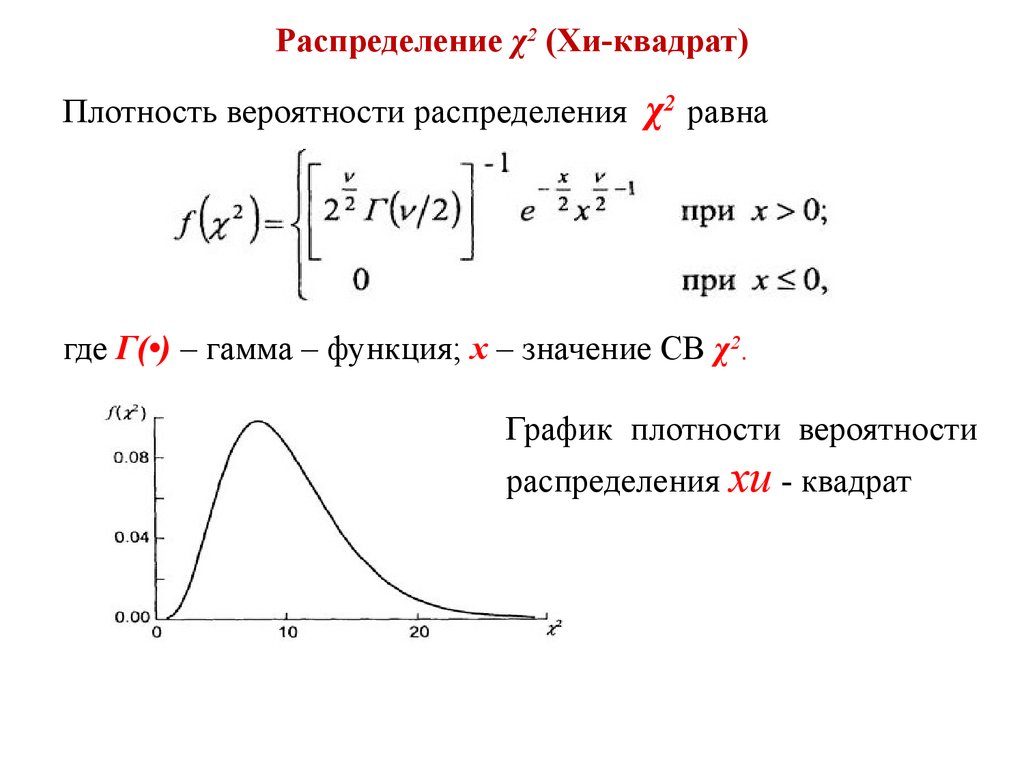
Иллюстрированный самоучитель по SPSS > Таблицы сопряженности > Тест хи-квадрат (X2) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Статистические критерии для таблиц сопряженности — Тест хи-квадрат Чтобы получить статистические критерии для таблиц сопряженности, щелкните на кнопке Statistics… (Статистика) в диалоговом окне Crosstabs. Откроется диалоговое окно Crosstabs: Statistics (Таблицы сопряженности: Статистика) (см. рис. 11.9). Рис. 11.9: Диалоговое окно Crosstabs: Statistics Флажки в этом диалоговом окне позволяют выбрать один или несколько критериев.
Эти критерии рассматриваются в двух последующих разделах, причем из-за того, что критерий хи-квадрат имеет большое значение в статистических вычислениях, ему посвящен отдельный раздел. Тест хи-квадрат (X2) При проведении теста хи-квадрат проверяется взаимная независимость двух переменных таблицы сопряженности и благодаря этому косвенно выясняется зависимость обоих переменных. Две переменные считаются взаимно независимыми, если наблюдаемые частоты (fо) в ячейках совпадают с ожидаемыми частотами (fe). Для того, чтобы провести тест хи-квадрат с помощью SPSS, выполните следующие действия:
Вы получите следующую таблицу сопряженности.
Кроме того, в окне просмотра будут показаны результаты теста хи-квадрат: Chi-Square Tests (Тесты хи-квадрат)
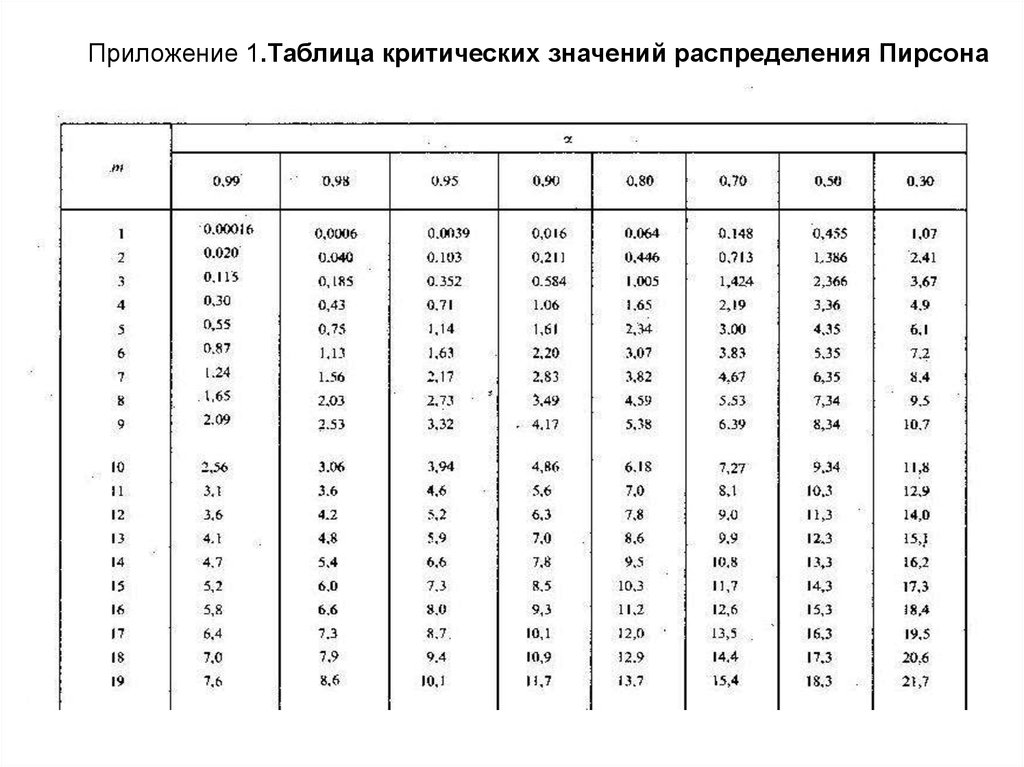
а. Для вычисления критерия хи-квадрат применяются три различных подхода:
Критерий хи-квадрат по Пирсону Обычно для вычисления критерия хи-квадрат используется формула Пирсона: Здесь вычисляется сумма квадратов стандартизованных остатков по всем полям таблицы сопряженности. Поэтому поля с более высоким стандартизованным остатком вносят более весомый вклад в
численное значение критерия хи-квадрат и, следовательно, — в значимый результат. Согласно правилу, приведенному в разделе 8.9,
стандартизованный остаток 2 (1,96) или более указывает на значимое расхождение между наблюдаемой и ожидаемой частотами в той или ячейке таблицы. В рассматриваемом примере формула Пирсона дает максимально значимую величину критерия хи-квадрат (р<0,0001). Если рассмотреть стандартизованные остатки в отдельных полях таблицы сопряженности, то на основе вышеприведенного правила можно сделать вывод, что эта значимость в основном определяется полями, в которых переменная psyche имеет значение «крайне неустойчивое». У женщин это значение сильно повышено, а у мужчин — понижено. Корректность проведения теста хи-квадрат определяется двумя условиями:
Однако в рассматриваемом примере это условие выполняется не полностью. Как указывает примечание после таблицы теста хи-квадрат, 25% полей имеют ожидаемую частоту менее 5.
Однако, так как допустимый предел в 20% превышен лишь ненамного и эти поля, вследствие своего очень малого стандартизованного остатка, вносят весьма незначительную долю в величину критерия хи-квадрат,
это нарушение можно считать несущественным. Критерий хи-квадрат с поправкой на правдоподобие Альтернативой формуле Пирсона для вычисления критерия хи-квадрат является поправка на правдоподобие: При большом объеме выборки формула Пирсона и подправленная формула дают очень близкие результаты. В нашем примере критерий хи-квадрат с поправкой на правдоподобие составляет 23,688. Тест Мантеля-Хэнзеля Дополнительно в таблице сопряженности под обозначением linear-by-linear («линейный-по-линейному») выводится значение теста Мантеля-Хэнзеля (20,391). Эта форма критерия хи-квадрат с поправкой Мантеля-Хэнзеля — еще одна мера линейной зависимости между строками и столбцами таблицы сопряженности. Она определяется как произведение коэффициента корреляции Пирсона на количество наблюдений, уменьшенное на единицу: Полученный таким образом критерий имеет одну степень свободы. Метод Мантеля-Хэнзеля используется всегда, когда в диалоговом окне Crosstabs: Statistics установлен флажок Chi-square.
Таблицы, подобные приведенной, называют таблицами сопряженности. Для проверки сформулированной выше нулевой гипотезы нам необходимо знать, какова была бы ситуация, если бы антитела действительно не оказывали никакого действия на выживаемость мышей. Другими словами, нужно рассчитать ожидаемые частоты для соответствующих ячеек таблицы сопряженности. Как это сделать? В эксперименте всего погибло 38 мышей, что составляет 34.2% от общего числа задействованных животных. Если введение антител не влияет на выживаемость мышей, в обеих экспериментальных группах должен наблюдаться одинаковый процент смертности, а именно 34.2%. Рассчитав, сколько составляет 34.2% от 57 и 54, получим 19.5 и 18.5. Это и есть ожидаемые величины смертности в наших экспериментальных группах.
Как видим, ожидаемые частоты довольно сильно отличаются от наблюдаемых, т. тестов хи-квадрат (Χ²) | Типы, формулы и примерыОпубликован в 23 мая 2022 г. по Шон Терни. Отредактировано 10 ноября 2022 г. Критерий хи-квадрат Пирсона — это статистический тест для категорийных данных. Он используется для определения того, значительно ли ваши данные отличаются от ожидаемых. Существует два типа критерия хи-квадрат Пирсона:
Хи-квадрат часто пишется как Χ 2 и произносится как «кай-квадрат» (рифмуется со словом «глаз-квадрат»). Его также называют хи-квадрат. Содержание
Практические вопросы Что такое критерий хи-квадрат?Критерии хи-квадрат Пирсона (Χ 2 ), часто называемые просто тестами хи-квадрат, являются одними из наиболее распространенных непараметрические тесты . Непараметрические тесты используются для данных, которые не соответствуют предположениям параметрических тестов, особенно предположению о нормальном распределении. Если вы хотите проверить гипотезу о распределении категориальной переменной , вам нужно использовать тест хи-квадрат или другой непараметрический тест. Проверка гипотез о частотных распределенияхСуществует два типа тестов хи-квадрат Пирсона, но оба они проверяют, значительно ли наблюдаемое частотное распределение категориальной переменной отличается от ее ожидаемого частотного распределения. Частотное распределение описывает, как наблюдения распределяются между различными группами. Частотные распределения часто отображаются с использованием таблиц частотного распределения . Таблица распределения частот показывает количество наблюдений в каждой группе.
Тест хи-квадрат (критерий согласия хи-квадрат) может проверить, значительно ли эти наблюдаемые частоты отличаются от ожидаемых, например равные частоты. Пример: хирость и национальность
Тест хи-квадрат (тест на независимость) может проверить, значительно ли эти наблюдаемые частоты отличаются от ожидаемых частот, если ручность не связана с национальностью. Формула хи-квадратОба критерия хи-квадрат Пирсона используют одну и ту же формулу для расчета статистики теста, хи-квадрат (X 2 ):
Где:
Чем больше разница между наблюдениями и ожиданиями ( O − E в уравнении), тем больше будет хи-квадрат. Чтобы решить, является ли разница достаточно большой, чтобы быть статистически значимой, вы сравниваете значение хи-квадрат с критическим значением. Предотвратите плагиат, запустите бесплатную проверку.Попробуй бесплатноКогда использовать критерий хи-квадратКритерий хи-квадрат Пирсона может быть подходящим вариантом для ваших данных, если все из следующего:
Типы тестов хи-квадратДва типа критерия хи-квадрат Пирсона:
Математически это один и тот же тест. Однако мы часто думаем о них как о разных тестах, потому что они используются для разных целей. Хи-квадрат критерия согласия Вы можете использовать критерий согласия хи-квадрат , когда у вас есть одна категориальная переменная .
Ожидание разных пропорций
Критерий независимости хи-квадратВы можете использовать критерий независимости хи-квадрат , когда у вас есть две категориальные переменные. Это позволяет вам проверить, связаны ли две переменные друг с другом. Если две переменные независимы (не связаны между собой), вероятность принадлежности к определенной группе одной переменной не зависит от другой переменной. Пример: Критерий независимости хи-квадрат
Другие типы тестов хи-квадрат Некоторые считают, что хи-квадрат критерий однородности является еще одной разновидностью критерия хи-квадрат Пирсона. Тест Макнемара — это тест, использующий статистику критерия хи-квадрат. Это не разновидность теста хи-квадрат Пирсона, но он тесно связан с ним. Вы можете провести этот тест, если у вас есть связанная пара категориальных переменных, каждая из которых имеет две группы. Он позволяет определить, равны ли пропорции переменных. Пример: тест Макнемара. Предположим, выборке из 100 человек предложили два вида мороженого и спросили, нравится ли им вкус каждого из них.
Существует несколько других типов тестов хи-квадрат, которые не являются тестами хи-квадрат Пирсона, включая тест одной дисперсии и критерий хи-квадрат отношения правдоподобия . Как выполнить тест хи-квадратТочная процедура выполнения теста хи-квадрат Пирсона зависит от того, какой тест вы используете, но обычно он состоит из следующих шагов:
Как сообщить о тесте хи-квадратЕсли вы решите включить критерий хи-квадрат Пирсона в свою исследовательскую работу, диссертацию или диссертацию, вы должны сообщить об этом в разделе результатов. Вы можете следовать этим правилам, если хотите сообщать статистику в стиле APA:
 Практические вопросына базе Typeform Часто задаваемые вопросы о критериях хи-квадрат
Процитировать эту статью ScribbrЕсли вы хотите процитировать этот источник, вы можете скопировать и вставить цитату или нажать кнопку «Цитировать эту статью Scribbr», чтобы автоматически добавить цитату в наш бесплатный генератор цитирования.
Процитировать эту статью Полезна ли эта статья? Вы уже проголосовали. Спасибо 🙂
Ваш голос сохранен 🙂
Обработка вашего голоса. Во время учебы в магистратуре и докторантуре Шон научился применять научные и статистические методы в своих исследованиях в области экологии. Теперь он любит учить студентов, как собирать и анализировать данные для собственных диссертаций и исследовательских проектов. Критерий независимости хи-квадрат — Учебные пособия по SPSSКритерий независимости хи-квадратКритерий независимости Хи-квадрат определяет, существует ли связь между категориальными переменными (т. е. являются ли переменные независимыми или связанными). Это непараметрический тест. Этот тест также известен как:
В этом тесте используется таблица непредвиденных обстоятельств для анализа данных. Таблица непредвиденных обстоятельств (также известная как перекрестная таблица , перекрестная таблица или двусторонняя таблица ) представляет собой схему, в которой данные классифицируются в соответствии с двумя категориальными переменными.
Общее использованиеКритерий независимости Хи-квадрат обычно используется для проверки следующего:
Критерий независимости Хи-квадрат может сравнивать только категориальные переменные. Он не может проводить сравнения между непрерывными переменными или между категориальными и непрерывными переменными. Кроме того, тест независимости хи-квадрат оценивает только ассоциаций между категориальными переменными и не может дать никаких выводов о причинно-следственной связи.
Требования к даннымВаши данные должны соответствовать следующим требованиям:
Гипотезы Нулевая гипотеза ( H 0 ) и альтернативная гипотеза ( H 1 ) критерия независимости Хи-квадрат могут быть выражены двумя разными, но эквивалентными способами: : «[ Переменная 1 ] не зависит от [ Переменная 2 ]» OR H 0 : «[ Variable 1 ] is not associated with [ Variable 2 ]» Статистика тестаСтатистический показатель для критерия независимости хи-квадрат обозначается как х 2 и рассчитывается как: 9{2}}{e_{ij}}}} $$ , где \(o_{ij}\) — наблюдаемое количество ячеек в строке i th и столбце j th таблица \(e_{ij}\) — это ожидаемое количество ячеек в строке i th и столбце j th таблицы, рассчитанное как $$ e_{ij} = \ frac{\ mathrm{ \textrm{row} \mathit{i}} \textrm{total} * \mathrm{\textrm{col} \mathit{j}} \textrm{total}}{\textrm{общий итог}} $$ Количество ( O IJ — E IJ ) иногда называют Rotual из ячейки I. Вычисленное значение х 2 затем сравнивается с критическим значением из таблицы распределения х 2 со степенями свободы df = ( R 915 C 64 905) и выбранный уровень достоверности. Если рассчитано х 2 значение > критическое х 2 значение, то мы отвергаем нулевую гипотезу. Настройка данныхСуществует два различных способа первоначальной настройки ваших данных. Формат данных будет определять, как продолжить выполнение теста независимости хи-квадрат. Как минимум, ваши данные должны включать две категориальные переменные (представленные в столбцах), которые будут использоваться в анализе. Категориальные переменные должны включать как минимум две группы. Ваши данные могут быть отформатированы одним из следующих способов: Если у вас есть необработанные данные (каждая строка является субъектом):
Если у вас есть частоты (каждая строка представляет собой комбинацию факторов):Пример использования критерия хи-квадрат для этого типа данных можно найти в учебном пособии «Взвешивание случаев».
Проведите тест независимости Хи-квадратВ SPSS критерий независимости хи-квадрат является опцией процедуры перекрестных таблиц. Напомним, что процедура Crosstabs создает таблицу непредвиденных обстоятельств или двустороннюю таблицу , которая обобщает распределение двух категориальных переменных. Чтобы создать кросс-таблицу и выполнить критерий независимости хи-квадрат, нажмите Анализ > Описательная статистика > Кросс-таблицы . A Строки: Одна или несколько переменных для использования в строках кросс-таблицы. Вы должны ввести хотя бы одну переменную Row. B Столбцы: Одна или несколько переменных для использования в столбцах кросс-таблицы. Вы должны ввести хотя бы одну переменную столбца. Также обратите внимание, что если вы укажете одну переменную строки и две или более переменных столбца, SPSS будет печатать перекрестные таблицы для каждой пары переменной строки с переменными столбца. C Слой: Необязательная переменная «стратификации». Если вы включили результаты теста хи-квадрат и указали переменную слоя, SPSS подмножит данные в соответствии с категориями переменной слоя, а затем запустит тесты хи-квадрат между переменными строки и столбца. (Это , а не эквивалентно тестированию на трехстороннюю ассоциацию или тестированию на ассоциацию между переменной строки и столбца после контроля переменной слоя.) D Статистика: Открывает окно Кросстаблицы: Статистика, которое содержит пятнадцать различных логических статистических данных для сравнения категориальных переменных. Чтобы выполнить тест независимости хи-квадрат, убедитесь, что установлен флажок хи-квадрат . E Ячейки: Открывает окно Кросс-таблицы: Отображение ячеек, которое определяет, какие выходные данные будут отображаться в каждой ячейке кросс-таблицы. (Примечание: в кросс-таблице ячейки являются внутренними разделами таблицы. Они показывают количество наблюдений для заданной комбинации категорий строк и столбцов.) В этом окне есть три параметра, которые полезны (но необязательны) при выполнении критерия независимости хи-квадрат: 1 Наблюдаемый : Фактическое количество наблюдений для данной ячейки. Эта опция включена по умолчанию. 2 Ожидаемое : Ожидаемое количество наблюдений для этой ячейки (см. формулу тестовой статистики). 3 Нестандартизированный Остатки : «Остаточное» значение, рассчитанное как наблюдаемое минус ожидаемое. F Формат: Открывает окно Кросс-таблицы: формат таблицы, в котором указывается способ сортировки строк таблицы. Пример: критерий хи-квадрат для таблицы 3×2Постановка задачиВ наборе выборочных данных респондентов спрашивали об их поле и о том, курят ли они сигареты. Было три варианта ответа: «Некурящий», «Курильщик в прошлом» и «Курильщик в настоящее время». Предположим, мы хотим проверить связь между поведением курильщика (некурящий, нынешний курильщик или курильщик в прошлом) и полом (мужской или женский), используя критерий независимости хи-квадрат (мы будем использовать 9).0170 α = 0,05). Перед тестом Прежде чем мы проверим «ассоциацию», полезно понять, как выглядит «ассоциация» и «отсутствие ассоциации» между двумя категориальными переменными. Один из способов визуализировать это — использовать сгруппированные гистограммы. Это диаграмма, которая получается, если вы используете Курение в качестве переменной строки и Пол в качестве переменной столбца (запуск синтаксиса позже в этом примере): «Кластеры» в гистограмме с кластерами определяются переменной строки (в данном случае — категориями курения). Цвет столбцов определяется переменной столбца (в данном случае — полом). Высота каждой полосы представляет собой общее количество наблюдений в этой конкретной комбинации категорий. Этот тип диаграммы подчеркивает различия внутри категорий переменной строки. Обратите внимание, что в каждой категории курения высота столбцов (т. е. количество мужчин и женщин) очень похожа. То есть некурящих мужчин и женщин примерно поровну; примерно равное количество бывших курильщиков мужского и женского пола; примерно равное количество курящих мужчин и женщин. Если бы существовала связь между полом и курением, можно было бы ожидать, что эти показатели будут каким-то образом различаться между группами. Запуск теста
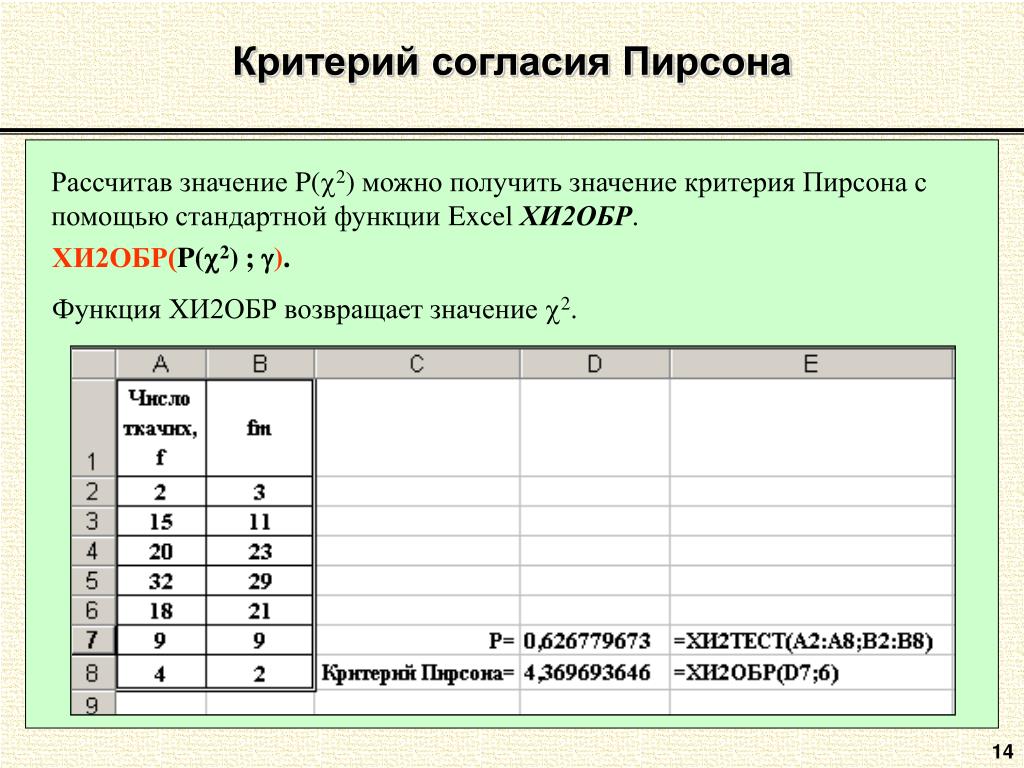
СинтаксисПЕРЕКРЕСТНЫЕ СТАБИЛИЗАЦИИ /TABLES=Курение ПО ПОЛУ /FORMAT=ЗНАЧЕНИЕ ТАБЛИЦ /СТАТИСТИКА=ЧИСК /CELLS=СЧЕТЧИК /COUNT КРУГЛАЯ ЯЧЕЙКА /БАРХАРТ. Выходные данныеТаблицы Первая таблица представляет собой сводку по обработке обращений, в которой указано количество достоверных наблюдений, использованных для анализа. В тесте могут быть использованы только случаи с непропущенными значениями как поведения в отношении курения, так и пола. Следующие таблицы представляют собой результаты кросс-табуляции и теста хи-квадрат. Ключевым результатом в таблице тестов хи-квадрата является хи-квадрат Пирсона.
Решение и выводы Поскольку значение p больше выбранного нами уровня значимости ( α = 0,05), мы не отвергаем нулевую гипотезу. Скорее, мы приходим к выводу, что недостаточно доказательств, чтобы предположить связь между полом и курением. По результатам можно констатировать следующее:
Пример: критерий хи-квадрат для таблицы 2×2Постановка задачиПродолжим пример с процентным соотношением строк и столбцов из учебника по кросс-таблицам, в котором описывалась взаимосвязь между переменными RankUpperUnder (старшеклассник/младший класс) и LivesOnCampus (живет в кампусе/живет за пределами кампуса). Вспомните, что проценты в столбце кросс-таблицы, по-видимому, указывают на то, что старшеклассники с меньшей вероятностью, чем младшие, живут в кампусе:
Предположим, что мы хотим проверить связь между классовым положением и проживанием в кампусе, используя критерий независимости Хи-квадрат (используя α = 0,05). Перед тестомГистограмма с кластерами из процедуры Crosstabs может служить дополнением к процентам в столбце выше. Давайте посмотрим на диаграмму, созданную процедурой Crosstabs для этого примера: Высота каждого столбца представляет общее количество наблюдений в этой конкретной комбинации категорий. «Кластеры» формируются переменной строки (в данном случае рангом класса). Этот тип диаграммы подчеркивает различия внутри групп младших и старшеклассников. Здесь разница в количестве студентов, проживающих в кампусе, по сравнению с количеством студентов, проживающих за пределами кампуса, гораздо более заметна в группах по классу. Запуск теста
ВыводСинтаксисПЕРЕКРЕСТНЫЕ СТАБИЛИЗАЦИИ /TABLES=RankUpperUnder ПО LiveOnCampus /FORMAT=ЗНАЧЕНИЕ ТАБЛИЦ /СТАТИСТИКА=ЧИСК /CELLS=КОЛИЧЕСТВО ОЖИДАЕМЫХ ОСТАТКОВ /COUNT КРУГЛАЯ ЯЧЕЙКА /БАРХАРТ. Таблицы Первая таблица представляет собой сводку обработки обращений, в которой указано количество действительных обращений, использованных для анализа. Следующая таблица представляет собой перекрестную таблицу. Если вы выбрали флажки для наблюдаемого количества, ожидаемого количества и нестандартизированных остатков, вы должны увидеть следующую таблицу:
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 Подтвердите выбор кнопкой Continue.
Подтвердите выбор кнопкой Continue. Residual
Residual Sig. (2-sided)
Sig. (2-sided) 


 2\) на (гипотетическом) примере из иммунологии. Представим, что мы выполнили эксперимент по установлению эффективности подавления развития микробного заболевания при введении в организм соответствующих антител. Всего в эксперименте было задействовано 111 мышей, которых мы разделили на две группы, включающие 57 и 54 животных соответственно. Первой группе мышей сделали инъекции патогенных бактерий с последующим введением сыворотки крови, содержащей антитела против этих бактерий. Животные из второй группы служили контролем – им сделали только бактериальные инъекции. После некоторого времени инкубации оказалось, что 38 мышей погибли, а 73 выжили. Из погибших 13 принадлежали первой группе, а 25 – ко второй (контрольной). Проверяемую в этом эксперименте нулевую гипотезу можно сформулировать так: введение сыворотки с антителами не оказывает никакого влияния на выживаемость мышей. Иными словами, мы утверждаем, что наблюдаемые различия в выживаемости мышей (77.2% в первой группе против 53.
2\) на (гипотетическом) примере из иммунологии. Представим, что мы выполнили эксперимент по установлению эффективности подавления развития микробного заболевания при введении в организм соответствующих антител. Всего в эксперименте было задействовано 111 мышей, которых мы разделили на две группы, включающие 57 и 54 животных соответственно. Первой группе мышей сделали инъекции патогенных бактерий с последующим введением сыворотки крови, содержащей антитела против этих бактерий. Животные из второй группы служили контролем – им сделали только бактериальные инъекции. После некоторого времени инкубации оказалось, что 38 мышей погибли, а 73 выжили. Из погибших 13 принадлежали первой группе, а 25 – ко второй (контрольной). Проверяемую в этом эксперименте нулевую гипотезу можно сформулировать так: введение сыворотки с антителами не оказывает никакого влияния на выживаемость мышей. Иными словами, мы утверждаем, что наблюдаемые различия в выживаемости мышей (77.2% в первой группе против 53. 7% во второй группе) совершенно случайны и не связаны с действием антител.
7% во второй группе) совершенно случайны и не связаны с действием антител. В рассматриваемом примере таблица имеет размерность 2х2: есть два класса объектов («Бактерии + сыворотка» и «Только бактерии»), которые исследуются по двум признакам («Погибло» и «Выжило»). Это простейший случай таблицы сопряженности: безусловно, и количество исследуемых классов, и количество признаков может быть бóльшим.
В рассматриваемом примере таблица имеет размерность 2х2: есть два класса объектов («Бактерии + сыворотка» и «Только бактерии»), которые исследуются по двум признакам («Погибло» и «Выжило»). Это простейший случай таблицы сопряженности: безусловно, и количество исследуемых классов, и количество признаков может быть бóльшим. Аналогичным образом рассчитываются и ожидаемые величины выживаемости: поскольку всего выжили 73 мыши, или 65.8% от общего их числа, то ожидаемые частоты выживаемости составят 37.5 и 35.5. Составим новую таблицу сопряженности, теперь уже с ожидаемыми частотами:
Аналогичным образом рассчитываются и ожидаемые величины выживаемости: поскольку всего выжили 73 мыши, или 65.8% от общего их числа, то ожидаемые частоты выживаемости составят 37.5 и 35.5. Составим новую таблицу сопряженности, теперь уже с ожидаемыми частотами: 2\) составило 5.79213. Мы можем отклонить нулевую гипотезу об отсутствии эффекта антител, рискуя ошибиться с вероятностью чуть более 1% (p-value = 0.0161).
2\) составило 5.79213. Мы можем отклонить нулевую гипотезу об отсутствии эффекта антител, рискуя ошибиться с вероятностью чуть более 1% (p-value = 0.0161).
 Категориальные переменные могут быть номинальными или порядковыми и представлять такие группы, как виды или национальности. Поскольку они могут иметь только несколько конкретных значений, они не могут иметь нормального распределения.
Категориальные переменные могут быть номинальными или порядковыми и представлять такие группы, как виды или национальности. Поскольку они могут иметь только несколько конкретных значений, они не могут иметь нормального распределения. Когда есть две категориальные переменные, вы можете использовать определенный тип таблицы частотного распределения, называемую таблицей непредвиденных обстоятельств , чтобы показать количество наблюдений в каждой комбинации групп.
Когда есть две категориальные переменные, вы можете использовать определенный тип таблицы частотного распределения, называемую таблицей непредвиденных обстоятельств , чтобы показать количество наблюдений в каждой комбинации групп.
 Если одна или несколько ваших переменных являются количественными, вам следует использовать другой статистический тест. В качестве альтернативы вы можете преобразовать количественную переменную в категориальную переменную, разделив наблюдения на интервалы.
Если одна или несколько ваших переменных являются количественными, вам следует использовать другой статистический тест. В качестве альтернативы вы можете преобразовать количественную переменную в категориальную переменную, разделив наблюдения на интервалы. Это позволяет вам проверить, значительно ли отличается частотное распределение категориальной переменной от ваших ожиданий. Часто, но не всегда ожидается, что категории будут иметь равные пропорции.
Это позволяет вам проверить, значительно ли отличается частотное распределение категориальной переменной от ваших ожиданий. Часто, но не всегда ожидается, что категории будут иметь равные пропорции.
 Он проверяет, происходят ли две совокупности из одного и того же распределения, определяя, имеют ли две совокупности одинаковые пропорции друг к другу. Вы можете считать это просто другим способом мышления о тесте независимости хи-квадрат.
Он проверяет, происходят ли две совокупности из одного и того же распределения, определяя, имеют ли две совокупности одинаковые пропорции друг к другу. Вы можете считать это просто другим способом мышления о тесте независимости хи-квадрат.



 ..
.. Категории для одной переменной отображаются в строках, а категории для другой переменной — в столбцах. Каждая переменная должна иметь две или более категории. Каждая ячейка отражает общее количество случаев для определенной пары категорий.
Категории для одной переменной отображаются в строках, а категории для другой переменной — в столбцах. Каждая переменная должна иметь две или более категории. Каждая ячейка отражает общее количество случаев для определенной пары категорий.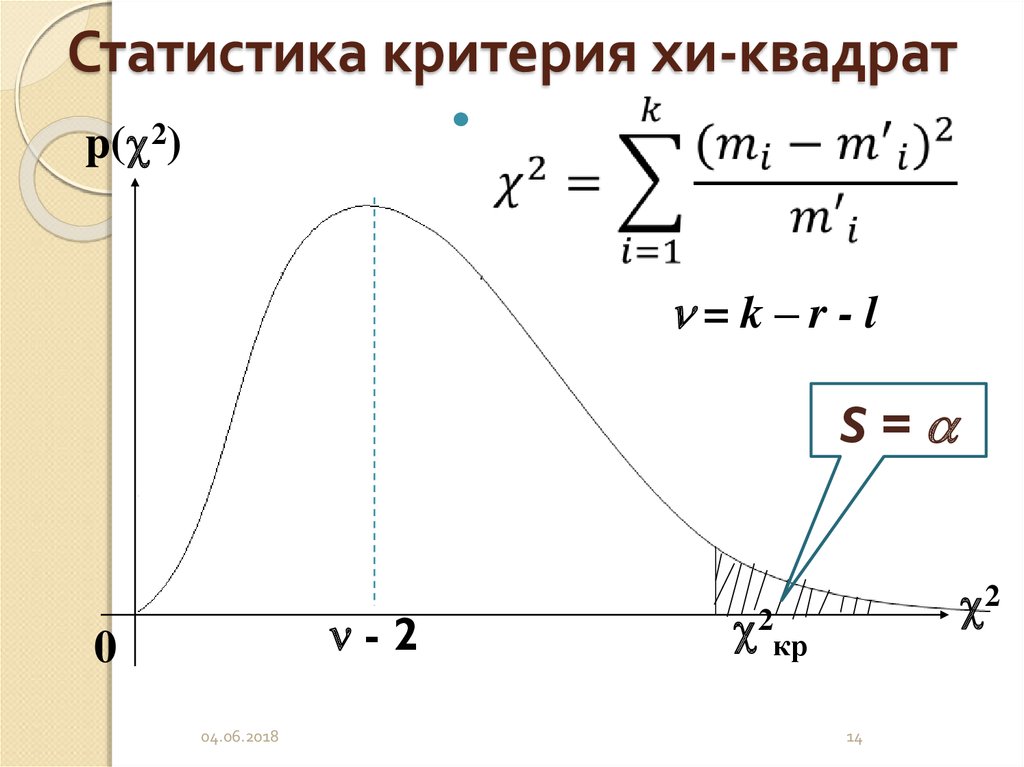
 ). }\).
). }\). То есть каждая строка представляет собой наблюдение уникального субъекта.
То есть каждая строка представляет собой наблюдение уникального субъекта.
 То же самое верно, если у вас есть одна переменная столбца и две или более переменных строки или если у вас есть несколько переменных строки и столбца. Для каждой таблицы будет проведен тест хи-квадрат. Кроме того, если вы включите переменную слоя, тесты хи-квадрат будут выполняться для каждой пары переменных строки и столбца на каждом уровне переменной слоя.
То же самое верно, если у вас есть одна переменная столбца и две или более переменных строки или если у вас есть несколько переменных строки и столбца. Для каждой таблицы будет проведен тест хи-квадрат. Кроме того, если вы включите переменную слоя, тесты хи-квадрат будут выполняться для каждой пары переменных строки и столбца на каждом уровне переменной слоя.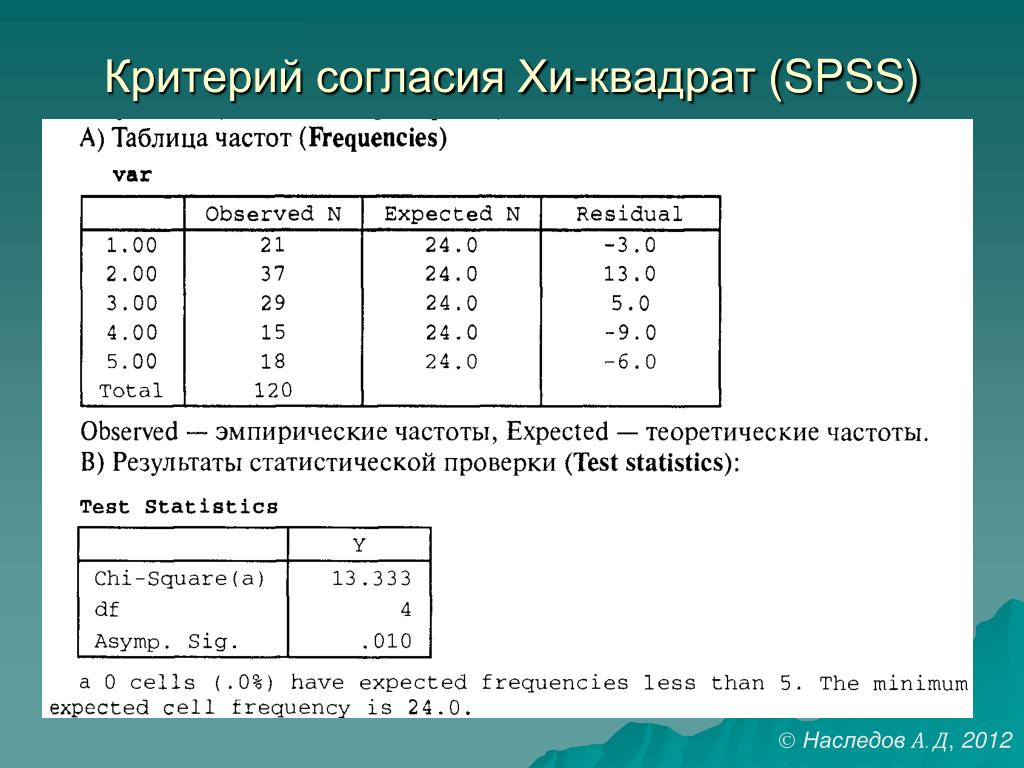

 Давайте посмотрим на кластеризованную гистограмму, созданную процедурой Crosstabs.
Давайте посмотрим на кластеризованную гистограмму, созданную процедурой Crosstabs.




 В тесте могут использоваться только случаи с неотсутствующими значениями как для классного звания, так и для проживания в кампусе.
В тесте могут использоваться только случаи с неотсутствующими значениями как для классного звания, так и для проживания в кампусе. 853 $$
853 $$