Указание логарифмической шкалы в отчете с разбивкой на страницы — Microsoft Report Builder & Power BI Report Builder
Twitter LinkedIn Facebook Адрес электронной почты
- Статья
- Чтение занимает 2 мин
Применимо к: Microsoft Report Builder (SSRS) Power BI Report Builder конструктор отчетов в SQL Server Data Tools
Если данные пропорциональны логарифму, в диаграмме в отчете с разбивкой на страницы можно использовать логарифмическую шкалу. Это может улучшить внешний вид диаграммы и повысить удобство работы с данными. Большинство логарифмических шкал использует логарифм с основанием 10.
Это может улучшить внешний вид диаграммы и повысить удобство работы с данными. Большинство логарифмических шкал использует логарифм с основанием 10.
Эта функция доступна только для оси значений. Ось значений обычно является вертикальной осью (осью Y). Однако в линейчатых диаграммах это горизонтальная ось (ось X).
Если ось логарифмическая, все остальные ее свойства будут логарифмически масштабированы. Например, если задать на оси логарифмическую шкалу с основанием 10, установка интервала шкалы, равного 2, на самом деле создаст интервалы, равные 10 в степени 2, то есть 100. Это означает, что будут отображены значения осей 1, 100, 10000, а не значения по умолчанию 1, 10, 100, 1000, 10000.
Примечание
Создать и изменить определение для отчета на страницу (RDL-файл) можно с помощью построителя отчетов (Майкрософт), построителя отчетов Power BI и конструктора отчетов в SQL Server Data Tools.
Задание логарифмической шкалы
Щелкните правой кнопкой мыши ось Y диаграммы и выберите пункт Свойства вертикальной оси.
 Откроется диалоговое окно Свойства вертикальной оси .
Откроется диалоговое окно Свойства вертикальной оси .В поле Свойства осивыберите Использовать логарифмическую шкалу.
В текстовом поле Основание логарифма введите положительное значение для основания логарифма. Если значение не задано, по умолчанию берется логарифм с основанием 10.
См. также:
Форматирование меток оси на диаграмме (построитель отчетов и службы SSRS)
Форматирование меток оси в виде значений даты или валюты (построитель отчетов и службы SSRS)
Диаграммы (построитель отчетов и службы SSRS)
Логарифмический масштаб — Большая Энциклопедия Нефти и Газа, статья, страница 3
Cтраница 3
Необходимость применения логарифмического масштаба по оси частот вызывается широким частотным диапазоном современных усилителей. [31]
[31]
При использовании логарифмического масштаба точка, соответствующая со 0, находится слева в минус бесконечности ( lg 0 — ) и ЛАХ строятся не от нулевой частоты, а от достаточно малого, но конечного значения со, которое и откладывается в точке пересечения кооординатных осей. [32]
| Кривые Gc / ( / m / sm для проектирования магнитных систем с магнитами из сплавов магнико ( 1 и алии 3 ( 2 с максимальным использованием энергии. [33] |
При использовании логарифмического масштаба по обеим осям зависимость оказывается линейной. [34]
Необходимость применения логарифмического масштаба по оси частот вызывается широким частотным диапазоном современных усилителей. [35]
| Логарифмический масштаб частоты. [36] |
При построении логарифмического масштаба частоты по оси абсцисс откладываются отрезки, пропорциональные не самим частотам со, a логарифмам частот lg со, как показано на рис. 2.16. Для удобства поль — зования логарифмическим масштабом частот на оси абсцисе обычно наносятся значения самих частот, логарифмы которых отложены по оси.
[37]
2.16. Для удобства поль — зования логарифмическим масштабом частот на оси абсцисе обычно наносятся значения самих частот, логарифмы которых отложены по оси.
[37]
Переход к
Что называется логарифмическим масштабом. [39]
| Диаграмма состояния систем, содержащих полупроводниковые фазы. а — с логарифмическим масштабом по абсциссе. Ь — диаграмма по. [40] |
Диаграммы с логарифмическим масштабом, как и частично крупномасштабные, могут оказать значительную помощь в случае соединений с очень узкой областью гомогенности при решении как теоретических, так и некоторых прикладных задач. [41]
Частота в логарифмическом масштабе измеряется в декадах. [42]
[42]
Затем в логарифмическом масштабе строят график зависимости понижения уровня s от времени t по фактически наблюдавшимся данным. [43]
Графики в логарифмическом масштабе имеют огромную ценность при анализе акций, потому что на них очень хорошо видно ускорение или замедление процентных темпов роста квартальной прибыли. Логарифмические графики точно показывают процентные изменения, потому что 1 дюйм в любом месте на шкале цен или прибыли представляет такое же процентное изменение. Иначе обстоит дело на графиках с арифметической шкалой. [44]
| R / S-анализ, функция Вейерштрасса. [45] |
Страницы: 1 2 3 4 5
Логарифмическая шкала Matplotlib — BMC Software
Блог о машинном обучении и больших данных В этой статье мы объясним, как использовать логарифмическую шкалу в Matplotlib.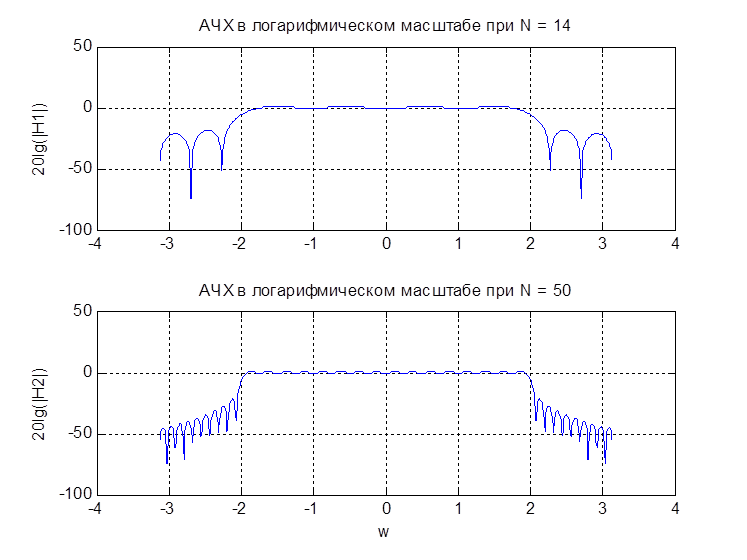
Логарифмическая шкала удобна для отображения данных, которые включают очень маленькие числа и очень большие числа, потому что шкала отображает данные так, что вы можете легко увидеть все числа, не сжимая маленькие числа слишком близко.
(Эта статья является частью нашего руководства по визуализации данных . Используйте правое меню для навигации.)
Логарифмы
Во-первых, давайте повторим немного математики средней школы. Логарифм — это способ заставить большое число казаться малым, рассматривая его как степень 10. Помимо 10 существуют и другие основания логарифма, например натуральный логарифм, используемый в математике, который задается константой e=2,718… . Но для наших целей мы будем использовать логарифмы по основанию 10.
Короче говоря:
log 10 x = y означает, что 10 в степени y равно x, т. е. 10 ** y = x. Итак, войдите 10 100=2, потому что 10**2 = 100.
Логарифмическая шкала в Matplotlib
Двумерная диаграмма в Matplotlib имеет шкалу y и шкалу x. Шкала означает градуировку или метки вдоль оси. Они могут быть любыми из:
Шкала означает градуировку или метки вдоль оси. Они могут быть любыми из:
- matplotlib.scale.LinearScale — это просто числа, например 1, 2, 3.
- matplotlib.scale.LogScale — это степени числа 10. , например 2 или значение натурального логарифма, которое задается числом e. Использование разных оснований сужает или расширяет расстояние между элементами на графике, облегчая видимость.
- matplotlib.scale.SsymmetricLogScale и matplotlib.scale.LogitScale — используются для чисел меньше 1, в частности, для очень маленьких чисел, чьи логарифмы представляют собой очень большие отрицательные числа.
Используя логарифмическую шкалу
Давайте построим график выручки некоторых крупных и небольших компаний.
Amazon, Alphabet (Google) и Intel во много раз крупнее небольших компаний Pete’s, Clock и Buckey’s BBQ (которые мы придумали). Разница между ними относительно Amazon огромна, поэтому график каждой более мелкой компании лежит на одной и той же вертикальной линии 0 на линейной шкале.
Matplotlib выбирает масштаб для осей, если вы не задали его явно. Здесь мы этого не сделали. Небольшое обозначение le11 внизу означает, что ось абсцисс представлена в экспоненциальном представлении, что в данном случае означает, что доход кратен 10**11 (100 миллиардов долларов). Доход Amazon в размере 232 887 000 000 долларов США составляет 2,325 * (10 ** 11). В то время как 600 000 долларов Пита в степени 11 составляют 0,000006 * (10 ** 11). Это объясняет, почему даже крупная компания Pepsi также близка к 0 на приведенной ниже диаграмме.
Итак, мы исправим эту проблему на следующем графике, используя логарифмическую шкалу. Ниже приведено объяснение кода.
импортировать matplotlib.pyplot как plt
импортировать numpy как np
импортировать matplotlib.pyplot как plt
импортировать numpy как np
импортировать панд как pd
данные = {
"У Пита": 600000,
«Часы»: 1600000,
«Барбекю Баки»: 2600000,
«Пепси»: 6466000000,
"Интел": 70848000000,
«Азбука»: 13681 00,
"Амазон": 232887000000
}
df = pd.
 DataFrame.from_dict (данные, ориентация = 'индекс', столбцы = ['Доход'])
dg =pd.to_numeric(df['Доход'])
dc = pd.Series(dg.index.values.tolist()).to_frame('Компания')
dat = df.assign(Company=dc.values)
данные = dat.sort_values (по = ['Доход'])
plt.scatter(данные['Доход'],данные['Компания'])
plt.grid()
plt.show()
DataFrame.from_dict (данные, ориентация = 'индекс', столбцы = ['Доход'])
dg =pd.to_numeric(df['Доход'])
dc = pd.Series(dg.index.values.tolist()).to_frame('Компания')
dat = df.assign(Company=dc.values)
данные = dat.sort_values (по = ['Доход'])
plt.scatter(данные['Доход'],данные['Компания'])
plt.grid()
plt.show()
Здесь все то же самое, за исключением того, что мы включили plt.xscale(«log») . Теперь нам легче увидеть значения, поскольку они являются степенями 10. Таким образом, небольшой доход Пита в размере 600 000 долларов легко увидеть как 6 * (10 ** 6). А Amazon примерно в 100 000 (10**5) раз больше.
импортировать matplotlib.pyplot как plt
импортировать numpy как np
импортировать панд как pd
данные = {
"У Пита": 600000,
«Часы»: 1600000,
«Барбекю Баки»: 2600000,
«Пепси»: 6466000000,
"Интел": 70848000000,
«Алфавит»: 1368100,
"Амазон": 232887000000
}
df = pd.DataFrame.from_dict (данные, ориентация = 'индекс', столбцы = ['Доход'])
dg =pd.
 to_numeric(df['Доход'])
dc = pd.Series(dg.index.values.tolist()).to_frame('Компания')
dat = df.assign(Company=dc.values)
данные = dat.sort_values (по = ['Доход'])
plt.scatter(данные['Доход'],данные['Компания'])
plt.grid()
plt.xscale("журнал")
plt.show()
to_numeric(df['Доход'])
dc = pd.Series(dg.index.values.tolist()).to_frame('Компания')
dat = df.assign(Company=dc.values)
данные = dat.sort_values (по = ['Доход'])
plt.scatter(данные['Доход'],данные['Компания'])
plt.grid()
plt.xscale("журнал")
plt.show()
Теперь вы можете более четко увидеть размер каждой компании по ее выручке
Объяснение кода
Часть этого кода может быть трудно понять без знакомства с наукой о данных, поскольку он использует Pandas и NumPy. Это иронично, поскольку Pandas был создан специально для облегчения работы с табличными данными.
На первом этапе данные, которые мы создали в виде словаря, преобразуются в кадр данных Pandas . Индексом для этих данных будет название компании. Мы сказали orient=’index’ , что означает взять первую запись в качестве значения индекса. Затем мы даем ему имя столбца с столбцов=[‘Доход’] . Название компании не имеет имени столбца, потому что это не столбец; это индекс строки.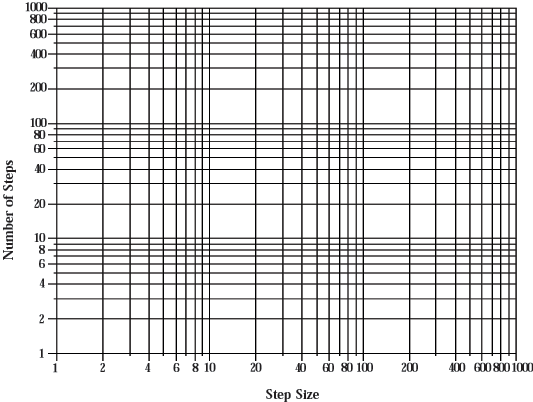
df = pd.DataFrame.from_dict(data,orient='index',columns=['Доход'])
Далее мы должны преобразовать строки доходов в числа. В противном случае они будут отсортированы matplotlib как буквы.
dg =pd.to_numeric(df['Revenue'])
Теперь мы хотим создать серию , которая представляет собой кадр данных только с одним столбцом. Значения будут индексом предыдущего кадра данных. Вот как мы получаем компании, перечисленные в виде столбца данных с именем 9.0017 Компания
dc = pd.Series(dg.index.values.tolist()).to_frame('Company') Затем мы добавляем значения ряда, который мы только что создали, в качестве еще одного столбца в кадре данных dat .
dat = df.assign(Company=dc.values)
Затем мы строим точечную диаграмму, давая кадры данных для значений x и y. Каждый из них имеет одинаковую форму (7,), которую вы можете проверить с помощью data[‘Revenue’].shape .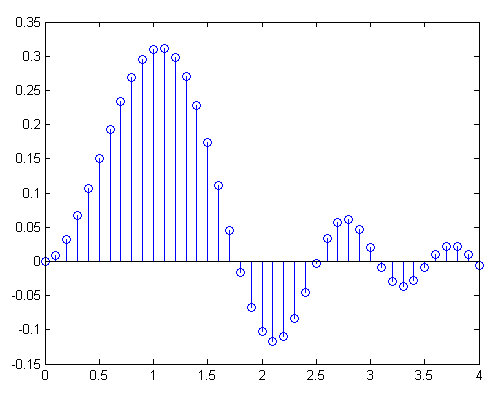 Shape — иногда сложная концепция NumPy. В основном это означает размерность массива. На графике xy они должны быть одинаковыми.
Shape — иногда сложная концепция NumPy. В основном это означает размерность массива. На графике xy они должны быть одинаковыми.
plt.scatter(data['Доход'],data['Компания'])
Остальное говорит само за себя:
plt.grid()
plt.xscale("журнал")
plt.show()
Эти сообщения являются моими собственными и не обязательно отражают позицию, стратегию или мнение BMC.
Видите ошибку или есть предложение? Пожалуйста, сообщите нам об этом по электронной почте [email protected].
Руководство по визуализации данных
BMC приносит A-Game
BMC работает с 86% Forbes Global 50, а также с клиентами и партнерами по всему миру, чтобы создать свое будущее. Благодаря нашей истории инноваций, ведущим в отрасли решениям для автоматизации, управления операциями и услугами в сочетании с непревзойденной гибкостью мы помогаем организациям высвободить время и пространство, чтобы стать автономным цифровым предприятием, которое завоевывает возможности в будущем.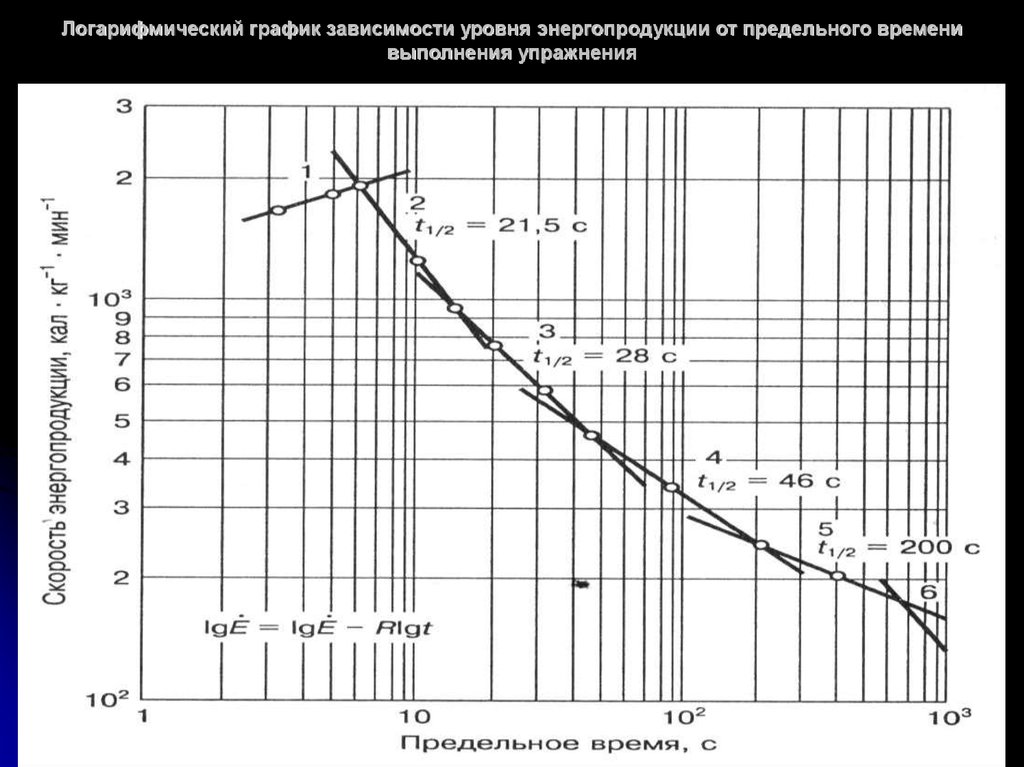
Узнайте больше о BMC ›
Вам также может понравиться
Об авторе
Уокер Роу
Уокер Роу — американский внештатный технический писатель и программист, проживающий на Кипре. Он пишет учебные пособия по аналитике и большим данным и специализируется на документировании SDK и API. Он является основателем Hypatia Academy Cyprus, онлайн-школы для обучения школьников программированию. Вы можете найти Уокера здесь и здесь.
Посмотреть все сообщения
Логарифмическая шкала — Энергетическое образование
Energy EducationМеню навигации
ИСТОЧНИКИ ЭНЕРГИИ
ИСПОЛЬЗОВАНИЕ ЭНЕРГИИ
ЭНЕРГЕТИЧЕСКОЕ ВОЗДЕЙСТВИЕ
ИНДЕКС
Поиск
Рис. 1. Полулогарифмический график с тремя различными функциями (щелкните, чтобы увеличить). [1]
[1]
Логарифмическая шкала — это нелинейная шкала, часто используемая при анализе большого диапазона величин. Вместо того, чтобы увеличиваться с равными приращениями, каждый интервал увеличивается на 9y=x[/math]
Это означает, что на каждые одно значение y значение x будет увеличиваться в раз десять , и наоборот. Использование логарифмической шкалы может быть полезно при создании графиков для уменьшения масштаба и упрощения понимания данных. При построении на полулогарифмическом графике, показанном на рис. 1, экспоненциальная функция 10 x выглядит линейной, тогда как на линейном графике она обычно быстро расходится.
Это полезно для многих приложений, некоторые из которых будут рассмотрены ниже. 9+[/math]
- Таким образом, на каждые одно уменьшение (из-за отрицательного знака) рН кислотность увеличивается в 10 раз (рН 3 в 10 раз кислее, чем рН 4 и в 100 раз более кислая, чем рН 5).
 6)=10 \times 6 = 60 дБ[/математика]
6)=10 \times 6 = 60 дБ[/математика]- Теперь, если два человека разговаривают одновременно, это только увеличивает дБ до 63 дБ. Таким образом, удвоение интенсивности звука приводит к +3 дБ . Болевой порог составляет около 120 дБ, что приводит к потере слуха.
Посетите страницу Гиперфизика для получения более подробной информации. - Шкала Рихтера — Землетрясения измеряются по шкале Рихтера, которая представляет собой логарифмическую шкалу с основанием 10. Эта шкала измеряет магнитуду землетрясения, то есть количество энергии, выделяемой им. Для каждого отдельного увеличения по этой шкале магнитуда увеличивается в 10 раз. [4] Посетите HowStuffWorks, чтобы узнать больше.
Ссылки
- ↑ Wikimedia Commons [онлайн], доступно: https://upload.wikimedia.org/wikipedia/commons/4/46/LogLinScale.svg
- ↑ Создано внутри компании членом группы Energy Education : адаптировано из Energy: its use and the Environment.