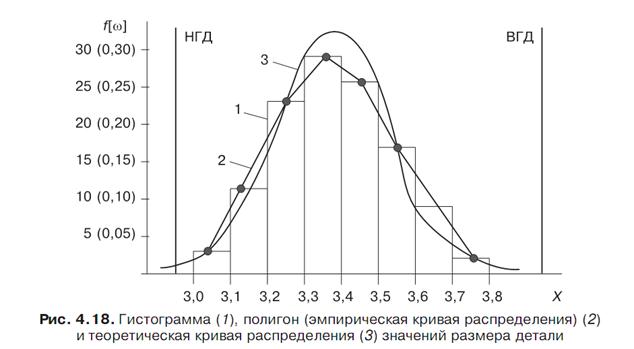
Гистограмма нормального распределения: Типы распределений и соответствующие им гистограммы | Бережливые шесть сигм | Статьи

Содержание

Типы распределений и соответствующие им гистограммы | Бережливые шесть сигм | Статьи | База знаний

Гистограммы помогают наглядно представить некоторые статистики выборки, а также визуально оценить закон распределения. Так как последний зачастую представляет наибольший интерес, визуальной оценке некоторых наиболее часто встречающихся распределений мы и уделим внимание в этой статье.

Для построения гистограмм воспользуемся генератором случайных чисел в программе Minitab. Подробное руководство и урок на одном листе уже опубликованы на нашем сайте, поэтому на самой процедуре получения чисел мы детально останавливаться не будем. Для каждого случая, за исключением отдельных примеров, будем генерировать по 1000 значений. Там, где это возможно, будем оставлять значения параметров по умолчанию. А там, где программа не предлагает таких значений, будем стараться разобрать на примере, какие величины мы могли бы внести.

Статья получилась довольно длинной, поэтому для удобства навигации добавлено содержание.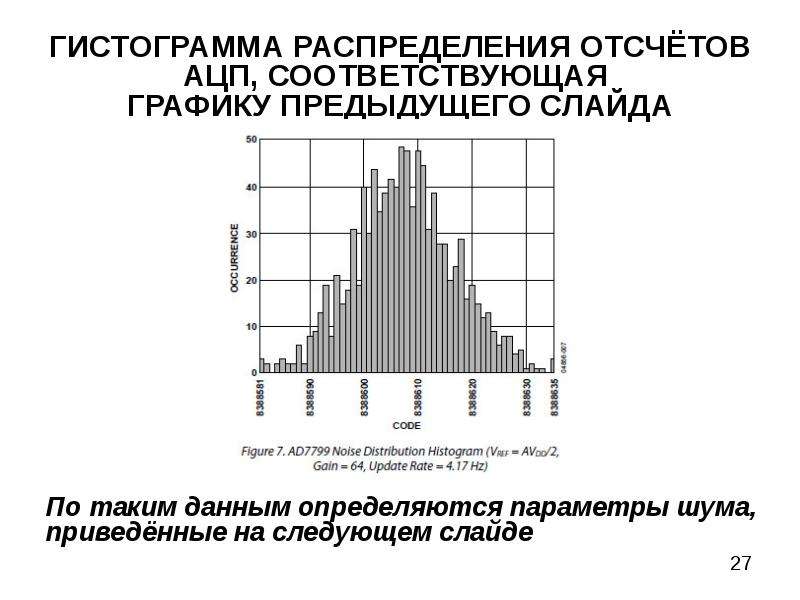

Каждому рассмотренному распределению соответствует отдельный самодостаточный раздел. Это значит, что нет необходимости читать все подряд, но можно обратиться к нужному разделу, чтобы найти информацию об интересующем распределении. Ну а если такой информации не нашлось, обязательно оставьте отзыв в комментариях под публикацией.

Содержание:

Нормальное распределение (Normal distribution) или распределение Гаусса

Начнем, разумеется, с нормального закона распределения. Из всех распределений в проектах шести сигм чаще всего приходится иметь дело именно с ним. Нормальному распределению может подчиняться практически любая переменная, на которую не влияют специальные факторы (например, связывающие или ограничивающие).

В силу того, что на любой процесс влияет огромное количество различных факторов, его результат никогда не принимает одно и тоже значение, но распределяется вокруг некоторого значения – математического ожидания или среднего арифметического значения, если говорить о выборке.

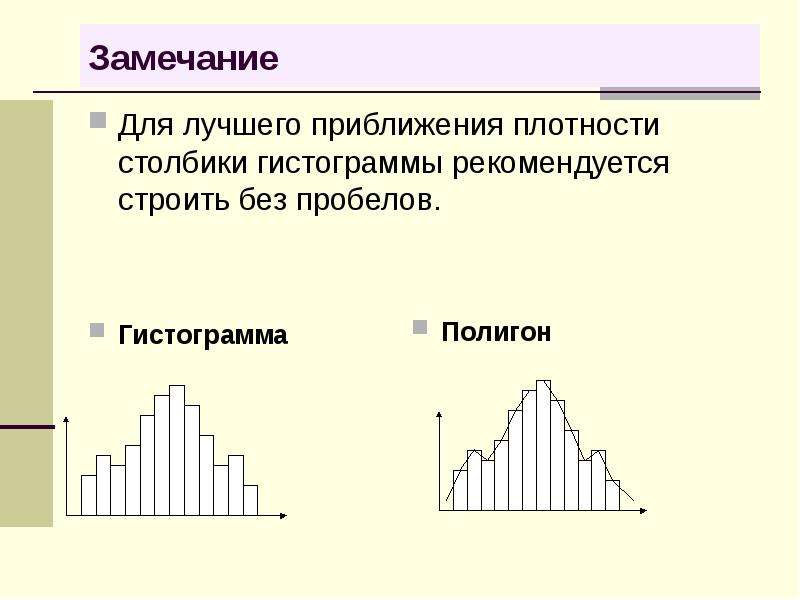
Следовательно, генерируя случайный набор чисел, подчиняющихся нормальному закону распределения, программа попросит нас задать среднее значение – Mean, а также Standard deviation – стандартное отклонение или меру рассеивания наблюдений вокруг математического ожидания:

Если построить гистограмму нормального распределения, то говорят, что она напоминает перевернутый колокол:

Примечательно, что какие бы величины параметров (математическое ожидание и стандартное отклонение) мы не задали, форма гистограммы от этого не поменяется. Чего не скажешь о следующем испытуемом.

Распределении Chi-square или χ² (хи-квадрат)

Попробуйте сгенерировать 2 набора данных, указав разное количество степеней свободы (Degrees of freedom) – k: 1 и 5, к примеру.

Гистограммы частично перекроют друг друга, однако на графике отчетливо видно, что с увеличением числа степеней свободы пик смещается вправо.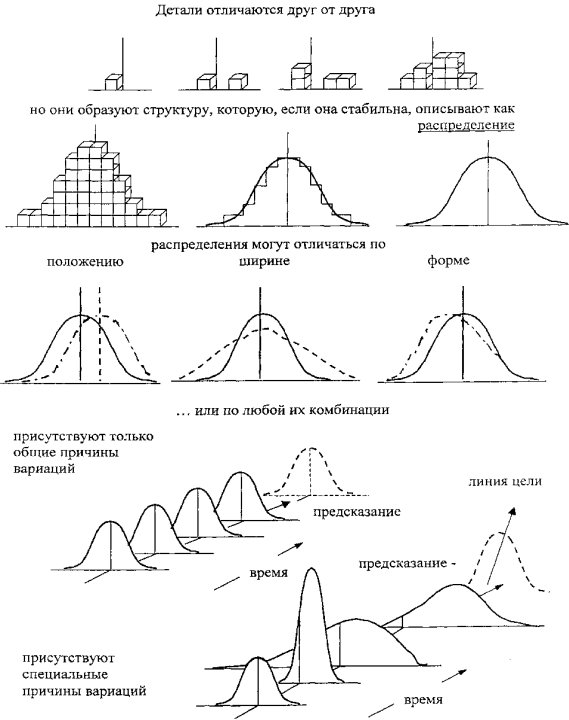 А если задать число степеней свободы 30 или выше, то гистограмма начнет напоминать нормальное распределение.

Практикам шести сигм довольно часто приходится иметь дело с распределением хи-квадрат. В частности, оно используется в тестах гипотез. Например, для оценки того, насколько хорошо выборка может быть описана распределением Пуассона (Stat \ Basic Statistics \ Goodness-of-Fit Test for Poisson), сопряженности номинальных данных (Stat \ Tables \ Chi-Square Test for Association) и т.д.

Больше о тестировании гипотез в среде Minitab вы можете в Карте выбора теста гипотез.

Распределение Фишера или Снедекора (F-distribution)

Движемся дальше – распределение Фишера или Снедекора (F), форма которого также будет зависеть от двух параметров: числителя и знаменателя числа степеней свободы – Numerator degrees of freedom и Denominator degrees of freedom соответственно.

По сути, это две независимые случайные величины, каждая из которых подчиняется распределению χ². Чтобы не влезать в дебри статистики и просто оценить их влияние, создайте 4 набора данных, задав следующие параметры:

Гистограммы для полученных таким образом числовых рядов будут выглядеть следующим образом:

Распределение Стьюдента (t-distribution)

Распределение Стьюдента (t) также часто применяется в статистическом анализе, к примеру, для построения доверительных интервалов, в тестах гипотез и т.д. T-критерий – частый “участник” проектов шести сигм.

Внешне гистограмма распределения Стьюдента может напоминать нормальное распределение: она также симметрична и также напоминает перевернутый колокол. Например, гистограмма распределения Стьюдента с числом степеней свободы 50 может иметь следующий вид:

Немного “упитаннее” и чуть короче хвосты, а в остальном полностью напоминает нормальное распределение.

Равномерное распределение (Uniform distribution)

На всех гистограммах выше был ярко выраженный пик. Но бывает и так, что на гистограмме присутствует большое количество пиков или вовсе нет выраженного пика. Иными словами, гистограмма представляет собой “плато”. Такие гистограммы встречаются довольно редко в проектах шести сигм и зачастую свидетельствуют о наличии специальных факторов вариации. Если каждый интервал гистограммы содержит примерно равное количество значений, то такая гистограмма называется однородной или гистограммой равномерного распределения (Uniform):

Для того, чтобы программа сгенерировала такой набор данных, нужно задать всего 2 параметра: начальную (Lower endpoint) и конечную точки (Upper endpoint). В примере выше это 0 и 20 соответственно.

Распределение Бернулли (Bernoulli distribution)

Распределение Бернулли (Bernoulli distribution) – распределение наблюдений, значения которых могут принимать лишь 2 взаимоисключающих значения: 0 или 1, успех или неудача, качественный или некачественный продукт и т.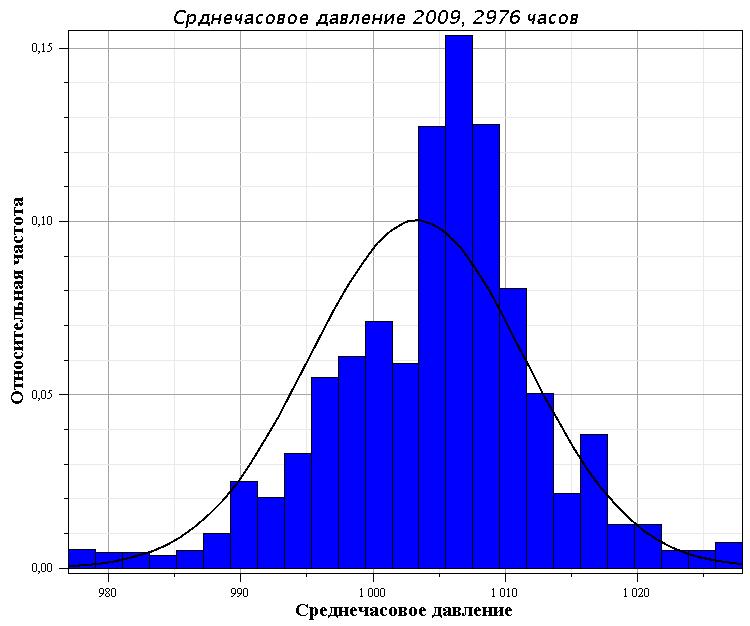 д.

При генерации чисел, программа просит задать лишь один параметр – вероятность события (Event probability), значение от 0 до 1 (от 0 до 100%):

Вероятность того, что событие не произойдет, соответственно, равно разнице между 1 и вероятностью того, что событие произойдёт. Гистограмма такого распределения, ожидаемо, ничем нас тоже не удивит – 2 колонки, отражающее, сколько раз событие произошло и сколько раз событие не произошло:

Биномиальное распределение (Binomial distribution)

Биномиальное распределение (Binomial distribution) – также частый “участник” проектов шести сигм. Оно описывает вероятность события в серии независимых экспериментов. Например, сколько раз может выпасть число 6, если вы кинете игральную кость 10 раз? Ну или сколько бракованных изделий вы найдете, если возьмете 10 образцов из очень большой партии изделий?

Параметры распределения: количество экспериментов (Number of trials) и вероятность события (Event probability).

А вот и ответ на наши вопросы в графическом виде:

Выходит, что вероятнее всего найти 1 дефектное изделие в выборке или выкинуть шестерку 1 раз.

Геометрическое распределение (Geometric distribution)

Геометрическое распределение (Geometric distribution) – еще одно распределение, описывающее вероятность события, с тем лишь отличием, что мы получаем количество опытов до первого “успеха”. Иными словами, скольким автомобилям в конце линии нужно заглянуть под капот, чтобы найти брак?

Minitab попросит нас задать лишь вероятность – значение от 0 до 1 (от 0 до 100%). Но не спешите нажимать Ok. На сей раз при генерации чисел в диалоговом окне доступна кнопка Options. Давайте нажмем ее и посмотрим, какие возможности нам предлагает программа:

Итак, мы можем выбрать Model the total number of trials (смоделировать количество экспериментов до первого события) или Model only the number of non-events (смоделировать количество “неудач” до первого “успеха”).

Что мы видим на диаграмме? При заданной вероятности (0,1) почти 200 раз из 1000 мы нашли брак, заглянув под капот первого, второго или третьего авто. Если же проверить 10 машин, то общее значение повышается до 720 из 1000. Иными словами, вероятность вырастет до 72%.

Понятно, что до 100% можно добраться, лишь контролируя все автомобили в конце конвейера. Что, по сути, и делается на всех автомобильных заводах. Однако график показывает нам, что за 50 переваливает лишь 5 наблюдений. Это означает, что проведя контроль 49 авто, мы найдем брак с вероятностью 99,5%.

Отрицательное биномиальное распределение (Negative binomial) или распределение Паскаля

Данное распределение моделирует количество экспериментов до получения требуемого количества событий. Проводя параллель с задачей, которую мы разбирали выше, можно сформулировать вопрос так: сколько капотов необходимо открыть, чтобы найти определенное количество бракованных машин.

В отличие от предыдущего распределения – геометрического, – мы ищем количество опытов не до первого события, а до заданного числа событий. Если задать вероятность (Event probability) 0,1 и число требуемых событий (Number of events needed) 1, то получим такую же гистограмму, что и выше. Она покажет, что до первого брака нам нужно взять выборку в 49-50 авто. Но задав (Number of events needed), например, 5, получим совсем другую картину:

Чтобы найти 5 бракованных авто, придется заглянуть под сотню капотов. 117, если быть точным и придерживаться уровня 99,5%.

Говорят: “В каждой шутке есть доля правды”. Вот и из этого шутливого примера с капотами можно сделать 2 вывода:

Хорошо, что современные производители машин производят на уровне 6 сигм и выше.
А что это там в стороне за стоянка, и почему там крутится столько техников?

Гипергеометрическое распределение (Hypergeometric distribution)

Также, как и предыдущее, гипергеометрическое распределение описывает количество событий в серии экспериментов, с тем лишь отличием, что генеральная совокупность ограничена. Можно с уверенностью сказать, что это – любимое распределение сотрудника отдела качества, так как дает ответ на вопрос: какую выборку взять из партии, чтобы найти в ней дефект.

Параметры распределения:

Размер популяции – Population size (N) – это наша партия. В начале статьи мы с вами условились, что будем генерировать по 1000 наблюдений. Но чуть ниже я поясню, почему в случае гипергеометрического распределения это было не самым удачным решением.
Количество событий в популяции – Event count in population (M) – количество бракованных образцов в партии. Вы его не знаете, но наверняка предполагаете исходя из вероятности или предыдущего опыта с поставщиком.
Размер выборки – Sample size (n).

Гистограмма, которую мы получим, покажется нам весьма знакомой:

Если вы промотаете выше, то заметите что это брат-близнец гистограммы биномиального распределения. Так и есть, и в этом нет ничего странного. Распределения очень похожи, и даже примеры, которые мы с вами рассматриваем, одни и те же: партия, выборка, брак…

Это сделано не для того, чтобы вас запутать, а скорее наоборот – показать практическое применение рассматриваемых распределений. Обычно, когда вы берете образец для контроля качества, вы же не возвращаете его, чтобы потом опять выбрать случайным образом следующий образец из целой партии. Следовательно, если вы не нашли дефекта на первом образце, то вероятность нахождения дефекта на втором образце возрастает. Для описания этого подходит гипергеометрическое распределение.

Учебник по статистике или Википедия вам так и скажет: “Моделирует количество удачных выборок без возвращения из конечной совокупности”. Вот только когда вы имеете дело с большими партиями, как например партия в 1000 изделий, оба распределения могут быть с одинаковым успехом применены.

Поэтому, рассматривая биномиальное распределение, мы говорили об “очень большой партии”, а рассматривая гипергеометрическое, просто о партии и о том, что условиться генерировать 1000 значений было не самым удачным решением.

Кстати, возвращаясь к полученной гистограмме гипергеометрического распределения, можно с грустью констатировать, что если выборка в ходе приемочного контроля качества равна 20, наши поставщики могут спать спокойно, а производство – готовиться к новым вызовам.

Дискретное распределение (Discrete distribution)

Следующее распределение в списке – это дискретное (Discrete distribution). Тут следует сделать оговорку, так как это меню в списке Minitab-а предлагает нам сгенерировать некий числовой ряд с заданными величинами и вероятностями их появления в этом ряду. Это не отдельный вид распределения, а лишь общее название для распределений со счетным числом значений. Под эту категорию подпадают уже рассмотренные выше распределения: Бернулли, биномиальное, гипергеометрическое и другие.

Что нам потребуется, чтобы сгенерировать такое распределение? Нам потребуется таблица с данными и вероятностями появления этих данных. Например, для игральной кости это может выглядеть так:

У кубика 6 сторон с числами от 1 до 6. Вероятность выпадения какого-либо из них 1/6 или 0,16667:

Гистограмма для этого набора данных и такого распределения нас не удивит – она будет напоминать гистограмму равномерного распределения:

Задай вы другие величины, их количество и вероятности, гистограмма приняла бы совершенно другой вид, напоминая любое другое распределение или их смесь.

Целочисленное распределение (Integer distribution)

Опять начнем с оговорки, что это не совсем распределение – скорее, синтетический способ генерирования чисел, который предлагает нам Minitab для понимания важных теорий и практик статистического анализа.

Параметры распределения, которые нам потребуется задать: минимальное и максимальное значения. Меню, как вы заметили, очень напоминает то, как мы моделировали данные для равномерного распределения. С тем лишь отличием, что в результате мы получим только целые числа. При равномерном распределении мы могли получить целые и дробные числа.

Разделом выше мы задали величины от 1 до 6 и равные вероятности для них. Для целочисленного распределения будет достаточно задать минимальное значение (Minimum value) равным 1 и максимальное (Maximum value) – равным 6:

Гистограмма, ожидаемо, будет напоминать гистограмму равномерного распределения, а также тот график, что мы получили для дискретного распределения:

Распределение Пуассона (Poisson distribution)

Еще один частый участник проектов шести сигм – распределение Пуассона. С его помощью можно моделировать очень много процессов: количество обращений в банк за день, количество запасов для покрытия еженедельного спроса, количество инцидентов на производстве или смертей в больнице… Сложно переоценить спектр применения и важность этого распределения.

Для моделирования данных программа попросит задать всего один параметр¹ – среднее значение (Mean). Давайте представим, что магазин электротоваров продает в среднем 5 пылесосов в день:

Полученная гистограмма даст возможность понять, к примеру, сколько пылесосов должно быть на складе, чтобы удовлетворить спрос с вероятностью 95%:

Чтобы не считать вручную, можно прибегнуть к анализу, который был рассмотрен в заметке Диаграмма распределения вероятностей (Probability Distribution Plot). Ну а продавай вы пылесосы десятками, можно было бы смело обратиться к нормальному распределению – с увеличением среднего распределение Пуассона все больше начинает напоминать нормальное распределение.

Бета-распределение (Beta distribution)

Данное распределение встречается реже в практике шести сигм, однако с его помощью, теоретически, можно моделировать любую случайную величину, значение которой ограничено определенным интервалом. Т.е. если стоит задача понять, когда на сайте появится новый читатель, какой срок согласования документов или любые другие SLA и т.д., то понадобится именно бета-распределение.

Для моделирования данных потребуется задать два параметра: α (альфа или First shape parameter) и β (бета или Second shape parameter). Гистограмма распределения будет зависеть от величины заданных параметров. Для понимания предлагаю сгенерировать наборы данных со следующими параметрами:

В результате получим 5 абсолютно различных гистограмм от параболической и равномерной до одновершинной симметричной и ассиметричной:

Глядя на эти графики, представьте, что α – это новый посетитель сайта SixSigmaOnline. ru, а β – пользователь Facebook. С какой вероятностью еще один человек оторвется от пролистывания темы и возьмется за ~~голову~~ шесть сигм?

Распределение Коши (Cauchy distribution)

Также известно как распределение Лоренца и Брейта-Вигнера. Вы наверняка встречались с этим распределением, проходя курс физики, но в проектах шести сигм это – не частый гость. Мне вот с ходу и не приходит на память проект, в котором я имел бы дело с этим распределением. Тем не менее, в списке Minitab-а это распределение есть – значит, наше дело нехитрое: генерируем данные и строим гистограмму.

У этого распределения нет математического ожидания и дисперсии, но есть коэффициент сдвига (Location) и коэффициент масштаба (Scale). Нам нет необходимости разбираться в статистике до малейших подробностей, поэтому можем условно представить, что коэффициент сдвига, даже если не представляет математическое ожидание, отражает положение пика гистограммы. А коэффициент масштаба – даже если не говорит о дисперсии – отражает размах.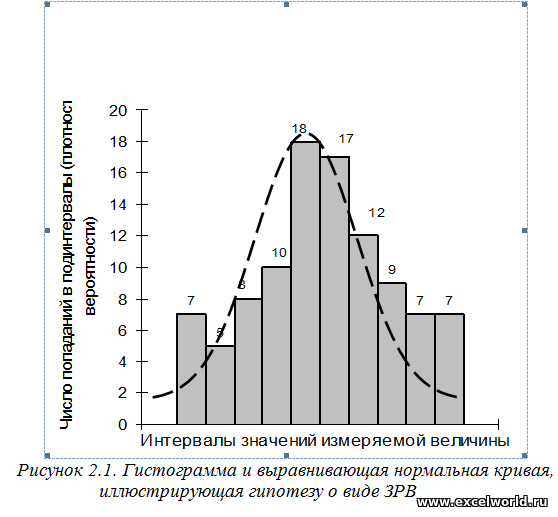 Также нет необходимости менять значения по умолчанию:

По сравнению с нормальным распределением, у гистограммы распределения Коши более длинные “хвосты” и острая вершина. К примеру, на графике ниже очень широкая шкала по оси X и заметна асимметрия вследствие того, что некоторые наблюдения значительно удалены от пика. Эксцесс (Kurtosis) – мера островершинности – равен 211 (у нормального распределения эксцесс близок к 0):

Экспоненциальное распределение (Exponential distribution)

Это непрерывное распределение моделирует время между двумя последовательными появлениями одного и того же события. Например, время между появлениями двух покупателей в магазине, метеоритов в небе, автобусов на остановке и даже период полураспада радиоактивных частиц будет случайной величиной с экспоненциальным распределением.

Параметры оставляем без изменений:

Scale – коэффициент интенсивности появления событий. С определенным допущением можем провести аналогию с распределением Пуассона и принять этот коэффициент за среднее значение.
Threshold – нижняя граница распределения – 0 (время между появлениями двух клиентов в магазине не может быть ниже 0).

Гамма-распределение (Gamma distribution)

Двухпараметрическое семейство абсолютно непрерывных распределений. Они применяются в различных отраслях экономики и техники, теории и практике испытаний надежности. В частности, гамма-распределению могут быть подчинены такие величины, как общий срок службы изделия, время наработки до k-го отказа (k = 1, 2, …, и т.д.). Также, это распределение используется в логистике для описания спроса в моделях управления запасами.

Параметры распределения могут называться по-разному. В Minitab это Shape parameter и Scale parameter. Чтобы оценить их влияние на распределение, сгенерируем 4 набора данных:

Также Minitab предлагает установить нижнюю границу распределения – Threshold, – но работает это так же, как и в случае с экспоненциальным распределением.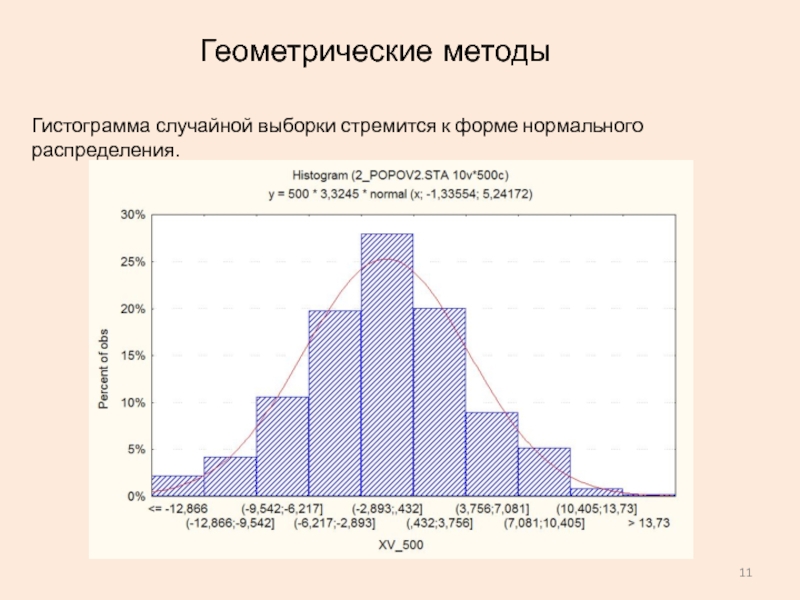 Поэтому дополнительно рассматривать влияние его значения м не будем.

Судя по полученным гистограммам:

Первый параметр отвечает за положение пика.
Второй – за “ширину” гистограммы.

Распределение Лапласа (Laplace distribution)

Распределение Лапласа не часто встречается в проектах шести сигм, однако широко применимо в биологии, экономике и финансах. Для получения данных потребуется установить два параметра: Location (коэффициент сдвига) и Scale (коэффициент масштаба). Оставим значения по умолчанию:

Гистограмма распределения весьма напоминает нормальное распределение, только с более острой вершиной:

Распределения экстремумов (Extreme Value Distribution)

В этом разделе мы рассмотрим 2 распределения: распределение минимального значения (Smallest extreme value distribution) и распределение максимального значения (Largest extreme value distribution). Еще к этому семейству относится распределение Вейбулла, но его мы рассмотрим отдельно.

Как следует из названия, эти распределения помогут нам понять экстремумы: минимум и максимум. Отсюда и область применения: там, где предвидеть экстремумы очень важно. А это – анализ надежности критических процессов, финансовых рисков, страхование… Например, распределение минимального значения (Smallest extreme value distribution) может нам помочь понять при какой минимальной температуре система откажет? А распределение максимального значения (Largest extreme value distribution) – наивысшие страховые потери.

Сгенерируем данные для Smallest extreme value distribution, оставив значения параметров Location (коэффициент сдвига – отвечает положению пика) и Scale (коэффициент масштаба – отвечает дисперсии наблюдений) по умолчанию. Затем повторим тот же алгоритм для Largest extreme value distribution, оставив значения параметров по умолчанию:

Гистограммы, соответствующие распределениям:

Логистическое распределение (Logistic distribution)

Логистическая функция распределения по форме похожа на функцию нормального распределения. Её главное предназначение – моделирование данных бинарного типа. Используется, например, в медико-биологических исследованиях для анализа эффекта различных лекарств, ядов и т.д. От нормального распределения логистическое отличается длинными “хвостами” – данными, находящимися в крайних, отдалённых от центра, позициях.

Сгенерируем данные, оставив значения параметров Location (коэффициент сдвига – отвечает положению пика) и Scale (коэффициент масштаба – отвечает дисперсии наблюдений) по умолчанию:

Гистограмма логистического распределения:

Лог-логистическое распределение (Log-logistic distribution)

Лог-логистическое распределение, в отличие от логистического, является трехпараметрическим. Оно полностью повторяет логистическое распределение, однако благодаря третьему параметру – Threshold или нижней границе распределения – позволяет моделировать только часть логистического распределения – данные больше 0.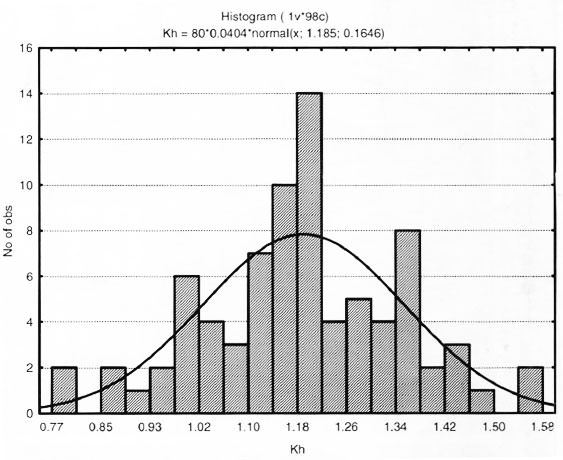

Сгенерируем данные, оставив значения параметров по умолчанию:

Гистограмма лог-логистического распределения:

Логнормальное распределение (Lognormal distribution)

Частным случаем нормального распределения является логнормальное распределение. Оно является непрерывным унимодальным распределением и имеет положительную асимметрию. Этому распределению с заданной степенью приближения подчиняется, например, размер фракций гравия или града. Аналогичные примеры: длительность часто повторяемого события (время выполнения операции на конвейере) или размер зарплат футболистов одного клуба. Как правило, значительно большее количество игроков имеет среднюю зарплату, но есть игроки-звезды мирового класса, которые зарабатывают значительно выше других игроков (правый хвост гистограммы).

Сгенерируем данные, оставив значения параметров по умолчанию, и построим гистограмму логнормального распределения:

Распределение Симпсона или треугольное распределение (Triangular distribution)

Довольно интересное распределение, которое не часто встретишь в проектах шести сигм.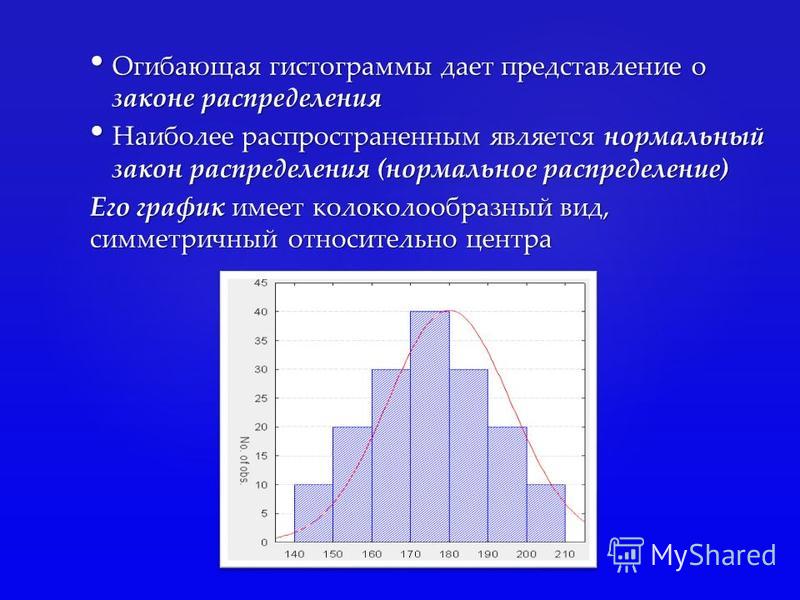 Его можно получить “синтетически”, как мы это сделаем ниже, задав начальную точку (Lower endpoint), моду (Mode), и конечную точку (Upper endpoint):

В таком случае этот упрощенный закон поможет нам помочь понять распределение при отсутствии или ограниченном количестве данных. Например, у нас может не быть достаточных данных для оценки стоимости постройки нового здания. Но мы можем оценить минимум, максимум и наиболее вероятное значение. И раз у нас недостаточно данных, чтобы сформулировать гипотезу об ином распределении, построим гистограмму треугольного распределения:

Мы также можем получить треугольное распределение путем сложения или вычитания двух переменных, подчиняющихся равномерному закону распределения. На отдельном листе я сгенерировал 2 колонки по 1000 наблюдений, подчиняющихся равномерному распределению:

Затем, используя функцию Calc \ Calculator, создал еще одну колонку, значения в которой являются результатом вычитания первой и второй колонок:

Гистограмма полученных таким образом наблюдений также будет напоминать треугольное распределение:

Это свойство позволяет применять треугольное распределение для моделирования сложных законов распределения.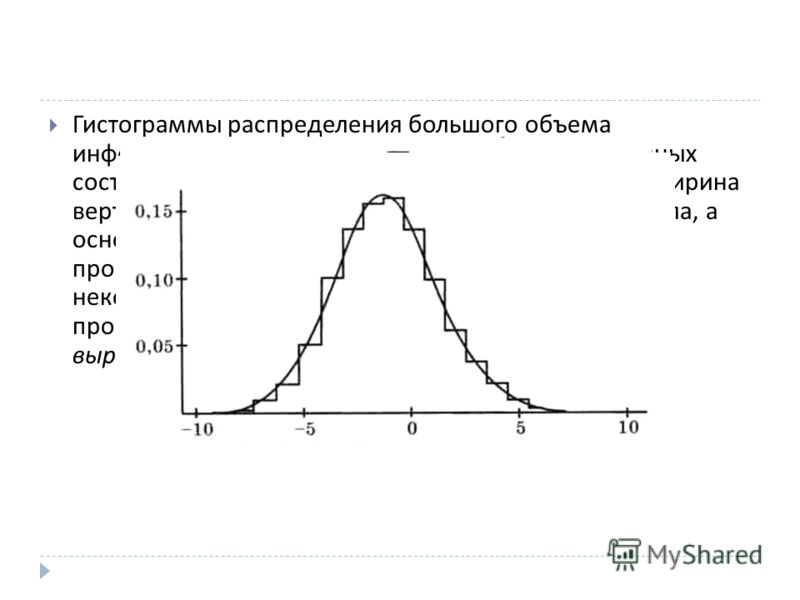 К примеру, так можно представить некоторые природные явления, бизнес-процессы, аудио размывание (audio blur)…

Распределение Вейбулла (Weibull distribution)

Распределение Вейбулла может быть применимо для моделирования широкого спектра задач. Однако в проектах шести сигм, это неизменный участник анализов надежности и определения времени до отказа.

Чтобы получить данные, задайте следующие параметры:

Shape parameter (k) – коэффициент формы.
Scale parameter (λ) – коэффициент масштаба.
Threshold parameter – нижняя граница распределения, оставляем значение по умолчанию.

Кстати, иногда говорят о распределении Вейбулла как о двухпараметрическом, а иногда – как о трех. Как вы видите выше, нам требуется задать 3 параметра. Т.е. распределение на самом деле трехпараметрическое. В то же время, задав Threshold равным 0, получаем двухпараметрическое распределение.

Давайте снова сгенерируем несколько наборов данных, чтобы оценить влияние параметров на форму гистограммы:

В результате получим 4 гистограммы, из которых можно заключить, что первый параметр – Shape parameter (коэффициент формы или k) – “двигает” пик, а второй — Scale parameter (коэффициент масштаба или λ) – определяет “ширину” гистограммы:

Многомерное нормальное распределение (Multivariate normal distribution)

Вы могли заметить, что двигаясь по списку доступных в меню Minitab распределений, мы упустили многомерное нормальное распределение. Это было сделано умышленно, так как и с данными, и с графиком нам придется повозиться. Но не стоит переживать. В этом распределении нет ничего сложного.

По сути, мы уже разобрали его частный случай – одномерное нормальное распределение. Просто мы не говорили, что оно одномерное. Многомерное можно представить как результат, зависимый от двух переменных, подчиняющихся нормальному закону распределения.

Давайте сгенерируем две колонки по 1000 наблюдений, удовлетворяющих нормальному закону распределения. Параметры – среднее и стандартное отклонение – в данном случае не имеют значения, хотя мы можем представить, что в одной колонке у нас будет температура (180°C), а в другой давление (760мм рт. ст.).

В меню Graph выберите Marginal Plots и в появившемся окне кликните на иконку With Histograms:

В следующем окне задайте колонки С1 и С2 в качестве переменных X и Y:

Нажав Ok, получим следующий результат:

Каждая точка на графике соответствует результату, который мы получим при определенной величине температуры и давления: где-то пирожки недопекутся, а где-то пригорят.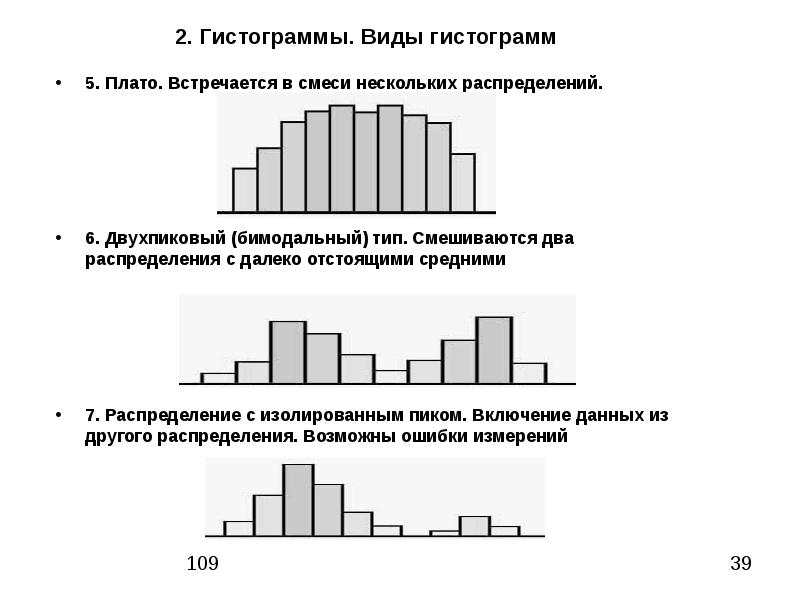

В проектах шести сигм многомерное нормальное распределение используется крайне редко. Однако некоторые методики анализа (факторный анализ, MANOVA) основываются на предположении, что данные подчиняются многомерному нормальному распределению.

Вот далеко не полный перечень типов существующих распределений и соответствующих им гистограмм. Внешнее отличие построенной вами гистограммы от перевернутого колокола еще совсем не означает, что данные собраны неправильно или что процесс нестабилен. Однако это всегда заставляет исследователя задуматься и постараться найти объяснение такому результату.

Нормальное распределение: понимание гистограмм и вероятностей

Добавлено 14 августа 2020 в 19:41

Сохранить или поделиться

В данной статье мы продолжаем исследование нормального распределения, рассматривая концепцию гистограмм и вводя функцию массы вероятности.

Данная статья является частью серии статей о статистике в электротехнике, которую мы начали с обсуждения статистического анализа и описательной статистики. Затем мы исследовали три описательных статистических показателя с точки зрения применения в обработке сигналов.

Затем мы коснулись стандартного отклонения (в частности, определения компенсации размера выборки при вычислении стандартного отклонения и понимания взаимосвязи между стандартным отклонением и среднеквадратичным значением).

В прошлой статье мы представили нормальное распределение в электротехнике, заложив основу для нашего текущего обсуждения: понимание вероятностей в измеренных данных.

Понимание гистограмм

В предыдущей статье мы начали обсуждение нормального распределения, обратившись к форме этой гистограммы:

Рисунок 1 – Гистограмма, иллюстрирующая нормальное или гауссово распределение

Я думаю, что большинство людей, работающих в области науки или техники, хотя бы смутно знакомы с гистограммами, но давайте сделаем шаг назад.

Что такое гистограмма?

Гистограммы – это визуальные представления 1) значений, присутствующих в наборе данных, и 2) частоты появления этих значений. Показанная выше гистограмма может представлять множество различных типов информации.

Представим, что она представляет собой распределение значений, полученных нами при измерении разницы, округленной до ближайшего милливольта, между номинальным и фактическим выходным напряжением линейного стабилизатора, который подвергался различным температурам и условиям эксплуатации. Так, например, примерно 8000 измерений показали разницу в 0 мВ между номинальным и фактическим выходными напряжениями, а примерно 1000 измерений показали разницу в 10 мВ.

Гистограммы – чрезвычайно эффективный способ обобщения больших объемов данных. Взглянув на гистограмму выше, мы можем быстро найти частоту отдельных значений в наборе данных и определить тенденции или закономерности, которые помогут нам понять взаимосвязь между измеренным значением и частотой.

Гистограммы с интервалами

Когда набор данных содержит так много разных значений, что мы не можем удобно связать их с отдельными столбцами гистограммы, мы используем объединение в интервалы (биннинг). То есть мы определяем диапазон значений как интервал, группируем результаты измерений в эти интервалы и создаем по одному столбцу для каждого интервала.

Следующая гистограмма, которая была сгенерирована из нормально распределенных данных со средним значением 0 и стандартным отклонением 0,6, использует интервалы вместо отдельных значений:

Рисунок 2 – Гистограмма с использованием интервалов вместо отдельных значений

Горизонтальная ось разделена на десять интервалов одинаковой ширины, и каждому интервалу назначен один столбец. Все результаты измерений, попадающие в числовой интервал, влияют на высоту соответствующего столбца (метки на горизонтальной оси показывают, что интервалы не одинаковой ширины, но это просто потому, что значения меток округлены).

Гистограммы и вероятность

В некоторых ситуациях гистограмма не дает нужной нам информации. Мы можем посмотреть на гистограмму и легко определить частоту измеренного значения, но не можем легко определить вероятность измеренного значения.

Например, если я посмотрю на первую гистограмму, я знаю, что примерно 8000 измерений показали разницу в 0 В между номинальным и фактическим напряжениями стабилизатора, но я не знаю, какова вероятность того, что результат случайно выбранного измерения или нового измерения сообщит о разнице в 0 В.

Это серьезное ограничение, потому что вероятность отвечает на чрезвычайно распространенный вопрос: каковы шансы, что…?

Каковы шансы, что у моего линейного стабилизатора погрешность выходного напряжения будет менее 2 мВ? Какова вероятность того, что частота битовых ошибок моего канала передачи данных будет выше 10^-3? Какова вероятность того, что из-за шума мой входной сигнал превысит порог срабатывания? И так далее.

Причина этого ограничения заключается в том, что гистограмма просто четко не передает размер выборки, то есть общее количество измерений (теоретически общее количество измерений можно определить, сложив значения всех столбцов гистограммы, но это было бы утомительно и неточно).

Если мы знаем размер выборки, мы можем разделить количество появлений на размер выборки и таким образом определить вероятность. Давайте рассмотрим пример.

Рисунок 3 – Пример того, как гистограмма может помочь нам определить вероятность путем деления количества появлений на размер выборки

Красные пунктирные линии заключают в себя столбцы, которые указывают на погрешности напряжения менее 2 мВ, а числа, написанные внутри столбцов, указывают точное количество появлений этих трех значений погрешности напряжения. Сумма этих трех чисел составляет 23 548. Таким образом, на основе этого примера по сбору данных вероятность получения погрешности менее 2 мВ составляет 23 548/100 000 ≈ 23,5%.

Функция массы вероятности

Если наша основная цель при создании гистограммы – передать информацию о вероятности, мы можем изменить всю гистограмму, разделив все счетчики вхождений на размер выборки.

Полученный график является аппроксимацией функции массы вероятности.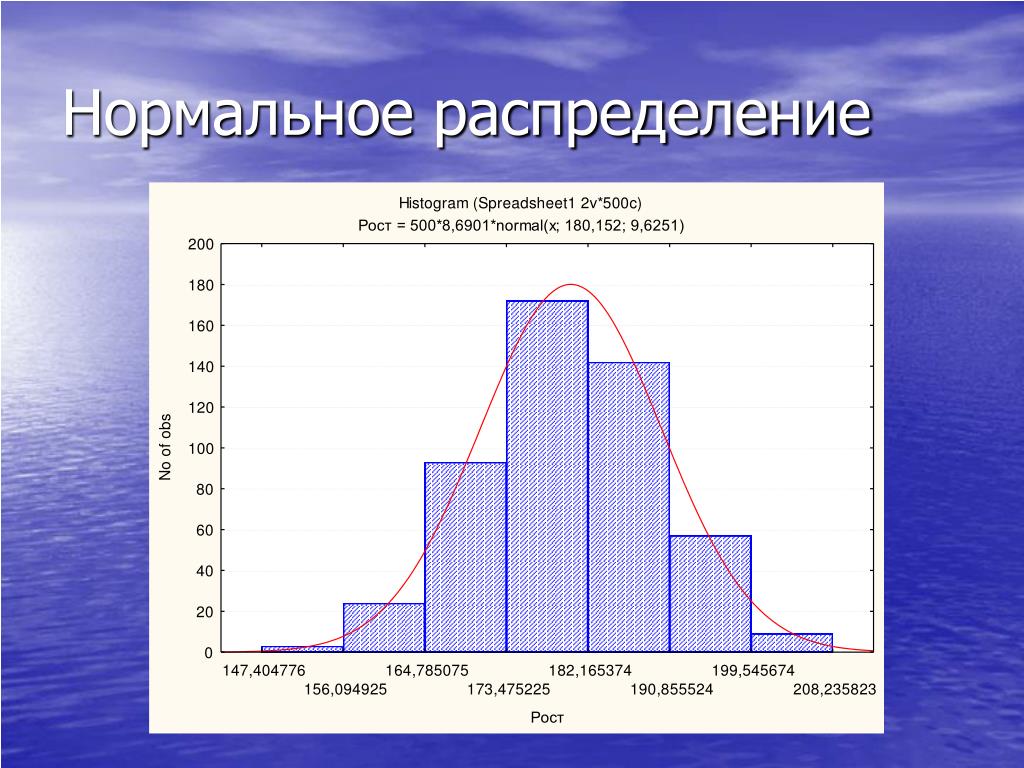 Например:

Рисунок 4 – Гистограмма, изображающая приблизительную функцию массы вероятности, полученную путем деления количества всех вхождений на размер выборки

Всё, что мы на самом деле выполнили, это изменили числа на вертикальной оси. Тем не менее, теперь мы можем посмотреть на отдельное значение или на группу значений и легко определить вероятность появления.

Хочу прояснить следующую деталь: я сказал, что мы аппроксимируем функцию массы вероятности, когда берем гистограмму и делим значения на размер выборки. Истинная функция массы вероятности представляет собой идеализированное распределение вероятностей, что означает, что для этого потребуется бесконечное количество измерений.

Таким образом, когда мы работаем с реалистичными размерами выборки, гистограмма, созданная на основе измеренных данных, дает нам только приближение функции массы вероятности.

Масса вероятности против плотности вероятности

Стоит подчеркнуть, что функция массы вероятности является дискретным эквивалентом функции плотности вероятности (о которой мы говорили в предыдущей статье).

В то время как функция плотности вероятности является непрерывной и предоставляет значения вероятности, когда мы интегрируем функцию в указанном диапазоне, функция массы вероятности дискретизируется и дает нам вероятность, связанную с конкретным значением или интервалом.

Эти две функции передают одну и ту же общую статистическую информацию о переменной или о сигнале, но делают это по-разному.

Обратите внимание на разницу между двумя названиями: вертикальная ось функции массы вероятности указывает массу вероятности, как количественное значение. Вертикальная ось функции плотности вероятности указывает плотность вероятности относительно горизонтальной оси; чтобы определить количественное значение вероятности, мы должны интегрировать эту плотность по горизонтальной оси.

Заключение

Мы рассмотрели функции массы и плотности вероятности, и теперь мы готовы изучить кумулятивную функцию распределения и исследовать вероятности нормального распределения с точки зрения стандартного отклонения. Об этом мы поговорим в следующей статье.

Оригинал статьи:

ГистограммаМасса вероятностиНормальное распределение / Гауссово распределениеПлотность вероятностиСтатистикаФункция массы вероятностиФункция плотности вероятности

Сохранить или поделиться

Гистограмма нормального распределения — Справочник химика 21

Счетное распределение частиц по размерам можно представить в виде гистограммы, выражающей процент частиц с размерами лежащими в данных интервалах и переходящей в пределе при бесконечном уменьшении этих интервалов в кривую распределения по размерам Распределение частиц по размерам в аэродисперсных системах является результатом ряда случайных причин и кривая распределения казалось бы должна быть гауссовой кривой, соответствующей нормальному распределению В действительности нормальное распределение частиц по размерам в аэрозолях ветре чается довольно редко, например в так называемых монодисперсных конденсационных аэрозолях впервые полученных в лабора тории Ла Мера В общем же случае наблюдается ясно выраженная асимметрия кривой распределения Но если по оси абсцисс откладывать логарифм диаметра частиц (вместо самого диаметра) асимметричная кривая весьма часто переходит в гауссову Логарифмически нормальное распределение выражается формулой [c. 222]
Аэродинамические неоднородности можно оценить функцией распределения скоростей потока в слое. Расчеты показали, что экспериментальные гистограммы при уровне значимости а — 0,05 могут быть описаны логарифмически нормальным законом с [c.159] Строим гистограмму распределения отклонений, состоящую из прямоугольников. Соединяя середины прямоугольников ломаной пунктирной линией, получим эмпирическую кривую распределения отклонений. Выравниваем эмпирическую кривую распределения по кривой нормального распределения, для чего определяем значение ординат теоретической кривой. [c.52]

ПРОВЕРКА НОРМАЛЬНОСТИ РАСПРЕДЕЛЕНИЯ РЕЗУЛЬТАТОВ ХИМИЧЕСКОГО АНАЛИЗА. ПОСТРОЕНИЕ ГИСТОГРАММ. [c.83]

На рис. 5.23 представлены гистограмма и кривая нормального распределения параметра Нормированное отклонение вычисляли как г а — а )I а- По форме гистограммы можно предположить, что вариация структурного параметра а у пентапласта следует нормальному закону. [c.185]

Под седьмым, восьмым и девятым столбцами печатаются значения критерия и указьшается число степеней свободы [64]. По данным первого, второго и третьего столбцов строятся гистограммы распределения и соответствующие им теоретические кривые нормального распределения. [c.67]

Хорошие результаты во многих случаях дает имитационное моделирование методом Монте-Карло. Для реализации метода необходимо задать допуски на вьшолнение проточной части машины и закон их распределения, Обьино принимается нормальное распределение, если неизвестен характер влияния технологического процесса изготовления. Однако вид распределения не влияет существенным образом на процесс моделирования. Необходимо выбрать детерминированную модель и процесс случайного выбора размеров. Далее проводится серия расчетов, которая дает либо оценку основных статистик дисперсии, размаха (разницы между максимальным и минимальным значениями параметра), асимметрии, эксцесса, либо, при достаточно большом числе экспериментов, распределение выходных параметров машины (гистограмму). [c.73]

Гистограмма частости значений давления перекачки приведена на рис. 1.30. Основная часть давлений ( 76 %) лежит в интервале (4,4-5,2) МПа. Доля больших давлений (Р > 5,2 МПа) составляет 1 %. Особенностью гистограммы, отличающей ее от нормального распределения, характерного для устойчивой работы НПС, является несколько большая доля давлений, не превышающих 0,8 МПа ( 10 %), и давлений из интервала (2,0-2,4) МПа (=6 %), что объясняется частыми остановками перекачки на станции (первый макси- [c.225]

Решение. Визуальное сходство гистограммы случайной величины с гистограммой, которая должна быть у нормально распределенной случайной величины не служит доказательством того, что случайная величина распределена по нормальному закону. Существует бесконечное множество случайных величин, гистограммы которых являются «идеальной горкой». Нормально распределенная величина — лишь одна из них. Поэтому, гистограмма в виде «горки» не дает никаких оснований не только к заключению, но и предположению о том, что случайная величина распределена нормально. [c.112]

Состав взвешенных частиц характеризуют концентрацией и дисперсностью. Концентрацию дисперсной фазы чаще всего представляют как массу частиц в единице объема дисперсионной фазы. Дисперсностью называют совокупность размеров всех частиц гетерогенной системы, которую для удобства описания разбивают на интервалы. Частицы с размерами, составляющими какой-либо интервал, относят к соответствующей фракции. Совокупность всех фракций аэрозоля называют фракционным составом его дисперсной фазы, которую можно представлять графически. Откладывая по оси абсцисс значения интервалов, составляющих фракции, а по оси ординат — доли или процентные содержания частиц соответствующих фракций, получают гистограммы — ступенчатые графики фракционного состава. С уменьшением интервалов фракций гистограммы приближаются к плавным кривым. Иногда такие кривые бывают близки по форме к кривой нормального распределения случайных величин, которая описывается двумя параметрами -средним диаметром частиц D и стандартным отклонением а от него [c. 24]

Приведены гистограммы, показывающие, что ошибки, характеризующие расхождение между результатами спектрального и химического анализов, не принадлежат к классу распределений, существенно отличному от нормального распределения. [c.416]

Приведем еще один весьма характерный вид гистограммы результатов химического анализа (рис. 16). Огибающая кривая имеет два максимума, один из которых выражен достаточно ярко, а второй несколько размыт. Кривая в целом асимметрична, но ход ее крайних ветвей аналогичен ходу ниспадающих крыльев кривой нормального распределения. Кривая может быть интерпретирована двумя отдельными кривыми, каждая из которых близка к канонической кривой нормального распределения со своими центрами рассеяния Хх и %2 И стандартами (71 и аг. [c.75]

Как было отмечено ранее, ошибки анализа могут быть систематическими или случайными. Систематические ошибки влияют на точность определения, т. е. на отклонение среднего значения от истинного значения, тогда как случайные ошибки приводят как к положительным, так и к отрицательным отклонениям от среднего значения, по которым рассчитывается разброс. Ошибки последнего типа обычно распределяются нормально вокруг среднего значения. Кривые нормального распределения хорошо известны экспериментаторам и хорошо изучены их можно получить из гистограмм при неограниченном увеличении числа измерений и уменьшении интервалов разбиения. В силикатном анализе 5 [c.67]

Для выяснения состояния качества готового продукта статистические данные показателей качества упорядочены. Для каждого из них составлена гистограмма, позволяющая выявить характер распределения и положение среднего значения. Установлено, что все они близки к нормальному распределению. При нахождении оптимальных значений показателей качества учитывались широта распределения по отношению к широте допуска, центр распределения по отношению к центру поля допуска. [c.41]

Необходимо отметить, что достаточно надежная проверка на нормальность, в том числе и качественная по форме стебля с листьями, требует довольно значительного объема исходной информации — нескольких десятков или даже сотен чисел.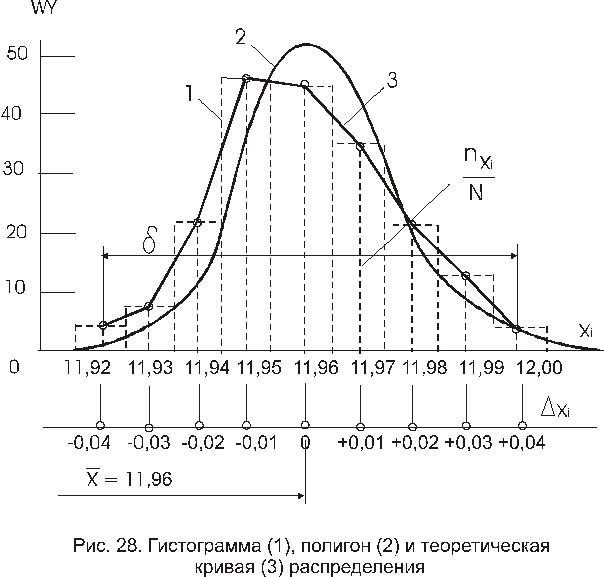 При недостаточном объеме выборки мала вероятность того, что эти числа будут давать нормальное распределение, даже если исходная совокупность чисел ему соответствовала. В качестве конкретной иллюстрации на рис. 23 приведено изменение формы гистограммы распределения чисел при увеличении выборки измерения диаметра образцов от 20 до 200. Видно, что более или менее удовлетворительная «нормальная» и стабильная форма кривой имеется только при числе наблюдений 100 и более. [c.92]

Гистограмма типичного распределения антител по аффинности в антисыворотке к данной антигенной детерминанте в сравнении с однородной по аффинности популяцией моноклональных антител к той же детерминанте. В отличие от поликлональных все моноклональные антитела характеризуются одинаковой аффинностью. Распределение поликлональных антител, содержащихся в антисыворотке, по аффинности отличается от нормального. [c.158]

Для осевых вентиляторов, регулируемых поворотом лопаток рабочего колеса или плавным изменением частоты вращения привода, сглаживание иа гистограммах статистических рядов достигается кривыми плотности нормального распределения Гаусса [10], при построении которых основные параметры такого распределения — математические ожидания и дисперсии — можно принимать приближенно равными [c. 215]

Гистограммы, аппроксимированные логарифмически нормальной функцией распределения, для двух способов загрузки свободной и с помогцью устройства с коаксиальными цилиндрами даны на рис. 4, а, б. [c.160]

Экспериментально определяемые величины, такие, как прочность, долговечность или концентрация свободных радикалов имеют широкий разброс значений. Это — стохастические переменные. В качестве предельного примера стохастической зависимости на рис. 3.1 дана гистограмма [3] долговечности 1 500 труб из ПЭВП, испытанных при одинаковых условиях. Показанная зависимость молнормальным логарифмическим распределением (рис. 3.2) со средним значением 1дг [ч], равным 2,3937, и вариацией 5 = 0,3043. Ожидаемое значение долговечности образца, подверженного испытанию, есть время, которое соответствует среднелогарифмическому значению, равному в данном случае 247,6 ч. Очевидно, что реально определяемые значения t имеют широкий разброс относительно данного ожидаемого значения.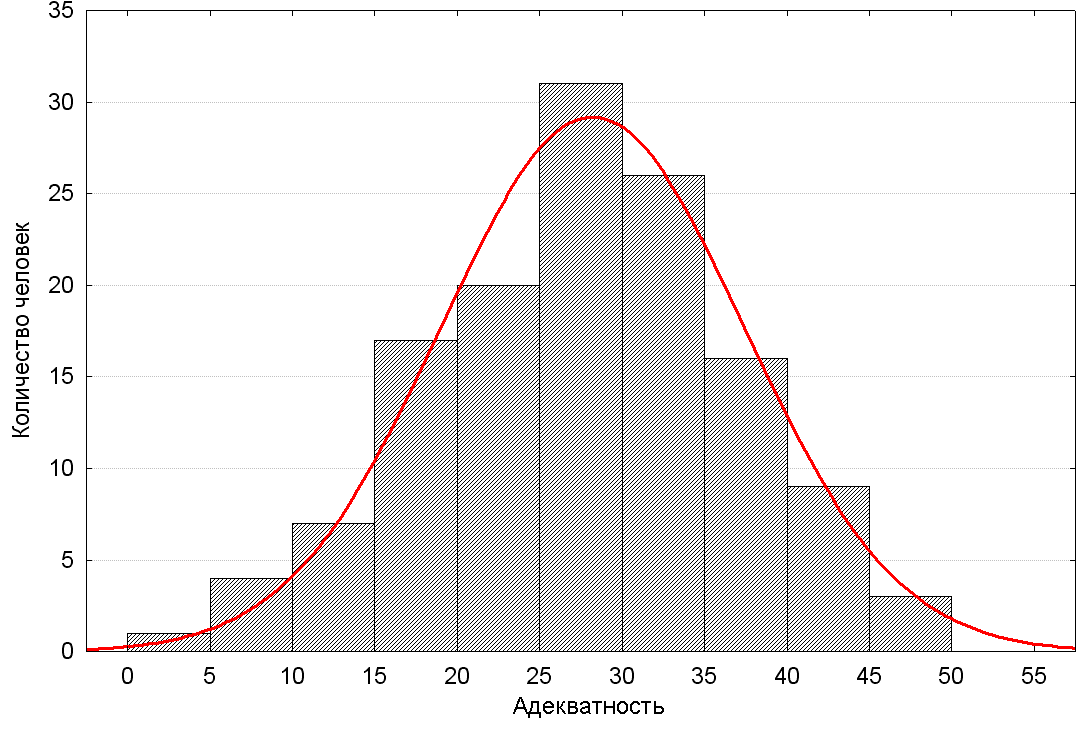 Несмотря на это, даже такое распределение можно получить путем испытания лишь нескольких случайно выбранных образцов. Для нормального распределения экспериментальных величин любые три случайных значения попадают в среднюю область 1,695, которая [c.59]

Хотя хронологическая шкала полярности, основанная на океанических магнитных аномалиях, внутренне менее точна, чем позднекайнозойская хронологическая шкала, приведенная на рис. 3.23, она довольно детальна и позволяет получить очень интересное представление о поведении геомагнитного поля за последние 80 млн. лет. Анализ, проведенный Ла Бреком и др. (LaBre que et al., 1977), показал, что за последние 71,62 млн. лет произошло 188 инверсий, включающих в себя ивенты полярности продолжительностью всего лишь по 10000 лет. Средняя продолжительность нормального (обратного) интервала полярности составляла 349 000 (412 500) лет. Следовательно, примерно 54,2% времени поле было обратным. Небольшая асимметрия полярности может быть просто артефактом, вызванным неточностью геомагнитной хронологической шкалы, но она может быть и следствием физических процессов, таких как термоэлектрические токи или NRM пород земной коры, которые оказывают влияние на динамо-процесс (Merrill et al, 1979). На рис. 3.25 приведена гистограмма, дающая распределение продолжительности интервалов инверсий полярности. Она демонстрирует приблизительно экспоненциальное уменьшение частоты встречаемости более длинных интервалов. [c.112]

Однако в ряде работ показано, что в некоторых случаях имеют место другие виды распределений. Проверка справедливости использования нормального распределения может быть проведена как экспериментальным построением гистограмм, так и расчетным способом (вычислением интеграла Гаусса пли исиользо-вание.м различных критериев). [c.85]

Гистограмма результатов изображена на рис. 30. Анализ гистограммы показывает, что огибающая ее кривая имеет вид, характерный для кривой нормального распределения. Стандартное отклонение для огибающей кривой в предположении о нормальном характере распределения оценено следующим образом в точке максимума (/П//п) = 0,19, но (т,//г)шах = ф(дг)т ДА = Д /(аУ2я), поскольку ф(х )Д е р // . Отсюда [c.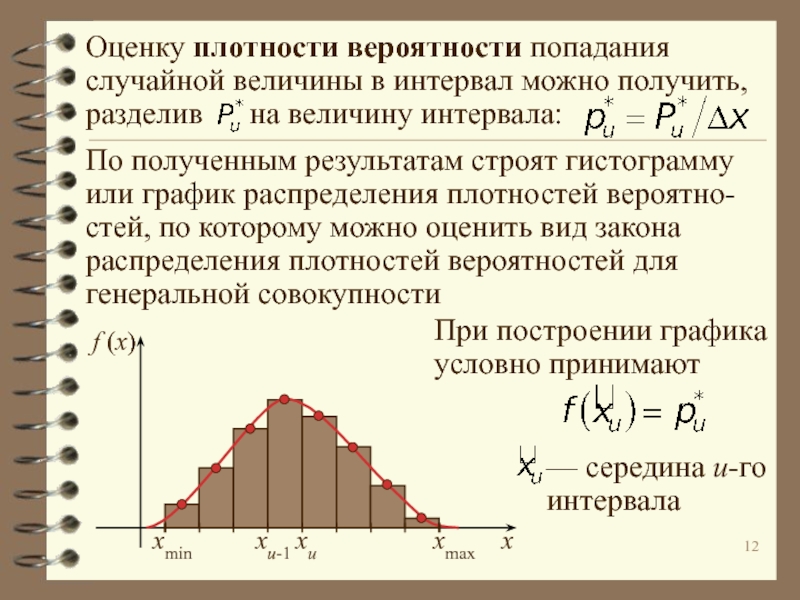 85]

При анализе нормальности распределения строят гистограммы распределения нормированных частот появления остатков в заБисимости от их чишовых значений. Подобные гистограммы должны приближенно отвечать нормальному закону распределения. При этом гипотеза о нормальности может 0ь1гь проверена по различным статистически.м критериям. Наряду с ней дополнительно проверяют также гипотезу о равенстве нулю математического ожщ1ания выборочного распределения, для чего используют как графические методы, так и методы линейного или нелинейного регрессионного анализа. [c.49]

Построены гистограммы распределения всех исследуег.их переменных, 4 из которых приведены иа рис.11-14. Цо критерию Пирсона проведена качественная оценка нормальнооги распрадоланий (прил — 2). На имеют нормального распределения переменные [c.59]

Тристрам [99] применил этот подход к некоторым другим белкам и заключил, что некоторые группы аминокислот распределяются в белках таким образом, что гистограммы последних носят характер одной или нескольких частично перекрывающихся кривых нормального распределения. Если такое распределение отражает какую-то природную закономерность, то это может указывать либо на то, что механизм синтеза белка более или менее одинаков для всех видов клеток, либо скорее на то, что механизмы синтеза избирательны и не допускают образования любых стереохимически возможных белков . [c.25]

Соответствие теоретического и эмпирического распределений оценивают критерием согласия Пирсона Принято считать, что эмпирическая кривая согласуется с теоретической, если вероятность согласия более 0,05. Если вероятность согласия больше принятого уровня, то считают, что эмпирическое распределение согласуется с теоретическим. Оценка соответствия теоретических кривых для гистограммы пределов прочности композиции 33-18с (см. рис. 19) дала следующие результаты вероятность согласия экспериментального распределения с кривой нормального распределения равна 0,02 (кривые распределения Седракяна и типа А можно считать соответствующими эмпирическому распределению, поскольку вероятность согласия и в том, и в другом случае равна 0,1 (>0,05). Для композиции АГ-4 уровень согласия для нормального распределения характеризуется вероятностью 0,47. 240 [c.240]

Форма гистограммы изменяется в зависимости от ширины выбранного интервала размера. Рекомендуется, чтобы эти интервалы составляли арифметическую прогрессию для нормального распределения и геометрическую прогрессию для нормальнологарифмического. [c.104]

При моделированйи для каждого варианта на ЭВМ просчитывается V случайных реализаций. За одну случайную реализацию принимается расчет характеристик фильтров для величин элементов, равных заданному номиналу, увеличенному на случайную величину Для индуктивностей и сопротивлений получается с помощью датчика случайных чисел (ДСЧ), нормально распределенных с нулевым средним значением и единичной дисперсией. Полученное случайное число умножается на а = А/3, а результат прибавляется к заданному значению номинала элемента. Для емкости изменение номинала получается с помощью датчика случайных чисел, равномерно распределенных в интервале (О, 1). Полученное случайное число легко преобразуется в случайное число, равномерно распределенное на интервале (—Д, -ЬЛ). Для каждой случайной реализации величин элементов вычисляются необходимые характеристики, для которых накапливаются по реализациям суммы различных степеней для получения моментов распределения этих характеристик. Для дальнейшего построения гистограмм и статистических функций распределения значений искомых величин накапливаются суммы числа попаданий полученных значений в определенные интервалы. [c.236]

Вьшолним визуальное сравнение гистограммы и кривой закона нормального распределения. [c.110]

Подтверждением этого являются гистограммы, приведенные па рис. 6.9, которые построены для двух указанных случаев регулирования вентилятора ВОД 30. Степень соответствия нормального распределения статистическому материалу по выборкам режимов из рабочих зон ряда вентиляторов проверена по критерию согласия Пирсона, посредством которого полученные на гистограммах распределения минимизировались относительно экстремальной теоретически вероятностной меры при показателе уровня значимости Рб>0 1 [Ю]- Этим показателем оценивается при принято1Ч законе распределения случайной величины вероятность ее попадания в разряды статистического ряда. [c.216]

Гистограмма частот в Excel 2016

Excel 2016 обзавелся новыми типами графиков. Причем, это не какие-нибудь дизайнерские новшества, а самые настоящие статистические диаграммы.

Так, «ящик с усами» применяется для анализа выборки. Диаграмма Парето пригодится при анализе вклада отдельных элементов в общую сумму. В этой заметке рассмотрим еще одну новую диаграмму из Excel 2016 – гистограмму частот.

На первый взгляд и в более ранних версиях Excel можно изобразить частоты с помощью диаграмм. Можно, но для этого предварительно необходимо числовые данные сгруппировать. То есть для каждой категории (интервала, группы, года и т.д.) нужно посчитать частоту. Теперь появилась возможность изобразить распределение данных буквально в один клик без предварительных расчетов и группировок.

Строится такая диаграмма в один клик. Выделяем ряд данных и нажимаем кнопку гистограммы частот.

Собственно, все. Тут же появляется соответствующая диаграмма.

Возникает вопрос: как Excel делит данные на интервалы? Справка Excel говорит, что с помощью формулы.

Количество интервалов получается достаточным для того, чтобы визуально прикинуть, каков характер распределения анализируемых данных.

Интервалы легко перестроить под свои потребности. Можно, например, задать нижнюю и верхнюю границу, за пределами которых данные будут объединены в один интервал.

При выборе опции выхода за нижнюю и верхнюю границы, судя по той же справке, их значения рассчитываются, как расстояние ±3σ от средней арифметической.

Однако рассчитываемые автоматически значения легко изменить в окне настроек.

Это был пример, когда данные разбиваются на интервалы. Такой вариант группировки установлен по умолчанию (см. окно параметров настройки оси выше).

Распределение частот можно получить и по имеющимся категориям (должен быть указан соответствующий столбец). Выбираем в настройках «По категориям» и получаем новые частоты.

Проведем эксперимент. С помощью функции СЛУЧМЕЖДУ смоделируем равномерно распределенную выборку в пределах, скажем, от 0 до 200. Пусть выборка состоит из 100 значений. Теперь изобразим гистограмму частот.

Как видно, частоты примерно одинаковы.

А теперь смоделируем нормальную выборку, со средней 100 и стандартным отклонением 30.

Отчетлива видна характерная конфигурация нормального распределения.

Поделиться в социальных сетях:

Создание и использование гистограмм—ArcGIS Insights

Гистограммы агрегируют числовые данные по группам с равными интервалами, которые называют бинами, и отображают частоту встречаемости значений в каждом из бинов.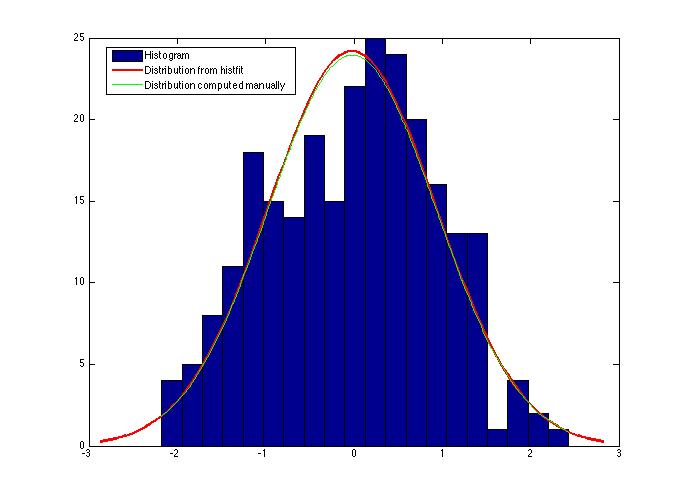 Гистограмма создается с помощью числового поля или поля доля/отношение.

Гистограммы помогают получить ответ на такой вопрос: каково распределение числовых значений и частота их появлений в наборе данных? Есть ли выбросы?

Пример

Негосударственная организация в области здравоохранения изучает показатели подросткового ожирения в США. Гистограмма частоты случаев ожирения у подростков может использоваться для того, чтобы определить, как распределены показатели ожирения по штатам, в том числе наиболее высокие и низкие показатели частоты ожирения и их общий уровень.

На приведенной выше гистограмме показано нормальное распределение, при котором наиболее часто встречающиеся показатели находятся в диапазоне 10-14 процентов.

Увеличивая и уменьшая число бинов, вы можете повлиять на характер анализа своих данных. Хотя сами данные и не изменяются, может измениться их вид. Чтобы правильно истолковать закономерности в данных, важно выбрать подходящее число бинов. Слишком маленькое число бинов может скрыть какие-то закономерности, а слишком большое – преувеличить значение небольших, допустимых изменений данных. Ниже представлен пример подходящего числа бинов данных. Каждый бин содержит примерно один процент данных, и данные можно рассмотреть в более крупном масштабе, что позволит выявить закономерности, невидимые при использовании шести бинов. В данном случае налицо нормальное распределение значений с незначительным, сдвигом влево.

Создание гистограммы

Для создания гистограммы выполните следующие шаги:

Выберите числовое поле или поле доли/отношения .
Для создания гистограммы выполните следующие шаги:
1. Перетащите выбранные поля в новую карточку.
2. Наведите курсор над областью размещения Диаграмма.
3. Поместите выбранные поля на Гистограмму.

Подсказка:

Также можно построить диаграммы с помощью меню Диаграмма над панелью данных или кнопки Тип визуализации на существующей карточке.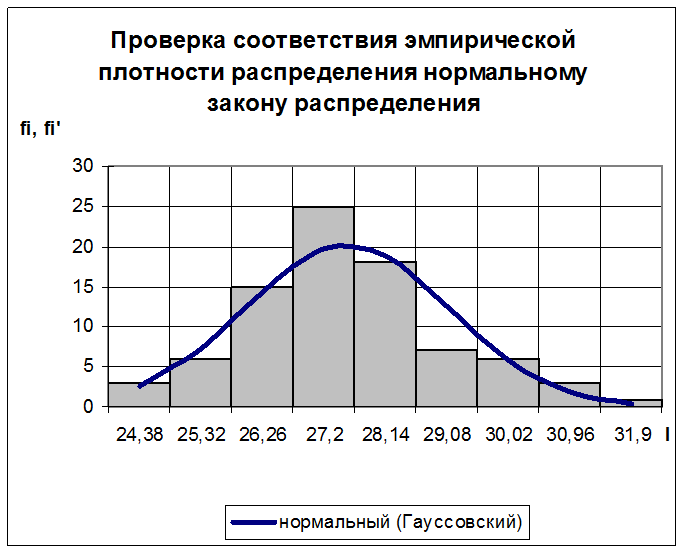 В меню Диаграммы будут доступны только диаграммы, которые применимы к имеющейся выборке данных. В меню Тип визуализации будут только подходящие варианты визуализаций (карты, диаграммы или таблицы).

Гистограмму также можно создать с помощью Просмотр гистограммы; для этого используйте кнопку Действие на вкладке Найти ответы > Распределение

Примечания по использованию

Гистограммы обозначаются отдельными символами. Вы можете использовать кнопку Легенда , чтобы изменить цвет символа и цвет контура, который будет применен ко всем бинам.

Когда гистограмма будет создана, Insights автоматически вычисляет приблизительное количество бинов для отображения ваших данных. Вы можете изменить количество бинов при помощи бегунка вдоль оси Х или щёлкнув на числе бинов и введя новое значение.

Для отображения среднего, медианного и нормального распределения данных используйте кнопку Статистика диаграммы . Кривая нормального распределения представляет ожидаемое распределение случайного поднабора непрерывных данных, где самая высокая частота значений центрируется вокруг среднего и частота значений уменьшается по мере увеличения или уменьшения значений по мере удаления от среднего. Кривая нормального распределения полезна при выявлении наличия провалов и выбросов в данных.

Эти статистики на обороте карточек включают среднее, медиану, дисперсию, стандартное квадратичное отклонение, эксцесс и сдвиг (упрощенный). Следующая таблица содержит описание асимметрии и эксцесса:


Статистика	Описание
Асимметрия	Скошенность определяет симметрично ли распределение данных. Мера скошенности определяет где лежит большинство значений в распределении – левее или правее среднего. Асимметрия нормального распределения равна нулю и показывает одинаковый объем данных по обе стороны от среднего. Значения асимметрии могут быть нулевыми, отрицательными или положительными: Нулевое – данные распределены симметрично. Отрицательное – данные асимметричны с эксцессом вправо. Самая высокая повторяемость значений находится справа от среднего, а левый «хвост» длиннее правого. Медиана больше, чем среднее. Положительное – данные асимметричны с эксцессом влево. Самая высокая повторяемость значений находится слева от среднего, а правый «хвост» длиннее левого. Среднее больше, чем медиана.
Эксцесс	Эксцесс описывает форму плотности распределения и определяет вероятность выбросов при данном распределении. Распределения с относительно тяжёлыми хвостами называются островершинными (лептокуртическими), и у них эксцесс больше нуля. Распределения с относительно тонкими хвостами называются плосковершинными (платикуртическими), и у них эксцесс меньше нуля. Эксцесс нормального распределения равен трём, а в случае использования упрощённого эксцесса – нулю (это вычисляется по той же формуле, что и эксцесс, минус три). Значения упрощённого эксцесса могут быть нулевыми, отрицательными или положительными: Нулевые – этот режим такой же, как среднее. Отрицательные – у такого распределения данных хвосты короче, а пик более плоский. Положительные – хвосты кривой длиннее, а пик выше.

Используйте кнопку Тип визуализации для прямого переключения между гистограммой и градуированными символами на карте или суммарной таблицей.

Отзыв по этому разделу?

Гистограммы—Справка | ArcGIS for Desktop

Доступно с лицензией Geostatistical Analyst.

Инструмент Гистограмма (Histogram) предоставляет одномерное (с одной переменной) описание данных. В диалоговом окне инструмента отображается частотное распределение интересующего набора данных и вычисляется суммарная статистика.

Частотное распределение

Частотное распределение представляет собой столбчатую диаграмму для отображения частотности попадания наблюдаемых значений в определенные интервалы или классы. Можно указать ряд классов с одинаковой шириной, которые будут использоваться в гистограмме. Относительная пропорция данных, которая распределяется по каждому классу, выражается высотой каждого столбца. Например, в гистограмме ниже показано частотное распределение (10 классов) для набора данных.

Пример диалогового окна Гистограмма (Histogram)

Суммарная статистика

Важные объекты распределения могут быть суммированы с помощью различных статистик, которые характеризуют их местоположение, распределение и форму.

Показатели расположения

Показатели расположения дают представление о том, где находятся центр и другие части распределения.

Среднее значение — это среднее арифметическое данных. Среднее представляет собой один из показателей центра распределения.
Значение медианы соответствует кумулятивной пропорции 0,5. Если данные организованы в порядке возрастания, 50 процентов значений будут находиться ниже медианы, а другие 50 процентов — выше медианы. Медиана предоставляет еще один показатель центра распределения.
Первая и третья квартили соответствуют кумулятивной пропорции 0,25 и 0,75. Если данные организованы в порядке возрастания, 25 процентов значений будут находиться ниже первой квартили, а еще 25 процентов — выше третьей квартили. Первая и третья квартили являются особыми случаями квантилей. Квантили вычисляются следующим образом:
```
quantile = (i - 0.5) / N
```
где i — упорядоченное i-тое^{значение данных.}

Показатели разброса

Разброс точек вокруг среднего значения — еще одна характеристика отображаемого частотного распределения.

Дисперсия данных представляет собой среднеквадратическое отклонение всех значений от среднего. Поскольку в нее включаются квадраты разностей, вычисляемая дисперсия чувствительна к необычно высоким или низким значениям. Дисперсия оценивается суммированием квадратических отклонений от среднего и делением суммы на (N-1).
Стандартное отклонение представляет собой квадратный корень из дисперсии и описывает разброс данных вокруг среднего. Чем меньше дисперсия и стандартное отклонение, тем гуще сконцентрирован кластер измерений вокруг среднего значения.

На диаграмме ниже показаны два распределения с различными стандартными отклонениями. Частотное распределение, представленное черной линией, более переменчиво (с широким разбросом), чем частотное распределение, представленное красной линией. Дисперсия и стандартное отклонение для черного частотного распределения больше, чем для красного.

Показатели диаграммы разброса

Показатели формы

Частотное распределение также характеризуется формой.

Коэффициент асимметрии — это показатель симметрии распределения. Для симметричных распределений коэффициент асимметрии равен нулю. Если у распределения есть длинный правый хвост больших значений, то у него положительная асимметрия, а если длинный левый хвост малых значений — то отрицательная.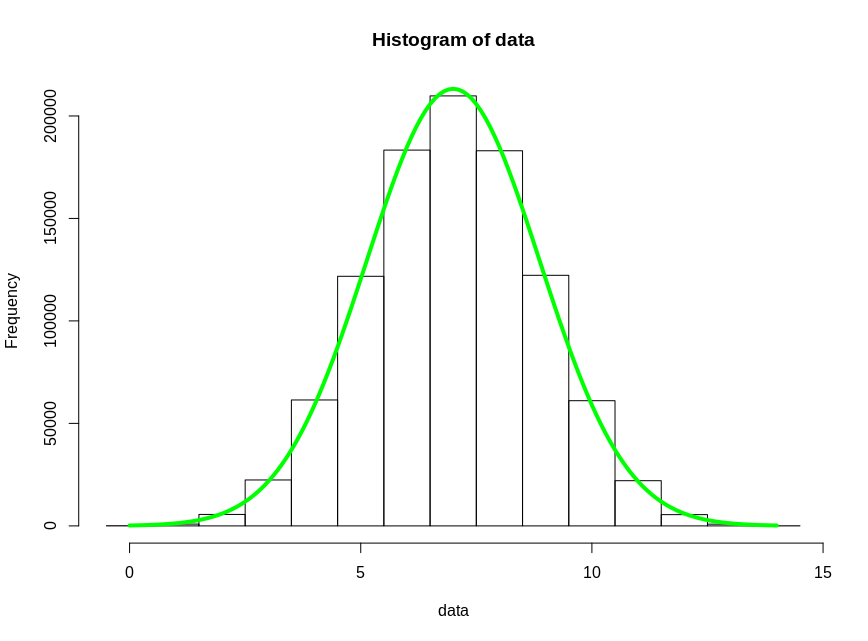 Среднее значение для распределений с положительной асимметрией больше, чем медиана, а для распределений с отрицательной асимметрией — наоборот. На рисунке ниже показано распределение с положительной асимметрией.Пример распределения с положительной асимметрией

Эксцесс основан на размере хвостов распределения и представляет собой показатель вероятности того, что распределение будет создавать выпадающие значения. Эксцесс нормального распределения равен трем. Распределения с относительно толстыми хвостами называются островершинными (лептокуртическими), и у них эксцесс больше трех. Распределения с относительно тонкими хвостами называются плосковершинными (платикуртическими), и у них эксцесс меньше трех. На следующей диаграмме нормальное распределение показано красным цветом, а островершинное (с толстыми хвостом) — черным.

Пример нормального распределения

Примеры

С помощью инструмента Гистограмма (Histogram) можно исследовать форму распределения путем прямого наблюдения. Просматривая статистику среднего значения и медианы, можно определить расположение центра распределения. На рисунке внизу обратите внимание на колоколообразное распределение, и так как значения среднего арифметического и медианы близки, это распределение близко к нормальному. Также можно выделить экстремальные значения в хвосте гистограммы и увидеть, как они расположены в пространстве на отображаемой карте.

Пример колоколообразной гистограммы

Если асимметрия данных слишком большая, можно протестировать эффекты трансформации на данных. На этом рисунке показано распределение с асимметрией перед применением преобразования.Пример гистограммы с асимметрией

К асимметричным данным применяется логарифмическое преобразование, и в этом случае преобразование приближает распределение к нормальному.Пример гистограммы логарифмического преобразования

Более подробно о преобразованиях, доступных в инструменте Гистограмма (Histogram), см. в разделе Преобразования по методу Box-Cox, арксинуса- и логарифмические.

Отзыв по этому разделу?

Математика и статистика, часть 2: практика в R

Выборки из распределений

На прошлом занятии мы познакомились с функциями, рассчитывающими значения функции распределения для различных распределений.

R позволяет также гененировать случайные выборки из различных распределений заданного объема. Для этого используются функции типа rdist(), где вместо dist указывается необходимое распределение. Первый аргумент этой функции всегда объем выборки, а затем – параметры распределения. Доступные распределения можно найти здесь.

Бинарное распределение

Например, сгененируем выборку объема 8 из бинарного распределения с параметром $p=\frac{1}{4}$. Для этого нужно попросить R сгенерировать выборку из биномиального распределения с параметрами $n=1$ и $p=\frac{1}{4}$ (так как бинарное распределение – это частный случай биномиального распределения).

rbinom(8, 1, 1/4)

## [1] 0 0 0 0 0 0 1 0

Каждый раз при реализации функции, генерирующей случайную выборку, у Вас будет появляться разная последовательность значений. Так и должно быть, ведь каждое из наблюдений выборки – случайная величина. В среднем, мы ожидаем, что четвертая часть выборки, то есть 2 наблюдения, должна содержать значения 1. Но при малельком размере выборки возможными также будут выборки, где 1 встречается чаще или реже.

По сути, мы имеем ситуацию, которую можно описать через модель серии испытаний Бернулли: количество единиц оказывается случайной величиной, и у каждого количества единиц в нашей выборке будет своя вероятность.

Мы можем примерно оценить, как часто нам выпадет выборка, где содержится 1 единица. Это вероятность одного успеха в серии из 8 испытаний Бернулли с тем же самым параметром вероятности успеха:

dbinom(1, 8, 1/4)

## [1] 0.2669678

dbinom(0, 8, 1/4)

## [1] 0.1001129

dbinom(8, 8, 1/4)

## [1] 1.525879e-05

Вы видим, что примерно в 10 случаях из 100 выборка не будет содержать ни одной 1, а вероятность сплошных единиц очень мала – следовательно, такая выборка (одни единицы) неправдоподобна.

Примечание. Для того, чтобы воспроизвести сгенерированную случайную выборку при повторной реализации функции, нужно прописать перед ней функцию set.seed(any_number). Например:

set.seed(111)

Нормальное распределение

Задание 3 из семинара 10

to be updated

Гистограммы в R

Гистограмма – график, который является аналогом графика функции плотности для распределний. Все наблюдения в выборке упорядочиваются по возрастанию. Затем упорядоченная выборка начиная от некоторого стартового значения (иногда это минимальное значение в выборке, а иногда – некоторое значение, меньшее, чем минимум) разбивается на $n$ равных интервалов. После этого подсчитывается количество наблюдений, которые попали в каждый интервал. Это количество откладывется на оси Y. По оси X откладываются значения наблюдений в выборке.

Вызовем встроенную в R базу данных, где содержатся измерения температуры тела двух бобров в течение дня. После реализации команды data() в памяти R (окошко Environment) появятся две базы данных – по одной на бобра. Описание базы данных можно найти здесь.

data(beavers)

Посмотрим на базу данных. Выведем первые 6 строчек базы данных beaver1 – это делается с помощью функции head().

head(beaver1)

Нам нужна колонка (по-другому колонки в базе данных называются переменными) temp. Чтобы обратиться к колонке внутри базы данных, нужно сначала прописать название базы данных, затем поставить знак $, а затем прописать название переменной.

beaver1$temp

##   [1] 36.33 36.34 36.35 36.42 36.55 36.69 36.71 36.75 36.81 36.88 36.89
##  [12] 36.91 36.85 36.89 36.89 36.67 36.50 36.74 36.77 36.76 36.78 36.82
##  [23] 36.89 36.99 36.92 36.99 36.89 36.94 36.92 36.97 36.91 36.79 36.77
##  [34] 36.69 36.62 36.54 36.55 36.67 36.69 36.62 36.64 36.59 36.65 36.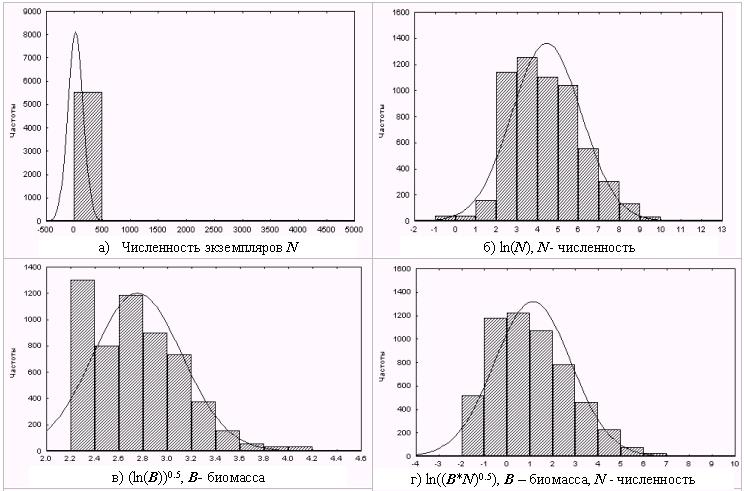 75
##  [45] 36.80 36.81 36.87 36.87 36.89 36.94 36.98 36.95 37.00 37.07 37.05
##  [56] 37.00 36.95 37.00 36.94 36.88 36.93 36.98 36.97 36.85 36.92 36.99
##  [67] 37.01 37.10 37.09 37.02 36.96 36.84 36.87 36.85 36.85 36.87 36.89
##  [78] 36.86 36.91 37.53 37.23 37.20 37.25 37.20 37.21 37.24 37.10 37.20
##  [89] 37.18 36.93 36.83 36.93 36.83 36.80 36.75 36.71 36.73 36.75 36.72
## [100] 36.76 36.70 36.82 36.88 36.94 36.79 36.78 36.80 36.82 36.84 36.86
## [111] 36.88 36.93 36.97 37.15

Чтобы построить гистограмму, нужна команда hist(). Аргументом является вектор: набор чисел, сохраненный в отдельный объект, или колонка из базы данных.

hist(beaver1$temp)

Настроим гистограмму.

hist(beaver1$temp,
     xlab = "Темература тела бобра", # изменить подпись оси OX
     ylab = "Количество наблюдений", # изменить подпись оси OY
     main = "Моя первая сливовая гистограмма про бобров", # изменить название гистограммы
     col = "plum" # поменять цвет гистограммы
     )

Дополнительно: кривая нормального распределения

Мы можем наложить на гистограмму кривую нормального распределения с параметрами, которые соответствуют выборочному среднему и выборочному стандартному отклонению.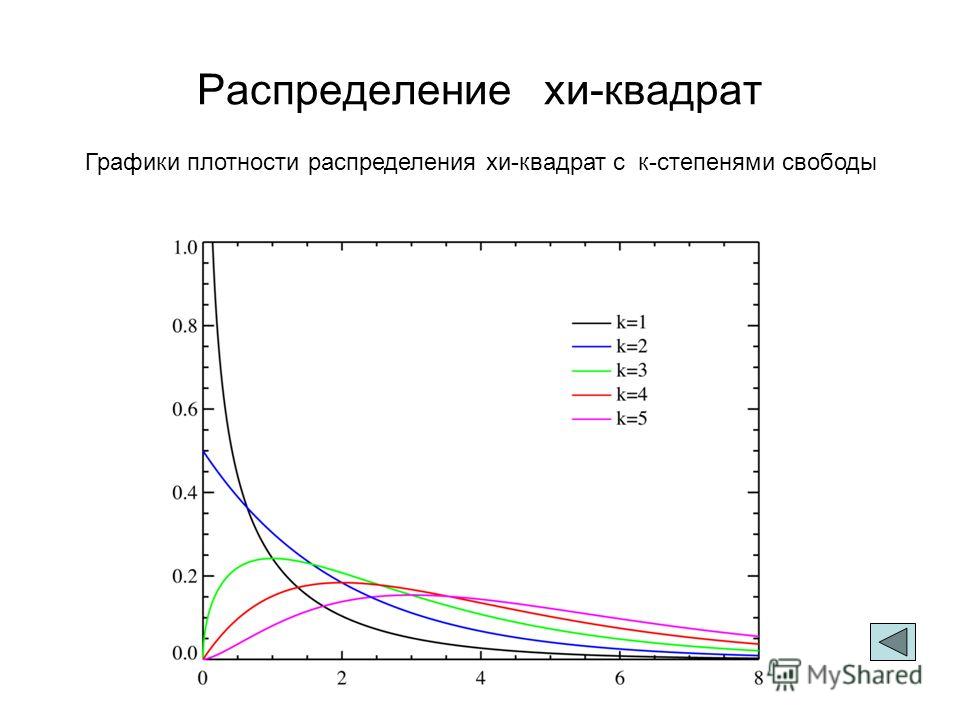 Иными словами, мы можем сравнить, похожа ли гистограмма на нормальное распределение, которое мы ожидали бы увидеть с заданными параметрами?

Прежде всего поменяем шкалу оси OY, указав аргумент freq = F. Тогда по оси Y будут отложены значения плотности: так, чтобы площадь под гистограммой была равна 1.

hist(beaver1$temp,
     xlab = "Темература тела бобра", # изменить подпись оси OX
     ylab = "Плотность", # изменить подпись оси OY
     main = "Моя первая сливовая гистограмма про бобров", # изменить название гистограммы
     col = "plum", # поменять цвет гистограммы
     freq = F # плотность
     )

После этого рассчитаем выборочные средние и стандартное отклонение через команды mean() и sd() соответственно. Сохраним в новые объекты.

mean_beaver <- mean(beaver1$temp)
sd_beaver <- sd(beaver1$temp)

Теперь нарисуем на гистограмме график плотности распределения через функцию curve(dnorm()).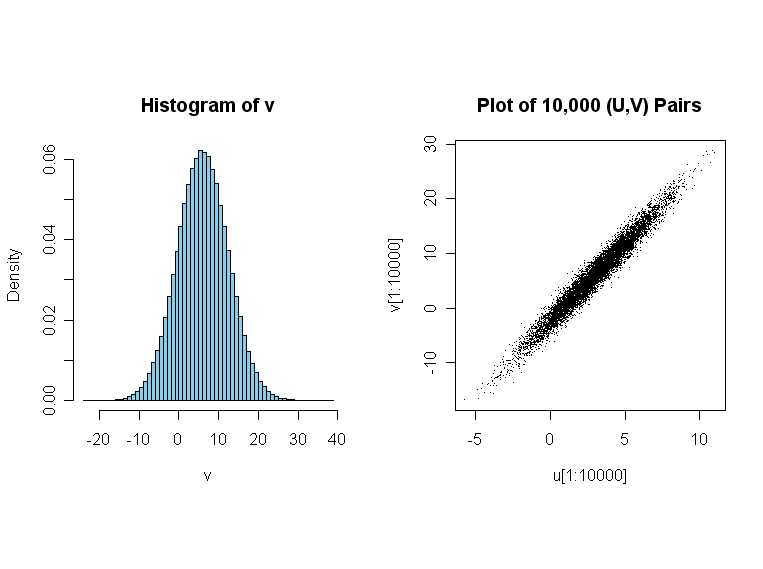

hist(beaver1$temp,
     xlab = "Темература тела бобра", # изменить подпись оси OX
     ylab = "Плотность", # изменить подпись оси OY
     main = "Моя первая сливовая гистограмма про бобров \nс кривой нормального распределения", # изменить название гистограммы
     col = "plum", # поменять цвет гистограммы
     freq = F # плотность
     )

curve(dnorm(x, # рассчитываем значения функции плотности нормального распределения
            mean = mean_beaver, # с выборочным средним
            sd = sd_beaver), # и выборочным стандартным отклонением
      add = T # дорисовываем кривую на предыдущем графике 
      )

Гистограмма напоминает нормальное распределение, но для заданных параметров график слишком вытянут вверх, и мы имеем более массивный левый хвост, хотя ожидали бы симметричное распределение.

Иллюстративно

Центральная предельная теорема

Сгенерируем игрушечную “генеральную совокупность”: выборку из равномерного распределения, определенного на отрезке $[0,~10]$.

set.seed(545)
population <- runif(1000, min = 0, max = 10)
hist(population, col = "paleturquoise1", main = "Выборка из равномерного распределения")

Рассчитаем “истинное среднее”.

mean(population)

## [1] 5.004849

Возьмем 1000 выборок объемом 20, для каждой из них посчитаем выборочное среднее, и для этих 1000 средних нарисуем гистограмму.

set.seed(545)
sample20_means <- c()
for (i in 1:1000) {
  sample20_mean <- mean(sample(population, 20))
  sample20_means <- c(sample20_means, sample20_mean)
}

hist(sample20_means, col = "paleturquoise1", 
     main = "Среднее для 1000 подвыборок размером 20",
     xlab = "Выборочное среднее",
     xlim = c(2,8), # границы на оси OX
     ylim = c(0, 0.6),
     freq = F)

curve(dnorm(x, mean = mean(sample20_means), sd = sd(sample20_means)), add = T)

Несмотря на то, что игрушечная “генеральная совокупность” не распределена нормально, распределение выборочных средних из этой “генеральной совокупности” подчиняется нормальному распределению! Этот вывод дает нам центральная предельная теорема.

Посчитаем среднее и стандартное отклонение для этих 1000 средних:

mean(sample20_means)

## [1] 5.000925

sd(sample20_means)

## [1] 0.6730099

Закон больших чисел

Теперь возьмем 1000 выборок объемом 100, для каждой из них посчитаем выборочное среднее, и для этих 1000 средних нарисуем гистограмму. Границы графика оставим те же, что и для предыдущей гистограммы.

set.seed(545)
sample100_means <- c()
for (i in 1:1000) {
  sample100_mean <- mean(sample(population, 100))
  sample100_means <- c(sample100_means, sample100_mean)
}

hist(sample100_means, col = "paleturquoise1", 
     main = "Среднее для 1000 подвыборок размером 100",
     xlab = "Выборочное среднее",
     xlim = c(2,8) # границы на оси OX
     )

Посчитаем среднее и стандартное отклонения для новых 1000 средних:

mean(sample100_means)

## [1] 4. 994113

sd(sample100_means)

## [1] 0.2803005

Среднее стало (немного) ближе к истинному среднему, а стандартное отлоклоение – меньше. Это значит, что с увеличением объема выборки оценка среднего становится точнее! Этот вывод дает нам закон больших чисел.

Нормальное приближение для гистограмм вероятностей

Гистограммы вероятностей

Гистограмма вероятности — это график, который показывает вероятность каждого результата на оси [latex] \ text {y} [/ latex].

Цели обучения

Объясните значение гистограммы как графического представления распределения данных

Основные выводы

Ключевые моменты

На гистограмме вероятностей высота каждого столбца показывает истинную вероятность каждого результата, если бы было очень большое количество испытаний (а не фактических относительных частот, определенных в ходе фактического проведения эксперимента).
Посмотрев на гистограмму вероятности, можно визуально увидеть, следует ли она определенному распределению, например нормальному распределению.
Как и во всех распределениях вероятностей, вероятности всех исходов должны в сумме равняться единице.

Ключевые термины

независимый : не зависимый; не случайный или зависящий от чего-то еще; бесплатно
дискретная случайная величина : получается путем подсчета значений, для которых нет промежуточных значений, таких как целые числа 0, 1, 2,….

Гистограммы

При изучении данных часто лучше создать графическое представление распределения. Визуальные графики, такие как гистограммы, помогают легко увидеть несколько очень важных характеристик данных, таких как их общий образец, заметные отклонения от этого образца, а также его форма, центр и разброс.

Гистограмма особенно полезна при большом количестве наблюдений. Гистограммы разбивают диапазон значений по классам и отображают только количество или процент наблюдений, попадающих в каждый класс. Обычные гистограммы имеют ось [latex] \ text {y} [/ latex], на которой указана частота. Гистограммы относительной частоты вместо этого имеют относительные частоты на оси [latex] \ text {y} [/ latex], с данными, взятыми из реального эксперимента. В этой главе особое внимание будет уделено гистограммам вероятностей, которые представляют собой идеализацию распределения относительной частоты.

Гистограммы вероятностей

Гистограммы вероятностей похожи на гистограммы относительной частоты в том, что ось [latex] \ text {y} [/ latex] помечена с вероятностями, но есть некоторые различия, которые следует отметить.На гистограмме вероятностей высота каждого столбца показывает истинную вероятность каждого результата, если бы было очень большое количество испытаний (а не фактических относительных частот , определенных в результате фактического проведения эксперимента). Поскольку все высоты являются вероятностями, они должны в сумме равняться единице. Думайте об этих гистограммах вероятностей как об идеализированных картинах результатов эксперимента. Просто глядя на гистограммы вероятностей, можно легко увидеть, какому типу распределения следуют данные.

Давайте посмотрим на следующий пример. Предположим, мы хотим создать гистограмму вероятности для дискретной случайной величины [latex] \ text {X} [/ latex], которая представляет количество орлов при четырех подбрасывании монеты. Допустим, монета сбалансирована, и каждый бросок не зависит от всех остальных бросков.

Мы знаем, что случайная величина [latex] \ text {X} [/ latex] может принимать значения 0, 1, 2, 3 или 4. Чтобы [latex] \ text {X} [/ latex] принимал при значении 0 орлов не будет, а это означает, что выпадут четыре решки.Назовем это ТТТТ. Чтобы [latex] \ text {X} [/ latex] принял значение 1, у нас может быть четыре разных сценария: HTTT, THTT, TTHT или TTTH. Чтобы [latex] \ text {X} [/ latex] принимал значение 2, у нас есть шесть сценариев: HHTT, HTHT, HTTH, THHT, THTH или TTHH. Чтобы [latex] \ text {X} [/ latex] принимал 3, у нас есть: HHHT, HHTH, HTHH или THHH.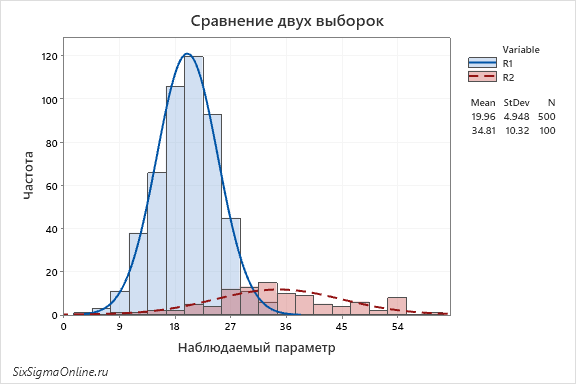 И, наконец, для [latex] \ text {X} [/ latex], чтобы взять на себя 4, у нас есть только один сценарий: HHHH.

Есть шестнадцать различных возможностей подбрасывать монету четыре раза.Вероятность каждого исхода равна [латекс] \ frac {1} {16} = 0,0625 [/ латекс]. Вероятность каждой из случайных величин [latex] \ text {X} [/ latex] равна:

[латекс] \ displaystyle {\ text {P} (\ text {X} = 0) = \ frac {1} {16} = 0,0625 \\ \ text {P} (\ text {X} = 1) = \ frac {4} {16} = 0,25 \\ \ text {P} (\ text {X} = 2) = \ frac {6} {16} = 0,375 \\ \ text {P} (\ text {X} = 3) = \ frac {4} {16} = 0,25 \\ \ text {P} (\ text {X} = 4) = \ frac {1} {16} = 0,0625 \\} [/ latex]

Обратите внимание, что, как и в любом другом распределении вероятностей, все вероятности в сумме составляют единицу.

Чтобы затем создать гистограмму вероятности для этого распределения, мы сначала построим две оси. Ось [latex] \ text {y} [/ latex] будет обозначена вероятностями в десятичной форме. На оси [latex] \ text {X} [/ latex] будут указаны возможные значения случайной переменной [latex] \ text {X} [/ latex]: в данном случае 0, 1, 2, 3 , и 4. Затем следует нарисовать прямоугольники одинаковой ширины в соответствии с их соответствующими вероятностями.

Обратите внимание, что эта конкретная гистограмма вероятности симметрична и напоминает нормальное распределение.Если бы вместо этого мы подбросили монету четыре раза во многих испытаниях и создали гистограмму относительной частоты, мы бы получили график, похожий на этот, но маловероятно, что он был бы идеально симметричным.

Гистограммы вероятностей и нормальная кривая

Нормальной кривой можно аппроксимировать множество различных типов распределений.

Цели обучения

Оценить нормальность с помощью графических инструментов для интерпретации данных

Основные выводы

Ключевые моменты

Возникновение нормального распределения в практических задачах можно условно разделить на три категории: точно нормальные распределения, приблизительно нормальные распределения и распределения, моделируемые как нормальные.
Просто взглянув на гистограмму вероятности, вы можете определить, является ли она нормальным, посмотрев на ее форму. Если график имеет приблизительно колоколообразную форму и симметричен относительно среднего значения, обычно можно предполагать нормальность.
График нормальной вероятности — еще один метод, используемый для оценки нормальности. Данные нанесены на график против теоретического нормального распределения таким образом, что, если данные нормальные, точки должны образовывать приблизительную прямую линию.

Ключевые термины

график нормальной вероятности : графический метод, используемый для оценки того, является ли набор данных приблизительно нормально распределенным
центральная предельная теорема : Теорема, которая гласит: если сумма независимых одинаково распределенных случайных величин имеет конечную дисперсию, то она будет (приблизительно) нормально распределенной.

При построении гистограмм вероятностей часто замечают, что распределение может близко совпадать с нормальным распределением. Возникновение нормального распределения в практических задачах можно условно разделить на три категории: точно нормальные распределения, приблизительно нормальные распределения и распределения, моделируемые как нормальные.

Точно нормальные распределения

Определенные величины в физике распределены нормально, например:

Скорости молекул в идеальном газе.В более общем плане скорости частиц в любой системе в термодинамическом равновесии будут иметь нормальное распределение из-за принципа максимальной энтропии.
Функция плотности вероятности основного состояния в квантовом гармоническом осцилляторе.
Положение частицы, которая испытывает диффузию.

Приблизительно нормальные распределения

Приблизительно нормальные распределения встречаются во многих ситуациях, как объясняется центральной предельной теоремой. Когда результатом является большое количество небольших эффектов, действующих аддитивно и независимо, его распределение будет близким к нормальному.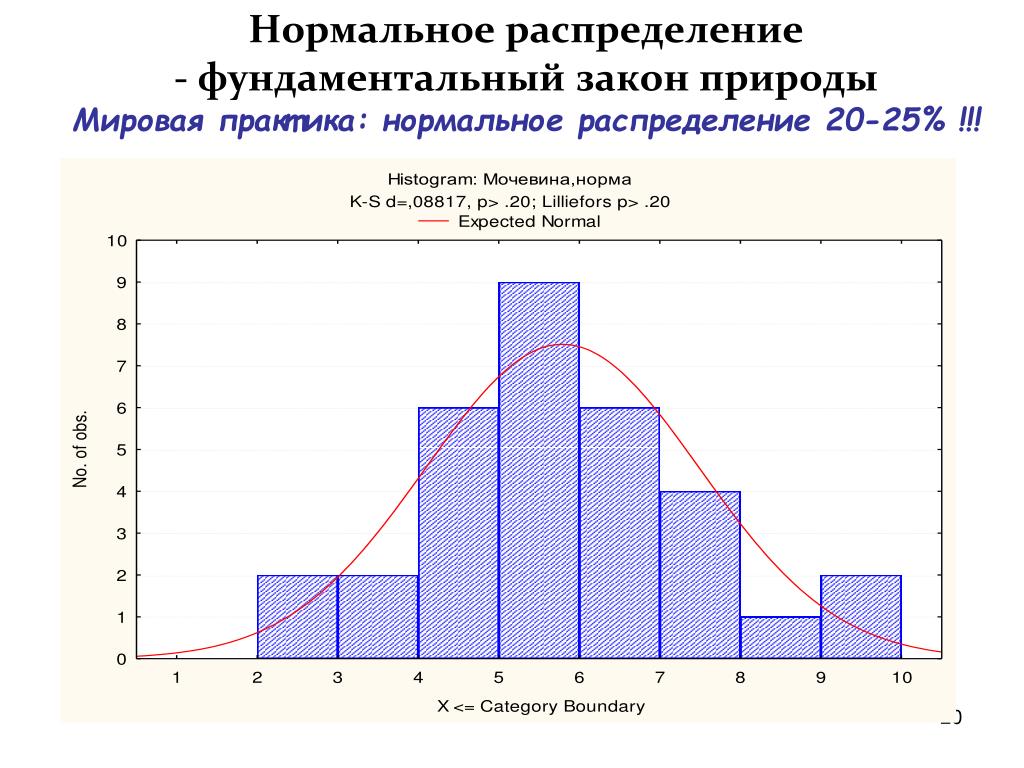 Нормальное приближение будет недействительным, если эффекты действуют мультипликативно (а не аддитивно) или если существует единственное внешнее влияние, которое имеет значительно большую величину, чем остальные эффекты.

Нормальное приближение может использоваться в задачах счета, где центральная предельная теорема включает приближение от дискретного к континуальному и где используются бесконечно делимые и разложимые распределения. Сюда входят биномиальные случайные величины, которые связаны с переменными двоичного ответа, и случайные величины Пуассона, которые связаны с редкими событиями.

Предполагаемая нормальность

В реальной жизни есть много примеров проблем, которые считаются нормальными. Если бы вы построили гистограмму вероятности этих событий с множеством испытаний, гистограмма выглядела бы в форме колокола. Примеры включают:

Определенные физиологические измерения, такие как артериальное давление у взрослых людей.
Погрешности измерений в физических экспериментах. Такое использование нормального распределения не означает, что предполагается, что ошибки измерения имеют нормальное распределение, скорее, использование нормального распределения дает наиболее консервативные прогнозы из возможных, учитывая только знания о среднем значении и дисперсии ошибок.
Результаты стандартизированного тестирования.

Как оценить нормальность

Как мы можем определить, являются ли данные на гистограмме вероятности нормальными или, по крайней мере, приблизительно нормальными? Самый очевидный способ — посмотреть на саму гистограмму. Если график имеет приблизительно колоколообразную форму и симметричен относительно среднего значения, обычно можно предполагать нормальность.

Однако есть другой метод, который может помочь: график нормальной вероятности. График нормальной вероятности — это графический метод проверки нормальности — оценки того, является ли набор данных приблизительно нормально распределенным.Данные нанесены на график против теоретического нормального распределения таким образом, что точки должны образовывать приблизительную прямую линию (,). Отклонения от этой прямой указывают на отклонения от нормы (,). Важно помнить, что нельзя слишком остро реагировать на незначительные колебания сюжета. Эти графики часто создаются не вручную, а с помощью технологических инструментов, таких как графический калькулятор.

Ненормальность — Гистограмма : Это выборка размером 50 из распределения со смещением вправо, построенная в виде гистограммы.Обратите внимание, что гистограмма не имеет формы колокола, что указывает на неправильное распределение.

Ненормальность — график вероятности : Это выборка размером 50 из распределения со смещением вправо, построенная как график нормальной вероятности. Обратите внимание, что точки на значке отклоняются, указывая на то, что распределение не является нормальным.

Приблизительно нормально — Гистограмма : Это выборка размером 50 из нормального распределения, нанесенная в виде гистограммы. Гистограмма имеет несколько колоколообразную форму, что указывает на нормальность.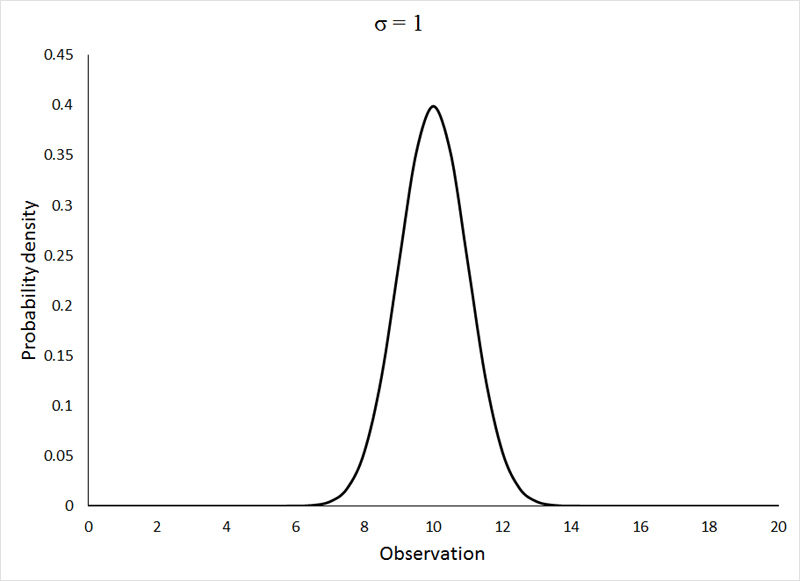

Примерно нормальный — график вероятности : Это выборка размером 50 из нормального распределения, построенная как график нормальной вероятности. Сюжет выглядит довольно прямым, что говорит о нормальности.

Заключение

Многие распределения в реальной жизни можно аппроксимировать с помощью нормального распределения.

Цели обучения

Объясните, как гистограмма вероятности используется для определения нормальности данных

Основные выводы

Ключевые моменты

На гистограмме вероятности высота каждого столбца показывает истинную вероятность каждого результата, если бы было очень большое количество испытаний (а не фактические относительные частоты, определенные при фактическом проведении эксперимента).
Самый очевидный способ определить, является ли распределение приблизительно нормальным, — это посмотреть на саму гистограмму. Если график имеет приблизительно колоколообразную форму и симметричен относительно среднего значения, обычно можно предполагать нормальность.
График нормальной вероятности — это графический метод проверки нормальности. Данные нанесены на график против теоретического нормального распределения таким образом, что точки образуют приблизительную прямую линию.
В реальной жизни многие вещи распределены приблизительно нормально, в том числе рост людей и артериальное давление.

Ключевые термины

график нормальной вероятности : графический метод, используемый для оценки того, является ли набор данных приблизительно нормально распределенным

Что такое гистограмма вероятности?

Часто бывает полезно отображать данные, собранные в эксперименте, в виде гистограммы. Наличие графического представления полезно, потому что оно позволяет исследователю визуализировать, какую форму принимает распределение.

Гистограммы вероятностей похожи на гистограммы относительной частоты в том, что по оси Y обозначены вероятности, но есть некоторые различия, которые следует отметить.На гистограмме вероятностей высота каждого столбца показывает истинную вероятность каждого результата, если бы было очень большое количество испытаний (а не фактических относительных частот , определенных в результате фактического проведения эксперимента). Поскольку все высоты являются вероятностями, они должны в сумме равняться единице. Думайте об этих гистограммах вероятностей как об идеализированных картинах результатов эксперимента. Просто глядя на гистограммы вероятностей, можно легко увидеть, какому типу распределения следуют данные.

Гистограмма вероятности : Эта гистограмма вероятности показывает вероятности того, что 0, 1, 2, 3 или 4 решки выпадут при четырех подбрасывании справедливой монеты.

Как мы можем определить, являются ли данные приблизительно нормальными?

Приведенный выше пример гистограммы вероятности является примером нормальной гистограммы. Как мы можем сказать? Самый очевидный способ — посмотреть на саму гистограмму. Если график имеет приблизительно колоколообразную форму и симметричен относительно среднего значения, обычно можно предполагать нормальность.

Однако есть другой метод, который может помочь: график нормальной вероятности. График нормальной вероятности — это графический метод проверки нормальности — оценки того, является ли набор данных приблизительно нормально распределенным. Данные нанесены на график против теоретического нормального распределения таким образом, что точки образуют приблизительную прямую линию. Отклонения от этой прямой линии указывают на отклонения от нормы. Важно помнить, что нельзя слишком остро реагировать на незначительные колебания сюжета.Эти графики часто создаются не вручную, а с помощью технологических инструментов, таких как графический калькулятор.

График нормальной вероятности : Точки данных не отклоняются далеко от прямой линии, поэтому мы можем предположить, что распределение является приблизительно нормальным.

Примерно нормальные распределения в реальной жизни

Мы тщательно изучаем нормальное распределение, потому что многие вещи в реальной жизни очень близки к нормальному распределению, в том числе:

Рост людей
Размеры выпускаемых машин
Погрешности измерений
Артериальное давление
Баллы по стандартизированному тесту

Нормальное распределение: понимание гистограмм и вероятностей

Эта статья является частью серии статей по статистике в электротехнике, которую мы начали с обсуждения статистического анализа и описательной статистики.Затем мы исследовали три описательных статистических показателя с точки зрения приложений обработки сигналов.

Затем мы коснулись стандартного отклонения — в частности, определения компенсации размера выборки при вычислении стандартного отклонения и понимания взаимосвязи между стандартным отклонением и среднеквадратичными значениями.

В прошлой статье мы представили нормальное распределение в электротехнике, заложив основу для нашего нынешнего обсуждения: понимание вероятностей в измеренных данных.

Знакомство с гистограммами

В предыдущей статье мы начали обсуждение нормального распределения, обратившись к форме этой гистограммы:

Гистограмма, иллюстрирующая нормальное распределение.

Что такое гистограмма?

Гистограммы — это визуальные представления 1) значений, которые присутствуют в наборе данных, и 2) частоты появления этих значений.Гистограмма, показанная выше, может представлять много различных типов информации.

Представим, что он представляет собой распределение значений, полученных нами при измерении разницы, округленной до ближайшего милливольта, между номинальным и фактическим выходным напряжением линейного регулятора, который подвергался различным температурам и условиям эксплуатации. Так, например, приблизительно 8000 измерений показали разницу в 0 мВ между номинальным выходным напряжением и фактическим выходным напряжением, а приблизительно 1000 измерений показали разницу в 10 мВ.

Гистограммы — чрезвычайно эффективный способ обобщения больших объемов данных. Взглянув на гистограмму выше, мы можем быстро найти частоту отдельных значений в наборе данных и определить тенденции или закономерности, которые помогут нам понять взаимосвязь между измеренным значением и частотой.

Гистограммы с ячейками

Когда набор данных содержит так много разных значений, что мы не можем удобно связать их с отдельными столбцами гистограммы, мы используем биннинг.То есть мы определяем диапазон значений как ячейку, группируем измерения в эти ячейки и создаем одну полосу для каждой ячейки.

Гистограмма, в которой вместо отдельных значений используются интервалы.

Горизонтальная ось разделена на десять интервалов одинаковой ширины, и каждому интервалу назначена одна полоса.Все измерения, попадающие в числовой интервал ячейки, влияют на высоту соответствующей полосы. (Метки на горизонтальной оси показывают, что ячейки имеют разную ширину, но это просто потому, что значения меток округлены.)

Гистограммы и вероятность

В некоторых ситуациях гистограмма не дает нам нужной информации. Мы можем посмотреть на гистограмму и легко определить частоту измеренного значения, но мы не можем легко определить вероятность измеренного значения.

Например, если я посмотрю на первую гистограмму, я знаю, что примерно 8000 измерений показали разницу в 0 В между номинальным и фактическим напряжением регулятора, но я не знаю , насколько вероятно , что случайно выбранное измерение , или новое измерение сообщит о разнице в 0 В.

Это серьезное ограничение, потому что вероятность отвечает на чрезвычайно распространенный вопрос: Каковы шансы, что…?

Какова вероятность того, что у моего линейного регулятора погрешность выходного напряжения будет менее 2 мВ? Какова вероятность того, что частота ошибок по битам моего канала передачи данных будет выше 10 ^–3? Какова вероятность того, что шум приведет к тому, что мой входной сигнал превысит порог обнаружения? И так далее.

Причина этого ограничения проста в том, что гистограмма четко не передает размер выборки, то есть общее количество измерений. (Теоретически общее количество измерений можно определить, сложив значения всех столбцов гистограммы, но это было бы утомительно и неточно.)

Если мы знаем размер выборки, мы можем разделить количество вхождений на размер выборки и таким образом определить вероятность. Давайте посмотрим на пример.

Пример того, как гистограмма может помочь нам определить вероятность путем деления количества вхождений на размер выборки.

Красные пунктирные линии заключают в себя столбики, показывающие ошибки напряжения менее 2 мВ, а числа, написанные внутри столбцов, указывают точное количество появлений этих трех напряжений ошибки. Сумма этих трех чисел составляет 23 548. Таким образом, исходя из этого упражнения по сбору данных, вероятность получения ошибки менее 2 мВ составляет 23 548/100 000 ≈ 23,5%.

Вероятностная массовая функция

Если наша основная цель при создании гистограммы — передать информацию о вероятности, мы можем изменить всю гистограмму, разделив все числа вхождений на размер выборки.

Полученный график является приближением функции массы вероятности . Например:

Гистограмма, изображающая приблизительную функцию массы вероятности, полученную путем деления числа всех вхождений на размер выборки.

Все, что мы действительно сделали, это изменили числа на вертикальной оси. Тем не менее, теперь мы можем посмотреть на отдельное значение или группу значений и легко определить вероятность появления.

Я хочу прояснить следующую деталь: я сказал, что мы аппроксимируем вероятностно-массовую функцию , когда мы берем гистограмму и делим числа на размер выборки. Истинная функция массы вероятностей представляет собой идеализированное распределение вероятностей, что означает, что для этого потребуется бесконечное количество измерений.

Таким образом, когда мы работаем с реалистичными размерами выборки, гистограмма, созданная на основе данных измерений, дает нам только приближение функции массы вероятности.

Вероятность массы в зависимости от плотности вероятности

Следует подчеркнуть, что функция массы вероятности является дискретным эквивалентом функции плотности вероятности (которую мы обсуждали в предыдущей статье).

Эти две функции передают одну и ту же общую статистическую информацию о переменной или форме сигнала, но делают это по-разному.

Обратите внимание на разницу между двумя именами: Вертикальная ось функции вероятности масса указывает массу вероятности, как в сумме . Вертикальная ось функции плотности вероятности указывает плотность вероятности относительно горизонтальной оси; мы должны интегрировать эту плотность вдоль горизонтальной оси, чтобы сгенерировать величину вероятности.

Заключение

Мы рассмотрели вероятностные функции массы и плотности, и теперь мы готовы изучить кумулятивную функцию распределения и исследовать вероятности нормального распределения с точки зрения стандартного отклонения. Об этом мы поговорим в следующей статье.

Что такое гистограммы? Анализ и распределение частот

Ищете более качественные инструменты?
Попробуйте «Планируй-Выполняй-Учеба-Действуй» (PDSA) Plus QTools ™ Training:
Глоссарий качества Определение: гистограмма
Частотное распределение показывает, как часто встречается каждое отдельное значение в наборе данных.Гистограмма — это наиболее часто используемый график для отображения частотного распределения. Это очень похоже на гистограмму, но между ними есть важные различия. Этот полезный инструмент сбора и анализа данных считается одним из семи основных инструментов качества.
Когда использовать гистограмму
Используйте гистограмму, когда:
Данные числовые
Вы хотите увидеть форму распределения данных, особенно при определении того, примерно нормально ли распределяются выходные данные процесса.
Анализ соответствия процесса требованиям заказчика
Анализируя, как выглядит результат процесса поставщика
Проверка того, произошло ли изменение процесса от одного периода времени к другому
Определение того, являются ли выходные данные двух или более процессов разными
Вы хотите быстро и легко сообщить другим о распределении данных
Пример гистограммы

Как создать гистограмму
Соберите не менее 50 последовательных точек данных из процесса.
Используйте рабочий лист гистограммы , чтобы настроить гистограмму. Это поможет вам определить количество полосок, диапазон чисел, которые входят в каждую полосу, и метки для краев полос. Вычислив W на шаге 2 рабочего листа, используйте свое суждение, чтобы отрегулировать его до удобного числа. Например, вы можете округлить 0,9 до 1,0. Значение W не должно иметь больше десятичных знаков, чем числа, которые вы будете отображать на графике.
Нарисуйте оси X и Y на миллиметровой бумаге.Отметьте и подпишите ось Y для подсчета значений данных. Отметьте и пометьте ось x значениями L из рабочего листа. Пробелы между этими числами будут столбиками гистограммы. Не допускайте промежутков между стержнями.
Для каждой точки данных отметьте один отсчет над соответствующей полосой знаком X или заштриховав эту часть полосы.
Анализ гистограммы
Прежде чем делать какие-либо выводы из вашей гистограммы, убедитесь, что процесс работал нормально в течение исследуемого периода времени.Если какие-либо необычные события повлияли на процесс в течение периода времени гистограммы, ваш анализ формы гистограммы, вероятно, не может быть обобщен на все периоды времени.
Проанализируйте значение формы вашей гистограммы. Ниже описаны типичные формы гистограмм и их значение.
Инструменты и шаблоны гистограмм
Шаблон гистограммы (Excel) Анализируйте частотное распределение до 200 точек данных с помощью этого простого, но мощного инструмента для создания гистограмм.
Шаблон контрольного листа (Excel) Анализируйте количество дефектов на каждый день недели. Начните с отслеживания дефектов на контрольном листе. Инструмент создаст гистограмму, используя введенные вами данные.
Нормальное распределение
Распространенным паттерном является колоколообразная кривая, известная как «нормальное распределение». При нормальном или «типичном» распределении точки с одинаковой вероятностью будут встречаться как на одной стороне среднего, так и на другой. Обратите внимание, что другие распределения похожи на нормальное распределение.Для доказательства нормального распределения необходимо использовать статистические расчеты.
Важно отметить, что «нормальный» относится к типичному дистрибутиву для конкретного процесса. Например, у многих процессов есть естественный предел с одной стороны, и они будут давать искаженные распределения. Это нормально — то есть типично — для этих процессов, даже если распределение не считается «нормальным».
Асимметричное распределение
Асимметричное распределение асимметрично, потому что естественный предел предотвращает результаты с одной стороны.Пик распределения смещен от центра к пределу, а хвост тянется от него. Например, распределение анализов очень чистого продукта будет искажено, потому что продукт не может быть чистым более чем на 100 процентов. Другими примерами естественных ограничений являются отверстия, размер которых не может быть меньше диаметра бурового долота, или время обработки вызовов, которое не может быть меньше нуля. Эти распределения называются скошенными вправо или влево в зависимости от направления хвоста.
Двухконечная или бимодальная
Бимодальное распределение похоже на спину двугорбого верблюда.Результаты двух процессов с разными распределениями объединяются в один набор данных. Например, распределение производственных данных при работе в две смены может быть двухрежимным, если каждая смена дает различное распределение результатов. Стратификация часто выявляет эту проблему.
Плато или мультимодальное распределение
Плато можно назвать «мультимодальным распределением». Объединены несколько процессов с нормальным распределением. Поскольку имеется много пиков, расположенных близко друг к другу, вершина распределения напоминает плато.
Распределение пограничных пиков
Распределение краевых пиков похоже на нормальное распределение, за исключением того, что у него есть большой пик на одном конце. Обычно это вызвано ошибочным построением гистограммы, когда данные сгруппированы в группу с пометкой «больше чем».
Расческа
При гребенчатом распределении стержни бывают попеременно высокими и короткими. Такое распределение часто является результатом округленных данных и / или неправильно построенной гистограммы.Например, данные о температуре, округленные до ближайших 0,2 градуса, покажут форму гребня, если ширина полосы для гистограммы составляет 0,1 градуса.
Усеченное или частичное распределение
Усеченное распределение выглядит как нормальное распределение с обрезанными хвостами. Поставщик может производить нормальное распределение материала, а затем полагаться на инспекцию, чтобы отделить то, что находится в пределах спецификации, от того, что не соответствует спецификации. В результате поставки клиенту изнутри спецификации — это сердце.
Раздача кормов для собак
В раздаче корма для собак чего-то не хватает — результаты близки к средним. Если покупатель получает такое распределение, то кому-то другому достается сердце, а покупателю остается «собачий корм» — мелочи, оставшиеся после трапезы хозяина. Несмотря на то, что то, что получает заказчик, находится в пределах технических характеристик, продукт делится на два кластера: один около верхнего предела спецификации, а другой — около нижнего предела спецификации.Этот вариант часто вызывает проблемы в работе клиента.
Адаптировано из The Quality Toolbox, Second Edition , ASQ Quality Press.
гистограмм — обзор | Темы ScienceDirect
3.2.4 Гистограммы
Как мы уже говорили ранее, гистограмма похожа на гистограмму, но используется с переменными интервала / отношения. Значения сгруппированы в интервалы (часто называемые ячейками или классами), которые обычно имеют одинаковую ширину. Прямоугольники нарисованы над каждым интервалом, а площадь прямоугольника представляет количество наблюдений в этом интервале.Если все интервалы имеют одинаковую ширину, то высота интервала, а также его площадь представляют частоту интервала. В отличие от гистограмм, между прямоугольниками нет пробелов, если в некотором интервале нет наблюдений.
Здесь мы демонстрируем построение гистограммы для данных о значениях систолического артериального давления пациентов в DIG200. Однако перед созданием гистограммы мы создаем одностороннюю таблицу, которая облегчит создание гистограммы.В таблице 3.7 представлена частота значений систолического артериального давления (САД) для каждого человека в DIG200. Обратите внимание, что имеется 199 наблюдений, поскольку у одного человека в группе плацебо отсутствует информация о своем систолическом артериальном давлении.
Таблица 3.7. Частота индивидуального систолического артериального давления (мм рт. Ст.): DIG200.
905 905 900 12 144
Значение Част. Значение Част. Значение Част. Значение Част. Значение Част. Значение Част.
85 1 105 1 116 8 128 3 138 3 138
90 5 106 2 118 5 130 23 139 2 152 2 152 2 108 2 120 25 131 1 140 26 155 1
155 1
110 16 122 4 132 2 142 1 160 3
100 14 112 1 124 4 134 1 1 144
102 1 114 5 125 3 135 2 145 1 165 1 104 2 126 1 136 1 148 1 170 5
После проверки данных вы должны заметить, что большая часть артериального давления значения заканчиваются нулем — фактически 137 из 199.Все значения являются четными числами, за исключением 17 наблюдений и 15 значений, оканчивающихся на 5. Это говорит о том, что человек, записавший значения артериального давления, возможно, предпочитал числа, оканчивающиеся на ноль. Этот тип находок не является необычным при исследованиях артериального давления; однако, несмотря на это возможное предпочтение цифр, мы собираемся создать некоторые гистограммы на основе этих значений, показанных в таблице 3.7.
Прежде чем мы сможем построить гистограммы для этих данных, необходимо ответить на следующие вопросы:
1.
Сколько должно быть интервалов?
2.
Насколько большими должны быть интервалы?
3.
Где должны быть расположены интервалы?
Тартер и Кронмал (1976) обсуждают эти вопросы достаточно глубоко. На эти вопросы нет однозначных и быстрых ответов; предоставляются только инструкции.
Количество интервалов зависит от количества наблюдений. Обычно используется от 5 до 15 интервалов, при этом меньшее количество интервалов используется для меньших размеров выборки.Существует компромисс между множеством небольших интервалов, которые позволяют получить более подробную информацию с небольшим количеством наблюдений в любой категории, и несколькими большими интервалами с небольшими деталями и множеством наблюдений в категориях.
Один метод определения количества интервалов предложен Стерджесом и разработан Скоттом (1979). Предлагаемая формула (log ₂ n + 1), где n — количество наблюдений, для вычисления количества интервалов, необходимых для построения гистограммы.Следовательно, ширину интервала можно рассчитать с помощью выражения (x _max — x _min) / (log ₂ n + 1). Поскольку в таблице 3.7 имеется 199 наблюдений, нам нужно найти значение log ₂ 199 + 1. Это значение равно 8,64, и мы округляем его до 9, что означает, что для построения гистограммы следует использовать 9 интервалов.
Мы отсылаем читателя к Приложению A для получения информации о логарифмах и о том, как вычислять логарифмы с разными основаниями.Показанный здесь график также дает некоторое представление о форме логарифмической кривой с 2 в качестве основания. Вкратце, log ₂ 199 можно вычислить, разделив log ₁₀ 199 на log ₁₀ 2, что составляет 7,64. Логарифм с основанием 10 доступен в большинстве калькуляторов или компьютерных программ. В качестве альтернативы значение журнала ₂ 199 можно прочитать на графике. Пунктирная линия на графике показывает, что значение log ₂199 составляет около 7,6.
Таблица 3.8 иллюстрирует 9 интервалов, и ширину интервала можно вычислить с помощью выражения ( x _max — x _min) / (log ₂ n + 1).Поскольку (170 — 85) / 8,64 = (85) / 8,64 = 9,84, мы округляем ширину интервала до 10 мм рт. Обратите внимание, что в Таблице 3.8 обозначение [85–95) означает все значения от 85 до 95, но не включая 95. Здесь мы используем скобку ([), чтобы указать, что значение должно быть включено в интервал, тогда как скобка ()) означает до значения, но не включая его. Мы начали интервалы со значением 85, хотя мы могли бы также начать первый интервал со значением 80.
Таблица 3.8. Интервалы гистограммы, предложенные Стерджесом для данных систолического артериального давления в таблице 3.7.
1
1 90,09
Класс (бункер) Ширина класса (ширина бункера) Частота Относительная частота Накопленная относительная частота Накопленная частота
1 1 1 1 6 3,02 3,02 6
2 [95–105) 20 10,05 13,07 26
3 3 13.57 26,63 53
4 [115–125) 48 24,12 50,75 101
5 905 1785 905 905 905 905 905 905 905 905 905 67,84 135
6 [135–145) 36 18,09 85,93 171
7 [14541–15538 [14541–15538] .47 188
8 [155–165) 5 2,51 96,98 193
9 [165–17541 3,01 905 905 905 [165–17541 3,0541 905 905 905 199
Итого 199 100,00
Это разумный подход, если нет относительно больших или малых значений. В этом случае исключите эти необычные значения из расчета разницы и соответствующим образом отрегулируйте минимальное и максимальное значения.Расположение интервалов тоже произвольно. Большинство исследователей либо начинают интервал с округленного числа, либо выбирают середину интервала круглым числом. Компьютерные пакеты создают гистограммы, используя процедуры, аналогичные предыдущему подходу, с опциями для удовлетворения запросов пользователей (см. Примечание к программе 3.3, на веб-сайте).
На рис. 3.8 показана гистограмма для данных в таблице 3.8.
Рисунок 3.8. Гистограмма 199 значений систолического артериального давления с использованием 9 интервалов размером 10, начиная с 85.
Пример 3.6
Создайте гистограммы для сравнения распределений систолического артериального давления между людьми в возрасте до 60 лет и лицами старше 60 лет с использованием набора данных DIG200. Мы начинаем с отображения количества наблюдений, минимального и максимального значения для каждой из возрастных групп.
Моложе 60 лет: n = 81, минимум = 90 мм рт. Ст., Максимум = 170 мм рт. Ст.
60 лет и старше: n = 118, минимум = 85 мм рт. максимум = 170 мм рт. ст.
Мы используем правило Стерджеса, чтобы определить количество интервалов, которые следует использовать для построения каждой гистограммы.Предлагаемое количество интервалов:
До 60 лет: (170-90) / (log ₂ 81 + 1) = 10,9 или 11 интервалов
60 лет и старше: (170-85) / (log ₂ 118 + 1) = 10,8 или 11 интервалов
Указывается такое же количество интервалов. Даже если указано разное количество интервалов, лучше оставить количество интервалов одинаковым для лучшего сравнения.
На рисунке 3.9 представлены две гистограммы для этих групп. Первая гистограмма отображает САД у пациентов младше 60 лет, а вторая гистограмма — для группы 60 лет и старше.
Рисунок 3.9. Гистограммы распределения систолического артериального давления по возрастным группам.
Обратите внимание, что в этом случае используются относительные частоты, а не частоты, главным образом потому, что гистограммы должны сравниваться, и две группы имеют неравное количество наблюдений, как только что показано (т. Е. 81 пациент моложе 60 лет и 118 пациентов. которым 60 лет и старше). Относительные частоты позволяют проводить сравнения между двумя или более группами, даже если в группах не одинаковое количество субъектов.Очевидно, что для субъектов в возрасте 60 лет и старше наибольший процент показаний систолического артериального давления приходится на интервалы между 105 и 145 мм рт. Субъекты в возрасте до 60 лет имеют треть своих наблюдений систолического артериального давления в интервале от 115 до 125 мм рт. После сравнения двух гистограмм легко увидеть, что в старшей возрастной группе выше концентрация субъектов со значениями систолического артериального давления выше 135 мм рт.
Гистограммы, построенные на основе одних и тех же данных, могут иметь разную форму. Формы гистограммы зависят от количества используемых интервалов и того, как установлены границы. Эти различия в построении гистограммы могут привести к разным представлениям о данных. Однако гистограммы говорят в основном одно и то же о распределении выборочных данных, хотя их формы различны.
В большинстве гистограмм используются интервалы равного размера. Если желательно использование интервалов неравного размера, мы должны внести некоторые коррективы.Поскольку площадь прямоугольника для категории на гистограмме отражает частоту категории, нам необходимо настроить высоту интервала неравномерного размера, чтобы сохранить размер области одинакового размера. Например, предположим, что мы заинтересованы в определении количества пациентов с САД 155 мм рт.ст. и выше. Мы можем свернуть два последних интервала гистограмм, представленных на рисунке 3.8, в один большой интервал, который вдвое шире, чем предыдущие интервалы. Гистограмма с объединенной категорией представлена на рисунке 3.10. Обратите внимание, что частота для комбинированного интервала равна 11, но высота этого интервала составляет 5,5, что составляет половину комбинированной частоты. Мы разделили высоту на 2, чтобы отразить тот факт, что ширина этого последнего интервала вдвое больше, чем других интервалов.
Рисунок 3.10. Гистограмма систолического артериального давления с неравномерными интервалами, DIG200.
Как создать гистограмму с нормальным распределением в программном обеспечении Tableau
В течение года бывают периоды, когда нам нужно идти в ногу с изменениями в нашей организации с точки зрения продаж или прибыли.Например, для компаний из сферы розничной торговли или электронной коммерции зимние праздники или Черная пятница представляют периоды, в которые регистрируется самый высокий рост продаж. С другой стороны, для ИТ-компаний или сервисных компаний праздники или отпуска часто приводят к снижению сроков привлечения новых клиентов и заключения новых контрактов.
Чтобы получить обзор наших результатов, необходимо оценить наши зарегистрированные данные. Чтобы добиться этого, мы должны учитывать средние продажи или поступления, их распределение и произошедшие отклонения.Таким образом, мы сможем увидеть, принесла ли наша деятельность желаемые результаты или нет.
Гистограмма с нормальным распределением
Программное обеспечение
Tableau предоставляет пользователям различные типы анализа, чтобы они могли более легко визуализировать свои записанные значения. Гистограмма с нормальным распределением — один из наиболее распространенных методов анализа, используемых для наблюдения за происходящими отклонениями. Этот тип анализа представлен наличием кривой, также называемой колоколообразной кривой. Нормальное распределение также известно как распределение Гаусса и представляет собой распределение симметричных вероятностей по сравнению со средним значением.Таким образом, данные, которые находятся ближе всего к верхней точке кривой, имеют более высокую частоту встречаемости, чем данные, расположенные дальше.
Гистограмма с нормальным распределением позволяет пользователям анализировать значения в наборе данных и наблюдать, имеют ли они нормальное распределение. Гистограмма отображает сумму значений, записанных в анализируемом наборе данных. Для нормального распределения наших значений они должны быть сконцентрированы в самой высокой точке кривой. Преимущество, которое предлагает кривая, заключается в том, что она показывает, как были распределены значения в наборе данных и имеет ли распределение нормальное поведение.
Далее мы покажем вам, как создать гистограмму с нормальным распределением, анализируя значения продаж из набора данных.

Шаг 1. Подключение к данным
→ В Tableau Desktop подключитесь к образцам данных Superstore, предоставленным Tableau.
Шаг 2: Создайте визуализацию
→ Создайте вычисляемое поле с именем Счетчик клиентов с формулой:
COUNTD ([Имя клиента])
→ Создайте выражение LOD , чтобы получить общую сумму продаж для клиента , с формулой:
{ФИКСИРОВАННОЕ [Имя клиента]: SUM ([Продажи])}
→ Создайте вычисляемое поле с именем Среднее значение с формулой:
{AVG ([Продажи по клиенту])}
У нас нет измерения, поскольку мы хотим, чтобы среднее значение вычислялось для всего набора данных.
→ Создайте вычисляемое поле для вычисления стандартного отклонения по формуле:
{СТАНДОТКЛОН ([Продажи по клиенту])}
→ Создайте параметр с именем Размер продаж (корзина) . В области типа данных выберите Integer и для Current Value введите значение 500.
→ Создайте новое вычисляемое поле с именем Продажи (корзина) с формулой:
INT ([Продажи по клиенту] / [Размер продаж (корзина)]) * [Размер продаж (корзина)]
→ Создайте вычисляемое поле с именем Нормальная кривая для вычисления нормального распределения по формуле:
(
1 / MAX ([Стандартное отклонение]) * SQRT (2 * PI ())
)
*
EXP
(
— КВАДРАТ (МАКС. ([Продажи (корзина)]) — МАКС. ([Среднее]))
/
(2 * КВАДРАТ (МАКС ( [Стандартное отклонение])))
)
→ Перетащите Продажи (корзина) на Столбец и измените тип визуализации на Бар .Щелкните его правой кнопкой мыши и преобразуйте его в размер .
→ Перетащите Счетчик клиентов на строк .
→ Перетащите Normal Curve на Rows и измените визуализацию на Line .
→ Щелкните правой кнопкой мыши по второй оси и выберите Dual Axis . Не синхронизировать ось.
→ Отрегулируйте всплывающую подсказку.
Автор Adelina Popescu
Загрузить программное обеспечение Tableau
Подгонка кривой Гаусса (нормального распределения) к гистограмме в Таблице
4 ноября, 2013 | Робин Кеннеди
Подгонка кривой Гаусса (нормального распределения) к гистограмме в Таблице
Недавно нас попросили помочь клиенту с помощью Tableau построить наиболее подходящую кривую Гаусса на основе его данных о поставщиках и их оценок.Хотя в Tableau нет встроенного статистического анализа такого рода, как только вы разберетесь с формулой нормального распределения, вам останется лишь настроить несколько вычисляемых полей.
Прежде всего, давайте посмотрим на наши данные в необработанном формате. Мы используем простой пример клиентов и показателей прибыли. На каждого покупателя выделяется 1 строка вместе с их общей прибылью по всем транзакциям. Если ваши данные содержат более 1 строки на клиента (возможно, 1 строку на заказ), вы можете выполнить некоторую предварительную агрегацию, прежде чем переносить данные в Tableau.
1. Гистограмма
Подключитесь к своим данным и проверьте наличие всех строк. Первый шаг — создать гистограмму из данных. Это одна из встроенных функций Tableau, которую очень легко сделать — просто нажмите «Прибыль» в окне данных, затем выберите опцию «Гистограмма» на вкладке «Показать меня» — бум! НО, мы хотим быть немного более гибкими, а также иметь возможность ссылаться на интервалы в последующих вычислениях, поэтому мы собираемся настроить гистограмму вручную.
Вместо того, чтобы использовать функцию автоматического биннинга Tableau, создайте свои собственные бинны вычисляемых полей, написав формулу для округления суммы прибыли до ближайшей тысячи
ИНТ ([Прибыль] / 1000) * 1000
Мы также можем ввести здесь параметр, чтобы пользователь мог легко изменять размер корзины.Если хотите, создайте параметр под названием «Размер корзины для прибыли», а затем измените формулу на…
INT ([Прибыль] / [Размер корзины]) * [Размер корзины]
ПРЕДУПРЕЖДЕНИЕ: Если ваши данные содержат негативы, следующий пункт действительно важен!
Поскольку формула INT округляется в меньшую сторону до нуля, любые отрицательные значения фактически округляются в большую сторону по числовой прямой (по-прежнему округляются в меньшую сторону по абсолютной величине). Это создает ситуацию, когда ваша нулевая ячейка, которая должна представлять от 0 до +1000 или независимо от того, на что установлен параметр размера ячейки, на самом деле представляет от –1000 до +1000.Нам нужно это исправить, и мы можем сделать это, сместив негативы вниз. Измените формулу на…
INT ([Прибыль] / [Размер корзины]) * [Размер корзины] + IF [Прибыль] <0 THEN - [Размер корзины] ELSE 0 END
Хорошо, теперь у нас есть вычисляемое поле для бункера — оно, вероятно, появилось в разделе «Измерения» окна данных, поэтому переместите его в раздел «Измерения», прежде чем добавлять его в столбцы в представлении, а затем добавлять количество записей в строки.
2. Расчет среднего и стандартного отклонения
Формула нормального распределения / Гаусса требует среднего и стандартного отклонения прибыли для всей совокупности наших клиентов.
Мы можем создать формулу для вычисления среднего значения, написав…
AVG ([Прибыль])
Но эта формула, когда она добавлена в представление гистограммы, будет разделена по нашей размерности биннинга, то есть мы получим среднее значение для бункера от 0 до 1000, среднее значение для бункера от 1000 до 2000 и т. Д. Нам нужно среднее значение для всего набор данных, поэтому мы должны использовать расчет таблицы…
ИТОГО (СРЕДНЕЕ ([Прибыль]))
… чтобы получить правильный результат. Аналогичным образом, для стандартного отклонения в формуле будет использоваться расчет таблицы ИТОГО
.
ИТОГО (СТАНДОТКЛОН ([Прибыль]))
3.2)))
Если вы добавите это новое вычисляемое поле в свое представление, вы должны увидеть красивую форму колоколообразной кривой — мы приближаемся, но чтобы подогнать кривую к нашей гистограмме, осталось сделать пару шагов.
Прежде всего, нам нужно масштабировать функцию в соответствии с шириной нашего бина (меньшие бины будут иметь меньшее количество записей), и мы делаем это, умножая всю формулу на 1000 (или параметр размера вашего бина)
Во-вторых, мы хотим преобразовать функцию плотности в функцию частоты, чтобы числа соответствовали нашей гистограмме — это делается путем умножения на общее количество записей.2))) * [Размер корзины прибыли] * ИТОГО (СУММА ([Количество записей]))
Добавьте это к своему виду как двойную ось, синхронизируйте и измените тип метки на линию, и вы должны получить ниже
графиков нормальной вероятности | BPI Consulting
июнь 2009 г.
В этом выпуске:
Введение
Информационный бюллетень прошлого месяца представил нормальное распределение. В информационном бюллетене за этот месяц будет рассказано, как ответить на следующий вопрос:
Распределение моих данных нормальное?
Нормальное распределение — одно из многих распределений.В прошлых информационных бюллетенях мы кратко говорили о двух дискретных распределениях: биномиальном распределении (базовое распределение для контрольных диаграмм n и np) и распределении Пуассона (базовое распределение для контрольных диаграмм c и u). С другой стороны, нормальное распределение используется с непрерывными данными.
Нормальное распределение — очень важное распределение в статистике. И, если ваши данные могут быть представлены нормальным распределением, вы можете многое узнать.Как показано в прошлом месяце, вы можете использовать значения z, чтобы определить, какой процент данных ниже некоторого значения, выше некоторого значения или между двумя значениями. Многие статистические методы основаны на предположении, что данные распределены нормально.
Обзор нормального распределения
Нормальное распределение — это знакомая колоколообразная кривая, показанная ниже.
Нормальное распределение имеет несколько интересных характеристик:
Форма распределения определяется средним значением μ (или X) и стандартным отклонением σ.
Самая высокая точка кривой — среднее значение.
Распределение симметрично относительно среднего.
По мере удаления от среднего значения точки появляются с меньшей частотой.
Большая часть площади под кривой (99,7%) находится между -3σ и + 3σ от среднего значения.
Полный обзор нормального распределения см. В информационном бюллетене за последний месяц.
Итак, как узнать, нормально ли распределены ваши данные? Есть два простых способа, которые зависят от того, сколько у вас данных.Если у вас много данных (100 точек и более), вы можете использовать гистограмму. Если у вас меньше данных, вы можете использовать график нормальной вероятности.
Гистограммы
Есть несколько способов определить, есть ли у вас нормальное распределение. Один из самых простых — построить гистограмму на основе данных. Просто изучите гистограмму и посмотрите, не кажется ли вам, что она имеет форму колокола. Если у вас много данных, это отличный способ определить, нормально ли распределены ваши данные.См. Наши информационные бюллетени за декабрь 2005 г. и январь 2006 г. для получения дополнительной информации о создании и использовании гистограмм.
Обратите внимание, что гистограмма реальных данных не будет выглядеть как идеальное нормальное распределение. Все, что вы пытаетесь определить, — это разумно ли описывать данные как нормальное распределение. Например, взгляните на гистограмму ниже. Это похоже на колоколообразную кривую? Выглядит нормально? Это не идеально, но кажется разумным предположить, что эти данные получены из нормального распределения.
Теперь рассмотрим гистограмму ниже. Это похоже на колоколообразную кривую? Это не похоже на колокольчик. Большинство значений стремятся к нулю. Имея эти данные, неразумно предполагать наличие нормального распределения.
Итак, вполне допустимо использовать гистограмму, чтобы определить, насколько вы считаете, что ваши данные могут быть разумно представлены нормальным распределением. Если у вас мало данных, гистограммы не будут очень полезны для определения того, есть ли у вас нормальное распределение.Вы можете случайным образом взять 20 выборок из нормального распределения, и результирующая гистограмма может не выглядеть нормально. В этих случаях необходимо использовать график нормальной вероятности.
Графики нормальной вероятности
График нормальной вероятности может использоваться для определения того, происходят ли небольшие наборы данных из нормального распределения. Это предполагает использование вероятностных свойств нормального распределения. В конечном итоге мы сделаем сюжет, который, как мы надеемся, будет линейным. Продемонстрируем процедуру, используя данные ниже.
Предположим, у нас есть десять образцов из нашего процесса.
100, 98, 101, 93, 123, 112, 85, 76, 119, 111
Мы хотим знать, можем ли мы разумно предположить, что эти данные получены из нормального распределения. Мы можем построить нормальный вероятностный график, который поможет нам в этом.
Следующие шаги используются для построения нормального графика вероятности этих данных.
1. Отсортируйте данные в порядке возрастания.
Данные
Сортировано Данные

100 76
98 85
101 93
93 98
123 100
112 101
85 111
76 112
119 119
111 123
2.Пронумеруйте отсортированные данные от 1 до n, где n — количество выборок (в данном примере 10).
Данные
Сортировано Данные

Номер
100 76 1
98 85 2
101 93 3
93 98 4
123 100 5
112 101 6
85 111 7
76 112 8
119 119 9
111 123 10
3.Рассчитайте (i-0,5) / n для каждого значения; это представляет собой совокупную вероятность.
Данные
Сортировано Данные

Номер
Кумулятивная Вероятность
100 76 1 0,05
98 85 2 0.15
101 93 3 0,25
93 98 4 0,35
123 100 5 0,45
112 101 6 0,55
85 111 7 0,65
76 112 8 0.75
119 119 9 0,85
111 123 10 0,95

4. Определите значение z из стандартного нормального распределения для каждой кумулятивной вероятности.
Есть несколько способов сделать это. Первое кумулятивное значение вероятности — 0,05. Вы можете использовать стандартную таблицу нормального распределения в информационном бюллетене за последний месяц, чтобы найти значение z, соответствующее 0.05 вероятность. Если вы посмотрите на таблицу, вы увидите, что z = -1,64 дает кумулятивную вероятность 0,0505, а z = -1,65 дает кумулятивную вероятность 0,0495. Таким образом, значение z, которое дает кумулятивную вероятность 0,05, находится в диапазоне от -1,65 до -1,64.
Самый простой способ сделать это — использовать функцию НОРМСТОБР в Excel. Например, НОРМСТОБР (0,05) = -1,64485. Остальные значения приведены в таблице ниже.
Данные
Сортировано Данные

Номер
Кумулятивная Вероятность
z Значение
100 76 1 0.05 -1,64485
98 85 2 0,15 -1,03643
101 93 3 0,25 -0,67449
93 98 4 0,35 -0,38532
123 100 5 0,45 -0,12566
112 101 6 0.55 0,125661
85 111 7 0,65 0,385321
76 112 8 0,75 0,67449
119 119 9 0,85 1.036433
111 123 10 0,95 1.644853
5.Постройте отсортированные данные в зависимости от значений z. Сюжет показан ниже.
Вопрос, который вы хотите задать себе: «Падают ли точки примерно по прямой линии?» Если это так, вы можете предположить, что у вас нормальное распределение. На графике выше видно, что точки падают по прямой линии. В Excel вы можете добавить наиболее подходящую линию, щелкнув правой кнопкой мыши точку на графике и выбрав «Добавить линию тренда». Полученный график показан ниже.
Поскольку данные располагаются по прямой линии, можно предположить, что у вас нормальное распределение.
Если данные не попадают в прямую линию, вы не можете предполагать, что у вас нормальное распределение. График нормальной вероятности для ненормальной гистограммы показан ниже. Обратите внимание на то, что на одном конце она заканчивается буквой S. Это часто типично для нестандартных дистрибутивов.
Сводка
Есть два простых метода определения того, нормально ли распределяются ваши данные.Если у вас много данных (100 точек и более), вы можете использовать гистограмму. Если гистограмма имеет несколько колоколообразную форму, можно предположить, что у вас нормальное распределение. Если у вас мало данных, постройте нормальный график вероятностей и посмотрите, попадают ли точки примерно по прямой линии. Если это так, вы можете предположить, что ваши данные распространяются нормально.
.

Значение	Част.	Значение	Част.	Значение	Част.	Значение	Част.	Значение	Част.	Значение	Част.
85	1	105	1	116	8	128	3	138	3	138
90	5	106	2	118	5	130	23	139	2	152		2	152		2	108	2	120	25	131	1	140	26	155	1
155	1
110	16	122	4	132	2	142	1	160	3
100	14	112	1	124	4	134	1	1	144
102	1	114	5	125	3	135	2	145	1	165	1	104	2	126	1	136	1	148	1	170	5

Класс (бункер)	Ширина класса (ширина бункера)	Частота	Относительная частота	Накопленная относительная частота	Накопленная частота
1	1	1	1	6	3,02	3,02	6
2	[95–105)	20	10,05	13,07	26
3	3		13.57	26,63	53
4	[115–125)	48	24,12	50,75	101
5	905 1785 905 905 905 905 905 905 905 905 905	67,84	135
6	[135–145)	36	18,09	85,93	171
7	[14541–15538	[14541–15538] .47	188
8	[155–165)	5	2,51	96,98	193
9	[165–17541 3,01 905 905 905	[165–17541 3,0541 905 905 905	199
	Итого	199	100,00

Моложе 60 лет:	n = 81, минимум = 90 мм рт. Ст., Максимум = 170 мм рт. Ст.
60 лет и старше:	n = 118, минимум = 85 мм рт. максимум = 170 мм рт. ст.

Данные	Сортировано Данные
100	76
98	85
101	93
93	98
123	100
112	101
85	111
76	112
119	119
111	123

Данные	Сортировано Данные	Номер
100	76	1
98	85	2
101	93	3
93	98	4
123	100	5
112	101	6
85	111	7
76	112	8
119	119	9
111	123	10

Типы распределений и соответствующие им гистограммы | Бережливые шесть сигм | Статьи | База знаний

Нормальное распределение: понимание гистограмм и вероятностей

Понимание гистограмм

Гистограммы с интервалами

Гистограммы и вероятность

Функция массы вероятности

Масса вероятности против плотности вероятности

Заключение

Теги

Гистограмма нормального распределения — Справочник химика 21

Гистограмма частот в Excel 2016

Создание и использование гистограмм—ArcGIS Insights

Пример

Создание гистограммы

Подсказка:

Примечания по использованию

Гистограммы—Справка | ArcGIS for Desktop

Частотное распределение

Суммарная статистика

Показатели расположения

Показатели разброса

Показатели формы

Примеры

Математика и статистика, часть 2: практика в R

Выборки из распределений

Бинарное распределение

Нормальное распределение

Задание 3 из семинара 10

Гистограммы в R

Дополнительно: кривая нормального распределения

Иллюстративно

Центральная предельная теорема

Закон больших чисел

Нормальное приближение для гистограмм вероятностей

Гистограммы вероятностей

Цели обучения

Основные выводы

Ключевые моменты

Ключевые термины

Гистограммы

Гистограммы вероятностей

Гистограммы вероятностей и нормальная кривая

Цели обучения

Основные выводы

Ключевые моменты

Ключевые термины

Точно нормальные распределения

Приблизительно нормальные распределения

Предполагаемая нормальность

Как оценить нормальность

Заключение

Цели обучения

Основные выводы

Ключевые моменты

Ключевые термины

Что такое гистограмма вероятности?

Как мы можем определить, являются ли данные приблизительно нормальными?

Примерно нормальные распределения в реальной жизни

Нормальное распределение: понимание гистограмм и вероятностей

Знакомство с гистограммами

Гистограммы с ячейками

Гистограммы и вероятность

Вероятностная массовая функция

Вероятность массы в зависимости от плотности вероятности

Заключение

Что такое гистограммы? Анализ и распределение частот

Когда использовать гистограмму

Как создать гистограмму

Анализ гистограммы

Инструменты и шаблоны гистограмм

Нормальное распределение

Асимметричное распределение

Двухконечная или бимодальная

Плато или мультимодальное распределение

Распределение пограничных пиков

Расческа

Усеченное или частичное распределение

Раздача кормов для собак

гистограмм — обзор | Темы ScienceDirect

3.2.4 Гистограммы