Глава 2. Элементарные функции MathCad.
Тригонометрические
sin(z) — синус,
cos(z) — косинус,
tan(z) — тангенс,
cot(z) — котангенс,
sec(z) — секанс
csc(z) — косеканс.
Обратные тригонометрические
asin(z) — арксинус,
acos(z) — арккосинус,
atan(z) — арктангенс
Гиперболические
sinh(z) — гиперболический синус,
cosh(z) — гиперболический косинус,
tanh(z) — гиперболический тангенс,
coth(z) — гиперболический котангенс,
sech(z) — гиперболический секанс
csch(z) — гиперболический косеканс.
Обратные гиперболические
asinh(z) — арксинус гиперболический,
acosh(z) — арккосинус гиперболический,
atanh(z) — арктангенс гиперболический
Показательные и логарифмические
exp(z) — экспонента,
ln(z) — натуральный логарифм,
log(z) —
десятичный логарифм.
Комплексного аргумента
Re(z) — вещественная часть,
Im(z) — мнимая часть,
|z| — модуль,
arg(z) — фаза (для формата экспоненты),
— сопряженный комплекс
Встроенные функции можно ввести в документ с помощью команды Insert / Function…или кнопкой f(x) Из одноименного окна диалога выбрать нужную категорию, а в ней соответствующую функцию.
Программа Visio
предназначена для создания различного
вида чертежей: от схем сетей до календарей,
от планов офиса до блок-схем. Microsoft Visio
— это универсальная графическая программа,
предоставляющая средства для визуализации
большинства технических и деловых задач
при помощи одного простого в использовании
продукта. Программы Microsoft Office Visio 2003 и
Microsoft Office Visio 2007 дают возможность всем
пользователям в таких отраслях, как
коммерция, проектирование и информационные
технологии, создавать и распространять
схемы процессов, систем и графики
числовых данных.
В Microsoft Office Visio 2007 представлены тысячи фигур и более шестидесяти шаблонов схем, одни из которых простые, а другие — довольно сложные. Каждый шаблон предназначен для конкретных целей — от создания планов водопроводных сетей до компьютерных сетей. Шаблоны разбиты по темам – например, план офиса, машиностроение, блок-схемы, расписание, бизнес, техника и прочее.
Кроме всего прочего Вы можете создавать свои Шаблоны со своими наборами фигур.
Файловые форматы
VSD — диаграмма
VSS — Фигура
VST — шаблон
VDX — диаграмма в формате XML
VSX
VTX
VSL — надстройка
Немного истории
Первоначально Visio
разрабатывался и выпускался компанией
Visio Corporation. Microsoft приобрела компанию в
2000 году, когда продукт назывался Visio
2000.
Был выполнен ребрендинг и продукт
был включен в состав Microsoft Office.
Visio 1.0 (Standard, Lite, Home)
Visio 2.0
Visio 3.0
Visio 4.0 (Standard, Technical)
Visio 4.1 (Standard, Technical)
Visio 4.5 (Standard, Professional, Technical)
Visio 5.0 (Standard, Professional, Technical)
Visio 2000 (6.0; Standard, Professional, Technical, Enterprise)
Visio 2002 (10.0; Standard, Professional)
Visio Enterprise Network Tools, Visio Network Center
Visio for Enterprise Architects 2003 (VEA 2003) (based on Visio 2002 and included with Visual Studio .NET 2003 Enterprise Architect)
Office Visio 2003 (11.0; Standard, Professional)
Office Visio for Enterprise Architects 2005 (VEA 2005) (based on Visio 2003 and included with Visual Studio 2005 Team Suite and Team Architect editions)
Office Visio 2007 (12.
0;
Standard, Professional).
Office Visio 2010 (14.0; планируемая версия, в настоящее время в статусе Release Candidate (RC))
Замечание: Не существует версий 7, 8, и 9, после покупки Visio компанией Microsoft, входила в состав Office, соответственно версия Visio соответствует версии Office.
Microsoft Office Visio относится к семейству продуктов Microsoft Office, но не входит ни в один стандартный комплект, поэтому приобретается отдельно. Программа выпускается в двух редакциях: Standard и Professional.
Ниже Вы найдете две таблицы со сравнением версий Visio Standard и Professional. Первая таблица посвящена сравнению функционала в области проектирования, во второй таблице приведено сравнение общезначимых функций программы.
|
|
|
переменные и
функции Числовые функции — это соответствие между элементами двух множеств, при котором каждому элементу одного множества (переменной, или аргументу) ставится в соответствие не более одного элемента другого множества (значение функции) |
|
периодические
функции Периодическая функция — для которой выполнено условие f(x)=f(x+Т)=f(x-Т). 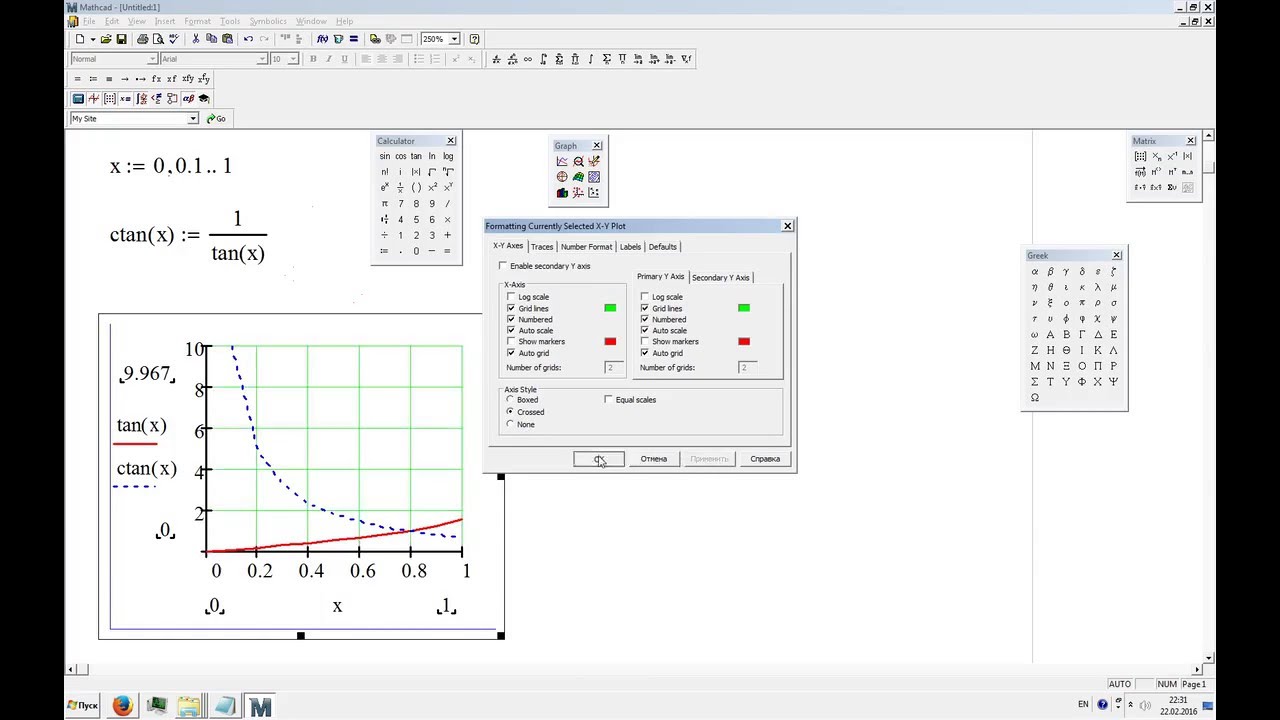 Число Т
называют периодом функции. |
|
радианы и
градусы Измерение угла: если окружность покрыть равномерной сеткой от 0 до 2π (или от 0 до 360°), то любой угол можно измерить в радианах (долях 2π) или градусах. Радианная мера угла α = (π/180)⋅(α в °). Очевидно: α = α ± 2π = α ± 360° |
|
сумма углов
треугольника и
многоугольника Сумма углов любого треугольника α1+α2+α3 равна π = 180°, сумма углов многоугольника (N-угольника) равна π⋅(N-2) = 180°⋅(N-2).  |
|
прямоугольный
треугольник Это треугольник, один из углов которого равен 90° = π/2. Стороны x, y при прямом угле называются катетами, а третья сторона — это гипотенуза |
|
теорема
Пифагора Прямоугольный треугольник задает простое соотношение между его сторонами: сумма квадратов длин катетов x, y равна квадрату длины гипотенузы: x² + y² = z² |
|
sin и cos, tg
и ctg Для острого угла α прямоугольного треугольника можно определить синус, как отношение противолежащего к углу катета y к гипотенузе z: sin(α) = y/z, косинус — как отношение прилежащего катета x к гипотенузе: cos(α) = x/z, тангенс и котангенс — как отношение катетов: tg(α) = y/x = sin(α)/cos(α) ctg(α) = x/y = 1/tg(α) |
|
теорема
синусов Для любого треугольника со сторонами х1, х2 и х3 и противолежащими им углами α1, α2 и α3 справедливо: x1/sin(α1) = x2/sin(α2) = x3/sin(α3) = 2R, где R — это радиус окружности, описанной вокруг треугольника |
|
теорема
косинусов Для любого треугольника со сторонами a,b,c и углом α между сторонами b,c справедливо: a² = b² + c² — 2⋅b⋅c⋅cos(α).  |
|
единичная
окружность Это окружность радиусом R=1. По точкам (x,y) на ней удобно отсчитывать углы и определять тригонометрические функции (в том числе, для α < 0 и α > π/2). В частности, синус sin(α) = y, косинус cos(α) = x, тангенс tg(α) = y/x, котангенс ctg(α) = x/y, секанс sec(α) = 1/cos(α) = 1/x, косеканс csc(α) = 1/sin(α) = 1/y. |
|
тригонометрические
функции: свойства Некоторые свойства тригонометрических функций: все они периодические sin(x)=sin(x+2π), четные cos(-x)=cos(x) или нечетные sin(-x)=-sin(x), tg(-x)=-tg(x) |
|
тригонометрические
тождества и формулы Основное тригонометрическое тождество: sin²(x)+cos²(x)=1, формулы приведения sin(k⋅π/2-x)=cos(x), tg(π/2+x)=-ctg(x) и т. 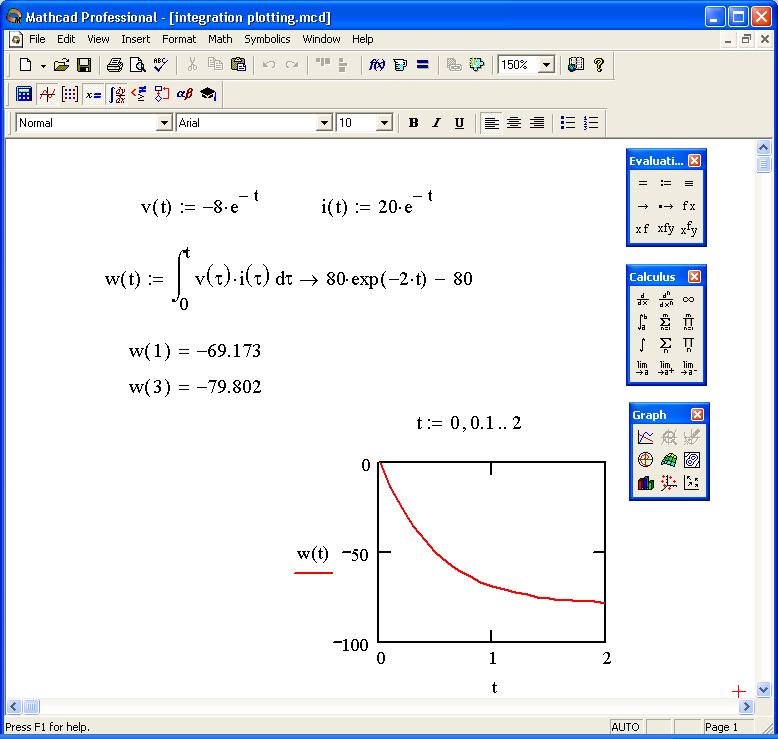 п.,
формулы сложения, двойного
угла, половинного угла,
преобразование суммы
тригонометрических функций в
произведение и т.д. |
|
arcsin,
arccos, arctg Обратные тригонометрические функции (круговые функции, аркфункции) — математические функции, являющиеся обратными к тригонометрическим функциям. Арксинус — это угол, синус которого равен х, т.е. если sin(α) = х, то арксинус arcsin(х) = α. Аналогично, арккосинус arccos(х) = α, если cos(α) = x и арктангенс arctg(х) = α, если tg(α) = x. 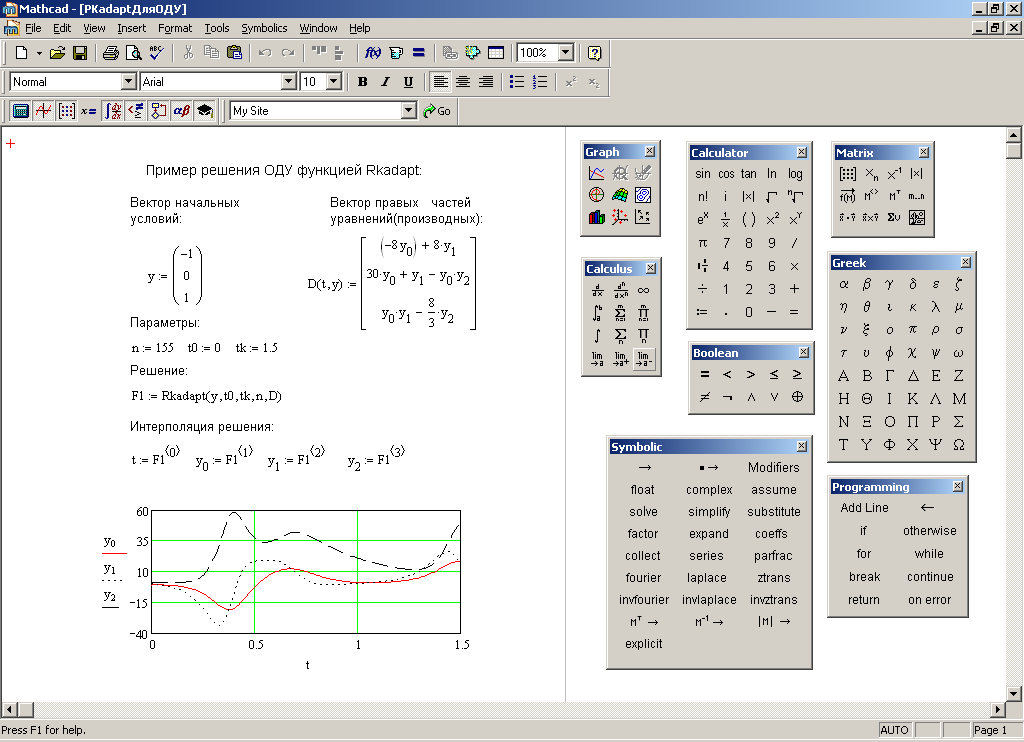 Причем arcsin определяет
-π/2 ≤ α ≤ π/2, а arccos для
0 ≤ α ≤ π. Очевидно:
arcsin(-х) = -arcsin(х),
arccos(-х) = π — arccos(х). |
|
гармонические
колебания Гармонический закон колебаний — это y(t) = A⋅cos(ω⋅t+φ) или y(t) = A⋅sin(ω⋅t+φ) = A⋅cos(ω⋅t+φ-π/2). Параметры A, ω, φ — это амплитуда, круговая частота и начальная фаза колебаний. Период колебаний равен Т = 2π/ω. |
|
Анна Малкова:
тригонометрия Курс по тригонометрии от А.  |