Системы счисления
Перед математиками и
конструкторами в 50-х годах XX столетия встала
задача найти такие системы счисления, которые бы
отвечали требованиям разработчиков ЭВМ и
программного обеспечения. В результате были
созданы “машинные” системы счисления:
— двоичная;
— восьмеричная;
— шестнадцатеричная.
Каждая из этих систем использует определенный
набор символов языка, которыми записываются
данные — символы алфавита.
В двоичной системе счисления их всего два: 0 и
1.
В восьмеричной системе их восемь:
0,1,2,3,4,5,6,7.
В шестнадцатеричной — шестнадцать: арабские
цифры 0-9, и символы латинского алфавита от А до
F. Причем символ А соответствует 10, В =11 и т.д
, F=15.
Каждая система счисления из
машинной группы применяется в различных случаях,
а именно, двоичная – для организации
преобразования информации, восьмеричная и
шестнадцатеричная – для представления машинных
кодов в удобном виде.
Десятичная система применяется для ввода данных
и вывода на устройства печати и на экран
дисплея.
Двоичная система счисления
Обработка информации в ПК основа
на обмене электрическими сигналами между
различными устройствами компьютера. Эти сигналы
возникают в определенной последовательности. ПК
“различает” два уровня этих сигналов – высокий
(1) и низкий (0). Таким образом, любая
информация в вычислительной технике
представляется как набор (код) двух символов 0 и
1. Каждый такой набор нулей и единиц называется
двоичным кодом.
Двоичная система счисления обладает такими же свойствами, что и десятичная, только для представления чисел используется не 10 цифр, а всего 2. Эта система счисления тоже является позиционной.
Официальное рождение двоичной
арифметики связано с именем Г.В. Лейбница,
опубликовавшего в 1703 г. статью, в которой он
рассмотрел правила выполнения арифметических
действий над двоичными числами.
Из истории известен курьезный случай с
восьмеричной системой счисления. Шведский король
Карл XII в 1717 году увлекался восьмеричной
системой счисления, считал ее более удобной, чем
десятичная, и намеревался королевским приказом
ввести ее как общепринятую.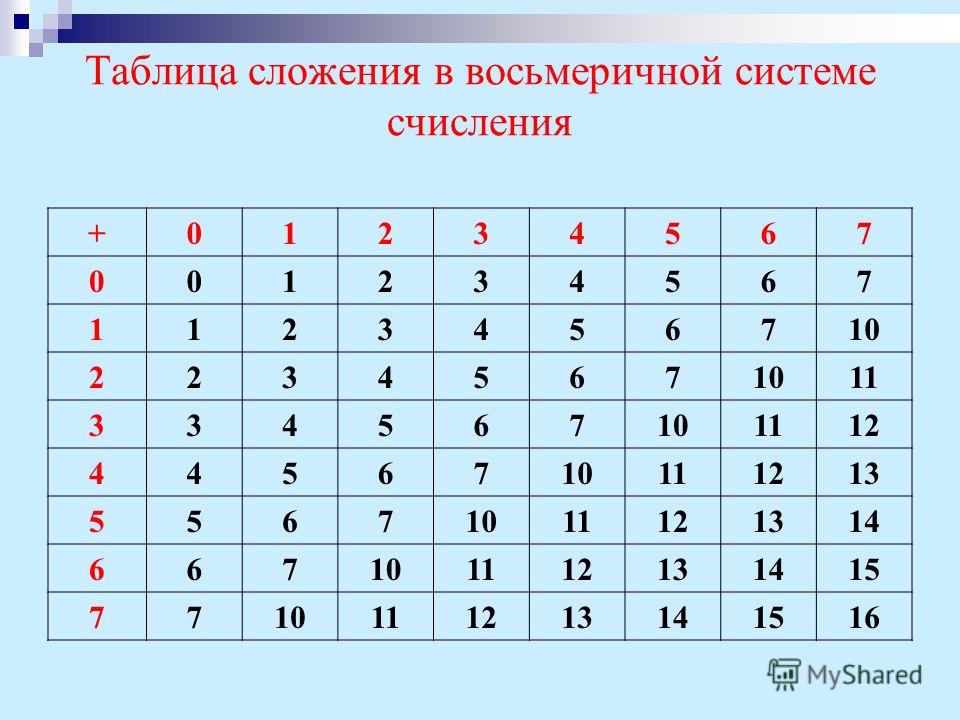
Восьмеричная и шестнадцатиричная системы счисления
Двоичные числа – длинные последовательности 0 и 1 – очень неудобны для восприятия. В связи с этим двоичные числа стали разбивать на группы по три (триада) или четыре (тетрада) разряда. Из трех нулей и единиц можно составить восемь различных двоичных чисел, а из четырех – шестнадцать. Для кодирования 3 бит требуется 8 цифр, и поэтому взяли цифры от 0 до 7, т.е. в соответствии с определением получили алфавит 8-ной системы счисления.
|
Восьмеричный алфавит |
Двоичное число (триада) |
|
0 |
000 |
|
1 |
001 |
|
2 |
010 |
|
3 |
011 |
|
4 |
100 |
|
5 |
101 |
|
6 |
110 |
|
7 |
111 |
Для кодирования 4 бит необходимо
16 знаков, для чего используются 10 цифр
десятичной системы и 6 первых букв латинского
алфавита.
|
Шестнадцатеричный алфавит |
Двоичное число (тетрада) |
|
0 |
0000 |
|
1 |
0001 |
|
2 |
0010 |
|
3 |
0011 |
|
4 |
0100 |
|
5 |
0101 |
|
6 |
0110 |
|
7 |
0111 |
|
8 |
1000 |
|
9 |
1001 |
|
A |
1010 |
|
B |
1011 |
|
C |
1100 |
|
D |
1101 |
|
E |
1110 |
|
F |
1111 |
Представление чисел в различных системах счисления
|
10-ная |
2-ная |
8-ная |
16-ная |
|
0 |
00 |
0 |
0 |
|
1 |
01 |
1 |
1 |
|
2 |
10 |
2 |
2 |
|
3 |
11 |
3 |
3 |
|
4 |
100 |
4 |
4 |
|
5 |
101 |
5 |
5 |
|
6 |
110 |
6 |
6 |
|
7 |
111 |
7 |
7 |
|
8 |
1000 |
10 |
8 |
|
9 |
1001 |
11 |
9 |
|
10 |
1010 |
12 |
A |
|
11 |
1011 |
13 |
B |
|
12 |
1100 |
14 |
C |
|
13 |
1101 |
15 |
D |
|
14 |
1110 |
16 |
E |
|
15 |
1111 |
17 |
F |
|
16 |
10000 |
20 |
10 |
ПЕРЕВОД ЧИСЕЛ ИЗ N-РИЧНОЙ СИСТЕМЫ В ДЕСЯТИЧНУЮ
Перевод чисел из одной системы счисления в
другую выполняет компьютер.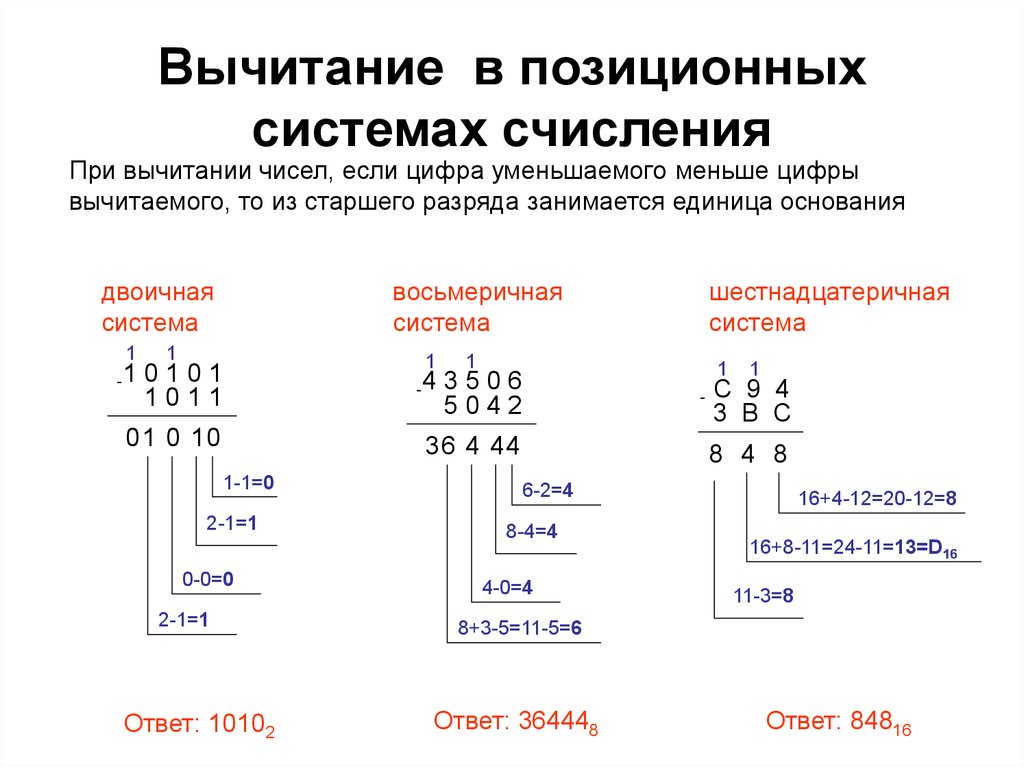
Эти операции
выполняются по определенным правилам.
Перевод числа из двоичной системы
счисления в десятеричную:
1) пронумеровать двоичный код начиная с младшего
разряда (его номер равен 0) к старшему;
2) записать двоичное число как сумму
произведений веса каждого разряда на основание
системы счисления исходного числа (2) в степени,
соответствующей номеру разряда;
3) выполнить вычисление произведений и суммы.
Например,
1010112 = 1*25+0*24+1*23+0*22+1*21+1*20
= 32+0+8+0+2+1=4310
Перевод числа из любой n-ричной системы счисления в десятеричную выполняется с описанным выше правилом (следует учесть, что для каждой системы счисления основание системы свое).
Задание:
Выполните перевод следующих чисел в десятичную:
123708 — ?10
ПЕРЕВОД ЧИСЕЛ ИЗ ДЕСЯТИЧНОЙ СИСТЕМЫ В N-РИЧНУЮ
Перевод числа из десятеричной в двоичную систему счисления:
1) выполнить последовательное
деление десятичного числа, а затем получаемых
целых частных на основание системы счисления, в
которую переводится число (2).
Деление
выполняется в записью целого частного и целого
остатка от деления до тех пор, пока целое
частное не будет равно 0.
2) записать код числа, записывая остатки от
деления, начиная с последнего из целых остатков
(в обратном порядке) символами алфавита
требуемой системы счисления.
|
Например,4210 — ?2 4210 = 1010102 |
Перевод числа из десятеричной в n-ричную систему счисления:
1) выполнить последовательное
деление десятичного числа, а затем получаемых
целых частных на основание системы счисления, в
которую переводится число (n).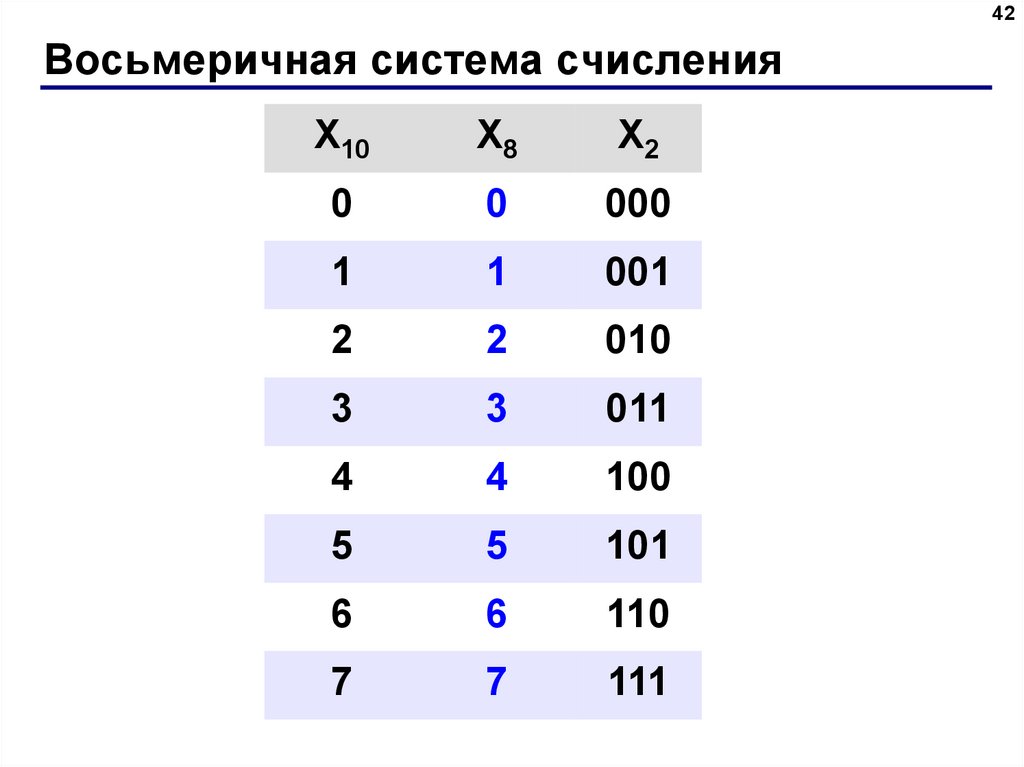
Деление
выполняется в записью целого частного и целого
остатка от деления до тех пор, пока целое
частное не будет равно 0.
2) записать код числа, записывая остатки от
деления, начиная с последнего из целых остатков
(в обратном порядке) символами алфавита
требуемой системы счисления.
Задание:
выполните перевод десятичных чисел 54 и 782
в 8-ричную и 16-ричную системы счисления каждое.
ПЕРЕВОД ЧИСЕЛ ИЗ ДВОИЧНОЙ СИСТЕМЫ В ВОСЬМЕРИЧНУЮ И ШЕСТНАДЦАТЕРИЧНУЮ
Правило перевода чисел из двоичной системы счисления в восьмеричную:
влево и вправо от запятой
двоичное число разбивается на двоичные триады,
при необходимости крайние группы дополняются
нулями; каждая триада заменяется соответствующей
цифрой восьмеричного алфавита (см.
таблицу).
|
100010011,112 = ?8 |
100 |
010 |
011, |
1102 |
=423,68 |
|
|
4 |
2 |
3 |
6 |
Правило перевода чисел из двоичной системы счисления в шестнадцатеричную:
влево и вправо от запятой
двоичное число разбивается на двоичные тетрады,
при необходимости крайние группы дополняются
нулями; каждая тетрада заменяется
соответствующей цифрой шестнадцатеричного
алфавита (см.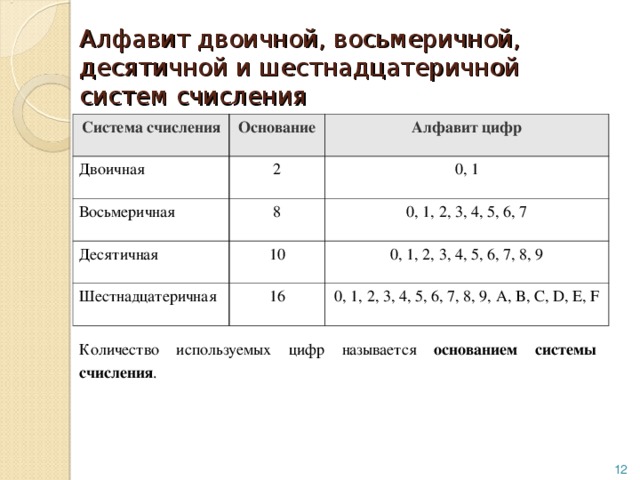
таблицу).
|
11111100011,1010102 = ?16 |
0111 |
1110 |
0011, |
1010 |
1000 |
= 7Е3,А816 |
|
|
7 |
Е |
3 |
А |
8 |
При переводе чисел из
восьмеричной и шестнадцатеричной систем
счисления в двоичную достаточно заменить каждую
цифру соответственно двоичной триадой или
тетрадой.
При этом незначащие нули
отбрасываются.
Примеры: 324,78 — ? 2
3 2 4, 78 = 11010100,1112
Е4А1, В516 — ?2
Е 4 А 1, В 516 =
1110010010100001,101101012
ПЕРЕВОД ЧИСЕЛ ИЗ ВОСЬМЕРИЧНОЙ И ШЕСТНАДЦАТЕРИЧНОЙ СИСТЕМЫ В ДВОИЧНУЮ
При переводе чисел из восьмеричной и шестнадцатеричной систем счисления в двоичную достаточно заменить каждую цифру соответственно двоичной триадой или тетрадой. При этом незначащие нули отбрасываются.
Примеры:
|
324,78 — ? 2 |
3 |
2 |
4, |
78 = |
11010100,1112 |
|
|
|
011 |
010 |
100 |
111 |
|
Е4А1, В516 — ?2 |
Е |
4 |
А |
1, |
В |
516 = |
1110010010100001,101101012 |
|
|
1110 |
0100 |
1010 |
0001 |
1011 |
0101 |
АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ В ДВОИЧНОЙ СИСТЕМЕ
С цифрами двоичного числа можно
выполнять арифметические операции.
При этом
выполняются правила двоичной арифметики:
|
0+0=0 |
0*0=0 |
|
1+0=1 |
1*0=0 |
|
0+1=1 |
0*1=0 |
|
1+1= 0 (+ перенос единицы
|
1*1= 1 |
Все арифметические операции над
двоичными числами можно свести к 2-м операциям:
сложению и сдвигу кодов.
Это позволяет
технически реализовать четыре арифметических
действия в одном арифметико-логическом
устройстве, используя одни и те же электронные
схемы. Впрочем, и в десятичной арифметике в
конечном итоге выполняются те же действия –
сложение и сдвиг.
Cложение двоичных чисел
Выполним сложение двух двоичных чисел 110012 и 100012
|
+ |
|
1 |
1 |
0 |
0 |
1 |
|
1 |
0 |
0 |
0 |
1 |
||
|
1 |
0 |
1 |
0 |
1 |
0 |
Задание:
Самостоятельно выполните сложение двоичных
чисел:
111002 и 100111112
Вычитание двоичных чисел
Вычитание – обратная операция
сложению так же может быть представлена в виде
сложения, но только с отрицательным числом.
Выполним вычитание двух двоичных чисел 110012
и 100012
|
— |
1 |
1 |
0 |
0 |
1 |
|
1 |
0 |
0 |
0 |
1 |
|
|
1 |
0 |
0 |
0 |
Задание:
выполните вычитание двух чисел 1011102
и 10012
Умножение и деление двоичных чисел
Умножение и деление производится
поразрядно и сводятся к двум операциям: сложению
и сдвигу.
Выполним умножение двоичных чисел 110012 и 10012
|
|
* |
1 |
1 |
0 |
0 |
1 |
|||
|
1 |
0 |
0 |
1 |
||||||
|
1 |
1 |
0 |
0 |
1 |
|||||
|
0 |
0 |
0 |
0 |
0 |
|||||
|
0 |
0 |
0 |
0 |
0 |
|||||
|
1 |
1 |
0 |
0 |
1 |
|||||
|
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
Задание:
самостоятельно перемножьте числа 11102
и 100012
Деление так же можно представить
как выполнение операций сложения и сдвига.
Задание:
выполните самостоятельно деление двоичного числа
1100110 на двоичное число 110
АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ В ВОСЬМЕТИЧНОЙ И ШЕСТНАДЦАТИРИЧНОЙ СИСТЕМЕ
Сложение и вычитание в 8-ной и 16-ной системах счисления
При выполнении действий сложения
и вычитания в 8-ной системе счисления необходимо
помнить:
в записи результатов сложения и вычитания могут
быть использованы только цифры восьмеричного
алфавита;
основание восьмеричной системы счисления равен
8, т.е. переполнение наступает, когда результат
сложения больше или равен 8. В этом случае для
записи результата надо вычесть 8, записать
остаток, а к старшему разряду прибавить единицу
переполнения;
если при вычитании приходится занимать единицу в
старшем разряде, эта единица переносится в
младший разряд в виде 8 единиц.
Примеры.
Сложить восьмеричные числа 7708 и 2368
.
|
|
1 |
1 |
|
|
|
+ |
7 |
7 |
0 |
|
|
2 |
3 |
6 |
||
|
1 |
2 |
2 |
6 |
Примеры на закрепление: выполнить
действия в восьмеричной системе счисления.
7158 + 3738
5248 + 578
Выполнить вычитание восьмеричных чисел 7508 и 2368.
|
|
|
4 |
8 |
|
|
_ |
7 |
5 |
0 |
|
|
2 |
3 |
6 |
||
|
|
5 |
1 |
2 |
Примеры на закрепление: выполнить
действия в восьмеричной системе счисления.
1378 — 72,38
4368 — 2578
При выполнении действий сложения
и вычитания в 16-ной системе счисления
необходимо помнить:
в записи результатов сложения и вычитания могут
быть использованы только цифры
шестнадцатеричного алфавита (0-9, A-F)
Основание шестнадцатеричной системы счисления
равно 16, т.е. переполнение наступает, когда
результат сложения больше или равен 16. В этом
случае для записи результата надо вычесть 16,
записать остаток, а к старшему разряду прибавить
единицу переполнения;
если при вычитании приходится занимать единицу в
старшем разряде, эта единица переносится в
младший разряд в виде 16 единиц.
Примеры.
Сложить шестнадцатеричные числа B0916
и EFA16
|
|
1 |
1 |
|
|
|
+ |
B |
0 |
9 |
|
|
E |
F |
A |
||
|
1 |
A |
0 |
3 |
Примеры на закрепление: выполнить
действия в шестнадцатеричной системе счисления.
A1316 + 1CF16
F0B,816 + 1DA,C116
Выполнить вычитание шестнадцатеричных чисел B0916 и 7FA16.
|
|
10 |
15 |
16 |
|
|
_ |
B |
0 |
9 |
|
|
7 |
F |
A |
||
|
|
3 |
0 |
F |
Примеры на закрепление: выполнить
действия в шестнадцатеричной системе счисления.
A1316 — 1CF16
DFA,B816 — 1AE,9416
Двоичная, восьмеричная и шестнадцатеричная системы счисления
Замечание 1
Данные системы счисления относятся к позиционным.
Двоичная система счисления
Эта система счисления свое название получила в результате того, что содержит в своем основании всего две цифры – $0$ и $1$. Таким образом, число $2$ и его степени $2, 4, 8$ и т.д. играют особую роль. Самая правая цифра числа показывает число единиц, следующая – число двоек, следующая — число четверок и т.д.
В двоичной системе счисления для формирования числа используются всего две цифры: $0$ и $1$. Пределом разряда является $1$, и как только при счете разряд достигает своего максимального значения, он обнуляется, а при этом образуется новый разряд. Ниже в таблице приведены соответствия двоичных и десятичных чисел.
Рисунок 1.
Замечание 2
Используя двоичную систему счисления, можно закодировать любое натуральное число, представляя его как последовательность нулей и единиц.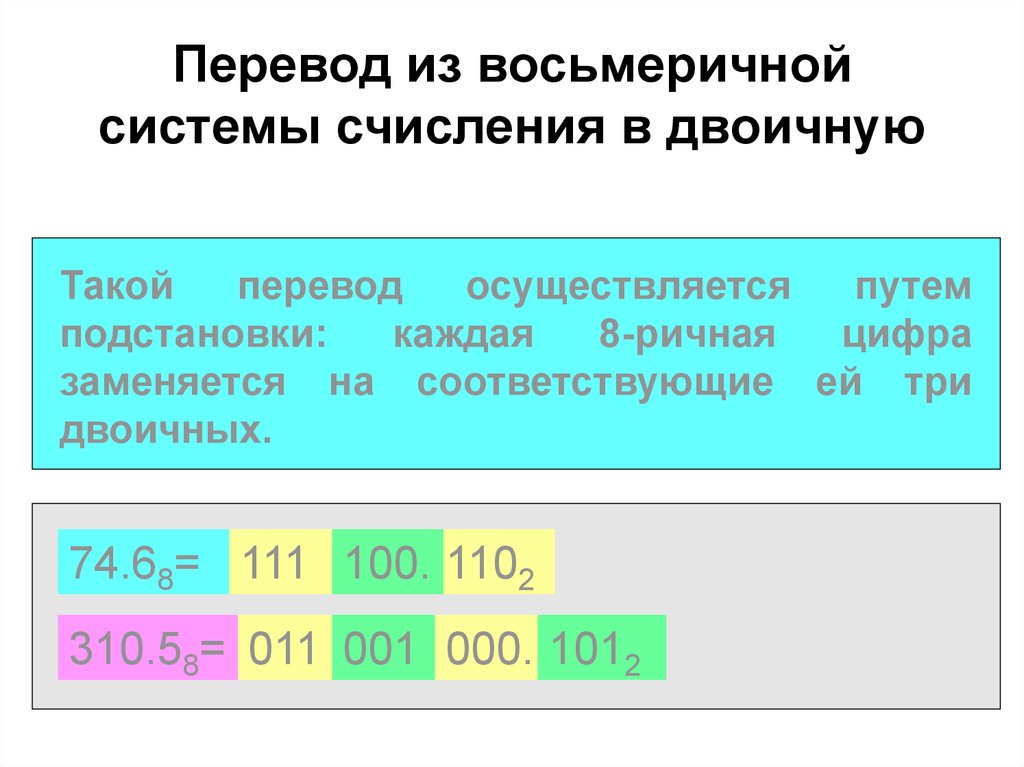
В двоичном виде можно представить не только числа, но и любую другую информацию: тексты, изображения, фильмы и аудиозаписи. Инженеров двоичное кодирование привлекает тем, что оно легко реализуется технически.
Именно на принципе двоичного кодирования работает вся вычислительная техника: $1$ означает, что электрический сигнал прошел, а $0$ – сигнал отсутствует. Наглядно это можно рассмотреть на примере перфокарт, которые использовались в вычислительных машинах первых поколений. Как уже упоминалось выше: в перфокартах пробивались отверстия в соответствующих рядах и столбцах цифр, таким образом, кодировались и сохранялись программы, поскольку жестких дисков, и тем более оптических, в те времена не было. Затем программы считывались при помощи электрического сигнала, который, если проходил в отверстие, значит, это был код $1$ и, наоборот, если не проходил сигнал – это был код $0$. Аналогичным способом в настоящее время записываются оптические диски при помощи лазерного луча, прожигающего невидимые микроотверстия на поверхности специальных дисков.
Принцип считывания закодированной информации с диска аналогичен предыдущему.
Из всего вышесказанного можно сделать вывод, что компьютер «понимает» всего два числа: $0$ и $1$. И именно один двоичный разряд и является минимальной единицей измерения памяти компьютера, которая называется «бит», т.е. бит – это ячейка памяти компьютера, в которую можно записать $1$ или $0$.
Другой единицей измерения информации является байт.
Байт – это восемь подряд расположенных битов. Общее количество комбинаций двоичных значений в байте равно $28 = 256$.
$1 \ байт = 8 \ битам$; $1 \ Кб = 210 \ байта = 1024 \ байта$; $1 \ Мб = 210 \ Кбайт = 1024 \ Кбайта$; $1 \ Гб = 210 \ байта = 1024 \ килобайта$; $1 \ Тб = 210 \ гигабайта = 1024 \ гигабайта$.
Замечание 3
Достоинства двоичной системы счисления заключаются в ее простоте, благодаря которой она широко используется в технике. Устройства, работающие в двух состояниях (включено, выключено), наиболее помехоустойчивы, и, как следствие, более надежны.
Восьмеричная система счисления
В основе данной системы счисления находятся $8$ цифр: от $0$ до $7$. Цифра $1$, указанная в самом младшем разряде, означает, как и в десятичном числе просто $1$. Та же цифра $1$ в следующем разряде означает $8$, в следующем $64$ и т.д. Число $100$ (восьмеричное) – это число $64$ (десятичное). Чтобы перевести в двоичную систему, например, число $611$ (восьмеричное), необходимо каждую цифру числа заменить эквивалентной тройкой двоичных чисел. Для перевода многозначного двоичного числа в восьмеричную систему счисления необходимо разбить его на тройки по правую сторону и по левую и заменить каждую тройку соответствующей восьмеричной цифрой.
В таблице приведены соответствия чисел в восьмеричной и десятичной системах.
Рисунок 2.
В технике данная система находит широкое применение, так с помощью нее можно компактно записывать двоичные числа.
Шестнадцатеричная система счисления
Запись числа в восьмеричной системе счисления достаточно компактная, но еще компактнее она выглядит в шестнадцатеричной системе.
В основу данной системы входят цифры от $0$ до $9$ и первые буквы латинского алфавита: $A$, $B$, $C$, $D$, $E$, $F$.
Цифра $1$, записанная в самом младшем разряде, означает просо единицу. Цифра $1$ в следующем разряде – $16$ (десятичное число), в следующем – $256$ и т.д. Цифра, обозначенная латинской буквой $F$, расположенная в самом младшем разряде означает $15$ ( десятичное число).
В таблице приведены соответствия чисел в шестнадцатеричной и десятичной системах.
Рисунок 3.
Широко используется в низкоуровневом программировании и компьютерной документации, поскольку в современных компьютерах минимальной единицей памяти является $8$-битный байт, значения которого удобно записывать двумя шестнадцатеричными цифрами. Такое использование началось с системы $IBM/360$, где вся документация использовала шестнадцатеричную систему, в то время как в документации других компьютерных систем того времени (даже с $8$-битными символами, как, например, $PDP-11$ или $БЭСМ-6$) использовали восьмеричную систему.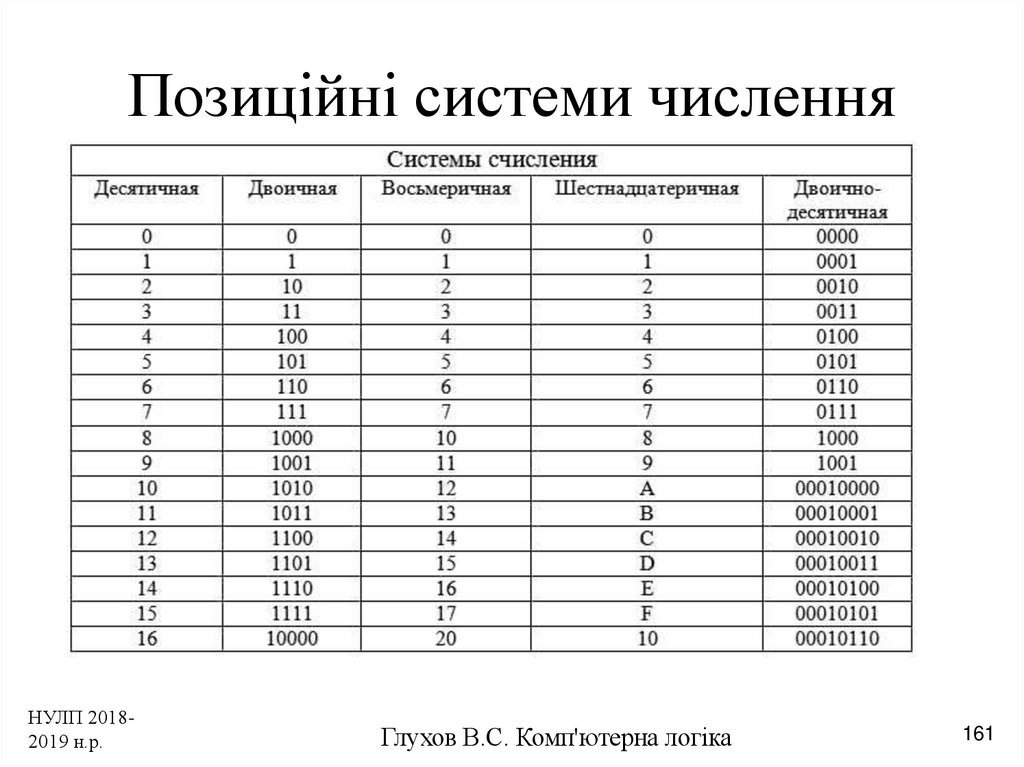
Двоичная, восьмеричная, шестнадцатеричная системы счисления.
Двоичная система счисления — это позиционная система счисления с основанием 2. В этой системе счисления, числа записываются с помощью двух символов (0 и 1).
Восьмери́чная систе́ма счисле́ния — позиционная целочисленная система счисления с основанием 8. Для представления чисел в ней используются цифры от 0 до 7.
Восьмеричная система часто используется в областях, связанных с цифровыми устройствами. Характеризуется лёгким переводом восьмеричных чисел в двоичные и обратно, путём замены восьмеричных чисел на триплеты двоичных. Ранее широко использовалась в программировании и вообще компьютерной документации, однако в настоящее время почти полностью вытеснена шестнадцатеричной.
Шестнадцатеричная
система счисления (шестнадцатеричные числа) — позиционная
система счисления по целочисленному
основанию 16.
Обычно в качестве
шестнадцатеричных цифр используются
десятичные цифры от 0 до 9 и латинские
буквы от A до F для обозначения цифр от
1010 до 1510, то есть (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C,
D, E, F).
Широко используется в низкоуровневом программировании и компьютерной документации, поскольку в современных компьютерах минимальной единицей памяти является 8-битный байт, значения которого удобно записывать двумя шестнадцатеричными цифрами. Такое использование началось с системы IBM/360, где вся документация использовала шестнадцатеричную систему, в то время как в документации других компьютерных систем того времени (даже с 8-битными символами, как, например, PDP-11 или БЭСМ-6) использовали восьмеричную систему.
Правило деления-умножения
Для
преобразования целых чисел используется
правило деления, а для преобразования
правильных дробей — правило умножения.
Для преобразования смешанных чисел
используются оба правила соответственно
для целой и дробной частей числа.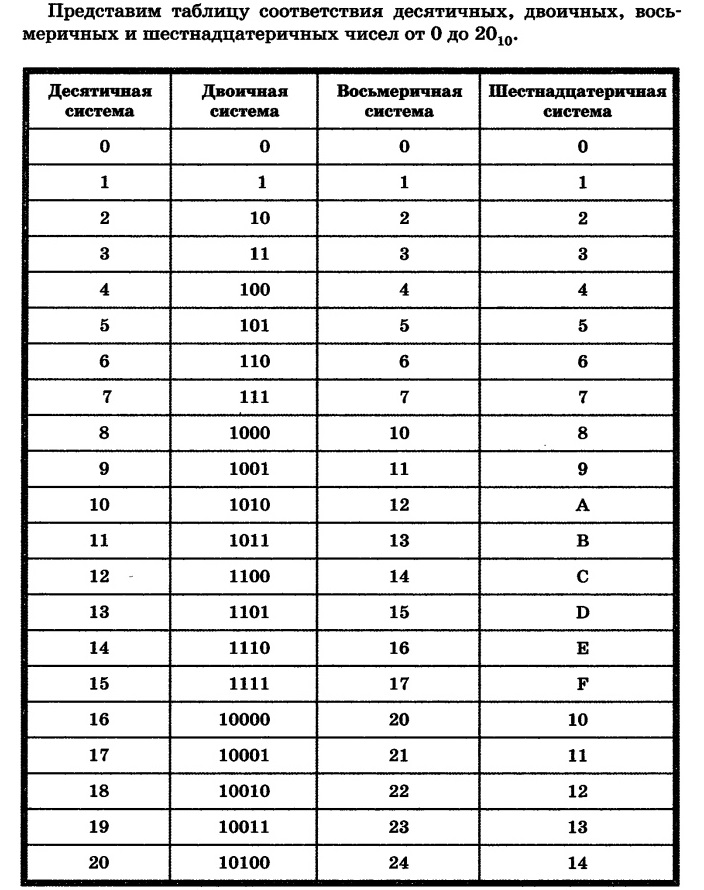
Проверим, не ошиблись ли мы в процессе преобразования? Для этого преобразуем получившееся двоичное
число в десятичную систему по обычной формуле разложения:1248.
1×82+7×81+4×80=6410+5610+410=124
Таблица 1. Таблица соответствия восьмеричных цифр и двоичного кода
Десятичныйэквивалент | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Двоичныйкод | 0 | 001 | 010 | 011 | 100 | 101 | 110 | 111 |
Восьмеричнаяцифра | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Используя
эту таблицу можно просто заменить каждую
восьмеричную цифру тремя двоичными
битами.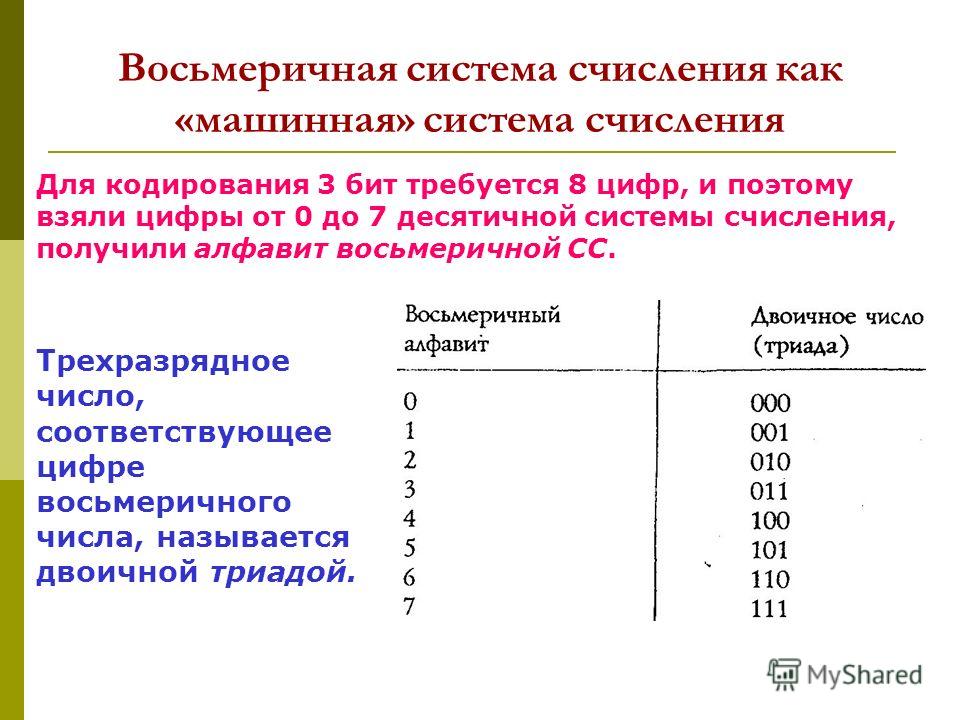
Три двоичных бита обычно называют
триадой или трибитом. Теперь давайте
переведём восьмеричное число 1748 в двоичную форму при помощи таблицы:
Аналогично можно выполнить перевод числа из двоичной системы в восьмеричную. Для этого двоичное число разбивают на триады относительно крайнего правого разряда (или двоичной запятой) и, используя таблицу , каждой триаде ставят в соответствие восьмеричную цифру.
10101001,101112 | 010 | 101 | 001, | 101 | 1102 | =251,568 |
2 | 5 | 1 | 5 | 6 |
Аналогичным
образом можно выполнить перевод числа
из шестнадцатеричной формы в двоичную
и обратно.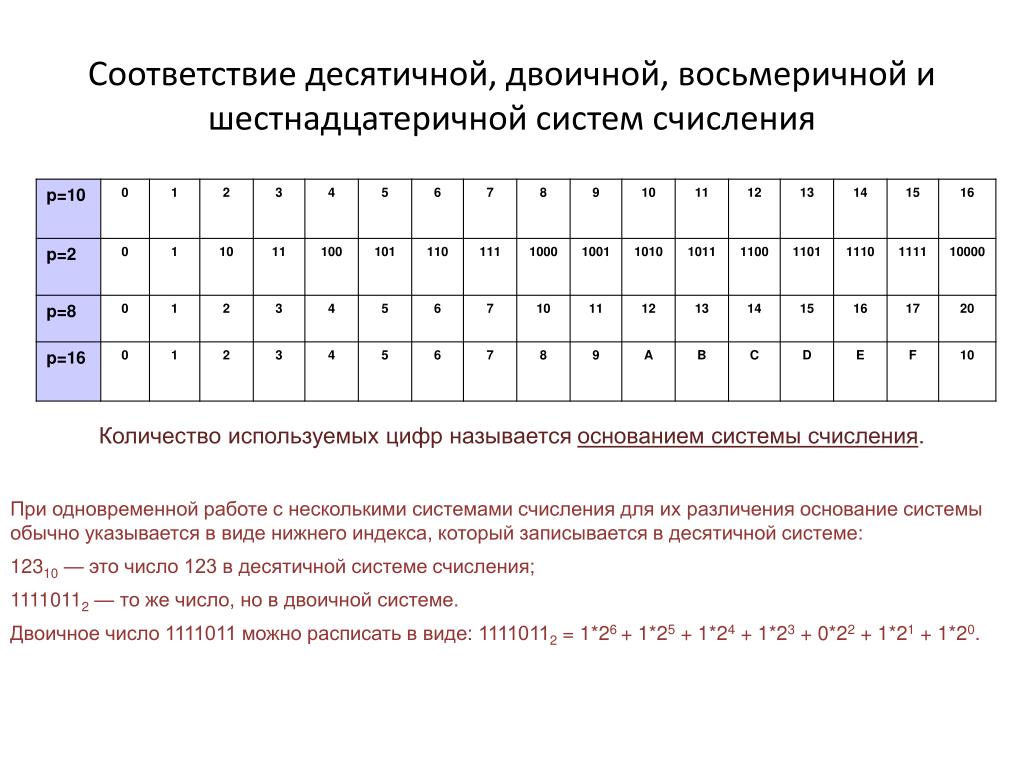
В этом случае для представления
шестнадцатеричной цифры потребуется
четыре двоичных разряда. Четыре двоичных
разряда обычно называют тетрадой
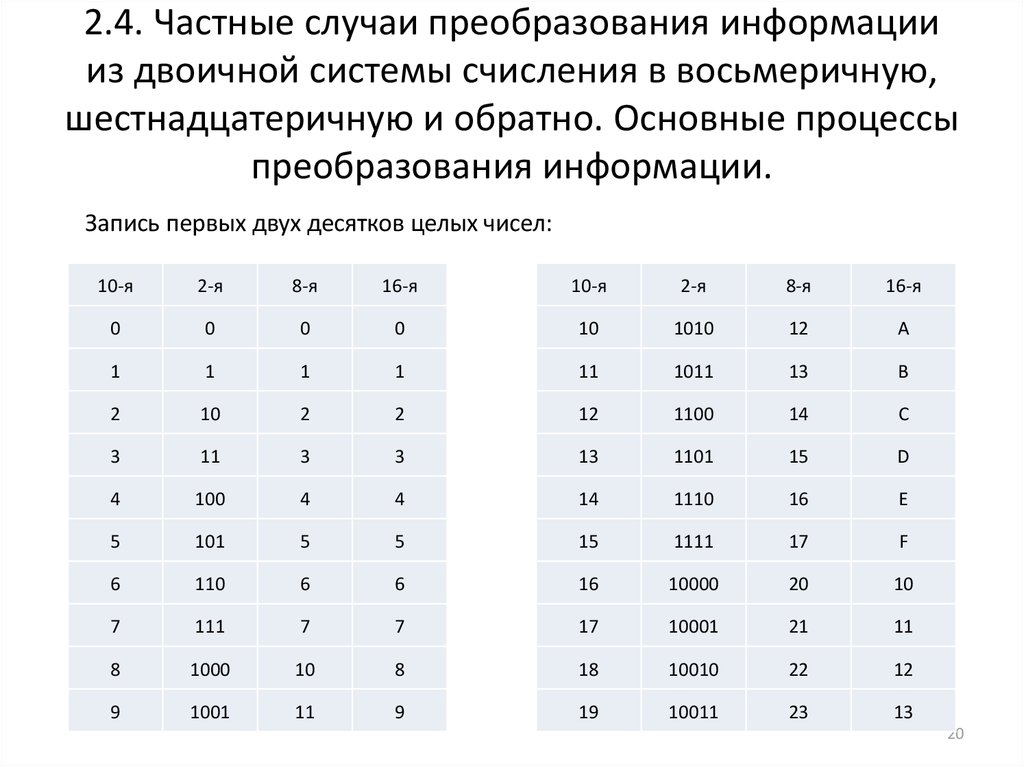
Таблица 2. Таблица соответствия шестнадцатеричных цифр и двоичного кода
Двоичный код | шестнадцатеричная цифра | Десятичный эквивалент |
0000 | 0 | 0 |
0001 | 1 | 1 |
0010 | 2 | 2 |
0011 | 3 | 3 |
0100 | 4 | 4 |
0101 | 5 | 5 |
0110 | 6 | 6 |
0111 | 7 | 7 |
1000 | 8 | 8 |
1001 | 9 | 9 |
1010 | a | 10 |
1011 | b | 11 |
1100 | c | 12 |
1101 | d | 13 |
1110 | e | 14 |
1111 | f | 15 |
10101001,101112 | 1010 | 1001, | 1011 | 10002 | =A9,B816 | |
A | 9 | B | 8 |
Восьмеричная система счисления – TheSassWay.
com Восьмеричная система счисления с основанием 8, в которой используются восемь цифр, от 0 до 7. Восьмеричные числа могут быть получены из двоичных чисел путем группировки двоичных цифр в группы по три (начиная справа) . Например, восьмеричное число 153 равно 1×82 + 5×81 + 3×80 или 1×64 + 5×8 + 3×1.
Octal использовался в ранней информатике, потому что многие ранние компьютерные архитектуры имели только 8-битные слова. В результате восьмеричное представление стало удобным способом представления двоичных данных в этих системах. Восьмеричный до сих пор используется в некоторых приложениях, например, в правах доступа к файлам Unix, где каждая цифра представляет собой другое разрешение.
В Octal любое целое число представлено восемью цифрами (0–7), также известными как основание 8. Поскольку каждый байт содержит восемь бит, в информатике иногда используется восьмеричное значение bytes. восьмеричное используется Linux и UNIX для назначения прав доступа к файлам. Восьмеричный код транспондера до сих пор используется в самолетах по всему миру.
Шестнадцатеричные цифры содержат 16 двоичных цифр, а восьмеричные цифры содержат три (8 = 23). Поскольку они меньше и содержат меньше цифр, десятичные или шестнадцатеричные числа использовать проще, чем буквенно-цифровые. Они способны преобразовать восьмеричное число в двоичное за считанные секунды.
Восьмеричные числа широко используются в компьютерных приложениях и цифровых системах счисления в дополнение к их использованию в компьютерных приложениях. Нет восьмеричных систем с 8 или 9 числами. Шестнадцатеричные числа могут использоваться для представления двоичных значений для людей без необходимости их записи. В десятицентовой системе используются десять (10) цифр от 0 до 9.
В результате некоторые могут задаться вопросом, почему восьмеричная и шестнадцатеричная системы не являются просто вариациями двоичной системы. Тысячи обычно представляют собой нули из-за пропуска цифр. Base-1000 будет 100 различных символов для каждых 0-999, тогда как это будет 1000 различных символов для каждого 0-999.
Большое спасибо.
Каковы различные применения чисел с восьмеричными числами? Широко используются восьмеричные числа, которые используются в компьютерных приложениях и цифровых системах счисления. В вычислительных системах 16-битные, 32-битные или 64-битные слова делятся на 8-битные слова. Восьмеричное число также может использоваться в авиационной промышленности в виде кода.
Восьмеричные и шестнадцатеричные типы данных, оба из которых являются целыми типами, могут использоваться в большинстве компьютерных языков. Они служат удобным обозначением целых значений в двоичной системе счисления. Значения двоичных цифр в памяти компьютера представляют собой все целые значения.
Восьмеричные числа содержат меньше цифр, чем десятичные и шестнадцатеричные числа, что дает им явное преимущество. В результате у него меньше вычислений и ошибок. У него нет ограничений на количество цифр, которые могут быть представлены в двоичном виде; для каждой цифры можно использовать только три бита, что упрощает преобразование из восьмеричной в двоичную и наоборот.
В каких ситуациях в информатике используются восьмеричные числа?
Кредит: Pinterest
Есть несколько ситуаций, в которых восьмеричные числа используются в информатике. Один из них — при работе с разрешениями в Unix-подобных операционных системах. Восьмеричные разрешения используют трехзначный код, где каждая цифра представляет другой уровень разрешения. Например, код «644» даст права на чтение и запись владельцу файла, а всем остальным — только чтение.
Другая ситуация, в которой используются восьмеричные числа, возникает в некоторых языках программирования при работе с escape-символами. Например, в C символ обратной косой черты (\) используется для экранирования других символов. Чтобы представить обратную косую черту в строке, вы должны использовать восьмеричный код «\\» (который эквивалентен шестнадцатеричному коду «0x5C»).
Восьмеричное число — это восьмеричное число, состоящее из восьми основных букв.
Он может быть представлен числом Q или O, и он делится на восьмерки и восьмеричные, когда представлен этими числами. Трехзначный формат двоичных цифр соответствует восьмеричному преобразованию в двоичное и наоборот. Восьмеричная система счисления использует восемь разных цифр для представления разных значений, что является общей системой счисления. Восьмеричные цифры могут быть представлены тремя битами информации, а разрядные значения могут быть выражены с использованием восьми степеней. Процесс преобразования восьмеричных чисел в десятичные эквиваленты аналогичен преобразованию двоичных чисел в десятичные эквиваленты.
Число представляет собой основание 8 и выражается как Q минус 8. Поскольку восьмеричные числа состоят только из 8 цифр, 255 чисел могут быть представлены только с их помощью. Из-за их большего диапазона, чем десятичные числа, двоичные числа часто представляются с использованием осенних чисел.
Понимают ли компьютеры восьмеричные числа?
Кредит: infourok.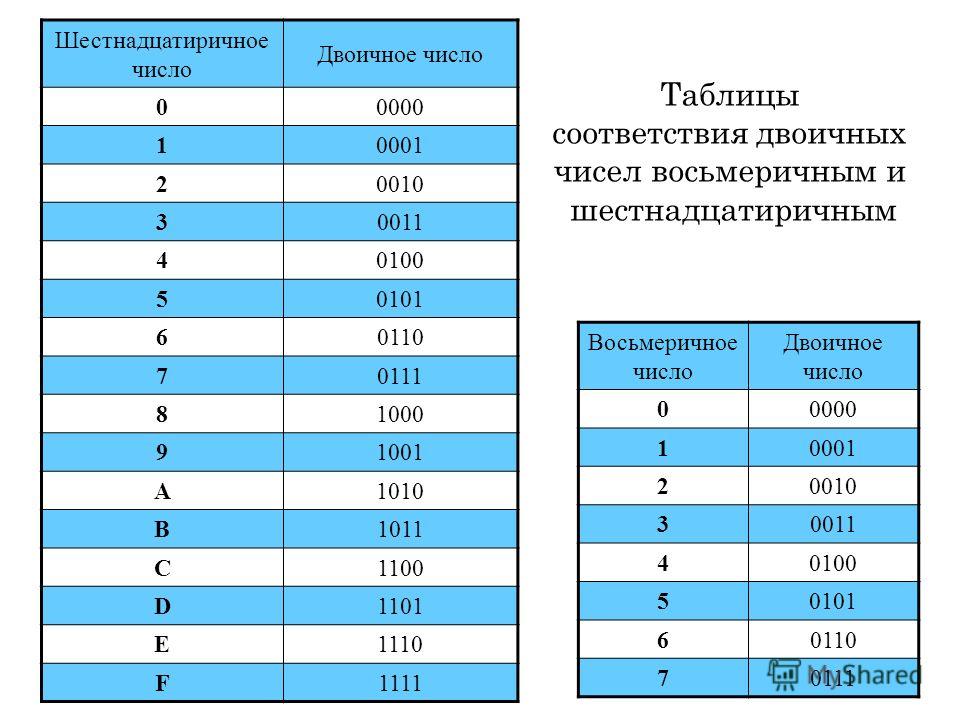
ru
Восьмеричные числа доступны в различных форматах. Восьмеричные числа используются в различных отраслях, включая секторы компьютерных приложений, цифровые системы счисления и системы компьютерных баз данных. Такие слова, как шестнадцать бит, шестнадцать бит и шестнадцать бит, используются в вычислительных системах, а также используются такие слова, как восемь бит, шестнадцать бит и шестнадцать бит. В авиации помимо восьмеричного числа используется код.
Хотя существует множество различных систем счисления, используемых людьми, они не единственные. Удобство, несомненно, является одним из наиболее важных факторов, влияющих на разнообразие, и это влияние зависит от контекста взаимодействия. В общем, в этой системе есть две базы: вторая база, также известная как вторая база, и база пять. В интерфейсе base 2 используются два разных символа, но существует множество случаев, что затрудняет представление материала. Таблицы умножения и символы, которые люди не помнят, необходимы для вычисления воображаемого основания 20.
В современном мире все еще используется шестидесятеричная система для времени, угла и географических координат. Древние вавилоняне пришли на смену древним шумерам в третьем тысячелетии до нашей эры, а затем переняли их. В некотором роде это может быть связано с двенадцатерично-пятеричной системой, основанной на базе 12 и 5.
Место Octal в современных вычислениях
Octal широко использовался в вычислениях в 1960-х и 1970-х годах, когда такие системы, как UniVAC 1050, PDP-8, ICL 1900 и мэйнфреймы IBM, использовали шесть, двенадцать, 24 или 36-битные слова. . Из-за трех двоичных цифр, которые составляют восьмеричные цифры (каждая восьмеричная цифра представляет три двоичных цифры), для этих машин было предпочтительнее использовать аббревиатуру для двоичных чисел. В результате компьютеры были способны обучаться только двоичному коду, состоящему из нулей и единиц, что облегчало им понимание системы счисления.
В современной вычислительной среде компьютеры распознают более широкий спектр систем счисления, включая шестнадцатеричные числа, в которых используются 16 цифр (0–9, a–f), и восьмеричные числа, в которых используются восемь цифр (0–7).
Восьмеричные (4-значные / 12-битные) коды транспондеров до сих пор используются в самолетах по всему миру, поскольку они менее подвержены ошибкам, чем шестнадцатеричные коды, и упрощают связь с УВД. Восьмеричное число
имеет место в современных вычислениях, в первую очередь из-за устаревших систем, которые все еще полагаются на него, несмотря на снижение его популярности. Как правило, компьютеры понимают двоичный код, состоящий из нулей и единиц, но в некоторых приложениях, таких как авиационная связь, необходимо использовать двузначную систему счисления.
Кто-нибудь использует Octal?
Кредит: www.pinkbike.com
На этот вопрос нет однозначного ответа. Некоторые люди могут использовать восьмеричные числа в определенных ситуациях, в то время как другим может вообще не понадобиться их использовать. Это действительно зависит от человека и того, над чем он работает.
Что такое восьмеричная система счисления в компьютере
Система счисления с основанием 8, также известная как система счисления, называется осенним числом.
Латинское слово «восемь» является основой для числа восемь. Для восьмеричной системы счисления используются числа 0-1-4-5-2-3-6-7. В вычислительной среде он обычно используется для представления двоичных чисел в виде троек путем группирования их в более мелкие единицы.
Система счисления используется для описания, представления или выражения чисел в различных формах. Это тип системы счисления, в которой используются числа от 0 до 7 с использованием восьмизначной базы. Восьмеричное числовое представление чисел с восьмеркой в качестве основания. Простой метод используется для преобразования восьмеричных чисел в десятичные числа. Набор чисел расширяется с помощью основания из восьми, где каждое число умножается, а степень сокращения 8 используется для вычисления числа. Шестнадцатеричная единица, которая представляет основание 16 с числами и алфавитами, является математической единицей. Восьмеричная система счисления представляет собой восьмизначную систему счисления с цифрами от 0 до 7.
Octal — это короткое латинское слово, означающее «краткий» на английском языке. Восьмеричные числа используются в различных приложениях и чрезвычайно ценны, особенно в компьютерных системах и цифровых системах счисления. Одна треть двоичной системы счисления состоит из восьмеричных чисел. Чтобы преобразовать восьмеричное число в десятичное, мы должны умножить восьмеричное основание на восьмикратную уменьшающую степень числа 8. Шестнадцатерично-десятичное состоит как из чисел, так и из алфавита и представлено основанием 16.
Восьмеричные числа, в отличие от квадратных чисел, записывается цифрами от 0 до 7. Каждое число (значение) в этой системе счисления равно 0, 1, 2, 3, 4, 5, 6 или 7. Поскольку в восьмеричных числах всего восемь цифр, они называются восьмеричными основаниями.
Поскольку она может представлять больше значений, чем двоичные числа, восьмеричная система счисления более универсальна. По сравнению с двоичными числами восьмеричные числа могут быть меньше по размеру.
Восьмеричная система счисления в двоичную
Восьмеричная система счисления, также известная как для краткости восьмерка, представляет собой систему счисления с основанием 8, в которой для каждого числа используются цифры от 0 до 7. Двоичное число можно составить из четырех групп по три, сгруппировав последовательные двоичные цифры в группы по три (начиная с правой).
Для понимания системы требуется основа. Основой системы является количество символов, из которых она состоит. В общем, основание десятичной системы, основание двоичной системы и основание восьмеричной системы равны 10. Несмотря на то, что каждая из этих систем имеет свою цель, все они работают одинаково. Мощность системы определяет ее позиционное значение по мере генерации числа. Число основано на десяти в десятичной системе. Другими словами, в заданном числе 10 представлено как 1, 2, 3, 4, 5, 6, 7, 8, 9., и 10. В двоичном коде в качестве основы для чисел используются два числа. Это означает, что числа с двумя разрядами равны нулю и единице.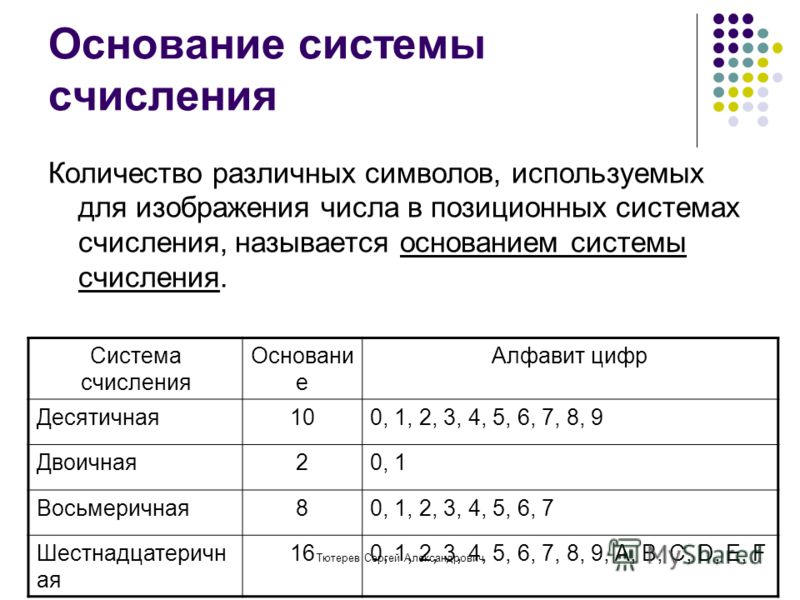
Согласно восьмеричным системам число 8 имеет разрядное значение. Иными словами, восемь чисел имеют разрядное значение 8, потому что у них есть ноль, 1, 2, 3, 4, 5, 6, 7 и 8.
Некоторые из этих систем используются особым образом, в то время как другие используются различными способами. Общепризнанно, что в повседневной жизни используются десятичные системы счисления. В десятичной системе используются числа, такие как 0 и 5. Двоичная система используется для создания компьютеров и других систем. Двоичные числа представлены такими числами, как 1010 и 1110. Восьмеричные системы могут использоваться в различных приложениях, включая телефонные номера и другие электрические системы. Восьмеричные системы, такие как 1111 и 1212, состоят из чисел.
Каждая из этих систем имеет свой набор преимуществ. Из-за своей простоты десятичная система проста для изучения. Поскольку двоичные системы могут обрабатывать большое количество данных одновременно, они могут быстро обрабатывать большой объем информации.
Когда вам нужно громко прочитать число, восьмеричная система удобна для чтения. Поскольку десятичное значение для этих чисел равно 10, они равны 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 и 11.
Восьмеричное в десятичное
восьмеричное число должно быть записано в обратном порядке, чтобы получить восьмеричное число. Числа в базе десять можно назвать десятичными числами. Числа 0-9используются большинством людей. Он состоит из двух частей: целой и десятичной.
Восьмеричная система счисления
Восьмеричная система счисления, или сокращенно октальная, представляет собой систему счисления с основанием 8, в которой используются цифры от 0 до 7. Восьмеричные числа могут использоваться для представления двоичных чисел и часто используются программистами в качестве сокращенный способ записи двоичного кода.
Значение основания в дробной системе счисления равно 8 в дополнение к его представлению в методах представления чисел. Если вы хотите указать число, добавьте префикс 0o или суффикс 8.
Каждая из восьмеричных позиций оказывает гораздо большее влияние на систему, чем предыдущая позиция. Когда для представления количества битов в слове используется число, кратное трем, количество битов в одном слове называется осенним. В системах UNIX он также используется для указания прав доступа к файлам. Система счисления более эффективна, поскольку в ней используется меньше цифр, чем в десятичной и шестнадцатеричной системах счисления. Он использует только три бита для представления любой цифры в двоичном формате и легко преобразует восьмеричное число в двоичное из одного бита.
8 используется как число для обозначения осенних чисел. Поскольку оно не основано на числе 8 и, следовательно, не является восьмеричным числом, 876 не попадает в эту категорию. Поскольку это восьмеричное число, число 786 основано на числе 8.
Kullabs
Обзор
Число с основанием восемь называется восьмеричным числом. Мы можем сгенерировать эти числа с комбинацией 0, 1, 2 3, 4, 5, 6, 7.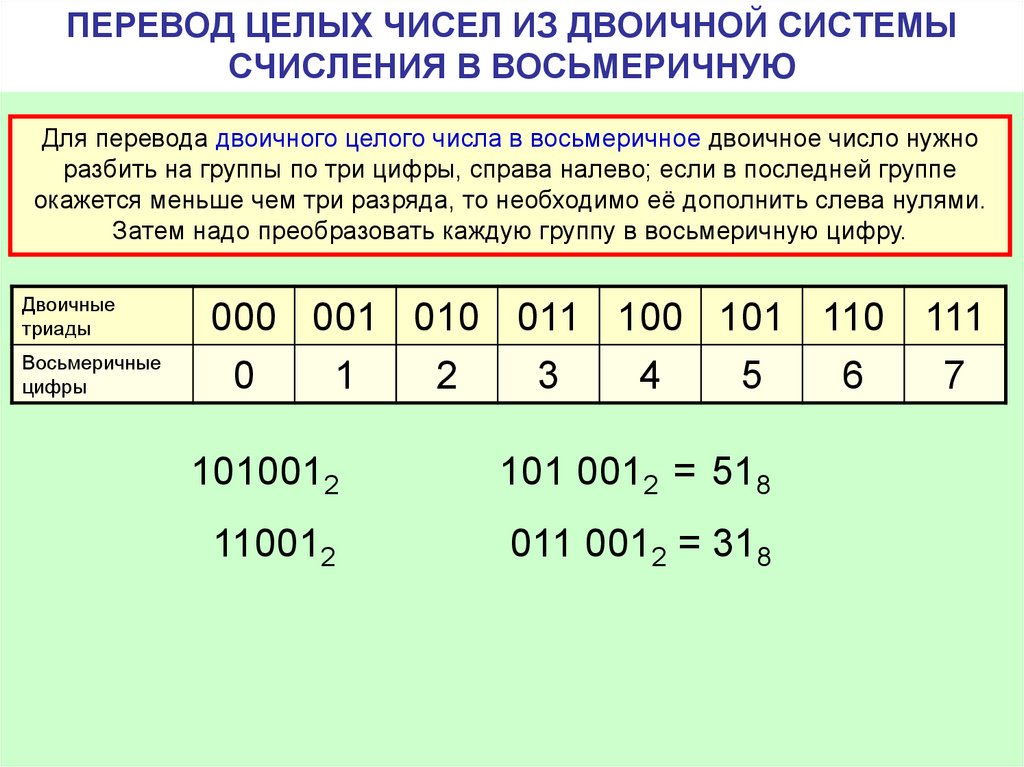
В этом примечании содержится информация о восьмеричной системе счисления и ее преобразованиях.- Примечание
- То, что нужно запомнить
- Видео
- Упражнение
- Контрольный опрос
Восьмеричная система счисления
Число с основанием восемь называется восьмеричным числом. Он представлен Q или O. Мы можем сгенерировать эти числа с комбинацией 0, 1, 2 3, 4, 5, 6, 7. Мы можем представить эти числа с суффиксом восемь.
Например, (5432) 8
Взвешенное значение
85 84 83 82 81 80 32768 4096 512 64 8 1 Conversions from Decimal to Octal
Десятичное число многократно делится на восемь, а остатки располагаются в виде восьмеричных чисел.
Пример
Преобразование (240) 10 в восьмеричном формате.
| 8 | 240 | 0 |
| 8 | 30 | 6 |
| 3 |
(240) 10 = (360) 8
Преобразуйте (356) 10 в восьмеричное число.
| 8 | 356 | 4 | |||
| 8 | 44 | 9 18 | 2 | 0121 4 |
(365) 10 =(444) 8
Преобразование из восьмеричного в десятичное.
Каждое восьмеричное число умножается на его взвешенную позицию. Сумма всех произведений известна как десятичная форма восьмеричного числа.
Пример
Преобразование октальных чисел в десятичные десятичные. (224) 10
Octal к биналью и биналью к оккулянту
- Преобразование каждой восьмеричной цифры в двоичную и группировка из трех цифр.
5= 101
6= 110 - группировка по 3 бита от последнего бита.
010 011 - преобразовать каждую группу в десятичные числа.
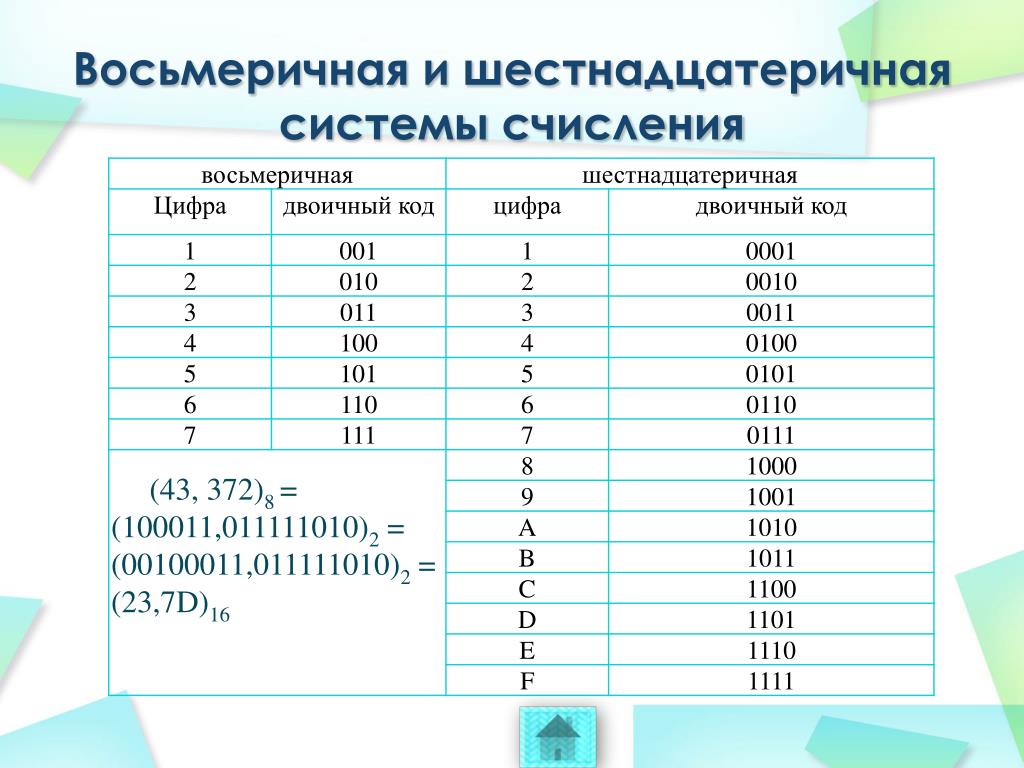
010 = 2
011 = 3
= (23) 8 - Convert octal into binary .
- сделать группы из 4-х бит от последнего бита.
- преобразовать каждую группу в десятичные числа.
- Преобразование в двоичное число
3=011, 4=100, 7=111, 6=110, 5=101
(011100111110101) 2 - Из последнего бита двоичного числа составить группу из четырех цифр.
0011 1001 1111 0101 (Добавьте 0 перед группой, чтобы получить четыре цифры)
3 9 15 5 (Преобразуйте в эквивалентные десятичные числа)
= (39F5) 16 Где F = 15 - Число с основанием восемь называется восьмеричным числом. Он представлен Q или O.
- Когда десятичное число многократно делится на восемь и остатки располагаются в виде восьмеричных чисел, то десятичное число преобразуется в восьмеричное.
- Каждое восьмеричное число умножается на его взвешенную позицию. Сумма всех произведений известна как десятичная форма восьмеричного числа.
- Трехзначный формат двоичных цифр используется для преобразования восьмеричного числа в двоичное или наоборот.
- Включает в себя все отношения, установившиеся между людьми.
- В обществе может быть более одного сообщества. Сообщество меньше, чем общество.
- Это сеть социальных отношений, которую нельзя увидеть или потрогать.
- общие интересы и общие цели не нужны обществу.
- Десятичный
- Десятичная система счисления — это система счисления, которую мы используем ежедневно. «Деци» означает 10, следовательно, действительны 10 числа от 0 до 9. Десятичное число — это число с основанием 10. система.
- Двоичный
- Двоичная система счисления — это система счисления, используемая
компьютеры, PLC/PAC и любое другое оборудование и
устройства, которые являются цифровыми. «Би» означает 2, поэтому
являются 2 допустимыми числами, 0 и 1. Двоичный — это «основание 2»
система счисления.
- Окталь
- Восьмеричная система счисления — это система счисления, используемая ранние PLC/PAC. «Окта» означает 8, следовательно, 8 действительные числа, от 0 до 7. Нет ни восьмерок, ни девяток. в этой системе счисления. Восьмеричное число с основанием 8 система.
- Шестнадцатеричный
- Шестнадцатеричная система счисления используется
всеми PLC/PAC, компьютерами и другим оборудованием и
устройства, которые являются цифровыми. «Гекса» означает 16, поэтому
есть 16 допустимых чисел, от 0 до 9и от А до Ф. Шестнадцатеричная — это система счисления с основанием 16.
- Номера BCD
- Двоично-десятичный код (BCD) на самом деле не является числом система. Это метод создания человеко-машинного интерфейса. (HMI) проще за счет представления десятичного числа 0–9в 4-битном двоичном коде. Если ты понимаешь шестнадцатеричные числа, вы поймете BCD.
- Отрицательные числа
- Большинство PLC/PAC хранят отрицательные числа в дополнении 2. Метод преобразования комплимента 2 подробно описан в Эта тема.
- Преобразование чисел
- Современное программное обеспечение для программирования PLC/PAC позволяет пользователю
изменить основание отображаемого числа.
Octal to Binarn и Binarn to Octal. цифровой формат двоичных цифр используется для восьмеричного преобразования в двоичное или наоборот.
Восьмеричное в двоичное
3-битные двоичные числа записываются для каждой восьмеричной цифры.
Пример
Преобразование (56) 8 (восьмеричное) в двоичное число.
Алгоритм:
Теперь наше эквивалентное двоичное число равно (56) 8 = (101110) 2
Преобразование (64102) 8 в двоичное число
6 = 110
4 = 100
1 = 001
0 = 000
2 = 010
Теперь наше эквивалентное двоичное число составляет (64102) 8 = (1101000010010) 2
BINAL.
0088Двоичные числа разбиваются на 3-битные секции, начиная с последнего бита, и преобразуются в восьмеричные эквиваленты каждой двоичной секции. В таблице показаны десятичные, восьмеричные и эквивалентные двоичные биты.
| Decimal | Octal | Binary |
| 0 | 0 | 000 |
| 1 | 1 | 001 |
| 2 | 2 | 010 |
| 3 | 3 | 011 |
| 4 | 4 | 100 |
| 5 | 5 | 101 |
| 6 | 6 | 110 |
| 7 | 7 | 111 |
Пример
Преобразование (10011) 2 в восьмеричное число.
Алгоритм
Преобразовать (1011010011) 2 в восьмеричное число.
001 011 010 011
001= 1
011= 3
010= 2
011= 3
= (1323) 8
Octal to Hexadecimal
Algorithm
Пример
1. (34765) 8 в шестнадцатеричном формате.
Что нужно помнить
Он представлен Q или O.Видео для восьмеричной системы счисления
Вопросы и ответы
Система счисления, в которой для представления различных значений используются восемь разных цифр, известна как восьмеричная система счисления.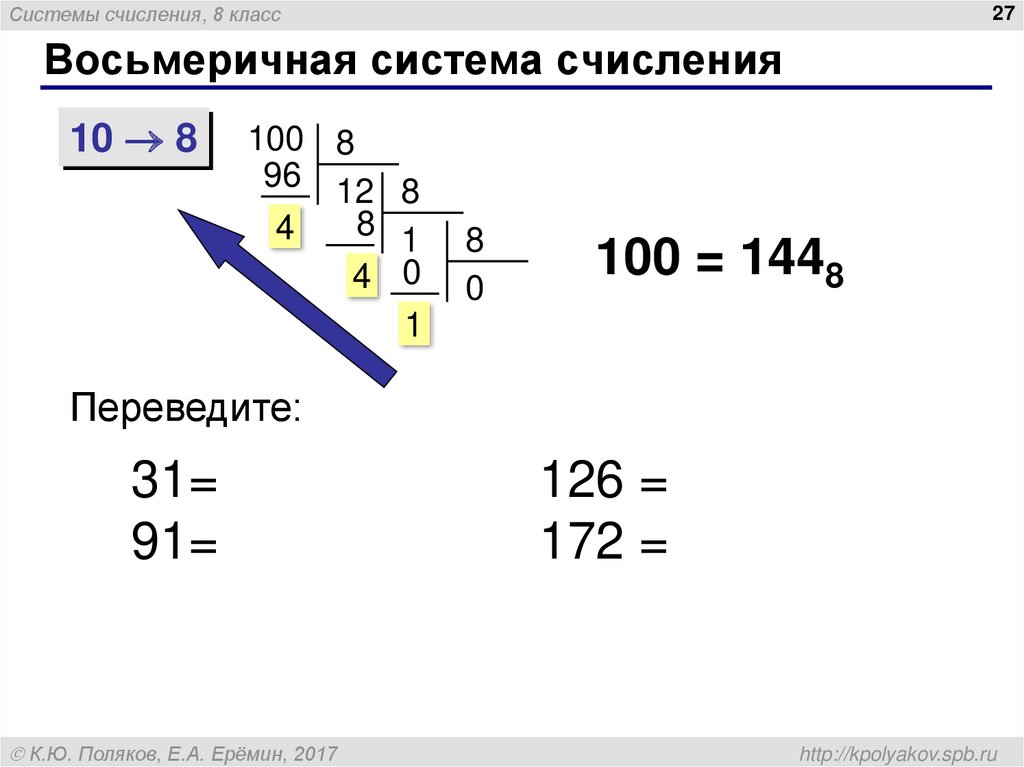
Основание восьмеричной системы счисления равно 8, потому что оно состоит из восьми цифр от 0 до 7. Восьмеричная система счисления используется в компьютере для представления двоичных чисел. Значения разрядов в восьмеричном числе могут быть выражены с использованием степеней числа 8.
Процедура преобразования восьмеричных чисел в их десятичные эквиваленты аналогична преобразованию двоичных чисел в их десятичные эквиваленты, но с той разницей, что в этом случае используется основание 8 вместо 2, используемого в двоичном формате.
Решение:
3 2 1 0 (вес)
Восьмеричное число: 5 2 6 4
Десятичный эквивалент: 5×8 3 + 2×8 2 + 6×9 4 9024 8 0
= 5×512 + 2×64 + 6×8 + 4×1
= 2560 + 128 + 48 + 4
= 2740
Следовательно, (5264) 8 = (2740) 10
Восьмеричная цифра представлена 3 битами.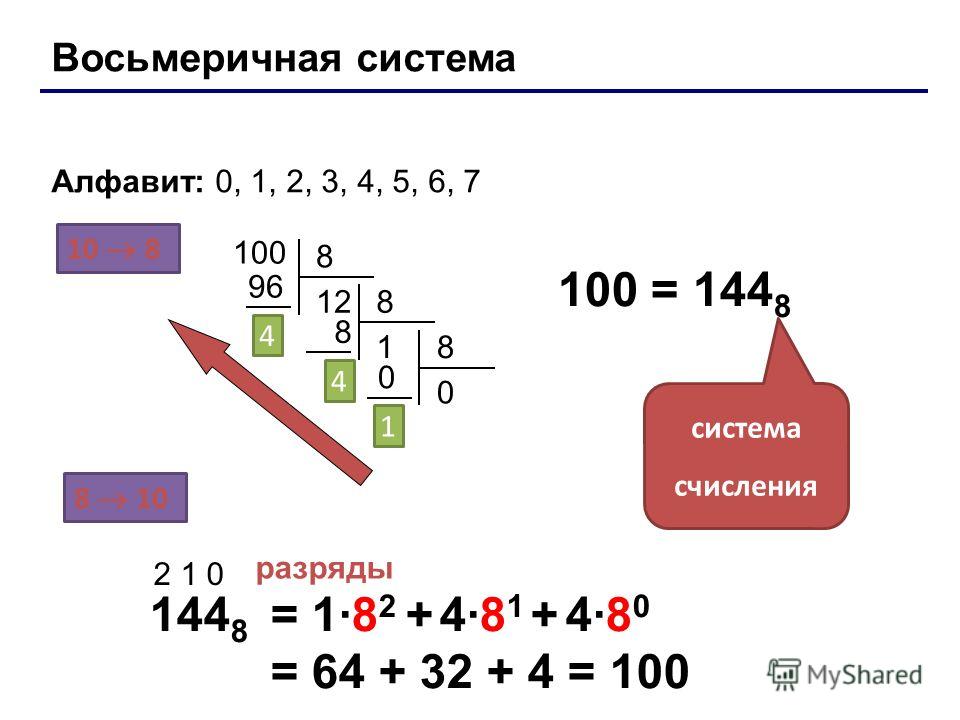
Восьмеричное число преобразуется в его двоичный эквивалент, просто подставляя соответствующее двоичное значение для каждой цифры восьмеричного числа.
Двоичная таблица
| Восьмеричная | Двоичная |
| 0 | 000 |
| 1 | 001 |
| 2 | 010 |
| 3 | 011 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
Прямого метода преобразования восьмеричного числа в восьмеричное нет. Итак, сначала данное восьмеричное число преобразуется в его двоичный эквивалент, затем результат будет преобразован в шестнадцатеричный, как и в предыдущих методах.
Восьмеричное число: 3 2 5 6
Двоичный эквивалент: 11 010 101 110 (из двоичной таблицы)
Опять же,
Парное шестнадцатеричное число
Эквивалент (4 бита от самой правой пары): 111 1010 1010
Шестнадцатеричный эквивалент: 6 A E (из двоичной таблицы)
Следовательно, (3256) 8 = (6AE) 16
Системы счисления
Системы счисленияДом История Проводка ввода/вывода Взаимодействие ввода/вывода Системы счисления Структура памяти Битовые инструкции Таймеры Счетчики Лаборатории ЛогиксПро Внешние ссылки Карта сайта Страница цитирования
Помпей Втрыскове дешевая обувь хуараче бомбы дешевые джорданы дешевый воздух макс дешевые кроссовки дешевые нфл трикотажные изделия дешевые Эйр Джорданс дешевая иорданская обувь дешевые оптовые Иордании
Самый частый вопрос студентов, которые учатся автоматизация: Почему мы должны изучать системы счисления?
Ну.
.. давайте подумаем об этом так. Если вы были в гостях у иностранца
страна, в которой вы хотели бы немного выучить язык,
говорят в этой стране. Фразы типа, где туалет?
Не могли бы вы направить меня на вокзал? Думайте о PLC/PAC как о
чужая страна, а язык, на котором говорят, — числа.
PLC/PAC используют четыре системы счисления:
(Нажмите на систему счисления для получения дополнительной информации
и преобразование в другие системы счисления.)
«Би» означает 2, поэтому
являются 2 допустимыми числами, 0 и 1. Двоичный — это «основание 2»
система счисления.
Шестнадцатеричная — это система счисления с основанием 16.