Целая часть | это… Что такое Целая часть?
График функции «пол» (целая часть числа)
График функции «потолок»
В математике, целая часть вещественного числа — округление до ближайшего целого в меньшую сторону. Целая часть числа также называется антье (фр. entier), или пол (англ. floor). Наряду с полом существует парная функция — потолок (англ. ceiling) — округление до ближайшего целого в большую сторону.
Содержание
|
Обозначения и примеры
Для целой части числа долгое время использовалось обозначение , введенное Гауссом[источник не указан 1264 дня]. Ни понятия функции потолок, ни специального обозначения для нее не существовало. В 1962 году Кеннет Айверсон предложил округления числа до ближайшего целого в меньшую и большую стороны называть «пол» и «потолок» и обозначать и соответственно [1].
В современной математике используются оба обозначения, и , однако существует тенденция перехода к терминологии и обозначениям Айверсона. Одна из причин этого — потенциальная неоднозначность понятия «целая часть числа» [1].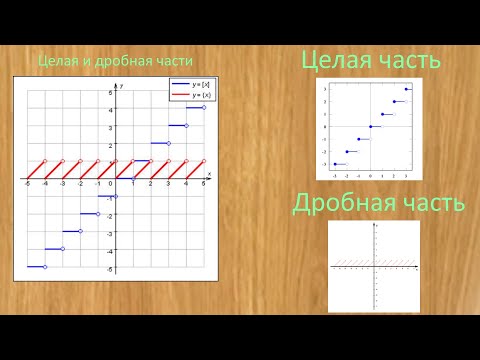
Например, целая часть числа 2,7 равна 2, но возможны два мнения на то, как определить целую часть числа −2,7. В соответствии с данным в этой статье определением , однако в некоторых калькуляторах имеется функция целой части числа INT, для отрицательных чисел определяемая как INT(-x) = -INT(x), так что INT(-2,7) = −2. В терминологии Айверсона отсутствуют возможные неоднозначности:
См. также: Округление
Определения
Функция пол определяется как наибольшее целое, меньшее или равное :
Функция потолок определяется как наименьшее целое, большее или равное :
Эти определения эквивалентны следующим неравенствам (где n — целое число) [2]:
Свойства
Везде ниже обозначают вещественные числа, а — целые.
Пол/потолок как функции вещественной переменной
Функции пол/потолок отображают множество вещественных чисел в множество целых чисел:
Функции пол/потолок имеют разрывны во всех целочисленных точках, это разрывы первого рода со скачком, равным единице.
При этом, функция пол является:
- полунепрерывной сверху
- непрерывной справа
Функция потолок является:
- полунепрерывной снизу
- непрерывной слева
Связь функций пола и потолка
Для произвольного [3]
Для целого пол и потолок совпадают:
Если — не целое, то потолок ровно на единицу выше пола:
Функции пола и потолка являются отражениями друг друга от обеих осей:
Пол/потолок: неравенства
Любое неравенство между вещественным и целым числами равносильно неравенству с полом и потолком между целыми числами [2]:
Два верхних неравенства являются непосредственными следствиями определений пола и потолка, а два нижние — обращение верхних от противного.
Функции пол/потолок являются монотонно возрастающими функциями:
Пол/потолок: сложение
Целочисленное слагаемое можно вносить/выносить за скобки пола/потолка [4]:
Предыдущее равенство, вообще говоря, не выполняется, если оба слагаемых — вещественные числа. Однако и в этом случае справедливы неравенства:
Пол/потолок под знаком функции
Имеет место следующее предложение:[5]
Пусть — непрерывная монотонно возрастающая функция, определенная на некотором промежутке, обладающая свойством:
Тогда
всякий раз, когда определены .
В частности,
если и — целые числа, и .
Пол/потолок: суммы
Если — целые числа, , то [6]
Вообще, если — произвольное вещественное число, а — целое положительное, то
Имеет место более общее соотношение [7]:
Так как правая часть этого равенства симметрична относительно и , то справедлив следующий закон взаимности:
Разложимость в ряд
Тривиальным образом функция Антье раскладывается в ряд с помощью функции Хевисайда:
где каждое слагаемое ряда создаёт характерные «ступеньки» функции.
Этот ряд сходится абсолютно, однако ошибочное преобразование его слагаемых может привести к «упрощённому» ряду
который расходится.
Применение
Целочисленные функции пол/потолок находят широкое применение в дискретной математике и теории чисел. Ниже приведены некоторые примеры использования этих функций.
Количество цифр в записи числа
Количество цифр в записи целого положительного числа в позиционной системе счисления с основанием b равно [8]
Округление
Основная статья: Округление
Ближайшее к целое число может быть определено по формуле
Бинарная операция mod
Основная статья: Остаток от деления
Операция «остаток по модулю», обозначаемая , может быть определена с помощью функции пола следующим образом. Если — произвольные вещественные числа, и , то неполное частное от деления на равно
- ,
а остаток
Дробная часть
Основная статья: Дробная часть
Дробная часть вещественного числа по определению равна
Количество целых точек промежутка
Требуется найти количество целых точек в замкнутом промежутке с концами и , то есть количество целых чисел , удовлетворяющий неравенству
В силу свойств пол/потолка, это неравенство равносильно
- .
Это есть точек в замкнутом промежутке с концами и , равное .
Аналогично можно подсчитать количество целых точек в других типах промежутков. Сводка результатов приведена ниже
(Через обозначена мощность множества ).
Первые три результата справедливы при всех , а четвертый — только при .
Теорема Рэлея о спектре
Пусть и — положительные иррациональные числа, связанные соотношением [10]
Тогда в ряду чисел
каждое натуральное встречается в точности один раз. Иными словами, последовательности
- и ,
называемые последовательностями Бетти (англ.), образуют разбиение натурального ряда.[11]
В информатике
В языках программирования
Во многих языках программирования существуют встроенные функции пола/потолка floor(), ceil().
В системах вёрстки
В TeX (и LaTeX) для символов пола/потолка , , , существуют специальные команды: \lfloor, \rfloor, \lceil, \rceil.
Поскольку wiki использует LaTeX для набора математических формул, то и в данной статье использованы именно эти команды.
Примечания
- ↑ 1 2 Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — С. 88.
- ↑ 1 2 Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — С. 90.
- ↑ Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — С. 89.
- ↑ Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — С. 90-91.
- ↑ Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — С. 93.
- ↑ Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — С. 108.
- ↑ Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — С. 112-117.
- ↑ Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — С. 91.
- ↑ Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — С. 95-96.
- ↑ Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — С. 99-100.
- ↑ А. Баабабов «Пентиум» хорошо, а ум лучше // Квант. — 1999. — № 4. — С. 36-38.
Паташник. Конкретная математика. — С. 95-96.См. также
- Дробная часть
- Нотация Айверсона
- Округление
- Десятичный разделитель
Литература
- Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — М.: «Мир», 1998. — 703 с. — ISBN 5-03-001793-3
- М. К. Потапов, В. В. Александров, П. И. Пасиченко. Алгебра и начала анализа. — АО Столетие, 1996.
Функции Int, Fix — Служба поддержки Майкрософт
Access для Microsoft 365 Access 2021 Access 2019 Access 2016 Access 2013 Access 2010 Access 2007 Еще…Меньше
Возвращает целую часть числа.
Синтаксис
Int ( число )
Fix( число )
Обязательный аргумент числоаргумент представляет собой значение типа Double или любое допустимое числовое выражение.
Замечания
Функции Int и Fix удаляют дробную часть числа и возвращают полученное целое значение.
Различие между функциями Int и Fix состоит в том, что при отрицательном значении числа функция Int возвращает первое отрицательное целое число, не превышающее число, а функция Fix — первое отрицательное целое число, которое больше числа или равно ему. Например, функция Int преобразует -8,4 в -9, а Fix преобразует -8,4 в -8.
Функция Fix(число) вычисляется следующим образом:
Sgn(number) * Int(Abs(number))
Примеры запросов
|
Выражение |
Результаты: |
|
SELECT Int([Discount]) AS Expr1 FROM ProductSales; |
Удаляет дробную часть всех значений в поле «Скидка» и возвращает итоги для всех значений. |
|
SELECT Fix([Discount]) AS Expr1 FROM ProductSales; |
Удаляет дробную часть всех значений в поле «Скидка» и возвращает итоги для всех значений. Для отрицательных дробей «Исправить» возвращает первое отрицательное integer, большее или равное числу. Например, для значения скидки «-223,20» возвращается значение -223,00. |
Для отрицательных дробей «Int» возвращает первое отрицательное integer, меньшее или равное числу. Например, для значения скидки «-223,20» возвращается значение -224,00.
Пример VBA
Примечание: В примерах ниже показано, как использовать эту функцию в модуле Visual Basic для приложений (VBA). Чтобы получить дополнительные сведения о работе с VBA, выберите Справочник разработчика в раскрывающемся списке рядом с полем Поиск и введите одно или несколько слов в поле поиска.
В данном примере показано, как функции Int и Fix возвращают целые части чисел. Если значением аргумента является отрицательное число, функция Int возвращает первое отрицательное целое число, не превышающее его, а функция Fix — первое отрицательное целое число, которое больше этого значения или равно ему.
Dim MyNumber
MyNumber = Int(99.8) ' Returns 99.
MyNumber = Fix(99.2) ' Returns 99.
MyNumber = Int(-99.8) ' Returns -100.
MyNumber = Fix(-99.8) ' Returns -99.
MyNumber = Int(-99.2) ' Returns -100.
MyNumber = Fix(-99.2) ' Returns -99.
Функции пола и потолка
Функции пола и потолка дают нам ближайшее целое число вверх или вниз.
Пример: Каковы пол и потолок 2.31?
Нижний предел числа 2.31 равен 2
Верхний предел числа 2.31 равен 3
Пол и потолок целых чисел
Что, если мы хотим получить пол или потолок числа, которое уже является целым числом?
Это просто: без сдачи!
Пример: Каковы пол и потолок 5?
Этаж 5 равен 5
Потолок 5 равен 5
Вот несколько значений для примера:
| x | Этаж | Потолок |
|---|---|---|
| −1,1 | −2 | −1 |
| 0 | 0 | 0 |
| 1,01 | 1 | 2 |
| 2,9 | 2 | 3 |
| 3 | 3 | 3 |
Символы
Символы для пола и потолка похожи на квадратные скобки [ ] без верхней или нижней части:
Но я предпочитаю использовать словоформу: пол (x) и потолок (x)
Определения
Как дать этому формальное определение?
Пример: Как определить нижний предел 2.
31?Ну, это должно быть целое число…
… и оно должно быть на меньше (или равно) 2,31, верно?
- 2 меньше 2,31 …
- , но 1 тоже меньше 2,31,
- и так 0 , и -1, -2, -3 и т.д.
О нет! Есть много целых чисел меньше 2,31.
Итак, какой из них мы выбираем?
Выберите наибольшее число (в данном случае это 2 )
Таким образом, мы получим:
наибольшее целое число , которое на меньше (или равно) 2,3005 9 2 приводит к нашему определению:
Функция пола: наибольшее целое число, меньшее или равное x
Аналогично для потолка:
Функция потолка: наименьшее целое число, большее или равное x
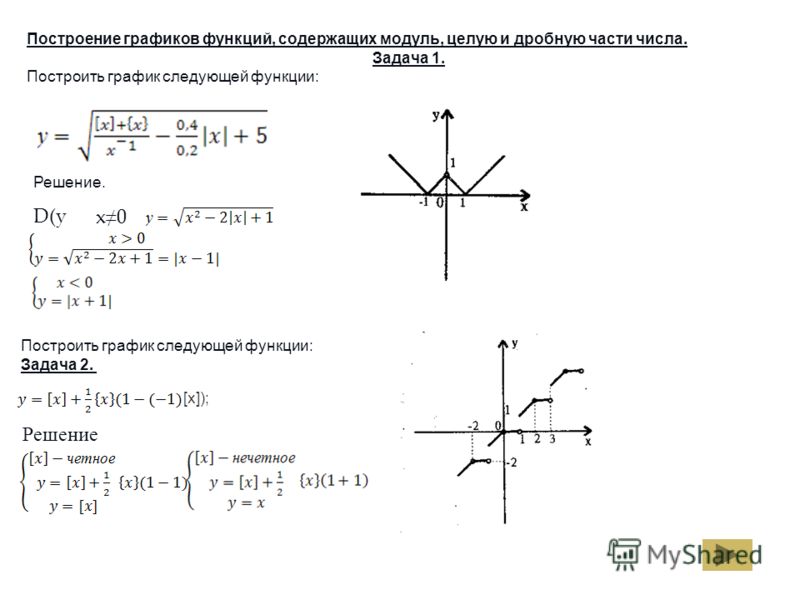
В виде графика
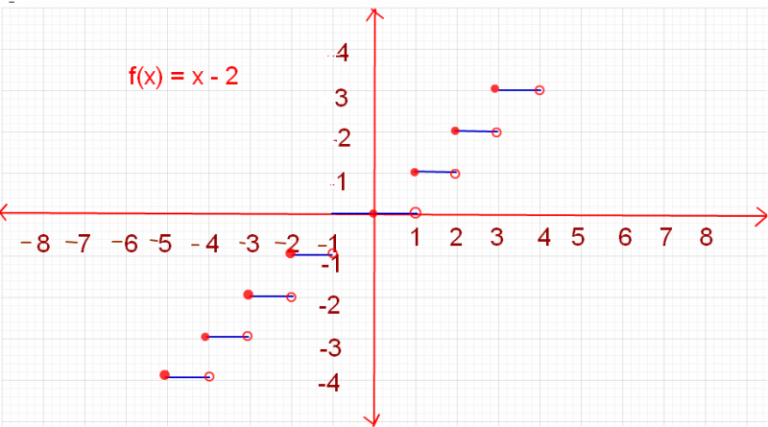
Функция этажа — это любопытная «ступенчатая» функция (как бесконечная лестница):
Функция этажа
Сплошная точка означает «включая», а открытая точка означает «не включая».
.
Пример: при
x=2 мы встречаем:- открытую точку при y=1 (поэтому она не включает x=2),
- и сплошная точка при y=2 (что означает, что включает x=2)
, поэтому ответ равен y=2
И это функция потолка:
Функция потолка
Функция «Int»
Функция «Int» (сокращение от «integer») похожа на Функция «пол», НО некоторые калькуляторы и компьютерные программы показывают разные результаты, когда заданы отрицательные числа:
- Некоторые говорят, что int(−3,65) = −4 (то же, что и функция Floor)
- Другие говорят, что int(−3,65) = −3 (соседнее целое число ближайший к нулю, или «просто выбросьте 0,65»)
Будьте осторожны с этой функцией!
Функция «ГРП»
С помощью функции Floor мы «отбрасываем» дробную часть. Эта часть называется функцией «фракция» или «дробная часть»:
frac(x) = x − floor(x)
Она выглядит как зуб пилы:
Функция Frac
Пример: что такое frac (3,65)?
гидроразрыв(х) = х — пол(х)
Итак: frac(3,65) = 3,65 − пол(3,65) = 3,65 − 3 = 0,65
Пример: что такое frac(−3,65)?
frac(x) = x − floor(x)
Итак: frac(−3,65) = (−3,65) − floor(−3,65) = (−3,65) − (−4) = −3,65 + 4 = 0,35
НО многие калькуляторы и компьютерные программы используют frac(x) = x − int(x) , поэтому их результат зависит от того, как они вычисляют int(x)
- 5 Некоторые говорят, что frac(−3,65) = 0,35 т.
- Другие говорят, что frac(−3,65) = −0,65 , то есть −3,65 − (−3)
е. −3,65 − (−4)Будьте осторожны, используя эту функцию с отрицательными значениями.
Функция наибольшего целого числа — график, домен, диапазон, примеры
Функция наибольшего целого числа также известна как ступенчатая функция. Он округляет число до ближайшего целого числа, меньшего или равного заданному числу. Наибольшая целочисленная функция имеет ступенчатую кривую, которую мы рассмотрим в следующих разделах. Область определения наибольшей целочисленной функции равна ℝ, а ее диапазон равен ℤ.
Таким образом, функция наибольшего целого числа просто округляет заданное число до наибольшего целого числа, меньшего или равного данному числу. Здесь мы узнаем больше о наибольшей целочисленной функции, ее графике и свойствах.
| 1. | Что такое функция наибольшего целого числа? |
2. | Домен и диапазон функции наибольшего целого числа |
| 3. | График функции наибольшего целого числа |
| 4. | Свойства функции наибольшего целого числа |
| 5. | Часто задаваемые вопросы о функции наибольшего целого числа |
Что такое функция наибольшего целого числа?
Функция наибольшего целого числа — это функция, которая возвращает наибольшее целое число, меньшее или равное заданному числу. Наибольшее целое число, меньшее или равное числу x, представляется как ⌊x⌋. Мы округлим данное число до ближайшего целого числа, которое меньше или равно самому числу. Математически функцию наибольшего целого числа ⌊x⌋ можно определить следующим образом:
- ⌊x⌋ = n, где n ≤ x < n + 1 и n — целое число.
Например, ⌊3,02⌋ = 3, поскольку 3 ≤ 3,02 < 4.
Ясно, что входная переменная x может принимать любое действительное значение.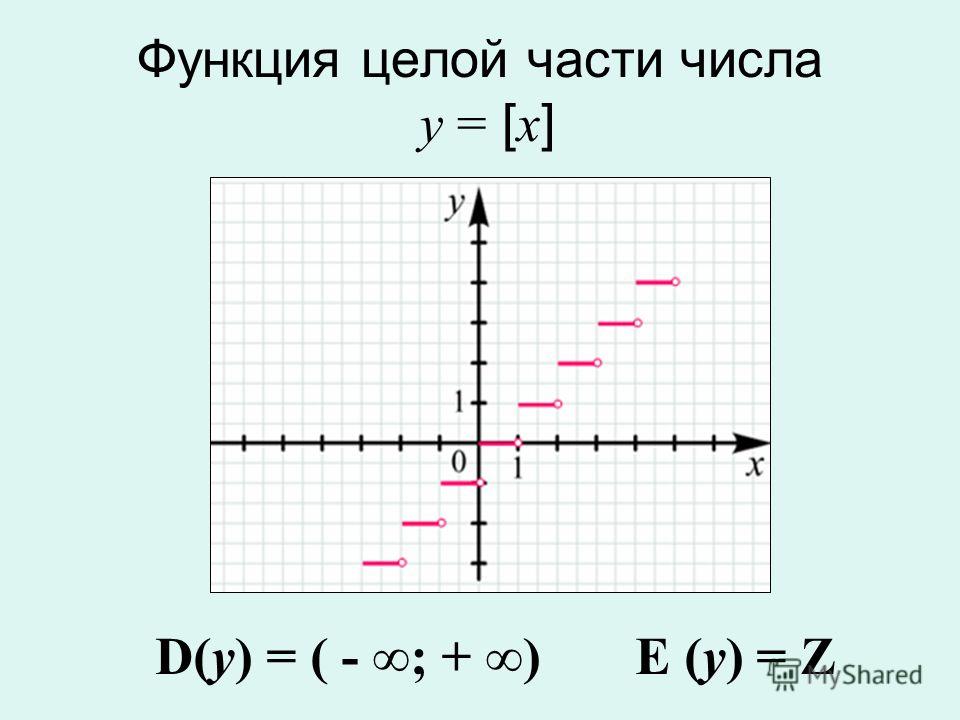
Однако на выходе всегда будет целое число. Кроме того, все целые числа будут встречаться в выходном наборе.
Домен и диапазон функции наибольшего целого числа
Наибольшая целочисленная функция имеет область определения функции как множество всех действительных чисел (ℝ), а ее областью значений является множество всех целых чисел (ℤ). Давайте поймем область определения и диапазон функции, наблюдая за следующими примерами наибольшей целочисленной функции в следующей таблице:
| Значения x | ф(х)=⌊х⌋ |
|---|---|
| 3.1 | f(3.1) = ⌊3.1⌋ = 3 |
| 2,999 | f(2,999) = ⌊2,999⌋ = 2 |
| −2,7 | f(−2,7) = ⌊−2,7⌋ = −3 |
| 4 | f(4) = ⌊4⌋ = 4 |
| −7 | f(−7) = ⌊−7⌋ = −7 |
Здесь значения x могут быть любыми действительными числами, поэтому область определения наибольшей целочисленной функции равна ℝ.
Но обратите внимание, что все значения f(x) (значения y) являются целыми числами, и, следовательно, диапазон равен ℤ.
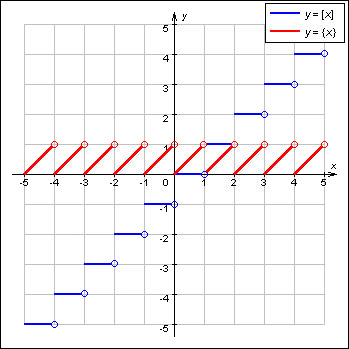
График функции наибольшего целого числа
График функции наибольшего целого числа известен как ступенчатая кривая из-за ступенчатой структуры кривой. Построим график наибольшей целочисленной функции. Во-первых, рассмотрим f(x) = ⌊x⌋, если x — целое число, то значением f будет сам x. Если x не является целым числом, то значением x будет целое число непосредственно перед x (слева от x).
Например,
- Для всех чисел, лежащих в интервале [0, 1), значение f будет равно 0.
- Для всего интервала [1, 2) f будет принимать значение 1.
- Для интервала [−1, 0) f примет значение −1 и так далее.
Таким образом, для целого числа n все числа, лежащие в интервале [n, n+1), будут иметь значение наибольшей целочисленной функции как n. Функция имеет постоянное значение между любыми двумя целыми числами.
Как только приходит следующее целое число, значение функции подскакивает на единицу. Это означает, что значение f при x = 1 равно 1 (а не 0), следовательно, будет полая точка в (1, 0) и сплошная точка в (1, 1), где пустая точка означает отсутствие значения, а сплошная точка означает включение значения. Эти наблюдения приводят нас к следующему графику.
Из приведенного выше графика ясно видно, что входными параметрами функции могут быть любые действительные числа, но на выходе всегда будут целые числа. Таким образом, областью определения этой функции являются действительные числа (ℝ), а ее диапазоном будут целые числа (ℤ).
Свойства функции наибольшего целого числа
Наибольшая целочисленная функция обладает многочисленными свойствами. Некоторые из важных свойств перечислены ниже.
- ⌊x+n⌋ = ⌊x⌋+n, где \(n \in \mathbb{Z}\)
- ⌊−x⌋ = \(\begin{cases} & {-\left\lfloor x\right\rfloor}, & \text{if} x \in \mathbb{Z} \\ &{-\left\lfloor x \right\rfloor-1}, & \text{if } x \notin \mathbb{Z} \\ \end{cases}\)
- Если ⌊f(x)⌋ ≥ L, то f(x) ≥ L
- Если ⌊f(x)⌋ ≤ L, то f(x) < L + 1,
Важные примечания о функции наибольшего целого числа:
Следующие пункты помогут обобщить важные моменты функции наибольшего целого числа.
- Если x число между последовательными целыми числами n и n+1, то ⌊x⌋=n. Если x целое число, то ⌊x⌋=x
- Область определения наибольшей целочисленной функции равна ℝ, а ее диапазон равен ℤ.
- График функции наибольшего целого числа содержит ступени, составленные из горизонтальных линий с одним концом в виде незаштрихованной точки и с другим концом в виде сплошной точки.
☛ Связанные темы:
Следующие ссылки связаны с функцией наибольшего целого числа
- Натуральные числа
- Представление действительных чисел в числовой строке
- Квадратный корень из двух иррационален
- Десятичное представление иррациональных чисел
- Комплексное сопряжение
- Рациональные числа
Примеры функции наибольшего целого числа
Пример 1: Какова область определения заданной функции наибольшего целого числа: f(x)=1/⌊x⌋?
Решение:
Знаменатель не должен быть равен 0, то есть ⌊x⌋≠0.
Наибольшая целая часть числа равна 0, если это число лежит в интервале [0,1).
Таким образом, для получения домена этот интервал необходимо исключить из множества действительных чисел.
Это означает, что область определения f равна R−[0,1).
Ответ: Домен = R−[0,1)
Пример 2: Найдите значение x такое, что ⌊x+1⌋ = 3.
Решение:
Из определения функции наибольшего целого числа имеем 3 ≤ x+1 < 4.
Вычтите 1 из этого неравенства.
Получаем, 2 ≤ x < 3
Ответ: x может принимать значения больше или равные 2 и меньше 3.
Пример 3: Найдите наибольшее целое значение для следующего: (i) [13,01] (ii) [13,99] (ii) [-2,4].
Решение:
Наибольшее целочисленное значение функции для вышеприведенных случаев приведено ниже: ] = -3
Ответ: (i) 13 (ii) 13 (iii) -3.
перейти к слайдуперейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Практические вопросы по функции наибольшего целого числа
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о функции наибольшего целого числа
Что означает функция наибольшего целого числа?
Функция наибольшего целого числа — это функция, которая дает наибольшее целое число, меньшее или равное x. Эта функция обозначается ⌊x⌋. Мы округлим данное число до ближайшего целого числа, которое меньше или равно самому числу.
Как найти наибольшую целочисленную функцию числа?
Самый простой способ найти наибольшую целочисленную функцию числа — просто нанести ее на числовую прямую и выбрать первое целое число, стоящее слева от нее.
Например, ⌊4,15⌋ = 4, ⌊-4,15⌋ = -5.
Каково другое название функции наибольшего целого числа?
Функция наибольшего целого числа также называется функцией пола. Здесь функция принимает наименьшее интегральное значение при округлении значения функции и, следовательно, называется функцией пола.
Почему функция наибольшего целого числа не дифференцируема?
Проверяя график функции наибольшего целого числа, мы видим, что он скачет всякий раз, когда достигает целого числа. Поскольку кривая разрывна в целых числах, она не дифференцируема в этих точках. Следовательно, для каждого целого числа функция наибольшего целого числа не дифференцируема.
Как вычислить функцию наибольшего целого числа отрицательного числа?
Найдем наибольшую целочисленную функцию от -3,2. т. е. ⌊-3,2⌋. Не думайте, что это равно -3. По определению у нас есть ⌊x⌋ = n, где n ≤ x < n + 1. Итак, подумайте, какое целое число находится непосредственно слева от -3,2, и ответ будет -4.
Следовательно, ⌊-3,2⌋ = -4.
Дифференцируема ли функция этажа?
Функция пола или функция наибольшего целого числа не дифференцируема в целых числах. Функция пола имеет скачкообразные значения в целых числах, поэтому ее кривая известна как ступенчатая кривая. Кривая функции пола разрывна в целых числах и, следовательно, не дифференцируема в целых числах.
Что такое область определения и область значений функции наибольшего целого числа?
Вводом функции наибольшего целого числа может быть любое действительное число, тогда как выходом функции наибольшего целого числа всегда является целое число. Таким образом, областью определения этой функции являются действительные числа (ℝ), а ее диапазон — целые числа (ℤ).
Как построить график функции наибольшего целого числа?
Построить график функции наибольшего целого числа очень просто. Это ступенчатая кривая. Здесь f(x) = ⌊x⌋, если x — целое число, то значением f будет сам x, а если x — нецелое число, то значением x будет целое число непосредственно перед x.