Это значение должно быть скаляром маткад: Значение должно быть скаляром, MathCad. — Спрашивалка

Рассмотрим следующие группы операторов. | Электронная библиотека

Прочее / Современные математические пакеты (MathCAD) /      Рассмотрим следующие группы операторов.

3.1. Арифметические операторы

     В MathCAD используются обычные операторы из курса математики. Они вызываются кнопкой 1 математической палитры (см. рис. 1.4):

     Сложение (X+Y) / вычитание (X—Y) (+ или — ): возвращает сумму (X+Y) / разность (X-Y). Если операнды не помещаются в одну строку, то взамен клавиши + можно использовать клавиши Ctrl+Enter. Тогда в документ будет вставлено       

   X…        или    X…

 +Y                 + -Y.

     Операнды должны иметь одинаковую размерность или быть скалярными величинами.

     Умножение (X*Y) (*): возвращает произведение X×Y. Операнды могут иметь одинаковую размерность, быть скалярами, а также может быть X – скаляр, Y – матрица. MathCAD  также поддерживает «подразумеваемое умножение» между константами и переменными. Например, можно записать 5X вместо 5*X. Подразумеваемое умножение для восьмеричных и шестнадцатеричных констант не поддерживается.

     Деление (Y/z) (/): возвращает частное от Y/z. Если z=0, то появляется сообщение об ошибке. Операнды Y  и z – скаляры, причем z  не равно 0. Если Y —  массив, то оператор делит каждый элемент массива на z. Если  Y=0  и z=0, то результат равен 0.

     Комплексно-сопряженное число (X) (“): меняет знак мнимой части комплексного числа X, т.е. из числа Re(X) + i Im(X) получаем число Re(X) — i Im(X).

     Факториал (n!) (!): возвращает факториал числа, равный 1×2×3×…×n. Число n должно быть положительным целым.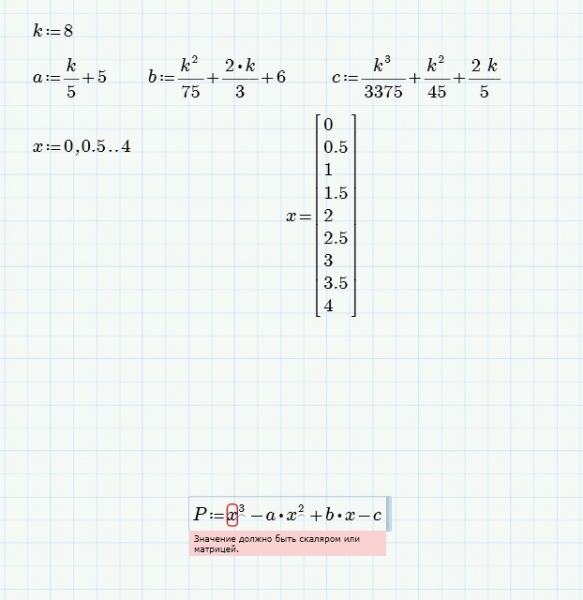

0.5)(): возвращает положительный квадратный корень для положительных z или главное значение для невещественных z.

    

3.2. Операторы векторов и матриц

Практические занятия Специальные операторы, функции и символьные вычисления в MathCad 6

Download 201,95 Kb. bet 1/2 Sana 22.04.2022 Hajmi 201,95 Kb. #573432 Turi Методические рекомендации

  1   2

Bog’liq
6 — 7 практическая занятия
Глава 6, Issiqlik texnologik jarayonlar va qurilmalarr, 36, Глава 6, Глава 6, Глава 6, boshqarish sistemalarining elementlari va qurilmalari (1), Шахснинг психологик характеристикаси, Глава 6, yarim otkazgichli asboblar, Глава 6, Оптика, Оптика, ichki yonuv dvigatellari va gaz turbinasi ishlarini organish, 1375683

6 – 7 Практические занятия Специальные операторы, функции и символьные вычисления в MathCad Цель: Научить студентов работать со специальными функциями и символами в среде MathCad. развивать знания и навыки расчетов. Оборудование: Компьютер. Методические рекомендации: Функция — это выражение, в котором вычисляются аргументы и определяется его числовое значение. Существует разница между аргументами и параметрами функции. Переменные, указанные в скобках после имени функции, являются ее аргументами, которые изменяются при вычислении функции. В левой части функции находятся параметры, не показанные в круглых скобках, которые необходимо установить перед определением функции. Функция должна возвращать одно значение. Возможности пакета MathCAD могут быть встроенными, т. е. предварительно установленными разработчиками и определяемыми пользователем. Символические вычисления. До сих пор Mathcad описывал количественный расчет выражений. В количественных расчетах возвращает одно или несколько чисел после знака Mathcad =. Хотя знать эти числа полезно, с их помощью трудно понять отношения между аргументами и выражениями. В дополнение к числовым вычислениям Mathcad также выполняет символьные вычисления. Это означает, что результаты расчетов могут быть описаны аналитически. Способы добавления встроенной функции: 1. Выберите меню Вставка → Функция. 2. Нажмите Ctrl + E. 3. Нажмите клавишу f (x). Специальные функции среды MathCad: Гиперболические функции acosh(z)-обратный гиперболический косинус. acoth (z) — обратный гиперболический котангенс. acsch(z)-обратно гиперболический косекан. asech(z)-обратная гиперболическая последовательность. asinh(z)-обратный гиперболический синус. atanh (z) — обратный гиперболический тангенс Результатом функции является действительная часть комплексного числа z. sh(z)-гиперболический синус: sh(x)=(ex — e-x)/2. ch(z)-гиперболический косинус: ch(x)=(ex+e-x)/2. tanh(z)-гиперболический тангенс: tanh(x)=(ex-e-x)/(ex+e-x). sech(z)-гиперболическая последовательность: sech(x)=l/ch(x). csch(z)-гиперболический котангенс: csch(x)=l/sh(x).coth(z)-гиперболический котангенс: coth(x)=1/th(x). Аргумент x должен быть скалярным. Логарифмическая и экспоненциальная функции exp(z) — это число e, умноженное на z. log(z[b]) — логарифм z по b; если b опущено, основание равно 10. ln (z) — логарифм z, основанный на e (натуральный логарифм z). Аргумент Z должен иметь скалярное и безразмерное числовое значение. Z для функций log и ln аргумент должен быть отличен от нуля. Для комплексных значений аргумента Z значения логарифмических функций выводятся из базовой ссылки называется: Для этих функций аргумент Z (действительный, комплексный или абстрактный) должен быть числом, определенным в радианах. Для комплексных чисел sin(z), cos(z), tan(z) определяются по следующим формулам: sin(z)=(эиз-э-из)/2i; сос(з)=(эиз+э-из)/2; tan(z)=(eiz-e-iz)/((eiz+e-iz)i).asin(z) — обратный тригонометрический синус. acos(z) — арктригонометрический косинус. asec(z) — обратная тригонометрическая последовательность.acsc(z) — обратная тригонометрическая косеканс. acot(z) — арктригонометрический котангенс. atan (z) — арктангенс тригонометрии asin (z), atan (z), asec (z), acot (z) — когда z является действительным числом, он возвращает углы в радианах между  и  / 2. Когда acos (z) -z является действительным числом, углы возвращаются в радианах от 0 до . Функции комплексных чисел arg(z) — определяет углы в радианах x от действительной оси до комплексного числа z. csgn(z) -if 0, если z = 0, 1, если Re(z)>0 или (Re(z)=0 и Im(z)>0), иначе возвращается -1. Im (z) — z отделяет абстрактную часть комплексного числа. Re(z) — z отделяет действительную часть комплексного числа. signum(z) — возвращает 1, если z = 0 и в противном случае z/z. Функции округления и числа. ceil (x) — возвращает наименьшее целое число, равное или превышающее x. Число x должно быть реальным: ячейка (15,7) = 16 ячейка (-3,9) = -3 floor (x) — возвращает наибольшее целое число, равное или меньшее x.Число x должно быть действительным: этаж (15,7) = 15 этаж (-3,9) = -4 round(x,n) — округляет действительное число x от десятичной точки вправо до знака n. Если n опущено, x округляется до первого целого числа. Если n раунд (15,71346,3) = 15,713 раунд (15,71346) = 16 раунд (1315,71346, -2) = 1,3 * 103 Сундук (x) -x возвращает целую часть действительного числа, не теряя дробной части: ствол (15,7) = 15 ствол (-3,9) = -3 Рекурсивная функция. Он также имеет возможность создавать рекурсивные функции в MathCad. Вычисление значения функции с помощью рекурсии означает использование той же функции внутри функции для вычисления значения функции. Это н! Рассмотрим пример расчета факт (n): = если (n = 0,1, n ∙ факт (n-1)) факт (3) = 6, факт (5) = 120. Функции, выполняемые на линии. MathCad имеет строковый тип переменных, значения которых приведены в скобках, и над ними можно выполнять множество операций. Когда Mathcad использует символьную математику, вместо результата вычисления появляется другое выражение, как показано ниже. Это может быть само выражение, умножение или деление и так далее. Чтобы использовать символьные символы в Mathcad, сделайте следующее. Символьные вычисления можно использовать в разделе меню «Символика» или с помощью значка в математической палитре. Символ → принимает выражение слева и дает упрощенную версию выражения справа. После выражения используйте команды в разделе «Символические символы», чтобы получить упрощенные варианты выражения в различных формах. возможный. Есть два основных инструмента для выполнения символьных вычислений: меню Symbolics; Математическая панель Символьная панель. Эти инструменты используются в более сложных символьных вычислениях. Теперь рассмотрим простейший способ выполнения простого символьного вычисления, то есть один из наиболее часто используемых методов — метод символьного равенства (→). Например, при решении неопределенных интегралов, дифференцировании и других подобных задач ее решение описывается аналитически. Ниже приводится последовательная процедура использования этого метода: 1. На панели «Математика» нажмите кнопку «Исчисление» на панели инструментов. 2. В открывшемся окне панели выберите Исчисление и нажмите на неопределенный интеграл (например, рассматривается неопределенный интеграл). 3. Заполняются поля ввода, т.е. вводятся имя функции и имя переменной. 4. Вводится символический знак равенства (→). Вы можете использовать команду Sumbolally или символ →, используя меню Symbolics — Evaluate — Symbolly или клавиши [Ctrl]>. Примеры: Download 201,95 Kb. Do’stlaringiz bilan baham:

  1   2

---

Ma’lumotlar bazasi mualliflik huquqi bilan himoyalangan ©hozir. org 2023
ma’muriyatiga murojaat qiling

Начало работы с PTC Mathcad API | ПТК

Написано Гость Автор

• 30.12.2021
• Время чтения: 3 мин.

Гостевой пост от Ioana Cernat

В этой статье представлен обзор интерфейса прикладного программирования PTC Mathcad (API) и его комплекта разработки программного обеспечения (SDK).

Чтобы найти SDK,

1. В PTC Mathcad откройте интерактивную справку (F1). Кроме того, вы можете получить онлайн-справку из веб-браузера, нажав здесь.
2. Щелкните Интеграция с другими продуктами > Руководство по API .

Что можно делать с API?

API предоставляет механизм для связи с Mathcad из другого приложения Windows, включая автономное приложение, написанное пользователями. API состоит из группы классов автоматизации, которые можно использовать для выполнения следующих действий (упомянем лишь некоторые из них):

• Открыть Mathcad
• Подсчитать результаты
• Назначение и извлечение переменных, матриц и строк
• Управление внешним видом окон
• Получить информацию о регионах
• Сохранение, печать или закрытие рабочего листа Mathcad
• Полностью закрыть Mathcad

При желании вы даже можете отправлять данные или присваивать значения переменных в PTC Mathcad Prime из другого приложения (например, Google Graphs) или отправлять результаты обратно в исходное приложение.

Таким образом, используя команды автоматизации, вы можете выполнять множество задач — от более простых до более сложных.

Знакомство с SDK

SDK содержит руководство пользователя, включающее документацию по командам автоматизации и примеры API, которые помогут вам лучше понять, как использовать и создавать собственные приложения. В зависимости от ваших навыков программирования вы можете использовать одну из следующих программ: C++, C#, VB, VBScript или JavaScript.

На изображении ниже показаны примеры, которые можно найти в Руководстве по API (см. изображение ниже), а также в установочном пакете Mathcad.

Изображение: Расположение примеров кода в Mathcad SDK.

Далее рассмотрим один из примеров.

Пример 10: GraphMat

В этом примере на C# показано, как запустить PTC Mathcad Prime, загрузить рабочий лист, передать скалярные значения на рабочий лист, вычислить рабочий лист и получить результат матрицы. Для создания решения он использует API-интерфейсы .NET, API-интерфейсы PTC Mathcad Prime и API Google Charts.

Выполните следующие шаги:

1. Загрузите пример здесь: C#_GraphMat.
2. Чтобы запустить пример, запустите GraphMatrix.exe. Откроется диалоговое окно GraphMat . Все поля ввода отключены.
3. Щелкните Файл > Открыть , чтобы открыть рабочий лист Force Google Graph. mcdx. Когда этот рабочий лист открывается, поля ввода GraphMat становятся доступными.
4. Обратите внимание на четыре области ввода в верхней части второй страницы и две области вывода в нижней части третьей страницы.
5. В диалоговом окне GraphMat вы можете изменить любое из четырех текстовых полей, прежде чем щелкнуть Отправить входные значения для отправки значений на рабочий лист.
6. На рабочем листе четыре области ввода теперь отражают значения, установленные в диалоговом окне GraphMat . Mathcad Prime пересчитывает рабочий лист и отправляет значения SForce и outstring в диалоговое окно GraphMat в виде диаграммы и строки чисел, отображаемой под диаграммой. Чтобы соответствовать ограничениям Google Charts, вектор силы масштабируется для создания SForce, чтобы гарантировать, что диапазон его элементов составляет 0-100.
7. Для следующего расчета установите новые значения диаметра или двигателя, затем щелкните . Отправить входные значения . График и строка чисел обновляются соответствующим образом.
8. В PTC Mathcad Prime щелкните Файл > Закрыть , а затем в диалоговом окне GraphMat щелкните Файл > Выход .

Вы можете переопределить исходные значения Mathcad, вставив новые значения в существующие поля. Вы увидите, как все мгновенно обновляется на рабочем листе Mathcad, как только вы отправите информацию в Mathcad из интерфейса.

После того, как вы установили Mathcad, вы можете получить доступ к этим примерам в папке установки и открыть код, чтобы проверить его, изучить его, создать новый на основе уже существующих и внести свои собственные данные и информацию. Затем, с момента компиляции кода, система предоставляет вам соответствующий интерфейс.

Альтернативный пример с демонстрацией JavaScript можно посмотреть в видео ниже:

 

 

Получите персональную помощь

Есть вопросы об API и SDK? Обратитесь к эксперту по Mathcad

СВЯЖИТЕСЬ С НАМИ

---

Об авторе

Приглашенные авторы отчета о жизненном цикле продукта являются отраслевыми лидерами в области тем и идей, связанных с IoT. Если вы хотите стать приглашенным автором, свяжитесь с Мишель Хопкинс по адресу [email protected].

API предоставляет механизм для связи с Mathcad из другого приложения Windows. Вот как вы можете использовать его для своих интеграций.

6.2 — Операции с матрицами

6.2 — Операции с матрицами

Равенство

Две матрицы равны тогда и только тогда, когда

• Порядок матриц тот же
• Соответствующие элементы матриц совпадают

Дополнение

• Порядок матриц должен быть одинаковым
• Сложить соответствующие элементы вместе
• Сложение матриц коммутативно
• Сложение матриц ассоциативно

Вычитание

• Порядок матриц должен быть одинаковым
• Вычесть соответствующие элементы
• Вычитание матриц не является коммутативным (как и вычитание действительных чисел)
• Вычитание матриц не является ассоциативным (как и вычитание действительных чисел)

Скалярное умножение

Скаляр — это число, а не матрица.

• Матрица может быть любого порядка
• Умножить все элементы матрицы на скаляр
• Скалярное умножение коммутативно
• Скалярное умножение ассоциативно

Нулевая матрица

• Матрица любого порядка
• Состоит из всех нулей
• Обозначается заглавной буквой O
• Аддитивная идентичность для матриц
• Любая матрица плюс нулевая матрица является исходной матрицей

Умножение матриц

A _m×n × B _n×p = C _m×p

• Количество столбцов в первой матрице должно быть равно количество строк во второй матрице. То есть внутренние размеры должны быть одинаковыми.
• Порядок произведения равен количеству строк в первой матрице на количество столбцов в вторая матрица. То есть размеры изделия – это наружные габариты.
• Так как количество столбцов в первой матрице равно количеству строк во второй матрица, вы можете спаривать записи.
• Каждый элемент в строке i из первой матрицы соединяется с элементом в столбце j из вторая матрица.
• Элемент в строке i , столбце j произведения образован путем умножения этих парных элементов и их суммирование.
• Каждый элемент произведения представляет собой сумму произведений элементов из строка i первой матрицы и столбец j второй матрицы.
• Будет n произведений, которые суммируются для каждого элемента произведения.

См. полный пример умножения матриц.

Умножение матриц не является коммутативным

• Умножение действительных чисел.
• Внутренние размеры могут не совпадать при изменении порядка матриц.

Не перемножайте соответствующие элементы

• Поскольку порядок (размеры) матриц не обязательно должен быть одинаковым, может не быть соответствующие элементы, чтобы умножить вместе.
• Умножить строки первого на столбцы второго и сложить.

Нет деления матрицы

• Не существует определенного процесса деления матрицы на другую матрицу.
• Матрица может делиться на скаляр.

Идентификационная матрица

• Квадратная матрица
• Единицы по главной диагонали
• Нули везде
• Обозначается I. Если индекс включен, это порядок единичной матрицы.
• I — мультипликативная идентичность для матриц
.
• Любая матрица, умноженная на единичную матрицу, является исходной матрицей.
• Умножение на единичную матрицу является коммутативным, хотя порядок изменить

Идентификационная матрица размера 2

I 2 =		1	0
		0	1

Идентификационная матрица размера 3

I 3 =		1	0	0
		0	1	0
		0	0	1

Свойства матриц

Недвижимость	Пример
Коммутативность сложения	А + В = В + А
Ассоциативность сложения	А + (В + С) = (А + В) + С
Ассоциативность скалярного умножения	(кд) А = с (дА)
Скалярная идентичность	1А = А(1) = А
Распределительный	с (А + В) = сА + сВ
Распределительный	(с + г) А = сА + дА
Дополнительный идентификатор	А + О = О + А = А
Ассоциативность умножения	А (ВС) = (АВ) С
Распределительный левый	А (В + С) = АВ + АС
Правый распределитель	( А + В ) С = АС + ВС
Скалярная ассоциативность/коммутативность	с (АВ) = (сА) В = А (сВ) = (АВ) с
Мультипликативная идентичность	ИА = АИ = А

Свойства действительных чисел, которые не являются свойствами матриц

Коммутативность умножения

• Вы не можете изменить порядок задачи на умножение и ожидать чтобы получить то же самое продукт. АБ≠БА
• Вы должны быть осторожны при факторизации общих факторов, чтобы убедиться, что они находятся на одно и тоже сторона. AX+BX = (A+B)X и XA+XB = X(A+B), но AX+XB не учитывается.

Свойство нулевого продукта

• Тот факт, что произведение двух матриц является нулевой матрицей, не означает, что одна из им была нулевая матрица.

Мультипликативное свойство равенства

• Если A=B, то AC = BC. Это свойство остается верным, но обратное не обязательно верно. Тот факт, что AC = BC, не означает, что A = B.
• Поскольку умножение матриц не является коммутативным, вы должны предварительно умножить или постумножить на обеих сторонах уравнения. То есть, если A=B, тогда AC = BC или CA = CB, но AC≠CB.

Нет деления матрицы

• Вы должны умножить на обратную матрицу

Оценка функции с использованием матрицы

Рассмотрим функцию f(x) = x ² — 4x + 3 и матрицу A

А =		1	2
		3	4

Первоначальная попытка вычислить f(A) состояла бы в замене каждого x с A, чтобы получить f(A) = A ² — 4А+3. Есть одно небольшое проблема однако. Константа 3 не матрица, и сложить нельзя матрицы и скаляры вместе. Итак, мы умножаем постоянная по матрице идентичности.

f(A) = A ² — 4A + 3I.

Вычислите каждый член функции, а затем сложите их вместе.

А 2 =		1	2		*		1	2		=		7	10
		3	4				3	4				15	22

-4 А = -4		1	2		=		-4	-8
		3	4				-12	-16

3I = 3		1	0		=		3	0
		0	1				0	3

ф(А) =		7	10		+		-4	-8		+		3	0		=		6	2
		15	22				-12	-16				0	3				3	9

Факторинг выражений

Показаны некоторые примеры факторинга. Упрощайте и решайте как обычно, но помните эта матрица умножение не коммутативно и нет матричного деления.

2Х + 3Х = 5Х

АХ + ВХ = (А+В)Х

ХА + ХВ = Х(А+В)

АХ + 5Х = (А+5I)Х

AX+XB не учитывает

Решение уравнений

Систему линейных уравнений можно записать в виде AX=B, где A — коэффициент матрица, X — вектор-столбец, содержащий переменные, а B — правая часть сторона. В следующем разделе мы научимся решать это уравнение.

Если имеется более одной системы линейных уравнений с одинаковым коэффициентом матрицу, то вы можете расширить матрицу B, чтобы иметь более одного столбца. Помещать каждую правую часть в свой столбец.

Умножение матриц

Умножение матриц включает суммирование произведения. Уместно там, где вы нужно умножить вещи вместе, а затем Добавить. Например, умножение количества единиц на стоимость единицы будет дать общее Стоимость.

Найдены единицы товара путем проведения модульного анализа на матрицы.