|
5.4.1. Реляционные базы данных Все реляционные базы данных используют в качестве модели хранения данных двумерные таблицы. Эта модель выбрана потому что она в основном знакома всем пользователям и рассматривается как «естественный» путь представления данных. Любая система данных, не имеет значения какой сложности, может быть сведена к набору таблиц (или «отношений» в терминологии СУРБД) с некоторой избыточностью. Избыточность контролируется путем приведения отношений к канонической «нормальной» форме, которая минимизирует ненужную избыточность без уменьшения связей между элементами данных.
Каждая строка олицетворяет уникальный элемент данных, который ею и описывается. Столбцы представляют собой отдельные куски информации (атрибуты данных), которые известны о данном элементе. Строки обычно называют записями, а столбцы — полями. Кроме того, для обработки отношений разрешены только следующие операции:
Другие операции с данными обычно не поддерживаются в базах с реляционной структурой. Добавление произвольных данных, которые, например, не соответствуют ни одному полю в описании данных, запрещено. Добавление поля для произвольных данных потребовало бы перестройки (реструктурирования) базы данных. А этот, зачастую очень длительный, процесс может выполняться только когда базой данных никто не пользуется. Вообще, лишь немногие реальные базы данных могут быть описаны при помощи единственной таблицы. Большинство приложений используют множество таблиц, которые содержат столбцы (поля) с одинаковым именем. Эти общие данные позволяют объединяя две (или несколько) таблицы, строить осмысленные ассоциации. Лучше всего это иллюстрируется примером. Рассмотрим два отношения «Служащий» и «Отдел», показанные на рис.5.14. Рис. 5.14. Отношения «Служащий» и «Отдел». В этом примере поля Номер Служащего и Номер Отдела выделены; это указывает на то, что эти поля — первичные ключи. Во многих случаях это объединение не такое простое. Предположим, нам требуется найти способ для определения, кто является Руководителем для любого Служащего. Мы могли бы создать следующую структуру данных (рис.5.15). Эта на вид интуитивная структура может вызвать проблемы из-за избыточности связи отношения «Руководитель», связанного с отношением «Служащий» как напрямую, так и через отношение «Отдел». Эта избыточность позволяет руководителю служащего отличаться от руководителя отдела служащего. Если это не разрешено, то приведенная структура таблиц не подходит. Рис. 5.15. Отношения «Служащий», «Отдел» и «Руководитель». Рис. 5.16. Вместо нее более подходящей была бы структура, представленная на рис.5.16. Эта структура удаляет избыточность, которая позволяет Служащему иметь Руководителя, отличного от Руководителя его Отдела. Но делая это, она удаляет прямую связь, которая может быть желательна с точки зрения производительности больших баз данных. Эта взаимосвязь между производительностью и целостностью данных присутствует фактически во всех моделях баз данных. Простой реальный пример может потребовать еще более сложной структуры. Пусть Служащий является членом более чем одного Отдела. Правила соединения в реляционных базах данных не разрешают связей «многие-ко-многим» (которые можно обозначить при помощи стрелки с двойным указателем на каждом конце). Чтобы представить отношение с такими связями (например, каждый Отдел имеет многочисленных Служащих и каждый Служащий может быть членом Многочисленных Отделов), нам надо создать отдельное отношение, которое является гибридом двух столбцов (рис. Рис. 5.17. Отношения «Служащий», «Назначение», «Отдел» и «Руководитель». Здесь отношение «Назначение» содержит запись для каждого отдела, сотрудником которого является служащий. То есть, если Служащий работает в Отделе, то соответствующие Номер Служащего и Номер отдела обнаруживаются точно в одной записи отношения «Назначение». Поле Номер Назначения фактически не нужно, так как Номер Служащего и Номер Отдела могут вместе служить ключем. В большинстве (но не во всех) СУРБД разрешены отношения с составными ключами. Для тех из них, в которых ключ должен быть представлен обязательно одним полем, структура будет такой, как представлена выше. «Естественный подход» с использованием таблиц может оказаться еще более «притянутым за уши», когда данные — разреженные. Разреженные данные означают, что не каждое поле в каждой записи содержит данные. В некоторых приложениях данные очень разреженные — только несколько из большого числа столбцов, определенных для данного отношения, могут содержать данные в каком-либо заданном ряду. Реляционные базы данных были бы совсем непригодны, если бы эти разреженные данные действительно хранились внутри прямоугольного массива, так как для этих пустых элементов данных надо было бы выделять пространство. |
Это означает, что элементы данных в этих полях единственным образом определяют запись (т.е. никакие две записи не имеют одинакового элемента данных в ключевом поле). Более того, поле N отдела обнаруживается в обеих таблицах. Это позволяет объединить две таблицы таким образом, чтобы, например, определять Название отдела для любого заданного Служащего.
5.17):
Двумерные таблицы — Студопедия
К наиболее часто используемым инструментам изучения взаимосвязи двух переменных относятся методы анализа таблицы сопряженности. Анализ таблицы является весьма простым и наглядным, и вместе с тем эффективным инструментом изучения одновременно двух переменных. Двумерная таблица сопряженности для переменных ql2 и q2 (табл. 2.1) составлена по данным исследования «Мониторинг социальных и экономических перемен в России», которые получены из ответов на вопросы:
qlOКак бы вы оценили в настоящее время материальное положение вашей семьи ?
4.
Хорошее, очень хорошее.
5. Среднее.
6. Плохое, очень плохое.
7. Затрудняюсь ответить.
q12 Как бы вы оцениkb в целом политическую обстановку в России ?
1. Благополучная, спокойная.
2. Напряженная.
3. Критическая, взрывоопасная.
4. Затрудняюсь ответить.
Таблица 2.1. Таблица сопряженности для переменных q10 nq12
| q10 Как бы вы оценили в настоящее время материальное положение вашей семьи? | q12Как бы вы оценили в целом политическую обстановку в России? | Все го | |||
| благопо лучная. спокойная | напря женная | критическая, взрыво опасная | затрудняюсь ответить | ||
| Хорошее, очень хорошее | |||||
| Среднее | |||||
| Плохое, очень плохое | И | ||||
| Затрудняюсь ответить | |||||
| Всего |
В табл.
2.1 на пересечении строк и столбцов находятся числа, показывающие, какое количество единиц анализа (в данном случае — респондентов) обладают одновременно данными градациями по переменным q10 и q12. Например, на пересечении первой строки и второго столбца стоит число 48 — это значит, что градацию «1» переменной q10 (считают материальное положение своей семьи хорошим или очень хорошим) и градацию «2» переменной q12 (считают политическую обстановку в России напряженной) одновременно отметили 48 человек.
Внизу таблицы сопряженности располагаются суммарные данные по всем колонкам, а с правого края таблицы — аналогичные суммы по всем строкам. Иными словами, сбоку справа и снизу находятся одномерные частотные распределения для переменных, использованных в таблице.
Можно ли по данным табл. 2.1 сразу дать ответ на вопрос о наличии зависимости между переменными q10 и q12? По всей вероятности, нет — стоящие в клетках таблицы числа ничего особенного не демонстрируют. Поставим вопрос иначе — а что, собственно, мы ищем? По всей видимости, при наличии зависимости между переменными q10 и q12 при разных значениях переменной q10 поведение данных по переменной q12 будет различным.
Если говорить о примере табл. 2.1 — это значит, что респонденты, по-разному оценивающие свое материальное положение, будут по-разному оценивать политическую обстановку в России.
Если бы количество респондентов, имеющих различные значения переменной q10, было одинаковым, в табл. 2.1 можно было бы сравнивать между собой строки и оценить, насколько схожи значения в клетках, располагающихся в одной колонке. Однако количество респондентов по строкам сильно разнится, поэтому для такого сравнения построим таблицу, в клетках которой располагаются не абсолютные количества единиц анализа, а процент от сумм по строкам. Другими словами, число респондентов в каждой строке берется за 100% и от этого числа считается процент в каждой клетке таблицы. Таким образом, мы как бы нормируем каждую строку таблицы и получаем возможность сравнения распределений по строкам (табл. 2.2).
Таблица 2.2 показывает, что оценка политической ситуации в России значительно отличается по группам респондентов, по-разному оценивающих материальное положение своей семьи, и, следовательно, имеется определенная зависимость между переменными q10 и q12.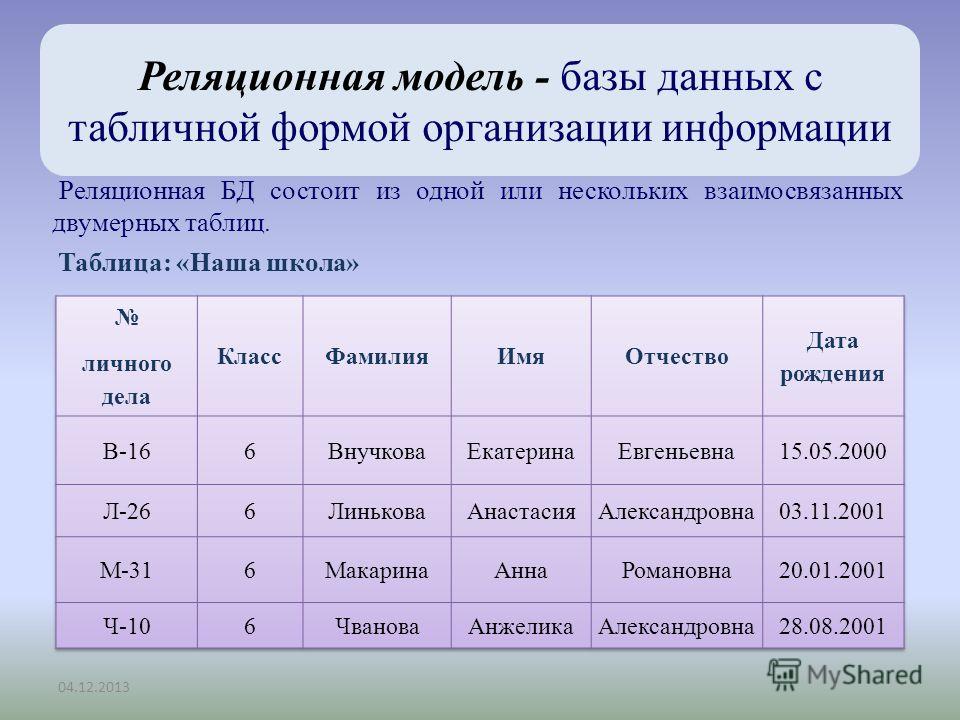
При анализе зависимостей двух переменных важнейшим является вопрос о том, какую из переменных считать зависимой, т.е. подверженной влиянию, а какую — независимой, т.е. влияющей. В табл. 2.1 и в последующих рассуждениях предполагалось, что оценка материального положения семьи — независимая переменная, иными словами.она влияет на оценку политической ситуации, которая, следовательно, выступает зависимой переменной. Если мы поменяем места ми переменные в модели и будем считать, что оценка политической ситуации оказывает влияние на оценку материального положения семьи, целесообразно изменить таблицу и проводить нормирование не от сумм по строкам, а от сумм по колонкам. Таблица 2.3 построена именно таким образом, т.е. использованы данные табл. 2.1, но нормированные по колонкам.
Таблица 2.2. Таблица сопряженности переменных q10 и q12, %
| q10 Как бы вы | q12 Как бы вы оценили в целом | Все | |||
| оценили | политическую обстановку в России? | го | |||
| в настоящее время материальное положение вашей семьи? | благопо
лучная.
спокойная
| напря женная | критическая. взрыво опасная | затруд няюсь отвеппъ | i |
| Хорошее, очень | 9,7 | 38,7 | 37,9 | 13,7 | 100,0 |
| хорошее | |||||
| Среднее | 1,5 | 36,7 | 51,2 | 10,6 | 100,0 |
| Плохое, очень | 1,2 | 16,8 | 73,6 | 8,5 | 100.0 |
| плохое | |||||
| Затрудняюсь | 21,4 | 53,6 | 25,0 | 100. 0
| |
| ответить | |||||
| Всего | 1,8 | 28,7 | 59,4 | 10,1 | 100.0 |
Очевидно, что при решении вопроса о зависимости между переменными q10 и q12 при анализе табл. 2.3 необходимо сравнивать распределения по разным колонкам таблицы, а не по строкам, как при анализе таблицы, представленной на рис. 2.2. Такое сравнение показывает, что среди респондентов, оценивающих политическую ситуацию в России как критическую, материальное положение своей семьи оценивают как плохое 49,1% респондентов (колонка 3, строка 3 табл. 2.3). В то же время среди оценивающих политическую ситуацию оптимистичнее, как напряженную, материальное положение своей семьи считают плохим 23,1% респондентов (колонка 3, строка 2 табл. 2.3).
Таблица 2.3. Таблица сопряженности переменных q10 n q12, %
| q10 Как бы вы оценили | q12 Как бы вы оценили в целом политическую обстановку в России? | Все го | |||
| в настоящее время материальное положение вашей семьи? | благопо
лучная.
спокойная
| напря женная | критическая, взрыво опасная | затруд няюсь ответить | |
| Хорошее, очень хорошее | 27,9 | 6,9 | 3,3 | 7,0 | 5,2 |
| Среднее | 46,5 | 69,1 | 46,6 | 56,8 | 54,1 |
| Плохое, очень плохое | 25,6 | 23,1 | 49,1 | 33,3 | 39,6 |
| Затрудняюсь ответить | 0,9 | 1,0 | 2,9 | 1,2 | |
| Всего | 100,0 | 100,0 | 100,0 | 100,0 | 100.0 |
Рис. 2.2. Меню команды Crosstabsпакета SPSS
При анализе таблиц сопряженности крайне важно помнить, что мы, по сути дела, ищем наличие (или отсутствие) определенных статистических, а не причинно-следственных зависимостей.
Вопрос о том, какая из переменных является причиной, т.е. оказывает влияние, а какая меняется вследствие этой причины, не может быть решен не только с помощью анализа таблиц, но и любым другим формально- статистическим методом. Это вопрос понимания той модели, которую мы проверяем методами построения таблиц либо другими статистическими приемами. Но результатом такой проверки не может быть утверждение: «наша модель верна», либо «наша модель неверна». Утверждать мы можем лишь то, что данные не противоречат (или, наоборот, противоречат) построенной модели, что само по себе отнюдь не является гарантией ее справедливости.
Иллюстрацию этой мысли можно найти у О. Генри. В рассказе «Вождь краснокожих» главный герой предложит изящную модель для ответа на вопрос о том, почему дует ветер — потому, что деревья качаются. Если собрать данные о ветре и поведении деревьев во время ветра, любой статистический метод покажет, что данные ни в коем случае не противоречат этой модели, что.видимо, и послужило Джиму основанием для столь глубокомысленного вывода.
Ряд распределения – упорядоченное распределение единиц совокупности оп определенному варьирующему признаку; это простая группировка, вкот известна численность едениц в группировках или удельный вес каждой группы в общем итоге. Ряды распр имеют 2 осн признака: 1. значение груп.признака (вариант Х), 2. частота- f или частость –w. Частота- f- численность отдельных вариантов, т.е.число, показывающее какое число раз (как часто встречается те или иные варианты. сумм f=N (N общий объем выборки). Частость— относительнымичастотами.–w-частота выраженная в % к итогу. W= f/ сумм f. Т.е. Относительные частоты – отношение частоты к объему выборки. Для создания частотной табл в SPSS: Выберите в меню команды Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Frequencies (Частоты) Появится диалоговое окно Frequencies.
Пр.: Задано распределение частот выборки объема = 20:
2 6 12
3 10 7
Написать распределение относительных частот.
Решение.Найдем относительные частоты, для чего разделим частоты на объем выборки:
=3/20 = 0,15, W2= 10/20 = 0,50, W3 = 7/20 = 0,35.
Напишем распределение относительных частот:
xi2 6 12
Wi0,15 0,50 0,35
Проверка: 0,15+0,50+ 0,35= 1.
В SPSS:Тест хи-квадрат (X2)
При проведении теста хи-квадрат проверяется взаимная независимость двух переменных таблицы сопряженности и благодаря этому косвенно выясняется зависимость обоих переменных. Две переменные считаются взаимно независимыми, если наблюдаемые частоты (f0) в ячейках совпадают с ожидаемыми частотами (fe).
Для того, чтобы провести тест хи-квадрат с помощью SPSS, выполните следующие действия:
· Выберите в меню команды Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Crosstabs… (Таблицы сопряженности)
· Кнопкой Reset (Сброс) удалите возможные настройки.
· Перенесите переменную sex в список строк, а переменную psyche — в список столбцов.
· Щелкните на кнопке Cells… (Ячейки). В диалоговом окне установите, кроме предлагаемого по умолчанию флажка Observed, еще флажки Expected и Standardized. Подтвердите выбор кнопкой Continue.
· Щелкните на кнопке Statistics… (Статистика).
Откроется описанное выше диалоговое окно Crosstabs: Statistics.
· Установите флажок Chi-square (Хи-квадрат). Щелкните на кнопке Continue, а в главном диалоговом окне — на ОК.
Вы получите следующую таблицу сопряженности.
Пол * Психическое состояние Таблица сопряженности
| Психическое состояние | Total | ||||||
| Крайне неустой-чивое | Неустой-чивое | Устой-чивое | Очень устойчивое | ||||
| Пол | женский | Count | |||||
| Expected Count | 7,9 | 16,6 | 17,0 | 2,5 | 44,0 | ||
Std. Residual
| 2,9 | ,3 | -1,9 | -.9 | |||
| Мужской | Count | ||||||
| Expected Count | 11,1 | 23,4 | 24,0 | 3,5 | 62,0 | ||
| Std. Residual | -2,4 | -,3 | 1,6 | ,8 | |||
| Total | Count | ||||||
| Expected Count | 19,0 | 40,0 | 41,0 | 6,0 | 106,0 |
Кроме того, в окне просмотра будут показаны результаты теста хи-квадрат:
Chi-Square Tests (Тестыхи-квадрат)
| Value (Значение) | df | Asymp. Sig. (2-sided) (Асимптотическая значимость (двусторонняя))
| |
| Pearson Chi-Square (Хи-квадрат по Пирсону) | 22,455 (а) | ,000 | |
| Likelihood Ratio (Отношение правдоподобия) | 23,688 | ,000 | |
| Linear-by-Linear Association (Зависимостьлинейный-линейный) | 20,391 | ,000 | |
| N of Valid Cases (Кол-во допустимых случаев) |
а. 2 cells (25,0%) have expected count less than 5. The minimum expected count is 2,49 (2 ячейки (25%) имеютожидаемуючастотуменее 5. Минимальная ожидаемая частота 2,49.)
Для вычисления критерия хи-квадрат применяются три различных подхода: формула Пирсона, поправка на правдоподобие и тест Мантеля-Хэнзеля. Если таблица сопряженности имеет четыре поля и ожидаемая вероятность менее 5, дополнительно выполняется точный тест Фишера.
Двумерные массивы
Каждая из команд объявления массива может создавать или изменять размер одномерных или двумерных массивов. Пример:
МАССИВ ТЕКСТ(atTopics;100;50) ` Создает текстовый массив, состоящий из 100 строк по 50 столбцов.
Двумерные массивы по сути являются объектами языка; вы не можете ни отобразить, ни распечатать их.
В предыдущем примере:
- atTopics — двумерный массив
- atTopics{8}{5} — 5-й элемент (5-й столбец…) 8-й строки
- atTopics{20} является 20-й строкой и представляет собой одномерный массив
- Size of array(atTopics) возвращает 100, т.е. количество строк
- Size of array(atTopics{17}) возвращает 50, что количество столбцов для 17-й строки
В следующем примере указатель на каждое поле каждой таблицы в базе данных хранится в двумерном массиве:
C_LONGINT($vlLastTable;$vlLastField)
C_LONGINT($vlFieldNumber)
` Создайте столько строк (пустых и без столбцов), сколько есть таблиц
$vlLastTable:=Получить номер последней таблицы
ARRAY POINTER(<>apFields;$vlLastTable;0) `2D-массив с X строк и нулевыми столбцами
` Для каждой таблицы
Для($vlTable;1;$vlLastTable)
If(Действителен ли номер таблицы($vlTable))
$vlLastField:=Получить номер последнего поля($vlTable)
` Задать значение элементов
$vlColumnNumber:=0
Для ($ vlField; 1; $ vlLastField)
If(Действителен ли номер поля($vlTable;$vlField))
$vlColumnNumber:=$vlColumnNumber+1
`Вставить столбец в строку текущей таблицы
ВСТАВИТЬ В МАССИВ(<>apFields{$vlTable};$vlColumnNumber;1)
`Назначить "ячейку" указателем
<>apFields{$vlTable}{$vlColumnNumber}:=Field($vlTable;$vlField)
Конец, если
Конец для
Конец, если
Конец для
При условии, что этот двумерный массив был инициализирован, вы можете получить указатели на поля для конкретной таблицы следующим образом:
` Получить указатели на поля таблицы, отображаемой в данный момент на экране:
COPY ARRAY(◊apFields{Table(Текущая таблица формы)};$apTheFieldsIamWorkingOn)
` Инициализировать логические поля и поля даты
For($vlElem;1;Размер массива($apTheFieldsIamWorkingOn))
Дело
:(Тип($apTheFieldsIamWorkingOn{$vlElem}->)=Дата)
$apTheFieldsIamWorkingOn{$vlElem}->:= Текущая дата
:(Type($apTheFieldsIamWorkingOn{$vlElem}->)=логический)
$apTheFieldsIamWorkingOn{$vlElem}->:=True
Конечный случай
Конец для
Примечание : Как видно из этого примера, строки двумерных массивов могут быть одного или разных размеров.
Программирование на Lua: 11.2
Программирование на Lua: 11.2 Это первое издание было написано для Lua 5.0. Несмотря на то, что они по-прежнему актуальны для более поздних версий, есть некоторые отличия.
Четвертое издание ориентировано на Lua 5.3 и доступно на Amazon и в других книжных магазинах.
Покупая книгу, вы также помогаете проекту Lua.
| Программирование на Луа | ||
| Часть II. Таблицы и объекты Глава 11. Структуры данных |
В Lua есть два основных способа представления матриц.
Первый — использовать массив массивов,
то есть таблица, в которой каждый элемент является другой таблицей.
Например, вы можете создать матрицу нулей с
размеры N по M со следующим кодом:
mt = {} -- создаем матрицу
для i=1,N сделать
mt[i] = {} -- создать новую строку
для j=1,M сделать
мт [я] [j] = 0
конец
конец
Поскольку таблицы в Lua являются объектами,
вам нужно создать каждую строку явно, чтобы создать матрицу.
С одной стороны, это, конечно, более многословно, чем просто
объявление матрицы, как в C или Pascal.
С другой стороны, это дает больше гибкости.
Например, вы можете создать треугольную матрицу, изменив
линия
для j=1,M сделать
в предыдущем примере к
для j = 1, я делаю
С этим кодом треугольная матрица использует только половину памяти.
оригинального. Второй способ представить матрицу в Lua — составить
два индекса в один.
Если два индекса являются целыми числами,
вы можете умножить первый на константу, а затем добавить
второй индекс.
При таком подходе
следующий код создаст
наша матрица нулей размерами N на M :
mt = {} -- создаем матрицу
для i=1,N сделать
для j=1,M сделать
мт[я*М + j] = 0
конец
конец
Если индексы являются строками,
вы можете создать один индекс, объединяющий оба индекса
с символом между ними, чтобы разделить их.
Например, вы можете проиндексировать матрицу m строковыми индексами s и t с кодом m[s. ,
при условии, что оба 
.':'..t] s и t не содержат двоеточий
(иначе пары типа ( "a:" , "b" ) и ( "a" , ":b" )
свернется в один индекс "a::b" ).
В случае сомнений,
вы можете использовать управляющий символ, например `\0 ´
для разделения индексов.
Довольно часто в приложениях используется разреженная матрица ,
матрица, в которой большинство элементов равно 0 или нулю.
Например, вы можете представить граф его матрицей смежности,
который имеет значение x в позиции m,n только когда
узлы м и н связаны стоимостью х ;
когда эти узлы не связаны,
значение в позиции m,n равно nil .
Чтобы представить граф с десятью тысячами узлов,
где каждый узел имеет около пяти соседей,
вам понадобится матрица со ста миллионами элементов
(квадратная матрица с 10 000 столбцов и 10 000 строк),
но примерно только пятьдесят тысяч из них будут не ниль (пять ненулевых столбцов для каждой строки,
соответствующие пяти соседям каждого узла).