Двоичные числа в десятичной записи. Двоичная система счисления
Понятие смешанной системы счисления
Среди систем счисления выделяют класс так называемых смешанных систем счисления .
Определение 1
Смешанной называется такая система счисления , в которой числа, заданные в некоторой системе счисления с основанием $P$ изображаются с помощью цифр другой системы счисления с основанием $Q$, где $Q
При этом в такой системе счисления во избежание разночтения для изображения каждой цифры системы с основанием $P$ отводится одинаковое количество разрядов системы с основанием $Q$, достаточное для представления любой цифры системы с основанием $P$.
Примером смешанной системы счисления является двоично-десятичная система.
Практическое обоснование использования двоично-десятичной системы счисления
Поскольку человек в своей практике широко использует десятичную систему счисления, а для компьютера свойственно оперирование двоичными числами и двоичной арифметикой, был введен в практику компромиссный вариант — система двоично-десятичной записи чисел , которая, как правило, используется там, где присутствует необходимость частого использования процедуры десятичного ввода-вывода (например, электронные часы, калькуляторы и т.
Замечание 1
В некоторых типах ЭВМ в арифметико-логических устройствах (АЛУ) имеются специальные блоки десятичной арифметики, которые выполняют операции над числами, представленными в двоично-десятичном коде. Это позволяет в некоторых случаях существенно повысить производительность ЭВМ.
К примеру, в автоматизированной системе обработки данных используется большое количество чисел, а вычислений при этом немного. В подобном случае операции перевода чисел из одной системы в другую существенно превысили бы время выполнения операций по обработке информации. Микропроцессоры же используют чистые двоичные числа, однако при этом понимают и команды преобразования в двоично-десятичную запись. АЛУ AVR-микроконтроллера (как и других микропроцессоров) выполняет элементарные арифметические и логические операции над числами, представленными в двоичном коде, а именно:
считывает результаты преобразования АЦП;
в формате целых чисел или чисел с плавающей точкой выполняет обработку результатов измерения.
Однако окончательный результат при этом выводится на индикатор в десятичном формате, удобном для восприятия человеком.
Принципы построения двоично-десятичной системы счисления
При построении двоично-десятичной системы счисления для изображения каждой десятичной цифры в ней отводится $4$ двоичных разряда, поскольку максимальная десятичная цифра $9$ кодируется как $10012$.
Например: $925_{10} = 1001 0010 0101_{2-10}$.
Рисунок 1.
В данной записи последовательные четверки двоичных разрядов изображают цифры $9$, $2$ и $5$ десятичной записи соответственно.
Для записи числа в двоично-десятичной системе счисления его необходимо сначала представить в десятичной системе, а затем каждую, входящую в состав числа, десятичную цифру представить в двоичной системе. При этом для написания различных десятичных цифр в двоичной системе счисления требуется разное количество двоичных разрядов. Чтобы обойтись без применения каких-либо разделительных знаков, при двоичном изображении десятичной цифры всегда записывается 4 двоичных разряда. Группа из этих четырех разрядов называется тетрадой .
Группа из этих четырех разрядов называется тетрадой .
Хотя в двоично-десятичной записи используются только цифры $0$ и $1$, она отличается от двоичного изображения данного числа, так как десятичный эквивалент двоичного числа в несколько раз больше десятичного эквивалента двоично-десятичного числа.
Например:
$1001 0010 0101_{(2)} = 2341_{(10)}$,
$1001 0010 0101_{(2)} = 925_{(2-10)}$.
Такая запись довольно часто используется как промежуточный этап при переводе числа из десятичной системы в двоичную и обратно. Так как число $10$ не является точной степенью числа $2$, то используются не все $16$ тетрад (тетрады, изображающие числа от $A$ до $F$ отбрасываются, так как эти числа считаются запрещенными), алгоритмы же арифметических операций над многозначными числами в этом случае более сложные, чем в основных системах счисления. И, тем не менее, двоично-десятичная система счисления используется даже на этом уровне во многих микрокалькуляторах и некоторых компьютерах.
Чтобы откорректировать результаты арифметических операций над числами, представленными в двоично-десятичном коде, в микропроцессорной технике используются команды, которые преобразуют результаты операций в двоично-десятичную систему счисления. При этом используется следующее правило: при получении в результате операции (сложения или вычитания) в тетраде числа, большего, чем $9$, к этой тетраде прибавляют число $6$.
Например: $75+18=93$.
$10001101 \ (8D)$
В младшей тетраде появилась запрещенная цифра $D$. Прибавим к младшей тетраде $6$ и получим:
$10010011 \ (93)$
Как видим, несмотря на то, что сложение осуществлялось в двоичной системе счисления результат операции получился в двоично-десятичной.
Замечание 2
Поразрядное уравновешивание часто осуществляют на основе двоично-десятичной системы счисления . Применение двоичной и двоично-десятичной системы счисления наиболее целесообразно, поскольку в этом случае число тактов уравновешивания оказывается наименьшим среди прочих систем счисления. Заметим, что применение двоичного кода позволяет примерно на $20\%$ уменьшить время обработки компенсирующего напряжения по сравнению с двоично-десятичным.
Заметим, что применение двоичного кода позволяет примерно на $20\%$ уменьшить время обработки компенсирующего напряжения по сравнению с двоично-десятичным.
Преимущества использования двоично-десятичной системы счисления
Преобразование чисел из десятичной системы в двоично-десятичную систему счисления не связано с вычислениями и его легко реализовать, используя при этом простейшие электронные схемы, так как преобразовывается небольшое количество (4) двоичных цифр. Обратное же преобразование происходит в ЭВМ автоматически с помощью особой программы перевода.
Применение двоично-десятичной системы счисления совместно с одной из основных систем счисления (двоичной) позволяет разрабатывать и создавать высокопроизводительные ЭВМ, так как использование блока десятичной арифметики в АЛУ исключает при решении задач необходимость программированного перевода чисел из одной системы счисления в другую.
Поскольку две двоично-десятичные цифры составляют $1$ байт, с помощью которого можно представить значения чисел от $0$ до $99$, а не от $0$ до $255$, как при использовании $8$-разрядного двоичного числа, то используя $1$ байт для преставления каждых двух десятичных цифр, можно формировать двоично-десятичные числа с любым требуемым числом десятичных разрядов.
В двоичной системе счисления используются всего две цифры 0 и 1. Другими словами, двойка является основанием двоичной системы счисления. (Аналогично у десятичной системы основание 10.)
Чтобы научиться понимать числа в двоичной системе счисления, сначала рассмотрим, как формируются числа в привычной для нас десятичной системе счисления.
В десятичной системе счисления мы располагаем десятью знаками-цифрами (от 0 до 9). Когда счет достигает 9, то вводится новый разряд (десятки), а единицы обнуляются и счет начинается снова. После 19 разряд десятков увеличивается на 1, а единицы снова обнуляются. И так далее. Когда десятки доходят до 9, то потом появляется третий разряд – сотни.
Двоичная система счисления аналогична десятичной за исключением того, что в формировании числа участвуют всего лишь две знака-цифры: 0 и 1. Как только разряд достигает своего предела (т.е. единицы), появляется новый разряд, а старый обнуляется.
Попробуем считать в двоичной системе:
0 – это ноль
1 – это один (и это предел разряда)
10 – это два
11 – это три (и это снова предел)
100 – это четыре
101 – пять
110 – шесть
111 – семь и т. д.
д.
Перевод чисел из двоичной системы счисления в десятичную
Не трудно заметить, что в двоичной системе счисления длины чисел с увеличением значения растут быстрыми темпами. Как определить, что значит вот это: 10001001? Непривычный к такой форме записи чисел человеческий мозг обычно не может понять сколько это. Неплохо бы уметь переводить двоичные числа в десятичные.
В десятичной системе счисления любое число можно представить в форме суммы единиц, десяток, сотен и т.д. Например:
1476 = 1000 + 400 + 70 + 6
1476 = 1 * 10 3 + 4 * 10 2 + 7 * 10 1 + 6 * 10 0
Посмотрите на эту запись внимательно. Здесь цифры 1, 4, 7 и 6 — это набор цифр из которых состоит число 1476. Все эти цифры поочередно умножаются на десять возведенную в ту или иную степень. Десять – это основание десятичной системы счисления. Степень, в которую возводится десятка – это разряд цифры за минусом единицы.
Аналогично можно разложить и любое двоичное число. Только основание здесь будет 2:
10001001 = 1*2 7 + 0*2 6 + 0*2 5 + 0*2 4 + 1*2 3 + 0*2 2 + 0*2 1 + 1*2 0
1*2 7 + 0*2 6 + 0*2 5 + 0*2 4 + 1*2 3 + 0*2 2 + 0*2 1 + 1*2 0 = 128 + 0 + 0 + 0 + 8 + 0 + 0 + 1 = 137
Т. е. число 10001001 по основанию 2 равно числу 137 по основанию 10. Записать это можно так:
е. число 10001001 по основанию 2 равно числу 137 по основанию 10. Записать это можно так:
10001001 2 = 137 10
Почему двоичная система счисления так распространена?
Дело в том, что двоичная система счисления – это язык вычислительной техники. Каждая цифра должна быть как-то представлена на физическом носителе. Если это десятичная система, то придется создать такое устройство, которое может быть в десяти состояниях. Это сложно. Проще изготовить физический элемент, который может быть лишь в двух состояниях (например, есть ток или нет тока). Это одна из основных причин, почему двоичной системе счисления уделяется столько внимания.
Перевод десятичного числа в двоичное
Может потребоваться перевести десятичное число в двоичное. Один из способов – это деление на два и формирование двоичного числа из остатков. Например, нужно получить из числа 77 его двоичную запись:
77 / 2 = 38 (1 остаток)
38 / 2 = 19 (0 остаток)
19 / 2 = 9 (1 остаток)
9 / 2 = 4 (1 остаток)
4 / 2 = 2 (0 остаток)
2 / 2 = 1 (0 остаток)
1 / 2 = 0 (1 остаток)
Собираем остатки вместе, начиная с конца: 1001101. Это и есть число 77 в двоичном представлении. Проверим:
Это и есть число 77 в двоичном представлении. Проверим:
1001101 = 1*2 6 + 0*2 5 + 0*2 4 + 1*2 3 + 1*2 2 + 0*2 1 + 1*2 0 = 64 + 0 + 0 + 8 + 4 + 0 + 1 = 77
Эта система имеет основание S = 10, но каждая цифра изображается четырехразрядным двоичным числом, называемым тетрадой. Обычно данная система счисления используется в ЭВМ при вводе и выводе информации. Однако в некоторых типах ЭВМ в АЛУ имеются специальные блоки десятичной арифметики, выполняющие операции над числами в двоично-десятичном коде. Это позволяет в ряде случаев существенно повышать производительность ЭВМ.
Например, в автоматизированной системе обработки данных чисел много, а вычислений мало. В этом случае операции, связанные с переводом чисел из одной системы в другую, существенно превысили бы время выполнения операций по обработке информации.
Перевод чисел из десятичной системы в двоично-десятичную весьма прост и заключается в замене каждой цифры двоичной тетрадой.
Пример.
Записать десятичное
число 572. 38 (10) в двоично-десятичной
системе счисления.
38 (10) в двоично-десятичной
системе счисления.
Обратный перевод также прост: необходимо двоично-десятичное число разбить на тетрады от точки влево (для целой части) и вправо (для дробной), дописать необходимое число незначащих нулей, а затем каждую тетраду записать в виде десятичной цифры.
Пример.
Записать двоично-десятичное число 10010.010101 (2-10) в десятичной системе счисления.
Перевод чисел из двоично-десятичной в двоичную систему осуществляется по общим правилам, описанным выше.
2.3. Восьмеричная система счисления
В восьмеричной системе счисления употребляются всего восемь цифр, т.е. эта система счисления имеет основание S = 8. В общем виде восьмеричное число выглядит следующим образом:
где
.
Восьмеричная
система счисления не нужна ЭВМ в отличие
от двоичной системы. Она удобна как
компактная форма записи чисел и
используется программистами (например,
в текстах программ для более краткой и
удобной записи двоичных кодов команд,
адресов и операндов). В восьмеричной
системе счисления вес каждого разряда
кратен восьми или одной восьмой, поэтому
восьмиразрядное двоичное число позволяет
выразить десятичные величины в пределах
0-255, а восьмеричное охватывает диапазон
0-99999999 (для двоичной это составляет 27
разрядов).
В восьмеричной
системе счисления вес каждого разряда
кратен восьми или одной восьмой, поэтому
восьмиразрядное двоичное число позволяет
выразить десятичные величины в пределах
0-255, а восьмеричное охватывает диапазон
0-99999999 (для двоичной это составляет 27
разрядов).
Поскольку 8=2 3 , то каждый восьмеричный символ можно представить трехбитовым двоичным числом. Для перевода числа из двоичной системы счисления в восьмеричную необходимо разбить это число влево (для целой части) и вправо (для дробной) от точки (запятой) на группы по три разряда (триады) и представить каждую группу цифрой в восьмеричной системе счисления. Крайние неполные триады дополняются необходимым количеством незначащих нулей.
Пример.
Двоичное число 10101011111101 (2) записать в восьмеричной системе счисления.
Пример.
Двоичное число 1011.0101 (2) записать в восьмеричной системе счисления.
Перевод
из восьмеричной системы счисления в
двоичную осуществляется путем
представления каждой цифры восьмеричного
числа трехразрядным двоичным числом
(триадой).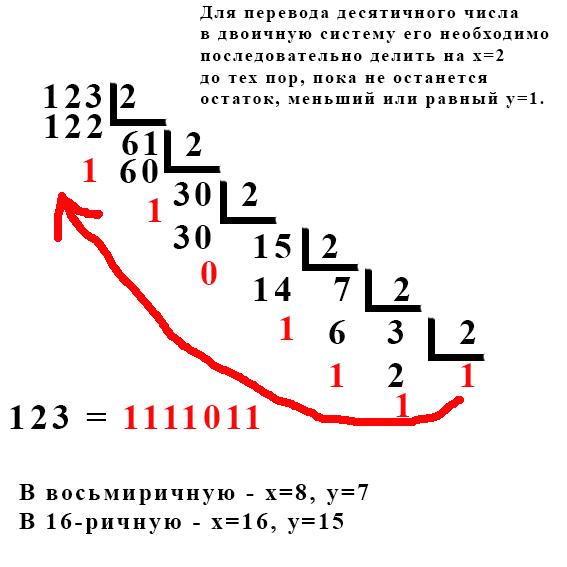
2.4. Шестнадцатеричная система счисления
Эта система счисления имеет основание S = 16. В общем виде шестнадцатеричное число выглядит следующим образом:где
.
Шестнадцатеричная система счисления позволяет еще короче записывать многоразрядные двоичные числа и, кроме того, сокращать запись 4-разрядного двоичного числа, т.е. полубайта, поскольку 16=2 4 . Шестнадцатеричная система также применяется в текстах программ для более краткой и удобной записи двоичных чисел.
Для перевода числа из двоичной системы счисления в шестнадцатеричную необходимо разбить это число влево и вправо от точки на тетрады и представить каждую тетраду цифрой в шестнадцатеричной системе счисления.
Пример.
Двоичное число 10101011111101 (2) записать в шестнадцатеричной системе.
Пример.
Двоичное число 11101.01111 (2) записать в шестнадцатеричной системе.
Для
перевода числа из шестнадцатеричной
системы счисления в двоичную, необходимо,
наоборот, каждую цифру этого числа
заменить тетрадой.
В заключение следует отметить, что перевод из одной системы счисления в другую произвольных чисел можно осуществлять по общим правилам, описанным в разделе “Двоичная система счисления”. Однако на практике переводы чисел из десятичной системы в рассмотренные системы счисления и обратно осуществляются через двоичную систему счисления.
Кроме того, следует помнить, что шестнадцатеричные и восьмеричные числа – это только способ представления больших двоичных чисел, которыми фактически оперирует процессор. При этом шестнадцатеричная система оказывается предпочтительнее, поскольку в современных ЭВМ процессоры манипулируют словами длиной 4, 8, 16, 32 или 64 бита, т.е. длиной слов, кратной 4. В восьмеричной же системе счисления предпочтительны слова, кратные 3 битам, например слова длиной 12 бит (как в PDP-8 фирмы DEC).
Примером смешанной системы счисления является двоично-десятичная система . В двоично-десятичной системе счисления для изображения каждой десятичной цифры отводится 4 двоичных разряда, поскольку максимальная десятичная цифра 9 кодируется как 1001 2 .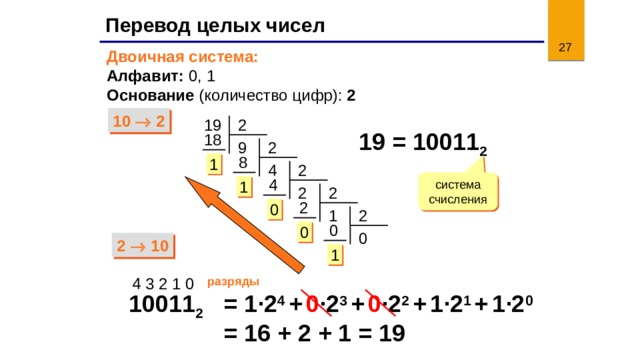 Например,
Например,
925 10 = 1001 0010 0101 2-10 .
Здесь последовательные четверки (тетрады) двоичных разрядов изображают цифры 9, 2 и 5 десятичной записи соответственно.
Хотя в двоично-десятичной записи используются только цифры 0 и 1, эта запись отличается от двоичного изображения данного числа. Например, двоичный код 1001 0010 0101 соответствует десятичному числу 2341, а не 925.
В случае если P=Q l (l – целое положительное число), запись любого числа в смешанной системе счисления тождественно совпадает с изображением этого числа в системе счисления с основанием Q. Примерами такой смешанной системы счисления являются двоично-восьмеричная и двоично-шестнадцатеричная.
Например,
A2 16 = 1010 0010 2 = 1010 0010 2-16
ПРЕДСТАВЛЕНИЕ ОТРИЦАТЕЛЬНЫХ ЧИСЕЛ В ФОРМАТЕ С ФИКСИРОВАННОЙ ЗАПЯТОЙ (ТОЧКОЙ)
В компьютерах в целях упрощения выполнения арифметических операций применяются специальные двоичные коды для представления отрицательных чисел: обратный и дополнительный.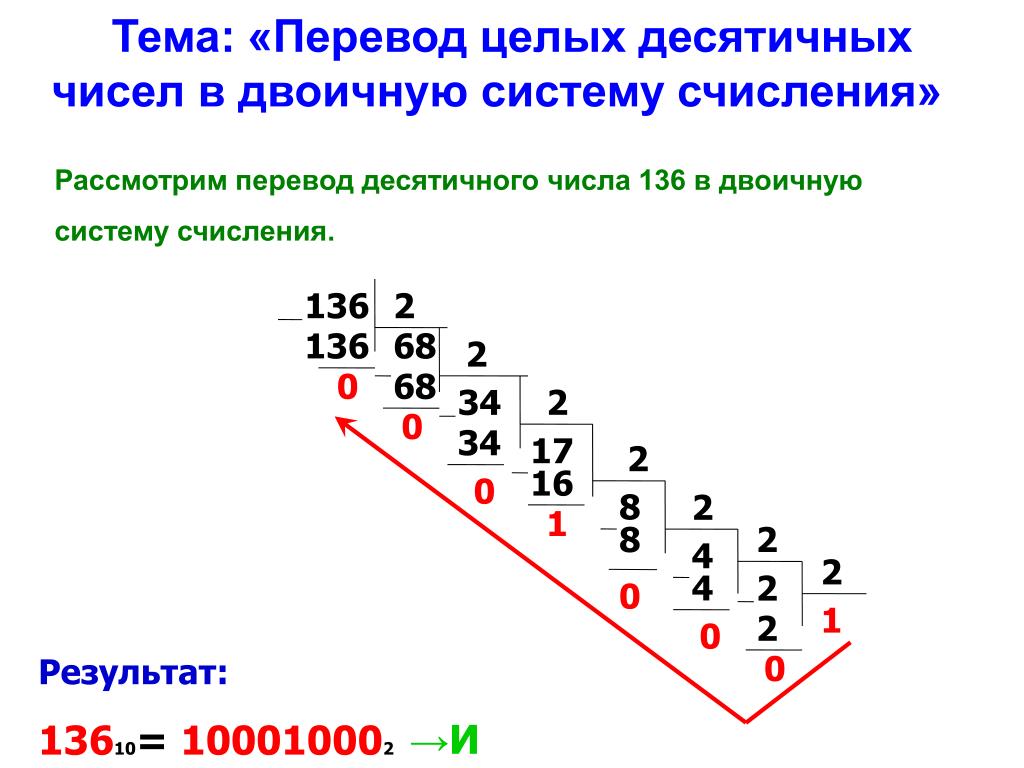 При помощи этих кодов упрощается определение знака результата операции при алгебраическом сложении. Операция вычитания (или алгебраического сложения) сводится к арифметическому сложению операндов, облегчается выработка признаков переполнения разрядной сетки. В результате упрощаются устройства компьютера, выполняющих арифметические операции.
При помощи этих кодов упрощается определение знака результата операции при алгебраическом сложении. Операция вычитания (или алгебраического сложения) сводится к арифметическому сложению операндов, облегчается выработка признаков переполнения разрядной сетки. В результате упрощаются устройства компьютера, выполняющих арифметические операции.
Известно, что одним из способов выполнения операции вычитания является замена знака вычитаемого на противоположный и прибавление его к уменьшаемому:
А — В = А + (- В)
Этим операцию арифметического вычитания заменяют операцией алгебраического сложения, которую можно выполнить при помощи двоичных сумматоров.
Для машинного представления отрицательных чисел используют коды прямой, дополнительный, обратный . Упрощенное определение этих кодов может быть дано следующим образом. Если число А в обычном двоичном коде — прямом двоичном коде, изобразить как
[A] пр = 0.an an-1 an-2…..a1 a0,
тогда число -А в этом же коде представляется как
[-A]пр = 1. an an-1 an-2…..a1 a0,
an an-1 an-2…..a1 a0,
а в обратном (инверсном) коде это число будет иметь вид:
[-A]об = 1.an an-1 an-2…..a1 a0,
ai = 1, если ai = 0,
ai = 0, если ai = 1,
a i — цифра i -того разряда двоичного числа. Следовательно, при переходе от прямого кода к обратному все цифры разрядов матиссы числа инвертируются.
Тогда число -A в дополнительном коде изображается в виде
[-A]доп = [-A]об + 1
Таким образом, для получения дополнительного кода отрицательных чисел нужно сначала инвертировать цифровую часть исходного числа, в результате чего получается его обратный код, а затем добавить единицу в младший разряд цифровой части числа.
Дополнительный код некоторого числа получается его заменой на новое число, дополняющее его до числа, равного весу разряда, следующего за самым старшим разрядом разрядной сетки, используемой для представления мантиссы числа в формате с фиксированной запятой. Поэтому такой код числа называется дополнительным.
Представим, что мы имеем только два разряда для представления чисел в десятичной системе счисления. Тогда максимальное число, которое можно изобразить будет 99, а вес третьего несуществующего старшего разряда будет 10 2 , т.е. 100. В таком случае для числа 20 дополнительным будет число 80, которое дополняет 20 до 100 (100 — 20 = 80). Следовательно по определению вычитание
можно заменить на сложение:
Здесь старшая единица выходит за пределы выделенной разрядной сетки, в которой остается только число 30, т.е. результат вычитания из 50 числа 20.
А теперь рассмотрим похожий пример для чисел, представленных 4-х разрядным двоичным кодом. Найдем дополнительное число для 0010 2 = 210. Надо из 0000 вычесть 0010, получим 1110, которое и является дополнительным кодом 2. Разряд, изображенный в квадратных скобках на самом деле не существует. Но так как у нас 4-х разрядная сетка, то выполнить такое вычитание в принципе невозможно, а тем более мы стараемся избавиться от вычитания. Поэтому дополнительный код числа получают способом, описанным ранее, т.е. сначала получают обратный код числа, а затем прибавляют к нему 1. Проделав все это с нашим числом (2), нетрудно убедиться, что получится аналогичный ответ.
Поэтому дополнительный код числа получают способом, описанным ранее, т.е. сначала получают обратный код числа, а затем прибавляют к нему 1. Проделав все это с нашим числом (2), нетрудно убедиться, что получится аналогичный ответ.
Подчеркнем, что дополнительный и обратный коды используются только для представления отрицательных двоичных чисел в форме с фиксированной запятой . Положительные числа в этих кодах не меняют своего изображения и представляются как в прямом коде.
Таким образом, цифровые разряды отрицательного числа в прямом коде остаются неизменными, а в знаковой части записывается единица.
Рассмотрим простые примеры.
Семерка в прямом коде представляется так:
пр = 0.0001112
Число -7 в прямом коде:
[-7]пр = 1.0001112,
а в обратном коде будет иметь вид
[-7]об = 1.1110002,
т.е. единицы заменяются нулями, а нули единицами. То же число в дополнительном коде будет:
[-7]доп = 1.1110012.
Рассмотрим еще раз как процедура вычитания, при помощи представления вычитаемого в дополнительном коде, сводится к процедуре сложения. Вычтем из 10 число 7: 10 — 7 = 3. Если оба операнда представлены в прямом коде, то процедура вычитания выполняется так:
Вычтем из 10 число 7: 10 — 7 = 3. Если оба операнда представлены в прямом коде, то процедура вычитания выполняется так:
-1.000111
А если вычитаемое, т.е. -7, представить в дополнительном коде, то процедура вычитания сводится к процедуре сложения:
+ 1.111001
1 0.000011 = 310.
В настоящее время в компьютерах для представления отрицательных чисел в формате с фиксированной запятой обычно используется дополнительный код.
Формой представления чисел в цифровых автоматах называется совокупность правил, позволяющих установить взаимное соответствие между записью числа и его количественным эквивалентом.
Машинное (автоматное) изображение числа это есть представление числа в разрядной сетке цифрового автомата . Условное обозначение машинного изображения числа, например, A будем представлять как [A] .
Из-за ограниченной длины машинных слов, множество чисел, которые можно представить в машине конечное. Сравнение различных форм представления чисел в компьютерах обычно производится на основе оценки диапазона и точности представления числа .
В повседневной практике наиболее распространенной является форма представления чисел в виде последовательности цифр, разделенной запятой на целую и дробную части. Числа, представленные в такой форме, называются числами с естественной запятой или числами в естественной форме . В естественной форме число записывается в естественном натуральном виде, например 12560 — целое число, 0,003572 — правильная дробь, 4,89760 — неправильная дробь.
При представлении чисел в такой форме обязательно требуется для каждого числа указание о положении его запятой в разрядной сетке, выделенной для представления числа в машине, что требует дополнительных аппаратных затрат достаточно большого объема. Поэтому в компьютерах получили распространение две другие формы представления: с фиксированной и плавающей запятой (точкой) .
Необходимость в указании положения запятой отпадает, если место запятой в разрядной сетки машины заранее фиксировано раз и навсегда. Такая форма представления чисел называется представлением с фиксированной запятой (точкой) .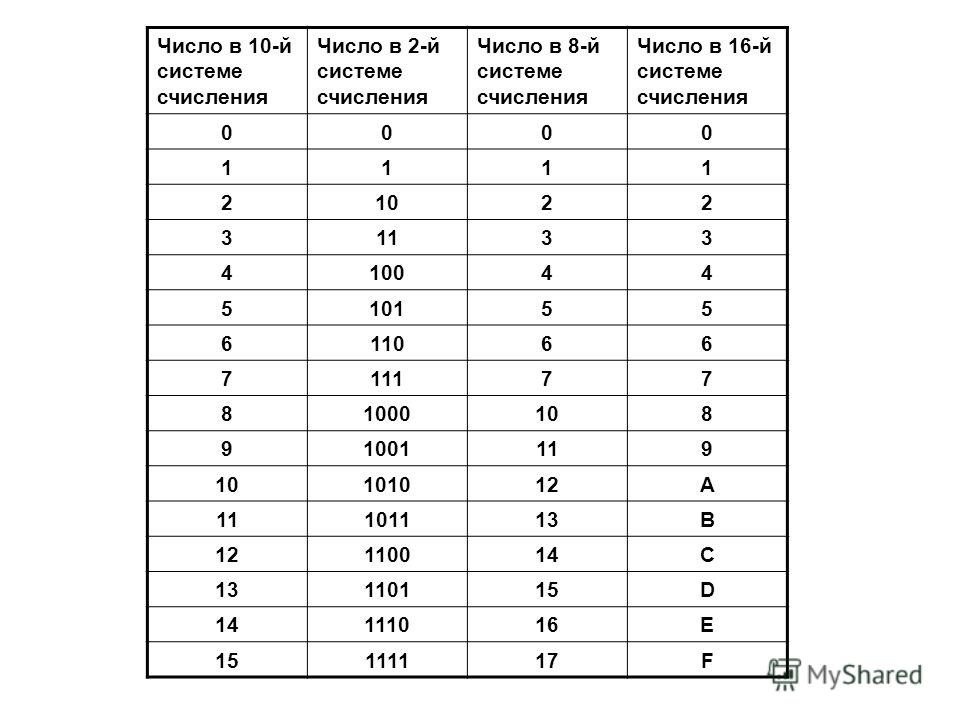
Так как числа бывают положительные и отрицательные, то формат (разрядная сетка) машинного изображения разбивается на знаковую часть и поле числа . В поле числа размещается само изображение числа, которое мы будем условно называть мантиссой числа. Для кодирования знака числа используется самый старший разряд разрядной сетки, отведенной для изображения двоичного числа, а остальные разряды отводятся под мантиссу числа. Положение запятой в разрядной сетке строго фиксируется, обычно или правее самого младшего разряда мантиссы, или левее самого старшего. В первом случае число представляется как целое, во втором — как правильная дробь . В настоящее время в подавляющем большинстве в компьютерах в формате с фиксированной точкой представляются целые числа.
В знаковую часть записывается информация о знаке числа. Принято, что знак положительного числа «+» изображается символом 0, а знак отрицательного числа «-» изображается символом 1.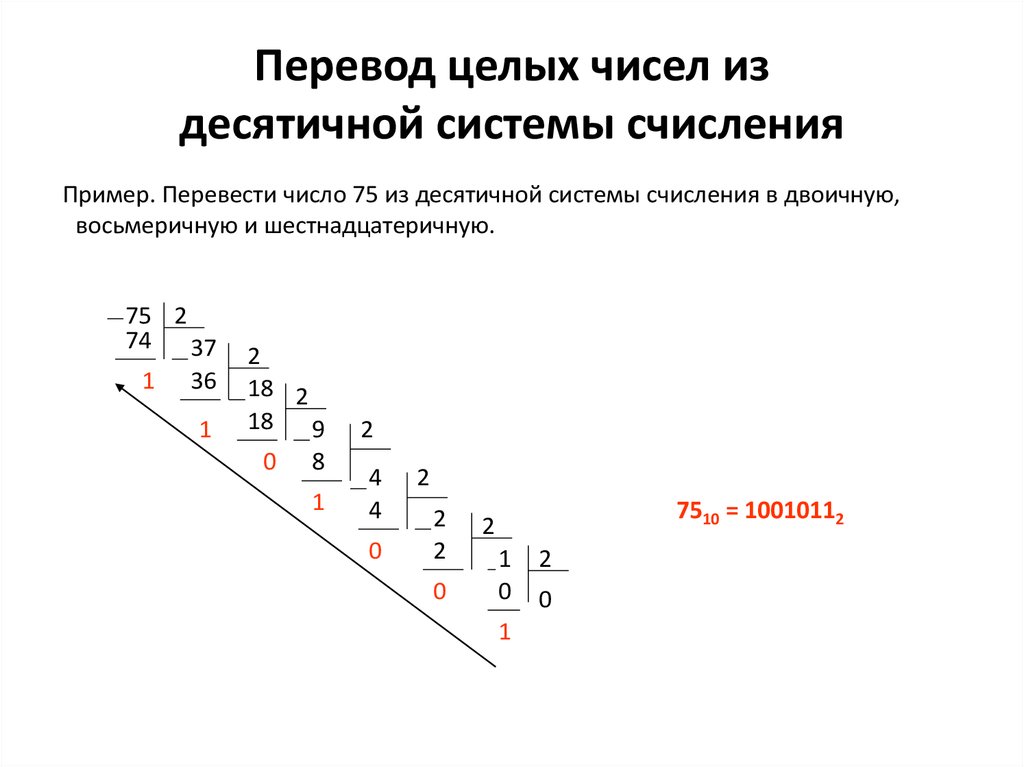
Например, в двоичном коде, используя 6-разрядную сетку, число 7 в форме с фиксированной запятой можно представить в виде:
где цифра левее точки это знак числа, а пять цифр правее точки — мантисса числа в прямом коде. Здесь подразумевается, что запятая фиксирована правее младшего разряда , а точка в изображении числа в данном случае просто разделяет знаковый бит от мантиссы числа.
В дальнейшем часто будет использоваться в примерах такой вид представления числа в машинной форме. Можно использовать и другую форму представления числа в машинной форме:
где знаковый разряд выделяется квадратными скобками.
Количество разрядов в разрядной сетке, отведенное для изображения мантиссы числа, определяет диапазон и точность представления числа с фиксированной запятой. Максимальное по абсолютной величине двоичное число изображается единицами во всех разрядах, исключая знаковый, т.е. для целого числа
|A|max = (2 (n -1) — 1),
где n — полная длина разрядной сетки. В случае 16-разрядной сетки
В случае 16-разрядной сетки
|A| max = (2 (16-1) — 1) = 32767 10 ,
т.е. диапазон представления целых чисел в этом случае будет от +3276710 до -3276710 .
Для случая, когда запятая фиксируется правее младшего разряда мантиссы, т.е. для целых чисел, числа, у которых модуль больше, чем
(2 (n-1) — 1) и меньше единицы не представляются в форме с фиксированной запятой. Числа, по абсолютной величине меньше единицы младшего разряда разрядной сетки, называются в этом случае машинным нулем.Отрицательный ноль запрещен.
В некоторых случаях, когда можно оперировать только модулями чисел, вся разрядная сетка, включая самый старший разряд, отводится для представления числа, что позволяет расширить диапазон изображения чисел.
Системы счисления. Двоичная система счисления (занятие кружка)
Цели занятия:
- Обучающая – формирование новых знаний, умений и навыков по переводу десятичных чисел в двоичную систему счисления и из двоичной системы в десятичную.
- Развивающая – развитие мышления учащихся посредством анализа, сравнения и обобщения изучаемого материала, развитие самостоятельности и речи;
- Воспитательная – активизация познавательной и творческой активности учащихся, воспитание чувства ответственности.
Ход занятия
1. ДЕСЯТИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ
Преимущества десятичной системы не математические, а зоологические.
Если бы у нас на руках было не десять пальцев, а восемь, то человечество
пользовалось бы восьмеричной системой.
Н. Н. Лузин
По-чукотски глагол “считать” (“рылгык”)
происходит от слова “рылг” — палец и значит,
собственно, “пальчить”. “Десять” по-чукотски
обозначается как “две руки”, а слово
“двадцать” происходит от слова “человек” —
весь человек, т. е. все пальцы на руках и ногах.
е. все пальцы на руках и ногах.
Вообще, видимо, сначала у многих народов господствовала не десятичная, а двадцатеричная система. Это отразилось и в строении числительных: например, по-французски 80 обозначается quatre-vingt, т. е. “четырежды 20”,- совсем как по-чукотски.
Слово “сорок” в русском языке резко отличается от других числительных, обозначающих десятки (трихдцать, пятьхдесят), а чтобы обозначить очень большое число, употребляют старинное выражение “сорок сороков”.
Не все народы и не всегда считают только с
помощью пальцев. Иногда для этого пользуются
другими частями тела. Например, одно из
папуасских племен Новой Гвинеи считает так:
мизинец левой руки, безымянный, средний,
указательный, большой палец, запястье, локоть,
плечо, левая сторона груди, правая сторона груди.
Но характерно, что и здесь используется в
качестве опоры именно человеческое тело. Лишь в
дальнейшем числительные отрываются от этой
опоры и начинают употребляться самостоятельно.
2. СИСТЕМЫ СЧИСЛЕНИЯ
Системы счисления — это способы записи чисел в виде, удобном для прочтения и выполнения арифметических операций.
При подсчете многих объектов удобно группировать их по нескольку штук. Такая группировка облегчает счет. Поскольку удобно считать на пальцах, предметы часто группируют по 5 или по 10 (впрочем, иногда и по 12- вспомните слово “дюжина”; иногда и по 7 — в неделе 7 дней).
В римской системе счисления1 есть особые знаки: для единицы — I, пяти — V, десяти — X, пятидесяти — L, ста — С, пятисот -D, тысячи — М. Примеры записи чисел в римской системе приведены в таблице. Римская система более или менее пригодна для выполнения операций сложения и вычитания, но совсем не удобна для умножения и деления.
Если в записи положение цифр (знаков) не играет
важной роли, то систему счисления называют
непозиционной. Непозиционными были системы
счисления у древних египтян, греков. У древних
вавилонян система счисления вначале тоже была
непозиционной, но впоследствии они научились
использовать информацию, заключенную в порядке
записи цифр, и перешли к позиционной системе
счисления. При этом в отличие от используемой
нами системы счисления, в которой значение цифры
меняется в 10 раз при перемещении на одну позицию,
у вавилонян при перемещении знака происходило
изменение значения числа в 60 раз. Следы
вавилонской системы счисления сохранились до
наших дней: в часе — 60 минут, в минуте – 60 секунд.
У древних
вавилонян система счисления вначале тоже была
непозиционной, но впоследствии они научились
использовать информацию, заключенную в порядке
записи цифр, и перешли к позиционной системе
счисления. При этом в отличие от используемой
нами системы счисления, в которой значение цифры
меняется в 10 раз при перемещении на одну позицию,
у вавилонян при перемещении знака происходило
изменение значения числа в 60 раз. Следы
вавилонской системы счисления сохранились до
наших дней: в часе — 60 минут, в минуте – 60 секунд.
Запись чисел в различных системах счисления
Десятичная |
Римская |
Двоичная |
Троичная |
Четверичная |
1 |
I |
1 |
1 |
1 |
2 |
II |
10 |
2 |
2 |
3 |
щ |
11 |
10 |
3 |
4 |
IV |
100 |
11 |
10 |
5 |
V |
101 |
12 |
11 |
б |
VI |
110 |
20 |
12 |
7 |
VII |
111 |
21 |
13 |
8 |
VIII |
1000 |
22 |
20 |
9 |
IX |
1001 |
100 |
21 |
10 |
X |
1010 |
101 |
22 |
11 |
XI |
1011 |
102 |
23 |
12 |
XII |
1100 |
110 |
30 |
13 |
XIII |
1101 |
111 |
31 |
14 |
XIV |
1110 |
112 |
32 |
15 |
XV |
1111 |
120 |
33 |
16 |
XVI |
10000 |
121 |
100 |
17 |
XVII |
10001 |
122 |
101 |
18 |
XVIII |
10010 |
200 |
102 |
19 |
XIX |
10011 |
201 |
103 |
20 |
XX |
10100 |
202 |
110 |
21 |
XXI |
10101 |
210 |
111 |
22 |
XXII |
10110 |
211 |
112 |
28 |
XXVIII |
11100 |
1001 |
130 |
48 |
XLVIII |
110000 |
1210 |
300 |
101 |
CI |
1100101 |
10202 |
1211 |
151 |
CLI |
10010111 |
12121 |
2113 |
1966 |
MCMLXVI |
11110101110 |
2200211 |
132232 |
1980 |
MCMLXXX |
11110111100 |
2201100 |
132330 |
1997 |
MCMXCVII |
11111001101 |
2201222 |
133031 |
2000 |
ММ |
11111010000 |
2202002 |
133100 |
5000 |
МММММ |
1001110001000 |
20212012 |
1032020 |
Долгое время в вавилонской системе счисления
не было нуля, т. е. знака для “пропущенного”
разряда. В IX в. появился особый знак для нуля.
е. знака для “пропущенного”
разряда. В IX в. появился особый знак для нуля.
Десятичная система распространилась по всему миру.
Например, записывая 2653, мы имеем в виду число 2·103+6·102+5·101+3·10°. Особая роль отводится числу десять; все числа представляются в виде суммы различных степеней десяти с коэффициентами, принимающими значения от 0 до 9. Поэтому эта система и называется десятичной.
А что будет, если вместо десяти использовать какое-нибудь другое число, например шесть? По аналогии нам потребуется шесть цифр-символов. В качестве их мы можем взять знакомые нам символы 0, 1, 2, 3, 4, 5, которые будут обозначать числа от нуля до пяти. Число шесть мы примем за единицу следующего разряда, и поэтому в нашей новой системе счисления оно будет записываться так: 10.
Продолжая аналогию, мы можем представить любое
натуральное число в виде суммы различных
степеней шестерки с коэффициентами от нуля до
пяти. Например: 7=1·61+1·6°, 45=1·62+1·61+1·6°.
Например: 7=1·61+1·6°, 45=1·62+1·61+1·6°.
Поэтому в новой системе счисления, которая называется шестеричной, естественно записывать число 710 как 116, 4510 как 1136 (индекс у числа означает, что это число записано в данной системе счисления).
Нетрудно понять, что в шестеричной системе счисления можно записать любое натуральное число. Покажем, как это сделать для числа 45010. Наибольшее число, являющееся степенью шестерки и не превосходящее 450,- это 216. Разделим 450 на 216 с остатком: 450=2-216+18.
Неполное частное равно 2. Поэтому первой цифрой шестеричной записи числа 450 будет 2.
Остаток от деления равен 18. Разделим его на
предыдущую степень шестерки (на первом этапе мы
делили на б3, а теперь -на б2), с
остатком: 18=0-36+18. Неполное частное равно нулю,
поэтому вторая цифра — 0. Остаток равен 18.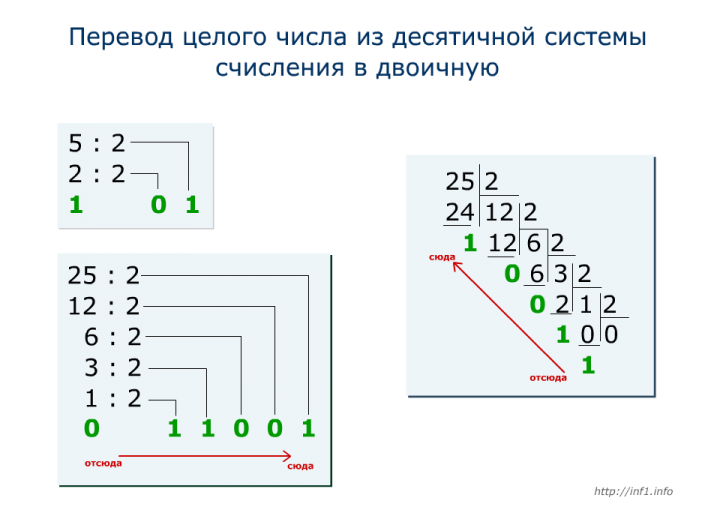 Разделим
с остатком 18 на б1: 18=3-6+0. Значит, третья
цифра равна 3, а остаток — 0. Таким образом,
последняя цифра равна 0. Итак, 45010=20306.
Разделим
с остатком 18 на б1: 18=3-6+0. Значит, третья
цифра равна 3, а остаток — 0. Таким образом,
последняя цифра равна 0. Итак, 45010=20306.
При построении новой системы счисления мы не пользовались никакими специфическими свойствами числа 6. Аналогично по любому натуральному числу л, большему 1, можно построить л-ичную систему счисления, в которой запись числа связана с его разложением по степеням числа л.
Еще в XVII в. немецкий математик Лейбниц
предложил перей-1и на двоичную систему счисления,
но этому помешала не только традиция, но и то, что
в двоичной системе счисления запись чисел
слишком длинна. Например: 10б=11010102. Однако в
XX в., когда были созданы компьютеры, оказалось,
что для выполнения арифметических операций на
машинах самой удобной является именно двоичная
система счисления. Удобным компромиссом между
человеком и машиной являются шее
шестнадцатеричная и восьмеричная системы
счисления. Дело I Юм, что очень легко переводить
числа из двоичной системы н любую из них, а по
краткости записи восьмеричная система почти
такая же, как десятичная, а шестнадцатеричная
даже короче.
Дело I Юм, что очень легко переводить
числа из двоичной системы н любую из них, а по
краткости записи восьмеричная система почти
такая же, как десятичная, а шестнадцатеричная
даже короче.
3.ДВОИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ
В двоичной системе счисления таблицы сложения и умножения удивительно просты:
| 0 + 0 = 0 | 0-0 = 0 |
| 0 + 1=1 | 0-1=0 |
| 1 + 1=10 | 1-1=1 |
Пользуясь этими таблицами, легко складывать и вычитать:
Эти примеры в десятичной системе выглядят следующим образом:
- 2 + 3 = 5;
- 7 + 5 = 12;
- 5-3 = 2;
- 435 + 23 = 458.
Умножение в двоичной системе:
В десятичной системе этот пример выглядят так: 29 * 5 = 145
В двоичной системе можно записывать не только целые числа. Например, двоичная запись 101,1010111 в десятичную систему переводится следующим образом
1·22+0·21+1·20+1·2-1+0·2-2+1·2-3+0·2-4+1·2-5+1·2-6+1·2-7= 4 + 1 + 1/2 + 1/8+ 1/64+ 1/128 = 5,6796875.
Операции над натуральными числами в n-ичной системе счисления выполняются в обычном порядке, с той лишь разницей, что для каждой системы счисления надо брать свои таблицы сложения и умножения. Например, для троичной системы счисления таблицы таковы:
+ 0 1 2 X 0 1 2 0 0 1 2 0 0 0 0 1 1 2 10 1 0 1 2 2 2 10 11 2 0 2 11
4. Решение задач.
Решение задач.
Задача 1.Сколько цифр необходимо иметь: а) в двоичной системе счисления; б) n-ичной системе счисления?
Задача 2.Запишите в десятичной системе счисления числа 101012, 101013, 2114, 1267, 15811.
Задача 3.Запишите число 10010 в двоичной, троичной, четверичной, пятеричной, шестеричной, семеричной, восьмеричной и девятеричной системах счисления.
Задача 4.Запишите число 11110 в одиннадцатеричной системе счисления (в качестве недостающей цифры 10 принято использовать букву А).
Задача 4.Запишите число 11101001112 в шестнадцатеричной системе счисления (в качестве недостающих цифр от 10 до 15 принято использовать буквы А, В, С, D, E, F).
Задача 5. Переведите число 100101110011012 из
двоичной в восьмеричную систему счисления.
Задача 6. Составьте таблицы сложения и умножения для систем счисления: а) четверичной; б) пятеричной ; в) пятнадцатеричной.
Задача 7. Вычислите:
а) 11002+11012;
б) 2013-1023.
Задача 8. Сначала выполните действия в десятичной системе, затем переведите числа в двоичную систему, выполните в ней те же действия, ответ переведите в десятичную систему: а) 20+40; б) 1998+23; г) 23·34534; д) 460·20.
Литература.
1. Петраков И.С. Математические кружки, М.:Просвещение,1987, стр.7-10
2. Факультативный курс по математике 7-9, М.:Просвещение, 1991, стр.4-22.
3. Спивак А.В. Тысяча и одна задача по математике, М.:Просвещение,2005,стр.128-133.
4. Методические разработки для первого курса
математического отделения ОЛ ВЗМШ, М. 2009.
Двоично-десятичная система. Двоично-десятичная система Понятие о двоично десятичной записи чисел
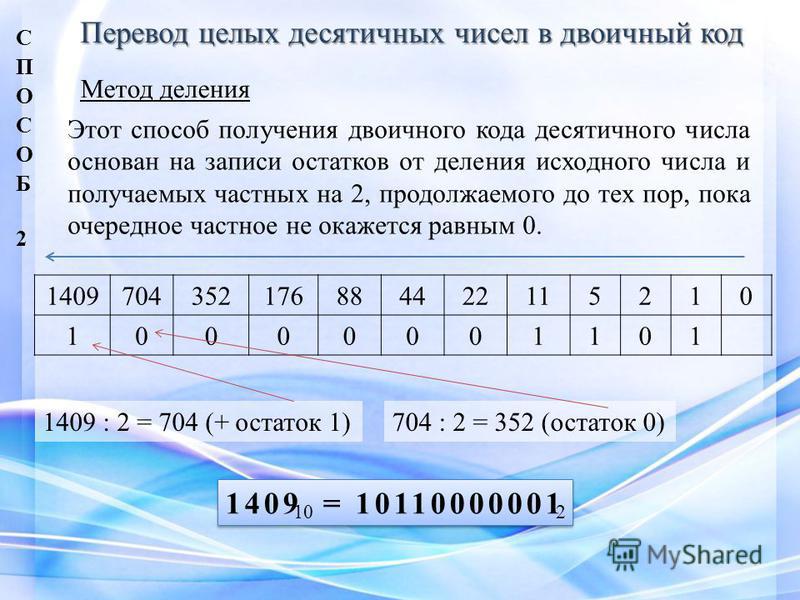
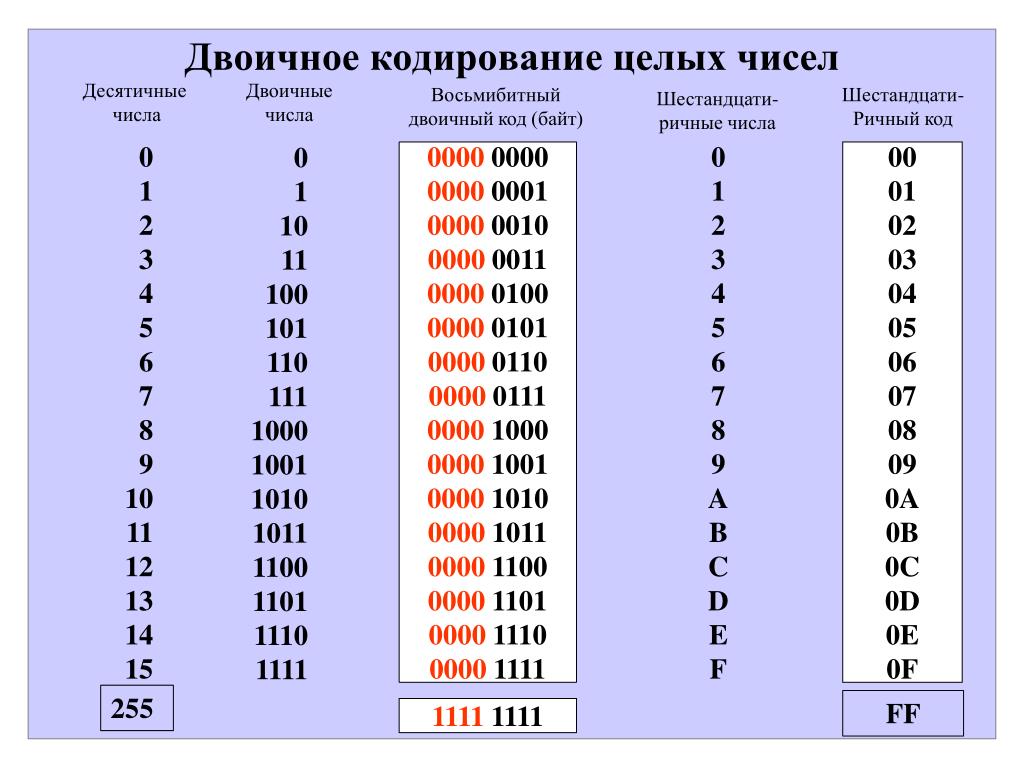
Двоично-десятичная система счисления. Десятичные цифры от 0 до 9 заменяются представляющими их двоичными тетрадами: 0=0000, 1=0001, 2=0010, 3=0011, 4=0100, 5=0101, 6=0110, 7=0111, 8=1000 и 9=1001. Такая запись очень часто используется как промежуточный этап перевода числа из десятичной системы в двоичную или обратно. Так как 10 не является точной степенью 2, то используются не все 16 тетрад, а алгоритмы арифметических операций над многозначными числами здесь более сложны, чем в основных системах счисления. И тем не менее, двоично-десятичная система счисления применяется даже на этом уровне во многих микрокалькуляторах и некоторых компьютерах (в частности, «Ямаха» стандарта MSX).
Поскольку человеку наиболее привычны представление и арифметика в десятичной системе счисления, а для компьютера — двоичное представление и двоичная арифметика, была введена компромиссная система двоично-десятичной записи чисел. Такая система чаще всего применяется там, где существует необходимость частого использования процедуры десятичного ввода-вывода. (электронные часы, калькуляторы, АОНы, и т.д.). В таких устройсвах не всегда целесообразно предусматривать универсальный микрокод перевода двоичных чисел в десятичные и обратно по причине небольшого объема программной памяти.
Такая система чаще всего применяется там, где существует необходимость частого использования процедуры десятичного ввода-вывода. (электронные часы, калькуляторы, АОНы, и т.д.). В таких устройсвах не всегда целесообразно предусматривать универсальный микрокод перевода двоичных чисел в десятичные и обратно по причине небольшого объема программной памяти.
Принцип построения этой системы достаточно прост: каждая десятичная цифра преобразуется прямо в свой десятичный эквивалент из 4 бит, например: 369110=0011 0110 1001 0001DEC:
Десятичное число 3 6 9 1 Двоично-десятичное число 0011 0110 1001 0001
Преобразуем двоично-десятичное число 1000 0000 0111 0010 в его десятичный эквивалент. Каждая группа из 4 бит преобразуется в её десятичный эквивалент. Получим 1000 0000 0111 0010DEC = 807210:
Двоично-десятичное число 1000 0000 0111 0010 Десятичное число 8 0 7 2
Микропроцессоры используют чистые двоичные числа, однако понимают и команды преобразования в двоично-десятичную запись. Полученные двоично-десятичные числа легко представимы в десятичной записи, более понятной людям.
Полученные двоично-десятичные числа легко представимы в десятичной записи, более понятной людям.
Преобразование двоичных чисел в двоично-десятичные
Арифметико-логическое устройство AVR-микроконтроллеров (как и других микропроцессоров) выполняет элементарные арифметические и логические операции над числами, представленными в двоичном коде. В двоичном коде считываются результаты преобразования АЦП, в двоичном коде (в формате целых чисел или чисел с плавающей точкой) удобно выполнять обработку результатов измерения. Однако, когда окончательный результат отображается на индикаторе, он должен быть преобразован в десятичный формат, удобный для восприятия человеком.
В данном разделе рассматриваются программы преобразования двоичных чисел в двоично-десятичные.
1. Форматы представления десятичных чисел
В настоящее время распространены два формата представления десятичных чисел в микропроцессорах — упакованный двоично-десятичный код (BCD-Binary-Coded Decimal) и неупакованный десятичный код .
Упакованный BCD-код — это такое представление десятичного числа, когда каждая десятичная цифра представляется 4-х битным двоичным позиционным кодом 8-4-2-1. При этом байт содержит две десятичные цифры. Младшая десятичная цифра занимает правую тетраду (биты 3: 0), старшая — левую тетраду (биты 7: 4). Многоразрядные BCD-числа занимают несколько смежных байт. Если число является знаковым, то для представления знака в BCD-формате отводится старшая тетрада старшего байта. Для кодирования знака можно использовать шесть двоичных кодовых комбинаций, которые не используются для представления десятичных цифр. Это коды 1010-1111 (A-F в шестнадцатеричном представлении). Обычно для кодирования знака плюс применяют код 1100 (С), а для знака минус — 1101 (D).
Неупакованный десятичный код является подмножеством международной таблицы кодирования символов ASCII (Таблица 1). Видно, что для хранения неупакованных десятичных чисел требуется в два раза больше памяти, так как каждая цифра представляется 8-битным кодом. Таблица 1: ASCII-коды десятичных цифр
Таблица 1: ASCII-коды десятичных цифр
2. Преобразование целых 16-битных чисел в двоично-десятичные числа
На сайте www.atmel.com предлагается программа «bin2bcd16» для преобразования целых 16-битных двоичных чисел в двоично-десятичные упакованные числа. В данной статье рассматривается программа «bin16bcd5» (см. Приложение, Программа 1), написанная Терешкиным А. В. согласно алгоритму, изложенному в , и выполняющая ту же задачу. Последняя программа по быстродействию, длине кода и количеству используемых регистров оказалась более эффективной, чем первая.
Алгоритм программы «bin16bcd5» заключается в следующем. Предположим, что имеется целое беззнаковое 16-битное число (диапазон от 0 до 65535). Очевидно, что необходимо найти 5 десятичных цифр. Способ преобразования заключается в том, чтобы, вычитая из исходного числа число 10000, сначала определить десятичную цифру десятков тысяч. Затем находится цифра тысяч последовательным вычитанием числа 1000 и т. д. Вычитание каждый раз производится до получения отрицательной разности с подсчетом числа вычитаний. При переходе к определению каждого следующего десятичного разряда в регистрах исходного числа восстанавливается последняя положительная разность. После того, как будет найдена десятичная цифра десятков, в регистрах исходного числа останется десятичная цифра единиц.
Вычитание каждый раз производится до получения отрицательной разности с подсчетом числа вычитаний. При переходе к определению каждого следующего десятичного разряда в регистрах исходного числа восстанавливается последняя положительная разность. После того, как будет найдена десятичная цифра десятков, в регистрах исходного числа останется десятичная цифра единиц.
Программа «bin16ASCII5» (см. Приложение, Программа 2) преобразует целое двоичное 16-битное число в десятичное неупакованное число. При этом используется тот же алгоритм.
3. Преобразование двоичной дроби в двоично-десятичную дробь
Двоичная дробь, по определению, представляется следующим выражением:
0.A-1A-2 … A-m = A-1*2-1 + A-2*2-2 + … A-m*2-m
Из этого представления следует алгоритм преобразования (Рис. 2), который содержит m шагов. На каждом шаге к двоично-десятичному результату прибавляется очередная двоичная цифра и весь результат делится на 2.
На изображены двоичный регистр, который содержит исходную двоичную дробь и регистр двоично-десятичного упакованного результата.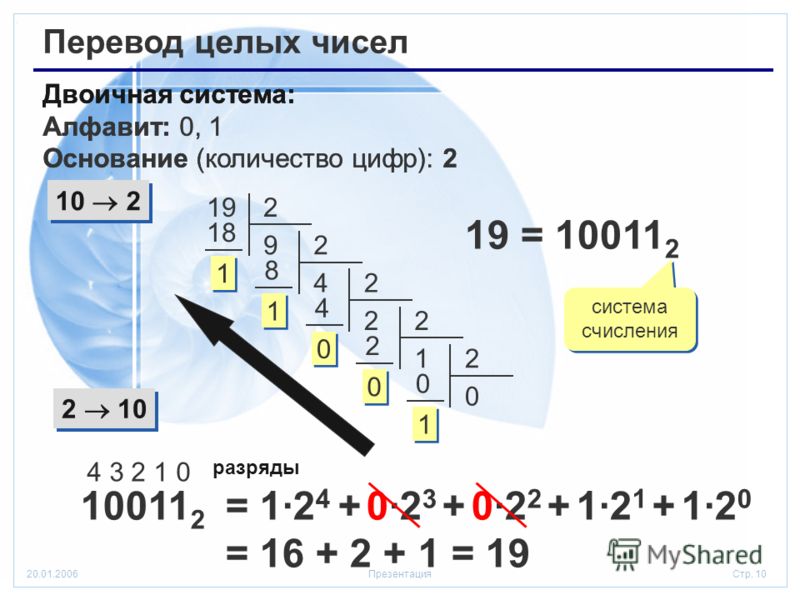 Для наглядности у обоих регистров также показаны разряд единиц и положение точки, которые в памяти микропроцессора никак не представлены, но положение которых всегда строго оговорено. Количество циклов рассматриваемого алгоритма равно количеству бит двоичной дроби. Разрядность двоично-десятичного регистра определяется требуемой точностью вычислений.
Для наглядности у обоих регистров также показаны разряд единиц и положение точки, которые в памяти микропроцессора никак не представлены, но положение которых всегда строго оговорено. Количество циклов рассматриваемого алгоритма равно количеству бит двоичной дроби. Разрядность двоично-десятичного регистра определяется требуемой точностью вычислений.
Сложить эту цифру с двоично-десятичным числом означает, что ее нужно поместить в разряд единиц двоично-десятичного числа, откуда при последующем делении на два цифра A-i сдвинется в старший разряд старшей тетрады десятичной дроби. При программировании мы можем представлять, что разрядом единиц десятичной дроби является бит переноса С.
При делении на два двоично-десятичного упакованного числа, так же как и при делении двоичного числа, его сдвигают вправо на один разряд. При этом на два делится каждая тетрада, то есть каждая десятичная цифра. При делении четной десятичной цифры в соответствующем разряде снова получается десятичная цифра, и никакой коррекции не требуется. При делении на 2 нечетной десятичной цифры остаток, равный 5, должен быть добавлен к более младшему десятичному разряду, но на самом деле при двоичном сдвиге в более младшую тетраду добавляется число 8 (вес старшего разряда тетрады). Поэтому требуется коррекция результата, которая заключается в вычитании числа 3 из содержимого тех тетрад, которые после сдвига вправо имеют установленные старшие разряды.
При делении на 2 нечетной десятичной цифры остаток, равный 5, должен быть добавлен к более младшему десятичному разряду, но на самом деле при двоичном сдвиге в более младшую тетраду добавляется число 8 (вес старшего разряда тетрады). Поэтому требуется коррекция результата, которая заключается в вычитании числа 3 из содержимого тех тетрад, которые после сдвига вправо имеют установленные старшие разряды.
4. Преобразование чисел с плавающей точкой в двоично-десятичные числа
Представление чисел с плавающей точкой имеет следующий вид:
где М — двоичная мантисса числа, П — двоичный порядок числа.
Такое представление часто используется и в десятичной системе счисления для представления очень больших или очень малых чисел. Мантисса и порядок представляют собой целые знаковые числа. Знак мантиссы является знаком всего числа. Порядок показывает истинное положение точки вместо того, которое она занимает в изображении мантиссы. Двоичное число с плавающей точкой отличается от привычного нам десятичного тем, что точка является двоичной, то есть порядок показывает на количество двоичных (а не десятичных) разрядов, на которое необходимо переместить эту точку влево или вправо.
Нормализованным представлением числа с плавающей точкой называют такое представление, когда мантисса является правильной дробью, и старшая ее цифра отличается от нуля. Но для двоичного числа требование того, что старшая цифра отличается от нуля означает, что эта цифра равна 1. Если старшая цифра точно известна, то ее можно не хранить в памяти.
В двоичной системе счисления используются всего две цифры 0 и 1. Другими словами, двойка является основанием двоичной системы счисления. (Аналогично у десятичной системы основание 10.)
Чтобы научиться понимать числа в двоичной системе счисления, сначала рассмотрим, как формируются числа в привычной для нас десятичной системе счисления.
В десятичной системе счисления мы располагаем десятью знаками-цифрами (от 0 до 9). Когда счет достигает 9, то вводится новый разряд (десятки), а единицы обнуляются и счет начинается снова. После 19 разряд десятков увеличивается на 1, а единицы снова обнуляются. И так далее. Когда десятки доходят до 9, то потом появляется третий разряд – сотни.
Двоичная система счисления аналогична десятичной за исключением того, что в формировании числа участвуют всего лишь две знака-цифры: 0 и 1. Как только разряд достигает своего предела (т.е. единицы), появляется новый разряд, а старый обнуляется.
Попробуем считать в двоичной системе:
0 – это ноль
1 – это один (и это предел разряда)
10 – это два
11 – это три (и это снова предел)
100 – это четыре
101 – пять
110 – шесть
111 – семь и т.д.
Перевод чисел из двоичной системы счисления в десятичную
Не трудно заметить, что в двоичной системе счисления длины чисел с увеличением значения растут быстрыми темпами. Как определить, что значит вот это: 10001001? Непривычный к такой форме записи чисел человеческий мозг обычно не может понять сколько это. Неплохо бы уметь переводить двоичные числа в десятичные.
В десятичной системе счисления любое число можно представить в форме суммы единиц, десяток, сотен и т.д. Например:
1476 = 1000 + 400 + 70 + 6
1476 = 1 * 10 3 + 4 * 10 2 + 7 * 10 1 + 6 * 10 0
Посмотрите на эту запись внимательно. Здесь цифры 1, 4, 7 и 6 — это набор цифр из которых состоит число 1476. Все эти цифры поочередно умножаются на десять возведенную в ту или иную степень. Десять – это основание десятичной системы счисления. Степень, в которую возводится десятка – это разряд цифры за минусом единицы.
Здесь цифры 1, 4, 7 и 6 — это набор цифр из которых состоит число 1476. Все эти цифры поочередно умножаются на десять возведенную в ту или иную степень. Десять – это основание десятичной системы счисления. Степень, в которую возводится десятка – это разряд цифры за минусом единицы.
Аналогично можно разложить и любое двоичное число. Только основание здесь будет 2:
10001001 = 1*2 7 + 0*2 6 + 0*2 5 + 0*2 4 + 1*2 3 + 0*2 2 + 0*2 1 + 1*2 0
1*2 7 + 0*2 6 + 0*2 5 + 0*2 4 + 1*2 3 + 0*2 2 + 0*2 1 + 1*2 0 = 128 + 0 + 0 + 0 + 8 + 0 + 0 + 1 = 137
Т.е. число 10001001 по основанию 2 равно числу 137 по основанию 10. Записать это можно так:
10001001 2 = 137 10
Почему двоичная система счисления так распространена?
Дело в том, что двоичная система счисления – это язык вычислительной техники. Каждая цифра должна быть как-то представлена на физическом носителе. Если это десятичная система, то придется создать такое устройство, которое может быть в десяти состояниях. Это сложно. Проще изготовить физический элемент, который может быть лишь в двух состояниях (например, есть ток или нет тока). Это одна из основных причин, почему двоичной системе счисления уделяется столько внимания.
Это сложно. Проще изготовить физический элемент, который может быть лишь в двух состояниях (например, есть ток или нет тока). Это одна из основных причин, почему двоичной системе счисления уделяется столько внимания.
Перевод десятичного числа в двоичное
Может потребоваться перевести десятичное число в двоичное. Один из способов – это деление на два и формирование двоичного числа из остатков. Например, нужно получить из числа 77 его двоичную запись:
77 / 2 = 38 (1 остаток)
38 / 2 = 19 (0 остаток)
19 / 2 = 9 (1 остаток)
9 / 2 = 4 (1 остаток)
4 / 2 = 2 (0 остаток)
2 / 2 = 1 (0 остаток)
1 / 2 = 0 (1 остаток)
Собираем остатки вместе, начиная с конца: 1001101. Это и есть число 77 в двоичном представлении. Проверим:
1001101 = 1*2 6 + 0*2 5 + 0*2 4 + 1*2 3 + 1*2 2 + 0*2 1 + 1*2 0 = 64 + 0 + 0 + 8 + 4 + 0 + 1 = 77
В курсе информатики, вне зависимости, школьном или университетском, особое место уделяется такому понятию как системы счисления. Как правило, на него выделяют несколько уроков или практических занятий. Основная цель — не только усвоить основные понятия темы, изучить виды систем счисления, но и познакомиться с двоичной, восьмеричной и шестнадцатеричной арифметикой.
Как правило, на него выделяют несколько уроков или практических занятий. Основная цель — не только усвоить основные понятия темы, изучить виды систем счисления, но и познакомиться с двоичной, восьмеричной и шестнадцатеричной арифметикой.
Что это значит?
Начнем с определения основного понятия. Как отмечает учебник «Информатика», система счисления — записи чисел, в которой используется специальный алфавит или определенный набор цифр.
В зависимости от того, меняется ли значение цифры от ее положения в числе, выделяют две: позиционную и непозиционную системы счисления.
В позиционных системах значение цифры меняется вместе с ее положением в числе. Так, если взять число 234, то цифра 4 в ней означает единицы, если же рассмотреть число 243, то тут она будет уже означать десятки, а не единицы.
В непозиционных системах значение цифры статично, вне зависимости от ее положения в числе. Наиболее яркий пример — палочковая система, где каждая единица обозначается с помощью черточки. Неважно, куда вы припишите палочку, значение числа измениться лишь на единицу.
Неважно, куда вы припишите палочку, значение числа измениться лишь на единицу.
Непозиционные системы
К непозиционным системам счисления относятся:
- Единичная система, которая считается одной из первых. В ней вместо цифр использовались палочки. Чем их было больше, тем больше было значение числа. Встретить пример чисел, записанных таким образом, можно в фильмах, где речь идет о потерянных в море людях, заключенных, которые отмечают каждый день с помощью зарубок на камне или дереве.
- Римская, в которой вместо цифр использовались латинские буквы. Используя их, можно записать любое число. При этом его значение определялось с помощью суммы и разницы цифр, из которых состояло число. Если слева от цифры находилось меньшее число, то левая цифра вычиталась из правой, а если справа цифра была меньше или равна цифре слева, то их значения суммировались. Например, число 11 записывалось как XI, а 9 — IX.
- Буквенные, в которых числа обозначались с помощью алфавита того или иного языка.
 Одной из них считается славянская система, в которой ряд букв имел не только фонетическое, но и числовое значение.
Одной из них считается славянская система, в которой ряд букв имел не только фонетическое, но и числовое значение. - в которой использовалось всего два обозначения для записи — клинья и стрелочки.
- В Египте тоже использовались специальные символы для обозначения чисел. При записи числа каждый символ мог использоваться не более девяти раз.
Позиционные системы
Большое внимание уделяется в информатике позиционным системам счисления. К ним относятся следующие:
- двоичная;
- восьмеричная;
- десятичная;
- шестнадцатеричная;
- шестидесятеричная, используемая при счете времени (к примеру, в минуте — 60 секунд, в часе — 60 минут).
Каждая из них обладает своим алфавитом для записи, правилами перевода и выполнения арифметических операций.
Десятичная система
Данная система является для нас наиболее привычной. В ней используются цифры от 0 до 9 для записи чисел. Они также носят название арабских. В зависимости от положения цифры в числе, она может обозначать разные разряды — единицы, десятки, сотни, тысячи или миллионы. Ее мы пользуемся повсеместно, знаем основные правила, по которым производятся арифметические операции над числами.
Ее мы пользуемся повсеместно, знаем основные правила, по которым производятся арифметические операции над числами.
Двоичная система
Одна из основных систем счисления в информатике — двоичная. Ее простота позволяет компьютеру производить громоздкие вычисления в несколько раз быстрее, нежели в десятичной системе.
Для записи чисел используется лишь две цифры — 0 и 1. При этом, в зависимости от положения 0 или 1 в числе, его значение будет меняться.
Изначально именно с помощью компьютеры получали всю необходимую информацию. При этом, единица означала наличие сигнала, передаваемого с помощью напряжения, а ноль — его отсутствие.
Восьмеричная система
Еще одна известная компьютерная система счисления, в которой применяются цифры от 0 до 7. Применялась в основном в тех областях знаний, которые связаны с цифровыми устройствами. Но в последнее время она употребляется значительно реже, так как на смену ей пришла шестнадцатеричная система счисления.
Двоично-десятичная система
Представление больших чисел в двоичной системе для человека — процесс довольно сложный. Для его упрощения была разработана Используется она обычно в электронных часах, калькуляторах. В данной системе из десятичной системы в двоичную преобразуется не все число, а каждая цифра переводится в соответствующий ей набор нулей и единиц в двоичной системе. Аналогично происходит и перевод из двоичной системы в десятичную. Каждая цифра, представленная в виде четырехзначного набора нулей и единиц, переводится в цифру десятичной системы счисления. В принципе, нет ничего сложного.
Для его упрощения была разработана Используется она обычно в электронных часах, калькуляторах. В данной системе из десятичной системы в двоичную преобразуется не все число, а каждая цифра переводится в соответствующий ей набор нулей и единиц в двоичной системе. Аналогично происходит и перевод из двоичной системы в десятичную. Каждая цифра, представленная в виде четырехзначного набора нулей и единиц, переводится в цифру десятичной системы счисления. В принципе, нет ничего сложного.
Для работы с числам в данном случае пригодится таблица систем счисления, в которой будет указано соответствие между цифрами и их двоичным кодом.
Шестнадцатеричная система
В последнее время все большую популярность приобретает в программировании и информатике система счисления шестнадцатеричная. В ней используются не только цифры от 0 до 9, но и ряд латинских букв — A, B, C, D, E, F.
При этом, каждая из букв имеет свое значение, так A=10, B=11, C=12 и так далее. Каждое число представляется в виде набора из четырех знаков: 001F.
Перевод чисел: из десятичной в двоичную
Перевод в системах счисления чисел происходит по определенным правилам. Наиболее часто встречается перевод из двоичной в десятичную систему и наоборот.
Для того, чтобы перевести число из десятичной системы в двоичную, необходимо последовательно делить его на основание системы счисления, то есть, число два. При этом, остаток от каждого деления необходимо фиксировать. Так будет происходить до тех пор, пока остаток от деления не будет меньше или равен единице. Проводить вычисления лучше всего в столбик. Затем полученные остатки от деления записываются в строку в обратном порядке.
Например, переведем число 9 в двоичную систему:
Делим 9, так как число не делится нацело, то берем число 8, остаток будет 9 — 1 = 1.
После деления 8 на 2 получаем 4. Снова делим его, так как число делится нацело — получаем в остатке 4 — 4 = 0.
Проводим ту же операцию с 2. В остатке получаем 0.
В итоге деления у нас получается 1.
Вне зависимости от итоговой системы счисления, перевод чисел из десятичной в любую другую будет происходить по принципу деления числа на основу позиционной системы.
Перевод чисел: из двоичной в десятичную
Довольно легко переводить числа и в десятичную систему счисления из двоичной. Для этого достаточно знать правила возведения чисел в степень. В данном случае, в степень двойки.
Алгоритм перевода следующий: каждую цифру из кода двоичного числа необходимо умножить на двойку, причем, первая двойка будет в степени m-1, вторая — m-2 и так далее, где m — количество цифр в коде. Затем сложить результаты сложения, получив целое число.
Для школьников этот алгоритм можно объяснить проще:
Для начала берем и записываем каждую цифру, умноженную на двойку, затем проставляем степень двойки с конца, начиная с нуля. Потом складываем полученное число.
Для примера разберем с вами полученное ранее число 1001, переведя его в десятичную систему, и заодно проверим правильность наших вычислений.
Выглядеть это будет следующим образом:
1*2 3 + 0*2 2 +0*2 1 +1*2 0 = 8+0+0+1 =9.
При изучении данной темы удобно использовать таблицу со степенями двойки. Это существенно уменьшит количество времени, необходимое для проведения вычислений.
Другие варианты перевода
В некоторых случаях перевод может осуществляться между двоичной и восьмеричной системой счисления, двоичной и шестнадцатеричной. В таком случае можно пользоваться специальными таблицами или же запустить на компьютере приложение калькулятор, выбрав во вкладке вид вариант «Программист».
Арифметические операции
Вне зависимости от того, в каком виде представлено число, с ним можно проводить привычные для нас вычисления. Это может быть деление и умножение, вычитание и сложение в системе счисления, которую вы выбрали. Конечно, для каждой из них действуют свои правила.
Так для двоичной системы разработаны свои таблицы для каждой из операций. Такие же таблицы используются и в других позиционных системах.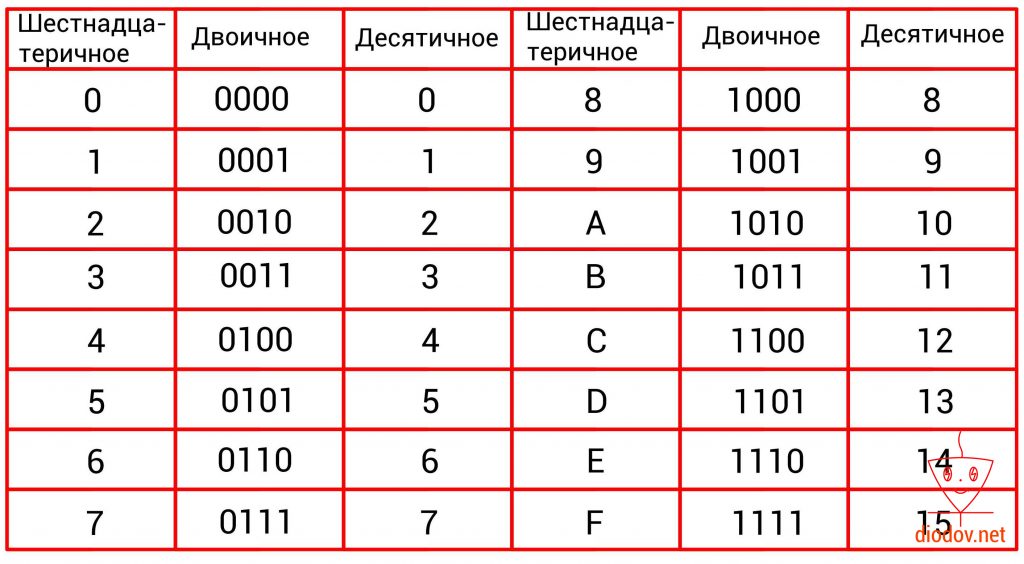
Заучивать их необязательно — достаточно просто распечатать и иметь под рукой. Также можно воспользоваться калькулятором на ПК.
Одна из важнейших тем в информатике — система счисления. Знание этой темы, понимание алгоритмов перевода чисел из одной системы в другую — залог того, что вы сможете разобраться в более сложных темах, таких как алгоритмизация и программирование и сможете самостоятельно написать свою первую программу.
Эта система имеет основание S = 10, но каждая цифра изображается четырехразрядным двоичным числом, называемым тетрадой. Обычно данная система счисления используется в ЭВМ при вводе и выводе информации. Однако в некоторых типах ЭВМ в АЛУ имеются специальные блоки десятичной арифметики, выполняющие операции над числами в двоично-десятичном коде. Это позволяет в ряде случаев существенно повышать производительность ЭВМ.
Например,
в автоматизированной системе обработки
данных чисел много, а вычислений мало.
В этом случае операции, связанные с
переводом чисел из одной системы в
другую, существенно превысили бы время
выполнения операций по обработке
информации.
Перевод чисел из десятичной системы в двоично-десятичную весьма прост и заключается в замене каждой цифры двоичной тетрадой.
Пример.
Записать десятичное число 572.38 (10) в двоично-десятичной системе счисления.
Обратный перевод также прост: необходимо двоично-десятичное число разбить на тетрады от точки влево (для целой части) и вправо (для дробной), дописать необходимое число незначащих нулей, а затем каждую тетраду записать в виде десятичной цифры.
Пример.
Записать двоично-десятичное число 10010.010101 (2-10) в десятичной системе счисления.
Перевод чисел из двоично-десятичной в двоичную систему осуществляется по общим правилам, описанным выше.
2.3. Восьмеричная система счисления
В восьмеричной системе счисления употребляются всего восемь цифр, т.е. эта система счисления имеет основание S = 8. В общем виде восьмеричное число выглядит следующим образом:
где
.
Восьмеричная
система счисления не нужна ЭВМ в отличие
от двоичной системы.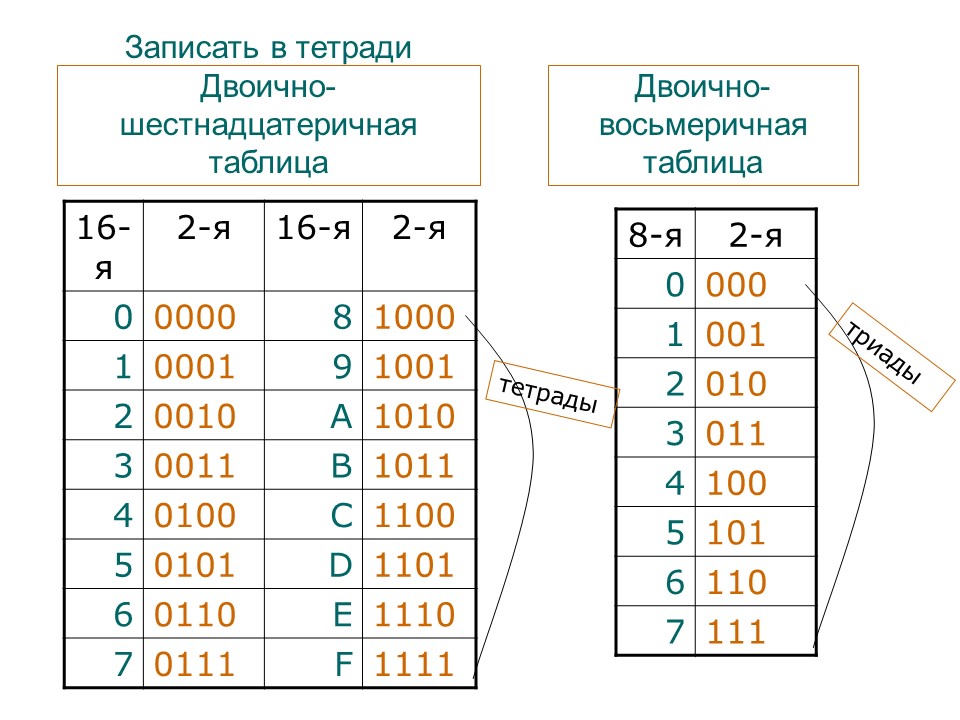 Она удобна как
компактная форма записи чисел и
используется программистами (например,
в текстах программ для более краткой и
удобной записи двоичных кодов команд,
адресов и операндов). В восьмеричной
системе счисления вес каждого разряда
кратен восьми или одной восьмой, поэтому
восьмиразрядное двоичное число позволяет
выразить десятичные величины в пределах
0-255, а восьмеричное охватывает диапазон
0-99999999 (для двоичной это составляет 27
разрядов).
Она удобна как
компактная форма записи чисел и
используется программистами (например,
в текстах программ для более краткой и
удобной записи двоичных кодов команд,
адресов и операндов). В восьмеричной
системе счисления вес каждого разряда
кратен восьми или одной восьмой, поэтому
восьмиразрядное двоичное число позволяет
выразить десятичные величины в пределах
0-255, а восьмеричное охватывает диапазон
0-99999999 (для двоичной это составляет 27
разрядов).
Поскольку 8=2 3 , то каждый восьмеричный символ можно представить трехбитовым двоичным числом. Для перевода числа из двоичной системы счисления в восьмеричную необходимо разбить это число влево (для целой части) и вправо (для дробной) от точки (запятой) на группы по три разряда (триады) и представить каждую группу цифрой в восьмеричной системе счисления. Крайние неполные триады дополняются необходимым количеством незначащих нулей.
Пример.
Двоичное число
10101011111101 (2) записать в восьмеричной
системе счисления.
Пример.
Двоичное число 1011.0101 (2) записать в восьмеричной системе счисления.
Перевод из восьмеричной системы счисления в двоичную осуществляется путем представления каждой цифры восьмеричного числа трехразрядным двоичным числом (триадой).
2.4. Шестнадцатеричная система счисления
Эта система счисления имеет основание S = 16. В общем виде шестнадцатеричное число выглядит следующим образом:
где
.
Шестнадцатеричная система счисления позволяет еще короче записывать многоразрядные двоичные числа и, кроме того, сокращать запись 4-разрядного двоичного числа, т.е. полубайта, поскольку 16=2 4 . Шестнадцатеричная система также применяется в текстах программ для более краткой и удобной записи двоичных чисел.
Для перевода числа из двоичной системы счисления в шестнадцатеричную необходимо разбить это число влево и вправо от точки на тетрады и представить каждую тетраду цифрой в шестнадцатеричной системе счисления.
Пример.
Двоичное число 10101011111101 (2) записать в шестнадцатеричной системе.
Пример.
Двоичное число 11101.01111 (2) записать в шестнадцатеричной системе.
Для перевода числа из шестнадцатеричной системы счисления в двоичную, необходимо, наоборот, каждую цифру этого числа заменить тетрадой.
В заключение следует отметить, что перевод из одной системы счисления в другую произвольных чисел можно осуществлять по общим правилам, описанным в разделе “Двоичная система счисления”. Однако на практике переводы чисел из десятичной системы в рассмотренные системы счисления и обратно осуществляются через двоичную систему счисления.
Кроме
того, следует помнить, что шестнадцатеричные
и восьмеричные числа – это только способ
представления больших двоичных чисел,
которыми фактически оперирует процессор.
При этом шестнадцатеричная система
оказывается предпочтительнее, поскольку
в современных ЭВМ процессоры манипулируют
словами длиной 4, 8, 16, 32 или 64 бита, т. е.
длиной слов, кратной 4. В восьмеричной
же системе счисления предпочтительны
слова, кратные 3 битам, например слова
длиной 12 бит (как в PDP-8 фирмы DEC).
е.
длиной слов, кратной 4. В восьмеричной
же системе счисления предпочтительны
слова, кратные 3 битам, например слова
длиной 12 бит (как в PDP-8 фирмы DEC).
Сложение положительных чисел Сложение многоразрядных чисел осуществляется по правилам двоичной арифметики; особенность проявляется при сложении двух единиц. При S = Ю(10)сумма двух единиц равна двум, что эквивалентно 10(2). Таким образом, вместо одного разряда образуется два. В этом…
(Вычислительная техника)
Арифметические действия над числами с плавающей запятой
Сложение чисел При сложении чисел с плавающей запятой результат определяется как сумма мантисс слагаемых с общим для слагаемых порядком. Если знаки обеих мантисс одинаковы, то они складываются в прямых кодах, если разные — в дополнительном или обратном кодах. В табл. 2.8 приведен порядок действий…(Вычислительная техника)
Числа в десятичной системе счисления
10° — единица 109 — миллиард 1024 — септиллион 101 — десять 1012 — триллион 1027 — октиллион 102 — сто 1015 — квадриллион Ю30 — нониллион 103 — тысяча 1018 — квинтиллион 1033 — дециллион 106 — миллион 1021 — . ..
..(Физика)
Системы счисления
Человеку издревле приходилось считать различные предметы и записывать их количество. Для этих целей возникла унарная система записи, при которой числа обозначались соответствующим количеством черточек (или засечек). Например, число 5 представлялось как 111 |. Унарная запись очень громоздкая и…(Архитектура ЭВМ)
Экономичность системы счисления
Число в системе счисления рек разрядами, очевидно, будет иметь наибольшее значение в том случае, если все цифры числа окажутся максимальными, т. е. равными (р — 1). Тогда (гр)тах =(/>-1)…(/>-!) = / -1. к цифр Количество разрядов числа при переходе от одной системы счисления…(Архитектура ЭВМ)
Корректура счисления пути по одной линии положения
При подходе к побережью обстановка может сложиться так, что судоводитель имеет возможность получить только одну линию положения. Например, открылась вершина горы, на которую можно измерить только пеленг, или прослушиваются сигналы только одного радиомаяка. Такая же обстановка складывается и при определении…
Такая же обстановка складывается и при определении…(Анализ и обработка навигационных измерений)
it-inform — Системы счисления
Главная / Системы счисления
Системы счисления – это знаковые системы, обеспечивающие запись чисел по установленным приёмам (правилам) с помощью принятых в этих системах символов, которые называются цифрами.
Или немного короче: система счисления – это совокупность правил записи чисел с помощью цифр.
Для написания чисел и выполнения математических операций с ними обычно используется десятичная система счисления. Ее название объясняется тем, что в основе этой системы лежит основание 10 (десять). Это означает, что в десятичной системе счисления любое число выражается упорядоченной последовательностью десяти различных цифр: 0, 1, 2, 3, …. 9.
Однако, применяют не только десятичную, но и другие системы счисления, например восьмеричную, шестнадцатеричную и т.д. Так, например, в компьютерах для хранения и преобразования чисел применяется не десятичная, а двоичная система счисления, то есть система счисления с основанием 2.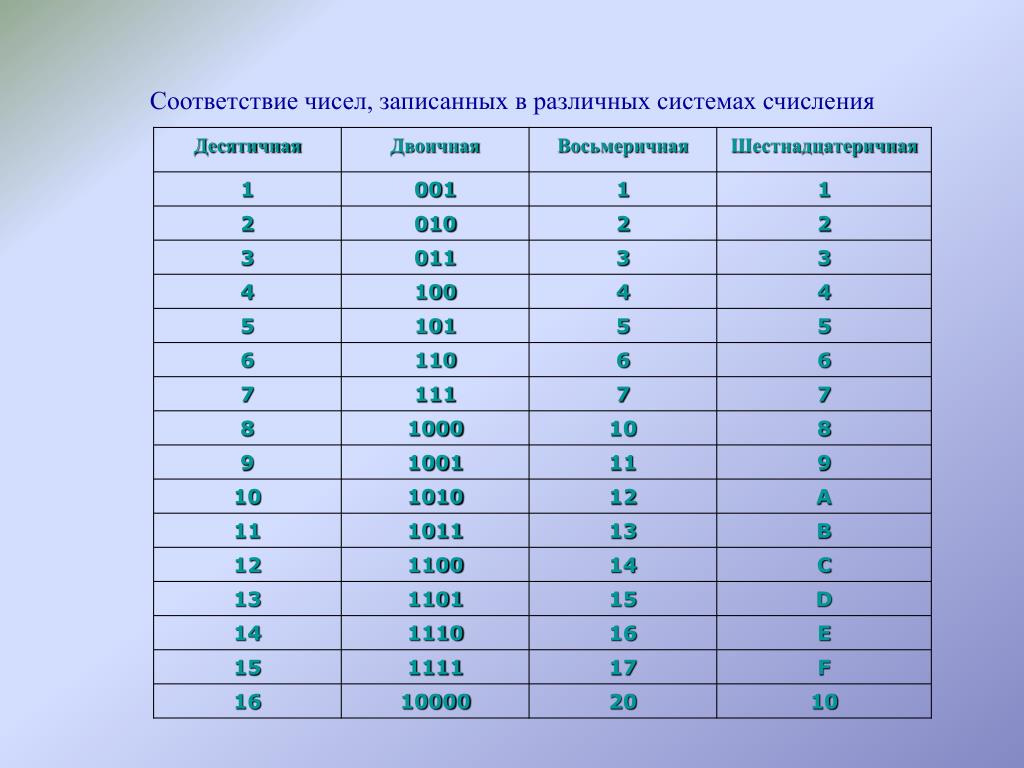 В этой системе любое число записывается с помощью двух цифр: 0 и 1, и поэтому такое число называется двоичным числом. Примеры двоичных чисел: 000; 001; 010011.
В этой системе любое число записывается с помощью двух цифр: 0 и 1, и поэтому такое число называется двоичным числом. Примеры двоичных чисел: 000; 001; 010011.
Существует два больших класса систем счисления: позиционные и непозиционные. В позиционных системах счисления значение любой цифры зависит от места (позиции), которое эта цифра занимает при записи конкретного числа. К непозиционным системам счисления можно отнести, например, римскую систему счисления, в которой для записи чисел используются буквы латинского алфавита: I (1), V (5), X (10), L (50), C (100), D (500), M (1000). Количество цифр, которое можно использовать для записи любого числа в позиционной системе счисления называется основанием этой системы счисления. Основание системы счисления указывает также на то, во сколько раз отличаются значения одинаковых цифр, находящихся в соседних позициях числа.
Рассмотрим любое десятичное число, например триста двадцать два (322). Это число состоит из суммы трех сотен, двух десятков и трех единиц:
В этом числе в двух соседних разрядах записаны одинаковые цифры (2), значения которых (2 и 20) отличаются между собой в десять раз.
Это же число в двоичной системе счисления имеет вид:
101000111.
Выбор двоичной системы счисления для хранения чисел в компьютерах связан, прежде всего, с удобством технической реализации устройств памяти. Запись двоичного числа является более громоздкой, чем десятичного, но для хранения двоичного числа в компьютерах требуются более простые элементы, которые обладают всего двумя устойчивыми состояниями.
В самых первых компьютерах такие элементы были построены на электронных лампах, позже – на транзисторах, а потом вместо транзисторов стали применять микросхемы. На магнитных дисках переключающимися элементами являются элементарные области намагниченности.
Запоминающие элементы в микросхеме или области намагниченности на магнитном диске называются ячейками памяти. Ячейка памяти состоит из разрядов. Количество разрядов соответствует количеству переключающихся элементов в этой ячейке. То есть, для физической реализации каждого разряда используется один переключающийся элемент. В каждом разряде хранится 0 или 1. С помощью одного разряда в двоичной системе можно закодировать два значения: 0 и 1. Ниже представлена таблица, в которой показано, какое максимальное число в двоичной системе счисления можно представить с помощью одного, двух и трех разрядов.
В каждом разряде хранится 0 или 1. С помощью одного разряда в двоичной системе можно закодировать два значения: 0 и 1. Ниже представлена таблица, в которой показано, какое максимальное число в двоичной системе счисления можно представить с помощью одного, двух и трех разрядов.
| Деся тичное число | 1 разряд для хранения числа | 2 разряда для хранения числа | 3 разряда для хранения числа |
| 0 | 0 | 00 | 00 |
| 1 | 1 | 01 | 01 |
| 2 | 10 | 10 | |
| 3 | 11 | 11 | |
| 4 | 100 | ||
| 5 | 101 | ||
| 6 | 110 | ||
| 7 | 111 |
Из приведенной таблицы видно, что в двух разрядах можно хранить уже вдвое больше различных значений. В трех разрядах количество этих значений опять удваивается. Таким образом, видно, что существует определенная закономерность. Она заключается в том, что добавление одного разряда для представления двоичного числа увеличивает количество возможных значений, представляемых в этих разрядах вдвое.
В трех разрядах количество этих значений опять удваивается. Таким образом, видно, что существует определенная закономерность. Она заключается в том, что добавление одного разряда для представления двоичного числа увеличивает количество возможных значений, представляемых в этих разрядах вдвое.
Важное достоинство двоичной системы счисления – удобство физического представления цифр и чисел. Недостатком двоичной системы является то, что для записи больших чисел в этой системе требуется довольно много цифр 0 и 1. Это затрудняет восприятие двоичных чисел человеком. Поэтому двоичную систему счисления применяют только для «внутренних нужд» компьютера, а человек, который работает с компьютером, имеет дело с обычными числами, представленными в десятичной системе счисления. Компьютер самостоятельно преобразует вводимые человеком числа в двоичную систему счисления, а результаты вычислений представляет опять в десятичной системе счисления.
Арифметические операции в двоичной системе счисления выполняются по тем же правилам, что и в десятичной или любой другой позиционной системе счисления.
Арифметические действия в двоичной системе счисления
Сложение двоичных чисел
Правила выполнения операции сложения чисел в двоичной системе счисления представлены в ниже:
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 10 (два)
Если при сложении двух цифр значение в каком-либо разряде становится равным или больше основания, то возникает единица переноса в следующий разряд, а в данном разряде записывается нуль. Пример:
11
+
01
Результат 100
При сложении трех единиц в данном разряде записывается единица, а 1 переносится в следующий разряд.
Точно также это правило справедливо и в десятичной системе счисления (если сумма двух цифр в десятичной системе счисления становится равной или больше основания (10), то возникает единица переноса в следующий разряд, а в данном разряде записывается цифра младшего разряда числа, полученного в результате сложения. Например:
17
+
16
Результат 33
В приведенном примере при сложении (7 + 6 = 13) возникает единица переноса в старший разряд, а в данный (текущий) разряд записывается цифра из младшего разряда результата сложения, то есть 3.
Таким образом, в любой системе счисления будет справедливо следующее правило: если при сложении двух чисел в любой системе счисления сумма двух цифр очередного разряда равна основанию системы счисления или превышает его, то в текущий разряд записывают младший разряд этой суммы, а в следующий разряд переносят разницу между текущим значением суммы и цифрой младшего разряда этой суммы.
Вычитание двоичных чисел
0 – 0 = 0
1 – 0 = 1
1 – 1 = 0
10 – 1 = 1
При двоичном вычитании в том случае, когда разность цифр становится меньше нуля, осуществляется заем из соседней левой цифры уменьшаемого, а нулевое значение данного разряда считается равным 2.
Например:
10111
—
01110
Результат 01001,
или
1001001
—
0011111
Результат 0101010.
То есть, арифметические действия в двоичной системе выполняются по тем
же правилам, что и в десятичной системе, но с учетом основания системы
счисления.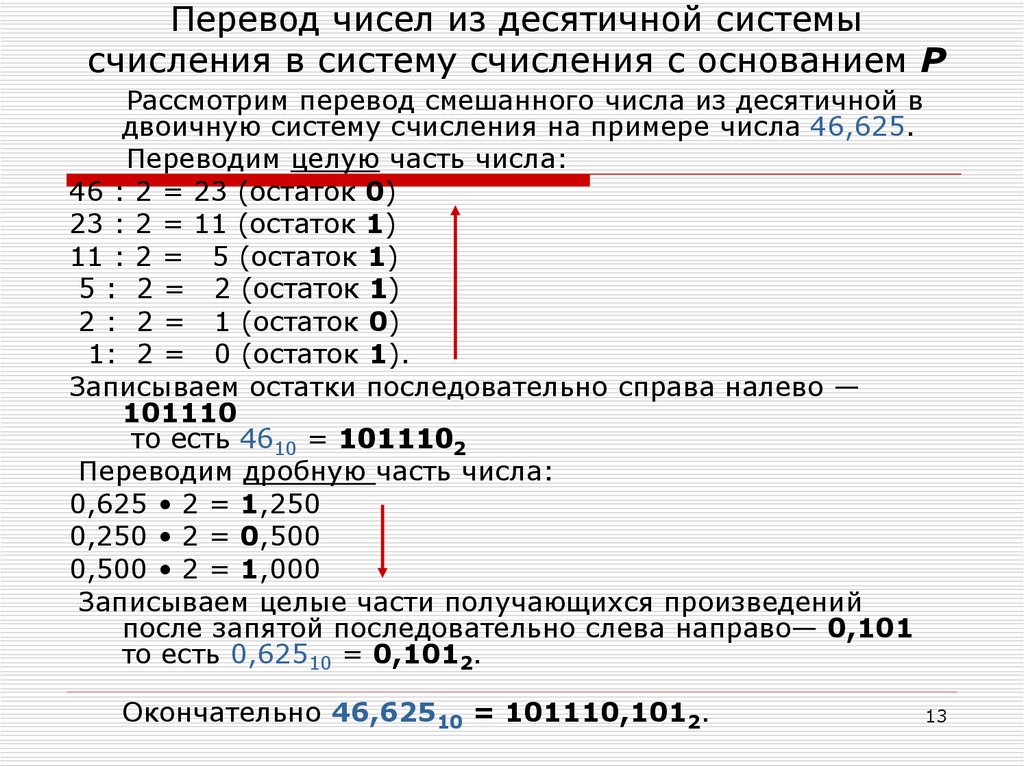
Сложение – важнейшая операция над двоичными числами в компьютерах. Другие операции – вычитание, умножение, деление – осуществляются в компьютерах обычно с помощью операции сложения.
Системы счисления. Двоичная система счисления
1. Системы счисления
1Системы
счисления
§ 7. Системы счисления
§ 8. Двоичная система счисления
§ 9. Восьмеричная система счисления
§ 10. Шестнадцатеричная система
счисления
§ 11. Другие системы счисления
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
2. Системы счисления
2Системы
счисления
§ 9. Системы счисления
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
3. Вспомним известное…
Системы счисления, 10 класс3
Вспомним известное…
Система счисления — это правила записи чисел с
помощью специальных знаков — цифр, а также
соответствующие правила выполнения операций с
этими числами.
Позиционная система: значение цифры определяется
ее позицией в записи числа.

Алфавит системы счисления — это используемый в
ней набор цифр.
Основание системы счисления — это количество
цифр в алфавите (мощность алфавита).
Разряд — это позиция цифры в записи числа. Разряды
в записи целых чисел нумеруются с нуля справа
налево.
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
4. Формы записи чисел
Системы счисления, 10 класс4
Формы записи чисел
тысячи
сотни десятки единицы
3
2
1
0
разряды
развёрнутая форма
записи числа
6 3 7 5 = 6·103 + 3·102 + 7·101 + 5·100
6000 300 70
5
Схема Горнера:
6 3 7 5 = ((6 10 + 3) 10 + 7) 10 + 5
для вычислений не нужно использовать
возведение в степень
удобна при вводе чисел с клавиатуры,
начиная с первой
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
5. Перевод в десятичную систему
Системы счисления, 10 класс5
Перевод в десятичную систему
Через развёрнутую запись:
=1
разряды: 3 2 1 0
12345 = 1 53 + 2 52 + 3 51 + 4 50 = 194
основание системы счисления
разряды: 3
2 1 0
a3a2a1a0 = a3 p 3 + a2 p 2 + a1 p 1 + a0 p 0
Через схему Горнера:
12345 = ((1 5 + 2) 5 + 3) 5 + 4 = 194
a3a2a1a0 = ((a3 p + a2) p + a1) p + a0
К.
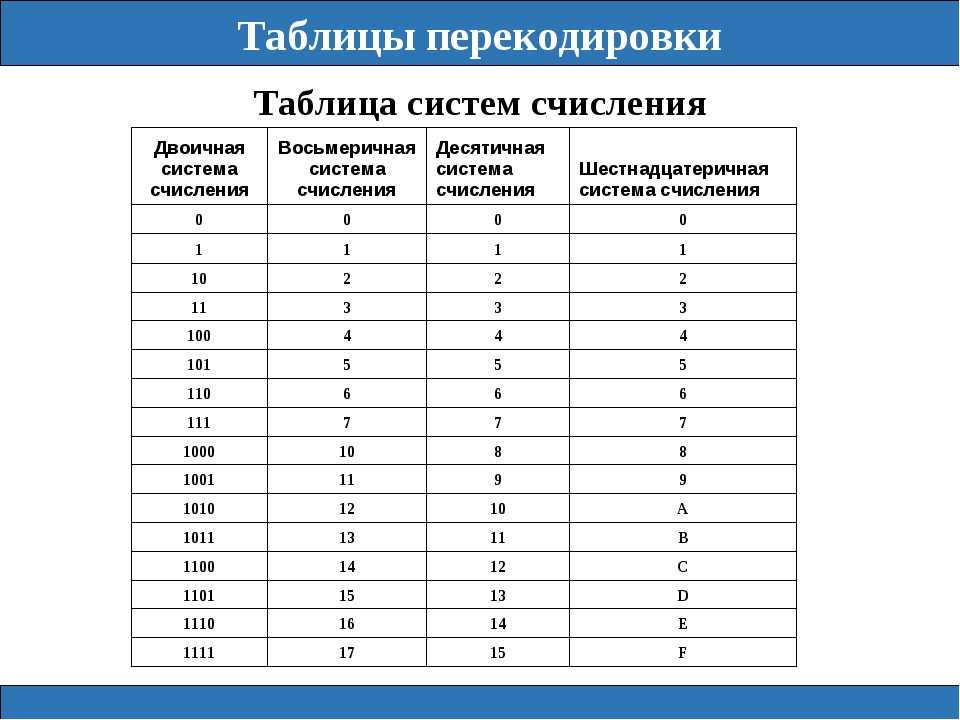 Ю. Поляков, Е.А. Ерёмин, 2018
Ю. Поляков, Е.А. Ерёмин, 2018http://kpolyakov.spb.ru
6. Перевод из десятичной в любую
Системы счисления, 10 класс6
Перевод из десятичной в любую
194 = 12345 = ((1 5 + 2) 5 + 3) 5 + 4
делится на 5
остаток от деления на 5
a3a2a1a0 = ((a3 p + a2) p + a1) p + a0
a3a2a1 = (a3 p + a2) p + a1
остаток от
частное от деления на p
деления на p
a1 — последняя цифра получившегося числа, которая равна
остатку от его деления на p.
Если запись числа в системе с основанием p оканчивается на 0
то число делиться на p, если оканчивается на два нуля, то
делится на p2.
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
7. Перевод из десятичной в любую
Системы счисления, 10 класс7
Перевод из десятичной в любую
10 5
194 5
190 38 5
4 35 7
3 5
2
194 = 12345
5
1
0
5
0
1
Делим число на p, отбрасывая остаток
на каждом шаге, пока не получится 0. Затем
надо выписать найденные остатки в обратном
порядке.

К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
8. Задачи
Системы счисления, 10 класс8
Задачи
Задача: в некоторой системе счисления число 71
записывается как «56x»? Определите основание
системы счисления X.
71 = 56X
• в записи есть цифра 6, поэтому X > 6
• переводим правую часть в десятичную систему
1 0
56x = 5·X1 + 6·X0= 5·X + 6
• решаем уравнение
71 = 5·X + 6 X = 13
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
9. Задачи
Системы счисления, 10 класс9
Задачи
Задача: в некоторой системе счисления число 71
записывается как «155x»? Определите основание
системы счисления X.
71 = 155X
• в записи есть цифра 5, поэтому X > 5
• переводим правую часть в десятичную систему
2 1 0
155x = 1·X2 + 5·X1 + 5·X0
= X2 + 5·X + 5
• решаем уравнение
71 = X2 + 5·X + 5
К.Ю. Поляков, Е.А. Ерёмин, 2018
X= 6
X = -11
http://kpolyakov.
 spb.ru
spb.ru10. Задачи
Системы счисления, 10 класс10
Задачи
Задача: найдите все основания систем счисления, в
которых запись десятичного числа 24 оканчивается на 3.
24 = k·X + 3
21 = k·X
X = 3, 7, 21
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
11. Задачи
Системы счисления, 10 класс11
Задачи
Задача: найдите все десятичные числа,
не превосходящие 40, запись которых в системе
счисления с основанием 4 оканчивается на 11.
N = k·42 + 1·4 + 1 = k·16 + 5
При k =0, 1, 2, 3, … получаем
N = 5, 21, 37, 53, …
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
12. Задачи
Системы счисления, 10 класс12
Задачи
Задача: Все 5-буквенные слова, составленные из букв А,
О и У, записаны в алфавитном порядке. Вот начало
списка:
1. ААААА
А 0
1. 00000
в троичной
2. ААААО
2. 00001
O 1
системе!
3. ААААУ
3. 00002
У 2
4. АААОА
4.
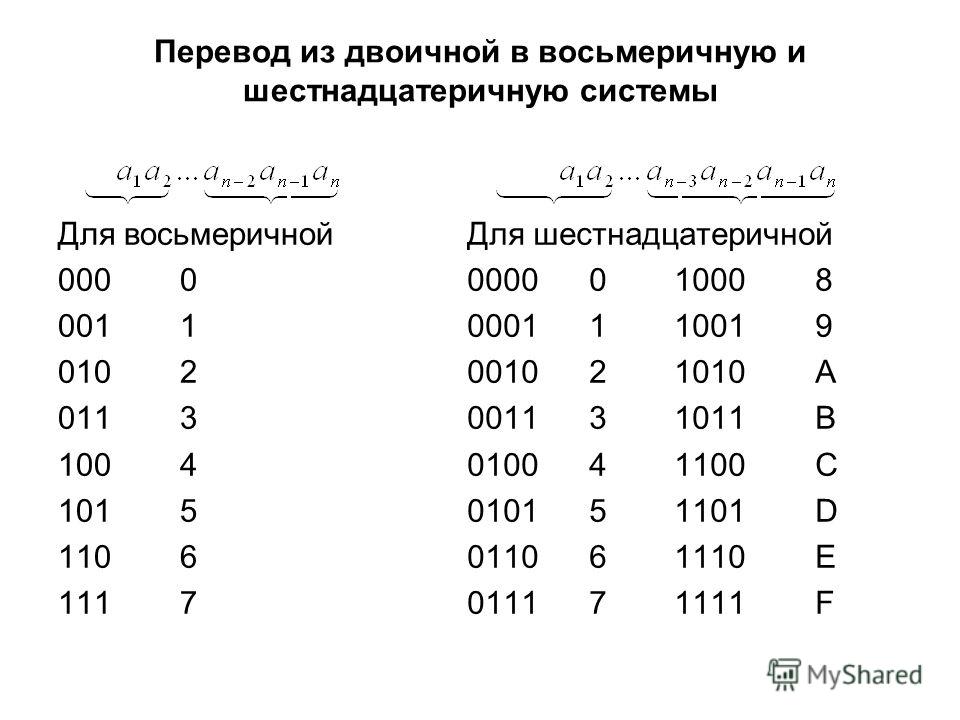 00010
000105. …
5. …
Найдите слово, которое стоит на 140-м месте от
начала списка.
на 1-м месте: 0
на 140-м месте: 139
?
Сколько всего?
К.Ю. Поляков, Е.А. Ерёмин, 2018
139 = 120113
ОУАОО
http://kpolyakov.spb.ru
13. Задачи
Системы счисления, 10 класс13
Задачи
Задача: Значение арифметического выражения
92017 + 32015 – 9
записали в системе счисления с основанием 3.
Сколько цифр 0, 1 и 2 содержится в этой записи?
Полезные свойства:
10N = 10…010
10N – 1= 9…910
N
N
10N – 10M = 10M (10N-M – 1) = 9…90…010
N–M M
3N = 10…03
N
К.Ю. Поляков, Е.А. Ерёмин, 2018
3N – 1= 2…23
N
3N – 3M = 2…20…03
N–M M
http://kpolyakov.spb.ru
14. Задачи
Системы счисления, 10 класс14
Задачи
Задача: Значение арифметического выражения
92017 + 32015 – 9
записали в системе счисления с основанием 3.
Сколько цифр 0, 1 и 2 содержится в этой записи?
Решение:
(32)2017 + 32015 – 32
34034 + 32015 – 32
2…20…03
+ 2013 2
10….
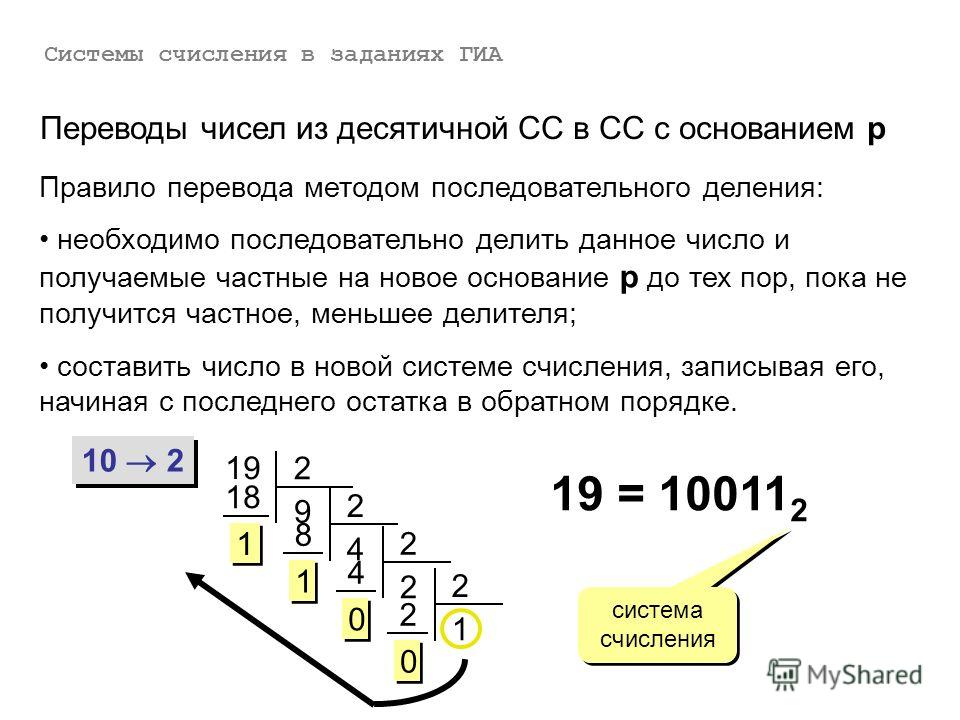 .…0…….…03
.…0…….…032 – 2013
1–1
0 – 2021
4034
10…..…2…20…03
4034-2013
2013
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
15. Дробные числа
Системы счисления, 10 класс15
Дробные числа
0,6375 = 6·0,1 + 3·0,01 + 7·0,001 + 5·0,0001
Развёрнутая форма записи:
разряды: -1 -2 -3 -4
0, 6 3 7 5 = 6·10-1 + 3·10-2 + 7·10-3 + 5·10-4
0, 1 2 3 45 = 1·5-1 + 2·5-2 + 3·5-3 + 4·5-4
перевод в десятичную систему
Схема Горнера:
0, 6375 = 10-1·(6 + 10-1·(3 + 10-1·(7 + 10-1·5)))
0,12345 = 5-1·(1 + 5-1·(2 + 5-1·(3 + 5-1·4)))
перевод в десятичную систему
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
16. Дробные числа: из десятичной в любую
Системы счисления, 10 класс16
Дробные числа: из десятичной в любую
0,12345 = 5-1·(1 + 5-1·(2 + 5-1·(3 + 5-1·4)))
5·(0,12345)= 1 + 5-1·(2 + 5-1·(3 + 5-1·4))
целая часть
дробная часть
0,a1a2a3a4 = p-1 (a1 + p-1 (a2 + p-1 (a1 + p-1 a0)))
p (0,a1a2a3a4) = a1 + p-1 (a2 + p-1 (a1 + p-1 a0))
?
К.
 Ю. Поляков, Е.А. Ерёмин, 2018
Ю. Поляков, Е.А. Ерёмин, 2018Как найти a2?
http://kpolyakov.spb.ru
17. Дробные числа: из десятичной в любую
Системы счисления, 10 класс17
Дробные числа: из десятичной в любую
10 5
0,9376
Вычисления
Целая часть
Дробная часть
0,9376 5 = 4,688
0,688 5 = 3,44
0,44 5 = 2,2
0,2 5 = 1
4
3
2
1
0,688
0,44
0,2
0
0,9376 = 0,43215
10 5
0,3
К.Ю. Поляков, Е.А. Ерёмин, 2018
?
Что делать?
http://kpolyakov.spb.ru
18. Дробные числа: из десятичной в любую
Системы счисления, 10 класс18
Дробные числа: из десятичной в любую
10 6
25,375 = 25 + 0,375
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
19. Системы счисления
19Системы
счисления
§ 11. Двоичная система
счисления
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
20. Двоичная система
Системы счисления, 10 класс20
Двоичная система
Основание (количество цифр): 2
Алфавит: 0, 1
10 2
19
18
1
2
9
8
1
2
4
4
0
2
2
2
0
2 10
43210
19 = 100112
2
1
0
2
0
система
счисления
1
разряды
100112 = 1·24 + 0·23 + 0·22 + 1·21 + 1·20
= 16 + 2 + 1 = 19
К.
 Ю. Поляков, Е.А. Ерёмин, 2018
Ю. Поляков, Е.А. Ерёмин, 2018http://kpolyakov.spb.ru
21. Метод подбора
Системы счисления, 10 класс21
Метод подбора
77
10 2
наибольшая степень двойки, которая
меньше или13
равна5заданному числу
1
77
1024 512
210
29
256
128
64
32
16
8
4
2
1
28
27
26
25
24
23
22
21
20
5+ 1…
1
77 = 64 + 813+ 4
…
Разложение по степеням двойки:
77 = 26 + 23 + 22 + 20
77 = 1 26 + 0 25 + 0 24 + 1 23 +1 22 +0 21 + 1 20
6543210
разряды
77 = 10011012
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
22. Перевод из двоичной в десятичную
Системы счисления, 10 класс22
Перевод из двоичной в десятичную
разряды
6543210
10011012 = 26 + 23 + 22 + 20
= 64 + 8 + 4 + 1 = 77
Схема Горнера:
Разряд
6
5
4
3
2
1
0
К.Ю. Поляков, Е.А. Ерёмин, 2018
1
0
0
1
1
0
1
Вычисления
1
1 2+0
2 2+0
4 2+1
9 2+1
19 2+0
38 2+1
Результат
1
2
4
9
19
38
77
http://kpolyakov.
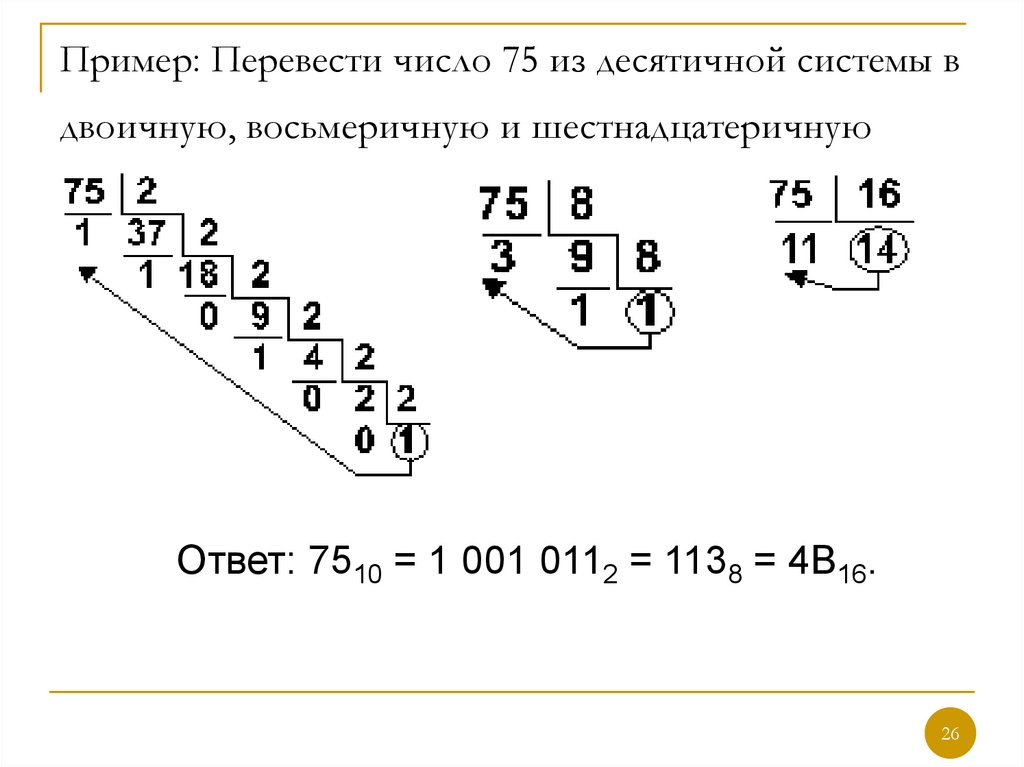 spb.ru
spb.ru23. Арифметические операции
Системы счисления, 10 класс23
Арифметические операции
сложение
вычитание
0+0=0 0+1=1перенос0-0=0 1-1=0
1+0=1 1+1=102
1-0=1 102-1=1
заём
1 + 1 + 1 = 112
11111
1 0 1 1 02
+ 1 1 1 0 1 12
1 0 1 0 0 0 12
К.Ю. Поляков, Е.А. Ерёмин, 2018
0 1 1 102 0 102
1 0 0 0 1 0 12
–
1 1 0 1 12
0 1 0 1 0 1 02
http://kpolyakov.spb.ru
24. Арифметические операции
Системы счисления, 10 класс24
Арифметические операции
1011012
+ 111112
101112
+1011102
1110112
+ 110112
1110112
+ 100112
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
25. Арифметические операции
Системы счисления, 10 класс25
Арифметические операции
1011012
– 111112
110112
–1101012
1100112
– 101012
1101012
– 110112
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
26. Арифметические операции
Системы счисления, 10 класс26
Арифметические операции
умножение
1 0 1 0 12
1 0 12
1 0 1 0 12
+ 1 0 1 0 12
1 1 0 1 0 0 12
К.
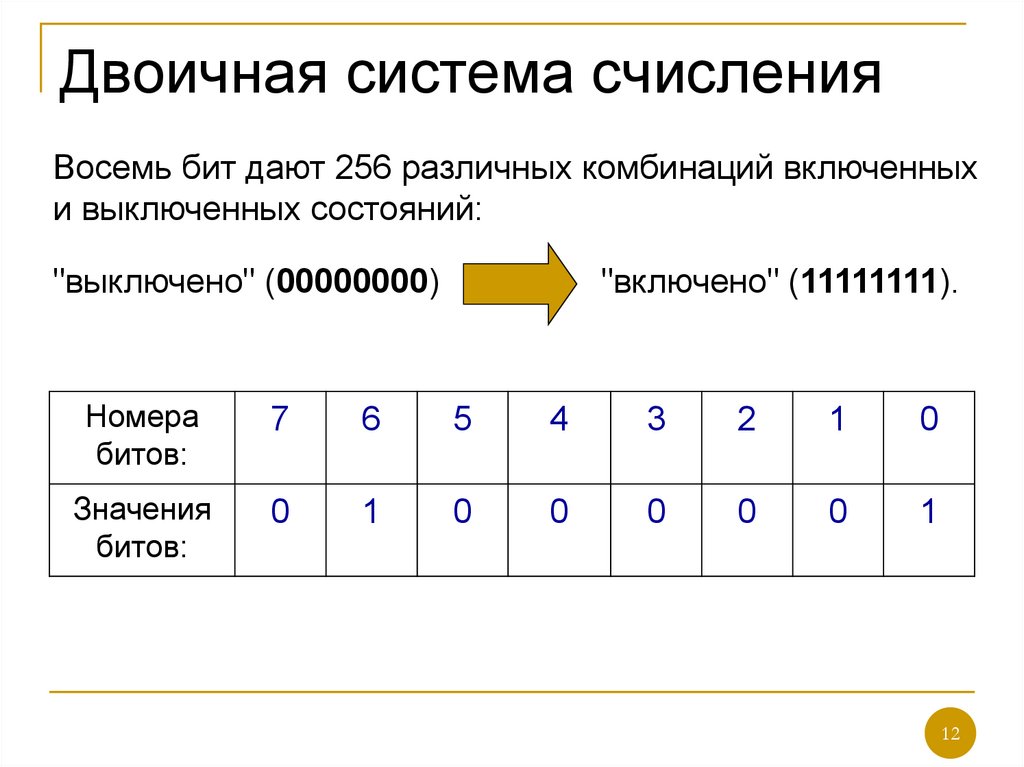 Ю. Поляков, Е.А. Ерёмин, 2018
Ю. Поляков, Е.А. Ерёмин, 2018деление
1 0 1 0 12 1 1 12
– 1 1 12 1 1
2
1 1 12
– 1 1 12
0
http://kpolyakov.spb.ru
27. Работа со степенями числа 2
Системы счисления, 10 класс27
Работа со степенями числа 2
Задача: Запишите значение выражения
212 + 27 – 25
в системе счисления с основанием 2.
Полезные свойства:
2N = 10…02
N
2N – 1= 1…12
2N – 2M = 1…10…02
N
N–M M
Решение:
27 – 25 = +
11000002
212 =
10000000000002
10000011000002
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
28. Работа со степенями числа 2
Системы счисления, 10 класс28
Работа со степенями числа 2
Задача: Запишите значение выражения
212 + 27 – 25– 23
в системе счисления с основанием 2.
Решение:
212 + 27 – 25– 23
пока забываем…
цепочка вычитаний
27 – 23 =
25 =
212 =
–
11110002
1000002
10110002
+
10000000000002
10000010110002
К.
 Ю. Поляков, Е.А. Ерёмин, 2018
Ю. Поляков, Е.А. Ерёмин, 2018http://kpolyakov.spb.ru
29. Работа со степенями числа 2
Системы счисления, 10 класс29
Работа со степенями числа 2
Задача: Сколько единиц и значащих нулей в двоичной
записи числа
Решение:
по убыванию
степеней!
4344
2136–
= 64 + 8 – 2
+
–
70
8128 + 4344 – 2136– 64 – 8 + 2
(23)128 + (22)344 – 2136 – 26 – 23 + 21
8128
2384 + 2688 – 2136 – 26 – 23 + 21
2688 + 2 384 – 2136 – 26 – 23 + 21
1
цепочка вычитаний
384 – 3 – 2 =
379
пока
забываем…
1
381
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
30. Дробные числа
Системы счисления, 10 класс30
Дробные числа
10 2
0,8125
Вычисления
Целая часть
Дробная часть
0,8125 2 = 1,625
0,625 2 = 1,25
0,25 2 = 0,5
0,5 2 = 1
1
1
0
1
0,625
0,25
0,5
0
0,8125 = 0,11012
10 2
0,6 = 0,100110011001… = 0,(1001)2
!
Бесконечное число разрядов!
К.
 Ю. Поляков, Е.А. Ерёмин, 2018
Ю. Поляков, Е.А. Ерёмин, 2018http://kpolyakov.spb.ru
31. Дробные числа
Системы счисления, 10 класс31
Дробные числа
• Большинство дробных чисел хранится в памяти с
некоторой погрешностью.
• При выполнении вычислений с дробными числами
погрешности накапливаются и могут существенно
влиять на результат.
• Желательно обходиться без использования дробных
чисел, если это возможно.
если A B то…
если A2 B то…
целые, 0
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
32. Двоичная система счисления
Системы счисления, 10 класс32
Двоичная система счисления
нужны только устройства с двумя состояниями
надёжность передачи данных при помехах
компьютеру проще выполнять вычисления
(умножение сводится сложению и т.п.)
длинная запись чисел: 1024 = 100000000002
запись однородна (только 0 и 1)
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
33. Системы счисления
33Системы
счисления
§ 12.
 Восьмеричная система
Восьмеричная системасчисления
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
34. Восьмеричная система счисления
Системы счисления, 10 класс34
Восьмеричная система счисления
PDP-11, ДВК,
Основание: 8
СМ ЭВМ, БЭСМ,
Алфавит: 0, 1, 2, 3, 4, 5, 6, 7
БК
10 8
100 8
96 12 8
8 1
4
4 0
100 = 1448
1
8 10
210
8
0
разряды
1448 = 1·82 + 4·81 + 4·80
= 64 + 32 + 4 = 100
34
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
35. Примеры
Системы счисления, 10 класс35
Примеры
134 =
75 =
1348 =
758 =
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
36. Восьмеричная система счисления
Системы счисления, 10 класс36
Восьмеричная система счисления
X8
X2
X8
X2
0
000
4
100
1
001
5
101
2
010
6
110
3
011
7
111
К.Ю. Поляков, Е.
 А. Ерёмин, 2018
А. Ерёмин, 2018http://kpolyakov.spb.ru
37. Перевод в двоичную систему счисления
Системы счисления, 10 класс37
Перевод в двоичную систему счисления
• трудоёмко
• 2 действия
10
8
2
8 = 23
!
Каждая восьмеричная цифра может быть
записана как три двоичных (триада)!
1
К.Ю. Поляков, Е.А. Ерёмин, 2018
7
2
{
{
{
{
17258 = 001 111 010 1012
5
http://kpolyakov.spb.ru
38. Примеры
Системы счисления, 10 класс38
Примеры
34678 =
21488 =
73528 =
12318 =
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
39. Перевод из двоичной в восьмеричную
Системы счисления, 10 класс39
Перевод из двоичной в восьмеричную
10010111011112
Шаг 1. Разбить на триады, начиная справа:
001 001 011 101 1112
Шаг 2. Каждую триаду записать одной
восьмеричной цифрой:
001 001 011 101 1112
1
Ответ:
1
3
5
7
10010111011112 = 113578
К.
 Ю. Поляков, Е.А. Ерёмин, 2018
Ю. Поляков, Е.А. Ерёмин, 2018http://kpolyakov.spb.ru
40. Примеры
Системы счисления, 10 класс40
Примеры
1011010100102 =
111111010112 =
11010110102 =
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
41. Арифметические операции
Системы счисления, 10 класс41
Арифметические операции
сложение
1 1 1
1 5 68
+ 6 6 28
1 0 4 08
К.Ю. Поляков, Е.А. Ерёмин, 2018
1 в перенос
1 в перенос
6+2=8=8+0
5 + 6 + 1 = 12 = 8 + 4
1+6+1=8=8+0
1 в перенос
http://kpolyakov.spb.ru
42. Примеры
Системы счисления, 10 класс42
Примеры
3 5 38
+ 7 3 68
К.Ю. Поляков, Е.А. Ерёмин, 2018
1 3 5 38
+ 7 7 78
http://kpolyakov.spb.ru
43. Арифметические операции
Системы счисления, 10 класс43
Арифметические операции
вычитание
4 5 68
– 2 7 78
1 5 78
К.Ю. Поляков, Е.А. Ерёмин, 2018
заём
(6 + 8) – 7 = 7
заём
(5 – 1 + 8) – 7 = 5
(4 – 1) – 2 = 1
http://kpolyakov.
 spb.ru
spb.ru44. Примеры
Системы счисления, 10 класс44
Примеры
1 5 68
–
6 6 28
К.Ю. Поляков, Е.А. Ерёмин, 2018
1 1 5 68
–
6 6 28
http://kpolyakov.spb.ru
45. Применение восьмеричной системы
Системы счисления, 10 класс45
Применение восьмеричной системы
• компактная запись данных в компьютерах
1960-х годов:
101001112 = 2478
• запись команд компьютеров PDP, ДВК, СМ
ЭВМ
• установка прав на доступ к файлу в Linux:
chmod 754 pass.txt
для
пользователя
для
группы
7 = 111 = rwx
5 = 101 = r-x
4 = 100 = r- К.Ю. Поляков, Е.А. Ерёмин, 2018
для
остальных
чтение, запись, выполнение
чтение, выполнение
чтение
http://kpolyakov.spb.ru
46. Системы счисления
46Системы
счисления
§ 13. Шестнадцатеричная
система счисления
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
47. Шестнадцатеричная система счисления
Системы счисления, 10 класс47
Шестнадцатеричная система счисления
Основание: 16
Алфавит: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
10 11 12 13 14 15
10 16 444 16
432 27
444 = 1BC16
16
12 16 1 16
С
11 0 0
B
1
16 10
2 1 0
разряды
1+C
B
1BC16= 1·162 + 11·16
12·160
= 256 + 176 + 12 = 444
К.
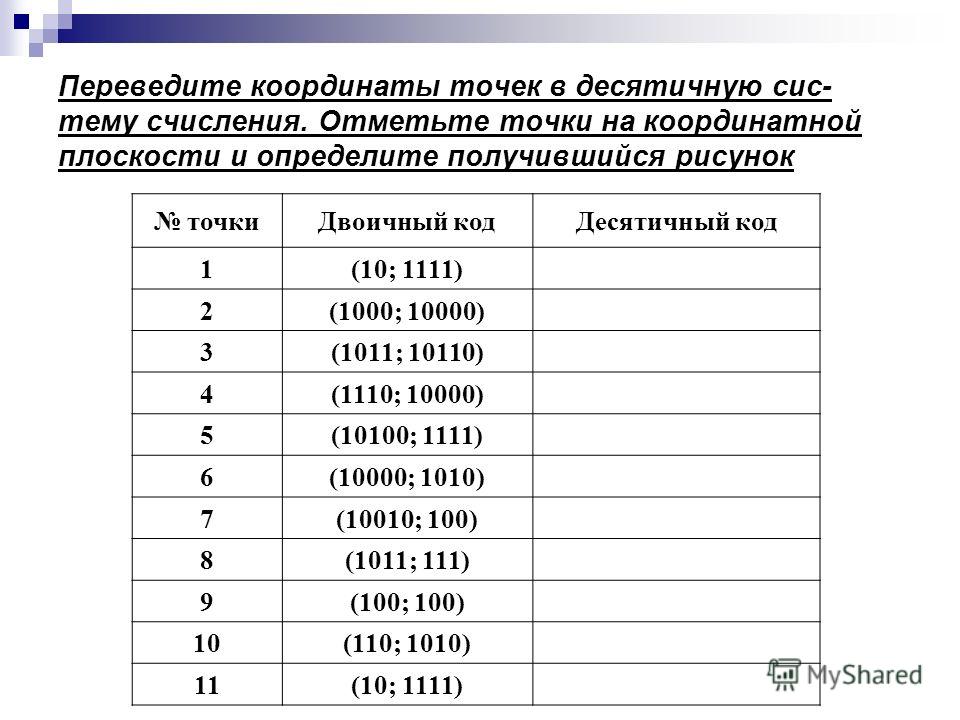 Ю. Поляков, Е.А. Ерёмин, 2018
Ю. Поляков, Е.А. Ерёмин, 2018http://kpolyakov.spb.ru
48. Примеры
Системы счисления, 10 класс48
Примеры
171 =
1C516 =
206 =
22B16 =
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
49. Шестнадцатеричная система счисления
Системы счисления, 10 класс49
Шестнадцатеричная система счисления
X10
X16
X2
X10
X16
X2
0
0
0000
8
8
1000
1
1
0001
9
9
1001
2
2
0010
10
A
1010
3
3
0011
11
B
1011
4
4
0100
12
C
1100
5
5
0101
13
D
1101
6
6
0110
14
E
1110
7
7
0111
15
F
1111
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
50. Перевод в двоичную систему
Системы счисления, 10 класс50
Перевод в двоичную систему
• трудоёмко
• 2 действия
10
16
2
16 = 24
!
Каждая шестнадцатеричная цифра может быть
записана как четыре двоичных (тетрада)!
7
К.
 Ю. Поляков, Е.А. Ерёмин, 2018
Ю. Поляков, Е.А. Ерёмин, 2018F
1
{
{
{
{
7F1A16 = 0111 1111 0001 10102
A
http://kpolyakov.spb.ru
51. Примеры
Системы счисления, 10 класс51
Примеры
C73B16 =
2FE116 =
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
52. Перевод из двоичной системы
Системы счисления, 10 класс52
Перевод из двоичной системы
10010111011112
Шаг 1. Разбить на тетрады, начиная справа:
0001 0010 1110 11112
Шаг 2. Каждую тетраду записать одной
шестнадцатеричной цифрой:
0001 0010 1110 11112
1
2
E
F
Ответ:
10010111011112 = 12EF16
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
53. Примеры
Системы счисления, 10 класс53
Примеры
10101011010101102 =
1111001101111101012 =
1101101101011111102 =
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
54. Перевод в восьмеричную и обратно
Системы счисления, 10 класс54
Перевод в восьмеричную и обратно
трудоёмко
10
8
16
2
Шаг 1.
 Перевести в двоичную систему:
Перевести в двоичную систему:3DEA16 = 11 1101 1110 10102
Шаг 2. Разбить на триады (справа):
011 110 111 101 0102
Шаг 3. Триада – одна восьмеричная цифра:
3DEA16 = 367528
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
55. Примеры
Системы счисления, 10 класс55
Примеры
A3516 =
7658 =
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
56. Арифметические операции
Системы счисления, 10 класс56
Арифметические операции
сложение
1
A 5 B16
+ C 7 E16
1 6 D 916
1
10 5 11
+ 12 7 14
1 6 13 9
1 в перенос
11+14=25=16+9
5+7+1=13=D16 1 в перенос
10+12=22=16+6
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
57. Примеры
Системы счисления, 10 класс57
Примеры
С В А16
+ A 5 916
F D В16
+ A B C16
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
58. Арифметические операции
Системы счисления, 10 класс58
Арифметические операции
вычитание
С 5 B16
– A 7 E16
1 D D16
заём
12 5 11
– 10 7 14
1 13 13
заём
(11+16)–14=13=D16
(5 – 1)+16 – 7=13=D16
(12 – 1) – 10 = 1
58
К.
 Ю. Поляков, Е.А. Ерёмин, 2018
Ю. Поляков, Е.А. Ерёмин, 2018http://kpolyakov.spb.ru
59. Примеры
Системы счисления, 10 класс59
Примеры
1 В А16
– A 5 916
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
60. Применение шестнадцатеричной системы
Системы счисления, 10 класс60
Применение шестнадцатеричной системы
• компактная запись данных :
0
1
0
1
1
5
• запись команд компьютеров
66 01 d8
код
команды
add
ax, bx
на языке
ассемблера
К.Ю. Поляков, Е.А. Ерёмин, 2018
1
1
0
5E16
E
ax
bx
ax ax + bx
http://kpolyakov.spb.ru
61. Системы счисления
61Системы
счисления
§ 14. Другие системы
счисления
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
62. Задача Баше о наборе гирь
Системы счисления, 10 класс62
Задача Баше о наборе гирь
Как с помощью 4-х гирь
взвесить от 0 до 40 кг?
+1
0
–1
гиря на правой чашке
гиря снята
гиря на левой чашке
!
Троичная система!
Веса гирь – степени числа 3:
1 кг, 3 кг, 9 кг, 27 кг
Пример:
27 кг + 9 кг + 3 кг + 1 кг = 40 кг
К.
 Ю. Поляков, Е.А. Ерёмин, 2018
Ю. Поляков, Е.А. Ерёмин, 2018http://kpolyakov.spb.ru
63. Троичная уравновешенная система
1Системы счисления, 10 класс63
Троичная уравновешенная система
ЭВМ «Сетунь» (1958) , Н.П. Брусенцов
Основание: 3
уравновешенная
Алфавит: 1 («-1»), 0, 1
система
Для N разрядов: всего 3N значений:
0 + по [3N/2] положительных
и отрицательных чисел
–4
–3
–2
–1
0
1
2
3
4
11
10
11
01
00
01
11
10
11
= (–1) 31 + (–1) 30
= (–1) 31 + 0 30
= (–1) 31 + 1 30
= 0 31 + (–1) 30
= 0 31 + 0 30
= 0 31 + 1 30
= 1 31 + (–1) 30
= 1 31 + 0 30
= 1 31 + 1 30
К.Ю. Поляков, Е.А. Ерёмин, 2018
и положительные, и
отрицательные числа
для изменения знака
нужно поменять знаки
у всех цифр
запись короче, чем в
двоичной системе
нужны элементы с
тремя состояниями
http://kpolyakov.spb.ru
64. Двоично-десятичная система (ДДС)
Системы счисления, 10 класс64
Двоично-десятичная система (ДДС)
Десятичные цифры, закодированные в двоичном коде.

Вinary coded decimal (BCD).
9024,19 = 1001 0000 0010 0100, 0001 1001ДДС
9
0
2
4
1
9
101010011,01111ДДС =
= 0001 0101 0011, 0111 1000ДДС = 153,78
легко переводить в десятичную систему
просто умножать и делить на 10
конечные десятичные дроби записываются точно
(аналог ручных расчётов)
длиннее, чем двоичная запись
сложнее арифметические операции
Использование – в калькуляторах.
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
65. Конец фильма
Системы счисления, 10 класс65
Конец фильма
ПОЛЯКОВ Константин Юрьевич
д.т.н., учитель информатики
ГБОУ СОШ № 163, г. Санкт-Петербург
[email protected]
ЕРЕМИН Евгений Александрович
к.ф.-м.н., доцент кафедры мультимедийной
дидактики и ИТО ПГГПУ, г. Пермь
[email protected]
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
66. Источники иллюстраций
Системы счисления, 10 класс66
Источники иллюстраций
1.
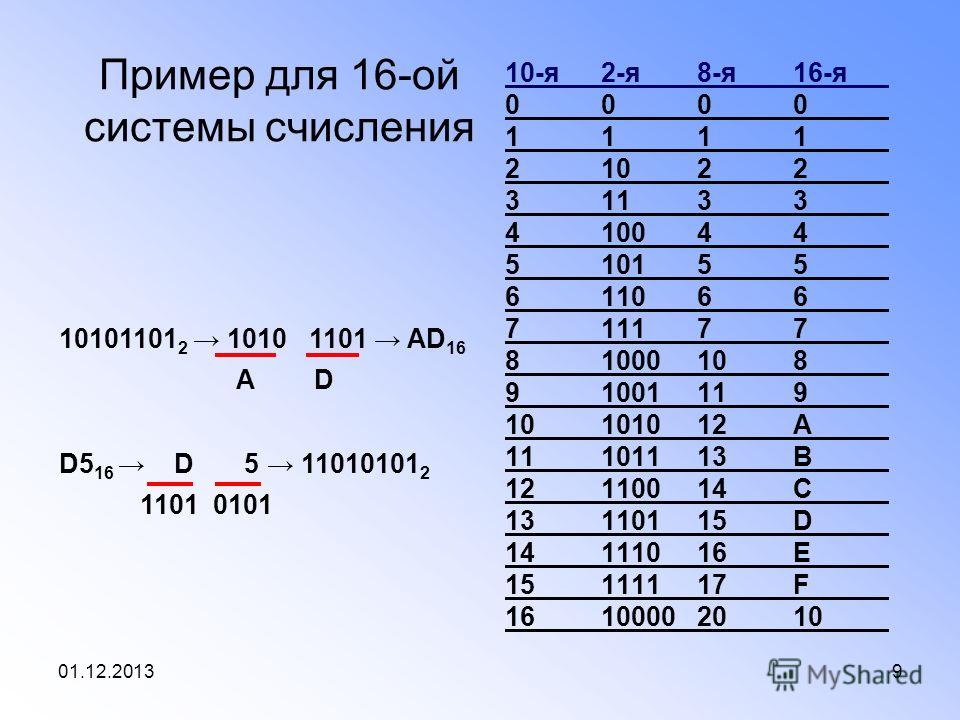
2.
3.
4.
5.
6.
7.
http://www.najboljamamanasvetu.com
http://www.tissot.ch
http://www.mindmeister.com
http://www.antiqueclocksshop.com/
http://en.wikipedia.org
http://ru.wikipedia.org
авторские материалы
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
Правила перевода из 10 в 2. Системы счисления
Для перевода чисел из одной системы счисления в другую необходимо владеть основными сведениями о системах счисления и форме представления чисел в них.
Количество s различных цифр, употребляемых в системе счисления, называется основанием, или базой системы счисления. В общем случае положительное число X в позиционной системе с основанием s может быть представлено в виде полинома:
где s — база системы счисления, — цифры, допустимые в данной системе счисления . Последовательность образует целую часть X , а последовательность — дробную часть X .
В вычислительной технике наибольшее применение нашли двоичная (BIN — binary),
и двоично кодированные системы счисления: восьмеричная (OCT — octal), шестнадцатеричная (HEX — hexadecimal) и двоично-кодированная десятичная (BCD — binary coded decimal).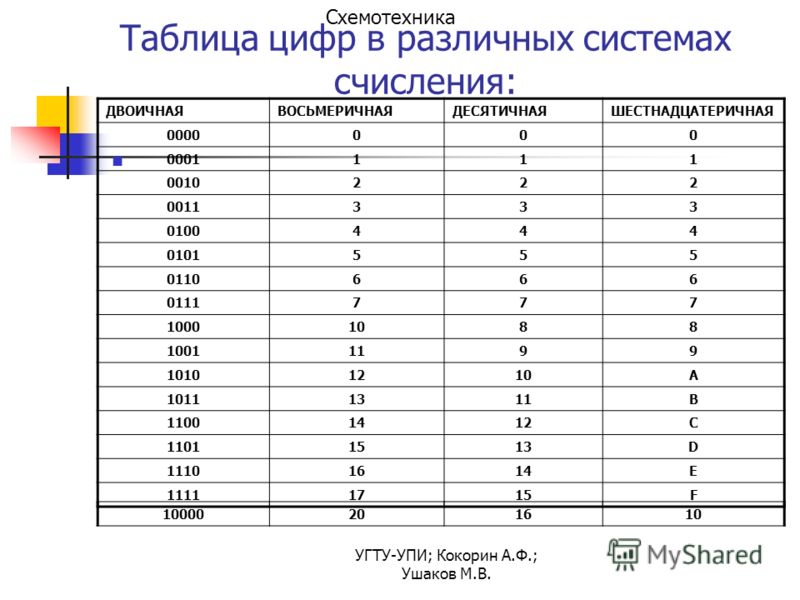
В дальнейшем для обозначения используемой системы счисления число будет заключаться в скобки, а в индексе указано основание системы. Число X по основанию s будет обозначено .
Двоичная система счисления
Основанием системы счисления служит число 2 (s = 2) и для записи чисел используются только две цифры: 0 и 1. Чтобы представить любой разряд двоичного числа, достаточно иметь физический элемент с двумя чётко различными устойчивыми состояниями, одно из которых изображает 1, а другое 0.
Прежде чем заняться переводом из любой системы счисления в двоичную, нужно внимательно изучить пример записи числа в двоичной системе счисления:
Если Вам не нужно углубляться в теорию, а нужно лишь получить результат, то воспользуйтесь Калькулятором онлайн Перевод целых чисел из десятичной системы счисления в другие системы .
Восьмеричная и шестнадцатеричная системы счисления
Эти системы счисления относятся к двоично-кодированным, в которых основание системы счисления
представляет собой целую степень двойки: —
для восьмеричной и — для шестнадцатеричной.
В восьмеричной системе счисления(s = 8) используются 8 цифр: 0, 1, 2, 3, 4, 5, 6, 7.
Прежде чем заняться переводом из любой системы счисления в восьмеричную, нужно внимательно изучить пример записи числа в восьмеричной системе:
В шестнадцатеричной системе счисления (s = 16) используются 16 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.
Пример записи числа в шестнадцатеричной системе:
Широкое применение восьмеричной и шестнадцатеричной систем счисления обусловлено двумя факторами.
Во-первых, эти системы позволяют заменить запись двоичного числа более компактным представлением
(запись числа в восьмеричной и шестнадцатеричной системах будет соответственно в 3 и 4 раза короче двоичной записи этого числа).
Во-вторых, взаимное преобразование чисел между двоичной системой с одной стороны и восьмеричной и шестнадцатиречной — с другой
осуществляется сравнительно просто. Действительно, поскольку для восьмеричного числа каждый разряд представляется
группой из трёх двоичных разрядов (триад), а для шестнадцатеричного — группой из четырёх двоичных разрядов (тетрад),
то для преобразования двоичного числа достаточно объединить его цифры в группы по 3 или 4 разряда соответственно, продвигаясь от
разделительной запятой вправо и влево.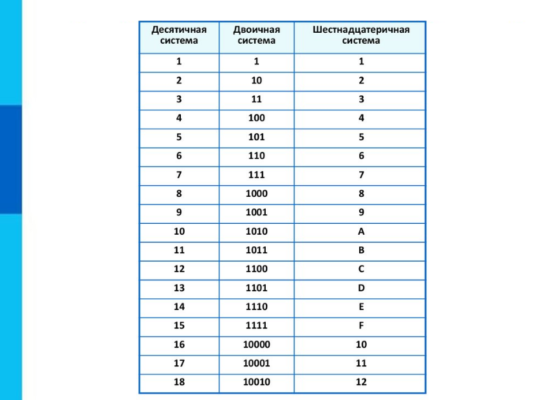 При этом, в случае необходимости, добавляют нули слева от целой части
и/или справа от дробной части и каждую такую группу — триаду или тетраду — заменяют эвивалентной восьмеричной или
шестнадцатеричной цифрой (см. таблицу).
При этом, в случае необходимости, добавляют нули слева от целой части
и/или справа от дробной части и каждую такую группу — триаду или тетраду — заменяют эвивалентной восьмеричной или
шестнадцатеричной цифрой (см. таблицу).
Если Вам не нужно углубляться в теорию, а нужно лишь получить результат, то воспользуйтесь Калькулятором онлайн Перевод целых чисел из десятичной системы счисления в другие системы .
Соответствие между цифрами в различных системах счисления
| DEC | BIN | OCT | HEX | BCD |
| 0 | 0000 | 0 | 0 | 0000 |
| 1 | 0001 | 1 | 1 | 0001 |
| 2 | 0010 | 2 | 2 | 0010 |
| 3 | 0011 | 3 | 3 | 0011 |
| 4 | 0100 | 4 | 4 | 0100 |
| 5 | 0101 | 5 | 5 | 0101 |
| 6 | 0110 | 6 | 6 | 0110 |
| 7 | 0111 | 7 | 7 | 0111 |
| 8 | 1000 | 10 | 8 | 1000 |
| 9 | 1001 | 11 | 9 | 1001 |
| 10 | 1010 | 12 | A | 0001 0000 |
| 11 | 1011 | 13 | B | 0001 0001 |
| 12 | 1100 | 14 | C | 0001 0010 |
| 13 | 1101 | 15 | D | 0001 0011 |
| 14 | 1110 | 16 | E | 0001 0100 |
| 15 | 1111 | 17 | F | 0001 0101 |
Для обратного перевода каждая OCT или HEX цифра заменяется соответственно триадой или тетрадой
двоичных цифр, причём незначащие нули слева и справа отбрасываются.
Для рассмотренных ранее примеров это выглядит следующим образом:
Если Вам не нужно углубляться в теорию, а нужно лишь получить результат, то воспользуйтесь Калькулятором онлайн Перевод целых чисел из десятичной системы счисления в другие системы .
Двоично-десятичная система счисления
В двоично-десятичной системе вес каждого разряда равен степени 10, как в десятичной системе, а каждая десятичная цифра кодируется четырьмя двоичными цифрами. Для записи десятичного числа в BCD-системе достаточно заменить каждую десятичную цифру эквивалентной четырёхразрядной двоичной комбинацией:
Любое десятичное число можно представить в двоично-десятичной записи, но следует помнить, что это не двоичный эквивалент числа. Это видно из следующего примера:
Перевод чисел из одной системы счисления в другую
Пусть X — число в системе счисления с основанием s , которое требуется
представить в системе с основанием h . Удобно различать два случая.
Удобно различать два случая.
В первом случае и, следовательно, при переходе к основанию h можно использовать арифметику этой системы. Метод преобразования состоит в представлении числа в виде многочлена по степеням s , а также в вычислении этого многочлена по правилам арифметики системы счисления с основанием h . Так, например, удобно переходить от двоичной или восьмеричной системы счисления к десятичной. Описанный приём иллюстрируют следующие примеры:
.
.
В обоих случаях арифметические действия выполняются по правилам системы счисления с основанием 10.
Во втором случае () удобнее пользоваться арифметикой по основанию s . Здесь следует учитывать, что перевод целых чисел и правильных дробей производится по различным правилам. При переводе смешанных дробей целая и дробная части переводятся каждая по своим правилам, после чего полученные числа записываются через запятую.
Перевод целых чисел
Правила перевода целых чисел становится ясным из общей формулы записи числа
в произвольной позиционной системе. Пусть число
в исходной системе счисления s имеет вид .
Требуется получить запись числа в системе счисления с основанием h :
Пусть число
в исходной системе счисления s имеет вид .
Требуется получить запись числа в системе счисления с основанием h :
.
Для нахождения значений разделим этот многочлен на h :
.
Как видно, младший разряд , то есть , равен первому остатку. Следующий значащий разряд определяется делением частного на h :
.
Остальные также вычисляются путём деления частных до тех пор, пока не станет равным нулю.
Для перевода целого числа из s-ичной системы счисления в h-ичную необходимо последовательно делить это число и получаемые частные на h (по правилам системы счисления с основанием h) до тех пор, пока частное не станет равным нулю. Старшей цифрой в записи числа с основанием h служит последний остаток, а следующие за ней цифры образуют остатки от предшествующих делений, выписываемые в последовательности, обратной их получению.
1. Порядковый счет в различных системах счисления.
В современной жизни мы используем позиционные системы счисления, то есть системы, в которых число, обозначаемое цифрой, зависит от положения цифры в записи числа. Поэтому в дальнейшем мы будем говорить только о них, опуская термин «позиционные».
Поэтому в дальнейшем мы будем говорить только о них, опуская термин «позиционные».
Для того чтобы научиться переводить числа из одной системы в другую, поймем, как происходит последовательная запись чисел на примере десятичной системы.
Поскольку у нас десятичная система счисления, мы имеем 10 символов (цифр) для построения чисел. Начинаем порядковый счет: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Цифры закончились. Мы увеличиваем разрядность числа и обнуляем младший разряд: 10. Затем опять увеличиваем младший разряд, пока не закончатся все цифры: 11, 12, 13, 14, 15, 16, 17, 18, 19. Увеличиваем старший разряд на 1 и обнуляем младший: 20. Когда мы используем все цифры для обоих разрядов (получим число 99), опять увеличиваем разрядность числа и обнуляем имеющиеся разряды: 100. И так далее.
Попробуем сделать то же самое в 2-ной, 3-ной и 5-ной системах (введем обозначение для 2-ной системы, для 3-ной и т.д.):
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 |
| 3 | 11 | 10 | 3 |
| 4 | 100 | 11 | 4 |
| 5 | 101 | 12 | 10 |
| 6 | 110 | 20 | 11 |
| 7 | 111 | 21 | 12 |
| 8 | 1000 | 22 | 13 |
| 9 | 1001 | 100 | 14 |
| 10 | 1010 | 101 | 20 |
| 11 | 1011 | 102 | 21 |
| 12 | 1100 | 110 | 22 |
| 13 | 1101 | 111 | 23 |
| 14 | 1110 | 112 | 24 |
| 15 | 1111 | 120 | 30 |
Если система счисления имеет основание больше 10, то нам придется вводить дополнительные символы, принято вводить буквы латинского алфавита. Например, для 12-ричной системы кроме десяти цифр нам понадобятся две буквы ( и ):
Например, для 12-ричной системы кроме десяти цифр нам понадобятся две буквы ( и ):
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
| 7 | 7 |
| 8 | 8 |
| 9 | 9 |
| 10 | |
| 11 | |
| 12 | 10 |
| 13 | 11 |
| 14 | 12 |
| 15 | 13 |
2.Перевод из десятичной системы счисления в любую другую.
Чтобы перевести целое положительное десятичное число в систему счисления с другим основанием, нужно это число разделить на основание. Полученное частное снова разделить на основание, и дальше до тех пор, пока частное не окажется меньше основания. В результате записать в одну строку последнее частное и все остатки, начиная с последнего.
В результате записать в одну строку последнее частное и все остатки, начиная с последнего.
Пример 1. Переведем десятичное число 46 в двоичную систему счисления.
Пример 2. Переведем десятичное число 672 в восьмеричную систему счисления.
Пример 3. Переведем десятичное число 934 в шестнадцатеричную систему счисления.
3. Перевод из любой системы счисления в десятичную.
Для того, чтобы научиться переводить числа из любой другой системы в десятичную, проанализируем привычную нам запись десятичного числа.
Например, десятичное число 325 – это 5 единиц, 2 десятка и 3 сотни, т.е.
Точно так же обстоит дело и в других системах счисления, только умножать будем не на 10, 100 и пр., а на степени основания системы счисления. Для примера возьмем число 1201 в троичной системе счисления. Пронумеруем разряды справа налево начиная с нуля и представим наше число как сумму произведений цифры на тройку в степени разряда числа:
Это и есть десятичная запись нашего числа, т. е.
е.
Пример 4. Переведем в десятичную систему счисления восьмеричное число 511.
Пример 5. Переведем в десятичную систему счисления шестнадцатеричное число 1151.
4. Перевод из двоичной системы в систему с основанием «степень двойки» (4, 8, 16 и т.д.).
Для преобразования двоичного числа в число с основанием «степень двойки» необходимо двоичную последовательность разбить на группы по количеству цифр равному степени справа налево и каждую группу заменить соответствующей цифрой новой системы счисления.
Например, Переведем двоичное 1100001111010110 число в восьмеричную систему. Для этого разобьем его на группы по 3 символа начиная справа (т.к. ), а затем воспользуемся таблицей соответствия и заменим каждую группу на новую цифру:
Таблицу соответствия мы научились строить в п.1.
| 0 | 0 |
| 1 | 1 |
| 10 | 2 |
| 11 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
Т.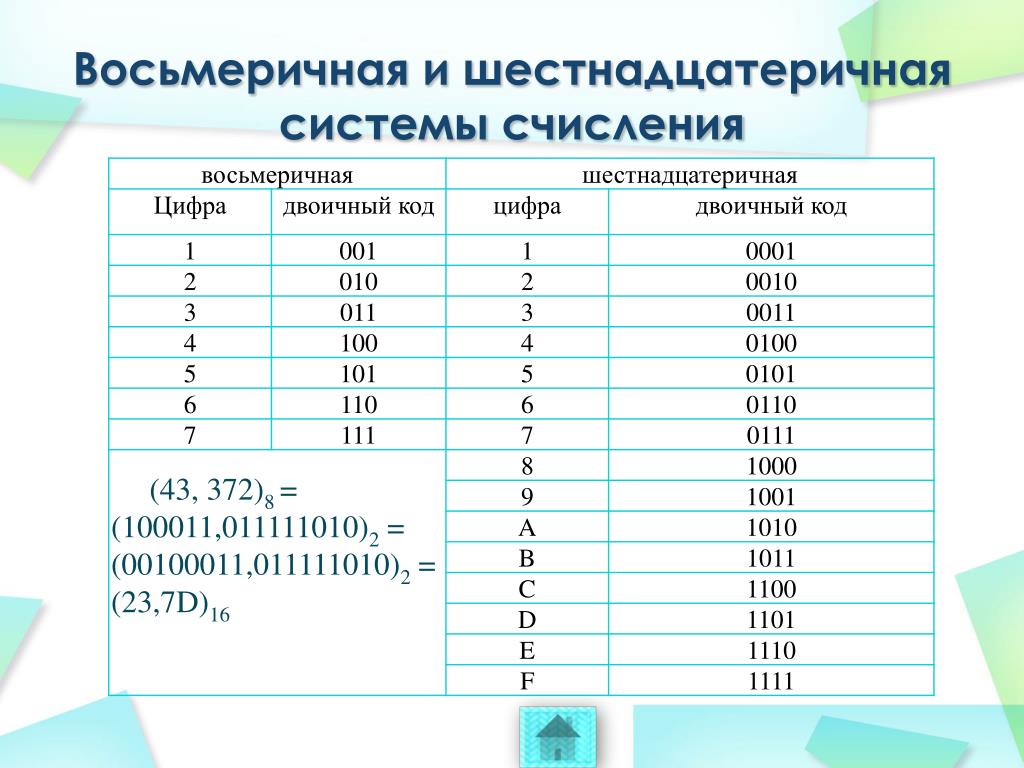 е.
е.
Пример 6. Переведем двоичное 1100001111010110 число в шестнадцатеричную систему.
| 0 | 0 |
| 1 | 1 |
| 10 | 2 |
| 11 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | A |
| 1011 | B |
| 1100 | C |
| 1101 | D |
| 1110 | E |
| 1111 | F |
5.Перевод из системы с основанием «степень двойки» (4, 8, 16 и т.д.) в двоичную.
Этот перевод аналогичен предыдущему, выполненному в обратную сторону: каждую цифру мы заменяем группой цифр в двоичной системе из таблицы соответствия.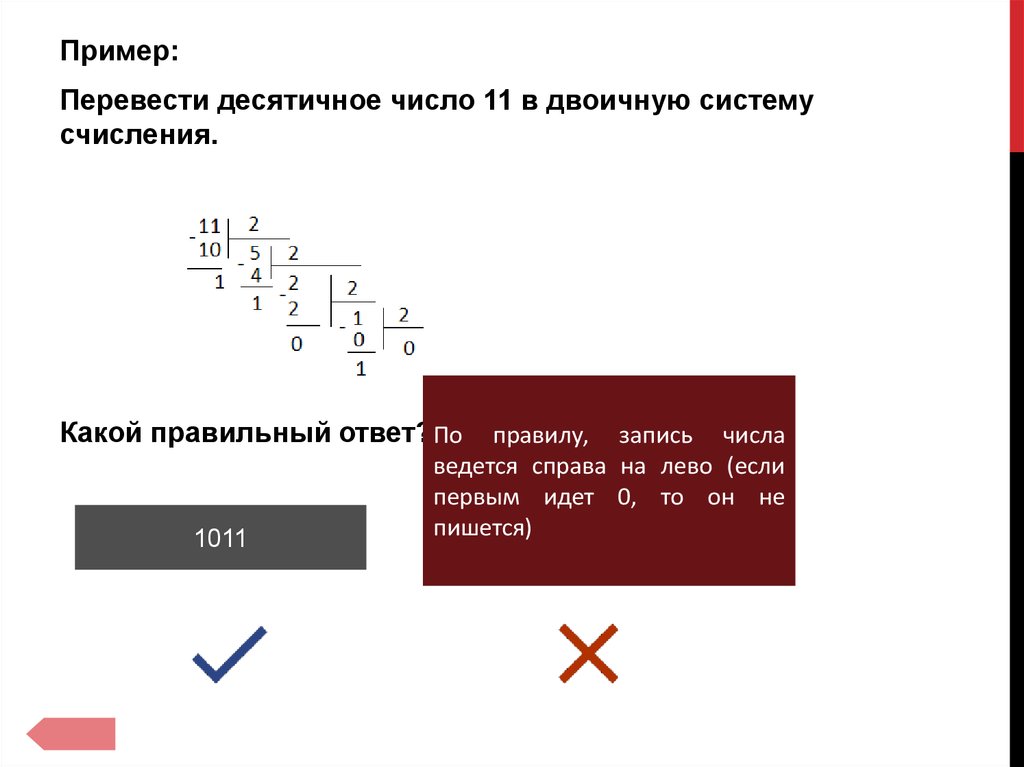
Пример 7. Переведем шестнадцатеричное число С3A6 в двоичную систему счисления.
Для этого каждую цифру числа заменим группой из 4 цифр (т.к. ) из таблицы соответствия, дополнив при необходимости группу нулями вначале:
Сдающим ЕГЭ и не только…
Странно, что в школах на уроках информатики обычно показывают ученикам самый сложный и неудобный способ перевода чисел из одной системы в другую. Это способ заключается в последовательном делении исходного числа на основание и сборе остатков от деления в обратном порядке.
Например, нужно перевести число 810 10 в двоичную систему:
Результат записываем в обратном порядке снизу вверх. Получается 81010 = 11001010102
Если нужно переводить в двоичную систему довольно большие числа, то лестница делений приобретает размер многоэтажного дома. И как тут собрать все единички с нулями и ни одной не пропустить?
В программу ЕГЭ по информатике входят несколько задач, связанных с переводом чисел из одной системы в другую. Как правило, это преобразование между 8- и 16-ричными системами и двоичной. Это разделы А1, В11. Но есть и задачи с другими системами счисления, как например, в разделе B7.
Как правило, это преобразование между 8- и 16-ричными системами и двоичной. Это разделы А1, В11. Но есть и задачи с другими системами счисления, как например, в разделе B7.
Для начала напомним две таблицы, которые хорошо бы знать наизусть тем, кто выбирает информатику своей дальнейшей профессией.
Таблица степеней числа 2:
| 2 1 | 2 2 | 2 3 | 2 4 | 2 5 | 2 6 | 2 7 | 2 8 | 2 9 | 2 10 |
| 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 |
Она легко получается умножением предыдущего числа на 2. Так, что если помните не все эти числа, остальные нетрудно получить в уме из тех, которые помните.
Таблица двоичных чисел от 0 до 15 c 16-ричным представлением:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
Недостающие значения тоже нетрудно вычислить, прибавляя по 1 к известным значениям.
Перевод целых чисел
Итак, начнем с перевода сразу в двоичную систему. Возьмём то же число 810 10 . Нам нужно разложить это число на слагаемые, равные степеням двойки.
- Ищем ближайшую к 810 степень двойки, не превосходящую его. Это 2 9 = 512.
- Вычитаем 512 из 810, получаем 298.
- Повторим шаги 1 и 2, пока не останется 1 или 0.
- У нас получилось так: 810 = 512 + 256 + 32 + 8 + 2 = 2 9 + 2 8 + 2 5 + 2 3 + 2 1 .
Далее есть два способа, можно использовать любой из них. Как легко увидеть, что в любой системе счисления её основание всегда 10. Квадрат основания всегда будет 100, куб 1000. То есть степень основания системы счисления — это 1 (единица), и за ней столько нулей, какова степень.
Способ 1 : Расставить 1 по тем разрядам, какие получились показатели у слагаемых. В нашем примере это 9, 8, 5, 3 и 1. В остальных местах будут стоять нули. Итак, мы получили двоичное представление числа 810 10 = 1100101010 2
.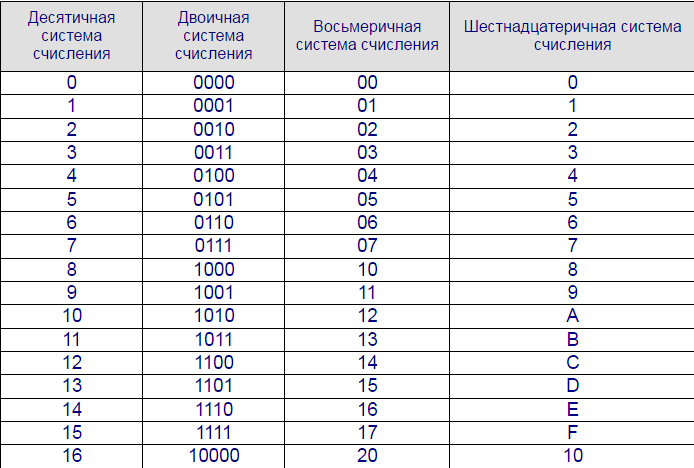 Единицы стоят на 9-м, 8-м, 5-м, 3-м и 1-м местах, считая справа налево с нуля.
Единицы стоят на 9-м, 8-м, 5-м, 3-м и 1-м местах, считая справа налево с нуля.
Способ 2 : Распишем слагаемые как степени двойки друг под другом, начиная с большего.
810 =
А теперь сложим эти ступеньки вместе, как складывают веер: 1100101010 .
Вот и всё. Попутно также просто решается задача «сколько единиц в двоичной записи числа 810?».
Ответ — столько, сколько слагаемых (степеней двойки) в таком его представлении. У 810 их 5.
Теперь пример попроще.
Переведём число 63 в 5-ричную систему счисления. Ближайшая к 63 степень числа 5 — это 25 (квадрат 5). Куб (125) будет уже много. То есть 63 лежит между квадратом 5 и кубом. Тогда подберем коэффициент для 5 2 . Это 2.
Получаем 63 10 = 50 + 13 = 50 + 10 + 3 = 2 * 5 2 + 2 * 5 + 3 = 223 5 .
Ну и, наконец, совсем лёгкие переводы между 8- и 16-ричными системами. Так как их основанием является степень двойки, то перевод делается автоматически, просто заменой цифр на их двоичное представление. Для 8-ричной системы каждая цифра заменяется тремя двоичными разрядами, а для 16-ричной четырьмя. При этом все ведущие нули обязательны, кроме самого старшего разряда.
Для 8-ричной системы каждая цифра заменяется тремя двоичными разрядами, а для 16-ричной четырьмя. При этом все ведущие нули обязательны, кроме самого старшего разряда.
Переведем в двоичную систему число 547 8 .
| 547 8 = | 101 | 100 | 111 |
| 5 | 4 | 7 |
Ещё одно, например 7D6A 16 .
| 7D6A 16 = | (0)111 | 1101 | 0110 | 1010 |
| 7 | D | 6 | A |
Переведем в 16-ричную систему число 7368. Сначала цифры запишем тройками, а потом поделим их на четверки с конца:
736 8 = 111 011 110 = 1 1101 1110 = 1DE 16
.
Переведем в 8-ричную систему число C25 16 . Сначала цифры запишем четвёрками, а потом поделим их на тройки с конца:
C25 16 = 1100 0010 0101 = 110 000 100 101 = 6045 8
. Теперь рассмотрим перевод обратно в десятичную. Он труда не представляет, главное не ошибиться в расчётах. Раскладываем число на многочлен со степенями основания и коэффициентами при них. Потом всё умножаем и складываем.
E68 16 = 14 * 16 2 + 6 * 16 + 8 = 3688
.
732 8 = 7 * 8 2 + 3*8 + 2 = 474
.
Теперь рассмотрим перевод обратно в десятичную. Он труда не представляет, главное не ошибиться в расчётах. Раскладываем число на многочлен со степенями основания и коэффициентами при них. Потом всё умножаем и складываем.
E68 16 = 14 * 16 2 + 6 * 16 + 8 = 3688
.
732 8 = 7 * 8 2 + 3*8 + 2 = 474
.
Перевод отрицательных чисел
Здесь нужно учесть, что число будет представлено в дополнительном коде. Для перевода числа в дополнительный код нужно знать конечный размер числа, то есть во что мы хотим его вписать — в байт, в два байта, в четыре. Старший разряд числа означает знак. Если там 0, то число положительное, если 1, то отрицательное. Слева число дополняется знаковым разрядом. Беззнаковые (unsigned) числа мы не рассматриваем, они всегда положительные, а старший разряд в них используется как информационный.
Для перевода отрицательного числа в двоичный дополнительный код нужно перевести положительное число в двоичную систему, потом поменять нули на единицы и единицы на нули. Затем прибавить к результату 1.
Затем прибавить к результату 1.
Итак, переведем число -79 в двоичную систему. Число займёт у нас один байт.
Переводим 79 в двоичную систему, 79 = 1001111. Дополним слева нулями до размера байта, 8 разрядов, получаем 01001111. Меняем 1 на 0 и 0 на 1. Получаем 10110000. К результату прибавляем 1, получаем ответ 10110001 . Попутно отвечаем на вопрос ЕГЭ «сколько единиц в двоичном представлении числа -79?». Ответ — 4.
Прибавление 1 к инверсии числа позволяет устранить разницу между представлениями +0 = 00000000 и -0 = 11111111. В дополнительном коде они будут записаны одинаково 00000000.
Перевод дробных чисел
Дробные числа переводятся способом, обратным делению целых чисел на основание, который мы рассмотрели в самом начале. То есть при помощи последовательного умножения на новое основание с собиранием целых частей. Полученные при умножении целые части собираются, но не участвуют в следующих операциях. Умножаются только дробные. Если исходное число больше 1, то целая и дробная части переводятся отдельно, потом склеиваются.
Переведем число 0,6752 в двоичную систему.
| 0 | ,6752 |
| *2 | |
| 1 | ,3504 |
| *2 | |
| 0 | ,7008 |
| *2 | |
| 1 | ,4016 |
| *2 | |
| 0 | ,8032 |
| *2 | |
| 1 | ,6064 |
| *2 | |
| 1 | ,2128 |
Процесс можно продолжать долго, пока не получим все нули в дробной части или будет достигнута требуемая точность. Остановимся пока на 6-м знаке.
Получается 0,6752 = 0,101011 .
Если число было 5,6752, то в двоичном виде оно будет 101,101011 .
Способы перевода чисел из одной системы счисления в другую.
Перевод чисел из одной позиционной системы счисления в другую: перевод целых чисел.
Чтобы перевести целое число из одной системы счисления с основанием d1 в другую с основанием d2 необходимо последовательно делить это число и получаемые частные на основание d2 новой системы до тех пор, пока не получится частное меньше основания d2. Последнее частное — старшая цифра числа в новой системе счисления с основанием d2, а следующие за ней цифры — это остатки от деления, записываемые в последовательности, обратной их получению. Арифметические действия выполнять в той системе счисления, в которой записано переводимое число.
Пример 1. Перевести число 11(10) в двоичную систему счисления.
Ответ: 11(10)=1011(2).
Пример 2. Перевести число 122(10) в восьмеричную систему счисления.
Ответ: 122(10)=172(8).
Пример 3. Перевести число 500(10) в шестнадцатеричную систему счисления.
Ответ: 500(10)=1F4(16).
Перевод чисел из одной позиционной системы счисления в другую: перевод правильных дробей.
Чтобы перевести правильную дробь из системы счисления с основанием d1 в систему с основанием d2, необходимо последовательно умножать исходную дробь и дробные части получающихся произведений на основание новой системы счисления d2. Правильная дробь числа в новой системе счисления с основанием d2 формируется в виде целых частей получающихся произведений, начиная с первого.
Правильная дробь числа в новой системе счисления с основанием d2 формируется в виде целых частей получающихся произведений, начиная с первого.
Если при переводе получается дробь в виде бесконечного или расходящегося ряда, процесс можно закончить при достижении необходимой точности.
При переводе смешанных чисел, необходимо в новую систему перевести отдельно целую и дробную части по правилам перевода целых чисел и правильных дробей, а затем оба результата объединить в одно смешанное число в новой системе счисления.
Пример 1. Перевести число 0,625(10) в двоичную систему счисления.
Ответ: 0,625(10)=0,101(2).
Пример 2. Перевести число 0,6(10) в восьмеричную систему счисления.
Ответ: 0,6(10)=0,463(8).
Пример 2. Перевести число 0,7(10) в шестнадцатеричную систему счисления.
Ответ: 0,7(10)=0,В333(16).
Перевод двоичных, восьмеричных и шестнадцатеричных чисел в десятичную систему счисления.
Для перевода числа P-ичной системы в десятичную необходимо использовать следующую формулу разложения:
аnan-1…а1а0=аnPn+ аn-1Pn-1+…+ а1P+a0 .
Пример 1. Перевести число 101,11(2) в десятичную систему счисления.
Ответ: 101,11(2)= 5,75(10) .
Пример 2. Перевести число 57,24(8) в десятичную систему счисления.
Ответ: 57,24(8) = 47,3125(10) .
Пример 3. Перевести число 7A,84(16) в десятичную систему счисления.
Ответ: 7A,84(16)= 122,515625(10) .
Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему счисления и обратно.
Для перевода числа из восьмеричной системы счисления в двоичную необходимо каждую цифру этого числа записать трехразрядным двоичным числом (триадой).
Пример: записать число 16,24(8) в двоичной системе счисления.
Ответ: 16,24(8)= 1110,0101(2) .
Для обратного перевода двоичного числа в восьмеричную систему счисления, необходимо исходное число разбить на триады влево и вправо от запятой и представить каждую группу цифрой в восьмеричной системе счисления. Крайние неполные триады дополняют нулями.
Пример: записать число 1110,0101(2) в восьмеричной системе счисления.
Ответ: 1110,0101(2)= 16,24(8) .
Для перевода числа из шестнадцатеричной системы счисления в двоичную необходимо каждую цифру этого числа записать четырехразрядным двоичным числом (тетрадой).
Пример: записать число 7A,7E(16) в двоичной системе счисления.
Ответ: 7A,7E(16)= 1111010,0111111(2) .
Примечание: незначащие нули слева для целых чисел и справа для дробей не записываются.
Для обратного перевода двоичного числа в шестнадцатеричную систему счисления, необходимо исходное число разбить на тетрады влево и вправо от запятой и представить каждую группу цифрой в шестнадцатеричной системе счисления. Крайние неполные триады дополняют нулями.
Пример: записать число 1111010,0111111(2) в шестнадцатеричной системе счисления.
С помощю этого онлайн калькулятора можно перевести целые и дробные числа из одной системы счисления в другую. Дается подробное решение с пояснениями. Для перевода введите исходное число, задайте основание сисемы счисления исходного числа, задайте основание системы счисления, в которую нужно перевести число и нажмите на кнопку «Перевести». Теоретическую часть и численные примеры смотрите ниже.
Теоретическую часть и численные примеры смотрите ниже.
Результат уже получен!
Перевод целых и дробных чисел из одной системы счисления в любую другую − теория, примеры и решения
Существуют позиционные и не позиционные системы счисления. Арабская система счисления, которым мы пользуемся в повседневной жизни, является позиционной, а римская − нет. В позиционных системах счисления позиция числа однозначно определяет величину числа. Рассмотрим это на примере числа 6372 в десятичном системе счисления. Пронумеруем это число справа налево начиная с нуля:
Тогда число 6372 можно представить в следующем виде:
6372=6000+300+70+2 =6·10 3 +3·10 2 +7·10 1 +2·10 0 .
Число 10 определяет систему счисления (в данном случае это 10). В качестве степеней взяты значения позиции данного числа.
Рассмотрим вещественное десятичное число 1287.923. Пронумеруем его начиная с нуля позиции числа от десятичной точки влево и вправо:
Тогда число 1287.923 можно представить в виде:
1287. 923 =1000+200+80 +7+0.9+0.02+0.003 = 1·10 3 +2·10 2 +8·10 1 +7·10 0 +9·10 -1 +2·10 -2 +3·10 -3 .
923 =1000+200+80 +7+0.9+0.02+0.003 = 1·10 3 +2·10 2 +8·10 1 +7·10 0 +9·10 -1 +2·10 -2 +3·10 -3 .
В общем случае формулу можно представить в следующем виде:
Ц n ·s n +Ц n-1 ·s n-1 +…+Ц 1 ·s 1 +Ц 0 ·s 0 +Д -1 ·s -1 +Д -2 ·s -2 +…+Д -k ·s -k
где Ц n -целое число в позиции n , Д -k — дробное число в позиции (-k), s — система счисления.
Несколько слов о системах счисления.Число в десятичной системе счисления состоит из множества цифр {0,1,2,3,4,5,6,7,8,9}, в восьмеричной системе счисления — из множества цифр {0,1,2,3,4,5,6,7}, в двоичной системе счисления — из множества цифр {0,1}, в шестнадцатеричной системе счисления — из множества цифр {0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F}, где A,B,C,D,E,F соответствуют числам 10,11,12,13,14,15.В таблице Таб.1 представлены числа в разных системах счисления.
| Таблица 1 | |||
|---|---|---|---|
| Система счисления | |||
| 10 | 2 | 8 | 16 |
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 |
| 3 | 11 | 3 | 3 |
| 4 | 100 | 4 | 4 |
| 5 | 101 | 5 | 5 |
| 6 | 110 | 6 | 6 |
| 7 | 111 | 7 | 7 |
| 8 | 1000 | 10 | 8 |
| 9 | 1001 | 11 | 9 |
| 10 | 1010 | 12 | A |
| 11 | 1011 | 13 | B |
| 12 | 1100 | 14 | C |
| 13 | 1101 | 15 | D |
| 14 | 1110 | 16 | E | 15 | 1111 | 17 | F |
Перевод чисел из одной системы счисления в другую
Для перевода чисел с одной системы счисления в другую, проще всего сначала перевести число в десятичную систему счисления, а затем, из десятичной системы счисления перевести в требуемую систему счисления.
Перевод чисел из любой системы счисления в десятичную систему счисления
С помощью формулы (1) можно перевести числа из любой системы счисления в десятичную систему счисления.
Пример 1. Переводить число 1011101.001 из двоичной системы счисления (СС) в десятичную СС. Решение:
1 ·2 6 +0 ·2 5 +1 ·2 4 +1 ·2 3 +1 ·2 2 +0 ·2 1 +1 ·2 0 +0 ·2 -1 +0 ·2 -2 +1 ·2 -3 =64+16+8+4+1+1/8=93.125
Пример 2. Переводить число 1011101.001 из восьмеричной системы счисления (СС) в десятичную СС. Решение:
Пример 3 . Переводить число AB572.CDF из шестнадцатеричной системы счисления в десятичную СС. Решение:
Здесь A -заменен на 10, B — на 11, C — на 12, F — на 15.
Перевод чисел из десятичной системы счисления в другую систему счисления
Для перевода чисел из десятичной системы счисления в другую систему счисления нужно переводить отдельно целую часть числа и дробную часть числа.
Целую часть числа переводится из десятичной СС в другую систему счисления — последовательным делением целой части числа на основание системы счисления (для двоичной СС — на 2, для 8-ичной СС — на 8, для 16-ичной — на 16 и т.д.) до получения целого остатка, меньше, чем основание СС.
Пример 4 . Переведем число 159 из десятичной СС в двоичную СС:
| 159 | 2 | ||||||
| 158 | 79 | 2 | |||||
| 1 | 78 | 39 | 2 | ||||
| 1 | 38 | 19 | 2 | ||||
| 1 | 18 | 9 | 2 | ||||
| 1 | 8 | 4 | 2 | ||||
| 1 | 4 | 2 | 2 | ||||
| 0 | 2 | 1 | |||||
| 0 |
Как видно из Рис. 1, число 159 при делении на 2 дает частное 79 и остаток 1. Далее число 79 при делении на 2 дает частное 39 и остаток 1 и т.д. В результате построив число из остатков деления (справа налево) получим число в двоичной СС: 10011111 . Следовательно можно записать:
1, число 159 при делении на 2 дает частное 79 и остаток 1. Далее число 79 при делении на 2 дает частное 39 и остаток 1 и т.д. В результате построив число из остатков деления (справа налево) получим число в двоичной СС: 10011111 . Следовательно можно записать:
159 10 =10011111 2 .
Пример 5 . Переведем число 615 из десятичной СС в восьмеричную СС.
| 615 | 8 | ||
| 608 | 76 | 8 | |
| 7 | 72 | 9 | 8 |
| 4 | 8 | 1 | |
| 1 |
При приведении числа из десятичной СС в восьмеричную СС, нужно последовательно делить число на 8, пока не получится целый остаток меньшее, чем 8. В результате построив число из остатков деления (справа налево) получим число в восьмеричной СС: 1147 (см. Рис. 2). Следовательно можно записать:
615 10 =1147 8 .
Пример 6 . Переведем число 19673 из десятичной системы счисления в шестнадцатеричную СС.
| 19673 | 16 | ||
| 19664 | 1229 | 16 | |
| 9 | 1216 | 76 | 16 |
| 13 | 64 | 4 | |
| 12 |
Как видно из рисунка Рис.3, последовательным делением числа 19673 на 16 получили остатки 4, 12, 13, 9. В шестнадцатеричной системе счисления числе 12 соответствует С, числе 13 — D. Следовательно наше шестнадцатеричное число — это 4CD9.
Для перевода правильных десятичных дробей (вещественное число с нулевой целой частью) в систему счисления с основанием s необходимо данное число последовательно умножить на s до тех пор, пока в дробной части не получится чистый нуль, или же не получим требуемое количество разрядов. Если при умножении получится число с целой частью, отличное от нуля, то эту целую часть не учитывать (они последовательно зачисливаются в результат).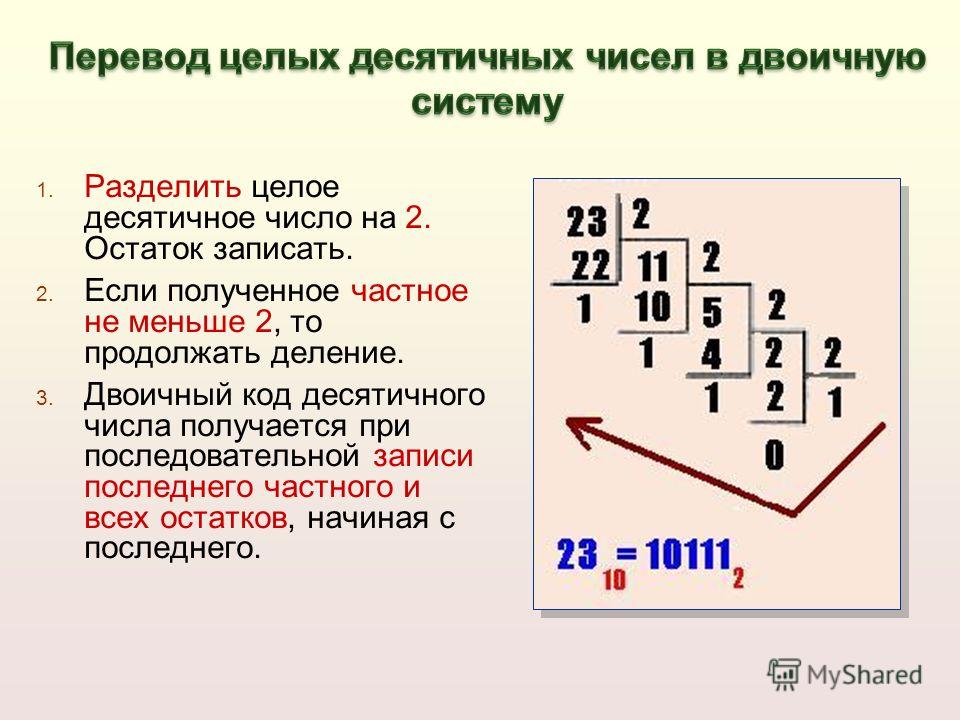
Рассмотрим вышеизложенное на примерах.
Пример 7 . Переведем число 0.214 из десятичной системы счисления в двоичную СС.
| 0.214 | ||
| x | 2 | |
| 0 | 0.428 | |
| x | 2 | |
| 0 | 0.856 | |
| x | 2 | |
| 1 | 0.712 | |
| x | 2 | |
| 1 | 0.424 | |
| x | 2 | |
| 0 | 0.848 | |
| x | 2 | |
| 1 | 0.696 | |
| x | 2 | |
| 1 | 0.392 |
Как видно из Рис.4, число 0.214 последовательно умножается на 2. Если в результате умножения получится число с целой частью, отличное от нуля, то целая часть записывается отдельно (слева от числа), а число записывается с нулевой целой частью. Если же при умножении получиться число с нулевой целой частью, то слева от нее записывается нуль. Процесс умножения продолжается до тех пор, пока в дробной части не получится чистый нуль или же не получим требуемое количество разрядов. Записывая жирные числа (Рис.4) сверху вниз получим требуемое число в двоичной системе счисления: 0.0011011 .
Если же при умножении получиться число с нулевой целой частью, то слева от нее записывается нуль. Процесс умножения продолжается до тех пор, пока в дробной части не получится чистый нуль или же не получим требуемое количество разрядов. Записывая жирные числа (Рис.4) сверху вниз получим требуемое число в двоичной системе счисления: 0.0011011 .
Следовательно можно записать:
0.214 10 =0.0011011 2 .
Пример 8 . Переведем число 0.125 из десятичной системы счисления в двоичную СС.
| 0.125 | ||
| x | 2 | |
| 0 | 0.25 | |
| x | 2 | |
| 0 | 0.5 | |
| x | 2 | |
| 1 | 0.0 |
Для приведения числа 0.125 из десятичной СС в двоичную, данное число последовательно умножается на 2. В третьем этапе получилось 0. Следовательно, получился следующий результат:
Следовательно, получился следующий результат:
0.125 10 =0.001 2 .
Пример 9 . Переведем число 0.214 из десятичной системы счисления в шестнадцатеричную СС.
| 0.214 | ||
| x | 16 | |
| 3 | 0.424 | |
| x | 16 | |
| 6 | 0.784 | |
| x | 16 | |
| 12 | 0.544 | |
| x | 16 | |
| 8 | 0.704 | |
| x | 16 | |
| 11 | 0.264 | |
| x | 16 | |
| 4 | 0.224 |
Следуя примерам 4 и 5 получаем числа 3, 6, 12, 8, 11, 4. Но в шестнадцатеричной СС числам 12 и 11 соответствуют числа C и B. Следовательно имеем:
0. 214 10 =0.36C8B4 16 .
214 10 =0.36C8B4 16 .
Пример 10 . Переведем число 0.512 из десятичной системы счисления в восьмеричную СС.
| 0.512 | ||
| x | 8 | |
| 4 | 0.096 | |
| x | 8 | |
| 0 | 0.768 | |
| x | 8 | |
| 6 | 0.144 | |
| x | 8 | |
| 1 | 0.152 | |
| x | 8 | |
| 1 | 0.216 | |
| x | 8 | |
| 1 | 0.728 |
Получили:
0.512 10 =0.406111 8 .
Пример 11 . Переведем число 159.125 из десятичной системы счисления в двоичную СС. Для этого переведем отдельно целую часть числа (Пример 4) и дробную часть числа (Пример 8).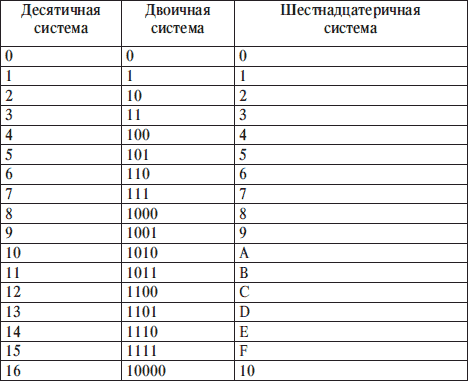 Далее объединяя эти результаты получим:
Далее объединяя эти результаты получим:
159.125 10 =10011111.001 2 .
Пример 12 . Переведем число 19673.214 из десятичной системы счисления в шестнадцатеричную СС. Для этого переведем отдельно целую часть числа (Пример 6) и дробную часть числа (Пример 9). Далее объединяя эти результаты получим.
Почему двоичные представления огромных чисел примерно в $3,3218$ раза длиннее их десятичных представлений?
$\begingroup$
Почему огромные двоичные числа примерно в $3,3218$ раза длиннее, чем их десятичные аналоги?
Я думал об этом, когда писал этот код на Python:
huge_number = 21**31**3 # ** — оператор мощности print((len(бин(огромное_число)) - 2) / len(str(огромное_число))) # -2 технический материал, игнорируйте его
Независимо от того, сколько $\texttt{huge_number}$ (оно должно быть огромным, это НЕ работает для маленьких чисел), вы получите $3,3218$. Почему?
- двоичный
$\endgroup$
7
$\begingroup$
Число разрядов представления натурального числа $n$ по основанию $k$ равно
$$\ell_k(n) := \lfloor \log_k n \rfloor + 1,$$
и поэтому отношение длины двоичного представления числа к его десятичной длине равно
$$\frac{\ell_2(n)}{\ell_{10}(n)} = \frac{\lfloor \log_2 n \rfloor + 1}{\lfloor \log_{10} n \rfloor + 1}. $$
$$
При больших $n$ постоянные члены в числителе и знаменателе не сильно влияют на отношение, равно как и различия между значениями $\log_k n$ и их соответствующими этажами (которые всегда находятся в $[0, 1)$), так что (для больших $n$) отношение удовлетворяет
$$\color{#df0000}{\boxed{\frac{\ell_2(n)}{\ell_{10}(n)} \ приблизительно \frac{\log_2 n}{\log_{10} n} = \log_2 10 = 3,32192\ldots}}.$$
Чуть точнее определение пола дает $\log_k n \leq \lfloor \log_k n \rfloor + 1 \leq \log_k n + 1$, и так
$$
\ гидроразрыва {\ log_2 п} {\ log_ {10} п + 1}
\leq \frac{\ell_2(n)}{\ell_{10}(n)}
\leq \frac{\log_2 n + 1}{\log_{10} n} .
$$
Используя некоторую простую алгебру, мы можем переписать это как
$$
\left(1 — \frac{1}{\log_{10} n + 1}\right) \log_2 10
\leq \frac{\ell_2(n)}{\ell_{10}(n)}
\leq \left(1 + \frac{1}{\log_2 n} \right) \log_2 10 .$$
При $n \to +\infty$ обе величины в скобках стремятся к $1$, поэтому теорема сжатия позволяет нам формализовать ваше наблюдение как утверждение
$$\lim_{n \to \infty} \frac{\ell_2(n)}{\ell_{10}(n)} = \log_2 10 . $$ 98}$:
$$ 98}$:
$\endgroup$
1
$\begingroup$
Количество цифр приблизительно (никогда не отличается более чем на 1) равно логарифму в этой системе счисления ($\log_{10}(x)\приблизительно$ количество цифр x в базе 10). Из-за логарифмической математики вы получаете:
$$\frac{\log_{10}(x)}{\log_2(x)}\приблизительно 3,32193$$
$\endgroup$
1
$\begingroup$
Интересный, хотя и неэффективный способ подсчета логов:
import string
импортировать математику
импортировать matplotlib.pyplot как plt
огромное_число = 21 ** 31 ** 3
b10len = длина (str (огромное_число))
ЦИФРЫ = строка.цифры + строка.нижний регистр
защита baseN (число, b):
цифры = []
в то время как число:
digits. append(ЦИФРЫ[число% b])
число = число // б
return ''.join (обратный (цифры))
базы = диапазон (2, 30)
длины = [len(baseN(huge_number, b)) для b в основаниях]
f, оси = plt.subplots (ncols = 2)
axs[0].plot(основания, [b10len/l для l в длинах])
axs[1].plot(основания, [math.log10(x) для x в основаниях])
plt.show()
93
$$
говорит вам, что для каждых десяти двоичных цифр требуется чуть более трех десятичных цифр. Ваш вопрос спрашивает о том, сколько именно больше трех (3,32...). Другие ответы (с использованием логарифмов, все хорошо) определяют источник этого числа.
append(ЦИФРЫ[число% b])
число = число // б
return ''.join (обратный (цифры))
базы = диапазон (2, 30)
длины = [len(baseN(huge_number, b)) для b в основаниях]
f, оси = plt.subplots (ncols = 2)
axs[0].plot(основания, [b10len/l для l в длинах])
axs[1].plot(основания, [math.log10(x) для x в основаниях])
plt.show()
93
$$
говорит вам, что для каждых десяти двоичных цифр требуется чуть более трех десятичных цифр. Ваш вопрос спрашивает о том, сколько именно больше трех (3,32...). Другие ответы (с использованием логарифмов, все хорошо) определяют источник этого числа.
$\endgroup$
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Как преобразовать длинное десятичное число в двоичное без использования калькулятора?
спросил
Изменено
1 год, 10 месяцев назад
Просмотрено
18 тысяч раз
$\begingroup$
Я знаю, что вы можете продолжать делить десятичное число на два, находя в процессе остатки, чтобы преобразовать число в двоичное.
Однако, когда я работаю с длинным десятичным числом, таким как 2147483647, есть ли более простой способ преобразовать его в двоичное? Для многократного деления этого числа вручную на два потребуется целая страница длинного деления, и вероятна человеческая ошибка.
Заранее спасибо.
РЕДАКТИРОВАТЬ: РЕШЕНИЕ. Благодаря помощи, которую я получил от joriki и pjs36, я обнаружил, что вместо деления на 2 я могу разделить на 16. Если деление на два даст вам двоичный результат, деление на 16 даст вам шестнадцатеричных в результате. Затем это шестнадцатеричное значение можно легко преобразовать в двоичное, и это гораздо более короткий процесс, чем деление на 2.
Благодаря помощи, которую я получил от joriki и pjs36, я обнаружил, что вместо деления на 2 я могу разделить на 16. Если деление на два даст вам двоичный результат, деление на 16 даст вам шестнадцатеричных в результате. Затем это шестнадцатеричное значение можно легко преобразовать в двоичное, и это гораздо более короткий процесс, чем деление на 2.
- двоичное
$\endgroup$
2 9к &256 и 128 и 64 и 32 и 16 и 8 и 4 и 2 и 1 \end{array}
Итак, нам понадобится $9$ бит. Чтобы найти их, мы, по существу, многократно вычитаем наибольшую степень 2$ из наших остатков (например, 409 - 256 = 153$): \начать{выравнивать*} 409 &= 256\cdot 1 + 153 \\ 153 &= 128 \cdot 1 + 25 \\ 25 &= 16 \cdot 1 + 9 \\ 9 &= 8 \cdot 1 + 1 \\ 1 &= 1 \cdot 1 \end{align*}
Поскольку мы увидели в процессе $256,\128,\16,\8,$ и $1$, у нас есть $$409{31} - 1$, и его двоичное представление буквально $$2147483647_{10} = \underbrace{111\ldots 1_2}_{31\text{times}}$$ (попробуйте меньшие числа, которые на единицу меньше степени $2$, например $7, 15, 31$, и вы увидите закономерность).
$\endgroup$
0
$\begingroup$
Вы можете преобразовать в другую степень двойки, например. восьмеричное или шестнадцатеричное, первое. Это в 3$ или 4$ раза меньше делений, а затем вы можете очень быстро преобразовать в двоичную систему, используя таблицу поиска для восьмеричных или шестнадцатеричных цифр.
$\endgroup$
$\begingroup$
Вот «цветовой» алгоритм преобразования $409$ в двоичное представление, и каждый шаг можно легко проверить, чтобы свести к минимуму вероятность человеческой ошибки:
Двоичное представление для $409$ получается путем взятия зеленых двоичных цифр. в последней строке и расположив их в обратном порядке,
$\quad 409 = 110011001_{\,\text{Base-}2}$
Обратите внимание, что этот алгоритм обработки строк может быть применен к любому целому числу, используя только конечное число арифметических правил, которых может быть жестко закодировал в логику. Например, самое большое целое число, которое когда-либо будет делиться на 2 доллара, равно 18 долларам.
Например, самое большое целое число, которое когда-либо будет делиться на 2 доллара, равно 18 долларам.
Реализацию этого алгоритма можно найти здесь.
$\endgroup$
$\begingroup$
Я чувствовал, что использовать метод остатка для меня довольно просто. если у вас есть остаток с десятичным числом при делении на 2, его следует рассматривать как 1 в битовой строке, а если остаток не имеет десятичного числа, это 0 строка битов.
тогда читай сверху вниз как справа налево. т.е. 110011001
- 409/2 = 204,5 - 1
- 204/2 = 102 - 0
- 102/2 = 51 - 0
- 51/2 = 25,5 - 1
- 25/2 = 12,5 - 1
- 12/2 = 6 - 0
- 6/2 = 3 - 0
- 3/2 = 1,5 - 1
- 1/2 = 0,5 - 1
$\endgroup$
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.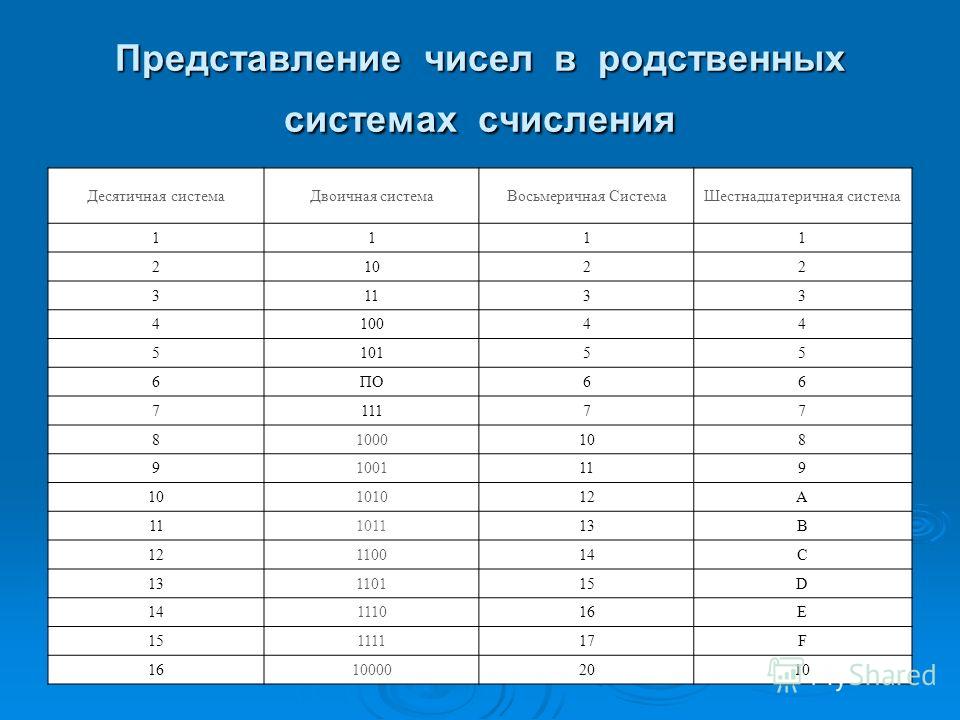
CSC 110 МОДУЛЬ 1.2
CSC 110 МОДУЛЬ 1.2Модуль 1 Раздел 2- Знакомство с двоичной системой счисления
В двоичной системе счисления все то же самое, что и в десятичной системе счисления. система с одним отличием: основание равно 2 вместо 10.Двоичный означает с основанием 2 (обратите внимание на префикс bi ). База 2 (двоичный) имеет 2 цифры: 0, 1. Поскольку двоичные числа состоят из двоичных цифры, мы часто называем двоичную цифру бит (сокращение от bi nary цифра т ). Мы также можем называть разрядную позицию битом. Другими словами, для записи двоичного числа «1010» требуется 4 бита, и эти биты равны «1», «0», «1» и «0».
Для любой системы счисления с основанием b первое b неотрицательное числа представлены самими цифрами. Для базы b=2 (двоичная), первые 2 цифры 0 и 1.
Счет в двоичном формате аналогичен счету в десятичном, за исключением того, что вы
цифры заканчиваются гораздо быстрее и приходится прибегать к более ценным местам
раньше. Чтобы подсчитать количество яиц в дюжине в двоичном формате, будет следующим образом:
0, 1, 10, 11, 100, 101, 110, 111, 1000, 1001, 1010, 1011, 1100. Следующие
таблица покажет, как эта последовательность выглядит как в двоичном, так и в десятичном виде, поэтому
вы можете сравнить их.
Чтобы подсчитать количество яиц в дюжине в двоичном формате, будет следующим образом:
0, 1, 10, 11, 100, 101, 110, 111, 1000, 1001, 1010, 1011, 1100. Следующие
таблица покажет, как эта последовательность выглядит как в двоичном, так и в десятичном виде, поэтому
вы можете сравнить их.
| Яйца | Десятичный | В двоичном формате | Комментарии |
|
|
|
||
|
|
|
Пока что последовательности точно такие же | |
|
|
|
Здесь в двоичном коде закончились цифры, и он должен перейти в другое место,
в то время как десятичный по-прежнему имеет больше цифр для использования. |
|
|
|
|
||
|
|
|
Опять же, в двоичном коде закончились цифры в разряде 2, и его необходимо расширить. на 4 место. Десятичная дробь еще не исчерпала своего 1-го места. | |
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
Наконец, десятичная дробь должна прибегать ко второму разряду значения, а затем к десяткам. |
|
|
|
|
||
|
|
|
- Вы не можете сказать, являются ли они двоичными или десятичными, просто взглянув на их . «10» — десятичная десятка или двоичная двойка? Там нет ничего о "10" чтобы дать вам эту информацию. Нам придется разобраться с этой проблемой скоро.
- Нечетные двоичные числа всегда заканчиваются на «1», а четные двоичные числа всегда заканчиваться на «0». Это видно, если сравнить цифры в таблице.
-
Всякий раз, когда вы удваиваете двоичное число, вам нужен еще один бит для представления
Это. Когда вы думаете о десятичных числах и о том, как они занимают
десятичная цифра для представления числа, когда вы умножаете его на десять, тогда оно
неудивительно, что вам понадобится еще один бит, когда вы умножаете
двоичное число на два.
 На самом деле, всякий раз, когда вы умножаете любое число по основанию
b на b , вам понадобится другое место для удержания
результат.
На самом деле, всякий раз, когда вы умножаете любое число по основанию
b на b , вам понадобится другое место для удержания
результат. - На самом деле, чтобы удвоить двоичное число, достаточно добавить ноль. бит с правой стороны .
- Десятичные числа занимают меньше места, чем двоичные числа . Это потому что есть больше цифр, из которых можно извлечь, а разрядные позиции не исчерпывается так быстро, как в бинарном.
- Двоичные числа занимают больше места, чем десятичные числа . Это обратное предыдущему наблюдению.
 Вот почему.
Вот почему.
Для начала разберемся, что означает слово цифровой . Двойник к цифре аналог . Вы можете понять разницу, подумав около часа... ну, два часа. Они здесь:
Цифровые часы способны отображать ограниченный объем информации.
Он может сообщить нам время, показывая использование 1 из 12 возможных часов, 1 из 60
возможные минуты, а также AM или PM. Нет пути для цифровых часов
чтобы показать нам, сколько минут прошло. Даже если вы добавили еще два
цифры для секунд, вы не сможете сказать, как далеко между секундами
Ты. И даже если вы добавите для этого больше цифр, фактическое время
всегда может быть «между» двумя возможными временами, которые могут показывать цифровые часы.
Вы должны иметь бесконечное количество цифр на дисплее, чтобы быть
могу сказать ровно сколько времени по цифровым часам. Из
конечно, это не практично! Цифровой может означать дискретный ,
как в этом примере. Это означает, что существует конечное число
то, что часы могут показать, даже если то, что они представляют (текущий
time) может иметь бесконечное количество фактических значений.
Это означает, что существует конечное число
то, что часы могут показать, даже если то, что они представляют (текущий
time) может иметь бесконечное количество фактических значений.
Аналоговые часы могут показывать бесконечное количество значений, т.к. руки проходят через непрерывный домен . Другими словами, когда время на самом деле между двумя минутами, стрелка будет находиться на полпути между двумя минутами на циферблате аналоговых часов. Цифровые компьютеры (например, цифровые часы) часто должны представлять аналоговую информацию, и сделайте это, выбрав ближайшее дискретное значение к непрерывному значению. Например, если время на самом деле 16:03:12, то наши цифровые часы будет показывать либо 16:03, либо 16:04.
Самый простой дискретный домен для работы и тот, который подходит для современных цифровых
с которыми работают компьютеры, имеет только два значения. Эти значения известны нескольким
имена. «ВЫКЛ» и «ВКЛ», «НЕТ» и «ДА», «ЛОЖЬ» и «ИСТИНА», и (как вы уже догадались
это) «0» и «1».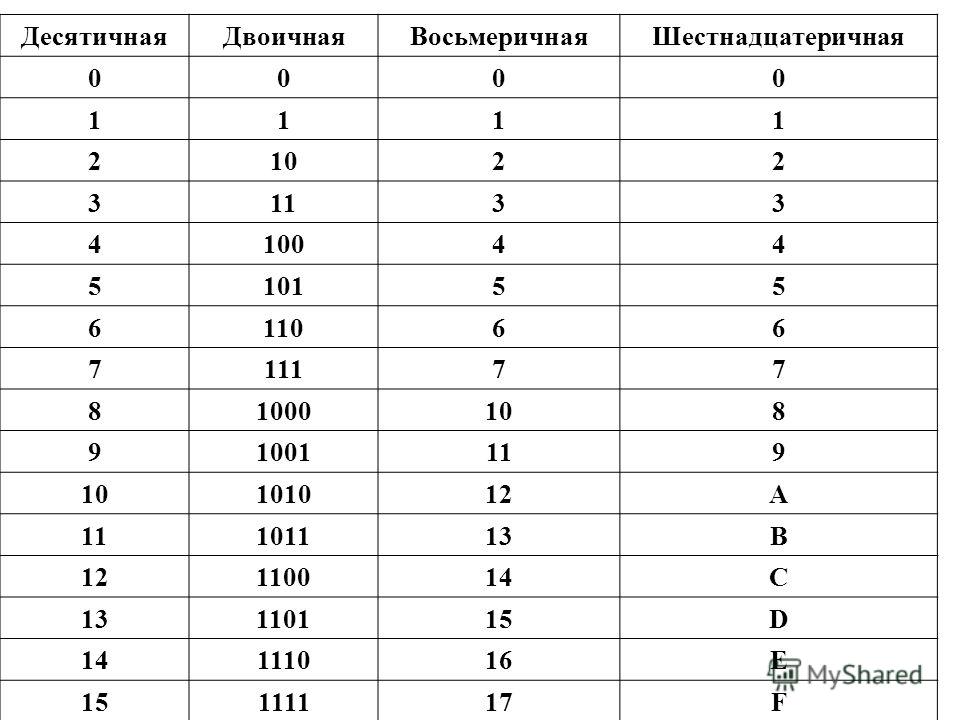 Причина, по которой компьютеры используют двоичный код, заключается в том, что значения
«0» и «1» могут быть представлены электричеством. Если есть электрический ток
на проводе, мы скажем, что провод сигнализирует «1». Если нет электрики
ток в проводе, то мы скажем, что он сигнализирует «0».
Причина, по которой компьютеры используют двоичный код, заключается в том, что значения
«0» и «1» могут быть представлены электричеством. Если есть электрический ток
на проводе, мы скажем, что провод сигнализирует «1». Если нет электрики
ток в проводе, то мы скажем, что он сигнализирует «0».
Компьютерные инженеры экспериментируют с компьютерами, потребляющими более два значения, но они еще не практичны. Эти компьютеры бы используйте разные уровни электрического тока для представления более дискретных значений. Например, ток не может быть равен «0», средний ток может быть равен «1», а высокий ток может быть «2», что даст вам тройной компьютер. За наши исследования, однако, мы ограничим себя бинарным компьютером. Это просто, и это современная технология.
Мы должны уметь применять расширенную запись к двоичным числам. За Например, двоичное число «10110», записанное в расширенной записи, будет выглядеть так:
Обратите внимание, что все записывается в двоичном формате.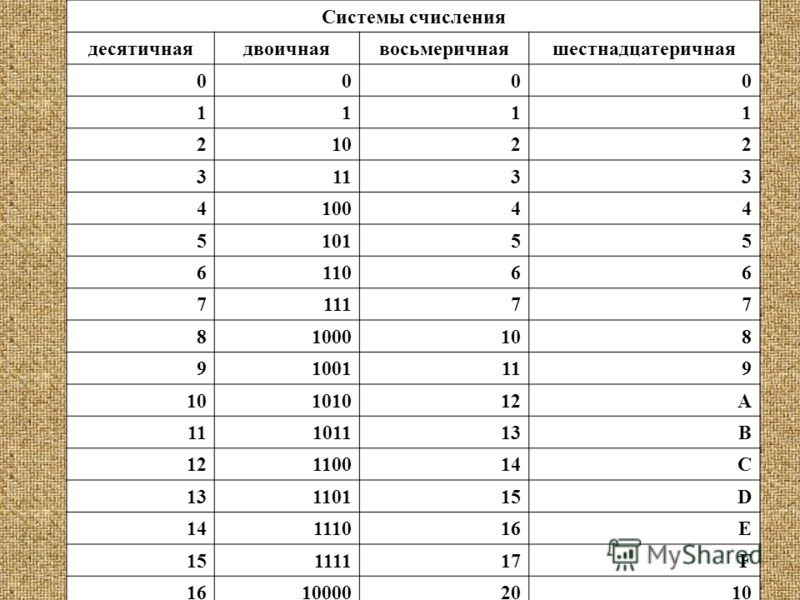 Вы бы прочитали это как "1
умножить на 2 до 4-го плюс 0 раз от 2 до 3-го плюс 1 раз от 2 до 2-го
плюс 1 умножить на 2 до 1 плюс 0 умножить на 2 до 0».
использовать расширенную нотацию в качестве инструмента для преобразования двоичного кода в десятичный. Так
перепишем расширенную запись в виде десятичного выражения:
Вы бы прочитали это как "1
умножить на 2 до 4-го плюс 0 раз от 2 до 3-го плюс 1 раз от 2 до 2-го
плюс 1 умножить на 2 до 1 плюс 0 умножить на 2 до 0».
использовать расширенную нотацию в качестве инструмента для преобразования двоичного кода в десятичный. Так
перепишем расширенную запись в виде десятичного выражения:
Теперь, фактически выполнив вычисление, мы можем сократить его до число с основанием 10 (десятичное), которое эквивалентно двоичному «10110». Запомнить, это одно и то же число, просто написанное по-разному. Таким образом, приведенное выше становится:
Таким образом, «10110» в двоичном формате совпадает с «22» в десятичном формате.
Другое наблюдение, которое вы, возможно, сделали, состоит в том, что каждый раз, когда '0' находится в
битовой позиции, он никогда не внесет в сумму ничего, кроме нуля.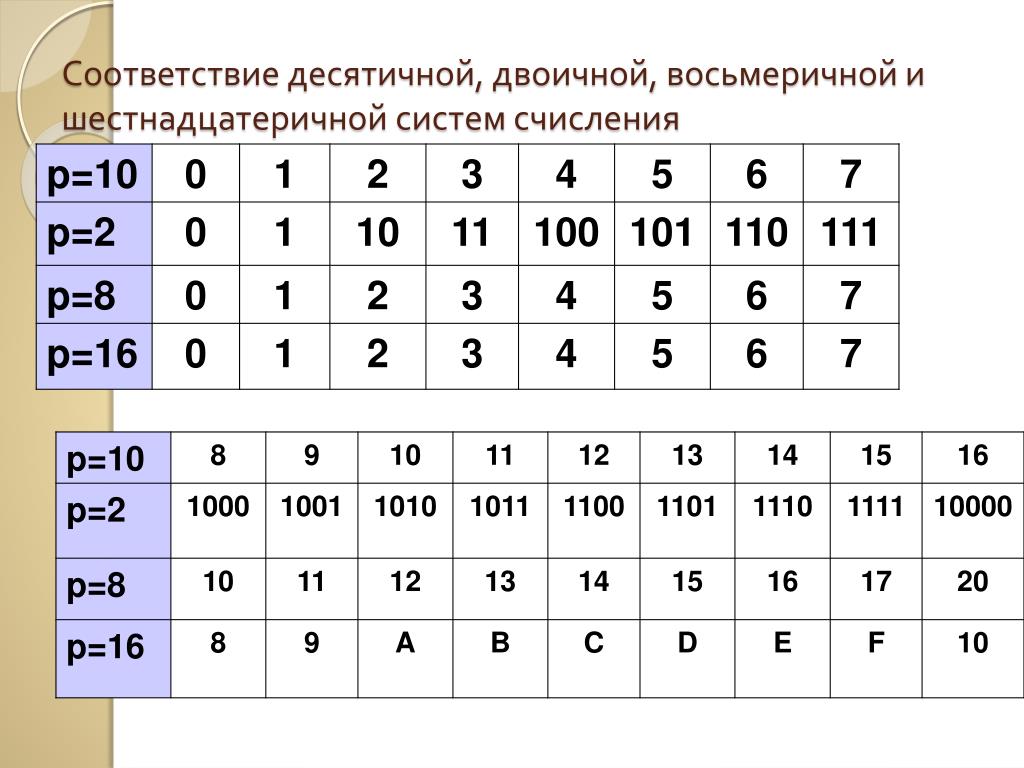 Так,
если мы собираемся преобразовать двоичное число в десятичное таким образом, мы можем сэкономить много
времени, просто не записывая биты '0' для начала. Например,
давайте преобразуем двоичное число «10010» в десятичное и запомним, что «0»
не участвует в сумме. Мы получаем:
Так,
если мы собираемся преобразовать двоичное число в десятичное таким образом, мы можем сэкономить много
времени, просто не записывая биты '0' для начала. Например,
давайте преобразуем двоичное число «10010» в десятичное и запомним, что «0»
не участвует в сумме. Мы получаем:
И еще одно наблюдение состоит в том, что биты '1' всегда вносят точный вклад эта сила двух. Другими словами, вы тратите время на умножение. Все, что вам нужно сделать, это записать ряд степеней двойки в виде суммы. Например, давайте преобразуем двоичное число «1011011», помня об этом:
Дроби также работают, как и десятичные числа. Отрицательные показатели
используются для обозначения отрицательных степеней двойки. Вместо «десятичной» точки
теперь у нас есть "бинарная" точка. Позиционное значение позиции справа
двоичной точки 2 -1 , или одна половина. Далее 2 -2 ,
или одну четвертую. Так что же такое двоичное число «100,101» в десятичном виде? Первый,
напишите расширенную запись:
Позиционное значение позиции справа
двоичной точки 2 -1 , или одна половина. Далее 2 -2 ,
или одну четвертую. Так что же такое двоичное число «100,101» в десятичном виде? Первый,
напишите расширенную запись:
Домашнее задание Вопросы
- 0
- 1
- 10
- 110
- 10.01
- 0,01
- 1101.01
- 100.01
- 111.11
- 0,1
Преобразование приведенных выше чисел (снова перечисленных ниже) в десятичные числа с использованием расширенного представления как промежуточная форма.
- 0
- 1
- 10
- 110
- 10.01
- 0,01
- 1101.
 01
01
- 100,01
- 111.11
- 0,1
Запишите следующие двоичные числа в расширенной записи, включая все информация, даже если она избыточна:
Предыдущий Раздел: Обзор десятичной системы счисления
Возврат к индексу модуля
Системы счисления
Системы счисленияВведение в двоичную и другие системы счисления
[ Примечание для тех, кто читает это шрифтом Брайля. Этот раздел содержит некоторые математические обозначения, которые могут отображаться некорректно при переводе на шрифт Брайля 2. Мы будем признательны за отзывы о любых проблемах. ]
Разрядность и десятичная система. Наша десятичная или десятичная система счисления является позиционной системой.
Это означает, что место или местоположение, в которое вы помещаете число, определяет соответствующее ему числовое значение. (Это аналогично кодам Брайля в том, что место, где вы помещаете ячейку
иногда определяет его значение.) Двойка вместо единицы означает два раза один или два. Двойка в тысячном разряде означает дважды одну тысячу или две тысячи.
Двойка в тысячном разряде означает дважды одну тысячу или две тысячи.
Значения разрядов увеличиваются справа налево. Первое место непосредственно перед запятой точка — или самое правое место, если нет десятичной точки — это место единицы, второе место или следующее место слева - это десятка, третье место - это сотый разряд и так далее.
На рис. 1 показаны разряды для первых шести целых разрядов десятичной дроби. система.
Всего мест: 6-е 5-е 4-е 3-е 2-е 1-е
Значения разрядов: 100000 10000 1000 100 10 1 Рис. 1. Разрядные значения (в десятичном формате) для десятичной системы счисления.
Порядковое значение места непосредственно перед слева "десятичной" точки равно один во всех разрядные системы счисления. (Сама точка должна иметь разные имена в разных числах. системы, но это различие обычно не делается.) Местное значение любого разряда слева от разряда единицы
представляет собой целое число , вычисленное из произведения (умножения), в котором основание числа
система повторяется как множитель на один меньшее число раз, чем положение места.
Например, четвертый разряд в нашей десятичной или десятичной системе будет иметь значение один
тысяча, так как десять повторяется в произведении четыре минус один или три раза:
10 х 10 х 10 = 1000.
Разрядное значение любого места до справа после запятой является дробью вычисляется из произведения, в котором обратная величина основания — или дробь с единицей в числитель и основание в знаменателе — повторяется как множитель ровно столько раз, сколько место находится справа от десятичной точки.
Например, место, где я поставил "X" в 0.00X00, который является третьим разрядом справа от десятичной точки, имеет место значение одной тысячной, так как одна десятая повторяется в произведении трижды:
(1/10) х (1/10) х (1/10) = (1/1000).
Прочие системы. Система счисления с основанием 16 называется шестнадцатеричный система с основанием 8 называется восьмеричной системой , а система с основанием 2 называется
называется двоичной системой .
Если вы пишете число, скажем, 101, и хотите, чтобы было ясно, что это двоичное число,
вы можете написать
101 (основание 2) или 101 2 .
Для этой и любой другой позиционной системы счисления действуют правила, аналогичные десятичной системе счисления. Местные значения для всех мест, кроме своего места, зависят от основания система счисления; наивысшее значение, которое вы можете выразить, используя только место всегда на единицу меньше основания. Это означает, что вам нужно столько же различных числительных, считая ноль, сколько оснований. Например, в двоичной системе с основанием 2 используются только две цифры: один и ноль.
На рис. 2 приведены значения разрядов, выраженные в десятичном виде, для первых шести целых разрядов восьмеричного числа. система. Четвертый разряд, например, имеет значение 512, что равно 8 х 8 х 8,9.0003
Всего мест: 6-е 5-е 4-е 3-е 2-е 1-е
Разрядные значения: 32768 4096 512 64 8 1 Рис. 2. Разрядные значения (в десятичном формате) для
восьмеричная система счисления.
2. Разрядные значения (в десятичном формате) для
восьмеричная система счисления.
Всего мест: 6-е 5-е 4-е 3-е 2-е 1-е
Значения разрядов: 32 16 8 4 2 1 Рис. 3. Разрядные значения (в десятичном формате) для двоичная система счисления.
Самое большое число, которое можно записать в двоичном формате, используя только шесть разрядов или шесть цифр.
равно 111111 (основание 2), которое, поскольку на каждом месте стоит единица, имеет десятичное значение
32+16+8+4+2+1 = 63. Это, конечно, согласуется с тем, что это 63 различных возможных ячейки Брайля.
Восьмеричные числа в двоичном коде. До сих пор мы использовали десятичных чисел , чтобы задать разрядность различных чисел. систем, но удобно использовать восьмеричных чисел , чтобы дать значения места для двоичная система счисления при интерпретации ячеек Брайля по этой системе.
Всего мест: 6-е 5-е 4-е 3-е 2-е 1-е
Разрядные значения: 40 8 20 8 10 8 4 8 2 8 1 8 Рис. 4. Разместите значения (в восьмеричном формате) для двоичной системы счисления. (Сравните с рис. 3 .)
Рис. 5. NUMBRL разрядные значения.
Хотя принято писать числа горизонтально, как на рис. 4, в этом нет необходимости. Их можно даже записать в виде сетки, подобной ячейке Брайля, как показано на рис. 5. Существует несколько различных способов присвоения разрядных значений позициям. Самое полезное соответствие - это позволить верхней позиции правой колонки быть 1-м или своим местом,
средняя позиция будет 2-м или 2-м местом, а нижняя позиция будет 3-м или
четвертое место, как это делается в NUMBRL.
Самое полезное соответствие - это позволить верхней позиции правой колонки быть 1-м или своим местом,
средняя позиция будет 2-м или 2-м местом, а нижняя позиция будет 3-м или
четвертое место, как это делается в NUMBRL.
В следующей таблице показаны десятичные значения от нуля до семи. записываются как двоичные, так и восьмеричные числа. Это все числа, которые можно записать в двоичном формате, используя только первые три разряда.
Двоичный | Сумма разрядов (восьмеричный) |
Окталь |
000 | 0+0+0 | 00 |
001 | 0+0+1 | 01 |
010 | 0+2+0 | 02 |
011 | 0+2+1 | 03 |
100 | 4+0+0 | 04 |
101 | 4+0+1 | 05 |
110 | 4+2+0 | 06 |
111 | 4+2+1 | 07 |
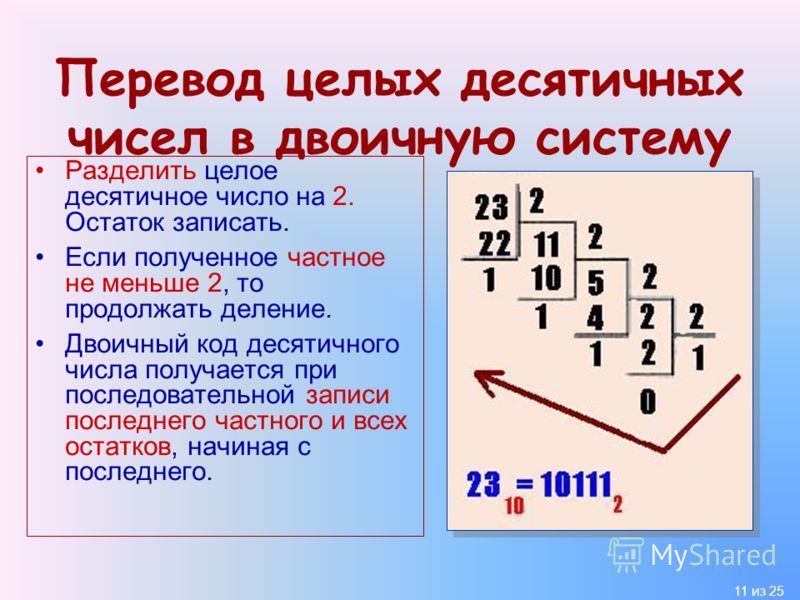
Если представить заполненные точки в ячейке Брайля как представление единиц и пустых позиций как представление нулей, то эти восемь двоичных или восьмеричных чисел представляют все восемь возможных шаблонов точек. (включая отсутствие точек) для одного столбца ячейки Брайля.
Если мы присвоим значения разряда позициям точек, как показано на рисунке 5, взаимосвязь между точечными узорами и восьмеричными числами будет следующей.
точка 1 10 точка 4 1
точка 2 20 точка 5 2
точки 1-2 30 точек 4-5 3
точка 3 40 точка 6 4
точки 1–3 50 точек 4–6 5
точки 2-3 60 точек 5-6 6
точки 1-2-3 70 точек 4-5-6 7
Следующая таблица показывает десятичные значения от восьми до пятидесяти шести, считая по восьмеркам,
снова записывается как двоичные, так и восьмеричные числа. Это все числа, которые можно записать в двоичном формате, используя только вторые три разряда. (Двоичные цифры записываются группами по три, чтобы сделать
их более читабельными.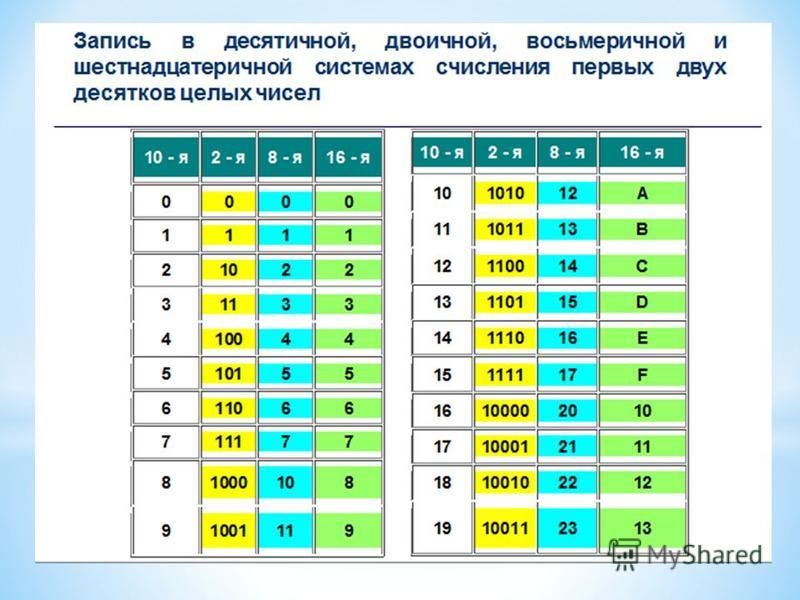 )
)
Двоичный | Сумма разрядов (восьмеричный) |
Окталь |
001 000 | 0+0+10+0+0+0 | 10 |
010 000 | 0+20+0+0+0+0 | 20 |
011 000 | 0+20+10+0+0+0 | 30 |
100 000 | 40+0+0+0+0+0 | 40 |
101 000 | 40+0+10+0+0+0 | 50 |
110 000 | 40+20+0+0+0+0 | 60 |
111 000 | 40+20+10+0+0+0 | 70 |
Сравнивая эту таблицу с предыдущей, мы видим симметрию.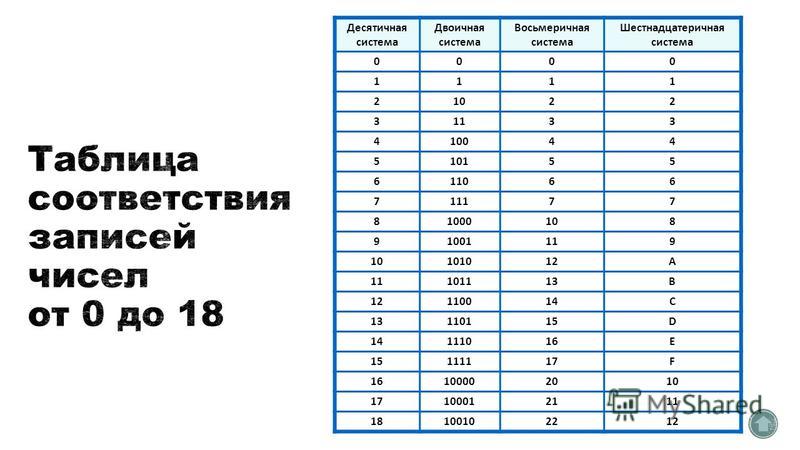 Одна и та же цифра или цифра соответствует одному и тому же образцу единиц и нулей в каждом случае;
единственное отличие состоит в том, что паттерн смещен влево.
Одна и та же цифра или цифра соответствует одному и тому же образцу единиц и нулей в каждом случае;
единственное отличие состоит в том, что паттерн смещен влево.
[Это конец информации о системах счисления, относящейся к шеститочечные ячейки Брайля. Обратите внимание, что 77 (основание 8) = (7x8) + (7x1) = 63.]
Возможно, вы уже думали о необходимых дополнительных символах. для однозначного цифры для десятичных значений 10-15 с использованием шестнадцатеричной системы счисления. Стандартным выбором является использование букв A-F для этих ценности! Кроме того, более распространено указывать шестнадцатеричное число, предваряя его с знак фунта стерлингов, "#", а не запись "(основание 16)" или использование нижнего индекса "16" с количество как упоминалось ранее для других баз. Таким образом, #A=10, #B=11, #C=12, #D=13, #E=14 и #F=15. Мы снова видим аналогию со шрифтом Брайля.
Какие существуют способы присвоения разрядных значений в бинарных представлениях?
В знаменитой книге Джонатана Свифта Путешествия Гулливера ,
есть рассказ о двух лагерях лилипутов, отличавшихся только тем, как они
ел яйца всмятку: одно разбило большой конец, другое маленькое.
Ученые-компьютерщики, у которых иногда есть чувство юмора, переняли эти имена, чтобы указать, как числа хранятся в компьютере. Число, хранящееся обычным образом, так, чтобы его меньший или «маленький» конец был обращен к говорят, что младшая часть компьютерного слова находится в Маленький порядок байтов форме, тогда как число, хранящееся в обратном порядке, называется формой Big Endian . Это означает, что сопоставление NUMBRL разрядных значений с позициями точек ячеек Брайля, показанное выше на рисунке 5, является либо «маленьким верхним», либо «большим нижним», если мы не раскроем ячейку Брайля, чтобы все шесть положений точек были линейными.
Двоичный код с обратным порядком байтов | Сумма разрядов (восьмеричный) |
Окталь |
000 | 0+0+0 | 00 |
100 | 1+0+0 | 01 |
010 | 0+2+0 | 02 |
110 | 1+2+0 | 03 |
001 | 0+0+4 | 04 |
101 | 1+0+4 | 05 |
011 | 0+2+4 | 06 |
111 | 1+2+4 | 07 |
Хотя последние два имени я придумал, термин Middle-Endian является фактическим техническим термином, который относится к любому смешанному заказу, такому как
американский способ написания дат в форме мм/дд/гг, а не европейский дд/мм/гг. или японское использование гг/мм/дд (для дат в западном стиле).
или японское использование гг/мм/дд (для дат в западном стиле).
Этот термин также правильно применяется к назначение позиций точек 3-2-1-4-5-6 на клавиши брайлера так, чтобы, например, оба указательных пальца используются для верхних точек столбцов. Изображение брайлера, показанное по последней ссылке, имеет соответствующие значения NUMBRL, 40-20-10-1-2-4, на этикетках над его клавишами. Эти метки показывают, что когда метод Брайлера для создания линейной ячейки Брайля применяется к NUMBRL значения позиции, NUMBRL пример формы "Middle-Endian" связывания значений места с позициями точек ячеек Брайля, поскольку первые три разряда перевернуты, как показано в Таблице 3.
Простая математика, лежащая в основе алгоритмов преобразования десятичных чисел в двоичные
Если вы поищете в Интернете «Как преобразовать десятичные числа в двоичные», вы найдете четыре простых алгоритма: два для целых чисел и два для дробей. Они представлены на примерах ниже в первой части статьи.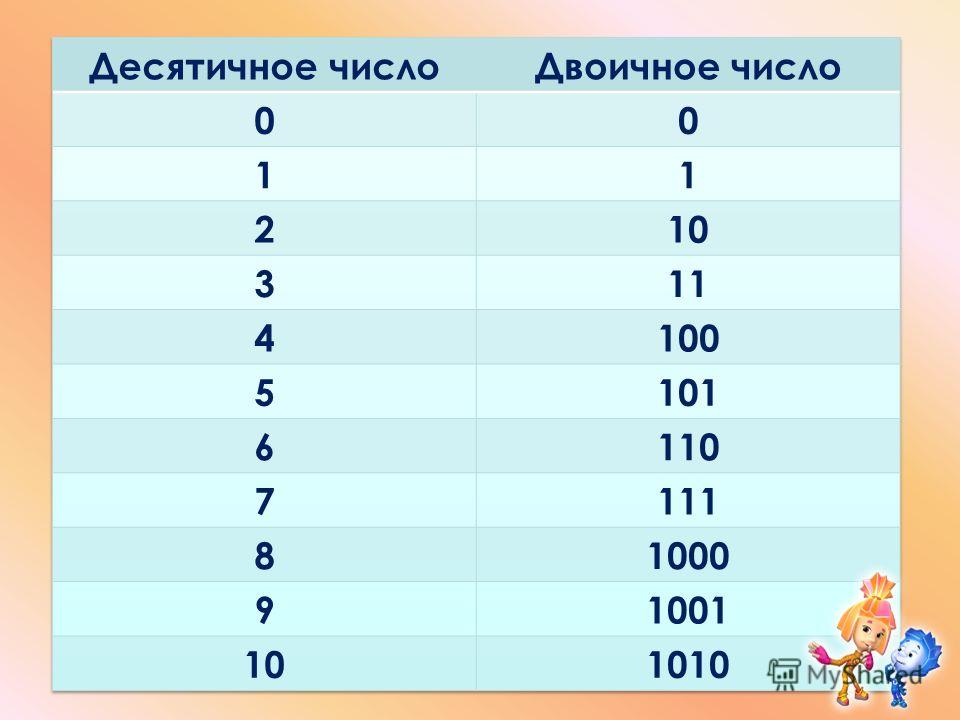 Но хотя почти всегда достаточно просто знать алгоритмы, я решил попытаться понять, почему они работают. Во второй части этой статьи объясняется самая основная математика, стоящая за каждым из них. Знание этого может помочь вам вспомнить любой из алгоритмов, если вы вдруг забудете их. Я настоятельно рекомендую вам взять блокнот и ручку и выполнять операции вместе со мной, чтобы лучше запомнить математику. Вот четыре алгоритма с примерами, которые вы можете найти в Интернете.
Но хотя почти всегда достаточно просто знать алгоритмы, я решил попытаться понять, почему они работают. Во второй части этой статьи объясняется самая основная математика, стоящая за каждым из них. Знание этого может помочь вам вспомнить любой из алгоритмов, если вы вдруг забудете их. Я настоятельно рекомендую вам взять блокнот и ручку и выполнять операции вместе со мной, чтобы лучше запомнить математику. Вот четыре алгоритма с примерами, которые вы можете найти в Интернете.
Преобразование десятичного целого числа в двоичное
Чтобы преобразовать целое число в двоичное, начните с рассматриваемого целого числа и разделите его на 2, обращая внимание на частное и остаток. Продолжайте делить частное на 2, пока не получите частное, равное нулю. Затем просто выпишите остатки в обратном порядке.
Вот пример такого преобразования с использованием целого числа 12.
Сначала разделим число на два, указав частное и остаток:
Теперь осталось просто выписать остаток в обратном порядке — 1100 . Итак, 12 в десятичной системе представляется как 1100 в двоичной.
Итак, 12 в десятичной системе представляется как 1100 в двоичной.
Преобразование десятичной дроби в двоичную
Чтобы преобразовать дробь в двоичную, начните с рассматриваемой дроби и умножьте ее на 2 , обращая внимание на полученную целую и дробную части. Продолжайте умножать на 2, пока не получите в результате дробную часть, равную нулю. Затем просто выпишите целые части из результатов каждого умножения.
Вот пример такого преобразования с использованием дроби 0,375 .
Теперь просто выпишем полученную целую часть на каждом шаге — 0,011 . Итак, 0,375 в десятичной системе представляется как 0,011 в двоичной.
Только дроби со знаменателем, равным степени двойки, могут быть конечно представлены в двоичной форме.Например, знаменатели 0,1 (1/10) и 0,2 (1/5) не являются степенями двойки, поэтому эти числа не могут быть конечно представлены в двоичном формате. Чтобы сохранить их как числа с плавающей запятой IEEE-754, их необходимо округлить до количества доступных битов для мантиссы — 10 бит для половинной точности, 23 бита для одинарной точности или 52 бита для двойной точности. В зависимости от того, сколько битов точности доступно, приближения с плавающей запятой 0,1 и 0,2 могут быть немного меньше или больше, чем соответствующие десятичные представления, но никогда не равны. Из-за этого у вас никогда не будет 0,1+0,2 == 0,3.
Преобразование двоичного целого числа в десятичное
Чтобы преобразовать двоичное целое число в десятичное, начните слева. Возьмите текущую сумму, умножьте ее на два и добавьте текущую цифру. Продолжайте до тех пор, пока не останется цифр. Вот пример такого преобразования с использованием дроби 1011 .
Преобразование целой дроби в десятичную
Чтобы преобразовать двоичную дробь в десятичную, начните справа с суммы, равной 0. Возьмите текущую сумму, добавьте текущую цифру и разделите результат на 2. Продолжайте, пока не останется цифр. . Вот пример такого преобразования с использованием дроби 0,1011 . Я просто заменил деление на 2 умножением на 1/2 .
Возьмите текущую сумму, добавьте текущую цифру и разделите результат на 2. Продолжайте, пока не останется цифр. . Вот пример такого преобразования с использованием дроби 0,1011 . Я просто заменил деление на 2 умножением на 1/2 .
Вот вам 4 простых алгоритма, которые позволят вам преобразовывать двоичные числа в десятичные и обратно.
Расширение числа по основанию q
Ключом к пониманию того, почему эти алгоритмы работают, является расширение числа по основанию q числа. Целое число в любой системе счисления может быть представлено в следующем виде:
where,
- N is integer
- x is the digit (0 through 9 for base-10 system, 0 and 1 for base-2 system)
- q является базовым значением (10 для системы с основанием 10, 2 для системы с основанием 2 ) , или просто
базовое расширение q. Посмотрим, как выглядит число 12 в десятичной и двоичной системах счисления:
Посмотрим, как выглядит число 12 в десятичной и двоичной системах счисления:Аналогично дробное число в любой системе счисления можно представить в следующем виде:
где,
- x — цифра (от 0 до 9 для системы счисления по основанию 10, 0 и 1 для системы счисления с основанием 2)
- Q является базовым значением (10 для системы базы-10, 2 для системы базы 2)
для числа 0,375
6666666666666666666666666666. выглядит следующим образом:Преобразование десятичного целого числа в двоичное
Как оказалось, мы можем использовать эту форму расширения base-q для преобразования числа из десятичной системы в двоичную. Давайте сделаем это для того же числа 12 . Во-первых, давайте притворимся, что мы не знаем, как оно представлено в двоичном виде, и запишем его, заменив неизвестные цифры на x :
Во-первых, давайте притворимся, что мы не знаем, как оно представлено в двоичном виде, и запишем его, заменив неизвестные цифры на x :
Наша задача — найти все x . Давайте посмотрим, что мы можем сделать здесь. Первое, на что мы должны обратить внимание, это то, что все слагаемые, кроме последнего, будут четными числами, потому что все они кратны двум. Теперь, используя эту информацию, мы можем вывести цифру для . x0 — if the integer being converted is even, then x0 is equal to 0 , if it's odd — then x0 должно быть 1 . Здесь у нас четное число 12, поэтому x0 равно нулю. Давайте запишем эту информацию:
Далее нам нужно найти значение для x1 . Since all summands from x1 to xN are multiples of two, we can factor out 2 to single out x1 . Сделаем так:
Since all summands from x1 to xN are multiples of two, we can factor out 2 to single out x1 . Сделаем так:
Также легко увидеть, что сумма значений в скобках равна 6 . Итак, мы можем записать наш первый шаг как:
Продолжим поиск оставшихся x . Мы можем записать многочлен в скобках как отдельное утверждение:
Здесь, применяя ту же логику, что и выше, мы можем видеть, что x1 равно 0 . Давайте перепишем его и снова вынесем 2:
Итак, наш второй шаг:
Теперь мы можем увидеть закономерность. Мы можем продолжить факторинг 2 , пока частное не станет равным нулю.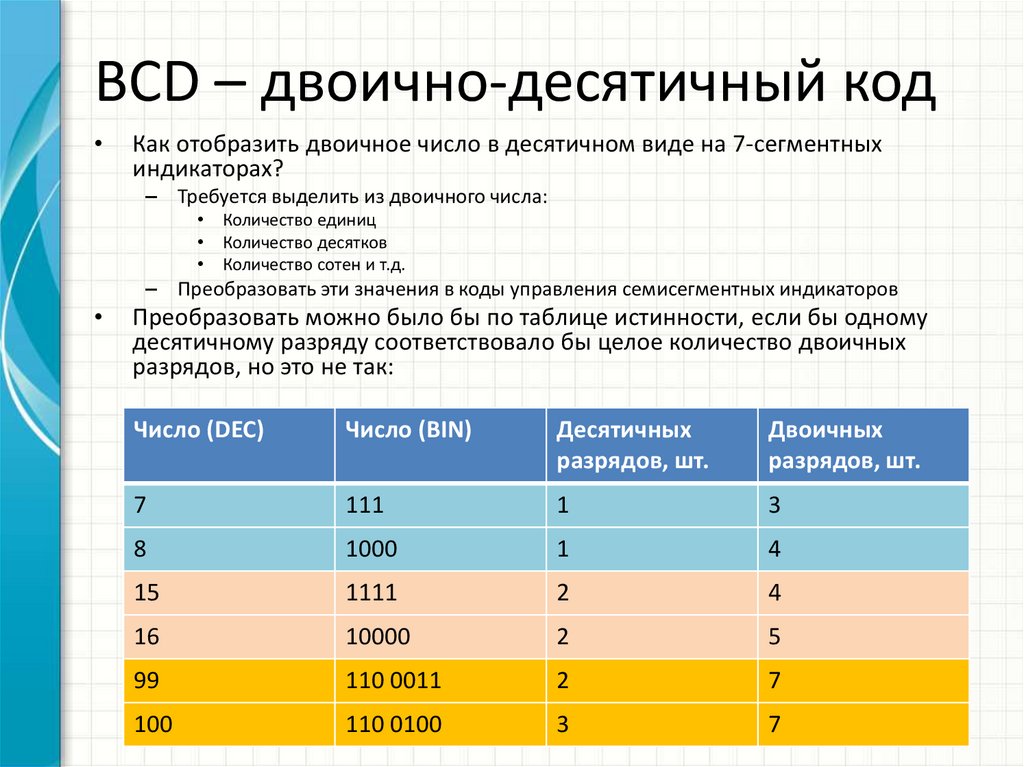 Давайте последуем этой схеме и посмотрим, что у нас получится.
Давайте последуем этой схеме и посмотрим, что у нас получится.
Поскольку частное равно 1, осталось только одно слагаемое, поэтому перепишем предыдущее выражение:
Итак, наш третий шаг:
Итак, мы получаем следующее:
Понятно, что x3 равно 1 . Но, так как для нашего алгоритма нам нужно частное, перепишем предыдущее выражение так, чтобы оно имело частное:
Поскольку мы получили частное 0 , больше не с чем работать, и это был наш последний шаг. Запишем:
Итак, мы закончили преобразование. Вот как выглядит наше преобразование по шагам:
Теперь понятно, что остаток на каждом шаге соответствует значению x на соответствующих позициях: первый остаток соответствует первому x, второй остаток второму х и так далее. Итак, число 12 в двоичном виде с использованием описанного выше алгоритма представляется как 1100 .
Помните, что мы начали с идеи показать, почему работает алгоритм, включающий погружение на 2 . Давайте выполним шаги, описанные выше, и переместим 2 в левую часть выражений:
Таким образом, вы можете увидеть, как мы пришли к алгоритму, описанному в начале. Мы также можем поместить вычисления для этих четырех шагов в одно представление, подобное этому 9.0003
Убедитесь, что вы понимаете, как мы пришли к такому представлению, так как оно понадобится нам при изучении того, как работает алгоритм преобразования из двоичного в десятичное.
Преобразование десятичной дроби в двоичную
Чтобы показать, почему мы умножаем на 2 и берем целую часть при преобразовании дробей в двоичную, я также буду использовать форму расширения по основанию q для дробей. Я буду использовать дробное число 0,375 из первой части статьи. Аналогично целой части, давайте представим, что мы не знаем, как это число представлено в двоичном виде, и запишем его, заменив неизвестные цифры на 9. 0109 x :
0109 x :
Как и в случае с целыми числами, наша задача состоит в том, чтобы найти все x , выделив x . Давайте посмотрим, как мы можем это сделать. Первое, на что следует обратить внимание, это то, что отрицательные степени числа 2 дают нам дроби со знаменателем числа 2 с положительными степенями. Давайте перепишем приведенное выше выражение:
Сразу видно, что мы можем просто вынести 1/2 в правой части выражения. Сделаем так:
А затем мы можем перенести 1/2 в левую часть
Хорошо, здесь мы выделили x1 , и мы знаем, что это может быть либо
, и мы знаем, что это может быть либо , и мы знаем, что это может быть либо 901, , и мы знаем, что это может быть либо 901, , и мы знаем, что это может или 0 .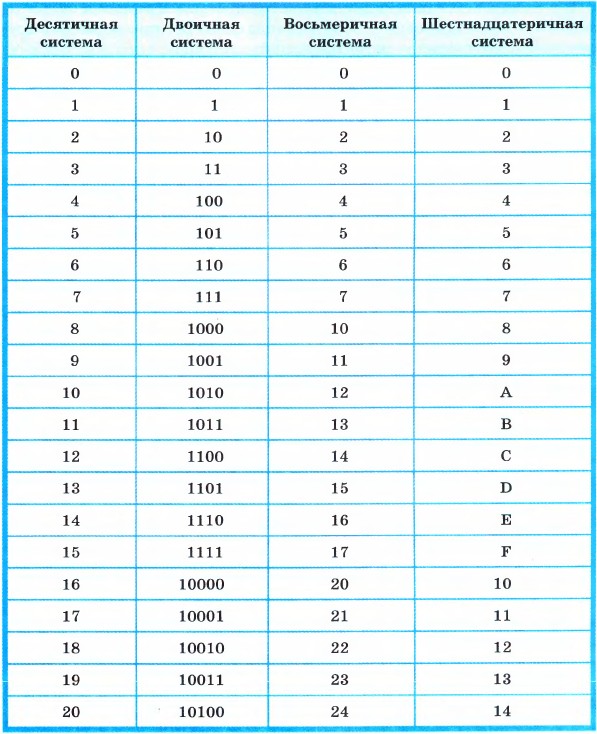 Чтобы определить, какая у него цифра, давайте посмотрим на оставшиеся слагаемые:
Чтобы определить, какая у него цифра, давайте посмотрим на оставшиеся слагаемые:Давайте подумаем, насколько большой может быть сумма этих чисел. Если максимальное количество цифр x равно 1, то мы можем просто заменить x с единицами и запишите сумму в виде:
Ну, это геометрический ряд дробей, и сумма такого ряда лежит в границах [0 < сумма < 1], поэтому максимальное количество таких сумма может дать нам 1. Давайте теперь снова посмотрим на наше выражение:
Теперь здесь должно быть ясно, что если правая часть меньше 1, то x1 не может быть равно 1 и, следовательно, равно 0 , а оставшаяся часть равна 0,75 .
Именно так выглядит первый шаг алгоритма, представленного в начале:
Отнимем дробную часть от 0,75 и вынесем еще 1/2 , чтобы выделить x2 0 0 9: и переместить 1/2 влево: Теперь, если x2 is equal to 0 , then the sum of left side of the expression cannot be greater than 1 , but the left side is 1. Опять же, это следует схеме в алгоритме, представленном в начале: Повторим те же действия для оставшейся дробной части 0,5 . Используя ту же логику, что и выше, мы можем видеть, что x3 равно 1 и нет оставшейся дробной части: вот как выглядит наш последний шаг: Итак, давайте еще раз выпишем все шаги: Это именно тот алгоритм, который я представил в начале. Точно так же, как мы делали с целыми числами, мы также можем поместить вычисления для этих трех шагов в одно представление, например: Опять же, важно, чтобы вы полностью усвоили это представление, так как оно понадобится нам при изучении двоичного преобразования в десятичное. Тот факт, что некоторые дроби, представленные конечно в десятичной системе, не могут быть представлены конечно в двоичной системе, является неожиданностью для многих разработчиков. Но именно эта путаница лежит в основе кажущегося странным результата прибавления 0,1 к 0,2. Так что же определяет, может ли дробь быть конечно представлена в системе счисления? Это довольно сложно. Но базовая версия такова — для конечного представления числа знаменатель в дроби должен быть степенью основания системы. Например, для системы с основанием 10 знаменатель должен быть степенью 10, поэтому мы можем конечно представить 0,625 в десятичном виде: и не может конечно представлять 1/3: То же самое относится и к системе с основанием 2: Но если мы проверим 0,1, знаменатель будет равен 10, и это не степень 2, поэтому 0,1 будет бесконечная дробь в двоичной системе. Давайте посмотрим на это, используя алгоритм, который мы изучили выше: Мы можем продолжать делать это бесконечно, но давайте запишем это как периодическую цепную дробь: Я собираюсь использовать то же самое двоичное целое число 1011 из первого раздела, чтобы показать вам, почему работает алгоритм умножения на 2. Поскольку все слагаемые кратны 2 , мы можем продолжать выносить 2 , пока частное не станет равным нулю. Давайте сделаем так: Теперь, если вы просто будете следовать порядку математических операций, вы получите точно такие же шаги, как я показал в начале, а именно: Таким образом, 1011 в двоичном виде равно 11 в десятичном виде. Вот мы и подошли к последнему алгоритму. Наверное, вы уже сами разобрались с механикой, стоящей за этим. Если нет, давайте посмотрим, почему это работает. Ключевым здесь также является расширение числа base-q от числа. Возьмем число 0,1011 из первого раздела. Опять же, поскольку все слагаемые кратны 1/2 , мы можем продолжать разлагать 1/2 до тех пор, пока не останется дробной части. Сделаем так: Следуя порядку математических операций, получается алгоритм, описанный в начале: Таким образом, 0,1011 в двоичном виде равно 0,6875 в десятичном. Десятичные числа могут быть представлены точно, если у вас достаточно места, но не плавающими двоичными точечными числами. Если вы используете десятичный тип с плавающей запятой (например, Давайте посмотрим на это с другой стороны - в системе счисления с основанием 10, с которой вам, вероятно, будет удобно, вы не сможете точно выразить 1/3. Проблема в том, что 3 — это простое число, которое не является множителем 10. Это не проблема, если вы хотите умножить число на 3: вы всегда можете умножить на целое число, не сталкиваясь с проблемами. Но когда вы 90 109 делите 90 110 на число, которое является простым и не является множителем вашего основания, вы можете столкнуться с проблемой (и 90 109 сделает то же самое, если вы попытаетесь разделить 1 на это число). Хотя 0,1 обычно используется в качестве простейшего примера точного десятичного числа, которое не может быть точно представлено в двоичном формате с плавающей запятой, возможно, 0,2 является более простым примером, поскольку это 1/5, а 5 — это простое число, которое вызывает проблемы между десятичными числами. и двоичный. Некоторые типы с плавающей запятой имеют фиксированный размер, например 0 Например, число 61,0 имеет точное двоичное представление, поскольку целая часть любого числа всегда точна. Но число 6,10 не точное. Все, что я сделал, это передвинул десятичную дробь на одно место, и внезапно я перешел от Экзактопии к Инексактвиллю. Этот второй пример побуждает нас задуматься о факторах, и мы можем видеть, что для любого Рациональное Таким образом, для основания 10 любое Итак, теперь возвращаясь к основаниям 10 и 2, мы видим, что любое рациональное число с завершающим 10-представлением будет иметь вид Но один из этих случаев является подмножеством другого! Всякий раз это очевидно также правда что или, другими словами, всякий раз, когда Итак, у нас есть ответ на ваш вопрос - , потому что простые делители 2 являются подмножеством простых делителей 10, все 2-конечные числа являются 10-конечными числами, но не наоборот. В заключение, если бы по какой-то причуде люди использовали (скажем) основание 17, а наши компьютеры использовали основание 5, ваша интуиция никогда бы не поддалась этому... не было бы и (ненулевых, нецелочисленных) чисел, которые завершались бы в обоих случаях! 6 Основная (математическая) причина в том, что когда вы имеете дело с целыми числами, они счетно бесконечны . Это означает, что даже если их бесконечное количество, мы могли бы «отсчитать» все элементы в последовательности, не пропуская ни одного. Это означает, что если мы хотим получить элемент в Однако действительные числа несчетно бесконечны . Вы не можете сказать «дайте мне настоящий номер на позиции Подробнее: http://en.wikipedia.org/wiki/Countable_set http://en.wikipedia.org/wiki/Uncountable_set Обновление: Прошу прощения, я, кажется, неправильно понял вопрос. Мой ответ о том, почему мы не можем представить каждое реальное значение , я не понял, что числа с плавающей запятой автоматически классифицируются как рациональные. 6 Повторяю то, что я сказал в своем комментарии мистеру Скит: мы можем представлять 1/3, 1/9, 1/27 или любое рациональное число в десятичной системе счисления. Мы делаем это, добавляя дополнительный символ. Например, линия над цифрами, которые повторяются в десятичной записи числа. Что нам нужно для представления десятичных чисел в виде последовательности двоичных чисел, так это 1) последовательность двоичных чисел, 2) точка счисления и 3) какой-либо другой символ для обозначения повторяющейся части последовательности. Цитата Hehner - способ сделать это. Он использует символ кавычек для обозначения повторяющейся части последовательности. Статья: http://www.cs.toronto.edu/~hehner/ratno.pdf и статья в Википедии: http://en.wikipedia.org/wiki/Quote_notation. Ничто не говорит о том, что мы не можем добавить символ в нашу систему представления, поэтому мы можем точно представлять десятичные рациональные числа, используя двоичные кавычки, и наоборот. 3 BCD — двоично-десятичное представление — точное. Они не очень компактны, но в этом случае вам придется пойти на компромисс ради точности. 2 Хороший вопрос. Весь ваш вопрос основан на том, "как мы представляем число?" ВСЕ числа могут быть представлены в десятичном или двоичном виде (дополнение до 2). Все!! НО некоторые (большинство из них) требуют бесконечного числа элементов ("0" или "1" для двоичной позиции или "0", "1" до "9" для десятичного представления). Как 1/3 в десятичном представлении (1/3 = 0,3333333... <- с бесконечным числом "3") Как 0,1 в двоичном ( 0,1 = 0,00011001100110011.... <- с бесконечным числом "0011") Все в этом понятии. Поскольку ваш компьютер может считать только конечными набор цифр (десятичных или двоичных), только некоторые числа могут быть точно представлены в вашем компьютере... И, как сказал Джон, 3 — простое число, которое не является множителем 10, поэтому 1/3 не может быть представлено конечным числом элементов по основанию 10. Даже при арифметических действиях с произвольной точностью система счисления позиций по основанию 2 не может полностью описать 6.1, хотя она может представлять 61. Для 6.1 мы должны использовать другое представление (например, десятичное представление или IEEE 854, который допускает основание 2 или основание 10 для представления значений с плавающей запятой) 2 Если вы сделаете достаточно большое число с плавающей запятой (как это может быть с экспонентой), то вы получите неточность и перед десятичной запятой. b) Обратите внимание, что мы сделали, чтобы умножить числа. Мы умножили мантиссы и сложили степени. Затем, поскольку мантисса закончилась больше двух, мы нормализовали результат, увеличив показатель степени. Это похоже на то, когда мы корректируем показатель степени после выполнения операции над числами в десятичной экспоненциальной системе счисления. В каждом случае значения, с которыми мы работали, имели конечное представление в двоичном виде, поэтому значения, выдаваемые базовыми операциями умножения и сложения, также давали значения с конечным представлением. 910b Именно округление мантиссы приводит к потере точности, которую мы связываем со значениями с плавающей запятой. На самом деле мы постоянно делаем подобные вещи, когда округляем десятичные числа до приемлемого размера и просто даем первые несколько цифр. Поскольку мы выражаем результат в десятичном виде, это кажется естественным. Но если бы мы округлили десятичное число, а затем преобразовали его в другое основание, это выглядело бы так же уродливо, как и десятичные числа, которые мы получаем из-за округления с плавающей запятой. Я удивлен, что никто еще не заявил об этом: используйте непрерывные дроби. Таким образом, любое рациональное число может быть представлено в конечной двоичной системе. Некоторые примеры: 1/3 (0,3333...) 5/9 (0,5555...) 10/43 (0,232558139534883720930. 9093/18478 (0,4 5 , so x 2 должно быть 1 и оставшаяся часть 0,5 . Давайте запишем это:
5 , so x 2 должно быть 1 и оставшаяся часть 0,5 . Давайте запишем это:
Почему не все дроби могут быть конечно представлены в двоичной системе
Преобразование двоичного целого числа в десятичное число
 Здесь мы также будем использовать расширение base-q формы числа. Давайте запишем это в такой форме:
Здесь мы также будем использовать расширение base-q формы числа. Давайте запишем это в такой форме: Преобразование двоичной дроби в десятичную
 Запишем в развернутом виде:
Запишем в развернутом виде: math - Почему десятичные числа не могут быть точно представлены в двоичном виде?
System.Decimal в .NET), то множество значений, которые не могут быть точно представлены в двоичном формате с плавающей запятой, могут быть точно представлены. Это 0,3333333... (повторяющееся). Причина, по которой вы не можете представить 0,1 как двоичное число с плавающей запятой, по той же причине. Вы можете представить 3 и 9, и 27 точно - но не 1/3, 1/9 или 1/27.
Это 0,3333333... (повторяющееся). Причина, по которой вы не можете представить 0,1 как двоичное число с плавающей запятой, по той же причине. Вы можете представить 3 и 9, и 27 точно - но не 1/3, 1/9 или 1/27. Дополнительное примечание для решения проблемы конечных представлений:
System. другие, такие как  Decimal
Decimal java.math.BigDecimal , являются «произвольно большими», но они будут в какой-то момент достичь предела, будь то системная память или теоретический максимальный размер массива. Однако это совершенно отдельный момент от основного этого ответа. Даже если бы у вас было действительно произвольно большое количество битов для игры, вы все равно не могли бы точно представить десятичное число 0,1 в представлении с плавающей двоичной точкой. Сравните это с обратным: учитывая произвольное количество десятичных цифр, вы может точно представлять любое число, которое можно точно представить как плавающую двоичную точку.
71198181621387596060179673...) С математической точки зрения между двумя числами не должно быть внутренней разницы — это просто числа 9.n = 22 , целое число. Однако
С математической точки зрения между двумя числами не должно быть внутренней разницы — это просто числа 9.n = 22 , целое число. Однако x = 1/3 этого не делает, потому что какие бы n мы ни выбрали, мы не сможем избавиться от 3. x = p/q (предполагается, что оно в наименьшем выражении), мы можем ответить на вопрос, сравнив простые факторизации b и q . Если q имеет какие-либо простые делители, не входящие в простую факторизацию числа б , мы никогда не сможем найти подходящий н чтобы избавиться от этих факторов. p/q , где q имеет простые делители, отличные от 2 или 5, не будет иметь завершающего представления. p/q в точности тогда, когда q имеет только 2 с и 5 с в его простая факторизация; и это же число будет иметь завершающее 2-представление ровно тогда, когда q имеет только 2 s в простой факторизации.
q имеет только 2 с в простой факторизации q имеет только 2 с и 5 с в простой факторизации p/q имеет завершающее 2-представление, p/q имеет завершающее 10-представление . Обратное, однако, , а не имеет место - всякий раз, когда q имеет 5 в своей простой факторизации, оно будет иметь завершающее 10-представление, но не завершающее 2-представление. Это пример 0.1 , упомянутый в других ответах. Дело не в 61 против 6.1, а в 10 против 2.
Дело не в 61 против 6.1, а в 10 против 2. 610000000000000 -й позиции в списке, мы можем вычислить это с помощью формулы. 610000000000000 » и получить ответ. Причина в том, что даже между
Причина в том, что даже между 0 и 1 существует бесконечное количество значений, когда вы рассматриваете значения с плавающей запятой. То же самое верно для любых двух чисел с плавающей запятой.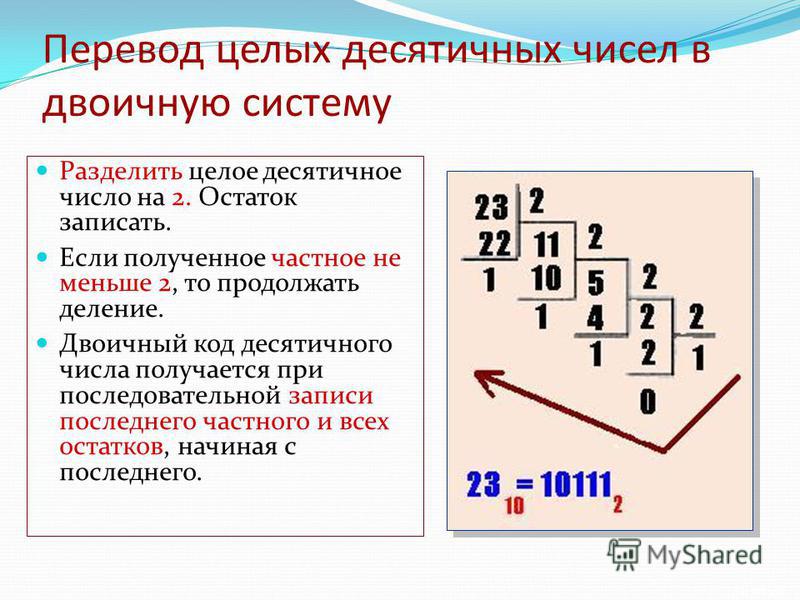
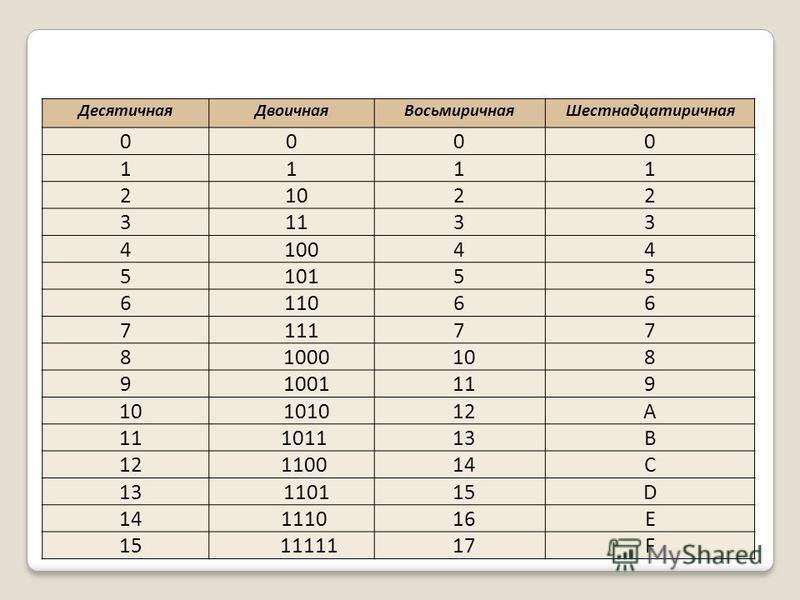
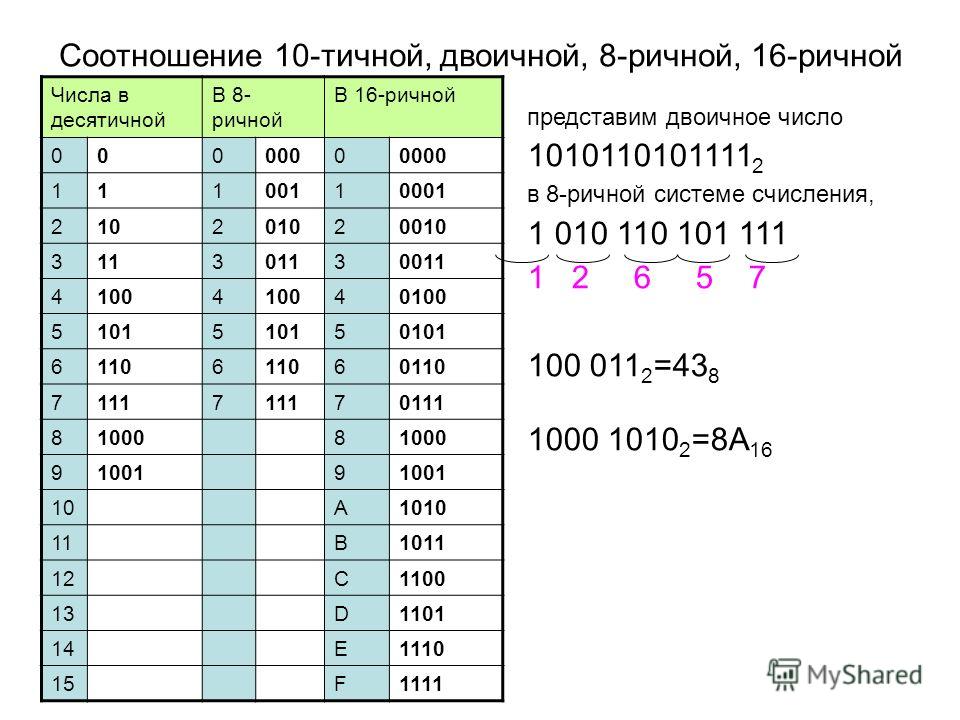 Поэтому я не думаю, что ваш вопрос полностью обоснован, потому что предпосылка неверна; дело не в том, что сдвиг на 10 всегда будет создавать большую точность, потому что в какой-то момент число с плавающей запятой должно будет использовать показатели степени для представления величины числа и таким образом также потеряет некоторую точность.
Поэтому я не думаю, что ваш вопрос полностью обоснован, потому что предпосылка неверна; дело не в том, что сдвиг на 10 всегда будет создавать большую точность, потому что в какой-то момент число с плавающей запятой должно будет использовать показатели степени для представления величины числа и таким образом также потеряет некоторую точность. Даже когда мантисса может быть выражена точно (например, при простом сложении двух чисел), мы все равно можем получить числовые потери, если мантисса требует слишком много цифр для соответствия после нормализации показателя степени.
Даже когда мантисса может быть выражена точно (например, при простом сложении двух чисел), мы все равно можем получить числовые потери, если мантисса требует слишком много цифр для соответствия после нормализации показателя степени. 0; 3
0; 1, 1, 4
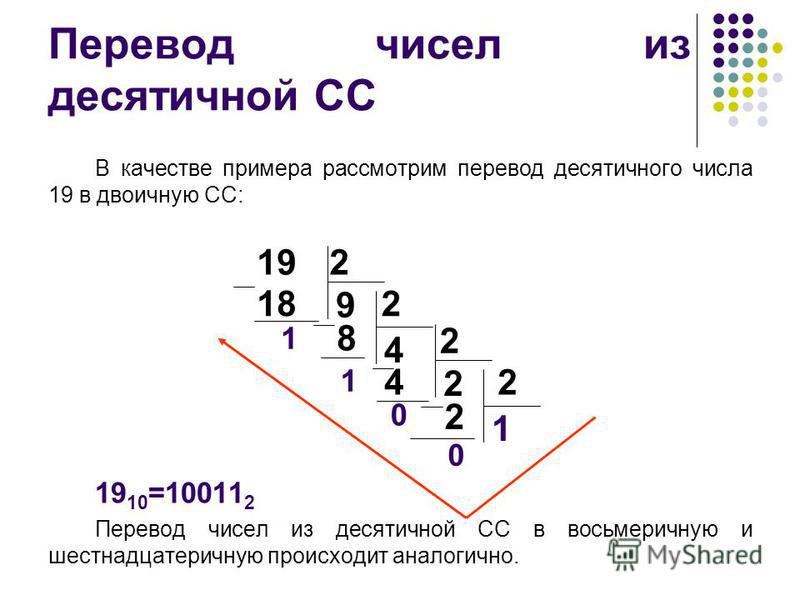 ..)
..) 0; 4, 3, 3
0; 2, 31, 7, 8, 5
Отсюда существует множество известных способов хранения последовательности целых чисел в памяти.
Помимо хранения вашего числа с идеальной точностью, непрерывные дроби также имеют некоторые другие преимущества, такие как наилучшее рациональное приближение. Если вы решите прервать последовательность чисел в непрерывной дроби досрочно, оставшиеся цифры (при объединении в дробь) дадут вам наилучшую возможную дробь. Вот как находятся приближения к пи:
Непрерывная дробь числа Пи:
3; 7, 15, 1, 292...
Завершая последовательность на 1, получаем дробь: 9(лог(0,41)/лог(2))
Проблема в том, что вы не знаете, действительно ли это число равно 61.0. Рассмотрим это:
поплавок а = 60; поплавок b = 0,1; поплавок с = а + b * 10;
Каково значение с? Это не точно 61, потому что b на самом деле не .1, потому что .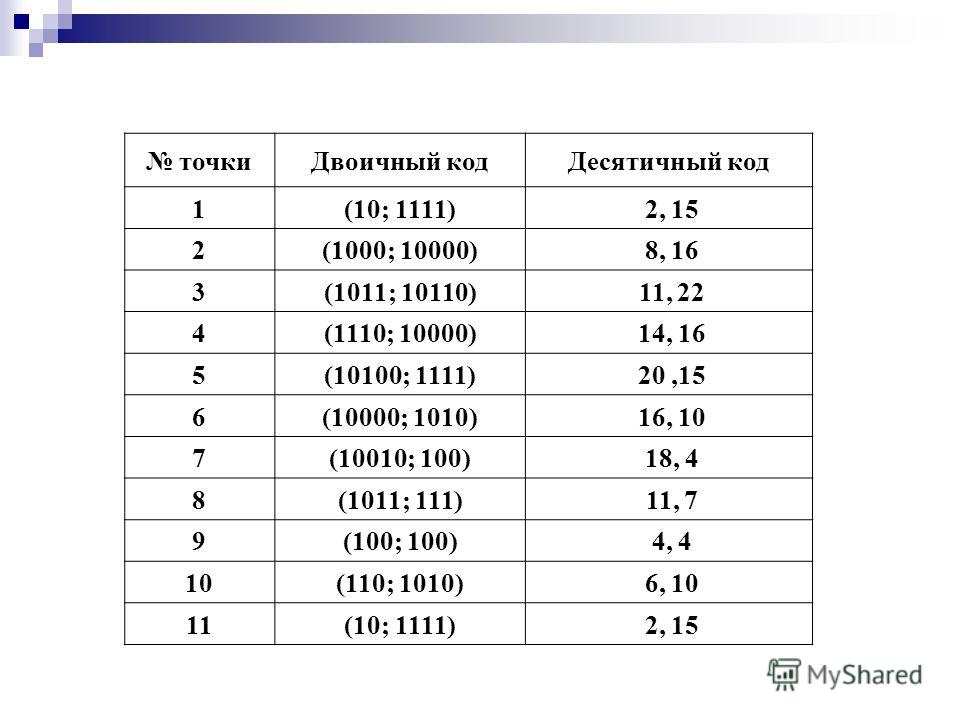 1 не имеет точного двоичного представления.
1 не имеет точного двоичного представления.
Число 61.0 действительно имеет точную операцию с плавающей запятой, но это неверно для всех целых чисел. Если вы написали цикл, добавляющий единицу к числу двойной точности с плавающей запятой и к 64-битному целому числу, в конечном итоге вы достигли бы точки, в которой 64-битное целое число идеально представляет число, а число с плавающей запятой — нет… потому что не хватает значащих битов. 9-1 равно 1/10, что определенно не является целым числом. Так вы окажетесь в Inexactville.
Параллель можно составить из дробей и целых чисел. Некоторые дроби, например 1/7, не могут быть представлены в десятичной форме без большого количества десятичных знаков. Поскольку число с плавающей запятой основано на двоичном коде, особые случаи меняются, но возникают те же проблемы с точностью.
Существует бесконечное число рациональных чисел и конечное число битов для их представления. См. http://en.wikipedia.org/wiki/Floating_point#Accuracy_problems. 9-4=0,0625
9-4=0,0625
Двоичное представление с плавающей запятой:
знак Показатель степени Дробь (я думаю, к дроби добавляется невидимая 1)
B11 B10 B9 B8 B7 B6 B5 B4 B3 B2 B1 B0
Ответ выше .
Сначала вы смешивали основание 2 и основание 10 в своем вопросе, затем, когда вы ставите справа число, которое не делится на основание, возникают проблемы. Как 1/3 в десятичном виде, потому что 3 не входит в степень 10 или 1/5 в двоичном формате, который не входит в степень 2.
Еще один комментарий, но НИКОГДА не используйте equal с числами с плавающей запятой, точка. Даже если это точное представление, в некоторых системах с плавающей запятой есть числа, которые могут быть точно представлены более чем одним способом (IEEE плохо относится к этому, это ужасная спецификация с плавающей запятой для начала, так что ожидайте головной боли). Никакой разницы здесь нет: 1/3 НЕ РАВНА числу на вашем калькуляторе 0,3333333, сколько бы троек не было справа от запятой. Это или может быть достаточно близко, но не равно. поэтому вы ожидаете, что что-то вроде 2 * 1/3 не будет равно 2/3 в зависимости от округления. Никогда не используйте равные с плавающей запятой.
Это или может быть достаточно близко, но не равно. поэтому вы ожидаете, что что-то вроде 2 * 1/3 не будет равно 2/3 в зависимости от округления. Никогда не используйте равные с плавающей запятой.
Как мы уже говорили, в арифметике с плавающей запятой десятичное число 0,1 не может быть идеально представлено в двоичном виде.
Представления с плавающей запятой и целыми числами обеспечивают сетки или решетки для представляемых чисел. По мере выполнения арифметических операций результаты выпадают из сетки и должны быть возвращены в сетку путем округления. Пример 1/10 в двоичной сетке.
Если мы будем использовать двоично-десятичное представление, как предложил один джентльмен, сможем ли мы хранить числа в сетке?
1
Для простого ответа: у компьютера нет бесконечной памяти для хранения дробей (после представления десятичного числа в виде научной записи). Согласно стандарту IEEE 754 для чисел с плавающей запятой двойной точности, у нас есть ограничение в 53 бита для хранения дроби. Для получения дополнительной информации: http://mathcenter.oxford.emory.edu/site/cs170/ieee754/
Для получения дополнительной информации: http://mathcenter.oxford.emory.edu/site/cs170/ieee754/
Я не буду повторять то, что уже подытожили другие 20 ответов, поэтому я просто отвечу кратко:
Ответ в вашем содержании:
Почему числа с основанием из двух не могут точно представлять определенные отношения?
По той же причине, по которой десятичных дробей недостаточно для представления определенных отношений, а именно неприводимых дробей со знаменателем, содержащим простые множители, отличные от двух или пяти, которые всегда будут иметь неопределенную строку по крайней мере в мантиссе своего десятичного разложения.
Почему десятичные числа не могут быть точно представлены в двоичном виде?
Этот вопрос на первый взгляд основан на неправильном представлении о самих ценностях. Никакой системы счисления недостаточно, чтобы представить какое-либо количество или отношение таким образом, чтобы сама вещь говорила вам, что она является одновременно и количеством, и в то же время сама по себе давала интерпретацию внутренней ценности представления. Как таковые, все количественные представления и вообще модели носят символический характер и могут быть поняты только апостериори, а именно после того, как человек научится читать и интерпретировать эти числа.
Как таковые, все количественные представления и вообще модели носят символический характер и могут быть поняты только апостериори, а именно после того, как человек научится читать и интерпретировать эти числа.
Поскольку модели являются субъективными вещами, которые истинны, поскольку отражают реальность, нам не обязательно интерпретировать двоичную строку как сумму отрицательных и положительных степеней двойки. Вместо этого можно заметить, что мы можем создать произвольный набор символов, использующих основание два или любое другое основание для точного представления любого числа или отношения. Просто учтите, что мы можем обращаться ко всей бесконечности, используя одно слово и даже один символ, не «показывая бесконечность» как таковую.
В качестве примера я разрабатываю двоичное кодирование для смешанных чисел, чтобы иметь большую точность, чем число с плавающей запятой IEEE 754. На момент написания этой статьи идея состояла в том, чтобы иметь знаковый бит, обратный бит, определенное количество битов для скаляра, чтобы определить, насколько «увеличить» дробную часть, а затем оставшиеся биты делятся поровну между целая часть смешанного числа, а последнее число с фиксированной запятой, которое, если установлен обратный бит, должно интерпретироваться как единица, деленная на это число. Преимущество этого заключается в том, что я могу представлять числа с бесконечным десятичным разложением, используя их обратные числа, которые до имеют завершающие десятичные расширения или, альтернативно, прямо как дробь, возможно, как приближение, в зависимости от моих потребностей.
Преимущество этого заключается в том, что я могу представлять числа с бесконечным десятичным разложением, используя их обратные числа, которые до имеют завершающие десятичные расширения или, альтернативно, прямо как дробь, возможно, как приближение, в зависимости от моих потребностей.
Вы не можете точно представить 0,1 в двоичном формате по той же причине, по которой вы не можете измерить 0,1 дюйма с помощью обычной английской линейки.
Английские линейки, как и двоичные дроби, состоят из половинок. Вы можете измерить полдюйма или четверть дюйма (что, конечно, составляет половину половины), восьмую, шестнадцатую и т. д.
Если вы хотите измерить десятую часть дюйма, вам не повезло. Это меньше одной восьмой дюйма, но больше шестнадцатой. Если вы попытаетесь уточнить, то обнаружите, что это чуть больше 3/32, но чуть меньше 7/64. Я никогда не видел настоящую линейку с градацией тоньше 64-х, но если вы посчитаете, то обнаружите, что 1/10 меньше 13/128, больше 25/256 и больше 51.