Деление в java: Java | Арифметические операции

НОУ ИНТУИТ | Лекция | Работа с числами в языке Java

Аннотация: Двоичное представление целых чисел. Позиционные и непозиционные системы счисления. Двоичное представление положительных целых чисел. Двоичное представление отрицательных целых чисел. Дополнительный код. Проблемы целочисленной машинной арифметики. Шестнадцатеричное представление целых чисел и перевод из одной системы счисления в другую. Побитовые маски и сдвиги. Двоичное представление вещественных чисел. Двоичные дроби. Мантисса и порядок числа. Стандарт IEEE 754 представления чисел в формате с плавающей точкой.

Ключевые слова: представление, система счисления, позиционная система счисления, алгоритмизация, кодирование информации, словосочетание, binary digit, архитектура компьютера, микрокоманда, порт ввода-вывода, аналого-цифровые преобразователи, двоичная система счисления, двоичное представление, дополнительный код, целочисленный тип, операции, бит, ячейка, криптография, инверсия, эквивалентность, значение, буфер, floating point, знаковый бит, мантисса, plain text, exponent, натуральный логарифмы, IEEE 754, IEC, экспонента, infinity, nan, IND, indeterminism, signaling, quiet

intuit.ru/2010/edi»>Данная часть посвящена изучению работы с числами на более глубоком уровне. В ней рассматривается машинное представление целых и вещественных чисел, эффективное для аппаратной реализации, а также объясняются особенности и проблемы, к которым приводит такое представление.

4.1. Двоичное представление целых чисел

Позиционные и непозиционные системы счисления

Позиционная система счисления — это такой способ записи числа, при котором вес цифры зависит от занимаемой позиции и пропорционален степени некоторого числа. Основание степени называется основанием системы счисления.

Например, число 2006 в десятичной системе счисления представляется в виде суммы тысяч, сотен, десятков и единиц:

то есть слагаемых с различными степенями числа 10. По основанию степени — числу десять — система называется десятичной. Другие позиционные системы счисления отличаются только числом в основании степени.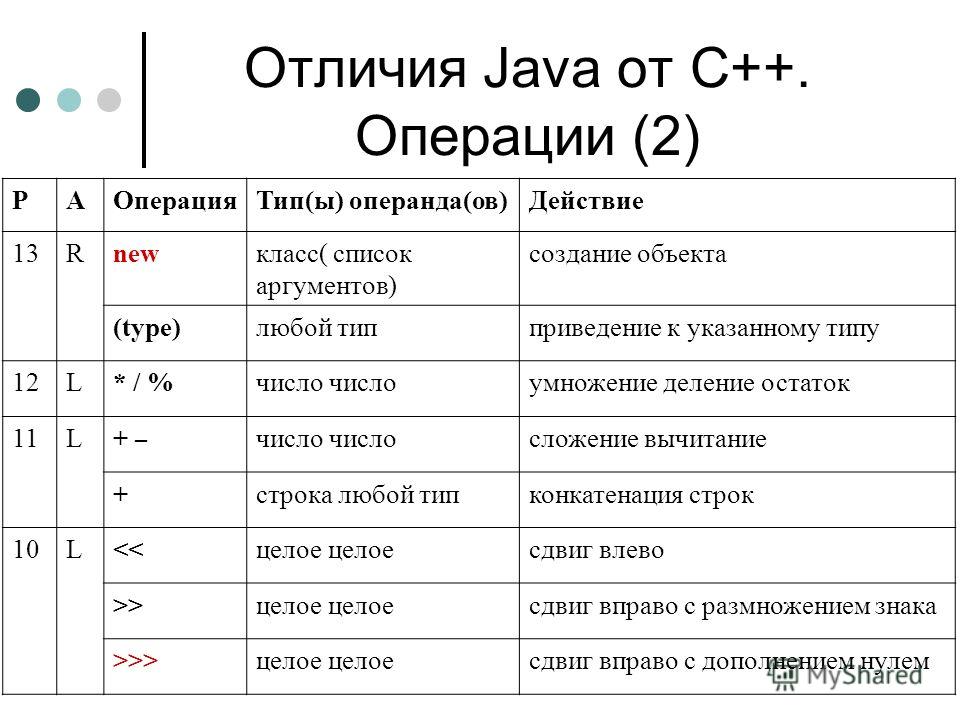

При написании программ чаще всего используют десятичную, шестнадцатеричную (основание шестнадцать), восьмеричную (основание восемь) и двоичную (основание два) системы. Число различных знаков — цифр, используемых для записи чисел — в каждой системе равно основанию данной системы счисления.

Таблица 4.1.

0,1	— цифры двоичной системы
0,1,2,3,4,5,6,7	— цифры восьмеричной системы
0,1,2,3,4,5,6,7,8,9	— цифры десятичной системы
0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F	— цифры шестнадцатеричной системы

intuit.ru/2010/edi»>

В шестнадцатеричной системе «обычных» десятичных цифр недостаточно, и для обозначения цифр, больших девяти, используются заглавные латинские буквы A,B,C,D,E,F.

В дальнейшем везде, где это необходимо, мы будем указывать основание системы счисления индексом рядом с числом: — в десятичной системе, — в шестнадцатеричной системе, — в восьмеричной системе, — в двоичной системе.

Существует множество непозиционных систем счисления, в которых числа изображаются и называются по своим правилам. Для римской системы чисел характерны сопоставление отдельного знака каждому большому числу ( V — пять, X — десять, L — пятьдесят, C — сто, M — тысяча ), повторение знака столько раз, сколько таких чисел во всем числе ( III — три, XX — двадцать), отдельные правила для предшествующих и последующих чисел (IV — четыре, VI — шесть, IX — девять). Множество непозиционных систем счисления связано с традиционными способами измерения конкретных величин — времени ( секунда, минута, час, сутки, неделя, месяц, год), длины ( дюйм, фут, ярд, миля, аршин, сажень), массы ( унция, фунт), денежных единиц.

Выполнение арифметических действий в таких системах представляет собой крайне сложную задачу.

Приведем пример самой простой из возможных систем счисления – унарную. В ней имеется всего одна цифра 1. В унарной системе счисления число 1 изображается как 1, число 2 изображается как 11, число 3 как 111, число 4 как 1111, и так далее. Первоначально вместо единицы использовались палочки (помните детский сад?), поэтому такая система счисления иногда называется палочковой. Как ни странно, она является позиционной.

Позиционные системы счисления с основанием 2 и более удобны для алгоритмизации математических операций с числами (вспомните способ сложения и умножения «столбиком»). Двоичная система является естественным способом кодирования информации в компьютере, когда сообщение представляется набором нулей («0» — нет сигнала на линии) и единиц («1» — есть сигнал на линии). Для обозначения двоичных цифр применяется термин «бит», являющийся сокращением английского словосочетания «двоичная цифра» (BInary digiT).

Архитектура компьютера накладывает существенное ограничение на длину информации, обрабатываемой за одну операцию. Эта длина измеряется количеством двоичных разрядов и называется разрядностью. С помощью восьми двоичных разрядов можно представить целых чисел. Порция информации размером 8 бит (8-ми битовое число) служит основной единицей измерения компьютерной информации и называется байтом (byte). Как правило, передача информации внутри компьютера и между компьютерами идет порциями, кратными целому числу байт.

Машинным словом называют порцию данных, которую процессор компьютера может обработать за одну операцию (микрокоманду). Первые персональные компьютеры были 16-разрядными, т.е. работали с 16-битными (двухбайтными) словами. Поэтому операционные системы для этих компьютеров также были 16-разрядными. Например, MS DOS. Операционные системы для персональных компьютеров следующих поколений были 32-разрядны (Windows® ’95/’98/NT/ME/2000/XP, Linux, MacOS®), так как предназначались для использования с 32-разрядными процессорами. Современные операционные системы либо 32-разрядны, либо даже 64-разрядны (версии для 64-разрядных процессоров).

Представление чисел в двоичной и шестнадцатеричной системах счисления, а также преобразование из одной системы в другую часто необходимо при программировании аппаратуры для измерений, контроля и управления с помощью портов ввода-вывода, цифро-аналоговых и аналого-цифровых преобразователей.

Двоичное представление положительных целых чисел

Целые числа в компьютере обычно кодируются в двоичном коде, то есть в двоичной системе счисления. Например, число 5 можно представить в виде .

Показатель системы счисления принято записывать справа снизу около числа.

Аналогично, , и так далее. Все очень похоже на обозначение чисел в десятичной системе счисления:

ru/2010/edi»>. Но только в качестве основания системы счисления используется число . У чисел, записанных в десятичной системе счисления, индекс 10 обычно не пишется, но его можно писать. Так что , и так далее.

В двоичной арифметике всего две цифры, 0 и 1. Двоичный код положительного целого числа – это коэффициенты разложения числа по степеням двойки.

Умножение числа на двоичное десять, то есть на , приводит к дописыванию справа нуля в двоичном представлении числа. Умножение на двоичное сто, то есть на — дописыванию двух нулей. И так далее.

Целочисленное деление на с отбрасыванием остатка производится путем отбрасывания последнего (младшего) бита, деление на — отбрасывания двух последних бит, и так далее. Обычно такие операции называют побитовыми сдвигами на n бит влево (умножение на ) или вправо (целочисленное деление на ).

intuit.ru/2010/edi»>Сложение двоичных чисел можно производить «в столбик» по полной аналогии со сложением десятичных чисел. Единственное отличие – то, что в двоичной арифметике только две цифры, 0 и 1, а не десять цифр (от 0 до 9) как в десятичной. Поэтому если в десятичной арифметике единицу более старшего разряда дает, к примеру, сложение 1 и 9, то в двоичной арифметике ее даст сложение 1 и 1. То есть

(в десятичной системе это равенство выглядит как 1+1=2). Аналогично, , и так далее.

Примеры сложения «в столбик»:

Совершенно аналогично выполняется умножение:

В машинной реализации целочисленного умножения используют побитовые сдвиги влево и сложения. Поскольку эти алгоритмы очень просты, они реализуются аппаратно.

1.2.2 Выражения Java

1.2.2 Выражения Java
Следующий: 1. 2.3 Приоритет операций Up: 1.2 Механика Java Предыдущий: 1.2.1 Обозначения и синтаксис В Java арифметические, логические и строковые выражения записываются на обычная математическая нотация инфикс , адаптированная к стандартный набор символов компьютера (называемый ASCII). Например, Выражение схемы

(и (< (+ (* x x) (* y y)) 25) (> x 0))
 

записывается на Java как

.
(х*х + у*у > 25) && (х > 0)
 

Подобно языку программирования C

, Java использует символ && для операция «и» над логическими значениями (true и false) и символ == для операции равенства чисел. (Символы и и = используются в C и Java для других целей.)

В следующей таблице перечислены основные инфиксные операторы. предоставлено Java:

+	добавление и объединение строк
—	вычитание
звезда	умножение
/	отделение
%	mod (остаток от целочисленного деления)
<	меньше
<=	меньше или равно
>	больше
>=	больше или равно
==	равно
!=	не равно
&&	и
||	или

Все арифметические операторы используют обычную компьютерную арифметику. соответствующие типам аргументов. Обычный компьютер арифметика не совсем соответствует стандартной математической соглашения. Например, выражение

5/3

дает результат

1

, что является частным от 5, деленного на 3. Целочисленное деление дает целочисленный, а не рациональный результат; он усекается до десятичной дроби представление рационального результата. Аналогично, выражение

5%3

дает результат

2

, остаток от деления 5 на 3. В тексте программы на Java пробелы между символами игнорируются; в выражение

5 / 3

эквивалентно выражению

5/3

Упражнение для пальцев: В среде программирования DrJava попробуйте вычисление следующих выражений:

5/3
5 % 3
5./3.
5 / 0
5./0.
5 < 6
5. < 6.
3 + .100000000 * .10000000 - 3.
 

Java-выражения непосредственно в Взаимодействия Окно. Вы получить ответы, которые вы ожидали?

Все бинарные инфиксные операторы в Java являются либо арифметическими, либо реляционное или логическое, за исключением +, когда он используется в соединение со струнами. Если любой из аргументов + имеет тип String, то Java приводит другой аргумент к типу String. Значения объекта приводятся к типу String с помощью их методов toString(). Как мы объясняли в Разделе 1.4.4, каждый объект имеет метод toString(). Примитивные значения преобразуются в строки с помощью встроенных процедур преобразования, таких как статический метод Integer.toString(int i), который преобразует int в соответствующую строку.

Обратите внимание, что порядок появления аргументов и использование круглые скобки в смешанных целочисленных и строковых выражениях, построенных из значения int и String влияют на процесс преобразования. Для например, выражение

9 + 5 + 1 + "S"

оценивается как строка "15S" а выражение

9 + (5 + (1 + "S"))

оценивается как строка "951S". Ассоциация правила для выражений Java объясняются в Разделе 1.2.3.

Java также поддерживает унарные префиксные операторы - (арифметические отрицание) и ! (логическое ``не''), используемое в обычных математические обозначения. Скобки используются для обозначения того, как выражения должны быть разложены на подвыражения.

Упражнение пальцами: Если окно DrJava Interactions , попробуйте вычисление следующих выражений:

-5 + 3
! (5 < 6)
 

Единственная чистая форма выражения в Java, которая отличается от общепринятой. математическая запись - это запись условного выражения

тест ? последовательное : альтернативное

заимствовано из C . Это выражение возвращает значение следствие , если тест истинен, и значение альтернатива , если тест ложен. Это соответствует Выражение схемы

(конд ( тест последующий ) (иначе альтернатива ))

Обратите внимание, что когда тест истинен, альтернатива не верна.