Шестнадцатеричное кодирование. Шестнадцатеричная нумерация и адресация
Шестнадцатеричная система счисления (также — шестнадцатеричный код) является позиционной системой счисления с целочисленным основанием 16. Иногда в литературе также используется термин hex (произносится «хекс», сокращение от англ. hexadecimal). Цифрами данной системы счисления принято использовать арабские цифры 0—9, а также первые символы латинского алфавита A—F. Буквы соответствуют следующим десятичным значениями:
- * A —10;
- * B —11;
- * C —12;
- * D —13;
- * E — 14;
- * F — 15.
Таким образом, десять арабских цифр вкупе с шестью латинскими буквами и составляют шестнадцать цифр системы.
Кстати, на нашем сайте вы можете перевести любой текст в десятичный, шестнадцатеричный, двоичный код воспользовавшись Калькулятором кодов онлайн .
Применение . Шестнадцатеричный код широко применяется в низкоуровневом программировании, а также в различных компьютерных справочных документах.
В кодировке Юникод для записи номера символа используется четыре шестнадцатеричных цифры. Запись цвета стандарта RGB (Red, Green, Blue — красный, зелёный, синий) также часто использует шестнадцатеричный код (например, #FF0000 — запись ярко-красного цвета).
Способ записи шестнадцатеричного кода.
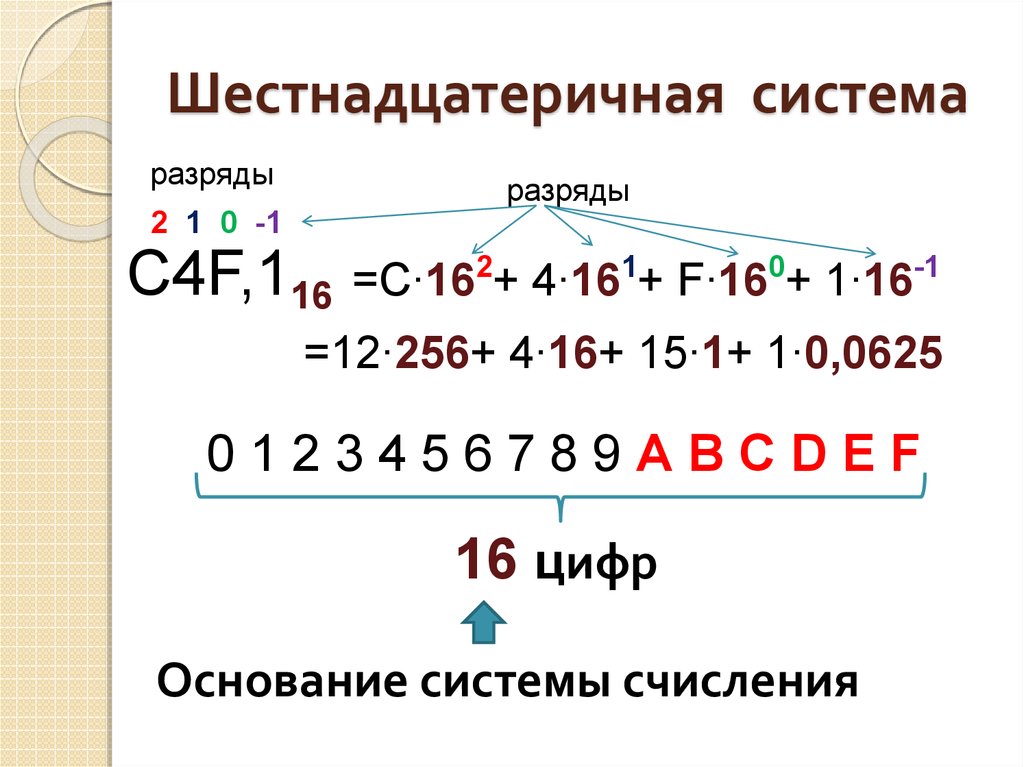
Математический способ записи . В математической записи основание системы записывают в десятичном виде в нижнем индексе справа от числа. Десятичную запись числа 3032 можно записать как 3032 10 , в шестнадцатеричной системе данное число будет иметь запись BD8 16 .
В синтаксисе языков программирования . Синтаксис различных языков программирования по-разному устанавливает формат записи числа, использующего шестнадцатеричный код :
* В синтаксисе некоторых разновидностей языка ассемблера используется латинская буква «h», которая ставится справа от числа, например: 20Dh. Если число начинается с латинской буквы, то перед ним ставится ноль, например: 0A0Bh. Это сделано для того, чтобы отличать от констант значения, использующие шестнадцатеричный код ;
* В прочих разновидностях ассемблера, а также в Pascal (и его разновидностях, таких как Delphi) и некоторых диалектах Basic, применяют префикс «$»: $A15;
* В языке разметки HTML, а также в каскадных файлах CSS, для указания цвета в формате RGB с шестнадцатеричной системой записи, используется префикс «#»: #00DC00.
Как перевести шестнадцатеричный код в другую систему?
Перевод из шестнадцатеричной системы в десятичную. Для совершения операции перевода из шестнадцатеричной системы в десятичную, требуется представить исходное число как сумму произведений цифр в разрядах шестнадцатеричного числа на степень основания.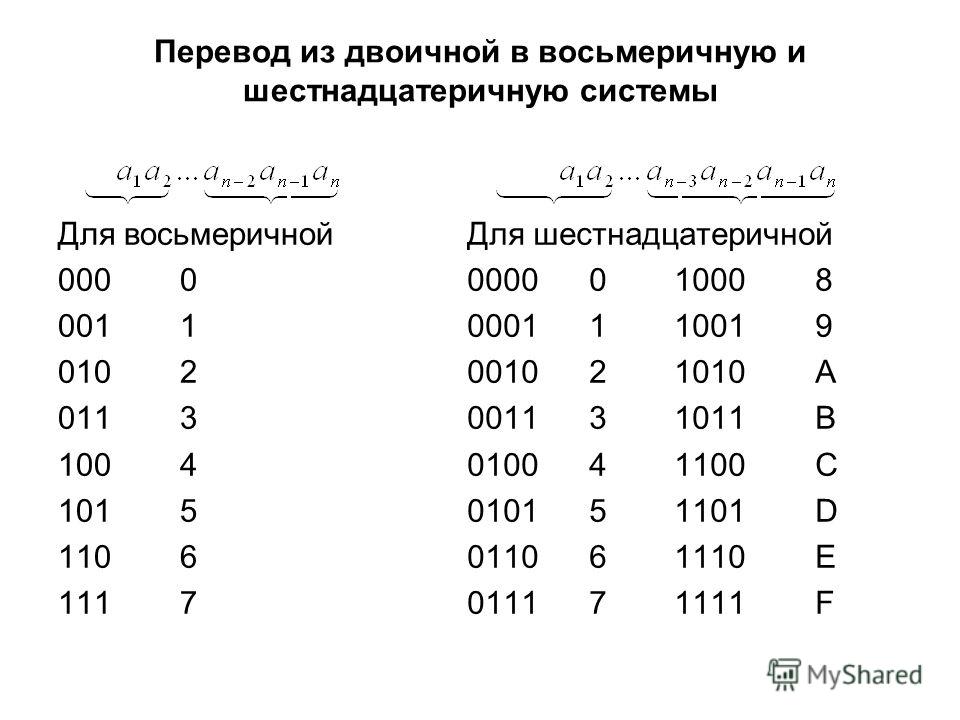
Двоичная СС | шестнадцатеричная СС |
Например, требуется выполнить перевод шестнадцатеричного числа A14: в нём три цифры. Используя правило, запишем его в виде суммы степеней с основанием 16:
A14 16 = 10.16 2 + 1.16 1 + 4.16 0 = 10.256 + 1.16 + 4.1 = 2560 + 16 + 4 = 2580 10
Перевод чисел из двоичной в шестнадцатеричную систему и наоборот.
Для перевода используется таблица тетрад. Чтобы выполнить перевод числа из двоичной в десятичную систему, необходимо произвести разбиение его на отдельные тетрады справа налево, после чего, используя таблицу, выполнить замену каждой тетрады на соответствующую шестнадцатеричную цифру. При этом, если количество цифр не кратно четырём, то необходимо добавить соответствующее количество нулей справа от числа, для того, чтобы общее число двоичных цифр стало кратно четырём.
Таблица тетрад для перевода.
Для перевода из шестнадцатеричной системы в двоичную, необходимо выполнить обратную операцию: выполнить замену каждой цифры на тетраду из таблицы.
Двоичная СС | Восьмеричная СС |
Пример перевода из шестнадцатеричной системы в двоичную : A5E 16 = 1010 0101 1110 = 101001011110 2
Пример перевода из двоичной системы в шестнадцатеричную : 111100111 2 = 0001 1110 0111 = 1E7 16
В этом примере количество цифр в исходном двоичном числе не было равным четырём (9), поэтому были добавлены незначащие нули — общее число цифр стало 12.
Автоматический перевод . Быстрый перевод из шестнадцатеричной системы счисления в одну из трёх популярных систем (двоичную, восьмеричную и десятичную), как и обратный перевод, можно выполнить, используя стандартный калькулятор из комплекта поставки ОС Windows. Откройте калькулятор, выберите в меню Вид -> Программист. В данном режиме можно устанавливать систему счисления, используемую в данный момент (см. меню слева: Hex, Dec, Oct, Bin). При этом изменение текущей системы счисления автоматически производит перевод.
Возникла в древнем Вавилоне. В Индии система работает в виде позиционной десятичной нумерации с использованием нуля, у индусов данную систему чисел позаимствовала арабская нация, у них, в свою очередь, взяли европейцы. В Европе эту систему стали называть арабской.
Позиционная система счисления — значение всех цифр зависит от позиции (разряда) данной цифры в числе.
Примеры , стандартная десятичная система счисления — это позиционная система.
Шестнадцатеричная система счисления.
Шестнадцатеричная система счисления (шестнадцатеричные числа) — позиционная система счисления. Основанием шестнадцатеричной системы счисления является число 16.
Записывая числа в восьмеричной системе счисления мы получаем довольно компактные выражения, однако в шестнадцатеричной системе мы получаем выражения более компактными.
Первыми десятью цифрами из шестнадцати шестнадцатеричных цифрах является стандартный интервал 0 — 9 , последующие шесть цифр выражают при помощи первых букв латинского алфавита: A , B , C , D , E , F .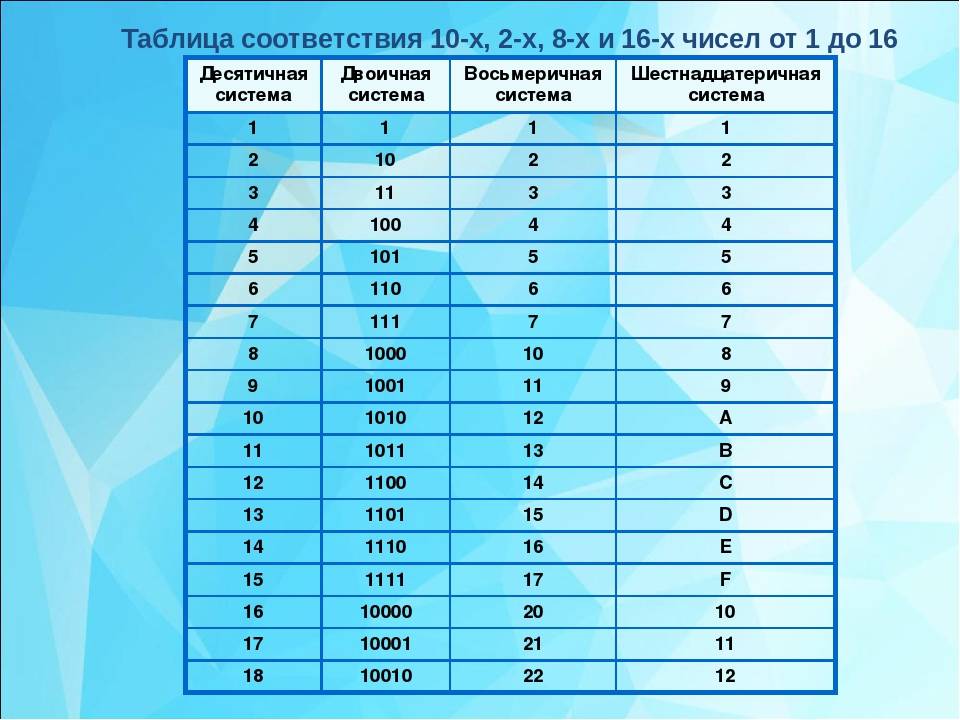
Перевод из шестнадцатеричной системы в двоичную систему и в обратную сторону делают аналогично процессу для восьмеричной системы.
Применение шестнадцатеричной системы счисления.
Шестнадцатеричную систему счисления довольно хорошо используют в современных компьютерах, например с ее помощью указывают цвет: #FFFFFF — белый цвет.
Перевод чисел из одной системы счисления в другую.
Перевод чисел из шестнадцатеричной системы в десятичную.
Что бы перевести шестнадцатеричное число в десятичное , нужно заданное число привести к виду суммы произведений степеней основания шестнадцатеричной системы счисления на соответствующие цифры в разрядах шестнадцатеричного числа.
Например , переведем шестнадцатеричное число 5A3 в десятичное. Здесь 3 цифры. Исходя их выше сказанного правила, приведем его к виду суммы степеней с основанием 16:
5A3 16 = 3·16 0 +10·16 1 +5·16 2 = 3·1+10·16+5·256 = 3+160+1280 = 1443 10
Перевод чисел из двоичной системы в шестнадцатеричную и наоборот.
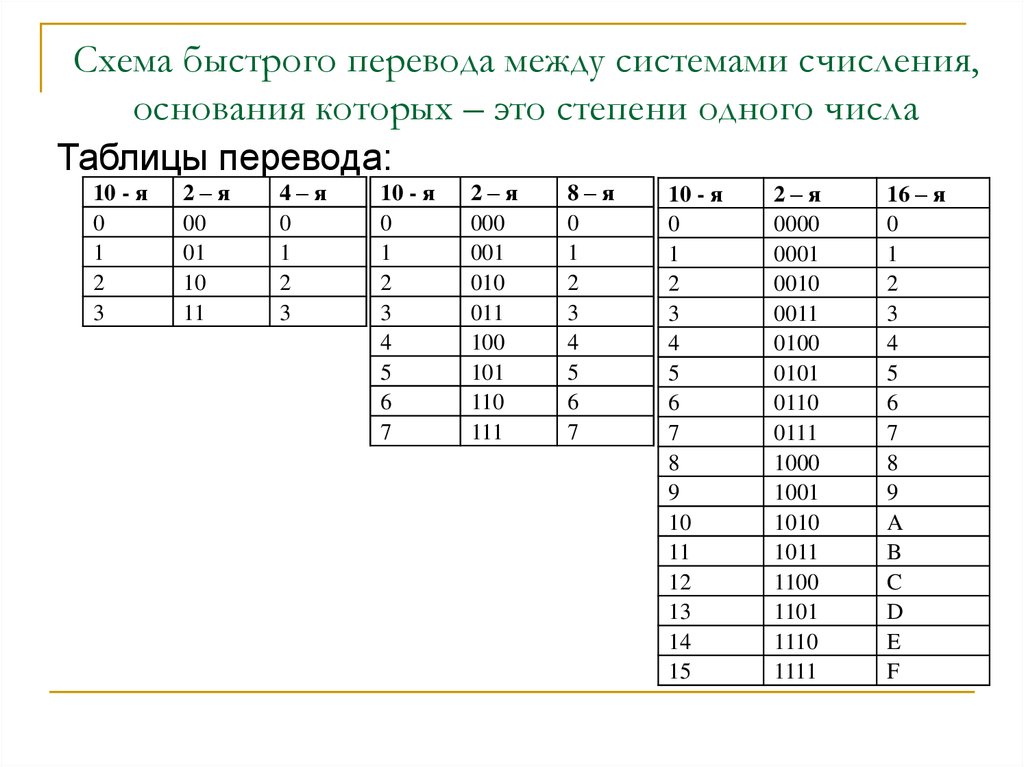
Для перевода многозначного двоичного числа в шестнадцатеричную систему необходимо разделить его на тетрады справа налево и поменять все тетрады соответствующей шестнадцатеричной цифрой. Для перевода числа из шестнадцатеричной системы в двоичную необходимо поменять каждую все цифры на соответствующие тетрады из таблицы перевода, которую вы найдете ниже.
Например :
010110100011 2 = 0101 1010 0011 = 5A3 16
Таблица перевода чисел.
Алгоритм перевода чисел из одной системы счисления в другую.
1. Из десятичной системы счисления:
- делим число на основание переводимой системы счисления;
- находим остаток от деления целой части числа;
- записываем все остатки от деления в обратном порядке;
2. Из двоичной системы счисления:
- для перевода в десятичную систему счисления находим сумму произведений основания 2 на соответствующую степень разряда;
- для перевода числа в восьмеричную разбиваем число на триады.
Например, 1000110 = 1 000 110 = 1068
- для перевода числа из двоичной системы счисления в шестнадцатеричную разбиваем число на группы по 4 разряда.
Например, 1000110 = 100 0110 = 4616.
Таблицы для перевода:
Двоичная СС | Шестнадцатеричная СС |
0000 | |
0001 | |
0010 | |
0011 | |
0100 | |
0101 | |
0110 | |
0111 | |
1000 | |
1001 | |
1010 | |
1011 | |
1100 | |
1101 | |
1110 | |
1111 |
Двоичная СС |
Привычная для человека система счисления – десятичная.
В ее основу входят десять цифр от 0 до 9. Шестнадцатеричную систему отличает наличие в ней первых шести букв латинского алфавита для записи чисел помимо основных цифр. То есть после цифры 9 следует символ «A», который соответствует числу 10 для десятичной системы. Соответственно, F в шестнадцатеричной системе – это 16 в десятичной. Использование шестнадцати символов в системе – неслучайный выбор.
Единица информации – бит. Восемь бит образуют байт. Существует понятие, как машинное слово – это единица данных, представляющая собой два , то есть шестнадцать бит. Таким образом, используя шестнадцать различных символов, можно описывать любую информацию, которая при обмене данных будет наименьшей частицей. С ними можно производить любые арифметические действия, результат, соответственно, получится тоже в шестнадцатеричной системе.
Для того чтобы отличать, что число записано в шестнадцатеричной системе, после него записывают букву «h» или нижний индекс «16».
Применение
Наиболее широкое применение шестнадцатеричной системы счисления – это коды ошибок программных продуктов, например, операционной системы.
Числа, заложенные в этих кодах, стандартизированы. Имея специальную таблицу, всегда можно определить, что именно означает та или иная ошибка.
В языках низкого уровня, максимально приближенным к машинным кодам шестнадцатеричная система применяется для написания программ. Многие программисты используют ее и при работе с языками высокого уровня, потому что числа в этой системе при помощи специальной таблицы соответствия легко переводятся в двоичную систему, на которой основана работа всей цифровой техники. Любая информация в компьютере, будь то музыкальный файл или текстовый документ, после трансляции представлена последовательностью исходного двоичного кода, а его удобнее просматривать представленным символами шестнадцатеричной системы.
Также одно из применений шестнадцатеричных символов – описание цветовых схем, то есть три компонента R, G, B описываются соответствующим данной системе способом. Данный подход к записи получил название шестнадцатеричный цвет
Возможность просмотреть программу в шестнадцатеричном коде позволяет отладить ее, внести изменения, а злоумышленниками данный подход используется для взлома программ.
Всем, кто общается с компьютером или другой цифровой техникой, приходилось встречать загадочные записи типа 10FEF, которые кажутся непосвященным каким-то шифром. Что скрывается за этими символами? Оказывается, это просто цифры. Те, которые использует шестнадцатиричная
Системы счисления
Каждый школьник знает или хотя бы где-то слышал, что все цифры, которые мы обычно используем, образуют Это название она носит просто потому, что различных символов в ней всего десять (от 0 до 9). Любое число в нашей привычной системе может быть записано с их помощью. Однако, оказывается, использовать ее удобно бывает далеко не всегда. Например, при обмене информацией между цифровыми устройствами проще всего применять систему счисления, в которой есть только две цифры: «0» — нет сигнала — или «1» — есть сигнал (напряжение или что-то еще). Она называется двоичной. Однако, чтобы описать процессы внутри таких устройств с ее помощью, придется выполнять слишком длинные и трудные для понимания записи.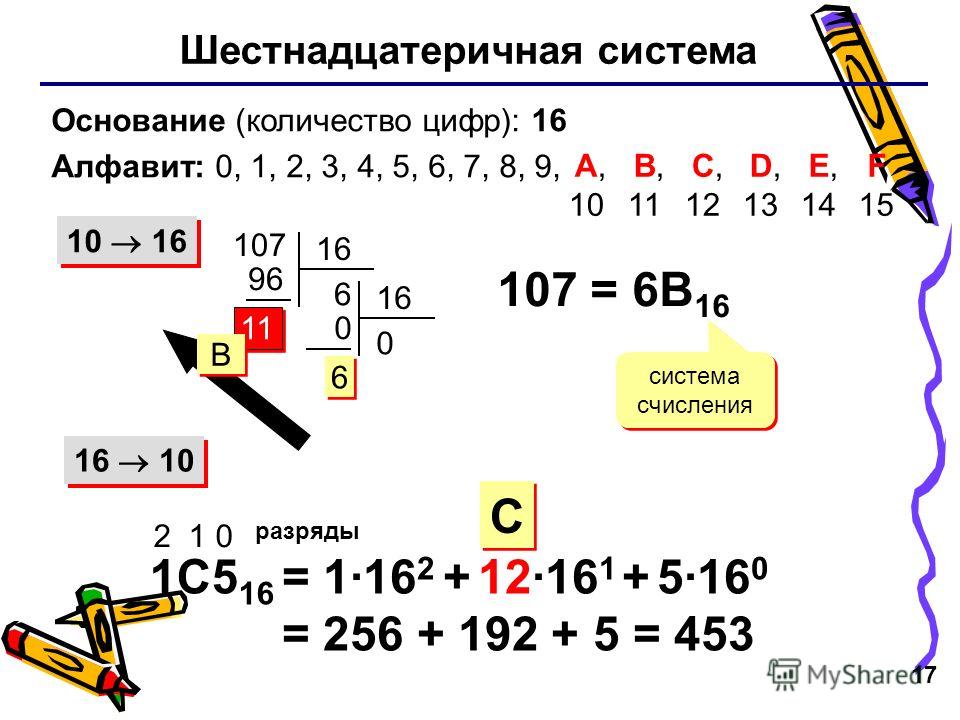
Поэтому была придумана шестнадцатиричная система счисления.
Понятие шестнадцатеричной системы
Почему же для цифровых устройств используется именно система, которая содержит шестнадцать разных символов? Как известно, информация в компьютерах передается в виде байтов, которые обычно содержат 8 бит. А единица данных — машинное слово — включает в себя 2 байта, то есть 16 бит. Таким образом, с помощью шестнадцати разных символов можно описать ту информацию, которая является мельчайшей частицей при обмене. Шестнадцатиричная система счисления включает наши привычные цифры (естественно, от 0 до 9), а также первые буковки (A, B, C, D, E, F). Именно с помощью этих символов принято записывать любую единицу информации. С ними можно производить любые арифметические действия. То есть сложение, вычитание, умножение, деление. Результатом также будет шестнадцатеричное число.
Где применяется
Шестнадцатиричная система используется для записи кодов ошибок. Они могут возникать при работе различных программных продуктов.
Например, так кодируются ошибки операционной системы. Каждое число при этом стандартное. Можно выяснить, какая именно ошибка произошла в процессе работы, расшифровав его с помощью инструкции. Также применяются такие символы при написании программ на языках низкого уровня, например ассемблере. Шестнадцатиричная система счисления любима программистами еще и потому, что ее составляющие очень легко могут быть переведены в двоичные, которые являются «родными» для всей цифровой техники. С помощью таких символов описывают также цветовые схемы. Кроме того, абсолютно все файлы в компьютере (и текстовые, и графические, и даже музыкальные или видео) представляются после трансляции в виде последовательности Просматривать исходный удобнее всего как раз в виде шестнадцатеричных символов.
Конечно, любое число можно записать в различных системах счисления. Это и десятичная, и двоичная, и шестнадцатеричная. Чтобы перевести слово из одной из них в другую, следует воспользоваться таким сервисом, как переводчик систем счисления, или сделать это самостоятельно с помощью определенного алгоритма.
Теперь предстоит совсем легкая прогулка, связанная с шестнадцатеричной системой счисления. В этом случае, надеемся, вы подозреваете и, видимо, справедливо, что у нас должно теперь быть 16 различных цифр.
Но, как мы знаем, традиционных («арабских») цифр всего десять. А требуется шестнадцать. Получается, что не хватает шести знаков.
Замечание
Таким образом, возникает чисто дизайнерская задача по теме «Знаки» — придумать недостающие символы для цифр .
Значит, в свое время специалистам необходимо было придумать какие-нибудь новые знаки. Но когда-то, в начале компьютерной эры, особого выбора в знаках не было. Программисты располагали только знаками цифр и букв. Поэтому они пошли по элементарному пути: взяли первые буквы латинского алфавита в качестве цифр, тем более что исторически это не первый случай (мы уже упоминали, что первоначально вместо цифр многие народы использовали буквы).
Замечание
Надеемся, что всем понятно, почему в этом случае нельзя использовать, например, числа «10», «11», «12» и т.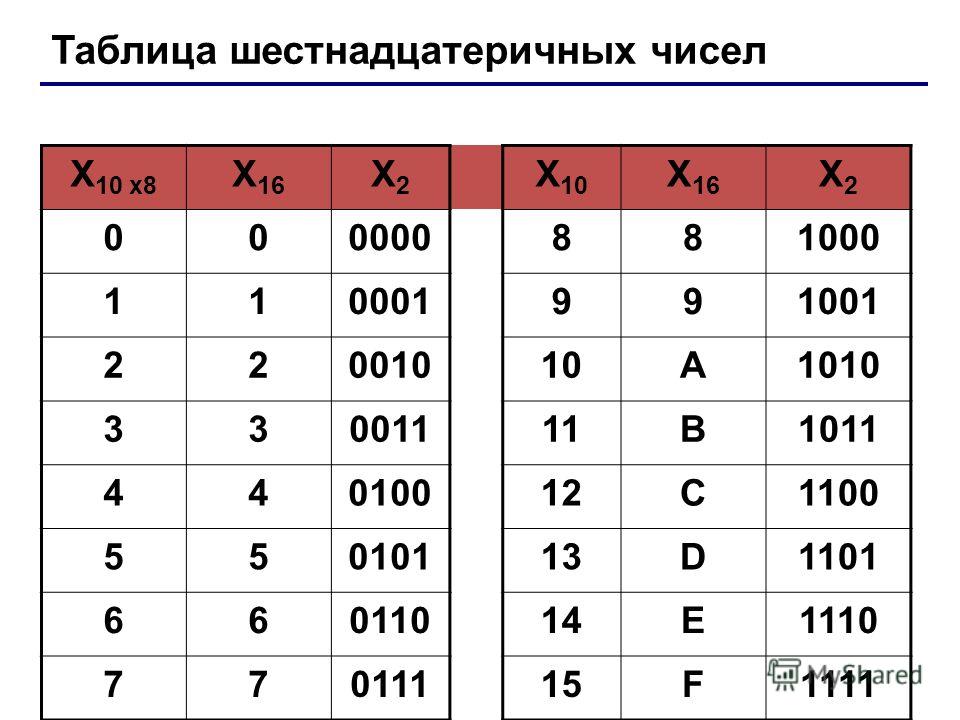
д.? Потому что, если мы говорим о шестнадцатеричной системе счисления, то должно быть шестнадцать цифр , а не чисел .
И десятичное число «10» стали обозначать латинской буквой «А» (точнее, «цифрой А»). Соответственно, дальше идут цифры «В», «С», «D», «Е» и «Р.
Поскольку мы намеревались построить шестнадцатеричную систему, то, начиная с нуля, здесь как раз и получится 16 цифр. Например, цифра «D» — это десятичное число «13», а цифра «F» — это десятичное число «15».
Когда к шестнадцатеричному числу «F» прибавляем единицу, то, поскольку эти цифры у нас кончились, в этом разряде ставим «О», а в следующий разряд переносим единицу, поэтому получается, что десятичное число «16» будет представлено в шестнадцатеричной системе счисления числом «10», т. е. получается «шестнадцатеричная десятка». Соединим десятичные и шестнадцатеричные числа в единую таблицу (табл. 4.5).
Таблица 4.5 . Соответствие десятичных и шестнадцатеричных чисел.
| Десятичное число | Шестнадцатеричное число | Десятичное число | Шестнадцатеричное число |
|---|---|---|---|
| 0-9 | 0-9 | 29 | 1D |
| 10 | А | 30 | 1Е |
| 11 | В | 31 | 1F |
| 12 | С | 32-41 | 20-29 |
| 13 | D | 42-47 | 2A-2F |
| 14 | Е | 48-255 | 30-FF |
| 15 | F | 256 | 100 |
| 16 | 10 | 512 | 200 |
| 17-25 | 11-19 | 1024 | 400 |
| 26 | 1А | 1280 | 500 |
| 27 | 1В | 4096 | 1000 |
| 28 | 1C |
Шестнадцатеричная система используется, чтобы более компактно записывать двоичную информацию.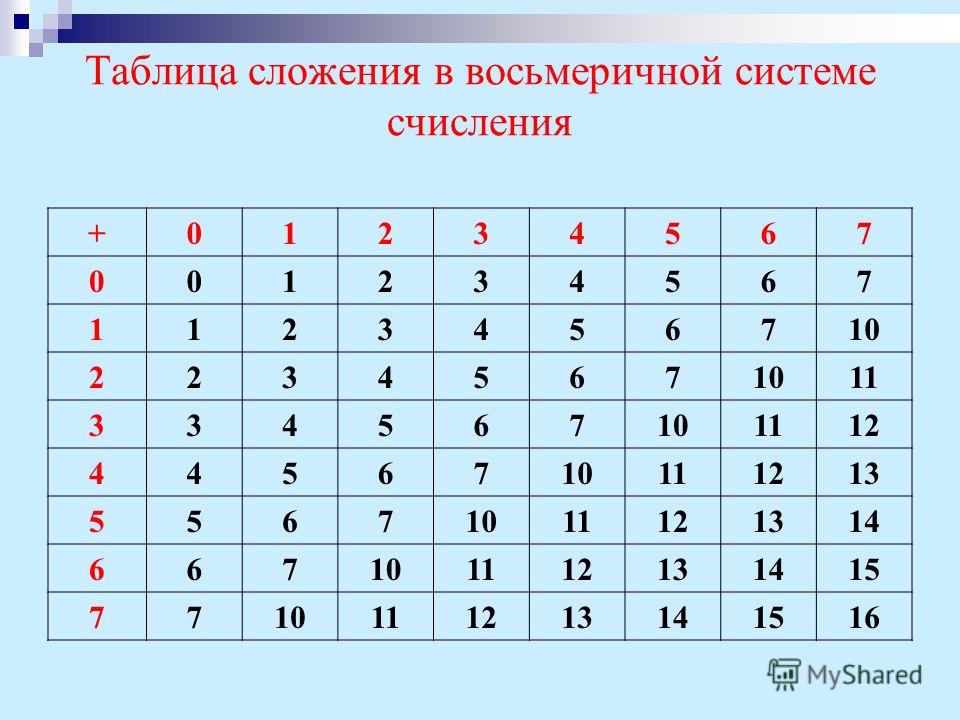
В самом деле, «шестнадцатеричная тысяча», состоящая из четырех разрядов, в двоичном виде занимает тринадцать разрядов (1000 16 = 1000000000000 2).
При обсуждении систем счисления неоднократно фигурировали «десятки», «сотни» и «тысячи», поэтому необходимо обратить внимание на так называемые «круглые» числа.
ДЕС (функция ДЕС) — Служба поддержки Майкрософт
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 for Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel для Mac 2011 Еще…Меньше
В этой статье описаны синтаксис формулы и использование десятичной формулы в Microsoft Excel.
Описание
Преобразует текстовое представление числа с указанным основанием в десятичное число.
Синтаксис
ДЕС(текст;основание)
Синтаксис функции ДЕС имеет аргументы, указанные ниже.
53, может привести к потере точности.
Основание системы счисления должно быть больше или равно 2 (двоичная система) или меньше или равно 36 (36-ричная система).
Для основания более 10 используются числовые значения 0–9 и буквы A–Z. Например, для основания 16 (шестнадцатеричного) используются цифры 0–9 и буквы A–F, а для основания 36 — цифры 0–9 и буквы A–Z.
Если хотя бы один из аргументов находится вне ограничений, decIMAL может вернуть #NUM! или значение ошибки #ЗНАЧ!.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД.
При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Формула |
Описание |
Результат |
Принцип действия |
|
‘=ДЕС(«FF»,16) |
Преобразует шестнадцатеричное значение FF (с основанием 16) в эквивалентное ему десятичное значение (с основанием 10). Результат — 255. |
=ДЕС(«FF»;16) |
«F» в позиции 15 в шестнадцатеричной системе счисления. |
|
‘=ДЕС(111;2) |
Преобразует двоичное значение 111 (с основанием 2) в эквивалентное ему десятичное значение (с основанием 10). Результат — 7. |
=ДЕС(111;2) |
«1» в позиции 1 в двоичной системе счисления. В приведенной ниже формуле показано, как число преобразуется в десятичное. |
|
Функция ДВ.В.ДЕС в ячейке C6 подтверждает этот результат. |
=ДВ.В.ДЕС(111) |
Формула |
|
|
=(1*(2^2))+(1*(2^1))+(1*(2^0)) |
|||
|
‘=ДЕС(«zap»;36) |
Преобразует значение «zap» с основанием 36 в эквивалентное десятичное значение (45745). |
0))
0))К началу страницы
Простая английская Википедия, бесплатная энциклопедия. Стандартная система счисления называется десятичной (основание 10) и использует десять символов: 0,1,2,3,4,5,6,7,8,9. Шестнадцатеричный использует десятичные числа и шесть дополнительных символов. Цифровых символов, представляющих значения больше девяти, не существует, поэтому используются буквы английского алфавита, в частности A, B, C, D, E и F. Шестнадцатеричный A = десятичный 10, а шестнадцатеричный F = десятичный 15.
Люди в основном используют десятичную систему (с основанием 10), где каждая цифра может иметь одно из десяти значений от нуля до десяти. Вероятно, это потому, что у людей десять пальцев на руках. Компьютеры обычно представляют числа в двоичном формате (с основанием 2). В двоичном формате каждая «двоичная цифра» называется битом и может иметь только одно из двух значений: единицу или ноль.
Поскольку два возможных значения одного бита представляют одну пятую часть информации, потенциально передаваемой десятью возможными значениями десятичной цифры, для двоичных представлений целых значений может потребоваться гораздо больше (двоичных) битов, чем десятичных цифр.
Например, трехзначное десятичное значение 219 требует, чтобы восемь битов были представлены в двоичном виде (11011011). Людям неудобно читать, запоминать и печатать длинные цепочки битов. Шестнадцатеричный формат позволяет более удобно представлять группы из четырех битов одной «шестнадцатеричной» цифрой, поэтому восьмибитное двоичное значение 11011011 требует только двух шестнадцатеричных цифр «DB».
Память компьютера организована в виде массива строк битов, называемых байтами. На современных компьютерах каждый байт обычно содержит восемь битов, которые удобно представить в виде двух шестнадцатеричных цифр. Инженеры и компьютерщики часто называют каждое из этих четырехбитных значений полубайтом (иногда пишется как nybble, см.
компьютерный жаргон).
Во избежание путаницы с десятичной, восьмеричной или другими системами счисления шестнадцатеричные числа иногда пишутся с «h» после или «0x» перед числом. Например, 63h и 0x63 означают 63 в шестнадцатеричном формате.
В отличие от современных компьютеров, многие ранние компьютеры имели шестибитные байты. Программисты этих систем обычно использовали альтернативную схему группировки битов, называемую восьмеричной. Каждая восьмеричная цифра эффективно представляет три бита, а шестибитный байт может быть представлен двумя восьмеричными цифрами. Три бита, каждый из которых может быть включен или выключен, могут представлять восемь чисел от 0 до 7: 000 = 0; 001 = 1; 010 = 2; 011 = 3; 100 = 4; 101 = 5; 110 = 6 и 111 = 7.
Шестнадцатеричная система счисления аналогична восьмеричной системе счисления (основание 8), поскольку каждую из них можно легко сравнить с двоичной системой счисления. Шестнадцатеричный использует четырехбитное двоичное кодирование.
Это означает, что каждая цифра в шестнадцатеричном формате равна четырем цифрам в двоичном формате. Octal использует трехбитную двоичную систему.
В десятичной системе первая цифра — это разряда единицы, следующая слева цифра — это разряда десятков, следующая — разряда сотен и т. д. В шестнадцатеричной системе каждая цифра может иметь 16 значений , а не 10. Это означает, что цифры имеют занимает место, шестнадцать занимает место, а следующий 256 занимает место. Таким образом, 1h = 1 десятичный, 10h = 16 десятичный и 100h = 256 десятичный.
Пример значений шестнадцатеричных чисел, преобразованных в двоичные, восьмеричные и десятичные.
|
Двоичный в шестнадцатеричный[изменить | изменить источник]
При изменении числа с двоичного на шестнадцатеричное используется метод группировки.
Двоичное число разделено на группы по четыре цифры, начиная справа. Затем эти группы преобразуются в шестнадцатеричные цифры, как показано в приведенной выше таблице для шестнадцатеричных чисел от 0 до F. Чтобы перейти от шестнадцатеричного, выполняется обратное. Каждая шестнадцатеричная цифра заменяется на двоичную, а группировка обычно удаляется.
| Двоичный | Группировки | Шестнадцатеричный | |||
|---|---|---|---|---|---|
| 01100101 | 0110 | 0101 | 65 | ||
| 010010110110 | 0100 | 1011 | 0110 | 4Б6 | |
| 1101011101011010 | 1101 | 0111 | 0101 | 1010 | Д75А |
Когда количество битов в двоичном числе не кратно 4, оно дополняется нулями, чтобы это было так.
Примеры:
- двоичное число 110 = 0110, то есть 6 шестнадцатеричных чисел.
- двоичный код 010010 = 00010010, что составляет 12 шестнадцатеричных чисел.
Шестнадцатеричное в десятичное[изменить | изменить источник]
Чтобы преобразовать число из шестнадцатеричного в десятичное, есть два распространенных способа.
Первый метод чаще используется при конвертации вручную:
- Используйте десятичное значение для каждой шестнадцатеричной цифры. Для 0-9 то же самое, но A = 10, B = 11, C = 12, D = 13, E = 14 и F = 15,
- Сохраняйте сумму чисел, преобразованных на каждом шаге ниже.
- Начните с младшей значащей шестнадцатеричной цифры. Это цифра справа. Это будет первый пункт в сумме.
- Возьмите вторую наименее значащую цифру. Это рядом с цифрой на правом конце. Умножьте десятичное значение цифры на 16. Добавьте это к сумме.
- Сделайте то же самое для третьей наименее значащей цифры, но умножьте ее на 16 2 (то есть 16 в квадрате или 256). Добавьте его к сумме.
- Продолжайте для каждой цифры, умножая каждый разряд на другую степень 16. (4096, 65536 и т. д.)
Добавьте его к сумме.| Местоположение | ||||||
|---|---|---|---|---|---|---|
| 6 | 5 | 4 | 3 | 2 | 1 | |
| Значение | 1048576 (16 5 ) | 65536 (16 4 ) | 4096 (16 3 ) | 256 (16 2 ) | 16(16 1 ) | 1 (16 0 ) |
Следующий метод чаще используется при преобразовании числа в программном обеспечении. Ему не нужно знать, сколько цифр в числе, прежде чем оно начнется, и оно никогда не умножается более чем на 16, но на бумаге оно выглядит длиннее.
- Используйте десятичное значение для каждой шестнадцатеричной цифры. Для 0-9 то же самое, но A = 10, B = 11, C = 12, D = 13, E = 14 и F = 15.
- Сохраняйте сумму чисел, преобразованных на каждом шаге ниже.
- Начните со старшей цифры (цифра крайняя слева). Это первый пункт в сумме.
- Если существует другая цифра, умножьте сумму на 16 и добавьте десятичное значение следующей цифры.
- Повторяйте вышеуказанный шаг, пока не закончатся цифры.
Пример: 5Fh и 3425h в десятичном виде, метод 1
|
|
Пример: 5Fh и 3425h в десятичном виде, метод 2
|
|
- Двоичная система счисления
- Восьмеричная система счисления
- Десятичная система счисления
Простая английская Википедия, бесплатная энциклопедия
Шестнадцатеричная система счисления , часто сокращаемая до «hex» , представляет собой систему счисления, состоящую из 16 символов (основание 16).
Стандартная система счисления называется десятичной (основание 10) и использует десять символов: 0,1,2,3,4,5,6,7,8,9. Шестнадцатеричный использует десятичные числа и шесть дополнительных символов. Цифровых символов, представляющих значения больше девяти, не существует, поэтому используются буквы английского алфавита, в частности A, B, C, D, E и F. Шестнадцатеричный A = десятичный 10, а шестнадцатеричный F = десятичный 15.
Люди в основном используют десятичную систему (с основанием 10), где каждая цифра может иметь одно из десяти значений от нуля до десяти. Вероятно, это потому, что у людей десять пальцев на руках. Компьютеры обычно представляют числа в двоичном формате (с основанием 2). В двоичном формате каждая «двоичная цифра» называется битом и может иметь только одно из двух значений: единицу или ноль. Поскольку два возможных значения одного бита представляют одну пятую часть информации, потенциально передаваемой десятью возможными значениями десятичной цифры, для двоичных представлений целых значений может потребоваться гораздо больше (двоичных) битов, чем десятичных цифр.
Например, трехзначное десятичное значение 219 требует, чтобы восемь битов были представлены в двоичном виде (11011011). Людям неудобно читать, запоминать и печатать длинные цепочки битов. Шестнадцатеричный формат позволяет более удобно представлять группы из четырех битов одной «шестнадцатеричной» цифрой, поэтому восьмибитное двоичное значение 11011011 требует только двух шестнадцатеричных цифр «DB».
Память компьютера организована в виде массива строк битов, называемых байтами. На современных компьютерах каждый байт обычно содержит восемь битов, которые удобно представить в виде двух шестнадцатеричных цифр. Инженеры и компьютерщики часто называют каждое из этих четырехбитных значений полубайтом (иногда пишется как nybble, см. компьютерный жаргон).
Во избежание путаницы с десятичной, восьмеричной или другими системами счисления шестнадцатеричные числа иногда пишутся с «h» после или «0x» перед числом. Например, 63h и 0x63 означают 63 в шестнадцатеричном формате.
В отличие от современных компьютеров, многие ранние компьютеры имели шестибитные байты. Программисты этих систем обычно использовали альтернативную схему группировки битов, называемую восьмеричной. Каждая восьмеричная цифра эффективно представляет три бита, а шестибитный байт может быть представлен двумя восьмеричными цифрами. Три бита, каждый из которых может быть включен или выключен, могут представлять восемь чисел от 0 до 7: 000 = 0; 001 = 1; 010 = 2; 011 = 3; 100 = 4; 101 = 5; 110 = 6 и 111 = 7.
Шестнадцатеричная система счисления аналогична восьмеричной системе счисления (основание 8), поскольку каждую из них можно легко сравнить с двоичной системой счисления. Шестнадцатеричный использует четырехбитное двоичное кодирование. Это означает, что каждая цифра в шестнадцатеричном формате равна четырем цифрам в двоичном формате. Octal использует трехбитную двоичную систему.
В десятичной системе первая цифра — это разряда единицы, следующая слева цифра — это разряда десятков, следующая — разряда сотен и т.
д. В шестнадцатеричной системе каждая цифра может иметь 16 значений , а не 10. Это означает, что цифры имеют занимает место, шестнадцать занимает место, а следующий 256 занимает место. Таким образом, 1h = 1 десятичный, 10h = 16 десятичный и 100h = 256 десятичный.
Пример значений шестнадцатеричных чисел, преобразованных в двоичные, восьмеричные и десятичные.
|
Двоичный в шестнадцатеричный[изменить | изменить источник]
При изменении числа с двоичного на шестнадцатеричное используется метод группировки. Двоичное число разделено на группы по четыре цифры, начиная справа. Затем эти группы преобразуются в шестнадцатеричные цифры, как показано в приведенной выше таблице для шестнадцатеричных чисел от 0 до F. Чтобы перейти от шестнадцатеричного, выполняется обратное. Каждая шестнадцатеричная цифра заменяется на двоичную, а группировка обычно удаляется.
| Двоичный | Группировки | Шестнадцатеричный | |||
|---|---|---|---|---|---|
| 01100101 | 0110 | 0101 | 65 | ||
| 010010110110 | 0100 | 1011 | 0110 | 4Б6 | |
| 1101011101011010 | 1101 | 0111 | 0101 | 1010 | Д75А |
Когда количество битов в двоичном числе не кратно 4, оно дополняется нулями, чтобы это было так. Примеры:
- двоичное число 110 = 0110, то есть 6 шестнадцатеричных чисел.
- двоичный код 010010 = 00010010, что составляет 12 шестнадцатеричных чисел.
Шестнадцатеричное в десятичное[изменить | изменить источник]
Чтобы преобразовать число из шестнадцатеричного в десятичное, есть два распространенных способа.
Первый метод чаще используется при конвертации вручную:
- Используйте десятичное значение для каждой шестнадцатеричной цифры. Для 0-9 то же самое, но A = 10, B = 11, C = 12, D = 13, E = 14 и F = 15,
- Сохраняйте сумму чисел, преобразованных на каждом шаге ниже.
- Начните с младшей значащей шестнадцатеричной цифры. Это цифра справа. Это будет первый пункт в сумме.
- Возьмите вторую наименее значащую цифру. Это рядом с цифрой на правом конце. Умножьте десятичное значение цифры на 16. Добавьте это к сумме.
- Сделайте то же самое для третьей наименее значащей цифры, но умножьте ее на 16 2 (то есть 16 в квадрате или 256). Добавьте его к сумме.
- Продолжайте для каждой цифры, умножая каждый разряд на другую степень 16. (4096, 65536 и т. д.)
| Местоположение | ||||||
|---|---|---|---|---|---|---|
| 6 | 5 | 4 | 3 | 2 | 1 | |
| Значение | 1048576 (16 5 ) | 65536 (16 4 ) | 4096 (16 3 ) | 256 (16 2 ) | 16(16 1 ) | 1 (16 0 ) |
Следующий метод чаще используется при преобразовании числа в программном обеспечении. Ему не нужно знать, сколько цифр в числе, прежде чем оно начнется, и оно никогда не умножается более чем на 16, но на бумаге оно выглядит длиннее.
- Используйте десятичное значение для каждой шестнадцатеричной цифры. Для 0-9 то же самое, но A = 10, B = 11, C = 12, D = 13, E = 14 и F = 15.