Безье сплайн: Сплайны Безье — Win32 apps

Аппроксимация данных сплайнами Безье — Виртуальные лаборатории

Вернуться к содержанию

  Сплайн (от англ. spline, – гибкое лекало, гибкая плазовая рейка – полоса металла, используемая для черчения кривых линий) – функция, область определения которой разбита на конечное число отрезков, на каждом из которых сплайн совпадает с некоторым алгебраическим многочленом. Максимальная степень из использованных полиномов называется степенью сплайна. Разность между степенью сплайна и получившейся гладкостью называется дефектом сплайна. Например, непрерывная ломаная есть сплайн степени 1 и дефекта 1. В современном понимании сплайны – это решения многоточечных краевых задач сеточными методами.

  Чтобы наглядно продемонстрировать приведенные понятия сплайна, степени сплайна и дефекта сплайна, рассмотрим следующую задачу: имеется совокупность экспериментальных данных, необходимо максимально точность аппроксимировать последовательность данных полиномиальной функцией n-го порядка с достоверностью не менее 95 %.

В качестве базового выбираем метод полиномиальной аппроксимации с помощью так называемого сплайна Безье. Данный метод наиболее актуален для реализации в компьютерном алгоритме.

   Сплайны (кривые) Безье или Кривые Бернштейна-Безье разработаны в 60-х годах XX века независимо друг от друга Пьером Безье из автомобилестроительной компании «Рено» и Полем де Кастельжо из компании «Ситроен», где применялись для проектирования кузовов автомобилей [1].

 Кривая Безье относится к полиномам третьего порядка и уникально определяется четырьмя точками. Обозначим эти точки p0 (начальная), p1, p2 (две управляющие) и p3 (конечная). Обозначенные точки будут иметь координаты: (

x0, y0), (x1, y1), (x2, y2) и (x3, y3). Полином третьего порядка, задающий координаты точек в двумерном пространстве, выражается параметрическими уравнениями общего вида:

где ax, bx, cx, dx, ay, by, cy и dy – константы, a параметр t меняется от 0 до 1.

  Любая кривая Безье уникально определяется этими 8 константами. Их значения зависят от координат четырех точек, задающих кривую. Цель этой задачи – вывести уравнения для расчета восьми констант по заданным координатам четырех точек.

  Первое допущение для вывода этих уравнений заключается в том, что кривая Безье начинается в точке с координатами (

x0, y0) при t = 0:

 Даже такое простое допущение позволяет продвинуться в выводе уравнений для констант. Подставив в параметрические уравнения t = 0, получим:

  Это означает, что две из констант – это просто координаты начальной точки:

   Второе допущение, касающееся кривой Безье: она заканчивается в точке с координатами (x3, y3) при t = 1:

   Подставив в параметрические уравнения (1) вместо t единицу, получаем:

что означает наличие следующей связи между константами и координатами конечной точки:

   Остальные допущения касаются первых производных параметрических уравнений, описывающих угол наклона кривой.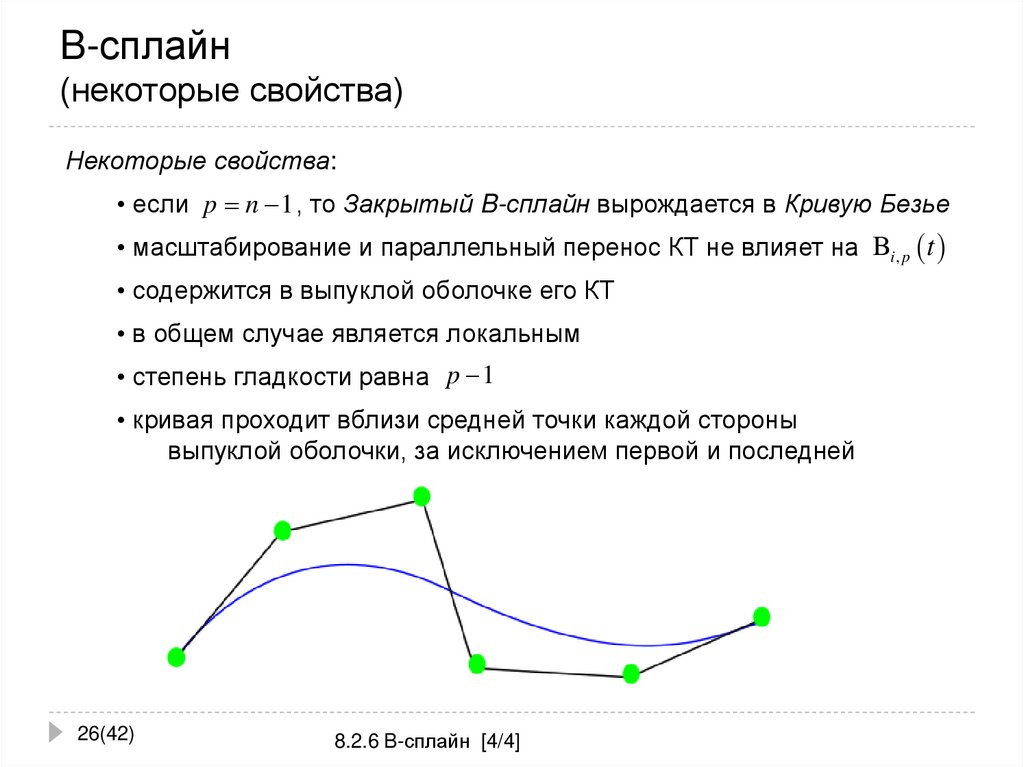

Первую производную параметрического уравнения общего вида, задающего полином третьего порядка как функцию переменной t, можно записать так:

    Нас, в частности, интересует угол наклона кривой в конечных точках. Как известно, прямая, проведенная из начальной точки через первую управляющую точку, проходит по касательной к кривой Безье и направлена в ту же сторону, что и кривая. Обычно эту прямую задают параметрическими уравнениями:

где t изменяется от 0 до 1. Но можно задать ее иначе:

где t изменяется от 0 до 1/3.

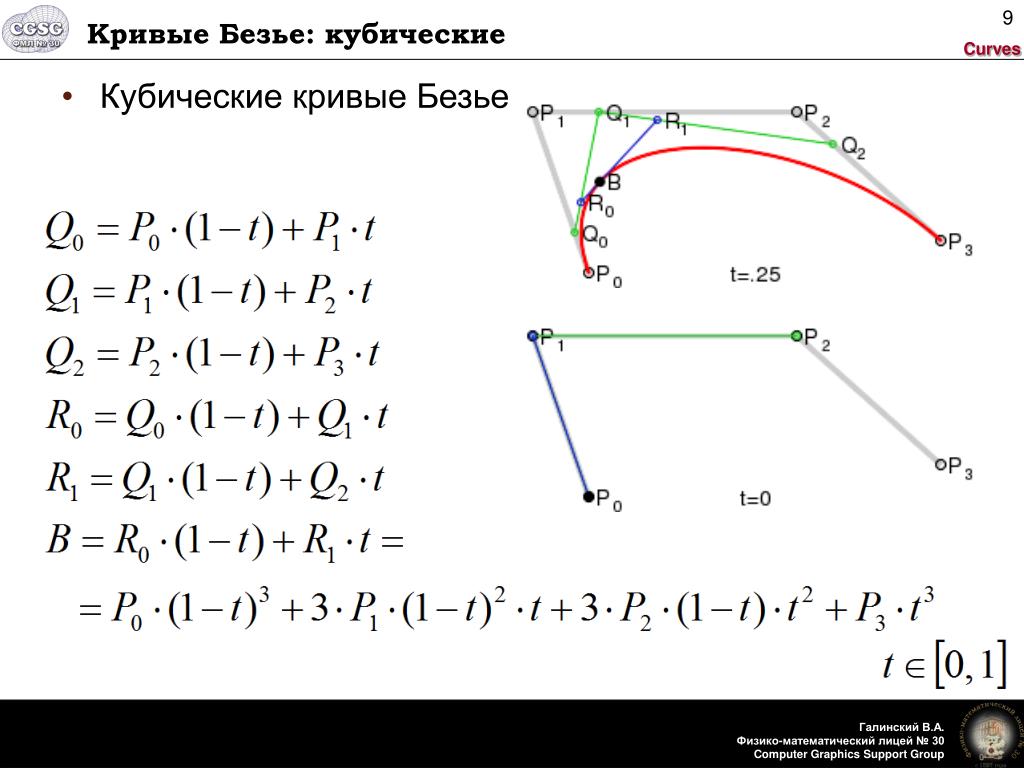   Почему именно 1/3? Дело в том, что длина той части кривой Безье, по касательной к которой проходит прямая, проведенная из точки p0 через p1, направленная в ту же сторону, что и кривая, равна 1/3 от общей длины кривой. Первые производные модифицированных параметрических уравнений можно записать так:

   Если нужно рассчитать по этим уравнениям угол наклона кривой Безье при t = 0, то:

   Подставив t = 0 в уравнение первой производной полинома третьего порядка, получим:

   Это позволяет записать равенство:

 Последнее допущение таково: прямая, проведенная из второй управляющей точки через конечную, является касательной к кривой Безье в ее конечной точке и направлена в ту же сторону, что и кривая. Иначе говоря:

    Из уравнений общего вида следует, что:

поэтому:

  Выражения (2), (4), (6) и (8) дают четыре уравнения с четырьмя неизвестными, которые можно решить относительно ax, bx, cx и dx, выразив их через x0, x1, x2 и x3.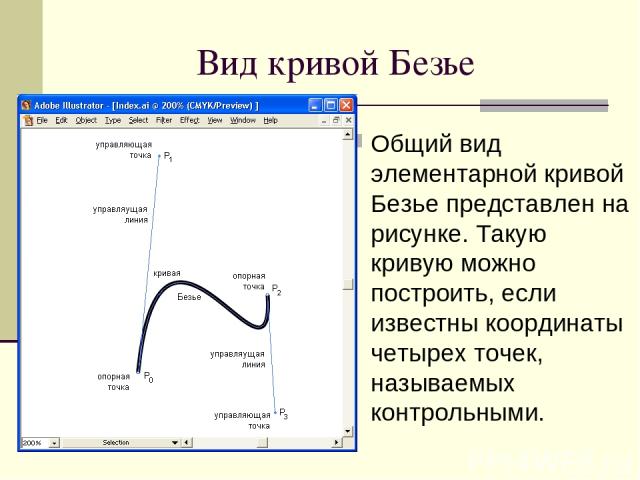 Выполнив ряд алгебраических преобразований, получаем:

  Выражения (3), (5), (7) и (9) позволяют сделать то же самое для коэффициентов y. После этого можно подставить константы обратно в параметрическое уравнение общего вида для полинома третьего порядка:

   В сущности, на этом можно было бы закончить. Но лучше раскрыть скобки и привести подобные слагаемые. В итоге получатся более элегантные параметрические уравнения, с которыми проще работать:

   Уравнения (10) и (11) позволяют построить кривую Безье в декартовых координатах.

  На первом этапе разработки компьютерного алгоритма аппроксимации экспериментальных данных мы будем задавать кривую Безье визуальным способом, перемещая ее узловые точки в декартовой системе координат графической области экрана. Пример графического представления кривой Безье представлен на рисунке 1. Точки P0 и P3 – начальная и конечная точки кривой соответственно,

P1 и P2 – управляющие точки (или точки направляющих отрезков).

Рисунок 1 – К построению кривой Безье

  В качестве средства разработки выбираем среду программирования Microsoft Visual Basic 6.0. На рисунке 2 представлена форма графического интерфейса, включающая графическое поле для построения кривых, и панель параметров, расположенную в левой части формы.

Рисунок 2 – Графический интерфейс пользователя программы математической аппроксимации кривой Безье

   С помощью указателя мыши пользователем задаются положения точек P0, P1, P2 и P3 сплайна Безье. Центр системы координат можно смещать, перемещая указатель мыши в графической области при нажатой правой кнопке мыши.

 Далее проведем кривую полиномиальной функции n-го порядка по кривой построенного сплайна Безье. Целью данной процедуры является переход от параметрических уравнений сплайна Безье к аналитической функции вида y=f(x) при аппроксимировании данных. На панели параметров в левой части экрана пользователем выбирается степень n полиномиальной функции. От данного параметра зависит, сколько опорных точек будет выделено на сплайне Безье, через которые проходит полиномиальная кривая, и, следовательно, точность приближения полиномиальной кривой к сплайну, также будет зависеть от выбранной степени полинома.

 Принцип построения полиномиальной кривой базируется на вычислении коэффициентов полинома:

где n – число точек на сплайне Безье, через которые проходит полиномиальная кривая.

  Для вычисления коэффициентов Ci необходимо задать опорные точки на сплайне Безье, координаты которых вычисляются по известным параметрическим уравнениям Безье (10 и 11), и подставить координаты опорных точек (xi, yi) в уравнение (12). В таком случае мы получаем систему линейных уравнений с n неизвестными:

где ai – коэффициенты системы уравнений, а0 – свободные члены.

   В представленном алгоритме система линейных уравнений вида (13) решается методом Крамера, подразумевающем преобразование системы уравнений в матрицы 3×3, 4×4, 5×5 и 6×6 для полиномиальной функции 2, 3, 4 и 5-го порядков, соответственно. Программно вычисления производятся с использованием двумерных массивов, в которые записываются столбцы основной и вспомогательных матриц Крамера, после чего производится вычисление их определителей, и находятся коэффициенты полиномиального уравнения.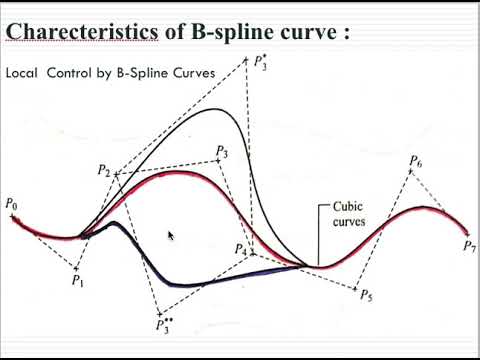

 В программе реализован алгоритм автоматической корректировки коэффициентов уравнения полинома. Сущность алгоритма заключается в цикличной проверке максимального расхождения полиномиальной кривой и кривой Безье в направлении оси Y (рисунок 3). Степень сплайна Безье es равна 3, а степень полиномиальной кривой ep выбирается пользователем (2, 3, 4 или 5). Теоретически, при ep ≥ es расхождение кривых сводится к нулю.

Рисунок 3 – К определению степени достоверности аппроксимации (до пересчета координат опорных точек)

   С заданным шагом (по оси абсцисс) вычисляются длины вертикальных отрезков, соединяющих кривую полинома и кривую Безье (закрашенная область на рисунке 3). Длины указанных отрезков записываются в одномерный массив, после чего определяется и фиксируется наибольшая длина отрезка (максимальная величина расхождения кривых Δ). С помощью генератора случайных чисел задаются новые координаты опорных точек на кривой Безье, тем самым происходит их случайное смещение по сплайну, при этом каждая итерация заканчивается пересчетом величины Δ. Если после новой итерации величина Δ уменьшилась по сравнению с предшествующей, то полиномиальная кривая перестраивается. Визуально мы наблюдаем сближение полиномиальной кривой со сплайном Безье (рисунок 4).

Рисунок 4 – К определению степени достоверности аппроксимации (максимальное приближение аппроксимирующей кривой к сплайну Безье)

  Разработанный алгоритм является эффективным инструментом для обработки эмпирических данных с использованием сплайнов. К примеру, если речь идет об интегральных кривых распределения, сплайном Безье можно задавать аппроксимирующую функцию, которая будет проходить через экспериментальные точки. При этом, конфигурация сплайна может задаваться не только ручным способом с помощью конечных и управляющих точек, а процедурно, путем проверки расходимости координат экспериментальных точек и точек, выделенных на сплайне с равной абсциссой. В конечном итоге мы получаем полиномиальную функцию n-й степени, которая будет максимально точно описывать последовательность эмпирических данных (например, как на рисунке 5).

Рисунок 5 – Схематичное представление процесса аппроксимации эмпирических данных

    В случае аппроксимации интегральных кривых распределения на выходе работы алгоритма мы получаем функцию y(x), дифференцирование которой позволит построить закономерную дифференциальную гистограмму распределения dy(x) (например, как на рисунке 6).

Рисунок 6 – Построение дифференциальной гистограммы распределения по аппроксимирующей полиномиальной кривой

Библиографические ссылки:

[1] – Кривая Безье: Материал из Википедии – свободной энциклопедии: Версия 64994710, сохраненная в 23:11 UTC 22 августа 2014 // Википедия, свободная энциклопедия. – Электрон. дан. – Сан-Франциско: Фонд Викимедиа, 2014.

Вернуться к содержанию

При копировании материалов ссылка на сайт www.sunspire.ru обязательна. Также, вы можете использовать библиографическую ссылку на учебное пособие:

 

«Белов, В.В. Компьютерная реализация решения научно-технических и образовательных задач: учебное пособие / В.В. Белов, И.В. Образцов, В.К. Иванов, Е.Н. Коноплев // Тверь: ТвГТУ, 2015. 108 с.»

Глава 13. Кривые Безье и другие сплайны

Глава 13. Кривые Безье и другие сплайны

Что такое сплайн? Даже изданные сравнительно недавно словари английского языка определяют значение слова «сплайн» (spline) как «гибкая форма для рисования кривых, сделанная из дерева, твердой резины или металла ¹» (если одним словом — лекало). Это определение вызывает в воображении образ инженера прошлых лет, который, согнувшись над чертежом, орудует чудным гибким инструментом в попытке соединить кривой разбросанные по бумаге точки.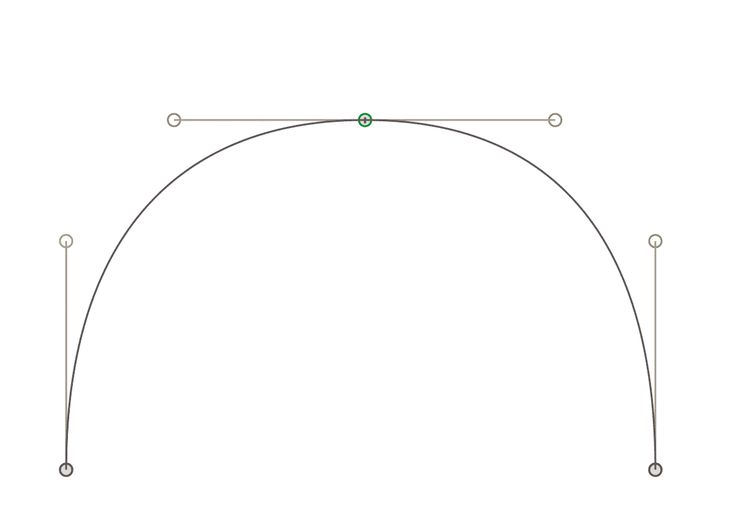 В современных словарях можно найти более точное определение слова сплайн: «заданная математической функцией плавная кривая, соединяющая ряд точек… см. также кривая Безье ²».

Пьер Этьен Безье родился в Париже в 1910 г. в семье инженера. В 1930 г. он завершил высшее образование, получив степень в машиностроении, а на следующий год дополнил ее степенью в электротехнике. В 1933 г. он был принят на работу в автомобильную компанию Рено (Франция), в которой и проработал до 1975 г. В 50-е Безье отвечал за внедрение одних из первых сверлильных и фрезерных станков с ЧПУ (т.е. с числовым программным управлением; в те дни этот термин встречался еще редко).

С 1960 г. Безье в основном занимался программой UNISURF — одной из первых систем автоматизированного проектирования и производства, использовавшейся в Рено для интерактивного конструирования автомобильных деталей. Для UNISURF нужно было разработать пригодную к промышленному внедрению методику математического определения сложных кривых, которая позволила бы конструкторам манипулировать кривыми, ничего не зная о задающих их функциях. В результате этой самой работы и появились на свет кривые, которые теперь носят имя Безье. Пьер Безье скончался в 1999 г ³.

Кривая Безье стала очень важным элементом компьютерной графики и занимает в табели о рангах третье место после прямой и эллиптической дуги. В языке PostScript все кривые визуализируются при помощи сплайнов Безье. Даже эллиптические дуги, и те аппроксимируют в PostScript кривыми Безье. Кривые Безье также используются для определения контуров шрифтов PostScript (в шрифтах TrueType применяется более простой и быстродействующий сплайн).

---

¹ Определение взято из словаря «American Heritage Dictionary of the English Language», 4-е издание (Boston: Houghton Mifflin, 2000).

² «Microsoft Computer Dictionary», 4-е издание (Redmond, WA: Microsoft Press, 1999).

³ Большая часть биографических сведений о П. Безье взята из его статьи «Style. Mathematics and NO», опубликованной в 22 томе журнала Computer-Aided Design, вышедшего в ноябре 1990 г. Две книги Безье были переведены на английский язык: «Numerical Control: Mathematics and Application» (London: John Wiley&Sons, 1972) и «The Mathematical Basis of the UNISURF CAD System» (London: Butter-worths, 1986). Также можно прочитать написанную им главу «How a Simple System Was Born» в книге Джеральда Фарма «Curves and Surfaces for Computer-Aided Geometric Design — A Practical Guide», 4-е издание (Sari Diego: Academic Press, 1997).

Сайт управляется системой uCoz

Сплайны Безье и другие некруглые кривые в SketchUp

Дизайн. Нажмите. Сборка

Дэйв Ричардс демонстрирует рисование кривых с помощью инструментов Classic Bezier Spline, Uniform B-Spline и Catmull Spline.

Дэвид Ричардс 18 декабря 2019 г.

В посте, который я сделал несколько недель назад, я продемонстрировал, как сделать язычки барашка на концах фасок с помощью этих тисков Moxon. Я использовал инструмент Classic Bezier Spline из расширения Bezier Spline от Fredo6. Один из наших читателей попросил дополнительную информацию о рисовании кривых с помощью этого инструмента. Безье и другие некруглые кривые используются во многих местах в деревообработке, поэтому я думаю, что этот набор инструментов очень полезен. Я довольно часто использую кривые Безье в своих моделях.

Изгибы сторон и бортика этого стола были созданы в виде сплайнов Безье…

…так же, как и профиль ручки в стиле шейкера…

…и многие кривые на этом токарном станке.

Я также использую эти кривые для моделирования выемки на сиденьях Windsor и других стульев, S-образных изгибов на ножках и профиле пьедестала для швейных стендов Shaker и многих других предметов мебели.

Для их моделирования можно использовать встроенные инструменты дуги в SketchUp, но для этого потребуется много манипуляций с инструментами «Перемещение» и «Масштабирование», а также гораздо больше времени.

В этом видео я немного покажу, как рисовать кривые с помощью инструментов Classic Bezier Spline, Uniform B-Spline и Catmull Spline. Одна ключевая вещь, которую следует иметь в виду при использовании этих инструментов, заключается в том, что кривые, создаваемые инструментами Classic Bezier и Uniform B-Spline, не проходят через контрольные точки. Если вы знаете координаты точек вдоль вашей кривой, сплайн Кэтмулла будет подходящим инструментом.

С Bezier и B-Spline не мучайтесь, получая кривую с первого раза. Особенно, если он более сложный. Получите кривую грубо, а затем уточните ее по мере необходимости. Вы, вероятно, обнаружите, что вам нужно отредактировать положение контрольных точек, чтобы настроить кривую в соответствии с требованиями. Вам также может понадобиться добавить контрольные точки, чтобы помочь вам уточнить кривую.

Попробуйте немного поэкспериментировать.

– Дэйв

 

Получайте советы по деревообработке, советы экспертов и специальные предложения на свой почтовый ящик

Зарегистрироваться

×

Получите все!

НЕОГРАНИЧЕННОЕ Членство — это как пройти мастер-класс по деревообработке за меньшие деньги чем 10 долларов в месяц.

Просмотреть все

Рекомендуемая мастерская

Он построил десятки круглых стендов Shaker за четыре десятилетия, так что нет никого более квалифицированного, чем Кристиан Бексвоорт, чтобы продемонстрировать создание этой классики. В этой серии видео из семи частей…

Избранные проекты и планы

Буфет Криса Гочнура сочетает в себе практичность, прочность и красоту в современном корпусе

Похожие статьи

Основные моменты

• Развивайте свои навыки

  при подписке на нашу электронную почту

  Плюс советы, рекомендации и специальные предложения от Fine Деревообработка .

• Наш подкаст, выходящий раз в две недели, позволяет редакторам, авторам и специальным гостям отвечать на ваши вопросы по деревообработке и связаться с онлайн-сообществом по деревообработке.

• Мы создали эти специальные коллекции контента, организованные для того, чтобы дать вам возможность глубоко погрузиться в ряд тем, которые имеют значение.

• Присоединяйтесь к нашим доверенным экспертам для углубленного онлайн-обучения.

Посмотреть все

Посмотреть Подробнее

Гладкий сплайн Безье через заданные точки

Опубликовано 17 июня 2012 г.
Предыдущая статья :: Следующая статья

В этой статье мы покажем вам, как создать гладкий сплайн через набор заданных точек. В статье также содержится интерактивная демонстрация SVG, которая позволяет вам попробовать это в режиме реального времени. Эта демонстрация может не работать, если вы читаете этот пост по электронной почте или на мобильном устройстве. В этом случае, пожалуйста, посетите статью из браузера вашего компьютера.

Введение

В научных вычислениях нам часто нужно построить линию, которая проходит через набор заданных контролируемых точек, или узлов . Типичным примером является создание сетки. Даже если мы используем бессеточный метод, нам нужно каким-то образом предписать внешнюю протяженность задачи. Обычно это достигается путем указания граничных сплайнов (аналогом в 3D являются патчи).

Сплайны Безье

Сплайн представляет собой набор многоугольных сегментов. Сегменты могут быть линейными, квадратичными, кубическими или полиномами даже более высокого порядка. В этой статье мы выводим уравнения, необходимые для построения гладкой кривой через набор контрольных точек с использованием кубического многочлена Безье. В Википедии есть очень хорошая статья о кривых Безье, в которой есть анимация, показывающая, как работают эти полиномы. 93\mathbf{P}_3$$

В этом определении точки 0 и 3 соответствуют конечным точкам (узлам). Две другие точки являются контрольными точками, определяющими форму кривой. Кривая, вообще говоря, не проходит через эти точки. Следуя шагам, описанным на codeproject.com, мы хотим, чтобы первая и вторая производные были непрерывными на границе сплайна. Это даст нам два уравнения (по одному для каждой производной) на каждом интерфейсе сплайна, которые мы используем для нахождения контрольных точек. 92\mathbf{P}_3$$
На левой границе «i-го» отрезка можно написать
$$ \mathbf{B}’_i(0)=\mathbf{B}’_{i-1 }(1)$$
или
$$ -3\mathbf{P}_{0,i}+3\mathbf{P}_{1,i}=-3\mathbf{P}_{2,i -1}+3\mathbf{P}_{3,i-1}$$
Теперь, поскольку кривая непрерывна, \(\mathbf{P}_{0,i}=\mathbf{P}_{ 3,i-1}=\mathbf{K}_i\), «i-я» узловая точка, и мы можем упростить это выражение как (1)
$$ 2\mathbf{K}_i=\mathbf{P }_{1,i}+\mathbf{P}_{2,i-1} \quad\quad\quad(1)$$

Мы также хотим, чтобы вторая производная была непрерывной. Вторая производная равна
$$ \mathbf{B}”(t)= 6(1-t)\mathbf{P}_0+3(-4+6t)\mathbf{P}_1+3(2-6t)\mathbf{P }_2+6t\mathbf{P}_3$$
на границе имеем
$$ 6 \mathbf{P}_{0,i}-12\mathbf{P}_{1,i}+6\mathbf {P}_{2,i}=6\mathbf{P}_{1,i-1}-12\mathbf{P}_{2,i-1}+6\mathbf{P}_{3, i-1}$$
Упрощая и учитывая общую точку узла, получаем уравнение (2),
$$ -2\mathbf{P}_{1,i}+\mathbf{P}_{2, i}=\mathbf{P}_{1,i-1}-2\mathbf{P}_{2,i-1} \quad\quad\quad(2)$$

Уравнения (1) и (2) определяются только на внутренних узлах – местах, где сходятся два сегмента. Математически это означает, что у нас есть \(2(n-1)\) уравнений для \(2n\) неизвестных. Для замыкания системы зададим еще два естественных граничных условия: \(\mathbf{B}»_0(0)=0\) и \(\mathbf{B}»_{n-1}(1)= 0\). Другими словами, сплайн становится линейным в конечных точках. Эти два оставшихся уравнения (3) и (4) равны
$$ \mathbf{K}_0-2\mathbf{P}_{1,0}+\mathbf{P}_{2,0}=0 \quad\quad\quad(3)$$
и
$$ \mathbf{P}_{1,n-1}-2\mathbf{P}_{2,n-1}+\mathbf{K}_n=0 \quad\quad\quad(4)$$

Мы можем упростить эту систему, подставив (1) в (2), чтобы получить
$$ \mathbf{P}_{1,i-1}+4\mathbf{P}_{1,i}+\ mathbf{P}_{1,i+1}=4\mathbf{K}_i+2\mathbf{K}_{i+1} \quad\quad i\in[1,n-2]$$.
На граничных узлах имеем из (3) и (4)
$$ 2\mathbf{P}_{1,0}+\mathbf{P}_{1,1}=\mathbf{K}_0+ 2\mathbf{K}_1$$
и
$$ 2\mathbf{P}_{1,n-2}+7\mathbf{P}_{1,n-1} = 8\mathbf{K}_{n-1}+\mathbf {K}_n$$

Это трехдиагональная система для \(P_1\), которую мы можем решить с помощью алгоритма Томаса. Определив \(\mathbf{P}_1\), мы получим \( \mathbf{P}_2\) из уравнений (1) и (4),
$$ \mathbf{P}_{2,i} =2\mathbf{K}_{i}-\mathbf{P}_{1,i} \quad\quad i\in [0,n-2]$$
и
$$ \mathbf{P}_ {2,n-1}= (1/2)(\mathbf{K}_n+\mathbf{P}_{1,n-1})$$

Интерактивная демонстрация

Ниже вы найдете интерактивную демонстрацию, которая реализует этот алгоритм. Если все загрузилось нормально, вы должны увидеть четыре желтых круга, соединенных плавной линией, состоящей из трех сегментов разного цвета. Вы можете перемещать любой из кругов с помощью мыши. Если вы не видите круги, не можете их двигать или сплайн неровный, сначала попробуйте перезагрузить страницу. Если это все еще не удается, попробуйте другой браузер. У меня демонстрация работала с Chrome, Firefox и Internet Explorer 9.под Windows. Я не мог заставить его работать на своем телефоне Android (графика не отображалась), и мой друг сообщил, что он не работает и на iPad. Если вы знаете, как заставить демо-версию работать на этих мобильных устройствах, сообщите мне об этом, оставив комментарий ниже.

В этой демонстрации используются SVG и Javascript (Вы можете найти массу примеров SVG на веб-сайте профессора Дейли. Еще одним хорошим ресурсом является учебник по SVG на «Веб-сайте Питера»). SVG (масштабируемая векторная графика) — это один из двух способов получить интерактивную графику на своем веб-сайте (второй — элемент HTML5). Из этих двух SVG кажется более универсальным. Существуют даже бесплатные программы векторной графики, такие как Inkscape, которые сохраняют изображения в формате SVG. Три линии, соединяющие круги, определены с использованием синтаксиса кубического пути Безье SVG. Всякий раз, когда вы перетаскиваете круг, код повторно вычисляет контрольные точки и обновляет определение пути. Затем ваш браузер автоматически перекрашивает представление. Довольно прикольно! Полный код вы найдете ниже.

Исходный код

Вы можете скачать исходный код здесь: circles. svg. Изображение встраивается с помощью тега . Вы также можете увидеть только Javascript: bezier-spline.js (этот код встроен в SVG).

Кстати, мне потребовалось слишком много времени, чтобы запустить код. Javascript отличается от Java тем, что, помимо прочего, не определяет типы переменных. Первоначально код использовал

 для (i=0;i<4;i++)
{
    x[i]=V[i].getAttributeNS(null,"cx")
    y[i]=V[i].getAttributeNS(null,"cy")
} 

, чтобы получить координаты четырех контрольных точек. Затем они были переданы другой функции, которая выполняла фактические вычисления. Проблема заключалась в том, что это на самом деле привело к тому, что x[i] был строкой, а не целым числом. Javascript не жаловался на это. Вместо этого, при необходимости, он автоматически преобразовывал строку в тип int. Однако оператор «плюс» привел к конкатенации строк вместо добавления двух чисел. Например, для x[i]="50" x[i]+30 дало 5030 вместо ожидаемого значения 80. В течение долгого времени я получал действительно странные результаты и не мог понять, почему, несмотря на перепроверку моей математики.