Геометрическая интерпретация комплексного числа
Содержание:
- Модуль комплексного числа
- Аргумент комплексного числа
Комплексные числа изображаются на так называемой комплексной плоскости. Ось, соответствующая в прямоугольной декартовой системе координат оси абсцисс, называется действительной осью, а оси ординат — мнимой осью (рис. 1).
Комплексному числу $z=a+b i$ будет однозначно соответствовать на комплексной плоскости точка $(a ; b)$: $z=a+b i \leftrightarrow(a ; b)$ (рис. 2). То есть на действительной оси откладывается действительная часть комплексного числа, а на мнимой — мнимая.
Например. На рисунке 3 на комплексной плоскости изображены числа $z_{1}=2+3 i$, $z_{2}=i$ и $z_{3}=-2$ .
Модуль комплексного числа
Комплексное число также можно изображать радиус-вектором
$\overline{O M}$ (рис. 2). Длина радиус-вектора, изображающего
комплексное число $z=a+b i$, называется модулем
этого комплексного числа.
У комплексно сопряженных чисел аргументы отличаются знаком (рис. 3).
Читать дальше: комплексно сопряженные числа.
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | sin(45 град. ) | |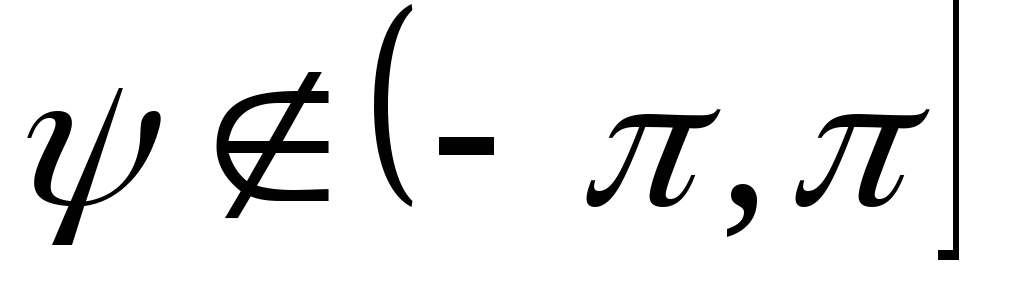
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. | |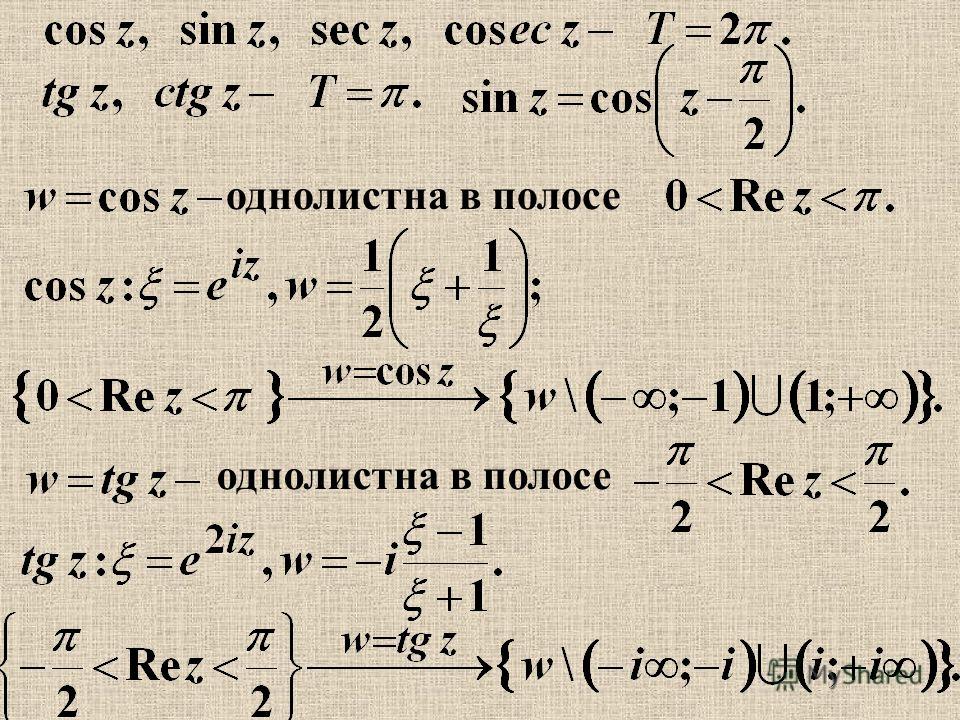
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Аргумент комплексного числа — определение, формула, примеры, часто задаваемые вопросы
Аргумент комплексного числа — это мера угла, образованного линией, представляющей комплексное число, с положительной осью x плоскости аргана.
Аргументом комплексного числа Z = a + ib является угол θ, который является обратной функцией тангенса мнимой части, деленной на действительную часть комплексного числа.Аргумент комплексного числа = θ = Tan -1 (b/a)
Аргумент комплексного числа определяет соотношение между действительной и мнимой частями комплексного числа. Давайте узнаем больше о принципе и общем аргументе комплексного числа, применениях аргумента комплексного числа, с помощью примеров, часто задаваемых вопросов.
| 1. | Что такое аргумент комплексного числа? |
| 2. | Принцип против общего аргумента комплексного числа |
| 3. | Модуль и аргумент комплексного числа |
| 4. | Применение аргумента комплексного числа |
| 5. | Примеры аргумента комплексного числа |
| 6. | Практические вопросы |
7.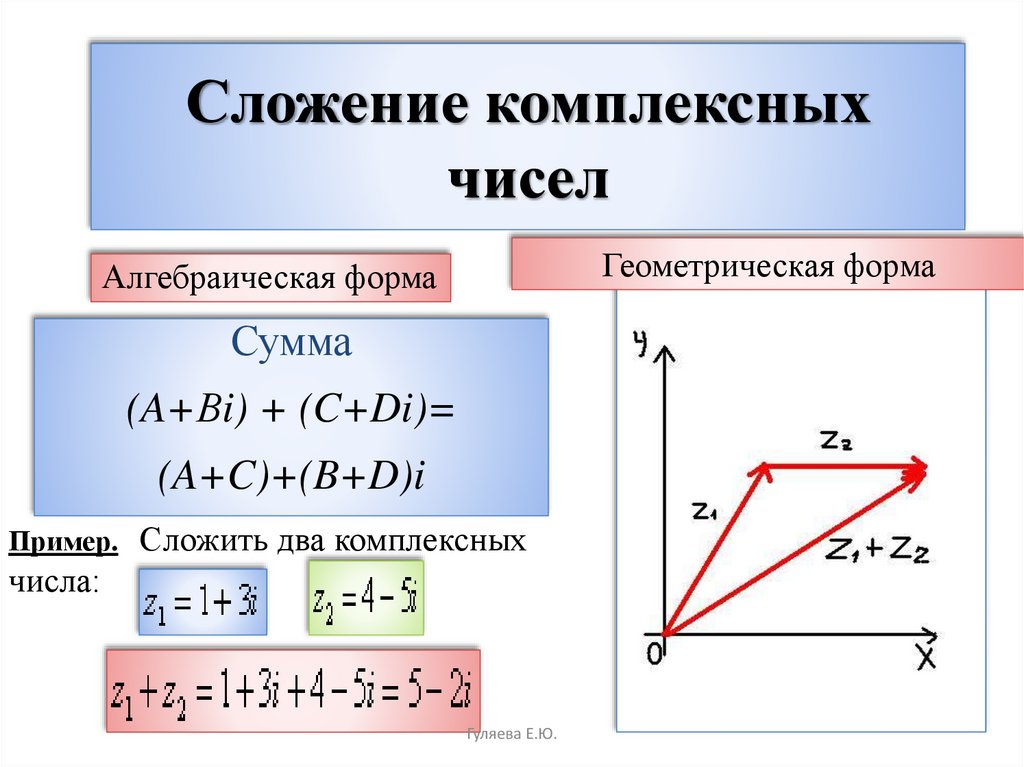 | Часто задаваемые вопросы по аргументу комплексного числа |
Что такое аргумент комплексного числа?
Аргумент комплексного числа — это угол, образованный линейным представлением комплексного числа с положительной осью x плоскости аргана. Любое комплексное число может быть представлено на плоскости арганда, где действительная часть отмечена по оси x, а мнимая часть — по оси y. А комплексное число Z = a + ib может быть представлено в виде точки A(a, b) на аргановой плоскости, а угол, который образует прямая OA с положительным x-ai, является аргументом комплексного числа.
Для комплексного числа Z = a + ib аргументом комплексного числа является угловая мера, равная обратной тригонометрической функции тангенса мнимой части, деленной на действительную часть комплексного числа.
Аргумент комплексного числа = θ = Tan -1 (b/a)
Принцип против общего аргумента комплексного числа
Аргумент комплексного числа измеряется как угол, образованный линейным представлением этого комплексного числа с положительной осью x.
Этот угол, основанный на его значениях, имеет основное значение и общее значение, которое приводит к главному аргументу и общему аргументу комплексного числа. Тригонометрическое значение Tan используется для нахождения аргумента комплексного числа, и, следовательно, оно основано на общем решении функции тригонометрического тангенса.
Основной аргумент комплексного числа = -π
< θ < πОсновной аргумент комплексного числа имеет значения от -π < θ <π. Кроме того, это 0 < θ < π, если брать в первых двух квадрантах, где угол измеряется относительно положительной оси x в направлении против часовой стрелки. И это -π < θ < 0 в третьем и четвертом квадранте относительно положительной оси x, где угол измеряется по часовой стрелке. Далее, общий аргумент комплексного числа равен 2nπ + θ.
Общий аргумент комплексного числа = 2nπ + θ
Таким образом, аргумент комплексного числа основан на тригонометрической функции и, следовательно, имеет принцип и общий аргумент.
Модуль и аргумент комплексного числа
Аргумент комплексного числа и модуль комплексного числа являются двумя важными характеристиками, которые полностью определяют комплексное число в плоскости арганда.
Модуль комплексного числа — это расстояние комплексного числа от начала координат, а аргумент комплексного числа — это угол, образуемый комплексным числом с положительной осью плоскости аргана. 92}\). Это расстояние между началом координат (0, 0) и точкой (a, b) на комплексной плоскости. Кроме того, мы также можем определить модуль комплексного числа как квадратный корень из суммы квадратов действительной и мнимой частей комплексного числа.
Аргумент комплексного числа: Аргумент комплексного числа Z = a + ib представлен как arg Z. Комплексное число Z = a + ib представлено в виде точки A(a, b) на аргановой плоскости с начало координат O(a, 0). А угол, который образует прямая ОА с положительной осью абсцисс против часовой стрелки, называется аргументом комплексного числа. Аргумент комплексного числа равен θ = Tan -1 (б/д).
Применение аргумента комплексного числа
Аргумент комплексного числа имеет множество применений при преобразовании комплексного числа в полярную форму, а также при нахождении связи между действительной и мнимой частями комплексного числа.
Значением аргумента комплексного числа является угол θ, который помогает определить, больше ли действительная часть или больше мнимая часть. Для θ = 45° действительная часть равна мнимой, для 0° < θ < 45° действительная часть больше мнимой, а для 45° < θ < 90º мнимая часть больше действительной части.
Полярная форма комплексного числа: Полярная форма комплексного числа: P = r(Cosθ + iSinθ). Здесь θ — аргумент комплексного числа, а r — аргумент комплексного числа. Полярная форма — еще одна важная форма представления комплексного числа в плоскости арганда. Полярная форма комплексного числа, представленного в декартовой форме, равна (rCosθ, rSinθ).
☛ Похожие темы
- Арган Плоскость
- Комплексный номер
- Комплексное сопряжение
- Величина и аргумент
- Модуль комплексного числа
Часто задаваемые вопросы по аргументу комплексного числа
Что такое аргумент комплексного числа?
Аргумент комплексного числа — это угол, образованный линейным представлением комплексного числа с положительной осью x плоскости аргана.
Любое комплексное число может быть представлено на плоскости арганда, где действительная часть отмечена по оси x, а мнимая часть — по оси y. Для комплексного числа Z = a + ib аргумент комплексного числа равен θ = Tan -1 (b/a)
Как найти аргумент комплексного числа?
Аргумент комплексного числа представляет собой угол, образуемый представлением комплексного числа с осью x плоскости аргана. Аргумент θ комплексного числа Z = a + ib равен обратному тангенсу тангенса мнимой части (b), деленному на действительную часть (a) комплексного числа. Аргумент комплексного числа равен θ = Tan -1 (b/a).
Какая польза от аргумента комплексного числа?
Аргумент комплексного числа полезен для нахождения пропорционального соотношения между действительной и мнимой частями комплексного числа. Аргумент комплексного числа также полезен при записи комплексного числа в полярной форме. Комплексное число Z = a + ib записывается в полярной форме как Z = r(Cosθ + iSinθ), где r — модуль комплексного числа, θ — аргумент комплексного числа.
В чем разница между общим и основным аргументом комплексного числа?
Основным аргументом комплексного числа является первое значение комплексного числа, находящееся между 0 и 2π. ( 0 < θ < 2π). И более высокие значения θ комплексного числа называются общим аргументом комплексного числа и θ = 2nπ + θ
Каковы свойства аргумента комплексного числа?
Два важных свойства аргумента комплексного числа заключаются в следующем.
- аргумент(Z 1 .Z 2 ) = аргумент(Z 1 ) + аргумент(Z 2 )
- аргумент(Z 1 /Z 2 ) = аргумент(Z 1 ) — аргумент(Z 2 )
Как аргумент комплексного числа связан с модулем комплексного числа?
Аргумент комплексного числа и модуль комплексного числа — это две различные характеристики комплексного числа. Модуль комплексного числа дает расстояние представления комплексного числа от начала координат, а аргумент комплексного числа дает наклон комплексного числа в аргандовой плоскости.
2}\), а аргумент комплексного числа равен θ = Tan 92}$$
, когда $z = x + iy$ — комплексное число.
Как вычислить аргумент $z$?
Спасибо.
- линейная алгебра
- тригонометрия
- комплексные числа
$\endgroup$
2
$\begingroup$
Вам следует знать, что любое комплексное число можно представить в виде точки на декартовой ($x$-$y$) плоскости. Другими словами, комплексное число $z=a+b\text i$ связано с некоторой точкой (скажем, $A$), имеющей координаты $(a,b)$ на декартовой плоскости. Возможно, вы слышали это как Диаграмма Аргана .
Пусть $\tan \theta$ будет отношением направлений вектора $\vec{OA}$ (Предположим, что линия, соединяющая начало координат , $O$ и точку $A$, является вектором)
Тогда $$\tan\theta =\frac ba \имплицитно \theta= \arctan \Большой (\фракция ба\Большой )$$
Однако мы пока не можем утверждать, что $\theta$ является $\operatorname {Arg}(z)$.
Есть небольшая деталь, которую нам нужно иметь в виду (спасибо пользователю за указание на это!). Нам нужно следить за квадрантом, в котором лежит наше комплексное число, и работать соответственно.
Пример Допустим, есть 2 комплексных числа $z=a+b\text i$ и $w=-a-b\text i$. Тогда $$\operatorname{Arg}(w)=\arctan\Big( \frac {-b}{-a} \Big )= \arctan\Big( \frac {b}{a} \Big )= \ имя_оператора{Arg}(z)$$
что просто нелепо. Это предполагает, что $w$, лежащий в третьем квадранте на диаграмме Аргана, имеет тот же аргумент, что и комплексное число ($z$), которое находится в первом квадранте. Чтобы исправить эту проблему, нам придется выдвинуть несколько простых условий. Как мы только что видели, один из них может выглядеть примерно так: $\text{ if } a,b<0 \text{ then } \operatorname{Arg}(z)=\theta -\pi$
Вот список условий для вычисления аргумента (это уже упоминалось в одном из ответов выше, и я просто публикую его здесь). Как только вы интуитивно почувствуете это, это должно прийти к вам естественным образом.
$\varphi = \arg(z) =
\begin{случаи}
\тета & \mbox{если} х > 0 \\
\theta + \pi & \mbox{если } x < 0 \mbox{ и } y \ge 0\\
\theta - \pi & \mbox{если } x < 0 \mbox{ и } y < 0\\
\frac{\pi}{2} & \mbox{если } x = 0 \mbox{ и } y > 0\\
-\frac{\pi}{2} & \mbox{если } x = 0 \mbox{ и } y < 0\\
\mbox{неопределенный} & \mbox{если } x = 0 \mbox{ и } y = 0.
\end{case}$
В качестве альтернативы вы можете использовать тот факт, что $|z| \sin \theta= b$ (или $|z| \cos \theta= a$), а затем найти $\theta$. Однако вам, возможно, все же придется внести последние поправки (как мы делали ранее), чтобы получить правильный ответ. Так что это не короче из двух методов.
$\endgroup$
6
$\begingroup$
Обратите внимание, что «ответ» $arctan(y/x)$ просто неверен. Чтобы увидеть это, посмотрите на пример $-1-i$: $\arctan(-1/-1) = 45°$, но правильно будет $225°$.