Аппроксимация данных: Линейная аппроксимация

Аппроксимация функции с помощью линии тренда

Аппроксимация, или приближение — научный метод, состоящий в замене одних объектов другими, в том или ином смысле близкими к исходным, но более простыми. В задачах, рассматриваемых в данном разделе и в следующем, используются исходные данные, полученные в результате табуляции заданной функции. Следует помнить, что в реальных задачах исходными данными являются результаты наблюдений (проведение опытов, научных экспериментов, наблюдение реальных событий и т.п.), которые подвержены ошибкам измерения и другим случайным факторам. Задача исследователя — подобрать по исходным точкам (которые на первый взгляд расположены хаотично) функциональную зависимость (если это вообще возможно), которая наилучшим образом описывает распределение исходных данных и в некоторых случаях попытаться сделать прогноз дальнейшего развития (например исследование временно́го ряда изменения котировок акций).

Задание. Построить таблицу значений функции F(x)=ax²+bx+c для 11 значений аргумента x в диапазоне –1 ≤ x ≤ +1. Построить график этой функции, затем выполнить аппроксимацию линиями тренда двух типов. С помощью линий тренда построить прогноз на два периода вперёд.

Как и в предыдущих задачах вводим исходные данные: начальное значение аргумента функции Xn, конечное значение аргумента функции Xk, количество точек разбиения функции (количество строк таблицы) N, формулу для шага аргумента функции dX, коэффициенты a, b, c, затем создаем основную таблицу и строим диаграмму (все эти действия были подробно описаны в разделе Табулирование функции одной переменной):

Как видно, в этой работе в формулах используются имена для ячеек, содержащих исходные значения (работа с именами была подробно описана в разделе Присваивание имен ячейкам).

Линии тренда на диаграмме

Линии тренда позволяют графически отображать тенденции изменения данных и прогнозировать их дальнейшие изменения. Подобный анализ называется также регрессионным анализом. Используя регрессионный анализ, можно продлить линию тренда в диаграмме за пределы реальных данных для предсказания будущих значений.

Линии тренда могут быть построены на всех двухмерных диаграммах (линию тренда нельзя добавить на объемных, лепестковых, круговых, кольцевых и пузырьковых диаграммах).

Существует шесть различных видов линий тренда:

• Линейная
• Полиномиальная
• Логарифмическая
• Экспоненциальная
• Степенная
• Скользящее среднее (линейная фильтрация)

Линии тренда, добавленные к графику функции, на сами данные и исходную диаграмму никак не влияют.

Формулы для вычисления линий тренда

Линейная. Используется для линейной аппроксимации данных по методу наименьших квадратов в соответствии с уравнением:

где: m — угол наклона, b — координата пересечения оси абсцисс.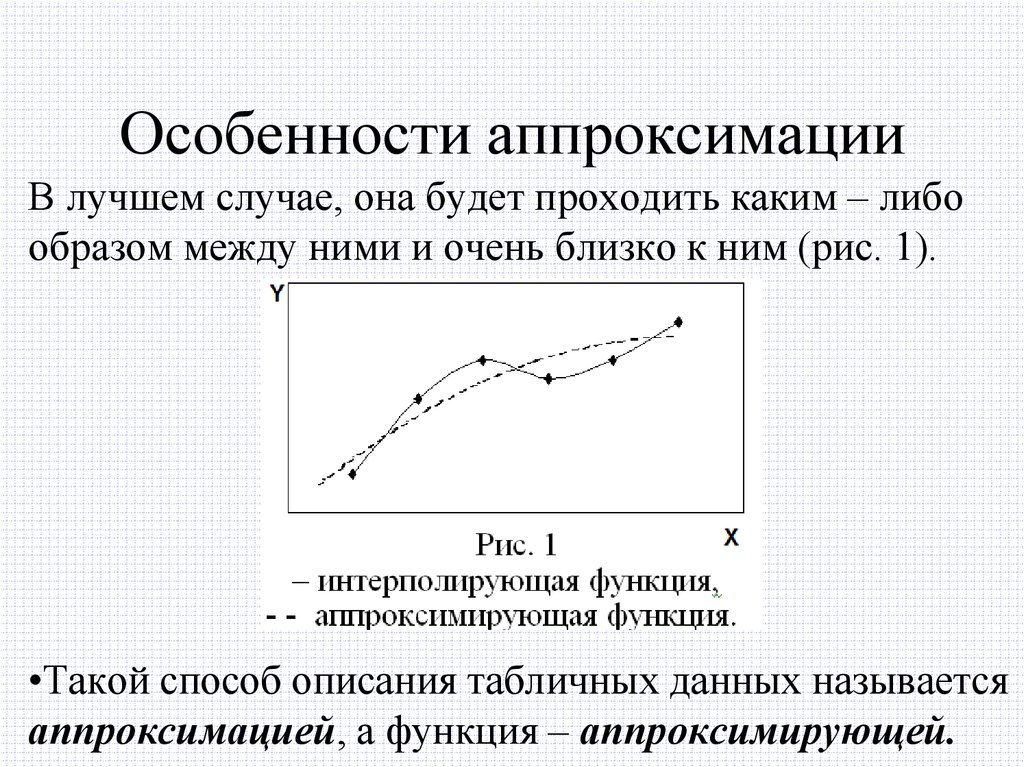

Полиномиальная. Используется для полиномиальной или криволинейной аппроксимации данных по методу наименьших квадратов в соответствии с уравнением:

где: b, c₁, c₂, … c₆ — константы.

Можно задать степень полинома от 2 до 6.

Логарифмическая. Используется для логарифмической аппроксимации данных по методу наименьших квадратов в соответствии с уравнением:

где: c и b — константы, ln — функция натурального логарифма.

Экспоненциальная. Используется для экспоненциальной аппроксимации данных по методу наименьших квадратов в соответствии с уравнением:

где: c и b — константы, e — основание натурального логарифма.

Степенная. Используется для степенной аппроксимации данных по методу наименьших квадратов в соответствии с уравнением:

где: c и b — константы.

Примечание. Экспоненциальная и степенная виды аппроксимации недоступны, если значения функции F(x) содержат отрицательные или нулевые значения. Кроме того, логарифмическая и степенная виды аппроксимации недоступны, если значения аргумента функции x содержат отрицательные или нулевые значения. Поскольку в заданиях к лабораторным работам используется отрицательное значение нижней границы аргумента Xn (x0), не выбирайте логарифмическую и степенную виды аппроксимации!

Скользящее среднее (линейная фильтрация). Скользящее среднее — это среднее значение за определенный период:

На диаграмме линия, построенная по точкам скользящего среднего, позволяет построить сглаженную кривую, более ясно показывающую закономерность в развитии данных.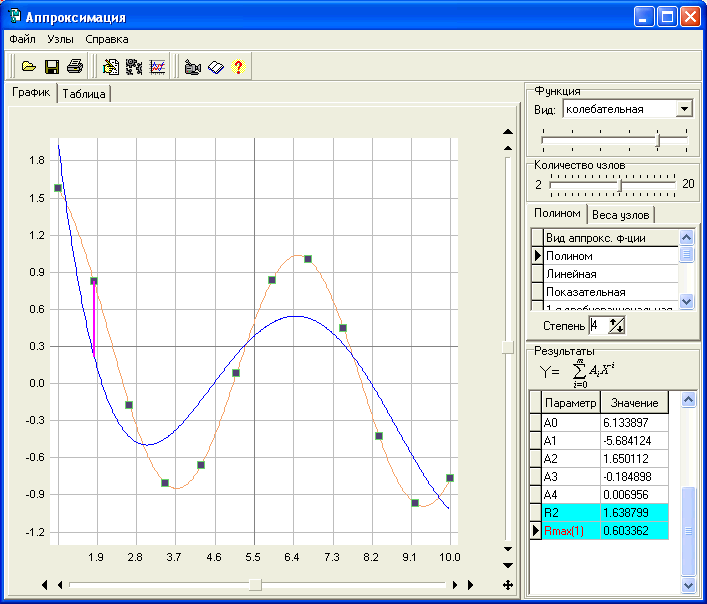

Добавление линии тренда к рядам данных

Выделяем диаграмму (щелкаем в любом пустом месте диаграммы), после чего на ленте меню появятся три дополнительные вкладки: Конструктор, Макет и Формат. На вкладке Макет в группе Анализ щелкаем по кнопке Линия тренда:

В открывшемся списке выбираем требуемый вид аппроксимации:

Через это меню удобно убирать все линии тренда с диаграммы, для этого используется первый пункт Нет.

Другой вариант. На диаграмме точно наводим курсор на любое место кривой функции, затем щелкаем правой кнопкой мыши (при этом на кривой в узлах появляются “пупырышки”). В открывшемся контекстном меню выбираем пункт Добавить линию тренда…:

Появится диалоговое окно Формат линии тренда:

На первой закладке выбираем вид аппроксимации (не выбирайте логарифмическую и степенную, если есть отрицательные значения аргумента функции x). Для того, чтобы рядом с линией тренда выводилось уравнение аппроксимирующей функции и величина достоверности аппроксимации R², поставьте галочки в соответствующих местах. Для дополнительной настройки вида линии тренда (цвет, толщина и т.п.) используйте закладки Цвет линии и Тип линии.

При выборе типа Полиномиальная в поле Степень можно указать степень аппроксимирующего полинома (от 2 до 6). При выборе типа Линейная фильтрация в поле Точки нужно задать число периодов, используемых для расчета скользящего среднего (от 2 до 10).

Величина достоверности R² показывает, насколько точно линия тренда аппроксимирует исходную функцию. При идеальном совпадении R²=1. На диаграмме видно, что экспоненциальная кривая в данном случае точнее описывает исходную функцию, чем линейная:

Для того, чтобы изменить параметры уже добавленной линии тренда, нужно точно навести курсор на любое место линии тренда, затем щелкнуть правой кнопкой мыши и в открывшемся контекстном меню выбрать пункт Формат линии тренда…:

« Назад

Вперед »

3.

3. Аппроксимация функции | Электронная библиотека

Естественные науки / Математическое моделирование процессов в машиностроении / 3.3. Аппроксимация функции

Аппроксимацией (приближением) функции  называется нахождение такой функции  (аппроксимирующей функции), которая была бы близка заданной. Критерии близости функций  и  могут быть различные.

Основная задача аппроксимации — построение приближенной (аппроксимирующей) функции, в целом наиболее близко проходящей около данных точек или около данной непрерывной функции. Такая задача возникает при наличии погрешности в исходных данных (в этом случае нецелесообразно проводить функцию точно через все точки, как в интерполяций) или при желании получить упрощенное математическое описание сложной или неизвестной зависимости.

Рис. 3.6 Метод Лагранжа

Концепция аппроксимации

Близость исходной и аппроксимирующей функций определяется числовой мерой

— критерием аппроксимации (близости).

Наибольшее распространение получил квадратичный критерий, равный сумме квадратов отклонений расчетных значений от «экспериментальных» (т.е. заданных), — критерий близости в заданных точках:

Здесь у_i — заданные табличные значения функции; у_i^расч — расчетные значения по аппроксимирующей функции; b_i — весовые коэффициенты, учитывающие относительную важность i-и точки (увеличение b,. приводит при стремлении уменьшить R к уменьшению, прежде всего отклонения в i—й точке, так как это отклонение искусственно увеличено за счет относительно большого значения весового коэффициента).

Квадратичный критерий обладает рядом «хороших» свойств, таких, как дифференцируемость, обеспечение единственного решения задачи аппроксимации при полиномиальных аппроксимирующих функциях.

Другим распространенным критерием близости является следующий:

Этот критерий менее распространен в связи с аналитическими и вычислительными трудностями, связанными с отсутствием гладкости функции и ее дифференцируемости.

Выделяют две основные задачи:

1)    получение аппроксимирующей функции, описывающей  имеющиеся данные, с погрешностью не хуже заданной;

2)    получение аппроксимирующей функции заданной структуры с наилучшей возможной погрешностью.

Чаще всего первая задача сводится ко второй перебором различных аппроксимирующих функций и последующим выбором наилучшей.

Метод наименьших квадратов

Метод базируется на применении в качестве критерия близости суммы квадратов отклонений заданных и расчетных значений. При заданной структуре аппроксимирующей функции

у_i^расч(х) необходимо таким образом подобрать параметры этой функции, чтобы получить наименьшее значение критерия близости, т.е. наилучшую аппроксимацию. Рассмотрим путь нахождения этих параметров на примере полиномиальной функции одной переменной:

Запишем выражение критерия аппроксимации при b_i =1 (i=1, 2,…, n) для полиномиального у_i^расч (х):

Искомые переменные а_j можно найти из необходимого условия минимума R по этим переменным, т.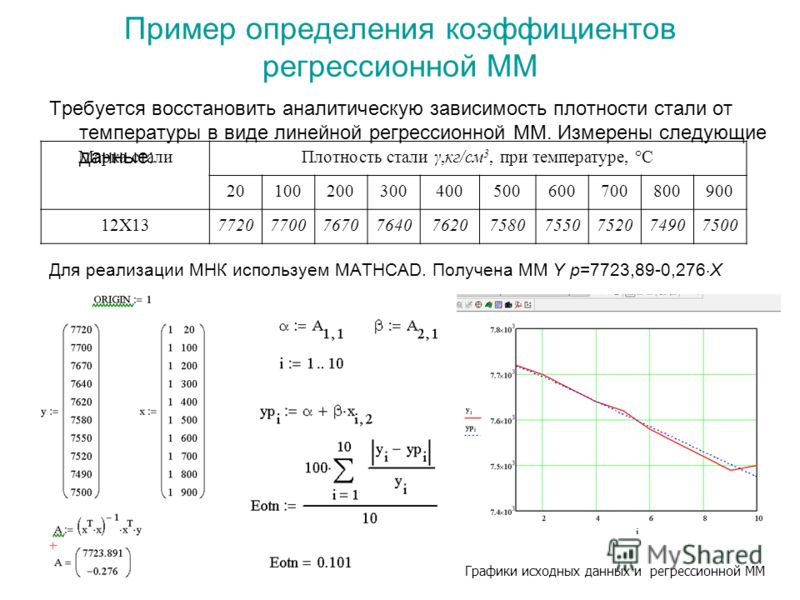 е. dR / dа_р = 0 (для _р =0, 1,2,…,k). Продифференцируем по а_р(р — текущий индекс):

После очевидных преобразований (сокращение на два, раскрытие скобок, изменение порядка суммирования) получим

Перепишем последние равенства

Получилась система n+1 уравнений с таким же количеством неизвестных а_j, причем линейная относительно этих переменных. Эта система называется системой нормальных уравнений. Из ее решения находятся параметры а_j аппроксимирующей функции, обеспечивающие minR, т.е. наилучшее возможное квадратичное приближение. Зная коэффициенты, можно (если нужно) вычислить и величину R (например, для сравнения различных аппроксимирующих функций). Следует помнить, что при изменении даже одного значения исходных данных (или пары значений х_i, у_i, или одного из них) все коэффициенты изменят в общем случае свои значения, так как они полностью определяются исходными данными. Поэтому при повторении аппроксимации с несколько изменившимися данными (например, вследствие погрешностей измерения, помех, влияния неучтенных факторов и т.п.) получится другая аппроксимирующая функция, отличающаяся коэффициентами. Обратим внимание на то, что коэффициенты

а_j полинома находятся из решения системы уравнений, т.е. они связаны между собой. Это приводит к тому, что если какой-то коэффициент вследствие его малости захочется отбросить, придется пересчитывать заново оставшиеся. Можно рассчитать количественные оценки тесноты связи коэффициентов. Существует специальная теория планирования экспериментов, которая

позволяет обосновать и рассчитать значения х_i, используемые для аппроксимации, чтобы получить заданные свойства коэффициентов (несвязанность, минимальная дисперсия коэффициентов и т.д.) или аппроксимирующей функции (равная точность описания реальной зависимости в различных направлениях, минимальная дисперсия предсказания значения функции и т.

д.).

Рис. 3.7 Влияние степени аппроксимирующего полинома М на точность аппроксимации

В случае постановки другой задачи — найти аппроксимирующую функцию, обеспечивающую погрешность не хуже заданной, — необходимо подбирать и структуру этой функции. Эта задача значительно сложнее предыдущей (найти параметры аппроксимирующей функции заданной структуры, обеспечивающей наилучшую возможную погрешность) и решается в основном путем перебора различных функций и сравнения получающихся мер близости. Для примера на рис. 3.7 приведены для визуального сравнения исходная и аппроксимирующие функции с различной степенью полинома, т.е. функции с различной структурой. Не следует забывать, что с повышением точности аппроксимации растет и сложность функции (при полиномиальных аппроксимирующих функциях), что делает ее менее удобной при использовании.

Рассмотрим решение задачи аппроксимации и интерполяции с шумом в

программе MathCAD (рисунок 3.8).

Пример 3.1. В ходе проведения эксперимента были получены данные, представленные в таблице 3. 1. Необходимо способом наименьших квадратов подобрать для заданных значений x и y квадратичную функцию . Построить на одной координатной плоскости экспериментальные данные и аппроксимирующую функцию.

Таблица 3.1 Данные эксперимента

х	80,5	77,0	70,8	56,7	39,7	29,9
у	281	272	259	224	186	170

Решение. Для определения коэффициентов  квадратичной функции построим дополнительную таблицу 3.2.

Таблица 3.2 Дополнительная таблица

1	80,5	6480,25	521660,13	41993640,0625	281	22620,5	1820950,25
2	77	5929	456533	35153041,0000	272	20944	1612688,00
3	70,8	5012,64	354894,91	25126559,7696	259	18337,2	1298273,76
4	56,7	3214,89	182284,26	10335517,7121	224	12700,8	720135,36
5	39,7	1576,09	62570,773	2484059,6881	186	7384,2	293152,74
6	29,9	894,01	26730,899	799253,8801	170	5083	151981,70
Σ	354,6	23106,88	1604673,972	115892072,1124	1392	87069,7	5897181,81

Строим систему уравнений

В нашем случае она будет иметь вид:

Из полученной системы уравнений находим

Искомая зависимость

Строим график экспериментальных данных и найденной зависимости.

Рис.3.8 Аппроксимация и интерполяция в задаче с помехами

Если требуется построить зависимость в виде показательной функции , то необходимо составить систему:

   (3.7)

Для этого строится таблица

1
…	…	…	…	…
n
Σ

Из системы 3.7 находим коэффициенты  и  (необходимо выразить ).

Если требуется построить зависимость в виде степенной функции , то составляется система:

   (3. 8)

Для этого строится таблица

1
…	…	…	…	…
n
Σ

Из системы 3.8 находим коэффициенты  и  (необходимо выразить ).

опасностей приближения данных | Валтех

04 ноября 2022 г.

Аппроксимация данных обычно используется для того, чтобы сделать определенные данные понятными и удобочитаемыми. Но в сфере маркетинга такое приближение уже нежелательно.

Аппроксимация данных — это процесс использования математически обоснованных методов для расчета приблизительных результатов на основе имеющихся данных. В то время как методы расчета являются надежными, результаты не могут быть определенными, когда имеешь дело с приближениями, и тем не менее, не осознавая этого, приближения везде, даже в самых серьезных областях.

Целью этого процесса является сделать сложные данные понятными как можно большему количеству людей. Хотя в определенных контекстах и ​​для определенных целей упрощение данных полностью оправдано (например, то, как страны часто оценивают свой годовой ВВП), оно может быть проблематичным для бизнеса при его маркетинговом использовании. Тем более, что технологии генерации данных значительно развились и эксплуатируют все более колоссальные объемы. Что нового, так это более сложные способы обработки данных, увеличение числа источников, из которых берутся данные, все более сложные алгоритмы, которым подвергаются данные, или архитектуры данных, становящиеся все более и более запутанными.

Когда дело доходит до обращения к потенциальным клиентам, последствия приблизительного использования данных могут быть минимальными, особенно в случае предложений или рекламных объявлений, не требующих высокого уровня приверженности. Тогда можно достичь части ваших целей с приблизительными данными. Но вы теряете эффективность. С другой стороны, когда речь идет об обращении к людям, которые уже являются клиентами, последствия могут быть гораздо более серьезными. Контракт на чтение с покупателем бренда или услуги должен выполняться со строгостью, которую могут обеспечить только самые точные данные.

Однако, за исключением специалистов по качеству данных, эта тема, похоже, мало волнует большинство предприятий. Вам нужно только посмотреть программы вебинаров и событий данных, чтобы убедиться. Спикеры, говорящие о сквозном качестве данных, встречаются редко. Кажется, все неявно указывает на то, что используемые данные надежны и хорошего качества. Однако это далеко не так. Темы, обсуждаемые на этих мероприятиях, касаются исключительно сбора данных, аспектов, связанных с RGPD, и уточненных данных. Остальная часть пути данных по-прежнему остается темой, которой специализированные команды все еще не уделяют должного внимания.

Если во Франции качество данных не является приоритетом для всех, то в Европе это совсем другая история. Некоторые швейцарские компании стали мастерами сквозного управления качеством и создали специальные группы, инструменты и процессы, чтобы гарантировать более чем убедительный результат. Слишком часто во Франции к этому аспекту данных относятся слишком традиционно, и им можно управлять только тогда, когда у команды есть достаточно времени для этого.

Однако существуют алгоритмы, которые можно использовать для контроля качества данных, и специализированные редакторы могут предоставить адаптированные решения. Есть также группы экспертов по этому вопросу. Конечно, для этого нужны финансовые и человеческие ресурсы. Крупные компании и группы имеют дело с такими большими объемами данных, что только алгоритмы могут отсортировать хорошие данные от плохих. Эту титаническую задачу не могут выполнить специалисты по данным в одиночку. Поэтому для этих компаний важно как можно скорее заняться этим вопросом и положить конец сближению.

В Valtech мы не используем приблизительные данные при развертывании наших услуг Data Science для клиентов. Наш сквозной контроль качества фокусируется на каждом аспекте использования и анализа данных, и мы делаем все возможное, чтобы давать рекомендации только на основе всех наиболее точных доступных данных. Позвоните нам сегодня, чтобы узнать больше о том, что наши специалисты по обслуживанию данных могут сделать для вашего бренда.

Страница не найдена – Khoury College Development

 

В мире, где информатика (CS) везде, CS для всех. CS пересекает все дисциплины и отрасли.

 

Колледж компьютерных наук Хури стремится создавать и развивать разнообразную инклюзивную среду.

 

Колледж Хури, первый в стране колледж компьютерных наук, основанный в 1982 году, вырос в размерах, разнообразии, программах на получение степени и превосходстве исследований.

 

В наших региональных кампусах, расположенных в промышленных и технологических центрах, Khoury College предлагает сильные академические программы в оживленных городах для жизни, работы и учебы.

 

Khoury College — это сообщество людей, преданных обучению, наставничеству, консультированию и поддержке студентов по всем программам.

 

Программы награждения колледжей и университетов проливают свет на выдающихся преподавателей, студентов, выпускников и отраслевых партнеров.

 

Наши реальные исследования, выдающиеся преподаватели, выдающиеся докладчики, динамичные выпускники и разные студенты рассказывают свои истории и попадают в новости.

 

В Колледже Хури обучение происходит в классе и за его пределами. Мероприятия в нашей сети кампусов обогащают образовательный опыт.

 

Информатика повсюду. Студенты Khoury College занимаются соответствующей работой, исследованиями, глобальными исследованиями и опытом обслуживания, которые помогают им расти.

 

Студенты магистратуры углубляют свои знания посредством проектной работы, профессионального опыта работы и стажировки в научных исследованиях.

 

Работа над исследованиями с преподавателями занимает центральное место в работе доктора философии. Докторанты колледжа Хури также могут проводить исследования с отраслевыми партнерами.

 

Преподаватели и студенты Колледжа Хури проводят эффективную работу по различным дисциплинам. Благодаря широкому спектру областей исследований мы каждый день решаем новые проблемы в области технологий.

 

Наши институты и исследовательские центры объединяют ведущих академических, отраслевых и государственных партнеров для использования вычислительной мощности.

 

Исследовательские проекты, разработанные и проводимые профессорско-преподавательским составом Khoury College мирового уровня, вовлекают студентов и других исследователей в получение новых знаний.

 

Исследовательские лаборатории и группы сосредотачиваются на ряде проблем в определенном контексте, поощряя исследования и сотрудничество.

 

Эта новая инициатива направлена ​​на устранение рисков для конфиденциальности и личных данных с помощью коллективных усилий на низовом уровне с упором на прозрачность и подотчетность.

 

Современное оборудование, бесшовные системы и инновационные лаборатории и помещения позволяют нашим преподавателям и студентам проводить передовые исследования.

 

9Колледж 0002 Khoury гордится нашим совместным инклюзивным сообществом. Каждый день мы стремимся создавать программы, которые приветствуют самых разных студентов в CS.

 

Более 20 компьютерных клубов в колледже Хури и Северо-Восточном колледже предлагают что-то для каждого студента. Мы всегда рады новым членам на каждом уровне.

 

Учащиеся учатся в современных классах, конференц-залах для совместной работы, а также в ультрасовременных лабораториях и исследовательских центрах.

 

Сети обеспечивают безопасную и бесперебойную работу кода, современное и надежное оборудование, а наша квалифицированная системная команда управляет поддержкой и обновлениями.

 

Заинтригован Колледжем Хури и Северо-восточным университетом? Начните здесь, чтобы увидеть общую картину: академические науки, экспериментальное обучение, студенческая жизнь и многое другое.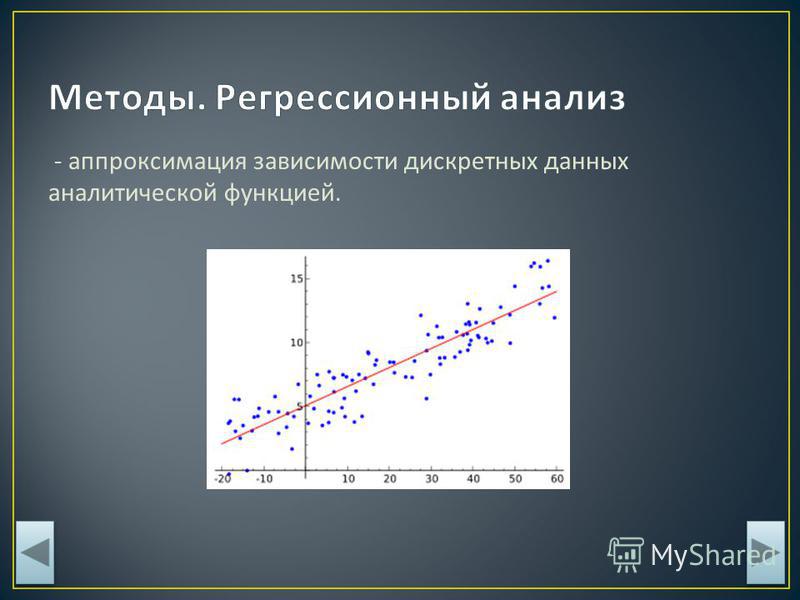

 

Готовы сделать следующий шаг в технической карьере? Наши магистерские программы сочетают в себе академическую строгость, исследовательское превосходство и значимые экспериментальные возможности.

 

Добро пожаловать в магистерскую программу Align, предназначенную для людей, готовых добавить информатику (CS) в свой набор навыков или переключиться на совершенно новую карьеру в сфере технологий.

 

Будучи аспирантом Хури, вы погрузитесь в строгую учебную программу, будете сотрудничать с известными преподавателями и окажете влияние в выбранной вами области исследований.

 

Где бы вы ни находились на пути бакалавриата в Хури, у нас есть консультанты, ресурсы и возможности, которые помогут вам добиться успеха и сделать информатику доступной для всех.

 

Где бы вы ни находились на пути к аспирантуре Хури, наши консультанты, информационные ресурсы и возможности помогут вам выбрать индивидуальный путь.

 

На любом этапе пути Align — и в любом из наших кампусов — консультанты Khoury, ресурсы и возможности поддержат вас на пути к карьере в сфере технологий.