2 журнал операций журнал: Журнал операций 2 с безналичными денежными средствами \ Акты, образцы, формы, договоры \ КонсультантПлюс

Как в 1С:Бухгалтерия государственного учреждения ред. 2.0 сформировать журнал операций по оплате труда № 6?

Вопрос:

Как в 1С:Бухгалтерия государственного учреждения ред. 2.0 сформировать журнал операций по оплате труда № 6?

Ответ:

1. Отчёт «Журнал операций» (ф. 0504071) размещён в пункте главного меню Учёт и отчётность — Отчёты — Регистры учёта (рис. 1).

 

Рисунок 1

2. Открываются отчёты раздела Регламентированные регистры учёта. Необходимо выбрать ссылку Журнал операций (ф. 0504071). Отчёт предназначен для получения журнала операций по унифицированной форме № 0504071 (рис. 2).

 

Рисунок 2

3. В диалоге настройки параметров вывода отчёта необходимо задать период, за который надо получить отчёт (месяц), номер журнала и учреждение (рис. 3).

Рисунок 3

4. Вид объектов аналитического учёта, для которого должен формироваться отдельный журнал, задаётся в справочнике «Журналы». Справочник «Журналы» содержит перечень регистров бюджетного учёта – журналов операций.

Элементы справочника используются в качестве значений реквизита «Номер журнала счетов плана счетов».

При первом запуске программы справочник «Журналы» автоматически заполняется перечнем журналов операций согласно Инструкции № 157н.

Для каждого журнала указаны:

— код – номер журнала. В типовой конфигурации номера журналов установлены согласно порядку следования журналов в инструкции по бюджетному учёту;

— приоритет.

Заполнение реквизита проводки «Номер журнала» определяется приоритетом журналов. Наивысший приоритет 1 задаётся для журнала операций с безналичными денежными средствами. Приоритет 2 – для журнала операций по счёту «Касса». Для остальных журналов автоматически приоритет не задаётся, но пользователь имеет возможность сам установить нужный приоритет журналов.

Если приоритет не задан (равен 0), то это самый низкий из возможных приоритетов.

При формировании проводки номер журнала присваивается равным номеру журнала с наивысшим приоритетом.

При равенстве приоритетов номер журнала определяется по счёту кредита.

Показатель – вид объектов аналитического учёта, данные о котором приводятся в графе «Наименование показателя» журнала.

Разделитель операций – вид объектов аналитического учёта, для которого должен формироваться отдельный журнал.

5. Журналы можно объединять в группы. Это позволяет формировать отчёты по группе однотипных журналов.

Можно также задать вариант формирования журнала: выводить остатки в разрезе показателя (будут выводиться остатки на начало и конец периода) либо не выводить остатки (в журнале будут отображаться только обороты за период), поставив галочку напротив нужного варианта.

Учреждение вправе самостоятельно определить порядок формирования журналов операций, закрепив это в учётной политике

(рис. 4).

Рисунок 4

6. Вызвать панель настроек отчёта можно с помощью кнопки Настройка слева.

В параметрах настроек отчёта задаются учреждение, подразделение (при необходимости), по которому следует получить отчёт.

Для печати в титульном листе наименования структурного подразделения, в котором формируется отчёт, должностей и расшифровок подписей ответственных лиц следует заполнить соответствующие реквизиты.

В отчёте можно установить следующие настройки: дата формирования, дополнительные группировки, макет оформления.

Опция «Сворачивать однотипные проводки» задаёт вывод в отчёт каждой проводки операции или сводных проводок (флажок включён).

Настройка «Дата формирования» задаётся посредством выбора необходимого элемента из открывающегося списка (рис. 5).

Настройка «Дополнительные группировки» задаётся посредством включения флажка и выбора необходимого элемента из списка (рис. 5).

Настройка «Макет оформления» задаётся посредством включения флажка и выбора необходимого элемента из открывающегося списка (рис. 5).

Также в отчёте можно выбрать расширенный вид настройки для изменения структуры отчёта (рис. 5).

Для формирования отчёта следует нажать кнопку Закрыть и сформировать (рис. 5).

Рисунок 5

7. В отчёте предусмотрен поиск по наименованию, например Фамилия или сумма (рис. 6).

Рисунок 6

Также в программе есть возможность сохранить сформированный отчёт в формате Excel, подписать электронной подписью, отправить по электронной почте, вывести на печать. Также можно развернуть или свернуть все группы при необходимости

(рис. 7).

Рисунок 7

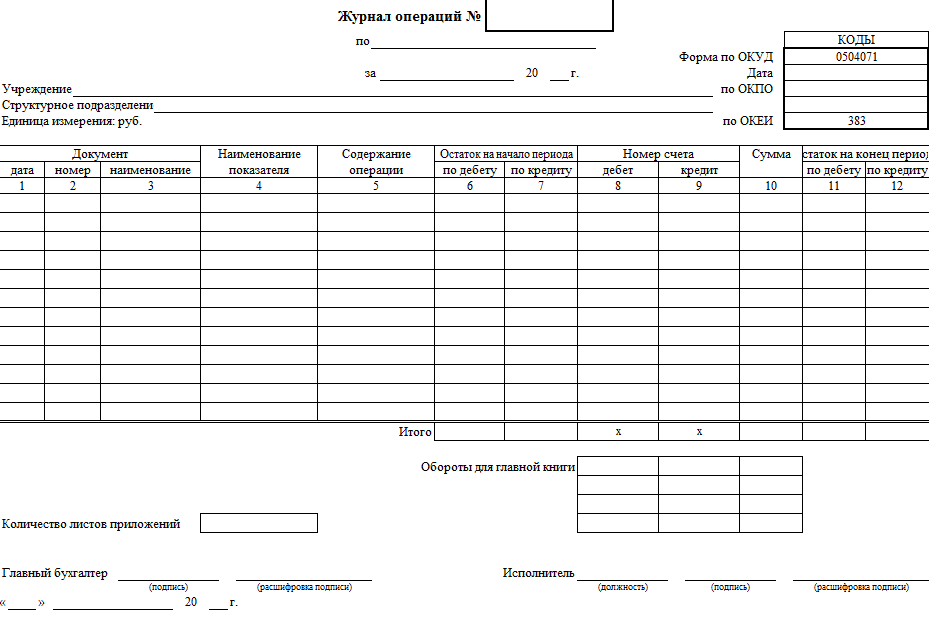
8. Сформированный отчёт открывается в виде табличного документа, который затем может быть выведен на печать.

В отчёте за заданный период (месяц) приводятся остатки на начало и конец отчётного периода и в хронологическом порядке все проводки, у счёта дебета или кредита которых реквизит Номер журнала равен номеру формируемого журнала.

Для каждой проводки выводится информация как о первичном, так и об электронном документе.

Подсчитывается итоговая сумма оборотов за период для переноса в главную книгу.

Для переноса в главную книгу (ф. 0504072) отбираются суммы по проводкам, у которых реквизит проводки № журнала соответствует выбранному журналу.

Журнал операций расчётов по оплате труда, денежному довольствию и стипендиям (№ 6) применяется для отражения операций по счетам 302 00 (в части расчётов по оплате труда и стипендиям), 303 01, 303 09, 304 02, 304 03. Записи в журнале операций расчётов по заработной плате, денежному довольствию и стипендиям отражаются на основании свода расчётно-платёжных ведомостей с приложением первичных документов. Свод ведомостей составляется раздельно по операциям за счёт различных источников финансового обеспечения. В главную книгу переносятся обороты по операциям, отражённым в журнале операций расчётов по заработной плате, кроме операций, которые отражаются в соответствующих журналах операций

(рис. 8).

Рисунок 8

Свидетельство о регистрации СМИ: Эл № ФС77-67462 от 18 октября 2016 г. Контакты редакции: +7 (495) 784-73-75, [email protected]

Электронный учебник 1С:Бухгалтерия 7.7 — Урок 6, вопр.2: Журнал операций.

Электронный учебник 1С:Бухгалтерия 7.7 — Урок 6, вопр.2: Журнал операций.

Оглавление     1   2   3   4   5   6   7   Далее >

Выход x

Урок 6 — продолжение Понятие и виды операций. Журнал операций. Журнал проводок. Ввод начального сальдо. Открыть журнал операций: Журналы ® Журнал операций или кнопкой  (Журнал операций). Журнал операций предназначен для просмотра списка операций. Каждая операция в нем представлена в виде отдельной строки. См. рис.8. Рис. 8. Журнал операций. В табличной части журнала операций имеются графы: Дата Дата операции Время Время операции (документа) Документ Вид документа (или указано ) Номер Номер операции или номер документа, которому принадлежит операция Содержание Содержание операции Сумма Сумма операции Интервал журнала операций устанавливается так же как и в журнале документов: Действия ® Интервал (или с помощью кнопки  Интервал в панели инструментов). Существует возможность разделения журнала операций на 2 подокна: для списка операций и для списка проводок текущей операции: Действия ® Показывать проводки. Работа с операциями и документами: Ввести новую операцию: нажмите кнопку  (Новая строка (Ins)). откроется окно диалога операции, заполните заголовок операции: дата, номер, сумма, содержание; далее введите проводки кнопкой  (Новая проводка (Ins)) или корреспонденции кнопкой  (Новая корреспонденция). Примечание: номера операций и проводок внутри операции уникальны. Ввести используя типовую операцию: нажмите кнопку , выбирите типовую операцию, заполните реквизиты заголовка операции, а затем все недостающие реквизиты проводок или корреспонденций. При вводе типовой операции суммы проводок рассчитываются автоматически. Для примера предлагается ввести типовую операцию Капитальные вложения в основные средства и нематериальные активы ® 1. Поступление оборудования от поставщика. Ввести документ: нажмите кнопку , выберите документ, заполните все его реквизиты, как и в журнале документов. Хотя такая возможность существует, все-таки удобнее вводить документы непосредственно в журналы документов. Редактировать операцию или реквизиты документа: выполните двойной щелчок по строке в журнале или нажмите Enter, откроется окно диалога операции. Можно также использовать кнопки  (Открыть операцию),  (Открыть документ). Копировать операцию: осуществляется аналогично копированию документов кнопкой  (Копировать строку). 1 2 3 4 Далее >

Оглавление     1   2   3   4   5   6   7   Далее >

Вверх ^

Сайт создан в системе uCoz

Operational Logging-A How To — LogBook

Что такое операционный журнал и почему он важен?

Итак, что такое операционный журнал?   Это хронологическая запись рабочих условий, наблюдений и действий, предпринятых с течением времени при управлении данной операцией. Это своего рода дневник. Он записывает, что знали операторы, когда они это знали и что они делали во время своей смены, когда контролировали операцию.

Короче говоря, это официальный отчет о том, что, черт возьми, произошло, почему это произошло — или, по крайней мере, наблюдаемые симптомы, которые присутствовали, и что было сделано по этому поводу кем.

Некоторые считают это бременем. «О, чувак, теперь я должен ввести это и ввести то». Да, вы должны задокументировать то, что произошло. Но умные операционные менеджеры знают, что это на благо ВСЕХ участников, включая тех, кто делает записи. Важность операционных записей должна быть признана и передана от группы управления операциями вниз по операционному персоналу.

Почему это важно? Потому что никто не хочет потерять деньги, причинить кому-то вред, потерять работу, поставить свою компанию под угрозу или быть оштрафованным органом по соблюдению нормативных требований. Давайте повторим это. Никто из тех, кто заслуживает быть в вашей команде, не хочет этого.

Итак, что происходит? Что люди делают в этой области, чтобы улучшить свой бизнес?

Они внедряют современные бортовые журналы и разрабатывают свои методы работы на основе бортового журнала, чтобы улучшить связь и максимально упростить ввод данных.

«Но у нас есть телеметрия, архиватор и система управления». Да, вы делаете. И они имеют решающее значение для вашей работы. Способ пойти.

Журналы предназначены для людей

Журналы учета записывают то, что знает человек, когда он это знает, и используются для документирования того, что он делает (их методы работы и когда они были сделаны), а также какие важные решения и действия были приняты во время смены .

Умные операционные менеджеры создают практики на основе своих бортовых журналов. Это включает оптимизацию и, в некоторых случаях, автоматизацию записей в их журналах. Они хотят, чтобы записи в журнале были быстрыми и эффективными, но в то же время полными. Одним из основных способов достижения этого является создание шаблонов или форм ввода данных, которые позволяют операторам записывать рутинные записи журнала, выбирая несколько простых вариантов. Это гарантирует, что записи легко вводить и что записи содержат соответствующие детали. Кроме того, эти записи берут то, что в противном случае было бы неструктурированным комментарием, и превращают его в структурированный контент.

Умные операционные менеджеры также вносят новшества, меняя методы проведения проверок (обходы или обходы). Они внедряют мобильные технологии (планшеты или смартфоны), которые позволяют легко документировать их раунды с использованием тех же типов шаблонов. Таким образом, наблюдения и данные, наблюдаемые во время этих циклов, также могут быть беспрепятственно помещены в операционный журнал, предоставляя еще больше данных, которые могут способствовать более быстрому и лучшему принятию решений операционной группой.

Все это объединено в решение, которое вводит подписи и утверждения, чтобы ключевой персонал был в курсе важных деталей, которые имеют значение. Когда вы добавите к этому диаграммы и аналитику, ценность станет очевидной.

big o — Что может привести к сложности алгоритма O(log log n)?

Термины O(log log n) могут появляться в самых разных местах, но обычно есть два основных маршрута, которые прибывают в эту среду выполнения.

Уменьшение квадратного корня

Как упоминалось в ответе на связанный вопрос, общий способ для алгоритма иметь временную сложность O (log n) заключается в том, что этот алгоритм работает, многократно уменьшая размер входных данных на некоторый постоянный коэффициент на каждой итерации. В этом случае алгоритм должен завершаться после O(log n) итераций, потому что после выполнения O(log n) делений на константу алгоритм должен уменьшить размер задачи до 0 или 1. Вот почему, например , бинарный поиск имеет сложность O(log n).

Интересно, что существует аналогичный способ уменьшения размера задачи, который дает время выполнения в виде O(log log n). Вместо того, чтобы делить ввод пополам на каждом уровне, что произойдет, если мы возьмем квадратный корень из размера на каждом уровне?

Например, возьмем число 65 536. Сколько раз мы должны разделить это число на 2, пока не получим 1? Если мы это сделаем, то получим

• 65 536 / 2 = 32 768
• 32 768 / 2 = 16 384
• 16 384 / 2 = 8 192
• 8 192 / 2 = 4 096
• 4096 / 2 = 2048
• 2048 / 2 = 1024
• 1024 / 2 = 512
• 512 / 2 = 256
• 256 / 2 = 128
• 128/2 = 64
• 64/2 = 32
• 32/2 = 16
• 16/2 = 8
• 8 / 2 = 4
• 4 / 2 = 2
• 2 / 2 = 1

Этот процесс занимает 16 шагов, а также тот случай, когда 65 536 = 2 ¹⁶ .

Но если мы возьмем квадратный корень на каждом уровне, мы получим

• √65 536 = 256
• √256 = 16
• √16 = 4
• √4 = 2

Обратите внимание, что для полного перехода к 2 требуется всего четыре шага. Почему это так?

Во-первых, интуитивное объяснение. Сколько цифр в числах n и √n? В числе n примерно log n цифр, и приблизительно log (√n) = log (n ^1/2 ) = (1/2) log n цифр в √n. Это означает, что каждый раз, когда вы извлекаете квадратный корень, вы примерно вдвое уменьшаете количество цифр в числе. Поскольку вы можете уменьшить вдвое число k O(log k) раз, прежде чем оно уменьшится до константы (скажем, 2), это означает, что вы можете извлечь квадратный корень только O(log log n) раз, прежде чем уменьшить число. к некоторой константе (скажем, 2).

Теперь давайте посчитаем, чтобы все было строго. Перепишем приведенную выше последовательность в терминах степеней двойки:

• √65 536 = √2 ¹⁶ = (2 ¹⁶ ) ^1/2 = 2 ⁸ = 256
• √256 = √2 ⁸ = (2 ⁸ ) ^1/2 = 2 ⁴ = 16
• √16 = √2 ⁴ = (2 ⁴ ) ^1/2 = 2 ² = 4
• √4 = √2 ² = (2 ² ) ^1/2 = 2 ¹ = 2

Обратите внимание, что мы следовали последовательности 2 ¹⁶ → 2 ⁸ → 2 ⁴ → 2 ² → 2 ¹ . На каждой итерации мы сокращаем показатель степени двойки вдвое. Это интересно, потому что это связано с тем, что мы уже знаем: вы можете разделить число k только пополам O(log k) раз, прежде чем оно упадет до нуля.

Итак, возьмите любое число n и запишите его как n = 2 ^k . Каждый раз, когда вы извлекаете квадратный корень из n, вы уменьшаете вдвое показатель степени в этом уравнении. Следовательно, может быть применено только O(log k) квадратных корней до того, как k упадет до 1 или ниже (в этом случае n упадет до 2 или ниже). Поскольку n = 2 ^k , это означает, что k = log ₂ n, и, следовательно, количество извлеченных квадратных корней равно O(log k) = O(log log n). Следовательно, если существует алгоритм, который работает путем многократного сведения проблемы к подзадаче, размер которой равен квадратному корню исходного размера задачи, этот алгоритм завершится после O(log log n) шагов.

Одним из реальных примеров этого является структура данных дерева ван Эмде Боаса (vEB-дерево). vEB-дерево — это специализированная структура данных для хранения целых чисел в диапазоне 0…N — 1. Оно работает следующим образом: корневой узел дерева имеет в себе √N указателей, разбивающих диапазон 0…N — 1 на √N сегментов, каждый из которых содержит диапазон примерно из √N целых чисел. Эти корзины затем внутренне подразделяются на √(√N) корзин, каждая из которых содержит примерно √(√N) элементов. Чтобы пройти по дереву, вы начинаете с корня, определяете, к какой корзине вы принадлежите, а затем рекурсивно продолжаете в соответствующем поддереве. Из-за того, как устроено vEB-дерево, вы можете определить за O(1) время, в какое поддерево спускаться, и, таким образом, после O(log log N) шагов вы достигнете нижней части дерева. Соответственно поиск в vEB-дереве занимает всего O(log log N).

Другим примером является алгоритм поиска ближайшей пары точек Хопкрофта-Фортуны. Этот алгоритм пытается найти две ближайшие точки в наборе двумерных точек. Он работает, создавая сетку сегментов и распределяя точки по этим сегментам. Если в какой-либо точке алгоритма обнаруживается ведро, содержащее более √N точек, алгоритм рекурсивно обрабатывает это ведро. Следовательно, максимальная глубина рекурсии равна O(log log n), и с помощью анализа дерева рекурсии можно показать, что каждый слой в дереве работает O(n). Следовательно, общее время выполнения алгоритма равно O(n log log n).

Алгоритмы O(log n) для малых входных данных

Существуют и другие алгоритмы, которые достигают времени выполнения O(log log n) за счет использования таких алгоритмов, как бинарный поиск на объектах размером O(log n). Например, структура данных x-fast trie выполняет бинарный поиск по слоям дерева высотой O(log U), поэтому время выполнения некоторых операций составляет O(log log U). Связанное y-быстрое дерево получает часть своего времени выполнения O(log log U) за счет поддержания сбалансированных BST из узлов O(log U) в каждом, что позволяет выполнять поиск в этих деревьях за время O(log log U). Дерево танго и связанные с ним структуры данных мультиэкранного дерева заканчиваются в своем анализе термином O(log log n), потому что они поддерживают деревья, содержащие O(log n) элементов каждое.