MATHCAD 14: Основные сервисы и технологии
Главная / Математика / MATHCAD 14: Основные сервисы и технологии / Тест 1
Упражнение 1:
Номер 1
Какое значение имеет переменная ORIGIN, если первый элемент матрицы :Ответ:
 (1) 11 
 (2) 1 
 (3) 0 
 (4) -1 
Номер 2
Какое значение имеет переменная ORIGIN, если элемент матрицы равен :Ответ:
 (1) 00 
 (2) 1 
 (3) 0 
 (4) 01 
Переменная ORIGIN=0, какой вид будет иметь первый элемент матрицы:Ответ:
 (1)  
 (2)  
 (3)  
 (4)  
Упражнение 2:
Номер 1
Для вычисления производной функции необходимо использовать панель
Ответ:
  (1) Calculus 
 (2) Symbolic 
 (3) Boolean 
 (4) Evaluation 
Номер 2
Для ввода производной функции необходимо использовать
Ответ:
 (1) Calculus 
 (2) Calculator 
 (3) Boolean 
 (4) Evaluation 
Номер 3
Для ввода и вычисления производной функции необходимо использовать
Ответ:
 (1) Calculus+Symbolic 
 (2) Calculator 
 (3) Calculus+ Evaluation 
 
Упражнение 3:
Номер 1
Параметр , чему равно значение функции в точке с точностью до 3 значащих цифр
Ответ:
 (1) 0. 156 
156 
 (2) 0.146 
 (3) 0.126 
 (4) 0.136  
Номер 2
Параметр , чему равно значение функции в точке с точностью до 4 значащих цифр
Ответ:
 (1) 0.1653 
 (2) 0.1553 
 (3) 0.1753 
 (4) 0.1853 
Номер 3
Параметр , чему равно значение функции в точке с точностью до 2 значащих цифр
Ответ:
 (1) 0.54 
 (2) 0,44 
 (3) 0.34 
 (4) 0.24 
Упражнение 4:
Номер 1
Ранжированная переменная задана в виде .Сколько элементов в массиве?
Ответ:
 (1) 3 
 (2) 4 
 (3) 5 
 (4) 6 
Ранжированная переменная задана в виде . Чему равен 5 элемент массива?
Ответ:
 (1) 5 
 (2) 7 
 (3) 8 
 (4) 9 
Номер 3
Ранжированная переменная задана в виде . Чему равна сумма элементов массива?
Ответ:
 (1) 20 
 (2) 30 
 (3) 40 
 (4) 50 
Упражнение 5:
Номер 1
Матрица задана в виде: .Чему равен элемент ?
Ответ:
 (1) 3 
 (2) 6 
 (3) 9 
 (4) 12 
Номер 2
Матрица задана в виде: . Чему равна сумма элементов матрицы?
Ответ:
 (1) 5 
 (2) 10 
 (3) 20 
 (4) 30 
Номер 3
Матрица задана в виде: . Сколько элементов в матрице?
Ответ:
 (1) 3 
 (2) 4 
 (3) 5 
 (4) 6 
Упражнение 6:
Номер 1
Матрица задана в виде: .Матрица задана в виде: Матрица Чему равен элемент ?
Ответ:
 (1) 15 
 (2) 10 
 (3) -10 
 (4) -15 
Номер 2
Матрица задана в виде: . Матрица задана в виде: Матрица Чему равна сумма элементов диагонали матрицы ?
Ответ:
 (1) 5 
 (2) 10 
 (3) -10 
 (4) 20 
Номер 3
Матрица задана в виде: . Матрица задана в виде: Матрица Чему равна сумма элементов 1 строки матрицы ?
Ответ:
 (1) 5 
 (2) -5 
 (3) 10 
 (4) -10 
Упражнение 7:
Номер 1
Заданы матрица , матрица .Какие действия можно произвести
Ответ:
 (1)  
 (2)
 (3) (умножение) 
 (4) (умножение) 
Номер 2
Заданы матрица , матрица . Какие действия можно произвести
Ответ:
 (1)  
 (2)  
 (3)  
 (4)
 Номер 3
Заданы функция , матрица .Какие действия можно произвести ?
Ответ:
 (1)  
 (2) (умножение) 
 (3)  
 (4) (умножение) 
Упражнение 8:
Номер 1
Заданы матрица , матрица . Какие действия можно произвести
Ответ:
 (1)  
 (2)  
 (3) (умножение) 
 (4) (умножение) 
Номер 2
Заданы матрица , матрица .Какие действия можно произвести
Ответ:
 (1)  
 (2)  
 (3)  
 (4)  
Номер 3
Заданы матрица , матрица . Какие действия можно произвести ?
Ответ:
 (1)  
 (2) (умножение) 
 (3)  
 (4) (умножение) 
Главная / Математика / MATHCAD 14: Основные сервисы и технологии / Тест 1
Дифференцирование и интегрирование в Mathcad
Download 0.
|
1 2 3
Bog’liq
Дифференцирование и интегрирование в Mathcad
5 — mavzu (lab topshiriqlari) (1), ehtimollar nazariyasi, 2- tema, 11 sinf, 8 sinflar uchun, Kombinatorika elementlari, КТ mustaqil ish mavzulari, Ma`ruza 1 2021, 3-ma\’ruza, Ma`ruza 17 2021, 2, 8, корреляция, 1, нулевая гипотеза
- Bu sahifa navigatsiya:
- Символика
| Дифференцирование и интегрирование в Mathcad Дифференцирование в Mathcad осуществляется или посредством выполнения самой операции над задаваемым выражением, или с использованием и отображением оператора производной. В первом случае достаточно ввести выражение, выделить переменную дифференцирования в выражении, войти в меню Символика, Переменная, Дифференцировать. 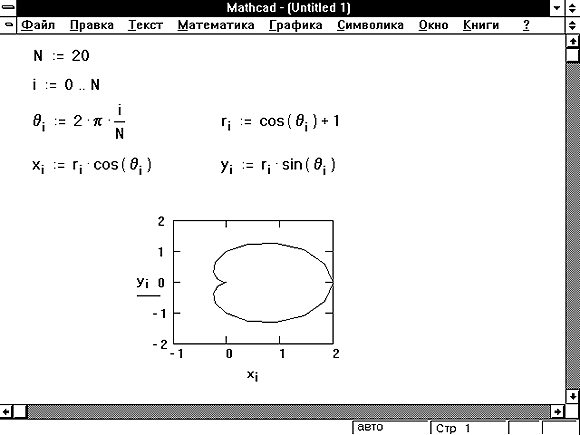 Несмотря на оперативность выполнения данной операции в Mathcad, при оформлении отчета о данных вычислениях, возникают неудобства, связанные с отсутствием самого символа (оператора ) производной. Например: Несмотря на оперативность выполнения данной операции в Mathcad, при оформлении отчета о данных вычислениях, возникают неудобства, связанные с отсутствием самого символа (оператора ) производной. Например:
sin(x)2 – 2. ln(x) Результат дифференцирования посредством меню Символика Аналогичного результата можно добиться, используя символику дифференцирования на панели инструментов “Исчисление”. Данный вариант в Mathcad является более предпочтительным при формировании отчета о результатах вычислений: Mathсad позволяет вычислить производную n-го порядка, что также можно осуществить используя панель инструментов “Исчисление”: Интегрирование в Mathcad выполняется аналогично символьному дифференцированию. Причем можно вычислить как определенный, так и неопределенный интеграл, используя команды меню “Символика” (Символика, Переменная, Интегрировать) или элементы панели инструментов “Символика”. При этом необходимо учитывать, что в результате вычисления неопределенного интеграла постоянная интегрирования автоматически не выводится, а должна вводится пользователем принудительно. Необходимо отметить, что при вычислениях с помощью операторов панели инструментов “Символика” и команд меню “Символика” могут получаться разные результаты. Это связано с тем, что команды меню применяются только к выделенному выражению, в то время как при использовании операторов панели инструментов “Символика” учитываются все предшествующие вычисления. Download 0.74 Mb. Do’stlaringiz bilan baham: |
1 2 3
Ma’lumotlar bazasi mualliflik huquqi bilan himoyalangan ©fayllar.org 2023
ma’muriyatiga murojaat qiling
Суммирование и продукты » MathCadHelp.com » Номер 1 в MathCad Assignments
Оператор суммирования суммирует выражение по всем значениям индекса. Оператор повторного продукта работает почти так же. Требуется произведение выражения на все значения индекса
Чтобы создать оператор суммирования на листе:
• Щелкните пустое место.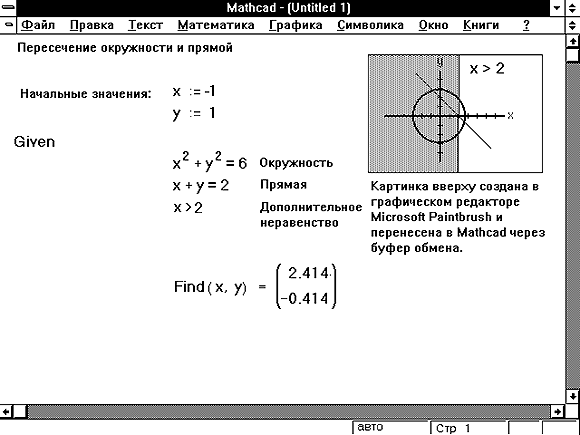 Затем введите [Ctrl][Shift]4. Появляется знак суммирования
Затем введите [Ctrl][Shift]4. Появляется знак суммирования
с четырьмя заполнителями
Суммирование и произведение
В поле слева от знака равенства введите имя переменной. Эта переменная является индексом суммирования. Он определен только внутри оператора суммирования, и поэтому L- _ не влияет на определения переменных вне оператора суммирования и не зависит от них.
Суммирование и произведение
• В заполнителе справа от знака равенства введите целое число или любое выражение, которое дает целое число
Суммирование и произведение
• В оставшемся заполнителе введите давление, которое вы хотите суммировать. Обычно это выражение включает в себя индекс пары круглых скобок вокруг заполнителя.
Суммирование и произведение
Повторяющиеся произведения аналогичны. Просто введите [Ctrl][Shift]3 и заполните заполнители, как описано ранее
. На рис. 12-1 показано несколько примеров использования операторов суммирования и произведения. Вы можете использовать суммирование или повторный продукт так же, как и любое другое выражение.
Вы можете использовать суммирование или повторный продукт так же, как и любое другое выражение.
Чтобы оценить несколько суммирования, поместите другое суммирование в последний заполнитель первого суммирования. Пример этого показан в нижней части рисунка 12-1.
Суммирование и произведение
При использовании оператора суммирования, показанного на рисунке 12-1, суммирование должно выполняться по целым числам с шагом в единицу. Mathcad предоставляет более общие версии этих операторов, которые могут использовать любую переменную диапазона, которую вы определяете как индекс суммирования. Чтобы использовать эти операторы, сначала определите переменную диапазона. В следующем примере введите i :1, 2; 10.Затем сделайте следующее:
Если вы не хотите тратить время на щелчок по каждому заполнителю, вы можете ввести предыдущее выражение, набрав
Также существует обобщенная версия повторного продукта. Чтобы использовать его, введите #. Затем заполните два заполнителя
.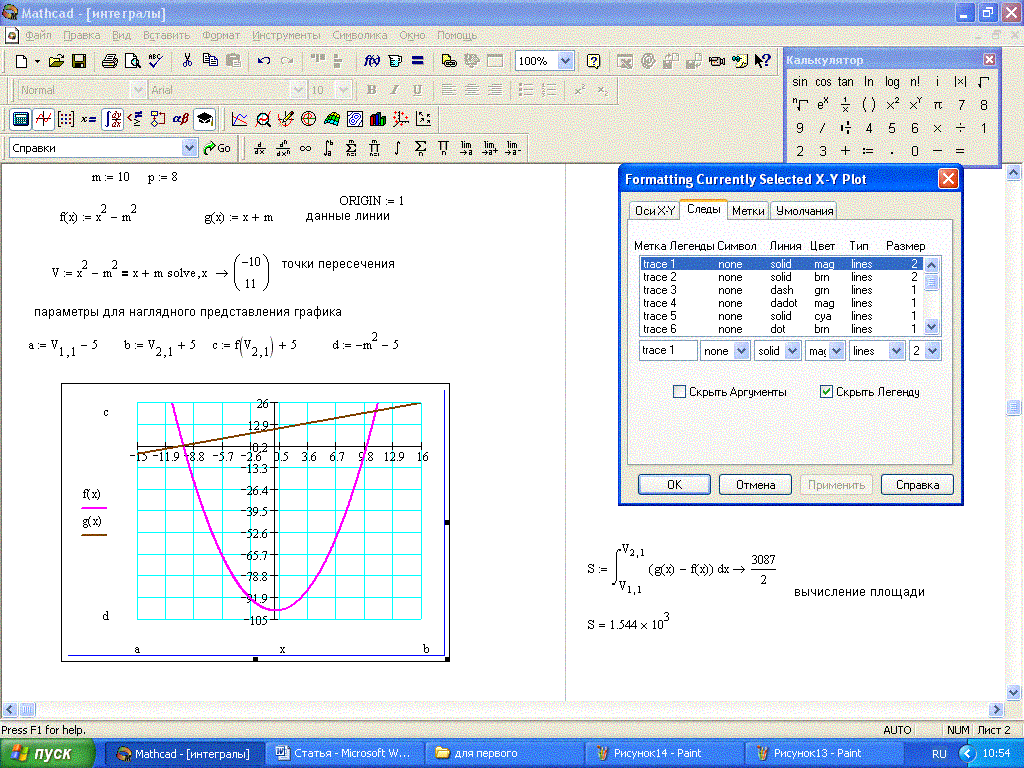 На рис. 12-2 показано несколько примеров применения операторов суммы диапазона и произведения диапазона. Эти операторы, в отличие от операторов суммирования и произведения, созданных с помощью [Ctrl][Shift]4 и [Ctrl][Shift]3, не могут работать по отдельности. Они требуют существования переменной диапазона. Однако обратите внимание, что одну переменную диапазона можно использовать с любым количеством этих операторов.
На рис. 12-2 показано несколько примеров применения операторов суммы диапазона и произведения диапазона. Эти операторы, в отличие от операторов суммирования и произведения, созданных с помощью [Ctrl][Shift]4 и [Ctrl][Shift]3, не могут работать по отдельности. Они требуют существования переменной диапазона. Однако обратите внимание, что одну переменную диапазона можно использовать с любым количеством этих операторов.
Вы можете использовать суммирование и повторные произведения так же, как и любое другое выражение. Чтобы оценить множественные суммы, используйте две переменные диапазона, как показано на рисунке 12-2.
Суммы диапазонов и произведения диапазонов.
Верхний предел суммирования переменных
Оператор суммирования диапазонов Mathcad проходит через каждое значение переменной диапазона, которое вы помещаете в нижний заполнитель. При разумном использовании логических выражений можно суммировать только до определенного значения. На рис. 12-3 терм i ~ x возвращает значение 1, когда оно истинно, и 0, когда оно ложно. Хотя оператор суммирования по-прежнему суммирует каждое значение индекса суммирования, те члены, для которых i > x, умножаются на 0 и, следовательно, не участвуют в суммировании.
12-3 терм i ~ x возвращает значение 1, когда оно истинно, и 0, когда оно ложно. Хотя оператор суммирования по-прежнему суммирует каждое значение индекса суммирования, те члены, для которых i > x, умножаются на 0 и, следовательно, не участвуют в суммировании.
Вы также можете использовать операторы суммирования и произведения с четырьмя заполнителями для вычисления сумм и произведений с переменным верхним пределом, но обратите внимание, что верхний предел в этих операторах должен быть целым числом
Переменный верхний предел суммирования
Вектор- оператор суммирования
Операция суммирования элементов вектора настолько распространена, что Mathcad предоставляет для нее специальный оператор. В то время как обычный оператор суммирования суммирует ранжированное выражение, оператор векторной суммы суммирует элементы вектора без использования переменной диапазона
Чтобы просуммировать все элементы вектора v, определенные в другом месте на листе, выполните следующие действия:
• Щелкните в пустом месте или на заполнителе.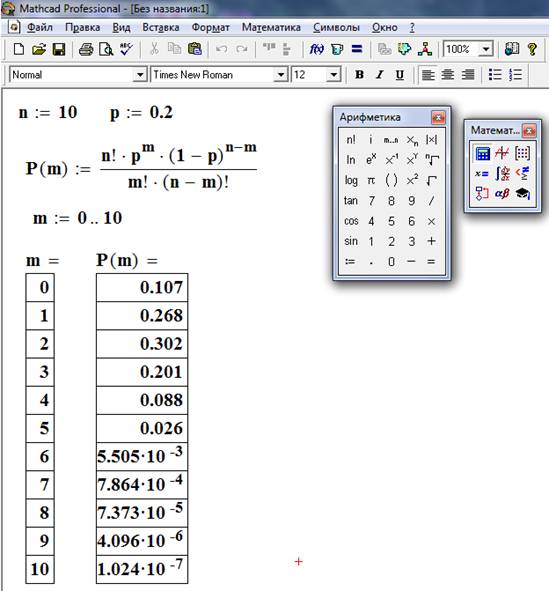 Затем нажмите [Ctrl]4.
Затем нажмите [Ctrl]4.
Переменный верхний предел суммирования
Производные
Вы можете использовать оператор производной Mathcad для вычисления производной функции в определенной точке первая производная должна быть точной в пределах 7 или 8 значащих цифр при условии, что значение, при котором вы оцениваете производную, не слишком близко к сингулярности функции. Точность этого алгоритма имеет тенденцию к уменьшению на одну значащую цифру при каждом увеличении порядка производной (см. раздел «Производные более высокого порядка» на стр. 245)
Примеры дифференцирования Mathcad.
Имейте в виду, что результатом дифференцирования является не функция, а одно число: вычисленная производная при указанном значении переменной дифференцирования. В предыдущем примере производная от x3 — это не выражение 3×2, а 3×2, оцененное при x = 2. Если вы хотите вычислить производные символически, см. главу 17, «Символическое вычисление». »
Хотя дифференцирование возвращает только одно число, вы все же можете определить одну функцию как производную от другой. Например
Например
Derivatives
Evaluatingfix) вернет численно вычисленную производную g(x) в .x .
Вы можете использовать эту технику для оценки производной функции во многих точках. Пример этого показан на Рисунке 12-5.
Вычисление производной функции в нескольких точках
Вычисление производной функции в нескольких значениях, хранящихся как элементы вектора.
Есть несколько важных моментов, которые следует помнить о дифференцировании в Mathcad:
• Дифференцируемое выражение может быть вещественным или комплексным.
• Переменная дифференцирования должна быть именем одной переменной. Если вы хотите вычислить производную при нескольких различных значениях, хранящихся в векторе, используйте метод, показанный на рис. 12-6. в определенной точке.
В качестве примера, вот как вы могли бы оценить третью производную от x9относительно x в точке x = 2:
• Сначала определите точку, в которой вы хотите оценить производную. Введите x:
Производные более высокого порядка
• Нажмите на выражение выше и справа от предыдущего заполнителя и введите 3. Это должно быть целое число от 0 до 5 включительно. Обратите внимание, что местозаполнитель в числителе автоматически отражает то, что вы ввели. При n = 0 он просто возвращает значение самой функции.
Это должно быть целое число от 0 до 5 включительно. Обратите внимание, что местозаполнитель в числителе автоматически отражает то, что вы ввели. При n = 0 он просто возвращает значение самой функции.
Расчет и построение диаграмм сдвига и изгибающего момента в Mathcad | PTC
Примечание редактора. Эта статья блога изначально была написана в виде рабочего листа PTC Mathcad Prime. Чтобы получить наилучшие впечатления от чтения, загрузите рабочий лист Mathcad Prime 8 здесь. Если вам нужна программа для просмотра листов Mathcad Prime, загрузите Mathcad Prime бесплатно здесь.
Грузовой автомобиль, едущий по мосту, вызывает отклонение опорных балок, что приводит к различным напряжениям в балках. Точно так же, когда вы идете по полу в своем доме, балки или балки прогибаются под вашим весом. Прогиб является результатом нагрузки, которая связана с сдвигом, изгибающим моментом, наклоном балки и прогибом балки. В этом блоге и нескольких последующих я расскажу, как можно использовать Mathcad для расчета, построения графиков и получения этих взаимосвязей.
Построение эпюр поперечного и изгибающего моментов свободно опертых балок является одним из заданий базового курса инженерной статики. Mathcad можно использовать для расчета сдвигов и моментов, а также для построения диаграмм сдвигающих и изгибающих моментов.
В этом блоге я покажу, как это сделать для свободно опертых балок с различными условиями нагрузки.
Я сторонник создания функций, которые можно использовать несколько раз, а не просто решать одну проблему. Итак, во-первых, давайте создадим несколько функций, которые помогут решить и построить диаграммы сдвига и изгибающего момента для равномерно нагруженной свободно опертой балки.
Рисунки в этом блоге были созданы в Microsoft PowerPoint как встроенные объекты. Если вы загрузите связанный файл Mathcad и дважды щелкните рисунок, он откроется в PowerPoint.
Сначала рассчитаем левую реакцию, R A , суммируя момент относительно точки B, а затем рассчитаем правую реакцию, R B , суммируя вертикальные нагрузки.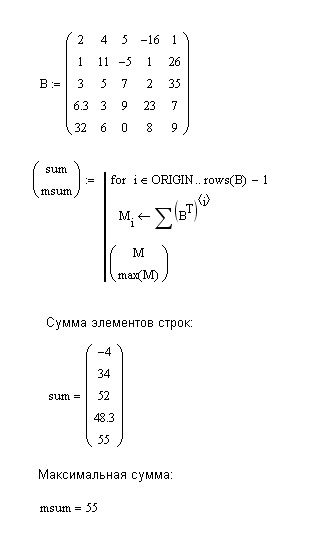
После написания этих функций результаты будут протестированы. Момент по часовой стрелке будем считать положительным.
Переменная «Пролет» — это длина балки, а переменная «w» — равномерная нагрузка (сила/длина) по длине балки. Поскольку Mathcad поддерживает единицы измерения, пролет и нагрузка могут быть выражены в любых единицах длины и силы.
Стрелка вправо в приведенных ниже функциях — это Оператор вычисления символов из раздела Symbolics на вкладке Math . Он обеспечивает символическое решение, а не числовое решение.
Далее напишите функцию для сдвига на расстоянии x путем суммирования вертикальных нагрузок. Сдвиг на расстоянии x слева равен левой реакции за вычетом нагрузки, приложенной к балке между левой и расстоянием x (w*x).
Теперь напишите функцию для момента на расстоянии x, суммируя моменты относительно x.
Теперь, когда уравнения написаны, рассчитайте и постройте диаграммы сдвига и момента, используя функции графика XY. Вставьте график из меню Plots в действие Traces s . Выберите XY Plot с помощью кнопки Insert Plot .
Вставьте график из меню Plots в действие Traces s . Выберите XY Plot с помощью кнопки Insert Plot .
Чтобы создать графики, определите значения для пролета и нагрузки, а затем создайте переменную диапазона для точек для построения. Переменная диапазона определяется начальным значением, второе значение которого устанавливает размер шага. Последнее число является конечным значением. Он создан так, как выглядит. Введите первое значение, затем введите запятую и введите второе значение, которое задает размер шага. Затем введите . . и введите конечное значение.
Уравнение для сдвига или момента будет отложено по оси Y.
Повторите проверку, используя метрические единицы. Задайте значения пролета и равномерной нагрузки, а также переменную диапазона z, которая установит точки для построения.
Теперь создадим диаграммы сдвига и момента для точечной нагрузки P, размещенной в любом месте вдоль балки на расстоянии «a» от левого конца.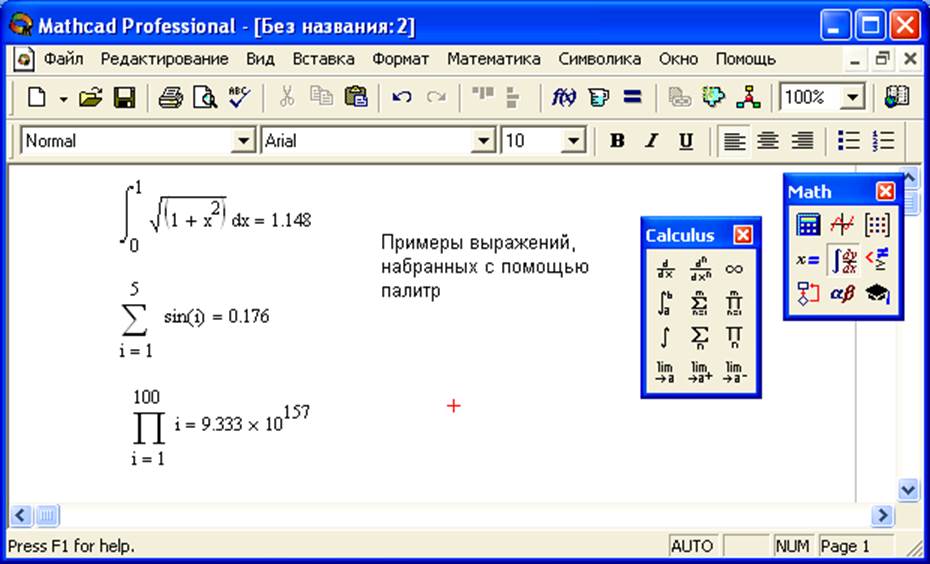 Создайте функции для описания нагрузки, сдвига и момента. Не обращайте внимания на вес бревна в этом упражнении. В этом примере я использую ключевое слово решить с помощью оператора символьного вычисления , чтобы продемонстрировать, как решать для R A .
Создайте функции для описания нагрузки, сдвига и момента. Не обращайте внимания на вес бревна в этом упражнении. В этом примере я использую ключевое слово решить с помощью оператора символьного вычисления , чтобы продемонстрировать, как решать для R A .
Теперь, когда уравнения для точечной нагрузки написаны, рассчитайте и постройте диаграммы сдвига и момента, используя функции графика XY.
Для создания графиков задайте значения для пролета, нагрузки и расстояния, а затем создайте переменную диапазона для точек для построения.
В этом последнем примере выводятся функции для треугольной нагрузки.
Как и в предыдущих примерах, создайте функции для реакций, а затем создайте функции для сдвига и момента.
В этом примере используется ключевое словоsolve с оператором символьного вычисления для получения функций для реакций.
Задайте значения для диапазона, нагрузки и переменной диапазона z, которые будут устанавливать точки для построения. Отобразите значения переменной диапазона и рассчитанные сдвиги и моменты, которые будут включены в график.
Отобразите значения переменной диапазона и рассчитанные сдвиги и моменты, которые будут включены в график.
Теперь, когда получены функции для равномерной нагрузки, точечной нагрузки и треугольной нагрузки, используйте эти функции для объединения нескольких условий нагружения.
Для этих примеров комбинирования нагрузок будут использоваться численные результаты, и должны быть предоставлены значения условий нагрузки. Переменные диапазона будут использоваться для определения точек для построения и местоположений для расчета сдвигов и моментов. Важно оценить переменную диапазона (используя знак =), чтобы преобразовать переменную диапазона в вектор значений. 9.) Это стрелка, указывающая вправо над выражением. Он указывает Mathcad выполнять операцию поэлементно.
В следующих примерах показано сочетание точечных, равномерных и треугольных нагрузок. В этом блог, я использовал диаграммы сдвига и изгибающего момента, чтобы проиллюстрировать многие возможности Mathcad. Кроме того, я показал, как комбинировать функции для равномерной нагрузки, треугольной нагрузки и точечной нагрузки для расчета и построения графиков реакций, сдвигов и изгибающих моментов. Эти примеры иллюстрируют:
Кроме того, я показал, как комбинировать функции для равномерной нагрузки, треугольной нагрузки и точечной нагрузки для расчета и построения графиков реакций, сдвигов и изгибающих моментов. Эти примеры иллюстрируют:
- Значительное использование функций
- Возможности использования оператора символьной оценки , включая использование ключевых слов
- Использование компонента Microsoft PowerPoint для создания графики
- Использование графиков XY
- Определение переменных диапазона для построения графика
- Оценка переменных диапазона для создания вектора значений
- Использование оператора векторизации для выполнения поэлементных операций
Мой следующий блог расширяет эти темы, показывая, как получить функции для максимального изгибающего момента балки для различных условий нагрузки.
Попробуйте Mathcad Prime
Загрузите бесплатную 30-дневную пробную версию Mathcad Prime, чтобы лично увидеть лучшие возможности Mathcad.
Об авторе
Брент Максфилд из Солт-Лейк-Сити, штат Юта. Это идеальное место для него из-за его любви к активному отдыху. Он любит пешие прогулки и катание на лыжах в близлежащих горах, а также любит исследовать каньоны красных скал и пустыни в Южной Юте.
Брент Максфилд — зарегистрированный профессиональный инженер-строитель в штате Юта. Он окончил с отличием Университет Бригама Янга по специальности «строительство» и получил степень магистра инженерного менеджмента в УБЯ. Он был практикующим инженером-строителем в течение 36 лет.
В 2012 году Совет инженеров штата Юта наградил его званием «Инженер года штата Юта». Он активно участвует в профессиональных ассоциациях, входил в состав Совета директоров Ассоциации инженеров-строителей штата Юта и отделения EERI в штате Юта.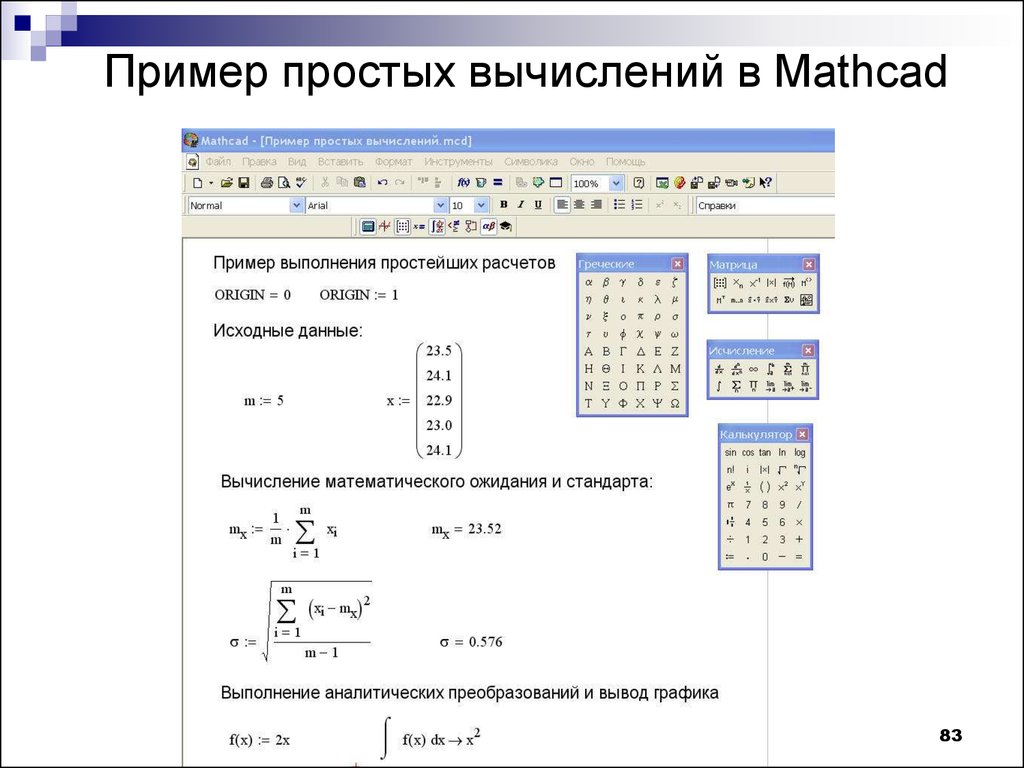
 74 Mb.
74 Mb.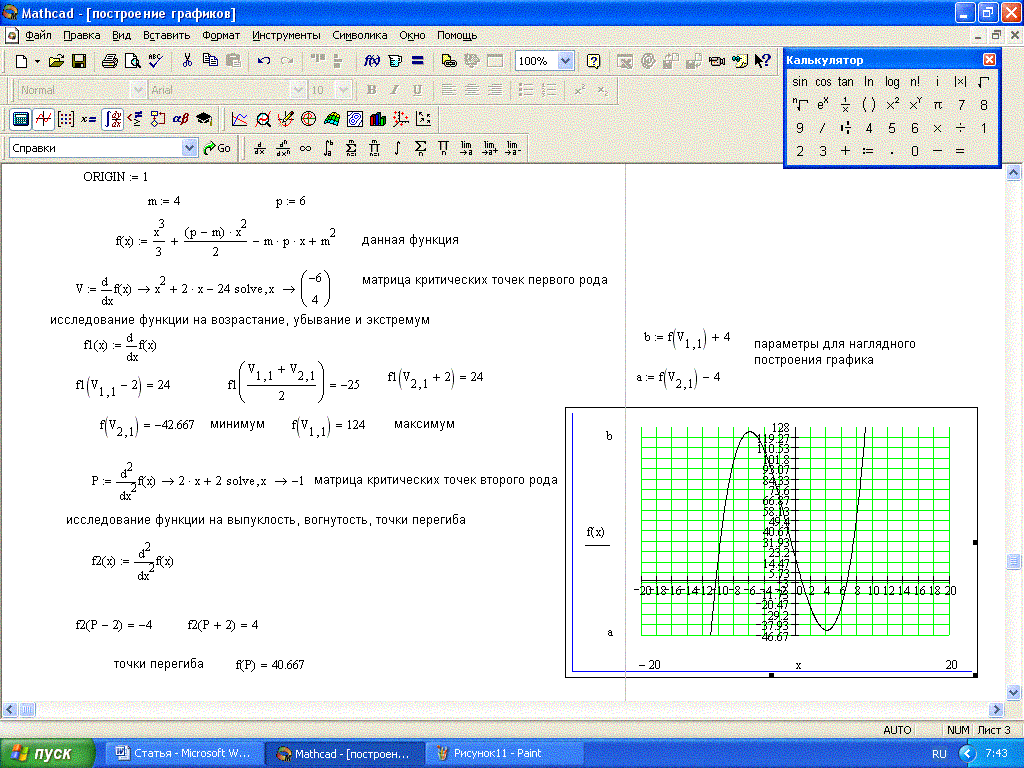 На Листинге приводится пример символьного интегрирования.
На Листинге приводится пример символьного интегрирования.