Символьное решение уравнений в mathcad: Урок 19. Символьные вычисления в Mathcad

Содержание

Урок 19. Символьные вычисления в Mathcad – ключевые слова и модификаторы

Navigation

Павел Демидов 29.09.2014 Уроки Mathcad 0

В этом уроке мы исследуем различные вариации результатов символьных вычислений с использованием ключевых слов и модификаторов. Мы будем применять их для нахождения символьного результата решения уравнений и для разложения функции в многочлен.

Решение уравнений

В качестве первого примера решим квадратичное уравнение:

Обратите внимание, что в записи используется булево равенство. Чтобы решить уравнение, щелкните по нему и вставьте оператор символьного преобразования. В результате получилось то же уравнение:

Нужно добавить ключевое слово “solve” в местозаполнителе над стрелкой:

Так как уравнение содержит четыре переменных, нужно указать, для какой именно следует решить уравнение. В нашем случае это переменная x. Для этого наберите запятую за словом “solve

”. В результате появится местозаполнитель для модификатора x:

Как видно, уравнение имеет два корня.

В следующем примере мы рассмотрим кубическое уравнение. Для констант следует указать значения, так как общее решение будет слишком громоздким.

Получено три корня уравнения, два из которых являются комплексными. Комплексное решение можно подавить, используя второе ключевое слово “assume” и модификатор “real” :

Другой пример – пересечение двух окружностей одного радиуса. Точки пересечений должны удовлетворять сразу двум уравнениям. Одна окружность смещена на расстояние ? вдоль оси абсцисс.

Чтобы решить систему, запишем уравнения в вектор. Так как нужно решить и для переменной x, и для переменной y, необходимо записать два модификатора:

Ответ представлен в качестве матрицы. Здесь два решения – две строки матрицы: «иксы» – первый столбец (они равны), «игреки» — второй (они различны).

Если ?>2r, решение будет комплексным.

Перед тем, как решать уравнение, упростите его, насколько можете. Но даже в этом случае решение может получиться громоздким, или оно вообще может быть не найдено.

Ключевые слова “series” и “coeffs”

Mathcad может разложить функцию в ряд – с помощью ключевого слова “series”. Вы можете добавить два местозаполнителя с помощью запятых:

Главный местозаполнитель содержит ключевое слово, второй – переменную, а третий – порядок разложения. Разложение выполняется в окрестности точки 0.

Если нужно разложить, например, натуральный логарифм в окрестности точки x=1, добавьте еще один модификатор:

Можно проверить, насколько полученное разложение соответствует изначальной функции:

В Mathcad можно вычислять сумму ряда символьно:

Тесно связанно с “series” ключевое слово “coeffs”. Проиллюстрируем ее на примере разложения экспоненты:

“Coeffs” дает вектор коэффициентов любого многочлена. Этот вектор начинается с низшего порядка.

Ключевые слова можно комбинировать:

Резюме

В этом уроке мы познакомились с ключевыми словами “solve”, “series” и “coeffs”:

Ключевые слова вводятся над стрелкой оператора аналитического преобразования.
Модификаторы следует вводить за ключевым словом через запятую.
Ключевое слово “solve” решает уравнение, введенное перед ним.
С помощью модификатора определите ключевому слову “solve”, для какой переменной следует решить уравнение.

Вывод можно ограничить, используя модификаторы с булевыми функциями.
Систему уравнений для решения с помощью “solve” следует поместить в вектор.
Ключевое слово “series” может разложить функцию в ряд.
Важные модификаторы для ключевого слова series:

переменная, по которой происходит разложение;
порядок разложения;
точка, в окрестности которой происходит разложение.

Вектор коэффициентов ряда (или другого многочлена) можно найти с помощью ключевого слова “coeffs”.

About Павел Демидов

Выпускник МГТУ им. Н.Э. Баумана, технический специалист по продуктам PTC Mathcad и Solid Edge.

View all posts by Павел Демидов →

Урок 18. Символьные вычисления в Mathcad

Урок 20. Преобразование выражений в Mathcad

5.1.3. Системы уравнений MathCAD 12 руководство

RADIOMASTER

Лучшие смартфоны на Android в 2022 году

Серия iPhone от Apple редко чем удивляет. Когда вы получаете новый iPhone, общее впечатление, скорее всего, будет очень похожим на ваше предыдущее устройство. Однако всё совсем не так в лагере владельцев устройств на Android. Существуют телефоны Android всех форм и размеров, не говоря уже о разных ценовых категориях. Другими словами, Android-телефон может подойти многим. Однако поиск лучших телефонов на Android может быть сложной задачей.

Документация Схемотехника CAD / CAM Статьи

MathCAD 12 MatLab OrCAD P CAD AutoCAD MathCAD 8 — 11

Главная
База знаний
CAD / CAM
MathCAD 12

Нелинейные алгебраические уравнения
5.1. Символьное решение уравнений
- 5.1.1. Вычислительный блок Given / Find
- 5.1.2. Одно уравнение
- 5.1.3. Системы уравнений
- 5.1.4. Решение уравнений при помощи меню
5.2. Численное решение уравнений
- 5.2.1. Системы уравнений: функция Find
- 5. 2.2. Уравнение с одним неизвестным: функция root
- 5.2.3. Корни полинома: функция polyroots
- 5.2.4. Локализация корней
5.3. О численных методах
- 5.3.1. Метод секущих: функция root
- 5.3.2. Градиентные методы: функция Find
- 5.3.3. Метод продолжения по параметру

Символьное решение системы алгебраических уравнений отличается от описанного случая одного уравнения только количеством соотношений, задаваемых после ключевого слова Given. Соответственно, число неизвестных также может быть любым, причем необязательно равным числу уравнений. Если система уравнений имеет не обособленные решения, а целые семейства решений, то соответствующие результаты выдаются символьным процессором Mathcad в виде выражений, формально зависящих от одной из переменных как от параметра (пример решения одного уравнения с тремя неизвестными был приведен ранее в последних двух строках листинга 5. 3).

Решение системы двух нелинейных уравнений иллюстрирует листинг 5.7. Нахождение символьным процессором его обоих корней визуализируется на графике, приведенном на рис. 5.2. На нем каждое из уравнений показывается в виде зависимости у(х): первое — сплошной кривой, а второе — пунктиром. Поскольку первое уравнение является квадратичным, то оно определяет на плоскости XY параболу, и поскольку второе уравнение линейное, то оно соответствует на графике прямой линии. Очевидно, что две точки пересечения кривых соответствуют одновременному выполнению обоих уравнений, т. е. их координаты равны искомым действительным корням системы.

Рис. 5.2. Графическая интерпретация решения системы двух уравнений (см. листинг 5.7)

Листинг 5.7. Символьное решение системы двух уравнений

Нравится

Твитнуть

Теги MathCad САПР

Сюжеты MathCad

Глава 1 Основы работы с системой Mathcad 11

9873 0

Глава 10 Работа с информационными ресурсами Mathcad 11

6913 0

Глава 2 Работа с файлами Mathcad 11

12323 0

Комментарии (0)

Вы должны авторизоваться, чтобы оставлять комментарии.

Вход

О проекте Использование материалов Контакты

Новости Статьи База знаний

Радиомастер
© 2005–2022 radiomaster.ru

При использовании материалов данного сайта прямая и явная ссылка на сайт radiomaster.ru обязательна. 0.2672 s

[PDF] Рабочий лист MathCAD 3 – Корни, решение блоков и символьные вычисления

Рабочий лист Ph46010 MathCAD 3 Корни, блоки решения и символьная математика Цель этого рабочего листа — познакомить вас с различными методами решения в MathCAD. К концу листа вы будете знать, как:  Использовать функцию root() для решения уравнений с одной переменной  Использовать функцию polyroots() для поиска нескольких корней многочлена  Использовать блок решения для решения более сложных систем уравнения  Используйте символьный процессор для обработки и решения уравнений

Этот рабочий лист представляет собой ряд примеров, которые иллюстрируют и знакомят с этими принципами. Проработайте столько из них, сколько сможете.

По крайней мере, вы должны прочитать весь лист, чтобы получить общее представление о теме.

Упражнение 1. Использование функции root() В этом упражнении мы будем использовать функцию root() для решения некоторых простых уравнений.      

Запустите MathCAD и создайте новый пустой рабочий лист. Первое уравнение, для которого мы попробуем найти решение, это ex = x2. Чтобы использовать корневую функцию, она должна быть в форме f(x )=0, поэтому перепишите уравнение в этой форме и начертите его. Добавьте линии сетки на график, чтобы помочь оценить точку, в которой кривая пересекает линию y=0. Вы должны настроить пределы осей графика, чтобы увеличить область, где линия пересекает ось. Когда вы закончите, ваш график должен выглядеть так, как показано ниже:

F (x)

x 2

1 F (x) 0

0,5

,2005

Ph46010 

MathCAD Example Sheet 3

Изучив график, вы можете увидеть, что решение будет лежать между –1 и –0,5, так как выборка и используйте корневую функцию, чтобы получить точное значение. 0,75

root( f( x)  x)  0,703

Успешно решив это уравнение, используйте тот же метод для решения следующих уравнений. В каждом случае используйте график функции, чтобы найти приближенные решения, прежде чем решать с помощью root(). 1,423  x

8,114238  x 8,537238 0

 

sin(x) cos(x)

90 Уравнение будет иметь кубические корни. Это будет иметь много решений



7 x

Сложные корни требуют комплексного предположения

2 x 6

Упражнение 2. Влияние допуска на решения Функция root() использует итеративный метод, который использует последовательные догадки, чтобы сойтись в решении. Существует системная переменная TOL, которая определяет, насколько близка функция к 0, прежде чем mathCAD решит, что она достигла решения. Небольшое значение TOL, как правило, дает более точные решения, но для получения результата может потребоваться больше времени. В этом упражнении мы увидим, как значение TOL меняет результат решения. Следующее квадратное уравнение имеет два совпадающих корня: 9 x

12 x 4

Постройте квадратное уравнение и увеличьте площадь корней. Используйте следующий сегмент рабочего листа, чтобы увидеть, как изменение значения TOL меняет решения, предлагаемые MathCAD. TOL

0,0001

S OLN1 CORT (F (x)  X)

S OLN1, 0,66898

F (S oln1)  4,82364  100003

0,5

9444 SO OLN224 SOLN224 SOLN224 SOLN 2

0,5

4 SH OLN222364 SOLN 2

0,5

944. root( f( x)  x)

s oln2 0,66364

f( s oln2)  8,2614  10

Значение TOL можно изменить с помощью пункта меню в mathCAD (Математика|Опции|Встроенные переменные|TOL), но метод явная установка системной переменной на листе предпочтительнее, поскольку она показывает, что изменяется. Поскольку TOL уже определен системой, вам придется заставить систему ввести оператор присваивания, используя клавишу «:» или выбрав := в оценочной палитре.

Ph46010

MathCAD Пример листа 3

Упражнение 3. Использование функции Polyroots() для получения корней многочленов многочлен за одну операцию. Его преимущество заключается в том, что все корни, как действительные, так и комплексные, возвращаются сразу и нет необходимости указывать предполагаемые значения. Например, чтобы найти все корни кубического уравнения из упражнения 1, сделайте следующее: 3

1,423  x

8.114238  x

8.537238 аргумент для функции polyroots(), вставив матрицу с 4 строками и одним столбцом. Теперь используйте polyroots() для поиска решений следующих многочленов.    

2 7 x 2 x 6 2 9 x 12 x 4 4 2 3 9 x 13 x 12 x 12 x 4 4 3 2 x 20  x 87  x 180  х 864

Можно ли с помощью поликорней найти 3 кубических корня из -1 и 4 корня четвертой степени из -1 ?

Ph46010

MathCAD Пример листа 3

Упражнение 4. Использование блока решения для решения более сложных задач. Блок решения — это еще один итеративный метод, доступный в mathCAD, который позволяет решать до 50 уравнений с 50 неизвестными. Уравнения не обязательно должны быть полиномами и могут включать неравенства (,,). Каждому из неизвестных должно быть присвоено начальное предполагаемое значение. Мы начнем с нескольких простых примеров и перейдем к более сложным ситуациям. В первом примере будет использоваться блок решения для нахождения квадратного корня из 3, начиная с предполагаемого значения 2. x

Дано 2

3 0

find( x)  1,73205

Начальное приближенное значение определяется первым завершает блок решения и возвращает решение(я)

Обратите внимание на использование полужирного знака равенства (=) или оператора «равно» в блоке решения. Это символ, отличный от оператора присваивания (:=) или оператора «вывести значение переменной» (=). Оператор «равно» широко используется в блоках решения, а также может использоваться в булевой логике. В следующем примере мы будем использовать блок решения, чтобы найти места, где единичный круг пересекается с линией x+y=0. Единичный круг (x2+y2=12) Решения

Строка x+y=0

Как и прежде, мы начинаем наш блок решения с предполагаемых значений для x- и y-

Ph46010 x

MathCAD Sheet Example 3 Y

Значения угадания

Указано 2

Уравнения в решающем блоке

y 1

x y 0

Найти (x  y) 

0,70711

Найти (x  y) 

0,70711

() возвращает вектор решений

0,70711

возвращает значения x,y для одной из точек пересечения. Чтобы вернуть координаты другой точки, мы можем либо начать с приближенных к ней значений, либо поместить условие в блок решения, чтобы принудительно найти решение. x

Указано 2

y 1

Дополнительное неравенство Добавлено в Block

x x x 0 Найти (x  y) 

0,70711 0,70711

MathCAD имеет ограничения на то, что может быть записано в блоке решения (между ‘given’ и ‘find()’), в частности, не разрешено помещать определение переменной или функции. В приведенных выше примерах мы использовали знак равенства «вывести значение» для печати значений x и y в решении. Создав вектор для хранения результатов, мы можем установить переменные для хранения решения за один шаг, как показано ниже: xval yval

find( x  y)

Multiple assignments in single step

xval  0.70711 yval 0.70711

Ph46010

MathCAD Example Sheet 3

Use a solve block to solve Следующие системы уравнений: 3  x 7  y 90

7  x 2  y 25

x 2 y z 4

y 3

3 x 4 y 2 z

x y 1

У вас должно быть 4 точки решения

6 x 2 y z 4

Для первого и последнего из них вы должны проверить свой результат, используя метод обращения матрицы из предыдущего рабочего листа. В конце этой брошюры приведено упражнение, взятое из предыдущего листа с примерами Ph25010, для построения траектории пушечного ядра. Создайте это упражнение на новом рабочем листе и используйте один из приведенных выше методов решения, чтобы определить время, через которое пушечное ядро упадет на землю после выстрела.

Упражнение 5. Символьная математика и работа с уравнениями Наряду с методами численного решения уравнений и систем уравнений, которые мы использовали до сих пор, MathCAD включает в себя мощный символьный процессор, который может обрабатывать уравнения и решать их с помощью алгебраических методов. При работе с символьным процессором полезно вызвать символьную панель инструментов. Чтобы увидеть, как символьный процессор может символически решать уравнения и вычислять выражения, выполните следующие упражнения.

Упрощение выражений Чтобы увидеть, как символьный процессор может помочь упростить выражения, введите следующее выражение в MathCAD. 6x

2x a 7x 3a x

с полем выбора В выражении нажмите «упростить» в палитре символов и посмотрите, как mathCAD упрощает выражение, собирая общие термины и отмена, где это возможно. 6 x

2 x a

7 x 3 a

x упростить

7 x

5 x 4 A

PH46010

MathCad Пример листа 3

Используйте символический процесс, чтобы упростить следующие выражения: 3 x x x x.

7 A

6.5  P

2 x

6 A

5,7  Q

6.9

1,2  P

7 A

(2 Q)

3 3 6 3 R S n 4 3 R M n

Расширение выражений Чтобы увидеть, как символьный процессор может расширять выражения, поместите прямоугольник выбора в выражение и нажмите «расширить» в символьной палитре. После ключевого слова расширения есть заполнитель, вы должны либо заполнить переменную, которую хотите расширить, либо удалить заполнитель. Похоже, в mathCAD есть ошибка, так как кажется, что не имеет значения, что находится в заполнителе.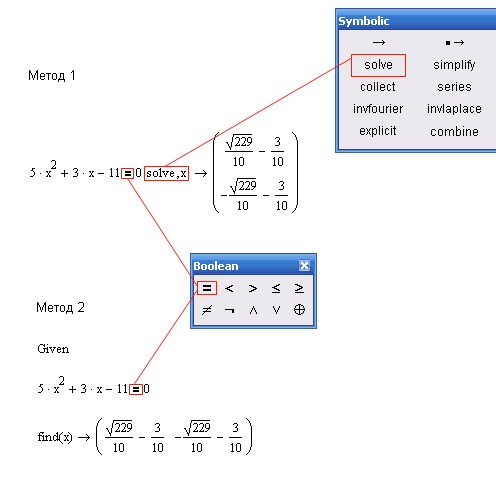 3

(g h) Расширение

3 G H

2 3 G  H

Распределите следующие примеры: 2 y  (x 7   h

. y)

(P  x q)  (r x s) 1,23  A

2 2

2 2 4.56  B  7,89  B

6.66 

2.7  a

4.2  b

«Неопределяемые» переменные При символьной обработке уравнений mathCAD будет использовать числовые значения любых уже определенных переменных. В качестве примера рассмотрим следующее биномиальное разложение: x

1 2

( x y) расширить

2 y y

Здесь mathCAD использовал значение 1 вместо x перед выполнением расширения. В зависимости от вашей проблемы это не всегда может быть тем, чего вы хотите достичь.

Ph46010

MathCAD Example Sheet 3

Чтобы отменить определение переменной, используйте оператор присваивания, чтобы установить переменную равной самой себе.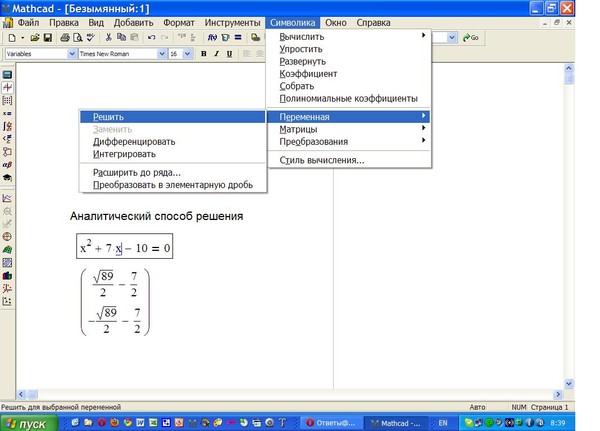 MathCAD понимает это рекурсивное определение, чтобы отменить определение переменной. Это показано ниже: x

1 2

(x y) Расширение x

2 y y y

x 2

(x y) Расширение

2 2 x y y

. Чтобы решить уравнение с помощью символьного процессора, введите уравнение, которое вы хотите решить, а затем нажмите «решить» на символьной панели инструментов. Заполните переменную, которую вы хотите найти, в заполнитель и нажмите, чтобы увидеть результат. 2

x 2 0 решение x

1 2

Обратите внимание, что MathCAD не может найти решение для описанного выше случая, когда x уже определен, вы должны отменить определение x, используя введенное выше рекурсивное определение. Теперь решите следующие уравнения с помощью символьного процессора: ( x 1)  ( x 1) 0 2

1 0

( y 2)  0 y 3 z

2 z

8 0

Ph46010

Math Sheet0003

Упражнение 6. Задача о консервной банке Это упражнение взято из листа с примерами для первого года обучения и показывает, как мы можем использовать символьный процессор в MathCAD для решения реальной задачи. Он представлен как проработанный пример, который вы должны скопировать и убедиться, что вы понимаете шаги для достижения решения. Производитель жестяных банок хочет максимально увеличить объем, содержащийся в банке, при минимизации количества металла, используемого для изготовления банки. Покажите, что при заданном количестве металла объем банки будет максимальным, если радиус равен половине высоты. Начните с записи выражений для объема и площади банки через радиус r и высоту h. 2 Том   r  ч

Площадь ( 2    r  h)

2   r

Используйте жирный знак равенства при построении этих двух уравнений, поскольку мы будем обрабатывать их с помощью символьного процессора. Скопируйте выражение для площади и используйте символьный решатель, чтобы получить выражение для h через площадь и r. Площадь (2  ϩ  r  H)

2  ϩ  R Solve H 2

1 2

ПЕАТЕЛЯ 2  УТАЖА и используйте символьную машину, чтобы заменить h в выражении выражением, которое вы только что получили: 2 Vol   r  h subs tituh 

Площадь 2  ϩ  r (ϩ  r)

1 2

VOL

1  2 r Площадь 2  ϩ r

У нас теперь есть выражение для объема банки с точки зрения площади и радиуса. Учитывая, что площадь постоянна, dVol/dr будет равно нулю при максимальном объеме. Скопируйте и вставьте выражение для объема и используйте символическое дифференцирование, чтобы дифференцировать его относительно r. d 1  2 r Область 2    r dr 2

1 2

Область 3    r

Используйте символ  из палитры символов или введите . Теперь у нас есть выражение для dVol/dr, мы можем найти значение r, где оно равно нулю. © DPL 2002,2005

PH46010

MathCad Пример листа 3 1

1 2

Площадь 3  ϩ  R

0 SOLVE R

1   2 6 (. Площадь) ( 6  ) 1

1    2 6 (  Площадь)  (6 )

MathCAD предоставил два решения, соответствующие положительным и отрицательным значениям r. Нас интересуют положительные значения r, поэтому мы скопируем первое решение и подставим обратно выражение для площади, чтобы получить выражение для r в точке максимального объема. 1

1    2 6 (Область) заместителя  (2  ϩ  r  H) (6 ϩ)

1      6 ϩ 2А (6).

2   r

Теперь у нас есть выражение для r через r и h, которое максимизирует объем. Итак, теперь мы можем найти r через h. 1

1       2 6 ϩ 2 ϩ r h 2 ϩ  r  (6 ϩ)

0 r s olve r

1 2

Пренебрегая случаем r=0, мы теперь имеем решение, согласно которому максимальный объем достигается при r=h/2. Обратите внимание, что можно комбинировать несколько символьных операций за один шаг, как показано ниже: (6 ϩ)

Solve r 0

Заместитель  (2  ϩ  r  H)

2 ϩ  r

2 ϩ r

1       6  2rh ( 6  )

2   r

В качестве упражнения вернитесь к задаче о пушечном ядре, упомянутой ранее, и, используя символьный процессор, выведите выражение для расстояния, которое пройдет пушечное ядро, прежде чем оно попадет в цель. земли с точки зрения начальной скорости, V0 и угла пушки, . Используйте символическое дифференцирование, чтобы найти угол , который максимизирует дальность полета пушки.

Ph46010

Лист примеров MathCAD 3

Приложение 1. Построение пути пушечного ядра. Это упражнение взято из предыдущего курса Ph25010 и показывает, как MathCAD может прогнозировать простую траекторию пушечного ядра. До сих пор мы использовали возможности построения графиков mathCAd для построения простой функции, такой как sin(x) против x, а также видели, как мы можем построить один вектор относительно другого. Часто мы хотим построить график одной функции относительно другой, например, у нас могут быть функции, которые описывают высоту и расстояние до снаряда как функцию времени. Сопоставляя одну функцию с другой, мы можем построить траекторию снаряда. В следующем упражнении показана траектория пушечного ядра, выпущенного под определенным углом с определенной начальной скоростью. 

30 DEG

Vinitial 50

M S

 () VXINITIAL VINITIALCOS

SEPERATE ИСТИННАЯ ВОЗДЕЙСТВА В X-& Y-COMPONENT пушка и начальная скорость, а затем продолжает разбивать скорость на компоненты в направлениях x и y. После того, как вы создали эти операторы, можно создать две функции для описания положения пушечного ядра в направлениях X и Y, используя простые уравнения движения при постоянном ускорении. Мы пренебрегаем сопротивлением воздуха, и положение по оси x легко вычисляется по начальной скорости по оси x. Точно так же положение в направлении y может быть рассчитано с использованием встроенного значения «g» для ускорения под действием силы тяжести. Это действует вниз, тогда как наше исходное направление для оси Y вверх, отсюда и знак минус в уравнении. Позиция X(t)

 VXIinitialt

Pos Y( t )

 VYInitialt

1 2 gt 2

Остается только выбрать подходящий диапазон временных шагов и построить графики функций. Хороший диапазон составляет от 0 до 6 секунд с шагом 0,1 секунды. Обратите внимание, что единицей времени должны быть секунды, и посмотрите, как это должно быть включено во все 3 условия, определяющие переменную диапазона.

Ph46010

Пример листа MathCAD 3

0 S  0,1 S  6 S

10 Posy (T) 0

9 100

150

50 0003

100

150

50 0003

150

50 0003

200

250

300

PosX ( t )

Я добавил линии сетки по оси Y, которые позволяют оценить, когда пушечное ядро упадет на землю, что в данном случае будет примерно дальность 220м. В качестве упражнения определите значение , дающее максимальный диапазон. Это то значение, которое вы ожидали?

Основы ускорительной физики и техники

PTC Mathcad (PTC 2018) — мощный программный вычислительный инструмент. Это позволяет пользователю создавать, решать и анализировать различные математические задачи. Здесь мы познакомим вас с некоторыми базовыми возможностями Mathcad , а затем применим их для расчета некоторых реальных параметров ускорителя.

Упражнение 1. Редактирование основных уравнений, расчеты и построение графиков 92}{13} = 11,841 \]

Создадим две переменные и решим одно и то же уравнение. Скопируйте уравнение, которое вы только что создали, в другое место на рабочем листе. Вы можете сделать это, щелкнув в любом месте поля уравнения, нажимая клавишу пробела, пока все уравнение не окажется внутри синих линий редактирования, а затем используйте функции копирования и вставки. Замените «7» на переменную, скажем «a», а «13» на другую, например «\(\beta\)» в уравнении, напечатав их. Один из способов вставить бета-версию греческого символа — выбрать «Панели инструментов» в меню «Вид», удерживать нажатой кнопку мыши и отпустить ее, когда курсор находится на греческом языке, а затем выбрать нужный символ. Далее, где-то над уравнением, введите 92}{\beta} = 11,841 \] Попробуйте ввести разные значения для a и \(\beta\).
Mathcad выполняет итерационные вычисления с использованием переменных диапазона . Всякий раз, когда Mathcad встречает переменную диапазона , он вычисляет уравнение для каждого значения этой специальной переменной.
Скопируйте наше существующее уравнение и переменную ‘\(\beta\)’ и вставьте их в другую область. Теперь превратите «a» в переменную диапазона, набрав a:7,14;70 . Matchcad должен ответить
\[ a := 7,14..70 \]
Теперь Mathcad определил ‘a’ так, чтобы он имел значения 7, 14, 21, … 70. Теперь наше уравнение вычисляется для каждого значения ‘a ‘ и результаты приведены ниже. Двойной щелчок в таблице ответов открывает окно параметров отображения. Поэкспериментируйте с ними, чтобы увидеть, на что способен Mathcad.
В Mathcad вы можете определить функцию и решить ее. Еще раз давайте воспользуемся нашим выражением выше. Начните с определения функции А(а): . Заполнитель появляется справа от того, что было напечатано. Либо введите, либо вставьте уравнение, которое мы использовали. Нам также нужно выбрать некоторые значения для «а», чтобы мы могли снова ввести a: 7, 14; 70 . Наконец, нам нужно вычислить некоторые решения нашей функции, поэтому введите A(a)= . Вы должны увидеть что-то вроде:
Другой способ решения этой функции — просто поместить значение «а», которое вы хотите найти, в скобки:
93 \]
Matchad также имеет графические возможности. Давайте построим график значения A(a) в зависимости от «a». Выберите Graph в меню Insert и выберите X-Y Plot . Заполнители отображаются для осей X и Y. Введите или скопируйте/вставьте a для оси X и A(a) для оси Y. Должен получиться график, подобный приведенному ниже:
Двойной щелчок в поле графика открывает окно параметров настройки. Проверь их. Поэкспериментируйте с другими особенностями поля графика.
Упражнение 2. Матрицы
Нажмите View > Toolbars > Matrix , чтобы открыть панель инструментов Matrix. Чтобы создать матрицу, щелкните значок матрицы на панели инструментов (левый верхний угол) или введите Ctrl-M . Создайте следующую матрицу 2X2:
Mathcad может выполнять различные операции с матрицей. Откройте панели инструментов Matrix и Symbolic. Чтобы транспонировать матрицу, используйте пробел, чтобы заключить всю матрицу в рамки редактирования. Выберите Символьная матрица Транспонируйте значок (нижний левый угол) на панели инструментов символов, затем нажмите Введите . Вы должны получить:
Чтобы инвертировать матрицу, выполните ту же процедуру еще раз. На этот раз выберите значок Symbolic Matrix inverse (нижний правый угол) на панели инструментов Symbolic. Mathcad должен создать:
Чтобы найти определитель, выполните ту же процедуру, но выберите определитель символьной матрицы (нижний правый угол) на панели инструментов Symbolic. Mathcad должен выдать:
Создайте еще одну матрицу M и выполните арифметические операции над двумя. Например:
Наконец, Mathcad также позволяет создавать и выполнять математические функции над векторами. Чтобы создать вектор, просто создайте матрицу из одного столбца:
.
Настройте Mathcad , чтобы сделать следующее:
Полезные советы
Ниже приведены некоторые полезные советы и подсказки при использовании Mathcad :
Чтобы изменить параметр, просто щелкайте по нему, пока справа от него не появится курсор, а затем удалите или измените его по своему усмотрению. Когда вы нажмете RETURN , Mathcad обновит весь рабочий лист.