13.1.1. Линейная интерполяция MathCAD 12 руководство
RADIOMASTER
Лучшие смартфоны на Android в 2022 году
Серия iPhone от Apple редко чем удивляет. Когда вы получаете новый iPhone, общее впечатление, скорее всего, будет очень похожим на ваше предыдущее устройство. Однако всё совсем не так в лагере владельцев устройств на Android. Существуют телефоны Android всех форм и размеров, не говоря уже о разных ценовых категориях. Другими словами, Android-телефон может подойти многим. Однако поиск лучших телефонов на Android может быть сложной задачей.
Документация Схемотехника CAD / CAM Статьи
MathCAD 12 MatLab OrCAD P CAD AutoCAD MathCAD 8 — 11
- Главная /
- База знаний /
- CAD / CAM /
- Интерполяция и регрессия
- 13.1. Интерполяция
- 13.1.1. Линейная интерполяция
- 13.1.2. Кубическая сплайн-интерполяция
- 13.1.3. Полиномиальная сплайн-интерполяция
- 13.1.4. Сплайн-экстраполяция
- 13.1.5. Экстраполяция функцией предсказания
- 13.1.6. Многомерная интерполяция
- 13.2. Регрессия
- 13.2.1. Линейная регрессия
- 13.2.2. Полиномиальная регрессия
- 13.2.3. Другие типы регрессии
- 13.2.4. Регрессия общего вида
- 13.3. Ввод/вывод данных
- 13.3.1. Ввод/вывод в текстовые файлы
- 13.3.2. Ввод/вывод в файлы других типов
- 13.3.3. Мастер импорта данных и функция READFILE
Самый простой вид интерполяции — линейная, которая представляет искомую зависимость А(Х) в виде ломаной линии.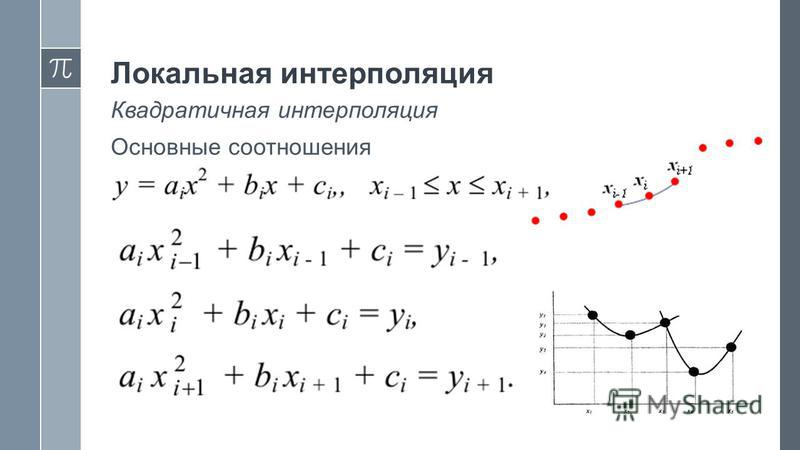
Рис. 13.2. Линейная интерполяция (продолжение листинга 13.1)
Для построения линейной интерполяции служит встроенная функция linterp (листинг 13.1):
- linterp(х,у,t) — функция, аппроксимирующая данные векторов х и у кусочно-линейной зависимостью:
- х — вектор действительных данных аргумента;
- у — вектор действительных данных значений того же размера;
- t — значение аргумента, при котором вычисляется интерполирующая функция.
ВНИМАНИЕ!
Элементы вектора х должны быть определены в порядке возрастания, т. е. Xl<X2<X3<. . .<XN.
Листинг 13.1. Линейная интерполяция
Как видно из листинга, чтобы осуществить линейную интерполяцию, надо выполнить следующие действия:
1. Ввести векторы данных х и у (первые две строки листинга).
Ввести векторы данных х и у (первые две строки листинга).
2. Определить функцию linterp (х, у, t).
3. Вычислить значения этой функции в требуемых точках, например, linterp(х,у,2.4)=3.52, или linterp(х,у,6)=5.9, или постройте ее График, как показано на рис. 13.2.
ПРИМЕЧАНИЕ
Обратите внимание, что функция A(t) на графике имеет аргумент t, а не х. Это означает, что функция A(t) вычисляется не только при значениях аргумента (т. е. в семи точках), а при гораздо большем числе аргументов в интервале (0,6), что автоматически обеспечивает Mathcad. Просто в данном случае эти различия незаметны, т. к. при обычном построении графика функции А(х) от векторного аргумента х (рис. 13.3) Mathcad по умолчанию соединяет точки графика прямыми линиями (т. е. скрытым образом осуществляет их линейную интерполяцию).
Рис. 13.3. Обычное построение графика функции от векторной переменной х (продолжение листинга 13.1)
Нравится
Твитнуть
Теги MathCad САПР
Сюжеты MathCad
Глава 1 Основы работы с системой Mathcad 11
9922 0
Глава 10 Работа с информационными ресурсами Mathcad 11
6948 0
Глава 2 Работа с файлами Mathcad 11
12413 0
Комментарии (0)
Вы должны авторизоваться, чтобы оставлять комментарии.
Вход
О проекте Использование материалов Контакты
Новости Статьи База знаний
Радиомастер
© 2005–2022 radiomaster.ru
При использовании материалов данного сайта прямая и явная ссылка на сайт radiomaster.ru обязательна. 0.2428 s
|
MATHCAD
Для построения линейной интерполяции служит встроенная функция linterp(х, у, t), которая аппроксимирует данные векторов х и у кусочно-линейной зависимостью. Здесь х – вектор действительных данных аргумента; у – вектор действительных данных значений того же размера; t – значение аргумента, при котором вычисляется интерполирующая функция. Элементы вектора х
должны быть определены в порядке возрастания, т.
х1 < х2 < х3 < . . . < xn.
Чтобы осуществить линейную интерполяцию с помощью MathCAD, выполняют следующие действия. В главном меню необходимо выбрать «Вид – Панели инструментов – Матрица», после чего в появившейся панели «Matrix» выбрать «Создать матрицу» на 1 строку и 7 столбцов (по числу экспериментальных точек) и ввести координаты по оси x. Далее с помощью элемента «Транспонирование матрицы» той же панели транспонировать матрицу данных
Аналогичную операцию проводим с координатами по оси у
Далее записываем функцию линейной интерполяции
Чтобы построить график,
необходимо выбрать в главном меню «Вид –
Панели инструментов – График»,
далее на появившейся панели «Graph» выбрать
элемент «Декартов график», после чего на рабочей области программы MathCAD
появится область построения графика. По оси ординат области построения графика
необходимо ввести «A(t), y», а по оси
абсцисс – «t, x». Далее двойным щелчком левой кнопки мыши по области
построения графика необходимо вызвать панель его форматирования, на которой выбрать
закладку «Трассировки», выделить мышью «trace2» и в поле «Символ» выбрать «dmnd». Встроенная функция linterp позволяет вычислить значения функции в требуемых точках. Например, для точки с аргументом x = 1,5 расчёт значения функции интерполяции A(t) будет выглядеть следующим образом: linterp(x, y, 1,5) = 3,05. Далее приведена программа линейной интерполяции.
Рис.
|
||||||||||
Функции интерполяции и прогнозирования » MathCadHelp.com » Номер 1 в назначениях MathCad
Интерполяция включает использование существующих точек данных для прогнозирования значений между этими точками данных. Mathcad позволяет либо соединять точки данных прямыми линиями (линейная интерполяция), либо соединять их участками кубического полинома (кубическая сплайн-интерполяция).
В отличие от функций регрессии, описанных в следующем разделе, эти функции интерполяции возвращают кривую, которая должна проходить через указанные вами точки. Из-за этого результирующая функция очень чувствительна к ложным точкам данных. Если ваши данные зашумлены, вам следует вместо этого рассмотреть возможность использования функций регрессии.
Линейное предсказание предполагает использование существующих значений данных для предсказания значений, выходящих за рамки существующих. Mathcad предоставляет функцию, которая позволяет прогнозировать будущие точки данных на основе прошлых точек данных.
Mathcad предоставляет функцию, которая позволяет прогнозировать будущие точки данных на основе прошлых точек данных.
Всякий раз, когда вы используете массивы в любой из функций, описанных в этом разделе, убедитесь, что каждый элемент в массиве содержит значение данных. Поскольку каждый элемент массива должен иметь значение, Mathcad присваивает 0 всем элементам, которым вы не присвоили явное значение
Линейная интерполяция
При линейной интерполяции Mathcad соединяет существующие точки данных прямыми линиями. Это достигается функцией linterp, описанной ниже.
Чтобы найти интерполированное значение для определенного x, Mathcad находит две точки, между которыми находится значение, и возвращает соответствующее значение y на прямой линии между двумя точками.
Для значений x перед первой точкой в vx Mathcad экстраполирует прямую линию между первыми двумя точками данных. Для значений x за пределами последней точки в vx Mathcad экстраполирует прямую линию между двумя последними точками данных.
Для достижения наилучших результатов значение x должно находиться между наибольшим и наименьшим значениями вектора vx. Функция linterp предназначена для интерполяции. не экстраполяция. Следовательно, расчетные значения x за пределами этого диапазона вряд ли будут полезны. На рис. 14-5 показаны некоторые примеры линейной интерполяции.
Примеры линейной интерполяции. Поскольку случайное число
Интерполяция кубическим сплайном
Интерполяция кубическим сплайном позволяет провести кривую через набор точек таким образом, что первая и вторая производные кривой непрерывны в каждой точке. Эта кривая собирается путем взятия трех соседних точек и построения кубического полинома , проходящего через эти точки. Затем эти кубические многочлены соединяются вместе, чтобы сформировать законченную кривую.
Чтобы построить кривую кубического сплайна через набор точек:
• Создайте векторы vx и vy, содержащие координаты x и y, через которые должен проходить кубический сплайн. Элементы vx должны быть в порядке возрастания. (Хотя мы используем имена vx, vy и vs, в этих названиях переменных нет ничего особенного; вы можете использовать любые имена в своей работе.)
Элементы vx должны быть в порядке возрастания. (Хотя мы используем имена vx, vy и vs, в этих названиях переменных нет ничего особенного; вы можете использовать любые имена в своей работе.)
• Сгенерировать вектор vs := cspline(vx, vy). Вектор vs — это вектор промежуточных результатов, предназначенный для использования с промежуточными значениями.
• Чтобы вычислить кубический сплайн в произвольной точке, скажем, xO, вычислите
(interp(vs, vx, vy, xO), где vs, vx и vy — векторы, описанные ранее.
Обратите внимание, что вы могли бы выполнить ту же задачу, оценив:
Однако с практической точки зрения вы, вероятно, будете оценивать интерполяцию для многих разных точек. Поскольку вызов cspline может занять много времени, а результат не изменится от одной точки к другой, имеет смысл сделать это один раз и просто повторно использовать результат, как описано выше.
На рис. 14-6 показано, как вычислить сплайн-кривую для примера на рис. 14-5.
Кривая сплайна для точек, сохраненных в x и y. Так как случайный
Так как случайный
Обратите внимание, что массив vs должен быть вычислен только один раз, даже для нескольких интерполяций. Поскольку расчеты сплайнов, которые приводят к vs, требуют много времени, более эффективно хранить эти промежуточные результаты в виде вектора, чем пересчитывать их по мере необходимости. В дополнение к cspline Mathcad поставляется с двумя другими функциями кубического сплайна, как описано ниже:
Эти три функции отличаются только граничными условиями:
• Функция !spline создает сплайн-кривую, которая приближается к прямой линии в конечных точках.
• Функция pspline создает сплайновую кривую, которая приближается к параболе в конечных точках.
• Функция cspline создает сплайновую кривую, которая может быть полностью кубической в конечных точках.
Чтобы найти интерполированное значение для определенного x, Mathcad находит две точки , между которыми оно находится. Затем он возвращает значение y для кубического сечения, заключенного между этими двумя точками.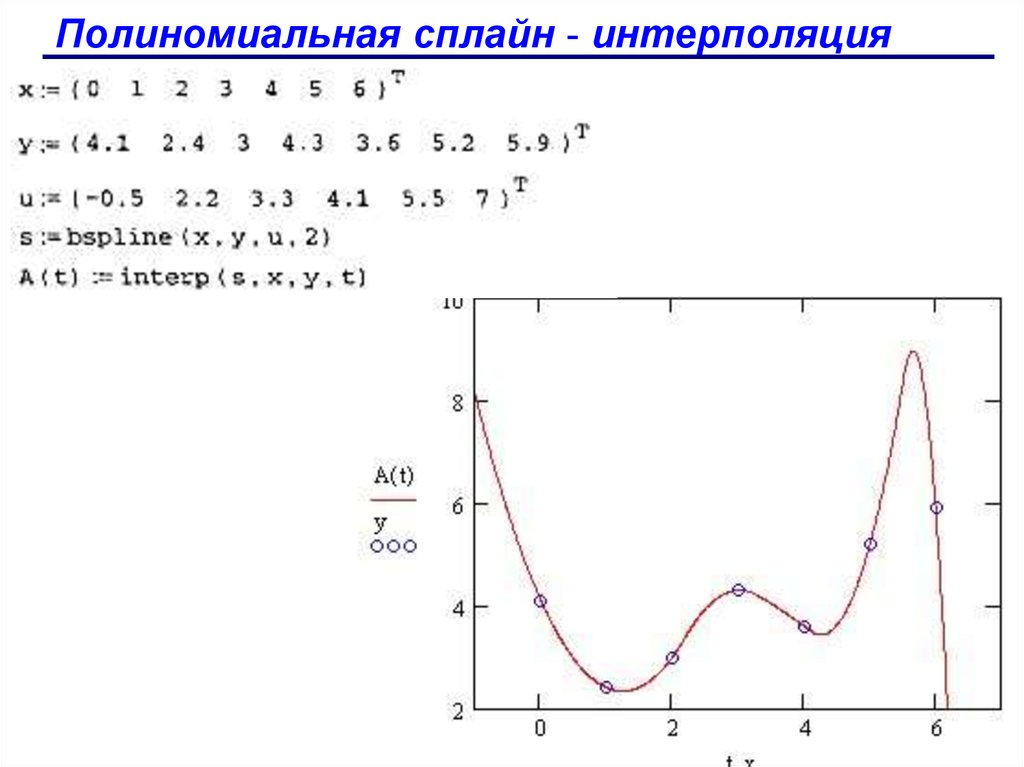 Для значений x до первой точки в vx Mathcad экстраполирует кубическое сечение , соединяющее первые две точки vx. Точно так же для значений x за пределами последней точки vx Mathcad экстраполирует кубическое сечение, соединяющее две последние точки vx.
Для значений x до первой точки в vx Mathcad экстраполирует кубическое сечение , соединяющее первые две точки vx. Точно так же для значений x за пределами последней точки vx Mathcad экстраполирует кубическое сечение, соединяющее две последние точки vx.
Для достижения наилучших результатов не используйте функцию интерполяции для значений x, далеких от установленных точек. Сплайны предназначены для интерполяции, а не экстраполяции. Следовательно, вычисленные значения для таких значений x вряд ли будут полезны.
Интерполяция вектора точек
Оператор векторизации можно использовать для возврата целого вектора интерполированных значений, соответствующего вектору точек данных. Это работает как с interp, так и с linterp.
На рис. 14-7 показано, как выполнить эту операцию. Чтобы применить оператор векторизации к функции, щелкните имя функции и нажимайте [Пробел], пока функция не окажется между двумя строками редактирования. Затем нажмите [Ctrl]- (удерживайте нажатой клавишу [Ctrl] и нажмите минус).
Интерполяция вектора точек. Обратите внимание, что, поскольку они являются случайными
Многомерная кубическая сплайн-интерполяция
Mathcad обрабатывает двумерную кубическую сплайн-интерполяцию почти так же, как и одномерный случай, рассмотренный ранее. Вместо того, чтобы проводить кривую через набор точек таким образом, чтобы первая и вторая производные кривой были непрерывны в каждой точке, Mathcad пропускает поверхность через сетку точек. Эта поверхность соответствует кубическому многочлену от x и y, в котором первая и вторая частные производные непрерывны в соответствующем направлении в каждой точке сетки.
Первый шаг в двумерной сплайн-интерполяции точно такой же, как и в одномерном случае: указать точки, через которые должна проходить поверхность. Однако процедура усложняется, поскольку теперь вам нужно указать сетку точек:
• Создайте матрицу n x 2 Mxy, элементы которой MXYi 0 и MXYi I’ задают координаты x и Y по диагонали прямоугольной сетки. • Создайте матрицу размера n x n Mz, ij-й элемент которой является координатой z, соответствующей точке x = MXYi, 0 и Y = MXYj, I . Это играет точно такую же роль, как vy в одномерном случае, описанном ранее. • Создать вектор vs:= cspline(Mxy, Mz). Вектор vs – это вектор промежуточных результатов, предназначенный для использования с интерп. Для достижения наилучших результатов не используйте функцию интерполяции для значений x и y, далеких от узлов сетки. Сплайны предназначены для интерполяции, а не экстраполяции. Следовательно, вычисленные значения для таких значений x и y вряд ли будут полезны. Линейный прогноз Функции, описанные до сих пор в этом разделе, позволяют находить точки данных, лежащие между существующими точками данных. Возвращает n прогнозируемых значений на основе m последовательных значений из вектора данных v. Элементы в v должны представлять выборки, взятые через равные промежутки времени. Функция прогнозирования использует последние m значений исходных данных для вычисления коэффициентов прогнозирования. Получив эти коэффициенты, он использует последние m точек для прогнозирования координат (m + 1)-й точки, фактически создавая движущееся окно шириной m точек. Использование функции прогнозирования для поиска будущих значений данных. ФОН Предварительные условия для интерполяции [PDF]
[ДОК] Цели интерполяции
[PDF]
[ДОК] Что такое интерполяция? [PDF]
[ДОК] История интерполяции [PDF]
[ДОК] Проверьте свои знания по
История интерполяции [HTML]
[ВСПЫШКА]
[PDF]
[ДОК] ФИЗИЧЕСКАЯ ПРОБЛЕМА Восходящая скорость ракеты дана как функция времени. ЧИСЛЕННЫЙ МЕТОД ПРЯМОЙ МЕТОД Предпосылки для прямого метода
Интерполяция [PDF]
[ДОК] Цели прямого метода
Интерполяция
[PDF]
[DOC] Как работает Direct
Метод работает? [PDF]
[ДОК] Линейная интерполяция [YOUTUBE
8:53] Квадратичная интерполяция
[YOUTUBE
8:17] Кубическая интерполяция — часть 1 из 2
[YOUTUBE
9:37] Кубическая интерполяция — Часть 2 из 2 [ЮТУБ 7:51] Презентация Power Point
[PDF]
[ППТ] Рабочие листы метода
[PDF]
[МКД] Проверьте свои знания прямого метода
[HTML]
[PDF]
[ДОК] МЕТОД ДЕЛЕНОЙ РАЗНОСТИ НЬЮТОНА Предварительные условия для разделенного Ньютона
Разностный полиномиальный метод [PDF]
[ДОК] Цели Newton’s Divided
Разностный полиномиальный метод
[PDF]
[DOC] Как делится число Ньютона
Разностный полиномиальный метод работает? [PDF]
[ДОК] Презентация Power Point
[PDF]
[ППТ] Рабочие листы метода
[PDF]
[МКД] Тест
Ваше знание метода [[HTML]
[FLASH] [PDF]
[ДОК] МЕТОД ЛАГРАНЖА Предпосылки для метода Лагранжа
[PDF]
[ДОК] Цели метода Лагранжа
[PDF]
[DOC] Как работает метод Лагранжа? [PDF]
[ДОК] Презентация Power Point
[PDF]
[ППТ] Рабочие листы метода [PDF]
[МКД] Проверьте свои знания метода Лагранжа
[HTML]
[FLASH] [PDF]
[ДОК] МЕТОД СПЛАЙНОВ Предпосылки для метода сплайнов
интерполяции [PDF]
[ДОК] Цели метода сплайнов
интерполяции
[PDF]
[DOC] Как работает метод сплайна?
[PDF]
[ДОК] Линейная сплайн-интерполяция: теория [YOUTUBE
7:56] Линейная сплайн-интерполяция: пример [YOUTUBE
5:27] Теория квадратичных сплайнов: часть 1 из 2 [YOUTUBE
9:49] Теория квадратичных сплайнов: часть 2 из 2 [YOUTUBE
5:27] Квадратичная сплайн-интерполяция: Пример:
Часть 1 из 2 [ЮТУБ
10:48] Квадратичная сплайн-интерполяция: Пример:
Часть 2 из 2 [ЮТУБ
7:05] Презентация Power Point
[PDF]
[ППТ] Рабочие листы метода
[PDF]
[МКД] Проверьте свои знания метода сплайнов
интерполяции
[HTML]
[FLASH] [PDF]
[ДОК] АНЕКДОТЫ Затаившиеся опасности
экстраполяции! [PDF]
[ДОК]
[МКД]
[PDF] Почему выше
Интерполяция ордеров — плохая идея?
[PDF]
[ДОК]
[МКД]
[PDF] Сравнение сплайна и полинома
Интерполяция. Как
Выбор точек интерполяции влияет на аппроксимацию!
[PDF]
[ДОК]
[МКД]
[PDF] Как
Сплайны могут помочь в разработке более короткого пути для робота! [PDF]
[ДОК]
[МКД]
[PDF] Рунге [HTML]
[PDF]
[ДОК] Ньютон [HTML]
[PDF]
[ДОК] Лагранж [HTML]
[PDF]
[ДОК] АУДИТОРИЯ | НАГРАДЫ
| ЛЮДИ | ТРЕК | РАСПРОСТРАНЕНИЕ
|
ПУБЛИКАЦИИ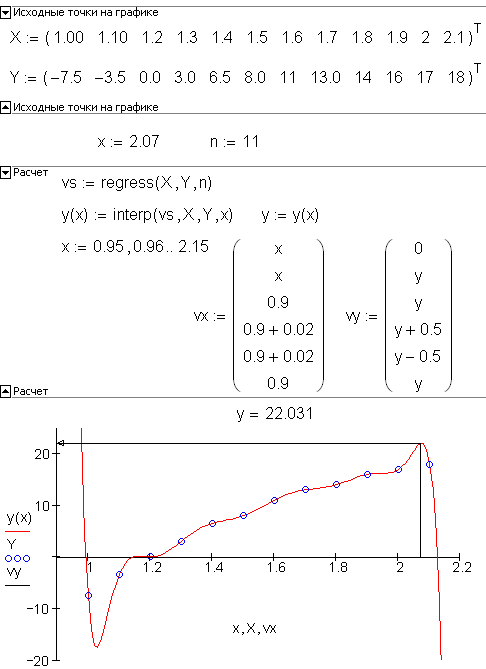 . Эта матрица играет точно такую же роль, как vx в одномерном случае, описанном ранее. Поскольку эти точки описывают диагональ, элементы в каждом столбце Mxy расположены в порядке возрастания (MxYi, k < MXYj, k, если i
. Эта матрица играет точно такую же роль, как vx в одномерном случае, описанном ранее. Поскольку эти точки описывают диагональ, элементы в каждом столбце Mxy расположены в порядке возрастания (MxYi, k < MXYj, k, если i
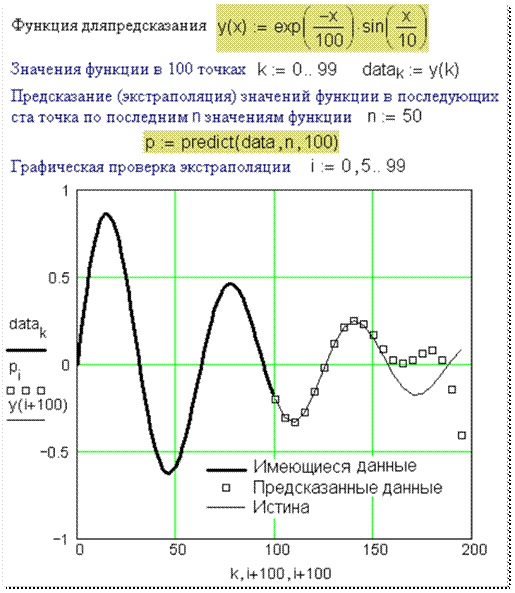
• Чтобы оценить кубический сплайн в произвольной точке, скажем, (xO, yO), оцените Однако вам может понадобиться найти точки данных, которые лежат за пределами ваших существующих. Mathcad предоставляет функцию прогнозирования, которая использует некоторые из ваших существующих данных для прогнозирования точек данных, лежащих за пределами существующих. Эта функция использует алгоритм линейного прогнозирования, который полезен, когда ваши данные являются гладкими и колебательными, хотя и не обязательно периодическими. Линейный прогноз можно рассматривать как разновидность метода экстраполяции, но его не следует путать с линейной или полиномиальной экстраполяцией.
Однако вам может понадобиться найти точки данных, которые лежат за пределами ваших существующих. Mathcad предоставляет функцию прогнозирования, которая использует некоторые из ваших существующих данных для прогнозирования точек данных, лежащих за пределами существующих. Эта функция использует алгоритм линейного прогнозирования, который полезен, когда ваши данные являются гладкими и колебательными, хотя и не обязательно периодическими. Линейный прогноз можно рассматривать как разновидность метода экстраполяции, но его не следует путать с линейной или полиномиальной экстраполяцией.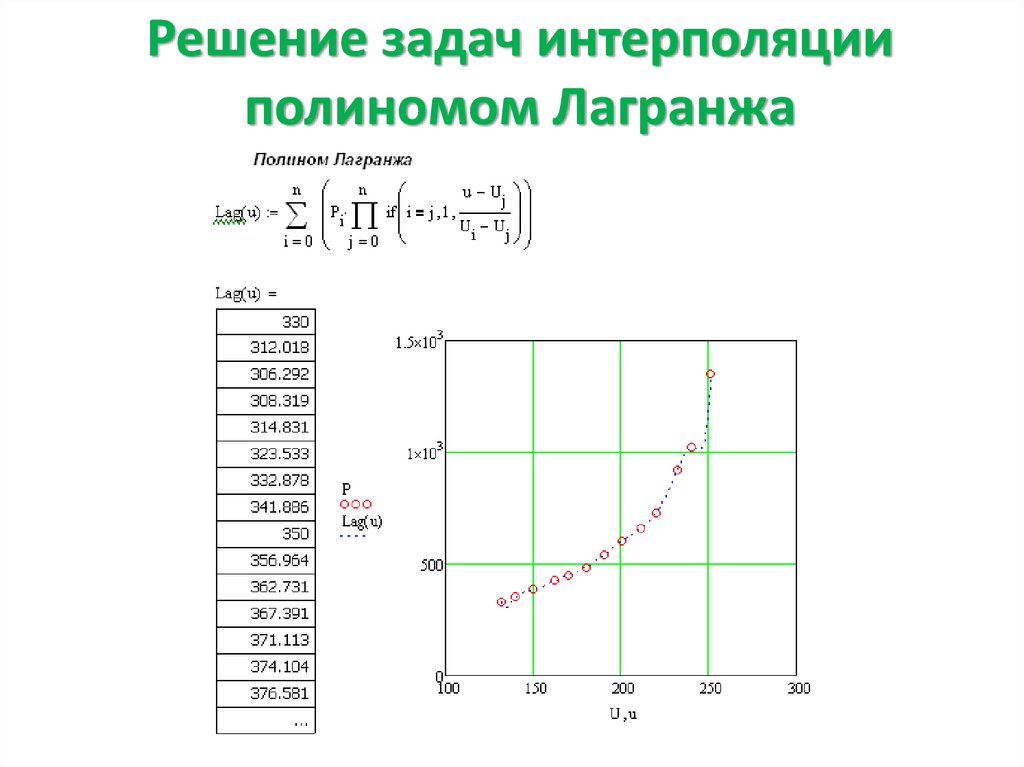
Численные методы интерполяции с использованием Mathcad для общего машиностроения
Численные методы интерполяции с использованием Mathcad для общего машиностроения
Инжиниринг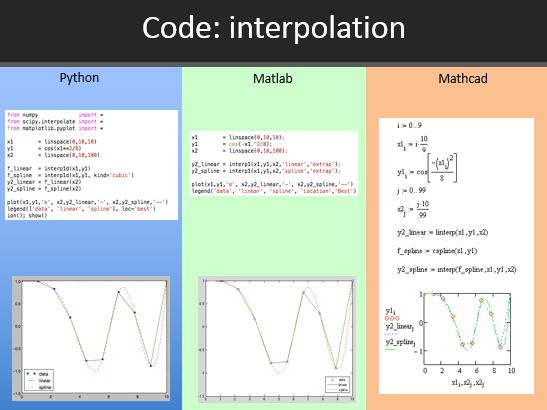 Чтобы найти скорость ракеты в какой-то другой момент времени, задача требует интерполяции.
[PDF]
[ДОК]
Чтобы найти скорость ракеты в какой-то другой момент времени, задача требует интерполяции.
[PDF]
[ДОК] [PDF]
[ДОК]
[МКД]
[PDF]
[PDF]
[ДОК]
[МКД]
[PDF] Авторские права:
Университет
Южной Флориды, 4202 E Fowler Ave, Tampa, FL 33620-5350. Все права защищены. Вопросы, предложения или
комментарии, контакт
[email protected].
Этот материал основан на работе, поддержанной Национальным научным фондом. 
 е.
е.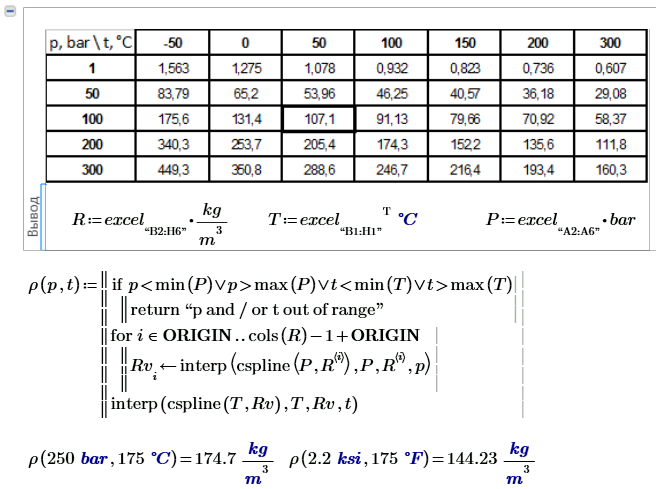

 Линейная интерполяция
Линейная интерполяция