Глава 1 Основы работы с системой Mathcad 11
Глава 1 Основы работы с системой Mathcad 11
Глава 2 Работа с файлами Mathcad 11
Глава 3 Редактирование документов Mathcad 11
Глава 4 Управление обзором (View) Mathcad 11
Глава 5 Работа со вставками Mathcad 11
Глава 6 Установки форматов объектов системы Mathcad 11
Глава 7 Управление вычислительными процессами Mathcad 11
Глава 8 Работа с символьным процессором Mathcad 11
Глава 9 Работа с окнами Mathcad 11
Глава 10 Работа с информационными ресурсами Mathcad 11
1. 1. История создания и возможности системы
Вскоре после окончания второй мировой войны потребность в автоматизации математических
расчетов привела к созданию компьютеров (computer — в буквальном переводе «счетная
машина»). Но широкого применения первые поколения таких машин на электронных
лампах не получили. Они были дороги и громоздки, а потому доступны лишь специалистам.
С развитием микроэлектроники появились специализированные, предназначенные для математических расчетов миниатюрные компьютеры личного пользования — программируемые калькуляторы [I]. Они широко применяются и сейчас. Однако в последние годы массовое распространение получили куда более мощные, быстрые и универсальные персональные компьютеры (ПК), имеющие превосходные графические возможности и используемые практически во всех сферах науки, производства, бизнеса и образования.
Одной из основных областей применения ПК и поныне являются математические и
научно-технические расчеты. Бесспорным лидером среди массовых ПК стали IBM-совместимые
ПК 486DX/Pentium/Pentium MMX/Pen-tium Pro/Pentium II, называемые так по типу
используемых в них микропроцессоров. На них и ориентированы современные математические
системы и, в частности, описываемая в этой книге новейшая система MathCAD 7.
0 PRO, появившаяся в 1997 г.
Само по себе появление компьютеров не упрощало математические расчеты, а лишь позволяло резко повысить скорость их выполнения и сложность решаемых задач. Пользователям ПК, прежде чем начинать такие расчеты, нужно было изучать сами компьютеры, языки программирования и довольно сложные методы вычислений, применять и подстраивать под свои цели программы для решения расчетных задач на языках Бейсик [2] или Паскаль. Поневоле ученому и инженеру, физику, химику и математику приходилось становиться программистом, к сожалению, порою довольно посредственным.
Необходимость в этом отпала лишь после появления интегрированных математических
программных систем для научно-технических расчетов: Eureka [З], PC MatLAB [4],
MathCAD [5-7, II], Maple V [12], Mathematica 2 или 3 [13] и др. Большое число
подобных разработок свидетельствует о значительном интересе к ним во всем мире
и бурном развитии компьютерных математических систем.
Широкую известность и заслуженную популярность еще в середине 80-х годов приобрели интегрированные системы для автоматизации математических расчетов класса MathCAD, разработанные фирмой MathSoft (США). По сей день они остаются единственными математическими системами, в которых описание решения математических задач дается с помощью привычных математических формул и знаков. Такой же вид имеют и результаты вычислений. Так что системы MathCAD вполне оправдывают аббревиатуру CAD (Computer Aided Design), говорящую о принадлежности к наиболее сложным и продвинутым системам автоматического проектирования — САПР. Можно сказать, что MathCAD — своего рода САПР в математике [7, 8].
С момента своего появления системы класса MathCAD имели удобный пользовательский
интерфейс — совокупность средств общения с пользователем в виде масштабируемых
и перемещаемых окон, клавиш и иных элементов. У этой системы есть и эффективные
средства типовой научной графики, они просты в применении и интуитивно понятны.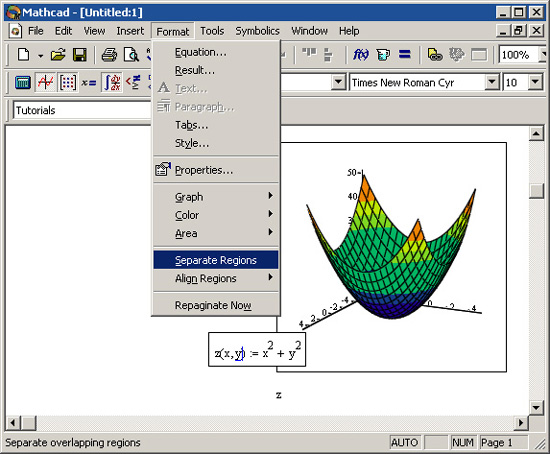
MathCAD — математически ориентированные универсальные системы. Помимо собственно вычислений они позволяют с блеском решать задачи, которые с трудом поддаются популярным текстовым редакторам или электронным таблицам. С их помощью можно не только качественно подготовить тексты статей, книг, диссертаций, научных отчетов, дипломных и курсовых проектов, они, кроме того, облегчают набор самых сложных математических формул и дают возможность представления результатов, в изысканном графическом виде.
В последнее время особый интерес проявляется к системам компьютерной алгебры,
способным выполнять не только числовые, но и аналитические вычисления. В 80-е
годы школа советского академика В. М. Глушкова внесла большой вклад в разработку
таких программных систем (язык Аналитик) и в создание инженерных мини-ЭВМ, аппаратно
реализующих аналитические вычисления (серия «Мир»).
К сожалению, эти ЭВМ были
вытеснены вначале машинами класса ЕС-ЭВМ, а затем и персональными компьютерами,
и теперь мы наблюдаем развитие нового поколения зарубежных систем компьютерной
алгебры, ориентированных на современные массовые ПК.
Однако прошло много лет, прежде чем серьезные системы символьной математики (компьютерной алгебры) появились на массовых IBM-совместимых ПК. К ним и относится новое поколение систем MathCAD под Windows [8, 11] и ряд других математических систем, таких, как Derive [10], Maple V и Mathe-matica 2 и 3. Применение их облегчает самые сложные математические, статистические и финансово-экономические расчеты, для проведения которых раньше приходилось привлекать научную элиту — математиков-аналитиков.
Пользователи, работающие с математическими программами, особенно в области
символьной математики, в недалеком прошлом не были избалованы удобными и красивыми
интерфейсами этих программ.
Все внимание было уделено математической корректности
программ и богатству их функциональных возможностей.
Многие известные математические программы для ПК класса IBM PC — от некогда популярного языка символьных вычислений Reduce [18] до мощной, быстрой и легко развиваемой системы MatLAB под MS-DOS — имели примитивный интерфейс, заимствованный из опыта начинающих программистов и любителей «дедушки» Бейсика, в новых версиях почитаемого и поныне. А системы с более современным (в конце 80-х годов) многооконным интерфейсом, например Eureka фирмы Borland [3], серьезному математику казались примитивными.
К сожалению, нашим пользователям пока очень мало известны возможности систем
символьной математики, поскольку соответствующей литературы до недавнего времени
почти не было. Наконец, в 1996 г., спустя три года после объявления о предстоящем
выходе, была издана книга автора [10] по системе символьной математики Derive
под MS-DOS.
Тем временем за рубежом каждой системе символьной математики уже
посвящены десятки книг.
Неплохо бы соединить приятное с полезным! К такому выводу первой пришла фирма MathSoft (США), разработчик подлинного шедевра среди математических систем — MathCAD. Из обзоров автора [7, 8] и его справочной книги [5] многие читатели уже знают, что отличительной чертой интегрированных математических систем MathCAD является подготовка документов, которые объединяют задание исходных данных, математическое описание их обработки и результаты вычислений (в виде числовых данных, таблиц и графиков). Вид документа в MathCAD почти ничем не отличается от вида научной статьи. Удачно решена в MathCAD проблема передачи изменений числовых данных в формулах по всей цепочке вычислений.
В начале 90-х годов произошло давно ожидаемое событие: серьезная математика
«в лице» интегрированной системы MathCAD 3. 0 прорвалась в окна системы
Windows [11]! Триумфальное шествие последней началось с того, что корпорация
Microsoft наводнила рынок графических операционных систем своей многооконной
и многозадачной системой Windows 3.
Ко времени выпуска MathCAD 3. 0 под Windows далеко не каждый наш пользователь имел под рукой ПК класса 386 или 486 с установленной на нем операционной системой Windows. Однако обзор западной литературы по информатике и тенденций развития вычислительной техники убедительно показывал, что система Windows стремительно выдвинулась на роль лидера среди современных операционных систем для персональных компьютеров. Большинство серьезных программных продуктов было переработано под Windows 3. 1/3. 11, а сейчас уже под 32-разрядную (в основном) операционную систему Windows 95. В то же время число программ под MS-DOS стремительно сокращается.
На Западе уже давно прекращен серийный выпуск ПК на микропроцессорах 286 и
386, сворачивается производство ПК на процессорах класса 486.
В России ситуация
также изменилась. Новое поколение ПК — это машины серии Pentium/ Pentiun MMX/Pentium
Pro/Pentium II. Стоимость их постоянно снижается, и ПК этого класса становятся
доступными не только для организаций, но и для домашних пользователей.
Сейчас наиболее часто приобретаемыми ПК уже становятся машины с микропроцессорами класса Pentium MMX 166/200, поддерживающими 57 новых команд для реализации средств мультимедиа. В последнее время парк ПК только в России ежегодно возрастает примерно на миллион машин, а общее число IBM-совместимых ПК превысило 200 миллионов.
Вероятно, уже в ближайшие год-два ПК с процессорами Pentium MMX и Pentium II
(упрощенный вариант Pentium PRO с мультимедиа-командами) станут основным типом
персональных компьютеров даже дома. Их производительность в сотни раз превышает
производительность первых ПК IBM PC XT. Именно на машины этого класса и ориентированы
версии MathCAD 7.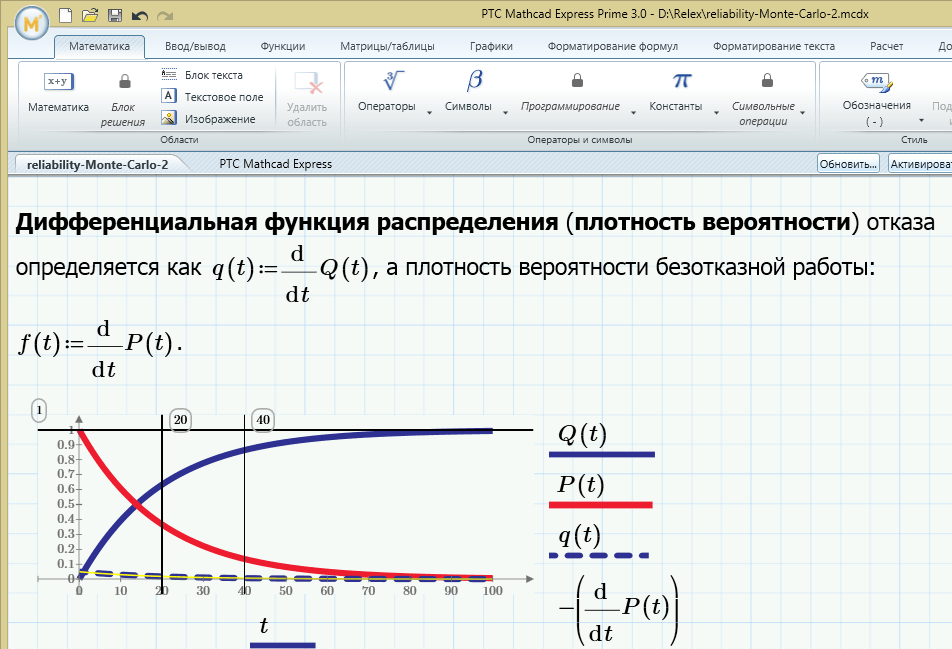
0 и PLUS 7. 0 PRO, хотя, в принципе, вполне возможна их работа
и на ПК с микропроцессором 486 (с частотой работы не менее 66 МГц).
Все это создает предпосылки к массовому переходу на старшие версии системы MathCAD под Windows. Тем более что пользователи, работающие с системой MathCAD под MS-DOS, всегда ощущали определенный дискомфорт из-за присущих ей принципиальных пороков, унаследованных от операционной системы MS-DOS. К примеру, при альтернативной кодировке символов знакогенераторов дисплея и принтера пропадала большая часть греческих букв, широко используемых в математических формулах. Много недоразумений возникало при печати документов на принтерах, искажались некоторые математические спецзнаки, нарушались форматы таблиц и т. д. Качество печати также оставляло желать лучшего. Шрифты не имели сменных наборов стилей, их размеры были фиксированными.
Не только профессионалы-аналитики, но и просто любители и почитатели математики
быстро теряли интерес к системе, как только возникала необходимость в выполнении
даже простейших символьных вычислений: нужных для этого средств версии системы
MathCAD под MS-DOS были попросту лишены.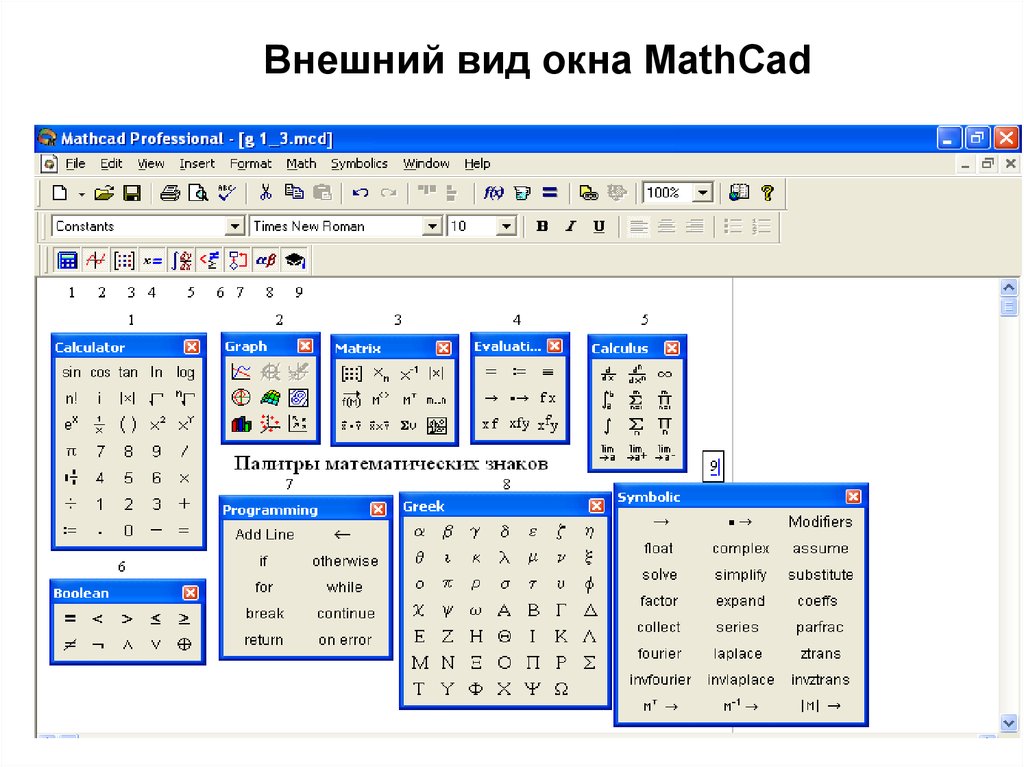
Да и набор математических формул (не
говоря уже об их поиске в справочных книгах) был занятием далеко не самым легким
и приятным, поскольку требовал знания десятков комбинаций различных клавиш.
Опыт работы автора даже с первой системой MathCAD под Windows (версия 3. 0) позволяет сделать вывод, что студенты, аспиранты, инженеры и ученые получили превосходный инструмент для повседневной работы. Теперь для написания научной статьи или диссертации они могут обойтись только системой MathCAD под Windows и встроенными в Windows средствами.
К средствам новых версий MathCAD относятся настройка под любой мало-мальски
известный тип печатающего устройства, богатый набор шрифтов, возможность использования
всех инструментов Windows, прекрасная графика и современный многооконный интерфейс.
А в версию MathCAD 7. 0 PRO включены эффективные средства цветового оформления
документов, создания анимационных (движущихся) графиков и звукового сопровождения.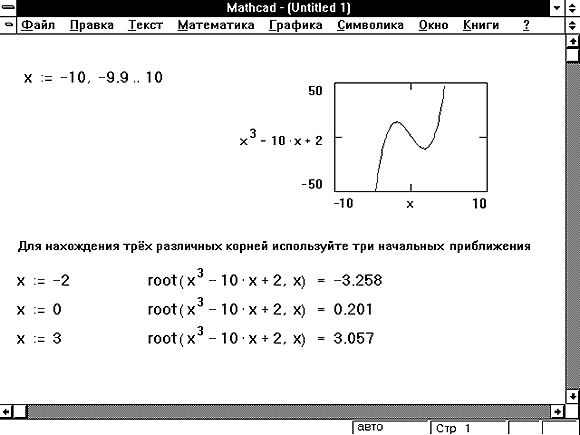
Тут же текстовый, формульный и графический редакторы, объединенные с мощным
вычислительным потенциалом. Предусмотрена и возможность объединения с другими
мощными математическими и графическими системами для решения особо сложных задач.
Отсюда и название таких систем — интегрированные системы.
Математики, физики и ученые из других, смежных отраслей науки давно мечтали
о математически ориентированном языке программирования для записи алгоритмов
решения математических и научно-технических задач в наиболее удобной, компактной
и доступной для понимания форме. Для этого они пытались приспособить различные
языки программирования высокого уровня — Фортран, Алгол, Бейсик, Паскаль и др.
Но их попытки так и не увенчались успехом: программы на этих языках, увы, ничем
не напоминали привычные математические и физические символы и формулы, с которыми
все привыкли работать и с помощью которых описываются решения математических
задач.
Кафедра РЛ-2 | Лазерные и оптико-электронные системы
В процессе обучения студенты выполняют практические работы, используя современное программное обеспечение.
ZEMAX – это пакет программ, с помощью которых можно моделировать, делать анализ и проектировать оптические системы. Интерфейс, с помощью которого осуществляется связь пользователя с компьютером, является очень простым в использовании и позволяет работать с достаточно высокой производительностью. Хотя программа во многом поможет пользователю в проектировании и анализе оптических систем, именно пользователь остается проектировщиком.
Mathcad — программа для выполнения и документирования инженерных и научных расчётов. Появившись в 1986 году для платформы MS-DOS, Mathcad впервые среди программ подобного рода использовал наборную математическую нотацию, совмещённую с автоматической системой вычислений. Кроме того, впервые было реализовано автоматическое вычисление и проверка единиц измерения.
Например, СИ. На сегодняшний день Mathcad включает некоторые возможности алгебраических систем для ЭВМ, но при этом сохраняет ориентацию на инженерные приложения. Рабочая область программы представляется как обыкновенный лист, на котором уравнения и выражения отображаются графически, а не в текстовом виде.
Язык MATLAB является высокоуровневым интерпретируемым языком программирования, включающим основанные на матрицах структуры данных, широкий спектр функций, интегрированную среду разработки, объектно-ориентированные возможности и интерфейсы к программам, написанным на других языках программирования. Пакет MATLAB включает различные интерфейсы для получения доступа к внешним подпрограммам, написанным на других языках программирования, данным, клиентам и серверам, общающимся через технологии Component Object Model или Dynamic Data Exchange, а также периферийным устройствам, которые взаимодействуют напрямую с MATLAB. Многие из этих возможностей известны под названием MATLAB API.
SolidWorks — продукт компании SolidWorks Corporation, система автоматизированного проектирования (САПР) в трёх измерениях, работает под управлением Microsoft Windows. Основной продукт SolidWorks включает инструменты для трехмерного моделирования, создания сборок, чертежей, работы с листовым металлом, сварными конструкциям и поверхностями произвольной формы. Присутствует возможность импортирования большого числа файлов 2D и 3D CAD программ. Имеется API для программирования в среде Visual Basic и C. Также включена программа для анализа методом конечных элементов начального уровня CosmosXpress.
Бесплатный доступ к лицензионному программному обеспечению
Студенты и аспиранты всех курсов и факультетов, а также преподаватели всех факультетов и научные сотрудники, занимающиеся некоммерческими исследованиями в МГТУ могут получить операционные системы, средства разработки ПО, серверные продукты и прочее. Чтобы получить программный продукт необходимо:
- иметь продлённый читательский билет библиотеки МГТУ;
- получить пароль от своего читательского билета в любом отделе обслуживания библиотеки для доступа к электронным ресурсам библиотеки;
- зайти на сайт ELMS для получения персональных ключей и скачивания дистрибутивов;
-
установить программный продукт на свой компьютер, воспользовавшись полученным персональным ключом.
Matlab и MathCad для студентов и сотрудников
Для использования лицензионных версий студентам достаточно подключиться к локальной сети университета (в т.ч. и через bmstu_lb) и установить Matlab или MathCad по инструкциям (доступны только из локальной сети). Все студенты и сотрудники университета имеют право пользоваться продуктами компании Mathworks (Matlab, Simulink, модули) на любых компьютерах: личных, домашних и т.п. Для самостоятельного получения лицензии следуйте инструкции.
Что нового — осень 2022 г.
Интерактивный инструмент блоков разрядов
Наш новый инструмент блоков разрядов идеально подходит для изучения системы разрядов целых чисел и визуализации относительных размеров цифр в разных местах. Вы также можете сравнивать числа и исследовать большие числа с помощью десятичных блоков. Это адаптировано из нашего популярного инструмента десятичных блоков.
Векторы и четырехугольники Рабочие листы
Сможете ли вы определить, какой тип четырехугольника получится, если вы будете следовать последовательности векторов?
Наши *бесплатные* рабочие листы по векторам и четырехугольникам дают возможность попрактиковаться в работе с векторами, побуждая думать о том, равны ли пары векторов по длине, параллельны или перпендикулярны, а также поощряют ментальную визуализацию.
Существуют упрощенная и более сложная версии этого рабочего листа.
Обновление учебного плана и учебников
Наш учебный план и учебники теперь готовы для всех классов 7, 8 и 9.
Каждая глава учебника содержит смесь практических упражнений, заданий в стиле головоломок и контрольных вопросов. Каждая концепция разбита на части и подробно рассмотрена, а вопросы регулярно основываются на знаниях из предыдущих глав, обеспечивая интегрированную практику.
Учебная программа 7 класса:
| 1. Место Значение | Ядро | Поддержка |
2. Расчеты | Ядро | Поддержка |
| 3. Негативы | Ядро | Поддержка |
| 4. Дроби | Ядро | Поддержка |
| 5. Индексы | Ядро | Поддержка |
| 6. Введение в алгебру | Ядро | Поддержка |
| 7. Меры | Ядро | Поддержка |
| 8. Форма, площадь и Пифагор | Ядро | Поддержка |
| 9. Дроби, десятичные дроби и проценты | Ядро | Поддержка |
Учебный план 8 класса:
| 1. Выражения | Ядро | Поддержка |
| 2. Уголки | Ядро | Поддержка |
| 3. Формулы | Ядро | Поддержка |
| 4. Площадь, объем и 3d | Ядро | Поддержка |
| 5. Составление и решение уравнений | Ядро | Поддержка |
6. Теория чисел и последовательности | Ядро | Поддержка |
| 7. Функции, координаты и графики | Ядро | Поддержка |
| 8. Введение в статистику | Ядро | Поддержка |
Учебная программа 9 класса:
| 1. Дроби, десятичные знаки и проценты | Высшее | Фундамент |
| 2. Линейные графики и градиент | Высшее | Фонд |
| 3. Преобразования | Высшее | Фундамент |
| 4. Соотношение и пропорция | Высшее | Фундамент |
| 5. Углы и подобия | Высшее | Фундамент |
| 6. Пифагор и тригонометрия | Высшее | Фундамент |
| 7. Вероятность | Высшее | Фундамент |
| 8. Карты и конструкции | Высшее | Фундамент |
9. Проценты/расчеты | Высшее | Фундамент |
преподавание математики | Доктор Атул Рана – онлайн-репетитор
Этот пост в блоге представляет собой отчет о моей шестой конференции по математике. #MathsConf19 прошла в гимназии Penistone Grammar School недалеко от Шеффилда 22 июня 2019 года. В конференциях, проводимых La Salle Education, принимают участие около 400 учителей математики, тренеров, издателей, поставщиков, ученых, репетиторов и других лиц, занимающихся математическим образованием.
TLDR ; Как реальные, так и виртуальные двусторонние счетчики очень универсальны, термин «радиус» является относительно новым словом для круговой вечеринки. Всего несколько альтернативных методов построения оживляют тему.
Прекрасный летний день для #MathsConf19 в идиллическом месте Пенистон. Фото @LaSalleEd
Перед конференцией Общение в пятницу вечером
Выпивка перед конференцией в пятницу вечером сама по себе является бесценной возможностью для неформального НПР.
У учителей так много вещей, которыми они хотят поделиться и поделиться своими мыслями с другими. Это та часть, которая мне так нравится, как репетиторство по математике в онлайн-группе одного человека, у которого нет возможности заниматься этим лично. Твиттер полезен для таких вещей, но на самом деле ничто не заменит личную встречу.
Например, мне нужно было узнать у учителей о новых уровнях A и о том, как проходило обучение первой полной первой группы. Я был так впечатлен встречей с парой учителей, которые преподают все, начиная от математики на уровне A и заканчивая учениками 7-го класса, от верхних до нижних наборов. Для этого нужно много навыков и разносторонности, которые нужны мне так же, как репетитору. Я собираюсь преподавать математику в будущем, поэтому я задал несколько вопросов по различным модулям для этого.
Некоторые из нас также играли в математические игры и головоломки. Я играл бессонницу Альберта, купленную Дрю Фостером. Игра с использованием ментальной математики и порядка операций.
Пиво, болтовня, игры и общение продолжались весь вечер. В отличие от Бристоля, на этот раз я провел раннюю ночь после закрытия бара. К счастью, после игры в бессонницу Альберта не было бессонницы Атула, и я был в хорошем настроении для следующего дня конференции.
Знакомство, твиттер и награда MacMillan
Генеральный директор La Salle Марк МакКорт начал со знакомства с математической конференцией. Глава отдела математики AQA Эндрю Тейлор также выступил с коротким докладом со слайдами «Угадайте, в каком году был задан этот вопрос», показывающим, как определенные стилистические элементы вопросов выходят из моды с 1940-х годов до настоящего времени. Марк также упомянул, что в стране насчитывается около 300 000 учителей математики, и призвал нас рассказать об этом событии в Твиттере, чтобы другие могли присоединиться к сети и узнать друг друга. Я не могу не согласиться с огромной силой, полученной от встреч и обучения у других учителей. La Salle действительно преуспела в создании этого сообщества; онлайн и лично через эти события.
И вы действительно не ошибетесь, если все название конференции будет хэштегом!
Марк был приятно удивлен объявлением из зала о вручении премии Дугласа Макмиллана 2019 года. Все организовано и номинировано Джулией Смит. Он всегда удваивает сумму (с некоторым щедрым округлением), полученную в день от продажи лотерейных билетов. У Марка также есть новая книга «Обучение для мастерства», которую я с нетерпением жду. Я был на трех из его полных дней CPD Complete Maths и продолжаю учиться на его обширном понимании преподавания математики.
Speed
знакомства с и некоторые новые идеи для обучения Затем были быстрые свидания, 4 «свидания», где каждый участник получает 120 секунд, чтобы поделиться своей любимой идеей обучения с другим участником. 120 секунд, чтобы поделиться всеми своими знаниями в области преподавания математики и своими лучшими идеями. Я думал, что это будет довольно сложно. После этого я многое узнал из этих свиданий о преподавании математики; от бесцельного решения проблем до сильно раздробленного подхода в преподавании некоторых тем.
Я говорил в основном о «обратном исчезновении в парах пример-задача» и «эффекте предварительного тестирования», которые я тестировал с некоторым успехом.
Семинар 1: Двусторонние счетчики
Этот семинар проводил Джонатан Холл, также известный как mathsbot. Он создал очень богатый ресурс онлайн-манипуляторов, которые я очень рекомендую использовать. Двусторонние счетчики опоздали для меня на эту манипулятивную вечеринку, так как я еще не начал использовать их с учениками. Так что этот мастер-класс послужит идеальным введением в их использование.
Цех двухсторонних счетчиков.
Это было намного больше, чем просто вступление. Джонатан показал, как этот простой и один из самых дешевых манипуляторов можно использовать для объяснения чисел, вероятности, алгебры и доказательства. У каждого делегата был свой набор манипуляторов, с которыми можно было играть. Для начала нам дали задачу об отеле с 12 закрытыми дверями, которую мы должны были попробовать в своих головах.
Очень быстро стало очевидно, что это будет довольно сложно сделать мысленно. Как только появились счетчики, было легко решить проблему с желтой стороной как «дверь открыта» и красной как «дверь закрыта».
Учащиеся могут исследовать закономерности, используя счетчики. Со временем пришли к собственным выводам по общей формуле закономерности. Слайд презентации @studymaths
Затем мы рассмотрели последовательности. Теперь я видел их на 13+ бумагах много раз в виде картинок, но на самом деле есть что-то еще в том, чтобы иметь настоящие жетоны в физической форме и на самом деле строить паттерны руками. Есть что-то приятное в процессе создания узоров вручную, и, несомненно, само это действие ведет к более глубокому пониманию. Мы рассмотрели пару примеров последовательностей, и хотя оба примера были для квадратичных последовательностей, счетчики очень хорошо работают и с линейными последовательностями. Затем нам показали несколько замечательных примеров визуального доказательства и вероятностных вопросов с использованием диаграмм Венна.
У каждого был лист формата А4, на котором можно было сделать диаграмму Венна и разместить счетчики. Каждое приложение в конечном итоге приводит к обобщенной форме, в которой можно использовать всего n счетчиков. Вероятность завершается рассмотрением примера парадокса Симпсона.
Меня очень впечатлило, что счетчики используются для факторизации и нахождения среднего значения. В этом примере у нас было три отдельные группы красных и желтых фишек (первый ряд на изображении), затем перераспределили их все, чтобы получить три одинаковых ряда по 2 желтых и 3 красных в каждом ряду, то есть 3(2y + 3r). Последняя строка на изображении изящно показывает, что среднее значение равно просто двум желтым и трем красным 2y + 3.
Первая строка из трех отдельных групп переставлена таким образом, чтобы показать как разложение на множители, так и нахождение среднего значения желтых и красных счетчиков. Слайд презентации @studymaths
Презентация завершилась демонстрацией различных вариантов использования двусторонних жетонов.
Эти существа; Направленное число, соотношение, последовательности и n-й член, доказательство, средние значения, сбор похожих терминов, факторизация, диаграммы Венна, вероятность, древовидные диаграммы, факторы, кратные и простые числа, квадратные и треугольные числа, длинное деление и задачи моделирования.
У меня уже есть набор счетчиков, и мне не терпится использовать их в своем обучении.
Семинар 2: Соотношение и пропорция
Следующее выступление было с Дэвидом Макьюэном, менеджером учебной программы по математике в AQA. Соотношение, пропорция, масштабирование, дроби, проценты — все это, конечно, взаимосвязанные темы. #MathsConf18 дал мне возможность по-настоящему оценить идею «масштабирования от единицы», поэтому я с нетерпением ждал этого конкретного семинара. У каждого из нас был список выдержек из спецификаций и экзаменационных вопросов, которые сопровождали семинар.
Мы начали с открытой дискуссии о том, как можно определить соотношение (см. изображение).
Открытая дискуссия о том, что означает соотношение.
Дэвид также упомянул, что отношение и пропорция появляются в той или иной форме в основном в материалах Фонда или Высшего Фонда. Анализируя серию за июнь 2018 года, он упомянул, что вопросы соотношения и пропорции появляются почти в начале статьи и равномерно распределяются почти в конце. А пропорция пропорции вопросов? Примерно 25% в Foundation и 20% в Higher. Игра слов здесь неизбежна, и в зале раздались смешки.
Дэвид показал эквивалентность дробей с отношениями, приводящими к равенству отношений. Наконец, связываем все это с действительно аккуратным методом перекрестного умножения, подходящим для всех расчетов эквивалентности отношений.
Используя линейчатое моделирование, каждая процентная задача может быть решена с использованием этого метода перекрестного умножения, если задача будет поставлена правильно. Найти процент, найти число, процентные изменения, обратные проценты можно было бы сделать с помощью модели столбцов.
Мне очень понравилась идея создать одно последовательное представление и следовать ему.
Аккуратный метод гистограммного моделирования и перекрестного умножения отношений, который можно использовать для решения различных типов процентных задач с одинаковым непротиворечивым представлением.
Нам также показали несколько слайдов, чтобы напомнить нам, что введение в тригонометрию также связано с отношениями и что учащиеся могут по существу познакомиться с тригонометрией в более раннем возрасте, когда знакомятся с прямоугольными подобными треугольниками. Также обсуждались таблицы соотношений, показывающие коэффициенты преобразования для масштабирования площади и объема, и несколько других концепций, показывающих ту же нить пропорциональных отношений. Было очень приятно получить такое ясное напоминание об этом.
Семинар 3: Эволюция словарного запаса в математическом образовании
Следующей была Джо Морган с докладом, посвященным использованию слов в математике и тому, как слова меняются, эволюционируют или исчезают из употребления с течением времени.
Слова обычно меняются со временем, потому что..
- Они устаревают (например, «кассета»)
- Выйти из моды («круто» или это слово из 90-х «безвкусица»)
- На смену им приходят новые способы разговора («телефон» становится просто «телефон»)
Я был очень рад услышать, что «трижды» действительно было словом. Я использовал его, когда жил в Индии и других странах. Я перестал использовать это слово в 11 классе, когда приехал в Великобританию, так как мои одноклассники сказали мне, что такого слова не существует. К тому времени он, должно быть, уже исчез здесь, в Великобритании. И, по-видимому, «twice» тоже скоро выйдет. Постепенно заменяется на «два раза». Упоминались также слова «четно-четный» (делится на 2 и еще раз на 2) и «четно-нечетный» (делится на 2 только один раз).
Джо Морган обсуждает «четно-четные» и «четно-нечетные» числа.
Затем Джо перешел к использованию некоторых слов в контексте решения и упрощения уравнений.
Транспозиция : «Акт переноса чего-либо в другое место». и ‘ concination ’ (упрощение в уравнении) появляются регулярно. То же самое можно сказать и о таких терминах, как « уничтожает », « очищает дроби » и глагол сам по себе « выявляет ».
Слово «сцепление» навело меня на мысль о слове « конкатенация » (соединять объекты в цепочку или ряд), которое я смутно припоминаю при использовании в вычислениях. Команда «сцепить» используется для объединения двух или более файлов в один большой с помощью командной строки MS DOS.
Далее геометрия окружности. Сейчас в это трудно поверить, но слово «радиус» — одно из самых молодых слов, используемых в кругах, и относительно недавно присоединилось к группе кругов. Математики очень долго обходились без слова и с помощью « полудиаметра ’ было достаточно. Самое раннее упоминание о радиусе в качестве математического термина на английском языке принадлежит Гоббсу, написанному в 1656 году.
Ромб «Назван так от греческого слова Rhombos, которое означает Рыбу, называемую Палтусом, и Стёкла в Окне». Ромбоиды также упоминались и обсуждались как то, что мы называем современным параллелограммом. И что интересно, продолговатый — это старое слово, используемое для обозначения прямоугольника. В этом новый продолговатый сильно отличается от старого.
В завершение семинара Джо рассказала о вкладе валлийского математика Роберта Рекорда в математику. Его книга The Grounde of Artes была написана с прекрасным наставником и студенческим рассказом, где Рекорд обучал своего воображаемого ученика, а ученик отвечал ему. Поощрение ученого «хорошо сказано». Значит, хорошая репетиторская практика оставалась неизменной все эти века!
Значение равных на языке оригинала Роберта Рекорда и его английский перевод. Слайд презентации @mathsjem
Нельзя упомянуть Роберта Рекорда, не упомянув его самый известный вклад, использование знака равенства = После небольшого обучения переводу древнеанглийского языка нам дали исходный текст для перевода, чтобы посмотреть, сможем ли мы найти упоминание о знак равенства.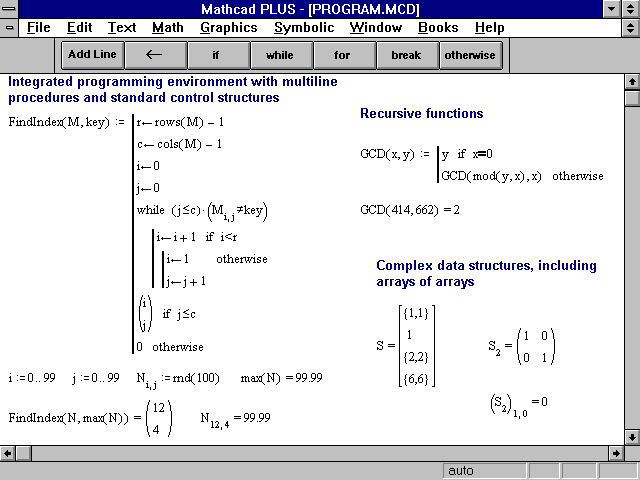
Рекорд также изобрел новые английские математические слова, многие из которых сегодня не используются. Язык меняется со временем, и, возможно, через 100 лет некоторые математические термины, которые мы используем сегодня, тоже устареют.
Мне очень понравился этот семинар, он проходил очень хорошо, в нужном темпе и вызывал у меня любопытство пойти и узнать больше.
Семинар 4: Обучение и преподавание без уловок с использованием плиток алгебры
Этот семинар провел Берни Уэстакотт, о котором я недавно узнал после его видеоподкаста с Крейгом Бартоном о манипуляциях. Очень рекомендую посмотреть этот видеоряд. У Берни невероятная глубина знаний в использовании манипулятивных средств и, в частности, в обучении маленьких детей абсолютно правильному обучению с первого раза. Не только это, но и введение алгебры в самом начале, когда дети впервые начинают свое математическое путешествие, еще не используя обозначения. На прошлой неделе я впервые встретился с ним на другом семинаре в Лондоне, и на этой неделе у него была полная аудитория, готовая заняться виртуальными манипуляциями.
Полный зал для презентации Берни Уэстакотта. Фото @LaSalleEd
Семинар был основан на использовании приложения для виртуального манипулирования brainingcamp. Мы потратили некоторое время на изучение использования двусторонних счетчиков, а затем алгебраических плиток. Берни также использует настоящие счетчики при обучении маленьких детей. Невероятно, но он делает это без использования каких-либо символов или письменных работ, но при этом он может помочь детям понять «правила отрицательных чисел» и даже простые уравнения. Маленьким детям совершенно комфортно с «перевернутым» миром отрицательных чисел, например, после того, как они поиграли со счетчиками.
Элементы алгебры в действии в приложении Brainingcamp.
Как и Джонатан Холл, он также начал с полевой аксиомы математики, предполагая существование «аддитивной инверсии», а не «выноса» идеи вычитания. Он подчеркнул, что нет такого понятия, как «вынос». Приложение — отличный способ показать аддитивную инверсию, нулевые пары могут быть выделены серым цветом, если их приблизить друг к другу, что довольно аккуратно.
Эти нулевые пары также можно использовать при обучении химии, поскольку положительные и отрицательные заряды можно использовать для моделирования электронов, протонов и т. д. Я также использую цветные точки при обучении химии. Но это вообще отдельная статья в блоге.
Берни очень элегантно показал нам с помощью счетчиков, как негатив из негатива превращается в позитив. Что значит добавить минус к плюсу и к минусу. И момент, который получил самый большой аааа момент, был демонстрацией того, как умножение негатива на другой негатив дает позитив. Ясность и очевидность этого представления с использованием идеи аксиомы поля неопровержимы.
И вот оно. Почему умножение двух отрицательных целых чисел дает положительное целое число. Очень просто в контексте аксиомы «аддитивного обратного» поля.
Тогда была небольшая демонстрация дисков Alge, которые, кажется, являются промежуточным звеном между плитками алгебры и счетчиками разрядов. Разница в том, что вместо чисел на счетчиках есть метки x и y.
Факторизация с использованием этих дисков, казалось, очень хорошо сочеталась с факторизацией, которую я видел ранее на семинаре Джонатана Холла.
Затем мы перешли к самим плиткам алгебры. Плитки можно использовать для многих вещей, и я использую их уже почти два года. Хотя я использую их только для демонстрации модели области и того, как их можно использовать для факторизации квадратных уравнений. С ними можно делать многое, включая нулевые пары, которые исчезают при объединении 9.0005
Наконец, Берни еще раз подчеркнул сделанное во введении замечание о том, что эти репрезентации предназначены только для того, чтобы учащиеся медленно учились и чувствовали, к чему должна привести абстрактная версия таких репрезентаций.
И что со временем использование манипулятивных средств должно выйти из употребления. Конечно, их всегда можно выкупить по мере необходимости по каждой теме в нелинейном путешествии по изучению математики по мере необходимости. Чем я и занимаюсь как репетитор. У Берни теперь также есть видеоканал, который я рекомендую посмотреть.
Семинар 5: Да, но конструкции
Заключительный семинар мероприятия провел Эд Саутхолл, автор книг «Да, но почему?» и «Геометрические закуски». Конструкции как тема мне очень интересны, так как во время учебы на инженера-механика я построил много конструкций. В первый год все чертежи выполняются на бумаге с использованием соответствующего оборудования, а затем переходят к САПР. А впоследствии практичный листовой металл требует применения конструкций с хорошим оснащением.
Эд Саутхолл обсуждает другие способы деления линии пополам.
Конструкции для обучения школьников не являются чем-то подобным, однако, это в основном шаткие циркуль, сломанные карандашные грифели и ничего, что никогда не выравнивается.
И преподавать это онлайн тоже больно, так как камера для документов мешает. Mathspad и Bitpaper помогают мне, и обычно этого достаточно. Но таким образом я делаю минимум.
Разумный порядок обучения конструкциям @solvemymaths
Прежде чем приступить к каким-либо строительным работам, важно убедиться, что все оборудование, которое будут использовать учащиеся, находится в приемлемом рабочем состоянии, затяните винт циркуля, чтобы он не шатался, и убедитесь, что карандаш не очень острый. Сохранение его немного тупым делает линии немного толще и дает возможность немного скрыть, когда вещи не совпадают. Простое привыкание к соединению двух точек в линию требует практики и беглости (в этом всегда есть некоторая степень случайности, поскольку карандаш может не следовать по линейке, как мы думаем) и привыкания к рисованию кругов разного диаметра.
Затем мы перешли к серединным перпендикулярам, разделив их пополам классическим способом. Но не забудьте нарисовать полные круги, чтобы симметрия и контекст, стоящий за всем этим, были ясно видны.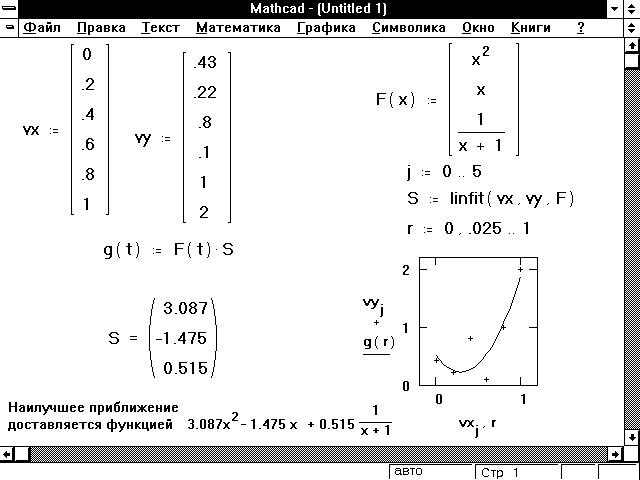
На самом деле всегда рекомендуется рисовать полные круги вместо дуг. За исключением того случая, когда ваша строка находится внизу страницы, что тогда? Введите альтернативные формы деления линии пополам.
Еще один способ построения серединного перпендикуляра к прямой.
Далее был метод деления угла «Дон» и еще один. Мы также сделали упражнение с кругами и линиями, что в конечном итоге привело к чему-то очень приятному для глаз в стиле исламского искусства.
«Донской» способ деления угла пополам
И я узнал об особом типе треугольника, называемом треугольником Рело. Наконец-то я знаю, как называется форма медиатора моей гитары и почему он так хорошо вращается!
Треугольник Рело. Хороший дизайн для гитарных медиаторов.
Также рисовали вписанную окружность квадрата, вписанную окружность треугольника и описанную окружность треугольника (см. видео).
Во время преподавания и выхода из класса, чтобы построить конструкции, Эд предложил иметь гифки конструкций в цикле, чтобы учащиеся могли посмотреть на них, если они пропустили определенный шаг во время презентации, чтобы они могли вернуться к нему и увидеть всю последовательность.