4.1. Взаимное расположение двух точек
Положение точки на чертеже определяется координатами. Точка расположена выше другой, если у нее больше координата Z. Точка находится ближе к наблюдателю, если у нее большая координатаY. От профильной плоскости проекции дальше удалена та точка, у которой больше координата Х.
Практический интерес вызывают точки, расположенные на одном перпендикуляре к плоскости проекций (рис. 4.1). Такие точки на чертеже называются конкурирующими.По ним определяется видимость элементов на чертеже. Из двух конкурирующих точек видимой считается та, у которой больше координата на другой плоскости проекций.
В данном случае видимой на фронтальной плоскости проекций будет точка b, так как у нее больше координатаY.
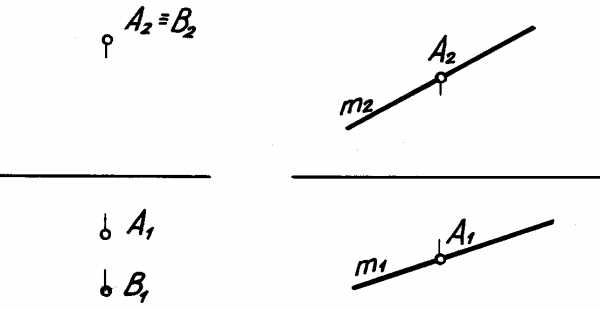
Рис. 4.1 Рис. 4.2
4.2. Взаимное расположение прямой и точки
Точка принадлежит прямой, если ее проекции принадлежат одноименным проекциям прямой (рис. 4.2).
4.3. Взаимное расположение двух прямых
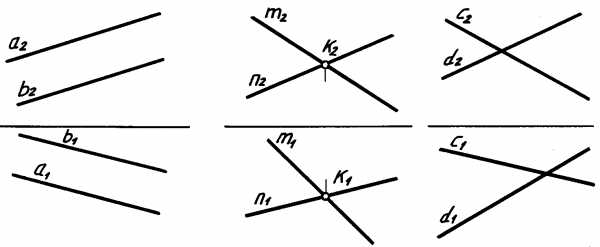
Прямые относительно друг друга могут быть параллельными (рис. 4.3, а), пересекающимися (б), скрещивающимися (в).
а б в
Рис. 4.3
4.4. Взаимное расположение точки и плоскости
Точка принадлежит плоскости, если она принадлежит прямой, лежащей в этой плоскости.
П р и м е р. Плоскость задана следами
(h0 f 0). Требуется построить
точку А, принадлежащую этой плоскости
(рис. 4.4).
f 0). Требуется построить
точку А, принадлежащую этой плоскости
(рис. 4.4).
Р е ш е н и е. Так как в плоскости можно построить бесчисленное множество точек, принадлежащих этой плоскости, то на одной из плоскостей проекций произвольно ставим одну проекцию точки (например, А2), но вторую проекцию А1находим из условия принадлежности точки плоскости. Для этого через А проводим прямую, т. е. через А2проводимh2до пересечения сf 0, определяем горизонтальную проекцию точки 1 и из 11параллельно горизонтальному следу проводимh1, на которой и отмечаем А1.
4.5. Взаимное расположение прямой и плоскости
Прямая принадлежит плоскости, если имеет две общие точки или одну общую точку и параллельна какой-либо прямой, лежащей в плоскости. Пусть плоскость на чертеже задана двумя пересекающимися прямыми. В данной плоскости требуется построить две прямыеmиnв соответствии с этими условиями(
 b))(рис. 4.5).
b))(рис. 4.5).Ре ш е н и е. 1. Произвольно проводимm2, так как прямая принадлежит плоскости, отмечаем проекции точек пересечения ее с прямымиаиbи определяем их горизонтальные проекции, через 11и 21проводимm1.
2. Через точку К плоскости проводим n2║m2 иn1║m1.
иn1║m1.
Прямая параллельна плоскости, если она параллельна какой-либо прямой, лежащей в плоскости.
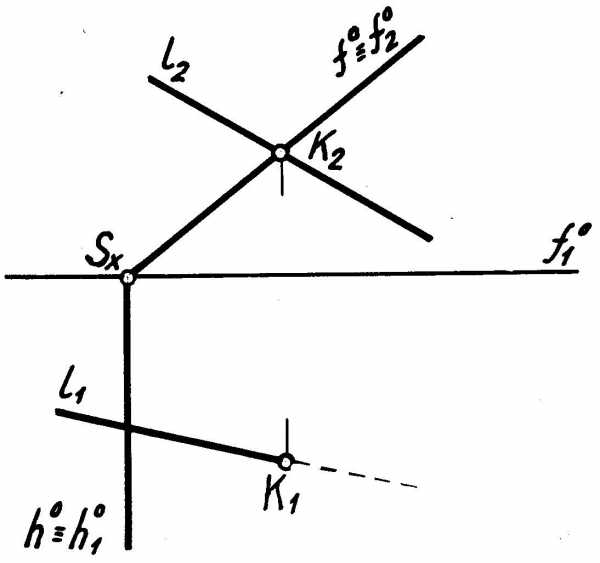
Пересечение прямой и плоскости.Возможны три случая расположения прямой и плоскости относительно плоскостей проекций. В зависимости от этого определяется точка пересечения прямой и плоскости.
Первый случай– прямая и плоскость – проецирующего положения. В этом случае точка пересечения на чертеже имеется (обе ее проекции), ее нужно только обозначить.
П р и м е р. На чертеже задана плоскость
следами Σ (h0 f 0)– горизонтально
проецирующего положения – и прямаяl– фронтально проецирующего положения.
Определить точку их пересечения (рис.
4.6).
f 0)– горизонтально
проецирующего положения – и прямаяl– фронтально проецирующего положения.
Определить точку их пересечения (рис.
4.6).
Точка пересечения на чертеже уже есть – К(К1К2).
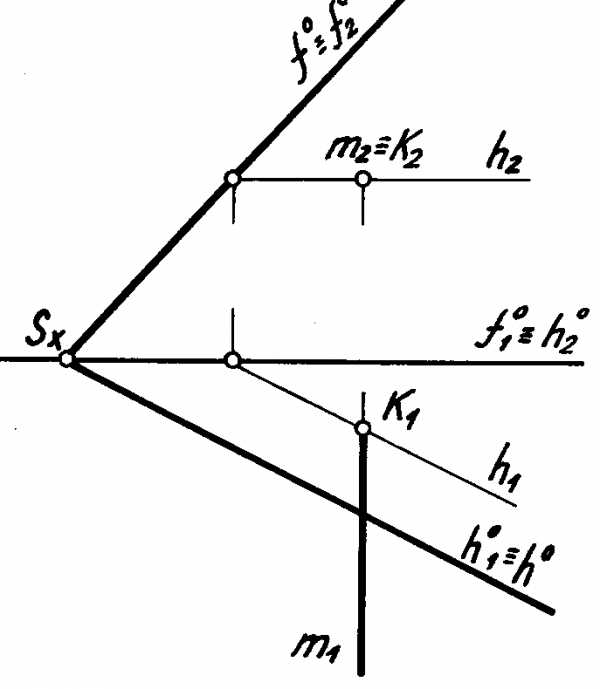
Второй случай – или прямая, или плоскость – проецирующего положения. В этом случае на одной из плоскостей проекций проекция точки пересечения уже имеется, ее нужно обозначить, а на второй плоскости проекций – найти по принадлежности.
а б
Рис. 4.7
Пр и м е р ы. На рис. 4.7, а изображена плоскость следами фронтально проецирующего положения и прямаяl– общего положения. Проекция точки пересечения К2на чертеже уже имеется, а проекцию К1необходимо найти по принадлежности точки К прямойl. На рис. 4.7, б плоскость общего положения, а прямаяm– фронтально проецирующего, тогда К2уже есть (совпадает сm2), а К1нужно найти из условия принадлежности точки К плоскости. Для этого через К проводят прямую (h– горизонталь), лежащую в плоскости.
Третий случай– и прямая, и плоскость – общего положения. В этом случае для определения точки пересечения прямой и плоскости необходимо воспользоваться так называемым посредником – плоскостью проецирующей. Для этого через прямую проводят вспомогательную секущую плоскость. Эта плоскость пересекает заданную плоскость по линии. Если эта линия пересекает заданную прямую, то есть точка пересечения прямой и плоскости.
П р и м е р ы. На рис. 4.8 представлены плоскость треугольником АВС – общего положения – и прямая l– общего положения. Чтобы определить точку пересечения К, необходимо черезlпровести фронтально проецирующую плоскость Σ, построить в треугольнике линию пересечения Δ и Σ (на чертеже это отрезок 1,2), определить К1и по принадлежности – К2. Затем определяется видимость прямойlпо отношению к треугольнику по конкурирующим точкам. На П1конкурирующими точками взяты точки 3 и 4. Видима на П1проекция точки 4, так как у нее координата Z больше, чем у точки 3, следовательно, проекцияl1от этой точки до К1будет невидима.
На П2конкурирующими точками взяты точка 1, принадлежащая АВ, и точка 5, принадлежащаяl
На рис. 4.9 изображены плоскость общего положения (задана следами) и прямая mтакже общего положения. Чтобы определить точку пересеченияmи плоскости, надо черезm2провести Σ2– фронтально проецирующую плоскость, построить линию пересечения двух плоскостей (отрезок 1,2), отметить К1и по принадлежности этой точки прямойlопределить К2.
studfiles.net
Взаимное положение точки и прямой
| т.А лежит на прямой т.В не лежит (III четверть) т.С выше прямой т.D перед прямой |
Если точка лежит на прямой, то её проекции лежат на одноимённых проекциях прямой.
1. Взаимное положение двух прямых
2 прямые в пространстве могут быть:
а) //,
б) пересекаться,
в) скрещиваться.
Если две прямые //, то их одноимённые проекции также //-ы друг другу.
Если две прямые пересекаются:
Одноимённые проекции двух пересекающихся прямых пересекаются и точки их пересечения лежат на одной линии связи. В противном случае прямые скрещиваются.

2. Проекции плоскостей. Способы задания и изображения плоскости на комплексном чертеже
Определителем плоскости называется совокупность геометрических элементов, однозначно задающих положение плоскости в пространстве.
На комплексном чертеже плоскость задаётся проекциями элементов своего определителя.
Способы задания плоскостей:
| 1) тремя точками, не лежащими на одной прямой |
| 2) прямой и точкой, не лежащей на этой прямой |
| 3) двумя пересекающимися прямыми |
| 4) двумя параллельными прямыми |
| 5) любой плоской фигурой |
Мы рассмотрим способы задания плоскости общего положения.
Плоскость считается заданной, если относительно любой точки пространства можно однозначно решить задачу о её принадлежности к этой плоскости.
3. Плоскости частного положения
К плоскостям частного положения относятся // или ^ к какой-либо плоскости проекций.
Плоскость, ^ плоскости проекций, называется проецирующей плоскостью.
^ к П1 – горизонтально проецирующая,
^ к П2 – фронтально проецирующая,
^ к П3 – профильно проецирующая.
горизонтально-проецирующая
Горизонтальные проекции всех точек, линий и фигур, лежащих в плоскости, проецируются на горизонтальную проекцию плоскости – собирательное свойство плоскости.
| фронтально-проецирующая |
Плоскость, // плоскости проекций, называется плоскостью уровня.
// П1 – горизонтальная плоскость уровня,
// П2 – фронтальная плоскость уровня,
// П3 – профильная плоскость уровня.

4. Точка в плоскости
Точка лежит в плоскости, если она принадлежит прямой, лежащей в этой плоскости.

5. Линии в плоскости
Среди множества прямых, лежащих в плоскости общего положения, можно выделить прямые частного положения.
Через любую точку плоскости общего положения всегда проходит 1 горизонталь, фронталь и профильная прямая уровня.

6. Параллельность прямой и плоскости
Прямая // плоскости, если в плоскости можно провести прямую, // данной.
1) Чаще всего приходится отвечать на вопрос: параллельны ли между собой заданная плоскость и прямая. Для этого на одной проекции плоскости проводится проекция прямой // проекции заданной прямой. Затем, из условия принадлежности прямой плоскости строится её вторая проекция и определяется, параллельна ли она второй проекции заданной прямой.
2) построить прямую, // данной плоскости
 | например, Задача имеет решений |
1) через заданную точку провести плоскость // данной прямой
 | 1) m||l Q(m,n)||l |
7. Параллельность плоскостей
Плоскости параллельны друг другу, если 2 пересекающиеся прямые одной плоскости //-ы двум пересекающимся прямым другой плоскости.
1) через заданную точку провести плоскость // данной.
2) заданы 2 плоскости, надо определить параллельны ли они между собой.
8. Классификация многогранников
Многогранником называется тело, ограниченное плоскими многоугольниками.
Многогранник называется выпуклым, если весь он лежит по одну сторону от плоскости любой его грани.
Многогранник называется правильным, если его боковые грани являются правильными многоугольниками.
Платон открыл 5 правильных выпуклых многогранников:
1) тетраэдр (четырёхгранник) – правильная треугольная пирамида;
2) гексаэдр(куб) – 8 вершин, 6 граней – квадратов;
3) октаэдр(8ми-гранник) – 6 вершин, 8 граней – треугольников;
4) икосаэдр(20ти-гранник) – 12 вершин, 20 граней – треугольников;
5) додекаэдр(12ти-гранник) – 20 вершин, 12 граней – пятиугольников.
Среди неправильных многогранников наибольший интерес представляют:
1) призмы – боковые рёбра // друг другу, а боковыми гранями являются параллелограммы;
2) пирамиды — боковые рёбра пересекаются в одной точке вершины;
3) призматоиды– многогранники, ограниченные какими-либо двумя многоугольниками, расположенными в //-ных плоскостях, называемыми основаниями, и треугольниками или трапециями, вершинами которых служат вершины оснований.
9. Изображение многогранников на комплексном чертеже
Многогранник на комплексном чертеже изображается проекциями своих вершин и рёбер.
Для придания однозначности чертежу вершины необходимо пронумеровать, а рёбра обвести с учётом видимости. Для определения видимости рёбер надо воспользоваться конкурирующими точками.
10. Понятие о поверхности
В математике под поверхностью понимается непрерывное множество точек, между координатами которых может быть установлена зависимость, определяемая в декартовой системе координат уравнением вида F(x,y,z)=0.
Похожие статьи:
poznayka.org
Взаимное расположение точки, прямой и плоскости — КиберПедия
Прямая может принадлежать и не принадлежать плоскости. Она принадлежит плоскости, если хотя бы две точки ее лежат на плоскости. На рисунке 93 показана плоскость Sum (axb). Прямая l принадлежит плоскости Sum, так как ее точки 1 и 2 принадлежат этой плоскости.
Если прямая не принадлежит плоскости, она может быть параллельной ей или пересекать ее.
Прямая параллельна плоскости, если она параллельна другой прямой, лежащей в этой плоскости. На рисунке 93 прямая m || Sum, так как она параллельна прямой l, принадлежащей этой плоскости.
Прямая может пересекать плоскость под различными углами и, в частности, быть перпендикулярной ей. Построение линий пересечения прямой с плоскостью приведено в §61.
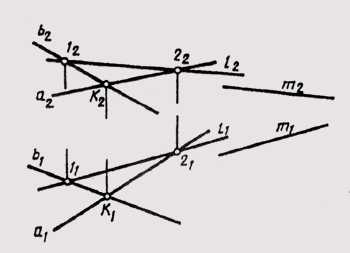
Рисунок 93 — Прямая, принадлежащая плоскости
Точка по отношению к плоскости может быть расположена следующим образом: принадлежать или не принадлежать ей. Точка принадлежит плоскости, если она расположена на прямой, расположенной в этой плоскости. На рисунке 94 показан комплексный чертеж плоскости Sum, заданной двумя параллельными прямыми l и п. В плоскости расположена линия m. Точка A лежит в плоскости Sum, так как она лежит на прямой m. Точка В не принадлежит плоскости, так как ее вторая проекция не лежит на соответствующих проекциях прямой.
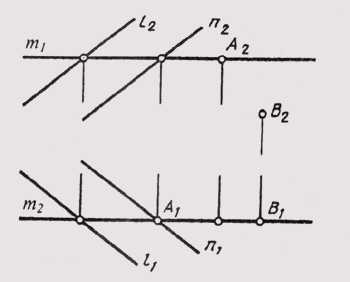
Рисунок 94 — Комплексный чертеж плоскости, заданной двумя параллельными прямыми
Коническая и цилиндрическая поверхности
К коническим относятся поверхности, образованные перемещением прямолинейной образующей l по криволинейной направляющей m. Особенностью образования конической поверхности является то, что при этом одна точка образующей всегда неподвижна. Эта точка является вершиной конической поверхности (рисунок 95, а). Определитель конической поверхности включает вершину S и направляющую m, при этом l‘~S; l‘^ m.
К цилиндрическим относятся поверхности, образованные прямой образующей /, перемещающейся по криволинейной направляющей т параллельно заданному направлению S (рисунок 95, б). Цилиндрическую поверхность можно рассматривать как частный случай конической поверхности с бесконечно удаленной вершиной S.
Определитель цилиндрической поверхности состоит из направляющей т и направления S, образующих l, при этом l’ || S; l’ ^ m.
Если образующие цилиндрической поверхности перпендикулярны плоскости проекций, то такую поверхность называют проецирующей.На рисунке 95, в показана горизонтально проецирующая цилиндрическая поверхность.
На цилиндрической и конической поверхностях заданные точки строят с помощью образующих, проходящих через них. Линии на поверхностях, например линия а на рисунок 95, в или горизонтали h на рисунке 95, а, б, строятся с помощью отдельных точек, принадлежащих этим линиям.
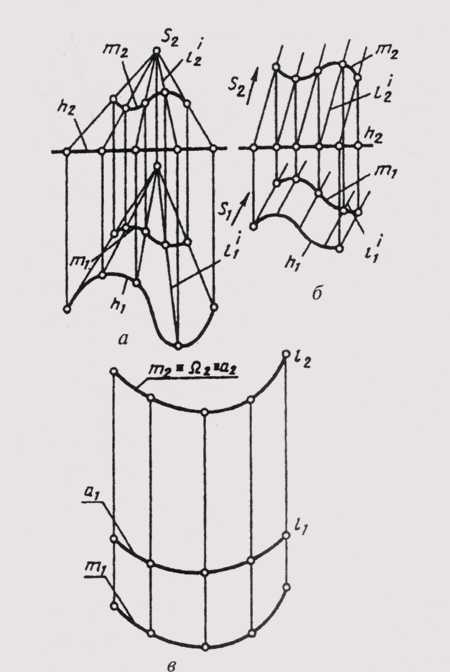
Рисунок 95 — Коническая и цилиндрическая поверхности
Торсовые поверхности
Торсовой называется поверхность, образованная прямолинейной образующей l , касающейся при своем движении во всех своих положениях некоторой пространственной кривой т, называемой ребром возврата(рисунок 96). Ребро возврата полностью задает торс и является геометрической частью определителя поверхности. Алгоритмической частью служит указание касательности образующих к ребру возврата.
Коническая поверхность является частным случаем торса, у которого ребро возврата т выродилось в точку S— вершину конической поверхности. Цилиндрическая поверхность — частный случай торса, у которого ребро возврата — точка в бесконечности.
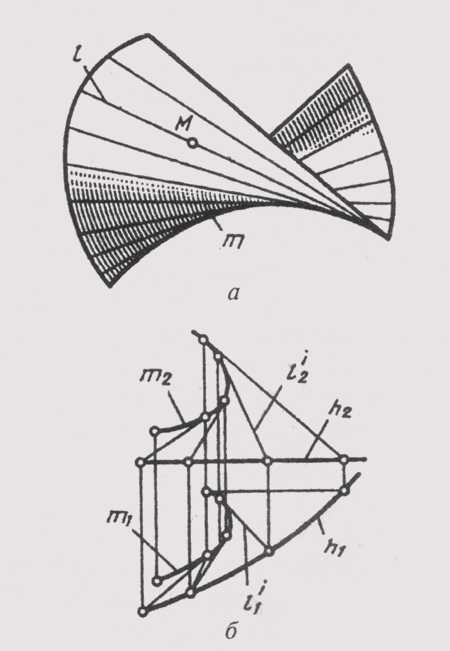
Рисунок 96 – Торсовая поверхность
Гранные поверхности
К гранным относятся поверхности, образованные перемещением прямолинейной образующей l по ломаной направляющей m. При этом если одна точка S образующей неподвижна, создается пирамидальная поверхность (рисунок 97), если образующая при перемещении параллельна заданному направлению S, то создается призматическая поверхность (рисунок 98).
Элементами гранных поверхностей являются: вершина S (у призматической поверхности она находится в бесконечности), грань (часть плоскости, ограниченная одним участком направляющей m и крайними относительно него положениями образующей l ) и ребро (линия пересечения смежных граней).
Определитель пирамидальной поверхности включает в себя вершину S, через которую проходят образующие и направляющие: l’ ~ S; l ^ т.
Определитель призматической поверхности, кроме направляющей т, содержит направление S, которому параллельны все образующие l поверхности: l||S; l^ т.
Рисунок 97 — Пирамидальная поверхность
Рисунок 98 — Призматическая поверхность
Замкнутые гранные поверхности, образованные некоторым числом (не менее четырех) граней, называются многогранниками. Из числа многогранников выделяют группу правильных многогранников, у которых все грани правильные и конгруэнтные многоугольники, а многогранные углы при вершинах выпуклые и содержат одинаковое число граней. Например: гексаэдр — куб (рисунок 99, а), тетраэдр — правильный четырехугольник (рисунок 99, 6) октаэдр — многогранник (рисунок 99, в). Форму различных многогранников имеют кристаллы.
Рисунок 99 — Многогранники
Пирамида— многогранник, в основании которого лежит произвольный многоугольник, а боковые грани — треугольники с общей вершиной S.
На комплексном чертеже пирамида задается проекциями ее вершин и ребер с учетом их видимости. Видимость ребра определяется с помощью конкурирующих точек (рисунок 100).

Рисунок 100 – Определение видимости ребра с помощью конкурирующих точек
Призма— многогранник, у которого основание — два одинаковых и взаимно параллельных многоугольника, а боковые грани — параллелограммы. Если ребра призмы перпендикулярны плоскости основания, такую призму называют прямой. Если у призмы ребра перпендикулярны какой-либо плоскости проекций, то боковую поверхность ее называют проецирующей. На рисунке 101 дан комплексный чертеж прямой четырехугольной призмы с горизонтально проецирующей поверхностью.
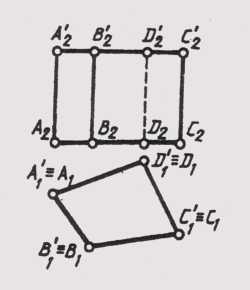
Рисунок 101 — Комплексный чертеж прямой четырехугольной призмы с горизонтально проецирующей поверхностью
При работе с комплексным чертежом многогранника приходится строить на его поверхности линии, а так как линия есть совокупность точек, то необходимо уметь строить точки на поверхности.
Любую точку на гранной поверхности можно построить с помощью образующей, проходящей через эту точку. На рисунке 100 в грани ACS построена точка М с помощью образующей S-5.
Винтовые поверхности
К винтовым относятся поверхности, создаваемые при винтовом движении прямолинейной образующей. Линейчатые винтовые поверхности называют геликоидами.
Прямой геликоид образуется движением прямолинейной образующей i по двум направляющим: винтовой линии т и ее оси i; при этом образующая l пересекает винтовую ось под прямым углом (рисунок 102, а). Прямой геликоид используется при создании винтовых лестниц, шнеков, а также силовых резьбах, в станках.
Наклонный геликоид образуется движением образующей по винтовой направляющей т и ее оси i так, что образующая l пересекает ось i под постоянным углом φ, отличным от прямого, т. е. в любом положении образующая l параллельна одной из образующих направляющего конуса с углом при вершине, равным 2φ (рисунок 102, б). Наклонные геликоиды ограничивают поверхности витков резьбы.

Рисунок 102 — Геликоиды
Поверхности вращения
К поверхностям вращения относятся поверхности, образующиеся вращением линии l вокруг прямой i, представляющей собой ось вращения. Они могут быть линейчатыми, например конус или цилиндр вращения, и нелинейчатыми или криволинейными, например сфера. Определитель поверхности вращения включает образующую l и ось i. Каждая точка образующей при вращении описывает окружность, плоскость которой перпендикулярна оси вращения. Такие окружности поверхности вращения называются параллелями. Наибольшую из параллелей называют экватором.Экватор .определяет горизонтальный очерк поверхности, если i _|_ П1. В этом случае параллелями являются горизонтали hэтой поверхности.
Кривые поверхности вращения, образующиеся в результате пересечения поверхности плоскостями, проходящими через ось вращения, называются меридианами.Все меридианы одной поверхности конгруэнтны. Фронтальный меридиан называют главным меридианом; он определяет фронтальный очерк поверхности вращения. Профильный меридиан определяет профильный очерк поверхности вращения.
Строить точку на криволинейных поверхностях вращения удобнее всего с помощью параллелей поверхности. На рисунке 103 точка М построена на параллели h4.
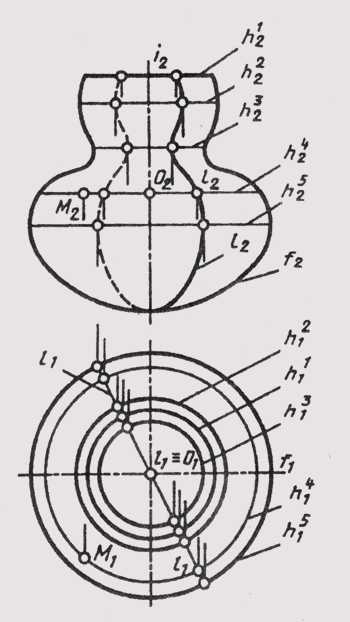
Рисунок 103 – Построение точки на криволинейной поверхности
Поверхности вращения нашли самое широкое применение в технике. Они ограничивают поверхности большинства машиностроительных деталей.
Коническая поверхность вращения образуется вращением прямой i вокруг пересекающейся с ней прямой — оси i (рисунок 104, а). Точка М на поверхности построена с помощью образующей l и параллели h. Эту поверхность называют еще конусом вращения или прямым круговым конусом.
Цилиндрическая поверхность вращения образуется вращением прямой l вокруг параллельной ей оси i (рисунок 104, б). Эту поверхность называют еще цилиндром или прямым круговым цилиндром.
Сфера, образуется вращением окружности вокруг ее диаметра (рисунок 104, в). Точка A на поверхности сферы принадлежит главному меридиану f, точка В — экватору h, а точка М построена на вспомогательной параллели h’.
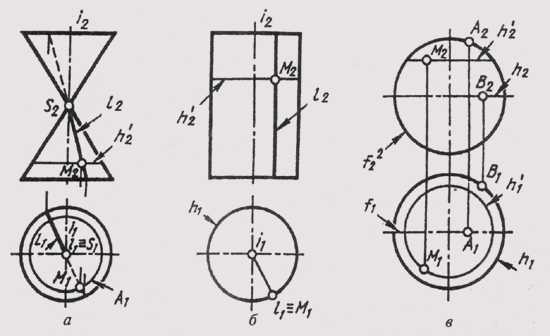
Рисунок 104 — Образование поверхностей вращения
Тор образуется вращением окружности или ее дуги вокруг оси, лежащей в плоскости окружности. Если ось расположена в пределах образующейся окружности, то такой тор называется закрытым (рисунок 105, а). Если ось вращения находится вне окружности, то такой тор называется открытым (рисунок 105, б). Открытый тор называется еще кольцом.
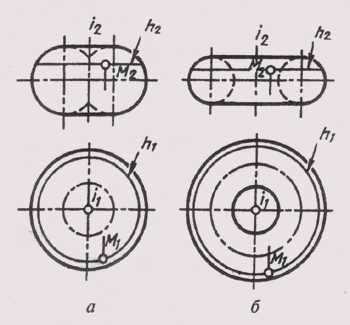
Рисунок 105 – Образование тора
Поверхности вращения могут быть образованы и другими кривыми второго порядка. Эллипсоид вращения (рисунок 106, а) образуется вращением эллипса вокруг одной из его осей; параболоид вращения (рисунок 106, б) — вращением параболы вокруг ее оси; гиперболоид вращения однополостный (рисунок 106, в) образуется вращением гиперболы вокруг мнимой оси, а двуполостный (рисунок 106, г) — вращением гиперболы вокруг действительной оси.
Рисунок 106 – Образование поверхностей вращения кривыми второго порядка
В общем случае поверхности изображаются не ограниченными в направлении распространения образующих линий (см рисунки 97, 98). Для решения конкретных задач и получения геометрических фигур ограничиваются плоскостями обреза. Например, чтобы получить круговой цилиндр, необходимо ограничить участок цилиндрической поверхности плоскостями обреза (см рисунок 104, б). В результате получим его верхнее и нижнее основания. Если плоскости обреза перпендикулярны оси вращения, цилиндр будет прямым, если нет — цилиндр будет наклонным.
Чтобы получить круговой конус (см рисунок 104, а), необходимо выполнить обрез по вершине и за пределами ее. Если плоскость обреза основания цилиндра будет перпендикулярна оси вращения — конус будет прямой, если нет — наклонный. Если обе плоскости обреза не проходят через вершину — конус получим усеченным.
С помощью плоскости обреза можно получить призму и пирамиду. Например, шестигранная пирамида будет прямой, если все ее ребра имеют одинаковый наклон к плоскости обреза. В других случаях она будет наклонной. Если она выполнена с помощью плоскостей обреза и ни одна из них не проходит через вершину — пирамида усеченная.
Призму (см рисунок 101) можно получить, ограничив участок призматической поверхности двумя плоскостями обреза. Если плоскость обреза перпендикулярна ребрам, например восьмигранной призмы, она прямая, если не перпендикулярна — наклонная.
Выбирая соответствующее положение плоскостей обреза, можно получать различные формы геометрических фигур в зависимости от условий решаемой задачи.
cyberpedia.su
Взаимное расположение прямой и точки.
Прямая на плоскости – необходимые сведения.
В этой статье мы подробно остановимся на одном из первичных понятий геометрии – на понятии прямой линии на плоскости. Сначала определимся с основными терминами и обозначениями. Далее обсудим взаимное расположение прямой и точки, а также двух прямых на плоскости, приведем необходимые аксиомы. В заключении, рассмотрим способы задания прямой на плоскости и приведем графические иллюстрации.
Навигация по странице.
- Прямая на плоскости — понятие.
- Взаимное расположение прямой и точки.
- Взаимное расположение прямых на плоскости.
- Способы задания прямой на плоскости.
Прямая на плоскости — понятие.
Прежде чем дать понятие прямой на плоскости, следует четко представлять себе что же представляет собой плоскость. Представление о …
плоскости позволяет получить, к примеру, ровная поверхность стола или стены дома. Следует, однако, иметь в виду, что размеры стола ограничены, а плоскость простирается и за пределы этих границ в бесконечность (как будто у нас сколь угодно большой стол).
Если взять хорошо заточенный карандаш и дотронуться его стержнем до поверхности «стола», то мы получим изображение точки. Так мы получаем представление о точке на плоскости.
Теперь можно переходить и к понятию прямой линии на плоскости.
Положим на поверхность стола (на плоскость) лист чистой бумаги. Для того чтобы изобразить прямую линию, нам необходимо взять линейку и провести карандашом линию на сколько это позволяют сделать размеры используемой линейки и листа бумаги. Следует отметить, что таким способом мы получим лишь часть прямой. Прямую линию целиком, простирающуюся в бесконечность, мы можем только вообразить.
К началу страницы
Взаимное расположение прямой и точки.
Точки принято обозначать большими латинскими буквами, например, точки А и F. В свою очередь прямые линии обозначают малыми латинскими буквами, к примеру, прямые a и d.
Возможны два варианта взаимного расположения прямой и точки на плоскости: либо точка лежит на прямой (в этом случае также говорят, что прямая проходит через точку), либо точка не лежит на прямой (также говорят, что точка не принадлежит прямой или прямая не проходит через точку).
Для обозначения принадлежности точки некоторой прямой используют символ « ». К примеру, если точка А лежит на прямой а, то можно записать . Если точка А не принадлежит прямой а, то записывают .
Справедливо следующее утверждение: через любые две точки проходит единственная прямая.
Это утверждение является аксиомой и его следует принять как факт. К тому же, это достаточно очевидно: отмечаем две точки на бумаге, прикладываем к ним линейку и проводим прямую линию. Прямую, проходящую через две заданные точки (например, через точки А и В), можно обозначать двумя этими буквами (в нашем случае прямая АВ или ВА).

Следует понимать, что на прямой, заданной на плоскости, лежит бесконечно много различных точек, причем все эти точки лежат в одной плоскости. Это утверждение устанавливается аксиомой: если две точки прямой лежат в некоторой плоскости, то все точки этой прямой лежат в этой плоскости.
Множество всех точек, расположенных между двумя заданными на прямой точками, вместе с этими точками называют отрезком прямой или просто отрезком. Точки, ограничивающие отрезок, называются концами отрезка. Отрезок обозначают двумя буквами, соответствующими точкам концов отрезка. К примеру, пусть точки А и В являются концами отрезка, тогда этот отрезок можно обозначить АВ или ВА. Обратите внимание, что такое обозначение отрезка совпадает с обозначением прямой. Чтобы избежать путаницы, рекомендуем к обозначению добавлять слово «отрезок» или «прямая».
Для краткой записи принадлежности и не принадлежности некоторой точки некоторому отрезку используют все те же символы и . Чтобы показать, что некоторый отрезок лежит или не лежит на прямой пользуются символами и соответственно. К примеру, если отрезок АВ принадлежит прямой а, можно кратко записать .
Следует также остановиться на случае, когда три различных точки принадлежат одной прямой. В этом случае одна, и только одна точка, лежит между двумя другими. Это утверждение является очередной аксиомой. Пусть точки А, В и С лежат на одной прямой, причем точка В лежит между точками А и С. Тогда можно говорить, что точки А и С находятся по разные стороны от точки В. Также можно сказать, что точки В и С лежат по одну сторону то точки А, а точки А и В лежат по одну сторону от точки С.
Для полноты картины заметим, что любая точка прямой делит эту прямую на две части – двалуча. Для этого случая дается аксиома: произвольная точка О, принадлежащая прямой, делит эту прямую на два луча, причем две любые точки одного луча лежат по одну сторону от точкиО, а две любые точки разных лучей – по разные стороны от точки О.
загрузка…
К началу страницы
refac.ru
4.1. Взаимное расположение двух точек
Положение точки на чертеже определяется координатами. Точка расположена выше другой, если у нее больше координата Z. Точка находится ближе к наблюдателю, если у нее большая координатаY. От профильной плоскости проекции дальше удалена та точка, у которой больше координата Х.
Практический интерес вызывают точки, расположенные на одном перпендикуляре к плоскости проекций (рис. 4.1). Такие точки на чертеже называются конкурирующими.По ним определяется видимость элементов на чертеже. Из двух конкурирующих точек видимой считается та, у которой больше координата на другой плоскости проекций.
В данном случае видимой на фронтальной плоскости проекций будет точка b, так как у нее больше координатаY.
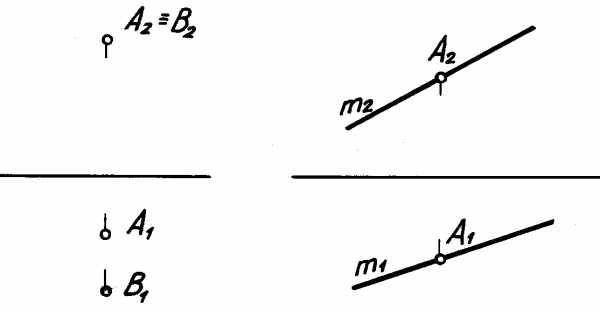
Рис. 4.1 Рис. 4.2
4.2. Взаимное расположение прямой и точки
Точка принадлежит прямой, если ее проекции принадлежат одноименным проекциям прямой (рис. 4.2).
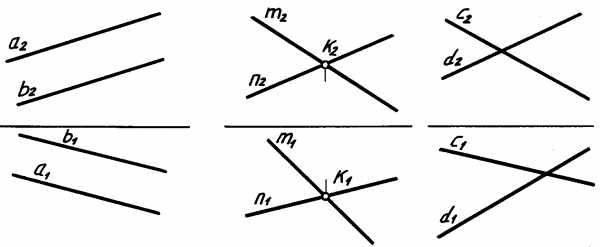
4.3. Взаимное расположение двух прямых
Прямые относительно друг друга могут быть параллельными (рис. 4.3, а), пересекающимися (б), скрещивающимися (в).
а б в
Рис. 4.3
4.4. Взаимное расположение точки и плоскости
Точка принадлежит плоскости, если она принадлежит прямой, лежащей в этой плоскости.
П р и м е р. Плоскость задана следами
(h0 f 0). Требуется построить
точку А, принадлежащую этой плоскости
(рис. 4.4).
f 0). Требуется построить
точку А, принадлежащую этой плоскости
(рис. 4.4).
Р е ш е н и е. Так как в плоскости можно построить бесчисленное множество точек, принадлежащих этой плоскости, то на одной из плоскостей проекций произвольно ставим одну проекцию точки (например, А2), но вторую проекцию А1находим из условия принадлежности точки плоскости. Для этого через А проводим прямую, т. е. через А2проводимh2до пересечения сf 0, определяем горизонтальную проекцию точки 1 и из 11параллельно горизонтальному следу проводимh1, на которой и отмечаем А1.
4.5. Взаимное расположение прямой и плоскости
Прямая принадлежит плоскости, если
имеет две общие точки или одну общую
точку и параллельна какой-либо прямой,
лежащей в плоскости. Пусть плоскость
на чертеже задана двумя пересекающимися
прямыми. В данной плоскости требуется
построить две прямыеmиnв соответствии с этими
условиями(Г(а b))(рис. 4.5).
b))(рис. 4.5).
Ре ш е н и е. 1. Произвольно проводимm2, так как прямая принадлежит плоскости, отмечаем проекции точек пересечения ее с прямымиаиbи определяем их горизонтальные проекции, через 11и 21проводимm1.
2. Через точку К плоскости проводим n2║m2 иn1║m1.
иn1║m1.
Прямая параллельна плоскости, если она параллельна какой-либо прямой, лежащей в плоскости.
Пересечение прямой и плоскости.Возможны три случая расположения прямой и плоскости относительно плоскостей проекций. В зависимости от этого определяется точка пересечения прямой и плоскости.
Первый случай– прямая и плоскость – проецирующего положения. В этом случае точка пересечения на чертеже имеется (обе ее проекции), ее нужно только обозначить.
П р и м е р. На чертеже задана плоскость
следами Σ (h0 f 0)– горизонтально
проецирующего положения – и прямаяl– фронтально проецирующего положения.
Определить точку их пересечения (рис.
4.6).
f 0)– горизонтально
проецирующего положения – и прямаяl– фронтально проецирующего положения.
Определить точку их пересечения (рис.
4.6).
Точка пересечения на чертеже уже есть – К(К1К2).
Второй случай – или прямая, или плоскость – проецирующего положения. В этом случае на одной из плоскостей проекций проекция точки пересечения уже имеется, ее нужно обозначить, а на второй плоскости проекций – найти по принадлежности.
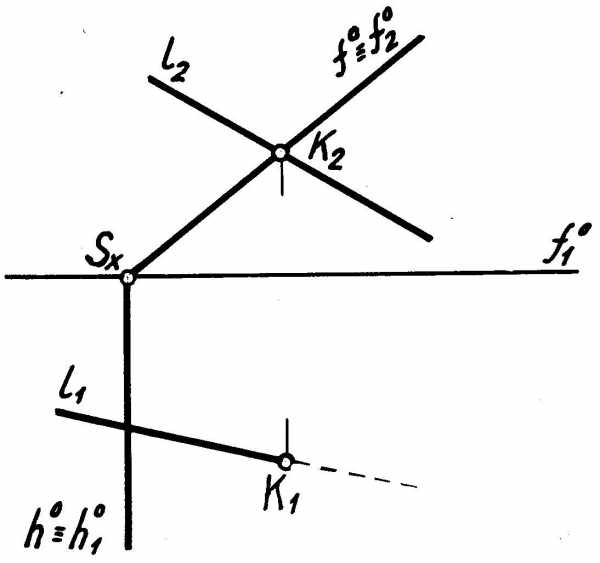
а б
Рис. 4.7
Пр и м е р ы. На рис. 4.7, а изображена плоскость следами фронтально проецирующего положения и прямаяl– общего положения. Проекция точки пересечения К2на чертеже уже имеется, а проекцию К1необходимо найти по принадлежности точки К прямойl. На рис. 4.7, б плоскость общего положения, а прямаяm– фронтально проецирующего, тогда К2уже есть (совпадает сm2), а К1нужно найти из условия принадлежности точки К плоскости. Для этого через К проводят прямую (h– горизонталь), лежащую в плоскости.
Третий случай– и прямая, и плоскость – общего положения. В этом случае для определения точки пересечения прямой и плоскости необходимо воспользоваться так называемым посредником – плоскостью проецирующей. Для этого через прямую проводят вспомогательную секущую плоскость. Эта плоскость пересекает заданную плоскость по линии. Если эта линия пересекает заданную прямую, то есть точка пересечения прямой и плоскости.
П р и м е р ы. На рис. 4.8 представлены плоскость треугольником АВС – общего положения – и прямая l– общего положения. Чтобы определить точку пересечения К, необходимо черезlпровести фронтально проецирующую плоскость Σ, построить в треугольнике линию пересечения Δ и Σ (на чертеже это отрезок 1,2), определить К1и по принадлежности – К2. Затем определяется видимость прямойlпо отношению к треугольнику по конкурирующим точкам. На П1конкурирующими точками взяты точки 3 и 4. Видима на П1проекция точки 4, так как у нее координата Z больше, чем у точки 3, следовательно, проекцияl1от этой точки до К1будет невидима.
На П2конкурирующими точками взяты точка 1, принадлежащая АВ, и точка 5, принадлежащаяl. Видимой будет точка 1, так как у нее координатаYбольше, чем у точки 5, и следовательно, проекция прямойl2 до К2невидима.
На рис. 4.9 изображены плоскость общего положения (задана следами) и прямая mтакже общего положения. Чтобы определить точку пересеченияmи плоскости, надо черезm2провести Σ2– фронтально проецирующую плоскость, построить линию пересечения двух плоскостей (отрезок 1,2), отметить К1и по принадлежности этой точки прямойlопределить К2.
studfiles.net
Взаимное расположение прямой и пары точек
Пусть заданы точки и общее уравнение некоторой прямой: Ax + By + C = 0. Вычислим значения величин и по формулам:
| (14) | (15) |
Взаимное расположение точек и относительно заданной прямой можно определить по следующим признакам:
1) числа и имеют одинаковые знаки, в этом случае точки и лежат по одну сторону от прямой;
2) числа и имеют противоположные знаки, в этом случае точки и лежат по разные стороны от прямой;
3) одно из чисел , равно нулю (или оба равны нулю), в этом случае точка или соответственно (или обе) принадлежит прямой.
Расстояние от точки до прямой
 Рис. 5
Рис. 5
| Расстояние d от точки до прямой Ax + By + C = 0 (рис. 5) вычисляется по формуле: . (16) |
Пучок прямых
Через одну фиксированную точку (рис. 6) на плоскости можно провести бесконечное множество прямых. Это множество называется цент-ральным пучком(пучком) прямых, а точка называется центром пучка. Каждую из прямых пучка (кроме той, которая параллельна оси
ординат) можно представить уравнением:
| (17) |
| где tg – угловой коэффициент прямой (см. рис. 6). Уравнение вида (17) называется уравнением пучка прямых с центром в точке | Рис. 6 |
Угол между прямыми
| Если пара прямых на плоскости задана общими уравнениями: (рис. 7, прямая f) и (рис. 7, прямая g), то косинус угла между этими прямыми может быть вычислен по формуле: | Рис. 7 |
| (18) |
Если пара прямых на плоскости задана уравнениями «с угловым коэффициентом»: и , то тангенс угла между этими прямыми рассчитывается по уравнению:
| tg | (19) |
Если пара прямых на плоскости задана своими каноническими уравнениями: и то косинус угла между этими прямыми определяется по формуле:
| (20) |
Условия параллельности и перпендикулярности прямых
Прямые, заданные общими уравнениями: и взаимно перпендикулярны тогда и только тогда, когда Данные прямые параллельны тогда и только тогда, когда
Прямые на плоскости, заданные в виде: и перпендикулярны только том случае, когда (при ). Данные прямые параллельны тогда и только тогда, когда их угловые коэффициенты равны, т. е.
Прямые, заданные своими каноническими уравнениями: и взаимно перпендикулярны тогда и только тогда, когда Данные прямые параллельны, если только выполнено условие:
Точка пересечения непараллельных прямых
Если на плоскости заданы две прямые: и , то согласно утверждению 2 координаты точки пересечения этих прямых можно вычислить по формулам:
| (21) | (22) |
3. ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
Варианты типового расчета «Прямая на плоскости»
Задание 1.Указать особенности в расположении прямых на плоскости (прямая общего положения, проходящая или не проходящая через начало координат; прямая, параллельная оси Ох или Оу) и сделать чертеж. Уравнения заданных прямых по вариантам представлены в табл. 1.
Таблица 1
Данные к заданию 1
Окончание табл. 1
Задание 2.Выбрать из имеющегося списка прямых на плоскости (табл. 2) пары: а) пересекающихся прямых; б) совпадающих прямых; в) прямых, не имеющих общих точек.
Таблица 2
Данные к заданию 2
Продолжение табл. 2
Окончание табл. 2
Задание 3.Две точки на плоскости заданы координатами: и , – некоторый угол (табл. 3). Составить: 1) уравнение прямой на плоскости, проходящей через точки и найти ее направляющие косинусы; 2) уравнение прямой, проходящей через точку и образующей с осью абсцисс угол .
Таблица 3
Данные к заданию 3
Окончание табл. 3
Задание 4. Дано общее уравнение прямой (табл. 4), записать для нее следующие виды уравнений:
1) каноническое
2) параметрические
3) «с угловым коэффициентом»
4) «в отрезках»
5) нормальное
Построить заданную прямую в системе координат хОу.
Таблица 4
Данные к заданию 4
Окончание табл. 4
Задание 5. Даны прямые и точка М (табл. 5). Составить уравнения прямых, проходящих: 1) через точку М параллельно прямой l; 2) через точку М перпендикулярно прямой l.
Найти угол между прямыми и и расстояние d от точки М до прямой l.
Таблица 5
Данные к заданию 5
Продолжение табл. 5
Задание 6.Отметить на координатной плоскости область решения системы линейных неравенств (табл. 6).
Таблица 6
Данные к заданию 6
Примеры выполнения заданий типового расчета
Задание 1.Указать особенности в расположении прямых на плоскости (прямая общего положения, проходящая или не проходящая через начало координат; прямая, параллельная оси Ох или Оу): 1) 2) 3) Сделать чертеж каждой прямой в системе координат
Решение.
1) Уравнение приведем к виду: – получили уравнение вида (см. подразд. 1.7, п. б), значит, данная прямая параллельна оси Оу и проходит через точку с координатами (рис. 8).
infopedia.su
ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ТОЧКИ, ПРЯМЫХ И ПЛОСКОСТЕЙ
Взаимное расположение точки и прямой
Возможны два варианта расположения точки относительно прямой:
1) точка принадлежит прямой (рис. 3.1 а), тогда, согласно основным свойствам прямоугольного проецирования[4], на КЧ ее проекции лежат на одноименных проекциях прямой.
;
2) точка не принадлежит прямой (рис. 3.1 б), если хотя бы одна из проекций точки не принадлежит проекции прямой.
; .
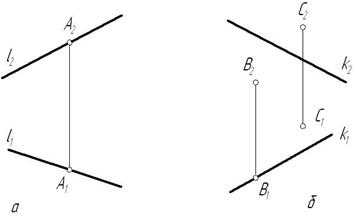
Рис. 3.1
Взаимное расположение прямых
Прямые в пространстве могут занимать относительно друг друга одно из трех положений:
1) быть параллельными;
2) пересекаться;
3) скрещиваться.
Параллельными называются прямые, лежащие в одной плоскости и не имеющие общих точек.
Рис. 3.2
Если прямые параллельны друг другу, то на КЧ их одноименные проекции тоже параллельны (см. п. 1.2).
.
Пересекающимися называются прямые, лежащие в одной плоскости и имеющие одну общую точку.
У пересекающихся прямых на КЧ одноименные проекции пересекаются в проекциях точки А. Причем фронтальная ( ) и горизонтальная ( )проекции этой точки должны находиться на одной линии связи.
.
Рис. 3.3
Скрещивающимися называются прямые, лежащие в параллельных плоскостях и не имеющие общих точек.
Рис. 3.4
Если прямые скрещивающиеся, то на КЧ их одноименные проекции могут пересекаться, но точки пересечений одноименных проекций не будут лежать на одной линии связи.
На рис. 3.4 точка С принадлежит прямой b, а точка D – прямой а. Эти точки находятся на одинаковом расстоянии от фронтальной плоскости проекций. Аналогично точки E и F принадлежат разным прямым, но находятся на одном расстоянии от горизонтальной плоскости проекций. Поэтому на КЧ их фронтальные проекции совпадают.
Принадлежность прямой и точки плоскости
Возможны два случая расположения точки относительно плоскости: точка может принадлежать плоскости или не принадлежать ей (рис. 3.5).
Признак принадлежности точки и прямой плоскости:
Точка принадлежит плоскости, если принадлежит прямой, лежащей в этой плоскости.
Прямая принадлежит плоскости, если имеет с ней две общие точки или имеет с ней одну общую точку и параллельна другой прямой, лежащей в этой плоскости.
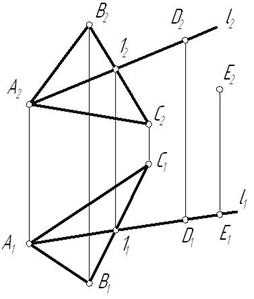
Рис. 3.5
На рис. 3.5 изображена плоскость и точки D и Е. Точка D принадлежит плоскости, т. к. принадлежит прямой l, имеющей с этой плоскостью две общие точки – 1 и А. Точка Е не принадлежит плоскости, т.к. через нее нельзя провести прямую, лежащую в данной плоскости.
На рис. 3.6 показана плоскость и прямая t, лежащая в этой плоскости, т.к. имеет с ней общую точку 1 и параллельна прямой а.
.
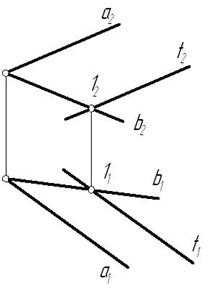
Рис. 3.6
Линии уровня плоскости
Линиями уровня плоскости называются прямые, лежащие в плоскости и параллельные одной из плоскостей проекций.
Существуют три линии уровня плоскости: горизонталь плоскости, фронталь плоскости и профильная прямая плоскости.
1. Горизонталь плоскости – прямая, лежащая в плоскости и параллельная горизонтальной плоскости проекций.
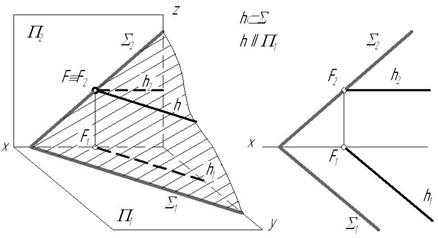
Рис. 3.7
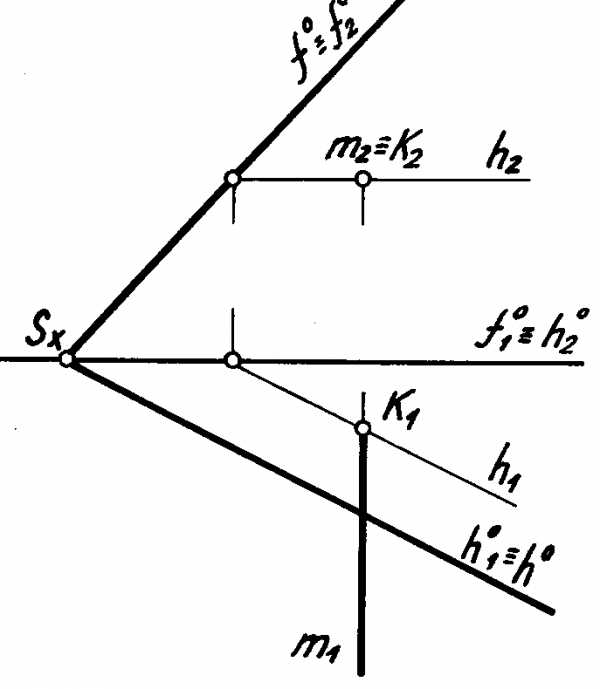
Признаки и свойства горизонтали плоскости:
1) все горизонтали плоскости параллельны друг другу;
2) фронтальный след горизонтали (точка F) принадлежит фронтальному следу плоскости;
3) горизонтальная проекция горизонтали параллельна горизонтальному следу плоскости.

Рис. 3.8
На рис. 3.8 приведена плоскость общего положения, заданная ,и принадлежащая ей горизонталь h. Если плоскость не задана следами, то построение горизонтали плоскости начинают с построения ее фронтальной проекции, идущей параллельно оси х. Т.к. горизонталь принадлежит плоскости, то она имеет с ней две общие точки – 1 и С. Зная их фронтальные проекции и , по линиям связи можно получить горизонтальные проекции и ,а затем, соединив между собой, получить горизонтальную проекцию горизонтали.
2. Фронталь плоскости – прямая, лежащая в плоскости и параллельная фронтальной плоскости проекций.
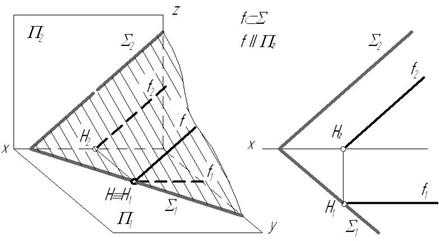
Рис. 3.9
Признаки и свойства фронтали плоскости:
1) все фронтали плоскости параллельны друг другу;
2) горизонтальный след фронтали (точка H) принадлежит горизонтальному следу плоскости;
3) фронтальная проекция фронтали параллельна фронтальному следу плоскости.
Если плоскость не задана следами, то построение фронтали плоскости начинают с построения ее горизонтальной проекции, идущей параллельно оси х (рис. 3.8). Т.к. фронталь принадлежит плоскости, то имеет с ней две общие точки – 2 и А. Имея их горизонтальные проекции и , по линиям связи можно получить фронтальные проекции и ,а затем, соединив между собой, получить фронтальную проекцию фронтали.
3. Профильная прямая плоскости – прямая лежащая в плоскости и параллельная профильной плоскости проекций (рис. 3.10).
Признаки и свойства профильной прямой плоскости:
1) все профильные прямые плоскости параллельны друг другу;
2) фронтальный след профильной прямой (точка F) принадлежит фронтальному следу плоскости, а ее горизонтальный след (точка H) – горизонтальному следу плоскости;
3) профильная проекция профильной прямой параллельна профильному следу плоскости.
Если плоскость не задана следами, то построение профильной прямой плоскости начинают с построения ее фронтальной или горизонтальной проекций, идущих перпендикулярно оси х (рис. 3.10).
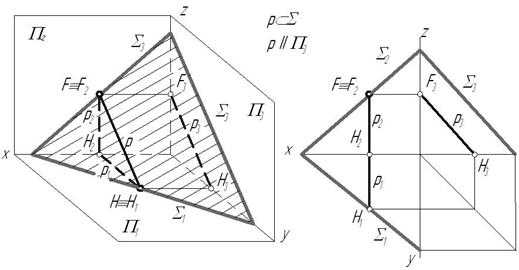
Рис. 3.10
infopedia.su