Восьмеричная система счисления таблица – Иллюстрированный самоучитель по цифровой графике › Системы счисления › Восьмеричная система счисления [страница — 41] | Самоучители по графическим программам

Восьмеричная система счисления — Программирование на C, C# и Java

Оглавление:
Перевод из десятичной системы счисления в восьмеричную
Перевод из восьмеричной системы счисления в десятичную
Перевод из двоичной системы счисления в восьмеричную
Перевод из восьмеричной системы счисления в двоичную
Перевод из восьмеричной системы счисления в шестнадцатеричную и из шестнадцатеричной системы в восьмеричную
Применение восьмеричной системы счисления

Восьмеричная система – одна из основных систем счислений наряду с двоичной, десятичной и шестнадцатеричной, применяемая в информационных технологиях.

Как мы знаем, компьютеры «воспринимают» лишь двоичную систему счисления, состоящую только из нулей и единиц. Однако человеку довольно непривычно и неудобно работать с такими числами. Например, привычное нам десятичное число 2 143 в двоичной системе будет выглядеть как 100001011111.  Переводить числа из двоичной системы в десятеричную также не очень удобно и бывает довольно муторно.

В итоге было решено использовать альтернативные и более простые системы счисления: восьмеричную и шестнадцатеричную. Числа 8 и 16 являются степенями двойки (2 в третьей и 2 в четвёртой степени соответственно), поэтому выполнять преобразования из двоичной системы и наоборот гораздо легче, чем при десятичной системе счисления, которая не может похвастаться своей причастностью к степеням числа 2.

Кроме того, числа в восьмеричной системе как минимум более приятны глазу и гораздо короче, чем их аналоги в двоичной системе. Так, например, в восьмеричной системе то же число 2 143 будет записываться как 4137.

В восьмеричной системе счисления, как уже можно было догадаться, основанием является цифра 8 и, соответственно, она вмещает в себя только восемь цифр: от 0 до 7. Поэтому числа в восьмеричной системе счисления очень похожи на десятичные, в отличие от шестнадцатеричных, где присутствуют буквы латинского алфавита или двоичных, состоящих только из двух цифр. Отличают эти две системы тем, что в восьмеричной отсутствуют цифры 8 и 9, а также, очевидно, нижними индексами: у числа в десятичной системе прибавляют нижний индекс с цифрой 10, а к числам в восьмеричной системе приписывают цифру 8, например:

 Теперь давайте научимся переводу чисел в восьмеричную систему счисления и наоборот.

Перевод из десятичной системы счисления в восьмеричную

Давайте попробуем изучить перевод десятичного числа в восьмеричное на примере. После этого примера вы без проблем сможете переводить любые числа в эту систему.

Возьмём десятичное число 15 450 и попробуем перевести его в восьмеричную систему счисления.

Для начала нам необходимо разделить исходное число на основание системы, в которую мы хотим это число перевести. Для восьмеричной системы это число 8. То есть мы делим 15 450 на 8.

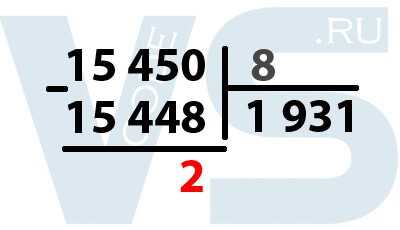
Происходит деление в столбик, но, в отличие от стандартного деления, мы не находим неполные частные, а делим сразу всё делимое на 8. Наибольшим числом, при котором 15 450 делится без остатка на 8 будет число 1 931. 1931 * 8 = 15 448. Теперь мы вычитаем из 15 450 полученное число 15 448, у нас получился остаток 2. Выделяем эту двойку, так как это уже кусочек нашего числа в восьмеричной системе.

Продолжаем: теперь делим полученное на предыдущем шаге частное на 8:

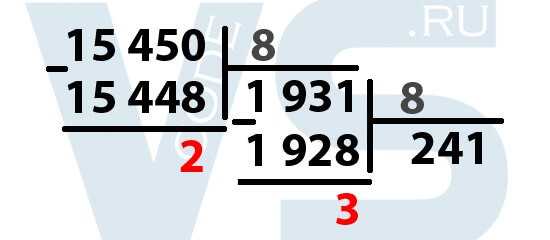
Всё точно так же: наибольшим числом, при котором 1 931 делится без остатка на 8 будет число 241. При умножении 241 на 8 получается число 1 928. Ищем разность между 1 931 и 1928 – получается 3. Выделяем её. Далее делим 241 на 8.

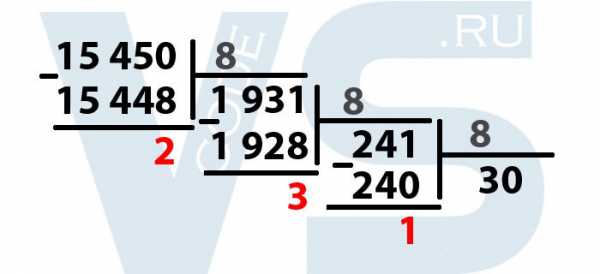
Получается число 30, умножив его на 8, получаем 240. Вычитаем из 241 это число, получается 1. Выделяем единицу.
Продолжаем деление до тех пор, пока частное не станет меньше 8!

Итак, делим 30 на 8, получается 3,75, отбрасываем дробную часть, получается 3. Умножаем 3 на 8, получается 24. 30 – 24 = 6. Выделяем шестёрку. Мы закончили деление так как 3 меньше 8. Обязательно выделяем последнее частное тоже (у нас это цифра 3).

Выделенные красным цифры – это и есть наше число в восьмеричной системе, НО они написаны наоборот. То есть, чтобы правильно прочитать число в восьмеричной системе, необходимо сделать это справа налево.

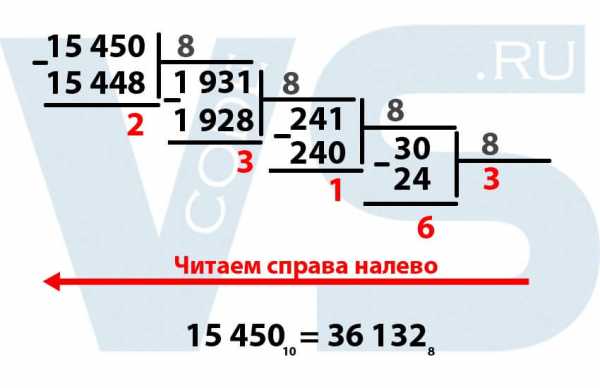
Таким образом, десятичное число 15 450₁₀ в восьмеричной системе будет выглядеть как 36 132₈.

Итого, алгоритм перевода чисел из десятичной системы в восьмеричную следующий:

1. Разделить исходное число на 8. Найти максимальное частное и убрать дробную часть от него. Например, исходное число 20 : 8 = 2,5. Значит в частное мы записываем число 2.
2. Умножить полученное частное на 8. Записать его под исходным числом.
3. Найти остаток между этими числами и выделить его – это кусочек переведённого в восьмеричную систему числа.
4. Затем разделить в столбик полученное частное на 8, записать ответ и проделать шаги 2 и 3.
5. Производить деление до тех пор, пока делимое не станет меньше 8. Выделить это делимое тоже.
6. Выписать все выделенные числа справа налево (т.е. последнее делимое будет на первом месте, затем идёт остаток, найденный на последнем шаге, затем остаток, найденный на предпоследнем шаге и т.д.). Полученное при такой записи число и будет нашим искомым восьмеричным.

Теперь перейдём к переводу восьмеричного числа в десятичную систему счисления.

Перевод из восьмеричной системы счисления в десятичную

Перевести восьмеричное число в десятичное даже проще, чем наоборот. Давайте рассмотрим пример: переведём восьмеричное число 3607₈ в десятичное.

Для начала мы делаем такую запись: с конца берём каждую цифру нашего исходного числа, каждое из них умножаем на 8, и все в целом складываем. Должно получиться примерно так:

Однако, это ещё не всё! После того, как мы сделали подобную запись, ко всем числам 8, на которые умножаются цифры исходного числа, необходимо добавить степени в порядке возрастания: 0, 1, 2 и т.д. Обязательно необходимо начинать с нулевой степени!

Всё, что остаётся после этого – просто посчитать. В итоге у нас получилось число 1927 в десятичной системе.

Перевод из двоичной системы счисления в восьмеричную

Перевод чисел из двоичной системы счисления в восьмеричную – довольно необычное дело для тех, кто никогда с этим не сталкивался. Однако на деле всё не так пугающе, как может показаться с первого раза.

Давайте попробуем. Допустим, у нас есть двоичное число 1010010001011101100.

Для начала нам необходимо разбить это число на триады – группы из трёх цифр. Почему именно три цифры? Как мы знаем, у систем счислений имеются основания. И у двоичной системы основание – 2. Нам необходимо перевести двоичное число в восьмеричную систему с основанием 8. Математически это можно записать так:

Найти i, пожалуй, не составит труда: i = 3, то есть, для записи одного восьмеричного числа в двоичной системе необходимо 3 бита или, говоря иначе – 3 двоичные цифры. Поэтому мы и будем разбивать двоичное число на триады. Однако надо запомнить, что делать это надо с младшего бита. Бит – это одна цифра в двоичном числе. Чем дальше бит от начала числа, тем он младше. Самый младший бит – это последняя цифра двоичного числа. Иными словами, мы разбиваем число на триады, начиная с конца.

Внимание: если старшая триада не заполнена, до конца, перед ней необходимо дописать столько нулей, чтобы получилась полноценная триада.

Теперь всё, что нам остаётся – это перевести каждую из этих триад из двоичной системы счисления в восьмеричную. Это можно сделать самостоятельно:

Для этого в каждой отдельной триаде (начиная с первой) нужно каждую цифру (начиная с последней) умножить на 2, возведённую в степени от 0 до 2, и сложить полученные три числа.

Затем, полученные результаты по каждой отдельной триаде надо выписать, начиная с самой первой. Записанное число и будет нашим конечным результатом в восьмеричной системой счисления.

Однако можно сильно облегчить себе задачу, не высчитывая все триады числа, а просто сверяя каждую из них по таблице соответствия двоичных чисел восьмеричным, например, по такой:

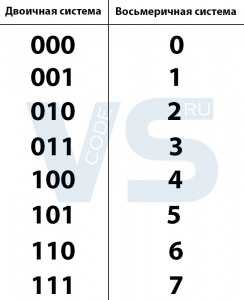
Теперь можно просто смотреть на триаду, сверять её с таблицей и записывать число, соответствующее ей в восьмеричной системе.

Перевод из восьмеричной системы счисления в двоичную

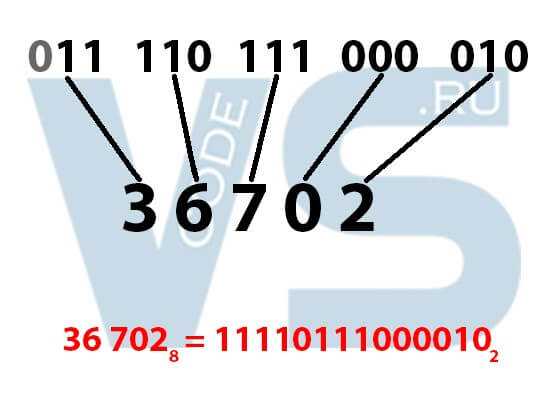
Самым удобным способом перевода из восьмеричной системы счисления в двоичную является использование таблицы соответствий. Итак, допустим, мы хотим перевести восьмеричное число 36702 в двоичную систему. Что же нам делать? Мы берём первую цифру нашего исходного числа – 3. Ищем её по таблице соответствия – в двоичной системе это 011. Берём следующую цифру – 6 и ищем её в таблице, находим 110, и так далее. Продолжаем, пока не переведём все восьмеричные цифры в триады. В итоге у нас получится необходимое двоичное число.

Внимание: Если в старших битах (то есть в самом начале двоичного числа) имеются нули, необходимо убрать их до первой единицы. Например, как на изображении ниже. В старшем бите у нас получился ноль при переводе восьмеричной тройки, и мы убрали его. Это делается для удобства, потому что зачем хранить и писать незначащие цифры.

Перевод из восьмеричной системы счисления в шестнадцатеричную и из шестнадцатеричной системы в восьмеричную

К сожалению, несмотря на то, что эти системы счисления близки друг к другу, напрямую перевести друг в друга нельзя. Легче всего при переводе этих двух систем друг в друга воспользоваться посредничеством двоичной системы. То есть, перевести восьмеричную систему счисления в двоичную, разделив число на триады и воспользовавшись таблицей соответствий, а затем перевести это число из двоичной системы в шестнадцатеричную с помощью тетрад. И наоборот: перевести число из шестнадцатеричной системы в двоичную, а затем уже из двоичной системы в восьмеричную описанными выше способами.

Применение восьмеричной системы счисления

В прошлом веке выпускались компьютеры, в которых использовались 12-ти, 24-х и 36-битные слова. Это, например, модель ICT 1900 (1964 год), а также PDP-8, выпущенная в 1965 году – это коммерчески довольно успешная модель миникомпьютера в своё время. Кроме того, некоторые мейнфреймы от компании IBM использовали восьмеричную систему. В компьютерах, размер машинного которых кратен тройке, очень удобно использовать систему с основанием восемь, поскольку всегда все биты из слова можно представить в виде целого количества цифр в восьмеричной системе. Например, слово из 24-х бит, можно записать в виде 8-ми восьмеричных чисел.

Если говорить про использование восьмеричной системы в жизни людей, то известно, что в индейских языках Юки (Калифорния) и Паме (Мексика) использовалась данная система. Индейцы считали предметы не по количеству пальцев на руках, а по количеству промежутков между ними.

 

Восьмеричная система счисления

5 (100%) 11 votes

Поделиться в соц. сетях:

vscode.ru

двоичная, восьмеричная, шестнадцатеричная — урок. Информатика, 8 класс.

Для кодирования информации в компьютере вместо привычной десятичной системы счисления используется двоичная система счисления.

Двоичной системой счисления люди начали пользоваться очень давно. Древние племена Австралии и островов Полинезии использовали эту систему в быту. Так, полинезийцы передавали необходимую  информацию, выполняя два вида ударов по барабану: звонкий и глухой. Это было примитивное представление двоичной системы счисления.

Двоичной системой счисления называется позиционная система счисления с основанием \(2\).

Для записи чисел в ней использовали только две цифры:  \(0\) и \(1\).

Для обозначения системы счисления, в которой представляется число, используют нижний индекс, указывающий основание системы. Например, 110112 —  число в двоичной системе счисления.

 

Цифры в двоичном числе являются коэффициентами его представления в виде суммы степеней с основанием \(2\), например:

 

1012=1 ·22+0 ·21+1 ·20.

 

В десятичной системе счисления это число будет выглядеть так:

 

1012=4+0+1=5.

 

Для перевода целого десятичного числа в двоичную систему счисления нужно последовательно выполнять деление данного числа и получаемых целых частных на \(2\) до тех пор, пока не получим частное, равное нулю. Исходное число в двоичной системе счисления составляется последовательной записью полученных остатков, начиная с последнего.

Пример:

Переведём десятичное число \(13\) в двоичную систему счисления. Рассмотренную выше последовательность действий (алгоритм перевода) можно изобразить так:

 

 

Получили 1310=11012.

Пример:

Если десятичное число достаточно большое, то более удобен следующий способ записи рассмотренного выше алгоритма:

 

\(224\)	\(112\)	\(56\)	\(28\)	\(14\)	\(7\)	\(3\)	\(1\)
\(0\)	\(0\)	\(0\)	\(0\)	\(0\)	\(1\)	\(1\)	\(1\)

 

22410=111000002.

Восьмеричной системой счисления называется позиционная система счисления с основанием \(8\).

 

Для записи чисел в восьмеричной системе счисления используются цифры:  \(0\), \(1\), \(2\), \(3\), \(4\), \(5\), \(6\), \(7\).

Для перевода целого восьмеричного числа в десятичную систему счисления следует перейти к его развёрнутой записи и вычислить значение получившегося выражения.

Для перевода целого десятичного числа в восьмеричную систему счисления следует последовательно выполнять деление данного числа и получаемых целых частных на 8 до тех пор, пока не получим частное, равное нулю. Исходное число в двоичной системе счисления составляется последовательной записью полученных остатков, начиная с последнего.

Пример:

Переведём восьмеричное число  154368 в десятичную систему счисления.

154368=1 ·84+5 ·83+4 ·82+3 ·81+6 ·80=694210

Пример:

Переведём десятичное число \(94\) в восьмеричную систему счисления.

 

 

9410=1368

Шестнадцатеричной системой счисления называется позиционная система счисления с основанием \(16\).

 

Для записи чисел в шестнадцатеричной системе счисления используются цифры:  \(0\), \(1\), \(2\), \(3\), \(4\), \(5\), \(6\), \(7\), \(8\), \(9\) и латинские буквы A, B, C, D, E, F. Буквы A, B, C, D, E, F имеют значения 1010, 1110, 1210, 1310, 1410, 1510.

Для перевода шестнадцатеричного числа в десятичное необходимо это число представить в виде суммы произведений степеней основания шестнадцатеричной системы счисления на соответствующие цифры в разрядах шестнадцатеричного числа.

Для перевода целого десятичного числа в шестнадцатеричную  систему счисления следует последовательно выполнять деление данного числа и получаемых целых частных на \(16\) до тех пор, пока не получим частное, равное нулю. Исходное число в системе счисления составляется последовательной записью полученных остатков, начиная с последнего.

Пример:

Переведём шестнадцатеричное число \(2\)\(A7\) в десятичное. В соответствии с вышеуказанными правилом представим его в виде суммы степеней с основанием \(16\):

2A716=2 ·162+10 ·161+7 ·160=521+160+7=679.

Пример:

Переведём десятичное число \(158\) в шестнадцатеричную систему счисления.

 

 

15810=9E16.

Для перевода числа из любой позиционной системы счисления в десятичную необходима использовать развернутую формулу числа, заменяя, если это необходимо, буквенные обозначения соответствующими цифрами.

Для перевода целых чисел десятичной системы счисления в число любой системы счисления последовательно выполняют деление нацело на основание системы счисления, пока не получат нуль. Числа, которые возникают как остаток от деления на основание системы счисление, представляют собой последовательную запись разрядов числа в выбранной системе счисления от младшего разряда к старшему. Поэтому для записи самого числа остатки от деления записывают в обратном порядке.

www.yaklass.ru

8 Восьмеричная система счисления. Запись чисел в восьмеричной системе счисления. Привести примеры.

В восьмеричной системе счисления основание равно 8, для записи чисел используются цифры от 0 до 7

A8 A2
0 000
1 001
2 010
3 011
4 100
5 101
6 110
7 111

Для записи каждой цифры восьмеричной с.с. требуется максимум 3 разряда.

Алгоритм перевода из 2-ой в 8-ую систему счисления

При переводе из 2-ой в 8-ую систему счисления надо число разбить на триады (по три разряда) и записать каждую триаду эквивалентным двоичным кодом, недостающее число разрядов надо дополнить слева нулями.

Примеры:

100111101₂= 100 111 101₂=475₈

1100010₂= 001 100 010₂=142₈

Алгоритм перевода из 8-ой в 2-ую

Для перевода из 8-ой в 2-ую используется обратное правило.

Каждую цифру 8-ого числа надо записать тремя разрядами соответствующего ей двоичного кода

Примеры:

Перевод из 8-ой в 2-ую	5638 = 1011100112
Перевод из 8-ой в 10-ую	5638 = 5*82 + 6*81 + 3*80 = 512+ 40 + 7 = 37110

9 Шестнадцатеричная система счисления. Запись чисел в шестнадцатеричной системе счисления. Привести примеры.

В шестнадцатеричной системе счисления основание системы равно 16, т.е. для записи чисел используется 16 символов: цифры от 0 до 9 и далее буквы латинского алфавита от AдоF

Ниже представлена таблица соответствия кодов чисел четырех систем счисления.

10-ая	8-ая	2-ая	16-ая
0	0	00000000	0
1	1	00000001	1
2	2	00000010	2
3	3	00000011	3
4	4	00000100	4
5	5	00000101	5
6	6	00000110	6
7	7	00000111	7
8	10	00001000	8
9	11	00001001	9
10	12	00001010	A
11	13	00001011	B
12	14	00001100	C
13	15	00001101	D
14	16	00001110	E
15	17	00001111	F

Для записи 1 цифры шестнадцатеричного числа в двоичной системе счисления требуется 4 разряда.

Алгоритм перевода чисел из 2-ой в 16-ую систему счисления

При переводе чисел из 2-ой в 16-ую систему счисления надо число разбить на тетрады (по четыре разряда) и записать каждую тетраду эквивалентным двоичным кодом, недостающее число разрядов надо дополнить слева нулями.

Примеры:

1. 1001 1110₂ = 9E₁₆

0010 0010₂ = 22₁₆

Алгоритм перевода чисел из 16-ой в 2-ую

Для перевода из 16-ой в 2-ую используется обратное правило.

Каждую цифру шестнадцатеричного числа надо записать четырьмя разрядами соответствующего ей двоичного кода

Перевод из 16-ой в 2-ую	17316 = 1011100112
Перевод из 16-ой в 10-ую	17316 = 1*162 + 7*161 + 3*160 = 256 + 112 + 3 = 37110

10 Перевод чисел из десятичной системы счисления в любую другую позиционную систему счисления. Привести примеры.

Для перевода целого десятичного числа N в систему счисления с основанием q необходимо N разделить с остатком («нацело») на q , записанное в той же десятичной системе. Затем неполное частное, полученное от такого деления, нужно снова разделить с остатком на q , и т.д., пока последнее полученное неполное частное не станет равным нулю. Представлением числа N в новой системе счисления будет последовательность остатков деления, изображенных одной q-ичной цифрой и записанных в порядке, обратном порядку их получения.

Пример: Переведем число 75 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:

В двоичную В восьмеричную В шестнадцатеричную

: 7510 = 1 001 0112 = 1138 = 4B16.

studfiles.net

Таблица перевода двоичных, восьмеричных, десятичных (от 1 до 255) и шестнадцатеричных чисел. Binary, Octal and Hexadecimal Numbers vs Decimal Numbers

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15	0 1 2 3 4 5 6 7 8 9 A B C D E F	000 001 002 003 004 005 006 007 010 011 012 013 014 015 016 017	00000000 00000001 00000010 00000011 00000100 00000101 00000110 00000111 00001000 00001001 00001010 00001011 00001100 00001101 00001110 00001111
16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31	10 11 12 13 14 15 16 17 18 19 1A 1B 1C 1D 1E 1F	020 021 022 023 024 025 026 027 030 031 032 033 034 035 036 037	00010000 00010001 00010010 00010011 00010100 00010101 00010110 00010111 00011000 00011001 00011010 00011011 00011100 00011101 00011110 00011111
Десятичное Dec	Шестнадцатеричное Hex	Восьмеричное Oct	Двоичное Bin
32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47	20 21 22 23 24 25 26 27 28 29 2A 2B 2C 2D 2E 2F	040 041 042 043 044 045 046 047 050 051 052 053 054 055 056 057	00100000 00100001 00100010 00100011 00100100 00100101 00100110 00100111 00101000 00101001 00101010 00101011 00101100 00101101 00101110 00101111
48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63	30 31 32 33 34 35 36 37 38 39 3A 3B 3C 3D 3E 3F	060 061 062 063 064 065 066 067 070 071 072 073 074 075 076 077	00110000 00110001 00110010 00110011 00110100 00110101 00110110 00110111 00111000 00111001 00111010 00111011 00111100 00111101 00111110 00111111
Десятичное Dec	Шестнадцатеричное Hex	Восьмеричное Oct	Двоичное Bin
64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79	40 41 42 43 44 45 46 47 48 49 4A 4B 4C 4D 4E 4F	100 101 102 103 104 105 106 107 110 111 112 113 114 115 116 117	01000000 01000001 01000010 01000011 01000100 01000101 01000110 01000111 01001000 01001001 01001010 01001011 01001100 01001101 01001110 01001111
80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95	50 51 52 53 54 55 56 57 58 59 5A 5B 5C 5D 5E 5F	120 121 122 123 124 125 126 127 130 131 132 133 134 135 136 137	01010000 01010001 01010010 01010011 01010100 01010101 01010110 01010111 01011000 01011001 01011010 01011011 01011100 01011101 01011110 01011111
96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111	60 61 62 63 64 65 66 67 68 69 6A 6B 6C 6D 6E 6F	140 141 142 143 144 145 146 147 150 151 152 153 154 155 156 157	01100000 01100001 01100010 01100011 01100100 01100101 01100110 01100111 01101000 01101001 01101010 01101011 01101100 01101101 01101110 01101111
Десятичное Dec	Шестнадцатеричное Hex	Восьмеричное Oct	Двоичное Bin
112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127	70 71 72 73 74 75 76 77 78 79 7A 7B 7C 7D 7E 7F	160 161 162 163 164 165 166 167 170 171 172 173 174 175 176 177	01110000 01110001 01110010 01110011 01110100 01110101 01110110 01110111 01111000 01111001 01111010 01111011 01111100 01111101 01111110 01111111
128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143	80 81 82 83 84 85 86 87 88 89 8A 8B 8C 8D 8E 8F	200 201 202 203 204 205 206 207 210 211 212 213 214 215 216 217	10000000 10000001 10000010 10000011 10000100 10000101 10000110 10000111 10001000 10001001 10001010 10001011 10001100 10001101 10001110 10001111
144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159	90 91 92 93 94 95 96 97 98 99 9A 9B 9C 9D 9E 9F	220 221 222 223 224 225 226 227 230 231 232 233 234 235 236 237	10010000 10010001 10010010 10010011 10010100 10010101 10010110 10010111 10011000 10011001 10011010 10011011 10011100 10011101 10011110 10011111
Десятичное Dec	Шестнадцатеричное Hex	Восьмеричное Oct	Двоичное Bin
160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175	A0 A1 A2 A3 A4 A5 A6 A7 A8 A9 AA AB AC AD AE AF	240 241 242 243 244 245 246 247 250 251 252 253 254 255 256 257	10100000 10100001 10100010 10100011 10100100 10100101 10100110 10100111 10101000 10101001 10101010 10101011 10101100 10101101 10101110 10101111
176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191	B0 B1 B2 B3 B4 B5 B6 B7 B8 B9 BA BB BC BD BE BF	260 261 262 263 264 265 266 267 270 271 272 273 274 275 276 277	10110000 10110001 10110010 10110011 10110100 10110101 10110110 10110111 10111000 10111001 10111010 10111011 10111100 10111101 10111110 10111111
Десятичное Dec	Шестнадцатеричное Hex	Восьмеричное Oct	Двоичное Bin
192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207	C0 C1 C2 C3 C4 C5 C6 C7 C8 C9 CA CB CC CD CE CF	300 301 302 303 304 305 306 307 310 311 312 313 314 315 316 317	11000000 11000001 11000010 11000011 11000100 11000101 11000110 11000111 11001000 11001001 11001010 11001011 11001100 11001101 11001110 11001111
208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223	D0 D1 D2 D3 D4 D5 D6 D7 D8 D9 DA DB DC DD DE DF	320 321 322 323 324 325 326 327 330 331 332 333 334 335 336 337	11010000 11010001 11010010 11010011 11010100 11010101 11010110 11010111 11011000 11011001 11011010 11011011 11011100 11011101 11011110 11011111
224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239	E0 E1 E2 E3 E4 E5 E6 E7 E8 E9 EA EB EC ED EE EF	340 341 342 343 344 345 346 347 350 351 352 353 354 355 356 357	11100000 11100001 11100010 11100011 11100100 11100101 11100110 11100111 11101000 11101001 11101010 11101011 11101100 11101101 11101110 11101111
Десятичное Dec	Шестнадцатеричное Hex	Восьмеричное Oct	Двоичное Bin
240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255	F0 F1 F2 F3 F4 F5 F6 F7 F8 F9 FA FB FC FD FE FF	360 361 362 363 364 365 366 367 370 371 372 373 374 375 376 377	11110000 11110001 11110010 11110011 11110100 11110101 11110110 11110111 11111000 11111001 11111010 11111011 11111100 11111101 11111110 11111111

www.dpva.ru

Восьмеричная система счисления

Разделы: Информатика, Конкурс «Презентация к уроку»

---

Презентация к уроку

Загрузить презентацию (2 МБ)

Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.

---

Тип урока: урок введения нового материала в 8 классе.

Дидактическая цель урока: ознакомление учащихся с восьмеричной системой счисления, с переводом чисел из восьмеричной в десятичную систему счисления, и обратно, а так же с переводом из восьмеричной системы счисления в двоичную систему счисления и обратно. Отработка навыков перевода из одной системы счисления в другую.

Развивающая цель урока: развитие умения рассуждать, сравнивать, делать выводы. Развитие памяти, внимательности, познавательного интереса к предмету с использованием соответствующих заданий.

Воспитательная: формирование самоконтроля у школьников. 

Этапы урока:

1. Организация начала урока – 2 мин.
2. Проверка домашнего задания – 10 мин.
3. Подготовка учащихся к усвоению новых знаний – 5 мин.
4. Введение нового материала – 8 мин.
5. Первичное закрепление нового материала – 5 мин.
6. Контроль и самопроверка знаний – 10 мин.
7. Информация о домашнем задании – 3 мин.
8. Подведение итогов урока – 2 мин.

Структура урока:

• Проверка домашнего задания.
• Знакомство с записями восьмеричных чисел.
• Перевод целого числа из восьмеричной системы счисления в десятичную с проверкой.
• Перевод числа из восьмеричной системы счисления в двоичную и обратно.
• Информация о домашнем задании.
• Подведение итогов урока.

Средства обучения:

1. Приложение операционной системы Windows XP-Калькулятор.
2. Индивидуальная карточка учащегося.
3. Алгоритм работы в приложении о.с. Windows XP-Калькулятор.
4. Презентация.
5. Карточка с заданием для перевода чисел из восьмеричной системы счисления в десятичную систему счисления.
6. Карточка с заданиями для перевода из одной системы счисления в другую с помощью двоично-восьмеричной таблицы.
7. Карточка с творческим заданием.

Ход урока

1 этап. Организация начала урока.

Цель этапа: подготовка учащихся к работе на занятиях.

Здравствуйте, ребята!

Сегодня на уроке мы с вами познакомимся с восьмеричной системой счисления и отработаем навыки перевода из одной системы счисления в другую.

Получают индивидуальные карточки, которые подписывают и куда будут вносить ответы заданий.

Ф.И.
№1	№2	№3

Приложение 1

2 этап. Проверка выполнения домашнего задания.

Цель этапа: установление правильности и осознанности выполнения домашнего задания всеми учащимися, выявление пробелов и их коррекция.

Проверим выполнение домашнего задания с помощью стандартного приложения ОС Windows XP-Калькулятор.

Домашнее задание: переведите числа из двоичной системы счисления в десятичную и сделайте проверку.

Получают листы с алгоритмом работы в приложении Калькулятор, проверяют домашнее задание за ПК.

Приложение 2

Ответы проверим с помощью презентации к уроку.

1. 10₂=2₁₀
2. 11₂=3₁₀
3. 100₂=4₁₀
4. 101₂=5₁₀
5. 110₂=6₁₀
6. 111₂=7₁₀

3 этап. Введение нового материала.

Цель этапа: обеспечение восприятия, осмысления и первичного запоминания знаний и способов действий, связей и отношений в объекте изучения.

Запишите тему сегодняшнего урока: «Восьмеричная система счисления».

Основание: 8

Алфавит цифр: 0, 1, 2, 3, 4, 5, 6, 7

Рассмотрим перевод целого числа из восьмеричной системы счисления в десятичную и выполним проверку.

Алгоритм перевода целого числа из восьмеричной системы счисления в десятичную.

Записать восьмеричное число в развернутой форме и вычислить ее значение.

Пример 1.

₁₀
21₈=2*8¹+1*8⁰=16+1=17₁₀

Выполним проверку.

Алгоритм перевода целого числа из десятичной системы счисления в восьмеричную.

1. Последовательно выполнять деление исходного целого десятичного числа на 8 до получения результата строго меньше основания системы.
2. Полученные остатки записать в обратной последовательности.

17₁₀→А₈

17₁₀=21₈

Пример 2.

₁₀
71₈=7*8¹+1*8⁰=56+1=57₁₀

4 этап. Первичное закрепление нового материала.

Цель этапа: установление правильности и осознанности усвоения нового учебного материала.

Задание №1 на первичное закрепление нового материала. Приложение 3

Перевести число из восьмеричной системы счисления в десятичную и выполнить проверку.

₂₁₀
114₈ =1*8²+1*8¹+4*8⁰=64+8+4=76₁₀

Проверка:

76₁₀=114₈

Выбрать правильный ответ под соответствующей буквой и записать букву в индивидуальную карточку.

О) 84₁₀
У) 76₁₀
Е) 97₁₀

5 этап. Контроль и самопроверка знаний.

Цель этапа: выявление качества и уровня овладения знаниями и способами действий.

Мы научились переводить числа из одной системы в другую, а теперь рассмотрим способы переводов, которые не требуют от нас каких-либо вычислений. Для этого в тетради начертим таблицу, состоящую из двух столбцов. Число в 8-ой системе счисления соответствует тройке цифр двоичной системы счисления. Например, 0₈=000₂, 1₈=001₂, далее обратимся к проверяемому в начале урока домашнему заданию. Таблица легко заполняется.

Двоично-восьмеричная система счисления.

8	2
0	000
1	001
2	010
3	011
4	100
5	101
6	110
7	111

При переводе восьмеричного числа в двоичное заменяют каждую восьмеричную цифру на соответствующую тройку цифр из таблицы. Для обратной операции, то есть для перевода из двоичной в восьмеричную систему, двоичное число разбивают на тройки цифр, потом заменяют каждую группу одной восьмеричной цифрой.

Например:

714₈=111 001 100₂
101 110 100₂=564₈.

Учащимся раздаются карточки с заданиями. После их решения, правильные ответы помещаются в индивидуальную карточку ученика.

Задания №2, №3 на контроль и самопроверку знаний. Приложение 4

Переведите числа из одной системы счисления в другую (с помощью двоично-восьмеричной таблицы).

2. Переведите число из восьмеричной системы счисления в двоичную систему счисления.

532₈ =А₂

ц) 1101001₂; р)101 011 010₂; в) 111001100₂;

3. Переведите из двоичной системы счисления в восьмеричную систему счисления.

111 111₂ =А₈

а) 77₈; о) 64₈; в) 29₈;

Сдайте индивидуальные карточки и раздаточный материал. Проверим ответы с помощью слайда № 7 презентации к уроку.

Правильные ответы:

№2 р)101 011 010₂

№3 а) 77₈

Индивидуальная карточка примет вид:

Ф.И.
№1	№2	№3
У	Р	А

Ученики получают раздаточный материал с творческим заданием. Даны координаты точек в разных системах счисления. Необходимо выполнить перевод координат в десятичную систему счисления, отметить и соединить точки на координатной плоскости.

Творческое задание. Приложение 5

Даны координаты точек:

1(100₂,1₂)
2(100₂, 110₂)
3(100₂, 1000₂)
4(10₈,10₈)
5(6₈,7₈)
6(10₈,6₈)

Выполните перевод чисел в десятичную систему счисления и в координатной плоскости поставьте и соедините все точки.

Ответ (в десятичной системе счисления):

1	2	3	4	5	6
(4,1)	(4,6)	(4,8)	(8,8)	(6,7)	(8,6)

Рисунок 1

6 этап. Информация о домашнем задании.

Цель этапа: обеспечение понимания цели, содержания и способов выполнения домашнего задания.

Переведите числа из восьмеричной системы счисления в двоичную, затем в десятичную систему счисления.

35₈ →А₂→А₁₀

65₈ → А₂→А₁₀

215₈ → А₂→А₁₀

7 этап. Подведение итогов урока.

Цель этапа: дать анализ и оценку успешности достижения цели.

Если у вас в индивидуальной карте получилось слово: УРА, то вы получили «5».

Если справились с 2-мя заданиями, то оценка «4».

Если решили 1-о задание, то вы получили «3».

Сегодня на уроке мы познакомились с восьмеричной системой счисления, рассмотрели разные способы перевода чисел из одной системы счисления в другую. Одни из способов требовали от нас решать задачи математическими методами, другие с привлечением компьютера, третьи не требовали от нас каких-либо вычислений.

Спасибо за урок.

17.12.2012

xn--i1abbnckbmcl9fb.xn--p1ai

3.6. Восьмеричная и шестнадцатеричная системы счисления

При наладке аппаратных средств и написании новых программ (особенно на языках низкого уровня типа ассемблера) часто возникает необходимость посмотреть содержимое той или иной ячейки памяти машины. Но там все заполнено длинными последовательностями нулей и единиц, очень неудобных для восприятия. Кроме того, естественные восможности человеческого мышления не позволяют быстро и точно оценить величину числа, представленного, например, комбинацией из 16 нулей и единиц. Для облегчения восприятия двоичного числа решили разбить его на группы разрядов, например по три и четыре разряда. Разбив таким образом число можно закодировать каждую группу разрядов отдельно, сократив при этом количество символов необходимых для записи числа. Последовательность из 3-х бит имеет 8 комбинаций, а из 4-х – 16 комбинаций. Для кодирования трех битов (триад) используются цифры от 0 до 7, а для кодирования четырех битов (тетрад) – цифры от 0 до 9 и буквы A, B, C, D, E, F (таблица 3.4). Полученные системы, имеющие в основании 8 и 16, назвали соответственно восьмиричной и шестнадцатиричной.

Таблица 3.4.

Восьмиричная система счисления		Шестнадцатиричная система счисления
Цифра	Триада	Цифра	Тетрада
0	000	0	0000
1	001	1	0001
2	010	2	0010
3	011	3	0011
4	100	4	0100
5	101	5	0101
6	110	6	0110
7	111	7	0111
		8	1000
		9	1001
		A	1010
		B	1011
		C	1100
		D	1101
		E	1110
		F	1111

Для перевода восьмиричного или шестнадцатиричного числа в двоичную форму достаточно заменить каждую цифру этого числа соответствующим трехзначным двоичным числом или четырехзначным двоичным числом (таблица 3.4). При этом отбрасываются ненужные нули в старших и младших (для дробной части) разрядах.

Пример. Перевести .

.

Пример. Перевести .

.

Для перехода от двоичной к восмиричной (шестнадцатиричной) системе поступают следующим образом: двигаясь от точки влево и вправо, разбивают двоичное число на группы по три (четыре) разряда, дополняя при необходимости нулями крайние левую и правую группы. Затем триаду (тетраду) заменяют соответствующей восьмиричной (шестнадцатиричной) цифрой.

Пример. Перевести .

.

Пример. Перевести .

.

Перевод из восьмиричной системы в шестнадцатиричную и обратно осуществляется через двоичную систему при помощи триад и тетрад.

Пример. Перевести .

.

3.7. Перевод чисел из системы с основанием p в систему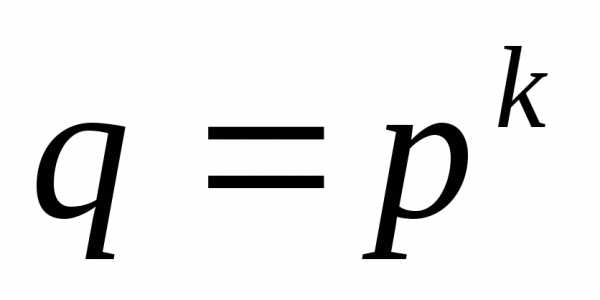

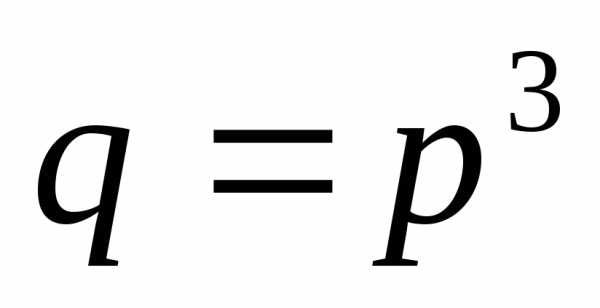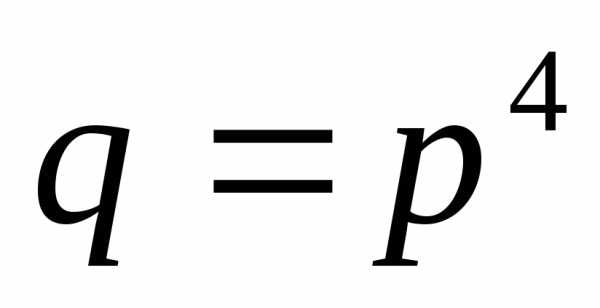Рассмотренный выше метод взаимного перевода чисел между двоичной и восьмиричной (шестнадцатиричной) системами счисления заслуживает более детального рассмотрения. Обозначим основание двоичной системы через p. Тогда основание восьмиричной системы , а для шестнадцатиричной. Именно поэтому перевод чисел между двоичной и восьмиричной (шестнадцатиричной) системами осуществляется простой группировкой цифр. При этом показатель степени определяет по сколько цифр системы с меньшим основанием необходимо группировать, чтобы получить одну цифру системы с большим основанием. Аналогичный метод справедлив для любыхp и q, связанных соотношением .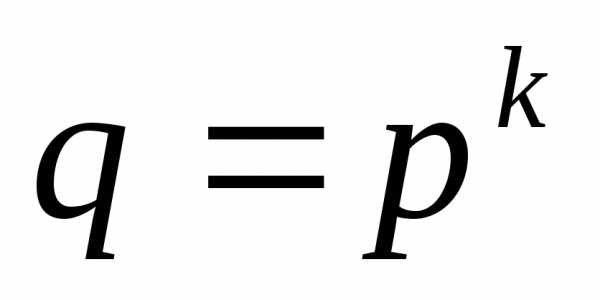

Пример. Перевести

Здесь p= 3, q= 9, k= 2. Составляем таблицу соответствия между системой с основанием 3 и системой с основанием 9.

Девятиричная система	Троичная система
0	00
1	01
2	02
3	10
4	11
5	12
6	20
7	21
8	22

3.8. Перевод чисел из системы основанием p в систему q (общий случай)

Предположим, что мы выполняем преобразование из системы с основанием p в систему с основанием q, когда p и q произвольные целые положительные числа. В основе большинства методов лежат операции умножения и деления, которые выполняются по одной из следующих схем (преобразование целых чисел).

Метод 1. Деление на q, при помощи арифметических действий над величинами с позиционным представлением по основанию p. Выше он рассматривался (метод деления для перевода чисел из десятичного представления в недесятичное) для частного случая когда p= 10, а q произвольно.

Метод 2. Умножение на p, при помощи арифметики основания q. Выше он рассматривался (метод перевода чисел из недесятичного представления в десятичное) для частного случая когда p произвольно, а q= 10.

Заметим, что на практике достаточно сложно выполнять арифметические действия над числами, записанными в системе счисления с произвольным основанием. Поэтому преобразование из системы с основанием p в систему с основанием q, когда p и q произвольные целые положительные числа, выполняется с использованием промежуточной системы счисления, выбираемой по соображениям удобства (десятичной, если вычисления производятся вручную и двоичной, если на компьютере).

studfiles.net

Таблица чисел в системах счисления

Таблица умножения чисел в шестнадцатеричной системе счисления

	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
1	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
2	0	2	4	6	8	A	C	E	10	12	14	16	18	1A	1C	1E
3	0	3	6	9	C	F	12	15	18	1B	1E	21	24	27	2A	2D
4	0	4	8	C	10	14	18	1C	20	24	28	2C	30	34	38	3C
5	0	5	A	F	14	19	1E	23	28	2D	32	37	3C	41	46	4B
6	0	6	C	12	18	1E	24	2A	30	36	3C	42	48	4E	54	5A
7	0	7	E	15	1C	23	2A	31	38	3F	46	4D	54	5B	62	69
8	0	8	10	18	20	28	30	38	40	48	50	58	60	68	70	78
9	0	9	12	1B	24	2D	36	3F	48	51	5A	63	6C	75	7E	87
A	0	A	14	1E	28	32	3C	46	50	5A	64	6E	78	82	8C	96
B	0	B	16	21	2C	37	42	4D	58	63	6E	79	84	8F	9A	A5
C	0	C	18	24	30	3C	48	54	60	6C	78	84	90	9C	A8	B4
D	0	D	1A	27	34	41	4E	5B	68	75	82	8F	9C	A9	B6	C3
E	0	E	1C	2A	38	46	54	62	70	7E	8C	9A	A8	B6	C4	D2
F	0	F	1E	2D	3C	4B	5A	69	78	87	96	A5	B4	C3	D2	E1

Таблица сложения чисел в шестнадцатеричной системе счисления

	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
0	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
1	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F	10
2	2	3	4	5	6	7	8	9	A	B	C	D	E	F	10	11
3	3	4	5	6	7	8	9	A	B	C	D	E	F	10	11	12
4	4	5	6	7	8	9	A	B	C	D	E	F	10	11	12	13
5	5	6	7	8	9	A	B	C	D	E	F	10	11	12	13	14
6	6	7	8	9	A	B	C	D	E	F	10	11	12	13	14	15
7	7	8	9	A	B	C	D	E	F	10	11	12	13	14	15	16
8	8	9	A	B	C	D	E	F	10	11	12	13	14	15	16	17
9	9	A	B	C	D	E	F	10	11	12	13	14	15	16	17	18
A	A	B	C	D	E	F	10	11	12	13	14	15	16	17	18	19
B	B	C	D	E	F	10	11	12	13	14	15	16	17	18	19	1A
C	C	D	E	F	10	11	12	13	14	15	16	17	18	19	1A	1B
D	D	E	F	10	11	12	13	14	15	16	17	18	19	1A	1B	1C
E	E	F	10	11	12	13	14	15	16	17	18	19	1A	1B	1C	1D
F	F	10	11	12	13	14	15	16	17	18	19	1A	1B	1C	1D	1E

Таблица сложения чисел в восьмеричной системе счисления

	0	1	2	3	4	5	6	7
0	0	1	2	3	4	5	6	7
1	1	2	3	4	5	6	7	10
2	2	3	4	5	6	7	10	11
3	3	4	5	6	7	10	11	12
4	4	5	6	7	10	11	12	13
5	5	6	7	10	11	12	13	14
6	6	7	10	11	12	13	14	15
7	7	10	11	12	13	14	15	16

Таблица умножения чисел в восьмеричной системе счисления

	0	1	2	3	4	5	6	7
0	0	0	0	0	0	0	0	0
1	0	1	2	3	4	5	6	7
2	0	2	4	6	10	12	14	16
3	0	3	6	11	14	17	22	25
4	0	4	10	14	20	24	30	34
5	0	5	12	17	24	31	36	43
6	0	6	14	22	30	36	44	52
7	0	7	16	25	34	43	52	61

studfiles.net