Степени счисления – Системы счисления — Перевод чисел и калькулятор

Системы счисления. Перевод из одной системы в другую.

1. Порядковый счет в различных системах счисления.

В современной жизни мы используем позиционные системы счисления, то есть системы, в которых число, обозначаемое цифрой, зависит от положения цифры в записи числа. Поэтому в дальнейшем мы будем говорить только о них, опуская термин «позиционные».

Для того чтобы научиться переводить числа из одной системы в другую, поймем, как происходит последовательная запись чисел на примере десятичной системы.

Поскольку у нас десятичная система счисления, мы имеем 10 символов (цифр) для построения чисел. Начинаем порядковый счет: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Цифры закончились. Мы увеличиваем разрядность числа и обнуляем младший разряд: 10. Затем опять увеличиваем младший разряд, пока не закончатся все цифры: 11, 12, 13, 14, 15, 16, 17, 18, 19. Увеличиваем старший разряд на 1 и обнуляем младший: 20. Когда мы используем все цифры для обоих разрядов (получим число 99), опять увеличиваем разрядность числа и обнуляем имеющиеся разряды: 100. И так далее.

Попробуем сделать то же самое в 2-ной, 3-ной и 5-ной системах (введем обозначение для 2-ной системы, для 3-ной и т.д.):

0	0	0	0
1	1	1	1
2	10	2	2
3	11	10	3
4	100	11	4
5	101	12	10
6	110	20	11
7	111	21	12
8	1000	22	13
9	1001	100	14
10	1010	101	20
11	1011	102	21
12	1100	110	22
13	1101	111	23
14	1110	112	24
15	1111	120	30

Если система счисления имеет основание больше 10, то нам придется вводить дополнительные символы, принято вводить буквы латинского алфавита. Например, для 12-ричной системы кроме десяти цифр нам понадобятся две буквы ( и ):

0	0
1	1
2	2
3	3
4	4
5	5
6	6
7	7
8	8
9	9
10
11
12	10
13	11
14	12
15	13

2.Перевод из десятичной системы счисления в любую другую.

Чтобы перевести целое положительное десятичное число в систему счисления с другим основанием, нужно это число разделить на основание. Полученное частное снова разделить на основание, и дальше до тех пор, пока частное не окажется меньше основания. В результате записать в одну строку последнее частное и все остатки, начиная с последнего.

Пример 1. Переведем десятичное число 46 в двоичную систему счисления.

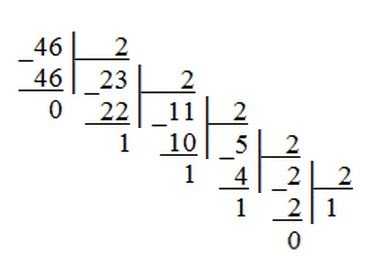
Пример 2. Переведем десятичное число 672 в восьмеричную систему счисления.

Пример 3. Переведем десятичное число 934 в шестнадцатеричную систему счисления.

3. Перевод из любой системы счисления в десятичную.

Для того, чтобы научиться переводить числа из любой другой системы в десятичную, проанализируем привычную нам запись десятичного числа.
Например, десятичное число 325 – это 5 единиц, 2 десятка и 3 сотни, т.е.

Точно так же обстоит дело и в других системах счисления, только умножать будем не на 10, 100 и пр., а на степени основания системы счисления. Для примера возьмем число 1201 в троичной системе счисления. Пронумеруем разряды справа налево начиная с нуля и представим наше число как сумму произведений цифры на тройку в степени разряда числа:

Это и есть десятичная запись нашего числа, т.е.

Пример 4. Переведем в десятичную систему счисления восьмеричное число 511.

Пример 5. Переведем в десятичную систему счисления шестнадцатеричное число 1151.

4. Перевод из двоичной системы в систему с основанием «степень двойки» (4, 8, 16 и т.д.).

Для преобразования двоичного числа в число с основанием «степень двойки» необходимо двоичную последовательность разбить на группы по количеству цифр равному степени справа налево и каждую группу заменить соответствующей цифрой новой системы счисления.

Например, Переведем двоичное 1100001111010110 число в восьмеричную систему. Для этого разобьем его на группы по 3 символа начиная справа (т.к. ), а затем воспользуемся таблицей соответствия и заменим каждую группу на новую цифру:

Таблицу соответствия мы научились строить в п.1.

0	0
1	1
10	2
11	3
100	4
101	5
110	6
111	7

Т.е.

Пример 6.

Переведем двоичное 1100001111010110 число в шестнадцатеричную систему.

0	0
1	1
10	2
11	3
100	4
101	5
110	6
111	7
1000	8
1001	9
1010	A
1011	B
1100	C
1101	D
1110	E
1111	F

5.Перевод из системы с основанием «степень двойки» (4, 8, 16 и т.д.) в двоичную.

Этот перевод аналогичен предыдущему, выполненному в обратную сторону: каждую цифру мы заменяем группой цифр в двоичной системе из таблицы соответствия.

Пример 7.

Переведем шестнадцатеричное число С3A6 в двоичную систему счисления.

Для этого каждую цифру числа заменим группой из 4 цифр (т.к. ) из таблицы соответствия, дополнив при необходимости группу нулями вначале:

Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России)                        +7 (495) 984-09-27 (бесплатный звонок по Москве)

Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.

ege-study.ru

Перевод из одной системы счисления в другую

Для перевода чисел из одной системы счисления в другую необходимо владеть основными сведениями о системах счисления и форме представления чисел в них.

Количество s различных цифр, употребляемых в системе счисления, называется основанием, или базой системы счисления. В общем случае положительное число

X в позиционной системе с основанием s может быть представлено в виде полинома:

где s — база системы счисления, — цифры, допустимые в данной системе счисления . Последовательность образует целую часть X, а последовательность — дробную часть X.

В вычислительной технике наибольшее применение нашли двоичная (BIN — binary), и двоично кодированные системы счисления: восьмеричная (OCT — octal), шестнадцатеричная (HEX — hexadecimal) и двоично-кодированная десятичная (BCD — binary coded decimal).

В дальнейшем для обозначения используемой системы счисления число будет заключаться в скобки, а в индексе указано основание системы. Число X по основанию s будет обозначено .

Если Вам не нужно углубляться в теорию, а нужно лишь получить результат, то воспользуйтесь Калькулятором онлайн Перевод целых чисел из десятичной системы счисления в другие системы.

Основанием системы счисления служит число 2 (s = 2) и для записи чисел используются только две цифры: 0 и 1. Чтобы представить любой разряд двоичного числа, достаточно иметь физический элемент с двумя чётко различными устойчивыми состояниями, одно из которых изображает 1, а другое 0.

Прежде чем заняться переводом из любой системы счисления в двоичную, нужно внимательно изучить пример записи числа в двоичной системе счисления:

Если Вам не нужно углубляться в теорию, а нужно лишь получить результат, то воспользуйтесь Калькулятором онлайн Перевод целых чисел из десятичной системы счисления в другие системы.

Эти системы счисления относятся к двоично-кодированным, в которых основание системы счисления представляет собой целую степень двойки: — для восьмеричной и — для шестнадцатеричной.

В восьмеричной системе счисления(s = 8) используются 8 цифр: 0, 1, 2, 3, 4, 5, 6, 7.

Прежде чем заняться переводом из любой системы счисления в восьмеричную, нужно внимательно изучить пример записи числа в восьмеричной системе:

В шестнадцатеричной системе счисления (s = 16) используются 16 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.

Пример записи числа в шестнадцатеричной системе:

Широкое применение восьмеричной и шестнадцатеричной систем счисления обусловлено двумя факторами.

Во-первых, эти системы позволяют заменить запись двоичного числа более компактным представлением (запись числа в восьмеричной и шестнадцатеричной системах будет соответственно в 3 и 4 раза короче двоичной записи этого числа). Во-вторых, взаимное преобразование чисел между двоичной системой с одной стороны и восьмеричной и шестнадцатиречной — с другой осуществляется сравнительно просто. Действительно, поскольку для восьмеричного числа каждый разряд представляется группой из трёх двоичных разрядов (триад), а для шестнадцатеричного — группой из четырёх двоичных разрядов (тетрад), то для преобразования двоичного числа достаточно объединить его цифры в группы по 3 или 4 разряда соответственно, продвигаясь от разделительной запятой вправо и влево. При этом, в случае необходимости, добавляют нули слева от целой части и/или справа от дробной части и каждую такую группу — триаду или тетраду — заменяют эвивалентной восьмеричной или шестнадцатеричной цифрой (см. таблицу).

Если Вам не нужно углубляться в теорию, а нужно лишь получить результат, то воспользуйтесь Калькулятором онлайн Перевод целых чисел из десятичной системы счисления в другие системы.

Соответствие между цифрами в различных системах счисления

DEC	BIN	OCT	HEX	BCD
0	0000	0	0	0000
1	0001	1	1	0001
2	0010	2	2	0010
3	0011	3	3	0011
4	0100	4	4	0100
5	0101	5	5	0101
6	0110	6	6	0110
7	0111	7	7	0111
8	1000	10	8	1000
9	1001	11	9	1001
10	1010	12	A	0001 0000
11	1011	13	B	0001 0001
12	1100	14	C	0001 0010
13	1101	15	D	0001 0011
14	1110	16	E	0001 0100
15	1111	17	F	0001 0101

Для обратного перевода каждая OCT или HEX цифра заменяется соответственно триадой или тетрадой двоичных цифр, причём незначащие нули слева и справа отбрасываются.

Для рассмотренных ранее примеров это выглядит следующим образом:

Если Вам не нужно углубляться в теорию, а нужно лишь получить результат, то воспользуйтесь Калькулятором онлайн Перевод целых чисел из десятичной системы счисления в другие системы.

В двоично-десятичной системе вес каждого разряда равен степени 10, как в десятичной системе, а каждая десятичная цифра кодируется четырьмя двоичными цифрами. Для записи десятичного числа в BCD-системе достаточно заменить каждую десятичную цифру эквивалентной четырёхразрядной двоичной комбинацией:

Любое десятичное число можно представить в двоично-десятичной записи, но следует помнить, что это не двоичный эквивалент числа. Это видно из следующего примера:

Пусть X — число в системе счисления с основанием s, которое требуется представить в системе с основанием h. Удобно различать два случая.

В первом случае и, следовательно, при переходе к основанию h можно использовать арифметику этой системы. Метод преобразования состоит в представлении числа в виде многочлена по степеням s, а также в вычислении этого многочлена по правилам арифметики системы счисления с основанием h. Так, например, удобно переходить от двоичной или восьмеричной системы счисления к десятичной. Описанный приём иллюстрируют следующие примеры:

.

.

В обоих случаях арифметические действия выполняются по правилам системы счисления с основанием 10.

Во втором случае () удобнее пользоваться арифметикой по основанию s. Здесь следует учитывать, что перевод целых чисел и правильных дробей производится по различным правилам. При переводе смешанных дробей целая и дробная части переводятся каждая по своим правилам, после чего полученные числа записываются через запятую.

Перевод целых чисел

Правила перевода целых чисел становится ясным из общей формулы записи числа в произвольной позиционной системе. Пусть число в исходной системе счисления s имеет вид . Требуется получить запись числа в системе счисления с основанием h:

.

Для нахождения значений разделим этот многочлен на h:

.

Как видно, младший разряд , то есть , равен первому остатку. Следующий значащий разряд определяется делением частного на h:

.

Остальные также вычисляются путём деления частных до тех пор, пока не станет равным нулю.

Для перевода целого числа из s-ичной системы счисления в h-ичную необходимо последовательно делить это число и получаемые частные на h (по правилам системы счисления с основанием h) до тех пор, пока частное не станет равным нулю. Старшей цифрой в записи числа с основанием h служит последний остаток, а следующие за ней цифры образуют остатки от предшествующих делений, выписываемые в последовательности, обратной их получению.

Пример 1. Перевести число 75 из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную системы.

Решение:

Если Вам не нужно углубляться в теорию, а нужно лишь получить результат, то воспользуйтесь Калькулятором онлайн Перевод целых чисел из десятичной системы счисления в другие системы.

Перевод правильных дробей

Правильную дробь , имеющую в системе с основанием s вид , можно выразить в системе счисления с основанием h как многочлен вида

Старшая цифра может быть найдена умножением этого многочлена на h, т.е.

Если это произведение меньше 1, то цифра равна 0, если же оно больше или равно 1, то цифра равна целой части произведения. Следующая цифра справа определяется путём умножения дробной части указанного выше произведения на h и выделения его целой части и т.д. Процесс может оказаться бесконечным, т.к. не всегда можно представить дробь по основанию h конечным набором цифр.

Для перевода правильной дроби из системы счисления с основанием s в систему счисления с основанием h нужно умножать исходную дробь и дробные части получающихся произведений на основание h (по правилам «старой» s-системы счисления). Целые части полученных произведений дают последовательность цифр дроби в h-системе счисления.

Описанная процедура продолжается до тех пор, пока дробная часть очередного произведения не станет равной нулю либо не будет достигнута требуемая точность изображения числа X в h-ичной системе счисления. Представлением дробной части числа X в новой системе счисления будет последовательности целых частей полученных произведений, записанных в порядке их получения и изображённых h-ичной цифрой. Абсолютная погрешность перевода числа X при p знаков после запятой равняется .

Пример 2. Перевести правильную дробь 0,453 из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную системы счисления.

* В двоичную систему:

Ответ:

** В восьмеричную систему:

Ответ:

*** В шестнадцатеричную систему:

Ответ: так как , то

Поделиться с друзьями

function-x.ru

Системы счисления — Перевод чисел из одной системы счисления в другую

Перевод чисел в десятичную систему счисления

Перевод из двоичной системы в десятичную

Преобразуем двоичное число 1001011 из первого примера

Пример Перевести число 11010101 из двоичной системы в десятичную.

Преобразуем число:

11010101₂= 1 * 2⁷ + 1 * 2⁶ + 0 * 2⁵ + 1 * 2⁴ + 0 * 2³ + 1 * 2² + 0 * 2¹ + 1 * 2⁰=128+64+0+16+0+4+0+1=213₁₀

Перевод из восьмеричной системы в десятичную

Преобразуем восьмеричное число 572.

Пример Перевести число 572 из восьмеричной системы в десятичную.

Преобразуем число:

572₈=5 * 8² + 7 * 8¹ + 2 * 8⁰=320+56+2=378₁₀

Перевод из шестнадцатеричной системы в десятичную

Числа в шестнадцатеричной системе состоят из цифр 0-9 и букв A, B, C, D, E, F, таблица соответствия:

десятичная	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
шестнадцатеричная	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F

Преобразуем шестнадцатеричное число A5C.

Пример Перевести число A5C из шестнадцатеричной системы в десятичную.

Преобразуем число:

A5C₁₆= 10 * 16² + 5 * 16¹ + 12 * 16⁰ =2560+80+12=2652₁₀

calcs.su

Перевод чисел между системами счисления, основания которых равно степени числа 2

Перевод чисел между системами счисления, основания которых равны значениям степеней числа 2 (т. е. P = 2 ⁿ), можно произвести по более простым алгоритмам. Получим эти правила.

Перевод между двоичной и восьмеричной системами счисления

Определим информационный вес двоичной цифры. Так как алфавит двоичной системы содержит две цифры (0 и 1), то используя формулу Хартли, имеем:
N = 2 ⁱ, 2 = 2 ⁱ, откуда i = 1 бит

Аналогично для восьмеричной цифры:
N = 2 ⁱ, 8 = 2 ⁱ, 2 ³ = 2 ⁱ, откуда i = 3 бит

Нетрудно заметить, что информационный вес восьмеричной цифры в три раза больше двоичного. Поэтому каждой восьмеричной цифре можно поставить в соответствие группу из трех двоичных разрядов (триаду):

0 – 000, 1 – 001, 2 – 010, 3 – 011, 4 – 100, 5 – 101, 6 – 110, 7 – 111

Последнее утверждение позволяет сформулировать алгоритм перевода двоичного числа в восьмеричную систему счисления:

1. Разбить двоичное число на триады, справа налево.
2. Если в правой группе меньше трех цифр, то добавить ведущие нули.
3. Каждую триаду перевести в восьмеричную систему счисления.
4. Записать полученные цифры в соответствующих разрядах восьмеричного числа.

Пример. Перевести двоичное число 1011101110₂ в восьмеричную систему счисления.

Для решения задачи воспользуемся выше приведенным алгоритмом:

1. 1.011.101.110
2. 001.011.101.110
3. 1 3 5 6
4. 1011101110₂ = 1356₈

Ответ. 1356

Алгоритм перевода восьмеричного числа в двоичную систему счисления:

1. Разбить двоичное число на триады, справа налево.
2. Поставить в соответствие каждой восьмеричной цифре двоичную триаду.
3. Соединить триады и записать двоичное число.
4. Удалить (если существуют) незначащие нули.

Пример. Перевести восьмеричное число 257₈ в двоичную систему счисления.

Используем алгоритм, приведенный выше:

1. 010.101.111
2. 010101111
3. 10101111

Таким образом, 257₈ = 10101111₂

Ответ. 10101111

Перевод между двоичной и шестнадцатеричной системами счисления

Определим информационный вес шестнадцатеричной цифры:

N = 2 ⁱ, 16 = 2 ⁱ, 2 ⁴ = 2 ⁱ, откуда i = 4 бит

Итак, информационный вес шестнадцатеричной цифры в четыре раза больше двоичного. Значит, каждой цифре шестнадцатеричной системы счисления можно поставить в соответствие группу из четырех двоичных разрядов (тетраду):

0 – 000, 1 – 001, 2 – 010, 3 – 011, 4 – 100, 5 – 101, 6 – 110, 7 – 111
8 – 0111, 9 – 1001, A – 1010, B – 1011, C – 1100, D – 1101, E – 1110, F – 1111

Алгоритм перевода двоичного целого числа в шестнадцатеричную систему счисления:

1. Разбить двоичное число на тетрады, справа налево.
2. Если в правой группе меньше четырех цифр, то добавить ведущие нули.
3. Каждую тетраду перевести в шестнадцатеричную систему счисления.
4. Записать полученные цифры в соответствующих разрядах шестнадцатеричного числа.

Пример. Перевести двоичное число 10011011102 в шестнадцатеричную систему счисления.

Воспользуемся выше приведенным алгоритмом:

1. 10.0110.1110
2. 0010.0110.1110
3. 2 6 E
4. 1001101110₂ = 26E₁₆

Ответ. 26E

Алгоритм перевода шестнадцатеричного числа в двоичную систему счисления:

1. Поставить в соответствие каждой шестнадцатеричной цифре двоичную тетраду.
2. Соединить тетрады и записать двоичное число.
3. Удалить (если существуют) незначащие нули.

Пример. Перевести шестнадцатеричное число 3AC₁₆ в двоичную систему счисления.

Используем алгоритм, приведенный выше:

1. 0011.1010.1100
2. 001110101100
3. 1110101100

Таким образом, 3AC₁₆ = 1110101100₂

Ответ. 1110101100

informatics-lesson.ru

Системы счисления — Компьютер для новичков

В настоящее время подавляющее число людей являются грамотными и умеют считать. Тем не менее, далеко не все в курсе, что за время человеческой цивилизации было придумано большое количество самых разнообразных систем счисления. Разные народы в различные исторические периоды использовали разные системы счета, которые видоизменялись с течением времени.

Считается, что самая первая система счета у всех народов состояла всего из одного числа, единицы. Соответственно для обозначения, какого то другого числа ее следовало повторить соответствующее количество раз. В качестве обозначения могло выступать что угодно, черточки, крестики и любые другие символы. Отсутствие письменности тоже не помеха, ведь можно использовать камешки, ракушки, плоды, веточки, делать зарубки, вязать узелки и так далее.

Таким образом, для записи числа 4 требовалось собрать 4 камешка или поставить 4 черточки: ||||. Это так называемая единичная система счисления, из которой впоследствии сформировались остальные. Все предельно просто, но очень не удобно для более менее больших чисел. Через какое то время люди догадались упростить запись, объединяя какое то количество элементов в группы и обозначая их другим символом. Чаще всего встречалась группировка по 3 и 5 элементов.

Таким образом, если договориться, что черные камни обозначают единицы, а один белый камень равен 3 черным, то для обозначения допустим 8 чужаков надо показать ●●●●●●●● черных камней или ○ белый и ●●●●● черных или ○○ белых и ●● черных. Любая из этих комбинаций обозначает в нашей условной системе число 8. Такой прием, конечно, заметно упрощал счет. Впоследствии многие народы использовали в качестве обозначения чисел буквы своего алфавита.

Римская система счисления

Одной из таких систем счисления является римская, которая до сих пор находит применение, например, для обозначения веков, цифр на циферблате аналоговых часов, разделов в документе и так далее. В ее основе лежат следующие числа и соответствующие им буквы латинского алфавита.

• 1 — I
• 5 — V
• 10 — X
• 50 — L
• 100 — C
• 500 — D
• 1000 — M

Все остальные числа получаются их комбинацией в соответствии с определенными правилами, причем 0 в римской системе отсутствует. Хотя сейчас правила довольно вольные и существует множество вариантов их трактовки отличающиеся различной степенью строгости. Мы не будем их расписывать, желающие могут найти их самостоятельно. Приведем лишь несколько примеров записи чисел в римской системе счисления.

• II — 2
• IV — 4
• XVI — 16
• XXIII — 23
• XLVIII — 48

Десятичная система счисления

Однако сейчас нам привычна система счисления основанная на цифрах от 1 до 9 и 0, это так называемые арабские цифры, хотя с исторической точки зрения это не совсем так. В итоге получается 10 цифр, поэтому она называется десятичной системой счисления с основанием системы равным 10. Считается, что она обязана своему появлению количеству пальцев на руках, что сильно упрощало жизнь. Ее особенностью является то, что в зависимости от местоположения цифры в числе меняется ее значение. Например, в числе 152 цифра 5 имеет значение 50, поскольку стоит в разряде десятков, а цифра 1 имеет значение 100 так как обозначает сотни. Это так называемая позиционная система счисления.

Так же существуют непозиционные системы, где значение цифр не зависит от их места в числе, а так же смешанные системы. Примером непозиционной системы может служить единичная система счета и с некоторой оговоркой римская.

Впрочем, еще относительно недавно в историческом масштабе, вплоть до конца XVIII века на Руси применялась пятеричная система, в которой были только цифры 0, 1, 2, 3, 4 и вытесненная из обихода современной десятичной.

Помимо уже названных систем счисления имеется множество других существовавших в разное время, а так же использующих в настоящее время в разных сферах деятельности человека. Для пересчета чисел из одной системы счисления в другую, вы можете воспользоваться онлайн конвертером систем счисления в конце статьи. Дальше мы рассмотрим несколько таких систем счисления применяющихся в компьютерной технике и программном обеспечении.

Двоичная система счисления

Почти все электронные вычислительные устройства, в том числе компьютеры используют вовсе не привычную для нас десятичную, а двоичную систему счисления, где основанием системы является 2. В ее основе лежит использование всего двух чисел 0 и 1. Это очень удобно для электронных устройств в силу технических причин, поскольку соответствует всего двум состояниям включено (1) и выключено (0) или высокий и низкий сигнал или «истина» и «ложь» и так далее. Наличие всего двух состояний упрощает техническую реализацию, повышает надежность работы, уменьшает габариты и обеспечивает высокую помехоустойчивость цифровых схем, в сравнение с аналоговыми.

В итоге любые числа представлены в виде комбинаций нулей и единиц. Например, число 4 в двоичной системе счисления записывается как 100, но читается каждый символ в отдельности, то есть «один ноль ноль». Это может запутать, поскольку запись числа 4 в двоичной системе счисления внешне не отличается от числа 100 из десятичной. В некоторых ситуациях из-за этого может возникнуть путаница. В таких случаях справа от числа подстрочным шрифтом принято указывать систему счисления, к которой относится данной число в десятичном формате. Числа из нашего примера можно записать следующим образом 4₁₀ и соответственно 100₂. Так же встречается вариант указания перед двоичным числом префиксов 0b или &, то есть 0b100 или &100.

Чтобы перевести десятичное число в двоичное, можно воспользоваться калькулятором расположенным ниже или применить метод Горнера. Для этого нужно десятичное число последовательно делить на основание системы, в данном случае 2. Если результат получается с остатком, то остаток отбрасываем, пишем 1 и снова делим на 2. Если результат получается без остатка, то пишем 0 и снова делим на 2. Запись нулей и единиц осуществляется справа налево, а деление продолжается пока в частном не получится ноль. Рассмотрим это на примере и преобразуем число 11₁₀ в двоичный вид.

11/2=5 остаток 1
5/2=2 остаток 1
2/2=1 остаток 0
1/2=0 остаток 1

В частном получился ноль, осталось записать получившиеся цифры справа налево от первой к последней и в итоге получаем, что 11₁₀=1011₂

Для обратной конвертации двоичных в десятичные, можно складывать последовательно цифры слева на право, умножая получившейся в предыдущем шаге результат на 2. Пересчитаем наш пример в обратную сторону.

Дано: &1011
1+0*2=1 (на первом шаге предыдущая сумма отсутствует, поэтому 0*2 )
0+1*2=2
1+2*2=5
1+5*2=11
Результат: 1110

Чтобы окончательно вас запутать, стоит упомянуть, что для записи чисел может применяться двоичный код, а система счета при этом использоваться десятичная. Такая комбинация называется двоично-десятичное кодирование и так же находит применение в вычислительной технике.

Шестнадцатеричная система счисления

Неудобством двоичных чисел является их громоздкость и трудность визуального восприятия человеком. Поэтому для представления двоичного кода в информатике широко используется шестнадцатеричная система счисления. Как вы уже наверно догадались, в ней используется шестнадцать символов, цифры от 0 до 9 и латинские буквы A, B, C, D, E, F соответствующие числам от 10 до 15 в десятичной системе. Шестнадцатеричное число может обозначаться словом hex.

Благодаря основанию системы равному 16 для записи 1 байта требуется всего 2 цифры в этой системе, для символов юникода требуется 4 шестнадцатеричных числа (иногда больше). Может использоваться для обозначения цветов в цветовой модели RGB, в програмировании, записи адресов IPv6, представления MAC-адреса сетевого оборудования, кодов ошибок операционных систем, записи хешей,  и так далее.

Чтобы перевести десятичное число в шестнадцатеричное используйте онлайн калькулятор систем счисления в конце статьи или воспользуйтесь алгоритмом, приведенным в примере с двоичной системой. Для примера пересчитаем число 382₁₀

382/16=23 остаток 14, пишем E
23/16=1 остаток 7, пишем 7
1/16=0 остаток 1, пишем 1
Результат: 17E16=38210

Чтобы пересчитать шестнадцатеричное число в десятичное, нужно разбить его на разряды и цифру каждого разряда умножить на 16 в степени соответствующего разряда и сложить получившиеся числа. Проще понять на примере, для этого выполним обратную операцию: 17E₁₆=1*16²+7*16¹+14*16⁰=1*256+7*16+14*1=382₁₀

Кроме рассмотренных систем существует и большое количество позиционных систем счисления с другими основаниями. Так в компьютерах одно время использовалась система с основанием 8, а такая древняя система счисления как шестидесятеричная, используется и в наше время для обозначения времени, координат и углов.

Калькулятор систем счисления

Работает только с целыми положительными числами.

beginpc.ru

Перевод чисел из одной системы счисления в другую, когда одно основание является целой степенью другого.

ТОП 10:

Как мы уже знаем, в ЭВМ наибольшее применение находит система с основаниями 2, 4, 8, 16, т.е. системы которые кратны степени 2. Поэтому целесообразно рассмотреть лишь правила перевода чисел в этих системах. Аналогичные правила будут справедливы и для других систем. Допустим, что имеется некоторое целое число N8 в 8-ой системе. Оно может быть представлено в виде: N8 = a1*8n-1 + a2*8n-2 + a3*8n-3 + … + an-2*82 + an-1*81 + an*80. Пусть каким-либо образом мы получили запись этого числа в виде двоичного, т.е.: N2 = b1*2k-1 + b2*2k-2 + … + bk-2*22 + bk-1*21 + bk*20. Разделим эти выражения на 23 = 8: a1*8n-2 + a2*8n-3 + a3*8n-4 + … + an-1*80 + an*8-1 ——- дробная часть b1*2k-4 + b2*2k-5 + … + bk-3*20 + bk-2*2-1 + bk-1*2-2 + bk*2-3 ————————- дробная часть Так как числа были равны, то получается одинаковые частные и одинаковые остатки: an*8-1 = bk-2*2-1 + bk-1*2-2 + bk*2-3. (6.2) Если снова разделим целые части на 23 = 8, то опять получим равные частные и равные остатки. При этом видим, что каждой восьмеричной цифре соответствует её двоичный эквивалент. Поэтому перевод выполняется простой заменой цифры восьмеричной системы её двоичным эквивалентом и обратно. Пример: 62,7538 = 110010,1111010112 Аналогично для 4-ой системы: 321,22334 = 111001,101011112 Аналогично для 16-ой системы: 1D876,72 = 00011101100001110110,011100102 Из этих примеров видим, что чем выше основание системы счисления, тем компактнее запись. Если умножить последние соотношения (6.2) на 8, то: an*8-1*8 = (bk-2*2-1 + bk-1*2-2 + bk*2-3)*23an = bk-2*22 + bk-1*21 + bk*20 7. Лекция: Способы представления чисел в ЭВМ Страницы: 1 | 2 | 3 | 4 | 5 | вопросы | » | учебники | для печати и PDA | ZIP Если Вы заметили ошибку — сообщите нам, или выделите ее и нажмите Ctrl+Enter В лекции представлены способы представления чисел в ЭВМ: фиксированная и плавающая запятая. Описаны прямой, дополнительный и обратный коды. Дано сложение чисел в дополнительном и обратном кодах. Как мы уже знаем, применяются два основных способа представления чисел — с фиксированной и плавающей запятой. Большинство универсальных ЭВМ работает с числами, представленными с плавающей запятой, а большинство специализированных — с фиксированной запятой. Однако целый ряд машин работает с числами в этих двух форматах. В общем виде способ представления чисел сильно влияет на характер программирования. Так, программирование для ЭВМ, работающих в системе с фиксированной запятой, значительно усложняется, поскольку помимо алгоритмических трудностей этот процесс требует ещё отслеживания положения запятой. Фиксированная запятая Оговоримся, что разрядная сетка машины имеет постоянное число разрядов — n. При представлении чисел с фиксированной запятой считают, что запятая всегда находится перед старшим разрядом, а все числа, которые участвуют в вычислениях, считаются по абсолютной величине меньше единицы: |X| < 1 Введём две характеристики чисел: диапазон изменения и точность представления. Диапазон изменения характеризуется теми пределами, в которых могут находиться числа, с которыми оперирует машина. Отличное от нуля самое малое число: Таким образом, диапазон чисел, с которыми работает ЭВМ, есть: |X|min |X| |X|max 2-n |X| 1 — 2-n Иными словами, числа, которые выходят за диапазон изменения, в ЭВМ не могут быть представлены точно. Если |X| < |X|min = 2-n, то такое число воспринимается как нуль. Если: |X| > |X|max = 1- 2-n, то такое число воспринимается как бесконечно большое. Этим двум случаям соответствуют понятия машинного нуля и машинной бесконечности. При оптимальном округлении абсолютная ошибка: |ΔX| 0,5*2-n Минимальная относительная ошибка: |ΔX| 0,5*2-n | x|min = _______ = -__________ 2-(n+1) |X|max 1-2-n так как 1-2-n 1 при большом «n» Максимальная относительная ошибка: |ΔX| 0,5*2-n | X|max = _____ = _____________ = 0,5 |X|min 2-n Ошибка представления числа зависит от величины самого числа и способа округления: 2-(n+1) | X| 0,5 Заметим, что для малых чисел ошибка может достигать большой величины.   Плавающая запятая В ЭВМ с плавающей запятой число представляется в виде: X = ± Mx * q±p, где: Mx — мантисса числа; q — основание системы счисления; p — порядок. Разрядная сетка машины принимает следующий вид: Это лишь условное изображение основных слогов в числе. Заметим, что в реальной ЭВМ может быть принят любой другой порядок расположения. Пусть «m» разрядов отведено под изображение мантиссы, а «k» разрядов под изображение порядка. Тогда для двоичной системы и нормализованного вида числа: q = 2; 0,1 Mx < 1 — нормализованная мантисса. То есть диапазон чисел: Абсолютная ошибка представления числа в ЭВМ с плавающей запятой равна: |ΔX| 0,5*2-m Так как 2-1 |Mx| 1-2-m, то минимальная относительная ошибка: |ΔX|min = (0,5*2-m) / (1 — 2-m) 2-(m+1), при m — большом, а максимальная относительная ошибка: |ΔX|max =(0,5*2-m) / (2-1) = 2-m Видно, что относительная ошибка в ЭВМ с плавающей запятой не зависит от порядка числа. При этом точность представления больших и малых чисел изменяется незначительно. Теоретически «плавающая запятая» имеет преимущества перед «фиксированной». Но соответствующее устройство получается намного сложнее. К тому же специфика выполнения операций с плавающей запятой требует большего числа микроопераций, что приводит к снижению быстродействия ЭВМ. Однако «плавающая запятая» снимает с программиста обязанность отслеживать положение запятой в вычислениях и значительно упрощает сам процесс программирования вычислительных задач. 

infopedia.su

Занятие 2

Повторение

1. Какие системы счисления называются позиционными? Приведите примеры.
2. Какие системы счисления называются непозиционными? Приведите примеры.
3. Почему непозиционные системы счисления не получили развития в математике?
4. Приведите примеры того, что, кроме десятичной позиционной системы счисления, человечество использовало и другие.
5. Как вычислить значение числа в римской системе счисления?
6. Запишите в римской системе счисления следующие числа: 144, 301, 1583, 2078, 959, 999.
7. Запишите в десятичной системе счисления, называя группы цифр: CMXLVI, CDLXIX, CMLXXX,MMCXC.
8. Дайте определения алфавита и основания (в позиционной) системе счисления.

Принципы записи чисел в позиционных системах счисления

&nbsp &nbsp Наряду с понятиями алфавита и основания в позиционных системах счисления будем использовать понятие базиса.
&nbsp &nbsp Базис позиционной системы счисления – это последовательность чисел, каждое из которых задает значение цифры «по месту» или «вес» каждого разряда.
&nbsp &nbsp В привычной нам десятичной системе счисления базисом являются степени числа десять – 1, 10, 100, 1000, 1000… Это означает, что в записи числа каждая последующая цифра «весит» больше предыдущей в 10 раз. Более наглядно это проявляется в так называемой развернутой форме записи числа.
&nbsp &nbsp 444=4*10⁰+4+10¹+4*10²; 658=8*10⁰+5*10¹+6*10².
&nbsp &nbsp Натуральный ряд чисел в десятичной системе счисления: 1..9, 10..99, 100…
&nbsp &nbsp Кроме десятичной, мы будем рассматривать и другие позиционные системы счисления.

&nbsp &nbsp В восьмеричной системе счисления основание равно 8, алфавит составляют цифры от 0 до 7, базисом является последовательность 1, 8, 8², 8³, 8⁴…, т.е., каждая последующая цифра в 8 раз больше предыдущей. В развернутой форме восьмеричное число записывается так: 345₈=5*8⁰+4*8¹+3*8²
&nbsp &nbsp Натуральный ряд чисел в восьмеричной системе счисления: 1..7,10, 11..77, 100…
&nbsp &nbsp Таким образом, справедливо, что 8₁₀=10₈.
&nbsp &nbsp В троичной системе счисления основание равно 3, алфавит составляют цифры 0,1,2, базисом являются числа 1, 3, 3², 3³, 3⁴…,т.е., единица каждого разряда в 3 раза больше предыдущей. В развернутой форме троичное число записывается так: 120=0*3⁰+2*3¹+1*3². Натуральный ряд чисел в троичной системе счисления: 1, 2, 10, 11, 12, 20, 21, 22, 100… Сравнивая десятичный и троичный рады натуральных чисел, получаем, что 3₁₀=10₃.
&nbsp &nbsp Двоичная система счисления имеет алфавит, состоящий из цифр 0 и 1, основание, равное двум, базисную последовательность 1, 2, 2², 2³,2⁴,… Развернутая запись числа 10110₂=0*2⁰+1*2¹+1*2²+1*2³+1*2⁴. Натуральный ряд чисел: 1, 10, 11, 100, 101, 110, 111… Таким образом, 2₁₀=10₂.
&nbsp &nbsp В шестнадцатеричной системе счисления в алфавите, кроме цифр 0..9, используются заглавные буквы латинского алфавита A, B, C, D, E, F, которые обозначают цифры 10, 11, 12, 13, 14, 15. Основание шестнадцатеричной системы счисления равно 16, базис составляют степени числа 16. Развернутая форма записи шестнадцатеричного числа 3А5₁₆=5*16⁰+10*16¹+3*16². Натуральный ряд чисел 1..9, А..F, 10, 11, 12… Значит, 16₁₀=10₁₆.

&nbsp &nbsp Т.о., позиционная система счисления с основанием P характеризуется тем, что с помощью ограниченного набора цифр можно записать сколь угодно большое и сколь угодно малое число в виде суммы произведений цифр на положительные и отрицательные степени числа Р.
&nbsp &nbsp В общем виде это можно записать так: a_na_n-1a_n-2…a₁a₀,b₁b₂…b_k=a_n*pⁿ+a_n-1*p^n-1+…+a₁*p¹+a₀*p⁰+b₁*p^-1+b₂*p^-2+…+b_k*p^-k
&nbsp &nbsp где р — основание системы счисления, а_i,b_i – цифры р-ичного числа.

Правила перевода чисел в десятичную систему счисления

&nbsp &nbsp Запишем в развернутой форме числа:
&nbsp &nbsp 143₁₀=3*10⁰+4*10¹+1*10²;
&nbsp &nbsp 143,78₁₀=3*10⁰+4*10¹+1*10²+7*10^-1+8*10^-2;
&nbsp &nbsp 56,31₈=6*8⁰+5*8¹+3*8^-1+1*8^-2;
&nbsp &nbsp 1011,01₂=1*2⁰+1*2¹+0*2²+1*2³+0*2^-1+1*2^-2;
&nbsp &nbsp FC,15₁₆=12*16⁰+15*16¹+1*16^-1+5*16^-2;
&nbsp &nbsp Если мы вычислим суммы, записанные в каждой строчке, то это будет не что иное, как число в десятичной системе счисления. Таким образом, получаем первый алгоритм (правило) перевода чисел в десятичную систему счисления.

1. Для перевода числа, записанного в системе счисления с основанием Р, в десятичную, нужно записать это число в развернутом виде, т.е. каждую цифру умножить не ее вес и вычислить сумму полученных произведений. Весом цифры называется соответствующая степень основания системы счисления.

   Полученный алгоритм можно переформулировать следующим образом:

2. Для перевода числа, записанного в системе счисления с основанием Р, в десятичную, нужно пронумеровать цифры его целой части справа налево, начиная с 0, и дробной части – слева направо, начиная с (-1), затем найти произведение каждой цифры числа на степень основания, где показателем степени является номер цифры, и сложить полученные значения.

&nbsp &nbsp Пусть число 341 записано цифрами девятеричной, восьмеричной, шестеричной и шестнадцатеричной систем счисления, найдем его десятичное значение.
&nbsp &nbsp 341₉=3*9²+4*9¹+1*9⁰=280₁₀;
&nbsp &nbsp 341₈=3*8²+4*8¹+1*8⁰=225₁₀;
&nbsp &nbsp 341₆=3*6²+4*6¹+1*6⁰=133₁₀;
&nbsp &nbsp 341₁₆=3*16²+4*16¹+1*16⁰=833₁₀;

Перевод чисел из десятичной системы счисления

&nbsp &nbsp Целые числа

&nbsp &nbsp Для обратного перевода нужно разложить десятичное число на слагаемые, содержащие максимальную степень основания нужной системы счисления. К примеру, переведем десятичное число 15 в двоичную, троичную и восьмеричную системы счисления соответственно:
&nbsp &nbsp 15₁₀=8+4+2+1=1*2³+1*2²+12¹+1*2⁰=1111₂;
&nbsp &nbsp 15₁₀=9+6=1*3²+2*3¹+0*3⁰=120₃;
&nbsp &nbsp 15₁₀=8+7=1*8¹+7*8⁰=17₈;
&nbsp &nbsp Так можно переводить любые натуральные числа в десятичную систему счисления.
&nbsp &nbsp Попробуйте самостоятельно выполнить следующие задания:
&nbsp &nbsp Переведите в двоичную систему счисления десятичные числа 39 и 157. Коротко эти задания можно записать так: 39₁₀→ Х₂ и 157₁₀→Х₂.
&nbsp &nbsp Если вы получили 100111₂ и 10011101₂ соответственно, то все выполнено правильно.

&nbsp &nbsp Получили, что для перевода целого десятичного числа в систему счисления с основанием Р нужно разложить это число на слагаемые, содержащие максимальную степень числа Р и выписать коэффициенты (множители) при этих степенях. Вместо отсутствующей степени нужно записать 0.
&nbsp &nbsp

Легко заметить, что множители при степенях Р не что иное, как остатки от последовательного деления десятичного числа на Р. Тогда запись Р-ичного числа превращается в последовательность остатков от деления на Р, записанных в обратном порядке.
&nbsp &nbsp Так получаем другой способ перевода целых чисел из десятичной системы счисления:
&nbsp &nbsp Для перевода целого десятичного числа в Р-ичную систему счисления, нужно последовательно делить число и получающиеся частные на Р, запоминая остатки, до тех пор, пока последнее частное не будет равно 0. После этого выписать полученные остатки в обратном порядке.
&nbsp &nbsp Сравните последовательность остатков, полученных при делении, с ответом, который вы получили в последнем примере.
&nbsp &nbsp При решении задач вы можете использовать любой из способов. Заметим лишь, что при переводе больших десятичных чисел в систему счисления с малым основанием (к примеру, в двоичную) первый способ гораздо быстрее приведет вас к результату.
&nbsp &nbsp Перевод правильных дробей и смешанных чисел
&nbsp &nbsp Напомним, что десятичная дробь называется правильной, если имеет нулевую целую часть.
&nbsp &nbsp Для перевода правильной десятичной дроби в Р-ичную систему счисления, ее нужно последовательно умножать на Р, запоминая и отбрасывая целую часть до тех пор, пока не произойдет одно из событий:

• Дробная часть не окажется равной нулю;
• Не будет выделен период в случае бесконечной периодической дроби;
• Не будет получено нужное количество знаков после запятой (не будет достигнута необходимая точность) в случае бесконечной непериодической дроби.

Р-ичную запись правильной дроби будут составлять целые части в порядке их получения.

&nbsp &nbsp Переведем правильную десятичную дробь 0,875 в двоичную систему счисления: Процесс умножения закончен, т.к. получена нулевая дробная часть. Последовательность целых частей, выписанных в порядке получения, является дробной частью числа в двоичной системе счисления. Целая часть двоичной дроби равна нулю. Итак, 0,875₁₀=0,111₂. Убедитесь в этом, выполнив обратный перевод.
&nbsp &nbsp Для смешанных чисел целая и дробная части переводятся отдельно по своим алгоритмам, полученные результаты складываются.

Задачи
К оглавлению

slbazhenova.narod.ru