Презентация по математике. Проект «способы записи чисел»
Описание презентации по отдельным слайдам:
1 слайд
Описание слайда:Проект подготовлен учениками 5 «Б» класса МБОУ «Судбищенская средняя общеобразовательная школа» Учитель: Киселёва Светлана Владимировна 2015 г. СПОСОБЫ ЗАПИСИ ЧИСЕЛ
2 слайд
Описание слайда:Рассмотреть историю возникновения числа. Какие символы используют для записи числа. Сколько цифр существует. Узнать, какими цифрами мы пользуемся сегодня. Придумать свои цифры, для записи чисел. Сравнить различные способы записи чисел. Цель:
Описание слайда:Математика каменного века Первобытные люди не знали ни скотоводства, ни земледелия. Они охотились на диких зверей, ловили рыбу, собирали ягоды, грибы и орехи, выкапывали из земли съедобные корни. Когда такой способ добычи стал трудным, люди стали возделывать землю и приручать некоторых животных. Чтобы с успехом заниматься сельским хозяйством, понадобились математические знания. Без подсчета дней трудно было определять, когда надо засевать поля, когда начинать полив, когда ждать потомства от животных. Надо было знать, сколько овец в стаде, сколько мешков зерна положено в амбары.
4 слайд
Описание слайда:Самым простым инструментом счета были пальцы на руках человека С их помощью можно было считать до 5, а если взять две руки, то и до 10. Первый счет
5 слайд
Описание слайда:Преимущества и неудобства Преимущества в том, что очень просто. Неудобства в том ,что для счета нужны люди.
6 слайд
Описание слайда:Египетская нумерация
Описание слайда:Египтяне придумали свою систему около 5 000 лет тому назад. Это одна из древнейших систем записи чисел, известная человеку Возникновение
8 слайд
Описание слайда:Как и большинство людей для счета небольшого количества предметов Египтяне использовали палочки Каждая единица изображалась отдельной палочкой Такими путами египтяне связывали коров Если нужно изобразить несколько десятков, то иероглиф повторяли нужное количество раз. Тоже самое относится и к остальным иероглифам. 1 10 Это мерная веревка, которой измеряли земельные участки после разлива Нила. 100 1000 Цветок лотоса Цифры Египта головастик 100 000 1 000 000 10 000 000 Египтяне поклонялись богу Ра, богу Солнца и, наверное, так изображали самое большое свое число Увидев такое число, обычный человек очень удивится и возденет руки к небу 1000 Поднятый палец — будь внимателен
9 слайд
Описание слайда:Число 1 245 386 в древнеегипетской записи будет выглядеть 1 2 4 5 3 8 6 Например:
10 слайд
Описание слайда:Преимущества и неудобства Преимущества в том, что на тот момент не было лучше счета. Неудобства в том ,что было тяжело писать.
Описание слайда:Римские цифры Римскую нумерацию придумали в Древнем Риме. И цифры в ней называются римскими. В римской нумерации семь цифр: I, V, X, L, C, D, M
12 слайд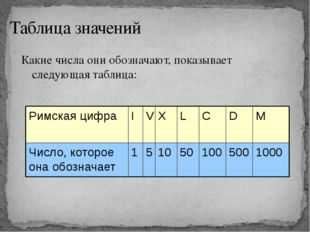
Описание слайда:Таблица значений Какие числа они обозначают, показывает следующая таблица: 1000 500 100 50 10 5 1 Число, которое она обозначает M D C L X V I Римская цифра
13 слайд
Описание слайда: Римская нумерация Римская нумерация непозиционная. На каком бы месте ни стояла цифра в записи числа, она везде обозначает одно и то же. Эта нумерация оказалась самой долговечной из древнейших. Мы пользуемся ей и сегодня.
14 слайд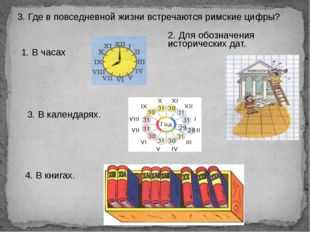
Описание слайда:3. Где в повседневной жизни встречаются римские цифры? 1. В часах 2. Для обозначения исторических дат. 3. В календарях. 4. В книгах.
15 слайд
Описание слайда:Преимущества и неудобства Эта нумерация очень удобна, даже в наше время её используют. Неудобства в объёмном написании.
Описание слайда:Славянская кириллическая нумерация
17 слайд
Описание слайда:Возникновение Славянская кириллическая нумерация была создана по подобию греческой записи чисел греческими же монахами братьями Кириллом и Мефодием. До XVII века эта форма записи чисел была официальной на территории России, Белоруссии, Украины, Болгарии, Венгрии, Сербии и Хорватии.
18 слайд
Описание слайда: Славянские цифры
19 слайд
Описание слайда:Преимущества и неудобства Преимущества в том, легко считать. Она до сих пор используется в православных церковных книгах. Неудобства в том ,что тяжелые правила написания.
20 слайд
Описание слайда:Вавилонская нумерация
21 слайд
Описание слайда:Возникновение В древнем Вавилоне примерно за 40 веков до нашего времени создалась позиционная нумерация, то есть такой способ записи чисел, при котором одна и та же цифра может обозначать разные числа, смотря по месту, занимаемому этой цифрой. В вавилонской поместной нумерации ту роль, которую у нас играет число 10, играет число 60, и потому эту нумерацию называют шестидесятеричной.
Описание слайда:Вавилонская нумерация Первой известной нам позиционной системой счисления была шестидесятеричная система вавилонян, возникшая примерно за 2500-2000 лет до н.э. Основанием ее служило число 60. Следовательно, в ней должно было быть 60 цифр.
23 слайд
Описание слайда:Например: Число 53 нужно было бы записать так:
24 слайд
Описание слайда:Преимущества и неудобства Преимущества легко считать. Неудобства в том ,что объёмное написание.
25 слайд
Описание слайда:Арабская нумерация
26 слайд
Описание слайда:Это, самая распространенная на сегодняшний день нумерация, которой мы пользуемся в настоящее время. Применяемые в настоящее время цифры : сложились в Индии около 400 г.н.э Арабы стали пользоваться подобной нумерацией около 800 г.н.э., Арабские цифры: В России арабская нумерация стала использоваться при Петре I Возникновение
Описание слайда:Арабская нумерация оказалась самой удобной в использовании (легко запоминать, легко записывать). Эта нумерация используется во всем мире.
28 слайд
Описание слайда:Наша нумерация
29 слайд
Описание слайда:Автор Блинкова Виктория
30 слайд
Описание слайда:Нумерация Моя нумерация Арабская + Красива Легче запоминать Легчесчитать — Долго писать Большие числа долго произносить
31 слайд
Описание слайда:Автор Болдина Яна
32 слайд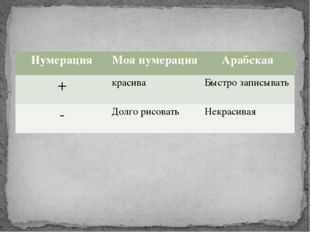
Описание слайда:Нумерация Моя нумерация Арабская + красива Быстро записывать — Долго рисовать Некрасивая
33 слайд
Описание слайда:Автор Еремина Ксения
34 слайд
Описание слайда:Нумерация Моя нумерация Арабская + Когда будешь записывать числа, можно рисовать. Числа будут выглядеть красиво. Напишешь пару примеров, а урок уже закончился Легко запомнить Легко писать — Очень сложно запомнить Долго писать, устанет рука запись числа получается очень большой Запись чисел очень скучная: нет ни цветочков, ни галочек.
35 слайд
Описание слайда:Автор Подливахина Дарья
36 слайд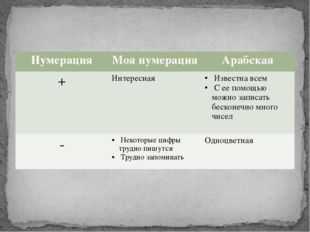
Описание слайда:Нумерация Моя нумерация Арабская + Интересная Известна всем С ее помощью можно записать бесконечно много чисел — Некоторыецифры трудно пишутся Трудно запоминать Одноцветная
37 слайд
Описание слайда:Автор Ходосеевич Светлана
38 слайд
Описание слайда:Нумерация Моя нумерация Арабская + Цветная Красивая Яркая Новая Легко писать цифры Числа занимают мало места — Числа надо долго писать Не модная
39 слайд
Описание слайда:Выводы Числа возникли из практических нужд человека. Числа сыграли большую роль в развитии человечества. Числа записывают с помощью десяти цифр. На уроках мы используем арабские цифры Лучше арабской системы счисления еще не придумали.
Курс повышения квалификации
Курс повышения квалификации
Курс профессиональной переподготовки
Учитель математики
Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:
Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое
Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс
Выберите учебник: Все учебники
Выберите тему: Все темы
также Вы можете выбрать тип материала:
Общая информация
Номер материала: ДВ-176664
ВНИМАНИЮ ВСЕХ УЧИТЕЛЕЙ: согласно Федеральному закону N273-ФЗ «Об образовании в Российской Федерации» педагогическая деятельность требует от педагога наличия системы специальных знаний в области обучения и воспитания детей с ОВЗ. Поэтому для всех педагогов является актуальным повышение квалификации по этому направлению!Дистанционный курс «Обучающиеся с ОВЗ: Особенности организации учебной деятельности в соответствии с ФГОС» от проекта «Инфоурок» даёт Вам возможность привести свои знания в соответствие с требованиями закона и получить удостоверение о повышении квалификации установленного образца (72 часа).
Подать заявку на курс
Похожие материалы
Вам будут интересны эти курсы:
Оставьте свой комментарийinfourok.ru
Способ — запись — число
Способ — запись — число
Cтраница 1
Способ записи чисел цифровыми символами определяется системой счисления. В современных ЭЦВМ находят применение десятичная и двоичная, а в качестве промежуточных — восьмеричная и шестнадцатиричная системы счисления. [1]
Этим способом записи чисел мы подчеркиваем ограниченную точность наших знаний — мы опускаем все цифры, в которых у нас нет достаточной уверенности. Например, когда речь идет о радиусе Земли и мы указываем, что он равен 6 37 — 10е м, а не 6 374 — 10 м или 6 370 — 10 м, то мы тем самым говорим, что вполне уверены в третьей значащей цифре, но не в четвертой. Число цифр, в которых мы вполне уверены, называется числом достоверных цифр. [2]
Системой счисления называется способ записи чисел при помощи цифр. Различают позиционные и непозиционные системы счисления. В позиционной системе значение каждой цифры, входящей в запись числа, зависит от ее положения ( позиции) в ряду цифр, изображающих число. Наиболее распространенная десятичная система счисления является позиционной. Изменение позиции цифры на один разряд вправо или влево изменяет ее значение в 10 раз. Число 10 определяет структуру десятичной системы и называется ее основанием. Примером непозиционной системы может служить запись числа римскими цифрами. [3]
Под системой счисления понимают способ записи чисел цифровыми знаками. Информация, характеризующая цифровую программу, может быть задана в различных системах счисления — десятичной, двоичной и двоично-десятичной. [4]
ДЕСЯТИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ, способ записи чисел, при к-ром один и тот же знак ( цифра) из десяти: О, 1, 2, 3, 4, 5, 6, 7, 8, 9 имеет разл. [5]
Наиболее распространенный в настоящее время способом записи чисел является позиционный способ, согласно которому один и тот же символ ( цифра) имеет различное значение в зависимости от занимаемого места в записи числа. Этот способ используется и в привычной для нас десятичной системе счисления. [6]
Этот метод основывается на еще одном способе записи чисел, соответствующих ключам. [7]
ПЛАВАЮЩАЯ ЗАПЯТАЯ, п р е д-ставление чисел с плавающей запя-той, — способ записи чисел в позиционной системе счисления с основанием R, при котором число JV представляется в виде N np-q, где р — целое число, называемое порядком числа N, а q — правильная дробь ( — g — 9l), называемая мантиссой числа N. [8]
Существует третий вид погрешностей, не зависящий ни от погрешностей исходных данных, ни от способа записи чисел, ни от точности вычислений. [9]
Способ записи чисел называют нумерацией или по-другому системой счисления. [10]
Для преобразования числа в ДДК необходимо преобразовать в двоичную систему счисления каждую цифру десятичного числа, сохранив при этом их порядок следования. Преимущество такого способа записи чисел состоит в том, что для преобразования чисел из одного представления в другое не требуются сложные расчеты. [11]
СТЕПЕННОЕ ПРЕДСТАВЛЕНИЕ ЧИСЛЕННЫХ ВЕЛИЧИН Представление численных величин в степенной форме позволяет избежать недоразумений при определении количества значащих цифр, а также избавляет от необходимости записывать большое количество нулей для очень малых или, наоборот, очень больших чисел. Многочисленные примеры помогают убедиться в удобстве такого способа записи чисел. [12]
Ранняя греческая система счисления была десятичной и аддитивной, как египетская и римская. В александрийскую эпоху, а может быть и раньше, появляется способ записи чисел, которым пятнадцать веков пользовались не только ученые, на и купцы и чиновники. Три архаичные буквы были добавлены к 24 буквам греческого алфавита, чтобы получить необходимые 27 знаков. С помощью такой системы любое число меньше 1000 можно было записать не более чем тремя знаками, например 14 как i6, так как i10, 6 4; числа, большие 1000, можно было выразить с помощью простого расширения такой системы. Архимеда, Ге-рона и всех других классических авторов. Имеются археологические данные о том, что этой системе обучали в школах. Такое отсутствие позиционности и использование не менее чем 27 знаков иной раз рассматривались как доказательство несовершенства системы. Но то, как легко ею пользовались математики древности, и то, что греческие купцы применяли ее даже при очень сложных расчетах — в Восточной Римской империи вплоть до ее гибели в 1453 г. — указывает, по-видимому, на наличие некоторых преимуществ. При известном опыте вычислений при такой системе мы действительно убеждаемся, что четыре основных действия можно выполнять достаточно легко, если твердо знать символы. Действия с дробями при подходящих обозначениях тоже просты, но греки не были при этом последовательны, так как у них не было единой системы: они пользовались египетскими основными дробями, вавилонскими шестиде-сятичнымн дробями и записью — дробей, напоминающей нашу. Десятичные дроби не были введены, это великое усовершенствование в Европе появляется в эпоху позднего Ренессанса, когда вычислительный аппарат был развит значительно больше, чем когда бы то ни было в древности. Но даже в этих условиях десятичные дроби не были приняты во многих школах до восемнадцатого и девятнадцатого столетия. [13]
Качественный материал этой главы может быть проработан за короткий срок. Точно так же немного времени займет и ознакомление с количественными методами измерения промежутков времени. Способ записи чисел с помощью числа десять в какой-то степени будет применяться на протяжении всего курса, и если он окажется незнакомым учащимся, следует на него обратить самое серьезное внимание. Определение порядка величин очень полезно, но иногда трудно для начинающих, и поэтому вначале не следует увлекаться этим. По мере того как на протяжении всего курса учащиеся будут решать задачи, они на практике оценят удобства этого метода оценки величин. [14]
Страницы: 1 2
www.ngpedia.ru
История развития понятия числа и деятельности счета. Способы записи чисел, история их развития.
Счет – математическое понятие, это операция, имеющая целью установить, сколько элементов содержит данное конечное множество.
1,5-2 года. Дети сопровождают свои операции с множеством такими словами как «вот», «еще» или числительными в любом порядке. Каждое повторение ребенок соотносит с одним предметом и одним движением, тем самым он устанавливает взаимнооднозначное соответствие между количеством предметов и количеством слов, движений.
2-4 года. Появляется интерес к сравнению множеств путем установления взаимнооднозначного соответствия. Последовательное называние числительных еще не означает овладение процессом счета, т.к. ребенок не понимает итога счета, т.е. не умеет отвечать на вопрос «сколько?» Счет еще не служит средством определения количества. Чаще всего названное числительное служит сигналом к остановке называния числительных.
4-5 лет. Дети начинают употреблять числительные в определенном порядке и отличать итог счета от процесса счета. Начинают понимать, что равночисленные множества всегда именуются одним числом.
5-6 лет. Усваивают последовательность называния числительных, понимают, что количество не зависит от направления счета, что число является показателем количества, осознают отношения между числами, т.е. осваивают обратный счет.
6-7 лет. Овладевают счетом группами, т.е. понимают, что единицей счета может быть не только отдельный предмет, а целая группа.
7-8 лет. Овладевают счетом десятками и новой деятельностью – вычислением. Счет связан с конкретным множеством, с определением количества в определенном множестве, а вычисление – абстрактная операция, здесь участвую только числа (без называния предмета).
Развитие понятия числа
3-4 года. Дети используют слова-числительные, но не понимают, что такое число. На этом этапе дети способны лишь сравнивать различные множества путем установления взаимнооднозначного соответствия.
4-5 лет. Дети могут сравнивать числа на основе сравнения множеств, но не воспринимают число абстрактно, без множества.
5-6 лет. Способны сравнивать любые числа на основе свойства транзитивности. При измерении понимают число как результат измерения, т.е. как отношение всей величины (целого) к условной мерке (части). Понимают, что число служит лишь показателем количества. Происходит абстрагирование числа от конкретных м ножеств.
Развитие представлений о натуральном ряде чисел
Натуральный ряд – последовательность целых положительных чисел, расположенных в порядке их возрастания.
2-4 года. На основе речи взрослых дети начинают рано употреблять слова-числительные: сначала хаотично, затем упорядочено. Осознание порядка следования чисел происходит сразу в 2-х направлениях:
— увеличиваются последовательности чисел, которые дети запоминают,
— начинают осознавать, что каждое числительное всегда занимает свое определенное место, но на этом этапе не понимают, почему это происходит.
У детей образуются рече-слухо-двигательные связи между называемыми числительными. Ребенок называет ряд натуральных чисел подобно бессмысленной считалке и не может продолжить ряд чисел с середины, т.к. дети не понимают отношений между числами.
4-5 лет. Дети не всегда могут ответить на вопрос, какое число идет до этого, а какое после. Не могут назвать предыдущие числа. Для них ряд движется как бы вперед (понимают только последние числа). Такое представление о натуральном ряде называется «пространственным образом натурального ряда чисел». Чтобы найти число на единицу больше дети мысленно или вслух начинают называть слова-числительные от начала ряда. Таким образом, разностные отношения между предыдущими и последующими числами еще не усвоены.
5-6 лет. Эмпирические представления о натуральном ряде как пространственном образе перестраиваются в понятие о натуральном ряде чисел. Дети начинают осознавать основной принцип построения натурального ряда (п` = п + 1).
Системы счисления.
Систе́ма счисле́ния — символический метод записи чисел, представление чисел с помощью письменных знаков. Системы счисления подразделяются на позиционные и непозиционные.
В позиционных системах счисления один и тот же числовой знак (цифра) в записи числа имеет различные значения в зависимости от того места, где он расположен. Такая система счисления основывается на том, что некоторое число n единиц (основание системы счисления) объединяется в одну единицу второго разряда, n единиц второго разряда объединяются в одну единицу третьего разряда и т. д. Основанием системы счисления может быть любое число, большее единицы.
Изобретение позиционной нумерации, основанной на поместном значении цифр, приписывается шумерам ивавилонянам
; развита была такая нумерация индусами и имела неоценимые последствия в истории человеческой цивилизации.К числу таких систем относится современная десятичная система счисления (с основанием n = 10), возникновение которой связано со счётом на пальцах. В средневековой Европе она появилась через итальянских купцов, в свою очередь заимствовавших ее у мусульман. В вычислительной технике применялись и широко применяются системы счисления не только с основанием 2, 4, 8, 16, 32, 64, 256. Например, использовалась и троичная система счисления, цифры которой кодировались отсутствием электрического сигнала и положительным или отрицательным его уровнем. При записи больших чисел заслуживают внимания основания систем счисления 100, 1000, 10000, 1000000.
В непозиционных системах счисления величина, которую обозначает цифра, не зависит от положения в числе. При этом система может накладывать ограничения на положение цифр, например, чтобы они были расположены в порядке убывания.
К позиционным системам счисления относятся: десятичная (используется 10 знаков для записи чисел – 0, 1, 2, …, 8, 9), двоичная (используется 2 знака – 0, 1) и т.п.
Правила перевода чисел из одной системы счисления в другую.
А) Чтобы перевести число из любой позиционной системы счисления в десятичную, надо представить это число в стандартном виде (например,
в десятичной системе счисления, 2134 = 2∙103+1∙102+3∙101+4∙100,
в двоичной системе счисления, 11012 = 1∙23 + 1∙22 + 0∙21 +1∙20,
затем выполнить все действия: 11012 = 1∙23 + 1∙22 + 0∙21 +1∙20 =
= 8 + 4 + 0 + 1 = 13.
Полученный результат и будет искомой записью числа в десятичной системе счисления, т.е. 11012 = 13.
Б) Чтобы перевести число из десятичной системы счисления в любую позиционную, надо делить это число на основание системы до тех пор, пока делимое не станет меньше делителя. Затем надо записать все остатки снизу вверх (или справа налево).
Полученный результат и будет искомой записью числа, т.е. 13 = 11012.
Арифметические действия с многозначными числами в любой позиционной системе счисления выполняются также как и в десятичной, т.е. числа записываются в столбик разряд под разрядом. А для выполнения действий с однозначными числами составляются таблицы. Например, в двоичной системе счисления:
cyberpedia.su
17.История развития понятия числа и деятельности счета. Способы записи чисел, история их развития.
Счет – математическое понятие, это операция, имеющая целью установить, сколько элементов содержит данное конечное множество.
1,5-2 года. Дети сопровождают свои операции с множеством такими словами как «вот», «еще» или числительными в любом порядке. Каждое повторение ребенок соотносит с одним предметом и одним движением, тем самым он устанавливает взаимнооднозначное соответствие между количеством предметов и количеством слов, движений.
2-4 года. Появляется интерес к сравнению множеств путем установления взаимнооднозначного соответствия. Последовательное называние числительных еще не означает овладение процессом счета, т.к. ребенок не понимает итога счета, т.е. не умеет отвечать на вопрос «сколько?» Счет еще не служит средством определения количества. Чаще всего названное числительное служит сигналом к остановке называния числительных.
4-5 лет. Дети начинают употреблять числительные в определенном порядке и отличать итог счета от процесса счета. Начинают понимать, что равночисленные множества всегда именуются одним числом.
5-6 лет. Усваивают последовательность называния числительных, понимают, что количество не зависит от направления счета, что число является показателем количества, осознают отношения между числами, т.е. осваивают обратный счет.
6-7 лет. Овладевают счетом группами, т.е. понимают, что единицей счета может быть не только отдельный предмет, а целая группа.
7-8 лет. Овладевают счетом десятками и новой деятельностью – вычислением. Счет связан с конкретным множеством, с определением количества в определенном множестве, а вычисление – абстрактная операция, здесь участвую только числа (без называния предмета).
Развитие понятия числа
3-4 года. Дети используют слова-числительные, но не понимают, что такое число. На этом этапе дети способны лишь сравнивать различные множества путем установления взаимнооднозначного соответствия.
4-5 лет. Дети могут сравнивать числа на основе сравнения множеств, но не воспринимают число абстрактно, без множества.
5-6 лет. Способны сравнивать любые числа на основе свойства транзитивности. При измерении понимают число как результат измерения, т.е. как отношение всей величины (целого) к условной мерке (части). Понимают, что число служит лишь показателем количества. Происходит абстрагирование числа от конкретных м ножеств.
Развитие представлений о натуральном ряде чисел
Натуральный ряд – последовательность целых положительных чисел, расположенных в порядке их возрастания.
2-4 года. На основе речи взрослых дети начинают рано употреблять слова-числительные: сначала хаотично, затем упорядочено. Осознание порядка следования чисел происходит сразу в 2-х направлениях:
— увеличиваются последовательности чисел, которые дети запоминают,
— начинают осознавать, что каждое числительное всегда занимает свое определенное место, но на этом этапе не понимают, почему это происходит.
У детей образуются рече-слухо-двигательные связи между называемыми числительными. Ребенок называет ряд натуральных чисел подобно бессмысленной считалке и не может продолжить ряд чисел с середины, т.к. дети не понимают отношений между числами.
4-5 лет. Дети не всегда могут ответить на вопрос, какое число идет до этого, а какое после. Не могут назвать предыдущие числа. Для них ряд движется как бы вперед (понимают только последние числа). Такое представление о натуральном ряде называется «пространственным образом натурального ряда чисел». Чтобы найти число на единицу больше дети мысленно или вслух начинают называть слова-числительные от начала ряда. Таким образом, разностные отношения между предыдущими и последующими числами еще не усвоены.
5-6 лет. Эмпирические представления о натуральном ряде как пространственном образе перестраиваются в понятие о натуральном ряде чисел. Дети начинают осознавать основной принцип построения натурального ряда (п` = п + 1).
studfiles.net
Способы записи чисел — презентация, доклад, проект
Обратная связь
Если не удалось найти и скачать доклад-презентацию, Вы можете заказать её на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:
Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:
Email: [email protected]
Мы в социальных сетях
Социальные сети давно стали неотъемлемой частью нашей жизни. Мы узнаем из них новости, общаемся с друзьями, участвуем в интерактивных клубах по интересам
ВКонтакте >
Что такое Myslide.ru?
Myslide.ru — это сайт презентаций, докладов, проектов в формате PowerPoint. Мы помогаем учителям, школьникам, студентам, преподавателям хранить и обмениваться своими учебными материалами с другими пользователями.
Для правообладателей >
myslide.ru
Числа и системы счисленияМ
Способ записи чиселКАК ЛЮДИ НАУЧИЛИСЬ СЧИТАТЬ?
Сколько тебе лет? Сколько у тебя друзей? Сколько лап у кота? Чтобы все подсчитать, нужно знать цифры. А как считали древние люди, которые их не знали? Вот познакомьтесь.Давным-давно, многие тысячи лет назад, наши далекие предки жили небольшими племенами. Они бродили по полям и лесам, по долинам рек и ручьев, разыскивая себе пищу. Питались листьями, плодами и корнями — различных растений. Иногда ловили рыбу, собирали ракушки или охотились. Одевались в шкуры убитых зверей. Жизнь первобытных людей мало чем отличалась от жизни животных. Да и сами люди отличались от животных только тем, что владели речью и умели пользоваться простейшими орудиями труда: палкой, камнем или камнем, привязанным к палке.
Первобытные люди, так же как и современные маленькие дети, не знали счета. Но теперь детей учат считать родители и учителя, старшие братья и сестры, товарищи. А первобытным людям не у кого было учиться. Их учителем была сама жизнь. Поэтому и «обучение шло медленно.
Наблюдая окружающую природу, от которой полностью зависела его жизнь, наш далекий предок из множества различных предметов сначала научился выделять отдельные предметы. Из стаи волков — вожака стаи, из стада оленей — одного оленя, из выводка плавающих уток — одну птицу, из колоса с зернами — одно зерно.
Поначалу они определяли это соотношение как «один» и «много».
Частые наблюдения множеств, состоявших из пары предметов (глаза, уши, рога, крылья, руки), привели человека к представлению о числе. Наш далекий предок, рассказывая о том, что видел двух уток, сравнивал их с парой глаз. А если он видел их больше, то говорил: «Много». Лишь постепенно человек научился выделять три предмета, ну а затем четыре, пять, шесть и т. д.
Учиться считать требовала жизнь. Добывая пищу, людям приходилось охотиться на крупных зверей: лося, медведя, зубра. Охотились наши предки большими группами, иногда всем племенем. Чтобы охота была удачной, нужно было уметь окружить зверя. Обычно старший ставил двух охотников за берлогой медведя, четырех с рогатинами — против берлоги, трех — с одной стороны и трех — с другой стороны берлоги. Для этого он должен был уметь считать, а так как названий чисел тогда еще не было, он показывал число на пальцах.
И ноги кстати сказать, пальцы сыграли немалую роль в истории счета, особенно когда люди начали обмениваться друг с другом предметами своего труда. Так, например, желая обменять сделанное им копье с каменным наконечником на пять шкурок для одежды, человек клал на землю свою руку и показывал, что против каждого пальца его руки нужно положить шкурку. Одна пятерня означала 5, две- 10. Когда рук не хватало, в ход шли и ноги. Две руки и одна нога — 15, две руки и две ноги — 20.
Следы счета на пальцах сохранились во многих странах. Так, в Китае и Японии предметы домашнего обихода (чашки, тарелки и др.) считают не дюжинами и полудюжинами, а пятерками и десятками. Во Франции и в Англии и поныне в ходу счет двадцатками.
Специальные названия чисел имелись — поначалу только для одного и двух. Числа же больше двух называли с помощью сложения: 3 — это два и один, 4 — это два да два, 5 — это два, еще два и один.
Названия чисел — у многих народов указывают на ; их происхождение.
Так, у индейцев два — глаза, у тибетцев — крылья, у других народов один — луна, пять — рука и т. д. У тех народов, которые еще сохранили первобытный уклад жизни, такие названия чисел используются до сих пор. Например, у одного из австралийских племен счет ведется так: 1 — энэа, 2 — петчевал, 3 — петчевал-энэа, 4 — петчевал-петчевал. А в другом племени считали так: 1 — мал, 2 — булан, 3 — гулиба, 4 — булан-булан, 5 — булан-гулиба, 6 — гулиба-гулиба. А на берегах реки Амазонки было обнаружено племя, которое знало только три числа- 1, 2 и 3, причем число 3 называлось «поэттаррароринкоароак». Вот как трудно было людям научиться считать!
КАК ЛЮДИ НАУЧИЛИСЬ ЗАПИСЫВАТЬ ЦИФРЫ?
В разных странах и в разные времена это делалось по-разному. Когда люди не умели еще делать бумагу, записи появлялись в виде зарубок на палках и костях животных, в виде отложенных ракушек или камешков или в виде узелков, завязанных на ремне или веревке.…Вглядись внимательно в рисунок. Какой-то человек воздел обе руки кверху. Ему было чему удивляться. Ведь он обозначал целый миллион. И это не шутка. Рисовали такого человечка древние египтяне, когда хотели изобразить миллион. Человечек исполнял обязанности числа.
Сейчас нам, привыкшим к начертанию цифр, даже не верится, что была какая-то другая система записи чисел.
Очень разные и порою даже забавные были эти «цифры» у разных народов.
В Древнем Египте числа первого десятка записывали соответствующим количеством палочек. А «десять» обозначалось скобочкой в виде подковы. Чтобы написать 15, надо было ставить 5 палочек и 1 подкову. И так до сотни. Для сотни придуман был крючок, для тысячи — значок вроде цветка. Десять тысяч обозначали рисунком пальца, сто тысяч — лягушкой, а миллион — знакомой нам фигуркой с поднятыми руками.
Не очень-то удобно было записывать таким способом большие числа и совсем неудобно было их складывать, вычитать, умножать, делить. Очень большая возня была с этими значками-иероглифами!
Гораздо лучше придумали запись чисел в древнем Вавилоне. Она очень похожа на современную, только мы считаем десятками, сотнями, тысячами и так далее, а жители древнего Вавилона объединяли единицы по 60, по 3600 (60×60=3600), а если надо, по 60x60x60=216000 и так далее. Писали в древнем Вавилоне на мягких глиняных табличках острыми палочками, а потом таблички обжигали, и они становились твердыми и прочными. При раскопках были найдены целые библиотеки и архивы из таких табличек.
Палочкой на глине трудно изображать сложные фигуры, поэтому вавилонская письменность состояла, в основном, из различных комбинаций клинышков (ее так и называют — клинопись). Единицы изображались узкими вертикальными клинышками, а десятки — широкими горизонтальными, все числа до 60 «собирали» из таких клинышков. Когда надо было записать число, большее, чем 60, то открывали следующий разряд —в него писали, сколько раз число 60 помещается в записываемом числе, а то, что оставалось (то есть остаток от деления на 60), записывали, как и раньше, в первый разряд. Между разрядами оставляли пробелы, чтобы цифры из разных разрядов не смешивались.
Такая запись чисел удобна тем, что если мы умеем умножать и складывать числа первого разряда, то очень легко научиться выполнять эти действия и с любыми числами — эти вычисления можно проводить «в столбик», как вас учат в школе.
Правда, вавилонская система была все-таки очень громоздкой из-за того, что 60 — довольно большое число, поэтому она больше нигде не использовалась. А вот система нумерации и вычислений, которая сложилась в Индии примерно к VI веку нашей эры, оказалась такой удобной и удачной, что ею сейчас пользуются во всем мире. Европейцы познакомились с ней в X — XIII веках через арабов, которые первыми оценили достоинства этого способа записи чисел, усвоили и перенесли в Европу, поэтому новые цифры в Европе стали называть арабскими. Произошло это еще и потому, что простейший счетный прибор, работающий в десятичной системе счисления, был всегда у человека под рукой — это его 10 пальцев.
Способ записи чисел называют нумерацией или счислением
Вначале индийских цифр было всего 9:1,2,3, 4, 5, 6, 7, 8 и 9. Цифра 0 появилась заметно позже, — скорее всего, около 500 года нашей эры. А поначалу, если оказывалось, что в каком-то разряде нет единиц, то между соседними разрядами оставляли пробел. Например, число 209 писали так: 2 9. Понятно, что при подсчете таких пробелов очень легко ошибиться. Чтобы избавиться от этих неприятностей, сначала вместо пустого разряда стали ставить точку, а потом — маленький кружочек, который постепенно превратился в цифру 0.Вот, оказывается, какая длинная история у этих знакомых значков!
Значительно позднее цифры стали изображать иначе. Вот посмотрите римскую нумерацию: I — один, II — два, III — три. На руке человека пять пальцев. Чтобы не писать пять палочек, стали изображать руку. Однако рисунок руки делали очень простым. Вместо того чтобы рисовать всю руку, ее изображали знаком V, и этот значок стал обозначать цифру 5. Потом к пяти прибавляли один и получали шесть. Вот так: шесть — VI, семь — VII. А сколько записано здесь: VIII? Правильно, восемь. Ну а как короче записать четыре? Четыре палочки долго пересчитывать, поэтому от пяти отнимали один и записывали так: IV — это пять без одного.
А как записать десять?
Вы знаете, что десять состоит из двух пятерок, поэтому в римской нумерации цифру «десять» изображали двумя пятерками: одна пятерка стоит как обычно, а другая перевернута вниз — X. Иначе десять можно записать двумя пересекающимися палочками. Если рядом с X написать одну палочку справа — XI, то будет одиннадцать, а если слева — IX — девять.
Запомните особенность римской записи: меньшая цифра, стоящая справа от большей, прибавляется к ней, стоящая слева — отнимается. Поэтому знак VI означает 5+1, то есть 6, а знак IV -5-1, то есть 4. Научиться читать числа, записанные в римской нумерации, нетрудно, и мы советуем это сделать обязательно. Позднее появились значки и для обозначения других чисел. Так 100 стали обозначать буквой С (первая буква соответствующего латинского слова — centum), число 1000 — буквой М (mille — тысяча), число 500 — буквой D, буквой L — число 50.
Когда возникла письменность, многие народы начали для обозначения чисел использовать алфавит.
Посмотрите, как обозначали числа древние греки и славяне.
Для того, чтобы отличать числа от слов, над буквами, изображающими числа, ставили специальный значок: греки — просто черточку, а славяне — волну, которая называлась «титло».
В славянской нумерации титло ставили только над одной буквой числа, а порядок цифр в записи числа был такой же, как в его названии. Например, в названии числа 15 (у славян — «пятьнадесять») сначала идет число единиц, а потом — десятков. Значение цифры не зависело от того места, которое она занимала в записи числа. Когда хотели записать числа, большие, чем 1000, перед цифрой ставили символ — наклонную перечеркнутую черту, при этом значение цифры умножалось на 1000. Два таких символа, записанных подряд, умножали значение цифры на миллион (греки в таких случаях ставили штрихи перед цифрами, обозначающими число единиц).
Для очень больших чисел использовались специальные названия. Например, поначалу число 10000 называли словом «тьма». Это же слово обозначало бесконечность {то, что нельзя пересчитать). По-гречески же число 10000 называлось «мириа», а словом «мириада», обозначали огромные, не поддающиеся счету количества. В таком значении это слово до сих пор используется в русском языке, например, когда хотят сказать, как много листьев в лесу, говорят «мириады листьев».
Позже число 10000 стали называть так же, как и мы сейчас — «десять тысяч», а словом «тьма» стали называть уже тысячу тысяч, то есть миллион. Число «тьма тем», то есть миллион миллионов, называлось «легион», число «легион легионов» называли «леодр», а «леодр леодров» называли «вороном».
В одной рукописи еще упоминалось число, которое называли «колода». Это число равно десяти воронам, и автор говорит, что «сего числа несть больше». Но вы-то уже знаете, что к любому, сколь угодно большому числу, можно прибавить единицу и получить еще большее число. Не надо думать, что наши предки были глупее нас с вами, просто этот пример показывает, как медленно и трудно люди накапливали те знания, которые мы получили от предыдущих поколений.
В старину на Руси среди простого народа широко применялись системы счисления, отдаленно напоминающие римскую. С их помощью сборщики податей заполняли квитанции об уплате подати (ясака) и делали записи в податной тетради. Вот перед вами текст закона об этих называемых ясачных знаках:
Яндекс.Реклама
sch69.narod.ru
Способы записи чисел
Published on
15-Jan-2016View
61Download
0
DESCRIPTION
78787878. IIIIIIIIIIII. . 5. LXXII. I. . I — 1. II — 2. III — 3. IIIIIIIII — 9. IIIIIIIIIIIIIII — 15. . I — 1. V — 5. X — 10. L — 50. C — 100. D — 500. M — 1000. II. III. IV. IX. VI. VIII. XIV. XI. — PowerPoint PPT Presentation
Transcript
IIIIIIIIIIIII — 1 IIIIIVIVIII XI XV XVI IVXIVIXXIX II — 2 III — 3 IIIIIIIII — 9 IIIIIIIIIIIIIII — 15 I — 1 V — 5 X — 10 L — 50 C — 100D — 500M — 1000 I — 1, V — 5, X — 10, L — 50, C — 100, D — 500, M — 1000 XXI LXVIII LXXIX DCXIV MMCCLXXI =LXVIII =LXXIX =DCXIV = MMCCL =10 + 10 + 1 = 2150 + 10 + 8 = 6850 + 10 + 10 + 9 = 79500 + 100 + 10 + 4 = 614 1000 + 1000 +100 + 100 + 50 = 2250 , , ?111222333444 555CXI CCXXIICCCXXXIIICDXLIVDLVI — 1, V — 5, X — 10, L — 50, C — 100, D — 500, M — 1000 555 = 500 + 50 + 5 = 5 100 + 5 10 + 5 , . , . , .c 200 004 085954 003 057 000 000831 000 820 00063 900 000 000 000 : a 1 4 7 12 20a + 6 6a : a 1 4 7 12 20a + 6 6a7101318266244272120 :34732110 97610 9847 2947 3011 298 542298 54362 457 99962 458 000 :347321>10 97610 98410010079 000 101007 60063 000 100 , .100100:79 000 :101007 600:63 000: 100 , .15 — 5 =10= 18 — 6 = 1215 : 5 =3x : y= 18 : 6 = 315 + 5 =20x + yx + y= 18 + 6 = 2415 2 =30= 2 18 = 365 3 =15= 3 6 = 1815 2 + 5 3 =45= 2 18 + 3 6 = 5415 2 5 3 =15= 2 18 — 3 6 = 18(15 2) : (5 3) =2= (2 18):(3 6) = 2 x= 18, y = 6x . 1 y . 1 15 . 5 . :1) a b;2) 38 m p; 3) 45 k;4) 8 n d. :1) a b;2a + b2) 38 m p; 38 : (m n)3) 45 k;45 3k4) 8 n d.8 (n + d) , , (. ). : ;2) , ;3) 3 ;4) ;5) , 3 , . , , (. ). : ;2) , ;3) 3 ;4) ;5) , 3 , . 1) + ;2) + ;3) 3 ( + ) ;4) ;5) 3 ( ). 1 1 1
docslide.net