Спираль архимеда в декартовых координатах – Как построить параметризированную геометрию спирали Архимеда

Содержание

Как построить параметризированную геометрию спирали Архимеда

Спирали Архимеда широко используются при построении геометрий для катушек индуктивности, спиральных теплообменников и микрогидродинамических устройств. В этой заметке мы покажем, как построить спираль Архимеда, используя аналитические выражения и их производные для задания необходимых кривых. Сначала мы создадим двухмерную геометрию, а затем, задав нужную толщину, преобразуем её в трёхмерную с помощью операции Extrude (Вытягивание).

Что такое спираль Архимеда?

Широко распространённые в природе спирали или завитки используются во многих инженерных конструкциях. Например, в электротехнике и электронике с помощью проводников спиралевидной формы наматывают катушки индуктивности или проектируют геликоидные антенны. В машиностроении спирали используются при проектировании пружин, косозубых цилиндрических передач или даже механизмов часов, один из которых изображён ниже.

Пример спирали Архимеда, которая используется в часовом механизме. Изображение представлено Greubel Forsey. Доступно по лицензии CC BY-SA 3.0 из Wikimedia Commons.

В данной статье мы разберём только один вид спирали, а именно, спираль Архимеда, которая изображена в механизме выше. Спираль Архимеда – это особый вид спирали с постоянным расстоянием между витками. Благодаря этому свойству она широко распространена при проектировании катушек и пружин.

Уравнение спирали Архимеда в полярной системе координат записывается, как:

r=a+b\theta

где a и b — параметры, определяющие начальный радиус спирали и расстояние между витками, которое равно 2 \pi b. Обратите внимание, что спираль Архимеда также иногда называют арифметической спиралью. Это имя связывают с арифметической зависимостью расстояния от начала кривой до точек спирали, находящихся на одной радиальной линии.

Задание параметризированной геометрии спирали Архимеда

Теперь, когда вы уже знаете, что такое спираль Архимеда, давайте приступим к параметризации и созданию геометрии в COMSOL Multiphysics.

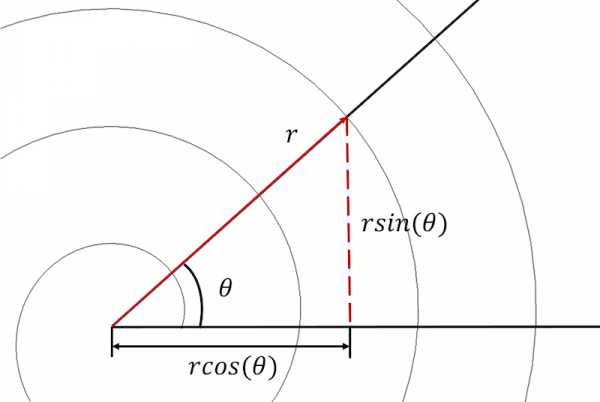
Спираль Архимеда может быть задана как в полярных, так и в декартовых координатах.

Для начала необходимо преобразовать уравнение спирали из полярной системы координат в декартову и выразить каждое уравнение в параметрической форме:

\begin{align*} x_{component}=rcos(\theta) \\ y_{component}=rsin(\theta) \end{align*}

После преобразования уравнения спирали в параметрической форме в декартовой системе координат примут вид:

\begin{align*} x_{component}=(a+b\theta)cos(\theta) \\ y_{component}=(a+b\theta)sin(\theta) \end{align*}

В COMSOL Multiphysics необходимо определить набор параметров, с помощью которых будем задавать геометрию спирали. В нашем случае — это начальный и конечный радиусы спирали a_{initial} и a_{final}, соответственно, и количество витков n. Показатель роста спирали b находится, как:

b=\frac{a_{final}-a_{initial}}{2 \pi n}

Также необходимо определить начальный и конечный углы спирали — theta_0 и theta_f, соответственно. Давайте с них и начнём — theta_0=0 и theta_f=2 \pi n. Исходя из заданной информации, определяем параметры для построения геометрии спирали.

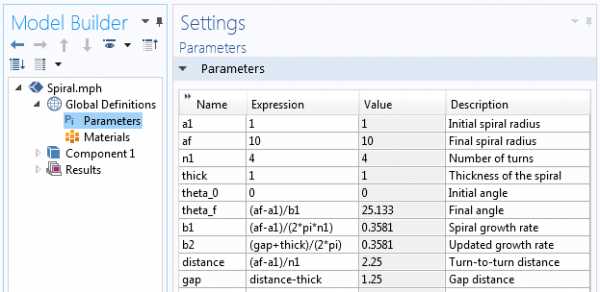
Параметры, которые используются для построения геометрии спирали.

Начнём наше построение, выбрав трёхмерную задачу (3D Component) и создадим Work Plane (Рабочую плоскость) в разделе Geometry (Геометрия). В геометрии для Work Plane добавляем Parametric Curve (Параметрическую кривую) и записываем параметрические уравнения, описанные выше, чтобы задать двухмерную геометрию спирали Архимеда. Данные уравнения можно сразу вписать в соответствующие поля во вкладке Expression либо сначала можно задать каждое уравнение отдельной

Аналитической функцией (Analytic function):

\begin{align*} X_{fun}=(a+bs)cos(s) \\ Y_{fun}=(a+bs)sin(s) \\ \end{align*}

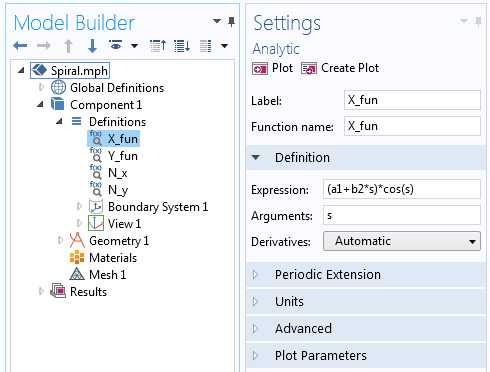
Выражение для X-компоненты уравнения спирали Архимеда, заданное аналитической функцией.

Аналитическая функция затем может использоваться в качестве выражения в узле Parametric Curve. Во вкладке Parameter задаём параметр s от начального угла, theta_0, до его конечного значения, theta_f=2 \pi n.

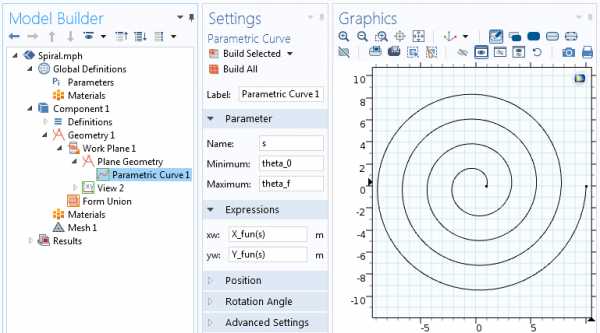
Настройки для Parametric Curve (Параметрической кривой).

Как только вы зададите все параметры и нажмёте на кнопку «Build Selected», будет построена кривая, изображённая на скриншоте выше. Теперь давайте зададим толщину спирали, чтобы получить твёрдотельную (solid) двухмерную фигуру.

До этого момента параметрами нашей кривой были начальный (a_{initial}) и конечный (a_{final}) радиусы и количество витков n. Теперь мы хотим добавить ещё один – толщину спирали.

Ещё раз напомним главное свойство спирали — расстояние между витками постоянно и равно 2 \pi b. Что эквивалентно \frac{a_{final}-a_{initial}}{n}. Чтобы добавить толщину в наши уравнения, представляем расстояние между витками суммой толщины спирали и зазора thick+gap.

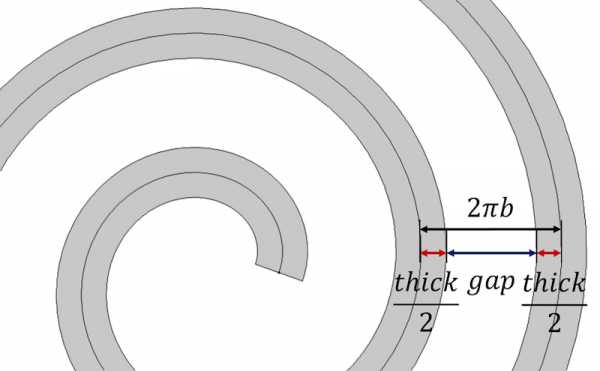
Расстояние между витками определяется толщиной спирали и величиной зазора.

Чтобы ввести параметр толщины и сохранить постоянное расстояние между витками, последнее перепишем, как:

\begin{align*} distance=\frac{a_{initial}-a_{final}}{n} \\ gap=distance-thick \end{align*}

После этого выражаем показатель роста спирали через толщину:

\begin{align*} distance=2\pi b \\ b=\frac{gap+thick}{2\pi} \end{align*}

Также нужно выразить конечный угол спирали через начальный угол и конечный радиус:

\begin{align*} \theta_{final}=2 \pi n \\ a_{final}=\text{total distance}+a_{initial} \\ a_{final}=2 \pi bn+a_{initial} \\ n=\frac{a_{final}-a_{initial}}{2 \pi b} \\ \theta_{final}=\frac{2 \pi (a_{final}-a_{initial})}{2 \pi b} \\ \theta_{final}=\frac{a_{final}-a_{initial}}{b} \end{align*}

Хотите задать отличный от нуля начальный угол спирали? Если так, то его надо будет добавить в выражение для определения конечного угла: theta_f=\frac{a_{final}-a_{initial}}{b}+theta_0.

Дублирование кривой спирали дважды со смещением на -\frac{thick}{2} и +\frac{thick}{2} по отношению к начальной кривой позволяет построить спираль заданной толщины. Чтобы правильно расположить внутреннюю и внешнюю спирали, необходимо убедиться, что начала данных кривых перпендикулярны линии, на которой расположены их начальные точки. Это можно сделать, домножив расстояние смещения \pm\frac{thick}{2} на единичный вектор, расположенный по нормали к начальной кривой спирали. Уравнения векторов нормали в параметрическом виде:

n_x=-\frac{dy}{ds} \quad \text{and} \quad n_y=\frac{dx}{ds}

где s — это параметр, используемый в узле Parametric Curve. Чтобы получить нормированные единичные вектора, необходимо эти выражения разделить на длину нормали:

\sqrt{(dx/ds)^2+(dy/ds)^2 }

Обновленные параметрические уравнения спирали Архимеда со смещением:

\begin{align*} x_{component}=(a+bs)cos(s)-\frac{dy/ds}{\sqrt{(dx/ds)^2+(dy/ds)^2}}\frac{thick}{2} \\ y_{component}=(a+bs)sin(s)+\frac{dx/ds}{\sqrt{(dx/ds)^2+(dy/ds)^2}}\frac{thick}{2} \end{align*}

Записывать такие длинные выражения довольно неудобно, поэтому введём следующие обозначения:

www.comsol.ru

Архимедова спираль | Математика, которая мне нравится

История спирали Архимеда

Архимедова спираль была открыта (правильно, Вы угадали!) Архимедом. Это произошло в III веке до н.э., когда он экспериментировал с компасом. Он тянул стрелку компаса с постоянной скоростью, вращая сам компас по часовой стрелке. Получившаяся кривая была спиралью, которая сдвигались на ту же величину, на которую поворачивался компас, и между витками спирали сохранялось одно и то же расстояние.

Использование архимедовой спирали в древности

Архимедову спираль использовали как наилучший способ определения площади круга. С ее помощью был улучшен древний греческий метод нахождения площади круга через измерение длины окружности. Спираль дала возможность более точного измерения длины окружности, а следовательно, и площади круга. Однако вскоре, когда Архимед попытался вычислить более точно значение , которое упрощало нахождение площади круга, было доказано, что спираль для этого не подходит.

Что такое обобщенная Архимедова спираль?

Обобщенная Архимедова спираль определяется как кривая, которая задается в полярных координатах уравнением (далее положим ). Спираль Архимеда, в частности, принадлежит множеству обобщенных Архимедовых спиралей.

Название спирали	Значение
Спираль Архимеда	1
Гиперболическая спираль	-1
Спираль Ферма	2
Литуус (lituus)	-2

Lituus – загнутый авгурский посох, жезл.

Общий вид в полярных координатах:

Спираль Архимеда:

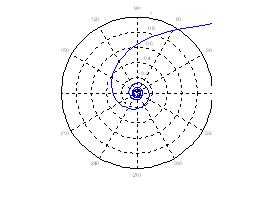
Гиперболическая спираль:

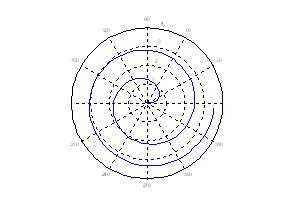
Спираль Ферма:

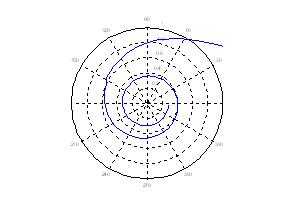
Литуус:

Параметризация спирали Архимеда

Начнем с уравнения спирали .

Воспользуемся теоремой Пифагора

– радиус окружности).

Также нам понадобятся формулы

Возведем уравнение спирали в квадрат:

Теперь аналогично выразим :

Вид параметризованной спирали:

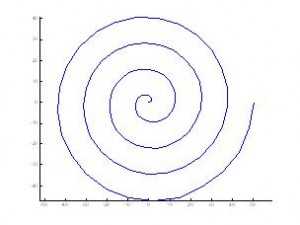
Спирали в реальной жизни

В технике нашли широкое применение плоские спиральные антенны, в том числе и антенны, имеющие вид Архимедовой спирали (http://library.tuit.uz/lectures/afu/anten_fider_ustr/lecture_11.htm):

http://online.redwoods.cc.ca.us/instruct/darnold/calcproj/sp06/leviowen/HistoryOfArchimedes.doc

hijos.ru

Уравнение кривых в полярных координатах

Благодаря радиальной природе полярной системы координат, некоторые кривые могут быть достаточно просто описаны полярным уравнением, тогда как уравнение в прямоугольной системе координат были бы намного сложнее. Среди самых известных кривых: полярная роза, архимедова спираль, Лемниската, улитка Паскаля и кардиоида.

Окружность

Круг, заданный уравнением .

Общее уравнение окружности с центром в () и радиусом имеет вид:

Это уравнение может быть упрощено для частных случаев, например

является уравнением, определяющим окружность с центром в полюсе и радиусом .^[15]

Прямая

Радиальные прямые (те, которые проходят через полюс) определяются уравнением

где — угол, на который прямая отклоняется от полярной оси, то есть, где — наклон прямой в прямоугольной системе координат. Нерадиальная прямая, перпендикулярно пересекает радиальную прямую в точке определяется уравнением

Полярная роза

Полярная роза задана уравнением .

Полярная роза — известная математическая кривая, похожая на цветок с лепестками. Она может быть определена простым уравнением в полярных координатах:

для произвольной постоянной (включая 0). Если — целое число, то это уравнение будет определять розу с лепестками для нечётных , либо с лепестками для чётных . Если — рациональное, но не целое, график, заданный уравнением, образует фигуру, подобную розе, но лепестки будут перекрываться. Розы с 2, 6, 10, 14 и т. д. лепестками этим уравнением определить невозможно. Переменная определяет длину лепестков.

Если считать, что радиус не может быть отрицательным, то при любом натуральном мы будем иметь — лепестковую розу. Таким образом, уравнение будет определять розу с двумя лепестками. С геометрической точки зрения радиус — это расстояние от полюса до точки и он не может быть отрицательным.

Спираль Архимеда

Одна из ветвей спирали Архимеда, задаваемая уравнением для .

Архимедова спираль названа в честь её изобретателя, древнегреческого математика Архимеда. Эту спираль можно определить с помощью простого полярного уравнения:

Изменения параметра приводят к повороту спирали, а параметра — расстояния между витками, которое является константой для конкретной спирали. Спираль Архимеда имеет две ветви, одну для а другую для . Две ветви плавно соединяются в полюсе. Зеркальное отображение одной ветви относительно прямой, проходящей через угол 90°/270°, даст другую ветвь. Эта кривая интересна тем, что была описана в математической литературе одной из первых, после конического сечения, и лучше других определяется именно полярным уравнением.

Конические сечения

Эллипс.

Коническое сечение, один из полюсов которого находится в полюсе, а другой где-то на полярной оси (так, что малая полуось лежит вдоль полярной оси) задаётся уравнением:

где — эксцентриситет, а — фокальный параметр. Если , это уравнение определяет гиперболу; если , то параболу; если , то эллипс. Отдельным случаем является , определяющее окружность с радиусом .

86. Вычисление определенного интеграла. Применение его к вычислению площадей плоских фигур, длины дуги кривой.

Вычисление площадей и длин дуг кривых в декартовых координатах

Пусть на плоскости x0y задана область, ограниченная снизу кривой y=f₁(x) , заданной в декартовых координатах, сверху – кривой y=f₂(x) , слева – прямой x=a (ее может и не быть, если f₁(a)=f₂(a) ), справа – прямой x=b.

Исходя из геометрического смысла определенного интеграла, площадь этой области можно вычислить по формуле

Здесь не нужно заботиться, какая из функций и где положительная, а какая отрицательная. Если, например, f₁(x)<0, то формула сама прибавит нужную площадь. Более сложные области всегда можно разбить так, чтобы выполнялись указанные условия.

Пусть на отрезке [a,b] уравнением y=f(x) задана плоская кривая. Ее длина вычисляется по формуле

Пример 1 :: Вычисление площадей и длин дуг в декартовых координатах

Вычислим площадь области, ограниченной кривыми и длину границы этой области.

Вычисление площадей и длин дуг при параметрическом задании кривых

Если область на плоскости снизу ограничена кривой, заданной параметрически, то есть

при этом x₁()=b, x₁()=b, а сверху – кривой

Тогда площадь такой плоской фигуры вычисляем по формуле

Эта формула совпадает с формулой вычисления площади в декартовых координатах, если учесть, что x'(t)dt=dx.

Пусть кривая на плоскости задана параметрически

Тогда длина этой кривой вычисляется по формуле

Пример 2 :: Вычисление площадей и длин дуг при параметрическом задании кривых.

Вычислим площадь фигуры, ограниченной кривыми , , . Вычислим длину дуги циклоиды , .

Вычисление площадей и длин дуг кривых в полярных координатах

Когда кривая, ограничивающая область, задана в полярных координатах =(), то площадь этой области вычисляем по формуле

Основная трудность в использовании этой формулы заключается в определении пределов интегрирования  ,  . Здесь нужно понимать, что кривая =() определена только, если  >0. Поскольку в формуле присутствует ² , то она учтет и не существующую площадь, когда . Решив уравнение ()=0 , найдем пределы интегрирования.

Если кривая, ограничивающая область, задана в полярных координатах =(), то ее длина вычисляется по формуле

Пределы интегрирования определяются из тех же соображений, что и при вычислении площади.

studfiles.net

Связь между декартовыми и полярными координатами

⇐ ПредыдущаяСтр 3 из 3

Пару полярных координат r и можно перевести в Декартовы координаты x и y путём применения тригонометрических функций синуса и косинуса:

x = rcos φ,

y = rsin φ,

в то время как две декартовы координаты x и y могут быть переведены в полярную координату r:

r² = y² + x² (по теореме Пифагора).

Для определения угловой координаты следует принять во внимание два следующие соображения:

Для вычисления в интервале , можно воспользоваться такими уравнениями (arctg обозначает обратную функцию к тангенсу):

Для вычисления в интервале , можно воспользоваться такими уравнениями:^[14]

Учитывая, что для вычисления полярного угла не достаточно знать отношение y к x, а ещё нужны знаки одного из этих чисел, многие из современных языков программирования имеют среди своих функций помимо функции atan, определяющей арктангенс числа, ещё и дополнительную функцию atan2, которая имеет отдельные аргументы для числителя и знаменателя. В языках программирования, поддерживающих необязательные аргументы (например, в Common Lisp), функция atan может получать значение координаты

Уравнение кривых в полярных координатах

Окружность

Круг, заданный уравнением .

Общее уравнение окружности с центром в ( ) и радиусом a имеет вид:

Это уравнение может быть упрощено для частных случаев, например

r(φ) = a

является уравнением, определяющим окружность с центром в полюсе и радиусом a.^[15]

Прямая

Радиальные прямые (те, которые проходят через полюс) определяются уравнением

φ = θ,

где θ — угол, на который прямая отклоняется от полярной оси, то есть, где m — наклон прямой в прямоугольной системе координат. Нерадиальная прямая, перпендикулярно пересекает радиальную прямую φ = θ в точке определяется уравнением

r(φ) = r₀sec(φ − θ).

Полярная роза

Полярная роза задана уравнением .

r(φ) = acos(kφ + θ₀)

для произвольной постоянной θ₀ (включая 0). Если k — целое число, то это уравнение будет определять розу с k лепестками для нечётных k, либо с 2k лепестками для чётных k. Если k — рациональное, но не целое, график, заданный уравнением, образует фигуру, подобную розе, но лепестки будут перекрываться. Розы с 2, 6, 10, 14 и т. д. лепестками этим уравнением определить невозможно. Переменная a определяет длину лепестков.

Если считать, что радиус не может быть отрицательным, то при любом натуральном k мы будем иметь k — лепестковую розу. Таким образом, уравнение r(φ) = cos(2φ) будет определять розу с двумя лепестками. С геометрической точки зрения радиус — это расстояние от полюса до точки и он не может быть отрицательным.

Спираль Архимеда

Одна из ветвей спирали Архимеда, задаваемая уравнением для .

r(φ) = a + bφ.

Изменения параметра a приводят к повороту спирали, а параметра b — расстояния между витками, которое является константой для конкретной спирали. Спираль Архимеда имеет две ветви, одну для φ > 0 а другую для φ < 0. Две ветви плавно соединяются в полюсе. Зеркальное отображение одной ветви относительно прямой, проходящей через угол 90°/270°, даст другую ветвь. Эта кривая интересна тем, что была описана в математической литературе одной из первых, после конического сечения, и лучше других определяется именно полярным уравнением.

[править] Конические сечения

Эллипс.

где e — эксцентриситет, а — фокальный параметр. Если e > 1, это уравнение определяет гиперболу; если e = 1, то параболу; если e < 1, то эллипс. Отдельным случаем является e = 0, определяющее окружность с радиусом .

Комплексные числа

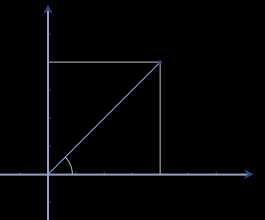
Пример комплексного числа , нанесённого на комплексную плоскость.

Пример комплексного числа, нанесённого на график, с использованием формулы Эйлера.

Каждое комплексное число может быть представлено точкой на комплексной плоскости, и, соответственно, эта точка может определяться в декартовых координатах (прямоугольная или декартова форма), либо в полярных координатах (полярная форма). Комплексное число z может быть записано в прямоугольной форме так:

z = x + iy,

где i — мнимая единица, или в полярной (см. формулы преобразования между системами координат выше):

и отсюда:

z = reⁱ^φ,

где e — число Эйлера. Благодаря формуле Эйлера, оба представления эквивалентны^[16] (Следует отметить, что в этой формуле, подобно остальным формулам, содержащим возведения в степень углов, угол задан в радианах)

Для перехода между прямоугольным и полярным представлением комплексных чисел, могут использоваться указанные выше формулы преобразования между системами координат.

Операции умножения, деления и возведения в степень с комплексными числами, как правило, проще проводить в полярной форме. Согласно правилам возведения в степень:

Возведение в степень (формула Муавра):

(reⁱ^φ)ⁿ = rⁿeⁱⁿ^φ.

Векторный анализ

Для полярных координат можно применить элементы векторного анализа. Любое векторное поле можно записать в полярной системе координат, используя единичные векторы:

в направлении , и

Связь между декартовыми компонентами поля F_x и F_y и его компонентами в полярной системе координат задаётся уравнениями:

F_x = F_rcos φ − F_φsin φ;

F_y = F_rsin φ + F_φcos φ.

arhivinfo.ru

Связь между декартовыми координатами и полярными

Часто можно легко выписать формулу, показывающую, как изменятся координаты точки М, если от одной системы координат перейти к другой. Выведем формулы связи между декартовыми координатами (x,y) и полярными r и φ.

Пусть даны: декартова система координат и полярная с полюсом в начале координат и полярной осью, совпадающей с осью X (рис. 7а), x и y – декартовы координаты точки, r и φ – ее полярные координаты. Из треугольника, образованного точками О, М и х, видно, что зависимость между полярными координатами r и φ точки М и ее прямоугольными координатами x и y выражается формулами, известными из тригонометрии:

y=rsinj, x=rcosj — вычисление декартовых координат по полярным

— вычисление полярных координат по декартовым (одной формулы для определения угла недостаточно).

То есть, зная декартовы координаты точки, мы можем определить ее полярные координаты. И наоборот. Зная ее полярные координаты, можно определить декартовы координаты.

Пример

Чему равны полярные координаты точки М, имеющей декартовы координаты один и минус один?

Подставив значения декартовых координат в формулы, которые задают выражение полярных координат через декартовы, получаем, что:

Так как точка М находится в четвертой четверти, то j=315° (рис. 7б)

Линии и их уравнения

Итак, при наличии системы координат каждой точке плоскости соответствует пара действительных чисел и, наоборот, каждой паре чисел соответствует определенная точка плоскости. Можно установить, что линиям на плоскости соответствует некоторое уравнение с двумя переменными x и y в декартовой системе координат и переменными r и j в полярной. Связь между уравнениями и линиями позволяет свести изучение геометрических свойств линий к исследованию аналитических свойств соответствующих им уравнений. Линии на плоскости соответствует некоторое уравнение с двумя переменными, которому удовлетворяют координаты любой точки, лежащей на линии, и не удовлетворяют координаты ни одной точки, не лежащей на ней. Такое уравнение называют уравнением данной линии. Входящие в него координаты x и y (или r и j) произвольной точки линии называются текущими координатами.

Уравнение линии на плоскости может быть аналитически задано в явном виде — y=f(x), r=f(j) или неявном виде — F(x,y)=0, F(r,j)=0. Полярную систему координат удобно использовать, когда длина радиуса-вектора точек, лежащих на линии, связана аналитической зависимостью со значением угла поворота j.

Примеры уравнений линий в декартовой и полярной системе координат

1.Уравнение прямой, отсекающей на оси Y отрезок величины b: y=kx+b, где k — значение tg угла наклона прямой к оси ОХ; параметр k называется угловым коэффициентом прямой. Уравнение линии задано в явном виде (рис. 8).

2.Уравнение линии, являющейся геометрическим местом точек, для которых расстояние до некоторой точки О с координатами а и b есть величина постоянная (обозначим ее через R). Выпишем условие равенства константе R расстояния от любой точки М(x,y) до точки O(a,b): . Возведя обе части равенства в квадрат, получаем каноническое уравнение окружности:

(x-a)²+(y-b)²=R²

Если система координат выбрана так, что центр окружности совпадает с началом координат, то a=0, b=0 и уравнение окружности принимает вид:

x²+y²=R²

Уравнение линии в этих примерах задано в неявном виде.

3.Уравнение окружности в полярной системе координат.

Введем полярную систему координат, центр которой совпадает с центром окружности, а направление полярной оси, например, горизонтальное. Окружность определяется, как геометрическое место точек, для которых расстояние до некоторой точки О есть величина постоянная (эту величину мы обозначали через R). Следовательно, уравнение окружности в полярных координатах: r=R

Окружность дает простейший пример линии, уравнение которой от перехода к полярной системе координат упрощается.

На рисунке 9 приведена окружность и ее уравнение в разных системах координат. Одновременно мы показали на этом простом примере, что вид линии не зависит от того, в какой системе координат написано ее уравнение. От выбора системы координат зависит лишь вид уравнения.

Рассмотрим примеры еще 2 кривых, длина радиуса-вектора которых связана аналитической зависимостью со значением его угла поворота j. Уравнения этих кривых удобно задавать именно в полярной системе координат.

Уравнение спирали Архимеда

Пусть по лучу, вращающемуся около полюса О с постоянной угловой скоростью w, движется точка М с постоянной скоростью v. Тогда точка М опишет линию, которая называется спиралью Архимеда. Для того чтобы вывести уравнение этой линии, введем полярную систему координат, центр которой совпадает с точкой О, тогда расстояние от точки М до полюса О r=ОМ пропорционально углу j (рис 10а). Это означает, что уравнение спирали Архимеда можно записать в виде:

r=kj.

В предыдущих главах мы строили опорные точки графика спирали Архимеда, руководствуясь именно этим свойством спирали – при изменении угла на величину nΔφ длину радиуса-вектора мы меняли на nΔr.

Из уравнения видно, что если j=2p (точка М совершила полный оборот вокруг центра О), то r₁=k×2p, после второго оборота r₂=k×4p=2r₁, после третьего r₃=k×6p=3r₁ и т.д. Величина k×2p=а называется шагом спирали. Шаг спирали — это величина смещения вдоль луча, соответствующее повороту луча на 2p.

Так как шаг спирали имеет ясный физический смысл, уравнение спирали Архимеда принято задавать в терминах именно шага спирали: . Коэффициент пропорциональности k и шаг спирали а связаны соотношением: и а=2pk.

infopedia.su

Кривые, заданные в полярных координатах

Р.Л. Ткачук

Вологда

Введение

Тема «Полярная система координат» позволяет познакомить учащихся с красивейшими результатами математической науки.

Полярная система координат на плоскости определяется заданием точки O(полюс), луча Ох (полярная ось) и единичного отрезка т. Кроме того, должен быть указан поворот луча Ох, называемый положительным. Пусть это будет поворот в направлении против движения часовой стрелки. Повороты луча, совершаемые в направлении, противоположном положительному, будем называть отрицательными.

Пусть М — произвольная точка плоскости, не совпадающая с полюсом. Обозначим через

длину отрезка ОМ, а через — величину угла, образованного лучами Ох и ОМ. Числа и такие, что р>0 и 0 ф называют первой полярной координатой, или полярным радиусом, число — второй полярной координатой, или полярным углом (рис. 1) Если точка М совпадает с полюсом, то = 0, а полярный утол считаем равным нулю. Заметим, что при заданных нами условиях > 0, 0 ≤

Введение таких координат очень естественно, ведь местонахождение любой точки на земной поверхности для неподвижного наблюдателя удобно определять с помощью расстояния от наблюдателя до этой точки и направления к точке от наблюдателя (в этом случае точка, в которой находится наблюдатель, служит полюсом).

Школьникам можно напомнить, что в повести Р.Л.Стивенсона «Остров сокровищ» описано, как старый пират Флинт определил местоположение закопанного клада: «Десять футов к северу от высокого дерева на склоне Подзорной Трубы» (рис. 2).

Построение кривых, заданных полярными уравнениями, имеет некоторые специфические особенности, которые мы проиллюстрируем на примерах. Как известно, математики Древней Индии заменяли доказательства теорем геометрическим чертежом, сопровождая его короткой подписью: «Смотри!». Мы пользовались тем же принципом, заменив долгие разъяснения рисунками, из которых видны все свойства кривых.

В дальнейшем, при построении кривых мы позволим углу

принимать любые неотрицательные значения, выделяя на рисунках жирной линией фрагменты кривых, получающиеся при ограниче-нии 0 ≤

Алгебраические спирали

Сначала рассмотрим так называемые алгебраические спирали, т.е. кривые, полярные уравнения которых являются алгебраическими относительно

и и имеют вид F(, ) = 0, ≥0, ≥ 0. Если перейти к прямоугольной системе координат, то эти уравнения уже не будут алгебраическими относительно х и у. Кривые, задаваемые такими уравнениями, принято называть трансцендентными.

Достаточно громоздкие декартовы уравнения упрощаются при переходе к полярной системе координат. Зависимость между полярными и декартовыми координатами весьма проста.

Пусть полюс Oсовпадает с началом декартовой системы координат, полярная ось совмещена с положительным направлением оси Ох; М(х; у) — произвольная точка декартовой плоскости. Легко убедиться, что

И обратно:

Спираль Архимеда

= .

Поместим точку на секундную стрелку часов и будем перемешать точку вдоль секундной стрелки с постоянной скоростью, не обращая внимания на равномерное движение стрелки часов по кругу. Тогда точка опишет кривую, называемую спиралью Архимеда. Изобретение этой кривой приписывается Конону Самосскому, хотя ее основные свойства описал именно Архимед (ок. 287-212 гг. до н.э.). Архимеду, в частности, было известно, что расстояние между двумя последовательными витками спирали является постоянной величиной и равно 2π (рис. 3).

Кстати, в силу этой особенности в расположении витков реальный образ спирали Архимеда можно видеть, например, наблюдая туго завернутый рулон бумаги с его торцевой стороны.

На внеклассных занятиях полезно показать построение первого витка спирали Архимеда.

Начертим окружность. Разделим ее и радиус ОА на п равных частей.

Пусть n = 8. Проведем ко всем точкам деления лучи из центра О окружности и пронумеруем их (рис. 4). На луче 1 отметим точку на расстоянии

=ОА от центра окружности. На луче 2 отметим точку на расстоянии = ОА, на луче 3 — точку на расстоянии =ОА и т.д. На луче 8 поставим точку на расстоянии =ОА.

Соединив последовательно плавной кривой полученные точки, мы увидим первый виток спирали Архимеда. Построение будет тем более точным, чем больше точек деления радиуса и окружности будет выбрано первоначально.

Спираль Архимеда используется в качестве линии, позволяющей разделить заданный угол на любое количество равных частей. В некоторых готовальнях в старину в состав рабочих инструментов входила металлическая пластинка с тщательно выгравированной на ней спиралью Архимеда. С помощью такого приспособления было нетрудно разделить угол на несколько равных частей. Например, для трисекции угла ВАС достаточно приложить пластину ее ровной частью к одному из лучей угла (рис. 5) и поделить получившийся отрезок АВ на 3 равные части. На дуге спирали следует сделать засечку радиусом АО = — АВ. Тогда угол САО будет равен одной трети угла ВАС.

В области техники спираль Архимеда находит применение в так называемых кулачковых механиз-мах, которые преобразуют вращательное движение шайбы в поступательное движение стержня. В некоторых механизмах (например, в часах) требуется, чтобы стержень двигался равномерно. Обеспечить это можно, очертив профиль шестеренки по спирали Архимеда.

В качестве второго объекта для применения спирали Архимеда в технике можно привести самоцентрирующийся патрон (рис. 6), направляющие канавки которого выполнены по спирали Архимеда. При одном повороте диска этого патрона кулачки перемещаются на величину радиального расстояния смежных канавок.

Кроме того, форму спирали Архимеда имеют звуковая дорожка на грампластинке и одна из деталей швейных машин — механизм для равномерного наматывания ниток на шпульку.

Логарифмическая спираль

= , = . При = 0 получаем = 1. При →+∞ видно, что →+∞ и спираль развертывается против хода часовой стрелки (рис. 7)

Логарифмическую спираль описывает точка, движущаяся по секундной стрелке не с постоянной скоростью (как в случае архимедовой спирали), а с возрастающей, причем это возрастание пропорционально расстоянию от центра часов.

Логарифмическую спираль можно построить с помощью так называемого золотого прямоугольника, т.е. такого, у которого отношение сторон равно золотому сечению:

mirznanii.com

Спираль Архимеда — Википедия

Материал из Википедии — свободной энциклопедии

Архимедова спираль — спираль, плоская кривая, траектория точки M (см Рис. 1), которая равномерно движется вдоль луча OV с началом в O, в то время как сам луч OV равномерно вращается вокруг O. Другими словами, расстояние ρ = OM пропорционально углу поворота φ луча OV. Повороту луча OV на один и тот же угол соответствует одно и то же приращение ρ.

Описание[ | ]

Уравнение Архимедовой спирали в полярной системе координат записывается так:

(1) ρ=kφ,{\displaystyle \rho =k\varphi ,}

где k — смещение точки M по лучу r, при повороте на угол равный одному радиану.

Повороту прямой на 2π{\displaystyle 2\pi } соответствует смещение a = |BM| = |MA| = 2kπ{\displaystyle 2k\pi }. Число a — называется шагом спирали. Уравнение Архимедовой спирали можно переписать так:

ρ=a2πφ.{\displaystyle \rho ={\frac {a}{2\pi }}\varphi .}

При вращении луча против часовой стрелки получается правая спираль (синяя линия) (см. Рис. 2), при вращении по часовой стрелке — левая спираль (зелёная линия).

encyclopaedia.bid