Шестнадцатеричные числа
Шестнадцатеричные числа в основании системы счисления имеют 16 символов, это числа от 0 до 9 и буквы английского алфавита от А до F:
16-ричное | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
10-ричное | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
Шестнадцатеричные числа всегда используются при отображении адресов и ссылок на память. Большие значения также можно выразить с помощью шестнадцатеричных чисел, используя всего несколько цифр, причем эти цифры легко преобразовать в двоичные значения. Шестнадцатеричные значения используются при написании программ для MASM и TASM. Для выделения шестнадцатеричных чисел используется буква «h» в конце числа. Например, 45h является шестнадцатеричным числом, тогда как 45 – десятичным.
Преобразование двоичных чисел в шестнадцатеричные
В таблице 2 показано соответствие двоичных чисел шестнадцатеричным цифрам. Большое двоичное число можно легко выразить с помощью шестнадцатеричных цифр.
Таблица 2. Соответствие двоичных и шестнадцатеричных чисел
Двоичное
Шестнадцетеричное
Двоичное
Шестнадцетеричное
0000
0
1000
8
0001
1
1001
9
0010
2
1010
A
0011
3
1011
B
0100
4
1100
C
0101
5
1101
D
0110
6
1110
E
0111
7
1111
F
Например, двоичное число 10101011100101111000011011100101 может быть легко представлено шестнадцатеричным значением АВ9786Е5:
А | В | 9 | 7 | 8 | 6 | Е | |
1010 | 1011 | 1001 | 0111 | 1000 | 0110 | 1110 | 0101 |
Преобразовывать шестнадцатеричное число в двоичное также очень легко, поскольку существует взаимно-однозначное соответствие между шестнадцатеричной цифрой и четырьмя двоичными разрядами. Например:
8А2640=
1000
1010
0010
0110
0100
0000
8
А
2
6
4
0
Несколько примеров:
0AF6h = 0000101011110110
D58Ch = 1101010110001100
F13Bh = 1111000100111011
Преобразование шестнадцатеричныx чисел в десятичные
Каждая позиция цифры в шестнадцатеричном числе соответствует степени числа 16. Например:
24C2h = 2*163+4*162+12*161+2*160 = 8192+1024+192+2 = 9410
Преобразование десятичных чисел в шестнадцатеричные
Последовательное деление на 16. Необходимо осуществить первое деление, после чего необходимо с полученным частным снова произвести деление, а полученный результат снова разделить на 16 и т. д. Остаток от каждого деления будет очередной шестнадцатеричной цифрой. Пример:
Десятичное число 12 268:
15 268 / 16 = 954, остаток 4
954 / 16 = 59, остаток 10 (А)
59 / 16 = 3, остаток 11 (В)
3 / 16 = 0, остаток 3
——————————————————
Шестнадцетеричное: 3ВА4
Числа со знаком
Двоичные числа могут быть как со знаком (signed), так и без знака (unsigned). Числа без знака используют все восемь битов для получения значения. Например, 11111111=255. Проссумировав значения всех битов, получим максимально возможное значение, которое может хранить байт без знака (255). Для слова без знака это значение будет составулять 65 535.
studfiles.netШестнадцатеричные числа — это… Что такое Шестнадцатеричные числа?
- Шестнадцатеричные числа
Шестнадцатеричная система счисления (шестнадцатеричные числа) — позиционная система счисления по целочисленному основанию 16. Обычно в качестве шестнадцатеричных цифр используются десятичные цифры от 0 до 9 и латинские буквы от A до F для обозначения цифр от 10 до 15.
Применение
Широко используется в низкоуровневом программировании и вообще в компьютерной документации, поскольку в современных компьютерах минимальной единицей памяти является 8-битный байт, значения которого удобно записывать двумя шестнадцатеричными цифрами. Такое использование началось с системы IBM/360, где вся документация использовала шестнадцатеричную систему, в то время как в документации других компьютерных систем того времени (даже с 8-битными символами, как, например, БЭСМ-6) использовали восьмеричную систему.
В стандарте Юникода номер символа принято записывать в шестнадцатеричном виде, используя не менее 4 цифр (при необходимости — с ведущими нулями).
Способы записи
В математике
В математике систему счисления принято писать в подстрочном знаке. Например, десятичное число 1443 можно записать как 144310 или как 5A316.
В языках программирования
В разных языках программирования для записи шестнадцатеричных чисел используют различный синтаксис:
- В Ада и
- В Си и языках схожего синтаксиса, например, в
- В некоторых ассемблерах используют букву «h», которую ставят после числа. Например, «5A3h». При этом, если число начинается не с десятичной цифры, впереди ставится «0» (ноль): «0FFh» (25510)
- Другие ассемблеры (AT&T, Motorola), а также Паскаль и некоторые версии Бэйсика используют префикс «$». Например, «$5A3».
- Некоторые иные платформы, например ZX Spectrum в своих ассемблерах (MASM, TASM, ALASM, GENS и т.д.) использовали запись #5A3, обычно выровненную до одного или двух байт: #05A3.
- Другие версии Бэйсика используют для указания шестнадцатеричных цифр сочетание «&h». Например, «&h5A3».
- В Unix-подобных операционных системах (и многих языках программирования, имеющих корни в Unix/linux) непечатные символы при выводе/вводе кодируются как \xCC, где CC — шестнадцатеричный код символа.
Перевод чисел из одной системы счисления в другую
Перевод чисел из шестнадцатеричной системы в десятичную
Для перевода шестнадцатеричного числа в десятичное необходимо это число представить в виде суммы произведений степеней основания шестнадцатеричной системы счисления на соответствующие цифры в разрядах шестнадцатеричного числа.
Например, требуется перевести шестнадцатеричное число 5A3 в десятичное. В этом числе 3 цифры. В соответствии с вышеуказанным правилом представим его в виде суммы степеней с основанием 16:
5A3
=5·256+10·16+3·1=1280+160+3=144310Перевод чисел из двоичной системы в шестнадцатеричную
Для перевода многозначного двоичного числа в шестнадцатеричную систему нужно разбить его на тетрады справа налево и заменить каждую тетраду соответствующей шестнадцатеричной цифрой.
Например:
101101000112=0101 1010 0011=5A316Таблица перевода чисел
0hex = 0dec = 0oct 0 0 0 0 1hex = 1dec = 1oct 0 0 0 1 2hex = 2dec = 2oct 0 0 1 0 3hex = 3dec = 3oct 0 0 1 1 4hex = 4dec = 4oct 0 1 0 0 5hex = 5dec = 5oct 0 1 0 1 6hex = 6dec = 6oct 0 1 1 0 7hex = 7dec = 7oct 0 1 1 1 8hex = 8dec = 10oct 1 0 0 0 9hex = 9dec = 11oct 1 0 0 1 Ahex = 10dec = 12oct 1 0 1 0 Bhex = 11dec = 13oct 1 0 1 1 Chex = 12dec = 14oct 1 1 0 0 Dhex = 13dec = 15oct 1 1 0 1 Ehex = 14dec = 16oct 1 1 1 0 Fhex = 15dec = 17oct 1 1 1 1 См. также
Ссылки
Wikimedia Foundation. 2010.
- Шестнадцатиричная система счисления
- Шестнадцать
Смотреть что такое «Шестнадцатеричные числа» в других словарях:
Шестнадцатиричные числа — Шестнадцатеричная система счисления (шестнадцатеричные числа) позиционная система счисления по целочисленному основанию 16. Обычно в качестве шестнадцатеричных цифр используются десятичные цифры от 0 до 9 и латинские буквы от A до F для… … Википедия
Hexspeak — Эта статья содержит незавершённый перевод с иностранного языка. Вы можете помочь проекту, переведя её до конца. Если вы знаете, на каком языке написан фрагмент, укажите его в этом шаблоне … Википедия
Шестнадцатеричная система счисления — Системы счисления в культуре Индо арабская система счисления Арабская Индийские Тамильская Бирманская Кхмерская Лаоская Монгольская Тайская Восточноазиатские системы счисления Китайская Японская Сучжоу Корейская Вьетнамская Счётные палочки… … Википедия
Шестнадцатеричная система — счисления (шестнадцатеричные числа) позиционная система счисления по целочисленному основанию 16. Обычно в качестве шестнадцатеричных цифр используются десятичные цифры от 0 до 9 и латинские буквы от A до F для обозначения цифр от 10 до 15.… … Википедия
Шестнадцатиричная система счисления — Шестнадцатеричная система счисления (шестнадцатеричные числа) позиционная система счисления по целочисленному основанию 16. Обычно в качестве шестнадцатеричных цифр используются десятичные цифры от 0 до 9 и латинские буквы от A до F для… … Википедия
Шестнадцатиричная система исчисления — Шестнадцатеричная система счисления (шестнадцатеричные числа) позиционная система счисления по целочисленному основанию 16. Обычно в качестве шестнадцатеричных цифр используются десятичные цифры от 0 до 9 и латинские буквы от A до F для… … Википедия
Монитор (интерактивная программа) — У этого термина существуют и другие значения, см. Монитор. Монитор компьютера Apple II Монитор интерактивная программа в компьютерах, особенно 1970 х годов, позволяющая осуществлять управление компьютером на низком уровне: просмотр… … Википедия
HIMEM.SYS — HIMEM.SYS драйвер дополнительной (extended memory) и HMA памяти для операционной системы MS DOS, обеспечивающий поддержку дополнительной памяти (extended или expanded). HIMEM.SYS был введён в состав операционной MS DOS 5.0 для возможности… … Википедия
Еггогология — Электроника МК 52 с сообщением «ERROR» (из за специфического отображения буквы r зачастую читалось как «ЕГГОГ») Еггогология& … Википедия
ЕГГОГ — Электроника МК 52 с сообщением ERROR (из за специфического отображения буквы r зачастую читалось как «ЕГГОГ» Еггогология изучение скрытых возможностей микрокалькуляторов. Содержание 1 Происхождение … Википедия
dic.academic.ru
Шестнадцатеричная Нумерация и Адресация
Шестнадцатеричная запись («Hex») — удобный способ представления двоичных значений. Так же, как десятичная система счисления имеет основание десять, а двоичная — два, шестнадцатеричная система имеет основание шестнадцать.
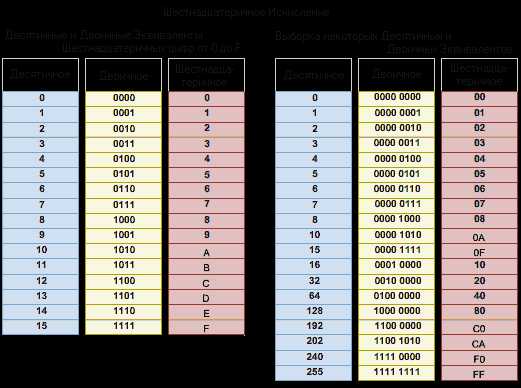
Система счисления с основанием 16 использует числа от 0 до 9 и буквы от A до F. Рисунок показывает эквивалентные десятичные, двоичные и шестнадцатеричные значения для двоичных чисел от 0000 до 1111. Для нас легче выражать значение в виде одной шестнадцатеричной цифры, чем в виде четырех битов.
Понимание Байтов
Учитывая, что 8 битов (байт) являются стандартной двоичной группировкой, двоичные числа от 00000000 до 11111111 могут быть представлены в шестнадцатеричной записи как числа от 00 до FF. Начальные нули всегда отображаются, чтобы завершить 8-разрядное представление. Например, двоичное значение 0000 1010 в шестнадцатеричном виде будет 0A.
Представление Шестнадцатеричных Значений
Отметьте: Важно отличать шестнадцатеричные значения от десятичных значений для символов от 0 до 9, как показано на рисунке.
Шестнадцатеричные значения обычно представляются в тексте значением, которому предшествует 0x (например 0x73), или с помощью нижнего индекса 16. Реже, они могут сопровождаться буквой H, например 73H. Однако, поскольку текст нижнего индекса не распознается ни в командной строке, ни в средах программирования, в техническом представлении шестнадцатеричных чисел им предшествует «0x» (нуль X). Поэтому, примеры выше были бы показаны в виде 0x0A и 0x73 соответственно.
Шестнадцатеричная запись используется, чтобы представлять MAC-адреса Ethernet и адреса IP Версии 6.
Шестнадцатеричные Преобразования
Преобразования чисел между десятичными и шестнадцатеричными значениями являются простыми, но быстрое деление или умножение на 16 не всегда удобно. Если такие преобразования необходимы, обычно легче преобразовать десятичное или шестнадцатеричное значение в двоичное, а затем преобразовать двоичное значение в десятичное или шестнадцатеричное, в зависимости от того, что требуется получить.
С практикой возможно распознать двоичные шаблоны битов, которые соответствуют десятичным и шестнадцатеричным значениям. Рисунок показывает эти шаблоны для некоторых 8-разрядных значений.
Далее: Разработка Схемы адресации — Сколько Узлов в Сети?
Смотрите также
Написать
datanets.ru
Шестнадцатеричная система счисления
Главная / Ассемблер / Для чайников / Системы счисления /Как мы увидели выше, с двоичным числом удобно работать при поразрядных операциях, однако запись двоичного числа получается довольно громоздкой. Чтобы немного упростить жизнь программистам, была придумана шестнадцатеричная система счисления, которая использует 16 цифр:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, FСоответственно, основание шестнадцатеричной системы равно 16.
Шестнадцатеричное число является компактным и лёгким для чтения. Его легко преобразовать в двоичное и наоборот. Каждый разряд шестнадцатеричного числа – это тетрада. Каждую тетраду легко преобразовать в двоичное число и наоборот (см. таблицу 2.3).
Таблица 2.3. Преобразование чисел.
| Десятичное | Двоичное | Шестнадцатеричное |
| 0 | 0000 | 0 |
| 1 | 0001 | 1 |
| 2 | 0010 | 2 |
| 3 | 0011 | 3 |
| 4 | 0100 | 4 |
| 5 | 0101 | 5 |
| 6 | 0110 | 6 |
| 7 | 0111 | 7 |
| 8 | 1000 | 8 |
| 9 | 1001 | 9 |
| 10 | 1010 | A |
| 11 | 1011 | B |
| 12 | 1100 | C |
| 13 | 1101 | D |
| 14 | 1110 | E |
| 15 | 1111 | F |
В конец шестнадцатеричного числа принято ставить букву h. Таким образом мы можем отличить шестнадцатеричное число от чисел в других системах исчисления. Например
11 – десятичное число 11 11b – двоичное число, которое эквивалентно десятичному числу 3 11h – шестнадцатеричное число, которое эквивалентно десятичному числу 17В исходных кодах программ на ассемблере, если шестнадцатеричное число начинается с буквы, то перед ним нужно поставить ноль, иначе ассемблер подумает, что это не число, а имя переменной. Например, число FF в исходном коде на ассемблере должно быть записано как 0FFh.
av-assembler.ru
Шестнадцатеричные цифры, преобразование шестнадцатеричного числа в десятичное
Умение преобразовывать шестнадцатеричные числа может быть полезно не только программистам, но и дизайнерам, ведь триада RRGGBB есть не что иное, как «машинные» компоненты для красного, зелёного и синего соответственно — от 0 до 255 каждое. Конечно, графические редакторы содержат палитры со встроенными преобразователями, а стандартный калькулятор операционной системы умеет справляться с этой задачей, но порой гораздо удобнее самому «накинуть +14» к требуемой компоненте, а не запускать сторонние программы.
Прежде, чем я покажу, как (легко) можно переводить числа из шестнадцатеричной системы и более привычную для нас, необходимы дополнительные мероприятия. Все мы в школе учили таблицу умножения, и можем убедиться, что данный навык остался (хотя некоторые им в повседневной жизни не пользуются). Теперь же потребуется немного углубить знания, выучив её вплоть до 16 × 16.
И последнее: я убеждён, что рядовому пользователю эти навыки не понадобятся с вероятностью 99.…%. В общем, вы предупреждены .

Таблица умножение от 11 до 16
| 11 11 × 2 = 22 11 × 3 = 33 11 × 4 = 44 11 × 5 = 55 11 × 6 = 66 11 × 7 = 77 11 × 8 = 88 11 × 9 = 99 11 × 10 = 110 11 × 11 = 121 11 × 12 = 132 11 × 13 = 143 11 × 14 = 154 11 × 15 = 165 11 × 16 = 176 | 12 12 × 2 = 24 12 × 3 = 36 12 × 4 = 48 12 × 5 = 60 12 × 6 = 72 12 × 7 = 84 12 × 8 = 96 12 × 9 = 108 12 × 10 = 120 12 × 11 = 132 12 × 12 = 144 12 × 13 = 156 12 × 14 = 168 12 × 15 = 180 12 × 16 = 192 | 13 13 × 2 = 26 13 × 3 = 39 13 × 4 = 52 13 × 5 = 65 13 × 6 = 78 13 × 7 = 91 13 × 8 = 104 13 × 9 = 117 13 × 10 = 130 13 × 11 = 143 13 × 12 = 156 13 × 13 = 169 13 × 14 = 182 13 × 15 = 195 13 × 16 = 208 |
| 14 14 × 2 = 28 14 × 3 = 42 14 × 4 = 56 14 × 5 = 70 14 × 6 = 84 14 × 7 = 98 14 × 8 = 112 14 × 9 = 126 14 × 10 = 140 14 × 11 = 154 14 × 12 = 168 14 × 13 = 182 14 × 14 = 196 14 × 15 = 210 14 × 16 = 224 | 15 15 × 2 = 30 15 × 3 = 45 15 × 4 = 60 15 × 5 = 75 15 × 6 = 90 15 × 7 = 105 15 × 8 = 120 15 × 9 = 135 15 × 10 = 150 15 × 11 = 165 15 × 12 = 180 15 × 13 = 195 15 × 14 = 210 15 × 15 = 225 15 × 16 = 240 | 16 16 × 2 = 32 16 × 3 = 48 16 × 4 = 64 16 × 5 = 80 16 × 6 = 96 16 × 7 = 112 16 × 8 = 128 16 × 9 = 144 16 × 10 = 160 16 × 11 = 176 16 × 12 = 192 16 × 13 = 208 16 × 14 = 224 16 × 15 = 240 16 × 16 = 256 |
Следующим шагом необходимо соотнести десятичные числа от 10 до 15 с шестнадцатеричными цифрами от A до F.
Таблица соответствия шестнадцатеричных цифр
| HEX (шестнадцатеричная) | DEC (десятичная) |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
| 7 | 7 |
| 8 | 8 |
| 9 | 9 |
| A | 10 |
| B | 11 |
| C | 12 |
| D | 13 |
| E | 14 |
| F | 15 |
А теперь вспомним поразрядное умножение из предыдущей статьи, для цифры 7. Здесь будет лишь поправка на другую систему счисления (не на 10, как там, а на 16).
Обычно в компьютерной литературе, для однозначного указания основания системы счисления, применяется следующая нотация:
— шестнадцатеричное число — 0x100 (256 в десятичной, признак — 0x в начале)
— десятичное число — 100 (наша, человеческая, система счисления)
— восьмеричное число — 0100 (64 в десятичной, признак — ведущий ноль)
— двоичное число — 0b100 (4 в десятичной, признак — 0b в начале)
Преобразование шестнадцатеричного числа в десятичное
Для начала, небольшой рисунок:
Для преобразования требуется каждую цифру числа умножить на «разряд», в котором оно находится. Из курса начальной школы мы помним, что позиции, занимаемые в числовой строке, называются (справа налево) единицы, десятки, сотни и т. д. Здесь почти то же самое, но с поправкой на систему счисления. Каждый следующий разряд — это +1 степень текущей системы счисления. Любое число в степени ноль — это ноль, в степени 1 — самом число, в степени 2 (квадрат) — число, умноженное само на себя и т. д.
Для наглядности привожу пример. Допустим, возьмём шестнадцатеричное число 0x1F8. Нам требуется перевести его в десятичную систему, поэтому запишем (0x — это признак основания!):
1F816 = 116 × 162 + F16 × 161 + 816 × 160 = 1 × 256 + 15 × 16 + 8 × 1 = 256 + 240 + 8 = 504
Обе таблички нам пригодились: благодаря второй мы переводим числа из шестнадцатеричной системы в десятичную, благодаря первой — легко перемножаем «больше» числа.
Небольшое отступление
А знаете ли вы, что у нас сейчас могла бы использоваться двенадцатеричная система счисления, используемая ещё шумерцами? По одной и версий, этому способствовало количество фаланг пальцев руки. Взгляните на рисунок:
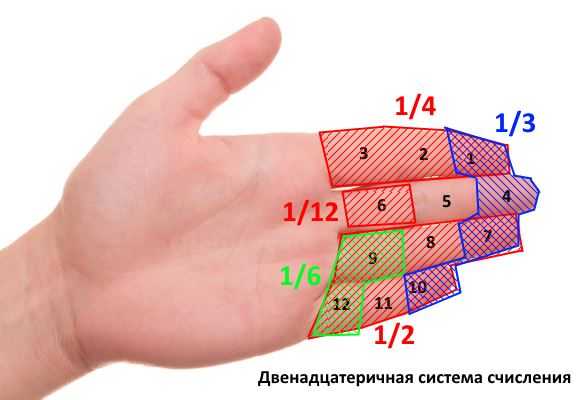
Скорее всего, вам сложно это представить. Но, взглянув на это под другим углом, можем убедиться, что выбор был бы очень хорош, ведь 12 делится без остатка на 2, 3, 4, 6 (в то время, как 10 можно разделить лишь на 2 и 5). Естественно, умножения и деления на степень числа 12 были так же просты, как сейчас аналогичные операции для степени числа 10.
Выучив эти таблицы, любой человек легко сможет переводить компьютерные байты в привычные числа. При желании, как следует потренировавшись и «расширив объём» краткосрочной памяти, станут доступны и более сложные варианты. Но, как уже говорилось чуть ранее, манипуляции с байтами мало кому нужны, не говоря о чём-то большем.
Автор публикации
1 892не в сети 3 дня
x64 (aka andi)
Комментарии: 2772Публикации: 385Регистрация: 02-04-2009 Загрузка…a-panov.ru
Шестнадцатеричные числа Википедия
| Системы счисления в культуре | |
|---|---|
| Индо-арабская | |
| Арабская Тамильская Бирманская | Кхмерская Лаосская Монгольская Тайская |
| Восточноазиатские | |
| Китайская Японская Сучжоу Корейская | Вьетнамская Счётные палочки |
| Алфавитные | |
| Абджадия Армянская Ариабхата Кириллическая Греческая | Грузинская Эфиопская Еврейская Акшара-санкхья |
| Другие | |
| Вавилонская Египетская Этрусская Римская Дунайская | Аттическая Кипу Майяская Эгейская Символы КППУ |
| Позиционные | |
| 2, 3, 4, 5, 6, 8, 10, 12, 16, 20, 60 | |
| Нега-позиционная | |
| Симметричная | |
| Смешанные системы | |
| Фибоначчиева | |
| Непозиционные | |
| Единичная (унарная) | |
Шестнадцатеричная система счисления — позиционная система счисления по целочисленному основанию 16. В качестве цифр этой системы счисления обычно используются цифры от 0 до 9 и латинские буквы от A до F. Буквы A, B, C, D, E, F имеют значения 1010, 1110, 1210, 1310, 1410, 1510 соответственно.
Применение
Широко используется в низкоуровневом программировании и компьютерной документации, поскольку в современных компьютерах минимальной адресуемой единицей памяти является 8-битный байт, значения которого удобно записывать двумя шестнадцатеричными цифрами. Такое использование началось с системы IBM/360, где вся документация использовала шестнадцатеричную систему, в то время как в документации других компьютерных систем того времени (даже с 8-битными символами, как, например, PDP-11 или БЭСМ-6) использовали восьмеричную систему.
В стандарте Юникода номер символа принято записывать в шестнадцатеричном виде, используя не менее 4 цифр (при необходимости — с ведущими нулями).
Шестнадцатеричный цвет — запись трёх компонентов цвета (R, G и B) в шестнадцатеричном виде.
Способы записи
В математике
В математике основание системы счисления принято указывать в десятичной системе в нижнем индексе. Например, десятичное число 1443 можно записать как 144310 или как 5A316.
В языках программирования
В разных языках программирования для записи шестнадцатеричных чисел используют различный синтаксис:
- В Ада и VHDL такие числа указывают так: «16#5A3#».
- В Си и языках схожего синтаксиса, например, в Java, используют префикс «0x». Например, «0x5A3».
- В некоторых ассемблерах используют букву «h», которую ставят после числа. Например, «5A3h». При этом, если число начинается не с десятичной цифры, то для отличия от имён идентификаторов (например, констант) впереди ставится «0» (ноль): «0FFh» (25510)
- Другие ассемблеры (AT&T, Motorola), а также Паскаль и некоторые версии Бейсика используют префикс «$». Например, «$5A3».
- В ассемблерах для IBM mainframe (Assembler F, Assembler 2, Assembler H) используется запись X’xx..xx’. Например X’05A3′.
- Некоторые иные платформы, например ZX Spectrum в своих ассемблерах (MASM, TASM, ALASM, GENS и т. д.) использовали запись #5A3, обычно выровненную до одного или двух байт: #05A3.
- Другие версии Бейсика, например Turbo Basic, используют для указания шестнадцатеричных цифр сочетание «&h» или «&H» перед числом. Например, «&h5A3».
- В Unix-подобных операционных системах (и многих языках программирования, имеющих корни в Unix/linux) непечатные символы при выводе/вводе кодируются как 0xCC, где CC — шестнадцатеричный код символа.
Перевод чисел из одной системы счисления в другую
Перевод чисел из шестнадцатеричной системы в десятичную
Для перевода шестнадцатеричного числа в десятичное необходимо это число представить в виде суммы произведений степеней основания шестнадцатеричной системы счисления на соответствующие цифры в разрядах шестнадцатеричного числа.
Например, требуется перевести шестнадцатеричное число 3A5 в десятичное. В этом числе 3 цифры. В соответствии с вышеуказанным правилом представим его в виде суммы степеней с основанием 16:
3A516 = 3·162+10·161+5·160== 3·256+10·16+5·1 = 768+160+5 = 93310
При переводе чисел, следует помнить, что в шестнадцатеричной системе счисления: A=10; B=11; C=12; D=13; E=14; F=15.
Перевод чисел из двоичной системы в шестнадцатеричную и наоборот
Для перевода многозначного двоичного числа в шестнадцатеричную систему нужно разбить его на тетрады справа налево и заменить каждую тетраду соответствующей шестнадцатеричной цифрой. Для перевода числа из шестнадцатеричной системы в двоичную нужно заменить каждую его цифру на соответствующую тетраду из нижеприведённой таблицы перевода.
Например:
Таблица перевода чисел
| 0hex | = | 0dec | = | 0oct | 0 | 0 | 0 | 0 | |||
| 1hex | = | 1dec | = | 1oct | 0 | 0 | 0 | 1 | |||
| 2hex | = | 2dec | = | 2oct | 0 | 0 | 1 | 0 | |||
| 3hex | = | 3dec | = | 3oct | 0 | 0 | 1 | 1 | |||
| 4hex | = | 4dec | = | 4oct | 0 | 1 | 0 | 0 | |||
| 5hex | = | 5dec | = | 5oct | 0 | 1 | 0 | 1 | |||
| 6hex | = | 6dec | = | 6oct | 0 | 1 | 1 | 0 | |||
| 7hex | = | 7dec | = | 7oct | 0 | 1 | 1 | 1 | |||
| 8hex | = | 8dec | = | 10oct | 1 | 0 | 0 | 0 | |||
| 9hex | = | 9dec | = | 11oct | 1 | 0 | 0 | 1 | |||
| Ahex | = | 10dec | = | 12oct | 1 | 0 | 1 | 0 | |||
| Bhex | = | 11dec | = | 13oct | 1 | 0 | 1 | 1 | |||
| Chex | = | 12dec | = | 14oct | 1 | 1 | 0 | 0 | |||
| Dhex | = | 13dec | = | 15oct | 1 | 1 | 0 | 1 | |||
| Ehex | = | 14dec | = | 16oct | 1 | 1 | 1 | 0 | |||
| Fhex | = | 15dec | = | 17oct | 1 | 1 | 1 | 1 | |||
См. также
Ссылки
wikiredia.ru
Шестнадцатиричные числа Википедия
| Системы счисления в культуре | |
|---|---|
| Индо-арабская | |
| Арабская Тамильская Бирманская | Кхмерская Лаосская Монгольская Тайская |
| Восточноазиатские | |
| Китайская Японская Сучжоу Корейская | Вьетнамская Счётные палочки |
| Алфавитные | |
| Абджадия Армянская Ариабхата Кириллическая Греческая | Грузинская Эфиопская Еврейская Акшара-санкхья |
| Другие | |
| Вавилонская Египетская Этрусская Римская Дунайская | Аттическая Кипу Майяская Эгейская Символы КППУ |
| Позиционные | |
| 2, 3, 4, 5, 6, 8, 10, 12, 16, 20, 60 | |
| Нега-позиционная | |
| Симметричная | |
| Смешанные системы | |
| Фибоначчиева | |
| Непозиционные | |
| Единичная (унарная) | |
Шестнадцатеричная система счисления — позиционная система счисления по целочисленному основанию 16. В качестве цифр этой системы счисления обычно используются цифры от 0 до 9 и латинские буквы от A до F. Буквы A, B, C, D, E, F имеют значения 1010, 1110, 1210, 1310, 1410, 1510 соответственно.
Применение
Широко используется в низкоуровневом программировании и компьютерной документации, поскольку в современных компьютерах минимальной адресуемой единицей памяти является 8-битный байт, значения которого удобно записывать двумя шестнадцатеричными цифрами. Такое использование началось с системы IBM/360, где вся документация использовала шестнадцатеричную систему, в то время как в документации других компьютерных систем того времени (даже с 8-битными символами, как, например, PDP-11 или БЭСМ-6) использовали восьмеричную систему.
В стандарте Юникода номер символа принято записывать в шестнадцатеричном виде, используя не менее 4 цифр (при необходимости — с ведущими нулями).
Шестнадцатеричный цвет — запись трёх компонентов цвета (R, G и B) в шестнадцатеричном виде.
Способы записи
В математике
В математике основание системы счисления принято указывать в десятичной системе в нижнем индексе. Например, десятичное число 1443 можно записать как 144310 или как 5A316.
В языках программирования
В разных языках программирования для записи шестнадцатеричных чисел используют различный синтаксис:
- В Ада и VHDL такие числа указывают так: «16#5A3#».
- В Си и языках схожего синтаксиса, например, в Java, используют префикс «0x». Например, «0x5A3».
- В некоторых ассемблерах используют букву «h», которую ставят после числа. Например, «5A3h». При этом, если число начинается не с десятичной цифры, то для отличия от имён идентификаторов (например, констант) впереди ставится «0» (ноль): «0FFh» (25510)
- Другие ассемблеры (AT&T, Motorola), а также Паскаль и некоторые версии Бейсика используют префикс «$». Например, «$5A3».
- В ассемблерах для IBM mainframe (Assembler F, Assembler 2, Assembler H) используется запись X’xx..xx’. Например X’05A3′.
- Некоторые иные платформы, например ZX Spectrum в своих ассемблерах (MASM, TASM, ALASM, GENS и т. д.) использовали запись #5A3, обычно выровненную до одного или двух байт: #05A3.
- Другие версии Бейсика, например Turbo Basic, используют для указания шестнадцатеричных цифр сочетание «&h» или «&H» перед числом. Например, «&h5A3».
- В Unix-подобных операционных системах (и многих языках программирования, имеющих корни в Unix/linux) непечатные символы при выводе/вводе кодируются как 0xCC, где CC — шестнадцатеричный код символа.
Перевод чисел из одной системы счисления в другую
Перевод чисел из шестнадцатеричной системы в десятичную
Для перевода шестнадцатеричного числа в десятичное необходимо это число представить в виде суммы произведений степеней основания шестнадцатеричной системы счисления на соответствующие цифры в разрядах шестнадцатеричного числа.
Например, требуется перевести шестнадцатеричное число 3A5 в десятичное. В этом числе 3 цифры. В соответствии с вышеуказанным правилом представим его в виде суммы степеней с основанием 16:
3A516 = 3·162+10·161+5·160== 3·256+10·16+5·1 = 768+160+5 = 93310
При переводе чисел, следует помнить, что в шестнадцатеричной системе счисления: A=10; B=11; C=12; D=13; E=14; F=15.
Перевод чисел из двоичной системы в шестнадцатеричную и наоборот
Для перевода многозначного двоичного числа в шестнадцатеричную систему нужно разбить его на тетрады справа налево и заменить каждую тетраду соответствующей шестнадцатеричной цифрой. Для перевода числа из шестнадцатеричной системы в двоичную нужно заменить каждую его цифру на соответствующую тетраду из нижеприведённой таблицы перевода.
Например:
Таблица перевода чисел
| 0hex | = | 0dec | = | 0oct | 0 | 0 | 0 | 0 | |||
| 1hex | = | 1dec | = | 1oct | 0 | 0 | 0 | 1 | |||
| 2hex | = | 2dec | = | 2oct | 0 | 0 | 1 | 0 | |||
| 3hex | = | 3dec | = | 3oct | 0 | 0 | 1 | 1 | |||
| 4hex | = | 4dec | = | 4oct | 0 | 1 | 0 | 0 | |||
| 5hex | = | 5dec | = | 5oct | 0 | 1 | 0 | 1 | |||
| 6hex | = | 6dec | = | 6oct | 0 | 1 | 1 | 0 | |||
| 7hex | = | 7dec | = | 7oct | 0 | 1 | 1 | 1 | |||
| 8hex | = | 8dec | = | 10oct | 1 | 0 | 0 | 0 | |||
| 9hex | = | 9dec | = | 11oct | 1 | 0 | 0 | 1 | |||
| Ahex | = | 10dec | = | 12oct | 1 | 0 | 1 | 0 | |||
| Bhex | = | 11dec | = | 13oct | 1 | 0 | 1 | 1 | |||
| Chex | = | 12dec | = | 14oct | 1 | 1 | 0 | 0 | |||
| Dhex | = | 13dec | = | 15oct | 1 | 1 | 0 | 1 | |||
| Ehex | = | 14dec | = | 16oct | 1 | 1 | 1 | 0 | |||
| Fhex | = | 15dec | = | 17oct | 1 | 1 | 1 | 1 | |||
См. также
Ссылки
wikiredia.ru