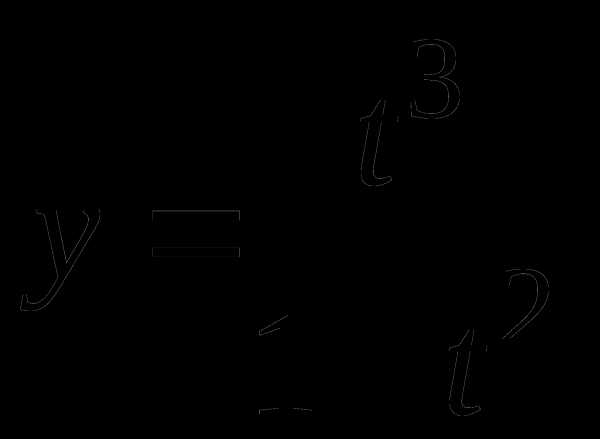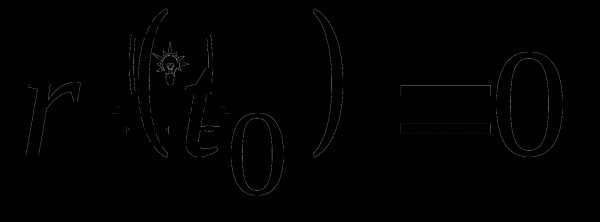Построение графика параметрически заданной функции

Содержание

13. Общая схема исследования функций и построения графиков.

13.1 Общая схема исследования и построения графика функции заданной явно.

Общее исследование функции следует проводить по приведенной ниже схеме:

1.Определить область существования функции, область непрерывности, точки разрыва.

2. Найти асимптоты функции.

3. Выяснить вопрос о периодичности.

4. Выяснить вопрос о четности или нечетности.

В случае, если функция окажется четной или нечетнойдостаточно исследовать функцию только при положительных значениях аргумента. При построении графика следует учесть, что график четной функции симметричен относительно оси ординат; график нечетной функции симметричен относительно начала координат.

5.Найти точки пересечения графика функции с осями координат:

с осью абсцисс — точки , где-решение уравнения;

с осью ординат- точки , где.

6. Найти промежутки монотонности и локальные экстремумы.

7.Найти интервалы выпуклости и вогнутости, точки перегиба.

8. Составить таблицу


Возрастает или убывает, Выпукла или вогнута	Возрастает или убывает, Выпукла или вогнута	Возрастает или убывает, Выпукла или вогнута	Возрастает или убывает, Выпукла или вогнута
знак	знак	знак	знак
знак	знак	знак	знак

Точки -все найденные в п.6-7 точки, в которых производные обращаются в нуль или не существуют.

9.На основании проведенного исследования построить график заданной функции.

Пример 26

Провести полное исследование и построить график функции .

Решение:

Область определения функции

Точка разрыва функции , функция непрерывна наи.

2. Асимптоты.

Вертикальная асимптота .

Поведение функции в окрестности :

Найдем наклонную асимптоту:

Прямая является наклонной асимптотой заданной кривой.

3. Функция не является периодической.

4. Четность функции

Условие четности или нечетности не выполнено. Заданная функция –функция общего вида.

5. Точки пересечения с осями.

График функции проходит через начало координат.

6. Промежутки монотонности, локальные экстремумы.

Найдем критические точки:

Исследуем знак производной методом интервалов:

знак

Найдем значения функции в критических точках:

7.Промежутки выпуклости и вогнутости. Точки перегиба.

Найдем вторую производную.

Точки, в которых равна нулю или несуществует:

Исследуем знак второй производной методом интервалов:

8. Составляем таблицу.


	0		—
+	0	+	—	—	0	+
—	0	+	—	+		+
	перегиб		разрыв		Мин.

13.2 Общая схема исследования и построения графика функции заданной параметрически.

Функция задана параметрически

1.Исследовать область изменения ипри изменении параметра.

2. Найти значения параметра , при которыхи.

3.а)Найти значения параметра , при котрых. Найти вертикальную асимптоту

б) Найти значения параметра , при котрых. Найти наклонную асимптоту

4. Вычисляем и.Находим все значения параметра, при которых хотя бы одна из полученных производных обращается в нуль или терпит разрыв. Найденные значения параметра будем называть критическими.По формуле (9) определяем знак производнойв каждом из полученных интервалов.

5. Вычисляем вторую производную по формуле (16) или (17). Определяем значения параметрапри которыхобращается в нуль или терпит разрыв. Определяем промежутки выпукдости вогнутости согласно (40) и (41).

6. Строим таблицу

Область изм.

Знак

Поведение

7. Строим график функции.

Пример 27

Построить кривую (декартов лист), заданную параметрическими уравненниями:

Решение:

1.Обе функции определены при .

При этом

2.при

при .

3.а) При

При этом

Таким образом, вертикальных асимптот график функции не имеет.

б) Найдем наклонную асимптоту:

Таким образом, график функции имеет наклонную асимптоту:

4. Найдем производные и.

Найдем критические значения параметра

При обе производные терпят разрыв.

Таким образом, получаем следующие критические значения параметра :

Найдем по формуле (9):

5. Найдем :

6. Строим таблицу

Область изм.	Область изм.	Область изм.	Знак	Знак	Знак	Знак	Знак	Поведение
								убывает, вогнута
								убывает, вогнута
								возрастает, вогнута
								убывает, вогнута
								возрастает, выгнута

7. Строим график

Задания 11. Провести полное исследование и построить график функции:

1.	2.	3.
4.	5.	6.
7.	8.	9.
10.	11.	12.

studfiles.net

6. Построение графика функции, заданной параметрически.

В среде Mathcad можно также построить график функции, заданной параметрической зависимостью. Чтобы получить такой график нужно:

Задать область изменения переменной t;
Записать аналитические выражения для x(t) и y(t);
Создать поле двумерного графика и указать на оси абсцисс x(t), а на оси ординат — y(t). (См. пример 6 и рис.12).

Пример 6.

рис.12. График функции, заданной параметрически.

7. Построение графика по массиву данных.

Mathcad позволяет построить график не только по аналитическому выражению, но и по массиву данных. Этот массив должен представлять собой матрицу, содержащую два столбца (в первом – абсциссы, а во втором – ординаты). Количество строк этой матрицы равно количеству точек. (См. пример 7). Если вы хотите, чтобы точки на графике обозначались определенными символами и не соединялись линиями, внесите соответствующие изменения в диалоговое окно Formatting Currently Selected X-Y Plot  Traces (см. п.2). Полученный график представлен на рис.10.

Пример 7.

рис.13. График, построенный по матрице данных.

Рассмотрим еще один пример.

Пример 8.

рис.14. График, построенный по массиву данных.

8. Увеличение фрагмента двумерного графика.

Вы можете увеличить интересующий вас фрагмент графического окна, с тем, чтобы более детально изучить поведение кривой на выбранном участке. Для этого сделайте следующее:

Активизируйте поле графика.
Вызовите команду Zoom одним из трех способов:

1) с помощью меню FormatGraphZoom;

2) щелкнув по кнопке “Zoom” из палитры “Graph”;

3) вызвав пункт Zoom из всплывающего меню, которое появится, когда вы щелкнете на графике правой кнопкой мыши.

После этого на экране появится диалоговое окно X-Y Zoom.

Выделите мышью тот фрагмент графика, который вы хотели бы увеличить.
Щелкните по кнопке (Zoom) в диалоговом окне X-Y Zoom.

После этого выбранный вами фрагмент будет увеличен до размеров исходного графика (временно). Щелкнув по кнопке (Unzoom) вы вернетесь к выбранному ранее масштабу. Если вы хотите, чтобы на графике остался только выбранный вами фрагмент, щелкните по кнопке “OK”, а кнопка “Cancel” отменяет выполненные ранее действия. Щелкнув по кнопке (Full View) вы выведете на экран всю область графика (т.е. в нашем примере – t от 0 до 10).

9. Считывание координат двумерного графика.

Вы можете узнать координаты любой точки кривой. Для этого:

Активизируйте поле графика.
Вызовите команду Trace одним из трех способов:

1) с помощью меню FormatGraphTrace;

2) щелкнув по кнопке “Trace” из палитры “Graph”;

3) вызвав пункт Trace из всплывающего меню, которое появится, когда вы щелкнете на графике правой кнопкой мыши.

После этого на экране появится диалоговое окно X-Y Trace.

Проведите мышью по той кривой в поле графика, координаты точек которой вы хотите узнать. После этого на графике появятся две пунктирные прямые, пересекающиеся на выбранной кривой.
Передвигая это перекрестье мышью или клавишами-стрелками, вы увидите в полях “X-Value”, “Y—Value” или “Y2—Value” координаты точки, на которой оно находится.

Щелкнув по кнопке “Copy X”, “Copy Y” или “Copy Y2” вы скопируете соответствующие координаты в буфер обмена.

Замечание. Если индикатор “Track data points” выключен, вы сможете узнать координаты любой точки поля графика, а не только точек, принадлежащих кривым.

studfiles.net

6. Построение графика функции, заданной параметрически.

Задать область изменения переменной t;
Записать аналитические выражения для x(t) и y(t);
Создать поле двумерного графика и указать на оси абсцисс x(t), а на оси ординат — y(t). (См. пример 6 и рис.12).

Пример 6.

рис.12. График функции, заданной параметрически.

7. Построение графика по массиву данных.

Пример 7.

р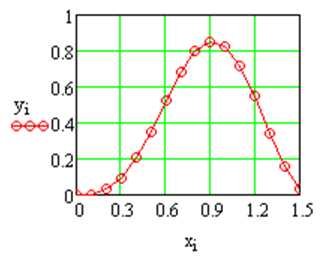ис.13. График, построенный по матрице данных.

Рассмотрим еще один пример.

Пример 8.

рис.14. График, построенный по массиву данных.

8. Увеличение фрагмента двумерного графика.

Активизируйте поле графика.
Вызовите команду Zoom одним из трех способов:

1) с помощью меню FormatGraphZoom;

2) щелкнув по кнопке “Zoom” из палитры “Graph”;

3) вызвав пункт Zoom из всплывающего меню, которое появится, когда вы щелкнете на графике правой кнопкой мыши.

После этого на экране появится диалоговое окно X-Y Zoom.

Выделите мышью тот фрагмент графика, который вы хотели бы увеличить.
Щелкните по кнопке (Zoom) в диалоговом окне X-Y Zoom.

9. Считывание координат двумерного графика.

Вы можете узнать координаты любой точки кривой. Для этого:

Активизируйте поле графика.
Вызовите команду Trace одним из трех способов:

1) с помощью меню FormatGraphTrace;

2) щелкнув по кнопке “Trace” из палитры “Graph”;

После этого на экране появится диалоговое окно X-Y Trace.

Проведите мышью по той кривой в поле графика, координаты точек которой вы хотите узнать. После этого на графике появятся две пунктирные прямые, пересекающиеся на выбранной кривой.
Передвигая это перекрестье мышью или клавишами-стрелками, вы увидите в полях “X-Value”, “Y—Value” или “Y2—Value” координаты точки, на которой оно находится.

Щелкнув по кнопке “Copy X”, “Copy Y” или “Copy Y2” вы скопируете соответствующие координаты в буфер обмена.

studfiles.net

Построение графиков функций, заданных параметрически — Мегаобучалка

Задание: Построить график функции

1. Решение этой задачи сведём к предыдущей задаче.

2. Запишем заголовки: в А1: t, в ячейку В1: х, в ячейку С1: у.

3. В столбце А с помощью маркера автозаполнения создать ряд значений для t от 0 до с шагом (либо при помощи набора команд: Правка Þ Заполнить Þ Црогрессия (шаг 0,314, предельное значение 6,28)).

4. В ячейку В2 вводим формулу =COS(2*A2)*SIN(A2)и копируем её в диапазоне В3:В22.

5. В ячейку С2 вводим формулу =COS(A2)*SIN(3*A2)и копируем её в диапазоне С3:С22.

6. Выделяем диапазон данных В2:С22 со значениями х и у, строим точечную диаграмму.

7. Результат работы представлен на рис. 7.

Построение графиков кусочно-непрерывной функции

Задание: Построить график функции , заданной тремя ветками на отрезке .

Для построения этого графика шаг изменения желательно выбирать поменьше, например, , и т. д. Далее в мастере диаграмм выбирать точечную диаграмму (первую в первой строке).

1. В ячейке A1 записываем заголовок X.

2. В ячейке В1 записываем заголовок f1.

3. В ячейке С1 записываем заголовок f2.

4. В ячейке D1 записываем заголовок f3.

5. В ячейке E1 записываем заголовок F(x).

6. В столбце А создаём ряд значений для х от -0,2 до 2,41 с шагом 0,03. Такой диапазон изменения взят с учётом промежутков, на которых задан каждый «кусок» функции. Так, по условию, у нас , поэтому можно взять в качестве крайнего левого значения аргумента. Кроме того, из третьего участка функции видно, что . Поэтому в качестве крайнего правого участка взято .

7. В ячейке B2 записываем формулу для вычисления функции по 1-й ветке: =ATAN(3,1*A2) и копируем её в столбце B.

8. В ячейке С2 записываем формулу для вычисления функции по 2-й ветке: =SIN(A2)^2*LN(A2) и копируем её в столбце С.

9. В ячейке D2 записываем формулу для вычисления функции по 3-й ветке: =КОРЕНЬ(A2^2+4*A2+11)и копируем её в столбце D.

10. В Е2 запишем формулу:

=ЕСЛИ(А2<0,47;В2;ЕСЛИ(А2>=2;D2;С2))

Скопируем её в столбце Е до конца диапазона изменения аргумента функции.

11. Выделим диапазон, состоящий из данных в столбце А и данных в столбце Е (используя клавишу CTRL) и строим точечную диаграмму.

12. Результат работы представлен на рис. 8.

Задания для самостоятельной работы

1. Построить график функции в прямоугольной системе координат. Диапазон изменения и шаг выберите самостоятельно:

10.

11.

12.

13.

14.

15.

2. Построить график функции, заданной в полярной системе координат:

10.

11.

12.

13.

14.

15.

3. Построить график функции, заданной параметрическим способом:

1. ,

2. ,

3. ,

4. ,

5. ,

6. ,

7. ,

8. ,

9. ,

10. ,

11. ,

12. ,

13. ,

14.

15.

4.Построить графики функций, используя функцию ЕСЛИ( )

а) Случай двух ветвей:

10.

11.

12.

13.

14.

15.

б) Случай трёх ветвей:

10.

11.

12.

13.

14.

15.

Лабораторный практикум № 4

megaobuchalka.ru

Построение графиков функций | Cubens

Как пользоваться программой

С помощью данной программы на Cubens можно построить график функции онлайн.

Десятичные дроби нужно разделять точкой
В некоторых случаях можно не писать знаки умножения
Можно строить множество графиков функций одновременно
Можно настроить названия осей и их интервалы
График можно скачать как PNG изображение
График можно распечатать
Можно получить ссылку на график чтобы поделиться им с другими
При наведении курсора на график его можно двигать, а также увеличивать или уменьшать масштаб

Предложения и замечания по работе программы можно оставить в комментариях ниже.

Режимы

На текущий момент в программе доступны четыре режима:

Обычный — в этом режиме можно строить графики функций, заданных уравнением
Параметрический — позволяет строить графики кривых, заданных параметрически, то есть, в виде и
Полярные координаты — позволяет строить графики кривых, заданных в полярной системе координат, то есть уравнением , где — радиальная координата, а — полярная координата
По точкам — этот режим предназначен для построения графиков функций указывая координаты их точек

График функции

Зависимость переменной от переменной называется функцией, если каждому значению соответствует единственное значение .

Функция обозначается или одной буквой или или равенством .

Область определения функции — это все значения, которые может принимать аргумент (переменная ).

Область значений функции — это все значения, которые может принимать функция (переменная ) при всех из области определения функции.

Функцию можно задать с помощью таблицы, графика или формулы. Формула задает правило, по которому каждому значению аргумента ставится в соответствие значение функции .

Графиком функции называется множество всех точек координатной плоскости с координатами , где первая координата пробегает всю область определения функции , а вторая координата — это соответствующее значение функции в точке .

cubens.com

Построение поверхности, заданной параметрически

При построении трехмерных поверхностей и объемных фигур можно использовать параметрическое задание описывающих их функций. При этом все три координаты задаются как функции от двух параметров u и v – X(u,v), Y(u,v), Z(u,v). Поверхности задаются значениями координат всех точек. При этом в шаблоне графики указываются три матрицы, хранящие массивы этих координат, X, Y Z.

Сначала необходимо задать векторы значений параметров и
Определить матрицы координат x(u,v), y(u,v) и y(u,v). Ввести как индексные переменные.
Вызвать график поверхности (Graph -> Surface Plot ). В шаблон занести имена матриц. Чтобы получилась фигура вращения, имена вводятся в скобках.
Настроить график.

Пример 3.11

Пример 3.11

На pис.3.28 показано построение объемной фигуры по точкам. (50 точек). Фигура задана параметрически, параметры – углы и. Координаты x,y,z вводятся как индексированные переменные, индексы – ранжированные переменные.

, ,

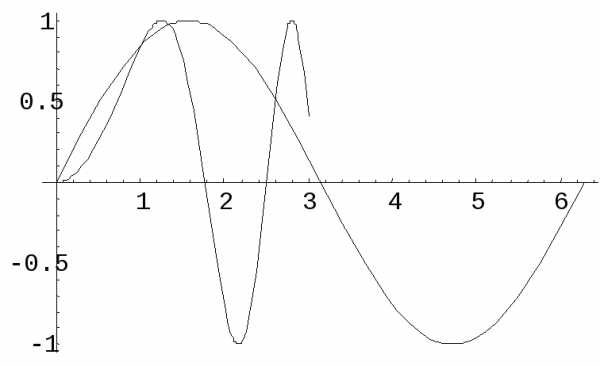
Рис. 3.28. Листинг примера. 3.11. Поверхность задана параметрически

Построение поверхности, заданной в векторной параметрической форме

Поверхность может быть задана в векторной форме. В этом случае функция вводится в виде матрицы, элементы которой – функции параметров, как и сама поверхность. На pис.3.27 показано построение объемной фигуры примера 3.11, заданной в виде матрицы от параметров — углов и. Количество линий сетки можно изменить в окне форматирования3-D Plot Format, вкладка QuickPlot Data .

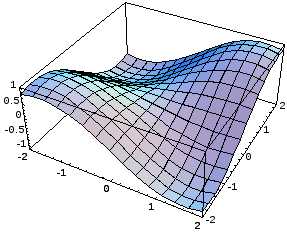
Рис. 3.29. Листинг примера. 3.11. Функция задана в векторной параметрической форме

3D точечный график

Трехмерный график можно представить в виде пространственной кривой. Пространственные кривые задаются, как правило, параметрически, и параметр является непрерывной действительной величиной. Рассмотрим два способа построения.

Пример 3.12

Построить пространственную кривую, у которой координаты определены следующим образом: ,,.

1 способ. Кривая в пространстве задается аналогично параметрическому заданию поверхности (пример 3.11).

Задать значения параметра t в виде ранжированной переменной, для t выбирается номер точки (0-100).
Определить координаты x, y, z как индексированные переменные параметра t.
Вызвать командой с панели Графика Graph / 3D Scatter Plot (график 3D точечный), в шаблон занести имена матриц в скобках (Рис.3.28).
Настроить график в окне форматирования.

На графике показаны максимальные минимальные значения

, ,

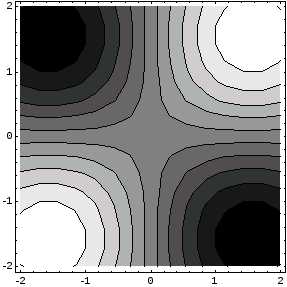
Рис. 3.30. Листинг примера 3.12. Параметрическое задание кривой

2 способ. (Рис.3.31). Векторная форма. Функция задается в виде матрицы-вектора. Для построения графика используется функция CreateSpace()

CreateSpace (R , t0, t1, tgrid, fmap): встроенная функция , создающая массив представляющий х-, у- и z-координаты параметрической пространственной кривой, заданной функцией R() ; и сетку точек на кривой, определенной функцией R() с параметрами , заданными аргументами ,

t0 и t1 – диапазон изменения параметровй, tgrid – размер сетки переменной, fmap – функция отображения аналогично функции CreateMesh() (необязательный параметр). Аргумент t выбирается из указанного интервала: t0=0 t1=10, сетка tgrid=100 точек. Создает сетку точек на кривой.

, ,

Рис. 3.31. Листинг примера 3.12. Векторное задание кривой. Использование CreateSpace()

studfiles.net

Использование excel для построения графиков функций заданных в параметрическом виде или в полярных координатах и графиков объемных функций цели урока

Бут Людмила Александровна

учитель информатики лицея №14 г.Жуковский

Использование Excel для построения графиков функций, заданных в параметрическом виде или в полярных координатах и графиков объемных функций.

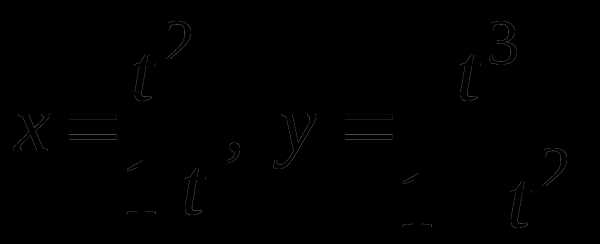Цели урока:

Образовательная:

Научить учащихся применять современное программное обеспечение в решении нестандартных задач;
Сформировать представление учащихся о способах построения объемных изображений средствами Excel.

Развивающая:

Продолжить развивать умения учащихся применять компьютер для решения конкретных задач из конкретной предметной области;
Развитие у школьников теоретического, творческого мышления, а также формирование операционного мышления, направленного на выбор оптимальных решений.

Воспитательная:

Задачи урока:

Воспитательная. Развитие познавательного интереса, воспитание информационной культуры.
Учебная. Изучить и закрепить основные навыки работы с электронными таблицами.
Развивающая. Развитие логического мышления, расширение кругозора.

Тип урока: Комбинированный — урок формирования и закрепления умений и навыков практического использования MS Excel.

План урока.

Организационная часть.
Повторение пройденного материала.
Обобщение и систематизация понятий для выполнения самостоятельной работы.
Самостоятельная работа.
Подведение итогов.
Домашнее задание.

Ход урока.

Вопросы для повторения:

Что такое относительная и абсолютная адресация?
Как протабулировать функцию, заданную в виде y=f(x)?
Как построить график функции, используя Мастер диаграмм?

На уроке мы рассмотрим особенности построения двух наиболее часто употребляемых в инженерной практике типов диаграмм – точечных (графиков) и поверхностных (или объемных).

Построение графиков функций, заданных в параметрическом виде или в полярной системе координат.

Параметрическое представление кривой на плоскости – это две функции, явно выражающие обе координаты x и y через значение некоторого производящего параметра:

Параметрические линии по форме могут быть более разнообразными, чем линии, описываемые одним уравнением. На них не распространяется ограничение по многозначности, поэтому линии могут быть самопересекающимися.

Для примера рассмотрим уравнение окружности с центром в начале координат и радиусом R.

Координаты точек окружности вычисляются по формулам:

Здесь центральный угол t является генерирующим параметром.

Для построения полной окружности радиуса R=100 составим таблицу, в которой значение параметра t меняется с шагом 0,1 от 0 до 2π.

Для построения графика выделим столбцы x и y таблицы и выберем тип диаграммы Точечная. Точечная диаграмма отображает взаимосвязь между числовыми значениями в нескольких рядах и представляет две группы чисел в виде одного ряда точек в координатах XY.

Получим диаграмму:

Полярные координаты и точки М на плоскости – это расстояние =ОМ от фиксированной точки О (полюса) до точки М и угол между лучами ОМ и ОР (полярная ось).

Полярные координаты являются наиболее употребительными после декартовых. Это нелинейные координаты. При построении кривых, заданных в полярных координатах, полярные координаты переводят в декартовы. Если полюс имеет координаты (x_0,y₀), то формулы преобразования таковы:

Для функций, заданных в полярных координатах формула имеет вид

, где – полярный угол.

Таблица должна содержать данные для построения кривой в полярной системе координат. Затем надо перевести данные из полярных координат в декартовы. Данные для построения точечного графика должны быть представлены в декартовой системе координат.

Рассмотрим Архимедову спираль, ее уравнение в полярных координатах:

ρ = aφ, где а — постоянная.

Составим таблицу для a=2, значение полярного угла меняется с шагом 0,1 от 0 до 6π. Такой диапазон выбран для того, чтобы увидеть несколько витков спирали.

Для построения графика выделим столбцы x и y таблицы и выберем тип диаграммы Точечная.

Получим диаграмму:

Задания для самостоятельной работы:

Построить графики замечательных кривых:

Астроида

Кардиоида

X=acost(1+cost)

Y=asint(1+cost)

или

ρ=a (1+cosφ)

n- лепестковая роза

ρ= asin mφ

или

ρ = a cos mφ

Лемниската Бернулли

ρ²-a²cos(2φ)=0

Элементы диаграммы можно видоизменять при помощи контекстного меню, вызываемого правой кнопкой мыши. Видоизменение, как правило, состоит в определении другого цвета для какого-то элемента, нового типа линии или маркера. Внести изменения можно, выбрав в контекстном меню первый пункт – Формат соответствующего объекта и определив нужные параметры.

Построение графика объемной функции.

Поверхности составляют широкое многообразие объектов трехмерного пространства. Инженерная деятельность человека связана непосредственно с конструированием, расчетом и, изготовлением различных поверхностей.

Поверхность будем рассматривать как непрерывное множество точек, между координатами которых может быть установлена зависимость, определяемая уравнением вида F(x,y,z)=0.

Рассмотрим зависимость, которая описывает сферу радиуса R.

X²+Y²+Z²=R²

Выразим z:

Поскольку z(x, y) является функцией двух переменных, то ее график будет объемным, т. к. по двум осям (x, y) будут откладываться значения аргументов, а по третьей (z) – вычисленные значения функции.

Сначала нужно создать таблицу значений функции в заданных диапазонах аргументов.

Если бы мы попытались сделать это известными способами, то нам потребовалось бы ввести большое множество значений аргументов, т. к. для каждого значения x пришлось бы ввести все значения диапазона y. При этом таблица имела бы очень большие размеры в длину или ширину. Однако можно построить таблицу по другому – в виде массива(матрицы): по строке отложить значения переменной x, а по столбцу – переменной y, а вычисленные значения функции – в ячейках на пересечении соответствующих значений аргументов. Это компактный способ представления данных.

Рассмотрим пример такой таблицы для R=3.

Значение квадрата радиуса вводится в ячейку B1.

В ячейки A3:A15 введите числа от -3 до 3 с шагом 0,5. Для этого воспользуемся в меню Правка подменю Заполнить подпунктом Прогрессия …Аналогично в ячейки B2:N2 введите числа от -3 до 3 с шагом 0,5. В ячейку B3 введите формулу =КОРЕНЬ($B$1-$A3^2-B$2^2). Для того, чтобы все значения x брались из строки 2, а все значения y из столбца A нужно использовать абсолютную адресацию. Замена относительных адресов в формуле на абсолютные производится с помощью клавиши F4, которая при выборе очередной ячейки при вводе формулы нажимается несколько раз до появления нужного вида адреса. Распространяя формулы на диапазон B3:O19, получим следующую таблицу( в ней удалены сообщения об ошибке в ячейках, где происходило извлечение квадратного корня из отрицательного числа).

Будем использовать стандартную объемную поверхностную диаграмму.

Поверхностные диаграммы отображают два или несколько рядов данных в виде поверхности.

В отличие от остальных диаграмм, в этом случае Excel применяет различные цвета для выделения значений, а не рядов данных.

Для построения графика выделим всю таблицу и выберем тип диаграммы Поверхность. Так как в таблице вычислены только положительные значения z , то на диаграмме будет изображена полусфера.

Получим объемный график.

Для видоизменения поверхностных диаграмм предоставляется больше возможностей. Вызвав через меню Диаграмма –Объемный вид диалоговое окно Формат трехмерной проекции, мы можем задать повороты в разных направлениях, перспективу, изменить высоту графика (задается в процентах от нормальной высоты), а также некоторые другие параметры.

Задания для самостоятельной работы:

Построить объемную диаграмму поверхностей второго порядка.

Эллиптический параболоид
Гиперболический параболоид
Вещественный конус
Однополостной гиперболоид
Двуполостной гиперболоид