1 класс. Математика. Точка. Прямая, кривая и ломаная линии. — Прямая линия. Кривая линия. Ломаная линия.
Комментарии преподавателя
На данном уроке Вы изучите простейшие геометрические понятия, о которых вам расскажет мама дракончиков. Вместе с дракончиками Вы изучите такие основные понятия, как прямая линия, луч, отрезок, угол, ломаная и кривая линия. У Вас будет возможность изучить предложенный материал на наглядных примерах.
Тема: Наглядная геометрия
Урок: Начальные геометрические понятия
На этом уроке будут изучены простейшие геометрические понятия. Для лучшего понимания рассмотрим сказку про дракончиков.
Далеко-далеко в горах живет большая-большая семья драконов: папа-дракон, мама-дракониха и много маленьких дракончиков. Когда дракончики были маленькие, они учились ползать, бегать, летать, прыгать, узнавали, что такое снег, дождь, звёзды, учились в горах ориентироваться, учились даже огнём дышать. Когда дракончики немножко подросли, мама решила их научить математики, в том числе геометрии. Дракончики очень удивились, они не поняли о чём идет речь. Мама предложила им сесть на площадке перед большой скалой и смотреть, что она будет рисовать. Она начала рисовать мелом на этом плоском куске скалы различные геометрические вещи, начиная с самых простых. Вначале мама-дракониха нарисовала линию, которая изображена на рисунке. (рис. 1)
Рис. 1
Мама-дракониха сказала, что эта линия называется прямая. Это такое геометрическое понятие.
Прямая линия – это линия, которая совершенно бесконечна.
Прямая линия идет бесконечно в одну сторону и в другую сторону. Есть такое даже выражение «Летит в небе по прямой».
Потом мама нарисовала точку и от неё провела линию. (рис. 2)
Рис. 2
Она объяснила, что точка – это начало, от нее идет линия в бесконечность. Это называется луч.
Луч — это полупрямая, которая имеет точку начала и не имеет конца.
Он так называется потому, что она как луч света. У луча света всегда есть начало. Он всегда начинается либо на солнце, либо на свечки, либо в фонарике, либо на звезде далекой. Дракончики поняли, что такое луч.
Потом мама-дракониха попросила представить дракончиков, что они от прямой отрежут кусочек. Такая фигура называется отрезок. (рис. 3)
Рис. 3
Отрезок — это часть прямой, которая ограничена с двух сторон.
Отрезок может быть длинным или коротким. Дракончики сразу не поняли. Тогда мама нарисовала еще несколько отрезков: длинные и короткие. (рис. 4)
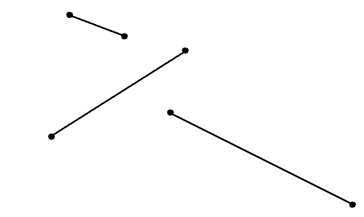
Рис. 4
Это всё отрезки. Теперь дракончики все поняли.
Потом мама-дракониха из одной точки отложила два луча, получилась фигура, которая называется угол. (рис. 5)

Рис. 5
Причем углом называется как вся фигура, так и что находится внутри неё.
Угол – это геометрическая фигура, образованная двумя лучами, выходящими из одной точки.
Потом мама-дракониха решила нарисовать еще одну форму линии. (рис. 6)
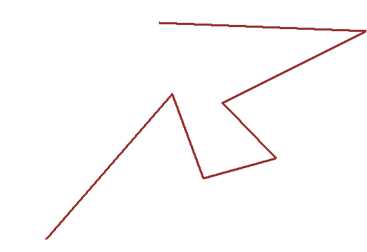
Рис. 6
Такая линия называется ломаная линия. Потому что взяли фактически прямую линию и поломали ее. И каждый кусочек на этой линии называется звено. Ломаные линии могут быть самые разные, по разному поломанные.
Следом мама нарисовала загогулину. (рис. 7)

Рис. 7
Это кривая линия. Таких кривых линий можно нарисовать много-много самых разных.
Потом мама-дракониха спросила у маленьких дракончиков, по какой линии они летаете в небе. Дракончики задумались. И один сказал, что он летает по кривой линии, он делает всякие пируэты, закладывает спирали, петли делает. А другой дракончик сказал, что когда они в снежки играли, он повисал в воздухе, махал крылышками, а в него кидали снежками. Он улетал от них и дёргался туда-сюда, туда-сюда. Получалась ломаная линия. Мама-дракониха сказала, что дракончики все поняли правильно. Драконы летают и по кривой линии, и по ломаной, иногда просто по прямой.
И тут мама заметила, что дракончики уже стали скучать и как-то вертеться, уже плохо её слушают. Она поняла, что пора их отпустить, она сказала, что урок закончен. Дракончики замахали крылышками, взлетели в небо, разлетелись над горами, весело кричали, смеялись. Мама смотрела на них и улыбалась, махала им лапой.
Итак, на уроке мы выучили такие простейшие геометрические понятия, как прямая линия, отрезок, луч, угол. Также мы рассмотрели ломаную и кривую линию. После изученного урока Вы будете знать простейшие геометрические понятия не хуже маленьких дракончиков.
Источник конспекта: http://interneturok.ru/ru/school/matematika/1-klass/beksperimentb/nachalnye-geometricheskie-ponyatiya?seconds=0
Источник видео: https://www.youtube.com/watch?v=o8Pu_Q8YFjk
www.kursoteka.ru
Урок 2. Кривые линии и волны.
Вы узнаете, как рисовать дудлинг, когда поймете его составляющие – основные элементы, из которых состоит любой рисунок. Первый урок состоит из упражнений с прямыми линиями, из которых составляются геометрические узоры. Самое главное, что важно в работе с повторяющимися линиями – это расстояние между линиями и их утолщение. Во втором уроке мы рассмотрим кривые, волнистые линии.
Большинство дудл-рисунков и клубков зентангл базируется именно на кривых линиях. В этом курсе мы изучаем дудлинг для начинающих, схемы этих уроков несложные, но они имеют важное значение, поскольку это базисные кирпичики, которые создают фундамент для дальнейшего познания все более сложных узоров. И в основе сложных узоров окажутся те же наши линии и точки: )
Для этого занятия вам понадобится бумага, желательно нелинованная. Для тренировки подойдет обычная бумага для печати. А для финальных рисунков можно завести отдельный блокнот с плотной бумагой или папку с бумагой для рисования. Плотная бумага особенно важна будет на тех этапах, когда мы включим в уроки рисование акварелью.
Также для рисования понадобится один линер (0,2 — 0,3) ( или тоненький маркер, или гелевая ручка). Если ничего этого нет под рукой, а потренироваться вы хотите прямо сейчас,то начните рисовать любым карандашом или обычной шариковой ручкой.
Упражнение 1.
В этом упражнении поработаем над рисованием волнистых линий, с определенными интервалами. Здесь развивается умение контролировать расстояние между линиями, и делать в определенных местах изменения, которые в итоге создадут интересный оптический эффект.
- Рисуем изогнутую линию, добавляем параллельные линии, постепенно увеличивая между ними шаг.
2- 5 . Рисуем волну с глубокими изгибами, добавляем с каждой стороны линии на равном удалении. Между линиями одинаковое расстояние, поэтому рисунок остается плоским. Этот прием мы будем использовать в ближайших занятиях, когда будем рисовать разные варианты лент.

упражнение 1
- Этот шаг упражнения похож на предыдущие, но здесь мы создаем не плоский, а объемный рисунок. Начинаем с дугообразной линии с небольшим искривлением. Следующую линию рисуем параллельно, но в области искривления (этот участок отмечен красным цветом), линию рисуем ближе к первой. Образуется оптическое углубление. На следующих шагах немного увеличиваем расстояние между линиями на «волне», оставляя небольшое расстояние у «углублении». Таким образом получается искривленная плоскость.
Упражнение 2.
В этом упражнении мы узнаем, как рисовать дудлинг с оптическим эффектом. Здесь приведен один из вариантов рисования объемных «трубок». Как видите, даже без спецэффектов – теней и бликов – желобки выглядят объемными, что достигается всего лишь изогнутыми линиями.
1-3. Основа задается волнистой линией. Далее можно пойти двумя путями: сразу нарисовать несколько базовых линий, и потом заполнять образовавшиеся дорожки (как в моем примере), либо нарисовать 2 линии, заполнить между ними пространство, и далее так добавлять по 1 линии и, соответственно, по 1 трубке.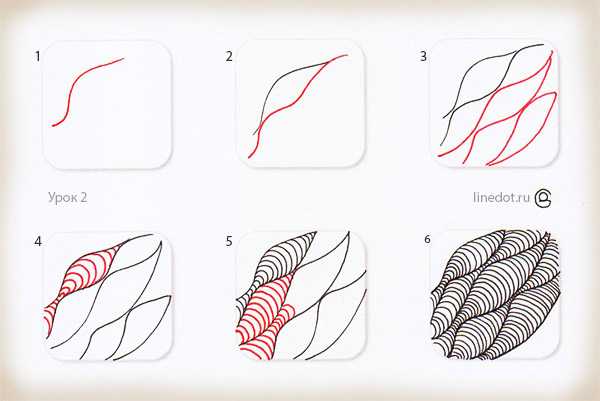
4-6. После того, как базовые линии, очерчивающие границы «трубок», созданы, начинаем рисовать параллельные линии в форме полукруга. Нарисованные поперечно они придают трубке округлость.
Вот пример таких линейных рисунков. Интересный оптический эффект, создаваемый кривыми линиями, популярен не только в зенарте, но и весьма характерен для стиля оп-арт, основной концепт которого — это оптические иллюзии.

Упражнение 3.
В этом блоке делаем разные утолщения, примерно, как на прямых линиях в предыдущем уроке.
- Здесь показано, как можно сделать эффект ленточки, утолщая линию по очереди то с одной, то с другой стороны.
- -3. Нарисуйте несколько волнообразных линий. Сначала поработайте над расширением линий с одной стороны. Затем на основе таких же параллельных линий сделайте узор с разными утолщениями.

Далее поработаем с такой же основой из нескольких параллельных волнообразных линий и сделаем сетчатый узор. Один из уроков полностью посвящен «сеткам», которые обязательно должны присутствовать в любом курсе дудлинг для начинающих Схемы таких узоров являются базисными. Сетчатый узор это одна из основных схем построения орнамента.
- Рисуем несколько изогнутых параллельных линий. Между ними располагаем в шахматном порядке диагональные прямые линии.
- Смягчаем уголки линиями, как бы срезая их.
- Закрашиваем образовавшиеся в уголках пустоты. Получилась сетка из прямых и кривых линий. Такой узор хорош для клубков зентангла, и его можно по разному трансформировать и детализировать.
Упражнение 4. Это упражнение больше экспериментальное, поскольку вам следует не повторять рисунок, а создать свои фрагменты узоров. Схемы здесь только для образца, как иллюстрация задания.
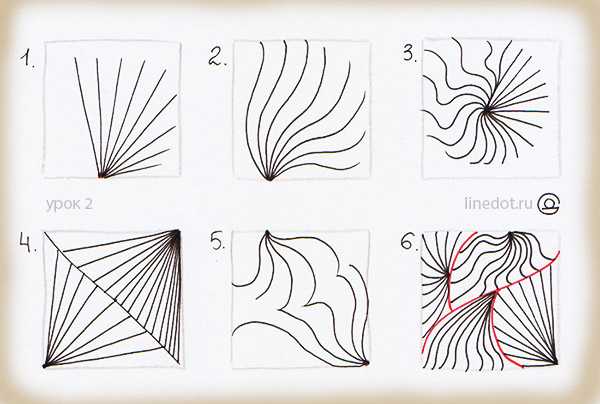
1-3. Рисуйте прямые и кривые линии из одной точки
4-5. Рисуйте прямые и кривые линии из разных точек. Линии соединяем, чтобы получить эффект выпуклостей и углублений. Экспериментируйте, чтобы понимать, какие получаются эффекты и как их можно применять в композициях.
- Делим площадь рисунка на сектора. В каждом секторе размещаем в любом месте точку, из которой рисуем прямые и кривые линии.
Мы сделали несколько упражнений, которые помогут понять, как рисовать дудлинг.Теперь осталось закрепить все пройденное в финальном рисунке.Если у вас еще остались силы, то можете это сделать прямо сейчас, либо отложите это на другое время, чтобы сделать рисунок с новыми силами красиво и аккуратно. Советую делать всегда финальные композиции прежде, чем перейдете к следующему уроку. В конце у вас соберется 25 рисунков, по которым вы отследите процесс и увидите результат!
Финальная композиция «Дудлинг с волнистыми линиями»
Делаем композицию с использованием нескольких отработанных элементов.
Для удобства ограничим пространство внешней границей. Можете нарисовать ее от руки в вольном стиле, начертить при помощи линейки, или просто возьмите какой-то предмет и очертите его. В моем случае под рукой оказался телефон.
Дальше можно разделить площадь на сектора и уже в секторах располагать элементы. Либо можно начать с какого- то места и продвигаться, заполняя всю площадь узорами. Действуйте, как вам нравится и постарайтесь включить в композицию разные отработанные варианты 1го и 2го урока.

На сегодня все. Надеюсь, этот урок был вам интересен и окажется полезным. Свои финальные композиции вы можете отправлять в предлагаемые новости на стену нашего клуба во Вконтакте http://vk.com/zenarts, в котором я тоже состою.
linedot.ru
Иллюстрированный самоучитель по компьютерной графике и звуку › CorelDRAW › Рисование линий [страница — 108] | Самоучители по средствам мультимедиа
Рисование линий
Как и в Фотошопе, в CorelDRAW можно рисовать произвольные линии и кривые Безье. Кроме того, Corel умеет создавать размерные линии для чертежей и несколько видов высокохудожественных линий, залитых симпатичными текстурками.
Произвольная линия
Карандашик Freehand рисует произвольную линию – ведет ее, пока нажата кнопка мышки. Как отпустили, так и прекратили рисовать. Тут же программа преобразует произвольную кривую в набор понятных ей простых кривых, расставит по линии узелки (начальный узелок будет самым большим), а внизу в информационной панели напишет что-то вроде: Curves on Layer 1 (кривая на первом слое) и Number of Nodes: 12 (число узелков 12).
Сразу же можно подвести карандашик к концевой или начальной точке своей линии и, убедившись, что программа вас поняла (курсор из вот такого: стал таким: ), продолжить рисование.
Стрелочку вместо кривульки курсор приобретает всякий раз, когда мышка попадает в зону вблизи начальной или конечной точки вашей линии.
По этому же признаку вы поймете, когда уже можно будет линию замкнуть – отпустить кнопку мыши. Замкнутую линию уже можно заливать цветом, градиентом или текстурой. Незамкнутую тоже можно, но заливка не будет видна. Она проявится только тогда, когда вы линию все же замкнете.
Возникает такой вопрос: а если мы собирались вовсе не продолжать линию, а начать новую вблизи этой точки, как быть?
Два ответа. Первый: нажать Esc или щелкнуть мышкой в стороне от линии, чтобы снять выделение с текущей линии, и начать рисование новой кривой. Второй: не снимая выделения, нажать клавишу CTRL, отчего курсор снова вместо стрелочки получит кривульку, и начать новую линию.
Противоположный вопрос: а как продолжить линию, если с нее уже снято выделение? Ответ напрашивается: выделить стрелочкой Pick, снова взять карандашик и продолжить.
Настройки линии показаны на рисунке 2.18, вся левая половина этой панели нам знакома, поговорим только о правой.
Рис. 2.18. Панель настроек инструмента Freehand
Три выпадающих списка чуть левее середины позволят создать в начальной и конечной точке стрелку и оперение (левый и правый списки), а также изменить стиль линии (штрих, пунктир и т. п.).
Кнопка Auto Close замыкает линию отрезком прямой. Самый правый движок всплывающая подсказка называет Freehand Smoothing, что переводится как «сглаживание произвольной линии». Именно этим параметром движок и управляет: при нуле нет никакого сглаживания, при 100% сглаживание максимально.
Из всех клавиш-модификаторов здесь действует только одна – SHIFT, причем весьма необычным образом. Стоит нажать эту клавишу (не отпуская мышки), как линия тянуться перестает. Таскаете мышку туда-сюда, а ничего не происходит. Но едва только вы отпустите SHIFT, как CorelDRAW соединит прямой линией текущее положение мышки с предыдущей точкой кривой и продолжит вычерчивание.
После того как кривая готова (неважно, замкнули вы ее или нет), можете менять ее форму, перетаскивая белые узелки. Когда с кривой снято выделение, вернуться к изменению размера или формы вы сможете, выбрав ее стрелочками выбора Pick или формы Shape, разговор о которых еще впереди.
В одиннадцатой версии CorelDRAW есть еще один инструмент, весьма похожий на карандашик , но более универсальный. Называется он Polyline (разные линии). Если нажать кнопку мыши и водить этим полилайном по странице, получается форменный Freehand. А если щелкать в разных точках страницы, то выйдет ломаная линия.
samoychiteli.ru
ᐈ Плавные линии на белом фоне
ᐈ Плавные линии на белом фоне — векторные изображения, рисунок плавные линии > скачать на Depositphotos®






alliesinteract
6900 x 5174



































rioillustrator
3000 x 2249


redshinestudio
4500 x 3267










ru.depositphotos.com
| «В этом уроке Вы познакомитесь с основными элементами рисунка: точкой, линией и пятном. Вы узнаете об их видах и использовании. Эти элементы являются средствами, при помощи которых можно создать любой рисунок как в иллюзии пространства на плоскости, так и в реальном пространстве. Затем мы познакомимся с другими, «производными» по отношению к упомянутым, элементами рисунка. Итогом нашей встречи станет рассмотрение различных способов рисования. ОТ ТОЧКИ К ФИГУРЕ В ПРОСТРАНСТВЕ Что такое точка Евклид (ок. 365-300 до н. э.) утверждал, что существует неделимая, не имеющая размеров математическая, геометрически воображаемая точка. Портрет Евклида (рис. 1) состоит из похожих, маленьких нарисованных точек с меньшей или большей степенью их концентрации (насыщенности). Практическое задание 1 Нарисуйте контуром, состоящим из точек, произвольную форму, например, человеческую фигуру. Практическое задание 2 При помощи произвольного инструмента зарисуйте точками формат небольшого квадрата, стараясь соблюдать одинаковую их светлоту, величину, а также одинаковые расстояния между ними. На втором рисунке такого же формата попытайтесь изменить одну из этих характеристик (валёр, размер или расположение). Практическое задание 3 Выполните подобный «frottage» в виде точек. Используйте её как основу (фон) для изображения объекта. Часть полученной фроттажной «графики» сотрите ластиком так, чтобы появившееся белое пятно напоминало определенную форму — к примеру, чашку, дерево, фигуру человека. Практическое задание 4 Выполните в подобной технике (тушью или капиллярной ручкой) рисунок любой другой несложной фигуры. Сами выберите вариант светотеневой моделировки формы объекта — с большей или меньшей концентрацией точек. Объемность в рисунке точками можно по¬лучить при помощи их дифференциации (различия, контраста) по размеру, светло¬те, форме, расположению и т.д. Выберите любую иллюстрацию, наложите на нее прозрачную кальку и перерисуйте изображение двумя способами: первый раз — используя точки одного вида, а второй -дифференцированные (по своему усмотрению). От точки к фигуре Оказывается, что любые формы, имеющиеся в натуре, можно получить, исходя из фиксации точки на плоскости — при помощи ее увеличения, изменения или придания объемности. Теперь рассмотрим, в чем именно состоит увеличение точки. Если к точке (рис. 14а) мы прибавим эту же точку, повторенную многократно и расположенную без разрыва одна за другой, то получим сначала короткий отрезок (14 б), а потом — линию (в). Изменяя направление развития точки, мы можем вместо прямой линии получить кривую (г). Если мы последовательно увеличим количество правильных точек, то получим линию с правильными краями, если увеличим неправильные точки — получим рваную линию (д).
Плоская фигура — это ограниченное формой пятно. Элемент рисунка-Его объемный эквивалент точка-объемная точка Предыдущие примеры, демонстрирующие увеличение, произвольное изменение или придание объемности точке, являющейся изображением (записью) на плоскости воображаемой математической точки, наглядно убеждают в том, что из неё можно получить все объемные элементы и формы, включая трехмерные фигуры. Очевидно, что более развитые элементы рисунка, находящиеся в цепочке на удаленных местах, можно получить из элементов, расположенных ближе к ее начальному звену — точке. К примеру, фигуру человека можно нарисовать точками, контуром, пятном, силуэтом и т. д. Перед тем, как мы рассмотрим более подробно некоторые примеры плоских и объемных элементов, встречающихся в натуре, запомним для себя простой, но важный вывод: все изображения на рисунке возникают из точки, линии, пятна и их взаимных комбинаций. ЧТО ТАКОЕ ЛИНИЯ Линия в натуральной перспективе Надеюсь, Вы хорошо усвоили, что натуральная сходящаяся перспектива подра¬зумевает воображаемые линии, сходящиеся в воображаемой точке схода, лежащей на линии горизонта. На рисунках из предыдущего урока, иллюстрирующих сходящуюся перспективу, нанесенных там линий в действительности не существует. Следует отличать видение линии в натуре от видения линии в рисунке. Мы уже говорили о том, что в природе нет линий, которыми были бы обведены какие-то формы, а значит, в натуре не существует контура — линии, очерчивающей форму. В то же время на рисунке мы можем увидеть следующие линии: самостоятельную, контурную или тонирующую (светотеневую). Самостоятельная линия Линии этого вида встречается очень часто. Они наиболее произвольны по своему характеру, направленности и не отображают конкретной формы. Такие линии выступают в рисунке «сами по себе», то есть как самостоятельный изобразительный элемент. Посмотрите на рисунок 19, который выполнен семилетней Евой. Здесь основой для изображаемой фигуры (моей!) являются, собственно, разновидности этого вида линии. Она будет еще часто появляться в иллюстрациях этого выпуска, а в каких именно — постарайтесь определить сами. Контурная линия и «воздействие» контура Еще раз посмотрите на рисунок Евы, которая на уровне незамысловатого детского воображения изобразила очертание фигуры. Аналогичным образом она нарисовала тучки, цветок и два других неизвестных растения. В её рисунке присутствуют контурные и самостоятельные линии. В ушах, чем-то напоминающих воздушные шарики, тоже есть замкнутые контуры. Помните мою фотографию, напечатанную в первом уроке? Сравните с ней рисунок. Очень удачный получился у ребенка портрет, неправда ли? Тонирующая линия — это, другими словами, светотеневая линия. Она применяется там, где, согласно нашему воображению или видению объектов в натуре, мы хотим на рисунке ввести тень. Мы можем наносить эти линии так, как это показано на рис. 27, где партию света играет естественная белизна бумажного листа. Штриховка — это один из наиболее распространенных приемов тонирования в рисунке или графике с помощью как идентичных параллельных, так и (или) пересекающихся линий. Нарисуйте контуром простой предмет, расположенный на горизонтальной плоскости. Затем, используя приемы разнообразной штриховки, постарайтесь выразить его форму с собственной падающей тенью и условной передачей фона и основания. Думаю, что иллюстрация рисунка Леонардо да Винчи поможет Вам правильно выполнить задание. Линия (черта) возникает из последовательного сочетания многих точек. В рисунке ее получают путем передвижения рисовального инструмента, оставляющего след на поверхности формата. Зарисовка всей плоскости формата линией Зарисовка квадратного формата мелким растром (сеткой из тонкой линии одного вида, то есть без каких-либо контрастов) привела к появлению своего рода серого пятна, плоскости в одинаковом валёре (рисунок 35а выполнен в компьютерной графике). Следующий рисунок более дифференцированный, поскольку вертикальные, под линейку нарисованные линии различаются между собой по светлоте и толщине, воздействуя при этом более сильно в той части, где они темнее и насыщеннее (356). На рис. 38 показана градация прямой вертикальной линии в шести стадиях: от темной широкой — до светлой тонкой (рис. 38а). Близлежащие линии между собой не контрастируют, зато если мы сравним крайние линии, то контраст между ними очевиден. Из прямой геометрической линии можно также получить линию иного вида, например, зигзагообразную, как на иллюстрации 39; где контраст наглядно виден уже между каждой линией. Для одного и того же вида линии возможны варианты преобразования, которые представлены на следующих рисунках. Рисунок 41а демонстрирует отдельную волнистую линию -промежуточную между биологической и геометрической, многократно повторенную с одинаковым промежутком в формате квадрата. Рисунок выглядит как изображение волнистой выпуклой или вогнутой плоскости. Если мы сделаем линии более толстыми, а также увеличим расстояния между ними, то получим такой набор линий, как на рис. 416, а если будем утолщать их и дальше — такой, как на рис. 41 в. В последнем рисунке введены контрасты за счет чередования тонкой и толстой линий, взятых из рис. 41а и 41в и изменения их наклона. Практическое задание 7 В иллюстрации рисунка Леонардо да Винчи, на который я уже дважды ссылался, попытайтесь найти линии, аналогичные представленным на рисунках 42.
Перекрывающее наложение линий Нанесение линий с перекрытием, то есть, таким образом, когда одна заслоняет другую, также часто используется в рисунках. В зависимости от степени контраста линий между собой, их размера и расположения, возникает определенный оптический эффект. |
tyblako.livejournal.com
2.5. Рисование прямых линий — «улыбки» кота
2.5.1. Выберите инструмент FreeHand (Кривая).Подведите перекрестье курсора к точке, где будет начинаться «улыбка» (см. рис. 9.). Щелкните и отпустите кнопку мыши. Перемещайте мышь. За курсором потянется линия. Когда она достигнет нужной длины, щелкните кнопкой мыши.
2.5.2. Для создания «улыбки» созданную прямую линию надо продолжить. Для этого подведите курсор к правому концу линии, щелкните на конце линии и проведите еще одну прямую. Создайте всю «улыбку» кота.
2.6. Рисование линий произвольной формы — усов кота
2.6.1. Выберите инструментFreeHand (Кривая).Щелкните в точке, где будет начинаться ус. Не отпуская кнопку мыши, нарисуйте коту ус, затем отпустите кнопку. Кривая имеет несколько узлов, выделенных белыми квадратиками.
2.6.2. Выберите инструмент Shape (Фигура). Щелкните на каком-нибудь узле. Помимо маркера, обозначающего сам узел, у выделенного узла появятся две касательных линии (вектора).
Изменяя положения и длины касательных линий, а также положение узловой точки, Вы можете изменять форму кривой и придать усам кота любую, нравящуюся Вам, форму.
Если в процессе работы Вам необходимо удалить узел, то выделите его и нажмите на кнопку со знаком минус на панели свойств (рис. 10). Если необходимо добавить узел, то щелчком мыши укажите его место. На линии появится круглая жирная точка, затем щелкните по кнопке со знаком плюс на панели свойств.
2.7. Редактирование кривых – «улыбки» кота
2.7.1.Выберите инструмент Shape(Фигура)(рис. 7). Выделите «улыбку» кота. В узлах соединения сегментов линии появятся хорошо заметные маркеры.
2.7.2. Выделите второй узел слева. Щелкните по кнопке Convert Line to Curve(Преобразовать в кривую)на панели свойств (рис. 10). Вид первого сегмента не изменился, но из его узлов идут касательные линии, позволяющие (как было описано выше) плавно менять форму кривой.
2.7.3. Преобразуйте все остальные участки ломаной линии. Для этого выберите все узлы и щелкните по кнопке Convert Line to Curve (Преобразовать в кривую).Теперь каждый узел, если его выделить, будет иметь касательные вектора.
2.7.4. Выберите все узлы, кроме среднего. В панели свойств щелкните по кнопке Make Node Symmetrical (Сглаженный).Углы ломаной линии превратятся в плавные переходы между сегментами.
2.7.5. Отредактируйте форму улыбки, пользуясь теми же приемами, как и для редактирования формы усов.
2.8. Копирование и вклеивание объектов
2.8.1. С помощью инструментаPick (Указатель)выделите пятиугольник – зубец короны.
2.8.2. Выберите в главном меню пункт Edit>Copy (Правка> Копировать) или одновременно нажмите клавиши «Ctrl+Insert»: Вы скопировали объект в буфер обмена.
2.8.3. Выберите в главном меню пункт Edit>Paste (Правка> Вставить) или одновременно нажмите клавиши «Shift+Insert». Объект из буфера будет вклеен на рабочую страницу поверх исходного.
2.8.4. С помощью инструмента Pick (Указатель)выделите и переместите объект. Поместите копию зубца короны на левом краю основания (рис. 11). Перемещение будет осуществляться строго в горизонтальном или вертикальном направлении, если удерживать нажатой клавишу «Ctrl».
Кроме копирования можно производить вырезание объектов — пункт меню Edit>Cut (Правка>Вырезать)или одновременное нажатие клавиш «Shift» и «Delete». При этом объект исчезает с экрана, но его копия попадает в буфер обмена и может быть вставлена в любой части рисунка.
studfiles.net
Плавная кривая линия — Большая Энциклопедия Нефти и Газа, статья, страница 1
Плавная кривая линия
Cтраница 1
Плавные кривые линии, составленные дугами окружностей различных радиусов, называют коробовыми кривыми линиями. [1]
Плавные кривые линии, которые нельзя заменить системой дуг окружностей, обводятся с помощью лекал линейными рейсфедерами. Вначале определяются точки будущей лекальной кривой. Чтобы иметь представление о характере кривой линии, полученные точки плавно соединяют карандашом от руки. [2]
Соединяя их плавной кривой линией, получаем график данной функциональной зависимости. Преимуществом графического изображения по сравнению с табличным являются его наглядность и легкая обозримость; недостатком — малая степень точности. Большое практическое значение имеет удачный выбор масштабов. [3]
Ось вала представляет собой плавную кривую линию, так как вал Прогибается под действием собственного веса и веса рабочих колес. [5]
Построенные точки соединим плавной кривой линией и получим приближенный график данной функции ( фиг. [6]
Соединив эти точки плавной кривой линией, получим приближенный график функции у 2 sin x ( фиг. [7]
Построенные точки соединим плавной кривой линией и получим приближенный график данной функции ( фиг. [8]
Соединив эти точки плавной кривой линией, получим приближенный график функции у 2 sin x ( фиг. [9]
Соединяя построенные точки плавными кривыми линиями, получаем очерк одного лепестка развертки. [10]
Построенные точки последовательно соединяют плавной кривой линией / с учетом ее видимости. [11]
Построенные точки последовательно соединяют плавной кривой линией / с учетом ее видимости. [12]
Построенные фронтальные проекции точек соединяют плавной кривой линией, точки пересечения которой т и п с фронтальной проекцией а Ь прямой А В являются фронтальными проекциями искомых точек пересечения прямой А В с поверхностью тора. По ним в проекционной связи строят горизонтальные проекции тип точек пересечения. Невидимый отрезок MN прямой А В проведен штриховой линией. [13]
Соединяя крайние точки построенных отрезков плавными кривыми линиями, получаем очерк одного звена ( лепестка) развертки неполной модели заданной поверхности вращения. На рис. 418 построено четыре таких звена. [14]
Страницы: 1 2 3 4
www.ngpedia.ru