Системы счисления
Система счисления – это способ представления чисел и соответствующие ему правила действий над числами. Система счисления – это знаковая система, в которой числа записываются по определенным правилам с помощью символов некоторого алфавита, называемых цифрами.Известно множество способов представления чисел. В любом случае число изображается символом или группой символов (словом) некоторого алфавита. Будем называть такие символы цифрами. Для представления чисел используются непозиционные и позиционные системы счисления.
В непозиционных системах каждая цифра имеет свой вес и ее значение не зависит от положения в числе – от позиции. Пример – римская система. Скажем, число 76 в этой системе выглядит так:
LXXVI, где L=50, X=10, V=5, I=1.
Как видно цифрами здесь служат латинские символы.
В позиционных системах значения цифр зависят от их положения (позиции) в числе.
Так, например, человек привык пользоваться десятичной позиционной системой — числа записываются с помощью 10 цифр. Самая правая цифра обозначает единицы, левее — десятки, ещё левее — сотни и т.д.
В любой позиционной системе число может быть представлено в виде многочлена.
Покажем, как представляют в виде многочлена десятичное число.
.
Система счисления – очень сложное понятие. Оно включает в себя все законы, по которым числа записываются и читаются, а так же те, по которым производятся операции над ними.
Самое главное, что нужно знать о системе счисления – ее тип: аддитивная или мультипликативная. В первом типе каждая цифра имеет свое значение, и для прочтения числа нужно сложить все значения использованных цифр:
XXXV = 10+10+10+5 = 35; CCXIX = 100+100+10–1+10 = 219;
Во втором типе каждая цифра может иметь разные значения в зависимости от своего местоположения в числе:
(иероглифы по порядку: 2, 1000, 4, 100, 2, 10, 5)
Здесь дважды использован иероглиф “2”, и в каждом случае он принимал разные значения “2000” и “20”.
2? 1000 + 4? 100+2? 10+5 = 2425
Для аддитивной (“добавительной”) системы нужно знать все цифры-символы с их значениями (их бывает до 4-5 десятков), и порядок записи. Например, в Латинской записи если меньшая цифра записана перед большей, то производится вычитание, а если после, то сложение (IV = (5–1) = 4; VI = (5+1) = 6).
Зачем числа?
«Все есть число», — говорили пифагорийцы (ученики древнегреческого математика Пифагора). Значит всё можно обозначить числом.
Так как многие предметы внешнего мира имеет схожую форму, возникла потребность их сосчитать. Например, сколько коров в стаде. Сколько добыто рыб, или зайцев. Т.е. число и арифметика возникли из практической деятельности человека.
Так как многие народы в древности не общались друг другом, то у разных народов возникли разные системы счисления и представления чисел и цифр.
Число — это обобщение, так как разными числами можно подсчитать разные предметы.
Цифры – это значки, с помощью которых записывают числа. Система счисления или нумерация – это способ записи чисел с помощью цифр.
Простая система счисления
У первобытных людей не было даже чисел, они количество предметов отображали равным количеством каких-либо значков. Такими значками могли быть зарубки, черточки, точки, а так же узелки на веревках.
Это самая простая система счисления. В этой системе счисления для записи чисел используется только одна цифра. Ее можно изобразить в виде палочки ?, кружочка 0, или любой другой фигуры. Тогда числа будут записываться примерно так:
|
1 |
? |
|
2 |
?? |
|
3 |
??? |
|
4 |
??? |
|
5 |
? ? ? ? ? и т. д. |
Такая система счисления использовалась, и до сих пор используется народами, не имеющими письменности.
Но иногда такой системой счисления пользуются и современные люди, например, отмечая зарубками количество прошедших дней, или карандашом отмечая черточками в тетради количество проданных товаров.
Позже, для облегчения счета, эти значки стали группировать по три или по пять. Такая система записи чисел называется единичной (унарной), так как любое число в ней образуется путем повторения одного знака, символизирующего единицу.
Но это удобно, пока числа небольшие. Вы только представьте себе число 1 000 записанное с помощью кучки камушков, а 1 000 000? Неудобно?
И люди начали изобретать системы счисления.
Позиционные и непозиционные системы счисления
Системы счисления бывают непозиционными (аддитивными) и позиционными (мультипликативными).
Чтобы разобраться в этом рассмотрим для примера нашу «арабскую» систему счисления. Например, число 3333 – три тысячи триста тридцать три. Здесь каждая цифра «3» в зависимости от того, в каком месте находиться обозначает свое число. Первая тройка слева, это три тысячи, вторая, три сотни, третья – три десятка, четвертая – три единицы. Т.е. это позиционная система. В таких же системах значение каждой цифры, зависит от ее положения (места, позиции) в записи числа. В непозиционных системах значение каждой цифры не зависит от ее положения (места, позиции) в записи числа.
Число 3333 можно представить в таком виде 3?1000 + 3?100 + 3?10 + 3. Т.е. для представления этого числа используется умножение (по-английски multiplication), отсюда название этой системы — мультипликативная.
В непозиционных же системах для представления числа используется сложение всех цифр, по-английски сложение – add. Поэтому другое название этих систем — аддитивные.
Основание системы счисления
Основание системы счисления – это число, на основе которого ведется счет. Например, если основание системы счисления равно десяти, то минимальная счетная группа этой системы счисления равна десяти, это значит, что, сосчитав какие-либо предметы до десяти, мы считаем снова с единицы, но при этом запоминаем число десятков. В нашей «арабской» системе основанием является число десять. Есть системы счисления и с другим основанием. Это такие системы счисления как пятеричная, двенадцатеричная, двадцатеричная, шестидесятеричная.
Десятеричная и пятеричная система возникла от того факта, что на одной руке человека пять пальцев, на обоих руках 10 пальцев.
Так проще считать. Если добавить пальцы и на ногах, то будет понятная и двадцатеричная система. Происхождение двенадцатеричной системы тоже связано со счетом на пальцах. Считали большой палец руки и фаланги остальных четырех пальцев.
Если двенадцать умножить на пять получим шестидесятеричную систему. Например, на одной руке загибаем пальцы, пока не получим, что отсчитано, пять штук, а на другой руке прикосновением большого пальца к суставам остальных четырех указываем количество этих пятерок.
В некоторых системах счисления используются для обозначения цифр буквы, такие системы счисления называются алфавитными.
Итак, бывают непозиционные (аддитивные) и позиционные (мультипликативные), пятеричные, десятичные, двенадцатеричные, двадцатеричные, шестидесятеричные и алфавитные системы счисления.
Вначале рассмотрим непозиционные (аддитивные) системы счисления.
Древнеегипетская десятичная
Примерно в третьем тысячелетии до нашей эры древние египтяне придумали свою числовую систему, в которой для обозначения ключевых чисел 1, 10, 100 и т.д. использовались специальные значки — иероглифы.
Все остальные числа составлялись из этих ключевых при помощи операции сложения. Система счисления Древнего Египта является десятичной, но непозиционной и аддитивной.
|
|
1. Как и большинство людей для счета небольшого количества предметов Египтяне использовали палочки. |
|
|
Если палочек нужно изобразить несколько, то их изображали в два ряда, причем в нижнем ряду должно быть столько же палочек, сколько и в верхнем, или на одну больше. |
|
|
10. Такими путами египтяне связывали коров |
|
|
Если нужно изобразить несколько десятков, то иероглиф повторяли нужное количество раз. Тоже самое относится и к остальным иероглифам. |
|
|
100. Это мерная веревка, которой измеряли земельные участки после разлива Нила. |
|
|
1 000. Вы когда-нибудь видели цветущий лотос? Если нет, то вам никогда не понять, почему Египтяне присвоили такое значение изображению этого цветка. |
|
|
10 000. «В больших числах будь внимателен!» — говорит поднятый вверх указательный палец. |
|
|
100 000. Это головастик. Обычный лягушачий головастик. |
|
|
1 000 000. Увидев такое число, обычный человек очень удивится и возденет руки к небу. Это и изображает этот иероглиф |
|
|
10 000 000. Египтяне поклонялись Амону Ра, богу Солнца, и, наверное, поэтому самое большое свое число они изобразили в виде восходящего солнца |
Записывались цифры числа начиная с больших значений и заканчивая меньшими. Если десятков, единиц, или какого-то другого разряда не было, то переходили к следующему разряду.
— 1205, — 1 023 029
Попробуйте сложить эти два числа, зная, что более 9 одинаковых иероглифов использовать нельзя, и вы сразу поймете, что для работы с этой системой нужен специальный человек. Обычному человеку это не под силу.
Недостатки непозиционной системы счисления
Непозиционные системы счисления имеют ряд существенных недостатков:
1. Существует постоянная потребность введения новых знаков для записи больших чисел.
2. Невозможно представлять дробные и отрицательные числа.
3. Сложно выполнять арифметические операции, так как не существует алгоритмов их выполнения. В частности, у всех народов наряду с системами счисления были способы пальцевого счета, а у греков был счетная доска абак – что-то наподобие наших счетов.
Но мы до сих пор пользуемся элементами непозиционной системы счисления в обыденной речи, в частности, мы говорим сто, а не десять десятков, тысяча, миллион, миллиард, триллион.
Далее рассмотрим позиционные системы счисления.
Вавилонская десятеричная / шестидесятеричная
В древнем Вавилоне примерно во II тысячелетие до нашей эры была такая система счисления — числа менее 60 обозначались с помощью двух знаков: для единицы, и для десятка. Они имели клинообразный вид, так как вавилоняне писали на глиняных табличках палочками треугольной формы. Эти знаки повторялись нужное число раз, например
— 3; — 20; — 32; — 59
Числа больше 60 записывались по разрядам, с небольшими пробелами между ними:
Так записывается число 302, то есть 5*60+2.
А это 1*60*60+2*60+5 = 3725.
Но представление не которых чисел в этой системе будет одинаковым, например, число 302, может быть и равно и 5*60*60 + 2 = 18002. Так как нет значка для обозначения нуля.
Лишь в V веке до нашей эры был введен особый знак — наклонный клин для обозначения пропущенных разрядов, игравший роль нуля.
это запись числа 7203 (2*60*60+3).
Однако отсутствие низшего разряда не обозначалось, и поэтому число 180 = 3*60 записывалось так , а обозначать эта запись могла и 3, и 180, и 10800 (3*60*60), и т. д.
Считается, что десятичная система была у шумеров, а после того как их завоевали семиты, их система была приспособлена под шестидесятеричную систему семитов.
Шестидесятеричная запись целых чисел не получила широкого распространения за пределами Ассиро-вавилонского царства, но шестидесятеричные дроби применяются до сих пор при измерении времени. Например, одна минута = 60 секунд, один час = 60 минут.
Древнекитайская десятеричная
Эта система одна из старейших и самых прогрессивных, поскольку в нее заложены такие же принципы, как и в современную «арабскую», которой мы с Вами пользуемся. Возникла эта система около 4 000 тысяч лет тому назад в Китае.
Числа в этой системе, так же как и у нас записывались слева направо, от больших к меньшим. Если десятков, единиц, или какого-то другого разряда не было, то сначала ничего не ставили и переходили к следующему разряду. (Во времена династии Мин был введен знак для пустого разряда — кружок — аналог нашего нуля). Чтобы не перепутать разряды использовали несколько служебных иероглифов, писавшихся после основного иероглифа, и показывающих какое значение принимает иероглиф-цифра в данном разряде.
 — 1*1 000 = 1000;
— 1*1 000 = 1000;
— 5 * 100+4* 10+8 = 548
Эта мультипликативная запись, так как в ней используется умножение. Она десятичная, в ней есть знак нуля, кроме этого она позиционная. Т.е. она почти соответствует «арабской» системе счисления.
Двадцатеричная система счисления индейцев Майя или долгий счет
Эта система очень интересна тем, что на ее развитие не повлияла ни одна из цивилизаций Европы и Азии. Эта система применялась для календаря и астрономических наблюдений. Характерной особенностью ее было наличие нуля (изображение ракушки). Основанием этой системы было число 20, хотя сильно заметны следы пятеричной системы. Первые 19 чисел получались путем комбинирование точек (один) и черточек (пять).
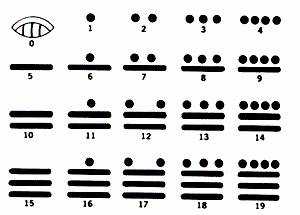
Число 20 изображалось из двух цифр, ноль и один наверху и называлось уиналу. Записывались числа столбиком, внизу располагались наименьшие разряды, вверху наибольшие, в результате получалась «этажерка» с полками. Если число ноль появлялось без единицы наверху, то это обозначало, что единиц данного разряда нет. Но, если хоть одна единица была в этом разряде, то знак нуля исчезал, например, число 21, это будет . Так же в нашей системе счисления: 10 – с нулем, 11 – без него. Вот несколько примеров чисел:

В двадцатеричной системе счета древних майя есть исключение: стоит прибавить к числу 359 только одну единицу первого порядка, как это исключение немедленно вступает в силу. Суть его сводится к следующему: 360 является начальным числом третьего порядка и его место уже не на второй, а на третьей полке.
Но тогда выходит, что начальное число третьего порядка больше начального числа второго не в двадцать раз (20×20=400, а не 360!), а только в восемнадцать! Значит, принцип двадцатеричности нарушен! Все верно. Это и есть исключение.
Дело в том, что у индейцев Майя 20 дней-кинов образовывали месяц или уинал. 18 месяцев-уиналов образовывали год или туну (360 дней в году) и так далее:
К’ин = 1 день.
Виналь = 20 к’ин = 20 дней.
Тун = 18 виналь = 360 дней = около 1 года.
К’атун = 20 тун = 7200 дней = около 20 лет.
Бак’тун = 20 к’атун = 144000 дней = около 400 лет.
Пиктун = 20 бак’тун = 2880000 дней = около 8000 лет.
Калабтун = 20 пиктун = 57 600 000 дней = около 160000 лет.
К’инчильтун = 20 калабтун = 1152000000 дней = около 3200000 лет.
Алавтун = 20 к’инчильтун = 23040000000 дней = около 64000000 лет.

Это довольно сложная система счисления, в основном использовалась жрецами для астрономических наблюдений, другая система индейцев Майя была аддитивной, похожей на египетскую и применялась в повседневной жизни.
anastasi-shherbakova.narod.ru
основание системы счисления — это… Что такое основание системы счисления?
- основание системы счисления
- base, base number, radix number, radix
Большой англо-русский и русско-английский словарь. 2001.
- основание робота
- основание скошенного шипа
Смотреть что такое «основание системы счисления» в других словарях:
основание (системы счисления) — основание логарифмов корень — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы основание логарифмовкорень EN radix … Справочник технического переводчика
основание системы счисления — показатель степени коэффициент абсолютное значение остаток целочисленного деления — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы показатель… … Справочник технического переводчика
основание системы счисления с плавающей точкой — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN floating point base … Справочник технического переводчика
отрицательное основание системы счисления — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN negative base … Справочник технического переводчика
смешанное основание системы счисления — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN mixed radix … Справочник технического переводчика
Основание позиционной системы счисления — в широком смысле конечный набор знаков (цифр), для представления чисел. Основание позиционной системы счисления в узком смысле количество знаков, используемых для записи чисел в той или иной позиционной системе счисления. Основание показывает, во … Финансовый словарь
СИСТЕМЫ СЧИСЛЕНИЯ — СИСТЕМЫ СЧИСЛЕНИЯ, способы счета, в которых используются различные ОСНОВАНИЯ. ДЕСЯТИЧНАЯ СИСТЕМА счисления, например, имеет основание из десяти цифр. ДВЕНАДЦАТИРИЧНАЯ СИСТЕМА счисления имеет основание из 12 цифр. Компьютеры осуществляют расчеты в … Научно-технический энциклопедический словарь
основание (позиционной системы счисления) — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN base radix … Справочник технического переводчика
Позиционные системы счисления — Позиционная система счисления система счисления, в которой один и тот же числовой знак (цифра) в записи числа имеет различные значения в зависимости от того места (разряда), где он расположен. Изобретение позиционной нумерации, основанной на… … Википедия
ЦИФРЫ И СИСТЕМЫ СЧИСЛЕНИЯ — Интуитивное представление о числе, по видимому, так же старо, как и само человечество, хотя с достоверностью проследить все ранние этапы его развития в принципе невозможно. Прежде чем человек научился считать или придумал слова для обозначения… … Энциклопедия Кольера
Нега-позиционные системы счисления — Нега позиционная система счисления это позиционная система счисления с отрицательным основанием. Особенностью таких систем является отсутствие знака перед отрицательными числами и, следовательно, отсутствие правил знаков. Всякое число любой из… … Википедия
dic.academic.ru
Двоичная система счисления
В двоичной системе счисления используются всего две цифры 0 и 1. Другими словами, двойка является основанием двоичной системы счисления. (Аналогично у десятичной системы основание 10.)
Чтобы научиться понимать числа в двоичной системе счисления, сначала рассмотрим, как формируются числа в привычной для нас десятичной системе счисления.
В десятичной системе счисления мы располагаем десятью знаками-цифрами (от 0 до 9). Когда счет достигает 9, то вводится новый разряд (десятки), а единицы обнуляются и счет начинается снова. После 19 разряд десятков увеличивается на 1, а единицы снова обнуляются. И так далее. Когда десятки доходят до 9, то потом появляется третий разряд – сотни.
Двоичная система счисления аналогична десятичной за исключением того, что в формировании числа участвуют всего лишь две знака-цифры: 0 и 1. Как только разряд достигает своего предела (т.е. единицы), появляется новый разряд, а старый обнуляется.
Попробуем считать в двоичной системе:
0 – это ноль
1 – это один (и это предел разряда)
10 – это два
11 – это три (и это снова предел)
100 – это четыре
101 – пять
110 – шесть
111 – семь и т.д.
Перевод чисел из двоичной системы счисления в десятичную
Не трудно заметить, что в двоичной системе счисления длины чисел с увеличением значения растут быстрыми темпами. Как определить, что значит вот это: 10001001? Непривычный к такой форме записи чисел человеческий мозг обычно не может понять сколько это. Неплохо бы уметь переводить двоичные числа в десятичные.
В десятичной системе счисления любое число можно представить в форме суммы единиц, десяток, сотен и т.д. Например:
1476 = 1000 + 400 + 70 + 6
Можно пойти еще дальше и разложить так:
1476 = 1 * 103 + 4 * 102 + 7 * 101 + 6 * 100
Посмотрите на эту запись внимательно. Здесь цифры 1, 4, 7 и 6 — это набор цифр из которых состоит число 1476. Все эти цифры поочередно умножаются на десять возведенную в ту или иную степень. Десять – это основание десятичной системы счисления. Степень, в которую возводится десятка – это разряд цифры за минусом единицы.
Аналогично можно разложить и любое двоичное число. Только основание здесь будет 2:
10001001 = 1*27 + 0*26 + 0*25 + 0*24 + 1*23 + 0*22 + 0*21 + 1*20
Если посчитать сумму составляющих, то в итоге мы получим десятичное число, соответствующее 10001001:
1*27 + 0*26 + 0*25 + 0*24 + 1*23 + 0*22 + 0*21 + 1*20 = 128 + 0 + 0 + 0 + 8 + 0 + 0 + 1 = 137
Т.е. число 10001001 по основанию 2 равно числу 137 по основанию 10. Записать это можно так:
100010012 = 13710
Почему двоичная система счисления так распространена?
Дело в том, что двоичная система счисления – это язык вычислительной техники. Каждая цифра должна быть как-то представлена на физическом носителе. Если это десятичная система, то придется создать такое устройство, которое может быть в десяти состояниях. Это сложно. Проще изготовить физический элемент, который может быть лишь в двух состояниях (например, есть ток или нет тока). Это одна из основных причин, почему двоичной системе счисления уделяется столько внимания.
Перевод десятичного числа в двоичное
Может потребоваться перевести десятичное число в двоичное. Один из способов – это деление на два и формирование двоичного числа из остатков. Например, нужно получить из числа 77 его двоичную запись:
77 / 2 = 38 (1 остаток)
38 / 2 = 19 (0 остаток)
19 / 2 = 9 (1 остаток)
9 / 2 = 4 (1 остаток)
4 / 2 = 2 (0 остаток)
2 / 2 = 1 (0 остаток)
1 / 2 = 0 (1 остаток)
Собираем остатки вместе, начиная с конца: 1001101. Это и есть число 77 в двоичном представлении. Проверим:
1001101 = 1*26 + 0*25 + 0*24 + 1*23 + 1*22 + 0*21 + 1*20 = 64 + 0 + 0 + 8 + 4 + 0 + 1 = 77
inf1.info
Система счисления — это… Что такое Система счисления?
| Системы счисления в культуре | |
|---|---|
| Индо-арабская система счисления | |
| Арабская Индийские Тамильская Бирманская | Кхмерская Лаоская Монгольская Тайская |
| Восточноазиатские системы счисления | |
| Китайская Японская Сучжоу Корейская | Вьетнамская Счётные палочки |
| Алфавитные системы счисления | |
| Абджадия Армянская Ариабхата Кириллическая | Греческая Эфиопская Еврейская Катапаяди |
| Другие системы | |
| Вавилонская Египетская Этруская Римская | Аттическая Кипу Майская |
| Позиционные системы счисления | |
| Десятичная система счисления (10) | |
| 2, 3, 4, 5, 6, 7, 8, 9, 12, 16, 20, 60 | |
| Нега-позиционная система счисления | |
| Симметричная система счисления | |
| Смешанные системы счисления | |
| Фибоначчиева система счисления | |
| Непозиционные системы счисления | |
| Единичная (унарная) система счисления | |
| Список систем счисления | |
Система счисле́ния — символический метод записи чисел, представление чисел с помощью письменных знаков.
Система счисления:
Системы счисления подразделяются на позиционные, непозиционные и смешанные.
Позиционные системы счисления
В позиционных системах счисления один и тот же числовой знак (цифра) в записи числа имеет различные значения в зависимости от того места (разряда), где он расположен. Изобретение позиционной нумерации, основанной на поместном значении цифр, приписывается шумерам и вавилонянам; развита была такая нумерация индусами и имела неоценимые последствия в истории человеческой цивилизации. К числу таких систем относится современная десятичная система счисления, возникновение которой связано со счётом на пальцах. В средневековой Европе она появилась через итальянских купцов, в свою очередь заимствовавших её у мусульман.
Под позиционной системой счисления обычно понимается -ричная система счисления, которая определяется целым числом , называемым основанием системы счисления. Целое число без знака в -ричной системе счисления представляется в виде конечной линейной комбинации степеней числа :
- , где — это целые числа, называемые цифрами, удовлетворяющие неравенству .
Каждая степень в такой записи называется весовым коэффициентом разряда. Старшинство разрядов и соответствующих им цифр определяется значением показателя (номером разряда). Обычно, в ненулевых числах , левые нули опускаются.
Если не возникает разночтений (например, когда все цифры представляются в виде уникальных письменных знаков), число записывают в виде последовательности его -ричных цифр, перечисляемых по убыванию старшинства разрядов слева направо:
Например, число сто три представляется в десятичной системе счисления в виде:
Наиболее употребляемыми в настоящее время позиционными системами являются:
В позиционных системах чем больше основание системы, тем меньшее количество разрядов (то есть записываемых цифр) требуется при записи числа.
Смешанные системы счисления
Смешанная система счисления является обобщением -ричной системы счисления и также зачастую относится к позиционным системам счисления. Основанием смешанной системы счисления является возрастающая последовательность чисел , и каждое число в ней представляется как линейная комбинация:
- , где на коэффициенты , называемые как и прежде цифрами, накладываются некоторые ограничения.
Записью числа в смешанной системе счисления называется перечисление его цифр в порядке уменьшения индекса , начиная с первого ненулевого.
В зависимости от вида как функции от смешанные системы счисления могут быть степенными, показательными и т. п. Когда для некоторого , смешанная система счисления совпадает с показательной -ричной системой счисления.
Наиболее известным примером смешанной системы счисления является представление времени в виде количества суток, часов, минут и секунд. При этом величина « дней, часов, минут, секунд» соответствует значению секунд.
Факториальная система счисления
В факториальной системе счисления основаниями являются последовательность факториалов , и каждое натуральное число представляется в виде:
- , где .
Факториальная система счисления используется при декодировании перестановок списками инверсий: имея номер перестановки, можно воспроизвести её саму следующим образом: число, на единицу меньшее номера (нумерация начинается с нуля) записывается в факториальной системе счисления, при этом коэффициент при числе i! будет обозначать число инверсий для элемента i+1 в том множестве, в котором производятся перестановки (число элементов меньших i+1, но стоящих правее его в искомой перестановке)
Пример: рассмотрим множество перестановок из 5 элементов, всего их 5! = 120 (от перестановки с номером 0 — (1,2,3,4,5) до перестановки с номером 119 — (5,4,3,2,1)), найдём 101-ую перестановку: 100 = 4!*4 + 3!*0 + 2!*2 + 1!*0 = 96 + 4; положим ti — коэффициент при числе i!, тогда t4 = 4, t3 = 0, t2 = 2, t1 = 0 , тогда: число элементов меньших 5, но стоящих правее равно 4; число элементов меньших 4, но стоящих правее равно 0; число элементов меньших 3, но стоящих правее равно 2; число элементов меньших 2, но стоящих правее равно 0 (последний элемент в перестановке «ставится» на единственное оставшееся место) — таким образом, 101-я перестановка будет иметь вид: (5,3,1,2,4) Проверка данного метода может быть осуществлена путём непосредственного подсчёта инверсий для каждого элемента перестановки.
Фибоначчиева система счисления
Фибоначчиева система счисления основывается на числах Фибоначчи. Каждое натуральное число в ней представляется в виде:
- , где — числа Фибоначчи, , при этом в коэффициентах есть конечное количество единиц и не встречаются две единицы подряд.
Непозиционные системы счисления
В непозиционных системах счисления величина, которую обозначает цифра, не зависит от положения в числе. При этом система может накладывать ограничения на положение цифр, например, чтобы они были расположены в порядке убывания.
Биномиальная система счисления
Представление, использующее биномиальные коэффициенты
- , где .
Система остаточных классов (СОК)
Представление числа в системе остаточных классов основано на понятии вычета и китайской теореме об остатках. СОК определяется набором взаимно простых модулей с произведением так, что каждому целому числу из отрезка ставится в соответствие набор вычетов , где
- …
При этом китайская теорема об остатках гарантирует однозначность представления для чисел из отрезка .
В СОК арифметические операции (сложение, вычитание, умножение, деление) выполняются покомпонентно, если про результат известно, что он является целочисленным и также лежит в .
Недостатками СОК является возможность представления только ограниченного количества чисел, а также отсутствие эффективных алгоритмов для сравнения чисел, представленых в СОК. Сравнение обычно осуществляется через перевод аргументов из СОК в смешанную систему счисления по основаниям .
Система счисления Штерна–Броко
Система счисления Штерна–Броко — способ записи положительных рациональных чисел, основанный на дереве Штерна–Броко.
Системы счисления разных народов
Единичная система счисления
По-видимому, хронологически первая система счисления каждого народа, овладевшего счётом. Натуральное число изображается путём повторения одного и того же знака (чёрточки или точки). Например, чтобы изобразить число 26, нужно провести 26 чёрточек (или сделать 26 засечек на кости, камне и т.д.). Впоследствии, ради удобства восприятия больших чисел, эти знаки группируются по три или по пять. Затем равнообъёмные группы знаков начинают заменяться каким-либо новым знаком — так возникают прообразы будущих цифр.
Древнеегипетская система счисления
Древнеегипетская десятичная непозиционная система счисления возникла во второй половине третьего тысячелетия до н. э. Для обозначения чисел 0, 1, 10, 10², 10³, 104, 105, 106, 107 использовались специальные цифры. Числа в египетской системе счисления записывались как комбинации этих цифр, в которых каждая из цифр повторялась не более девяти раз. Значение числа равно простой сумме значений цифр, участвующих в его записи.[2]
Вавилонская система счисления
Алфавитные системы счисления
Алфавитными системами счисления пользовались древние армяне, грузины, греки (ионическая система счисления), арабы (абджадия), евреи (см. гематрия) и другие народы Ближнего Востока. В славянских богослужебных книгах греческая алфавитная система была переведена на буквы кириллицы.[2]
Еврейская система счисления
Еврейская система счисления в качестве цифр использует 22 буквы еврейского алфавита. Каждая буква имеет своё числовое значение от 1 до 400 (см. т. ж. Гематрия). Ноль отсутствует. Цифры, записанные таким образом, наиболее часто можно встретить в нумерации лет по иудейскому календарю.
Греческая система счисления
Римская система счисления
Каноническим примером почти непозиционной системы счисления является римская, в которой в качестве цифр используются латинские буквы:
I обозначает 1,
V — 5,
X — 10,
L — 50,
C — 100,
D — 500,
M — 1000
Например, II = 1 + 1 = 2
здесь символ I обозначает 1 независимо от места в числе.
На самом деле, римская система не является полностью непозиционной, так как меньшая цифра, идущая перед большей, вычитается из неё, например:
IV = 4, в то время как:
VI = 6
Система счисления майя
Майя использовали 20-ричную систему счисления за одним исключением: во втором разряде было не 20, а 18 ступеней, то есть за числом (17)(19) сразу следовало число (1)(0)(0). Это было сделано для облегчения расчётов календарного цикла, поскольку (1)(0)(0) = 360 примерно равно числу дней в солнечном году.
Для записи основными знаками были точки (единицы) и отрезки (пятёрки).
Кипу инков
Прообразом баз данных, широко использовавшихся в Центральных Андах (Перу, Боливия) в государственных и общественных целях в I—II тысячелетии н. э., была узелковая письменность Инков — кипу, состоявшая как из числовых записей десятичной системы[3], так и не числовых записей в двоичной системе кодирования[4]. В кипу применялись первичные и дополнительные ключи, позиционные числа, кодирование цветом и образование серий повторяющихся данных[5]. Кипу впервые в истории человечества использовалось для применения такого способа ведения бухгалтерского учёта как двойная запись[6].
См. также
Примечания
Ссылки
dic.academic.ru
Дневники чайника
Дневники чайникаПро цифры, числа и верёвки
Я сделал всё, чтобы статья была понятна и интересна всем читателям.
Но если для вас здесь всё ясно, как 2×2, — не обижайтесь.
Ведь не все же такими умными сразу родились. ;)
Итак, система счисления — это всего лишь письменный и устный способ представления чисел.
Про устную составляющую мы говорить вообще не будем, займёмся правилами записи чисел. То есть главный предмет — цифры и отношения между ними.
Хорошо бы ещё понять, что такое число, номер, цифра, количество…
Начнём с самого простого.
Цифра
Одна цифра есть один условный письменный знак, который представляет число.
«0,1,2,3,4,5,6,7,8,9» — это цифры, принятые для нашей системы счисления.
«A,B,C,D,E,F» — это цифры, принятые в шестнадцатиричной системе для представления чисел 10d,11d,12d,13d,14d,15d.
Номер
Ещё совсем недавно большинство людей не имели представления об отвлечённых числах. Посмотрите, даже Даль в своём словаре толкует номер как число, и это отражает язык бытовых понятий, но сейчас взглянем на вопрос по-другому.
Мы привыкли думать, что номер выдаётся конкретному объекту, например: маршрут автобуса, место в театре или даже телефон обладают номером. То есть номер не существует вне связи с конкретным объектом, а это очень важное отличие от современного понятия числа.
Номер — это именование объекта в числовом виде.
Количество
Вот тут я на 100% согласен с Далем. Мы говорим: количество и качество чего-либо. Таким образом, говоря о количестве, мы измеряем свойство объекта. Выразить количество (веса, объёма, штук…) можно только через число, но не всякое число можно использовать для выражения количества. Простой пример: +20 градусов и -20 градусов есть одинаковое количество от нуля, но разные числа.
А от номера количество отличается тем, что оно есть у любого объекта, это обязательное свойство предмета.
Число
Необъяснимое понятие.
Человечество только начало постигать эту загадочную субстанцию. Всё, чему мы научились, — выражать числа через отношения к единице или другим числам. С точки зрения науки нельзя определять понятие через само себя. А других способов я не знаю.
Чтобы не сильно мудрить, сразу ограничим разговор целыми числами, и по большей части речь пойдёт о натуральных (положительных целых) числах. Однако нужно сознавать, что бывают и более сложные виды чисел: рациональные, иррациональные, мнимые и даже те, которые мы ещё никак не называем, потому что просто ничего о них не знаем.
Мне кажется, для простого объяснения хотя бы натуральных чисел будет полезно быстренько пройтись по цепочке развития от обезьяны до Битфрая (поверьте, цепочка не очень длинная =).
Счёт
Наш мозг имеет множество подходов к обработке чисел. Главным образом их можно разделить по таким свойствам:
дискретный счёт — выделение объектов в единицы или их части,
и чувственный счёт — восприятие изменений целиком.
Изначально для вычислений цифры были не нужны. Потому что никто даже не разделял предметы на единицы. Чтоб вы точно поняли, о чём я говорю, приведу пример:
\
\
\
\
\
Любой трезвый человек безошибочно определит, что эта «палка» расположена не вертикально (при наличии некоторой базы). Однако у нас нет транспортира. Как мы это делаем? Проводим цифровые вычисления? Или используем шаблон?
Нет, просто у каждого из нас есть свой хитрый компьютер для подобных целей. Результатом действий этого компьютера будет чувство разности — в данном случае чувственная разность между запомненной вертикалью (от видимой базовой линии) и положением этой «палки».
Большинство животных умеют выделять объекты, и они прекрасно чувствуют количество этих объектов. Научных доказательств у меня нет, но что-то подсказывает: некоторые животные всё-таки могут считать дискретно и даже передавать друг другу цифровую информацию (те же пчёлы).
Давайте предположим, как могли быть осознаны целые единицы и как возникли специальные знаки для их представления.
Как появились цифры
В одной умной книге (см. Историю математики, том I) написано, что первым шагом к цифровому счёту было установление «взаимно однозначного соответствия» между разными предметами.
Даже обезьяны могут разделить бананы среди детёнышей по штукам. Каждому малышу мама отдаёт один банан.
Таким образом, она неосознанно проводит «взаимно однозначное соответствие» между разными объектами (бананами и малышами).
Для того чтобы сделать самый элементарный выбор, желательно произвести осознанный прогноз. Счёт здесь просто необходим.
Нужно знать: сколько воды взять с собой в дорогу, сколько дней пути, сколько камней обработать для топоров… Так что совсем не удивительно, что через некоторое время появились существа, до которых дошло простейшее осознание постоянно повторяющегося вокруг них процесса.
Они специально начали выставлять предметы счёта друг перед другом, для того чтобы узнать, каких меньше.
Видимо, так и выглядел первый шаг к осознанию понятия числа.
Следующий шаг, очевидно, сделали люди. Они усовершенствовали этот метод.
«Колдуны», самые умные представители древних общин, выделили особые предметы для счёта.
Возможно, изначально это были камушки, возможно палочки, а может быть, и косточки врагов. Но со временем у большинства такими предметами стали части тела (ведь оно всегда с собой), в частности, пальцы.
Спустя некоторое время появился знак «I». Предположим, в виде зарубки на стволе дерева или угольной чёрточки на скале. Так числа обрели письменную форму.
Уже здесь можно говорить о принятии самой простой системы счисления.
Это система, основанная на сложении (аддитивная). Система с одним символом.
I = 1 II = 2 III = 3 IIII = 4 ...
Даже такой способ записи из одного символа (и счёт сложением) очень помог рассмотреть мир вокруг, а это позволило выжить и развиться.
Давайте рассмотрим эту систему по элементам.
Такая система счисления может представлять только целые положительные числа (натуральные).
Метод представления — сложение единственного символа в системе с другими такими же.
Отвлечённые числа
Параллельно с предметным счётом стали развиваться абстрактные категории.
Люди осознали, что число может быть не только предметным, то есть три стрелы, три собаки, три дня, но и отвлечённым — просто III.
По самым скромным подсчётам, от обезьяны с бананами до восприятия отвлечённых целых чисел прошло ~2,5 миллиона лет =).
Насколько мне известно, отвлечённые числа пришли к нам через геометрию, но об этом я писать не буду, хотя тема очень интересная. Почитайте сами в учебнике про то, как из условной записи геометрических задач началась алгебра.
Естественная потребность развития языка — называть всё, что видишь. Очень быстро каждая следующая единица обрела своё собственное имя. У разных народов этот процесс, видимо, происходил по-разному. Кто-то называл единицы как части тела (один — нос, два — глаза, или один — палец, два — кулак, три — локоть…), кто-то — как природные явления или предметы, а некоторые вперемешку. С развитием письменности стали возникать и соответствующие знаки (цифры).
Здесь, пожалуй, стоит посмотреть на римскую систему записи чисел.
I II III IV V VI VII VIII IX X XI XII XIII XIV XV XVI XVII XVIII ...
Что же мы видим?
Всё та же арифметика, натуральные числа.
Но теперь цифр много, и число формируется не только сложением, а ещё и вычитанием. В некотором роде прогресс.
Восприятие такого числа начинается не слева направо или наоборот, а с младшей цифры в числе.
Если она стоит слева от следующей по старшинству цифры, то её нужно отнимать, а если справа — то прибавлять.
Такая система даёт возможность относительно коротко записывать большие натуральные числа.
Однако здесь не хватает ещё одной мелочи, можно сказать, ничтожной мелочи, да нет, это даже не мелочь, это просто ничего — ноль.
0
Вы, наверное, слышали, что слово цифра — искажённый перевод древнего арабского слова со значением «пустое», так когда-то именовали ноль. Да и в русском языке слово цифра раньше означало именно ноль.
Как же люди могли додуматься использовать такую совершенно абстрактную категорию?
С одной стороны, при вычитании бОльшего числа из меньшего возникает странная субстанция, назовём её долг.
Она не давала покоя многим учёным, и не только им. Ведь ни один ростовщик никогда не смирится с тем, что долг считать нельзя.
C другой стороны — интерес к познанию мира.
На тот момент центром развития оказался Восток (главным образом, Индия и Китай). Заметьте, именно там люди особенно много думают о гармонии. Мудрецы всю свою жизнь ищут баланс, центр сил, точку равновесия. Найденные ответы выражаются самыми разными способами и один из них — математика.
Примерно в нулевом году (+-~300 лет) ноль-таки был обозначен известными нам цивилизациями.
«0» — made in China =)
Не удивляйтесь. Вполне возможно, запись числа ноль пришла из Китая.
Во всяком случае, насколько мне известно, самые древние записи нуля (маленькая точка) были найдены именно на территории тогдашней Китайской империи. Книги свидетельствуют, что китайцы сначала использовали пустую ячейку для представления числа ноль.
Хотя данный вопрос не так принципиален.
Намного интереснее, что можно сделать, зная о таком числе и имея подобную цифру?
Очень много. Ноль — самая могущественная сила во Вселенной, он может всё!
Ноль создаёт порядок в математике, и он же вносит в неё хаос… Впрочем, об этом можно рассуждать до бесконечности и даже дальше — до нуля :).
Применительно к нашей теме ноль позволил повсеместно использовать позиционную систему счисления.
Отдохните перед главными мыслями этой статьи.
Позиционные системы счисления
Теперь рекомендую долго и старательно медитировать в процессе чтения.
Тем, кто не поймёт вопроса, дальше идти некуда. =(
Представьте такую незамысловатую верёвку.
Верёвка наглядно демонстрирует нашу систему счёта.
Что здесь есть?
Во-первых — направление счёта. Очень важный фактор для наглядного представления.
Во-вторых — 10 узелков
Ну и, конечно, нельзя забывать про 10 отрезков.
На рисунке выше пронумерованы отрезки.
Целью счёта мы определим именно отрезки.
Отрезки — предметы измерения.
Но что тогда будут символизировать узелки?
А вот что:
Ведь на нижнем узелке ещё нет отрезков.
Значит, туда мы поставим цифру 0.
А узел с цифрой 9 сообщает, что посчитано девять отрезков.
Таким образом, можно сказать:
узлы — «цифры»,
отрезки — «числа».
Вообразите, что мы измеряем этой верёвкой размер земельного участка, фундамент будущего дома, оконные проёмы и мелкую мебель внутри.
Верёвка должна быть длиннее участка, но ведь при десяти узелках на такой длиннющей верёвке небольшие предметы измерять не получится. Что же делать?
Можно измерять маленькие предметы частями одного отрезка между целыми узелками (дробями). Не самый удобный способ (я дроби вообще не очень люблю =), но довольно долго мы так и делали. И вот наконец-таки для удобства маленькие отрезки мы тоже обозначили более мелкими узелками. Задумайтесь над этим.
Есть и другой способ. Сразу завести маленькую верёвку для небольших предметов…
Если при измерении большой верёвкой остался неизмеренный кусок меньше целого отрезка, можно там приложить эту маленькую верёвку и домерить.
Короче говоря, решений очень много, но все они рано или поздно приведут к позиционной системе счисления.
Так же, как и счёт: горшками, бочками, телегами и любыми более крупными объектами, чем конечные предметы счёта.
Вот как можно представить позиционный принцип записи чисел через наши верёвки:
Маленькая верёвка ровно умещается в одном отрезке большой верёвки.
Люди сообразили, что удобнее, когда на всех верёвках равное количество узелков.
Каждая следующая верёвка в 10 раз больше предыдущей.
10*10=100, столько маленьких отрезков во второй верёвке.
Давайте попробуем записать цифрами результат подсчёта ширины будущей дороги.
Три отрезка большой верёвки и один отрезок маленькой.
Запишем это так же, как на рисунке. Каждая бОльшая верёвка будет слева (дело было на Востоке =):
Выходит 31.
Но, как всегда, мы решили сэкономить на дороге. Ну, пусть не будет этого маленького отрезка.
Вот тут и пригодится запись цифры ноль.
Три отрезка большой верёвки и нет отрезков на маленькой, получается = 30.
Это и называется позиционный метод записи чисел.
Позиция здесь — очередное место для цифры (слева).
Конечно, можно записывать числа таким же методом, не используя цифру 0, но всё равно в позиции, где нет отрезков, будет хотя бы пустое место. Например, сверху мы пишем номер позиции, а снизу её значение:
Номер позиции - 4321 Значение - 4 3
Так я записал число 4030.
А можно записать, как в древности это делали китайцы:
В любом случае, экономия средств (речевых и письменных) — одна из важнейших сил развития языка. Ноль просто обязан был обзавестись собственным символом. А нам остаётся только радоваться, что это уже произошло.
Основные характеристики позиционных систем
Рассмотрим систему, получившуюся с верёвками.
Опять только целые числа, однако теперь к положительным (1,2,3…) прибавился ещё и ноль.
Как и раньше, система не ограничена, но направленна. Ведь мы можем предположить сколько угодно верёвок и все будем складывать только «вперёд».
Система построена на умножении, а не на сложении, как более древние.
И наконец-таки, важнейшая характеристика подобного представления.
Каждая следующая верёвка в P раз больше предыдущей.
Узелков на всех верёвках одинаковое количество = P.
P — это основание.
Основание — главная характеристика позиционной системы счисления. Оно равно количеству символов в системе.
Ещё нам пригодится такой термин, как разряд.
Разряд = номер позиции цифры минус один.
Разряд — положение цифры в числе за вычетом единицы. Рост разрядов у нас принят влево и считается от нуля.
Перевод чисел в разные системы счисления
Чтоб не запутаться в разных основаниях, назовём в этой статье количество предметов измерения просто количеством.
Количество — реальное число измеряемых предметов или отвлечённое число.
Выражать в тексте количество будем в системе с основанием 10d, так как она наша родная.
Но само количество не зависит от записи чисел, это вы должны хорошо понимать. Ведь как бы мы ни записывали, а от этого реальное число предметов совершенно не изменится.
Составим формулу, опираясь на верёвки (рисуйте их сами, если такой образ помогает).
Возьмём верёвки с четырьмя узелками и отрезками на каждой (основание — 4).
Измерим что-нибудь и получим такой результат:
3 самых маленьких отрезка, 2 отрезка из следующей верёвки, 0 отрезков из верёвки ещё большего размера и 2 самых больших отрезка.
То есть в четверичной системе счисления мы получаем:
2023
Основание = 4, значит, каждая следующая верёвка в 4 раза больше предыдущей.
Или по-другому: каждый следующий разряд в 4 раза больше.
Наша задача найти общую сумму самых маленьких отрезков (то есть количество).
Начиная с младшего разряда, мы будем складывать количества.
3 — уже определено, это и есть количество 3.
2 — это два отрезка по четыре маленьких в каждом 2*4= количество 8
0 — он и в Африке ноль
2 — это два отрезка, в которых 4 более маленьких, в которых 4 более маленьких, в которых 4 самых маленьких =).
Можно сначала посчитать количество в старшем разряде так:
2 *4=8. Мы узнали, сколько в четвёртой верёвке отрезков из третьей. 8 *4=32, теперь перевели в отрезки второй верёвки. И вот, наконец: 32*4= количество 128
Запишем по-человечески:
2*43=128
Все количества по отдельности мы узнали.
Очевидно, что если просто сложить количества, то получится искомый результат.
128+0+8+3=139
Если взять ещё несколько примеров из этой серии и чуть-чуть подумать, то записать красиво наш пример можно так:
2*43 + 0*42 + 2*41 + 3*40 = 139
Суть вот в чём:
значение цифры * основание, возведённое в степень разряда = количество за этой цифрой в данной позиции.
За базовую систему взята привычная нам dec. Поэтому, сложив все количества вместе, мы имеем десятичную запись числа.
Но если бы расчёты проводились, например, в hex-системе, мы получили бы шестнадцатиричное представление.
Обобщённый вид этой формулы вы уже видели, и теперь она не должна показаться такой страшной.
Есть ещё один забавный вопрос, вызывающий некоторые сложности при нулевом знакомстве с нашей системой счёта.
А почему старшая цифра — «9»?
Все, наверное, знают, что десятичная система связана с пальцами рук, но, возможно, не все могут сказать, почему она не одиннадцатиричная. Ведь по сути каждый палец обозначает один предмет, а как я уже сказал, в позиционной системе основание равно количеству цифр. Значит, десять пальцев — это десять предметов плюс цифра ноль, получается = 11. Некоторые народы так и считали, но почему же десятичная система оказалась устойчивей?
Ответ кроется в кулаках =).
Возможно, на кулаках и была построена древнейшая позиционная система.
Дело в том, что загибая десятый палец, мы получаем два кулака.
Так вот, если два сжатых кулака становятся следующим разрядом, то можно сказать, что десятый палец и кулак — одна сущность = 10.
Давайте представим это в наших верёвочных образах.
Вы, наверное, заметили: на верхнем конце верёвок нет узелка.
Значит, старшая цифра 9 обозначает, что посчитано девять предметов счёта.
Куда же делся верхний узелок?
Хм… Попробуем доработать верёвку, замкнув её. Вот так:
Смотрите, как красиво получилось.
Всё сошлось — десять узелков, десять отрезков и нет никаких «обрезков».
Мы ведь на самом деле ведём счёт от нуля до нуля.
То есть в позиционной системе счисления цифра 0 одновременно и самая младшая, и самая старшая!
Пройдя круг, сделаем +1 к следующему разряду, создавая, таким образом, бесконечный цикл.
Из такого представления вытекает много интересных закономерностей.
Например, запись «10»:
цифра «0» и слева стоящая цифра «1» всегда будут выражать основание.
Ведь на верёвке может быть сколько угодно узелков (от двух до бесконечности) и каждый из них может иметь цифру, но при этом мы всегда будем прибавлять единицу к следующему разряду только когда пройдём ноль.
Допустим, двоичная система может быть представлена так:
Да, круга не получилось. =/
Тут вообще на глаз один отрезок. Однако если мы вспомним про направление счёта, то станет понятно:
надо дойти до единицы и затем вернуться к нулю, только после этого выполняется +1 к следующему разряду.
Значит, мы были правы, 10b= количество 2.
Запомните это равенство:
10 = основание,
а по правилам современной математической записи:
10(p)=P,
где P — основание.
В позиционных системах оно будет выполняться всегда, пока мы используем для записи единичного количества и отсутствия предмета цифры 1 и 0 соответственно.
Теперь очень легко можно решать простые задачки вроде этой:
110=35+42
В какой системе это записано?
Достаточно сложить младший разряд:
5+2= количество 7
Затем старший:
3+4= количество 7
Получилось равенство:
110= количество 77
Осталось только сократить:
10= количество 7
Ответ: в семеричной системе.
Ах да, чуть не забыл, уроки-то про Ассемблер =).
Всё! Сворачиваем отвлечение и возвращаемся к практике программирования.
Больше не будем говорить о математике. Сдалась она нам вообще? ;)
Bitfry
А для тех, кто серьёзно заинтересовался темой систем счисления, приведу полезную ссылку на статью «Система счисления» из Википедии.
Именно эта статья указана по нескольким причинам. Во-первых, она постоянно обновляется, во-вторых, там довольно интересный список литературы и ссылки уже долго «живут». Начать рекомендую с брошюрки «Популярные лекции по математике», выпуск 40.
Хотя я бы включил в список обязательного прочтения ещё одну книгу:
«История математики с древнейших времён до начала XIX столетия» (в трёх томах, под редакцией А. П. Юшкевича, изд-во «Наука», М., 1970).
Сам сейчас читаю ещё только первый том, и больше всего для этой статьи я почерпнул именно оттуда.
Впрочем, смотрите сами, что вам будет интересно.
bitfry.narod.ru
Иллюстрированный самоучитель по цифровой графике › Системы счисления › Основания и степени в системе счисления [страница — 43] | Самоучители по графическим программам
Основания и степени в системе счисления
Наконец, пришло время для итоговой таблицы всех рассмотренных систем счисления. В табл. 4.6 представлены числа в нескольких интересующих нас системах счисления, но не все числа, а только те, которые являются «круглыми» в одной из систем (они выделены полужирным шрифтом).
Таблица 4.6. «Круглые» числа в нескольких системах счисления.
| Двоичная | Восьмеричная | Десятичная | Шестнадцатеричная |
|---|---|---|---|
| 10 = 21 | 2 | 2 | 2 |
| 100 = 22 | 4 | 4 | 4 |
| 1010 | 12 | 10 = 101 | А |
| 1000 = 23 | 10 = 81 | 8 | 8 |
| 10000 = 24 | 20 | 16 | 10 = 161 |
| 1 00000 = 25 | 40 | 32 | 20 |
| 1000000 = 26 | 100 = 82 | 64 | 40 |
| 1100100 | 144 | 100 = 102 | 64 |
| 1 0000000 = 27 | 200 | 128 | 80 |
| 100000000 = 28 | 400 | 256 | 100 = 162 |
| 1000000000 = 29 | 1000 = 83 | 512 | 200 |
| 1111101000 | 1750 | 1000 = 103 | ЗЕ8 |
| 1 0000000000 = 210 | 2000 | 1024 | 400 |
| 100000000000 = 211 | 4000 | 2048 | 800 |
| 1 00000000000 = 212 | 10000 = 84 | 4096 | 1000 = 163 |
Обратите внимание на одну интересную закономерность, заметную при рассмотрении этой таблицы. «Круглые» числа во всех системах счисления расположены там, где происходит добавление следующего разряда, а количество нулей соответствует степени числа на том же основании.
Пример
«Шестнадцатеричная тысяча» (три нуля) равна третьей степени основания системы счисления (16), «восьмеричные десять тысяч» (четыре нуля) равны четвертой степени основания системы счисления (8) и, наконец, «двоичный миллиард» (двенадцать нулей) равен двенадцатой степени основания системы счисления (2).
Это еще один аргумент в пользу мысли, что законы математики едины (законы арифметики также). Изменяется всего-навсего основание в каждой конкретной арифметике.
Тот факт, что нам до сих пор привычной представлялась только десятичная система счисления, не может служить препятствием для перехода к другим системам счисления: двоичной, восьмеричной и шестнадцатеричной, как того требуют компьютерные технологии.
- Коды пронизывают нашу жизнь. Код – это совокупность знаков и система определенных правил.
- В компьютерных технологиях все виды информации кодируются только цифрами или, точнее, числами, которые представляются в двоичной системе счисления – способе представления любых чисел с помощью двух знаков (цифр) по позиционному принципу.
- Позиционная система счисления состоит в использовании ограниченного числа цифр, зато позиция каждой цифры в числе обеспечивает значимость (вес) этой цифры. Позиция цифры в числе на математическом языке называется разрядом.
- Основание позиционной системы счисления – это количество различных знаков или символов (цифр), используемых для отображения чисел в данной системе.
- Для того чтобы двоичные числа, отличающиеся довольно значительной длиной, было легче воспринимать и отображать, их сжимают в восьмеричную и шестнадцатеричную системы счисления.
Если данная тема понятна, следует обратить внимание еще на один аспект, ради которого, собственно, и был затеян этот длинный экскурс в элементарную математику, а именно связь двоичных разрядов и количества кодов, которые можно ему присвоить.
samoychiteli.ru
Числа и системы счисленияМ
Шестнадцатеричная система счисления«Все есть число», — говорили пифагорийцы, подчеркивая необычайно важную роль чисел в практической деятельности.
Известно множество способов представления чисел. Но в любом случае число изображается символом или группой символов (словом) некоторого алфавита. Такие символы называются цифрами, символические изображения чисел — кодами, а правила их получения — системами счисления (кодирования).
Система счисления — это способ записи чисел с помощью заданного набора специальных знаков и соответствующие ему правила выполнения действий над числами.
Все системы счисления делятся на две большие группы: позиционные и непозиционные.
| Позиционные | Непозиционные |
| Это такие системы счисления, в которых величина, которую обозначает цифра в записи числа, зависит от положения цифры в этом числе. | Это такие системы счисления, в которых величина, которую обозначает цифра в записи числа, не зависит от положения цифры в этом числе. |
| Например: 10-, 2-, 3-, 8-, 16-чная и т.д. | Например: римская система счисления. |
Алфавит системы счисления — это совокупность цифр и букв, с помощью которых записываются числа.
Основание системы счисления — это количество цифр в алфавите.
Наименьшее возможное основание позиционной системы счисления равно 2. Такая система называется двоичной.
НЕМНОГО ИЗ ИСТОРИИ
Первая позиционная система счисления была придумана еще в древнем Вавилоне, причем вавилонская нумерация (система счисления) была шестидесятеричной, т.е. в ней использовались шестьдесят цифр! Интересно, что до сих пор при измерении времени мы используем основание, равное 60 (в 1 минуте содержится 60 секунд, а в 1 часе — 60 минут).Сегодня мы привыкли пользоваться в повседневной жизни десятичной системой счисления. Десятичными цифрами выражаются время, номера домов и телефонов, цены, бюджет, на них базируется метрическая система мер.
Арифметические действия над десятичными числами производятся с помощью достаточно простых операций, в основе которых лежат известные каждому школьнику таблицы умножения и сложения. Изучаемые в самом раннем возрасте, эти правила в результате повседневной практики усваиваются так прочно, что мы оперируем ими уже подсознательно. По этой причине сегодня многие люди даже не догадываются о существовании других систем счисления.
Так например, в некоторых областях Украины еще несколько десятков лет назад продавали яблоки, яйца и многое другое на «копы» — кучи по 60 штук.
До нашего времени дошли многие древние вавилонские глиняные таблички, на которых в шестидесятеричной системе счисления решены сложнейшие задачи, такие, как вычисление корней, отыскание объема пирамиды и другие. Для записи чисел использовалось всего два знака: клин вертикальный (единицы) и клин горизонтальный (десятки). Все числа от 1 до 59 записывались в десятичной непозиционной системе, а число в целом — в позиционной системе счисления с основанием 60. Например, число 1972 записывалось так:
_ _ _II_ _ _ _ _ _ II
32 · 60 + 52 = 1972
В Китае долгое время пользовались пятеричной системой счисления.
Широкое распространение до первой трети ХХ века имели элементы двенадцатеричной системы счисления, некоторые отголоски которой дошли до нашего времени: в сутках две дюжины часов, час делится на 5 дюжин минут, круг содержит тридцать дюжин градусов и т.д. Влияние двенадцатеричной системы счисления ощущается сегодня хотя бы в том, что карандашей или фломастеров в наборе обычно бывает 6, 12, 24, количество приборов в сервизах равно 6, 12 и т.д.
Наиболее распространенными в настоящее время позиционными системами счисления являются: десятичная, восьмеричная и шестнадцатеричная. Каждая позиционная система имеет определенный алфавит цифр и основание.
| Система счисления | Основание | Алфавит цифр |
| Десятичная | 10 | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 |
| Двоичная | 2 | 0, 1 |
| Восьмеричная | 8 | 0, 1, 2, 3, 4, 5, 6, 7 |
| Шестнадцатеричная | 16 | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А(10), В(11), С(12), D(13), E(14), F(15) |
Десятичная система счисления
Наиболее распространенной позиционной системой счисления является десятичная система. Она характеризуется тем, что в ней 10 единиц какого-либо разряда образуют единицу следующего, старшего разряда. Другими словами, единицы различных разрядов представляют собой различные степени числа 10.Так, например, в числе 555 цифры 5, находящиеся на разных позициях, имеют различные количественные значения — 5 сотен, 5 десятков, 5 единиц. При перемещении цифры на соседнюю позицию ее вес (количественный эквивалент) изменяется в 10 раз.
Число 555 — записано в свернутой форме и привычно для нас. Мы настолько привыкли к такой форме записи, что уже не замечаем, как в уме умножаем цифры числа на различные степени числа 10.
В развернутой форме записи числа такое умножение производится в явной форме:
55510 = 5· 102 + 5· 101 + 5· 100
Для записи десятичных дробей используются разряды с отрицательными значениями степеней основания.
555,5510 = 5· 102 + 5·1 + 5· 100 + 5· 10-1 + 5· 10-2
Двоичная система счисления
Из всех позиционных систем счисления особенно проста и поэтому интересна двоичная система счисления. В ней для записи чисел используются всего две цифры: 0 и 1. Основание равно 2. Двоичное число 111012 записано в свернутой форме.
Двоичное число 111012 в развернутой форме будет записано так:
11101,012 = 1· 24 + 1· 23 + 1· 22 + 0· 21 + 1· 20 + 0· 2-1 + 1· 2-2
Восьмеричная система счисления
Основание равно 8. Алфавит: 0, 1, 2, 3, 4, 5, 6, 7Восьмеричное число 237,018 записано в свернутой форме.
Восьмеричное число 237,018 в развернутой форме будет записано так:
237,018 = 2· 82 + 3· 81 + 7· 80 + 0· 8-1 + 1· 8-2
Шестнадцатеричная система счисления
Основание равно 16.Алфавит: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, B, C, D, E, F
Шестнадцатеричное число 3А,С16 записано в свернутой форме.
Шестнадцатеричное число 3А,С16 в развернутой форме будет записано так:
3А,С16 = 3· 161 + 10· 160 + 12· 16-1
Яндекс.Реклама
sch69.narod.ru