70. Определение истинной величины углов — 11. Метрические задачи
Задачу на определение истинной величины углов (плоских) удобнее решать путем преобразования исходного чертежа способом вращения вокруг линии уровня. Истинная величина углов между пересекающимися прямыми с и d (рис. 143) определена следующим образом: плоскость угла повернута вокруг своей фронтали f (1, 2) до совмещения ее с фронтальной плоскостью уровня Ф (Ф1), проходящей через
Рис. 143
фронталь f Проекция MI совмещения вершины М угла между прямыми с и d находится на проекции Sum2 фронтально проецирующей плоскости Sum, в которой вращается точка М. Определив с помощью прямоугольного треугольника О2М2М натуральную величину радиуса вращения r и отложив ее на проекции Е
Эта задача также может быть решена способом замены плоскостей проекций. Для этого двойной заменой плоскостей проекций нужно сделать плоскость угла плоскостью уровня, решив последовательно сначала третью исходную задачу, а затем — четвертую.
Натуральная величина угла между скрещивающимися прямыми определяется как угол между двумя пересекающимися прямыми, параллельными данным скрещивающимся прямым.
Угол а между прямой l и плоскостью 6 может быть определен через дополнительный угол р между заданной прямой l и перпендикуляром п к данной плоскости, проведенной из любой точки прямой (рис. 144). Угол Р дополняет искомый угол а до 90°. Определив истинную величину угла Р путем вращения вокруг прямой уровня плоскости угла, образованного прямой l и перпендикуляром и, остается дополнить его до прямого угла. Этот дополнительный угол и даст истинную величину угла а между прямой l и плоскостью 0.
Истинная величина двугранного угла — между двумя плоскостями Q и л. — может быть определена или путем замены плоскости проекций с целью преобразования ребра двугранного угла в проецирующую прямую (задачи 1 и 2), или если ребро не задано, как угол между двумя перпендикулярами n1 и n2, проведенными к данным плоскостям (см. § 61) из произвольной точки
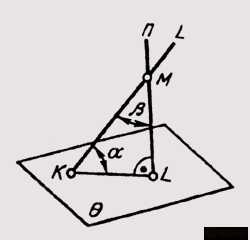
Рис. 144
Рис. 145
угла а и Р, которые соответственно равны линейным углам двух смежных углов (двугранных), образованных плоскостями q и л,. Определив истинную величину углов между перпендикулярными n1 и n2 путем вращения вокруг прямой уровня, тем самым определим и линейный угол двугранного угла, образованного плоскостями q и л.
intellect.ml
4.5. Измерение угла между двумя плоскостями (гранями)
У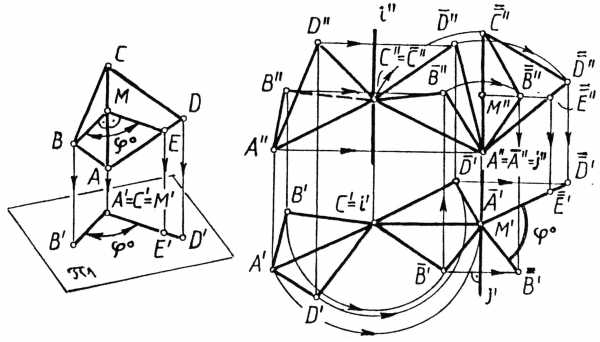
гол
φ0 (рис.14) между двумя плоскостями измеряется
линейным углом этого двугранного угла.
Стороны линейного угла, как известно,
перпендикулярны к линии пересечения
заданных плоскостей (граней). Таким
образом, «решающим положением»
оригинала в данной задаче будет такое,
при котором линия пересечения двух
плоскостей будет проецирующей прямой,
то есть рассматриваемая задача сводится
ко второй основной задаче на преобразование
комплексного чертежа.Рис. 14. Рис. 15.
Пример №5. Определить натуральную величину двугранного угла φ0 при ребре АС.
Решим эту задачу способом вращения вокруг проецирующих прямых (рис.15).
Проведем через точку С ось вращения i, перпендикулярную горизонтальной плоскости проекций и повернем заданную фигуру до положения, при котором отрезок (ребро)
»
»
»
».
Выберем новую ось вращенияj
, проходящую через точку 
и перпендикулярную плоскости π2.
Повернем полученную фигуру 
»
»
»
»
вокруг осиj
до положения, при котором ребро СА станет горизонтально проецирующей
линией 
.
Тогда, двугранный угол при этом ребре
спроецируется на горизонтальную
плоскость проекций в натуральную
величину (угол
‘
‘
‘
— искомый угол φ 0).4.6. Измерение угла между прямой и плоскостью
Известно,
что угол между прямой и плоскостью
измеряется линейным углом между самой
прямой и ее ортогональной проекцией на
данную плоскость. «Решающим положением»
оригинала в данной задаче должно быть
такое положение, при котором стороны
искомого угла φ°
оказались бы параллельными одной из
плоскостей проекций, например, плоскости
π
Такого положения можно добиться путем последовательного преобразования чертежа согласно следующему алгоритму:
I) провести в заданной плоскости линию уровня, а затем преобразовать чертеж так, чтобы эта линия уровня стала проецирующей прямой. При этом плоскость, содержащая эту линию уровня, станет проецирующей;
2) преобразовать полученную фигуру так, чтобы в новом положении проецирующая плоскость стала плоскостью уровня. При этом, прямая и ее проекция на плоскости уровня совпадут в одну линию, т.е. плоскость искомого угла станет проецирующей;
З) путем следующего преобразования нужно сделать плоскость искомого угла плоскостью уровня по отношению к соответствующей плоскости проекций. На рис.16 этот угол обозначен углом φ°.
Р
ис.
16.
П
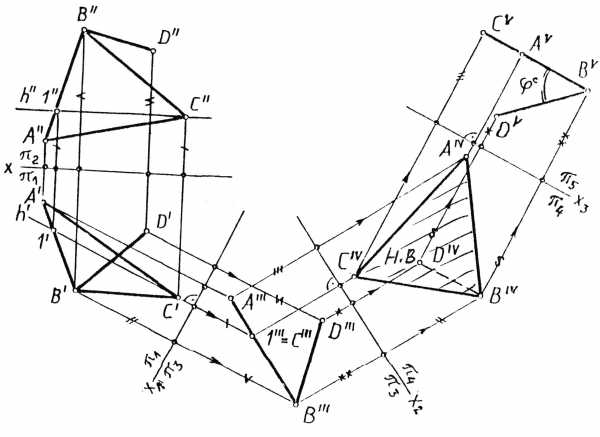ример
№6.
Рис. 17.
Последовательность решения задачи, согласно приведенному выше алгоритму, понятна из чертежа. Задача в данном случае решена способом замены плоскостей проекций. Ход решения указан стрелками, а конгруэнтные отрезки — соответствующими значками (черточками).
КОНТРОЛЬНЫЕ ВОПРОСЫ
Почему одна проекция не определяет положение точки в пространстве?
Как построить третью проекцию точки, если заданы на комплексном чертеже две другие проекции?
Под каким углом к оси проекции должны проходить линии связи?
Где расположена сама точка, заданная своими проекциями?
Как задается на комплексном чертеже прямая линия?
Чем отличается прямая общего положения от прямой частного положения?
Какие виды прямых частного положения Вы знаете?
Как изображаются на чертеже прямые уровня: горизонталь, фронталь, профильная прямая?
Как изображаются проецирующие прямые, перпендикулярные к горизонтальной, фронтальной и профильной плоскостям?
Назовите условие принадлежности точки прямой линии.
Как разделить прямую, заданную своими проекциями, в данном отношении (теорема Фаллеса)?
Какие взаимные положения двух прямых Вы знаете?
Назовите условие, при котором две прямые пересекаются.
Назовите условие, при котором две прямые являются скрещивающимися.
Какие две точки называются конкурирующими?
Как при помощи конкурирующих точек определить видимость на чертеже?
Способы задания плоскости на комплексном чертеже?
Что такое плоскость общего положения?
Какие виды плоскости частного положения Вы знаете?
Определение линии пересечения двух плоскостей. Изложите порядок графических построений – алгоритм решения задачи.
Какие виды взаимных положений прямой и плоскости Вы знаете?
Определение точки пересечения прямой с плоскостью. Изложите порядок графических построений – алгоритм решения.
Дайте определение позиционных и метрических задач.
Определение натуральной величины прямой общего положения способом прямоугольного треугольника.
Определение натуральной величины прямой общего положения способом перемены плоскостей проекций.
Преобразование плоскости общего положения в проецирующую и в плоскость уровня.
ЛИТЕРАТУРА
Гордон В.О., Семнцов-Огиевский М.А. Курс начертательной геометрии, М.: Высш. шк., 2002.-272 с: ил.
Гордон В.О., Иванов Ю.Б., Солнцева Т.Е. Сборник задач по курсу начертательной геометрии, М.: Высш. шк., 1998.-320 с: ил.
Локтев О.В. Краткий курс начертательной геометрии. М.: Высш. шк., 2002
Начертательная геометрия/ Крылов Н.Н. и др. — М.: Высш. шк., 2000
Фролов С.А., Начертательная геометрия: Учебник для втузов. М.: Машиностроение, 1983. – 240 с., ил
ЕСКД. Основные положения. ГОСТ 2.104-68. Основные надписи. М.: Изд-во стандартов, 2001, 343с.
ЕСКД. Общие правила выполнения чертежей. ГОСТ 2.301-68 – ГОСТ 2.304-81. М.: Изд-во стандартов, 2001, 238с.
18
studfiles.net
70. Определение истинной величины углов
Задачу на определение истинной величины углов (плоских) удобнее решать путем преобразования исходного чертежа способом вращения вокруг линии уровня. Истинная величина углов между пересекающимися прямыми с и d (рис. 143) определена следующим образом: плоскость угла повернута вокруг своей фронтали f (1, 2) до совмещения ее с фронтальной плоскостью уровня Ф (Ф1), проходящей через
Рис. 143
фронталь f Проекция MI совмещения вершины М угла между прямыми с и d находится на проекции Sum2 фронтально проецирующей плоскости Sum, в которой вращается точка М. Определив с помощью прямоугольного треугольника О2М2М натуральную величину радиуса вращения r и отложив ее на проекции Е2 от фронтальной проекции центра вращения, получаем изображение точки М на плоскости П2 в совмещенном с плоскостью Ф положении. Соединяя фронтальные проекции неподвижных точек 1 и 2 с построенной точкой М, получаем проекции с2 и d2, совмещенных с плоскостью Ф прямых с и d. Угол между прямыми с2 и d2 определяет натуральную величину искомого угла между пересекающимися прямыми с и d.
Эта задача также может быть решена способом замены плоскостей проекций. Для этого двойной заменой плоскостей проекций нужно сделать плоскость угла плоскостью уровня, решив последовательно сначала третью исходную задачу, а затем — четвертую.
Натуральная величина угла между скрещивающимися прямыми определяется как угол между двумя пересекающимися прямыми, параллельными данным скрещивающимся прямым.
Угол а между прямой l и плоскостью 6 может быть определен через дополнительный угол р между заданной прямой l и перпендикуляром п к данной плоскости, проведенной из любой точки прямой (рис. 144). Угол Р дополняет искомый угол а до 90°. Определив истинную величину угла Р путем вращения вокруг прямой уровня плоскости угла, образованного прямой l и перпендикуляром и, остается дополнить его до прямого угла. Этот дополнительный угол и даст истинную величину угла а между прямой l и плоскостью 0.
Истинная величина двугранного угла — между двумя плоскостями Q и л. — может быть определена или путем замены плоскости проекций с целью преобразования ребра двугранного угла в проецирующую прямую (задачи 1 и 2), или если ребро не задано, как угол между двумя перпендикулярами n1 и n2, проведенными к данным плоскостям (см. § 61) из произвольной точки М пространства (см. рис. 145). В плоскости этих перпендикуляров при точке М получаем два плоских
Рис. 144
Рис. 145
угла а и Р, которые соответственно равны линейным углам двух смежных углов (двугранных), образованных плоскостями q и л,. Определив истинную величину углов между перпендикулярными n1 и n2 путем вращения вокруг прямой уровня, тем самым определим и линейный угол двугранного угла, образованного плоскостями q и л.
lib.qrz.ru
Определить двугранный угол
Дано:
(ABC)
(ABD)
Для определения линейного угла , измеряющего двугранный угол, достаточно расположить его так, чтобы ребро [АВ] оказалось перпендикулярным плоскости проекций.
1.Преобразуйте ребро [АВ] общего положения в прямую уровня, применив первую основную задачу преобразования комплексного чертежа.
П2 П4 П1; П4 ||[AB]
X12 X14|| [A1B1]
2.Преобразуйте ребро [АВ] в проецирующую прямую, применив вторую исходную задачу.
На плоскости проекции П5 ребро [AB] вырождается в точку, а грани АВС и АВD вырождаются в отрезки прямых.
На П4 линейный угол спроецируется в натуральную величину.
П1 П5 П4
П5 [AB]
= ,
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
1.Зачем необходимо преобразование комплексного чертежа?
2. Какие основные задачи решаются путем преобразования чертежа?
3. В чем сущность способа замены плоскостей проекций?
4. Как надо расположить новые плоскости проекций, чтобы отрезок прямой общего положения спроецировался в натуральную величину, в точку?
5. Как нужно расположить новую плоскость проекций, чтобы плоскость общего положения стала проецирующей?
ТЕСТ №7
1. На каком чертеже введена плоскость П4 для определения
угла наклона отрезка (АВ) к П1?
2. На каком чертеже в результате замены будет определен угол
наклона отрезка (АВ) к П2?
3. На каком чертеже одной заменой возможно преобразование
прямой в проецирующее положение?
4На каком чертеже для преобразования прямой в
проецирующее положение ось задана неверно?
9. ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ ПЛОСКОСТЯМИ
Сечением называется плоская фигура, полученная в результате пересечения тела плоскостью и содержащая точки, принадлежащие как поверхности тела, так и секущей плоскости.
Плоскости, которые образуют сечения, называют секущими. Плоскость, пересекая поверхность многогранника, дает сечение в виде многоугольника. Вершинами такого многоугольника являются точки пересечения ребер многогранника с секущей плоскостью, а сторонами – прямые линии пересечения граней с секущей плоскостью (рис.66).
— пирамида
Г – секущая плоскость
MNK – сечение (треугольник)
Рис.66
Рис.67
Плоскость, пересекая кривые поверхности, в общем случае дает криволинейную фигуру (окружность, эллипс и т.д.) (рис.67).
— цилиндр
– секущая плоскость
m- линия сечения (эллипс)
Построение линий сечения поверхности плоскостью значительно упрощается, если секущая плоскость является проецирующей. В этом случае одна из проекций линии сечения совпадает с проекцией проецирующей плоскости.
9.1 Пересечение пирамиды проецирующей плоскостью
Построить линию пересечения
пирамиды плоскостью Г
Дано: — пирамида
Г- плоскость
ГП2
Построить: Г=m
1.Фронтально проецирующая плоскость Г пересекает три ребра пирамиды:
ГSA=1
ГSB=2
ГSC=3
m = (1-2-3)
Фронтальная проекция линии пересечения m 2(12-22-32) совпадает с фронтальной проекцией Г2
2. Горизонтальные проекции линии (11-21-31) получают с помощью вертикальных линий связи, перенося все точки с фронтальной проекции на горизонтальную проекцию.
3. Соединяя последовательно точки 11,21,31 отрезками прямых, получают горизонтальную проекцию линии сечения.
studfiles.net
Определить натуральную величину двугранного угла ABCD при ребре ВС. Задачу решить методом замены плоскостей проекций. Исходные данные к задаче представлены в таблице 1.
Образование Определить натуральную величину двугранного угла ABCD при ребре ВС. Задачу решить методом замены плоскостей проекций. Исходные данные к задаче представлены в таблице 1.
Количество просмотров публикации Определить натуральную величину двугранного угла ABCD при ребре ВС. Задачу решить методом замены плоскостей проекций. Исходные данные к задаче представлены в таблице 1. — 1132
| Наименование параметра | Значение |
| Тема статьи: | Определить натуральную величину двугранного угла ABCD при ребре ВС. Задачу решить методом замены плоскостей проекций. Исходные данные к задаче представлены в таблице 1. |
| Рубрика (тематическая категория) | Образование |
Рисунок 5
Решение:
Величину угла можно замерить, в случае если грани угла будут выглядеть как отрезки сторон обычного угла. Чтобы получить проекцию угла на некоторую плоскость и замерить его, крайне важно спроецировать ребро при вершине угла в точку.
Алгоритм решения задачи следующий:
1 Находим натуральную величину ребра ВС.
2 Спроецируем ребро ВС так, чтобы в новой системе получить точку.
Замерим полученный угол.
Приложение А
Пример оформления титульного листа
Определить натуральную величину двугранного угла ABCD при ребре ВС. Задачу решить методом замены плоскостей проекций. Исходные данные к задаче представлены в таблице 1. — понятие и виды. Классификация и особенности категории «Определить натуральную величину двугранного угла ABCD при ребре ВС. Задачу решить методом замены плоскостей проекций. Исходные данные к задаче представлены в таблице 1.» 2014, 2015.
Читайте также
Толстая линза. Матрица толстой линзы. Главные плоскости. Матрица толстой линзы: = , где , — оптические силы двух сферических поверхностей, — толщина линзы, — показатель преломления линзы. Главные плоскости оптической системы — сопряженные плоскости с единичным… [читать подробнее].
T2 second ; Tl first; Словари Yes Ben B i l l Jessica John Mary Monica Sju B i l l Monica B i l l John Monica Sju Ben Bin Jessica Mary Monica В определении класса mар используется тип pair, который описан в заголовочном файле <utility> следующим образом: … [читать подробнее].
referatwork.ru
Определение натуральной величины двугранного угла
Дом Определение натуральной величины двугранного углапросмотров — 535
Мерой угла между плоскостями служит линейный угол, образованный двумя прямыми–сечениями граней этого угла плоскостью, перпендикулярной к их ребру (рис.31).
| Рис.32 |
На рис.32 показано определение двугранного угла, образованного плоскостями Λ (АВС) и S (ВАD), когда ребро (АВ) искомого угла задано. Задача решена преобразованием ребра (АВ) в проецирующую прямую. При таком преобразовании общее ребро двугранного угла «вырождается» в точку, а грани угла – в линии. Угол между линиями является искомым двугранным углом. При построении, как правило используется способ замены плоскостей проекций.
Задача 2.Определить натуральную величину двугранного угла при ребре АS.
Решение:
Шаг 1. По заданным координатам точек строятся проекции двухгранного угла с учётом видимости рёбер (рис.33). Видимость определяется способом конкурирующих точек.
| Рис.33 |
Шаг 2. Вводится дополнительная плоскость проекций П4 перпендикулярно к П1, чтобы ребро AS стало прямой уровня относительно П4. Из каждой точки А1, B1, C1, S1 проводятся линии связи, перпендикулярные оси х1,4. На них от оси х1,4 откладываются расстояния, соответственно равные расстоянию от оси х1,2 до фронтальной проекции каждой точки (рис. 34).
| Рис.34 |
Шаг 2. Для того чтобы ребро AS стало проецирующим, вводится дополнительная плоскость проекций П5 перпендикулярно к П4 (рис.35). Из каждой точки А4, B4, C4, S4 проводятся линии связи, перпендикулярные оси х4,5. На них от оси х4,5. откладываются расстояния, соответственно равные расстоянию от оси х1,4 до горизонтальной проекции каждой точки Ребро AS выродилась в точку А5 ≡ S5, а грани отобразились прямыми линиями, угол между которыми и есть искомый двухгранный угол при ребре. AS.
| Рис.35 |
Читайте также
Мерой угла между плоскостями служит линейный угол, образованный двумя прямыми–сечениями граней этого угла плоскостью, перпендикулярной к их ребру (рис.31). Рис.32 На рис.32 показано определение двугранного угла, образованного плоскостями &… [читать подробенее]
oplib.ru
Определить двугранный угол
Дано:
(ABC)
(ABD)
Для определения линейного угла , измеряющего двугранный угол, достаточно расположить его так, чтобы ребро [АВ] оказалось перпендикулярным плоскости проекций.
1.Преобразуйте ребро [АВ] общего положения в прямую уровня, применив первую основную задачу преобразования комплексного чертежа.
П2 П4 П1; П4 ||[AB]
X12 X14|| [A1B1]
2.Преобразуйте ребро [АВ] в проецирующую прямую, применив вторую исходную задачу.
На плоскости проекции П5 ребро [AB] вырождается в точку, а грани АВС и АВD вырождаются в отрезки прямых.
На П4 линейный угол спроецируется в натуральную величину.
П1 П5 П4
П5 [AB]
= ,
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
1.Зачем необходимо преобразование комплексного чертежа?
2. Какие основные задачи решаются путем преобразования чертежа?
3. В чем сущность способа замены плоскостей проекций?
4. Как надо расположить новые плоскости проекций, чтобы отрезок прямой общего положения спроецировался в натуральную величину, в точку?
5. Как нужно расположить новую плоскость проекций, чтобы плоскость общего положения стала проецирующей?
ТЕСТ №7
1. На каком чертеже введена плоскость П4 для определения
угла наклона отрезка (АВ) к П1?
2. На каком чертеже в результате замены будет определен угол
наклона отрезка (АВ) к П2?
3. На каком чертеже одной заменой возможно преобразование
прямой в проецирующее положение?
4На каком чертеже для преобразования прямой в
проецирующее положение ось задана неверно?
9. ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ ПЛОСКОСТЯМИ
Сечением называется плоская фигура, полученная в результате пересечения тела плоскостью и содержащая точки, принадлежащие как поверхности тела, так и секущей плоскости.
Плоскости, которые образуют сечения, называют секущими. Плоскость, пересекая поверхность многогранника, дает сечение в виде многоугольника. Вершинами такого многоугольника являются точки пересечения ребер многогранника с секущей плоскостью, а сторонами – прямые линии пересечения граней с секущей плоскостью (рис.66).
— пирамида
Г – секущая плоскость
MNK – сечение (треугольник)
Рис.66
Рис.67
Плоскость, пересекая кривые поверхности, в общем случае дает криволинейную фигуру (окружность, эллипс и т.д.) (рис.67).
— цилиндр
– секущая плоскость
m- линия сечения (эллипс)
Построение линий сечения поверхности плоскостью значительно упрощается, если секущая плоскость является проецирующей. В этом случае одна из проекций линии сечения совпадает с проекцией проецирующей плоскости.
9.1 Пересечение пирамиды проецирующей плоскостью
Построить линию пересечения
пирамиды плоскостью Г
Дано: — пирамида
Г- плоскость
ГП2
Построить: Г=m
1.Фронтально проецирующая плоскость Г пересекает три ребра пирамиды:
ГSA=1
ГSB=2
ГSC=3
m = (1-2-3)
Фронтальная проекция линии пересечения m 2(12-22-32) совпадает с фронтальной проекцией Г2
2. Горизонтальные проекции линии (11-21-31) получают с помощью вертикальных линий связи, перенося все точки с фронтальной проекции на горизонтальную проекцию.
3. Соединяя последовательно точки 11,21,31 отрезками прямых, получают горизонтальную проекцию линии сечения.
studfiles.net