Онлайн построение в полярной системе координат – График функции в полярной системе координат

Содержание

Примеры графиков функций в полярных координатах

Поделиться в соцсетях:

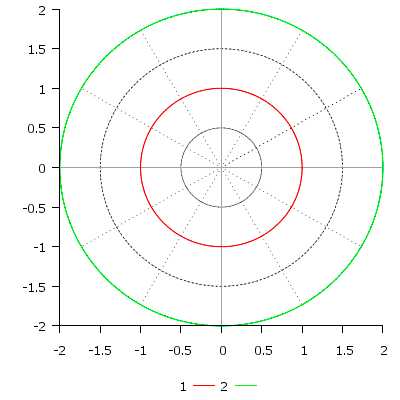
\[ r(t) = 1, \quad t \in [0; 2\pi] \\ r(t) = 2, \quad t \in [0; 2\pi] \]

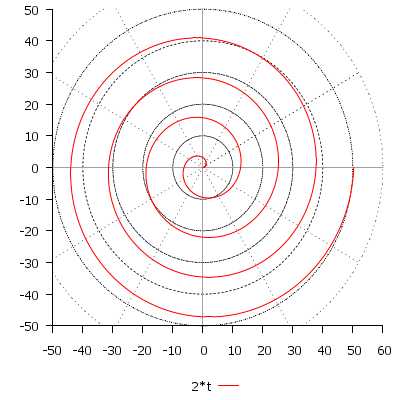
\[ r(t) = 2t, \quad t \in [0; 8\pi] \]

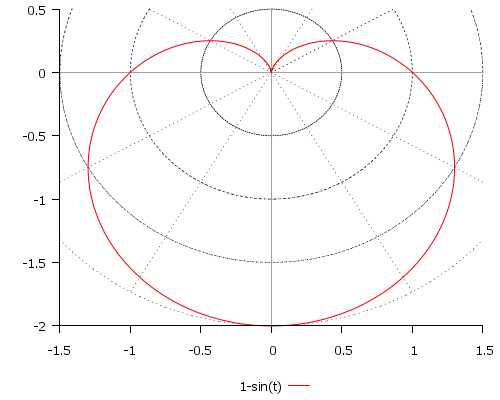
\[ r(t) = 1 — \sin(t), \quad t \in [0; 2\pi] \]

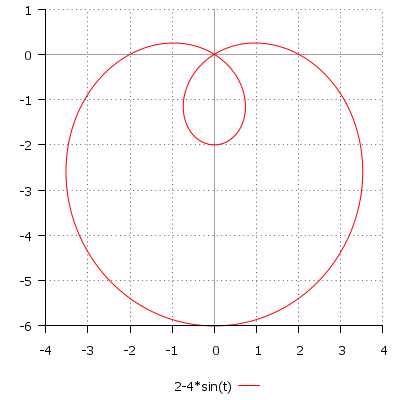
\[ r(t) = 2 — 4\sin(t), \quad t \in [0; 2\pi] \]

\[ r(t) = \frac{1}{1 — \cos(t)}, \quad t \in [0; 2\pi] \]

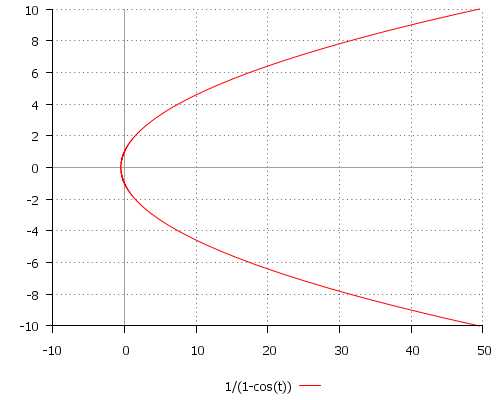
\[ r(t) = \sin(6t), \quad t \in [0; 2\pi] \]

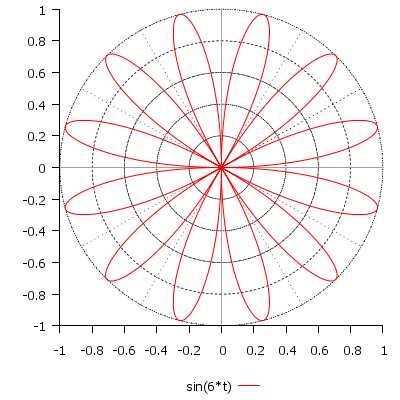
\[ r(t) = \sin\Big(\frac{7}{4}t\Big), \quad t \in [0; 8\pi] \]

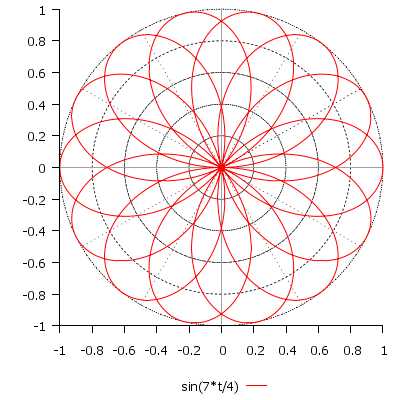
\[ r(t) = \sin\Big(\frac{3}{4}t\Big), \quad t \in [0; 8\pi] \]

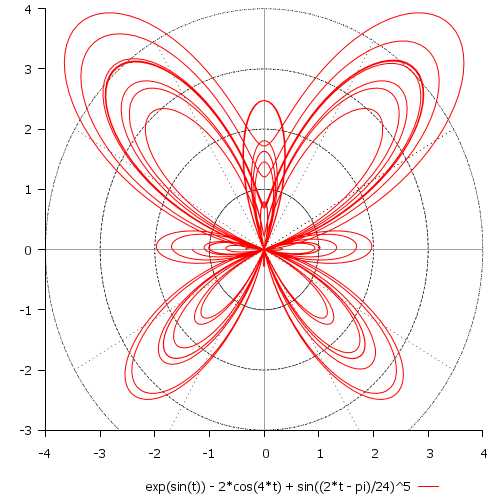
\[ r(t) = \mathrm{e}^{\sin(t)} — 2\cos(4t) + \sin^5\Big(\frac{2t — \pi}{24}\Big) \\ t \in [{-8\pi}; 8\pi] \]

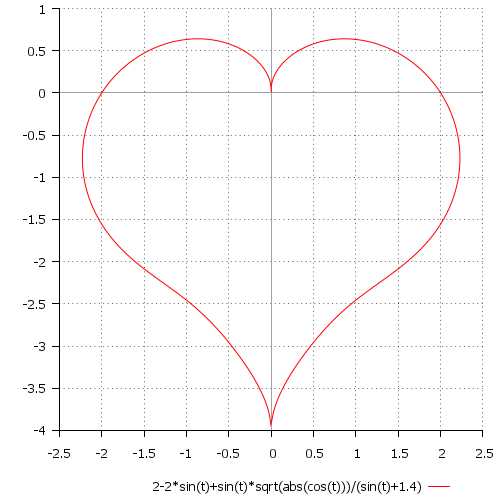
\[ r(t) = 2 — 2\sin(t) + \sin(t)\frac{\sqrt{|\cos(t)|}}{\sin(t) + 1,4} \\ t \in [0; 2\pi] \]

grafikus.ru

Построение графика в полярных координатах. Контрольные онлайн

Построение графика в полярных координатах

Дано уравнение  кривой в полярной системе координат .
Требуется:
   а) построить кривую по точкам, придавая j  значения из промежутка  с шагом ; 
   б) записать уравнение этой кривой в  декартовой прямоугольной системе координат, согласованной с полярной, и определить  тип этой кривой.

Решение
а) Составим таблицу значений функции.

p/8

p/4

3p/8

p/2

5p/8

3p/4

7p/8

9p/8

5p/8

11p/8

3p/2

13p/8

7p/4

15p/8

2,8

2,32

1,72

1,5

1,26

1,11

1,02

1,11

1,26

1,5

1,72

2,32

2,8

По этим данным отметим точки на плоскости и, плавно соединяя соседние точки, построим линию.

б) Перейдём к декартовой прямоугольной системе координат, пользуясь формулами , .
Заданное уравнение примет вид .
Преобразуем это уравнение: ,

, , , .
Выделив полные квадраты переменных и , получим или .

Это уравнение эллипса с центром в точке и полуосями и .

www.matem96.ru

Полярная система координат: основные понятия и примеры

Полярная система координат определяется заданием некоторой точки O, называемой полюсом, исходящего из этой точки луча OA (обозначается также и как Ox), называемого полярной осью, и масштаба для изменения длин. Кроме того, при задании полярной системы координат должно быть определено, какие повороты вокруг точки O считаются положительными (на чертежах обычно положительными считаются повороты против часовой стрелки).

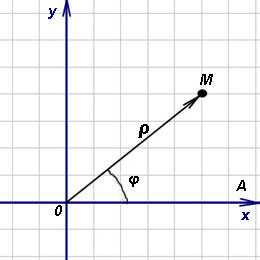
Итак, выберем на плоскости (рисунок выше) некоторую точку O (полюс) и некоторый выходящий из неё луч Ox. Кроме того, укажем единицу масштаба. Полярными координатами точки

M называются два числа ρ и φ, первое из которых (полярный радиус ρ) равно расстоянию точки M от полюса O, а второе (полярный угол φ, который называют также амплитудой) — угол, на который нужно повернуть против часовой стрелки луч Ox до совмещения с лучом OM.

Точку M с полярными координатами ρ и φ обозначают символом M(ρ, φ).

Установим связь между полярными координатами точки и её декартовыми координатами. Будем предполагать, что начало декартовой прямоугольной системы координат находится в полюсе, а положительная полуось абсцисс совпадает с полярной осью. Пусть точка M имеет декартовы координаты x и y и полярные координаты ρ и φ.Тогда

x = ρ cos φ)

y = ρ sin φ).

Полярные координаты ρ и φ точки M определяются по её декартовым координатам следующим образом:

Для того, чтобы найти величину угла φ, нужно, используя знаки x и y, определить квадрант, в котором находится точка M, и, кроме того, воспользоваться тем, что тангенс угла φ равен .

Приведённые выше формулы называются формулами перехода от декартовых координат к полярным.

Пример 1. В полярной системе координат на плоскости даны точки

A(3; π/4);

B(2; —π/2);

C(3; —π/3).

Найти полярные координаты точек, симметричных этим точкам относительно полярной оси.

Решение. При симметрии длина луча не меняется. Следовательно, первая координата — длина луча — у симметричной относительно полярной оси точки будет как и у данной точки. Как видно из рисунка в начале урока, при построении симметричной относительно полярной оси точки данную точку нужно повернуть вокруг полярной оси на тот же угол φ. Следовательно, в полярной системе координат второй координатой симметричной точки будет угол для исходной точки, взятый с противоположным знаком, то есть -φ. Итак, полярные координаты точки, симметричной данной относительно полярной оси будут отличаться лишь второй координатой, и эта координата будет с противоположным знаком. Полярные координаты искомых симметричных точек будут следующими:

A’(3; —π/4);

B’(2; π/2);

C’(3; π/3).

Пример 2. В полярной системе координат на плоскости даны точки

(1; π/4);

B(5; π/2);

C(2; —π/3).

Найти полярные координаты точек, симметричных этим точкам относительно полюса.

Решение. При симметрии длина луча не меняется. Следовательно, первая координата — длина луча — у симметричной относительно полюса точки будет как и у данной точки. Симметричная относительно полюса точка получается вращением исходной точки на 180 градусов против часовой стрелки, то есть на угол π. Следовательно, вторая координата точки, симметричной данной относительно полюса рассчитывается как φ + π (если в результате получится числитель больше знаменателя, то вычтем из полученного числа один полный оборот, то есть 2π). Получаем следующие координаты точек, симметричных данным относительно полюса:

A’(1; 3π/4);

B’(5; —π/2);

C’(2; 2π/3).

Пример 3. Полюс полярной системы координат совпадает с началом декартовых прямоугольных координат, а полярная ось совпадает с положительной полуосью абсцисс. В полярной системе координат даны точки

A(6; π/2);

B(5; 0);

C(2; π/4).

Найти декартовы координаты этих точек.

Решение. Используем формулы перехода от полярных координат к декартовым:

x = ρ cos φ)

y = ρ sin φ).

Получаем следующие декартовы координаты данных точек:

A(0; 6);

B(5; 0);

C’(√2; √2).

Пример 4. Полюс полярной системы координат совпадает с началом декартовых прямоугольных координат, а полярная ось совпадает с положительной полуосью абсцисс. В декартовой прямоугольной системе координат даны точки

A(0; 5);

B(-3; 0);

C(√3; 1).

Найти полярные координаты этих точек.

Решение. Определяем первую из полярных координат по формуле , а тангенс угла φ — второй из полярных координат как . Получаем следующие полярные координаты данных точек:

A(5; π/2);

B(3; π);

C(2; π/6).

Поделиться с друзьями

Весь блок «Аналитическая геометрия»

Векторы
Плоскость
Прямая на плоскости

function-x.ru

Окружность в полярных координатах | Формулы и расчеты онлайн

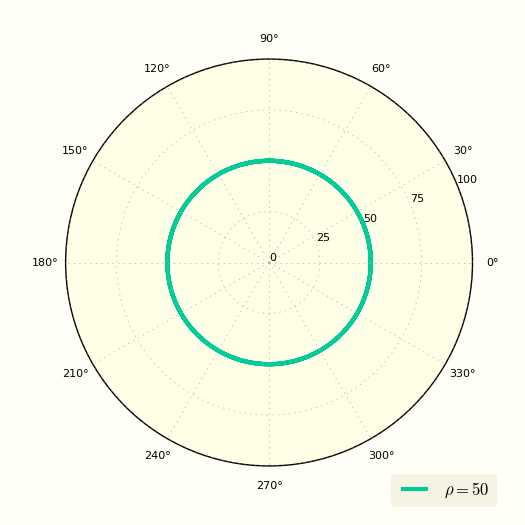
Уравнение окружности в полярных координатах выглядит очень просто

\[ ρ = R = \const \]

Это уравнение показывает, что ρ вообще не зависит от угла φ.

Построение окружности по простому уравнению в полярной системе координат

Еще одно уравнение окружности в полярных координатах

Первый пример был очень простым, теперь возьмем окружность смещенную по оси X в декартовых координатах и получим ее полярное уравнение.

Известно, что окружность в декартовой прямоугольной системе координат описывается уравнением:

\[ (x-R)^2 + y^2 = R^2 \]

Также известны формулы перевода декартовых координат в полярные

Используя эти формулы и подставив их в (1) мы получим:

Уравнение окружности в полярных координатах

Изначально после подстановки имеем

\[ ρ^2-2Rρ\cos(φ) = 0 \]

И этого уравнения получается система

\[ \lvbig ρ = 0
ρ = 2R\cos(φ) \r.\]

Первое уравнение системы описывает полюс окружности.

Второе описывает саму окружность в полярной системе координат.

В итоге получаем:

\[ ρ = 2R\cos(φ) \]

Построение окружности в полярной системе координат

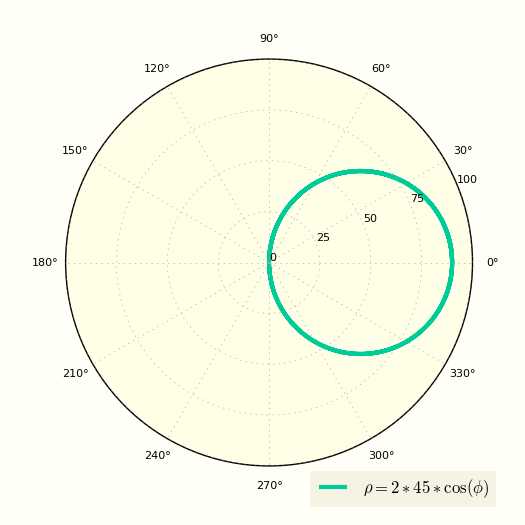
Теперь сместим окружность по вверх, очередное уравнение окружности в полярных координатах

В данном варианте мы сместим окружность по оси Y в декартовых координатах и получим ее полярное уравнение.

При таком смещении окружность описывается уравнением:

\[ x^2 + (y-R)^2 = R^2 \]

Снова используем формулы перевода декартовых координат в полярные

получаем:

\[ ρ^2-2Rρ\sin(φ) = 0 \]

И этого уравнения получается система

\[ \lvbig ρ = 0
ρ = 2R\sin(φ) \r.\]

Первое уравнение системы описывает полюс окружности.

Второе описывает саму окружность в полярной системе координат.

В итоге получаем:

\[ ρ = 2R\sin(φ) \]

Построение окружности в полярной системе координат смещенной вверх относительно полюса

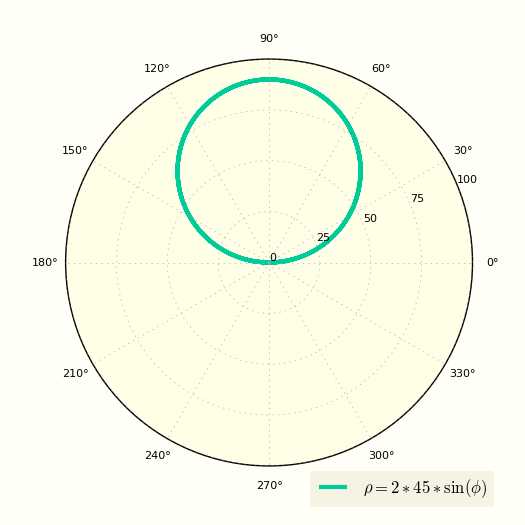
www.fxyz.ru

Лепестковая диаграмма в Excel в полярной системе координат

Лепестковая диаграмма по внешнему виду напоминает паутину или звезду. Достаточно специфическое изображение, позволяющее отображать данные каждой категории вдоль отдельной оси. Каждая ось начинается в центре рисунка и заканчивается на внешнем круге.

Что показывает лепестковая диаграмма

Лепестковая диаграмма – разновидность круговой, которая отлично подходит для представления данных, сгруппированных по определенному признаку (по годам, месяцам, категории товаров и т.п.).

В каких ситуациях полезна именно лепестковая диаграмма:

нужна максимальная наглядность;
необходимо проиллюстрировать изменчивость показателей сразу по нескольким направлениям;
важно показать на одном графике зависимость переменных величин от набора стабильных значений.

График паутинообразного типа напоминает по форме колесо. Каждый набор переменных отображается вдоль отдельной оси-спицы. Построение полярной кривой лепестковыми диаграммами выполняется очень просто. Вся графическая область этого типа диаграмм имеет полярную систему координат.

Как построить лепестковую диаграмму в Excel

На пустом листе создаем таблицу с данными. Или запускаем книгу, где хранится готовая информация для диаграммы лепесткового типа. Будьте внимательны: независимые переменные (причины) находятся в строках. Зависимые (воздействия) – в столбцах. Данные имеют одинаковый формат.
Выделяем данные, которые нужно отобразить на диаграмме. Переходим на вкладку «Вставка» в группу «Диаграммы». Лепестковые находятся в «Других диаграммах». Для примера выберем подтип «заполненной».
После нажатия ОК появится рисунок. Чтобы изменить цвет заливки, стиль, размер построенной диаграммы, используйте вкладки «Макет», «Формат», «Конструктор». В примере – объемная диаграмма лепесткового типа.

* При выделении ячеек с данными для включения в график названия тоже можно выделять. Excel распознает их и включает в подписи к секторам.

В примере получился такой рисунок, т.к. в таблице только один столбец с переменными значениями. Возьмем для построения диаграммы лепесткового типа данные из другого диапазона:

Добавились столбцы с переменными. Их нужно включить в диаграмму. Для этого щелкаем правой кнопкой мыши по области построения и нажимаем «Выбрать данные». В открывшемся диалоговом окне добавляем элементы легенды.

Получаем такой рисунок:

* Чтобы не перегружать рисунок, количество столбцов с данными не должно быть больше семи.

Построение графика в полярной системе координат с помощью Excel

В разных областях науки и техники существуют декартовые координаты и полярная система координат. Примеры знаменитых кривых в полярных координатах – уравнение кардиоиды, архимедова спираль, уравнение розы и др.

Инструмент «Лепестковая диаграмма» позволяет легко и быстро строить графики в полярной системе координат:

для каждой категории предусмотрена отдельная ось, а все оси выходят из одной точки – центра;
значение ряда данных – расстояние от центра до маркера – величина радиуса;
категория – угловая координата точки – наклон радиуса.

Известны следующие значения точек:

π /8	π /6	π /4	π /3	3π/8	5π/12	π/2	7 π/12
5 π/8	4 π/6	3 π/4	5 π/6	7 π*8	11 π/12	π

Уравнение функции:

r = 3 * sin (6 * ^φ)/

Заполним таблицу данных в Excel. Программа понимает число π и автоматически рассчитывает синусы.

Формулы для заполнения первого столбца берем из таблицы значений точек:

В соседнем столбце запишем формулу, по которой Excel будет считать значение функции r:

Выделим найденные значения функции. Перейдем на вкладку «Вставка». Подтип лепестковой диаграммы – «Лепестковая с маркерами». Получим в результате вот такой график в системе полярных координат:

На одной графической области в полярных координатах с помощью диаграммы лепесткового типа можно построить два и более графика.

exceltable.com

Полярная система координат, построение графика, примеры — смотреть онлайн видео урок бесплатно! Автор: alWEBra — Аналитическая геометрия

Это видео посвящено вопросу о том, что такое полярная система координат, построение графика, примеры. Вы уже наверняка знаете, что такое прямоугольная декартова система координат на плоскости. На одном из уроков эта тема уже рассматривалась. Она часто используется при решении многих задач и позволяет установить взаимно однозначное соответствие между точками плоскости и действительными числами. Но в некоторых случаях более эффективным является использование полярной системы координат. В этом видео уроке подробно рассказывается об этой системе. Вы узнаете, что такое полярная ось, полюс, полярный радиус, полярный угол, полярные координаты точки и многое другое. На приведенном примере вы узнаете, как построить график в полярной системе координат. Затем будет установлена связь между полярными и декартовыми координатами, т.е. по известным полярным координатам, при помощи формул, вычисляются координаты декартовой системы координат и наоборот. Во втором примере будет рассмотрена задача, в которой даны декартовы координаты точки, а требуется найти полярные координаты этой точки. Видео урок «Полярная система координат, построение графика, примеры» вы можете смотреть онлайн совершенно бесплатно. Удачи Вам!

Автор: alWEBra
Длительность: 6:06
Дата: 01.11.2013
Смотрели: 332
Рейтинг: 0.0/0

Если у Вас есть качественные видео уроки, которых нет на нашем сайте, то Вы можете добавить их в нашу коллекцию. Для этого Вам необходимо загрузить их на видеохостинг (например, YouTube) и добавить код видео в форму добавления уроков. Возможность добавлять свои материалы доступна только для зарегистрированных пользователей.

videourokionline.ru

площадь фигуры в полярных координатах — 22 Марта 2015 — Примеры решений задач

Площадь фигуры, заданной в полярных координатах

Рассмотрим примеры вычисления площади фигуры, заданной в полярных координатах кривой ρ= ρ(φ), с помощью определенного интеграла по формуле

Пример 1. Вычислить площадь, ограниченную одним лепестком розы

Решение.

Шаг 1. Выполним рисунок графика функции с помощью калькулятора построения графиков функций в полярных координатах.

Шаг 2. Из рисунка видно, что угол φ в первой четверти изменяется от 0 до π/2, следовательно границы интегрирования φ₁=0, φ₂=π/2

Шаг 3. Уравнение кривой , и границы φ₁=0, φ₂=π/2, подставляем в формулу

получаем площадь фигуры:

Замечание. Вычислить площадь фигуры в полярных координатах можно с помощью калькулятора