Изображение и построение углов
1. При помощи ЧП. Повернув головку на заданное число градусов, можно построить любой угол.
2. При помощи транспортира. Приложив центр транспортира к заданной вершине А искомого угла и отметив около шкалы транспортира нулевую точку и точку, соответствующую заданному числу градусов, соединяем обе эти точки с точкой А.
3. При помощи рейсшины и угольников. На Чертеже-№110, а показаны приемы построения углов в 15°, 30°, 45°, 60°, 75° и 90° и дополнительные к ним до 180°.
4. При помощи циркуля и линейки. Таким приемом удобно строить углы, показанные на Чертеже — №110, б.
Деление углов на равные части
Деление произвольного угла пополам. Наиболее удобным приемом деления произвольного угла пополам является деление при помощи циркуля и линейки; последовательность построения биссектрисы угла показана на Чертеже-№111.
Деление прямого угла на три равные части:
1. При помощи ЧП. На Чертеже — №112, а показано, что вдоль кромки линейки, повернутой на 30°. проведен из вершины А луч, а вдоль кромки линейки, повернутой на угол 60°, проведен из вершины А второй луч; получились три угла по 30°.
3. При помощи рейсшины и угольника в 30° — 60° — 90°.
На Чертеже — №112, б показано проведение из вершины А луча, наклоненного на угол 60°, и проведение луча, наклоненного на угол 30°.
4. При помощи циркуля и линейки. Построение сводится к проведению двух засечек D и Е и лучей через них из вершины А; радиус R берется произвольный. Порядок построения показан цифрами в кружках.
Уклоны и конусность
Уклоны. Уклоном прямой по отношению к какой-либо другой прямой называется величина се наклона к этой прямой, выраженная через тангенс угла между ними. Следовательно, уклоном прямой АС относительно прямой АВ называется отношение i = h ÷ l = tg α.
Как видно из чертежа — №113, а, уклон линии выявляется отношением величин двух катетов прямоугольного треугольника ABC, один из которых, например АВ, имеет направление линии, по отношению к которой задан уклон; гипотенузой является отрезок АС прямой заданного уклона. При обозначении уклона перед размерным числом пишут слово «уклон» параллельно линии, по отношению к которой он задан.
Взамен слова «уклон» допускается применять знак <, вершина угла которого должна быть направлена в сторону уклона (чертеж — №113, в).
Этот знак рекомендуется применять, когда направление уклона неясно выражено.
Проведение через точку А прямой заданного уклона h : l (по отношению к горизонтальной линии). На чертеже — №113, г показаны приемы вспомогательных построений для проведения прямой заданного уклона через заданную точку А: из данной точки А проводят горизонтальный луч и на нем от точки А откладывают длину L (равную числовому значению делителя данного уклона) — получают точку К, через которую проводят вертикальную линию и на ней от точки К откладывают длину h (равную числовому значению делимого данного уклона) — получают точку В. Прямая, проведенная через точки А и В, будет иметь требуемый уклон. Построение можно начинать с проведения вертикального луча из точки А и откладывания на нем величины h.
УПРАЖНЕНИЕ 3
Начертить контур шаблона с применением построения уклона (чертеж-№113, е).
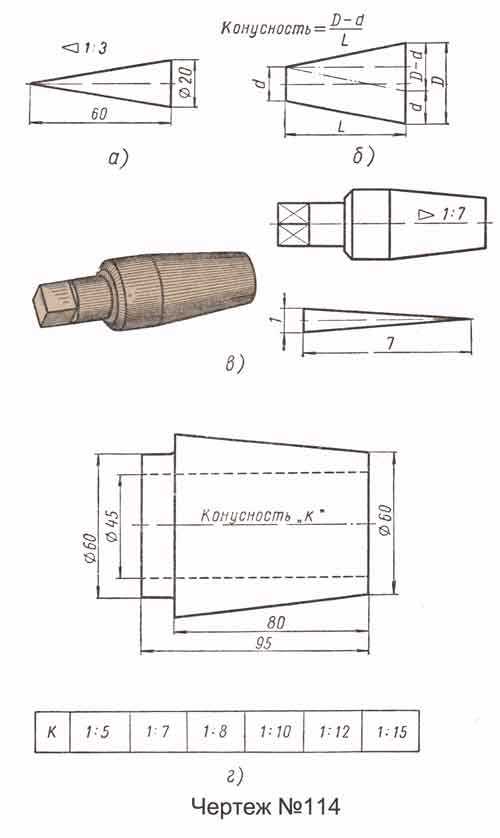
Конусность. Конусностью называется отношение диаметра D основания конуса к его высоте h. Перед размерным числом конусности следует писать знак >, вершина которого должна быть направлена в сторону вершины конуса (чертеж-№114, а).
Если на чертеже направление конусности выявлено вполне ясно, допускается взамен знака писать слово «конусность» (параллельно оси конуса).
Определение конусности по чертежу и проведение наклонных линий — образующих конуса — согласно данному числовому значению конусности аналогично определению уклонов и проведению прямых заданного уклона.
На чертеже-№114,в показан пример применения построения конусности при изображении детали — пробки.
УПРАЖНЕНИЕ 4
Пример 1. Начертить изображение конической втулки С применением построений, указанных конусностей, согласно чертежу-№114, г.
Пример 2. Перечертить один из вариантов по заданным размерам с построением указанной конусности (чертеж-№114, д).
Угловые (пропорциональные) масштабы
Угловыми (пропорциональными) масштабами называют графически выраженные числовые масштабы, о которых было сказано (на стр. Масштабы и компоновка чертежей )
Для уменьшения линий чертежа (чертеж-№115,б) отмеряем разметочным циркулем размер стороны α и, отложив его от вершины А на горизонтальной стороне углового масштаба 1 : 2,5 поворачиваем циркуль вокруг правой иглы и берем по вертикальному направлению до гипотенузы размер α 1, который будет равен α ÷ 2,5
Этот размер переносим на проведенную из заранее намеченной точки К1 вертикальную линию. Из верхней конечной точки проводим вправо горизонтальный луч; на нем откладываем размер стороны b, уменьшенный в 2,5 раза, т. е. b1 (полученный аналогично размеру α1; из конечной точки проводим вниз вертикальную линию и на ней откладываем размер с1 и т. д. В результате получим чертеж данной фигуры, выполненный в масштабе 1 : 2,5.
Чтобы не чертить каждый раз требуемый угловой масштаб, рекомендуется выполнить на миллиметровой бумаге общий угловой масштаб для уменьшений 1 : 2; 1 : 2,5; 1 : 4; 1 : 5; 1 : 10, такой же, какой показан на чертеже-№115, в.
Чертежи используемые в данной главе: >>> Чертежи №110 №111 №112 >>> Чертеж №113 >>> Продолжение чертежа №114 >>> Чертеж №115 >>> Смотри далее Окружность дуга и многоугольник…..
www.viktoriastar.ru
Расчет и нанесение уклона на обмерных чертежах
С необходимостью посчитать уклон постоянно сталкиваются проектировщики, строители, архитекторы, а также люди ряда других профессий, в силу того, что на земной поверхности очень трудно найти идеально ровный участок. Уклон выражается в градусах или в процентах. Обозначение в градусах показывает угол кривизны поверхности. Но уклон может быть представлен и в виде тангенса этого угла, умноженного на 100%.
Как рассчитать уклон поверхности?
Уклон – это отношение превышения (ВС) к заложению (АС) и обозначается в текстовых документах буквой i.
Например, i=1:6
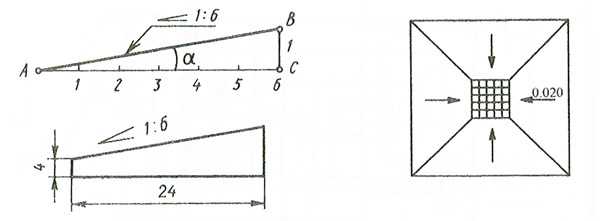
Разделите противолежащий катет (вертикальное расстояние) на прилежащий (расстояние между точками). Если вам нужно получить уклон в процентах, умножьте полученное число на 100%. Чтобы получить уклон в промилле, умножьте результат деления на 1000‰.
Если вам необходимо получить уклон в градусах, воспользуйтесь тем, что полученный при делении катетов результат – тангенс угла наклона. Посчитайте его арктангенс при помощи инженерного калькулятора, в результате вы получите значение уклона в градусах.
На видах (фасадах), разрезах, сечениях и схемах перед размерным числом, определяющим величину уклона, наносят знак , острый угол которого должен быть направлен в сторону уклона.
Обозначение уклона наносят непосредственно над линией контура или на полке линии-выноски.
На планах направление уклона плоскостей указывают стрелкой, на которой, при необходимости, проставляют величину уклона (см.рис.).
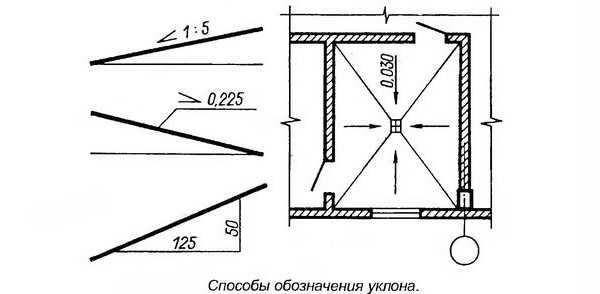
Построение и обозначение уклона. Пример изображения уклона на планах.
Величину уклона (тангенс угла наклона) указывают в виде простой или десятичной дроби с точностью до третьего знака.
Уклон (в строительстве) — показатель крутизны склона (а также ската кровли).
Укло́н (в геодезии) — показатель крутизны склона; отношение превышения местности к горизонтальному проложению, на котором оно наблюдается. Иными словами, величина уклона равна тангенсу угла между поверхностью склона и горизонталью.
Уклон поверхности равен тангенсу угла α, tgα = h/l — отношение перпендикуляра, опущенного из точки поверхности на прямую поверхность, к длине прямой поверхности от начала склона (при вершине угла α) до перпендикуляра.
Например, подъёму 12 м на 100 м перемещения по горизонтали соответствует уклон, равный 0,12 (12 % или 120 ‰).
При чтении нотации знак «%» произносится «сотых», а «‰» — «тысячных».
Источник:
книга: Единые требования по выполнению строительных чертежей.
М.: Изд-во «Архитектура-С», 2004.
Справочное пособие.
Автор: Георгиевский О.В.
Аннотация:
Справочное пособие по строительному черчению для студентов средних и высших учебных заведений. Пособие выполнено в соответствии с требованиями ГОСТов.
Настоящее справочное пособие выполнено в соответствии с требованиями ГОСТов ЕСКД (Единой системы конструкторской документации) и СПДС (Системы проектной документации для строительства).
Пособие может быть использовано при выполнении заданий по архитектурно-строительному черчению, а также при выполнении курсовых и дипломных проектов студентами всех строительных специальностей средних и высших учебных заведений.
распечатать
Вконтакте
Одноклассники
Google+
photogrammetria.ru
Обозначение: высота, ширина, длина. Ширина
Построение чертежей — дело непростое, но без него в современном мире никак. Ведь чтобы изготовить даже самый обычный предмет (крошечный болт или гайку, полку для книг, дизайн нового платья и подобное), изначально нужно провести соответствующие вычисления и нарисовать чертеж будущего изделия. Однако часто составляет его один человек, а занимается изготовлением чего-либо по этой схеме другой.
Чтобы не возникло путаницы в понимании изображенного предмета и его параметров, во всем мире приняты условные обозначения длины, ширины, высоты и других величин, применяемых при проектировании. Каковы они? Давайте узнаем.
Величины
Площадь, длина, ширина, высота и другие обозначения подобного характера являются не только физическими, но и математическими величинами. 
Единое их буквенное обозначение (используемое всеми странами) было уставлено в середине ХХ века Международной системой единиц (СИ) и применяется по сей день. Именно по этой причине все подобные параметры обозначаются латинскими, а не кириллическими буквами или арабской вязью. Чтобы не создавать отдельных трудностей, при разработке стандартов конструкторской документации в большинстве современных стран решено было использовать практически те же условные обозначения, что применяются в физике или геометрии.
Любой выпускник школы помнит, что в зависимости от того, двухмерная или трехмерная фигура (изделие) изображена на чертеже, она обладает набором основных параметров. Если присутствуют два измерения — это ширина и длина, если их три – добавляется еще и высота.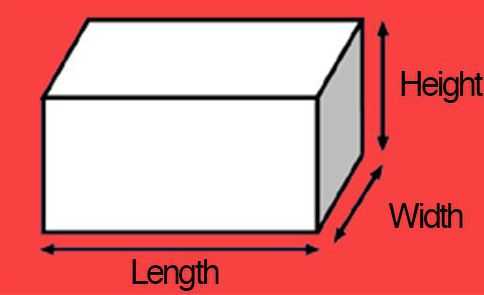 
Итак, для начала давайте выясним, как правильно длину, ширину, высоту обозначать на чертежах.
Ширина
Как было сказано выше, в математике рассматриваемая величина является одним из трех пространственных измерений любого объекта, при условии что его замеры производятся в поперечном направлении. Так чем знаменита ширина? Обозначение буквой «В» она имеет. Об этом известно во всём мире. Причем, согласно ГОСТу, допустимо применение как заглавной, так и строчной латинских литер. Часто возникает вопрос о том, почему именно такая буква выбрана. Ведь обычно сокращение производится по первой букве латинского, греческого или английского названия величины. При этом ширина на английском будет выглядеть как «width».
Вероятно, здесь дело в том, что данный параметр наиболее широкое применение изначально имел в геометрии. В этой науке, описывая фигуры, часто длину, ширину, высоту обозначают буквами «а», «b», «с». Согласно этой традиции, при выборе литера «В» (или «b») была заимствована системой СИ (хотя для других двух измерений стали применять отличные от геометрических символы).
Большинство полагает, что это было сделано, дабы не путать ширину (обозначение буквой «B»/«b») с весом. Дело в том, что последний иногда именуется как «W» (сокращение от английского названия weight), хотя допустимо использование и других литер («G» и «Р»). Согласно международным нормам системы СИ, измеряется ширина в метрах или кратных (дольных) их единицах. Стоит отметить, что в геометрии иногда также допустимо использовать «w» для обозначения ширины, однако в физике и остальных точных науках такое обозначение, как правило, не применяется.
Длина
Как уже было указано, в математике длина, высота, ширина – это три пространственных измерения. При этом, если ширина является линейным размером в поперечном направлении, то длина — в продольном. Рассматривая ее как величину физики можно понять, что под этим словом подразумевается численная характеристика протяжности линий.
В английском языке этот термин именуется length. Именно из-за этого данная величина обозначается заглавной или строчной начальной литерой этого слова — «L». Как и ширина, длина измеряется в метрах или их кратных (дольных) единицах.
Высота
Наличие этой величины указывает на то, что приходится иметь дело с более сложным — трехмерным пространством. В отличие от длины и ширины, высота численно характеризует размер объекта в вертикальном направлении.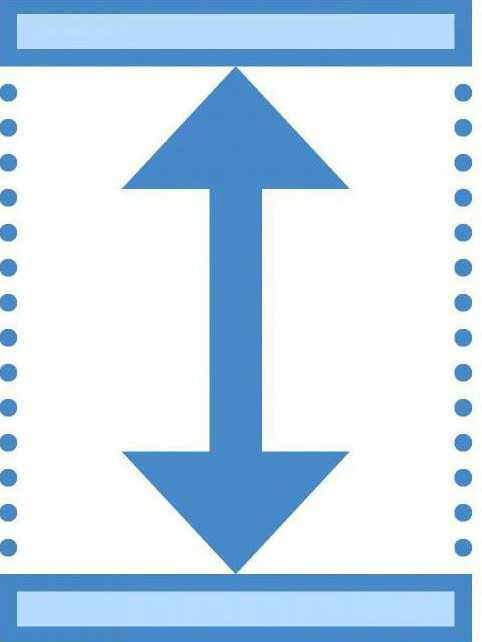 
На английском она пишется как «height». Поэтому, согласно международным нормам, ее обозначают латинской литерой «Н»/«h». Помимо высоты, в чертежах иногда эта буква выступает и как глубины обозначение. Высота, ширина и длина – все все эти параметры измеряются в метрах и их кратных и дольных единицах (километры, сантиметры, миллиметры и т. п.).
Радиус и диаметр
Помимо рассмотренных параметров, при составлении чертежей приходится иметь дело и с иными. 
Например, при работе с окружностями возникает необходимость в определении их радиуса. Так именуется отрезок, который соединяет две точки. Первая из них является центром. Вторая находится непосредственно на самой окружности. На латыни это слово выглядит как «radius». Отсюда и общепринятое сокращение: строчная или заглавная «R»/«r».
Чертя окружности, помимо радиуса часто приходится сталкиваться с близким к нему явлением – диаметром. Он также является отрезком, соединяющим две точки на окружности. При этом он обязательно проходит через центр.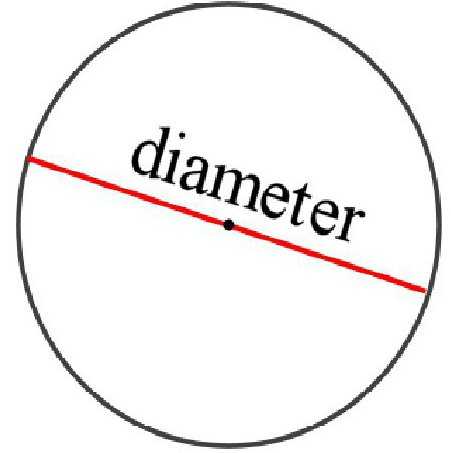 
Численно диаметр равен двум радиусам. По-английски это слово пишется так: «diameter». Отсюда и сокращение – большая или маленькая латинская буква «D»/«d». Часто диаметр на чертежах обозначают при помощи перечеркнутого круга – «Ø».
Хотя это распространенное сокращение, стоит иметь в виду, что ГОСТ предусматривает использование только латинской «D»/«d».
Толщина
Большинство из нас помнят школьные уроки математики. Ещё тогда учителя рассказывали, что, латинской литерой «s» принято обозначать такую величину, как площадь. Однако, согласно общепринятым нормам, на чертежах таким способом записывается совсем другой параметр – толщина.
Почему так? Известно, что в случае с высотой, шириной, длиной, обозначение буквами можно было объяснить их написанием или традицией. Вот только толщина по-английски выглядит как «thickness», а в латинском варианте — «crassities». Также непонятно, почему, в отличие от других величин, толщину можно обозначать только строчной литерой. Обозначение «s» также применяется при описании толщины страниц, стенок, ребер и так далее.
Периметр и площадь
В отличие от всех перечисленных выше величин, слово «периметр» пришло не из латыни или английского, а из греческого языка. Оно образовано от «περιμετρέο» («измерять окружность»). И сегодня этот термин сохранил свое значение (общая длина границ фигуры). Впоследствии слово попало в английский язык («perimeter») и закрепилось в системе СИ в виде сокращения буквой «Р».
Площадь — это величина, показывающая количественную характеристику геометрической фигуры, обладающей двумя измерениями (длиной и шириной). В отличие от всего перечисленного ранее, она измеряется в квадратных метрах (а также в дольных и кратных их единицах). Что касается буквенного обозначения площади, то в разных сферах оно отличается. Например, в математике это знакомая всем с детства латинская литера «S». Почему так – нет информации.
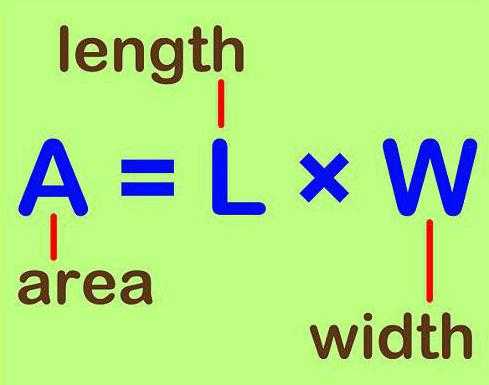Некоторые по незнанию думают, что это связано с английским написанием слова «square». Однако в нем математическая площадь – это «area», а «square» — это площадь в архитектурном понимании. Кстати, стоит вспомнить, что «square» — название геометрической фигуры «квадрат». Так что стоит быть внимательным при изучении чертежей на английском языке. Из-за перевода «area» в отдельных дисциплинах в качестве обозначения применяется литера «А». В редких случаях также используется «F», однако в физике данная буква означает величину под названием «сила» («fortis»).
Другие распространенные сокращения
Обозначения высоты, ширины, длины, толщины, радиуса, диаметра являются наиболее употребляемыми при составлении чертежей. Однако есть и другие величины, которые тоже часто присутствуют в них. Например, строчное «t». В физике это означает «температуру», однако согласно ГОСТу Единой системы конструкторской документации, данная литера — это шаг (винтовых пружин, заклепочных соединений и подобного). При этом она не используется, когда речь идет о зубчатых зацеплениях и резьбе.
Заглавная и строчная буква «A»/«a» (согласно все тем же нормам) в чертежах применяется, чтобы обозначать не площадь, а межцентровое и межосевое расстояние. Помимо различных величин, в чертежах часто приходится обозначать углы разного размера. Для этого принято использовать строчные литеры греческого алфавита. Наиболее применяемые — «α», «β», «γ» и «δ». Однако допустимо использовать и другие.
Какой стандарт определяет буквенное обозначение длины, ширины, высоты, площади и других величин?
Как уже было сказано выше, чтобы не было недопонимания при прочтении чертежа, представителями разных народов приняты общие стандарты буквенного обозначения. Иными словами, если вы сомневаетесь в интерпретации того или иного сокращения, загляните в ГОСТы. Таким образом вы узнаете, как правильно обозначается высота, ширины, длина, диаметр, радиус и так далее.
Для Российской Федерации таким нормативным документом является ГОСТ 2.321-84. Он был внедрен еще в марте 1984 г. (во времена СССР), взамен устаревшего ГОСТа 3452—59.
fb.ru
Обозначение на чертежах.
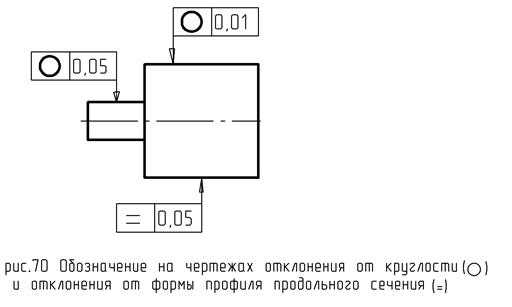
Все рассмотренные показатели устанавливаются ГОСТом 24643-81, причем для каждого вида погрешности установлено 16 степеней точности (1 — самая точная, 16 — самая грубая). В зависимости от соотношения между допусками формы ( ) и размера ( ) установлено 3 уровня относительной геометрической точности:
1) А – нормальная.
Для плоских тел: .
Для круглых тел:
2) В – повышенная точность.
Для плоских тел:
Для круглых тел:
3) С – высокая точность.
Для плоских тел:
Для круглых тел:
§ 26. Взаимозаменяемость по расположению поверхностей деталей. Обозначения на чертежах.
При нормировки этих отклонений реальные профили поверхности заменяются прилегающими и измеряется отклонение этих прилегающих поверхностей относительно баз номинальных поверхностей.
Различают конструкторские, измерительные, технологические базы.
Для снижения погрешности изготовления детали целесообразно совмещать их в производстве и измерении.
Отклонение от параллельности плоскости.
а – минимальное расстояние от базы до прилегающей контрольной плоскости (ПКП).
b – максимальное расстояние от базы до прилегающей контрольной плоскости (рис. 71).
Δ= = b – a ≤ Т=.
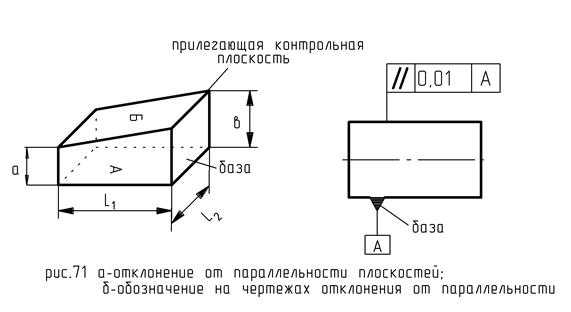
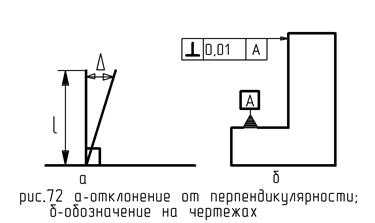
Отклонение от перпендикулярности.
Указывается в линейных единицах относительно базовых поверхностей, реального угла от номинального (рис. 72).
Лекция №17
Отклонение угла наклона относительно плоскости или оси.
Отклонения угла наклона относительно плоскости или оси — отклонение нормируемой плоскости от базовой угла наклона, выраженное в линейных единицах на длине нормируемого участка. Допустим, задан какой-то номинальный угол наклона на длине нормируемого участка 100мм. Нормируемое отклонение обозначается ∆<. Плоскость, относительно которой происходит нормирование, обозначена на рисунке базой А. Отклонение нормируемой плоскости происходит на угол ∆<, само отклонение нормируется в линейных величинах, поэтому присутствует соответствующий размер (100мм) (рис. 73).
Отклонение от соосности.
Отклонение от соосности — наибольшее расстояние между базовой и действительной осью.
Допустим, что действительная ось не совпадает с базовой. Максимальное отклонение действительной оси от базовой на длине участка (200мм) опять выражается в линейных единицах. Обозначается это отклонение значком ∆Θ. Это отклонение можетбыть записано как в радиальном ∆TΘ/2 , так и в диаметральном выражении ∆TΘ. Приведем пример отклонения от соосности. Здесь отклонение от соосности в диаметральном выражении двух отверстий относительно базы А составляет 0,1 мм.
Отклонение от симметричности.
Отклонение от симметричности — это наибольшее расстояние от оси нормируемого элемента до оси симметрии базового элемента.
К примеру, в элементе с осью симметрии необходимо выполнить отверстие. Чертеж читается так: отклонение от оси базового элемента А оси симметрии нормируемого элемента не должно превышать в диаметральном выражении 0,1мм (рис. 75).
Отклонение от пересечения полей.
Важно, например, когда изготавливаются форсуночные элементы, которые имеют достаточно большое количество пересечений осей, а в случае неточного пересечения осей форсунок могут возникнуть завихрения прогоняемых веществ (окислителя, горючего).
Суммарное отклонение формы и расположения поверхности.
Основные типы отклонений формы и расположения поверхности:
1) радиальное биение;
2) торцовое биение.
Биения обозначаются значком ∆↑.
Радиальное биение.
Радиальное биение представляет собой разность максимального и минимального отклонения реального профиля от базовой оси.
Изобразим профиль реальной окружности. Для того, что найти у этого реального профиля отклонение от круглости необходимо описать вокруг него прилегающую окружность. Эта окружность имеет свою ось и центр, но ось, как правило, не совпадает с базовой осью (рис. 77).
Максимальное расстояние от базовой оси состоит из радиуса прилегающей окружности R и отклонения о соосности ∆↑. Минимальное же расстояние равно разнице радиуса R и отклонения ∆↑. Тогда биение:
∆↑=Rmax — Rmin=∆Θ + ∆o.
На чертеже это обозначается следующим образом (рис. 78).
Радиальное биение относительно базовой оси А не должно превышать 0,1мм, в случае полного радиального биения, когда требуется нормировать всю цилиндрическую поверхность.
Торцевое биение.
Торцовое биение — разность максимального и минимального расстояния реального профиля торца от плоскости, перпендикулярной оси (рис.79).
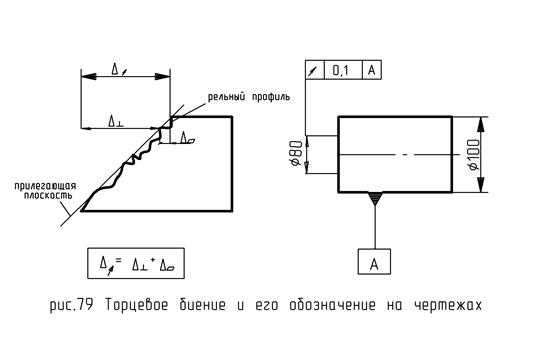
Лекция №18
Похожие статьи:
poznayka.org
Величины |
| Вес |
| Время |
| Высота |
| Давление |
| Диаметр |
| Длина |
| Длина пути |
| Импульс (количество движения) |
| Количество вещества |
| Коэффициент жесткости (жесткость) |
| Коэффициент запаса прочности |
| Коэффициент полезного действия |
| Коэффициент трения качения |
| Коэффициент трения скольжения |
| Масса |
| Масса атома |
| Масса электрона |
| Механическое напряжение |
| Модуль упругости (модуль Юнга) |
| Момент силы |
| Мощность |
| Объем, вместимость |
| Период колебания |
| Плотность |
| Площадь |
| Поверхностное натяжение |
| Постоянная гравитационная |
| Предел прочности |
| Работа |
| Радиус |
| Сила, сила тяжести |
| Скорость линейная |
| Скорость угловая |
| Толщина |
| Ускорение линейное |
| Ускорение свободного падения |
| Частота |
| Частота вращения |
| Ширина |
| Энергия |
| Энергия кинетическая |
| Энергия потенциальная |
| Длина волны |
| Звуковая мощность |
| Звуковая энергия |
| Интенсивность звука |
| Скорость звука |
| Частота |
Тепловые величины и величины молекулярной физики |
| Абсолютная влажность |
| Газовая постоянная (молярная) |
| Количество теплоты |
| Коэффицент полезного действия |
| Относительная влажность |
| Относительная молекулярная масса |
| Постоянная (число) Авогадро |
| Постоянная Больцмана |
| Постоянная (число) Лошмидта |
| Температура Кюри |
| Температура па шкале Цельсия |
| Температура термодинамическая (абсолютная температура) |
| Температурный коэффицент линейного расширения |
| Температурный коффицент объемного расширения |
| Удельная теплоемкость |
| Удельная теплота парообразования |
| Удельная теплота плавления |
| Удельная теплота сгорания топлива (сокращенно: теплота сгорания топлива) |
| Число молекул |
| Энергия внутренняя |
Электрические и магнитные величины |
| Диэлектрическая проницаемость вакуума (электрическая постоянная) |
| Индуктивность |
| Коэффицент самоиндукции |
| Коэффицент трансформации |
| Магнитная индукция |
| Магнитная проницаемость вакуума (магнитная постоянная) |
| Магнитный поток |
| Мощность электрической цепи |
| Напряженность магнитного поля |
| Напряженность электрического поля |
| Объемная плотность электрического заряда |
| Относительная диэлектрическая проницаемость |
| Относительная магнитная проницаемость |
| Плотность энергии магнитного поля удельная |
| Плотность энергии электрического поля удельная |
| Плотность заряда поверхностная |
| Плотность электрического тока |
| Постоянная (число) Фарадея |
| Проницаемость диэлектрическая |
| Работа выхода электрона |
| Разность потенциалов |
| Сила тока |
| Температурный коэффицент электрического сопротивления |
| Удельная электрическая проводимость |
| Удельное электрическое сопротивление |
| Частота электрического тока |
| Число виток обмотки |
| Электрическая емкость |
| Электрическая индукция |
| Электрическая проводимость |
| Электрический момент диполя молекулы |
| Электрический заряд (количество электричества) |
| Электрический потенциал |
| Электрическое напряжение |
| Электрическое сопротивление |
| Электродвижущая сила |
| Электрохимический эквивалент |
| Энергия магнитного поля |
| Энергия электрического поля |
| Энергия Электромагнитная |
| Длина волны |
| Освещенность |
| Период колебания |
| Плотность потока излучения |
| Показатель (коэффицент) преломления |
| Световой поток |
| Света сила объектива |
| Сила света |
| Скорость света |
| Увеличение линейное |
| Увеличение окуляра, микроскопа, лупы |
| Угол отражения луча |
| Угол падения луча |
| Фокусное расстояние |
| Частота колебаний |
| Энергия излучения |
| Энергия световая |
| Атомная масса относительная |
| Время полураспада |
| Дефект массы |
| Заряд электрона |
| Масса атома |
| Масса нейтрона |
| Масса протона |
| Масса электрона |
| Постоянная Планка |
| Радиус электрона |
Величины ионизирующих излучений |
| Поглощеная доза излучения (доза излучения) |
| Мощность поглощенной дозы излучения |
| Активность нуклида в радиоактивном источнике |
stroyvolga.ru
13. Основные правила нанесения размеров на чертеже
По изображениям предмета на чертеже судят о его величине и величине его отдельных частей. Основанием для этого служат размерные числа, независимо от того, в каком масштабе и с какой точностью
Рис. 7
Рис. 8
Рис. 9
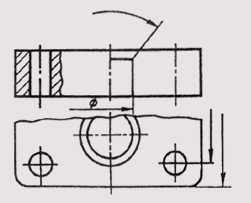
Рис. 10
Рис. 11
Рис. 12
Рис. 13
выполнены изображения. Правила нанесения размеров на чертежах установлены ГОСТ 2.307—68.
Размеры на чертеже указывают размерными числами, размерными и выносными линиями. Размерные числа на чертежах, как правило, указывают в миллиметрах без указания единиц измерения. В тех случаях, когда необходимо применять другие единицы измерения длины, их показывают после размерного числа.
Размерные числа наносят над размерной линией, возможно ближе к ее середине. Зазор между размерным числом и размерной линией должен быть около 1,0 мм. Высоту цифр размерных чисел принимают не менее 3,5 мм (рис. 7).
Размерная линия проводится параллельно отрезку, размер которого над ней наносится. Ее проводят между выносными линиями, проведенными перпендикулярно размерным. Допускается размерные линии проводить непосредственно к линиям видимого контура, осевым и центровым. В отдельных случаях размерная линия может проводиться не перпендикулярно выносной (рис. 8). Размерные линии ограничивают стрелки (рис. 9). В отдельных случаях их проводят не полностью, а с обрывом стрелки с одной стороны (рис. 10). Размер стрелки выбирают от принятой на чертеже толщины сплошной толстой основной линии. В пределах одного чертежа величина стрелок должна быть по возможности одинаковой. Не рекомендуется в качестве размерных линий использовать контурные, осевые, центровые и выносные линии.
Если длина размерной линии мала для размещения стрелок, то размерную линию продолжают за выносные линии, и размеры наносят, как показано на рис. 11.
Выносные линии проводят от границ измерений, они являются вспомогательными и служат для размещения между ними размерных линий. Выносные линии следует по возможности располагать вне контура изображения, перпендикулярно прямолинейному отрезку, размер которого необходимо указать. Выносные линии должны выходить за концы стрелок размерных линий на 1…5 мм (рис. 12).
Минимальное расстояние от размерной линии до параллельной ей линии должно быть 10 мм, а между параллельными размерными линиями — 7 мм.
Угловые размеры на чертежах проставляются в градусах, минутах и секундах с указанием единиц измерения. Размер угла наносят над размерной линией, которая проводится в виде дуги с центром в его вершине. Выносные линии в этом случае проводятся радиально (рис. 13).
При различных наклонах размерных линий размерные числа линейных размеров располагают так, как показано на рис. 14, а, а угловые размеры — как показано на рис. 14, б. Если размерная линия будет находиться в зоне, которая на чертеже заштрихована, размерные числа наносят на полках линий-выносок (рис. 15).
Если для написания размерного числа мало места над размерной линией или это место занято другими элементами изображения и впи-
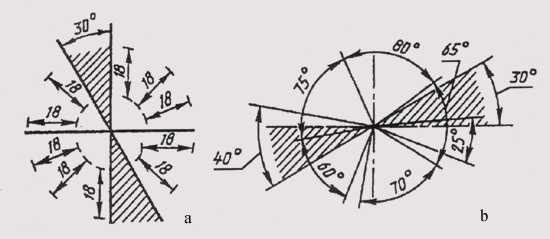
Рис. 14
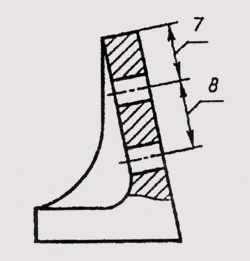
Рис. 15
Рис. 16
Рис. 17
сать в него размерное число невозможно, размерное число наносят по одному из вариантов, приведенных на рис. 16.
С целью упрощения ряда изображений, создания удобств для чтения чертежа стандарт предусматривает применение условных обозначений в виде букв латинского алфавита и графических знаков, которые ставятся перед размерными числами. На чертежах применяются
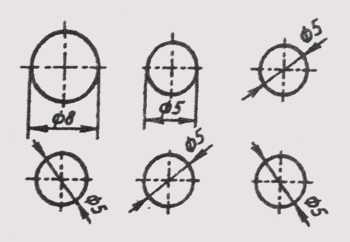
Рис. 18
Рис. 19
Рис. 20
Рис. 21
Рис. 22
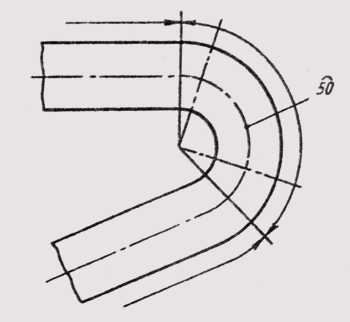
Рис. 23
Рис. 24
знаки и буквы для обозначения диаметра и радиуса, длины дуги и квадрата, уклона и конусности, сферы, толщины и длины детали.
Перед размерным числом диаметра наносится знак 0 (рис. 17). Причем между знаком и числом никаких пропусков не предусмотрено. Для окружностей малого диаметра размерные линии стрелки и сам размер наносят по одному из вариантов, приведенных на рис. 18.
Перед размерным числом радиуса дуги всегда ставится знак в виде прописной латинской буквы R. Размерную линию в этом случае проводят по направлению к центру дуги и ограничивают только одной стрелкой, упирающейся в дугу или ее продолжение (рис. 19). Если величина радиуса на чертеже менее 6 мм, стрелку рекомендуется распо-
Рис. 25
лагать с внешней стороны дуги. При необходимости задания положения центра дуги его отмечают пересечением центровых или выносных линий (рис. 20). В тех случаях, когда на чертеже изображена дуга большого радиуса, для которой центр можно не обозначать, размерную линию обрывают, не доводя до центра (рис. 21). Если же в этом случае центр необходимо отметить, допускается приближать его к дуге (рис. 22). Размерная линия в этом случае показывается с изломом 90°, и оба участка размерной линии проводятся параллельно. Не следует располагать на одной прямой размерные линии, выходящие из одного центра и предназначенные для обозначения размерных дуг. Радиусами рекомендуется обозначать дуги до 180°; дуги, величина которых составляет более 180°, обозначаются диаметром.
Знак дуги наносится над размерным числом (рис. 23). Длину дуги задают в линейных единицах, а размерное число, обозначающее дугу, наносится над размерной линией в соответствии с обычными требованиями.
Для простановки размеров квадрата применяют соответствующий знак D, высота которого равна 7/10 высоты размерного числа (рис. 24, а). При ином расположении квадрата наносят размеры его сторон (рис. 24, б). Следует отметить, что знак квадрата наносят только на том изображении, на котором он проецируется в линию.
Знак конусности поверхности наносится на полке линии-выноски, расположенной параллельно оси конуса или на оси конуса (рис. 25, а). Знак конусности располагают так, чтобы его острый угол был направлен в сторону вершины конуса. Величину конусности определяют отношением разности диаметров двух поперечных сечений конуса к расстоянию между этими сечениями, т. е. k = D — dll, где D — диаметр большого сечения; d — диаметр меньшего сечения; l — расстояние между сечениями. Конусность указывают в виде простого дробного числа (рис. 25, б).
Знак уклона прямой указывают на полке линии-выноски. Уклон i представляет собой тангенс угла между данной прямой и горизонтальной или вертикальной прямой (рис. 26, а). Знак уклона располагается
Рис. 26
Рис. 27
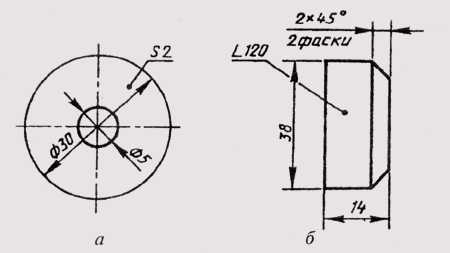
Рис. 28
так, чтобы острый угол его был направлен в сторону уклона прямой (рис. 26, б). Уклон, как и конусность, на чертеже задают простой дробью, в процентах или в промилях.
Для обозначения сферы на чертеже применяют знак диаметра или радиуса. В тех случаях, когда по чертежу сферу трудно отличить от других поверхностей, перед знаком радиуса или диаметра допускается добавлять слово «Сфера». Надпись на чертеже выполняется по типу «Сфера диаметр 17» или «Сфера R10» (рис. 27).
Простые плоские детали изображаются в виде одной проекции. В этих случаях ее толщину обозначают строчной буквой s и надпись на чертеже выполняется по типу s2 и располагается на полке линии-выноски (рис. 28, а). Длину предмета указывают буквой / (рис. 28, б).
Фаски на чертежах наносят двумя линейными размерами (рис. 29, а) или одним линейным и одним угловым (рис. 29, б). В том случае, если
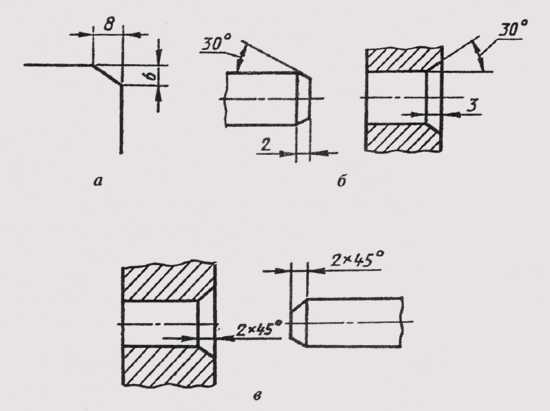
Рис. 29
угол наклона образующей конуса равен 45°, применяют упрощенное обозначение фаски, когда размерная линия проводится параллельно оси конуса, а надпись выполняется по типу «2 х 45» (рис. 29, в).
lib.qrz.ru
ЕСКД. Обозначения графические материалов и правила их нанесения на чертежах
ГОСТ 2.306-68
МЕЖГОСУДАРСТВЕННЫЙ СТАНДАРТ
ЕДИНАЯ СИСТЕМА КОНСТРУКТОРСКОЙ ДОКУМЕНТАЦИИ
ОБОЗНАЧЕНИЯ ГРАФИЧЕСКИЕ
МАТЕРИАЛОВ И ПРАВИЛА
ИХ НАНЕСЕНИЯ НА ЧЕРТЕЖАХ
ИПК
ИЗДАТЕЛЬСТВО СТАНДАРТОВ
Москва
МЕЖГОСУДАРСТВЕННЫЙ СТАНДАРТ
Дата введения 01.01.71
1. Настоящий стандарт устанавливает графические обозначения материалов в сечениях и на фасадах, а также правила нанесения их на чертежи всех отраслей промышленности и строительства.
(Измененная редакция, Изм. № 2).
la. Общее графическое обозначение материалов в сечениях независимо от вида материалов должно соответствовать черт. 1а.
Черт. la
(Введен дополнительно, Изм. № 1).
2. Графические обозначения материалов в сечениях в зависимости от вида материалов должны соответствовать приведенным в табл. 1.
Допускается применять дополнительные обозначения материалов, не предусмотренных в настоящем стандарте, поясняя их на чертеже.
Таблица 1
|
Материал |
Обозначение |
|
1. Металлы и твердые сплавы |
|
|
2. Неметаллические материалы, в том числе волокнистые монолитные и плитные (прессованные), за исключением указанных ниже |
|
|
3. Древесина |
|
|
4. Камень естественный |
|
|
5. Керамика и силикатные материалы для кладки |
|
|
6. Бетон |
|
|
7. Стекло и другие светопрозрачные материалы |
|
|
8. Жидкости |
|
|
9. Грунт естественный |
Примечания:
1. Композиционные материалы, содержащие металлы и неметаллические материалы, обозначают как металлы.
2. Графическое обозначение п. 3 следует применять, когда нет необходимости указывать направление волокон.
3. Графическое обозначение п. 5 следует применять для обозначения кирпичных изделий (обожженных и необожженных), огнеупоров, строительной керамики, электротехнического фарфора, шлакобетонных блоков и т.п.
(Измененная редакция, Изм. № 1, 2).
3. Устанавливают следующие обозначения сетки и засыпки из любого материала (в сечении), указанные на черт. 1.
а — сетка; б – засыпка
Черт. 1
4. При выделении материалов и изделий на виде (фасаде) графические обозначения их должны соответствовать указанным в табл. 2.
Таблица 2
|
Материал |
Обозначение |
|
1. Металлы |
|
|
2. Сталь рифленая |
|
|
3. Сталь просечная |
|
|
4. Кладка из кирпича строительного и специального, клинкера, керамики, терракоты, искусственного и естественного камней любой формы и т.п. |
|
|
5. Стекло |
Примечания:
1. (Исключено, Изм. № 1).
2. Для уточнения разновидности материала, в частности, материалов с однотипным обозначением, графическое обозначение следует сопровождать поясняющей надписью на поле чертежа.
3. В специальных строительных конструктивных чертежах для армирования железобетонных конструкций должны применяться обозначения по ГОСТ 21.501.
4. Обозначение материала на виде (фасаде) допускается наносить не полностью, а только небольшими участками по контуру или пятнами внутри контура.
5. Наклонные параллельные линии штриховки должны проводиться под углом 45° к линии контура изображения (черт. 2a) или к его оси (черт. 2б), или к линиям рамки чертежа (черт. 2).
Черт. 2а
Черт. 2б
Если линии штриховки, приведенные к линиям рамки чертежа под углом 45°, совпадают по направлению с линиями контура или осевыми линиями, то вместо угла 45° следует брать угол 30° или 60° (черт. 3 и 4).
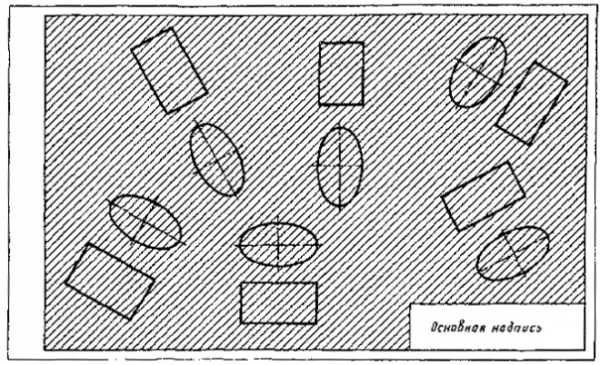
Черт. 2
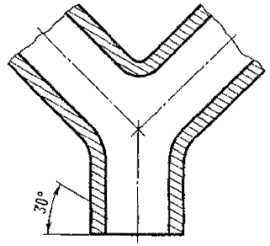
Черт. 3
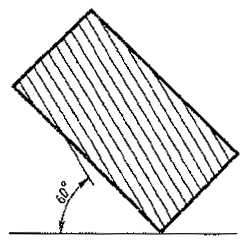
Черт. 4
Линии штриховки должны наноситься с наклоном влево или вправо, но как правило, в одну и ту же сторону на всех сечениях, относящихся к одной и той же детали, независимо от количества листов, на которых эти сечения расположены.
(Измененная редакция, Изм. № 1).
6. Расстояние между параллельными прямыми линиями штриховки (частота) должно быть, как правило, одинаковым для всех выполняемых в одном и том же масштабе сечений данной детали и выбирается в зависимости от площади штриховки и необходимости разнообразить штриховку смежных сечений. Указанное расстояние должно быть от 1 до 10 мм в зависимости от площади штриховки и необходимости разнообразить штриховку смежных сечений.
(Измененная редакция, Изм. № 2).
7. Узкие и длинные площади сечений (например, штампованных, вальцованных и других подобных деталей), ширина которых на чертеже от 2 до 4 мм, допускается штриховать полностью только на концах и у контуров отверстий, а остальную площадь сечения — небольшими участками в нескольких местах (черт. 5 и 6). Линии штриховки стекла (черт. 7) следует наносить с наклоном 15-20° к линии большей стороны контура сечения.
Черт. 5
Черт. 6
Черт. 7
(Измененная редакция, Изм. № 4)
8. Узкие площади сечений, ширина которых на чертеже менее 2 мм, допускается показывать зачерненными с оставлением просветов между смежными сечениями не менее 0,8 мм (черт. 8, 9).
В строительных чертежах допускается на сечениях незначительной площади любой материал обозначать как металл или вообще не применять обозначение, сделав поясняющую надпись на поле чертежа.
Черт. 8
Черт. 9
9. Обозначение, указанное в п. 3 табл. 1, и обозначение засыпки в сечении выполняют от руки.
(Измененная редакция, Изм. № 1).
10. Для смежных сечений двух деталей следует брать наклон линий штриховки для одного сечения вправо, для другого — влево (встречная штриховка).
При штриховке «в клетку» для смежных сечений двух деталей расстояние между линиями штриховки в каждом сечении должно быть разным.
В смежных сечениях со штриховкой одинакового наклона и направления следует изменять расстояние между линиями штриховки (черт. 10) или сдвигать эти линии в одном сечении по отношению к другому, не изменяя угла их наклона (черт. 11).
Черт. 10
Черт. 11
11. При больших площадях сечений, а также при указании профиля грунта допускается наносить обозначение лишь у контура сечения узкой полоской равномерной ширины (черт. 12).
(Измененная редакция, Изм. № 1).
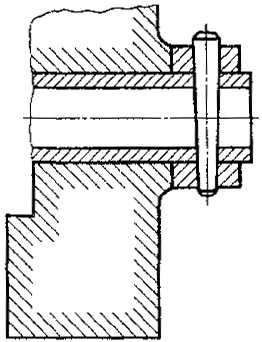
Черт. 12
ИНФОРМАЦИОННЫЕ ДАННЫЕ
1. РАЗРАБОТАН И ВНЕСЕН Комитетом стандартов, мер и измерительных приборов при Совете Министров СССР
РАЗРАБОТЧИКИ
В.Р. Верченко, Е.А. Панфилов, Ю.И. Степанов, Я.Г. Старожилец, Б.Я. Кабаков, Л.В. Матвеев, Н.И. Ермин, В.Н. Взоров, М.Г. Арановский
2. УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Постановлением Комитета стандартов, мер и измерительных приборов при Совете Министров СССР в декабре 1967 г.
3. (Исключен, Изм. № 4)
4. Взамен ГОСТ 3455-59 и ГОСТ 11633-65
5. ССЫЛОЧНЫЕ НОРМАТИВНО-ТЕХНИЧЕСКИЕ ДОКУМЕНТЫ
6. ИЗДАНИЕ (апрель 2000 г.) с Изменениями № 1, 2, 3, утвержденными в августе 1980 г., сентябре 1987 г., марте 1989 г. (ИУС 11-80, 12-87, 7-89)
aquagroup.ru