Как найти истинную величину отрезка – Иллюстрированный самоучитель по созданию чертежей › Изображение линий на чертеже › Определение натуральной величины отрезка прямой линии [страница — 50] | Самоучители по инженерным программам

Определение натуральной величины отрезка

Если отрезок параллелен плоскости, то он проецируется на неё без искажений. В остальных случаях для нахождения его натуральной величины применяют метод прямоугольного треугольника или способы преобразования ортогональных проекций.

Содержание

1. Метод прямоугольного треугольника
2. Способ параллельного переноса
3. Поворот вокруг оси

Метод прямоугольного треугольника

Сущность данного метода заключается в нахождении гипотенузы прямоугольного треугольника, у которого один катет равен горизонтальной (или фронтальной) проекции отрезка, а величина другого катета представляет собой разность удаления концов отрезка от горизонтальной (или, соответственно, фронтальной) плоскости проекции.

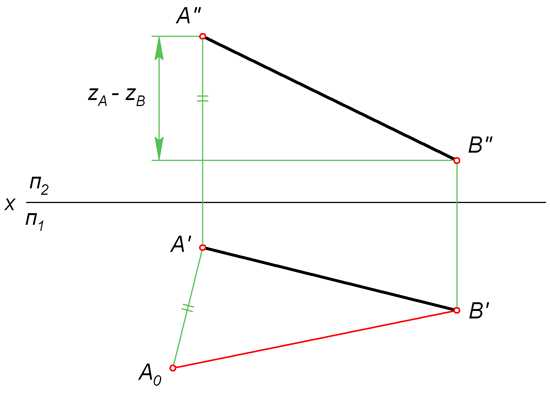
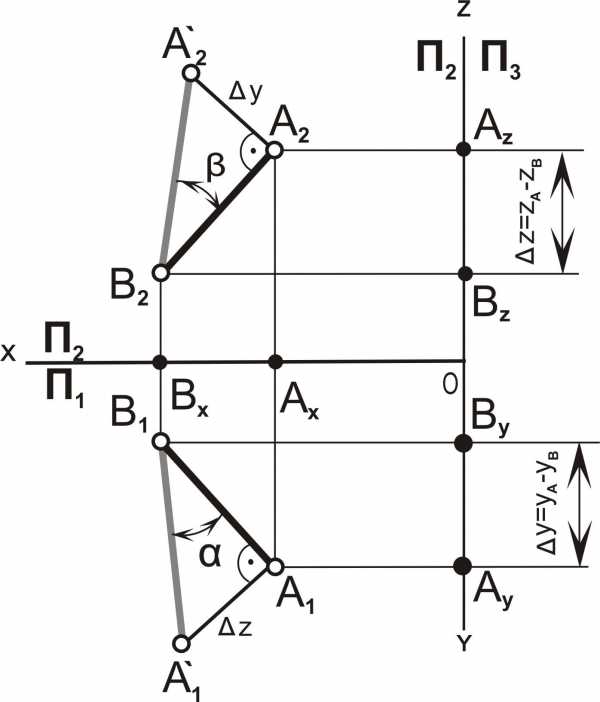
Для того чтобы найти натуральную величину отрезка AB (рисунок выше), строим прямоугольный треугольник A₀A’B’. Его первый катет A’B’ – это горизонтальная проекция AB. Второй катет A’A

0 равен величине Z_A – Z_B, то есть разности удаления точек A и B от горизонтальной плоскости П₁.

Откладываем A’A₀ = Z_A – Z_B перпендикулярно A’B’. Затем проводим гипотенузу A₀B’ треугольника A₀A’B’. На рисунке она обозначена красным цветом. Её величина соответствует настоящей длине AB.

Способ параллельного переноса

Параллельный перенос представляет собой перемещение геометрической фигуры параллельно одной из плоскостей проекций. При этом величина проекции фигуры на эту плоскость не меняется. Например, если перемещать отрезок EF параллельно горизонтальной плоскости П₁, то длина его проекции E’F’ не изменится, когда она займет новое положение E’₁F’₁ (как это показано на рисунке ниже).

Еще одно важное свойство параллельного переноса заключается в том, что при любом перемещении точки параллельно горизонтальной плоскости проекции, её фронтальная проекция движется по прямой, параллельной оси X. Если точка перемещается параллельно фронтальной плоскости, то её горизонтальная проекция движется по прямой, параллельной оси X.

Пример построения

Чтобы определить действительный размер отрезка EF, на свободном месте чертежа строим его новую горизонтальную проекцию E’₁F’₁ = E’F’ так, чтобы она была параллельна оси X . Затем по линиям связи находим точки E»₁ и F»₁. Расстояние между ними и есть искомая величина, поскольку мы перенесли EF в положение, параллельное фронтальной плоскости.

Метод параллельного переноса, описанный здесь, иногда называют параллельным перемещением. Посмотреть дополнительные примеры и получить более подробную информацию по данной теме можно в этой статье.

Поворот вокруг оси

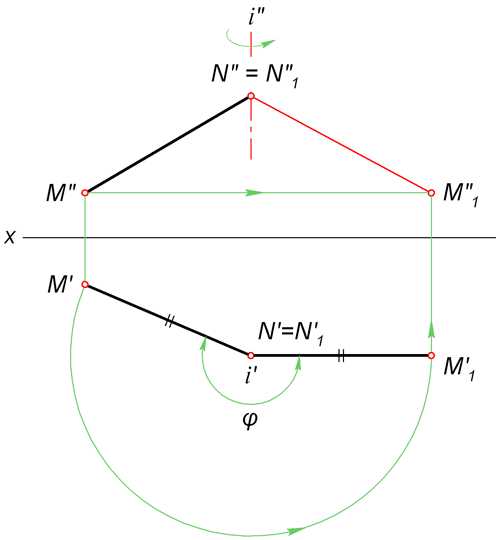
Для того, чтобы отрезок стал параллелен плоскости проекции и без искажения отразился на ней, он может быть повернут вокруг проецирующей прямой, проходящей через один из его концов.

Пример построения

Определим длину произвольного отрезка MN. Для этого через точку N проводим горизонтально проецирующую прямую i. Вокруг неё поворачиваем MN так, чтобы его проекция M’N’ заняла положение M’₁N’₁, параллельное оси X.

По линиям связи находим точку M»₁. При этом исходим из того, что M» в процессе вращения движется параллельно горизонтальной плоскости.

Точка N не изменит своего положения, так как лежит на оси поворота. Поэтому осталось только соединить N»₁ и M»₁ искомым отрезком. На рисунке он выделен красным цветом.

Более подробную информацию о решении задач методом поворота вокруг оси вы можете получить, ознакомившись со следующим материалом.

ngeometry.ru

3.4. Определение натуральной величины отрезка

Если отрезок прямой занимает общее положение, то определить истинную величину прямой на плоскостях проекций нельзя. Поэтому для определения длины отрезка по его проекциям используют способ прямоугольного треугольника: длина отрезка измеряется гипотенузой прямоугольного треугольника, одним катетом которого является проекция отрезка на плоскость, а другим – разность расстояний концов его до этой плоскости. Рассмотрим прямую общего положения в пространстве.

Рис. 9

Треугольник АВВ₁–прямоугольный. Гипотенуза АВ является натуральной длиной отрезка (рис. 9, а), а проекция А₁В₁– катетом. Второй катет ВВ

1определяет превышение одного конца отрезка над другим относительно плоскости проекций П₁и проецируется без искажения на фронтальную плоскость проекций П₂. Угол= ВАВ₁– это угол наклона прямой АВ к горизонтальной плоскости проекций.

Построения см. на рис. 9, б. Из точки В₁ проведём перпендикуляр к проекции А₁В₁, отложим на нём отрезок В₁В_о= В_хВ₂и соединим прямой точки А₁и В_о. Построенный треугольник А₁В_оВ₁= АВВ₁(рис. 9, а), так как равны их катеты и угол между ними составляет 90°. Следовательно, отрезок А₁В_о равен отрезку АВ и угол В₁А₁В_оопределяет угол наклона отрезка АВ к горизонтальной плоскости проекций.

Аналогичное построение можно сделать на фронтальной плоскости проекций, только в качестве второго катета нужно будет взять разность глубин его концов В

1В_х(рис. 9, в).

Определение длины отрезка с использованием способа замены плоскостей проекций будем рассматривать в вузе.

Вопросы для самопроверки

1. Какое положение может занимать прямая относительно плоскостей проекций ?

2. Прямая общего положения (начертить комплексный чертёж).

3. В каком случае прямая обращается в точку и как называются такие прямые ? Привести пример.

4. Какие точки называются конкурирующими ?

5. Сформулировать признак принадлежности точки, прямой (см. выше).

6. Сформулировать правило прямоугольного треугольника.

4. Плоскость

Плоскость может быть задана аналитически (уравнением) или графически (проекциями). Для графического задания плоскости достаточно построить проекции определяющих её элементов (

рис. 10):

1) трёх точек, не лежащих на одной прямой;

2) прямой и точки, не лежащей на этой прямой;

3) двух пересекающихся прямых;

4) двух параллельных прямых;

5) любой плоской фигурой.

Рис. 10

В зависимости от положения плоскости относительно плоскостей проекций различают плоскости общего и частного положения.

Плоскость, не перпендикулярную ни одной из основных плоскостей проекций называют плоскостью общего положения (рис. 10.5).

Плоскости частного положения можно разделить на две группы:

проецирующие и плоскости уровня.

4.1. Проецирующие плоскости

Проецирующие плоскости– это плоскости, перпендикулярные к одной из плоскостей проекций (

рис. 11). К ним относятся:

1) горизонтально-проецирующая П₁;

2) фронтально-проецирующая П₂;

3) профильно-проецирующая П₃.

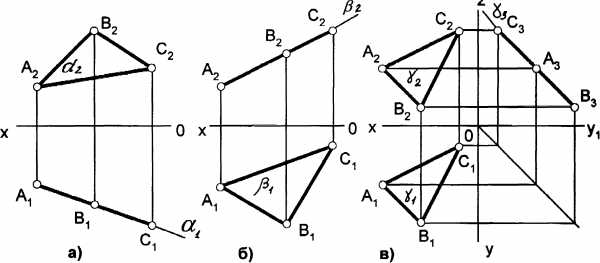
Рис. 11

Отличительной особенностью проецирующих плоскостей является то, что все геометрические образы, принадлежащие проецирующей плоскости, проецируются на перпендикулярную к ней плоскость в одну прямую, совпадая с главной проекцией (следом):

горизонтально-проецирующая плоскость А₁В₁С₁(рис. 11, а),

фронтально-проецирующая плоскость А₂В₂С₂(рис. 11, б),

профильно-проецирующая плоскость А₃В₃С

3(рис. 11, в).

studfiles.net

§ 5. Способ прямоугольного треугольника. Определение натуральной величины отрезка прямой линии и углов наклона прямой к плоскостям проекций

Построение проекций отрезка прямой общего и частного положения позволяет решать не только позиционные задачи (расположение относительно плоскостей проекций), но и метрические – определение длины отрезка и углов наклона к плоскостям проекций. Но эта задача может быть решена только в случае, если отрезок параллелен или перпендикулярен к одной или нескольким плоскостям. Рассмотрим способ решения такой задачи для отрезка общего положения.

Пусть дан отрезок АВ общего положения относительно плоскостей ₁ и ₂. АВ’В – прямоугольный треугольник (рис. 3.10), в котором катет АВ’ = А₁В₁ (проекции отрезка АВ на плоскость ₁

), а катет ВВ’ равен z – разности расстояний точек А и В до плоскости ₁. Угол  в прямоугольном треугольнике АВ’В определяет угол наклона прямой АВ к плоскости ₁.

Рассмотрим треугольник ВА’А (рис. 3.11), где катет ВА’ равен проекции А₂В₂ (ВА’ = А₂В₂), а второй катет АА’ равен  y – разности расстояний точек А и В от плоскости  ₂. Угол в прямоугольном треугольнике ВАА’ определяет угол наклона прямой АВ к плоскости₂.

Таким образом, натуральная длина отрезка прямой общего положения определяется гипотенузой прямоугольного треугольника, у которого один катет равен проекции отрезка, а второй катет – алгебраической разности расстояний от концов отрезка до одной из плоскостей проекций.

Рис. 3.10	Рис. 3.11

 

§ 6. Определение натуральной величины отрезка прямой общего положения

Для определения натуральной величины отрезка прямой линии общего положения по ее проекциям применяют метод прямоугольного треугольника.

Рассмотрим последовательность этого положения (табл. 3.4).

Таблица 3.4

Вербальная форма	Графическая форма
Определить на комплексном чертеже Аz, Bz, Ay, By:  z – разность расстояний от точек А и В до плоскости 1;  y – разность расстояний от точек А и В до плоскости 2
а) либо перпендикуляр к А2В2 через точку В2 или А2; б) либо перпендикуляр к А1В1 через точку В1 или А1

или от точки B1 отложить  z
4. Соединить A2 и В’2; A1 и В’1
5. Обозначить натуральную величину отрезка АВ (гипотенузу треугольника): |АВ| = А1В’1 = А2В’2

 –угол наклона отрезка АВ к плоскости 1; –угол наклона отрезка АВ к плоскости 2

При решении подобной задачи находить натуральную величину отрезка можно только один раз (либо на  ₁, либо на  ₂). Если требуется определить углы наклона прямой к плоскостям проекций, то данное построение выполняется дважды – на фронтальной и горизонтальной проекциях отрезка.

studfiles.net

4.3. Определение натуральной величины отрезка прямой

Рис. 4.9. Определение натуральной величины отрезка АВ

Длину отрезка и угол наклона его к плоскости проекций можно определить, пользуясь методом прямоугольного треугольника (рис. 4.9).

Алгоритм определения натуральной величины отрезка прямой линии.

1. Определить по чертежу разность расстояний удаления точек А и В до плоскостей проекций П₁ и П₂, Δz = z_А– z_В, Δy = y_А–y_В.

2. В плоскости П₂построить треугольникA₂А`<sub>2</sub>B<sub>2</sub>, катет [A<sub>2</sub>А`₂] = Δy.

3. В плоскости П₁построить треугольникA₁А`<sub>1</sub>B<sub>1</sub>, катет [A<sub>2</sub>А`₂] = Δz.

4. [А`<sub>2</sub>B<sub>2</sub>] =[А`₁B₁] =IABI.

5. Угол – угол наклона отрезка прямой линии АВ к плоскости П₂, угол– угол наклона отрезка прямой линии АВ к плоскости П₁.

4.4. Взаимное положение прямых линий

Две прямые в пространстве могут быть параллельными, пересекаться и скрещиваться.

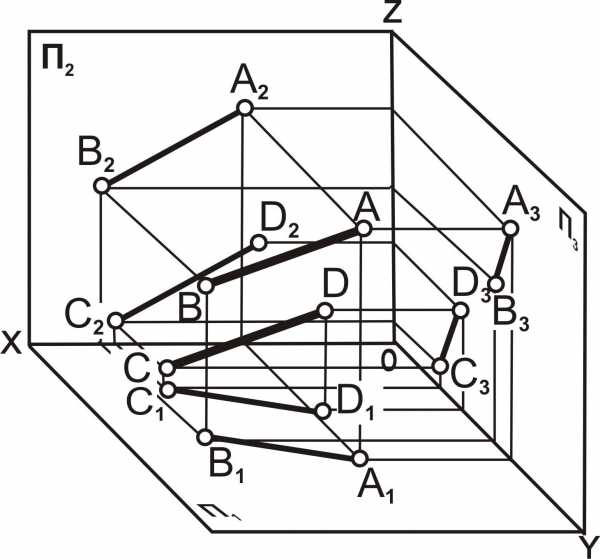
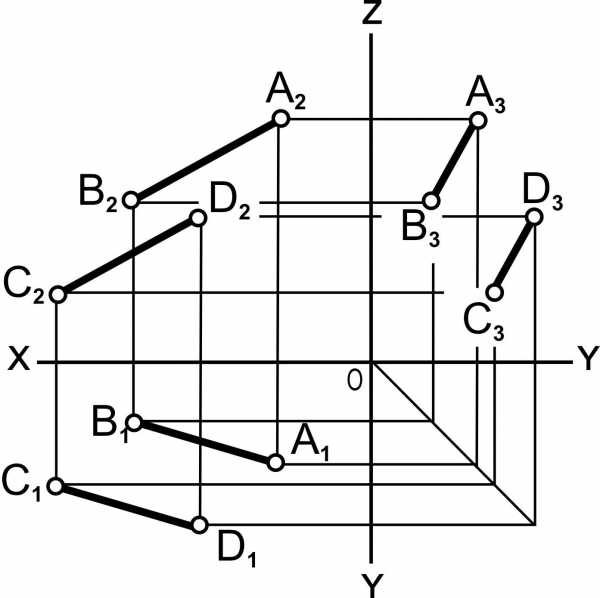
Параллельные прямые. Если прямые параллельны, то их одноименные проекции параллельны¹² (рис. 4.10). Если ABIICD, то [A₁B₁]II[C₁D₁]; [A₂B₂]II[C₂D₂]; [A₃B₃]II[C₃D₃] (рис. 4.10). В свою очередь, если проекции прямых линий на всех плоскостях проекций параллельны, то прямые линии параллельны.

Особый случай представляют собой прямые линии, параллельные одной из плоскостей проекций. Например, фронтальные и горизонтальные проекции профильных прямых линий параллельны, но для оценки их взаимного положения необходимо построить профильные проекции прямых, которые в рассмотренном случае на плоскости П₃ пересекаются, следовательно, AB и CD не параллельны [A₁B₁]II[C₁D₁]; [A₂B₂]II[C₂D₂]; [A₃B₃]∩[C₃D₃] (рис. 4.11).

а	б
Рис. 4.10. Прямые линии, параллельные: а – наглядное изображение; б – комплексный чертёж
а	б
Рис. 4.11. Прямые линии, непараллельные: а – наглядное изображение; б – комплексный чертёж

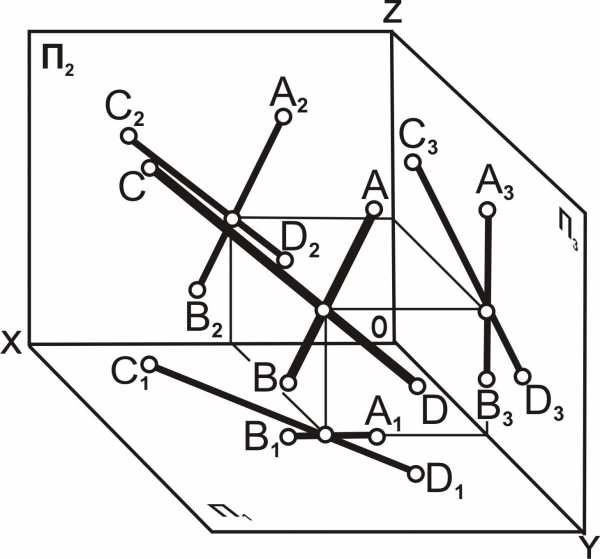
Пересекающиеся прямые. Если прямые пересекаются, то их проекции также пересекаются, а точки пересечения проекций находятся в проекционной связи¹³ (рис. 4.12). Рассмотрим два частных случая.

1. Если одна из прямых параллельна какой-либо плоскости проекций, например, профильной, то по двум проекциям невозможно судить об их взаимном расположении (рис. 4.13).

2. Пересекающиеся прямые расположены в общей для них проецирующей плоскости, например перпендикулярной фронтальной плоскости проекций. О взаимном расположении прямых, лежащих в этой плоскости, можно судить по одной горизонтальной проекции [А₁В₁]∩[С₁D₁]ÞАВ∩СD (рис.4.14).

а	б
Рис. 4.12. Прямые линии пересекающиеся: а – наглядное изображение; б – комплексный чертёж
Рис. 4.13. Прямые линии не пересекаются		Рис. 4.14. Прямые линии пресекаются

Скрещивающиеся прямые. Если одна из двух прямых линий лежит в некоторой плоскости, а другаяпрямаялиния пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые – скрещивающиеся (рис. 4.15).

а	б
Рис. 4.15. Прямые линии скрещивающиеся: а – наглядное изображение; б – комплексный чертёж

studfiles.net

Определение натуральной величины отрезка прямой общего положения методом прямоугольного треугольника

 

Ортогональная проекция отрезка прямой общего положения на любую плоскость проекций всегда меньше длины самого отрезка. Для определения натуральной величины отрезка прямой служит метод прямоугольного треугольника, который заключается в следующем.

Предположим, что точки А и В лежат в I октанте (рис. 20, а). Соединим эти точки и получим отрезок некоторой прямой АВ.

 

Из точки А проведем линию параллельную А¢В¢, которая в пересечении с линией проекционной связи даст точку В₀.

Рассмотрим прямоугольный треугольник АВВ_О:

— гипотенуза АВ определяет истинную величину этого отрезка;

— катет АВ₀ равен горизонтальной проекцией А¢В¢;

— катет ВВ₀ равен Dz = z_В – z_А.

На ортогональном чертеже оказывается достаточно данных для построения на чертеже треугольника, равного рассмотренному (рис. 20, б). Для этого к горизонтальной проекции А¢В¢ «пристроен» второй катет — разность координат Dz. Гипотенуза построенного треугольника есть натуральная величина отрезка АВ.

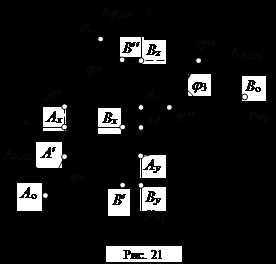Если прямоугольный треугольник строится на фронтальной проекции, то второй катет окажется равным разности координат Dy (табл. 3). Для треугольника, построенного на профильной проекции, вторым катетом будет Dx (рис. 21).

Координаты концов отрезка могут иметь разные знаки. Тогда разность координат определяется с учетом знака. Например, если координата z точки А положительная, а точки В отрицательная, то разность координат будет равна

Dz_АВ = z_A – (-z_B) = z_A + z_B.

Таблица 3

Геометрические элементы при определении истинной величины отрезка прямой методом прямоугольного треугольника

Проекция отрезка прямой, выбираемая в качестве первого катета треугольника	Разность координат, откладываемая в качестве второго катета	Плоскость проекций, к которой определяется угол наклона	Обозначение угла наклона
горизонтальная: А¢В¢	DzАВ=|AzBz|	p1	j1
фронтальная: А²В²	DyAB=|AyBy|	p2	j2
профильная: А¢¢¢В¢¢¢	DxAB=|AxBx|	p3	j3

 

В общем случае натуральная величина отрезка прямой общего положения равна гипотенузе прямоугольного треугольника, одним катетом которого является проекция отрезка прямой, а вторым — разность «третьих» координат.

Угол наклона прямой к плоскости проекций – это угол между прямой и ее проекцией. Следовательно, определяя истинную величину отрезка прямой методом прямоугольного треугольника, одновременно можно найти и угол ее наклона к плоскости проекций (j₁, j₂, j₃). Угол между гипотенузой и соответствующей проекцией отрезка равен углу наклона этой прямой к данной плоскости проекций.

Пример 3. Определить истинную величину отрезка АВ и угол наклона к плоскости p₁ (рис. 22).

1. По таблице 3 определяем, что для нахождения угла наклона к плоскости p₁ надо построить прямоугольный треугольник, в котором одним катетом будет горизонтальная проекция отрезка А¢В¢, а вторым – разность координат по оси z.

2. Определяем координаты по оси z точек А и В и их разность:

Dz_АВ = z_В – (-z_А) = z_В + z_А .

3. Строим прямоугольный треугольник, в котором за катет принимаем горизонтальную проекцию А¢В¢. В качестве второго катета откладываем расстояние, равное Dz_АВ.

4. Гипотенуза построенного треугольника есть истинная величина отрезка АВ, а угол при вершине А¢ (угол j₁) – угол наклона прямой к плоскости p₁.

Лекция 3

 

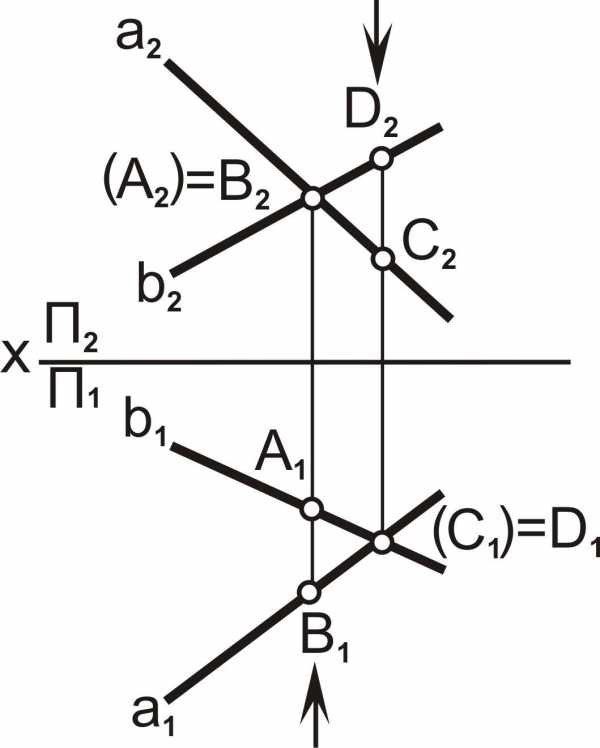
СЛЕДЫ ПРЯМОЙ

 

Следом прямой называется точка пересечения прямой линии с плоскостью проекций (является точкой частного положения – лежит в плоскости проекций).

Прямая общего положения пересекает все три плоскости проекций и, следовательно, имеет три следа. Прямая линия частного положения не имеет следа на плоскости проекций, если она параллельна этой плоскости.

Выберем две точки: точку М, лежащую в плоскости проекций p_1, и точку N – в плоскости проекций p₂ (рис. 23, а). Через эти точки проведем прямую.

 

Точка пересечения (M) прямой линии с горизонтальной плоскостью проекций называется горизонтальным следом прямой; точка пересечения (N) прямой линии с фронтальной плоскостью проекций называется фронтальным следом прямой; точка пересечения (P) прямой линии с профильной плоскостью проекций называется профильным следом прямой.

Следы прямой совпадут с проекциями этих следов в той плоскости, где они расположены: М º M¢, N º N¢¢, P º P¢¢¢.

Поскольку точка М лежит в плоскости p₁, то ее фронтальная проекция М¢¢ располагается на оси x, а профильная М¢¢¢ – на оси y. Горизонтальная проекция точки N — N¢ также располагается на оси x, а профильная проекция N¢¢¢ лежит на оси z. Горизонтальная проекция профильного следа P¢ лежит на оси y, а фронтальная проекция P¢¢ — на оси z.

Охарактеризуем положение каждой проекции каждого из трех следов на ортогональном чертеже (рис. 23, б).

1) Построение проекций горизонтального следа:

M¢¢ — фронтальная проекция горизонтального следа лежит на пересечении фронтальной проекции прямой с осью x;

М¢ — горизонтальная проекция горизонтального следа лежит на пересечении линии проекционной связи, проведенной из проекции M¢¢ перпендикулярно оси x, с горизонтальной проекцией прямой;

M¢¢¢ — профильная проекция горизонтального следа лежит на пересечении профильной проекции прямой с осью y_p3.

2) Построение проекций фронтального следа:

N¢ — горизонтальная проекция фронтального следа лежит в точке пересечения горизонтальной проекции прямой с осью x;

N¢¢ — фронтальная проекция фронтального следа лежит на пересечении фронтальной проекции прямой с линией проекционной связи, проведенной из точки N¢ перпендикулярно оси x;

N¢¢¢ — профильная проекция фронтального следа лежит на пересечении профильного следа прямой с осью z.

3) Построение проекций профильного следа:

P¢ — горизонтальная проекция профильного следа лежит на пересечении горизонтальной проекции прямой с осью y_p1.

P¢¢ — фронтальная проекция профильного следа лежит на пересечении фронтальной проекции прямой с осью z.

Пример 4. Построить проекции следов отрезка прямой АВ (рис. 24). 1. Находим фронтальную проекцию горизонтального следа М², продолжив А¢¢В¢¢ до пересечения с осью x. 2. Из точки М¢¢ проводим линию проекционной связи до ее пересечения с продолжением А¢В¢. Здесь расположена точка М¢. 3. По двум проекциям М¢ и М¢¢ строим третью — М¢¢¢, которая совпадает с точкой пересечения профильной проекции прямой с осью yp3. 4. Находим горизонтальную проекцию фронтального следа N¢ в пересечении А¢В¢ с осью x. 5. Через точку N¢ проводим линию проекционной связи до ее пересечения с фронтальной проекцией прямой A¢¢B¢¢ и получаем точку N¢¢.

P¢¢¢ — профильная проекция профильного следа находится в точке пересечения профильной проекции прямой с линией проекционной связи, проведенной из P¢¢ перпендикулярно оси z.

 

 

6. По двум проекциям фронтального следа N¢ и N¢¢ строим третью его проекцию — N¢¢¢, которая совпадает с точкой пересечения профильной проекции прямой с осью z.

7. В пересечении А¢В¢^{с осью y_p1строим точку Р¢ (горизонтальную проекцию профильного следа).}

8. В пересечении А²В² с осью z получаем точку фронтальную проекцию профильного следа — Р².

9. По двум проекциям Р¢ и Р¢¢ строим профильную проекцию — Р¢¢¢ (проекции Р¢¢ и Р¢¢¢ находятся на горизонтальной линии проекционной связи).

 

ВЗАИМНОЕ ПОЛОЖЕНИЕ ДВУХ ПРЯМЫХ

 

Две прямые могут пересекаться, быть параллельными друг другу и скрещиваться.

1) Пересекающиеся прямые имеют одну общую точку. Если прямые линии пересекаются, то одноименные проекции этих прямых тоже пересекаются (рис. 25, а), причем проекции точки пересечения лежат на одной линии проекционной связи.

2) Параллельные прямые лежат в одной плоскости и не имеют общих точек. Одноименные проекции двух параллельных прямых параллельны между собой (рис. 25, б).

3) Скрещивающиеся прямые, в отличие от пересекающихся и параллельных прямых, не лежат в одной плоскости. Хотя одноименные проекции двух скрещивающихся прямых и могут пересекаться, но точки их пересечения не могут лежать на одной линии проекционной связи (рис. 25, в).

Две точки, лежащие на скрещивающихся прямых и на одном перпендикуляре к плоскости проекций, называются конкурирующими. Проекции конкурирующих точек лежат в точке пересечения одноименных проекций скрещивающихся прямых (точки 1 и 2 на фронтальной плоскости проекций, точки 3 и 4 на горизонтальной плоскости проекций – см. рис. 25, в).

Построение их проекций применяется для определения взаимнойвидимостигеометрических элементов1.

 

 

 

 

 

 

(которые совпадают с самими следами), которые обозначаются соответственно h¢_0a, f²_0a и p¢¢¢_0a. Каждый след плоскости проходит через две точки схода следов. Следовательно, любые два следа плоскости позволяют определить все три параметра плоскости.

 

Таким образом, любые два следа плоскости однозначно определяют ее положение в пространстве. Также как положение точки в пространстве определяются тремя ее координатами, так и положение плоскости может быть задано аналитически тремя ее параметрами.

Плоскость, пересекающая все три плоскости проекций, называется плоскостью общего положения. Если плоскость параллельна одной или двум осям координат, то она называется плоскостью частного положения.

 

 

ПЛОСКОСТИ ЧАСТНОГО ПОЛОЖЕНИЯ

Плоскости, параллельные одной оси координат

1) Плоскость, параллельная оси z (рис. 32).

 

У такой плоскости параметры Х_a, и U_a — конечные величины, а параметр Z_a = ¥. Следовательно, фронтальный и профильный следы такой плоскости, которые должны пройти через точку схода следов Z_a, будут параллельны оси z. Плоскость, параллельная оси z перпендикулярна горизонтальной плоскости проекций и называется горизонтально-проецирующей плоскостью.

Рассмотрим точку А, лежащую в горизонтально-проецирующей плоскости a, и построим горизонтальную проекцию этой точки. Для этого из точки А опустим перпендикуляр на плоскость проекций p₁. Горизонтальная проекция любой точки, лежащей в горизонтально-проецирующей плоскости, будет всегда располагаться на горизонтальном следе плоскости.

 

4) Плоскость, параллельная оси y (рис. 33).

 

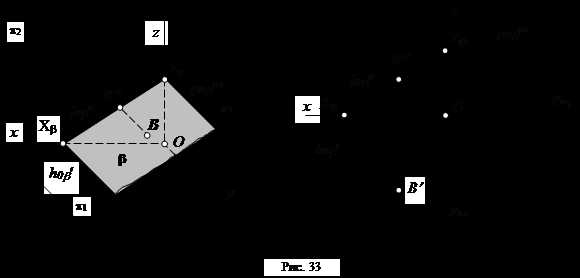Если плоскость параллельна оси y, то ее параметр по этой оси равен бесконечности (Y_b = ¥) и, следовательно, горизонтальный и профильный следы плоскости будут параллельны оси y. Плоскость, параллельная оси y, перпендикулярна фронтальной плоскости проекций p₂ и называется фронтально-проецирующей плоскостью.

Фронтальная проекция любой точки, лежащей в этой плоскости (например, точки В), всегда расположена на фронтальном следе плоскости.

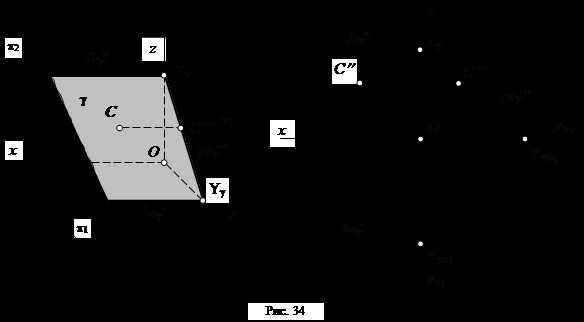
4) Плоскость, параллельная оси x (рис. 34).

У такой плоскости параметр по оси x равен бесконечности (Х_{g =} ¥), поэтому ее фронтальный и горизонтальный следы будут параллельны оси x. Такая плоскость перпендикулярна профильной плоскости проекций p₃ и называется профильно-проецирующей плоскостью.

Профильная проекция любой точки, лежащей в этой плоскости (например, точки С), всегда расположена на профильном следе плоскости.

Осевая плоскость.

Осевая плоскость проходит через одну из осей координат.

 

 

У осевой плоскости два следа совпадают с одной из осей координат (в нашем примере на рис. 35 – с осью x), а плоскость является проецирующей.

Так как плоскость не может быть задана двумя совпадающими друг с другом следами, то для однозначного определения ее положения необходимо знать положение еще хотя бы одной точки, лежащей в этой плоскости, одна из проекций которой лежит на соответствующем следе этой плоскости (в нашем примере на рис.35 – проекция D¢¢¢).

 

Похожие статьи:

poznayka.org

Определение натуральной величины отрезка прямой линии — Мегаобучалка

При решении задач инженерной графики в ряде случаев появляется необходимость в определении натуральной величины отрезка прямой линии. Решить эту задачу можно несколькими способами: способом прямоугольного треугольника, способом вращения, плоскопараллельного перемещения, заменой плоскостей проекций. Правило прямоугольного треугольника. Для того чтобы определить Н.В. отрезка необходимо: построить прямоугольный треугольник, одним катетом которого является одна из проекций отрезка (А1В1 или А2В2), а другим катетом – разность удалений концов отрезка от оси Х, взятая с другой плоскости проекции. Гипотенуза этого треугольника – Н.В. отрезка.

Способ вращения.Способ вращения заключается в том, что отрезок прямой линии или плоскую фигуру вращают вокруг выбранной оси до положения, параллельного плоскости проекций.

Построение на чертеже начинают с горизонтальной проекции (рис. 173, б). Из точки а, как из центра, радиусом, равным ab, описывают дугу окружности bb1 до пересечения с прямой, проведенной из точки а параллельно оси х. Получают новую горизонтальную проекцию b1 точки В. Фронтальную проекцию b`1 точки b1 получают, восставив из нее перпендикуляр к оси х. Соединив прямой точку а’ с точкой b` получают натуральную длину отрезка АВ.

Способ перемены плоскостей проекций. Этот способ отличается от способа вращения тем, что проецируемая линия или фигура остается неподвижной, а одну из плоскостей проекций заменяют новой дополнительной плоскостью, на которую и проецируют изображаемый элемент. Применение этого способа характеризуется тем, что пространственное положение заданных элементов остается неизменным, а изменяется система плоскостей проекций, на которых строятся новые изображения геометрических образов. Дополнительные плоскости проекций вводятся таким образом, чтобы на них интересующие нас элементы изображались в удобном для конкретной задачи положений.

 

Способ плоскопараллельного перемещения

Способ плоскопараллельного перемещения основан на том, что при параллельном переносе геометрического тела относительно плоскости проекций проекция его на эту плоскость не меняет своей формы и размеров, хотя и меняет положение. При этом если точка перемещается в плоскости, параллельной П1, то ее фронтальная проекция изображается в виде прямой, параллельной оси П2/П1. Если же точка перемещается в плоскости, параллельной П2, то ее горизонтальная проекция изображается в виде прямой, параллельной той же оси.

 

 

megaobuchalka.ru

Определение натуральной величины отрезка прямой

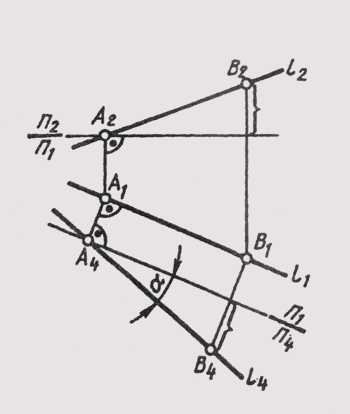
Определение натуральной величины отрезка прямой общего положения и углов наклона ее к плоскостям проекций производится способом прямоугольного треугольника.

Как видно из рисунка 1.3.7, длину отрезка прямой АВ можно определить из прямоугольного треугольника АВ¹В₁, в котором: катет АВ₁=А₁В₁ (проекция отрезка АВ на плоскость П₁), а катет ВВ¹=– разности расстояний точек А и В

от плоскости П₁ (Δz=z_А-z_В). Угол φ в этом же треугольнике определяет угол наклона отрезка прямой АВ к плоскости П₁.

 

Рисунок 1.3.7 – Определение натуральной величины отрезка способом прямоугольного треугольника

 

Чтобы понять принцип нахождения натуральной величины отрезка прямой и угла наклона его к плоскости проекций на комплексном чертеже, совместим треугольник АВ¹В₁ с горизонтальной плоскостью проекций. Для этого примем горизонтальную проекцию А₁В₁ за один из катетов этого треугольника. Через точку В₁ проведем на плоскости П₁ прямую, перпендикулярную к А₁В₁, и отложим на ней от точки В₁ отрезок ВВ¹=Δz, равный длине второго катета. Соединив точки А₁ и В₁¹ прямой, получим прямоугольный треугольник А₁В₁В₁¹ = АВ¹В, так как А₁В₁=АВ¹, В₁В₁¹=ВВ¹ и угол А₁В₁В₁¹=90º.

В соответствии с рисунком 1.3.8 выполняются построения по нахождению натуральной величины отрезка АВ и его угла наклона к горизонтальной плоскости проекций на комплексном чертеже.

Рисунок 1.3.8 – Определение натуральной величины отрезка способом прямоугольного треугольника на комплексном чертеже

 

Аналогичные построения можно выполнить, использовав фронтальную проекцию А₂В₂ в качестве одного из катетов треугольника, тогда другой катет — Δy будет равен разности расстояний точек А и В от плоскости П₂. Гипотенуза треугольника будет также равна АВ, а угол ψ определит угол наклона отрезка прямой АВ к плоскости П₂.

Выводы:

— натуральная величина прямой общего положения равна гипотенузе прямоугольного треугольника, одним катетом которого будет являться проекция отрезка на любую плоскость проекций, а другим – разность расстояния концов отрезка от той же плоскости;

— угол между катетом-проекций и гипотенузой равен натуральной величине угла наклона отрезка к той плоскости проекций, на которой выполнены построения.

Похожие статьи:

poznayka.org