Как начертить изометрию?
Начнем с того, что определимся с направлением осей в изометрии.

Возьмем для примера не очень сложную деталь. Это параллелепипед 50х60х80мм, имеющий сквозное вертикальное отверстие диаметром 20 мм и сквозное прямоугольное отверстие 50х30мм.

Начнем построение изометрии с вычерчивания верхней грани фигуры. Расчертим на требуемой нам высоте тонкими линиями оси Х и У. Из получившегося центра отложим вдоль оси Х 25 мм (половина от 50) и через эту точку проведем отрезок параллельный оси У длиной 60 мм. Отложим по оси У 30 мм (половина от 60) и через полученную точку проведем отрезок параллельный оси Х длиной 50 мм. Достроим фигуру.

Мы получили верхнюю грань фигуры.
Не хватает только отверстия диаметром 20 мм. Построим это отверстие. В изометрии окружность изображается особым образом — в виде эллипса. Это связано с тем, что мы смотрим на нее под углом. Изображение окружностей на всех трех плоскостях я описал в отдельном уроке, а пока лишь скажу, что в изометрии окружности проецируются в эллипсы с размерами осей a=1,22D и b=0,71D. Эллипсы, обозначающие окружности на горизонтальных плоскостях в изометрии изображаются с осью а расположенной горизонтально, а ось b — вертикально. При этом расстояние между точками расположенными на оси Х или У равно диаметру окружности (смотри размер 20 мм).

Теперь, из трех углов нашей верхней грани начертим вниз вертикальные ребра — по 80 мм и соединим их в нижних точках. Фигура почти полностью начерчена — не хватает только прямоугольного сквозного отверстия.

Чтобы начертить его опустим вспомогательный отрезок 15 мм из центра ребра верхней грани (указан голубым цветом). Через полученную точку проводим отрезок 30 мм параллельный верхней грани (и оси Х). Из крайних точек чертим вертикальные ребра отверстия — по 50 мм. Замыкаем снизу и проводим внутреннее ребро отверстия, оно параллельно оси У.

На этом простая изометрическая проекция может считаться завершенной. Но как правило, в курсе инженерной графики выполняется изометрия с вырезом одной четверти. Чаще всего, это четверть нижняя левая на виде сверху — в этом случае получается наиболее интересный с точки зрения наблюдателя разрез (конечно же все зависит от изначальной правильности компоновки чертежа, но чаще всего это так). На нашем примере эта четверть обозначена красными линиями. Удалим ее.

Как видим из получившегося чертежа, сечения полностью повторяют контур разрезов на видах (смотри соответствие плоскостей обозначенных цифрой 1), но при этом они вычерчены параллельно изометрическим осям. Сечение же второй плоскостью повторяет разрез выполненный на виде слева (в данном примере этот вид мы не чертили).
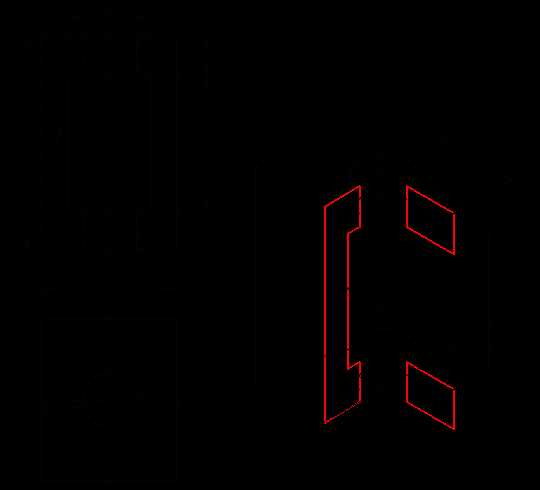
Надеюсь, этот урок оказался полезным, и построение изометрии вам уже не кажется чем-то совершенно неведомым. Возможно, некоторые шаги придется прочитать по два, а то и по три раза, но в конечном итоге понимание должно будет прийти. Удачи вам в учебе!
Как начертить окружность в изометрии?
Как вы наверняка знаете, при построении изометрии окружность изображается в виде эллипса. Причем вполне конкретного: длина большой оси эллипса AB=1.22*D, а длина малой оси CD=0.71*D (где D — диаметр той самой исходной окружности, которую мы хотим начертить в изометрической проекции). Как начертить эллипс зная длину осей? Об этом я рассказывал в отдельном уроке. Там рассматривалось построение больших эллипсов. Если же исходная окружность имеет диаметр где-то до 60-80 мм, то скорее всего мы сможем начертить ее и без лишних построений, используя 8 опорных точек. Рассмотрим следующий рисунок:
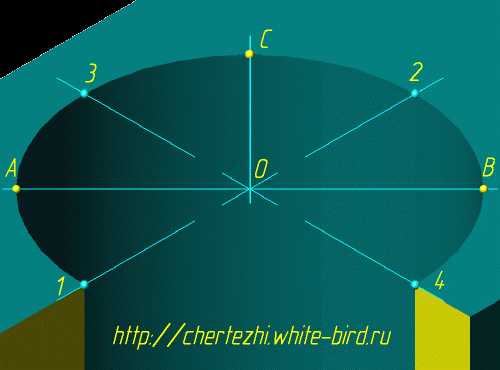
Это фрагмент изометрии детали, полный чертеж которой можно увидеть ниже. Но сейчас мы говорим о построении эллипса в изометрии. На данном рисунке AB — большая ось эллипса (коэффициент 1.22), CD — малая ось (коэффициент 0.71). На рисунке половина короткой оси (ОD) попала в вырезанную четверть и отсутствует — используется полуось СО (не забудьте об этом, когда будете откладывать значения по короткой оси — полуось — имеет длину равную половине короткой оси). Итак, мы уже имеем 4 (3) точки. Теперь отложим по двум оставшимся изометрическим осям точки 1,2,3 и 4 — на расстоянии равном радиусу исходной окружности (таким образом 12=34=D). Через полученные восемь точек уже можно провести достаточно ровный эллипс, либо аккуратно от руки, либо по лекалу.
Для лучшего понимания направления осей эллипсов в зависимости от того, какое направление имеет циллиндр, рассмотрим три разных отверстия в детали, имеющей форму параллелепипеда. Отверстие — тот же цилиндр, только из воздуха 🙂 Но для нас это особого значения не имеет. Полагаю, что ориентируясь на эти примеры вы без труда сможете правильно расположить оси своих эллипсов. Если же обобщить, то получится так: большая ось эллипса перпендикулярна той оси, вокруг которой образован цилиндр (конус).



Изометрическая проекция — это… Что такое Изометрическая проекция?
 Стол в прямоугольной изометрической проекции
Стол в прямоугольной изометрической проекцииИзометри́ческая прое́кция — это разновидность аксонометрической проекции, при которой в отображении трёхмерного объекта на плоскость коэффициент искажения (отношение длины спроектированного на плоскость отрезка, параллельного координатной оси, к действительной длине отрезка) по всем трём осям один и тот же. Слово «изометрическая» в названии проекции пришло из греческого языка и означает «равный размер», отражая тот факт, что в этой проекции масштабы по всем осям равны. В других видах проекций это не так.
Изометрическая проекция используется в машиностроительном черчении и САПР для построения наглядного изображения детали на чертеже, а также в компьютерных играх для трёхмерных объектов и панорам.
Необходимо отметить, что параллельные проекции, разновидностью которых являются аксонометрические и, в том числе, изометрические проекции, делятся также на ортогональные (перпендикулярные), с направлением проекции перпендикулярным к плоскости проекции, и косоугольные, с углом между направлением и плоскостью, отличным от прямого. По советским стандартам (см. ниже) аксонометрические проекции могут быть и ортогональными, и косоугольными
Стандартные изометрические проекции[1]
Расположение осей координат в изометрических проекциях…
…прямоугольной
…косоугольной фронтальной
…косоугольной горизонтальной
Прямоугольная (ортогональная) изометрическая проекция
В прямоугольной изометрической проекции аксонометрические оси образуют между собой углы в 120°, ось Z’ направлена вертикально. Коэффициенты искажения () имеют числовое значение . Как правило, для упрощения построений изометрическую проекцию выполняют без искажений по осям, то есть коэффициент искажения принимают равным 1, в этом случае получают увеличение линейных размеров в раза.
Косоугольная фронтальная изометрическая проекция
Ось Z’ направлена вертикально, угол между осью X’ и Z’ равен 90°, ось Y’ с углом наклона 135° (допускается 120° и 150°) от оси Z’.
Фронтальная изометрическая проекция выполняется по осям X’, Y’ и Z’ без искажения.
Кривые параллельные фронтальной плоскости проецируются без искажений.
Косоугольная горизонтальная изометрическая проекция
Ось Z’ направлена вертикально, между осью Z’ и осью Y’ угол наклона равен 120° (допускается 135° и 150°), при этом сохраняется угол между осями X’ и Y’ равным 90°.
Горизонтальную изометрическую проекцию выполняют без искажения по осям X’, Y’ и Z’.
Кривые, параллельные горизонтальной плоскости[2] проецируются без искажений.
Визуализация
Изометрический вид объекта можно получить, выбрав направление обзора таким образом, чтобы углы между проекцией осей x, y, и z были одинаковы и равны 120°. К примеру, если взять куб, это можно выполнить направив взгляд на одну из граней куба, после чего повернув куб на ±45° вокруг вертикальной оси и на ±arcsin (tan 30°) ≈ 35.264° вокруг горизонтальной оси. Обратите внимание: на иллюстрации изометрической проекции куба контур проекции образует правильный шестиугольник — все рёбра равной длины и все грани равной площади.
Подобным же образом изометрический вид может быть получен, к примеру, в редакторе трёхмерных сцен: начав с камерой, выровненной параллельно полу и координатным осям, её нужно повернуть вниз на ≈35.264° вокруг горизонтальной оси и на ±45° вокруг вертикальной оси.
Другой путь визуализации изометрической проекции заключается в рассмотрении вида кубической комнаты с верхнего угла с направлением взгляда в противолежащий нижний угол. Ось x здесь направлена диагонально вниз и вправо, ось y — диагонально вниз и влево, ось z — прямо вверх. Глубина также отражается высотой картинки. Линии, нарисованные вдоль осей, имеют угол 120° между собой.
Матричные преобразования
Имеется 8 различных вариантов получения изометрической проекции в зависимости от того, в какой октант смотрит наблюдатель. Изометрическое преобразование точки в трёхмерном пространстве в точку на плоскости при взгляде в первый октант может быть математически описано с помощью матриц поворота следующим образом. Вначале, как объяснено в разделе Визуализация, выполняется поворот вокруг горизонтальной оси (здесь x) на α = arcsin (tan 30°) ≈ 35.264° и вокруг вертикальной оси (здесь
Затем применяется ортогональная проекция на плоскость x-y:
Другие семь возможных видов получаются поворотом к противостоящим сторонам и/или инверсией направления взгляда.[3]
Ограничения аксонометрической проекции
Изометрический рисунок с голубым шаром на два уровня выше красногоКак и в других видах параллельных проекций, объекты в аксонометрической проекции не выглядят больше или меньше при приближении или удалении от наблюдателя. Это полезно в архитектурных чертежах и удобно в спрайто-ориентированных компьютерных играх, но, в отличие от перспективной (центральной) проекции, приводит к ощущению искривления, поскольку наши глаза или фотография работают иначе.
Это также легко приводит к ситуациям, когда глубину и высоту невозможно оценить, как показано на иллюстрации справа. В этом изометрическом рисунке голубой шар на два уровня выше красного, но это нельзя увидеть, если смотреть только на левую половину картинки. Если выступ, на котором находится голубой шар, расширить на один квадрат, то он окажется точно рядом с квадратом, на котором находится красный шар, создавая оптическую иллюзию, будто оба шара на одном уровне.
Дополнительная проблема, специфичная для изометрической проекции — сложность определения, какая сторона объекта наблюдается. При отсутствии теней и для объектов, которые относительно перпендикулярны и соразмерны, сложно определить, какая сторона является верхней, нижней или боковой. Это происходит из-за приблизительно равных по размеру и площади проекций такого объекта.
Большинство современных компьютерных игр избегают этого за счёт отказа от аксонометрической проекции в пользу перспективного трёхмерного рендеринга. Однако эксплуатация проекционных иллюзий популярна в оптическом искусстве — таком, как работы из серии «невозможной архитектуры» Эшера. Водопад (1961) — хороший пример, в котором строение в основном изометрическое, в то время как блеклый фон использует перспективную проекцию. Другое преимущество заключается в том, что в черчении даже новички легко могут строить углы в 60° с помощью только циркуля и линейки.
Изометрическая проекция в компьютерных играх и пиксельной графике
Рисунок телевизора в почти-изометрической пиксельной графике. У пиксельного узора видна пропорция 2:1В области компьютерных игр и пиксельной графики аксонометрическая проекция была весьма популярна в силу лёгкости, с которой двухмерные спрайты и плиточная графика (англ.) могли быть использованы для представления трёхмерной игровой среды — поскольку во время перемещения по игровому полю объекты не меняют размер, компьютеру не требуется масштабировать спрайты или выполнять вычисления, необходимые для моделирования визуальной перспективы. Это позволяло старым 8-битным и 16-битным игровым системам (и, позднее, портативным игровым системам) легко отображать большие трёхмерные пространства. И хотя неразбериха с глубиной (см. выше) иногда могла быть проблемой, хороший дизайн игры способен её смягчить. С приходом более мощных графических систем аксонометрическая проекция стала терять свои позиции.
Проекция в компьютерных играх обычно несколько отличается от «истинной» изометрической в силу ограничений растровой графики — линии по осям x и y не имели бы аккуратного пиксельного узора, если бы рисовались под углом в 30° к горизонтали. Хотя современные компьютеры могут устранять эту проблему с помощью сглаживания, ранее компьютерная графика не поддерживала достаточную цветовую палитру или не располагала достаточной мощностью процессоров для его выполнения. Вместо этого использовалась пропорция пиксельного узора 2:1 для рисования осевых линий x и y, в результате чего эти оси располагались под углом arctan 0,5 ≈ 26,565° к горизонтали. (Игровые системы с неквадратными пикселями могли, однако, приводить к другим углам, включая полностью изометрические). Поскольку здесь из трёх углов между осями (116,565°, 116,565°, 126,87°) равны только два, такой вид проекции более точно характеризуется как вариация диметрической проекции. Однако большинство представителей сообществ компьютерных игр и растровой графики продолжает называть эту проекцию «изометрической перспективой». Также, часто используются термины «вид 3/4 (англ.)» и «2.5D».
Термин применялся и к играм, не использующим пропорцию 2:1, общую для многих компьютерных игр. Fallout[4] и SimCity 4[5], в которых используется триметрическая проекция, были отнесены к «изометрическим». Игры с косоугольной проекцией, такие как The Legend of Zelda: A Link to the Past[6] и Ultima Online[7], а также игры с перспективной проекцией с видом «с воздуха» (англ.)русск., такие как The Age of Decadence (англ.)[8] и Silent Storm[9], также иногда относят к изометрическим или «псевдо-изометрическим».
Кадр из игры «echochrome»Интересный пример использования особенностей изометрической проекции наблюдается в игре echochrome (яп. 無限回廊 муген кайро:?). Слоган игры — «В этом мире то, что ты видишь, становится реальностью». Смысл игры заключается в том, что иллюзия, возникающая при взгляде на изометрически построенный трёхмерный уровень с определённой точки, перестаёт быть иллюзией. Например, если посмотреть на уровень таким образом, чтобы площадки, находящиеся на разной высоте, выглядели так, будто они находятся на одной и той же высоте (см. изображение с синим и красным шарами из предыдущего раздела), игрой они будут расцениваться как находящиеся на одной высоте, и человек (игрок) сможет запросто «перешагнуть» с одной площадки на другую. Затем, если повернуть карту уровня и посмотреть на конструкцию так, чтобы было отчётливо видно разницу в высоте, можно понять, что в действительности человек «перешагнул» на другую высоту, пользуясь тем, что изометрическая иллюзия на какой-то момент стала реальностью. На приведённом в качестве иллюстрации кадре из игры положение площадки, находящейся вверху лестницы, можно представить двояко: в одном случае она находится на одной высоте с площадкой, на которой находится игрок (можно перешагнуть), а в другом случае — под ней (можно спрыгнуть через чёрное отверстие). Оба случая будут одновременно являться правдой. Очевидно, этот эффект достигается отсутствием перспективы в изометрии.
История изометрических компьютерных игр
 Q*bert (1982), одна из первых игр с изометрической графикой
Q*bert (1982), одна из первых игр с изометрической графикойПервыми играми, использующими изометрическую проекцию, были аркадные игры начала 1980-х: так, Q*bert[10] и Zaxxon (англ.)[11] выпущены в 1982 году. Q*bert показывает статичную пирамиду, нарисованную в изометрической перспективе, по которой должен прыгать управляемый игроком персонаж. Zaxxon предлагает прокручиваемые изометрические уровни, над которыми летает управляемый игроком самолётик. Год спустя, в 1983 году, была выпущена аркадная игра Congo Bongo (англ.)[12], работавшая на тех же игровых автоматах, что и Zaxxon. В этой игре персонаж перемещается по большим изометрическим уровням, включающим трёхмерные подъёмы и спуски. То же самое предлагается и в аркадной игре Marble Madness (1984).
С выходом Ant Attack (англ.) (1983) для ZX Spectrum изометрические игры перестали быть изюминкой только аркадных игровых автоматов и пришли также и в домашние компьютеры. Журнал CRASH присудил этой игре 100 % в категории «графика» за новую «трёхмерную» технологию.[13] Год спустя для ZX была выпущена игра Knight Lore, которая расценивается как революционное произведение[14], определившее последующий жанр изометрических квестовых игр[15]. На домашних компьютерах было отмечено столько изометрических игр-последователей Knight Lore, что эта игра стала считаться вторым наиболее клонируемым образцом программного обеспечения после текстового редактора WordStar (англ.).[16] Среди клонов большой успех имела игра Head Over Heels (1987)[17]. Однако, изометрическая перспектива не ограничивалась только аркадами и квестовыми играми — например, стратегическая игра Populous (1989) также использовала изометрическую перспективу.
На протяжении 1990-х некоторые очень успешные игры вроде Civilization II и Diablo использовали фиксированную изометрическую перспективу. С приходом 3D ускорителей на персональные компьютеры и игровые консоли игры с трёхмерной перспективой в основном переключились на полноценную трёхмерность вместо изометрической перспективы. Это можно видеть в преемницах вышеназванных игр — начиная с Civilization IV в этой серии используется полная трёхмерность. Diablo II, как и ранее, использует фиксированную перспективу, но опционально применяет перспективное масштабирование спрайтов на расстоянии, получая псевдо-трёхмерную перспективу.[18]
См. также: Категория:Компьютерные игры с изометрической графикой
Примечания
Ссылки
- Introduction to 3 Dimensional graphics (англ.). Blueprint project. IDER group, Manufactuing Systems Engineering Centre, University of Hertfordshire. — Пояснения и учебник по рисованию в изометрической перспективе из Хертфорширдского университета.(недоступная ссылка — история) Проверено 29 сентября 2008.
- Herbert Glarner. Isometric Projection (англ.) (19 марта 2007). Архивировано из первоисточника 19 февраля 2012. Проверено 29 сентября 2008.
- PixelDam (англ.). — A collaborative pixelart community. Архивировано из первоисточника 19 февраля 2012. Проверено 29 сентября 2008.
- Tom Gersic. Rendering Isometric Tiles in Blender 3D (англ.). — Учебник с примерами по созданию изометрических плиток в программе Blender 3D. Архивировано из первоисточника 19 февраля 2012. Проверено 29 сентября 2008.
Литература
- Богданов В. Н., Малежик И. Ф., Верхола А. П. и др. Справочное руководство по черчению. — М.: Машиностроение, 1989. — С. 864. — ISBN 5-217-00403-7
- Фролов С. А. Начертательная геометрия. — 2-е изд., перераб. и доп. — М.: Машиностроение, 1983. — С. 240.
dic.academic.ru
Аксонометрические проекции. Изометрическая проекция — Черчение
Для тoгo чтобы получить аксонометрическую проекцию предмета (рис. 106), необходимо мысленно: поместить предмет в систему координат; выбрать аксонометрическую плоскость проекций и расположить предмет перед ней; выбрать направление параллельных проецирующих лучей, которое не должно совпадать ни с одной из аксонометрических осей; направить проецирующие лучи через все точки предмета и координатные оси до пересечения с аксонометрической плоскостью проекций, получив тем самым изображение проецируемого предмета и координатных осей.
На аксонометрической плоскости проекций получают изображение — аксонометрическую проекцию предмета, а также проекции осей систем координат, которые называют аксонометрическими осями.
Аксонометрической проекцией называется изображение, полученное на аксонометрической плоскости в результате параллельного проецирования предмета вместе с системой координат, которое наглядно отображает его форму.
Система координат состоит из трех взаимно пересекающихся плоскостей, которые имеют фиксированную точку — начало координат (точку О) и три оси (X, У, Z), исходящие из нее и расположенные под прямым углом друг к другу. Система координат позволяет производить измерения по осям, определяя положение предметов в пространстве.

Рис. 106. Получение аксонометрической (прямоугольной изометрической) проекции
Можно получить множество аксонометрических проекций, по- разному располагая предмет перед плоскостью и выбирая при этом различное направление проецирующих лучей (рис. 107).
Наиболее употребляемой является так называемая прямоугольная изометрическая проекция (в дальнейшем будем использовать ее сокращенное название — изометрическая проекция). Изометрической проекцией (см. рис. 107, а) называется такая проекция, у которой коэффициенты искажения по всем трем осям равны, а углы между аксонометрическими осями составляют 120°. Изометрическая проекция получается с помощью параллельного проецирования.
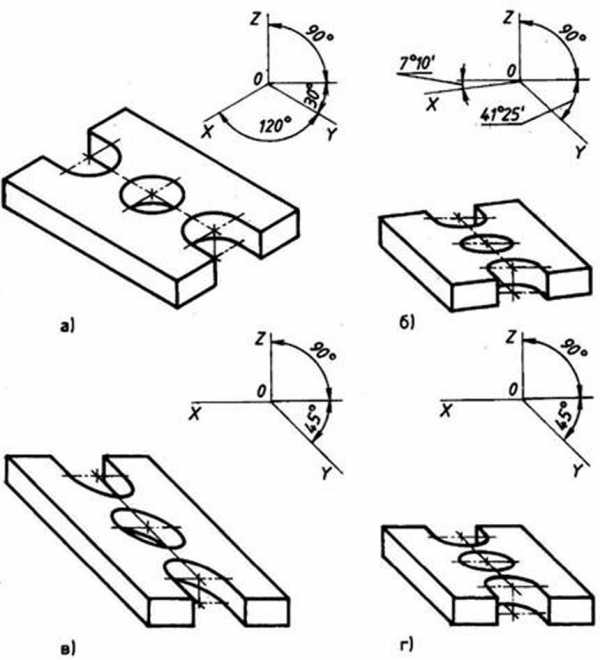
Рис. 107. Аксонометрические проекции, установленные ГОСТ 2.317—69:
а — прямоугольная изометрическая проекция; б — прямоугольная диметрическая проекция;
в — косоугольная фронтальная изометрическая проекция;
г — косоугольная фронтальная диметрическая проекция
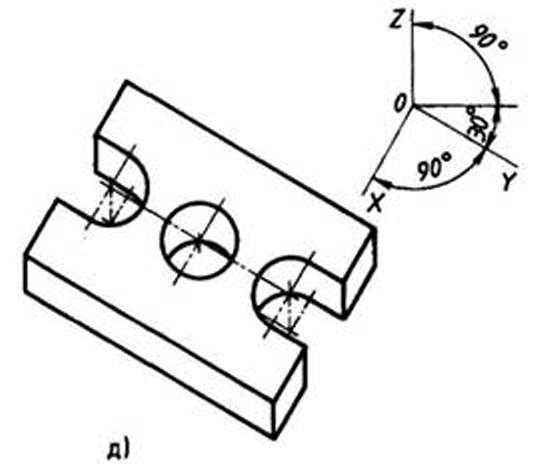
Рис. 107. Продолжение: д — косоугольная горизонтальная изометрическая проекция
При этом проецирующие лучи перпендикулярны аксонометрической плоскости проекций, а координатные оси одинаково наклонены к аксонометрической плоскости проекций (cм. рис. 106). Если сравнить линейные размеры предмета и соответствующие им размеры аксонометрического изображения, то можно увидеть, что на изображении эти размеры меньше, чем действительные. Величины, показывающие отношение размеров проекций отрезков прямых к действительным их размерам, называют коэффициентами искажения. Коэффициенты искажения (К) по осям изометрической проекции одинаковы и равны 0,82, однако для удобства построения используют так называемые практические коэффициенты искажения, которые равны единице (рис. 108).

Рис. 108. Положение осей и коэффициенты искажения изометрической проекции
Существуют изометрические, диметрические и триметрические проекции. К изометрическим проекциям относятся такие проекции, которые имеют одинаковые коэффициенты искажения по всем трем осям. Диметрическими проекциями называются такие проекции, у которых два коэффициента искажения по осям одинаковые, а величина третьего отличается от них. К триметрическим проекциям относятся проекции, у которых все коэффициенты искажения различны.
cherch.ru
1. Прямоугольные изометрические проекции
Прямоугольной изометриейназывается аксонометрическая проекция, у которой коэффициенты искажения по всем трём осям равны, а углы между аксонометрическими осями 120. На рис. 1 представлено положение аксонометрических осей прямоугольной изометрии и способы их построения.
а) б) в)
Рис. 1. Построение аксонометрических осей прямоугольной изометрии с помощью: а) отрезков; б) циркуля; в) угольников или транспортира.
При практических построениях коэффициент искажения (К) по аксонометрическим осям согласно ГОСТ 2.317- 2011 рекомендуют равный единице. При этом изображение получают более крупным по сравнению с теоретическим или точным изображением при коэффициентах искажения 0,82. Увеличение равно 1,22. На рис. 2 приведён пример изображения детали в прямоугольной изометрической проекции.
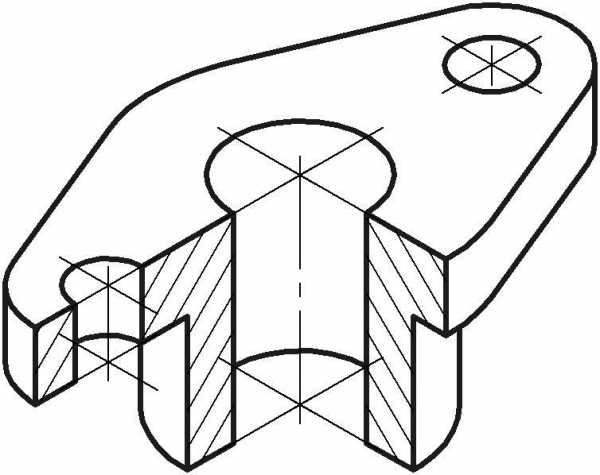
Рис. 2. Изометрия детали.
Построение в изометрии плоских фигур
Задан правильный шестиугольник АВСDЕF, расположенный параллельно горизонтальной плоскости проекций Н (П1).
а) Строим изометрические оси (рис.3).
б) Коэффициент искажения по осям в изометрии равен 1, поэтому от точки О0 по осям откладываем натуральные величины отрезков: А0О0 = АО; О0D0 = ОD; К0О0 = КО; О0Р0 = ОР.
в) Линии, параллельные координатным осям, проводятся в изометрии также параллельно соответствующим изометрическим осям в натуральную величину.
В нашем примере стороны ВС и FЕ параллельны оси Х.
В изометрии они вычерчиваются также параллельно оси Х в натуральную величину В0С0 = ВС; F0Е0= FЕ.
г) Соединяя полученные точки, получим изометрическое изображение шестиугольника в плоскости Н (П1).
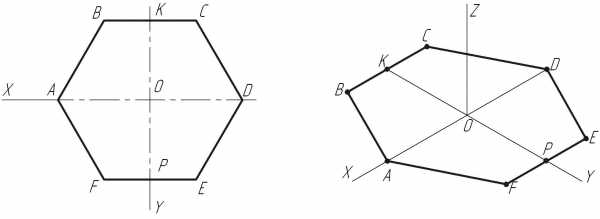
Рис. 3. Изометрическая проекция шестиугольника на чертеже
и в горизонтальной плоскости проекции
На рис. 4 представлены проекции наиболее распространенных плоских фигур в различных плоскостях проекций.
Наиболее распространённой фигурой является окружность. Изометрическая проекция окружности в общем случае представляет собой эллипс. Эллипс строят по точкам и обводят по лекалу, что в практике черчения весьма неудобно. Поэтому эллипсы заменяют овалами.
На рис. 5 построен в изометрии куб с окружностями, вписанными в каждую грань куба. При изометрических построениях важно правильно расположить оси овалов в зависимости от плоскости, в которой предполагается изобразить окружность. Как видно на рис. 5 большие оси овалов располагаются по большей диагонали ромбов, в которые спроецировались грани куба.
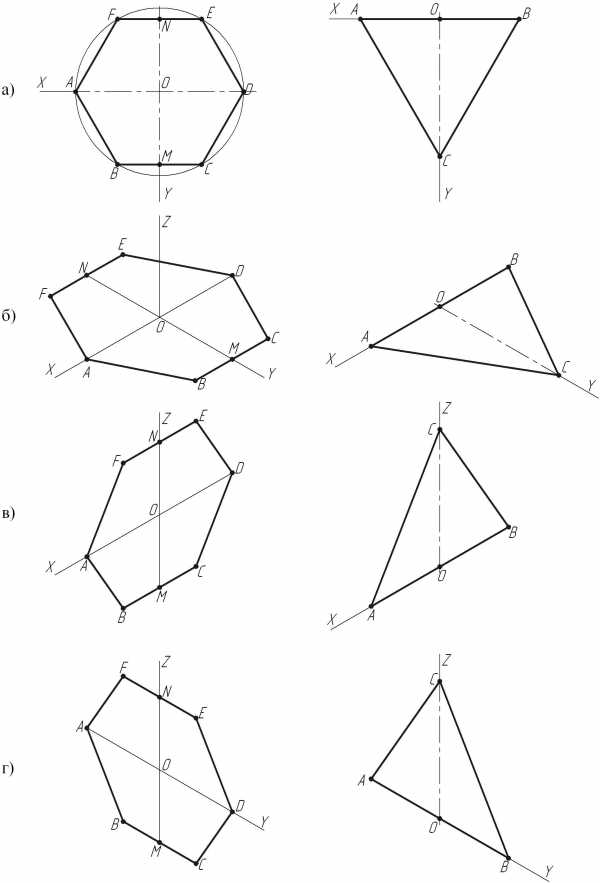
Рис. 4 Изометрическое изображение плоских фигур
а) на чертеже; б) на плоскости Н; в) на плоскости V; г) на плоскостиW.
Для прямоугольной аксонометрии любого вида правило определения главных осей эллипса овала, в который проецируется окружность, лежащая в какой-либо плоскости проекции, может быть сформулировано следующим образом: большая ось овала располагается перпендикулярно к той аксонометрической оси, которая отсутствует в данной плоскости, а малая совпадает с направлением этой оси. Форма и размеры овалов в каждой плоскости изометрических проекций одинаковы.
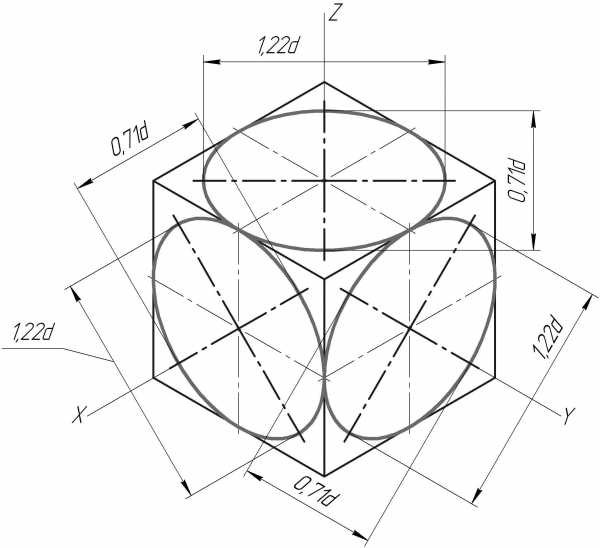
Рис. 5
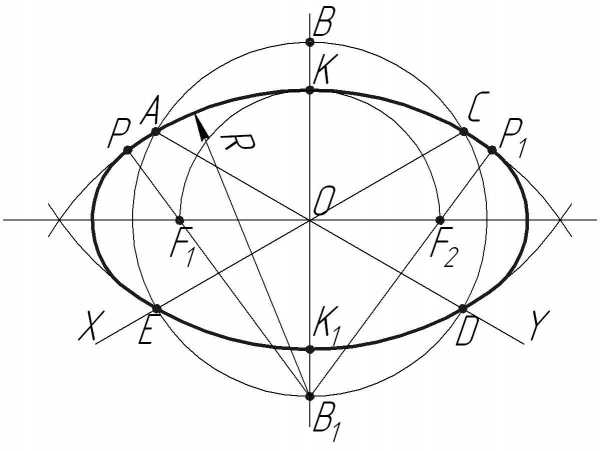
Рис. 6
studfiles.net
Способы построения изометрической проекции плоских фигур, геометрических тел и деталей
Для выполнения изометрической проекции любой детали необходимо знать правила построения изометрических проекций плоских и объемных геометрических фигур.
Правила построения изометрических проекций геометрических фигур. Построение любой плоской фигуры следует начинать с проведения осей изометрических проекций.
При построении изометрической проекции квадрата (рис. 109) из точки О по аксонометрическим осям откладывают в обе стороны половину длины стороны квадрата. Через полученные засечки проводят прямые, параллельные осям.
При построении изометрической проекции треугольника (рис. 110) по оси X от точки 0 в обе стороны откладывают отрезки, равные половине стороны треугольника. По оси У от точки О откладывают высоту треугольника. Соединяют полученные засечки отрезками прямых.
Рис. 109. Прямоугольная и изометрические проекции квадрата
Рис. 110. Прямоугольная и изометрические проекции треугольника
При построении изометрической проекции шестиугольника (рис. 111) из точки О по одной из осей откладывают (в обе стороны) радиус описанной окружности, а по другой — H/2. Через полученные засечки проводят прямые, параллельные одной из осей, и на них откладывают длину стороны шестиугольника. Соединяют полученные засечки отрезками прямых.
Рис. 111. Прямоугольная и изометрические проекции шестиугольника

Рис. 112. Прямоугольная и изометрические проекции круга
При построении изометрической проекции круга (рис. 112) из точки О по осям координат откладывают отрезки, равные его радиусу. Через полученные засечки проводят прямые, параллельные осям, получая аксонометрическую проекцию квадрата. Из вершин 1, 3 проводят дуги CD и KL радиусом 3С. Соединяют точки 2 с 4, 3 с С и 3 с D. В пересечениях прямых получаются центры а и б малых дуг, проведя которые получают овал, заменяющий аксонометрическую проекцию круга.
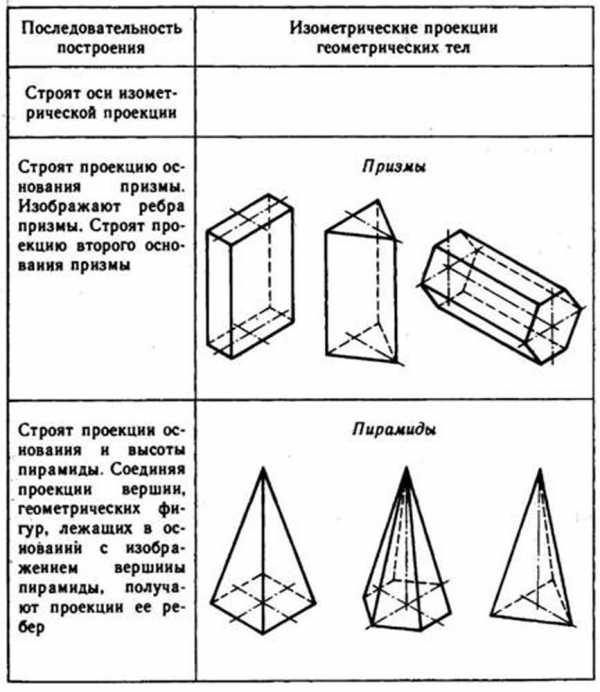
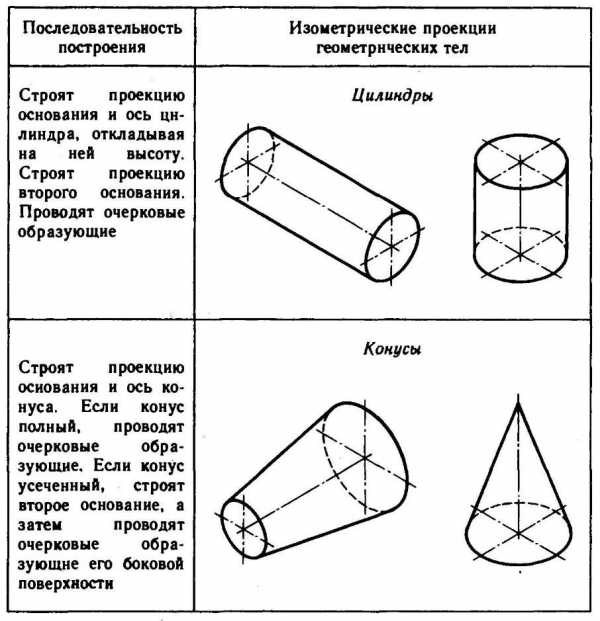
Используя описанные построения, можно выполнить аксонометрические проекции простых геометрических тел (табл. 10).
10. Изометрические проекции простых геометрических тел
Способы построения изометрической проекции детали:
1. Способ построения изометрической проекции детали от формообразующей грани используется для деталей, форма которых имеет плоскую грань, называемую формообразующей; ширина (толщина) детали на всем протяжении одинакова, на боковых поверхностях отсутствуют пазы, отверстия и другие элементы. Последовательность построения изометрической проекции заключается в следующем:
1) построение осей изометрической проекции;
2) построение изометрической проекции формообразующей грани;
3) построение проекций остальных граней посредством изображения ребер модели;
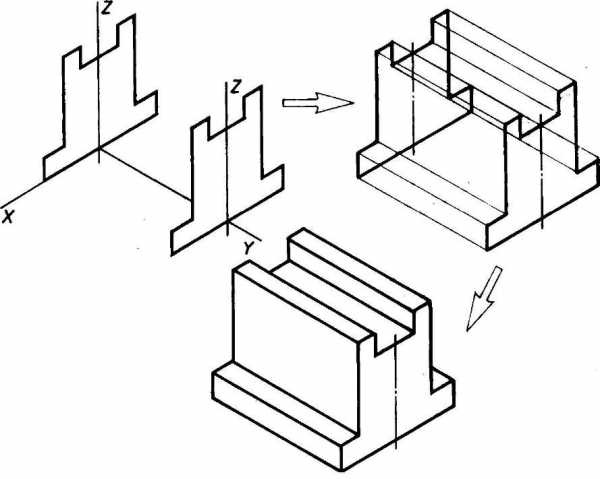
Рис. 113. Построение изометрической проекции детали, начиная от формообразующей грани
4) обводка изометрической проекции (рис. 113).
- Способ построения изометрической проекции на основе последовательного удаления объемов используется в тех случаях, когда отображаемая форма получена в результате удаления из исходной формы каких-либо объемов (рис. 114).
- Способ построения изометрической проекции на основе последовательного приращения (добавления) объемов применяется для выполнения изометрического изображения детали, форма которой получена из нескольких объемов, соединенных определенным образом друг с другом (рис. 115).
- Комбинированный способ построения изометрической проекции. Изометрическую проекцию детали, форма которой получена в результате сочетания различных способов формообразования, выполняют, используя комбинированный способ построения (рис. 116).
Аксонометрическую проекцию детали можно выполнять с изображением (рис. 117, а) и без изображения (рис. 117, б) невидимых частей формы.

Рис. 114. Построение изометрической проекции детали на основе последовательного удаления объемов

Рис. 115 Построение изометрической проекции детали на основе последовательного приращения объемов
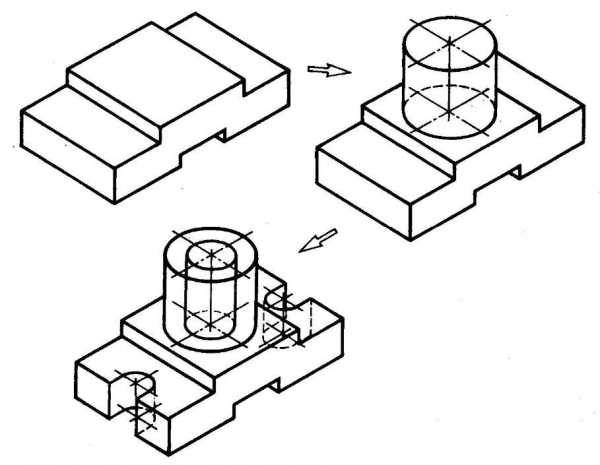
Рис. 116. Использование комбинированного способа построения изометрической проекции детали
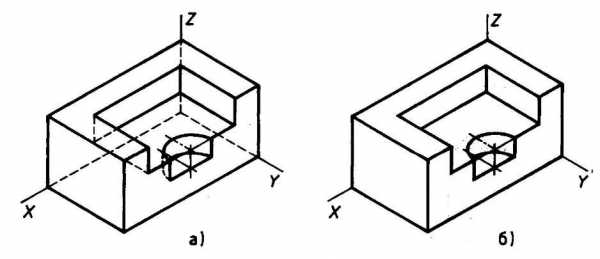
Рис. 117. Варианты изображения изометрических проекций детали: а — с изображением невидимых частей;
б — без изображения невидимых частей
cherch.ru
Чем отличается изометрия от аксонометрии
Отображать различные геометрические предметы с помощью чертежей и посредством компьютерной графики можно с применением принципов изометрии и аксонометрии. В чем специфика каждого из них?
Что представляет собой аксонометрия?
Под аксонометрией или аксонометрической проекцией понимается способ графического отображения тех или иных геометрических предметов посредством параллельных проекций.
 Аксонометрия
АксонометрияГеометрический предмет в данном случае чаще всего рисуется с использованием определенной системы координат — так, чтобы та плоскость, на которую он проецируется, не соответствовала положению плоскости других координат соответствующей системы. Получается, что предмет отображается в пространстве посредством 2 проекций и выглядит объемно.
При этом по той причине, что плоскость отображения предмета не расположена строго параллельно какой-либо из осей системы координат, отдельные элементы соответствующего отображения могут искажаться — по одному из 3 следующих принципов.
Во-первых, искажение элементов отображения предметов может наблюдаться по всем 3 осям, используемым в системе, в равной величине. В этом случае фиксируется изометрическая проекция предмета, или изометрия.
Во-вторых, искажение элементов может наблюдаться только по 2 осям в равной величине. В этом случае наблюдается диметрическая проекция.
В-третьих, искажение элементов может фиксироваться как различающееся по всем 3 осям. В этом случае наблюдается триметрическая проекция.
Рассмотрим, таким образом, специфику первого типа искажений, формируемых в рамках аксонометрии.
к содержанию ↑Что представляет собой изометрия?
Итак, изометрия — это разновидность аксонометрии, которая наблюдается при прорисовке предмета в случае, если искажение его элементов по всем 3 осям координат одинаковое.
 Изометрия
ИзометрияРассматриваемый вид аксонометрической проекции активно применяется в промышленном проектировании. Он позволяет хорошо просматривать те или иные детали в рамках чертежа. Распространено использование изометрии и при разработке компьютерных игр: с помощью соответствующего типа проекции становится возможным эффективно отображать трехмерные картинки.
Можно отметить, что в сфере современных промышленных разработок под изометрией в общем случае понимается прямоугольная проекция. Но иногда она может быть представлена и в косоугольной разновидности.
к содержанию ↑Сравнение
Главное отличие изометрии от аксонометрии заключается в том, что первый термин соответствует проекции, являющейся только лишь одной из разновидностей той, которая обозначается вторым термином. Изометрическая проекция, таким образом, существенно отличается от других разновидностей аксонометрии — диметрии и триметрии.
Отобразим более наглядно то, в чем разница между изометрией и аксонометрией, в небольшой таблице.
к содержанию ↑Таблица
| Изометрия | Аксонометрия |
| Что общего между ними? | |
| Изометрия — разновидность аксонометрии, способ графического отображения предметов с помощью параллельных проекций | |
| В чем разница между ними? | |
| Характеризуется равенством искаженных элементов проекции по всем 3 осям используемой системы координат | Может быть представлена также диметрией (равенством искажений по 2 осям), триметрией (отсутствием равенства искажений при их сопоставлении по 3 осям) |
thedifference.ru
Изометрическая проекция
Во многих случаях используется изометрическая проекция: в компьютерных играх для трёхмерных объектов и панорам, в рисовании схем проезда и т.д. Рассмотрим, как можно рисовать изометрическую проекцию в Inkscape.
Для начала немного теории. Начнем с Википедии: Изометрическая проекция — это разновидность аксонометрической проекции, при которой в отображении трёхмерного объекта на плоскость коэффициент искажения (отношение длины спроектированного на плоскость отрезка, параллельного координатной оси, к действительной длине отрезка) по всем трём осям один и тот же. Слово «изометрическая» в названии проекции пришло из греческого языка и означает «равный размер», отражая тот факт, что в этой проекции масштабы по всем осям равны. По западным стандартам изометрическая проекция, помимо равенства масштабов по осям, включает условие равенства 120° углов между проекциями любой пары осей.
В прямоугольной изометрической проекции аксонометрические оси образуют между собой углы в 120°, ось Z’ направлена вертикально. Коэффициенты искажения (kx,ky,kz) имеют числовое значение . Как правило, для упрощения построений изометрическую проекцию выполняют без искажений по осям, то есть коэффициент искажения принимают равным 1, в этом случае получают увеличение линейных размеров в раза.
Изометрический вид объекта можно получить, выбрав направление обзора таким образом, чтобы углы между проекцией осей x, y, и z были одинаковы и равны 120°. К примеру, если взять куб, это можно выполнить направив взгляд на одну из граней куба, после чего повернув куб на ±45° вокруг вертикальной оси и на ±arcsin (tan 30°) = 35.264° вокруг горизонтальной оси. Обратите внимание: при изометрической проекции куба контур проекции образует правильный шестиугольник — все рёбра равной длины и все грани равной площади.
Подобным же образом изометрический вид может быть получен, к примеру, в редакторе трёхмерных сцен: начав с камерой, выровненной параллельно полу и координатным осям, её нужно повернуть вниз на =35.264° вокруг горизонтальной оси и на ±45° вокруг вертикальной оси.
Попробуем нарисовать предмет в изометрической проекции. Для опытов возьмём некий блочный предмет. Это может быть коробка, дом, книга, полка и т.п.
Описываемый здесь способ удобен, когда нужно нарисовать готовый объект с картинками и текстами в изометрической проекции, так как к этим элементам композиции также будут правильно применены операции масштабирования и сдвига.
Нарисуем развертку блочного элемента при помощи инструмента Rectangle, состоящую из трёх частей: передняя часть, боковая часть и верхняя часть.
Обратите внимание, что должны совпадать высоты передней и боковой части, а также ширина боковой и высота верхней части (в противном случае фигура просто не сложится). Размеры прямоугольников выберите по своему вкусу.
Мы не будем сейчас добавлять текст и другие элементы украшения, а сфокусируемся на технике создания изометрической проекции.
Для удобства можно раскрасить каждый прямоугольник блока в собственный цвет. Далее откройте диалоговое окно Fill and Stroke (Shift+Ctrl+F) и на вкладке Stroke style установите ширину границ в 1 пиксель.
При создании проекции каждая сторона меняет свои размеры (сужается) и сдвигается (искажается). А верхняя часть к тому же ещё и вращается. Делается это за несколько шагов.
Начнем с передней части. Выберите её при помощи инструмента Select. Далее вызовите диалоговое окно Transform через меню Object | Transform… (Shift+Ctrl+M). Перейдите на вкладку Scale и установите ширину прямоугольника в 86.603%, что эквивалентно cos(30°). Щелкните на кнопке Apply. После этой операции прямоугольник станет уже и изменит свое местоположение. Подвиньте его к остальным прямоугольникам.
Далее нам необходимо произвести операцию сдвига на 30°. Это легко сделать при помощи инструмента Select. Щёлкните на прямоугольнике два раза, чтобы включить режим поворота и сдвига. Когда вы это сделаете, то в центре фигуры увидите крестик — центр поворота. Вокруг этой точки осуществляется поворот фигуры или сдвига. Перетащите крестик в верхний правый угол прямоугольника. Будьте аккуратны и постарайтесь разместить крестик точно в указанном углу.
Теперь необходимо сделать сдвиг прямоугольника. Удерживая клавишу Ctrl, щёлкните и потащите стрелку сдвига на левой стороне прямоугольника. По умолчанию, при нажатой клавише Ctrl сдвиг происходит по шагам на 15°. Смотрите на строку состояния и сдвиньте прямоугольник на -30°
Повторите предыдущие шаги для боковой стороны. Измените ее ширину на 86.603% и сдвиньте на 30°. Единственная разница заключается в том, что центр поворота теперь нужно расположить в верхнем левом углу.
Финальная часть нашего упражнения — работа с верхним прямоугольником. Здесь есть свои особенности. Во-первых, для верхнего прямоугольника необходимо масштабировать не ширину (её оставляем равным 100%), а высоту на 86.603%. Во-вторых, для сдвига перемещаем центр поворота в нижний левый угол и сдвигаем на 30° (удерживаем клавишу Ctrl для аккуратного точного сдвига). Но это еще не всё. Далее берёмся за верхнюю левую стрелку и поворачиваем фигуру по часовой стрелке на 30°, опять удерживая клавишу Ctrl.
Если вы всё сделали правильно, то у вас получилась изометрическая проекция объекта.
Аксонометрическая сетка
В Inkscape есть специальная аксонометрическая сетка (File | Document Properties… | Вкладка Grids/Файл | Свойства документа | Сетки). В выпадающем списке выберите Axonometric grid. Использование аксонометрической сетки позволят создавать объекты в изометрии. Чтобы облегчить рисование ещё больше, можно также включить прилипание. Настройка сетки включает в себя изменения параметров единицы, основной линии и интервала по оси Y. Для большего удобства, можно также задать свои цвета основным и обычным линиям сетки.
Далее вы можете трансформировать объекты, как в верхнем примере, но при этом вам будет помогать сетка.
Общий алгоритм: Object | Transform…| Scale/Объект | Трансформировать | Масштаб, уменьшить ширину на 86,603%. Затем, в том же меню трансформации, следует изменить наклон по вертикали на 30 или −30 градусов (в зависимости от желаемого угла). Либо менять наклон вручную.
Создание параллелепипедов в 3D
С помощью инструмента «Рисовать параллелепипеды в 3D» (Shift+F4) можно создать объекты в изометрической проекции. Необходимо изменить направление точек схода всех трех углов от «конечных» до «бесконечных». А углы параллелепипеда установить в следующие значениях: X:150, Y:90, Z:30.
Чтобы редактировать цвет и обводку отдельной грани, не потеряв свойства трехмерного объекта, можно воспользоваться инструментом «Редактирования узлов и рычагов» (F2). На изображении — верхняя грань сделана прозрачной и стали видны внутренние стенки. А если уменьшить высоту стенок, то можно увидеть и дно.
Реклама
designer.alexanderklimov.ru