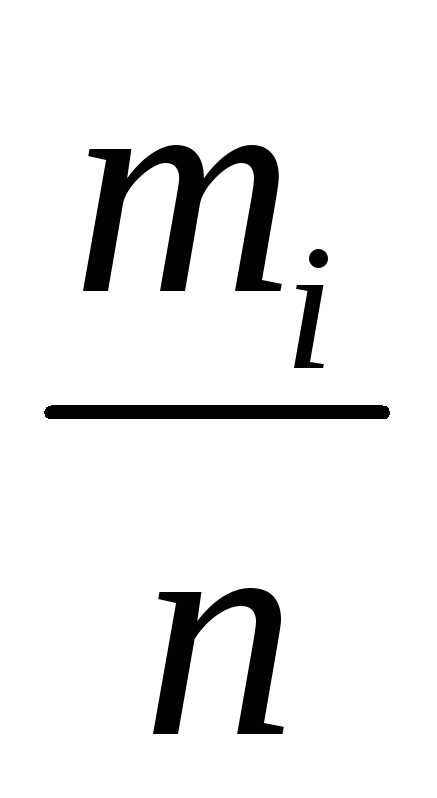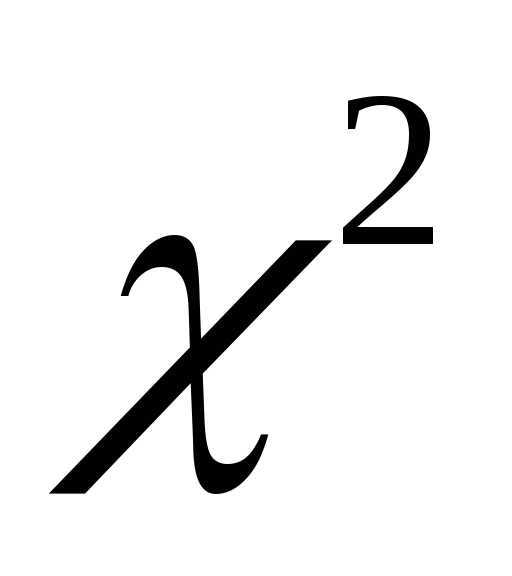Гистограмма нормального распределения – Типы распределений и соответствующие им гистограммы | Бережливые шесть сигм | Тематический раздел | База знаний

Типы распределений и соответствующие им гистограммы | Бережливые шесть сигм | Тематический раздел | База знаний

В предыдущей статье нам удалось выделить основные характеристики числового ряда, которые можно показать с помощью гистограмм – это среднее значение популяции, разброс и функция распределения. Так как последняя характеристика зачастую представляет наибольший интерес, ее анализ и примеры некоторых, наиболее часто встречающихся распределений требуют дополнительного внимания.

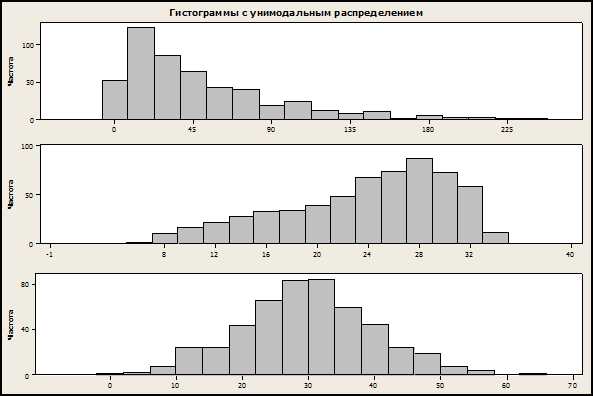
Гистограмма позволяет анализировать частотное распределение числового ряда, а соответственно дает возможность выделить наиболее вероятные число или диапазон – другими словами, пик. Гистограмма с ярко выраженным пиком называется унимодальной:

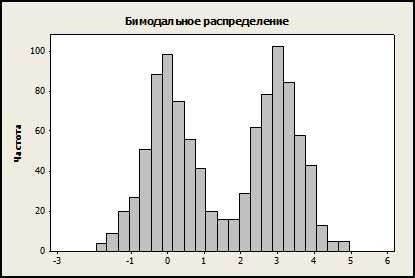
Если мы можем различить у гистограммы два ярко выраженных пика, то гистограмма называется бимодальной. Во многих случаях это значит, что выборки происходят из двух разных популяций, так как наличие двух мод в одной популяции маловероятное явление:

Гистограммы с большим количеством пиков (многомодальные) встречаются крайне редко и, зачастую свидетельствуют о присутствии специальных факторов, влияющих на исследуемую систему или процесс. Если каждый интервал гистограммы содержит примерно равное количество значений, то такая гистограмма называется однородной или гистограммой равномерного распределения:

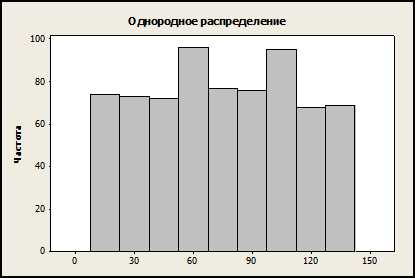
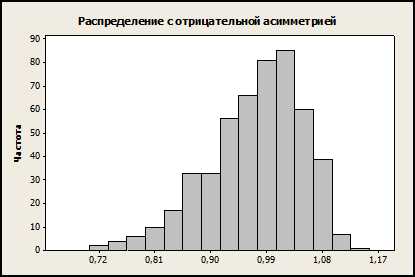
Гистограмма называется симметричной, если она имеет симметричную форму относительно центральной линии (правая и левая стороны одинаковой формы). Ассиметричные гистограммы бывают со скосом влево или вправо от осевой линии. Если левая сторона гистограммы вытянута значительно больше, чем правая (или левый «хвост” значительно длиннее правого), то говорят, что гистограмма имеет отрицательную асимметрию:

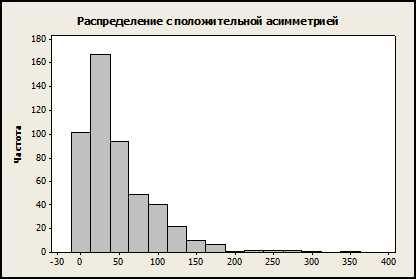
Соответственно, у гистограммы с положительной асимметрией больше в сторону выдаётся правая сторона (или правый «хвост” значительно длиннее левого):

Если наблюдаемая величина подчиняется нормальному закону распределения, гистограмма числового ряда будет иметь унимодальную симметрическую форму:

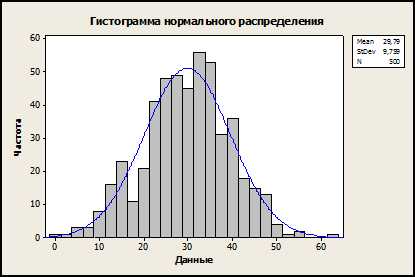
Нормальному закону распределения может подчиняться любая величина, на которую не влияют специальные факторы (например, связывающие или ограничивающие): когда она подвержена влиянию большого числа случайных помех. Считается, что из всех распределений чаще всего встречается именно нормальное.

Частным случаем нормального распределения является логарифмическое распределение. Оно является непрерывным унимодальным распределением и имеет положительную асимметрию. Этому распределению с заданной степенью приближения, подчиняется, например, размер фракций гравия, камня и т.п. Аналогичные примеры: длительность часто повторяемого события (время выполнения операции на конвейере), или размер зарплат на предприятии – как правило, значительно большее количество сотрудников имеет среднюю зарплату, но есть персонал, у которого она значительно выше (правый хвост гистограммы).

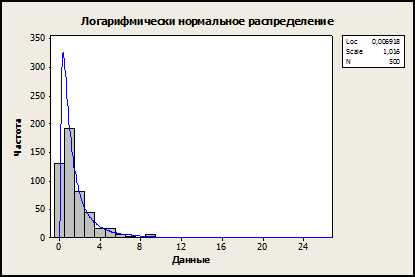
Гамма-распределение – это двухпараметрическое семейство абсолютно непрерывных распределений. Они применяются в различных отраслях экономики и техники, теории и практике испытаний надежности. В частности, гамма-распределению могут быть подчинены такие величины, как общий срок службы изделия, время наработки до k-го отказа (k = 1, 2, …, и т.д.). Также, это распределение используется в логистике для описания спроса в моделях управления запасами.

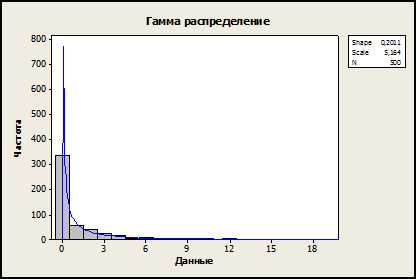
Экспоненциальное распределение – непрерывное распределение, моделирующее время между двумя последовательными свершениями одного и того же события. Например, время между появлениями двух последовательных клиентов (заказчиков в бизнесе или просто покупателей в магазине) будет случайной величиной с экспоненциальным распределением:

Логистическая функция распределения – по форме похожа на функцию нормального распределения, её главное предназначение – моделирование данных бинарного типа. Используется, например, в медико-биологических исследованиях для анализа эффекта различных лекарств, ядов и т.д. От нормального распределения логистическое отличается длинными «хвостами” – данными, находящимися в крайних, отдалённых от центра, позициях:

Вот далеко не полный перечень типов распределений и соответствующих им гистограмм. Внешнее отличие построенной Вами гистограммы от перевернутого колокола еще совсем не означает, что данные собраны неправильно или, что процесс нестабилен. Однако это всегда заставляет исследователя задуматься и постараться найти объяснение такому результату.

sixsigmaonline.ru

Гистограмма — QUORACE

Гистограммы позволяют сделать при контроле качества предварительную оценку закона распределения случайной величины, т.е. понять, как происходит разброс значений, есть ли влияющие факторы и как они влияют на измеряемый результат.
Гистограмма является столбчатым графиком и позволяет наглядно представить характер распределения случайной величины

Построение гистограммы происходит следующим образом
1. Создаётся план исследования, проводятся измерения, результаты заносятся в таблицу. Результатом может быть, как фактическое измеренное значение, например, момент затяжки 20 Н*м, так и отклонение от требуемого значения, например, запись отклонения в 0,05 мм при оценке диаметра изделия.

В Таблице 1 приведён пример для 40 результатов измерений момента силы (Н*м).
Заданный момент силы равен 25,5 Н*м, отклонения ±1,5 Н*м. Он будет рассмотрен для построения гистограмм.
Таблица 1.

2. В полученной выборке находят минимальное и максимальное значение X_min и X_max (Таблица 2).
3. Вычисляют разницу R=X_max-X_min (Таблица 2).
4. Разницу R разбивают на z равных интервалов (L), где z=√N, N – объём всей выборки (количество измеренных значений параметра) (Таблица 2). Для точного анализа выборка должна быть представительной, т.е. быть достаточной для проведения анализа и его точной интерпретации. Представительной считается выборка от 35 до 100 значений, обычно N=100. Длина интервала

L=R/x должна быть больше цены деления шкалы измерительного устройства, которым выполнялись измерения.
Таблица 2.

5. Подсчитываются частоты попадания значений в интервалы, составляется таблица распределения и строится его графическое изображение. При этом частоты значений, оказавшиеся на границе интервалов, поровну распределяют между соседними интервалами (Рис.1)

Рис.1
Имея таблицу распределения значения X(среднее арифметическое) и S² (стандартное отклонение) можно рассчитать по формулам

Где x_i – среднее значение i-го интервала

Или воспользовавшись соответствующими функциями в MS Excel
СРЗНАЧ() для X
СТАНДОТКЛОН.В() или СТАНДОТКЛОН.Г() для S²
Зная X и S² можно оценить индекс воспроизводимости процесса (С_р), который будет рассмотрен в другой статье.

Исходя из гистограммы, рассмотренной в примере, можно сделать вывод о том, что часть значений находится вне допусков и большинство значений уходят в сторону двух пиков по левую и правую границу допусков, что характерно для выборки, объединяющей результаты двух процессов, когда происходит смешивание двух распределений с далеко отстоящими средними значениями. В данном случае необходимо применить метод стратификации и провести анализ ещё раз. В данном случае можно предположить, что измерения проводились двумя различными ключами, что и дало такой результат. Разделение данных по различным ключам позволит исключить двойные пики в гистограмме.

Таким образом, существуют некоторые основные типы гистограмм исходя из графического представления которых можно сделать выводы о характере популяции.

Существует восемь основных типов гистограмм:

1. Нормальное распределение. Обычный тип. Форма колокола.
   
   Симметричная форма с пиком примерно в центре интервала характерна для нормального распределения. Отклонения от данной формы могут указывать на наличие различных причин, влияющих на распределение.
2. Распределение с двумя пиками.
   
   В центре интервала низкая частота попадания, зато есть два пика по левую и правую стороны интервала. Подобное распределение говорит о том, что в выборку включены значения, объединяющие различные процессы, например, смешаны результаты контроля двух станков или была произведена различная настройка контролирующего инструмента.
3. Плато
   
   При подобном распределении можно говорить о влиянии условий, аналогичных предыдущей гистограмме, отличие в том, что средние значения нескольких распределений отличаются незначительно. Необходимо провести расслоение данных, снизить вариабельность процессов.
4. Распределение гребенчатого типа.
   
   Чередующиеся высокие и низки значения обычно указывают на ошибки измерений или ошибки в способе группировки данных, также на систематическую погрешность в способе округления данных. Существуют незначительная вероятность того, что это распределение типа плато. Если значения в таблицу заносятся человеком, то наличие пиков на целых числах может быть обусловлено влиянием человека при округлении значений. Человеку свойственно отдавать предпочтения при записи круглым числам
5. Положительно или отрицательно скошенное распределение.
   
   Среднее значение гистограммы локализовано слева или справа от центра размаха. Частоты резко спадают к противоположному от пика концу. Форма ассиметрична. Подобное распределение возможно, когда невозможно получение значений больше или меньше определённой величины, либо при наличии одностороннего поля допуска, также это может быть влияние точности заготовок при их механической обработке.
6. Усечённое распределение, с обрывом справа или слева.
   
   Среднее арифметическое гистограммы локализовано далеко слева или справа от центра размаха, частоты резко спадают в противоположном от пика направлении. Подобные распределения встречаются при стопроцентном просеивании изделий из-за плохой воспроизводимости процессов, т.е., например, часть распределения изъята при контроле качества.
7. Распределение с изолированным пиком.
   
   На ряду с обычным распределением любого типа по одну сторону от распределения находится маленький пик. Причиной может быть включение данных из другого распределения или появление ошибки измерения. Стоит перепроверить измерения и вычисления, может возможно выделить условия (оборудование, время), которые могут служить причиной образования изолированного пика.
8. Распределение с пиком на краю.
   
   Имеется большой пик по одну из сторон размаха. Подобное распределение может быть при объединении всех несоответствий, близких к одному из концов размаха в одну категорию, либо на неаккуратную запись данных.
   Если существуют границы допуска, то следует нанести их на гистограммы. Исходя из положения распределения относительно границ допуска на гистограмме можно делать выводы о необходимости принятия решений.

Есть пять типичных случаев расположения распределения относительно границ допуска

1. Гистограмма находится в допуске.
   
   Состояние процесса стабильно, необходимо поддерживать процесс в данном состоянии
2. Гистограмма находится в допуске, но вплотную к границам.
   
   Необходимо уменьшить разброс до меньшего значения.
3. Гистограмма за границами допуска слева (или справа).
   
   Необходимо сместить среднее значение ближе к центру.
4. Гистограмма за границами допуска слева и справа.
   
   Необходимы действия, направленные на снижение вариаций процесса.
5. Гистограмма за границами допуска слева и справа, пик смещён вправо (или влево).
   

Необходимо провести действия, аналогичные для 3 и 4 случая одновременно, для снижения вариаций и смещения среднего.

quorace.com

Визуальный анализ гистограмм распределения | Металловедение

В прошлой статье мы научились строить гистограммы распределения в Excel, а теперь посмотрим, как их можно использовать для анализа.  Пока будет рассмотрен только качественный анализ гистограмм, представляющий собой, грубо говоря, оценку «на глаз».

Несмотря на то, что качественный анализ и не дает конкретных цифр (количественных характеристик), такая визуальная оценка может помочь избежать ошибок, от которых при осуществлении анализа распределения с помощью количественных показателей не застрахован даже опытный человек.

А то может получиться вот что:  работа проделана огромная, был обработан здоровенный массив данных, глаза уже болят, пятая точка приросла к стулу и сама уже тоже как будто одеревенела, а в голову словно вату напихали, а вот все результаты и выеденного яйца не стоят, т.к. всех наших умных вычислений и преобразований и делать-то было не нужно. А могло это произойти, к примеру, потому что наблюдаемая величина, не подчиняется закону нормального распределения или выборка была «загрязнена» данными из другой выборки, и все наши супер-формулы для определения дисперсий, отклонений и т.п. оказались не применимы.

В общем, метод очень даже полезен, и его стоит использовать в качестве предварительной оценки, чтобы не делать «зряшную работу», как любит говорить один мой сотрудник.

Рассмотрим возможные виды гистограмм, которые мы можем получить.

Симметричная форма

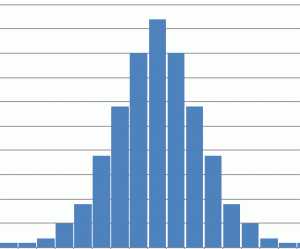Похожа на колокол и присуща нормальному распределению. Среднее значение и максимум гистограммы соответствуют середине разбега данных. Такая форма свидетельствует о стабильности процесса.

Скошенное распределение

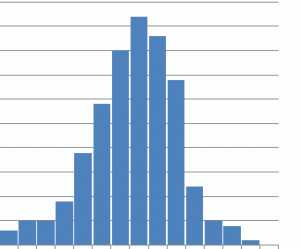Несимметричная форма. К нашему колоколу изрядно приложились молотком. Среднее значение гистограммы располагается либо правее, либо левее середины разбега данных, происходит резкое уменьшение частоты (высоты столбиков) с одного края.
Такая форма образуется, когда

а) крайнее значение невозможно достигнуть (например, при оценке количества вязкой составляющей после испытаний падающим грузом — больше 100% ведет быть не может),

б) либо если одна из границ регулируется теоретически, то есть кто-то сознательно подтасовывает данные (например, накидывает с десяток-другой мегапаскалей к значению временного сопротивления после получения результатов испытаний на растяжение).

Распределение с обрывом

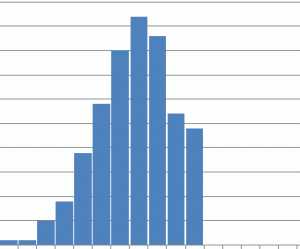Похожа на предыдущую только еще резче. Здесь тоже видим асимметричную форму и смещение максимума в одну из сторон, при этом с одной из сторон наблюдается резкий обрыв.
Такая форма часто встречается при 100 %-ном контроле изделий вследствие плохой воспроизводимости процесса, или опять же, кто-то мухлюет, только еще наглее =)

Гребень

Мультимодальный тип. Столбики через один или два интервала то выше, то ниже. Такое случается, когда

а) количество единичных наблюдений (измерений), входящих в интервал, колеблется от интервала к интервалу. То есть так уж получилось;

б) или данные были округлены по какому-то правилу. Чтобы провести нормальный анализ, скорее всего, нужно будет искать исходные неокругленные данные. Я, например, не представляю, как, даже зная правило округления, вернуть данным исходные значения. Если кто знает способ, подскажите.

Плато

В середине гистограммы видим примерно одинаковые частоты, т.е. образуется ровная площадка на возвышении (потому и «плато»).
Так может получиться, когда произошло объединение нескольких распределений со средними значениями близко расположенными друг к другу. Например, вот только сегодня на работе, делал отчет и смотрел, как различные параметры нагрева и прокатки влияют на  механические свойства, и получил такое распределение. Оказалось, что я не учел вот чего: часть проката была прокатана в два карата по длине (то есть в два раза больше, чем нужно заказчику, а потом резали пополам). Металл один, режимы — тоже (конечно же, в пределах отклонений по хим. составу, работы оборудования и т.п.), но вот исходные заготовки разные. Для дальнейшего анализа в таких случаях  рекомендуется

а) проверить свою выборку (может все-таки удастся найти следы второй выборки) и разбить ее на две. У меня это получилось, легко, так как можно было достать данные об исходной заготовке.

б) заняться очисткой выборки. Для это существует метод стратификации. О нем пока ничего не знаю =).

Гистограмма с провалом

Как выломанный забор. Форма такой гистограммы близка к нормальному распределению, но присутствует интервал с меньшей частотой по сравнению с соседними. Такое может получиться,

а) когда ширина интервала не кратна единице измерения, или

б) когда неправильно сняты показания шкалы (тут уж, наверное, ничего не поделаешь).

Распределение с изолированным пиком.

Около обычного распределения появляется изолированный пик.
Такая форма образуется также при «загрязнении» выборки данными из другого распределения. Это может происходить из-за

а) ошибок при измерении,

б) нарушения управляемости процессом,

в) или, попросту, как в моем случае, из-за включения данных из другого процесса.

Вот и все!

А теперь разгадываем кроссворд и подписываемся на обновления блога!

Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.

Поделиться ссылкой:

metallovedeniye.ru

«Гистограмма распределения» Теоретические сведения — Документ

Лабораторная работа №2
по курсу «Компьютерный анализ статистических данных»
на тему «Гистограмма распределения»

Теоретические сведения

Гистограмма распределения показывает, насколько часто встречаются те или иные значения X (аналог плотности распределения). Каждый столбец гистограммы показывает частоту попадания значения выборки в интервал значений — чем выше столбец, тем вероятнее соответствующие значения показателя.

Для построения гистограммы необходимо:

1. Разбить диапазон значений показателя на интервалы (обычно используются равные интервалы).

2. Посчитать число значений, попавших в каждый интервал – частоты.

3. Посчитать высоту столбцов гистограммы в соответствии с правилом нормировки: сумма площадей столбцов гистограммы равна 1 (без учета зазоров между столбцами).

4. Построить график.

Рассмотрим каждый шаг подробнее.

Выделение интервалов

Весь диапазон значений показателя необходимо разбить на части – интервалы. Не допускается наличие «дырок» между интервалами и перекрытие интервалов. Чаще всего интервалы имеют одинаковую ширину.

Интервал задается своей нижней и верхней границей: a_i и b_i, i – номер интервала (1,2,3…).

Иногда разбиение выполняют в соответствии с общепринятой традицией. Например, принято распределять население по возрастным группам, как показано в таблице (по 5 лет).

Иногда разбиение производят исходя из простоты, например, на интервалы шириной 10. Например:

1. [20;30)

2. [30;40)

3. [40;50)

4. [50;60)

5. [60;70]

Но в этом случае может получиться так, что в крайние интервалы попадает слишком мало значений.

Распределение населения по возрастным группам

	Тыс. человек
	2001	2006	2007
Все население		146304	142754	142221
в том числе    в возрасте, лет:
0-4		6367	7037	7223
5-9		7762	6418	6376
10-14		11789	7790	7283
15-19		12322	11825	11088
20-24		11106	12405	12671
25-29		10451	11049	11165
30-34		9620	10295	10442
35-39		11333	9417	9459
40-44		12651	10949	10368
45-49		11434	12054	12067
50-54		9409	10645	10804
55-59		4995	8590	8985
60-64		8906	4407	4336
65-69		5903	7609	7458
70 и более		12256	12264	12496

Третий вариант – определить оптимальное количество интервалов исходя из мощности выборки (чем больше наблюдений, тем больше интервалов). Для этого используется формула Стерджесса:

Затем весь диапазон значений от минимального до максимального разбивается на равные части. Ширина интервала определяется по формуле:

Тогда первый интервал начинается в X_min, а последний (с номером m) заканчивается в X_max.

a₁ = X_minb₁ = a₁ + w

a₂ = b₁b₂ = a₂ + w

…

a_m = b_m–1b_m = a_m + w = X_max

Частота (частость) попадания в каждый интервал считается явно: сколько из всех значений находятся внутри интервала, т.е. и . Обозначается n_i.

Сумма всех частот должна быть равна мощности выборки, иначе какие-то значения «потерялись»:

В примере с населением частота попадания в интервал 20-24 года в 2007г. составила 12671 тыс. чел.

Высота столбца гистограммы вычисляется через частоту и ширину интервалов:

Проверим, что при этом выполняется правило нормировки. Площадь каждого столбца (прямоугольника) – это высота умножить на ширину:

Сумма площадей:

Для визуального анализа гистограмму наносят на график и сравнивают с известными законами распределения.

Чаще всего гистограмма близка к нормальному закону распределения. Большинство значений сосредоточены в центре, к краям высоты столбцов плавно снижается. Пример такой гистограммы в сравнении с теоретическим нормальным законом (красная линия):

Другой возможный вариант – равномерное распределение, когда все значения примерно поровну распределены по столбцам гистограммы, нет заметных максимумов и минимумов:

В идеале, высоты столбцов должны быть почти одинаковыми, но в реальности так получается редко.

Существуют и другие варианты гистограммы распределения:

Гистограмма смещена влево (асимметрия влево)

Гистограмма смещена вправо (асимметрия вправо)

Бимодальность

Гистограмма отображает два совмещенных процесса. Такая ситуация может произойти если результаты измерений получены от двух разных устройств, двух операторов, контролеров, разных измерительных инструментов, или с разных точек измерения.

Гистограмма усечена

Распределение не является нормальным т.к. нет постепенного снижения частоты результатов измерений от центра к границам. Такой вид гистограммы возникает, если чересчур малые и большие наблюдения невозможны или потеряны.

Гистограмма не имеет центра

Достаточно редкая ситуация, когда столбцы в центре диаграммы близки к 0. Может быть случаем бимодальности.

«Тяжелые хвосты»

По краям гистограммы наблюдаются высокие столбцы. Означает сильное «расслоение» показателя, когда много как очень больших, так и очень маленьких значений.

Кумулята или кумулятивная кривая, в отличие от гистограммы строится по накопленным частотам. При этом на горизонтальной оси также отмечают интервалы значений признака, а на вертикальной оси – накопленные частоты.

Накопленная частота – это сумма частот обычной гистограммы, от первого интервала до текущего:

…

Высота столбца кумуляты рассчитывается как накопленная частота деленная на общее количество наблюдений:

Кумулята является аналогом закона распределения, и поэтому возрастает от 0 до 1. Правило нормировки для нее не действует.

Визуально кумуляту труднее анализировать, но с вертикальной оси можно снимать значения вероятностей: высота столбца кумуляты равна вероятности того, что случайная величина меньше верхней границы соответствующего интервала.

Задание

Имеется статистическая выборка с наблюдениями показателя X – ежемесячного дохода лиц, совершивших определенный тип преступлений, тыс. у.е.. Необходимо построить гистограмму распределения:

1. Определить мощность выборки, минимальное, максимальное, среднее значения и стандартное отклонение.

2. Определить число интервалов по формуле Стерджесса и их ширину.

3. Определить границы и середины интервалов («карманов»).

4. Вычислить частоты попаданий в интервалы двумя способами: через «Анализ данных» и через формулы.

5. Построить график гистограммы.

6. Построить график кумуляты.

7. Сравнить полученную гистограмму с нормальным законом распределения (визуально).

8. Сравнить полученную гистограмму с равномерным законом распределения (визуально).

Сделать выводы о предположительном законе распределения (нормальный, равномерный, другой). Если это возможно, определить, в каком диапазоне дохода совершение преступления а) наиболее вероятно; б) наименее вероятно. Какова вероятность совершения данного преступления для лиц с доходом менее 10 тыс. у.е?

Исходные данные

Исходные выборки находятся в файле «КАСД Л.р. Варианты.xlsx» на листе «Л.р.2». Вариант задается по номеру в списке группы.

Подготовка исходных данных

Работа выполняется в том же файле, что и первая, но на новом листе. Переименуйте «Лист 2» в «Л.р.2».

Скопируйте данные для своего варианта на лист «Л.р.2», начиная со второй строки и столбца A. Укажите название столбца (X).

Пример

Все расчеты показаны на примере выборки:

32,32	43,69	55,62	33,28	59,92
61,78	39,15	39,94	51,83	55,95
67,22	52,41	40,67	55,92	42,29
54,48	40,87	57,46	49,89	59,24
64,71	45,79	30,92	34,2	56,32
59,6	51,18	46,25	37,62	63,64
64,25	46,88	43,76	48,74	48,74
55,39	56,84	40,61	51,05	56,89
50,88	59,99	51,16	43,99	61,4
60,91	56,38	63,22	46,57	42,99
49,05	58,19	44,96	53,84	37,59
53,29	56,08	68,03	58,3	42,58
57,67	54,15	50,71	56,01	46,73
31,14	59,29	57,91	44,76	28,71
50,4	44,7	41,5	46,79	23,02
53,17	44,9	54,87	65,09	26,01
55,89	62,02	59,35	36,57	32,53

Указания к выполнению работы

1. Мощность выборки, минимальное и максимальное значения, среднее и стандартное отклонение рассчитываются по аналогии с 1 лабораторной работой (любым способом).

В примере выборка содержит 85 наблюдений, от 23,02 до 68,03. Средний доход составляет 49,89, стандартное отклонение – 10,16.

2. Число интервалов определим по формуле Стерджесса:

Полученное число необходимо округлить до большего значения.

Функции: ОКРУГЛВВЕРХ(число; знаков_после_запятой) Округлить число в сторону большего до указанного знаков после запятой (0 – до целых). LOG10(число) Десятичный логарифм числа (lg).

Чтобы определить ширину интервала, воспользуемся формулой:

Ширину интервала округлять не нужно.

Таким образом, необходимо исходные данные распределить по 8 интервалам шириной 5,626тыс.у.е.

3. Определим границы интервалов («карманов») и подготовим таблицу для будущих расчетов. Число строк в таблице равно числу интервалов, столбцы мы будем добавлять по мере необходимости (всего их будет 9, пока подготовим 3).

a_i – нижняя граница;

b_i – верхняя граница;

c_i – середина интервала.

Нижняя граница первого интервала – это минимальное значение выборки (в примере 23,02). Нижняя граница каждого следующего интервала – это предыдущий интервал плюс ширина интервала:

.

Не забудьте зафиксировать ячейку с w в формуле, прежде чем растянуть ее!

Верхняя граница интервала совпадает с нижней границей следующего интервала и рассчитывается по такой же формуле.

.

Верхняя граница последнего интервала должна быть в точности равна максимальному значению выборки.

Середина интервала рассчитывается как среднее между его границами.

Чтобы в столбце отображалось только 2 знака после запятой (как в исходных данных), выделите значения ci (F12:F19), кликните по ним правой кнопкой, выберите «Формат ячеек», вкладка «Число», Выберите тип «Числовой». В поле «Число десятичных знаков» можно задать, сколько показывать знаков после запятой (по умолчанию – 2).

Таким образом, исходную выборку мы разбили на 8 числовых интервалов:

1. [23,02;28,65)

2. [28,65;34,27)

3. [34,27;39,9)

4. [39,9;45,53)

5. [45,53;51,15)

6. [51,15;56,78)

7. [56,78;62,4)

8. [62,4;68,03]

Квадратная скобка означает, что число на границе входит в интервал, круглая – что не входит. Например, 28,65 входит во второй интервал, но не входит в первый.

Обратите внимание, в последний интервал входят обе границы.

4. Далее необходимо определить частоты попадания в интервал, т.е. сколько наблюдений из исходной выборки попадает в каждый интервал.

В Excel это можно сделать двумя способами: через «Анализ данных» и через формулы.

Способ 1.

Убедитесь, что на вкладке «Данные» есть кнопка «Анализ данных» (как ее включить см. в л.р.1).

Нажмите «Анализ данных» – «Гистограмма» – «ОК».

В поле «Входной интервал» укажите все значения X.

В поле «Интервал карманов» – верхние границы интервалов, кроме последней.

В «Параметрах вывода» выберите «Выходной интервал» и укажите любую ячейку под таблицей.

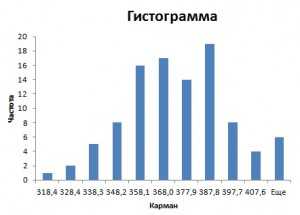
В результате получим таблицу вида:

Как видите, в качестве «карманов» указаны границы интервалов. Карман «Еще» соответствует последнему интервалу и считает все значения, не вошедшие в остальные интервалы.

Способ 2.

Способ более трудоемкий, но позволяет автоматически пересчитывать гистограмму при добавлении новых значений.

Значения по способу 2 мы внесем в следующий столбец нашей таблицы, обозначив его n_i.

Воспользуемся формулой СЧЁТЕСЛИМН(диапазон1; условие1; диапазон2; условие2; …) Она похожа на функцию СЧЁТ, но считает не все значения подряд, а только те, которые удовлетворяют заданным условиям. В нашем случае условия – число должно входить в интервал, т.е. быть и . Для записи первого условия (дял первого интервала) потербуется такая конструкция: «>=»&D12 «>=» — знак & — чтобы Excel понял, что дальше пойдет ячейка D12 — адрес ячейки со значением a1. Аналогично для условия : «&E12 Но! В последнем интервале в условии будет » Диапазон1 и диапазон 2 — что считать, т.е. значения X. Не забудьте зафиксировать диапазон, чтобы «растянуть» формулу. Таким образом, для первого интервала получим формулу: =СЧЁТЕСЛИМН($A$2:$A$86;»>=»&D12;$A$2:$A$86;»

Проверьте себя – сумма n_i должна быть равна n. Если сумма получилась на 1 меньше, проверьте последний интервал, стоит ли там »

Результат для обоих способов должен совпадать.

5. Построим график гистограммы. Для этого потребуются некоторые дополнительные расчеты, т.к. частоты – это еще не гистограмма. Для нее должно выполняться правило нормировки – сумма площадей всех столбцов гистограммы должна быть равна 1. Исходя из этого правила, высота столбца гистограммы вычисляется по формуле:

Добавим соответствующие расчеты.

Проверьте себя! Сумма h_i умноженная на w должна быть равна 1.

Построим график гистограммы. Выделите значения h_i вместе с заголовком и на вкладке «Вставка» выберите «Диаграмма» – «Гистограмма».

Удалите заголовок. Чтобы под столбцами отображались не номера интервалов, а их границы, нужно кликнуть по гистограмме правой кнопкой – «Выбрать данные…», нажать кнопку «Изменить» справа, в разделе «Подписи горизонтальной оси» и выделить значения a_i и b_i (без заголовков).

В результате получим график вида:

6. Кумулята (накопленная гистограмма) – это аналог закона распределения. В отличие от обычной гистограммы, которая учитывает только значения, попадающие в интервал от a_i до b_i, кумулята считает все значения меньше b_i т.е. суммарное (накопленное, кумулятивное) число попаданий во все интервалы с первого по текущий.

Для кумуляты также отдельно рассчитываются частоты (k_i) и высота столбцов (H_i).

Частоты можно вычислить следующим образом.

Частота первого интервала одинакова для гистограммы и кумуляты:

Остальные частоты рассчитываются как предыдущая частота кумуляты плюс текущая частота гистограммы:

Например, для 2 и 3 столбца получится:

и т.д.

Добавим в таблицу столбец k_i:

Обратите внимание, в последнем интервале должна получиться мощность выборки n.

Теперь можно вычислить высоты столбцов кумуляты:

Для кумуляты правило нормировки не действует, поэтому частоты делятся просто на n. В последней строке должна получиться 1.

По значениям кумуляты можно сказать, например, что только в 2,35% случаев данный вид преступлений совершают лица с доходом ниже 23,02 тыс. у.е. А почти в половине случаев (49,4%) доход преступника составляет до 51,15тыс. у.е. (много это или мало, зависит от курса у.е.).

График кумуляты строится аналогично обычной гистограмме. Можно скопировать уже созданную диаграмму и изменить исходные данные.

7. Сравним полученную в п.5 гистограмму с нормальным законом распределения, который очень часто встречается на практике.

Добавим в таблицу еще один столбец для расчета плотности нормального распределения.

Воспользуемся формулой НОРМРАСП(x;m;S;тип) x — для какого значения рассчитываем (середин интервалов) m, S — среднее и стандартное отклонение тип = 0, показывает, что нужно рассчитать именно плотность, а не интегральный закон (кумуляту)

Добавим его на график с гистограммой. Кликните по ней правой кнопкой – «Выбрать данные», нажмите «Добавить» и укажите столбец с f_норм.

В результате диаграмма примет вид:

Но плотность распределения принято изображать не столбцами, а гладкой линией. Для этого выделите новые столбцы (красные), кликните по любом из них правой кнопкой – «Изменить тип диаграммы для ряда». Выберите тип — «График с маркерами», нажмите «ОК». Столбцы превратятся в линию. Еще раз кликните по ней правой кнопкой – «Формат ряда данных» – «Тип линии», поставить галочку «сглаженная линия».

В результате получим:

Вывод: хотя отдельные столбцы достаточно близки к нормальному закону, в других отличия слишком велики. В целом, гистограмма распределения не соответствует нормальному закону: она не симметрична (справа столбцы высокие, слева низкие, мода не в цнтре распределения). Имеются «провалы» в 3 и 5 интервалах, а 2 и 7 столбцы, наоборот, значительно выше нормальной плотности распределения.

Примечание

Более точно на этот вопрос позволяют ответить специальные критерии, например, критерий Пирсона, Колмогорова. Их расчет выходит за рамки данной лабораторной, но они чаще всего строятся на основе гистограммы.

8. Сравним гистограмму с еще одним распространенным законом распределения – равномерным. У равномерного закона отсутствует мода, нет более или менее вероятных интервалов – все допустимые значения равновероятны.

Значения плотности равномерного распределения во всех точках одинаковы и рассчитываются по формуле:

Также добавим равномерный закон на график гистограммы.

Вывод: Гистограмма распределения далека от равномерного закона. Заметно, что высоты столбцов сильно отличаются друг от друга. В правой части гистограммы столбцы выше, т.е. более высокий доход вероятнее, чем низкий.

9. Напишите вывод по работе (на листе под расчетами). Ответьте на вопросы, приведенные в конце задания.

Пример

Среднее значение дохода лиц, совершивших данный тип преступления – 49,9тыс.у.е. Наиболее вероятен доход приблизительно от 40 до 60 тыс. у.е. Маловероятно совершение данного типа преступления для лиц с доходом более 70 и 20 тыс. у.е.

Закон распределения нельзя считать ни нормальным, ни равномерным. Он асимметричный, смещен вправо, с модой в диапазоне от 51,15 до 56,78.

Для лиц с доходом менее 10 тыс. у.е. вероятность совершения данного преступления близка к 0.

Примечание

На практике на этом останавливается не следует — необходимо сравнить картину со средним доходом в целом по региону. Возможно, он такой же, как и для лиц. совершивших преступления, тогда сам факт совершения преступления с доходом никак не связан.

gigabaza.ru

Построение гистограмм распределения в Excel

Очень давно не писал блог. Расслабился совсем. Ну ничего, исправляюсь.

Продолжаю новую рубрику блога, посвященную анализу данных с помощью всем известного Microsoft Excel.

В современном мире к статистике проявляется большой интерес, поскольку это отличный инструмент для анализа и принятия решений, а также это отличное средство для поиска причин нарушений процесса и их устранения. Статистический анализ применим во многих сферах, где существуют большие массивы данных: естественно, в первую очередь я скажу, что металлургии, а также в экономике, биологии, политике, социологии  и… много где еще. Статья эта будет, как несложно догадаться по ее названию, про использование некоторых средств статистического анализа, а именно — гистограммам.
Ну, поехали.

Статистический анализ в Excel можно осуществлять двумя способами:
• С помощью функций
• С помощью средств надстройки «Пакет анализа». Ее, как правило, еще необходимо установить.

Чтобы установить пакет анализа в Excel, выберите вкладку «Файл» (а в Excel 2007 это круглая цветная кнопка слева сверху), далее — «Параметры», затем выберите раздел «Надстройки». Нажмите «Перейти» и поставьте галочку напротив «Пакет анализа».

А теперь — к построению гистограмм распределения по частоте и их анализу.

Речь пойдет именно о частотных гистограммах, где каждый столбец соответствует частоте появления* значения в пределах границ интервалов. Например, мы хотим посмотреть, как у нас выглядит распределение значения предела текучести стали S355J2 в прокате толщиной 20 мм за несколько месяцев. В общем, хотим посмотреть, похоже ли наше распределение на нормальное (а оно должно быть таким).

*Примечание: для металловедческих целей типа оценки размера зерна или оценки объемной доли частиц этот вид гистограмм не пойдет, т.к. там высота столбика соответствует не частоте появления частиц определенного размера, а доле объема (а в плоскости шлифа — площади), которую эти частицы занимают.

График нормального распределения выглядит следующим образом:

График функции Гаусса

Мы знаем, что реально такой график может быть получен только при бесконечно большом количестве измерений. Реально же для конечного числа измерений строят гистограмму, которая внешне похожа на график нормального распределения и при увеличении количества измерений приближается к графику нормального распределения (распределения Гаусса).

Построение гистограмм с помощью программ типа Excel является очень быстрым способом проверки стабильности работы оборудования и добросовестности коллектива: если получим «кривую» гистограмму, значит, либо прибор не исправен или мы данные неверно собрали, либо кто-то где-то преднамеренно мухлюет или же просто неверно использует оборудование.

data-ad-client=»ca-pub-9341405937949877″
data-ad-slot=»7116308946″>

А теперь — построение гистограмм!

Способ 1-ый. Халявный.

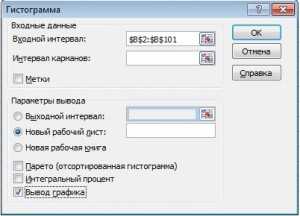
1. Идем во вкладку «Анализ данных» и выбираем «Гистограмма».

 




2. Выбираем входной интервал.
3. Здесь же предлагается задать интервал карманов, т.е. те диапазоны, в пределах которых будут лежать наши значения. Чем больше значений в интервале — тем выше столбик гистограммы. Если мы оставим поле «Интервалы карманов» пустым, то программа вычислит границы интервалов за нас.
4. Если хотим сразу же вывести график,то ставим галочку напротив «Вывод графика».



5. Нажимаем «ОК».
6. Вот, вроде бы, и все: гистограмма готова. Теперь нужно сделать так, чтобы по вертикальной оси отображалась не абсолютная частота, а относительная.



7. Под появившейся таблицей со столбцами «Карман» и «Частота» под столбцом «Частота» введем формулу «=СУММ» и сложим все абсолютные частоты.
8. К появившейся таблице со столбцами «Карман» и «Частота» добавим еще один столбец и назовем его «Относительная частота».
9. Во всех ячейках нового столбца введем формулу, которая будет рассчитывать относительную частоту: 100 умножить на абсолютную частоту (ячейка из столбца «частота») и разделить на сумму, которую мы вычислил в  п. 7.

 

Способ 2-ой. Трудный, но интересный.

Будет полезен тому, кто по каким-либо причинам не смог установить Пакет анализа.

1. Перво-наперво нужно задать интервалы тех самых карманов, которые мы не стали вычислять в способе, описанном выше.
2. Интервал карманов вычисляют так: разность максимального значения и минимального значений массива, деленная на количество интервалов: (Xmax-Xmin)/n.
   Для оценки оптимального для нашего массива данных количества интервалов можно воспользоваться формулой Стерджесса: n~1+3,322lgN, где N — количество всех значений величины. Например для N=100, n=7,6. Естественно, округляем до 8.
3. Для нахождения максимального и минимального значений воспользуемся соответствующими функциями: =МАКС(наш диапазон значений) и =МИН(наш диапазон значений).
   
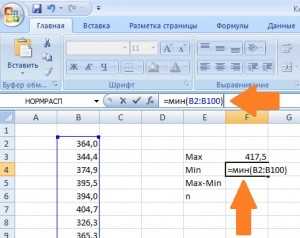
4. Найдем разность этих значений и разделим его на количество интервалов, которое нам захочется. Пусть будет 10. Так мы вычислили ширину нашего «кармана».
5. Теперь в каждой ячейке шаг за шагом прибавляем полученное значение ширины кармана: сначала к минимальному значению нашего массива (п. 3), затем в следующей ячейке ниже — к полученной сумме и т.д. Так постепенно доходим до максимального значения. Вот мы и построили интервалы карманов в виде столбца значений. Интервалом считается следующий диапазон : (i-1; i] или i<значения<=i (нестрогая верхняя граница интервала — это значение в ячейке, нижняя строгая граница — значение в предыдущей ячейке).
6. Выделяем столбец рядом с нашими карманами, нажимаем «F2» и вводим функцию: =ЧАСТОТА(массив данных; диапазон карманов) и нажимаем Ctr+Shift+Ener.




7. В выделенном нами столбце напротив границ интервалов (а из п. 5 мы знаем, что это нестрогие верхние границы) появилось количество значений исходного массива, которые попадают в интервал.
8. Далее, как и в предыдущем способе, нужно вычислить сумму частот (п.7.), создать столбец «относительная частота» и вычислить относительные частоты (разделить значения из столбца с абсолютными частотами на ихсумму и умножить на 100).
9. Теперь с помощью стандартного инструмента для построения гистограмм («вставка/гистограмма» и т.д.) можно построить гистограмму распределения.

На этом все. Ура!

Гистограмму-то мы построили, а что с ней делать дальше? В следующей статье расскажу о том, какую информацию можно извлечь из гистограмм.  Так что не пропустите! А чтобы не пропустить, можно подписаться на обновления блога.

Успехов!

 

>>Скачать бесплатно видеокурc по Excel

Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.

Поделиться ссылкой:

metallovedeniye.ru

взгляд на распределение данных, страница 4

Сравните гистограмму значений данных (рис. 3.2.2) и столбиковую диаграм­му, приведенную на рис. 3.2.3. Обратите внимание, что столбики на гистограмме показывают количество отраслей в каждом из диапазонов заработной платы, а столбики на столбиковой диаграмме — фактическое значение заработной платы в конкретной отрасли. Полезны оба графических изображения. Столбиковую диаграмму лучше ис­пользовать, когда желательно идентифицировать все значения из набора дан­ных, при условии, что набор данных достаточно небольшой. Однако для получе­ния общего представления о наборе данных больше подходит гистограмма, осо­бенно при больших наборах данных с множеством чисел

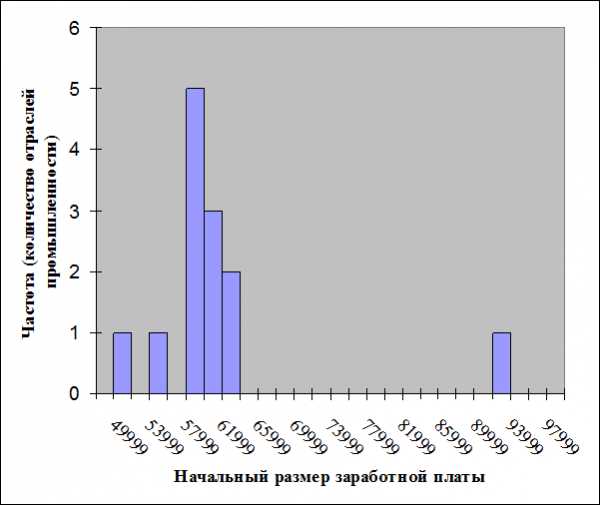
Рис. 3.2.2. Гистограмма значений начального размера зара­ботной платы.

Обратите внимание, что каждый столбик может представлять больше одной отрасли (см. число на вертикальной оси слева). Столбики по­казывают, какие диапазоны заработной платы чаще, а какие реже встречаются в этом наборе данных

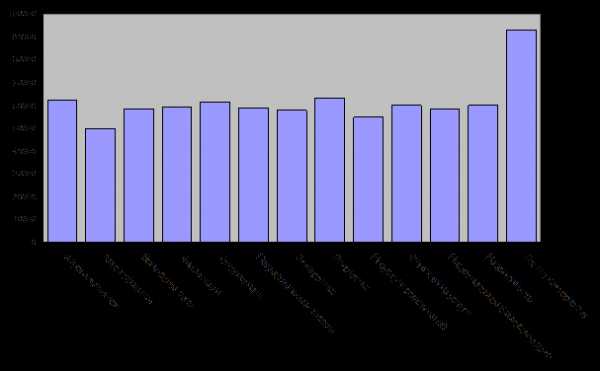
Рис. 3.2.3. Столбиковая диаграмма значений начального размера заработной платы.

Обратите внимание, что каждый стол­бик представляет одну отрасль промышленности

3.3. Нормальное распределение

Нормальное распределение представляет собой теоретическую гладкую гисто­грамму в форме колокола без случайных отклонений. Такая кривая представля­ет идеальный набор данных, в котором большинство чисел сконцентрировано в средней части диапазона значений, а оставшиеся значения с затуханием симмет­рично расположены по обе стороны от вершины колокола. Такая степень глад­кости не присуща реальным данным. На рисункеприведена кривая нормаль­ного распределения.

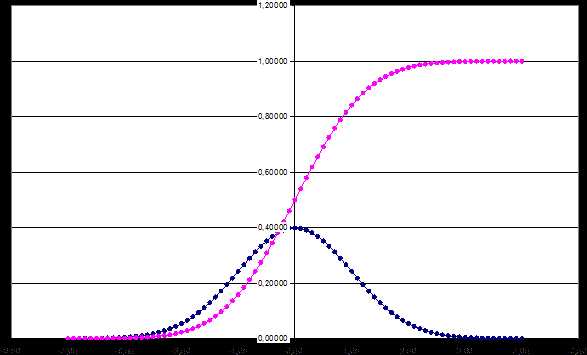
 Идеальная (теоретическая) кривая нормального распределения. Реальные нормально распределенные на­боры данных имеют некоторые случайные отклонения от этой идеально гладкой кривой

Для любознательных приведем формулу этой колоколоподобной кривой:        

где

m— центр, определяет горизонтальное положение наивысшей точки, а s определяет ширину колокола (изменчивость или масштаб).

Фактически существует много различных кривых нормального распределе­ния, форма которых напоминает симметричный колокол. Они отличаются рас­положением центра и масштабом (шириной колокола). Чтобы построить кон­кретную кривую нормального распределения, следует взять базовую кривую в форме колокола, переместить ее по горизонтали в точку, где предполагается разместить центр, а затем растянуть (или сжать).

Почему нормальное распределение играет такую важную роль в статистике? Обычно предполагают, что распределение данных приблизительно соответствует нормальному. В частности, многие стандартные методы для вычисления доверительных интервалов и про­верки статистических гипотез (о которых вы узнаете позже) требуют, чтобы данные были рас­пределены нормально (по крайней мере, приблизительно). Специалисты-статистики знают свойства нормаль­ного распределения и используют их всякий раз, когда гистограмма похожа на кривую нормального распределения.

В каком случае можно сказать, что набор данных подчиняется нормальному распределению? Хороший способ заключается в том, чтобы внимательно изучить гистограмму.

Действительно ли в реальной жизни все наборы данных подчиняются нор­мальному распределению? Конечно, нет. Используя гистограмму, важно опреде­лить, являются ли данные нормально распределенными. Это особенно важно, ес­ли дальнейший анализ предполагает использование стандартных статистических процедур, которые требуют нормального распределения данных.

3.4. Несимметричные распределения и преобразование данных

Несимметричное (скошенное) распределение не является ни симметричным, ни нормальным, поскольку значения данных на одной стороне кривой затухают быстрее, чем на другой. В бизнесе часто можно встретить асимметрию в наборах данных, которые отражают величины, выраженные положительными числами (например, объемы продаж или размеры активов). Это связано с тем, что такие данные не могут принимать отрицательные значения (наличие границы с одной стороны) и значения не ограничены сверху. В результате на гистограмме много значений данных сконцентрировано около нуля, и количество значений становится все меньше и меньше при движении по горизонтальной оси гистограммы вправо.

Пример. Активы коммерческих банков

vunivere.ru

Гистограмма распределения

Интер- рвалы
mi
pi = =

6. Определяют частоту появления p_i величины Х в данном разряде

p_i = 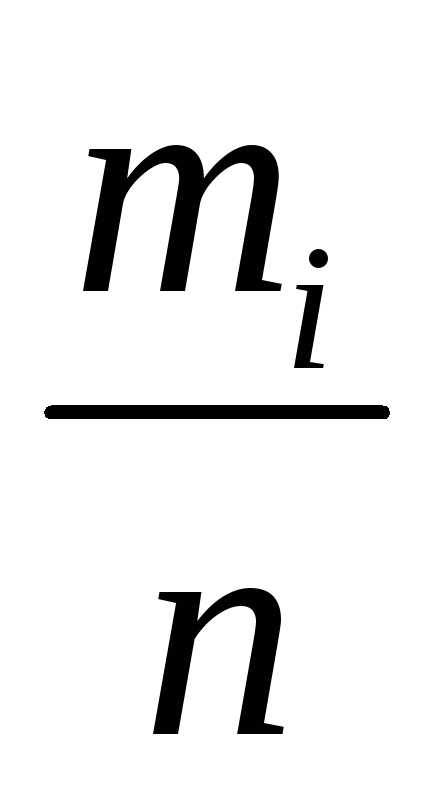, (5.9)

где n — общее число всех опытных данных.

7. В системе координат p_i = f(X) на ширине разряда h откладывают величину p_i как высоту и строят прямоугольник.

Очевидно, что площадь элементарного прямо-угольника

s_i = hy_i, = p_i, (5.10)

а площадь всей гистограммы

S = 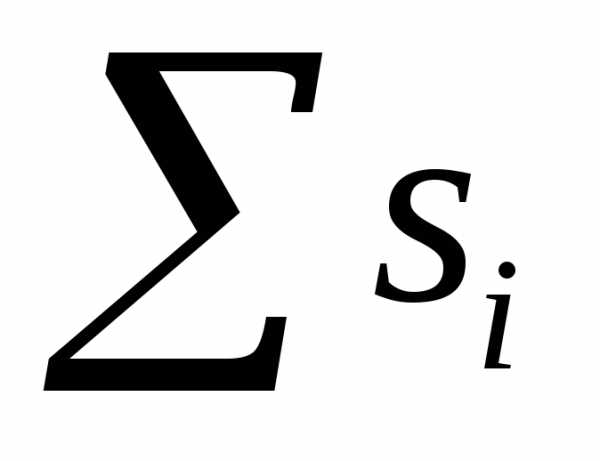= = 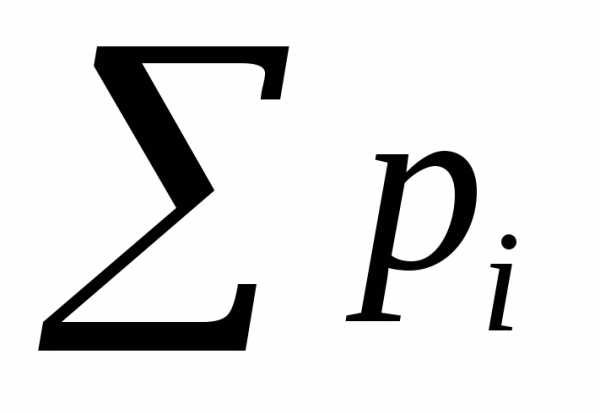1. (5.11)

Таким образом, гистограмма представляет собой совокупность прямоугольников (рис. 5.1).

Полигон (рис. 5.1, кривая 2) строят как ломаную прямую, соединяющую интервалы середин интервалов.

В пределе гистограмма (полигон) стремится к нормальному закону распределения, плотность функции распределения которого описывается уравнением (5.12).

В качестве закона распределения случайных величин чаще всего используют нормальный закон распределения, он же закон Гаусса (K.F. Gauss – немецкий математик ХIХ века). Плотность нормального закона распределения

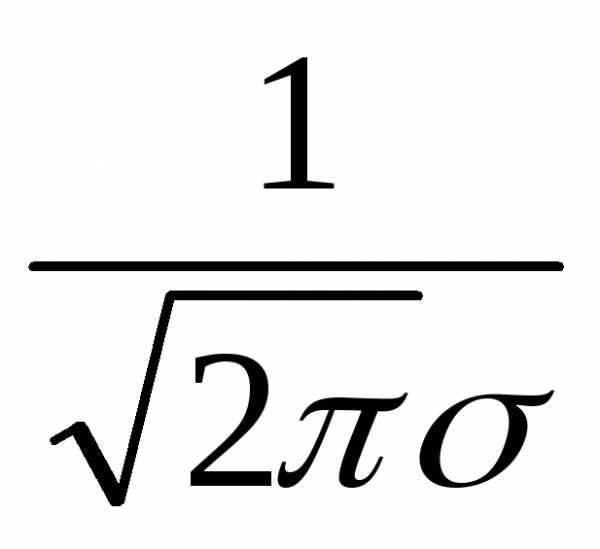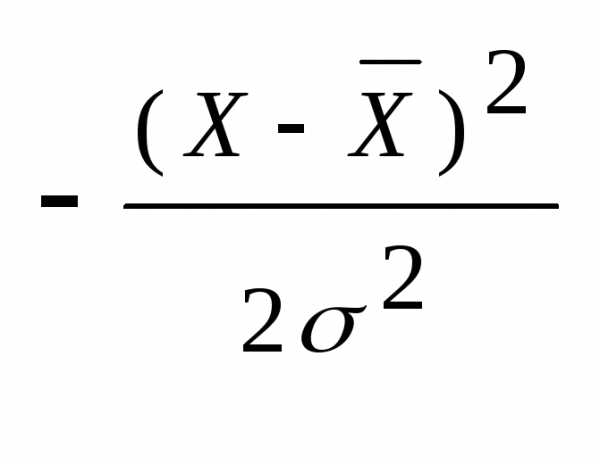f(Х) = e. (5.12)

Функция плотности распределения позволяет определить вероятность появления данного конкретного значения Х.

Данные, снятые для построения гистограммы и полигона, могут быть использованы для построения статистического ряда распределения (рис. 5. 2).

Статистический же ряд распределения стремится к функции распределения, которая описывается следую-щим уравнением:

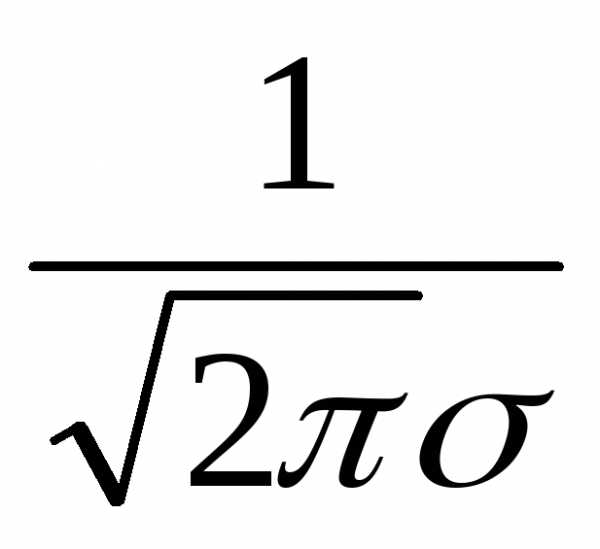
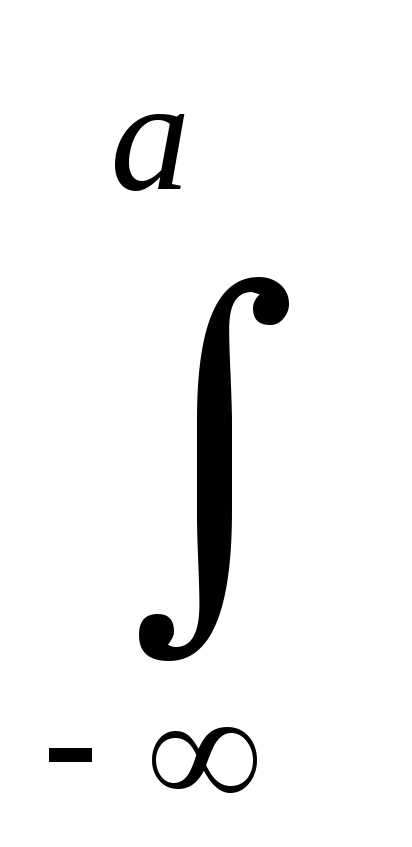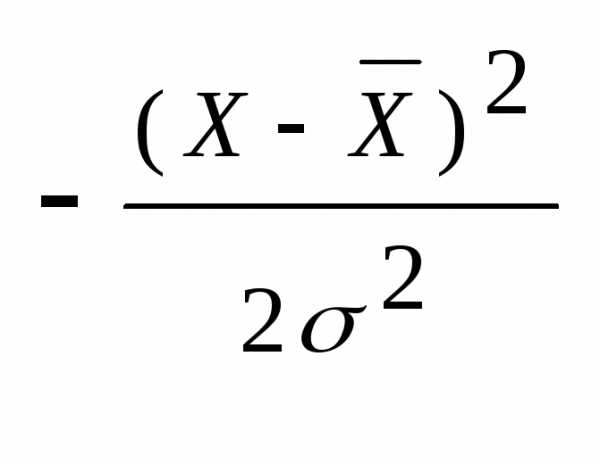F(X) = = edX. (5.13)

f(X) 2

1

Х

Рис. 5.1. Гистограмма (1) и полигон (2) распределения

величины Х

F(X)

1

Х

Рис. 5.2. Статистический ряд распределения

величины Х

Функция распределения позволяет определить вероятность появления значения Х в интервале от — до числаа.

Критерий (от греч.  — мерило) Пирсона (К.Pearson – английский математик, биолог и философ, работавший в конце ХIХ – начале ХХ века) – один из

важнейших непараметрических критериев. С его помощью проверяют гипотезу (от греч.  – основание, предположение) о согласии выборочного распределения с нормальным законом распределения. Применение критерия 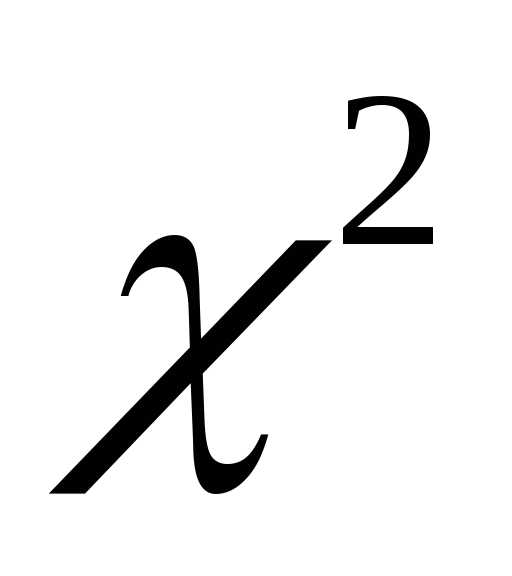допустимо лишь тогда, когдаnp_i  5.

Для проверки нормальности закона распределения результатов измерений заполняют табл. 5.2.

Таблица 5.2

Проверка по критерию 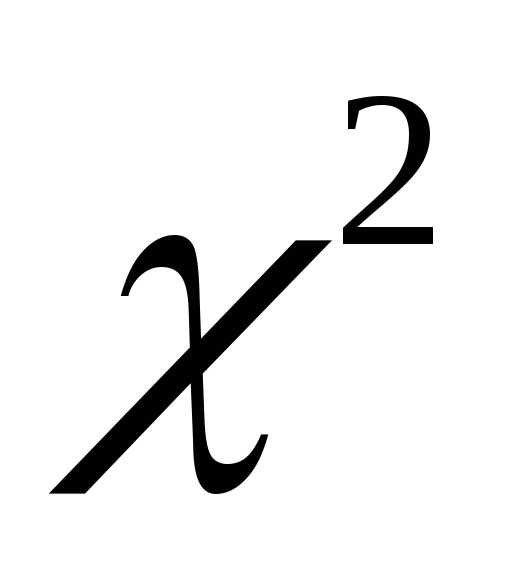Пирсона

Начало интер- вала	mi	ti	Ф(ti)	pi	mi-npi	(mi-npi)2 npi
… … …
Сумма		—	—		—

Данные первых двух столбцов надо взять из табл. 5.1. В третьем столбце записывают отношение

t_i = . (5.14)

Четвёртый столбец заполняют соответствующими значениями интеграла вероятностей Ф(t_i) из справочной литературы 6.

Интеграл (лат. integer – целый) вероятностей Ф(t) равен

Ф(t) = , (5.15)

где t = .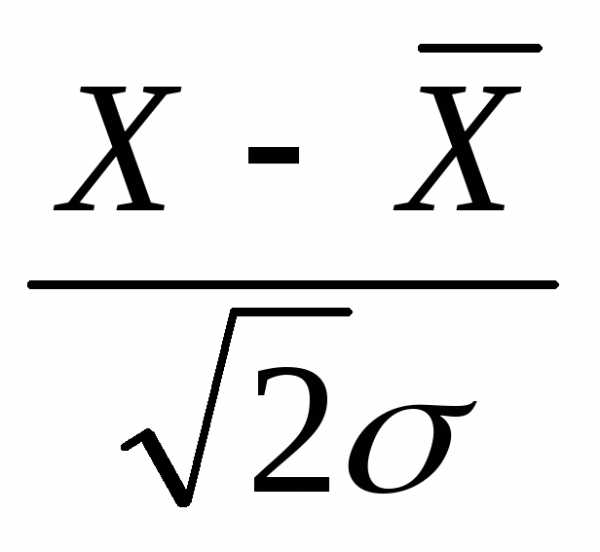

По значениям Ф(_i) в пятом столбце вычисляют вероятность p_i как разность соответствующих значений Ф(t)

p_i = Ф(t_i) — Ф(t_i-1). (5.16)

Напомним, что Ф() = — 0,5.

Последние столбцы таблицы в пояснении не нуждаются.

Сумма чисел последнего столбца даёт значение

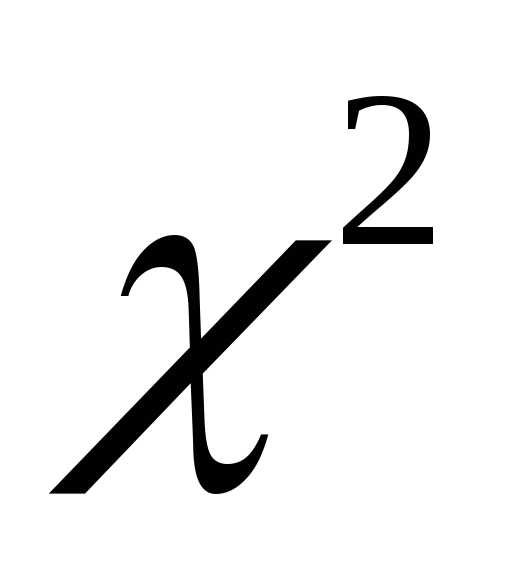= (5.17)

где n – число всех результатов измерений.

Если окажется больше критического значения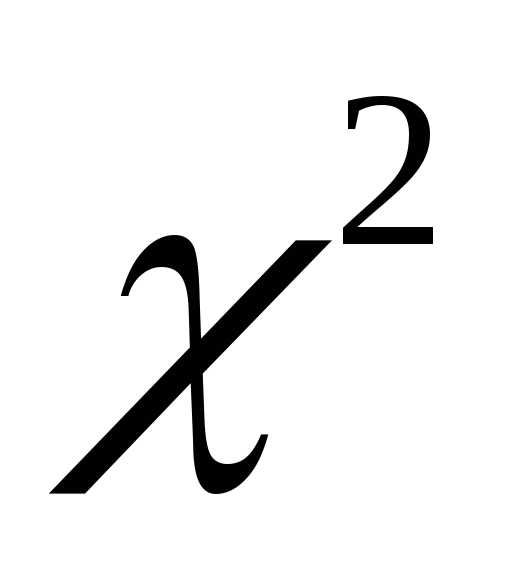_крит при некоторой доверительной вероятности Р и числе степеней свободы k = l — 3, где l – число всех интервалов, то с вероятностью Р можно считать, что распределение вероятностей результатов измерения в рассматриваемой серии измерений отличается от нормального. В противном случае для такого вывода нет достаточных оснований.

Указанное число степеней свободы k = l – 3 относится только к тому случаю, когда оба параметра нормального закона распределения определяют по результатам измерений, т.е. когда вместо точных значений Х и применяют их эмпирические оценки.

Если значение Х известно точно (например, при измерении эталона – в нашем случае концевой меры длины), то число степеней свободы равно k = l – 2.

studfiles.net