Аксонометрическая проекция окружности
ПОСТРОЕНИЕ АКСОНОМЕТРИЧЕСКИХ ПРОЕКЦИЙ ОКРУЖНОСТИ.
1. Построение изометрической проекции окружности, лежащей в одной из плоскостей проекции.
I, а. Дана окружность диаметра D, лежащая в плоскости П1 (фиг.278). Намечаем на ней несколько равномерно расположенных (но не менее восьми) точек, проекции которых на плоскости П1 обозначим А1,В1,С1,D1,Е1,F1,G1,H1. Определяем их координаты.
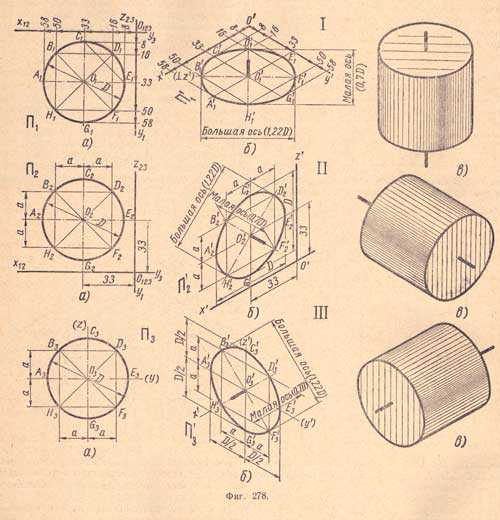
I, б. Проводим аксонометрические оси х’ и у’ и строим на плоскости Щ вторичные изометрические проекции всех указанных точек. Соединив их плавной замкнутой кривой, получим вторичную и вместе с тем изометрическую проекцию данной окружности — эллипс, у которого малая ось будет иметь направление не лежащей в данной плоскости изометрической оси г (т. е. вертикальной) и равняться 0,7 D, а большая ось будет перпендикулярна малой оси (т. е. иметь горизонтальное направление) и равняться 1,22 D.
II, а. Дана ортогональная проекция той же окружности, но лежащей в плоскости П2. Вместо того, чтобы определять координаты всех намеченных точек, можно определять только координаты центра О2 и размеры а и а от центровых линий до намеченных точек В2,D2,H2,F2.
II, б. Построение вторичной и вместе с тем изометрической проекции этой окружности аналогично указанному на (фиг.278, I, б). Малая ось полученного эллипса расположена по направлению не лежащей в д’анной плоскости аксонометрической оси у’, а большая ось перпендикулярна ей.
Длина осей эллипса такая же, как и на (фиг.278, I, б).
II, в. Показан пример применения изометрической проекции окружности, лежащей во фронтальной плоскости при изображении цилиндра.
III, а. Дана ортогональная проекция той же окружности, но лежащей в плоскости П3; центр окружности не координирован. Определяем размеры а и а от центровых линий до намеченных точек В3, D3, F3 и Н3.
III, б. Построение эллипса начинаем с проведения прямых, заменяющих аксонометрические оси z и у, затем через полученную в пересечении точку O3 проводим линию малой оси по направлению не лежащей в данной плоскости аксонометрической оси х и линию большой оси, перпендикулярную к малой оси; в остальном построение эллипса аналогично указанному на чертеже II, б. Малая ось эллипса расположена по направлению не лежащей в данной плоскости аксонометрической оси х’, а большая перпендикулярна ей.
III, в. Показан пример применения изометрической проекции окружности, лежащей в профильной плоскости, при изображении цилиндра. Обычно при выполнении аксонометрических проекций заменяют эллипс очень близким ему по очертанию и размерам овалом, построение которого гораздо проще.
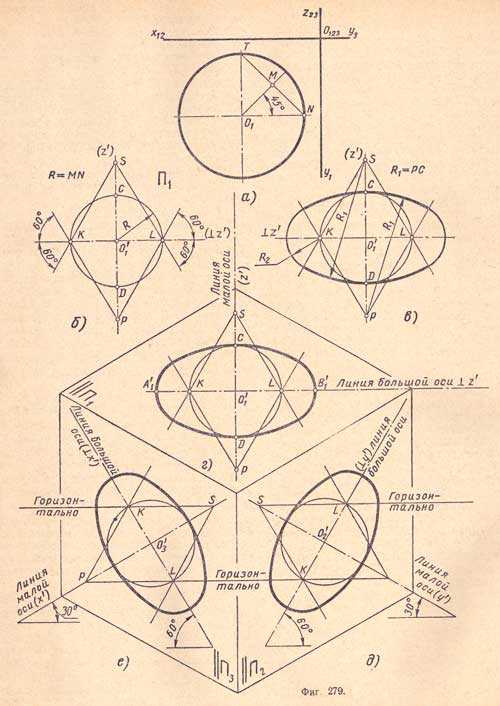
Через намеченную в любом месте точку O’1 проводим линии осей будущего овала (направление малой оси такое же, как и у не лежащей в данной плоскости аксонометрической оси z’ , а большой оси — перпендикулярное к малой оси).
Приняв за центр точку O’1, проводим окружность радиусом R = MN (т. е. равным половине хорды TN), получим точки С, D и K, L. Через точки К и L проводим прямые линии под углом 60°, получим точки Р и S (фиг.279,б).
Приняв за центры точки К и L, проводим замыкающие овал дуги радиусом R2, размер которого определяется предыдущим построением (фиг.279,г).
Построение овалов, заменяющих эллипсы при изображении изометрической проекции окружности, лежащей в плоскости проекций П2 или П3, аналогично указанному; причем большая ось овала будет наклонена на угол 60° в первом случае (П2) вправо, а во втором (П3) — влево (фиг.279, д и е).
3. Построение овалов, заменяющих эллипсы при изображении диметрических проекций окружности (фиг.280).
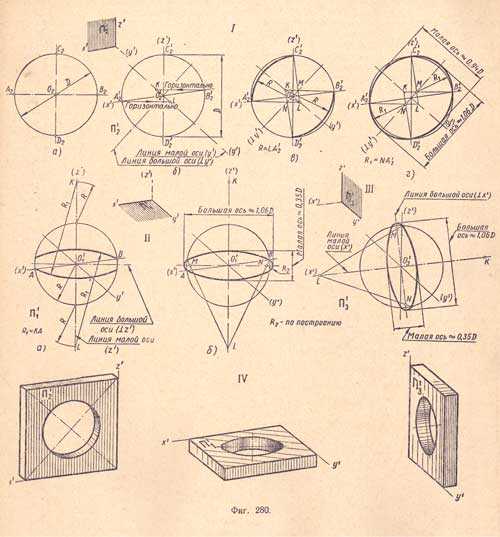
I, а. Дана окружность диаметра D, расположенная в плоскости П2 (или в любой фронтальной плоскости).
I, б. Через намеченную точку O’2, диметриче-скую проекцию точки О
Из центра O’2 проводим вспомогательную окружность диаметром D данной окружности; в пересечении получим точки А’2, В’2, С’2 и D’2 Из точек А’2 и В’2 проводим горизонтальные лучи до пересечения с линией малой оси, получим точки К и L.
I, в. Соединяем отрезками прямых точки К и D’2, а также точки L и С’2, получаем точки М и N. Приняв за центр точку L, радиусом R = LA’2, проводим дугу между точками А’2 и С’2 приняв за центр точку К, тем же радиусом проводим дугу между точками В’2и D’2
I, г. Приняв за центры точки М и N, проводим радиусом R1 = NA’2 замыкающие овал дуги.
Если данная окружность будет расположена в плоскости П 1 (или в любой горизонтальной плоскости), то построение упрощенного очертания ее диметрической проекции (овала) рекомендуется выполнять в такой последовательности:
II, а. Через намеченную точку О’1 проводим прямые линии параллельно диметрическим осям х’ и у’, а также линию малой оси овала по направлению диметрической оси z’ и перпендикулярно линию большой оси овала. Из центра О’1 проводим вспомогательную окружность радиусом R данной окружности, получаем точки А и В; на вертикальной центровой на расстоянии радиуса R выше и ниже проведенной окружности намечаем точки К и L; приняв эти точки за центры, проводим радиусом R1 = КA дуги внутри окружности;
II, б. Точку L соединяем отрезками прямых с концами верхней дуги, на линии большой оси получим точки М и N; приняв их за центры, проводим замыкающие овал дуги.
III. На данном чертеже показано построение овала приближенного очертания диметрическои проекции окружности, расположенной в профильной плоскости, которое выполняется аналогично предыдущему построению.
Построение аксонометрических проекций различных геометрических тел (полных, усеченных и пересекающихся) показано на последующих фигурах вместе с построением ортогональных проекций этих тел.
Призма…..
www.viktoriastar.ru
Изометрия окружности
Окружности проецируются на плоскость проекций в натуральную величину, когда они параллельны этой плоскости. А так как все плоскости наклонены к аксонометрической плоскости, то окружности, лежащие на них, будут проецироваться на эту плоскость в виде эллипсов. Во всех видах аксонометрий эллипсы заменяются овалами.
При изображении овалов надо, прежде всего, обратить внимание на построение большой и малой оси. Начинать надо с определения положения малой оси, а большая ось всегда ей перпендикулярна.
Существует правило: малая ось совпадает с перпендикуляром к этой плоскости, а большая ось ей перпендикулярна или направление малой оси совпадает с осью, не существующей в этой плоскости, а большая ей перпендикулярна (рис.10.7)
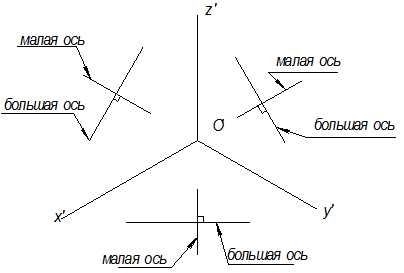
Рис.10.7
Большая ось эллипса перпендикулярна той координатной оси, которая отсутствует в плоскости окружности.
Большая ось эллипса равна 1,22 ´ d окр; малая ось эллипса равна 0,71 ´ d окр.
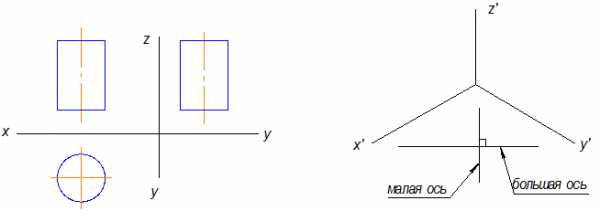
Рис.10.8
На рисунке 10.8 в плоскости окружности отсутствует ось Z, поэтому большая ось перпендикулярна оси
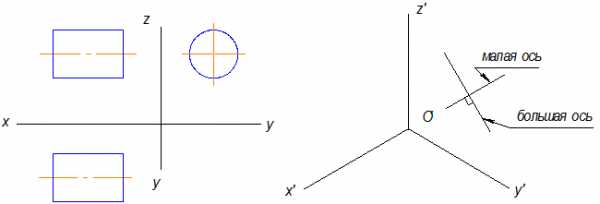
Рис.10.9
На рисунке 10.9 в плоскости окружности отсутствует ось Х, поэтому большая ось перпендикулярна оси Х‘.
А теперь рассмотрим, как вычерчивается овал в одной из плоскостей, например, в горизонтальной плоскости XY. Существует множество способов построения овала, познакомимся с одним из них.
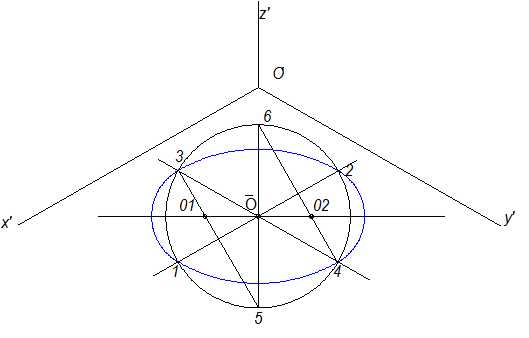
Рис.10.10
Последовательность построения овала следующая (рис.10.10):
1. Определяется положение малой и большой оси.
2.Через точку пересечения малой и большой оси проводим линии, параллельные осям X’ и Y’.
3.На этих линиях, а также на малой оси, из центра радиусом, равным радиусу заданной окружности, откладываем точки 1 и 2, 3 и 4, 5 и 6.
4. Соединяем точки 3 и 5, 4 и 6 и отмечаем точки пересечения их с большой осью эллипса (01 и 02). Из точки 5, радиусом 5-3, и из точки 6, радиусом 6-4, проводим дуги между точками 3 и 2 и точками 4 и 1.
5. Радиусом 01-3 проводим дугу, соединяющую точки 3 и 1 и радиусом 02-4— точки 2 и 4. Аналогично строятся овалы в других плоскостях (рис.10.11).
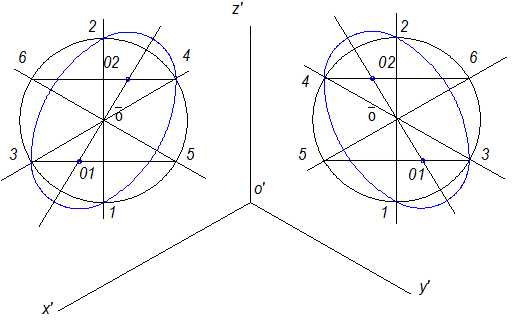
Рис.10. 11
Далее рассмотрим примеры построения аксонометрии конуса вращения и цилиндра.
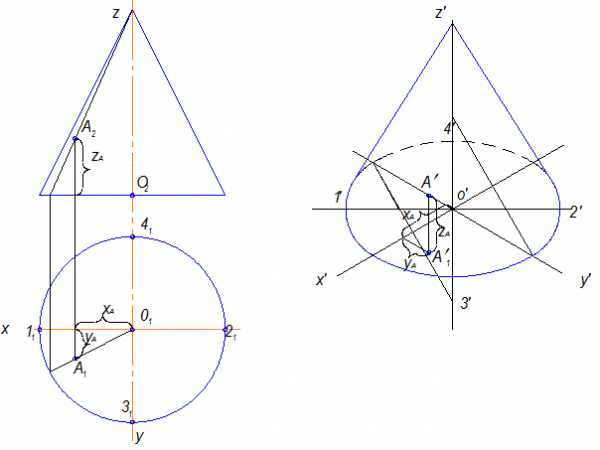
Рис.10.12
Чтобы построить точку А, принадлежащую поверхности надо построить ее три координаты XA, YA и ZA. Точка на поверхности цилиндра и других поверхностях строится аналогично (рис.10.13).
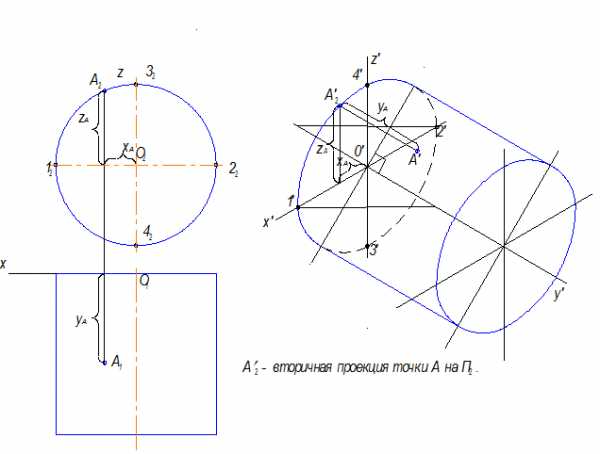
Рис.10.13
Большая ось овала перпендикулярна оси Y‘.
При построении аксонометрии детали, ограниченной несколькими поверхностями, следует придерживаться следующей последовательности:
Вариант 1.
1. Деталь мысленно разбивается на элементарные геометрические фигуры.
2. Вычерчивается аксонометрия каждой поверхности, линии построения сохраняются.
3. Строится вырез 1/4 детали, чтобы показать внутреннюю конфигурацию детали.
4. Наносится штриховка по ГОСТ 2.317-70.
Рассмотрим пример построения аксонометрии детали, внешний контур которой состоит из нескольких призм, а внутри детали цилиндрические отверстия разных диаметров.
Вариант 2. (Рис. 10.5)
1. Строится вторичная проекция детали на плоскости проекций П .
2. Откладываются высоты всех точек.
3. Строится вырез 1/4 части детали.
4. Наносится штриховка.
Для данной детали более удобным для построения будет вариант 1.
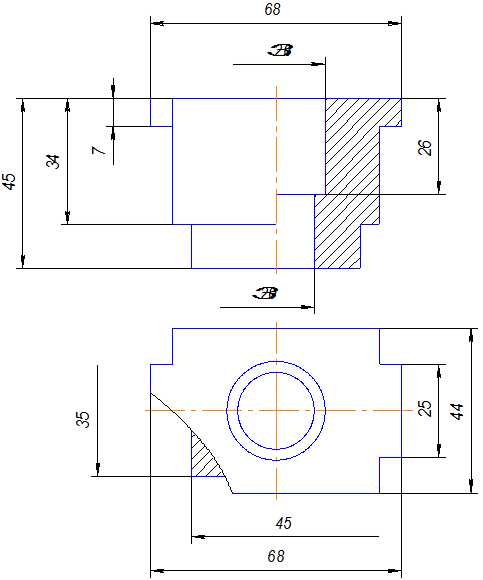
Рис.10.14
Похожие статьи:
poznayka.org
Построение окружностей в стандартных аксонометрических проекциях.
Изометрическими проекциями окружностей, расположенных в плоскостях проекций или в плоскостях, параллельных им, являются эллипсы с одинаковыми соотношениями осей (рис.47).
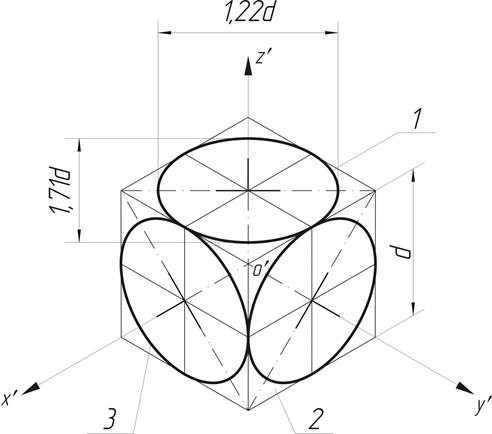
Рис.47. Изометрические проекции окружности
Большие оси эллипсов равны 1,22d, а малые — 0,71 d , где d — диаметр изображаемой окружности.
Для упрощения построений допускается заменять эллипсы овалами, очерченными дугами окружностей.
На рис.48 приведена последовательность построения четырехцентровых овалов, приближенно заменяющих проекции окружности, расположенной в плоскости проекций или ей параллельной. Данный способ является наиболее простым в построении.
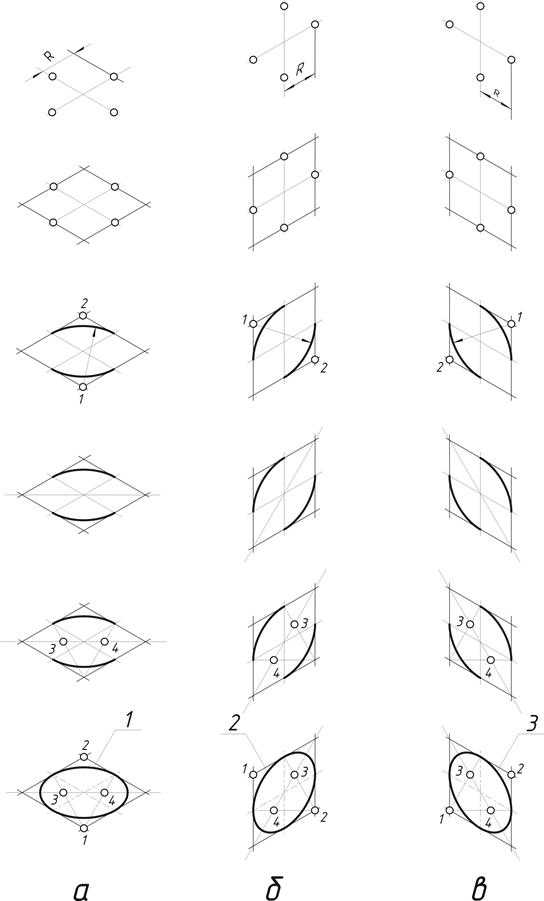
а б в
Рис.48. Построение овалов: а — в координатной плоскости х1 01 у1 , б — в координатной плоскости у1 01 z1; в — в координатной плоскости у1 01 z1
Разрезы в аксонометрии, как правило, выполняют плоскостями,
отличными о тех, которыми производят разрезы на комплексном чертеже (рис.49,а, 49,б). Плоскости разрезов аксонометрии должны либо совпадать с координатными плоскостями, либо располагаться параллельно им.
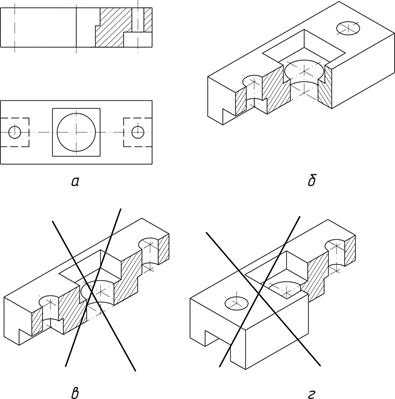
Рис.49. Разрезы в аксонометрии
Чаще всего плоскости разрезов в аксонометрии совпадают с главными плоскостями симметрии предмета (рис 49,б).
Нельзя применять в аксонометрии только одну секущую плоскость, изображая половину предмета, так как при этом исчезает один из трех габаритных размеров и изображений теряет наглядность (рис.498,в))
Разрезы в аксонометрии должны всегда просматриваться и быть обращенными к наблюдателю (рис.49,г).
Последовательность построения аксонометрической проекции предмета
Похожие статьи:
poznayka.org
Как начертить эллипс в аксонометрии
Окружность в аксонометрии представляет собой эллипс. Возвести его дозволено с подмогой параллельного проецирования окружности заданного радиуса на плоскость.
Вам понадобится
- — бумага;
- — линейка;
- — карандаш;
- — ластик;
- — треугольник с прямым углом;
- — циркуль;
- — транспортир.
Инструкция
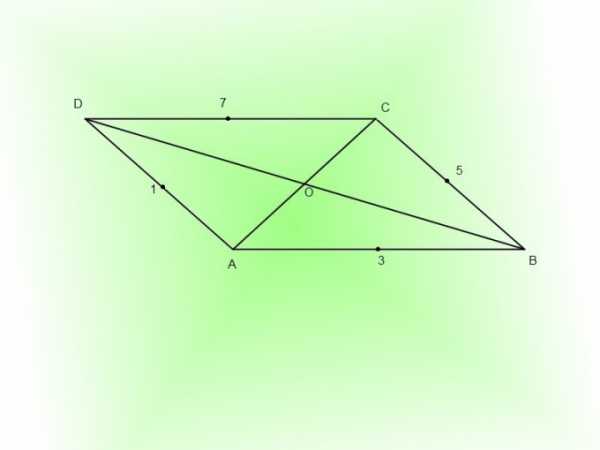
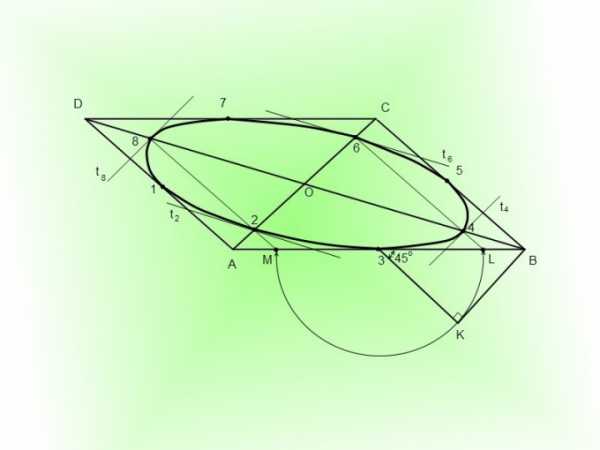
1. Дабы начертить эллипс в аксонометрии, вначале нужно возвести параллелограмм ABCD. В получившемся параллелограмме нужно провести диагонали. Для этого объедините точки A и C, B и D. Получите диагонали AC и BD. Точку их пересечения обозначьте буквой О.
2. Подметьте середины сторон параллелограмма точками 1, 3, 5, 7. Вы можете примитивно поделить длины сторон напополам и подметить середины. Либо вы можете приложить линейку к стороне параллелограмма AB и вести ее параллельно AB до пересечения с точкой О. Остановите линейку и подметьте на боковых сторонах параллелограмма AD и BC точки 1 и 5. После этого повторите ту же процедуру и подметьте середины верхней и нижней стороны параллелограмма точками 3 и 7.
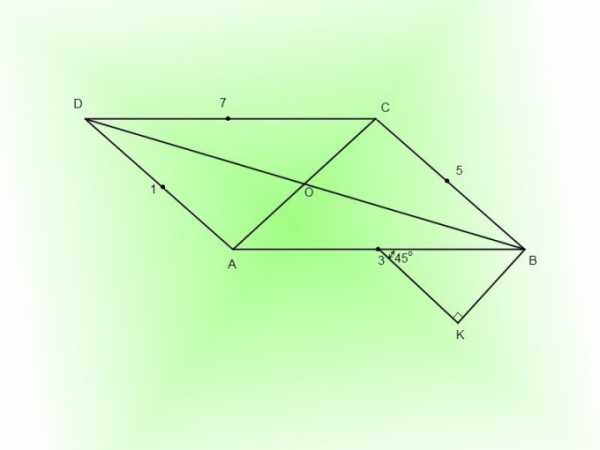
3. На отрезке 3B постройте вниз равнобедренный прямоугольный треугольник 3KB, где 3B является гипотенузой треугольника. С поддержкой транспортира отмерьте вниз и вправо угол в 45° около точки 3. После этого подметьте 45° вниз и налево от точки B. Проведите прямые по подмеченным углам. Точка их пересечения — вершина прямого угла K.
4. Возьмите циркуль и проведите полуокружность из точки 3 радиусом 3K до пересечения со стороной параллелограмма AB. Точки пересечения обозначьте L и M. Эти точки делят отрезок 3A и равный ему 3B в отношении 3:7. Если у вас нет циркуля, испробуйте поделить половины стороны AB в соотношении 3:7 с подмогой линейки, но это сокращает точность построения.
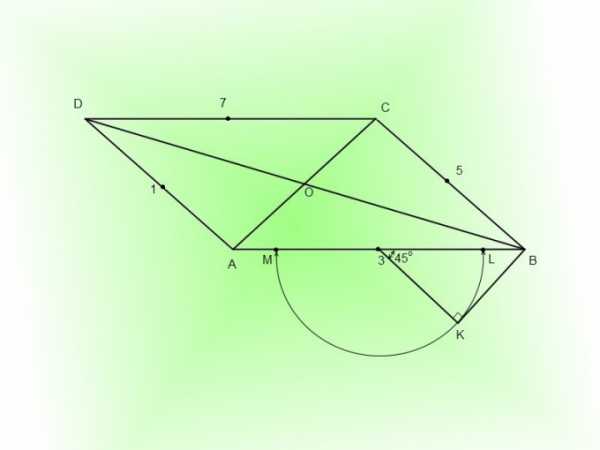
5. Проведите через точки L и M прямые параллельно боковым сторонам AD и BC до пересечения с диагоналями параллелограмма. Подметьте точки 2, 4, 6, 8.
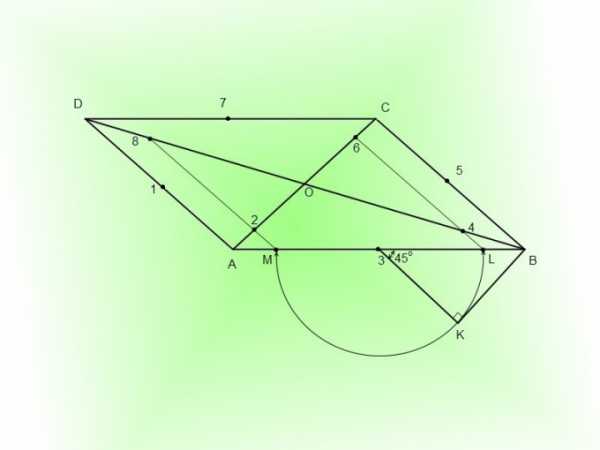
6. Постройте в точках 2 и 6 касательные t? и t? параллельные диагонали BD и в точках 4 и 8 касательные t? и t? параллельные диагонали AC. Они будут являться касательными к эллипсу в точках 2, 4, 6 и 8.

7. У вас получилось возвести 8 точек эллипса 1, 2, 3, 4, 5, 6, 7 и 8 и столько же касательных к эллипсу AD, t?, AB, t?, BC, t?, CD и t?. Сейчас вы можете с довольной точностью начертить в параллелограмме эллипс. Вначале начертите слабый силуэт, после этого обведите эллипс толстой линией.
Обратите внимание!
Если вам не необходимы вспомогательные линии, сотрите ластиком все лишнее позже того, как вы начертите эллипс.
Полезный совет
Если под рукой нет транспортира, вы можете возвести треугольник 3KB с подмогой треугольной линейки с прямым углом. Направьте прямой угол треугольника вниз между точками 3 и B. Спускайте линейку до тех пор, пока боковые стороны треугольника не пересекутся с точками 3 и B. Очертите треугольник.
jprosto.ru
Как построить окружность в аксонометрии
Аксонометрические проекции используют, дабы передать на чертеже представление о форме предмета с различных сторон. При этом вид предмета с различных сторон проецируется на плоскости куба. Наклон плоскостей в аксонометрической проекции придает окружности форму эллипса. Из-за сложности построения эллипсов на практике их заменяют овалами.
Вам понадобится
- Лист бумаги, карандаш, циркуль, транспортир, линейка либо угольник.
Инструкция
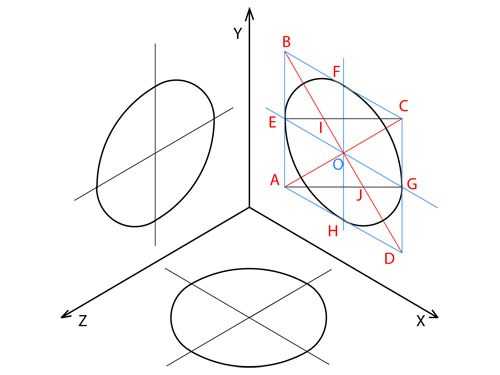
1. Возвести окружность в аксонометрии помогает квадрат, в тот, что вписана заданная окружность . На плоскости под наклоном квадрат принимает форму ромба. Следственно вначале постройте в надобной плоскости ромб. Его стороны обязаны быть равны диаметру окружности и параллельны соответствующим осям проекции. Центр ромба должен совпадать с центром окружности.
2. Ступенчато обозначьте углы построенного ромба точками A, B, C и D. При этом точка A должна располагаться в том углу ромба, тот, что особенно близок к точке пересечения осей на аксонометрической проекции.
3. Начертите диагонали получившегося ромба, объединив отрезками точки A и C, а также B и D. Диагональ AC образует малую ось овала, а диагональ BD – крупную.
4. Пересечение овалов образует центр ромба и окружности на плоскости. Обозначьте его буквой O.
5. Проведите через центр ромба O две линии, которые параллельны осям проекции и разделяют ромб на 4 части.
6. Ступенчато обозначьте точки, в которых линии параллельные осям проекции пересекают стороны ромба буквами E, F, G и H. Точка E должна следовать за точкой A в том же направлении, в котором ступенчато обозначались углы ромба.
7. Объедините точки A и G, а также C и E отрезками.
8. Обозначьте точки, в которых огромная ось ромба пересекает отрезки AG и EC буквами I и J. При этом точка I должна лежать на отрезке EC, а точка J на отрезке EC.
9. С поддержкой циркуля начертите дугу между точками E и F. Центр окружности для дуги размещен в точке I, а её радиус равен длине отрезка EI. Подобно начертите дугу между точками G и H.
10. Начертите две дуги, которые завершат построение овала на проекции. Первая дуга с центром окружности в точке A соединяет точки F и G. Радиус первой дуги равен длине отрезка AG. Вторая дуга с центром окружности, тот, что размещен в точке C, соединяет точки E и H. Ее радиус равен отрезку EC. Когда вы завершите чертить вторую дугу, вы получите построенную окружность на плоскости аксонометрической проекции.
Окружность еще древние греки считали самой идеальной и слаженной из всех геометрических фигур. В их ряду окружность является примитивной косой, а ее безупречность заключается в том, что все составляющие ее точки располагаются на идентичном расстоянии от ее центра, вокруг которого она «скользит сама по себе». Неудивительно, что методы построения окружности начали волновать математиков еще в древности.

Вам понадобится
- * циркуль;
- * бумага;
- * лист бумаги в клеточку;
- * карандаш;
- * веревка;
- * 2 колышка.
Инструкция
1. Самый примитивный и знаменитый с древности и по сей день — построение окружности при помощи особого инструмента — циркуля (от лат. «circulus» — круг, окружность). Для такого построения сперва необходимо подметить центр грядущей окружности — скажем, пересечением 2х штрихпунктирных линий под прямым углом, и выставить шаг циркуля, равный радиусу грядущей окружности. Дальше установите ножку циркуля в подмеченный центр и, поворачивая ножку с грифелем вокруг него, проведите окружность.
2. Без циркуля окружность возвести тоже допустимо. Для этого понадобится карандаш и лист бумаги в клеточку. Подметьте предисловие грядущей окружности — точку А и запомните легкой алгорифм: три – один, один – один, один – три. Для построения первой четверти окружности продвиньтесь из точки А на три клетки вправо и на одну вниз и зафиксируйте точку В. Из точки В — на одну клетку вправо и одну вниз и подметьте точку С. И из точки С — на одну клетку вправо и три вниз в точку D. Четверть окружности готова. Сейчас для комфорта дозволено развернуть лист супротив часовой стрелки так, дабы точка D оказалась вверху, и по тому же алгорифму достроить оставшиеся 3/4 окружности.
3. Но что делать, если нам необходимо возвести окружность большего размера, чем разрешает тетрадный лист и шаг циркуля — скажем, для игры? Тогда нам понадобится веревочка длины, равной радиусу желаемой окружности, и 2 колышка. Колышки привяжите к концам веревки. Один из них воткните в землю, а иным при натянутой веревке начертите окружность.Абсолютно допустимо, что одним из этих методов построения окружности воспользовался и изобретатель колеса — по сей день одного из самых феноменальных изобретений общества.
Видео по теме
Аксонометрическая проекция дюже главна в таких науках, как черчение и геометрия. Она является дюже наглядным трехмерным изображением предмета. А как строить аксонометрию ?

Инструкция
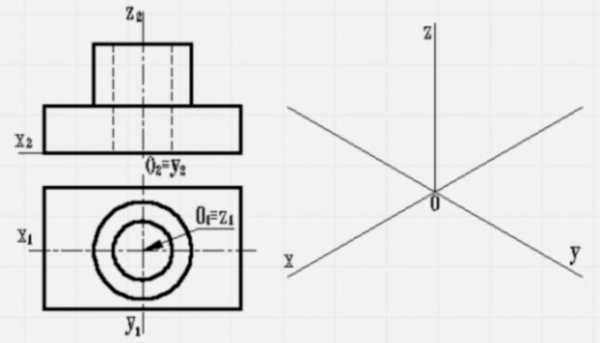
1. Пускай перед вами стоит задача исполнить построение аксонометрической проекции заданного тела вращения. В первую очередь надобно соотнести данное тело с какой-нибудь прямоугольной системой координат. Потому что дано тело вращения, то в данном случае для комфорта счёта одну из осей системы координат нужно совместить с осью тела вращения.

2. Сейчас необходимо вычертить вторую ортогональную проекцию тела, как показано на рисунке.

3. После этого нужно перейти к построению аксонометрических осей. Учтите, что их необходимо так располагать на листе, дабы большей части поверхности предмета была обеспечена видимость. Для того, дабы упростить задачу построения класснее каждого будет взять координатную ось, используемую в прямоугольной изометрической проекции, изображенную на рисунке. Вследствие такому выбору, показатели искажения по всякой из осей становятся равными единице. Если же делать типовые аксонометрические оси, в которых соседние оси образуют угол в 120 градусов, то показатель искажения станет равен 0,82. Это сделает добавочные трудности при изображении предмета.
4. Все элементы заданной фигуры нужно спроецировать в соотношении один к одному по аксонометрических осей. Для того, дабы изображение было больше наглядным, в ближайшей четверти детали делается вырез, с дальнейшей штриховкой. Линии штриховки по правилам наносят параллельно какой-нибудь из диагоналей условного квадрата, лежащего в рассматриваемой координатной плоскости. Стороны этого квадрата обязаны быть параллельны аксонометрическим осям. В одной детали различные сечения нужно заштриховывать с наклоном в различные стороны.
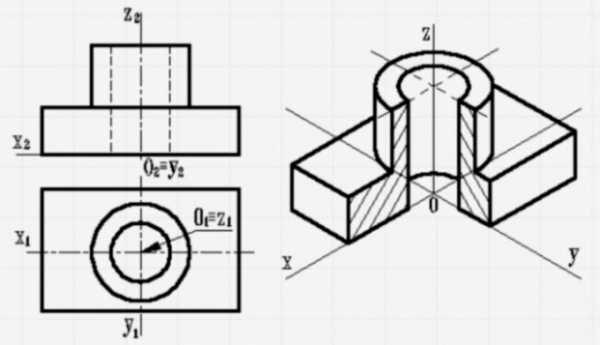
Полезный совет
Построение аксонометрических проекций предметов во многих учебниках по черчению рекомендуется начинать с построения их оснований, после этого теснее к основаниям понемногу добавляются аксонометрические проекции других элементов: ребер, граней, вершин, оснований.
Аксонометрические проекции деталей и узлов машин неоднократно применяются в конструкторской документации для того, дабы наглядно показать конструктивные особенности детали (сборочного узла), представить, как выглядит деталь (узел) в пространстве. В зависимости от того, под каким углом расположены оси координат, аксонометрические проекции подразделяются на прямоугольные и косоугольные.

Вам понадобится
- Программа для построения чертежей, карандаш, бумага, ластик, транспортир.
Инструкция
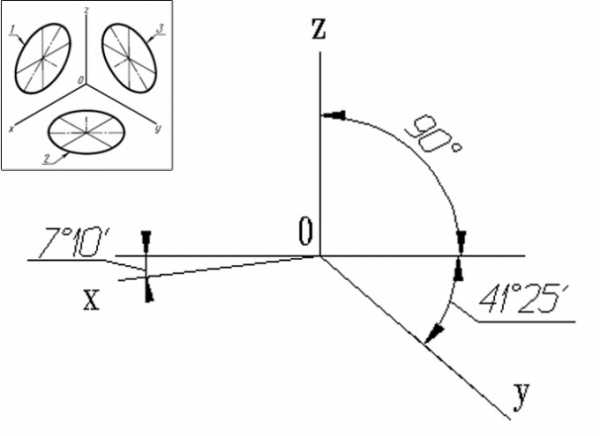
1. Прямоугольные проекции. Изометрическая проекция. При построении прямоугольной изометрической проекции рассматривают показатель искажения по осям X, Y, Z, равный 0,82, при этом окружности, параллельные плоскостям проекций, проецируются на аксонометрические плоскости проекций в виде эллипсов, огромная ось которых равна d, а малая ось – 0,58d, где d – диаметр начальной окружности. Для простоты расчетов изометрическую проекцию исполняют без искажения по осям (показатель искажения равен 1). В этом случае проецируемые окружности будут иметь вид эллипсов с крупной осью, равной 1,22d, и малой осью, равной 0,71d.
2. Диметрическая проекция. При построении прямоугольной диметрической проекции учитывается показатель искажения по осям X и Z, равный 0,94, а по оси Y – 0.47. На практике диметрическую проекцию упрощенно исполняют без искажения по осям X и Z и с показателем искажения по оси Y = 0,5. Окружность, параллельная общей плоскости проекций, проецируется на нее в виде эллипса с крупный осью, равной 1,06d и малой осью, равной 0,95d, где d – диаметр начальной окружности. Окружности, параллельные двум иным аксонометрическим плоскостям, проецируются на них в виде эллипсов с осями, равными соответственно 1.06d и 0,35d.
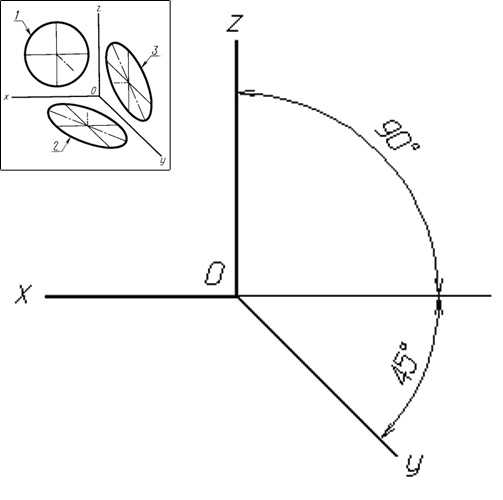
3. Косоугольные проекции. Общая изометрическая проекция. При построении общей изометрической проекции эталоном установлен наилучший угол наклона оси Y к горизонтали 45 градусов. Допускаются углы наклона оси Y к горизонтали — 30 и 60 градусов. Показатель искажения по осям X, Y и Z равен 1. Окружность 1, расположенная параллельно общей плоскости проекций, проецируется на нее без искажений. Окружности, параллельные горизонтальной и профильной плоскостям проекций, выполняются в виде эллипсов 2 и 3 с огромный осью, равной 1.3d и малой осью, равной 0,54d, где d – диаметр начальной окружности.
4. Горизонтальная изометрическая проекция. Горизонтальная изометрическая проекция детали (узла) строится на аксонометрических осях, расположенных, как показано на рис. 7. Допускается изменять угол между осью Y и горизонталью на 45 и 60 градусов, оставляя постоянным угол 90 градусов между осями Y и X. Показатель искажения по осям X, Y, Z равен 1. Окружность, лежащая в плоскости, параллельной горизонтальной плоскости проекций, проецируется в виде окружности 2 без искажения. Окружности, параллельные общей и профильной плоскостям проекций, имеют вид эллипсов 1 и 3. Размеры осей эллипсов связаны с диаметром d начальной окружности следующими зависимостями:эллипс 1 – огромная ось равна 1,37d, малая ось – 0, 37d; эллипс 3 – огромная ось равна 1,22d, малая ось – 0.71d.

5. Общая диметрическая проекция. Косоугольная общая диметрическая проекция детали (узла) строится на аксонометрических осях, сходственных осям общей изометрической проекции, но отличаются от нее показателем искажения по оси Y, тот, что равен 0,5. По осям X и Z показатель искажения равен 1. Также возможно метаморфоза угла наклона оси Y к горизонтали до значений 30 и 60 градусов. Окружность, лежащая в плоскости, параллельной общей аксонометрической плоскости проекций, проецируется на нее без искажений. Окружности, параллельные плоскостям проекций горизонтальной и профильной, вычерчиваются в виде эллипсов 2 и 3. Размеры эллипсов от размера диаметра окружности d выражаются зависимостью:огромная ось эллипсов 2 и 3 равна 1,07d; малая ось эллипсов 2 и 3 равна 0,33d.
Видео по теме
Обратите внимание!
Аксонометрическая проекция (от др.-греч. ???? «ось» и др.-греч. ?????? «измеряю») — метод изображения геометричеук4уеских предметов на чертеже при помощи параллельных проекций.
Полезный совет
Плоскость, на которую производится проецирование, именуется аксонометрической либо картинной. Аксонометрическая проекция именуется прямоугольной, если при параллельном проецировании проецирующие лучи перпендикулярны картинной плоскости ( =90 ) и косоугольной, если лучи составляют с картинной плоскостью угол 0
Вам понадобится
- — лист бумаги,
- — карандаш,
- — линейка,
- — транспортир.
Инструкция
1. Аксонометрия может быть исполнена как в прямоугольной проекции, так и в косоугольной. Для начала постройте куб в прямоугольной изометрической проекции, то есть проецирование происходит перпендикулярно плоскости проекции и масштаб по каждой оси идентичен. Обыкновенно, для простоты показатель искажения тут принимают равным 1. Нарисуйте три оси координат. Для этого с помощью линейки и карандаша нарисуйте вертикальную линию приблизительно от середины листа вверх. С помощью транспортира от этой линии отложите угол в 120 градусов в обе стороны и проведите соответствующие линии. Получилась ось координат в пространстве. Сейчас на этих осях отложите идентичные отрезки. Из полученных точек проведите линии, параллельные оси координат. Для этого вновь нужно от каждой точки отложить по 120 градусов в обе стороны. И на каждом луче с помощью линейки отложите отрезок той же величины, что и раньше. Сейчас объедините получившиеся точки параллельными линиями. Получился куб в прямоугольной изометрической проекции. Она еще носит наименование ортогональной.
2. Дабы получить прямоугольную диаметрическую проекцию, сбережете размеры в по любым двум осям, а по оставшейся — исказите в нужной либо произвольной степени. Реально куб превращается в прямоугольный параллелепипед. Помимо прямоугольной существуют косоугольные проекции, при которых проецирование происходит под любым иным углом к плоскости, помимо прямого. Различают фронтальную изометрическую проекцию, фронтальную диметрическую и горизонтальную изометрическую проекцию.
3. Для того дабы возвести фронтальную косоугольную проекцию, отложите следующие углы между осями: между вертикальной и горизонтальной — 90 градусов, а третью ось наклоните касательно вертикальной на 135 градусов. Помимо того, допускаются и другие отклонения — на 120 либо 150 градусов. Позже этого постройте проекции подобно предыдущему случаю, но лишь во фронтальной проекции сбережете пропорции. Для горизонтальной проекции пропорции сбережете в горизонтальной плоскости.
Обратите внимание!
При изометрических проекциях сложно оценить глубину и высоту рисунка.
Полезный совет
Аксонометрия почаще каждого применяют в машиностроительном черчении и САПР и в компьютерных играх для построения трёхмерных объектов и панорам.
Видео по теме
jprosto.ru
Построение окружности в аксонометрии — МегаЛекции
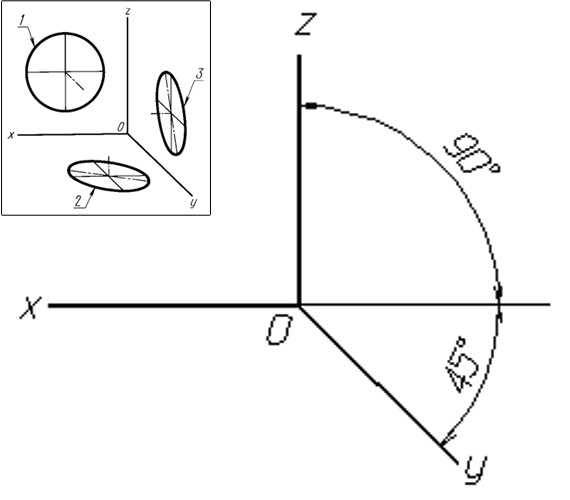
Окружности, лежащие в плоскостях, параллельных плоскостям проекций, проецируются на аксонометрическую плоскость проекций в эллипсы.
Малая ось эллипса всегда располагается вдоль отсутствующей оси в плоскости проекций. Большая ось эллипса перпендикулярна его малой оси. Так, в плоскости ХОY малая ось расположена вдоль оси Z, в плоскости ХОZ – вдоль оси Y, в плоскости YОZ – вдоль оси Х.
В прямоугольной изометрии большая ось эллипсов 1, 2, 3 равна 1,22 диаметра окружности, а малая – 0,71 диаметра окружности (рис. 2.29).
В прямоугольной диметрии большая ось эллипсов 1, 2, 3 равна 1,06 диаметра окружности, а малая ось эллипса 1 – 0,95d, эллипсов 2, 3 – 0,35d. Величину большой и малой оси подсчитывают или определяют графическим путем (рис. 2.30).
В косоугольной фронтальной диметрии окружности, лежащие в плоскостях, параллельных фронтальной плоскости проекций, проецируются на аксонометрическую плоскость в виде окружности; окружности, лежащие в плоскостях, параллельных горизонтальной и профильной плоскостям проекций, – в виде эллипсов (рис. 2.31). При этом большая ось эллипсов равна 1,07d, а малая ось – 0,33d. Большая ось горизонтального эллипса с осью Х составит угол 7°14′, и тот же угол будет между осью Z и большой осью профильного эллипса.
Фронтальную диметрию целесообразно применять в тех случаях, когда необходимо сохранить неискаженными фигуры, расположенные во фронтальных плоскостях.
На практике принято заменять эллипсы овалами, что значительно облегчает построение.
Пример выполнения овала, расположенного в горизонтальной плоскости проекций, дан на рис. 2.32.
Построение овала начинают с проведения осей симметрии и аксонометрических осей. Большая ось равна 1,22d, малая ось – 0,71d, где d – диаметр изображаемой окружности. Через точку О – начало аксонометрических осей – проводят окружности, диаметры которых соответственно равны большой и малой осям эллипса. На вертикальном диаметре большой окружности отмечают центры О1 и О2, а на горизонтальном диаметре малой окружности – О3 и О4. Эти точки являются центрами сопряжения дуг овала. Проводят прямые О2О3, О2О4, О1О3, на которых расположены точки со-
пряжения дуг овала. Две дуги радиуса R1 = О3В описывают из центров О3 и О4, а две другие радиуса R2 = О1А – из центров О1 и О2.
Для построения овала, расположенного в горизонтальной плоскости проекций, можно использовать и другой способ (рис. 2.33). В прямоугольной изометрии малую ось овала будем располагать вдоль оси Z, большую ось проведем перпендикулярно к малой оси. Из точки О пересечения этих осей циркулем сделаем засечки на осях Х и Y радиусом, равным радиусу заданной окружности.
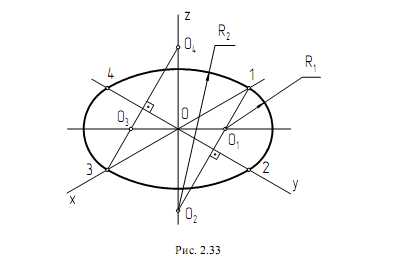
Полученные точки 1, 2, 3, 4 являются точками сопряжения дуг овала.
Из точки 1, лежащей на оси Х, проведем перпендикуляр к оси Y. На пересечении перпендикуляра с большой и малой осями получим две точки О1 и О2, которые являются центрами сопряжения дуг овала. Из точек О1 и О2 радиусами R1 = О1 – 1 и R2 = О2 – 1 опишем дуги окружностей. Аналогично построим две другие дуги. Построение будем проводить из точки 3. Перпендикуляр, проведенный из точки 3 к оси Y, даст нам еще два центра: О3 и О4, из которых радиусами R1= О3 – 3 и R2 = О4 – 3 опишем дуги окружностей.
Во фронтальной и профильной плоскостях построение овалов аналогично.
Рассмотрим построение прямоугольной диметрии овала, заменяющего эллипс, в который проецируется окружность, расположенная в плоскости П1 (рис. 2.34). Через точку О проводим оси диметрии ОХ, ОY, ОZ и направление большой оси овала перпендикулярно оси ОZ. Малая ось совпадет с направлением оси ОZ. Вдоль большой оси овала откладывают длину, равную 1,06d; вдоль малой оси – величину 0,35d. Для определения положения центра О1 сопряжения большой дуги овала откладывают вдоль малой оси от точки О величину 1,06d. От точки В откладывают величину ВО2, равную 0,09d, и определяют положение центра сопряжения О2 малой дуги овала.
Проводят линии центров О1О2 и т.д. Из центра О2 радиусом R = О2В проводят дугу овала до пересечения с линией центров в точке сопряжения. Из центра О1 радиусом R = О1А проводят большую дугу овала. Аналогично проводят дуги из двух не указанных на чертеже центров.

При построении прямоугольной диметрии овала, расположенного в плоскости П2 (рис. 2.35), через точку О проводят оси диметрии ОХ, ОY, ОZ. Через точку О проводят направление большой оси овала перпендикулярно оси Оу. Малая ось совпадает с направлением оси ОY. На осях ОY и ОZ откладывают величину d изображаемой окружности и получают точки М, N, K, L, являющиеся точками сопряжения дуг овала. Через точки М и N проводят горизонтальные прямые, которые в пересечении с осью Оу и перпендикуляром к ней дают точки О1, О2, О3, О4 – центры дуг овала. Из центров О1 и О3 описывают дуги радиусом R1 = О3L, а из центров О4 и О2 – дуги радиусом R2 = О4М.
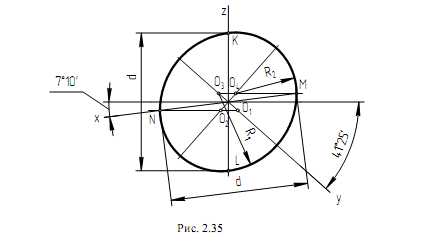
В профильной плоскости построение овала аналогично построению овала в горизонтальной плоскости с учетом расположения большой и малой осей овала.
Рекомендуемые страницы:
Воспользуйтесь поиском по сайту:
megalektsii.ru
Как начертить эллипс в аксонометрии
Окружность в аксонометрии представляет собой эллипс. Построить его можно с помощью параллельного проецирования окружности заданного радиуса на плоскость.Вам понадобится
- — бумага;
- — линейка;
- — карандаш;
- — ластик;
- — треугольник с прямым углом;
- — циркуль;
- — транспортир.
Инструкция
- Чтобы начертить эллипс в аксонометрии, сначала необходимо построить параллелограмм ABCD. В получившемся параллелограмме необходимо провести диагонали. Для этого соедините точки A и C, B и D. Получите диагонали AC и BD. Точку их пересечения обозначьте буквой О.
- Отметьте середины сторон параллелограмма точками 1, 3, 5, 7. Вы можете просто разделить длины сторон пополам и отметить середины. Или вы можете приложить линейку к стороне параллелограмма AB и вести ее параллельно AB до пересечения с точкой О. Остановите линейку и отметьте на боковых сторонах параллелограмма AD и BC точки 1 и 5. Затем повторите ту же процедуру и отметьте середины верхней и нижней стороны параллелограмма точками 3 и 7.
- На отрезке 3B постройте вниз равнобедренный прямоугольный треугольник 3KB, где 3B является гипотенузой треугольника. С помощью транспортира отмерьте вниз и вправо угол в 45° около точки 3. Затем отметьте 45° вниз и влево от точки B. Проведите прямые по отмеченным углам. Точка их пересечения — вершина прямого угла K.
- Возьмите циркуль и проведите полуокружность из точки 3 радиусом 3K до пересечения со стороной параллелограмма AB. Точки пересечения обозначьте L и M. Эти точки делят отрезок 3A и равный ему 3B в отношении 3:7. Если у вас нет циркуля, попробуйте разделить половины стороны AB в соотношении 3:7 с помощью линейки, но это уменьшает точность построения.
- Проведите через точки L и M прямые параллельно боковым сторонам AD и BC до пересечения с диагоналями параллелограмма. Отметьте точки 2, 4, 6, 8.
- Постройте в точках 2 и 6 касательные t₂ и t₆ параллельные диагонали BD и в точках 4 и 8 касательные t₄ и t₈ параллельные диагонали AC. Они будут являться касательными к эллипсу в точках 2, 4, 6 и 8.
- У вас получилось построить 8 точек эллипса 1, 2, 3, 4, 5, 6, 7 и 8 и столько же касательных к эллипсу AD, t₂, AB, t₄, BC, t₆, CD и t₈. Теперь вы можете с достаточной точностью начертить в параллелограмме эллипс. Сначала начертите слабый контур, затем обведите эллипс толстой линией.
completerepair.ru