Циклоида построение онлайн – Плоские кривые - Построение кривых - Геометрические построения, Лекальные кривые, построение синусоиды, построение циклоиды, построение эвольвенты, построение параболы, построение эллипса, касательная к эллипсу, построение биссектрисы угла

Содержание

Построение локальных кривых — циклоида, эпициклоида и гипоциклоида

Циклоида. Незамкнутая плоская кривая, которую описывает точка, лежащая на производящей окружности, катящейся без скольжения по прямой линии, называется циклоидой (рис. 1). Окружность радиуса R делят на восемь равных частей и мысленно катят ее слева направо по горизонтальной прямой 8—8. Очевидно, расстояние между точками 8—8 будет равно длине окружности 2пR. Это расстояние делят также на восемь равных частей. Из полученных точек 1, 2, 3 и т. д. восставляют перпендикуляры для того, чтобы получить центры 11, 21, З1 и др. перемещающейся окружности на линии 6—2. Если теперь из центра 11 провести окружность радиуса R, то в пересечении ее с прямой 7—1 будет найдена точка I циклоиды. Аналогично строят другие точки. Для более точного построения кривой используют деление окружности на 12 или даже 16 равных частей.

n
nTBegin—>TEnd—>n
n

Рис. 1. Построение циклоиды

n

n

Эпициклоида

. Эпициклоидой называют плоскую кривую, которую описывает точка производящей окружности при качении ее без скольжения снаружи направляющей окружности (рис. 2, а). Зная диаметр производящей окружности D и радиуснаправляющей окружности R, определяют центральный угол а = 180°(D/R). Это важно для того, чтобы расположить эпициклоиду симметрично.

n
nTBegin—>

TEnd—>n
n

Рис. 2. Построение эпициклоиды

Делят производящую окружность и дугу направляющей окружности АВ на 12 равных частей, находят центры 1,2 и т. д. на линии центров OO₁, проводят дуги 11—1, 10—2 и т. д. и находят точки эпициклоиды на пересечении дуг так, как в случае циклоиды. Разница только в том, что здесь вместо прямых 11—1 и др. имеются дуги 11-1 и др. Если центральный угол определен, то делят на равные части не направляющую окружность АВ, а непосредственно линию центров OO₁.

Если диаметры производящей и направляющей окружностей равны (рис. 2, б), т. е. если R равно половине D, то эпициклоида будет замкнутой кривой линией. Такая эпициклоида называется кардиоидой. Кардиоиду применяют для очертания деталей машин, предназначенных для осуществления возвратно-поступательного движения.

Гипоциклоида. Гипоциклоидой называют кривую, которую описывает точка производящей окружности при качении ее без скольжения внутри направляющей окружности (рис. 3, а). Центральный угол а определяют по той же формуле, что и для эпициклоиды. Так же производят и построение точек. По дуге направляющей окружности АВ откладывают двенадцатые части производящей окружности, т. е. делят дугу АВ на 12 равных частей. Соединяя точки деления с центром направляющей окружности, получают центры вспомогательных окружностей, 2, 3 и т. д. на линии центров OO₁. Проводят вспомогательные концентрические дуги 11—1, 10—2 и т. д. На пересечении этих дуг с окружностями, проведенными из соответствующих центров, получают точки гипоциклоиды, которые и соединяют плавной кривой линией по лекалу.

n
nTBegin—>TEnd—>n
n

Рис. 3. Построение гипоциклоиды

Если радиус направляющей окружности будет вдвое больше диаметра производящей окружности, то гипоциклоида будет иметь четыре полные ветви. Замкнутая кривая, образованная при этом, носит название астроиды (рис. 3, б).

Циклические кривые рассмотренных видов используются при построении профиля зубьев зубчатых колес.

Работа на forex, статьи, индикаторы рынка, новости, отзывы, статистика, графики.

polynsky.com.kg

Плоские кривые — лемнискаты, циклоиды, гипоциклоиды, цепная линия, трохоида

ЛЕМНИСКАТЫ
Уравнение в полярных координатах:
r² = a²cos2θ

Уравнение в прямоугольных координатах:
(x² + y²)² = a²(x² — y²

)

Угол между AB’ или A’B и осью x = 45^o

Площадь одной петли = a²/2

ЦИКЛОИДА
Уравнения в параметрической форме:

Площадь одной дуги = 3πa²

Длина дуги одной арки = 8a

Это кривая, описываемая точкой Р на окружности радиусом а, которая катится вдоль оси х.

ГИПОЦИКЛОИДЫ С ЧЕТЫРЬМЯ ОСТРИЯМИ
Уравнение в прямоугольных координатах:
x^2/3 + y^2/3 = a^2/3

Уравнения в параметрической форме:

Площадь, ограниченная кривой = 3πa²/8

Длина дуги целой кривой = 6a

Это кривая, описываемая точкой Р на окружности радиусом a/4, которая катится внутри окружности радиусом a.

КАРДИОИДА
Уравнение: r = a(1 + cosθ)

Площадь, ограниченная кривой = 3πa²/2

Длина дуги кривой = 8a

Это кривая, описываемая точкой Р на окружности радиусом a, которая катится снаружи окружности радиусом a. Эта кривая также является частным случаем улитки Паскаля.

ЦЕПНАЯ ЛИНИЯ
Уравнение:
y = a(e^x/a + e^-x/a)/2 = acosh(x/a)

Это кривая, по которой бы повисла цепь, подвешенная вертикально от точки А к В.

ТРЕХЛЕПЕСТКОВАЯ РОЗА
Уравнение: r = acos3θ

Уравнение r = acos3θ подобно кривой, полученной вращением против часовой стрелки по кривой 30^o или π/6 радиан.

В общем, r = acosnθ или r = asinnθ имеет n лепестков если n является нечетным.

ЧЕТЫРЕХЛЕПЕСТКОВАЯ РОЗА
Уравнение: r = acos2θ

Уравнение r = asin2θ подобно кривой, полученной вращением против часовой стрелки по кривой 45^o или π/4 радиан.

В общем r = acosnθ или r = asinnθ имеет 2n лепестков если n — четное.

ЭПИЦИКЛОИДА
Параметрические уравнения:

Это кривая, описываемая точкой Р на окружности радиуса b, когда она катится по внешней стороне окружности радиусом а. Кардиоида является частным случаем эпициклоиды.

ОБЩАЯ ГИПОЦИКЛОИДА
Параметрические уравнения:

Это кривая, описываемая точкой Р на окружности радиуса b, когда она катится по внешней стороне окружности радиусом а.

Если b = a/4, кривая является гипоциклоидой с четырьмя остриями.

ТРОХОИДА
Параметрические уравнения:

Это кривая, описываемая точкой Р на дистанции b от центра окружности с радиусом а, когда она катится по оси x.
Если b укороченной циклоидой.
Если b > a, кривая имеет форму, показанную на рис. 11-11 и называется троходой.
Если b = a, кривая есть циклоидой.

ТРАКТРИСА
Параметрические уравнения:

Это кривая, описываемая конечной точкой Р натянутой струны длиной PQ, когда другой конец Q перемещается вдоль оси х.

ВЕРЗЬЕРА (ВЕРЗИЕРА) АНЬЕЗИ (ИНОГДА ЛОКОН АНЬЕЗИ)
Уравнение в прямоугольных координатах: y = 8a³/(x² + 4a

Параметрические уравнения:

В. На рисунке переменная линия OA пересекающая y = 2a и круг с радиусом a с центром (0,a) в A и B соотвественно. Любая точка P на «локоне» определяется построением линий, параллельных к осям x и y, и через B и A соответственно и определяющие точку пересечения P.

ДЕКАРТОВ ЛИСТ
Уравнение в прямоугольных координатах:
x³

www.math10.com

Плоские кривые — Построение кривых — Геометрические построения, Лекальные кривые, построение синусоиды, построение циклоиды, построение эвольвенты, построение параболы, построение эллипса, касательная к эллипсу, построение биссектрисы угла

Решение практических задач по формированию сложных технических контуров наталкивается на такую проблему, как невозможность представления всего контура единственной кривой. Это и породило необходимость конструирования составных кривых (кривых, сформированных из дуг простых).

В технике такие кривые получили название обводов, в математике они более известны как сплайны (spline). Основной характеристикой обвода является гладкость. Под гладкостью понимают число совпавших производных (уравнений стыкующихся кривых) в точках стыка.

Наиболее простой вариант построения составной кривой — из дуг окружностей.

Окружности могут сопрягаться таким образом, что в точках стыка будут располагаться общие касательные. Такой стык соответствует первому порядку гладкости (совпадают только первые производные).

Для построения этого обвода используется идея радиусо-графического сопряжения дуг окружностей. Исходной информацией является точечный ряд (1, 2, 3, …, n) и касательная на одном из концов этого ряда, например, ti (рисунок 1).

Вследствие того, что окружность трехпараметрическая кривая, для её построения кроме точки i нужно определить еще одну, например (i+1) или (i-1). Не нарушая общности рассуждений, рассмотрим вариант с (i+1)-ой точкой (рисунок ниже).

Рисунок 1 — Построение дуги окружности с заданными параметрами

Рисунок 2 — Построение обвода первого порядка гладкости

Графическое решение выглядит следующим образом: через точку i проводится нормаль n. Конечные точки i и (i+1) соединяются хордой. В средней точке хорды строится перпендикуляр h. Пересечение нормали n и перпендикуляра h и определит положение центра искомой окружности. Радиус окружности совпадает с отрезками [o-i] и [o-(i+1)]. Касательная к построенной окружности будет перпендикулярна радиусу, проведенному в (i+1)-ю точку.

Центры соприкасающихся окружностей лежат на одной прямой, проходящей через точку касания. Таким образом, определение центра окружности сопрягающейся с i-той найдется на пересечении линии Оi(i+1) с перпендикуляром к середине хорды (i+1)(i+2) (рисунок 2).

Построение кривых

Ниже приведено построение наиболее наиболее употребительных кривых. На картинке приведена кривая и сохранены все построения. Ниже описан алгоритм построения кривой.

Лекальные кривые

Построение синусоиды

Рисунок 3 — Построение синусоиды

Синусоидой называется плоская кривая, графически изображающая изменение синуса в зависимости от его аргумента (угла). Для построения синусоиды окружность радиуса R делят на произвольное количество равных частей. На горизонтальной прямой откладывают отрезок, равный половине длины окружности (R*3.14), и делят его на такое же число равных частей. Из концов этих отрезков (точки 1′,2′,3′) проводят вертикальные прямые до пересечения с горизонтальными прямыми, исходящими из концов соответствующих радиусов (точки 1,2,3).

Построение циклоиды

Рисунок 4 — Построение циклоиды

Циклоидой называется кривая, образованная точкой окружности, катящейся без скольжения по прямой линии. Для построения циклоиды окружность радиуса R делят на произвольное количество равных частей. На горизонтальной прямой откладывают отрезок, равный половине длины окружности (R*3.14), и делят его на такое же число равных частей. Из концов этих отрезков (точки 1′,2′,3′) проводят вертикальные прямые до пересечения с горизонтальной осевой линией. Эти точки будут центрами окружностей радиуса R. Пересечения окружностей с соответствующими горизонтальными прямыми, исходящими из концов радиусов (точки 1,2,3), дадут точки циклоиды.

Построение эвольвенты

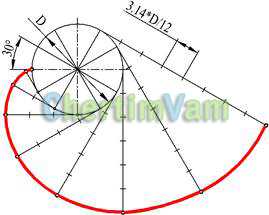
Рисунок 5 — Построение эвольвенты

Эвольвентой окружности называется кривая, которую описывает точка прямой линии, катящейся без скольжения по неподвижной окружности. Окружность диаметра D делят на произвольное число равных частей. Из точек деления проводят касательные к окружности, на которых откладывают соответственно 1, 2, 3 и т.д. части окружности.

Построение параболы

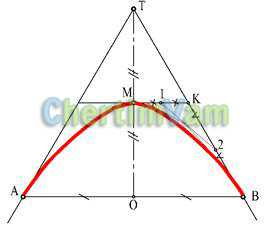
Рисунок 6 — Построение параболы

Параболойназывается, кривая, полученная при пересечении конуса и плоскости, параллельной образующей конуса. При задании параболы граничными точками А и В и точкой пересечения касательных Т кривая строится методом пропорционального деления.

Отрезок АВ делится пополам в точке О, отрезок ОТ – тоже пополам в точке М, отрезок МК — в точке 1, КВ — в точке 2 и т.д.

Построение эллипса

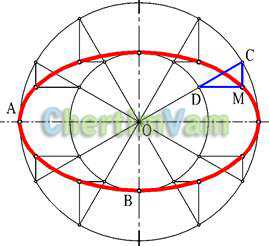
Рисунок 7 — Построение эллипса

Эллипсомназывается кривая, полученная при пересечении конуса и плоскости, пересекающей все образующее конуса.

Эллипс удобнее стоить по его полуосям (большой ОА и малой ОВ).

Для построения эллипса проводятся две соосные окружности радиусами ОВ и ОА Проведение произвольной прямой ОС и дальнейшее построение ”ключа” (треугольника СDМ со сторонами параллельными осям эллипса) позволяет определить положение текущей точки эллипса М.

Геометрические построения

Ниже даны изображения наиболее распространенных видов геометрических построений и описан алгоритм построения.

Касательная к эллипсу

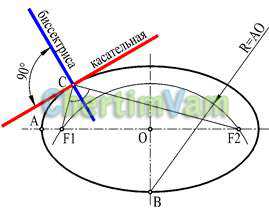
Рисунок 8 — Касательная к эллипсу

Построение касательной к эллипсу (с полуосями ОА и ОВ) в заданной точке С нужно начинать с построения фокусов эллипса, точек F1 и F2.

Построить окружность с центром в точке В и радиусом, равным большой полуоси ОА. В пересечении окружности с горизонтальной осью отметить точки F1 и F2. Построить биссектрису угла F1СF2. Прямая, перпендикулярная биссектрисе и проходящая через точку С, будет касательной к эллипсу в заданной точке.

Построение биссектрисы угла

Рисунок 9 — Построение биссектрисы угла

Из вершины угла произвольным радиусом построить дугу окружности. Из точек пересечения дуги окружности со сторонами угла построить равные окружности произвольного радиуса R. Прямая, проходящая через вершину угла и точки пересечения окружностей, — биссектриса угла.

Геометрическое построения сопряжения прямых

Рисунок 10 — Сопряжение прямых окружностью заданного радиуса R

На расстоянии R от заданных прямых построить вспомогательные прямые, им параллельные. Из точки пересечения вспомогательных прямых построить сопрягающую окружность заданного радиуса R. Отметить точки сопряжения. Они лежат на перпендикулярах, проведенных из центра сопрягающей окружности к заданным прямым.

Построение сопряжения прямой и дуги

Рисунок 11 — Сопряжение окружностью заданного радиуса R прямой и дуги

На расстоянии R от заданной прямой построить вспомогательную прямую, ей параллельную. Из центра сопрягаемой дуги провести дугу окружности с радиусом r + R. Из точки пересечения построенной дуги и вспомогательной прямой построить сопрягающую окружность. Отметить точки сопряжения.

Построение сопряжения двух окружностей

Рисунок 12 — Внешнее сопряжение окружностью с заданным радиусом R двух окружностей с радиусами R1 и R2

Из центров заданных окружностей провести дуги вспомогательных окружностей с радиусами R1+R и R2+R. Из точки пересечения дуг вспомогательных окружностей построить сопрягающую окружность радиуса R. Отметить точки сопряжения. Они лежат на прямых, соединяющих центры окружностей.

Геометрические построения смешанного сопряжения

Рисунок 13 — Смешанное сопряжение окружностью с заданным радиусом R двух окружностей с радиусами R1 и R2

Из центров заданных окружностей провести дуги вспомогательных окружностей с радиусами R1-R и R2+R. Из точки пересечения дуг вспомогательных окружностей построить сопрягающую окружность радиуса R. Отметить точки сопряжения. Они лежат на прямых, соединяющих центры окружностей.

chertimvam.ru

Циклоиды.

И так продолжаем тему геометрических фигур и сегодня поговорим о циклоиде, как она определяется и какие есть ее виды.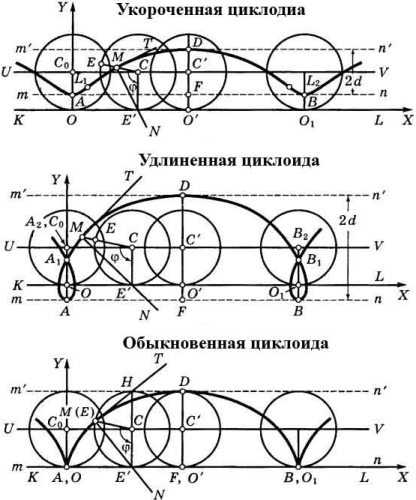

Определение. Циклоидой называется линия, которую описывает точка, закрепленная в плоскости круга (производящий круг), когда этот круг катится (без скольжения) по некоторой прямой KL (направляющая).

Если точка М, описывающая циклоиду, взята внутри производящего круга (т. е. расстояние CM = d от центра С меньше радиуса r), то циклоида называется укороченной; если вне круга (т. е. d > r), — удлиненной; если же точка М лежит на окружности (т. е. d = r), то линия, описываемая этой точкой, называется обыкновенной циклоидой или чаще просто циклоидой.

Пример. Когда вагон движется по рельсам, внутренняя точка колеса описывает укороченную циклоиду, точка на ободе — удлиненную, а точка окружности колеса — обыкновенную.

Начальной точкой фигуры называется такая ее точка, которая лежит на прямой (С₀О)у соединяющей центр С₀ производящего круга с точкой его опоры (О), и расположена по ту же сторону от центра С₀, что и точка опоры О. Точка В на рисунках — тоже начальная.

Начальные точки обыкновенной циклоиды лежат на направляющей и совпадают с соответствующими точками опоры производящего круга.

Вершиной циклоиды (D на рисунке) называется такая ее точка, которая лежит на прямой С’О’ соединяющей центр С’ производящего круга с точкой опоры О’, но расположена на продолжении отрезка С’О’ за точку С’.

Отрезок АВ, который соединяет две соседние начальные точки, будет называтся основанием циклоиды; а перпендикуляр DF, который опущен из вершины циклоиды на ее основание, — высотой. Дуга, которая описывается точкой М между двумя соседними начальными точками, также имеет свое название — арка циклоиды; прямая UV, которая описывается центром С производящего круга, — линия центров.

Как мы видим — это очень интересная геометрическая кривая у которой есть ещё очень много разных свойств, по ней даже можно оформить заказ кандидатской диссертации и доказать не одну полезную теорему.

Материалы по теме:

Поделиться с друзьями:

Загрузка…

matemonline.com

Циклоида | Основы программирования

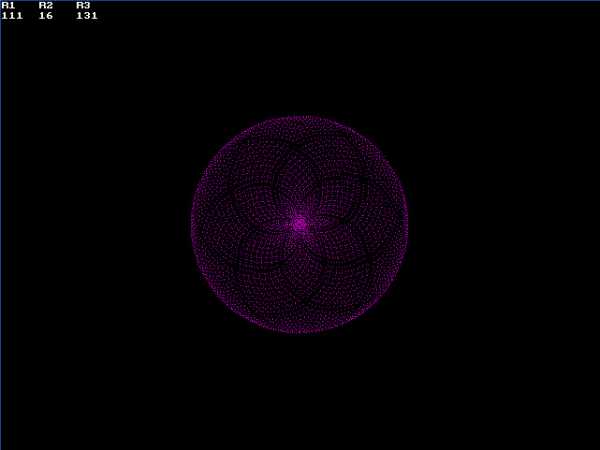
Построить циклоиду.

Чтобы нарисовать циклоиду, достаточно пройтись в цикле по формулам:

X = Int((R1 + R2) * Cos(R2 * T / R1) — R3 * Cos((R1 + R2) / R1 * T))
Y = Int((R1 + R2) * Sin(R2 * T / R1) — R3 * Sin((R1 + R2) / R1 * T))

Здесь R1 — радиус круга, по которому катится колесо, R2 — радиус колеса, катящегося по кругу, если с минусом, то внутри его и R3 — радиус, на котором лежит рисуемая точка на колесе. Т — счетчик цикла, он же полярный угол, на котором лежит центр колеса в данный момент.

#include <stdio.h>
#include <conio.h>
#include <graphics.h>
#include <math.h>
#include <STDLIB.H>
#include <dos.h>
 
#define  K  0.45
 
 
void zicloida(int R1,int R2,int R3,float T );
char* s1_s2(char *s1,char *s2);
 
int main(){
    int R1,R2,R3;
    int gd ,gm;
 
    printf("Enter R1,R2,R3 :\n");  //R1 - радиус круга, по которому катится колесо, R2 - радиус колеса, катящегося по кругу,
    scanf("%d%d%d",&R1,&R2,&R3);   // если с минусом, то внутри его и R3 - радиус, на котором лежит рисуемая точка на колесе
 
 
    detectgraph(&gd, &gm);   //инициализация графики
    initgraph(&gd, &gm,"");
 
    zicloida(R1,R2,R3,0.0);
 
    getch();
    closegraph();
 
    return 0;
}
 
void zicloida(int r1,int r2,int r3,float t )
{
  int X,Y,xo,yo,R1,R2,R3,col;
  float T;
  char str1[20],str2[8],str3[8];
 
   randomize();
   xo = getmaxx()/2;
   yo = getmaxy()/2;
 
   for(R1 = r1 ; R1 <= 187 ; R1 += 5)
 
    for(R2 = r2 ; R2 <= 240 ; R2 += 5)
 
       for(R3 = r3; R3 <= 240 ; R3 += 5)
       {
	  outtextxy(1,1,"R1   R2   R3 ");      //вывод на экран значений R1, R2, R3
	  col =random(16) + 1;
	  itoa(R1, str1,10);
	  itoa(R2, str2,10);
	  itoa(R3, str3,10);
 
	  s1_s2(str1,"  ");
	  s1_s2(str1,str2);
	  s1_s2(str1,"   ");
	  s1_s2(str1,str3);
	  outtextxy(1,12,str1);
 
	  for(T = t ;T <= 600.0  ; T += 0.1){ // Т - счетчик цикла, он же полярный угол, на котором лежит центр колеса в данный момент
	     X = (R1 + R2) * cos(R2 * T / R1) - R3 * cos((R1 + R2) / R1 * T);  //формула построения циклоиды
	     Y = (R1 + R2) * sin(R2 * T / R1) - R3 * sin((R1 + R2) / R1 * T);
 
	     putpixel(X*K+xo,Y*K+yo,col);
 
	     if ( kbhit()) exit(1);
	 }
	    delay(50);
	    cleardevice();
 
     }
 }
 
 char* s1_s2(char *s1,char *s2){ //рассчет R2, R3
    int i,j;
 
 
    i=j=0;
    while (s1[i]!='\0')
	i++;
 
    while( (s1[i++]=s2[j++]) !='\0') ;
 
 
 
   return s1;
}

Ключевые слова:

фрактал циклоида

Вложение	Размер
cikloid.rar	37.52 кб

www.opita.net

Циклоида

Федеральное агентство по образованию

ГОУ ВПО «Красноярский государственный педагогический университет им. В.П. Астафьева

Факультет математики и информатики

Кафедра математического анализа и методики его преподавания

Курсовая работа

по математическому анализу на тему

«Циклоида»

Выполнила студентка 43 группы

Ковальчук М.В.

Научный руководитель

доцент кафедры мат. анализа и мп

Шатохина М.П

Красноярск 2010

Оглавление

1. Введение

2. Исторические сведения

3. Основные свойства циклоиды

4. Построение циклоиды

5. Геометрическое определение циклоиды

6. Параметрическое уравнение циклоиды и уравнение в декартовых координата

7. Задачи на нахождение частей циклоиды и фигур, образованных циклоидой

8. Заключение

Литература

Введение

Кривая циклоида очень интересна для изучения, однако не так просто найти литературу ей посвященную. В большинстве таких источников циклоида упоминается только вскользь или рассматривается не достаточно полно. Однако она используется при решении различных задач. В виду того, что в школах вводится углубленное изучение математических дисциплин, в скором времени может понадобиться подробная информация о различных кривых, в том числе и о циклоиде. Так же задачи связанные с циклоидой встречаются и в физике и в высшей математике. Поэтому я посчитала данную тему актуальной и интересной для изучения.

Цель работы: описать основные свойства циклоиды, привести решение геометрических задач, связанных с циклоидой.

1. Исторические сведения

Первым кто стал изучать циклоиду, был Галилео Галилей (1564-1642)_ знаменитый итальянский, астроном, физик и просветитель. Он же и придумал название «циклоида» , что значит : «напоминающая о круге». Сам Галилей о циклоиде ничего не писал, но о его работах в этом направлении упоминают ученики и последователи Галилея: Вивиани, Торичелли и другие.

Великий античный философ — «отец логики» — Аристотель из Стагиры (384—322 годы до н. э.), занимаясь логическим обоснованием понятия движения, рассматривал, между прочим, следующий парадокс.

рис. 1

Пусть кружок, изображенный на рис. 1 жирной линией, катится по прямой АВ. Когда кружок этот сделает полный оборот, точка М вернется на прямую АВ и займет положение М_х . При этом, как мы знаем, отрезок ММ_Х будет равен длине «жирной» окружности. Рассмотрим начерченный кружок с центром О, изображенный тонкой линией. Когда точка М придет в положение М₁ этот маленький кружок тоже сделает полный оборот и его точка К придет в положение К₁ . При этом в каждый момент времени какая-то одна единственная точка маленькой окружности совмещается с единственной же точкой отрезка КК₁ . Каждой точке окружности соответствует единственная точка отрезка и каждой точке отрезка — единственная точка окружности. Поэтому напрашивается вывод: длина маленькой «тонкой» окружности равна длине отрезка КК₁ — ММ₁ т. е. равна длине большой («жирной») окружности. Итак, круги различных радиусов имеют окружности одинаковой длины! В этом и состоит парадокс Аристотеля.

Ошибка здесь в следующем. Из того, что каждой точке окружности радиуса ОК соответствует единственная точка отрезка КК₁ вовсе не следует, что длина этой окружности равна КК₁ . Так, например, на рис. 2 точки отрезка АВ приведены при помощи лучей, проходящих через точку D, во «взаимно однозначное» соответствие с точками вдвое большего отрезка СЕ, но никому в голову не придет утверждать, что отрезки АВ и СЕ имеют одинаковую длину! Это же относится не только к отрезкам прямых, но и кривых линий. Парадоксу Аристотеля можно придать следующую, более грубую, а потому и более ясную форму: рассмотрим две концентрические окружности (рис. 3). На них «поровну» точек: соответствующие точки соединены на рис. 3 прямыми линиями (радиусами). И все же никто не станет утверждать, что длины этих окружностей одинаковы.

рис 2 рис. 3

Аристотель рассматривал именно то движение, которое через 1900 лет привело Галилея к открытию циклоиды; но он не заинтересовался кривыми, которые вычерчиваются точками окружности катящегося круга.

В самом начале XVII века юный Галилей пытался экспериментально проверить свою догадку о том, что свободное падение — равноускоренное движение. Когда он перенес наблюдения с Пизанской башни в лаборатории, ему стало очень мешать то, что тела падают «слишком быстро». Чтобы замедлить это движение, Галилей решил заменить свободное падение тел их движением по наклонной плоскости, предположив, что и оно будет равноускоренным. Проводя эти опыты, Галилей обратил внимание на то, что в конечной точке величина скорости тела, скатившегося по наклонной плоскости, не зависит от угла наклона плоскости, а определяется только высотойH и совпадает с конечной скоростью тела, свободно упавшего с той же высоты (как вы хорошо знаете, в обоих случаях |v ̄|=

Изучив движения по наклонным плоскостям, Галилей перешел к рассмотрению движения материальной точки под действием силы тяжести по ломаным линиям. Сравнивая времена движения по различным ломаным, соединяющим фиксированную пару точек А и В , Галилей заметил, что если через эти две точки А, В провести четверть окружности и вписать в нее две ломаные М иL , такие, что ломанаяL «вписана» в ломаную М, то материальная точка из А в В быстрее попадает по ломаной М, чем по ломаной L. Увеличивая у ломаной число звеньев и переходя к пределу, Галилей получил, что по четверти окружности, соединяющей две заданные точки, материальная точка спустится быстрее, чем по любой вписанной в эту четверть окружности ломаной. Из этого Галилей сделал ничем не аргументированный вывод, что четверть окружности, соединяющая пару заданных точек А, В (не лежащих на одной вертикали), и будет для материальной точки, движущейся под действием силы тяжести, линией наискорейшего спуска (позже линию наискорейшего спуска стали называть брахистохроной). Впоследствии выяснилось, что это утверждение Галилея было не только необоснованным, но и ошибочным.

Свойства касательной и нормали к циклоиде были впервые изложены Торичелли (1608—1647) в его книге «Геометрические работы» (1644 год). Торичелли использовал при этом сложение движений. Несколько позже, но полнее, разобрал эти вопросы Роберваль (псевдоним французского математика Жилля Персонна, 1602—1672). В 1634 году Роберваль –вычислил площадь, ограниченную аркой циклоиды и ее основанием. Свойства касательной к циклоиде изучал также Декарт; он изложил свои результаты, не прибегая к помощи механики.

2. Основные свойства циклоиды

Определение циклоиды, введенное ранее, никогда не удовлетворяло ученых: ведь оно опирается на механические понятия — скорости, сложения движений и т. д. Поэтому геометры всегда стремились дать циклоиде чисто геометрическое определение» Но для того, чтобы дать такое определение, нужно прежде всего изучить основные свойства циклоиды, пользуясь ее механическим определением. Выбрав наиболее простое и характерное из этих свойств, можно положить его в основу геометрического определения.

Начнем с изучения касательной и нормали к циклоиде. Что такое касательная к кривой линии, каждый представляет себе достаточно ясно; точно определение касательной дается в курсах высшей математики, и мы его приводить здесь не будем. Нормалью называется перпендикуляр к касательной, восставленный в точке касания. На рис. 16 изображена касательная и нормаль к кривой АВ в ее точке М

Рассмотрим циклоиду (рис. 17),круг катящийся по прямой АВ. Допустим, что вертикальный радиус круга, проходивший в начальный момент через нижнюю точку циклоиды, успел повернуться на угол φ и занял положение ОМ. Иными словами, мы считаем, что отрезок М_о Т составляет такую долю отрезка М_о М₁ , какую угол φ составляет от 360° (от полного оборота).

Касательная к циклоиде

При этом точка М₀ пришла в точку М. Точка М и есть интересующая нас точка циклоиды.

СтрелочкаOH изображает скорость движения центра катящегося круга. Такой же горизонтальной скоростью обладают все точки круга, в том числе и точка М. Но, кроме того, точка М принимает участие во вращении круга. Скорость МС, которую точка М на окружности получает при этом вращении, направлена по касательной МС₁ к окружности, т. е. перпендикулярно к радиусу ОМ. А т.к. в этом случае скорость МС по величине равна скорости MP (т. е. скорости ОН). Поэтому параллелограмм скоростей в случае нашего движения будет ромбом (ромб МСКР на рис. 17). Диагональ МК этого ромба как раз и даст нам касательную к циклоиде.

Все сказанное дает возможность решить следующую «задачу на построение»: дана направляющая прямая АВ циклоиды, радиус г производящего круга и точка М, принадлежащая циклоиде (рис. 17). Требуется построить касательную МК к циклоиде.

Имея точку М, мы без труда строим производящий круг, в том его положении, когда точка на окружности попадает в М. Для этого предварительно найдем центр О при помощи радиуса МО =r (точка О должка лежать на прямой, параллельной АВ на расстоянии г от нее). Затем строим отрезок MP произвольной длины, параллельный направляющей прямой. Далее строим прямую МС₁ , перпендикулярную к ОМ На этой прямой откладываем от точки М отрезок МС, равный MP. На МС и MP, как на сторонах, строим ромб. Диагональ этого ромба и будет касательной к циклоиде в точке М.

mirznanii.com

Урок по теме моделирование

Коткова Лидия Леонидовна

учитель информатики

ГОУ СОШ № 728 г.Москвы

Урок по теме «Моделирование физического процесса.Циклоида»

Цель: формирование умения построения графической модели в Excel.

Необходимые знания и умения к данному уроку.

Учащиеся должны знать понятия моделирования, модели, формы информационных моделей. Уметь в электронной таблице Excel заполнять ячейки, работать с формулами, строить диаграммы.

ПЛАН УРОКА

Организационный момент.
Постановка задачи.
Эксперимент.
Историческая справка о циклоиде.
Практическая работа: построение графика кривой в Excel.
Повторение.
Задание на дом.

1. Организационный момент (учащиеся сидят за партами). Мы продолжаем изучение темы моделирование. Напомните, что означает моделирование, что называется моделью? Сегодня вы будете строить графическую модель, но сначала вспомним, какие графические модели нам известны? (графы, графики, чертежи, схемы и т.д.).

2. Постановка задачи. Возьмём колесо, обруч, круг. Зафиксируем точку круга. Будем катить круг по прямой. Какую кривую опишет зафиксированная точка круга? Следите внимательно за траекторией точки (в большинстве учащиеся отвечают, что точка опишет окружность, но кто-то догадается и скажет, что точка опишет дугу).

Учитель показывает на большом экране:

(нажмите кнопку «Движение»)

3. Эксперимент. Проверим наше предположение. Прикрепим к обручу или кругу кусок мела и покатим вдоль стены, мел будет вычерчивать «кругообразную» кривую, называемую циклоидой. Одному обороту обруча соответствует одна «арка» циклоиды, если обруч будет катиться дальше, то будут получаться еще и еще арки той же циклоиды.

Учитель показывает на большом экране:

(нажмите кнопку «Движение»)

4. Историческая справка о циклоиде. Первым из учёных обратил внимание на циклоиду Николай Кузанский в XV веке, но серьёзное исследование этой кривой началось только в XVII веке. Название циклоида придумал Галилей (во Франции эту кривую сначала называли рулеттой). Содержательное исследование циклоиды провёл современник Галилея Мерсенн.

Паскаль писал о циклоиде: « … является линией столь обычной, что после прямой и окружности нет более часто встречающейся линии; она так часто вычерчивается перед глазами каждого, что надо удивляться тому, как не рассмотрели её древние… ибо это не что иное, как путь, описываемый в воздухе гвоздём колеса.».

Эта кривая быстро завоевала популярность и подверглась глубокому анализу, в котором участвовали Декарт, Ферма, Ньютон, Лейбниц, братья Бернулли и другие корифеи науки XVII—XVIII веков.

Циклоида имеет ряд удивительных свойств:

ü «Перевёрнутая» циклоида является кривой скорейшего спуска. Более того, она имеет также свойство таутохронности: тяжёлое тело, помещённое в любую точку арки циклоиды, достигает горизонтали за одно и то же время.

ü Период колебаний материальной точки, скользящей по перевёрнутой циклоиде, не зависит от амплитуды, этот факт был использован Гюйгенсом для создания точных механических часов.

Итак, циклоида — плоская кривая, описываемая точкой Р окружности, катящейся без скольжения по неподвижной прямой.

Координаты точки окружности в данный момент времени вычисляются по формулам:

x = a ( t — sin t ),

y = a (1- cos t ),

где а — радиус окружности.

5. Практическая работа (учащиеся садятся за компьютеры). Построим в Excel график этой кривой.

Памятка.

Ø  Для переменной t достаточно ввести значения 0 и 1, навестись мышкой на маркер заполнения и растянуть до нужной ячейки.

Ø  Для переменных x и y надо ввести в ячейки В2 и С2 формулы соответственно (см. рисунок). Потом растянуть ячейки до нужных ячеек с помощью маркера заполнения
 ( в ячейку С2 ввести =5*(1-cos(A2)).

Ø  Для построения графика надо выделить ячейки с В2 по С21. Выбрать пункт меню «Вставка» - «Диаграмма». Выбрать вид – точечная диаграмма.

Дополнительное задание (для тех, кто быстро построил график кривой).

Сделайте так, чтобы значение радиуса a задавалось в отдельной ячейке.

Задайте разные значения a и посмотрите как меняется график кривой.

6. Повторение. Итак, вы сегодня построили графическую модель кривой, которую описывает некоторая точка окружности, катящейся без скольжения по неподвижной прямой.

ü Как называется эта кривая?

ü Какие интересные свойства циклоиды вы запомнили?

ü Предположем, что катится гимнастический обруч. Внешняя и внутренняя точки обруча будут описывать одинаковые кривые?

ответ…

7. Домашнее задание. Поищите в справочниках, интернете, какие существуют ещё интересные кривые. Модели каких кривых мы можем построить в электронной таблице Excel?

school-728.narod.ru