Что такое интерполяция линейная – Линейная интерполяция — Википедия

Линейная интерполяция Онлайн

можно использовать:

дроби

1/2, -3/4, 5/7

дробные числа

1.52 или 0,19 можно иcпользовать как «.» так и «,»

квадратный корень

sqrt(4), sqrt(4/3)

тригонометрия

sin(1), cos(1), tan(1), atan(1)

возведение в степень

pow(3, 2) = 3*3 !при pow(3,2, 4,3) — система поймет что вы хотите 3.2 возвести в степень 4.3

арифметические операции

(3/4 + sqrt(5/7)) * pow(2, 4)

Сервис интерполяции и экстраполяции онлайн (линейная интерполяция/экстраполяция) поможет вам вычислить значение линейной функции, имея в распоряжении f(x) в двух различных точках, а также рассчитает уравнение прямой. Данный сервис автоматически определит нужный способ расчета — вам лишь надо ввести значения в двух произвольных точках, и указать необходимую точку, в которой нужно рассчитать значение. Если установить «галку» внутри кнопки «Рассчитать», калькулятор будет рассчитывать значение автоматически при любом изменении входных данных. Пример расчета интерполяции

Интерполяция — (от латинского interpolatio изменение, переделка), в математике и статике это способ вычислить промежуточное значение функции по нескольким уже известным ее значениям. Например.: Имеется функция f(x), известны результаты значения f(x) в точке x₀ и точке x₂, интерполяця помогает найти значение f(x₁) при условии что x₁ принадлежит интервалу от x₀ до x₂. Если x₁ лежит вне интервала (x₀, x₂), интерполяция не поможет, для этого нужно использовать «экстраполяцию». Этот метод часто называют «линейная интерполяция«, он дает 100% верный результат для уравнения прямой. Для вычесления резултата функций с двумя переменными существует «Билинейная интерполяция (Двойная интерполяция)». Также для рассчета интерполяции можно воспользоваться сервисом Интерполяция — полином Ньютона и Интерполяция — полином Лагранжа

Экстраполяция — в математике и статике это способ вычислить значение функции по нескольким уже известным ее значениям. Например.: Имеется функция f(x), известны результаты значения f(x) в точке x₁ и точке x₂, экстраполяция помогает найти значение f(x₀) либо f(x₃) при условии что x₀ либо x₃ меньше либо больше интервала x₁ до x₂. Если x_n лежит в интервале (x₁, x₂), экстраполяция не поможет, для того вам нужно использовать «интерполяцию» — для функций с одной переменной, и «двойная интерполяция» — для функций с двумя переменными.

Этот метод часто называют «линейная экстраполяция«, он дает 100% верный результат для уравнения прямой.

Как для интерполяции так и для экстраполяции в основе их рассчета лежит пропорция (y1 — y0)/(y2 — y0) = (x1 — x0)/(x2 — x0), прирощение значения в первой точке к прирощению значения во второй точке относится также как прирощение переменной в первой точке к прирощению переменной во второй точке (все относительно нулевой точки отсчета), из этой пропорции легко получить формулу рассчета любого значения

www.bl2.ru

Линейная интерполяция — это… Что такое Линейная интерполяция?

Лине́йная интерполя́ция — интерполяция алгебраическим двучленом P₁(x) = ax + b функции f, заданной в двух точках x₀ и x₁ отрезка [a, b]. В случае, если заданы значения в нескольких точках, функция заменяется кусочно-линейной функцией.

Геометрическая интерпретация

Геометрически это означает замену графика функции прямой, проходящей через точки и .

График: пример линейной интерполяции

Уравнение такой прямой имеет вид:

отсюда для

Это и есть формула линейной интерполяции

, при этом

где  — погрешность формулы:

Справедлива оценка

Применение

Линейная интерполяция применяется для уплотнения таблиц.

Формула линейной интерполяции является частным случаем интерполяционной формулы Лагранжа и интерполяционной формулы Ньютона.

См. также

dic.academic.ru

ЛИНЕЙНАЯ ИНТЕРПОЛЯЦИЯ — это… Что такое ЛИНЕЙНАЯ ИНТЕРПОЛЯЦИЯ?



ЛИНЕЙНАЯ ИНТЕРПОЛЯЦИЯ

способ приближенного вычисления значения функции f(x), основанный на замене функции f(х).линейной функцией

параметры аи b к-рой выбираются таким образом, чтобы значения L(х).совпадали со значениями f(x).в заданных точках х ₁ и х ₂:

Этим условиям удовлетворяет единственная функция

приближающая заданную функцию f(х)на отрезке [

x₁ , x₂]с погрешностью

Вычисления, необходимые для Л. и., легко реализуются при ручном счете, благодаря чему этот способ широко используется при интерполировании табличных данных.

Лит.:[1] Б а х в а л о в Н. С., Численные методы, 2 изд., М., 1975; [2] Б е р е з и н И. С., Жидков Н. П., Методы вычислений, 3 изд., т. 1, М., 1966. М. К. Самарин.

Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.

• ЛИНЕЙНАЯ ЗАВИСИМОСТЬ
• ЛИНЕЙНАЯ КЛАССИЧЕСКАЯ ГРУППА

Смотреть что такое «ЛИНЕЙНАЯ ИНТЕРПОЛЯЦИЯ» в других словарях:

• линейная интерполяция — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN linear interpolation …   Справочник технического переводчика

• Линейная интерполяция — Линейная интерполяция  интерполяция алгебраическим двучленом P1(x) = ax + b функции f, заданной в двух точках x0 и x1 отрезка [a, b]. В случае, если заданы значения в нескольких точках, функция заменяется кусочно линейной функцией.… …   Википедия

• линейная интерполяция — tiesinė interpoliacija statusas T sritis fizika atitikmenys: angl. linear interpolation vok. lineare Interpolation, f rus. линейная интерполяция, f pranc. interpolation linéaire, f …   Fizikos terminų žodynas

• интерполяция — Вычисление промежуточных значений между двумя известными точками. Например: linear линейная интерполяция exponential экспоненциальная интерполяция Процесс вывода цветного изображения, когда пикселы, относящиеся к области между двумя цветными… …   Справочник технического переводчика

• интерполяция — и, ж. interpolation f. < лат. interpolatio изменение; переделка, искажение. 1. Вставка позднейшего происхождения в каком л. тексте, не принадлежащая оригиналу. БАС 1. В древних рукописях много интерполяций, внесенных переписчиками. Уш. 1934. 2 …   Исторический словарь галлицизмов русского языка

• Интерполяция — О функции, см.: Интерполянт. Интерполяция, интерполирование  в вычислительной математике способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений. Многим из тех, кто сталкивается с научными и… …   Википедия

• Интерполяция (матем.) — О функции, см.: Интерполянт. Интерполяция  в вычислительной математике способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений. Многим из тех, кто сталкивается с научными и инженерными расчётами часто …   Википедия

• Билинейная интерполяция — Билинейная интерполяция  в вычислительной математике расширение линейной интерполяции для функций двух переменных. Ключевая идея заключается в том, чтобы провести обычную линейную интерполяцию сначала в одном направлении, затем в другом …   Википедия

• Интерполирование — О функции, см.: Интерполянт. Интерполяция  в вычислительной математике способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений. Многим из тех, кто сталкивается с научными и инженерными расчётами часто …   Википедия

• Таблица поиска — (англ. lookup table)  это структура данных, обычно массив или ассоциативный массив, используемая с целью заменить вычисления на операцию простого поиска. Увеличение скорости может быть значительным, так как получить данные из памяти… …   Википедия

dic.academic.ru

Линейная интерполяция — Википедия (с комментариями)

Материал из Википедии — свободной энциклопедии

Лине́йная интерполя́ция — интерполяция алгебраическим двучленом P₁(x) = ax + b функции f, заданной в двух точках x₀ и x₁ отрезка [a, b]. В случае, если заданы значения в нескольких точках, функция заменяется кусочно-линейной функцией.

Геометрическая интерпретация

Геометрически это означает замену графика функции <math>f</math> прямой, проходящей через точки <math>(x_0, f(x_0))</math> и <math>(x_1, f(x_1))</math>.

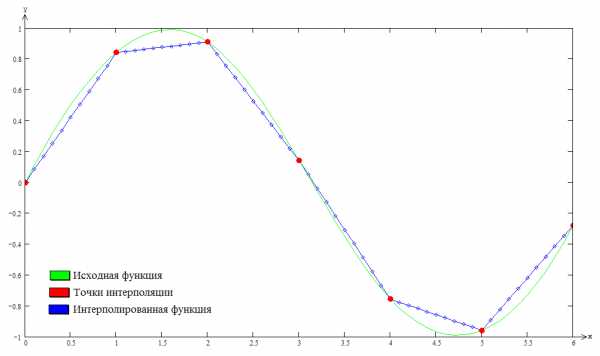
Уравнение такой прямой имеет вид:

<math>\frac{y — f(x_0)}{f(x_1) — f(x_0)} = \frac{x — x_0}{x_1 — x_0}</math>

отсюда для <math>x \in [x_0, x_1]</math>

<math>f(x) \approx y = P_1(x) = f(x_0) + \frac{f(x_1) — f(x_0)}{x_1 — x_0}(x — x_0)</math>

Это и есть формула линейной интерполяции, при этом

<math>f(x) = P_1(x) + R_1(x)\quad</math>

где <math>R_1(x)</math> — погрешность формулы:

<math>R_1(x) = \frac{f(\psi)}{2}(x — x_0)(x — x_1),\quad \psi \in [x_0, x_1]</math>

Справедлива оценка

<math>|R_1(x)|\leqslant \frac{M_2}{2} \max |(x — x_0)(x — x_1)| = \frac{M_2 h^2}{8},\quad M_2 = \max_{[x_0,x_1]} |f(x)|,\quad h = x_1 — x_0.</math>

Матричная форма

можно записать P(x) = ax + b следующим образом <math>P(x)= \begin{pmatrix} a & b \end{pmatrix} \begin{pmatrix} x \\ 1 \\ \end{pmatrix} </math>

условия будут записаны так: <math> \begin{pmatrix} a & b \end{pmatrix} \begin{pmatrix} x_{0} & x_{1} \\ 1 & 1 \\ \end{pmatrix} = \begin{pmatrix} P_{0} & P_{1}\\ \end{pmatrix} </math>

отсюда можно найти: <math> \begin{pmatrix} a & b \end{pmatrix} = \begin{pmatrix} P_{0} & P_{1}\\ \end{pmatrix} \begin{pmatrix} x_{0} & x_{1} \\ 1 & 1 \\ \end{pmatrix}^{-1} </math>
Получаем:
<math> P(x)= \begin{pmatrix} P_{0} & P_{1}\\ \end{pmatrix} \begin{pmatrix} x_{0} & x_{1} \\ 1 & 1 \\ \end{pmatrix}^{-1} \begin{pmatrix} x \\ 1 \\ \end{pmatrix} </math>
Распространяя на:

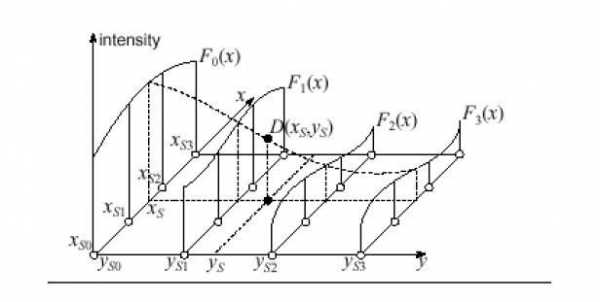
<math> P(x,y)= \begin{pmatrix} P_{0} & P_{1} & P_{2}\\ \end{pmatrix} \begin{pmatrix} x_{0} & x_{1} & x_{2} \\ y_{0} & y_{1} & y_{2} \\ 1 & 1 & 1 \\ \end{pmatrix}^{-1} \begin{pmatrix} x \\ y \\ 1 \\ \end{pmatrix} </math>

<math> P(x,y,z)= \begin{pmatrix} P_{0} & P_{1} & P_{2}& P_{3}\\ \end{pmatrix} \begin{pmatrix} x_{0} & x_{1} & x_{2} & x_{3}\\ y_{0} & y_{1} & y_{2} & y_{3} \\ z_{0} & z_{1} & z_{2} & z_{3} \\ 1 & 1 & 1 & 1 \\ \end{pmatrix}^{-1} \begin{pmatrix} x \\ y \\ z \\ 1 \\ \end{pmatrix} </math>

Применение

Линейная интерполяция применяется для уплотнения таблиц.

Формула линейной интерполяции является частным случаем интерполяционной формулы Лагранжа и интерполяционной формулы Ньютона.

См. также

Напишите отзыв о статье «Линейная интерполяция»

Отрывок, характеризующий Линейная интерполяция

– Что бы ни случилось с вами, – сказал он, – вы должны с мужеством переносить всё, ежели вы твердо решились вступить в наше братство. (Пьер утвердительно отвечал наклонением головы.) Когда вы услышите стук в двери, вы развяжете себе глаза, – прибавил Вилларский; – желаю вам мужества и успеха. И, пожав руку Пьеру, Вилларский вышел.
Оставшись один, Пьер продолжал всё так же улыбаться. Раза два он пожимал плечами, подносил руку к платку, как бы желая снять его, и опять опускал ее. Пять минут, которые он пробыл с связанными глазами, показались ему часом. Руки его отекли, ноги подкашивались; ему казалось, что он устал. Он испытывал самые сложные и разнообразные чувства. Ему было и страшно того, что с ним случится, и еще более страшно того, как бы ему не выказать страха. Ему было любопытно узнать, что будет с ним, что откроется ему; но более всего ему было радостно, что наступила минута, когда он наконец вступит на тот путь обновления и деятельно добродетельной жизни, о котором он мечтал со времени своей встречи с Осипом Алексеевичем. В дверь послышались сильные удары. Пьер снял повязку и оглянулся вокруг себя. В комнате было черно – темно: только в одном месте горела лампада, в чем то белом. Пьер подошел ближе и увидал, что лампада стояла на черном столе, на котором лежала одна раскрытая книга. Книга была Евангелие; то белое, в чем горела лампада, был человечий череп с своими дырами и зубами. Прочтя первые слова Евангелия: «Вначале бе слово и слово бе к Богу», Пьер обошел стол и увидал большой, наполненный чем то и открытый ящик. Это был гроб с костями. Его нисколько не удивило то, что он увидал. Надеясь вступить в совершенно новую жизнь, совершенно отличную от прежней, он ожидал всего необыкновенного, еще более необыкновенного чем то, что он видел. Череп, гроб, Евангелие – ему казалось, что он ожидал всего этого, ожидал еще большего. Стараясь вызвать в себе чувство умиленья, он смотрел вокруг себя. – «Бог, смерть, любовь, братство людей», – говорил он себе, связывая с этими словами смутные, но радостные представления чего то. Дверь отворилась, и кто то вошел.

wiki-org.ru

Линейная интерполяция — Википедия. Что такое Линейная интерполяция

Материал из Википедии — свободной энциклопедии

Лине́йная интерполя́ция — интерполяция алгебраическим двучленом P₁(x) = ax + b функции f, заданной в двух точках x₀ и x₁ отрезка [a, b]. В случае, если заданы значения в нескольких точках, функция заменяется кусочно-линейной функцией.

Геометрическая интерпретация

Геометрически это означает замену графика функции f{\displaystyle f} прямой, проходящей через точки (x0,f(x0)){\displaystyle (x_{0},f(x_{0}))} и (x1,f(x1)){\displaystyle (x_{1},f(x_{1}))}.

График: пример линейной интерполяции

Уравнение такой прямой имеет вид:

y−f(x0)f(x1)−f(x0)=x−x0x1−x0{\displaystyle {\frac {y-f(x_{0})}{f(x_{1})-f(x_{0})}}={\frac {x-x_{0}}{x_{1}-x_{0}}}}

отсюда для x∈[x0,x1]{\displaystyle x\in [x_{0},x_{1}]}

f(x)≈y=P1(x)=f(x0)+f(x1)−f(x0)x1−x0(x−x0){\displaystyle f(x)\approx y=P_{1}(x)=f(x_{0})+{\frac {f(x_{1})-f(x_{0})}{x_{1}-x_{0}}}(x-x_{0})}

Это и есть формула линейной интерполяции, при этом

f(x)=P1(x)+R1(x){\displaystyle f(x)=P_{1}(x)+R_{1}(x)\quad }

где R1(x){\displaystyle R_{1}(x)} — погрешность формулы:

R1(x)=f″(ψ)2(x−x0)(x−x1),ψ∈[x0,x1]{\displaystyle R_{1}(x)={\frac {f»(\psi )}{2}}(x-x_{0})(x-x_{1}),\quad \psi \in [x_{0},x_{1}]}

Справедлива оценка

|R1(x)|⩽M22max|(x−x0)(x−x1)|=M2h38,M2=max[x0,x1]|f″(x)|,h=x1−x0.{\displaystyle |R_{1}(x)|\leqslant {\frac {M_{2}}{2}}\max |(x-x_{0})(x-x_{1})|={\frac {M_{2}h^{2}}{8}},\quad M_{2}=\max _{[x_{0},x_{1}]}|f»(x)|,\quad h=x_{1}-x_{0}.}

Матричная форма

можно записать P(x) = ax + b следующим образом P(x)=(ab)(x1){\displaystyle P(x)={\begin{pmatrix}a&b\end{pmatrix}}{\begin{pmatrix}x\\1\\\end{pmatrix}}}

условия будут записаны так: (ab)(x0x111)=(P0P1){\displaystyle {\begin{pmatrix}a&b\end{pmatrix}}{\begin{pmatrix}x_{0}&x_{1}\\1&1\\\end{pmatrix}}={\begin{pmatrix}P_{0}&P_{1}\\\end{pmatrix}}}

отсюда можно найти: (ab)=(P0P1)(x0x111)−1{\displaystyle {\begin{pmatrix}a&b\end{pmatrix}}={\begin{pmatrix}P_{0}&P_{1}\\\end{pmatrix}}{\begin{pmatrix}x_{0}&x_{1}\\1&1\\\end{pmatrix}}^{-1}}
Получаем:
P(x)=(P0P1)(x0x111)−1(x1){\displaystyle P(x)={\begin{pmatrix}P_{0}&P_{1}\\\end{pmatrix}}{\begin{pmatrix}x_{0}&x_{1}\\1&1\\\end{pmatrix}}^{-1}{\begin{pmatrix}x\\1\\\end{pmatrix}}}
Распространяя на:

P(x,y)=(P0P1P2)(x0x1x2y0y1y2111)−1(xy1){\displaystyle P(x,y)={\begin{pmatrix}P_{0}&P_{1}&P_{2}\\\end{pmatrix}}{\begin{pmatrix}x_{0}&x_{1}&x_{2}\\y_{0}&y_{1}&y_{2}\\1&1&1\\\end{pmatrix}}^{-1}{\begin{pmatrix}x\\y\\1\\\end{pmatrix}}}

P(x,y,z)=(P0P1P2P3)(x0x1x2x3y0y1y2y3z0z1z2z31111)−1(xyz1){\displaystyle P(x,y,z)={\begin{pmatrix}P_{0}&P_{1}&P_{2}&P_{3}\\\end{pmatrix}}{\begin{pmatrix}x_{0}&x_{1}&x_{2}&x_{3}\\y_{0}&y_{1}&y_{2}&y_{3}\\z_{0}&z_{1}&z_{2}&z_{3}\\1&1&1&1\\\end{pmatrix}}^{-1}{\begin{pmatrix}x\\y\\z\\1\\\end{pmatrix}}}

Применение

Линейная интерполяция применяется для уплотнения таблиц.

Формула линейной интерполяции является частным случаем интерполяционной формулы Лагранжа и интерполяционной формулы Ньютона.

См. также

wiki.sc

линейная интерполяция — это… Что такое линейная интерполяция?



линейная интерполяция

simple interpolation

Большой англо-русский и русско-английский словарь. 2001.

• линейная интенсивность изнашивания
• линейная итерация

Смотреть что такое «линейная интерполяция» в других словарях:

• линейная интерполяция — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN linear interpolation …   Справочник технического переводчика

• Линейная интерполяция — Линейная интерполяция  интерполяция алгебраическим двучленом P1(x) = ax + b функции f, заданной в двух точках x0 и x1 отрезка [a, b]. В случае, если заданы значения в нескольких точках, функция заменяется кусочно линейной функцией.… …   Википедия

• линейная интерполяция — tiesinė interpoliacija statusas T sritis fizika atitikmenys: angl. linear interpolation vok. lineare Interpolation, f rus. линейная интерполяция, f pranc. interpolation linéaire, f …   Fizikos terminų žodynas

• ЛИНЕЙНАЯ ИНТЕРПОЛЯЦИЯ — способ приближенного вычисления значения функции f(x), основанный на замене функции f(х).линейной функцией параметры аи b к рой выбираются таким образом, чтобы значения L(х).совпадали со значениями f(x).в заданных точках х 1 и х 2: Этим условиям… …   Математическая энциклопедия

• интерполяция — Вычисление промежуточных значений между двумя известными точками. Например: linear линейная интерполяция exponential экспоненциальная интерполяция Процесс вывода цветного изображения, когда пикселы, относящиеся к области между двумя цветными… …   Справочник технического переводчика

• интерполяция — и, ж. interpolation f. &LT; лат. interpolatio изменение; переделка, искажение. 1. Вставка позднейшего происхождения в каком л. тексте, не принадлежащая оригиналу. БАС 1. В древних рукописях много интерполяций, внесенных переписчиками. Уш. 1934. 2 …   Исторический словарь галлицизмов русского языка

• Интерполяция — О функции, см.: Интерполянт. Интерполяция, интерполирование  в вычислительной математике способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений. Многим из тех, кто сталкивается с научными и… …   Википедия

• Интерполяция (матем.) — О функции, см.: Интерполянт. Интерполяция  в вычислительной математике способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений. Многим из тех, кто сталкивается с научными и инженерными расчётами часто …   Википедия

• Билинейная интерполяция — Билинейная интерполяция  в вычислительной математике расширение линейной интерполяции для функций двух переменных. Ключевая идея заключается в том, чтобы провести обычную линейную интерполяцию сначала в одном направлении, затем в другом …   Википедия

• Интерполирование — О функции, см.: Интерполянт. Интерполяция  в вычислительной математике способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений. Многим из тех, кто сталкивается с научными и инженерными расчётами часто …   Википедия

• Таблица поиска — (англ. lookup table)  это структура данных, обычно массив или ассоциативный массив, используемая с целью заменить вычисления на операцию простого поиска. Увеличение скорости может быть значительным, так как получить данные из памяти… …   Википедия

dic.academic.ru

это… Определение, особенности расчета и примеры интерполяции :: SYL.ru

Многие из нас сталкивались с непонятными терминами в разных науках. Но находится очень мало людей, которых не пугают непонятные слова, а наоборот, приободряют и заставляют всё больше углубиться в изучаемый предмет. Сегодня речь пойдёт о такой вещи, как интерполяция. Это способ построения графиков по известным точкам, позволяющий с минимальным количеством информации о функции предсказать её поведение на конкретных участках кривой.

Перед тем как перейти к сути самого определения и рассказать о нём подробнее, немного углубимся в историю.

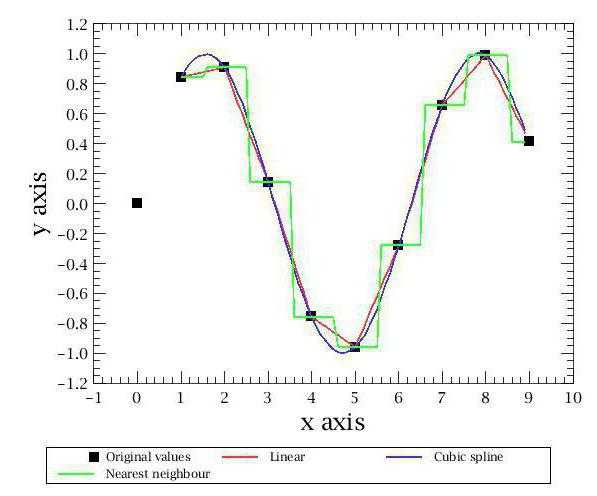
История

Интерполяция была известна ещё с древнейших времён. Однако своим развитием это явление обязано нескольким самым выдающимся математикам прошлого: Ньютону, Лейбницу и Грегори. Именно они развили это понятие с помощью более продвинутых математических способов, доступных в то время. До этого интерполяцию, конечно, применяли и использовали в вычислениях, но делали это совершенно неточными способами, требующими большого количества данных для построения модели, более-менее близкой к реальности.

Сегодня мы можем даже выбирать, какой из способов интерполяции подходит больше. Всё переведено на компьютерный язык, который с огромной точностью может предсказывать поведение функции на определённом участке, ограниченном известными точками.

Интерполяция представляет собой достаточно узкое понятие, поэтому её история не так богата фактами. В следующем разделе разберёмся, что такое интерполяция на самом деле и чем она отличается от своей противоположности — экстраполяции.

Что такое интерполяция?

Как мы уже говорили, это общее название способов, позволяющих построить график по точкам. В школе в основном это делают с помощью составления таблицы, выявления точек на графике и примерного построения линий, их соединяющих. Последнее действие делается исходя из соображений похожести исследуемой функции на другие, вид графиков которых нам известен.

Однако есть другие, более сложные и точные способы выполнить поставленную задачу построения графика по точкам. Итак, интерполяция — это фактически «предсказание» поведения функции на конкретном участке, ограниченном известными точками.

Существует схожее понятие, связанное с этой же областью, — экстраполяция. Она представляет собой также предсказание графика функции, но за пределами известных точек графика. При таком способе предсказание делается на основе поведения функции на известном промежутке, и потом эта функция применяется и для неизвестного промежутка. Такой способ очень удобен для практического применения и активно используется, например, в экономике для прогнозирования взлётов и падения на рынке и для предсказания демографической ситуации в стране.

Но мы отошли от основной темы. В следующем разделе разберёмся, какая бывает интерполяция и с помощью каких формул можно произвести эту операцию.

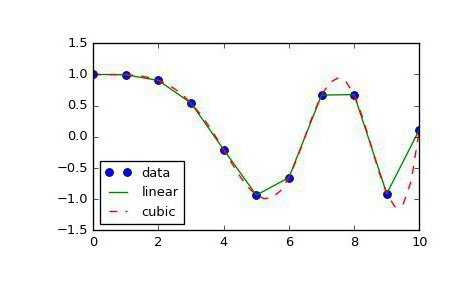
Виды интерполяции

Самым простым видом является интерполяция методом ближайшего соседа. С помощью этого способа мы получаем очень приблизительный график, состоящий из прямоугольников. Если вы видели хоть раз объяснение геометрического смысла интеграла на графике, то поймёте, о каком графическом виде идёт речь.

Кроме этого, существуют и другие методы интерполяции. Самые известные и популярные связаны с многочленами. Они более точны и позволяют предсказывать поведение функции при достаточно скудном наборе значений. Первым методом интерполяции, который мы рассмотрим, будет линейная интерполяция многочленами. Это самый простой способ из данной категории, и им наверняка каждый из вас пользовался в школе. Суть его заключается в построении прямых между известными точками. Как известно, через две точки плоскости проходит единственная прямая, уравнение которой можно найти исходя из координат данных точек. Построив эти прямые, мы получаем ломаный график, который худо-бедно, но отражает примерные значения функций и в общих чертах совпадает с реальностью. Так и осуществляется линейная интерполяция.

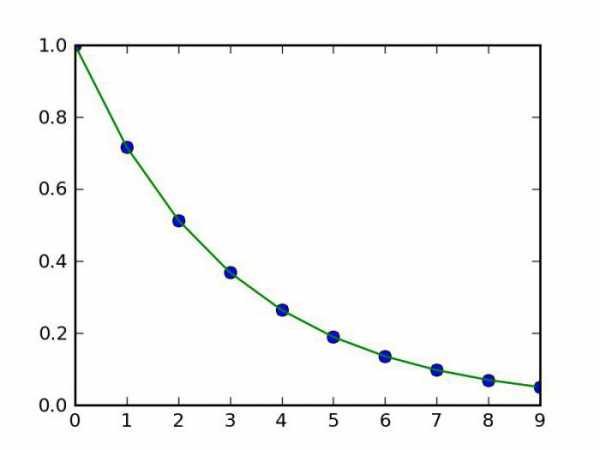
Усложнённые виды интерполяции

Есть более интересный, но при этом более сложный способ интерполяции. Его придумал французский математик Жозеф Луи Лагранж. Именно поэтому расчет интерполяции по этому методу назван его именем: интерполяция по методу Лагранжа. Фокус тут вот в чём: если способ, изложенный в предыдущем абзаце, использует для расчета только линейную функцию, то разложение методом Лагранжа предполагает также использование многочленов более высоких степеней. Но не так просто найти сами формулы интерполяции для разных функций. И чем больше точек известно, тем точнее получается формула интерполяции. Но есть и масса других методов.

Существует и более совершенный и приближенный к реальности метод расчета. Формула интерполяции, используемая в нём, представляет собой совокупность многочленов, применение каждого из которых зависит от участка функции. Такой метод называется сплайн-функцией. Кроме того, есть ещё и способы, позволяющие провести такую вещь, как интерполяция функций двух переменных. Тут всего два метода. Среди них билинейная или двойная интерполяция. Этот способ позволяет без труда построить график по точкам в трёхмерном пространстве. Другие методы затрагивать не будем. Вообще, интерполяция — это универсальное называние для всех этих способов построения графиков, но многообразие способов, которыми можно осуществить это действие, заставляет делить их на группы в зависимости от вида функции, которая подлежит этому действию. То есть интерполяция, пример которой мы рассмотрели выше, относится к прямым способам. Есть также обратная интерполяция, которая отличается тем, что позволяет вычислить не прямую, а обратную функцию (то есть x от y). Рассматривать последние варианты мы не будем, так как это достаточно сложно и требует хорошей математической базы знаний.

Перейдём к, пожалуй, одному из важнейших разделов. Из него мы узнаем, как и где обсуждаемая нами совокупность методов применяется в жизни.

Применение

Математика, как известно, царица наук. Поэтому даже если вы сначала не видите смысла в тех или иных операциях, это не значит, что они бесполезны. Вот, например, кажется, что интерполяция — это бесполезная вещь, с помощью которой только графики строить можно, которые сейчас мало кому нужны. Однако при любых расчётах в технике, физике и многих других науках (например, биологии), крайне важно представлять достаточно полную картину о явлении, имея при этом определённый набор значений. Сами значения, разбросанные по графику, не всегда дают чёткие представления о поведении функции на конкретном участке, значениях её производных и точек пересечения с осями. А это очень важно для многих областей нашей с вами жизни.

А как это пригодится в жизни?

На подобный вопрос бывает очень сложно ответить. Но ответ прост: никак. Именно эти знания вам никак не пригодятся. А вот если вы поймёте этот материал и методы, с помощью которых осуществляются эти действия, вы потренируете свою логику, которая в жизни очень пригодится. Главное — не сами знания, а те навыки, которые человек приобретает в процессе изучения. Ведь недаром существует поговорка: «Век живи — век учись».

Смежные понятия

Вы можете сами понять, насколько важна была (и до сих пор не теряет свою важность) эта область математики, взглянув на многообразие других концепций, связанных с данной. Мы уже говорили об экстраполяции, но есть ещё и аппроксимация. Может быть, вы уже слышали это слово. В любом случае то, что оно обозначает, мы тоже разбирали в этой статье. Аппроксимация, как и интерполяция, — это понятия, связанные с построением графиков функций. Но отличие первой от второй в том, что она представляет собой приблизительное построение графика на основе сходных известных графиков. Эти два понятия очень похожи между собой, и тем интереснее изучать каждое из них.

Заключение

Математика — не такая сложная наука, как кажется на первый взгляд. Она, скорее, интересная. И в этой статье мы попытались вам это доказать. Мы рассмотрели понятия, связанные с построением графиков, узнали, что такое двойная интерполяция, и разобрали на примерах, где она применяется.

www.syl.ru