Что может принадлежать плоскости – —

2.3. Принадлежность точки и прямой плоскости

Признаки принадлежности хорошо известны из курса планиметрии. Наша задача рассмотреть их применительно к проекциям геометрических объектов.

Точка принадлежит плоскости, если она принадлежит прямой, лежащей в этой плоскости.

Принадлежность прямой плоскости определяется по одному из двух признаков:

а) прямая проходит через две точки, лежащие в этой плоскости;

б) прямая проходит через точку и параллельна прямой, лежащим в этой плоскости.

Используя эти свойства, решим в качестве примера задачу. Пусть плоскость задана треугольником АВС. Требуется построить недостающую проекцию D₁ точки D, принадлежащей этой плоскости. Последовательность построений следующая (рис. 2.5).

Рис. 2.5. К построению проекций точки, принадлежащей плоскости

Через точку D₂ проводим проекцию прямой d, лежащей в плоскости АВС, пересекающую одну из сторон треугольника и точку А₂. Тогда точка 1₂ принадлежит прямым А₂D₂ и C₂В₂. Следовательно, можно получить ее горизонтальную проекцию 1₁ на C₁В₁ по линии связи. Соединив точки 1₁ и А₁, получаем горизонтальную проекцию d₁. Ясно, что точка D₁ принадлежит ей и лежит на линии проекционной связи с точкой D₂.

Достаточно просто решаются задачи на определение принадлежности точки или прямой плоскости. На рис. 2.6 показан ход решения таких задач. Для наглядности изложения задачи плоскость задаем треугольником.

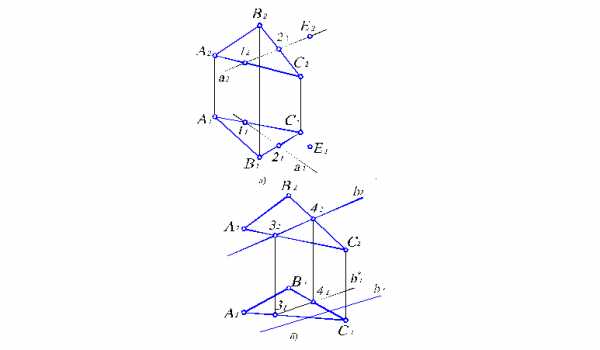
Рис. 2.6. Задачи на определение принадлежности точки и прямой плоскости.

Для того, чтобы определить принадлежит ли точка Е плоскости АВС, проведем через ее фронтальную проекцию Е₂ прямую а₂. Считая, что прямая а принадлежит плоскости АВС, построим ее горизонтальную проекцию а₁ по точкам пересечения 1 и 2. Как видим (рис. 2.6, а), прямая а₁ не проходит через точку Е₁. Следовательно, точка Е АВС.

В задаче на принадлежность прямой в плоскости треугольника АВС (рис. 2.6, б), достаточно по одной из проекций прямой в₂ построить другую в₁* считая, что в

АВС. Как видим, в₁* и в₁ не совпадают. Следовательно, прямая в  АВС.

2.4. Линии уровня в плоскости

Определение линий уровня было дано ранее. Линии уровня, принадлежащие данной плоскости, называются главными. Эти линии (прямые) играют существенную роль при решении ряда задач начертательной геометрии.

Рассмотрим построение линий уровня в плоскости, заданной треугольником (рис. 2.7).

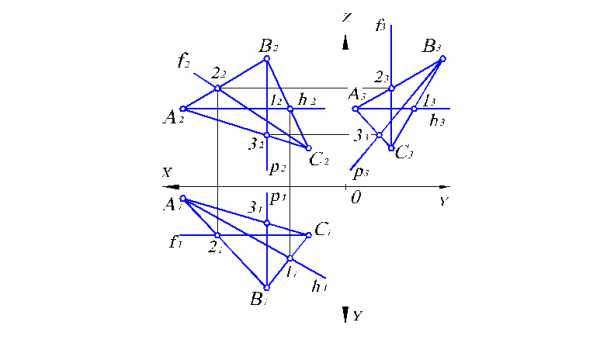
Рис. 2.7. Построение главных линий плоскости, заданной треугольником

Горизонталь плоскости АВС начинаем с вычерчивания ее фронтальной проекции h₂, которая, как известно, параллельна оси ОХ. Поскольку эта горизонталь принадлежит данной плоскости, то она проходит через две точки плоскости 

АВС, а именно, точки А и 1. Имея их фронтальные проекции А₂ и 1₂, по линии связи получим горизонтальные проекции (А₁ уже есть) 1₁. Соединив точки А₁ и1₁, имеем горизонтальную проекцию h₁ горизонтали плоскости АВС. Профильная проекция h₃ горизонтали плоскости АВС будет параллельна оси ОХ по определению.

Фронталь плоскости АВС строится аналогично (рис. 2.7) с той лишь разницей, что ее вычерчивание начинается с горизонтальной проекции f₁, так как известно, что она параллельна оси ОХ. Профильная проекция f₃ фронтали должна быть параллельна оси ОZ и пройти через проекции С₃, 2₃ тех же точек С и 2.

Профильная линия плоскости АВС имеет горизонтальную

р₁ и фронтальную р₂ проекции, параллельные осям OY и OZ, а профильную проекцию р₃ можно получить по фронтальной, используя точки пересечения В и 3 с  АВС.

При построении главных линий плоскости необходимо помнить лишь одно правило: для решения задачи всегда нужно получить две точки пересечения с данной плоскостью. Построение главных линий, лежащих в плоскости, заданной иным способом, ничуть не сложнее рассмотренного выше. На рис. 2.8 показано построение горизонтали и фронтали плоскости, заданной двумя пересекающимися прямыми аив.

Рис. 2.8. Построение главных линий плоскости, заданной пересекающимися прямыми.

studfiles.net

Д12. Плоскость общего положения. Принадлежность точки плоскости

37

Следует помнить, что плоскость безгранична, поэтому точки, линии и плоские фигуры, принадлежащие плоскости, могут находиться в пределах или выходить за пределы геометрических фигур, задающих плоскость.

Плоскость может занимать различные положения относительн плоскостей проекций:

-общее, если плоскость наклонена ко всем трем плоскостям проекций;

-проецирующее, если плоскость перпендикулярна одной из плоскостей проекций;

-положение уровня, если плоскость параллельна одной плоскости проекций.

Плоскостью общего положения называется плоскость, не параллельная

и не перпендикулярная ни одной из плоскостей проекций.
Плоскость	общего	положения	может	быть	задана , способ
перечисленными выше (рис. 35).
Например, если плоскость задана тремя точками(рис. 36а), то, соединив
эти точки отрезками прямых, получим задание плоскости треугольником (						АВС
на рис. 36б). Можно через заданные три точки провести две параллельные
прямые (а || b на рис. 36в) и т.д.
Если плоскость задана на чертеже, то это значит, что					может	быть
построена любая точка, принадлежащая данной плоскости.

Точка в плоскости строится из условия принадлежности:

точка принадлежит плоскости, если она принадлежит какой-либопрямой этой плоскости.

Плоскость β, заданная двумя пересекающимися прямымиа иb, и точка

СÎ β изображены на рис. 37.

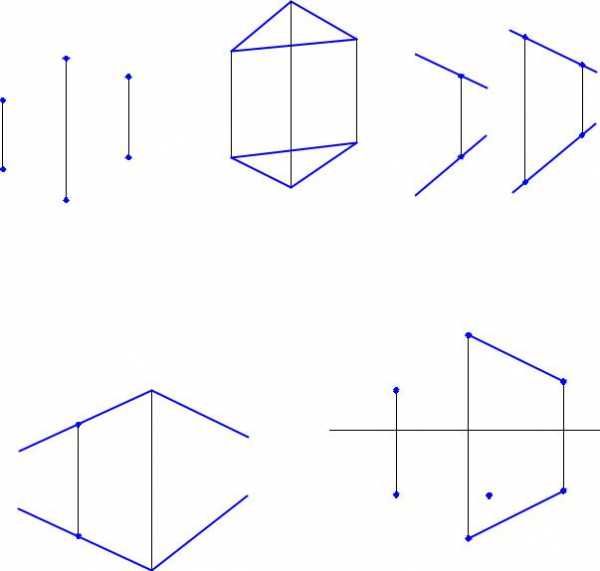
38

Точка С принадлежит заданной плоскости, так как она принадлежит

прямой а этой плоскости.
	а)			б)		в)
				В2		В2
	В		А2	С			b2С
	2	С		2	А2
А2						а2	2
		2
				С		а1	С
			А1		А		1
А1В1		С		1			b1
				В1	1	В1
		1
			Рис.36
					В2		С
				А2
	С		b2				2
а2				х
	2
				А1		М1	С
а1			b1				1
	С				В1
	1
		Рис.37			Рис.38

ЗАДАЧА. Построить недостающую проекциюМ2 точкиМ, принадлежащей плоскостиα (А,ВС) (рис.38).

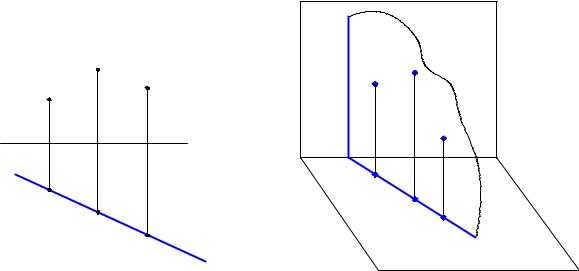
39

Д13. Проецирующие плоскости. Принадлежность точки плоскости

Проецирующей называется плоскость, перпендикулярная к одной из плоскостей проекций.

Плоскость, перпендикулярная к плоскости проекцийП1, называетсягоризонтально-проецирующей;плоскость перпендикулярная к плоскостиП2,–

фронтально-проецирующей;плоскость перпендикулярная к плоскостиП3,–

профильно-проецирующейплоскостью.

Проецирующая плоскость, как и плоскость общего положения, может быть задана тремя точками, не лежащими на одной прямой(например,

горизонтально-проецирующаяплоскостьα на рис. 39), прямой и точкой, не лежащей на этойпрямой(фронтально-проецирующаяплоскостьβ на рис. 40),

двумя пересекающимися прямыми(профильно-проецирующаяплоскостьγ на рис. 41) и т.д.

а)		В2		б)	a
			С		А	В
	А2		2
						С
х
	А1	В1			А1	В1С	a1
				a1
			С					p
						1
			1					1

Рис.39

						40
а)						б)
F2			m2=b2
х
F1			m1
						Рис.40
а)		l2	z			б)
n			n =l		3	=g
	D		3			3
2				D3
	2
х			О			у
n		l1
1
	D1		у
						Рис.41

Проецирующая плоскость изображается в виде прямой линии на той

плоскости проекций, перпендикулярно	которой она	расположена; на двух
других плоскостях проекций она изображается множеством точек.
Например, на рис. 39 плоскость α	изображается	в виде прямойα1 на

плоскости проекций П1; на плоскостиП2 плоскостьα изображается точками

А2, В2, С2.

Проекция плоскости – прямая линия обладает собирательным свойством:

на эту прямую проецируются все точки и прямые, принадлежащие данной

Построить горизонтально-

проецирующую плоскость,

проходящую через прямую т

(рис.42).

41

плоскости (например, на рис. 40 точка F и прямаяm, принадлежащие плоскости

β, проецируются на прямуюβ2).

Проекция плоскости в виде прямой линии вполне определяетпрое цирующую плоскость, поэтому на чертеже проецирующая плоскость может быть задана одной своей проекцией.

т2 ЗАДАЧА.

х

т

1

Рис.42

Д14. Плоскости уровня. Принадлежность точки плоскости

Плоскостью уровня называется плоскость, параллельная одной из

плоскостей проекций. К двум другим плоскостям проекций плоскость уровня расположена перпендикулярно.

Плоскость, параллельная плоскости П1, называется горизонтальной

(рис.43), параллельная плоскости П2 – фронтальной (рис.44), параллельная

плоскости П3 – профильной плоскостью (рис.45).

Плоскость уровня может быть задана теми же способами, которыми

задается плоскость общего положения.
На	плоскостях	проекций, перпендикулярно	которым	расположена

плоскость уровня, она изображается в виде прямых линий, параллельных осям проекций; на плоскости проекции, параллельно которой расположена плоскость

studfiles.net

Принадлежность прямой плоскости — КиберПедия

Прямая принадлежит плоскости если она проходит через две точки, лежащих в этой плоскости.

Дано: задана плоскость α(∆АВС) и одна из проекций прямой l₁ которая принадлежит этой плоскости (рис. 41).

Определитьнедостающею проекцию прямой l₂ при условии, что прямая l Ì α(∆АВС).

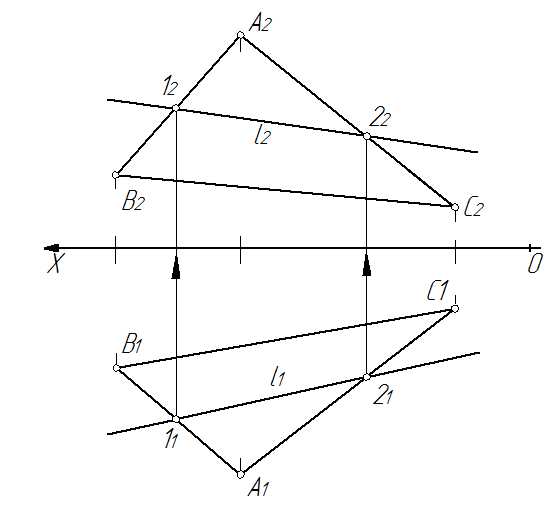
Рис. 41

Алгоритм решения.

1. Выбираются проекции двух точек одновременно принадлежащие заданным плоскости и прямой (А₁В₁∩l₁=1₁ и А₁С₁∩l₁=2₁).

2. По принадлежности точки 1ÌАВ и 2ÌАС определяются недостающие проекции точек 1₂ и 2₂.

3. Через полученные проекции точек 1₂ и 2₂ достраивается недостающая проекция прямой l₂ принадлежащей плоскости α.

Принадлежность точки плоскости

Точка принадлежит плоскости если она принадлежит прямой лежащей в этой плоскости.

Дано: задана плоскость α(∆АВС) и одна из проекций точки К, которая принадлежит этой плоскости (рис. 42).

Определитьнедостающею проекцию точки К.

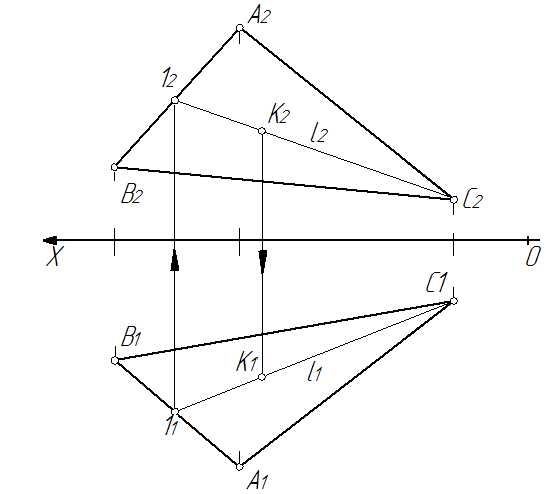
Рис. 42

Алгоритм решения.

1. Через известную проекцию точки К₁ проводим проекцию прямой l₁ в предположение, что эта прямая принадлежит заданной плоскости (l Ì α).

2. По вышеуказанному алгоритму определяется недостающая проекция прямой l₂.

3. По принадлежности точки К прямо l достраивается искомая проекция точки К₂.

Главные прямые плоскости

Основными главными линиями плоскости являются: горизонтали плоскости; фронтали плоскости; линии наибольшего ската; линии наибольшего наклона.

Горизонталь плоскости. Горизонталь плоскости – прямая, которая лежит в этой плоскости и параллельна горизонтальной плоскости проекций. На рис. 43 показана горизонталь h плоскости α.

Алгоритм построения горизонтали (рис. 44).

1. Горизонталь плоскости как прямая, параллельная горизонтальной плоскости проекций, имеет фронтальную проекцию h₂, параллельную оси 0Х. Поэтому вначале на фронтальной проекции заданной плоскости строится характерный признак горизонтали. На рис. 44 h₂(С₂1₂)∥0X.

2. По принадлежности прямой плоскости (алгоритм принадлежности прямой плоскости) достраивается недостающая проекция горизонтали плоскости h₁.

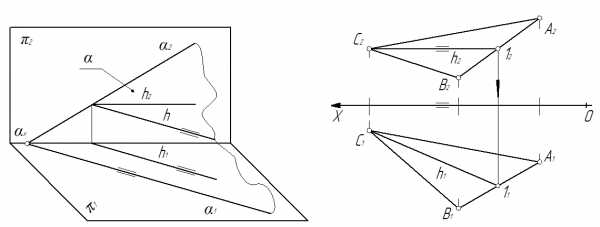
Рис. 43 Рис. 44

Следует отметить, что все горизонтали плоскости параллельны между собой и параллельны горизонтальному следу плоскости.

Фронталь плоскости. Фронталь плоскости – прямая, которая лежит в этой плоскости и параллельна фронтальной плоскости проекций. На рис. 45 показана фронталь f плоскости α.

Алгоритм построения фронтали (рис. 46).

1. Фронталь плоскости как прямая, параллельная фронтальной плоскости проекций, имеет горизонтальную проекцию f₁, параллельную оси 0Х. Поэтому вначале на горизонтальной проекции заданной плоскости строится характерный признак фронтали. На рис. 46 f₁(A₁1₁)∥0X.

2. По принадлежности прямой плоскости (алгоритм принадлежности прямой плоскости) достраивается недостающая проекция горизонтали плоскости f₂.

Линия наибольшего ската. Линия наибольшего ската – прямая, которая лежит в этой плоскости и перпендикулярная горизонталям этой плоскости. Угол α (рис. 47) между линией наибольшего ската и ее горизонтальной проекцией равен углу наклона плоскости к горизонтальной плоскости проекций. Поэтому линия наибольшего ската характеризует угол наклона плоскости к горизонтальной плоскости проекций.

Алгоритм построения линии наибольшего ската (рис. 48).

1. В заданной плоскости проводится горизонталь h.

2. Используя теорему о прямом угле, на первой проекции плоскости, строится проекция линии наибольшего ската l₁(В₁2₁)^h₁(C₁1₁).

Рис. 45 Рис. 46

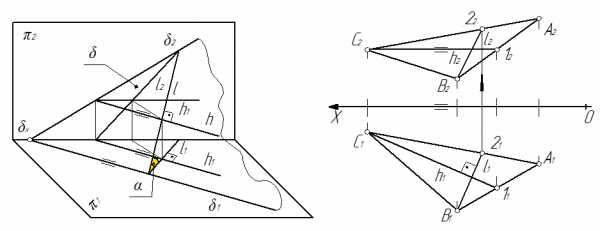
Рис. 47 Рис. 48

3. По принадлежности прямой плоскости достраивается недостающая проекция l₂ линии наибольшего ската.

Следует отменить, что все линии наибольшего ската параллельны между собой и перпендикулярны горизонтальному следу плоскости.

Линия наибольшего наклона. Линия наибольшего наклона – прямая, которая лежит в этой плоскости и перпендикулярная фронталям этой плоскости. Угол β (рис. 49) между линией наибольшего наклона и ее фронтальной проекцией равен углу наклона плоскости к фронтальной плоскости проекций. Поэтому линия наибольшего наклона характеризует угол наклона плоскости к фронтальной плоскости проекций.

Алгоритм построения линии наибольшего наклона (рис. 50).

1. В заданной плоскости проводится фронталь f.

2. Используя теорему о прямом угле, на второй проекции плоскости, строится проекция линии наибольшего наклона f₂(В₂2₂)^f₂(A₂1₂).

3. По принадлежности прямой плоскости достраивается недостающая проекция l₁ линии наибольшего наклона.

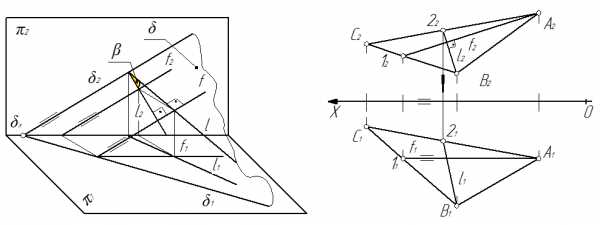
Рис. 49 Рис. 50

Следует отменить, что все линии наибольшего наклона параллельны между собой и перпендикулярны фронтальному следу плоскости.

cyberpedia.su

Принадлежность прямой плоскости | Начертательная геометрия

Принадлежность прямой плоскости на комплексном чертеже определяется согласно аксиомам инцидентности или отношения принадлежности между элементами евклидова пространства, которые гласят: — если точка A принадлежит прямой k, а прямая k принадлежит плоскости α, то точка A принадлежит плоскости α; — если две точки A и B, принадлежащие прямой k, принадлежат плоскости α, то и прямая k принадлежит плоскости α.

Задача на принадлежность прямой плоскости может быть выражена следующим образом: — заключить прямую k(k`, k») в; — провести через прямую k(k`, k») плоскость α общего положения

Принадлежность прямой плоскости

Положение плоскости α в пространстве определяется тремя точками: — точка A ∉ k; — точки 1 и 2 ∈ k Здесь принадлежность прямой плоскости α общего положения определяется двумя точками — 1 и 2 взятыми на прямой k. Проведя прямые через точки 1 и A и 2 и A получим искомую плоскость , заданную пересекающимися прямыми a и b соответственно.

Принадлежность прямой плоскости

Положение плоскости α в пространстве определяется двумя параллельными прямыми: — a // b и точки 1 ∈ a и 2 ∈ b — точки 1 и 2 ∈ k Здесь принадлежность прямой плоскости α общего положения определяется двумя точками — 1 и 2 взятыми на прямой k. Проведя прямые a // b через точки 1 и 2 соответственно получим искомую плоскость , заданную прямыми a // b.

Провести через прямую k(k`, k») плоскость α общего положения, заданную следами

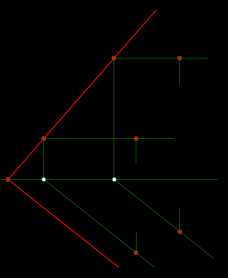
Принадлежность прямой плоскости

Положение плоскости α в пространстве определяется двумя параллельными прямыми — горизонталями плоскости: — h₁ // h₂ и точки 1 ∈ h₁ и 2 ∈ h₂ — точки 1 и 2 ∈ k Здесь принадлежность прямой плоскости α общего положения определяется двумя точками — 1 и 2 взятыми на прямой k. Проведя прямые h₁ // h₂ через точки 1 и 2 соответственно, получим искомую плоскость α, заданную следами α_H и α_V.

+

ngeo.fxyz.ru

Принадлежность прямой и точки плоскости

Дом Принадлежность прямой и точки плоскости

просмотров — 208

Плоскость. Способы ее задания, положение относительно плоскостей проекций

Положение плоскости в пространстве может быть однозначно определœено:

— тремя точками, не лежащими на одной прямой;

— прямой и точкой, не лежащей на этой прямой;

— двумя параллельными прямыми;

— двумя пересекающимися прямыми;

— плоской фигурой;

— следом плоскости.

Всегда от одного способа задания плоскостей можно перейти к другому.

След плоскости — ϶ᴛᴏ линия пересечения заданной плоскости с одной из плоскостей проекций.

Соответственно различают горизонтальный, фронтальный и профильный следы плоскости.

Рис.3.5

Плоскостью общего положения принято называть плоскость не параллельная и не перпендикулярная ни одной из плоскостей проекций.

Плоскостями частного положения относительно плоскостей проекций называются плоскости параллельные или перпендикулярные им.

Плоскость перпендикулярная одной из плоскостей проекций принято называть проецирующей плоскостью.

Существует три вида проецирующих плоскостей: горизонтально-проецирующая, фронтально-проецирующая и профильно-проецирующая плоскости. Такие плоскости вырождаются в прямую линию (след плоскости) на ту плоскость проекций, к которой они перпендикулярны.

1. Горизонтально-проецирующая плоскость— плоскость перпендикулярная горизонтальной плоскости проекций.

Рис. 3.6

2. Фронтально-проецирующая плоскость –плоскость перпендикулярная фронтальной плоскости проекций.

Рис. 3.7

3. Профильно-проецирующая плоскость – плоскость, перпендикулярная профильной плоскости проекций.

Рис. 3.8

Плоскость, параллельная одной из плоскостей проекций, принято называть плоскостью уровня.

Существует три вида плоскостей уровня: горизонтальная, фронтальная и профильная плоскости уровня.

1. Горизонтальная плоскость– плоскость, параллельная горизонтальной плоскости проекций.

Рис. 3.9

2. Фронтальная плоскость— плоскость, параллельная фронтальной плоскости проекций.

Рис. 3.10

3. Профильная плоскость – плоскость, параллельная профильной плоскости проекций.

Рис. 3.11

Возможны два случая расположения точки относительно плоскости: точка может принадлежать плоскости или не принадлежать ей (рис. 3.12).

Точка принадлежит плоскости, если принадлежит прямой, лежащей в этой плоскости.

Прямая принадлежит плоскости, если имеет с ней две общие точки или имеет с ней одну общую точку и параллельна другой прямой, лежащей в этой плоскости.

Рис. 3.12

На рис. 3.12 изображена плоскость S(DАВС) и точки D и Е. Точка D принадлежит плоскости, т. к. принадлежит прямой l, имеющей с этой плоскостью две общие точки – 1 и А. Точка Е не принадлежит плоскости, т.к. через нее нельзя провести прямую, лежащую в данной плоскости. На рис. 3.13. показана плоскость Q(aÇb) и прямая t, лежащая в этой плоскости, т.к. имеет с ней общую точку 1 и параллельна прямой..

Рис. 3.13

Читайте также

— Принадлежность прямой и точки плоскости

Принадлежность прямой и точки плоскости. Проекции плоских фигур. Главные линии плоскости Принадлежность прямой и точки плоскости основываются на аксиомах геометрии. Прямая принадлежит плоскости, если две любые различные точки прямой принадлежат данной плоскости…. [читать подробенее]

— Принадлежность прямой и точки плоскости

Возможны два случая расположения точки относительно плоскости: точка может принадлежать плоскости или не принадлежать ей (рис. 3.5). Признак принадлежности точки и прямой плоскости: Точка принадлежит плоскости, если принадлежит прямой, лежащей в этой плоскости. Прямая… [читать подробенее]

oplib.ru

Точка принадлежит плоскости, если она принадлежит какой-нибудь прямой, лежащей в этой плоскости

Построение точки в плоскости сводится к двум операциям: построению в плоскости вспомогательной прямой и построению точки на этой прямой.

Задача: Плоскость Sзадана пересекающимися прямыми а и b (рис. 2-3). Точка М(М₂ ) принадлежит плоскости.

Найти М_1.

Краткая запись условия задачи: S(а Ç b), М(М₂ )Î S; М₁ = ?

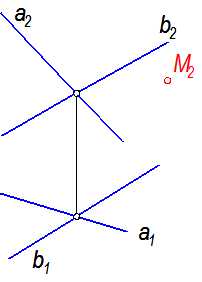
Рис. 2-3

Решение: Через точку М₂(рис. 2-4) проводим вспомогательную прямую

kÌ S: k₂ Ç a₂ =1₂; k₂ Ç b₂ =2₂;

затем находим горизонтальные проекции точек 1 и 2 по условию принадлежности прямым а и b соответственно; через две точки 1₁ и 2₁проводим прямую k₁ и на ней, с помощью линии связи, находим точку М₁. И таких прямых можно провести сколько угодно, то есть, вариантов решения бесчисленное множество.

Рис. 2-4

Прямая принадлежит плоскости, если она:

1. Проходит через две точки плоскости;

Проходит через одну точку плоскости и параллельна какой-нибудь прямой, лежащей в этой плоскости.

 

В предыдущем примере мы рассмотрели, как построить прямую в плоскости по двум точкам. Для второго случая плоскость Г зададим треугольником АВС.

Задача: Плоскость Г задана DАВС (рис. 2-5).

Точка М(М₁) принадлежит Г. Найти М₂.

М(М₁)Î Г(АВС). М₂ = ?

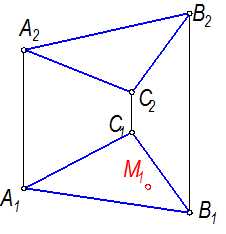
Рис. 2-5

Решение:

Через точку М₁ (рис.2-6) проведём прямую k, параллельную стороне треугольника АВ. Она пересечёт сторону АС в точке 1: k₁ || A₁ B₁ ; k­₁ A₁ Ç C₁ =1₁; с помощью линии связи найдём 1₂, проведём k₂ параллельно А₂В₂ней найдём точку М₂:

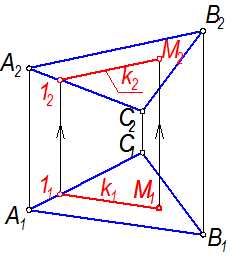
Рис. 2-6

Алгоритмическая запись решения:

1₁Î A₁C₁ Þ 1₂Î A₂C₂; 1₂Î k₂, k₂ || A₂B₂; M₂Î k₂.

Как вы думаете?

Сколько решений имеет эта задача?

Плоскости частного положения

Плоскости, параллельные или перпендикулярные одной из плоскостей проекций, называются плоскостями частного положения.

Имеется две группы таких плоскостей:

1. Проецирующие плоскости
2. Плоскости уровня

Проецирующие плоскости

Если плоскость перпендикулярна только одной плоскости проекций, то она называется проецирующей.

Одна из её проекций вырождается в прямую линию, называемую главной проекцией и обладающую собирательными свойствами.

Горизонтально проецирующая плоскость

Это плоскость, перпендикулярная горизонтальной плоскости проекций: Г^^ П₁

(рис. 2-7а, 2-7б).

Графический признак:

Горизонтальная проекция Г₁ горизонтально проецирующей плоскости прямая линия, не параллельная и не перпендикулярная линиям связи. Это главная проекция.

Например:

Г ^^ П₁ — горизонтально проецирующая плоскость.

Г^ П₁ Þ Г₁ — прямая линия, главная проекция.

Ðb — угол наклона плоскости Г к П₂.

Рис. 2-7а

Пространственный чертеж

Рис. 2-7б

Плоский чертеж

 

megaobuchalka.ru

Принадлежность точки плоскости | Начертательная геометрия

Принадлежность точки плоскости на комплексном чертеже определяется согласно аксиоме инцидентности или отношения принадлежности между элементами евклидова пространства, которая гласит: — если точка E принадлежит прямой k, а прямая k принадлежит плоскости α, то точка E принадлежит плоскости α: E ∈ k ∧ k ∈ α ⇒ E ∈ α.

Задача на принадлежность точки плоскости может быть выражена следующим образом: — заключить точку E(E`, E») в; — провести через точку E(E`, E») плоскость α общего положения

Принадлежность точки плоскости

Положение плоскости α в пространстве определяется тремя точками — вершинами ΔABC. Здесь принадлежность точки плоскости α общего положения определяется ее принадлежностью прямой k, которая принадлежит плоскости α, потому что две ее точки A и D принадлежат этой плоскости. Проведя прямую в плоскости через точку E

Принадлежность точки плоскости

доказываем тем самым ее принадлежность заданной плоскости. Заключить точку M в плоскость α заданную параллельными прямыми a и b

Принадлежность точки плоскости

Здесь принадлежность точки плоскости α общего положения определяется ее принадлежностью прямой k, которая принадлежит плоскости α, потому что две ее точки 1 и 2 принадлежат этой плоскости. Построение искомой плоскости α: — проводим прямую через точку M; — через точки 1 и 2 взятые на прямой k проводим взаимно параллельные прямые a и b соответственно.

Через точку M провести плоскость α заданную следами

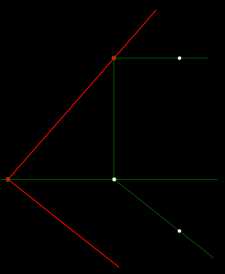
Принадлежность точки плоскости

Здесь принадлежность точки плоскости α общего положения определяется ее принадлежностью прямой h, которая, в то же время, принадлежит плоскости α и является ее горизонталью. Построение искомой плоскости α: — проводим прямую h (горизонталь искомой плоскости) через точку K; — проводим горизонтальный след α_H // h` ⇒ α_x; — через точки α_x и h_V проводим фронтальный след α_V.

+

ngeo.fxyz.ru