22. Частная корреляция.
Как неоднократно подчеркивалось, экономические явления чаще всего приходится описывать многофакторными моделями. В связи с этим возникают две задачи:
1) определение тесноты связи одной из переменных с совокупностью остальных переменных, включенных b анализ; это является задачей изучения множественной корреляции;
2) определение тесноты связи между двумя переменными при фиксировании или исключении влияния остальных. Интенсивность такой связи оценивается с помощью коэффициентов частной корреляции. Если переменные коррелируют друг с другом, то на величине коэффициента парной корреляции частично сказывается влияние других переменных. Если, например, между х1 и х2 существует тесная связь, и, кроме того, у зависит от х1, то у будет также коррелировать с
Измерение частного воздействия отдельных переменных выполняется на основе частной регрессии и частной корреляции. Следуя форме записи коэффициента частной детерминации, обозначим через ry1∙2 коэффициент частной корреляции, с помощью которого оценивается интенсивность связи между переменными у и х1 при исключении влияния х2. В соответствии с данным определением, например, r12.у также будет коэффициентом частной корреляции, измеряющим тесноту связи между переменными х1 и х2 при исключении влияния у.
В то время как при рассмотрении множественной корреляции используется мера зависимости одной из переменных с совокупностью других, при изучении частной корреляции определяется частное воздействие каждой отдельной переменной при предположении ее связи с остальными переменными.
Рассмотрим задачи исследования частной корреляции на примере взаимосвязи трех переменных. Проанализируем коэффициент частной корреляции между переменными у и х1 при исключении влияния х2. Основываясь на формуле (2.48)
b1
построим коэффициент детерминации по аналогии с (2.49)
(2.49)
и потребуем в соответствии с (= — коэф. кореляции), чтобы этот коэффициент детерминации был равен квадрату коэффициента частной корреляции. Это требование вполне оправдано, так как коэффициент детерминации должен вычисляться по данным, из которых исключено влияние переменной х2. Итак, получаем
(2.50)
Учитывая, что = 0, (2.50) можно привести к виду
(2.51)
Формула (2.51) мало пригодна для практических вычислений. Для получения более удобного выражения выполним некоторые преобразования. Подставим (2.48) в (2.51). Учитывая далее
а также то, что коэффициенты частной регрессии равны коэффициентам множественной регрессии, получим
(2.52)
Введем следующие обозначения. Пусть by1.2 — коэффициент частной регрессии у на x1; b0(12) — постоянная, а b12 — коэффициент регрессии x1 на х2; b0(У2) — постоянная, а by2 — коэффициент регрессии у на х2.
В соответствии c
получим выражение
(2.53)
которое будет необъясненной дисперсией для регрессии х1 на х2. Отсюда делаем заключение, что знаменатель в (2.52) представляет собой необъясненную дисперсию для регрессии у на х2. Исходя из этих соображений (2.52) записываем в виде
(2.54)
Мы знаем, что общую дисперсию можно разложить на две составляющие — объясненную и необъясненную дисперсии. Используем это обстоятельство в дальнейших наших рассуждениях. Разделим обе части тождества
на и, учитывая (2.6), после некоторых простых преобразований получим
(2.55)
По аналогии можно записать
(2.56)
Подставим (2.56) в (2.54)
(2.57)
Теперь подставим (2.24) в (2.57) и выполним некоторые преобразования:
(2.58)
Таким образом, мы получили формулу коэффициента частной корреляции, удобную для практических вычислений. По аналогии можно легко записать выражения для других коэффициентов частной корреляции.
Вычисление коэффициентов частной корреляции сводится к нахождению коэффициентов парной корреляции. Благодаря выведенным формулам легко установить соотношения между этими коэффициентами. Так, если rу2 = r12 = 0, то rу1.2 = rу1. Если r12 =
0 (т.е. переменные х1 и х2 не коррелированы), то |ry1.2| > |rу1| и |rу2.1| > |rу2| . Итак, с уменьшением взаимодействия между х1 и х2 следует ожидать увеличения коэффициента частной корреляции по сравнению с соответствующим коэффициентом парной корреляции. Это увеличение тем сильнее, чем больше |rу1| или |rу2|. Далее, |ry1.2| > |rу1|, если rу2 = 0 и |rу2.1| > |rу2|, если rОбобщим теперь выражение коэффициента частной корреляции на любое число объясняющих переменных. Воспользуемся для этого формулой (2.57). После извлечения корня квадратного из обеих частей равенства получим
(2.59)
По аналогии запишем
(2.60)
Так как r1y.2 = ry1.2, то, перемножая соответственно правые и левые части (2.59) и (2.60), получим
(2.61)
В соответствии с (2.28) и (2.29)
(2.62)
Обобщая, можно записать
(2.63)
Формула (2.63) позволяет нам вычислять коэффициент частной корреляции по коэффициентам частной регрессии.
По аналогии с (2.58), обобщая на любое число объясняющих переменных, получим
(2.64
Как видно из (2.64), вычисление коэффициента частной корреляции порядка m сводится к определению коэффициентов частной корреляции порядка m-1. При использовании (2.64) сначала необходимо знать коэффициенты парной корреляции, а затем приступать к вычислению коэффициентов корреляции более высокого порядка. При более чем четырех переменных вычисление частных коэффициентов корреляции желательно производить на КВМ.
studfiles.net
Частная корреляция в эконометрике, Частные коэффициенты корреляции
Ранжирование факторов в множественной линейной регрессии, может быть проведено через стандартизованные коэффициенты регрессии. Эту цель можно достигнуть с помощью частных коэффициентов корреляции для линейных связей. При нелинейной связи исследуемых признаков эту функцию выполняют частные индексы детерминации. Помимо этого, частные коэффициенты корреляции широко используют при решении проблемы отбора факторов: целесообразность включения фактора в модель может определяться величиной частных коэффициентов корреляции.
Частные коэффициенты корреляции характеризуют тесноту связи между результатом и фактором при устранении влияния другого фактора (или факторов), которые включенны в уравнение регрессии.
Показатели частной корреляции определяются как отношение сокращения остаточной дисперсии за счет дополнительного включения в анализ нового фактора к остаточной дисперсии, имевшей место до введения его в регрессионную модель.
Частные коэффициенты корреляции, рассчитанные по рекуррентной формуле могут находиться в пределах от -1 до +1, а по формулам через множественные коэффициенты детерминации — от 0 до 1. Сравнивая их друг с другом можно ранжировать факторы по тесноте их связи с результатом.
Частные коэффициенты на основе стандартизованных коэффициентов регрессии (бета-коэффициентов) дают меру тесноты связи каждого фактора с показателем (результатом) в чистом виде. Если из стандартизованного уравнения регрессии следует, что бета 1 > бета 2 > бета 3, т.е. по силе влияния факторов на результат их порядок таков: х1, х2, х3, такой же порядок факторов определяется и по соотношению частных коэффициентов корреляции.
Для уравнения регрессии в стандартизованном виде, коэффициенты могут быть определены по формулам, исходя из решения системы нормальных уравнений:
Расчет частных коэффициентов корреляции, решая задачи по эконометрике, обычно проводят по формулам Т.е. в двухфакторном анализе частные коэффициенты корреляции — это стандартизованные коэффициенты регрессии, которые умноженны на квадратный корень из соотношения долей остаточных дисперсий фиксируемого фактора на фактор и на результат. В эконометрике коэффициенты частной корреляции в основном не имеют самостоятельного значения. Их, как правило, используют на стадии формирования модели, зачастую в процедуре отсева факторов.univer-nn.ru
Иллюстрированный самоучитель по SPSS 10/11 › Корреляции › Частная корреляция [страница — 205] | Самоучители по математическим пакетам
Частная корреляция
Если исследовать достаточно большую совокупность мужчин и сопоставить размер их обуви с уровнем образованности, то между этими двумя переменными можно заметить хоть и небольшую, но в то же время значимую корреляцию. Это корреляция может послужить примером так называемой ложной корреляции. Здесь статистически значимый коэффициент корреляции является не проявлением некоторой причинной связи между двумя рассматриваемыми переменными, а в большей степени обусловлен некоторой третьей переменной.
В рассматриваемом примере такой переменной является рост. С одной стороны существует некоторая незначительная корреляция между ростом и уровнем образованности, а с другой – вполне объяснимая и логичная связь между ростом и размером обуви. Вместе эти две корреляции приводят к упоминавшейся ложной корреляции. Для исключения одной такой искажающей переменной необходим расчет так называемой частной корреляции.
Если присвоить коррелирующим переменным индексы 1 и 2, а искажающей переменной – индекс 3, и попарно рассчитать корреляционный коэффициент (Пирсона) r12,r13, и r23, то для частных корреляционных коэффициентов получим:
Достаточно давно в социологических исследованиях, проводимых в Германии, выяснялось отношение населения к приезжим рабочим-иностранцам. Для этого было сформулировано несколько отдельных вопросов. Ответы на вопросы суммировались. Сумма могла принимать значения от 0 до 30, причем большее значение соответствует более негативному отношению к приезжим рабочим.
Среди многочисленных дополнительных переменных учитывались: возраст опрашиваемых и частота посещения церкви. Последней характеристике были присвоены значения от 1 (никогда) до 6 (по меньшей мере, 2 раза в неделю). Небольшая выборка из оригинальных данных опроса (35 респондентов с этими тремя переменными) наводится в файле kirche.sav. Откройте этот файл, если Вы хотите самостоятельно провести следующие расчеты.
Если подсчитать корреляции между этими тремя переменными, то при выборе коэффициентов Пирсона для анализа взаимосвязи, получатся следующие результаты закроем глаза на то, что одна из переменных, а именно частота посещения церкви, имеет порядковую шкалу):
Correlations (Корреляции)
| ALTER (Возраст) | GAST (Приезжий) | KIRCHE (Церковь) | ||
| ALTER (Возраст) | Pearson Correlation (Корреляция по Пирсону) | 1 | 0.468** | 0.779** |
| Sig. (2-tailed) (Значимость (2-сторонняя)) | 0.000 | 0.005 | 0.000 | |
| N | 35 | 35 | 35 | |
| GAST (Приезжий) | Pearson Correlation (Корреляция по Пирсону) | 0.468** | 1 | 0.432** |
| Sig. (2-tailed) (Значимость (2-сторонняя)) | 0.005 | 0.000 | 0.010 | |
| N | 35 | 35 | 35 | |
| KIRCHE (Церковь) | Pearson Correlation (Корреляция по Пирсону) | 0.779** | 0.432** | 1 |
| Sig. (2-tailed) (Значимость (2-сторонняя)) | 0.000 | 0.010 | 0.000 | |
| N | 35 | 35 | 35 | |
- ** Correlation is significant at the.01 level (2-tailed). Корреляция является закономерной на уровне 0.01 (2-стороння).
Принимая во внимание полярность, полученные результаты можно трактовать, к примеру, таким образом, что частые посещения церкви коррелируют с отрицательным отношением к приезжим рабочим (r = 0.432). Прежде, чем поставить в упрек церкви враждебность по отношению к иностранцам, нужно учесть влияние возраста. Он также коррелирует с враждебным отношением к иностранным рабочим (r = 0.468) и сильно коррелирует с частотой посещения церкви (r = 0.779). Таким образом, возникает подозрение, что возраст является искажающим признаком, виновным в ложной корреляции между частотой посещения церкви и отрицательным отношением к иностранным рабочим. Докажем это путем расчета частных корреляционных коэффициентов.
- Откройте файл kirche.sav.
- Выберите в меню Analyse… (Анализ) › Correlate… (Корреляция) › Partial… (Частная)
Откроется диалоговое окно Partial Correlations (Частные корреляции).
- Перенесите переменные gast и kirche в поле признаков, а переменную Alter в поле контрольных переменных и оставьте предварительную установку для двухстороннего теста значимости.
При помощи щелчка на кнопке Options… (Опции) наряду с традиционной обработкой пропущенных значений, Вы можете организовать расчет среднего значения, стандартного отклонения и вывод «корреляций нулевого порядка» (то есть простых корреляционных коэффициентов).
В случае одной искажающей переменной, как в приведенном примере, возможен расчет частной корреляции первого порядка, при наличии нескольких искажающих переменных, SPSS выдает корреляции высших порядков.
- Начните расчет щелчком на кнопке ОК. В окне просмотра появится результат.
Вас, возможно, удивит, что в данном случае все еще выводится старый вариант таблицы результатов, соответствующий прежним версиям SPSS. Результаты включают: частный корреляционный коэффициент, число степеней свободы (число наблюдений минус 3) и уровень значимости. Исходя из полученных результатов, можно сделать вывод, что при исключении искажающей переменной Alter больше не наблюдается существенной корреляции между частотой посещения церкви и отрицательным отношением к иностранным рабочим.
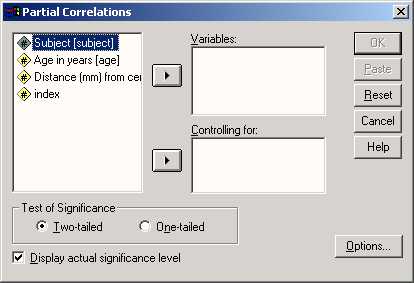
Рис. 15.3: Диалоговое окно Partial Correlations (Частичные корреляции)
samoychiteli.ru
Частная корреляция
Количество просмотров публикации Частная корреляция — 415
Приизучении влияния отдельных факторов методом корреляции возможен подход, при котором учитывается их воздействие на результативный признак, в случае если воздействие других факторов при этом не учитывается. Но возможен и другой способ измерения, когда изучается воздействие одного или нескольких факторов при закреплении остальных факторов на постоянном уровне. Такой метод изучения связи принято называть частной или чистой корреляцией.
В случае если при расчете частного коэффициента корреляции исключается влияние одного фактора, такой коэффициент корреляции принято называть частным коэффициентом корреляции первого порядка, при исключении влияния двух факторов – частный коэффициент корреляции второго порядка и т.д.
Частный коэффициент корреляции первого порядка между признаками у и х при исключении влияния признака z вычисляется следующим образом:
,
где r – парные коэффициенты между признаками.
Коэффициент частной корреляции второго порядка исчисляется по формуле:
.
Частными коэффициентами корреляции можно воспользоваться и для расчета совокупного коэффициента корреляции. В этом случае формула имеет вид:
.
Коэффициент множественной корреляции можно вычислить и на базе стандартизованных коэффициентов:
,
где b1, b2, b3, b4 – параметры системы.
2.2. Имитирование (интерпретация)
регрессионных моделей
Итак, на базе регрессионных моделей определяется влияние отдельных (или комплекса) факторов на результативный признак.
Базовую модель регрессионного анализа можно представить следующим образом:
,
где yi — результативный признак i-го вида;
xij — факторы j-го вида, которые влияют на i-ый результативный признак;
aij — влияние отдельных факторов j-го вида на i-ый результативный признак;
ai(u) — исходный уровень i-го результативного признака.
По существу базовая регрессионная модель позволяет исследовать количественные характеристики спроса, предложения, ценообразования, рентабельности производства, продукции; прибыли и других технико-экономических показателей. При этом, как правило, обосновываются, выбираются основные переменные величины, которые крайне важно ввести в базовую регрессионную модель, в частности переменные величины, характеризующие ассортимент выпуска продукции с учетом их качественных оценок; переменные величины, характеризующие количественные оценки отдельных технико-экономических показателей.
В процессе решения системы выявляются численные значения зависимостей между отдельными показателями, к примеру между спросом и ценой, между прибылью и издержками (себестоимости продукции) и т.д.
Рекомендуется дифференциация базовой регрессионной модели исходя из характера решаемых экономических задач. В частности рекомендуется базовые регрессионные модели спроса, предложения, ценообразования, прибыли и других.
Различают линейные и нелинейные виды регрессионных моделей.
Линейный аналог регрессионных моделей имеет следующий вид:
y = a0 + a1x1 + a2x2 + … + akxk,
где x1, x2,…, xk — факторы, влияющие на результативный признак;
a1, a2,…, ak — уровень влияния каждого фактора на результативный признак;
a0— начало отсчета͵ ᴛ.ᴇ. исходный уровень результативного признака.
Нелинейная регрессионная модель имеет следующий вид:
.
Как правило, в линейных регрессионных моделях поведение результативного признака носит прямо пропорциональный характер исходя из переменных величин, а в нелинейных наоборот — колебания результативного показателя являются неадекватными, ᴛ.ᴇ. носят непропорциональный характер.
В отдельных случаях для оценки (интерпретации) упомянутых моделей возможно применение следующих функций (рис. 1-18).
На рис. 1 изображенная функция оказывает линейную зависимость, на рис. 2 – обратнопропорциональную, на рис. 3 – тоже обратнопропорциональную зависимость, но совершенно в других обстоятельствах. Привлекают внимание функции: , , , , , , , , (рис. 7, 8, 10, 12, 13, 15, 16, 17, 18) для оценки экономических показателей в условиях оживления экономики. Функция (рис. 8) имитирует более умеренный процесс экономической динамики и т.д.
Учитывая зависимость отрешаемых экономических задач различают три типа регрессионных моделей: простые, сложные, суперсложные.
В простых регрессионных моделях, как правило, исследуются два, в отдельных случаях три фактора.
В сложных моделях исследование осуществляется под влиянием более трех факторов на базе различных функций.
В суперсложных моделях исследование осуществляется на базе комплекса внутренних и внешних факторов.
referatwork.ru
Частные коэффициенты корреляции.
ранжирование факторов, участвующих во
множественной линейной регрессии, может
быть проведено через стандартизованные
коэффициенты регрессии ( -коэффициенты).
Эта же цель может быть достигнута с
помощью частных коэффициентов корреляции
(для линейных связей). Кроме того, частные
показатели корреляции широко используются
при решении проблемы отбора факторов:
целесообразность включения того или
иного фактора в модель можно доказать
величиной показателя частной корреляции.
-коэффициенты).
Эта же цель может быть достигнута с
помощью частных коэффициентов корреляции
(для линейных связей). Кроме того, частные
показатели корреляции широко используются
при решении проблемы отбора факторов:
целесообразность включения того или
иного фактора в модель можно доказать
величиной показателя частной корреляции.
Частные коэффициенты корреляциихарактеризуют тесноту связи между результатом и соответствующим фактором при элиминировании (устранении влияния) других факторов, включенных в уравнение регрессии.
Показатели частной корреляции представляют собой отношение сокращения остаточной дисперсии за счет дополнительного включения в анализ нового фактора к остаточной дисперсии, имевшей место до введения его в модель.
В общем виде при наличии 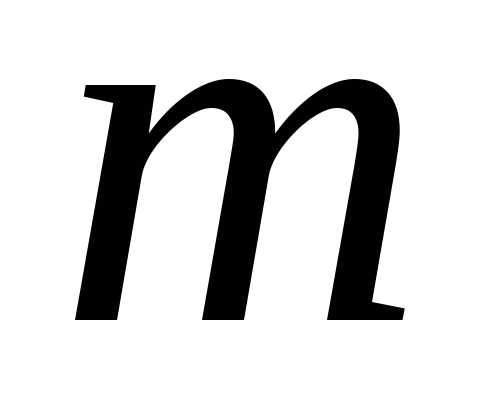 факторов для уравнения
факторов для уравнения
коэффициент частной корреляции,
измеряющий влияние на  фактора
фактора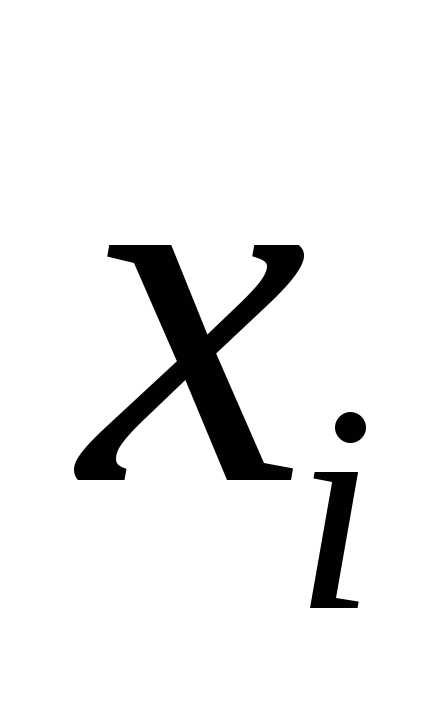 ,
при неизменном уровне других факторов,
можно определить по формуле:
,
при неизменном уровне других факторов,
можно определить по формуле:
, (2.18)
где 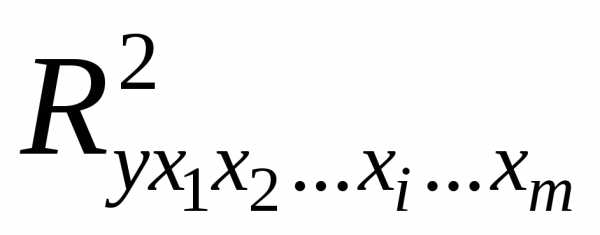 – множественный коэффициент детерминации
всех
– множественный коэффициент детерминации
всех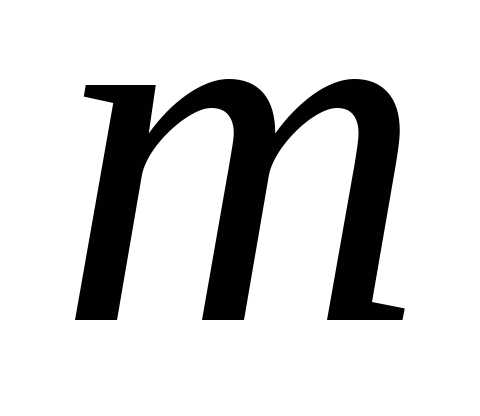 факторов с результатом;– тот же показатель детерминации, но
без введения в модель фактора
факторов с результатом;– тот же показатель детерминации, но
без введения в модель фактора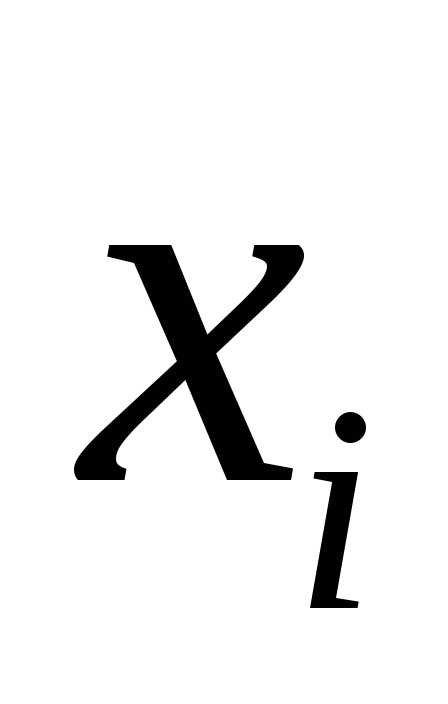 .
.
При двух факторах формула (2.18) примет вид:
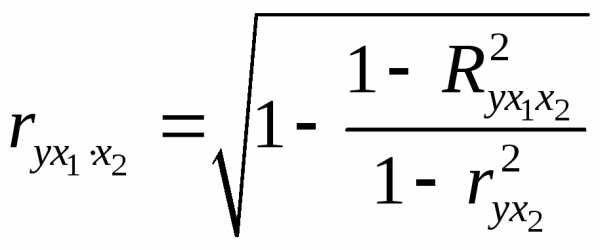 ;
;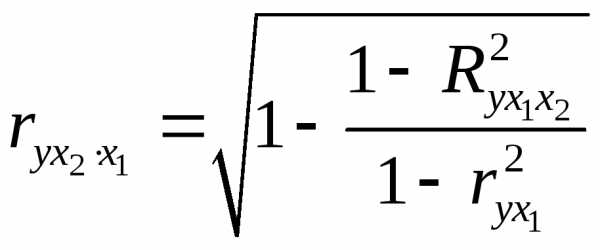 . (2.18а)
. (2.18а)
Порядок частного коэффициента корреляции
определяется количеством факторов,
влияние которых исключается. Например, 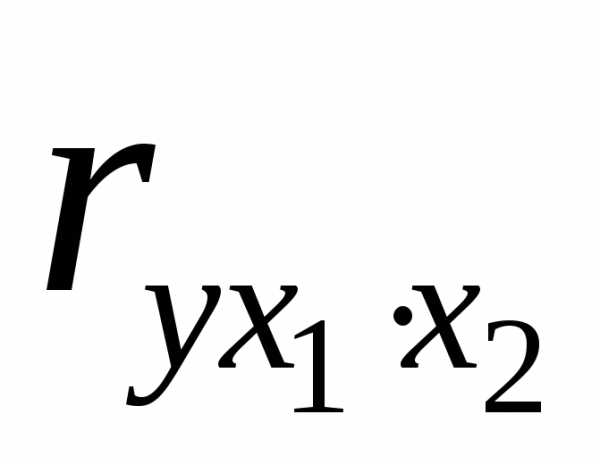 – коэффициент частной корреляции
первого порядка. Соответственно
коэффициенты парной корреляции называются
коэффициентами нулевого порядка.
Коэффициенты частной корреляции более
высоких порядков можно определить через
коэффициенты частной корреляции более
низких порядков по рекуррентной формуле:
– коэффициент частной корреляции
первого порядка. Соответственно
коэффициенты парной корреляции называются
коэффициентами нулевого порядка.
Коэффициенты частной корреляции более
высоких порядков можно определить через
коэффициенты частной корреляции более
низких порядков по рекуррентной формуле:
.(2.19)
При двух факторах данная формула примет вид:
;. (2.19а)
Для уравнения регрессии с тремя факторами частные коэффициенты корреляции второго порядка определяются на основе частных коэффициентов корреляции первого порядка. Так, по уравнению возможно исчисление трех частных коэффициентов корреляции второго порядка:
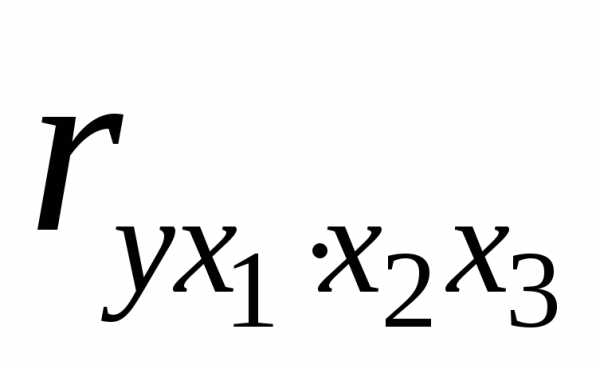 ,
, 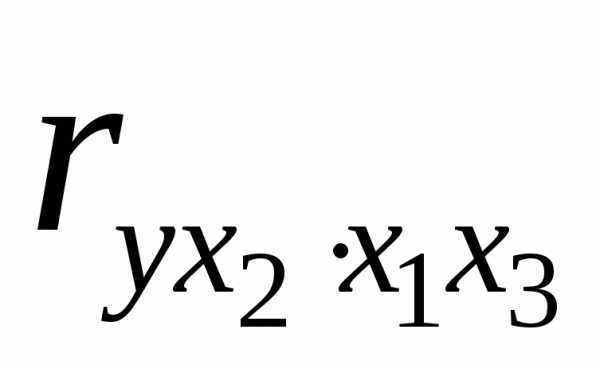 ,
, 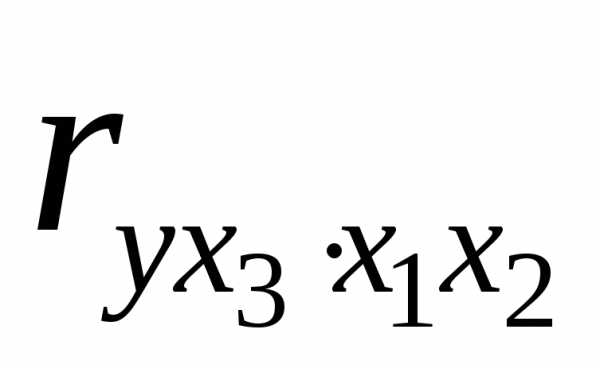 ,
,
каждый из которых определяется по
рекуррентной формуле. Например, при 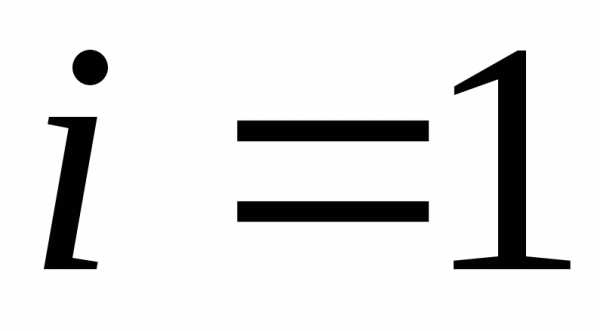 имеем формулу для расчета
имеем формулу для расчета 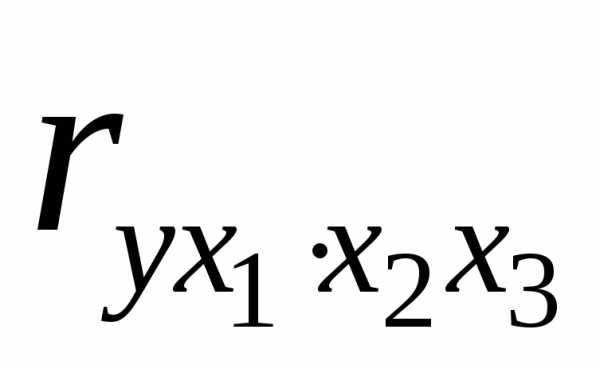 :
:
. (2.20)
Рассчитанные по рекуррентной формуле
частные коэффициенты корреляции
изменяются в пределах от –1 до +1, а по
формулам через множественные коэффициенты
детерминации – от 0 до 1. Сравнение их
друг с другом позволяет ранжировать
факторы по тесноте их связи с результатом.
Частные коэффициенты корреляции дают
меру тесноты связи каждого фактора с
результатом в чистом виде. Если из
стандартизованного уравнения регрессии
следует, что,
т.е.noсиле влияния на
результат порядок факторов таков: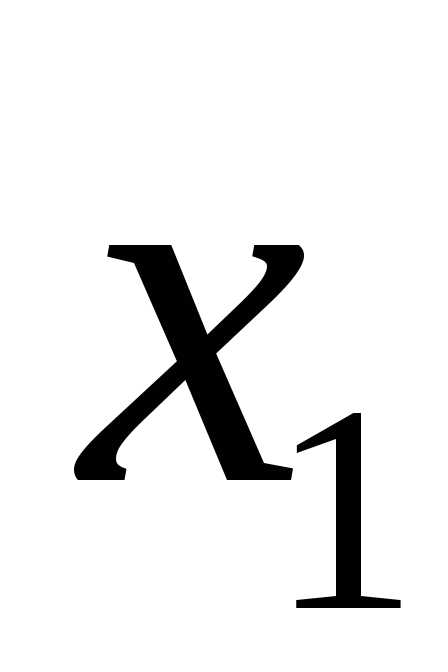 ,
,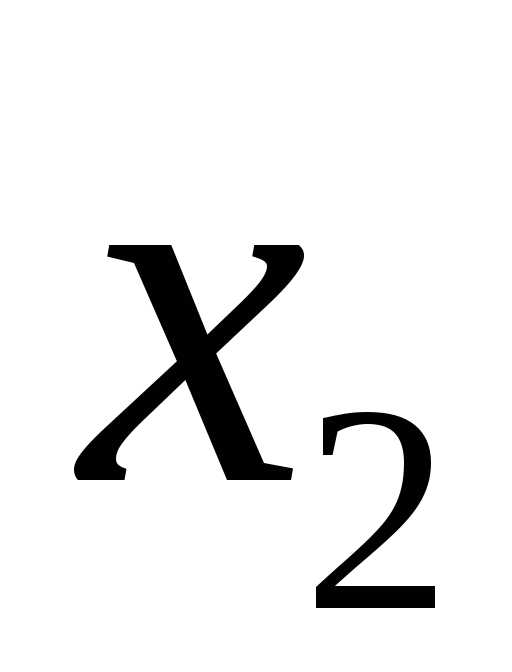 ,
,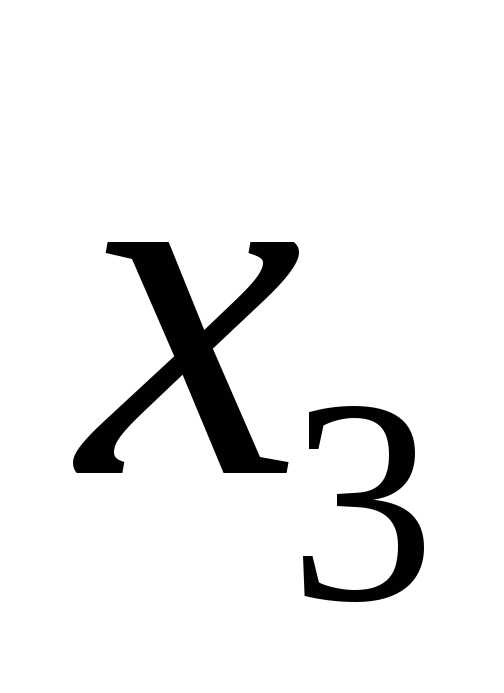 ,
то этот же порядок факторов определяется
и по соотношению частных коэффициентов
корреляции,
.
,
то этот же порядок факторов определяется
и по соотношению частных коэффициентов
корреляции,
.
В эконометрике частные коэффициенты
корреляции обычно не имеют самостоятельного
значения. Их используют на стадии
формирования модели. Так, строя
многофакторную модель, на первом шаге
определяется уравнение регрессии с
полным набором факторов и рассчитывается
матрица частных коэффициентов корреляции.
На втором шаге отбирается фактор с
наименьшей и несущественной по  -критерию
Стьюдента величиной показателя частной
корреляции. Исключив его из модели,
строится новое уравнение регрессии.
Процедура продолжается до тех пор, пока
не окажется, что все частные коэффициенты
корреляции существенно отличаются от
нуля. Если исключен несущественный
фактор, то множественные коэффициенты
детерминации на двух смежных шагах
построения регрессионной модели почти
не отличаются друг от друга,
-критерию
Стьюдента величиной показателя частной
корреляции. Исключив его из модели,
строится новое уравнение регрессии.
Процедура продолжается до тех пор, пока
не окажется, что все частные коэффициенты
корреляции существенно отличаются от
нуля. Если исключен несущественный
фактор, то множественные коэффициенты
детерминации на двух смежных шагах
построения регрессионной модели почти
не отличаются друг от друга,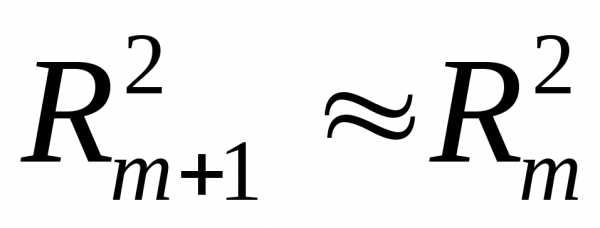 ,
где
,
где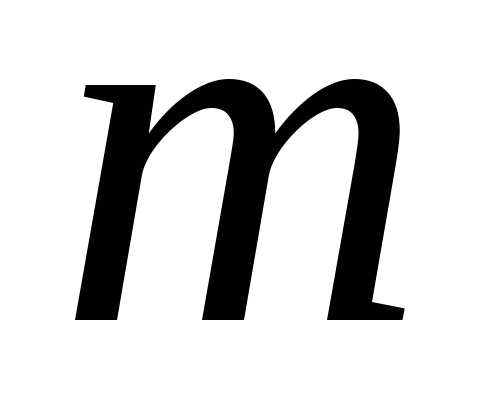 – число факторов.
– число факторов.
Из приведенных выше формул частных коэффициентов корреляции видна связь этих показателей с совокупным коэффициентом корреляции. Зная частные коэффициенты корреляции (последовательно первого, второго и более высокого порядка), можно определить совокупный коэффициент корреляции по формуле:
. (2.21)
В частности, для двухфакторного уравнения формула (2.21) принимает вид:
. (2.21)
При полной зависимости результативного
признака от исследуемых факторов
коэффициент совокупного их влияния
равен единице. Из единицы вычитается
доля остаточной вариации результативного
признака 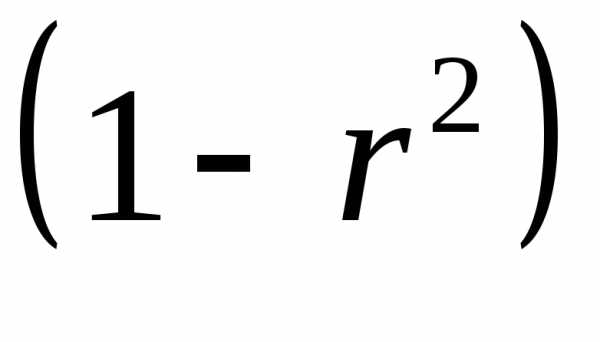 ,
обусловленная последовательно включенными
в анализ факторами. В результате
подкоренное выражение характеризует
совокупное действие всех исследуемых
факторов.
,
обусловленная последовательно включенными
в анализ факторами. В результате
подкоренное выражение характеризует
совокупное действие всех исследуемых
факторов.
studfiles.net
Коэффициент частной корреляции
Коэффициент частной корреляции (Partial Correlation) показывает степень (тесноту) взаимосвязи двух переменных относительно друг друга, без учета влияния третьей переменной.
Для вычисления частного коэффициента корреляции между тремя переменными требуется знать их коэффициенты корреляции Пирсона.
Формула частного коэффициента корреляции для коэффициента корреляции Пирсона следующая:
где коэффициенты корреляции r-Пирсона исследуемых переменных между собой.
Формула частного коэффициента корреляции для коэффициента корреляции Кендала (в отличие от коэффициента корреляции Спирмена) следующая:
где коэффициенты корреляции r-Пирсона исследуемых переменных между собой.
Однако следует помнить, что частная корреляция не обязательно говорит о причинности существующей между переменными, для этих целей лучше использовать дисперсионный анализ.
statpsy.ru
Тема 10. Множественная и частная корреляция
В настоящее время при построении корреляционных моделей исходят из условия нормальности многомерного закона распределения генеральной совокупности. Эти условия обеспечивают линейный характер связи между изучаемыми признаками, что делает правомерным использование в качестве показателей тесноты связи парного, частного коэффициентов корреляции и коэффициента множественной корреляции.
Частные коэффициенты корреляции характеризуют связи двух признаков из совокупности признаков при условии, что все связи этих признаков с другими признаками элиминированы, т. е. закреплены на условно-постоянном (среднем) уровне.
Если парный коэффициент корреляции между двумя случайными величинами оказался больше частного коэффициента между теми же случайными величинами, то это говорит о том, что третья фиксированная величина усиливает взаимосвязь между изучаемыми величинами, т.е. более высокое значение парного коэффициента обусловлено присутствием третьей величины.
Более низкое значение парного коэффициента корреляции в сравнении с соответствующими частными свидетельствует об ослаблении связи между изучаемыми величинами действием фиксируемой величины.
Частный коэффициент корреляции, например, характеризует степень линейной зависимости между двумя величинами yх1 при исключенном влиянии третьей величины х2, включенной в модель. Он определяется по формуле:
.
Тогда зависимость у отх2 при исключении влиянияx1:
.
Можно рассчитать взаимосвязь факторных признаков при устранении влияния результативного признака:
.
Частный коэффициент корреляции изменяется в пределах от -1 по +1. Если частный коэффициент корреляции равен ±1, то связь между двумя величинами функциональная, а равенство нулю свидетельствует о линейной независимости этих величин.
Если есть матрица парных коэффициентов корреляции R, то переход к матрице частных коэффициентов корреляции осуществляется на основании последовательного расчета коэффициентов частной корреляции и замены ими в матрицеR коэффициентов парной корреляции с использованием формулы
,
где rij — коэффициент частной корреляции междуi-м иj—u признаками;
Аij — алгебраическое дополнение к элементуrij матрицы парных коэффициентов корреляции;
Аii ,Аjj — дополнения к элементам матрицы парных коэффициентов корреляцииrii иrjj соответственно. Знак частному коэффициенту корреляции присваивается по знаку соответствующего коэффициента регрессии в модели связи.
Частные коэффициенты корреляции как статистические величины подвергаются в анализе оценке на достоверность. С этой целью используется t-критерий Стьюдента, который определяется по формуле:
.
Значение t-критерия сравнивают с табличнымt, где— заданный уровень значимости;= (n—k-1) — число степеней свободы.
Если выполняется неравенство tрасч> t, , то значение коэффициента корреляции признается значимым, т.е. нулевая гипотеза, утверждающая равенство нулю коэффициента корреляции, отвергается и делается вывод о том, что между исследуемыми переменными есть тесная статистическая взаимосвязь.
Если частные коэффициенты корреляции возвести в квадрат, то получим частные коэффициенты детерминации.
Частный коэффициент детерминациипоказываетдолю вариации признака под действием одного из факторов при неизменном значении другого фактора.
В случае двухфакторной линейной модели коэффициент множественной корреляцииопределяется по следующей формуле:
.
Коэффициент колеблется в пределах от 0 до 1, чем ближе он к 1, тем в большей степени учтены факторы, влияющие на результативный признак
Когда известна матрица парных коэффициентов корреляции R, коэффициент множественной корреляции получают, решив матричное уравнение вида
,
где |R|— определитель матрицы парных коэффициентов корреляции;
|R* |— определитель матрицы парных коэффициентов корреляции, в которой вычеркнуты строка и столбец, характеризующие связи независимых переменныхxj, с зависимой переменнойy.
Для проверки существенности коэффициента множественной корреляции можно использоватьF-критерий, который определяется по формуле:
,
при k и n — k — 1 степенях свободы.
Наиболее достоверные результаты при корреляционном анализе можно получить, когда число объектов наблюдения (n) превышает число анализируемых признаков (m) в 6-8 раз.
studfiles.net