Алгоритм crc16 – Иллюстрированный самоучитель по задачам и примерам Assembler › Вычисление CRC › Табличные алгоритмы вычисления CRC [страница - 188]

Содержание

CRC16 Курсовая работа

Курсовая работа
Петров Дмитрий, 3 курс, группа КБ-301, мат-мех УрГУ, 2003 год.
Руководитель — М. Баклановский

Введение
Способы обнаружения искажений в пакете
СRC-арифметика
Стандарты для CRC-полиномов
Алгоритм
Требования к CRC-полиномам
Исследование
Приложение 1. Примеры
Приложение 2. Другие CRC-полиномы
Приложение 3. Аббревиатуры
Библиография и ссылки
Утилита для вычисления СRC (Скачать)

Введение.

С развитием технологии стали возникать все более и более интересные вещи. Так оказалось, что отправляя, файл по модему, или же копируя его с дискеты мы не можем быть уверены в том, что мы получим то, что хотели и без искажений. Как только был обнаружен этот факт (а это было уже довольно давно) разработчики программного и аппаратного обеспечения решили внедрят различные алгоритмы обнаружения ошибок в полученном сообщении. Но так или иначе практически каждый алгоритм обладал рядом недостатков. В ходе отбора стали применяться алгоритмы CRC (Циклических избыточных сумм). CRC обладает рядом преимуществ и, вообще, на CRC наложены достаточно жестокие требования, чтобы он мог обнаруживать разнообразные виды ошибок. Цель данной работы исследовать известные алгоритмы нахождения CRC 16 бит и узнать действительно ли выполняются те требования, которые накладывались на него при разработке. Следует сразу отметить, что CRC отнюдь не ограничиваются 16-ю битами, применяются (или же применялись) так же CRC 8, 10, 24 и 32 бит, но CRC 16-бит оказались наиболее удобными для исследования в силу их длины.

Возникновение ошибки из-за шума можно показать так:

Изначальный сигнал, который посылается отправителем.

В линии возникает помеха, некий шум.

В итоге шум налагается на сигнал, и получатель видит искаженную информацию.

Способы обнаружения искажений в пакете.

Чтобы обнаружить искаженную информацию существует и применяется несколько способов, которые добавляют лишнюю информацию, по которой получатель может определить была ли ошибка.

Посимвольный контроль четности.

Пример.

Поблочный контроль четности.

Вычисление контрольных сумм.
Контроль циклически избыточным кодом.

Вообще вышеизложенные способы являются хэш-фуенкциями, т.е.: Хэш функцией называется математическая, либо другая функция, которая преобразует входные данные произвольной длины в данные фиксированной длины (значение хэш функции). Как правило, выходные данные хеш-функции имеют меньший размер, чем входные. Как правило, в качестве хеш-функций выступают односторонние функции. Главная задача хеш-функции состоит в том, чтобы по выходным данным невозможно было восстановить входные. Например для проверки пароля можно проверять его соответствие хэшу. В этом случае не требуется хранить пароль в открытом виде. Пример простейшей хеш-функции — сумма всех элементов массива. [7] CRC и является односторонней хэш-функцией.

Что же такое особенное есть в CRC, что позволяет обнаруживать большую часть ошибок? Это безусловно метод его нахождения. Для нахождения CRC используется специальная CRC-арифметика, которая является полиномиальной арифметикой по модулю 2. Т.е. битовое значение 1001001112=16710 может быть представлено в виде: 1*x^8+0*x^7+0*x^6+1*x^5+0*x^4+0*x^3+1*x^2+1*x^1+1. Для того чтобы получить искомое значение, можно подставить x=2. Эта арифметика обладает одним весьма не маловажным свойством — операции сложения и вычитания идентичны, и поэтому можно оставить лишь одну операцию, т.е.

Сложение и вычитание ведется по следующим правилам: 0-0=0, 0-1=1, 1-0=1, 1-1=0. Таким образом можно заметить, что результат вычитания в арифметике без переносов, аналогичен операции XOR. Для нашего рассмотрения особый интерес представляет операция деления, так как в основе любого алгоритма вычисления CRC лежит представление исходного сообщения в виде огромного двоичного числа, делении его на другое двоичное число и использование остатка от этого деления в качестве значения CRC. Говоря иначе: M — исходное сообщение, n — степень порождающего полинома, G — порождающий полином, тогда CRC — это остаток от M*x^n/G.

Например, сообщение M=0x54, G=0x11021 (Xmodem). M’=0101,0100,0000,0000,0000,0000 G=1,0001,0000,0010,0001

	
	010101000000000000000000|00010001000000100001
         10001000000100001	|частное никого не интересует
	------------------------  
         00100000000100001000000
           10001000000100001
	------------------------
           000010000101001010000
	       10001000000100001
	------------------------
	       00001101001110001
      	       0001,1010,0111,0001=0x1a71 - остаток от деления

После получения этого остатка — остаток добавляется в конец передаваемого сообщения и сообщение передается. Есть 2 способа обнаружения ошибок:

Приемник может получить сообщение отделить последние 16 бит, посчитать CRC оставшегося и сравнить с тем 16 битами.
Или же приемник может поделить полученное сообщение на G, и таким образом обнаружить ошибку

Несколько протоколов определяют CRC-полиномы используемые для обнаружения ошибок: CCITT X.25, BiSynch, SDLC, HDLC. Они определяют полином и метод нахождения остатка. Используемые полиномы:

CRC X.25 (CCITT), X-modem:x¹⁶ + x¹² + x⁵ + 1
CRC-16 (Bisynch): x¹⁶ + x¹⁵ + x² + 1

Полином 1 стандартизирован в спецификации V. 41 CCITT «Кодонезависимая система контроля ошибок».
Полином 2 стандартизирован в спецификации V. 42 того же CCITT. Также он используется в протоколе двоичной синхронной (бисинхронной) передаче данных от компании IBM

Не все протоколы используют обычную схему нахождения остатка, так, например, рассмотрим CCITT X.25. S=0x54, G=0x11021, n=16. В приложении CCITT сначала меняется порядок битов сообщения, т.е. S=0x54 становится S=0x2a. К тому же начальное значение CRC инициализируется единицами. Это тоже, что XOR первых 16-ти бит с 16-ю единицами.


	110101011111111100000000 |10001000000100001 
	10001000000100001	 |частное не имеет значения 
	-------------------------
	010111011110111110000000
         10001000000100001
	-------------------------
  	 00110011110011111000000
      	   10001000000100001
	-------------------------
           010001110010111010000
            10001000000100001
	-------------------------
            00000110010011011000

Остаток равен 0110,0100,1101,1000. Последовательность бит так же меняется, т.е. 0001,1011,0010,0110. Затем результат обращается и две восьмерки битов меняются местами, Итак CRC=1101100111100100, или CRC=0xd9e4.

Протокол Xmodem был разработан специально для программного применения. Он использовал тот же полином, что CCITT X.25. Протокол Xmodem использует обычный алгоритм нахождения CRC. И поэтому довольно просто в применении там, где невозможно реализовать таблицы.

Надо отметить, что различные стандарты так же имеет различные отклонения от обычной математической реализации. Многие стандарты инициализируют начальное значение CRC в единицы, но Xmodem, BiSynch — в нули. Старый CCITT стандарт так же инициализировал в нули, на X.25 инициализирует в единицы. Многие утилиты использующие алгоритм Xmodem’а так же инициализируют начальное значение в 1’ы. Особенности X.25 были показаны выше. Между прочим, существует множество модификаций протокола Xmodem, но не один из них не менял полином. [4] В SDLC и HDLC используется тот же алгоритм и тот же полином, что и в CCITT X.25.

Упомяну о других CRC полиномах. Существуют и стандартизированы CRC полиномы разрядности — 8, 10, 24, 32. Полиномы меньшей разрядности используются там, где передаваемые сообщения малы, тогда как полиномы разрядности 24 могут обнаружить ошибку в сообщения длины свыше одного мегабайта, а 32 уже свыше 256 мегабайт.

В самом алгоритме вычисления CRC нет ничего сложного, его можно на любом языке, потому что операции XOR и SHL встроены практически в любой язык. Коротко весь алгоритм можно записать так:

G — полином, M — битовое сообщение.

Дополнить исходное сообщение 16-ю нулями. M’=M*x16.
Инициализировать начальное значение CRC 0x0000.
Выполнять операцию сдвиг влево последовательности бит сообщения M’ до тех пор, пока бит в ячейке (ячейка — то место, где изначально находился старший бит M’) не станет равным единице или количество бит станет меньше чем в делителе.
Если старший бит станет равным единице, то производим операцию XOR между сообщением и полиномом. И повторяем шаг 2.
То что в конце остается от последовательности M’ и называется CRC.
Возможно потребуется обратить результат.

В случае зеркального алгоритма применяемого при вычислении CCITT X.25 и IBM Bisynch CRC есть некоторые отличия, а именно M — не само сообщение, а его зеркальное отражение и еще в X.25 начальное значение — инициализируется в 0xffff — это всего лишь операция XOR первых 16 бит сообщения с 0xffff. Во всем остальном алгоритм работает так же.

Таким образом, алгоритм вычисления CRC имеет несколько параметров:

начальное значение
порядок прохода битов сообщения (зеркальный или прямой)
обращение результата.

Следует отметить, что старшая единица в полиноме не имеет значения. И поэтому очень часто вместо, например, 0x11021 можно видеть запись 0x1021.

В силу ассоциативности операции XOR можно представить:

E=A XOR F

Таким образом, можно заметить, что количество сдвигов полностью зависит от старшего байта. Величина F полностью предсказуема и определяется значением байта и значением полинома. Следовательно, для одного полинома величина F может принимать 256 значений. Значит, все значения величины F можно свести в одну таблицу. Это ускорит процесс вычисления CRC в несколько раз, потому что таблица вычисляется лишь один раз и в отличии от прямого алгоритма не надо сдвигать каждый бит и тем более последовательность бит дополнять нулями. Так же следует отметить, что единственный разумный способ работать с зеркальным алгоритмом вычисления CRC.

Табличный алгоритм.

G — полином, М — байтовое сообщение.

Вычислить значение в таблице для каждого байта от 0x00 до 0xff:
- Производится сдвиг влево на 8 бит (из 0x001a -> 0x1a00).
- Выполнять 8 раз операцию сдвиг влево, причем, если старший бит равен 1, то производится XOR с полиномом G.
- Все что осталось от двух байт — становится значением в таблице.
Просматривается каждый байт сообщения M:
- Над старшим байтом текущего значения CRC и текущим байтом сообщения выполняется операция XOR — это индекс в таблице.
- Младший байт текущего значения CRC сдвигается влево на 8 и становится старшим, затем объединяется по XOR со значением таблицы — это становится новым значением CRC.
В результате получено значение CRC.

Зеркальный алгоритм работает так же, но с незначительными изменениями:

G — полином, М — байтовое сообщение.

Вычислить значение в таблице для каждого байта от 0x00 до 0xff:
- Выполнять 8 раз операцию сдвиг вправо, причем, если младший бит равен 1, то производится XOR с полиномом G.
- Все что осталось от двух байт — становится значением в таблице.
Текущее значение CRC = 0xffff, если CCITT и CRC=0x0000, если BiSynch.

Просматривается каждый байт сообщения M:
- Над младший байтом текущего значения CRC и текущим байтом сообщения выполняется операция XOR — это индекс в таблице.
- Старший байт текущего значения CRC сдвигается вправо на 8 и становится младшим, затем объединяется по XOR со значением таблицы — это становится новым значением CRC.
В результате получено значение CRC.
(Для CCITT X.25) Меняется старший и младший байт CRC местами и результат обращается (операция логического отрицания).

Безусловно, это не все существующие на данный момент алгоритмы CRC, но все остальные, так или иначе, являются модификациями табличного алгоритма. И преследуют следующие цели:

переход от цикла по битам к циклам по большим порциям данных — байтам и словам
повышение разрядности порождающего полинома.

Рассмотрев алгоритм CRC16 можно его модифицировать, как для полиномов большей степени, так и для полиномов меньшей степени.

Используемые в расчетах полиномы, данны в шестнадцатеричном формате.

X.25: 0x18408 (обратный к 0x11021)
X-modem: 0x11021
CRC-16 (BISYNCH): 0x1a001 (обратный к 0x18005)
CRC-16* (IBM): 0x18005

*- вообще-то это то же, что CRC-16 (BISYNCH), но использует обычный математический алгоритм нахождения CRC, а следовательно не нуждается в обращении. Неизвестно стандарта, в котором бы он использовался и не удивительно, что он дает худшие результаты.

Выбор полинома весьма непростое дело. Итак, из каких соображений находят полином. Передаваемое сообщение T=M’+CRC, где M’ — исходное сообщение с добавленными 15-ю нулями в конец, а CRC — остаток от деления. Поскольку сложение также и вычитание — M’ уменьшается до ближайшего кратного к делителю G. Если сообщение пришло с ошибками, т.е. T’=T+E, тогда приемник просто T’ делит на G, получая (T+E)modG=E mod G, т.к. T mod G=0. Т.е. качество качество полинома определяется количеством E кратных ему.

Обнаруживать ошибку в 1-бите. Для этого в полиноме должно быть больше 1-й единицы.
Обнаруживать ошибки в 2-х различных битах для пакетов длины меньше, чем 2¹⁵ бит. Надо подобрать G для которые не кратны числам типа 011, 0101, 01001, и.т.д.
Обнаруживать ошибки в нечетном количестве бит. Для этого в G должно быть четное количество единичных бит.
Обнаруживать идущие подряд ошибочные биты длины меньше 17. E=000…011…10…000. Вектор ошибок можно представить в виде: E=(100…00)*(111…1). Если в G младший бит единица, то левый множитель не кратен G, и если G длиннее правого множителя, то ошибка будет отловлена.

Обнаруживать идущие подряд ошибочные биты длины 17, кроме 1/2¹⁵.
Обнаруживать все другие ошибки, кроме 1/2¹⁶.

Сразу же следует отметить, что выполнение этих всех условий одновременно, задача нереальная, да к тому же и не нужная. Какая бы ошибка во время передачи не возникала — она локальна, точнее сказать она — скорее всего, локальна. От возникновения нескольких ошибок в результате помехи спасает уменьшение размеров передаваемых пакетов, так что в каждом пакете лишь одна ошибка (один ли несколько подряд идущих ошибочных битов). Поэтому при нахождении CRC-полиномов было сделано одно допущение — если возникла ошибка, то она локальна (ну разве что в теории CRC-полиномы могут обнаружить 2 однобитные ошибки и нечетное количество ошибок, но на практике все несколько хуже).

Концепция сдвига вносит некоторые ограничения. Поскольку степени x — это ненулевые элементы 2¹⁶, если сдвиг начался с некоторого ненулевого состояния, то в это же состояние мы вернемся через 2¹⁵ шагов и не раньше. Таким образом, возникает ограничение на размер сообщения — 4094 байта.

Было проведено исследование. Цель, которого состояла в том, чтобы узнать выполняются ли на самом деле условия наложенные на полиномы. Для этого использовалось 10⁵ строк длины 5 байт, содержащих цифры от 0 до 9. Значение CRC для каждой такой строки было получено при помощи написанной мной программы, которую можно скачать здесь.

В этом исследованим понадобилось обрабатывать большие объемы данных с довольно хорошей скоростью. Наиболее подходящим для этого инструментом стал MS Visual FoxPro 6.0. Были созданы базы данных, которые вы можете скачать здесь . Названия файлов говорят, сами за себя, чего не скажешь о названиях столбцов. Итак:

Crc — Знаение CRC, которое совпало.
Cin1 и Cin2 — строки, значение CRC, которых совпало.
Nin1 и Nin2 — те же строки, только не в символьном придставлении, а в числовом.
Nx — XOR между двумя значениями Nin1 и Nin2, чтобы выявить разлиные биты.
Rasst — расстояние между крайними битами
Razlbit — количество различных бит
Rez — максимальное расстояние между двумя различными битами
Sinbit — количество одиноких единичных битов (биты рядом, с которыми нет других единичных битов)
Burst — максимальная длина потока единичных ошибочных битов.

Можно заметить, что кое-какие из этих столбоцов являются вспомогательными, поэтому в некоторых таблицах присутствуют не все эти столбцы.

Xmodem (0x1021, инициализируется 0).
- Повторов: 112320
- Нет ни одного случая с одной 1-битной ошибкой.
- Все пары 1-битных ошибок находит.
- Совпадений CRC при четном количестве различных битов — 35840, при нечетном количестве бит — 76480. Есть совпадения CRC при нечетном количестве различных одиночных бит
- Если встречаются группы ошибочных бит, то их несколько.
CRC-16* (0x8005, инициализируется 0)
- Повторов: 327424
- Нет ни одного случая с одной 1-битной ошибкой.
- 16000 раз встречается совпадение CRC в случае с 2 различными битами. Причем биты находятся на расстоянии в 1 бит.
- Совпадений CRC при четном количестве различных битов — 150912, при нечетном количестве бит — 176512. Нет совпадений CRC при нечетном количестве различных одиночных бит
- Если встречаются группы ошибочных бит, то их несколько.
X.25 (0x8408, инициализируется в 0xffff)
- Повторов: 98560
- Нет ни одного случая с одной 1-битной ошибкой.
- Все пары 1-битных ошибок находит
- Совпадений CRC при четном количестве различных битов — 35840, при нечетном количестве бит — 62720. Есть совпадения CRC при нечетном количестве различных одиночных бит
- Если встречаются группы ошибочных бит, то их несколько.
CRC-16 (0xa001, инициализируется в 0)
- Повторов: 274816
- Нет случаев с одной однобитной ошибкой.
- 6000 раз встречается совпадение CRC в случае с 2 различными битами. Причем биты находятся на расстоянии в 1 бит.
- Совпадений CRC при четном количестве различных битов — 134272, при нечетном количестве бит — 140544. Нет совпадений CRC при нечетном количестве различных одиночных бит
- Если встречаются группы ошибочных бит, то их несколько.

Из данного исследования можно сделать определенные выводы. Больше всего удивляет расхождение с теорией по нечетному количеству ошибочных бит. С нечетным количеством различных бит совпадений было не меньше, а больше и это несмотря на то, что такого вообще быть не должно! Другое дело, что нечетное количество одиночных ошибочных бит почему-то пропуcкают, как X25 и X-modem, однако не пропускает полином IBM Все прекрасно ловят группы ошибочных бит, здесь нареканий никаких.

Полином CRC-16 был разработан для бисинхронной передачи данных довольно известной в узких кругах компанией IBM. И как они могли допустить совпадение CRC в 2 сообщениях с двумя различными битами? Но если присмотреться можно заметить, что если два бита есть и совпадает CRC, то они находятся на расстоянии в 1 бит. Всегда, по крайней мере? для 40 бит. Можно подумать, что для полинома CRC-16 служат кратными полиномы вроде (0..01010..0). Но таких полиномов в массе гораздо меньше, чем всех остальных. Вполне возможно, что CRC-16 может отловить все остальные, не отлавливая этот конкретный случай.

Так почему же используется всего 2 полинома? Дело в том, что при улучшении каких-то показателей по отдельным пунктам, ухудшаются остальные, а нахождение максимально лучшего полинома может стать своего рода «шаманством», недаром ведь полиномы называют «magic word», что значит магическое слово. Можно взглянуть на эти два применяемых в индустрии полинома и, казалось бы, что X.25 и Xmodem находят CRC гораздо лучше, но судить рано, ведь может быть при больших объемах все будет несколько иначе.

При написании утилиты столкнулся с тем, что тяжело найти примеры с вычисленными для них CRC. Поэтому привожу данную таблицу.

CRC значения представлены в 16-ричном формате, значение после 0x и есть 16 бит значения CRC.

Строка	Xmodem	CRC-16*	CRC-16	CCITT X.25
«abcdefgh»	0xabff	0x7d68	0x7429	0xa8a6
«T»	0x1a71	0x81fb	0xff01	0xd9e4
«THE,QUICK,BROWN,FOX,0123456789»	0x0498	0x38da	0xb96e	0x6e20
«TeSt»	0xaaae	0x7ce1	0xf83c	0xe8ab

Так же значения CRC совпадают с примерами из [1]

CRC-8 [1]:x⁸ + x² + x + 1. Используется в SMBUS.
CRC-10[1]:x¹⁰ + x⁹ + x⁵ + x⁴ + x + 1. Используется в протоколе ATM (Asynchronous Transfer Mode)
CRC-12[8]:x¹² + x¹¹ + x ³ + x² + x + 1.
CRC-24[1]:x²⁴ + x²³ + x¹⁸ + x¹⁷ + x¹⁴ + x¹¹ + x¹⁰ + x⁷ + x⁶ + x⁵ + x⁴ + x³ + x + 1. Используется в протоколе Military Standard 188/184. Название говорит само за себя.
CRC-32[1]:x³² + x²⁶ + x²³ + x²² + x¹⁶ + x¹² + x¹¹ + x¹⁰ + x⁸ + x⁷ + x⁵ + x⁴ + x² + x + 1. Стандарт V. 42 CCITT. Используется в технологии Ethernet, под именем Ethernet и известен.

CRC — Cyclic Redundancy Code, циклически избыточный код.
CCITT — Comite Consultatif International Telegraphique et Telephonique. Международный Комитет Консультантов по Телефонии и Телеграфии.
HDLC — High-level Data Link Control. Высокоуровневый контроль управления каналом. [6]
SDLC — Synchronous Data Link Control. Синхронное управление передачей данных. [6]
IBM — International Business Machines
BISYNCH — Протокол IBM бисинхронной передачи данных
XOR — операция побитового исключающего ИЛИ.
SMBUS — System Management Bus

Craig Watson, «CRC info» [Online]
Владимир Замятин, Алексей Эстрекин, «CRC-алгоритмы обнаружения ошибок» [Online]
Assembler: практикум/ В. Юров — СПб.: Питер, 2002
Stuart Baker, «Kermit and Xmodem — A Comparison» [Online]
CISCO Networking Academy Course [Online]
Основы компьютерных сетей. : Пер. с англ. — М.: Издательский дом «Вильямс», 2002.
Passwords.ru [Online]
http://doc.lipetsk.ru/book.itep.ru/2/27/erdet_27.htm

Для целей, поставленных в данной курсовой работе я написал программку для вычисления различных стандартных 16-ти битных CRC.

Здесь вы ее можете скачать

О замеченных ошибках и опечатках просьба сообщить. Буду признателен.

2003 г., Екатеринбург.

cs.usu.edu.ru

Прямой табличный алгоритм crc16

Необходимость дополнения исходной строки завершающими нулевыми байтами представляет большое неудобство при реализации общей схемы табличного алгоритма. Поэтому на практике используют другую схему вычисления CRC, не требующую завершения исходного сообщения нулевыми байтами. В этой схеме очередной байт исходной строки объединяется операцией XOR со старшим байтом регистра, выдвинутым с левой стороны этого регистра.

Полученное в результате объединения значение используется в качестве индекса для доступа к CRC-таблице. Извлекаемое из CRC-таблицы значение объединяется операцией XOR с содержимым регистра. Описанный алгоритм называют прямым табличным алгоритмом.

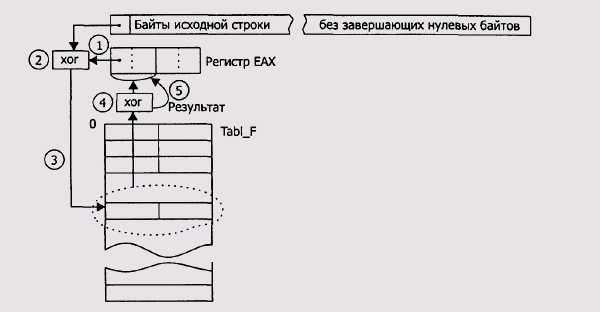Рис. 12.6. Схема вычислений CRC с использованием прямого табличного алгоритма

На схеме вычислений CRC с использованием прямого табличного алгоритма цифрами обозначена последовательность шагов вычисления CRC.

Выдвижение старшего байта регистра АХ в байтовую ячейку.
Выполнение операции XOR над выдвинутым на шаге 1 в байтовую ячейку старшим байтом регистра АХ и очередным байтом исходной строки.
Полученное на шаге 2 значение используется в качестве индекса для доступа к элементу CRC-таблицы.
Извлеченное из CRC-таблицы значение объединяется по XOR со значением в регистре АХ.
Результат выполнения на шаге 4 операции XOR помещается обратно в регистр АХ.

После обработки последнего байта исходной строки регистр АХ содержит значение CRC.

Все существующие алгоритмы вычисления CRC являются, по сути, различными модификациями описанного выше табличного алгоритма. Эти модификации преследуют разные цели, перечислим некоторые из них:

переход от цикла по всем битам к циклу по большим порциям данных – байтам, словам и т. д.;
повышение разрядности порождающего полинома;
отражение особенностей функционирования аппаратуры передачи данных (наличие этой цели обусловлено тем, что микросхемы, поддерживающие работу последовательного порта компьютера, передачу байта начинают с его младших битов, поэтому описанные ниже алгоритмы расчета CRC, учитывающие эту особенность, называются зеркальными).

Алгоритмы вычисления CRC получили свое закрепление в некоторых стандартах. Перечислим отличительные особенности основных алгоритмов вычисления CRC. Итак, основные алгоритмы вычисления CRC различаются:

по значению и степени порождающего полинома, при этом значение полинома обычно указывается без ведущей единицы в старшем разряде;
по начальному содержимому регистра, в котором формируется значение CRC;
по тому, производится ли обращение битов каждого байта перед его обработкой;
по способу прохода байтов через регистр – способ может быть косвенным или прямым;
по тому, производится ли обращение конечного результата;
по конечному значению, с которым производится объединение по XOR результата вычисления CRC.

После появления 32-разрядных микропроцессоров наибольшей популярностью стали пользоваться 32-разрядные алгоритмы вычисления CRC. В различных источниках рассматривают два типа таких алгоритмов – прямой и зеркальный. Рассмотрим их конкретные реализации, рекомендуемые стандартами.

Как и любой табличный алгоритм, табличный алгоритм вычисления CRC32 требует задания CRC-таблицы. Ее можно задать в программе статически, явно прописав значения элементов таблицы в сегменте кода, или динамически, вычислив значения элементов таблицы перед началом расчета CRC.

В заключение обсудим «зеркальный» вариант табличного алгоритма – алгоритм CRC32 (V.42 МККТТ). Этот вариант вычисления CRC обязан своим возникновением существованию последовательного интерфейса, который посылает биты, начиная с наименее значимого (бит 0) и заканчивая самым старшим (бит 7), то есть в обратном порядке. В «зеркальном» регистре все биты отражены относительно центра. Например, 10111011001 есть отражение значения 10011011101.

Вместо того чтобы менять местами биты перед их обработкой, можно зеркально отразить все значения и действия, участвующие в прямом алгоритме. При этом направление расчетов поменяется – байты теперь будут сдвигаться вправо, полином 04clldb7h зеркально отразится относительно его центра, в результате получится значение 0edb88320h. СRС32-таблица будет зеркальным отражением аналогичной таблицы для прямого алгоритма (рис. 12.7).

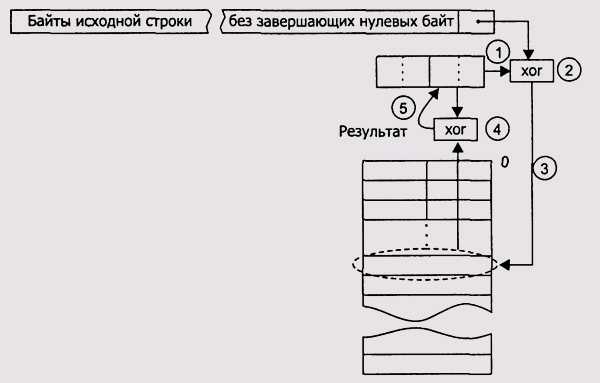Рис. 12.7. Схема «Зеркального» табличного алгоритма

Для зеркального алгоритма вычисления CRC32 процесс вычисления такой же, за исключением порядка – сдвиги и заполнение регистра осуществляются вправо.

Этот вариант работы алгоритма вычисления CRC32 удобен тем, что не нужно знать длину собственно исходной последовательности (без значения CRC). Достаточно просто обработать весь входной поток, не различая в строке завершающую ее подстроку с CRC. Далее необходимо сравнить содержимое регистра ЕАХ с 6b202ca2h. Если эти значения равны, значит, исходная последовательность нарушена не была. Для получения собственно строки достаточно отбросить последние 4 байта сообщения, полученного приемником.

studfiles.net

Простой и эффективный расчёт Modbus CRC16 в ПЛК и МК без побитового сдвига и таблиц

Сакральный алгоритм расчёта CRC16, описанный в литературе и связанный с побитовым сдвигом, плохо вписывается в формат вычислительных возможностей ПЛК и МК. Во-первых, постольку, поскольку его реализация отнимает изрядный объем вычислительных ресурсов вышеозначенных устройств, во-вторых, потому что в ходе такого расчета существенно растягивается время скана программы. Рост скана программы обусловлен тем, что, вследствие словной или байтовой организации аккумулятора арифметико-логического устройства, результирующие битовые операции со словами/байтами в нём выполняются гораздо дольше операций со словами/байтами целиком. В отдельных устройствах операции побитового сдвига и вовсе не поддерживаются, тогда как алгоритм подразумевает выполнение восьми циклов с такими операциями.

В целях сокращения объема вычислений и, как следствие, времени сканирования при обработке CRC, часто применяется иной алгоритм — табличный, когда таблица масок рассчитывается и заполняется единожды в первом скане программы. Тем не менее, и этот способ не лишён недостатка, ибо также потребляет ресурсы. 512 байт (или 256 двухбайтных слов), порою, отнюдь не лишние.

А можно ли видоизменить алгоритм расчёта CRC таким образом, чтобы отказаться от применения побитовых сдвигов и таблиц? Безусловно, да. Достаточно лишь внимательно приглядеться к алгоритму с побитовым сдвигом.

Напомню его суть:

осуществляется сложение по модулю 2 очередного байта массива посылки с младшим байтом двухбайтной CRC;
осуществляется ациклический сдвиг CRC на один бит от старшего 15-го разряда к младшему, нулевому, с выдвижением младшего бита, при этом старший разряд обнуляется;
если значение выдвинутого бита единичное, выполняется сложение CRC по модулю 2 c полиномом 16#A001.
шаги 2 и 3 повторяются ещё 7 раз.

Почему это реализовано так, а не иначе? Да потому, что такая алгоритмизация представлялась наиболее подходящей для реализации посредством аппаратной логики.

Внимательно взглянув на этот алгоритм, нетрудно обнаружить, что фактически мы имеем дело с циклическим побитовым сдвигом слова. За его цикличность отвечает старший бит полинома. В результате, значение старшего битового разряда CRC после каждого сдвига идентично значению выдвинутого младшего. Таким образом, при осуществлении циклического побитового сдвига, полином, с которым затем необходимо производить сложение по модулю 2, трансформируется в 16#2001.

Подобных сдвигов выполняется восемь… Проще говоря, в глобальном плане речь идёт о перемене местами младшего байта CRC со старшим её байтом. А это наводит на мысль, что, после сложения по модулю 2 очередного байта массива посылки с младшим байтом CRC, достаточно поменять местами младший и старший байт CRC, а затем, последовательно проанализировав восемь бит старшего её байта, начав с младшего его разряда, восьмого, произвести сложение СRC по модулю 2 c известными константами, предопределёнными значением полинома, значение которого для Modbus CRC16, как уже указано выше, эквивалентно 16#2001.

Итоговый алгоритм для учёта в CRC очередного байта массива посылки выглядит следующим образом:

Осуществляется сложение по модулю 2 очередного байта массива посылки с младшим байтом двухбайтовой CRC, после чего младший и старший байт CRC меняются местами;

Если значение 8-го бита СRC единичное, выполняется её сложение по модулю 2 с константой 16#0240;
Если значение 9-го бита СRC единичное, выполняется её сложение по модулю 2 с константой 16#0480;
Если значение 10-го бита СRC единичное, выполняется её сложение по модулю 2 с константой 16#0900;
Если значение 11-го бита СRC единичное, выполняется её сложение по модулю 2 с константой 16#1200;
Если значение 12-го бита СRC единичное, выполняется её сложение по модулю 2 с константой 16#2400;
Если значение 13-го бита СRC единичное, выполняется её сложение по модулю 2 с константой 16#4800;
Если значение 14-го бита СRC единичное, выполняется её сложение по модулю 2 с константой 16#9000;
Если значение 15-го бита СRC единичное, выполняется её сложение по модулю 2 с константой 16#2001, расчёт окончен.

Преимущества такого способа расчёта:

1) По сравнению с алгоритмом побитового сдвига:

а) предложенный алгоритм позволяет избавиться от команд вложенного цикла FOR-NEXT и команд побитового сдвига в таком цикле, при том, число количество исполняемых команд сложения по модулю 2 сохраняется неизменным;

б) в контроллерах c поддержкой команды SWAP, восьмикратный побитовый сдвиг CRC заменяется единственной командой, а в контроллерах, такую команду не поддерживающих, — одной или двумя командами пересылки, входящими в число базовых команд контроллера и отнимающими минимальное время;

2) По сравнению с табличным методом расчёта, этот метод не нуждается в выделении места в памяти данных под таблицу, в её предварительном заполнении, в выборке соответствующей маски из таблицы с последующим ее наложением на байт CRC.

Проработка предложенного алгоритма расчёта СRC16 изначально велась для ПЛК Mitsubishi моделей FX3S/3G, не поддерживающих инструкций расчёта СRC и перемены местами байт в слове, между тем, предельное суммарное время расчета СRC с применением указанного алгоритма для массива посылки, состоящего из 128 байт, не превышает 2,4мс.

habr.com

Циклический избыточный код | Контроль Разума

/*
  Name  : CRC-8
  Poly  : 0x31	x^8 + x^5 + x^4 + 1
  Init  : 0xFF
  Revert: false
  XorOut: 0x00
  Check : 0xF7 ("123456789")
  MaxLen: 15 байт (127 бит) - обнаружение
    одинарных, двойных, тройных и всех нечетных ошибок
*/
const unsigned char Crc8Table[256] = {
    0x00, 0x31, 0x62, 0x53, 0xC4, 0xF5, 0xA6, 0x97,
    0xB9, 0x88, 0xDB, 0xEA, 0x7D, 0x4C, 0x1F, 0x2E,
    0x43, 0x72, 0x21, 0x10, 0x87, 0xB6, 0xE5, 0xD4,
    0xFA, 0xCB, 0x98, 0xA9, 0x3E, 0x0F, 0x5C, 0x6D,
    0x86, 0xB7, 0xE4, 0xD5, 0x42, 0x73, 0x20, 0x11,
    0x3F, 0x0E, 0x5D, 0x6C, 0xFB, 0xCA, 0x99, 0xA8,
    0xC5, 0xF4, 0xA7, 0x96, 0x01, 0x30, 0x63, 0x52,
    0x7C, 0x4D, 0x1E, 0x2F, 0xB8, 0x89, 0xDA, 0xEB,
    0x3D, 0x0C, 0x5F, 0x6E, 0xF9, 0xC8, 0x9B, 0xAA,
    0x84, 0xB5, 0xE6, 0xD7, 0x40, 0x71, 0x22, 0x13,
    0x7E, 0x4F, 0x1C, 0x2D, 0xBA, 0x8B, 0xD8, 0xE9,
    0xC7, 0xF6, 0xA5, 0x94, 0x03, 0x32, 0x61, 0x50,
    0xBB, 0x8A, 0xD9, 0xE8, 0x7F, 0x4E, 0x1D, 0x2C,
    0x02, 0x33, 0x60, 0x51, 0xC6, 0xF7, 0xA4, 0x95,
    0xF8, 0xC9, 0x9A, 0xAB, 0x3C, 0x0D, 0x5E, 0x6F,
    0x41, 0x70, 0x23, 0x12, 0x85, 0xB4, 0xE7, 0xD6,
    0x7A, 0x4B, 0x18, 0x29, 0xBE, 0x8F, 0xDC, 0xED,
    0xC3, 0xF2, 0xA1, 0x90, 0x07, 0x36, 0x65, 0x54,
    0x39, 0x08, 0x5B, 0x6A, 0xFD, 0xCC, 0x9F, 0xAE,
    0x80, 0xB1, 0xE2, 0xD3, 0x44, 0x75, 0x26, 0x17,
    0xFC, 0xCD, 0x9E, 0xAF, 0x38, 0x09, 0x5A, 0x6B,
    0x45, 0x74, 0x27, 0x16, 0x81, 0xB0, 0xE3, 0xD2,
    0xBF, 0x8E, 0xDD, 0xEC, 0x7B, 0x4A, 0x19, 0x28,
    0x06, 0x37, 0x64, 0x55, 0xC2, 0xF3, 0xA0, 0x91,
    0x47, 0x76, 0x25, 0x14, 0x83, 0xB2, 0xE1, 0xD0,
    0xFE, 0xCF, 0x9C, 0xAD, 0x3A, 0x0B, 0x58, 0x69,
    0x04, 0x35, 0x66, 0x57, 0xC0, 0xF1, 0xA2, 0x93,
    0xBD, 0x8C, 0xDF, 0xEE, 0x79, 0x48, 0x1B, 0x2A,
    0xC1, 0xF0, 0xA3, 0x92, 0x05, 0x34, 0x67, 0x56,
    0x78, 0x49, 0x1A, 0x2B, 0xBC, 0x8D, 0xDE, 0xEF,
    0x82, 0xB3, 0xE0, 0xD1, 0x46, 0x77, 0x24, 0x15,
    0x3B, 0x0A, 0x59, 0x68, 0xFF, 0xCE, 0x9D, 0xAC
};
 
unsigned char Crc8(unsigned char *pcBlock, unsigned char len)
{
    unsigned char crc = 0xFF;
 
    while (len--)
        crc = Crc8Table[crc ^ *pcBlock++];
 
    return crc;
}

mind-control.wikia.com

Описание и расчёт CRC16

Documents войти Загрузить ×

Математика

advertisement advertisement

Document 4540531

Лабораторная работа №5 Реализация алгоритма обнаружения

Очиститель и обезжириватель Degreaser65

Восемь лет назад был принят Федеральный закон «Об общих

Блок подъездный контрольно сигнальный «Цифрал-Интел КСБ-400» Руководство пользователя

Вопросы к экзамену по курсу «Разработка программных приложений»

Протокол обмена по последовательному порту стационарного

Сегодня самые консервативные из государств осознали, что без

Андрей Шеремет, заместитель председателя

Организация и учебно-методическое обеспечение самостоятельной работы студентов Текущая СРС.

СИСТЕМАТИЧЕСКОЕ КОДИРОВАНИЕ КОДОВ n РЕГИСТРА СДВИГА

Алгоритм Шора, Гровера

Мыцко Е. А. Примеры аппаратных реализаций вычисления

studydoc.ru

c — Функция для вычисления контрольной суммы CRC16

Есть несколько деталей, которые вам нужно «совместить» для конкретной реализации CRC. Даже при использовании одного и того же полинома могут быть разные результаты из-за незначительных различий в том, как обрабатываются биты данных, используя определенное начальное значение для CRC (иногда это ноль, иногда 0xffff) и/или инвертирование бит CRC. Например, иногда одна реализация будет работать из младших бит байтов данных, тогда как иногда они будут работать с битами верхнего порядка вниз (как это делается в настоящее время).

Кроме того, вам нужно «вытолкнуть» последние бит CRC после запуска всех бит данных.

Имейте в виду, что алгоритмы CRC были разработаны для аппаратного обеспечения, поэтому некоторые из способов обработки битового заказа могут не иметь особого смысла с точки зрения программного обеспечения.

Если вы хотите сопоставить CRC16 с полиномом 0x8005, как показано на странице калькулятора CRM lammertbies.nl, вам необходимо внести следующие изменения в функцию CRC:

a) запускать биты данных через цикл CRC, начиная с младшего значащего бита, а не из самого значащего бита
b) вытащите последние 16 бит CRC из регистра CRC после того, как вы закончили с входными данными.
c) отменить бит CRC (я предполагаю, что этот бит переносится с аппаратных реализаций)

Итак, ваша функция может выглядеть так:

#define CRC16 0x8005

uint16_t gen_crc16(const uint8_t *data, uint16_t size)
{
    uint16_t out = 0;
    int bits_read = 0, bit_flag;

    /* Sanity check: */
    if(data == NULL)
        return 0;

    while(size > 0)
    {
        bit_flag = out >> 15;

        /* Get next bit: */
        out <<= 1;
        out |= (*data >> bits_read) & 1; // item a) work from the least significant bits

        /* Increment bit counter: */
        bits_read++;
        if(bits_read > 7)
        {
            bits_read = 0;
            data++;
            size--;
        }

        /* Cycle check: */
        if(bit_flag)
            out ^= CRC16;

    }

    // item b) "push out" the last 16 bits
    int i;
    for (i = 0; i < 16; ++i) {
        bit_flag = out >> 15;
        out <<= 1;
        if(bit_flag)
            out ^= CRC16;
    }

    // item c) reverse the bits
    uint16_t crc = 0;
    i = 0x8000;
    int j = 0x0001;
    for (; i != 0; i >>=1, j <<= 1) {
        if (i & out) crc |= j;
    }

    return crc;
}

Эта функция возвращает 0xbb3d для меня, когда я передаю "123456789".

qaru.site

Иллюстрированный самоучитель по задачам и примерам Assembler › Вычисление CRC › Табличные алгоритмы вычисления CRC [страница — 188] | Самоучители по программированию

Табличные алгоритмы вычисления CRC

Прямой табличный алгоритм CRC16

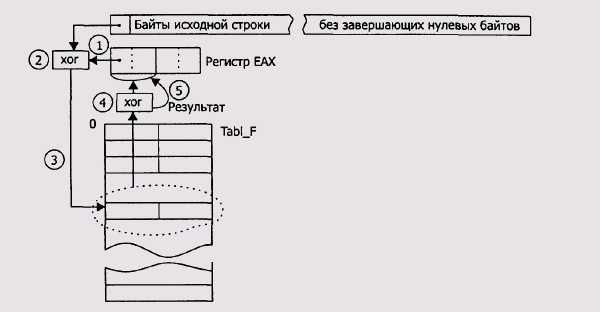
Рис. 9.9. Схема вычислений CRC с использованием прямого табличного алгоритма

Выдвижение старшего байта регистра АХ в байтовую ячейку.
Выполнение операции XOR над выдвинутым на шаге 1 в байтовую ячейку старшим байтом регистра АХ и очередным байтом исходной строки.
Полученное на шаге 2 значение используется в качестве индекса для доступа к элементу CRC-таблицы.
Извлеченное из CRC-таблицы значение объединяется по XOR со значением в регистре АХ.
Результат выполнения на шаге 4 операции XOR помещается обратно в регистр АХ.

После обработки последнего байта исходной строки регистр АХ содержит значение CRC. Программа вычисления CRC с использованием прямого табличного алгоритма приведена ниже.

:prg09_04.asm – программа вычисления CRC с использованием прямого табличного алгоритма.
………. >>
.data
;исходная битовая последовательность в символах
bit_string db "6476c8"
1en_bi t_string=$-bi t_stri ng
adr_bit_string dd bit_string
tabl_16 dw 256 dup (0) iCRC-таблица
Ien_tab1_16=$-tabl_16 adr_tabl_16 dd tabl_16
polinom dw 1021h
.code
.-------------расчитываем CRC-таблицу---…..-------------
les di.adr_tabl_16
add di.len_tabl_16-2
std:идем назад по таблице
mov ex.255
mov bx.polinom
ml: xor ax,ax
mov ah.cl:индекс в таблице для вычисления CRC
push ex сложенные циклы
mov ex.8
m2: shi ax.l
jnc m3;старшие разряды не равны – выполняем сдвиг (частное нас не интересует)
:старшие разряды равны – выполняем XOR:
xor ax.bx:ax XOR polinom
тЗ: loop m2
pop ex
stosw
loop ml
-------------закончили расчет CRC-таблицы………
хог ах,ах
xor bx.bx
Ids si.adrbitstring
mov cx.len_bit_string
m4: mov bl.ah
shl ax.8
xor bl.[si]
xor ax.tabl_16[bx]
inc si
1oop m4
;………

Рассмотрением этого алгоритма введение в проблему вычисления CRC можно было бы и закончить. Все существующие алгоритмы вычисления CRC являются, по сути, различными модификациями описанного выше табличного алгоритма. Эти модификации преследуют разные цели, перечислим некоторые из них:

переход от цикла по всем битам к циклу по большим порциям данных – байтам, словам и т. д.;
повышение разрядности порождающего полинома;
отражение особенностей функционирования аппаратуры передачи данных (наличие этой цели обусловлено тем, что микросхемы, поддерживающие работу последовательного порта компьютера, передачу байта начинают с его младших битов, поэтому описанные ниже алгоритмы расчета CRC, учитывающие эту особенность, называются зеркальными).

по значению и степени порождающего полинома, при этом значение полинома обычно указывается без ведущей единицы в старшем разряде;
по начальному содержимому регистра, в котором формируется значение CRC;
по тому, производится ли обращение битов каждого байта перед его обработкой;
по способу прохода байтов через регистр – способ может быть косвенным или прямым;
по тому, производится ли обращение конечного результата;
по конечному значению, с которым производится объединение по XOR результата вычисления CRC.

samoychiteli.ru