Золотое сечение в живописи — Ф. В. Ковалев
История зототого сечения
История золотого сечения интересна и увлекательна. Она еще раз подтверждает, что тайны природы скрыты и ревниво ею охраняются. Тайна золотого сечения — не исключение.
В 1911 г. французский художник Анри Матисс (1869 — 1954) посетил Россию. В Москве он увидел старинные русские иконы. «Русские и не подозревают, какими художественными богатствами они владеют… Ваша учащаяся молодежь имеет здесь, у себя дома, несравненно лучшие образцы искусства…, чем за границей. Французские художники должны ездить учиться в Россию: Италия в этой области дает меньше», — писал художник позже 1.
Много лет спустя Матисс вспоминал, как «тронуло» его древнерусское искусство и какое воздействие оказало на его творчество: «Ему предаешься тем сильнее, чем яснее видишь, что его достижения подкреплены традицией — традицией древней» 2. Матисс, несомненно, имел в виду традиции искусства Греции классической поры.
Он увидел, что Русь через Византию унаследовала живую традицию античного искусства и в своих исторических и национальных условиях продолжала ее. Пока Италия возрождала античность, пытаясь из обломков и развалин составить цельное представление о древности, искусство живописи и архитектуры на Руси достигло больших высот.
Приехав в Советский Союз, американский художник Антон Рефрежье восторженно воспринимает сохранившиеся росписи, выполненные древнерусскими художниками. «Я смотрю на величественные росписи древнерусских храмов, и меня снова и снова потрясает глубина гуманизма искусства, которое поднялось над церковной догмой до уровня выражения эмоционального духа народа. И я с изумлением смотрю на построение композиции, на пропорции фризов на стенах. Здесь также мы можем учиться знанию закона динамической симметрии, абсолютной вере художников в эти законы, раскрытые древними греками и подтвержденные во все великие периоды архитектуры и живописи», — писал он в статье «На языке, понятном массам», опубликованной в газете «Советская культура» 21мая 1974 г.
Принято считать, что понятие о золотом делении ввел в научный обиход Пифагор, древнегреческий философ и математик (VI в. до н. э.). Есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамоиа свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании.
Греки были искусными геометрами. Даже арифметике обучали своих детей при помощи геометрических фигур. Квадрат Пифагора и диагональ этого квадрата были основанием для построения динамических прямоугольников (рис. 23, а).
Платон (427 — 347 гг. до н. э.) также знал о золотом делении. Его диалог «Тимей» посвящен математическим и эстетическим воззрениям школы Пифагора и, в частности, вопросам золотого деления.
В фасаде древнегреческого храма Парфенона присутствуют золотые пропорции. При его раскопках обнаружены циркули, которыми пользовались архитекторы и скульпторы античного мира.
В Помпейском циркуле (музей в Неаполе) также заложены пропорции золотого деления (рис. 23, б).
Рис. 23. Динамические прямоугольники (а) и античный циркуль золотого сечения (б)
В дошедшей до нас античной литературе золотое деление впервые упоминается в «Началах» Евклида. Во 2-й книге «Начал» дается геометрическое построение золотого деления. После Евклида исследованием золотого деления занимались Гипсикл (II в. до н. э.), Папп (III в. н. э.) и др. В средневековой Европе с золотым делением познакомились по арабским переводам «Начал» Евклида. Переводчик Дж. Кампано из Наварры (III в.) сделал к переводу комментарии. Секреты золотого деления ревностно оберегались, хранились в строгой тайне. Они были известны только посвященным.
В историю золотого сечения косвенным образом вплетено имя итальянского математика монаха Леонардо из Пизы, более известного под именем Фибоначчи (сын Боначчи). Он много путешествовал по Востоку, познакомил Европу с индийскими (арабскими) цифрами.
| Месяцы | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | и т.д. |
| Пары кроликов | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 89 | 144 | и т. д. |
Ряд цифр 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и т. д. стал известен в наука как ряд Фибоначчи. Его особенность состоит в том, что каждый его член, начиная с третьего, равен сумме двух предыдущих: 2 + 3=5; 3+5 = 8; 5 + 8=13; 8+13 = 21; 13+21 = 34 и т. д., а отношение чисел ряда все больше и больше приближается к отношению золотого деления. Так, 21 : 34 = 0,617, а 34:55 = 0,618. Это отношение обозначается символом Ф. Только это отношение — 0,618:0,382 — дает непрерывное деление отрезка прямой в золотой пропорции, увеличение его или уменьшение до бесконечности, когда меньший отрезок так относится к большему, как больший ко всему. Ряд Фибоначчи мог бы остаться только математическим казусом (случаем), если бы не то обстоятельство, что все исследователи золотого деления в растительном мире, а также и в животном, не говоря уже об искусстве, неизменно приходили к этому ряду как арифметическому выражению закона золотого деления.
В эпоху Возрождения усиливается интерес к золотому делению среди ученых и художников в связи с его применением как в геометрии, так и в искусстве, особенно в архитектуре.
Леонардо да Винчи, художник и ученый, видел, что у итальянских художников эмпирический опыт большой, а знаний мало. Он задумал и начал писать книгу по геометрии, но в это время появилась книга монаха Луки Пачоли, и Леонардо оставил свою затею. По мнению современников и историков науки, Лука Пачоли был настоящим светилом, величайшим математиком Италии в период между Фибоначчи и Галилеем. Лука Пачоли был учеником художника Пьеро делла Франчески, написавшего две книги, одна из которых называлась «О перспективе в живописи». Его называют творцом начертательной геометрии.
Лука Пачоли прекрасно понимал значение науки для искусства. В 1496 г. по приглашению герцога Моро он приезжает в Милан, где читает лекции по математике. В Милане при дворе Моро в то время работал и Леонардо да Винчи. Они стали друзьями. В 1509 г. в Венеции была издана книга Луки Пачоли «Божественная пропорция» с блестяще выполненными иллюстрациями, ввиду чего полагают, что их сделал Леонардо да Винчи. Книга была восторженным гимном золотой пропорции.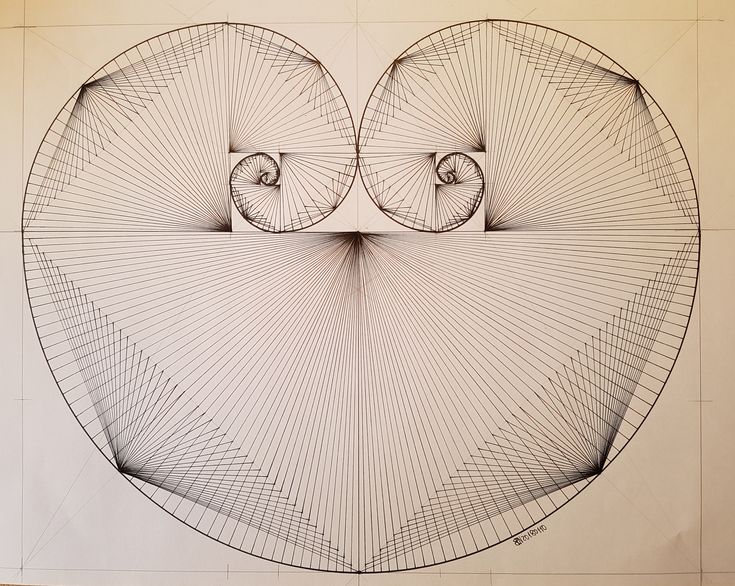
Среди многих достоинств золотой пропорции монах Лука Пачоли не преминул назвать и ее «божественную суть» как выражение божественного триединства: бог сын, бог отец и бог дух святой (подразумевалось, что малый отрезок есть олицетворение бога сына, больший отрезок — бога отца, а весь отрезок — бога духа святого). На золотую пропорцию был наброшен мистический покров.
Леонардо да Винчи также много внимания уделял изучению золотого деления. Он производил сечения стереометрического тела, образованного правильными пятиугольниками, и каждый раз получал прямоугольники с отношениями сторон в золотом делении. Поэтому он дал этому делению название золотое сечение. Так оно и держится в науке до сих пор как самое популярное.
Характерно, что в то же время на севере Европы, в Германии, над теми же проблемами трудился Альбрехт Дюрер. Он делает наброски введения к первому варианту трактата о пропорциях. Дюрер пишет: «…Необходимо, чтобы тот, кто что-либо умеет, обучил этому других, которые в этом нуждаются.
Это я и вознамерился сделать» 3.
Дюрер сетует, что секреты древних утеряны, что отцы церкви не должны так яростно уничтожать все, что осталось от древних. Судя по одному из писем Дюрера, он встречался с Лукой Пачоли во время пребывания в Италии. Альбрехт Дюрер подробно разрабатывает теорию пропорций человеческого тела. Важное место в своей системе соотношений Дюрер отводил золотому сечению. Рост человека делится в золотых пропорциях линией пояса, а также линией, проведенной через кончики средних пальцев опущенных рук, нижняя часть лица — ртом и т. д. Известен пропорциональный циркуль Дюрера.
Великий астроном XVI в. Иоган Кеплер назвал золотое сечение одним из сокровищ геометрии. Он первый обращает внимание на значение золотой пропорции для ботаники (рост растений и их строение).
В последующие века правило золотой пропорции превратилось в академический канон и, когда со временем в искусстве началась борьба с академической рутиной, в пылу борьбы «вместе с водой выплеснули и ребенка».
Вновь «открыто» золотое сечение было в середине XIX в. В 1855 г. немецкий исследователь золотого сечения профессор Цейзинг опубликовал свой труд «Эстетические исследования». С Цейзингом произошло именно то, что и должно было неминуемо произойти с исследователем, который рассматривает явление как таковое, без связи с другими явлениями. Он абсолютизировал пропорцию золотого сечения, объявив ее универсальной для всех явлений природы и искусства. У Цейзинга были многочисленные последователи, но были и противники, которые объявили его учение о пропорциях «математической эстетикой».
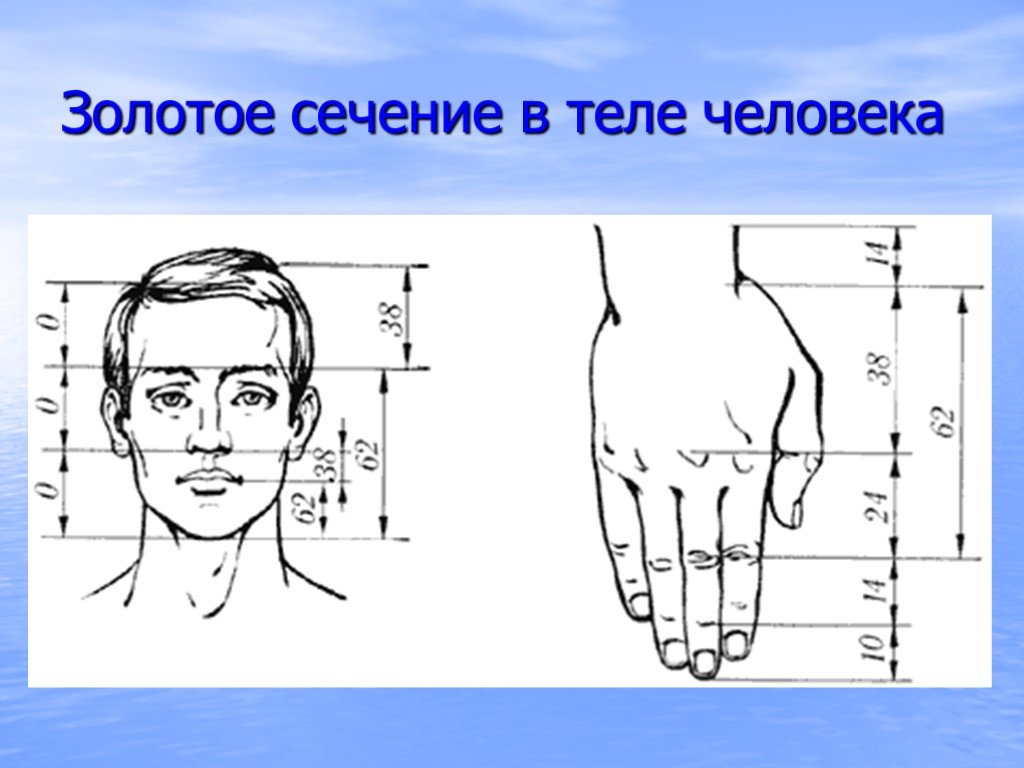
Цейзинг проделал колоссальную работу. Он измерил около двух тысяч человеческих тел и пришел к выводу, что золотое сечение выражает средний статистический закон. Деление тела точкой пупа — важнейший показатель золотого сечения. Пропорции мужского тела колеблются в пределах среднего отношения 13 : 8=1,625 и несколько ближе подходят к золотому сечению, чем пропорции женского тела, в отношении которого среднее значение пропорции выражается в соотношении 8:5=1,6.
У новорожденного пропорция составляет отношение 1:1, к 13 годам она равна 1,6, а к 21 году равняется мужской. Пропорции золотого сечения проявляются и в отношении других частей тела — длина плеча, предплечья и кисти, кисти и пальцев и т. д.
Верность своей теории Цейзинг проверял на греческих статуях. Наиболее подробно он разработал пропорции Аполлона Бельведерского. Подверглись исследованию греческие вазы, архитектурные сооружения различных эпох, растения, животные, птичьи яйца, музыкальные тона, стихотворные размеры. Цейзинг дал определение золотому сечению, показал, как оно выражается в отрезках прямой и в цифрах. Когда цифры, выражающие длины отрезков, были получены, Цейзинг увидел, что они составляют ряд Фибоначчи, который можно продолжать до бесконечности в одну и в другую сторону. Следующая его книга имела название «Золотое деление как основной морфологический закон в природе и искусстве». В 1876 г. в России была издана небольшая книжка, почти брошюра, с изложением этого труда Цейзинга.
Автор укрылся под инициалами Ю. Ф. В. Характерно, что в этом издании не упомянуто ни одно произведение живописи.
В конце XIX — начале XX вв. появилось немало чисто формалистических теорий о применении золотого сечения в произведениях искусства и архитектуры. С развитием дизайна и технической эстетики действие закона золотого сечения распространилось на конструирование машин, мебели и т. д.
Анархия капиталистического производства привела в XX в. к тому, что продукция, изготовленная одним предприятием, сильно отличалась от аналогичной продукции других предприятий. При перевозке такой продукции нередко оказывалось, что она не соответствует размерам транспортных средств. Такое же положение наблюдалось и в строительном деле.
Французский архитектор Ле Корбюзье (1887 — 1965) разрабатывает единую систему величин. За основу был взят средний рост человека, равный 175 см. Была построена шкала золотого сечения, которая и дала необходимые размеры. Эту шкалу Ле Корбюзье назвал модулором.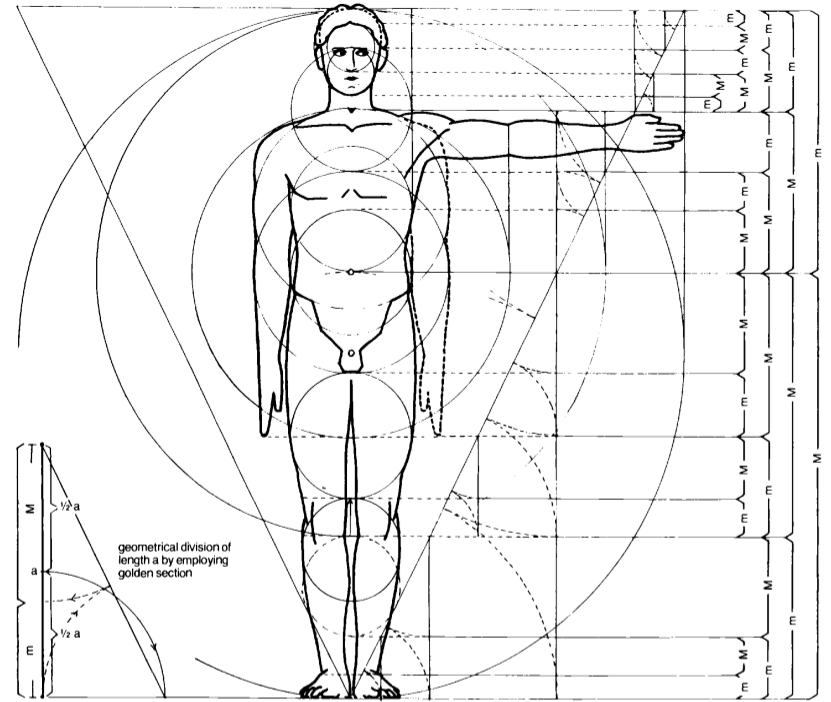
Пользуясь своим «модулором», Ле Корбюзье строил отдельные здания и целые комплексы сооружений.
На девятой выставке «Триеннале» в Милане в 1951 г. три дня были посвящены золотому сечению. В эти дни было проведено первое международное совещание на тему пропорций в искусстве, а выставка «Триеннале» 1954 г. была полностью посвящена «божественной пропорции» и явилась восхвалением золотого сечения — «древнейшей тропы человечества, указанной Пифагором» (Ле Корбюзье). К сожалению, речь там шла в основном об архитектуре.
Следует упомянуть заслуги Г. Б. Борисовского. В книге «Наука. Техника. Искусство» (М., 1969) автор отдает должное золотому сечению, но указывает на его слабую сторону: золотое сечение характеризует только количественные отношения. Он приводит слова Жолтовского о колбасе (сказанные в шутку), что если разрезать тухлую колбасу в золотом сечении, то она не станет вкуснее. Отношения, свойственные золотой пропорции, выраженные арифметически или геометрически, действительно определяют только количественные отношения.
Но эти же отношения, воплотившиеся в живых формах листьев, цветов, животных, доставляют нам эстетическое удовлетворение, радость, мы наслаждаемся красотой формы. Тем более они приятны нам в произведениях рук человеческих: зданиях, статуях, картинах, коврах, вазах и т. д., которые мы пробуем не на вкус, а смотрим на них глазами.
В нашей стране в довоенные годы были изданы книги о золотом сечении в архитектуре: Н. Врунов. Пропорции античной и средневековой архитектуры. — М., 1935; Г. Д. Гримм. Пропорциональность в архитектуре. — Л.; М., 1935. Осуществлялись переводные издания: Г. Е. Тимердинг. Золотое сечение. — М., 1924; М. Гика. Эстетика пропорций в природе и искусстве. — М., 1936; Д. Хэмбидж. Динамическая симметрия в архитектуре. — М., 1936. И в этих книгах проявление закона золотого сечения в живописи не затрагивалось.
В редакционном примечании к книге М. Гика «Эстетика пропорций в природе и искусстве» указывается, что многие ученые, занимавшиеся золотым сечением, не идут дальше простой констатации факта: «Между тем, задача заключается в том, чтобы объяснить его причины.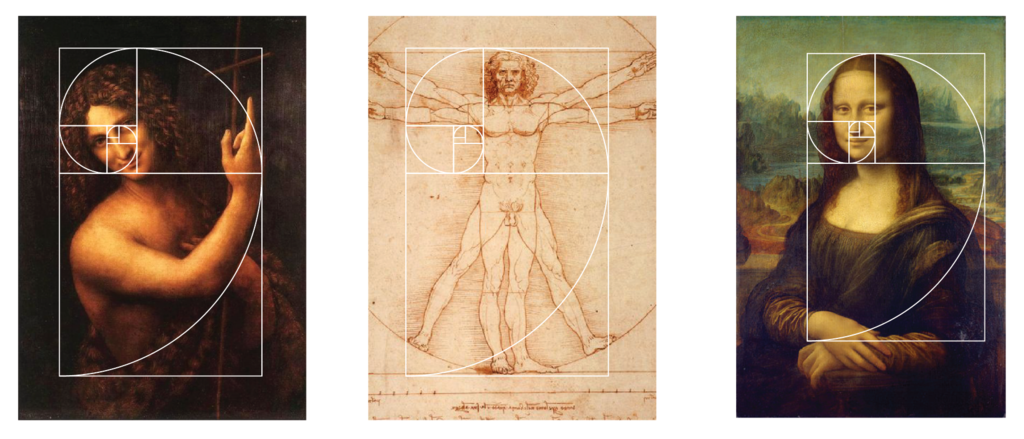
Такую попытку делает советский исследователь Ф. И. Зубарев, работы которого о золотом сечении подготовляются сейчас к печати» 4. Неизвестно, были опубликованы работы Ф. Зубарева или нет.
В послевоенные годы заметно расширение и углубление внимания ученых различных специальностей к проблеме золотого сечения. В 1974 г. И. И. Шафрановский публикует работу «Динамическая симметрия в кристаллографии, минералогии, петрографии и органическом мире» (Записки Ленингр. горн, ин-та им. Г. В. Плеханова. — Т. XII, вып. 2). В 1977 г. напечатана книга А. П. Стахова «Введение в алгоритмическую теорию измерения», а в 1979 г. — его же «Алгоритмическая теория измерения» (М., Знание), в которых изложено применение чисел ряда Фибоначчи и золотой пропорции для улучшения работы аналого-цифровых преобразователей. В 1979 г. И. Шмелев в журнале «Архитектура СССР» публикует статью «Канон. Ритм, пропорция, гармония» (№ 2), в которой излагает дальнейшее развитие идеи «модулора» Ле Корбюзье, что позволило ему раскрыть механизм гармонии ритмических взаимосвязей в пропорциях мужского и женского тела, их динамическую дополнительность по отношению друг к другу, что снимает недоверие к золотому сечению на том основании, что пропорции тела женщины не соответствуют золотым.
Особый интерес представляет статья М. А. Марутаева «О гармонии как закономерности» в сборнике «Принцип симметрии» (М., 1978). Он отмечает, что в современной науке существуют три проблемы: 1) природа золотого сечения, 2) загадка числа 137 и 3) природа приблизительной симметрии, которая относится к живой природе, искусству, а в последнее время и к физике. Далее он показывает, что все три проблемы представляют собой одну проблему: нарушенная симметрия (приблизительная симметрия), число 137 и золотая пропорция взаимосвязаны. Это подтверждает, по мнению автора, фундаментальность принципа золотого сечения и позволяет объяснить многие факты, которые раньше рассматривались как противоречащие принципу золотого сечения.
Болгарский журнал «Отечество» (1983 — № 10) опубликовал статью Цветана Цекова-Карандаша о «втором золотом сечении», которое вытекает из основного сечения и дает новое отношение 44:56. Эта пропорция обнаружена в архитектуре, а также имеет место при построении композиций картин удлиненного горизонтального формата.
Рис. 24. Второе золотое сечение: а — геометрическое построение; 6 — линия второго золотого сечения на картине
Отрезок АВ делится в пропорции золотого сечения (рис. 24, а). Из точки С восставляется перпендикуляр СД. Радиусом АВ находится точка D, которая соединяется линией с точкой А. Прямой < АСД делится пополам. Из точки С проводитсялиния до пересечения с линией AD. Точка Е делит отрезок AD в отношении 56:44. На рис. 24, б показано нахождение линии второго золотого сечения на картине. Она находится посередине между линией золотого сечения и средней линией картины.
1 Матисс А. Сборник статей о творчестве. — М.,1958. — С. 99.
2 Там же. — С. 104.
3 Дюрер А. Дневники, письма, трактаты. — Л.; М., 1957. — Т. 2.- С. 37,
4 Гика М. Эстетика пропорций в природе и искусстве. — М., 1936. — С. 301.
<<<�предыдущая вверх следующая>>>
Конспект урока «Золотое Сечение»
«…Геометрия владеет двумя сокровищами-
Теоремой Пифагора и золотым сечением, и
если первое из них можно сравнить с мерой
золота, то второе- с драгоценным камнем».
(Иоганн Кеплер)
Золотое
сечение
Цели: 1.Образовательные: дать представление о золотом сечении в математике, природе, архитектуре, живописи, теле человека. Узнать, что существует такая золотая точка на любом отрезке, которая обеспечивает присутствие красоты, соразмерности всех частей.
2.Развивающие: Активизировать самостоятельную деятельность; развивать познавательную активность и мировоззренческие представления о единстве красоты природы; учить обобщать и систематизировать полученную информацию.
3.Воспитательные: расширить кругозор учащихся ,способствовать
развитию познавательного интереса; воспитывать гармонически развитую личность.
Содержание:
— История «Золотого сечения». — Золотое сечение в математике. — Золотое сечение в природе — Золотое сечение в архитектуре. – Золотое сечение в живописи. – Золотое сечение в теле человека.
История «Золотого сечения»
В дошедшей до нас античной литературе деление отрезка в
крайнем и среднем отношении впервые встречается в «Началах» Евклида (около 300
лет до н.
э.). Принято считать, что понятие о золотом делении ввел в
научный обиход Пифагор, древнегреческий философ и математик(6 в. до н.э.) Есть
предположение, что Пифагор свое знание золотого деления позаимствовал у
египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов,
барельефов,предметов быта и украшений из гробницы Тутурхамона свидетельствуют,
что египетские мастера пользовались соотношениями золотого деления при
их создании.
Платон(427…347гг. до н.э.) также знал о золотом делении .Его
диалог «Тимей» посвящен математическим и эстетическим воззрениям школы Пифагора
и , в частности, вопросам золотого деления.
Термин «золотое
сечение» был введен в обиход Мартином Омом в1835 году. В последующие века
правило золотого сечения превратилось в академический закон и , когда со
временем в искусстве началась борьба с академической рутиной, в пылу борьбы
«вместе с водой выплеснули и ребенка».
Вновь «открыто» золотое сечение
было в середине 19 века немецким исследователем Цейзингом.
Золотое сечение занимало почетное место в ряду символических величин. Это иррациональное соотношение возникает при делении отрезка на две неравные части, при котором весь отрезок относится к большей части, как большая к меньшей.
Золотое сечение в математике
Усилием математиков золотая пропорция была объяснена, изучена и глубоко проанализирована. Золотое сечение-это такое деление целого на две неравные части, при котором целое так относится к большей части, как большая к меньшей. Рассмотрим деление отрезка на части в отношении равном «золотому сечению». Пусть точка М делит отрезок АВ в золотом отношении.
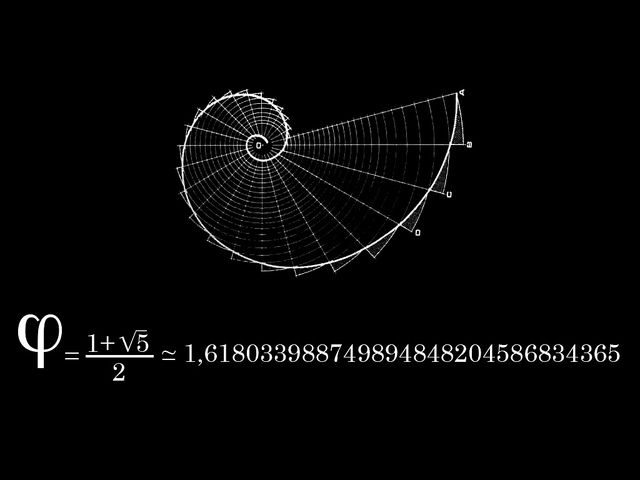
Итак «Золотое сечение»- это иррациональное число,
оно приблизительно равно 1,618.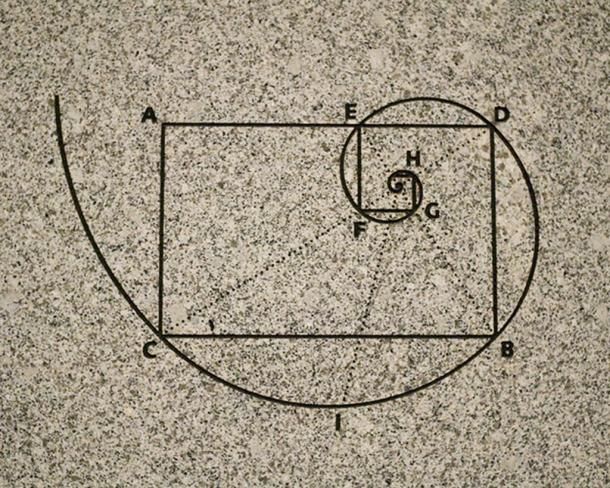
В процентном округленном значении золотое сечение – это деление какой- либо величины в отношении 62 % и 38 %.
На золотом сечении базируются основные геометрические фигуры. Окружающие нас предметы дают примеры золотого прямоугольника: обложки многих книг, журналов, тетрадей, открытки, картины. Крышки столов, экраны телевизоров и т.д. о близки по размерам к золотому прямоугольнику.(отношение длины прямоугольника к его ширине равно 1,618) Разумеется есть и золотой треугольник. Это равнобедренный треугольник, у которого отношение длины боковой стороны к длине основания равняется 1,618.
Золотое сечение в природе
«Великая книга природы написана на
языке математики». (Галилео Галилей). Корни золотой пропорции в живой природе
уходят также глубоко, как и корни самой жизни.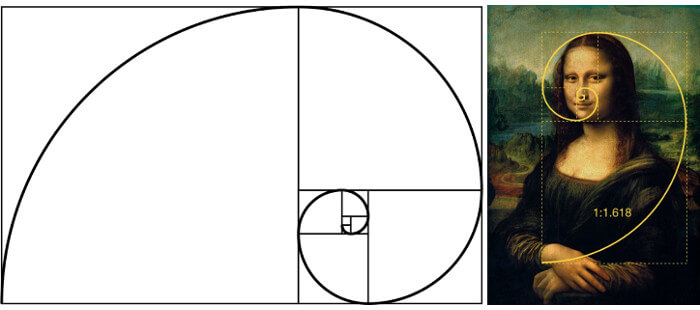
Мир природы-это, прежде всего, мир гармонии, в котором действует «закон золотого сечения». Все, что приобретало какую-то форму, образовывалось, росло, стремилось занять место в пространстве и сохранить себя. Это стремление осуществляется в двух вариантах-рост вверх или расстилание по поверхности земли и закручивание по спирали. Среди придорожных трав растет непримечательное растение – цикорий. Приглядимся к нему внимательно. От основного стебля образовался отросток. Тут же расположился первый листок.
Отросток делает сильный выброс в
пространство, останавливается, выпускает листок, но уже короче первого, снова
делает выброс в пространство, но уже меньшей силы, выпускает листок еще
меньшего размера и снова выброс. Длина лепестков подчинена золотой
пропорции. (62 : 38
=1,631).
Давно подметили винтообразное и спиралевидное расположение
листьев на ветках деревьев.
Спираль увидели в расположении семян подсолнечника,
в шишках сосны, улитках, кактусах и т. д.
Совместная работа ботаников и математиков пролила свет на эти удивительные явления природы. Выяснилось, что в расположении листьев на ветке, семян подсолнечника, шишек сосны проявляет себя закон золотого сечения. Паук плетет паутину спиралеобразно. Спирально закручивается ураган. Испуганное стадо северных оленей разбегается по спирали. Молекула ДНК закручена двойной спиралью. Гете называл спираль «кривой жизни».
Испуганное стадо северных оленей разбегается по спирали
Ураган закручивается спиралью
Золотое сечение в архитектуре
Великолепные
памятники архитектуры оставили нам зодчие древней Греции и среди них первое
место по праву принадлежит храму Парфенон при построении которого,
великий скульптор и архитектор Фидий использовал золотую пропорцию, поэтому она
была обозначена буквой (фи) – первой буквой его имени.
Парфенон — главный храм
в древних Афинах, посвященный покровительнице этого города и всей Аттики, богине
Афине-Девственнице. Он красовался на самом высоком пункте афинского акрополя,
там, где перед тем стоял не вполне достроенный храм той же богини, заложенный
еще до нашествия. По окончании персидских войн, в правление Перикла, приступили
к сооружению, на месте прежнего святилища, нового, более обширного и роскошного
храма. Строителями Парфенона называют Иктина и Калликрата.Велики скульптор
Фидий и сам Перикл наблюдали за постройкой, продолжавшейся около десяти лет, с
448 по 438 г. До Р. Хр. На прямоугольной платформе (в 68,4 м длины и в 30,38 м
ширины), сложенной из пирейского камня и на которую можно было со всех сторон
подниматься по трем ступеням, высился построенный из пентелийского мрамора
величественный периптер дорического стиля с восемью колоннами в каждом коротком
фасе и с семнадцатью в каждом длинном.
Вышиной эти колонны были в 11 м, диаметр
их разреза в нижнем конце равнялся 1,8 м. Окруженный этой колоннадой, стоит и
посей день.
Отношение длины здания Парфенона в Афинах к его высоте равно Ф (фи)
.
Известный русский архитектор Казаков Матвей Федорович в своем творчестве широко использовал “золотое сечение”. Его талант был многогранным, но в большей степени он раскрылся в многочисленных осуществленных проектах жилых домов и усадеб. Например золотое сечение можно обнаружить в архитектуре здания сената в Кремле. По проекту Казакова построена в Москве Голицынская больница, которая в настоящее время называется “Первая клиническая” больница имени Пирогова.
Петровский дворец в Москве построен по проекту М.Ф. Казакова.
Петровский дворец в Москве 1776-1796 гг
Еще один архитектурныйшедевр Москвы – дом Пашкова (1786 г.
)– является одним из наиболее совершенным произведением архитектуры Василия
Ивановича Баженова.
Прекрасное творение прочно вошло в ансамбль центра современной Москвы. Наружный вид сохранился почти без изменения до наших дней, ныне Российская государственная библиотека.
Многие высказывания зодчего заслуживают внимания и в наши дни. О своем любимом искусстве В. Баженов говорил: “Архитектура – главнейшие имеет три предмета: красоту, спокойность и прочность здания … К достижению сего служит руководством знание пропорции , перспективы , механики или вообще физики ,а всем им общим вождем является рассудок
Золотое сечение в живописи
Переходя к примерам “золотого сечения” в живописи, нельзя не остановить своего внимания на творчестве Леонардо да Винчи.
Леонардо да Винчи
Его личность одна из загадок истории.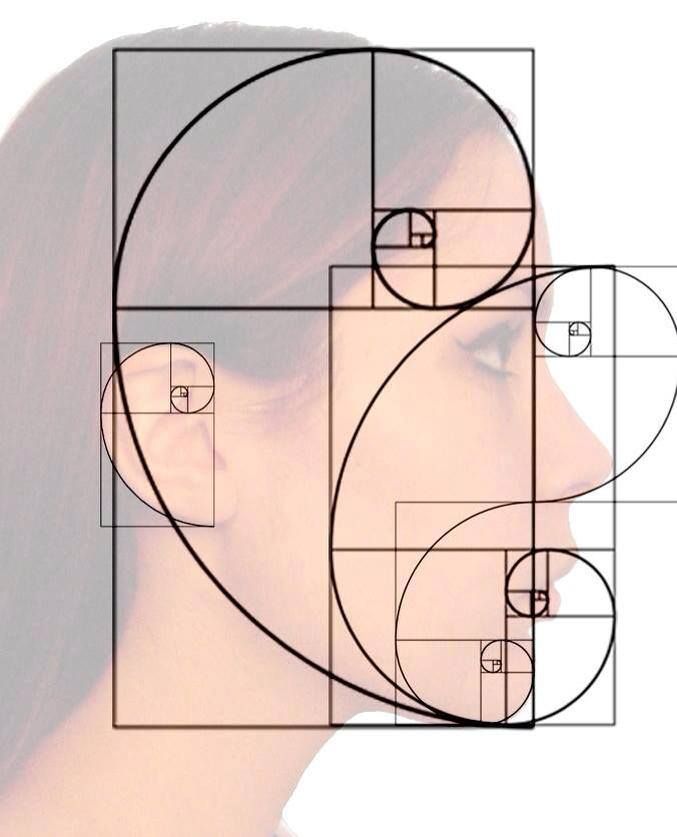
Сам Леонардо да Винчи говорил
: “Пусть никто, не будучи математиком, не дерзнет читать мои труды”. Сам
термин “золотое сечение” ввел Леонардо да Винчи. Он говорил о пропорции
человеческого тела.
“Если мы человеческую фигуру – самое совершенное творение Вселенной – перевяжем поясом и отмерим потом расстояние от пояса до ступней, то эта величина будет относиться к расстоянию от того же пояса до макушки, как весь рост человека к длине от пояса до ступней”
В наиболее известной картине Леонардо, портрете Моны Лизы (так называемой “Джоконды”, около 1503, Лувр) образ богатой горожанки предстает таинственным олицетворением природы как таковой, не теряя при этом чисто женского лукавства; внутреннюю значительность композиции придает космически-величавый и в то же время тревожно-отчужденный пейзаж, тающий в холодной дымке. Ее композиция основана на золотых треугольниках.
В
картине Сальвадора Дали «Тайная вечеря» также использован принцип золотого
сечения.
Золотое сечение в теле человека
. Человек – это универсальная форма для проверки законов золотого сечения. Конечно, от природы далеко не у всех людей пропорции идеальны, что создает определенные сложности с подбором одежды. В дневнике Леонардо да Винчи есть рисунок вписанного в окружность обнаженного человека, находящегося в двух наложенных друг на друга позициях. Опираясь на исследования римского архитектора Витрувия, Леонардо подобным образом пытался установить пропорции человеческого т
Адольф Цейзинг,
исследуя пропорциональность человека, проделал колоссальную работу. Он измерил
порядка двух тысяч человеческих тел, а также множество античных статуй и вывел,
что золотое сечение выражает среднестатистический закон.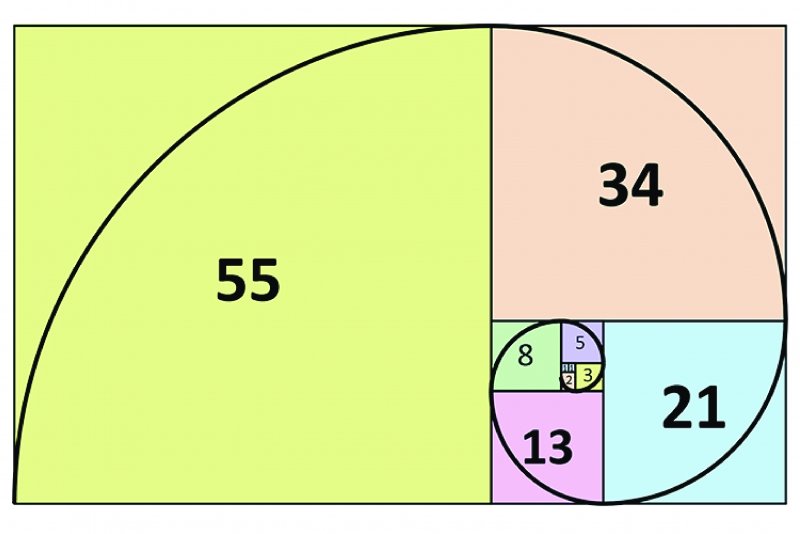
В человеке ему
подчинены практически все части тела, но главный показатель золотого сечения это деление тела талией. В результате огромной работы немецкий профессор Цейзинг
(измерил более 2000 тел) установил, что пропорции мужского тела 13:8=1,625
ближе к золотому сечению, чем пропорции женского тела 8:5=1,6. Так
что пропорции мужчин ближе к «золотому сечению», чем пропорции женщин
(однако женщина в обуви на каблуках может оказаться ближе к «золотому
сечению). Пропорции золотого сечения проявляются и в отношении других частей
тела-длина плеча, предплечья и кисти, кисти и пальцев . Сапоставляя расстояния
между отдельными частями лица, также можно найти «золотые» соотношения.
Практическая работа на нахождение «золотого сечения».
Учащиеся разбиваются на группы и выполняют практическую работу.
1 группа находит отношение роста мальчика к длине (от талии
до пола).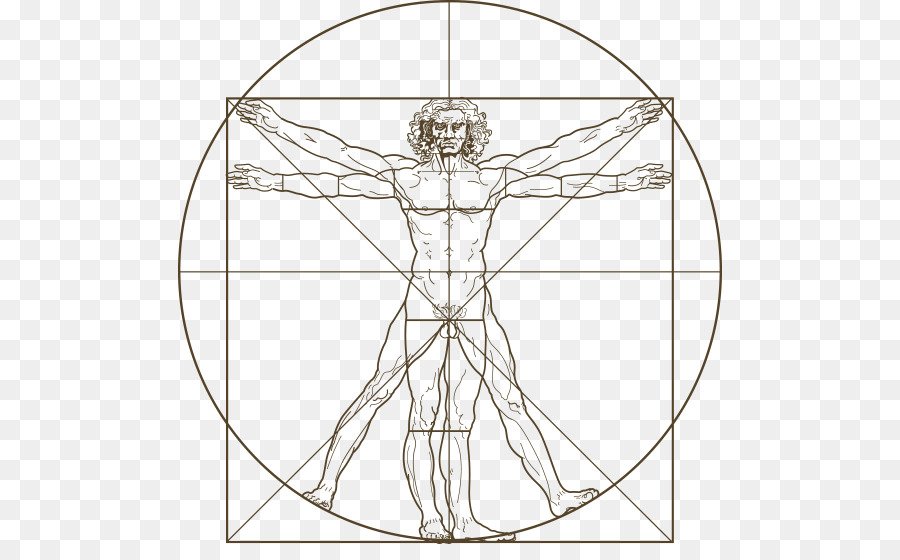
2 группа находит отношение роста девочки к длине (от талии до пола).
3 группа находит отношение длины мизинца к длине среднего пальца.
Заключение. «Золотое сечение» представляется тем моментом истины, без выполнения которого невозможно, вообще» что-либо сущее. Чтобымы не взяли элементом исследования, «золотое сечение» будет везде; если даже нет видимого его соблюдения, то оно обязательно имеет место на энергетическом, молекулярном или клеточном уровнях.
изображений золотого сечения | Скачать бесплатные картинки на Unsplash
Golden Ratio Pictures | Скачать бесплатные изображения на Unsplash- A Photophotos 10K
- А.
Лаура Гилкрист
Подсолнух фото и картинкирастение
Людде Лоренц
архитектурная лестница
–––– –––– –––– – –––– ––––– –– – –– –––– – – –– ––– –– – ––– – –.Len Cruz
Hd abstract wallpapersHd windows wallpapersHd dark wallpapers
Ryan Searle
Light backgroundslondonglow
Arun Clarke
australiamelbourne vicvictoria
nic chi
Hd white wallpapersstaircaseHd blue wallpapers
Zoltan Tasi
Hd grey wallpapersFlower imagesblossom
Didssph
sea lifeHd black wallpapersWhite backgrounds
Gidon Wessner
snailsnail shellsnails
Didssph
spiralsea creatureone subject
Tevei Renvoyé
Hd gold wallpapersfrench polynesiatahiti
Lahiru Supunchandra
sri lankagolden ratio seashellssand
Ali Choubin
fashionstylePeople images & images
Варанонт (Джо)
таиландбангкокхрам золотой горы
Shibupavizha George
golden sand beachindiathiruvananthapuram
Courtney Hill
golden gate bridgesan franciscobridge
Linoleum Creative Collective
gold coast qldgolden retrieverDog images & pictures
Helena Lopes
Brown backgroundspetcanine
Zane Lee
Nature imagesoutdoorsfield
Келли Сиккема
Соединенные Штаты Ямайка Плейнбостон
Подсолнечник images & imagesplant
Hd abstract wallpapersHd windows wallpapersHd dark wallpapers
australiamelbourne vicvictoria
Hd grey wallpapersFlower imagesblossom
sea lifeHd black wallpapersWhite backgrounds
Hd gold wallpapersfrench polynesiatahiti
thailandbangkokgolden mount temple
gold coast qldgolden retrieverDog images & pictures
Nature imagesoutdoorsfield
–––– –––– –––– – –––– – –––– –– – –– –––– – – –– ––– –– –––– – –.
architecturestairssverige
Light backgroundslondonglow
Hd white wallpapersstaircaseHd blue wallpapers
snailsnail shellsnails
spiralsea creatureone subject
sri lankagolden ratio seashellssand
fashionstylePeople images & pictures
golden sand beachindiathiruvananthapuram
golden gate bridgesan franciscobridge
Related collections
спираль Фибоначчи золотое сечение золотая середина
63 photos · Curated by Eye SeeGolden ratio
7 photos · Curated by Cristina DCGolden Ratio
7 photos · Curated by Haley ChaffinBrown backgroundspetcanine
united statesjamaica plainboston
Sunflower images & picturesplant
Light backgroundslondonglow
snailsnail shellsnails
Hd золотые обоифранцузская полинезиятаити
мост золотые воротасан-францискомост
united statesjamaica plainboston
architecturestairssverige
australiamelbourne vicvictoria
Hd grey wallpapersFlower imagesblossom
sea lifeHd black wallpapersWhite backgrounds
fashionstylePeople images & pictures
golden sand beachindiathiruvananthapuram
gold coast qldgolden retrieverDog images & pictures
Nature imagesoutdoorsfield
–––– –––– –––– – –––– – –––– –– – –– –––– – – –– ––– –– –––– – –.
Hd abstract wallpapersHd windows wallpapersHd dark wallpapers
Hd white wallpapersstaircaseHd blue wallpapers
spiralsea creatureone subject
sri lankagolden ratio seashellssand
Related collections
spiral fibonacci golden ratio golden mean
63 photos · Curated by Eye SeeЗолотое сечение
7 фото · Куратор Кристина DCЗолотое сечение
7 фото · Куратор Хейли Чаффинтаиландбангкокзолотой горы храм
Коричневый фонspetcanine
Просматривайте премиум-изображения на iStock | Скидка 20% на iStock
Логотип UnsplashСделайте что-нибудь потрясающее
Немного истории о золотом сечении и правиле третей
Правило третей — это первое, чему учат в фотографии. Кажется, что у него есть некоторое сходство с золотым сечением, но на самом деле это нечто совершенно иное. Давайте подробнее рассмотрим историю этих так называемых правил, чтобы лучше их понять.
Правило третей — довольно простое правило. Разделите изображение на девять равных частей, проведя две горизонтальные и две вертикальные линии по третям от краев. Поместите объект на одну из линий или на пересечение линий, и все готово. Вроде, как бы, что-то вроде.
Хотя в некоторых ситуациях это может помочь добиться приемлемой композиции, правило третей никогда не предназначалось для этого. На самом деле происхождение не имеет абсолютно никакого отношения к рисованию линий на третях изображения. На первый взгляд сходство с золотым сечением создает впечатление, что они связаны. Нет ничего более далекого от истины. Поясню почему, углубившись в историю.
Золотое сечение, Фибоначчи и Архимед
Золотое сечение — изобретение математиков. Это не имело ничего общего с композицией в картинах. Грек по имени Евклид, живший где-то около 400 г. до н.э., обнаружил, что деление линии по определенному соотношению может продолжаться бесконечно. Это отношение является иррациональным числом, а значит, его нельзя записать в виде натуральной дроби.
Это иррациональное число является золотым сечением. Это число 1,618, за которым следует бесконечное количество цифр, а греческая буква для него — фи.
Золотое сечение. Все дело в игре с числами. Номер совершенно особенный. Его нельзя записать в виде натуральной дроби.
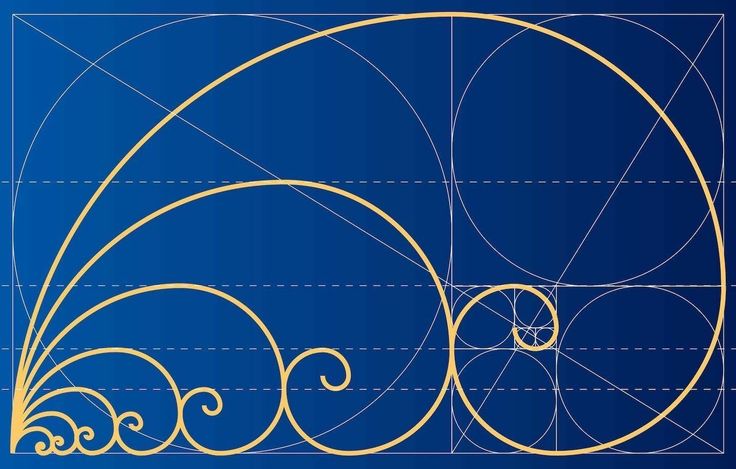
Потребовалось 16 столетий, прежде чем Леонардо Пизанский придумал весьма необычную последовательность чисел. Каждое число было суммой двух предыдущих, и последовательность была бесконечной. Эта последовательность чисел была названа в честь его прозвища: последовательность Фибоначчи.
Астроном Иоганн Кеплер наконец обнаружил связь между золотым сечением и последовательностью Фибоначчи. Он выяснил, как деление числа Фибоначчи на предыдущее число в последовательности будет приближаться к золотому сечению с возрастающей точностью.
Хорошо известный квадрат, основанный на золотом сечении. Добавляются порядковые номера Фибоначчи. Все подходит как влитой.
Все знают об Архимеде.
Он выкрикнул «эврика», когда узнал, как узнать, была ли золотая корона короля Гиеро Сиракуз подделкой или нет. Но Архимед также был одержим спиралями. Одной из сделанных им спиралей была Spirabilis Mirabilis, основанная на золотом сечении. Сегодня мы лучше знаем эту спираль под названием Спираль Фибоначчи (мы сожалеем об этом, Архимед).Архимед сделал спираль, но мы назвали ее в честь Фибоначчи.
Лука Пачоли и золотое сечение для композиции
Кажется, мы находим в природе множество примеров, где присутствует золотое сечение и спираль Фибоначчи. Конечно, у нас есть привычка смотреть на эти сходства и игнорировать все, что не имеет сходства. Тем не менее, золотое сечение — это то, что часто проявляется в вещах, растущих в природе, например, в распределении листьев на стебле или семенах подсолнуха.
Возможно, именно поэтому итальянский монах по имени Лука Пачоли придумал общее правило композиции. Где-то между 15 и 16 веками он утверждал, что картина станет наиболее реалистичной, если композиция будет создана по математическим правилам.
Для этого было выбрано золотое сечение.Ветряные мельницы в Вейк-бий-Дурстеде от художника Якоба ван Рейсдала со спиралью Фибоначчи.
(общественное достояние, Creative Commons)Сегодня мы пытаемся увидеть золотое сечение во всем, что было построено, нарисовано или нарисовано. Мы ищем золотое сечение в таких зданиях, как Парфенон, пирамиды и даже современные здания. Мы рисуем спираль Фибоначчи по известным картинам, таким как «Мона Лиза» Леонардо да Винчи или «Девушка с жемчужной сережкой» Иоганна Вермеера.
Спираль Фибоначчи проецируется на картины Леонардо да Винчи «Мона Лиза» (общественное достояние, Creative Commons) и «Девушка с жемчужной сережкой» Йоханнеса Вермеера (общественное достояние, Creative Commons).
Правило третей
Для происхождения правила третей мы должны отправиться во времени в 1797 год. В то время некий сэр Джошуа Рейнольдс преподавал в Королевской академии художеств в Лондоне, упоминая в своих беседах, как Картина работает лучше всего, когда соотношение света и тени составляет примерно 1/3:2/3.
Никогда не упоминалось о правиле третей, пока английский художник по имени Джон Томас Смит не придумал это правило, прочитав речи сэра Джошуа Рейнольдса. Он пошел еще дальше в делении 1/3:2/3 и сказал, что его следует использовать для всего в композиции.
Заметки о сельском пейзаже 1797 года Джона Томаса Смита, в которых впервые упоминается правило третей. (Project Gutenberg)
Уже тогда было много людей, которым не нравилось правило третей. Некий Джордж Филдс писал о недостатках правила третей в 1845 году, говоря, что использование правила приводит к скучным и монотонным изображениям.
«Хроматика: или аналогия, гармония и философия цветов» Джорджа Филда, написанная в 1845 году с комментариями об использовании правила третей. (Project Gutenburg, 2014)
Сегодня правило третей сводится к набору линий на фотографии. Вы должны разместить предмет на одной из линий или на пересечении этих линий. Это придало бы изображению много напряжения и энергии. Не все согласны по понятным причинам.
Первоначальная идея правила третей о том, как должны распределяться свет и тьма в изображении, утеряна и забыта.Композиция с правилом третей. Я думаю, что это работает довольно хорошо. Но это не имеет ничего общего с первоначальной концепцией правила.
Использование правила третей или золотого сечения
Снова вернемся в современность. Большинство фотографов научились использовать правило третей. Я считаю, что это работает в некоторых случаях. Но, возможно, разумнее использовать линии для распределения предмета в кадре. Это вовсе не обязательно должно быть на третях, особенно если в итоге вы остаетесь с двумя другими третями, которые почти пусты. Баланс и визуальный поток в изображении гораздо важнее.
Правило третей в формате 5:4. Кажется, это работает довольно хорошо, потому что распределение элементов сбалансировано.
Я думаю, во многих случаях лучше использовать что-то вроде золотого сечения. Спираль Фибоначчи может помочь найти визуальный поток на изображении.
Однако есть одна проблема. Поскольку мы часто визуализируем эти правила, используя инструмент обрезки в таких программах, как Lightroom и Photoshop, мы смотрим на линии, не понимая, что композиция вообще не следует золотому сечению.Золотое сечение проецируется на соотношение сторон 5:4. Он не может полностью заполнить кадр.
Эти инструменты обрезки проецируют правила внутри соотношения сторон самого изображения. Это может быть 3:2, 4:3 или 5:4. Но таким образом вы больше не смотрите на линии золотого сечения, потому что оно имеет соотношение сторон 1,618:1. Итак, вы можете думать, что используете его, но это не так. С другой стороны, правило третей не зависит от соотношения сторон изображения.
Найти баланс
Приятно иметь все эти правила, и я считаю важным знать о его происхождении, чтобы понять, почему вы должны использовать его или нет. Это также показывает, что буквальное использование этих правил часто не очень художественно. Вы можете стать больше математиком, чем фотографом.
Он выкрикнул «эврика», когда узнал, как узнать, была ли золотая корона короля Гиеро Сиракуз подделкой или нет. Но Архимед также был одержим спиралями. Одной из сделанных им спиралей была Spirabilis Mirabilis, основанная на золотом сечении. Сегодня мы лучше знаем эту спираль под названием Спираль Фибоначчи (мы сожалеем об этом, Архимед).
Для этого было выбрано золотое сечение.
Первоначальная идея правила третей о том, как должны распределяться свет и тьма в изображении, утеряна и забыта.
Однако есть одна проблема. Поскольку мы часто визуализируем эти правила, используя инструмент обрезки в таких программах, как Lightroom и Photoshop, мы смотрим на линии, не понимая, что композиция вообще не следует золотому сечению.