Зд макс уроки: 110+ уроков 3ds Max по моделированию и визуализации в 2021

3Ds Max уроки для начинающих. Урок 1. Кратко об инструментах

Этот первый урок для начинающих свое знакомство с 3Д Максом, мы посвятим собственно тому, каким образом происходит работа по создания 3Д-моделей в данном редакторе и какими инструментами мы при этом будем пользоваться. В этом уроке я просто собрал краткую справку, стараясь убрать лишние слова, чтобы проще было запомнить и всегда можно было вернуться и посмотреть, если что-то забудется. И так приступим.

Выбор объекта – левый клик мышки.

При создании объекта, после того как мы его создадим – делаем правый клик, чтобы сбросить кнопку создания.

Трансформация объектов (W,E,R)

(горячие клавиши – чтобы легче запомнить – подряд идут клавиши W,E,R)

W – Сдвиг

E – Вращение

R – Масштабирование

Не надо двигать объект хватаясь за него! Только по осям чтобы не было ошибок! При любой трансформации!

W – Сдвиг – Move – появились осевые стрелки

Надо навести курсор на ось (ось подсветится желтым) и тогда двигать по нужной нам оси.

Можно двигать в плоскости, плоскость между осями подсветится желтым (навести надо на внешний угол четырехугольника). Зажимаем левую кнопку и двигаем

Чтобы задать точные значения, кликаем Правой кнопкой мышки на кнопку из панельки нужной трансформации (например на Move) и появится окно с координатами:

Слева столбик в мировой системе координат

Правый столбец – относительно текущего местоположения

Трансформация вращения – E:

Для вращения нужно хвататься мышкой за окружности.

Наводить аккуратно на нужную ось. Зажимаем левую кнопку и крутим.

Трансформация масштабирование – R.

3 режима:

1 – масштабирование по одной оси

2 – масштабирование по 2м осям – наводим на четырехугольник (неунифицированное масштабирование оно же non uniform scale )

3 – Без изменений пропорций – курсор в центр

Клонирование Ctrl+V

Пункт меню Edit -> Clone либо  Ctrl+V или сдвинуть объект зажав SHIFT

Появится меню:

Самый частый случай – обычное копирование – Copy

Отмена действия – Ctrl-Z

Можно сгруппировать объекты

Меню edit –>  GROUP/UNGROUP

Выделить несколько объектов

Стандартно зажимаем Ctrl при клике либо зажать левую кнопку мыши и выделить рамкой.

RENDERING (визуализация объекта) SHIFT-Q

Рендер активного окна – либо на главной панели самый правый значок чайника (эту панель можно прокручивать) либо SHIFT-Q

После рендера можно сохранить полученное изображение

Настройки параметров Rendering (F10)

В меню Rendering ->Render Setup (F10)

Основная вкладка Common

Размер картинки рендера

Вкладка Common – > секция Output Size

Выбор DPI

Меню Rendering -> Print Size Assistant…

Выбор фона (8)

Меню Rendering -> Environment… (клавиша 8 с клавиатуры), секция Background , св-во Color

Сменить цвета объектов в сцене

На командной панели есть кнопка color

Жмем и выбираем. Галочка Assign Random Color каждый объект с уникальным цветом (включена по умолчанию)

Навигация/перемещение по сцене

Привыкайте использовать горячие клавиши. Не надо пользоваться кнопками, что будут сейчас перечислены для ознакомления ниже:

Увеличение/уменьшение/zoom

Крутим колесо мышки, если зажать попутно Alt то шаг зума уменьшится.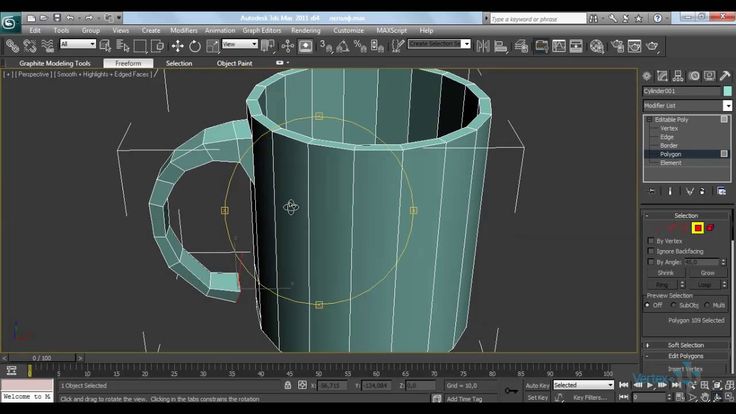  Кнопка 1

Масштабирование во всех окнах

Zoom All – почти никогда не используется (горячей клавиши нет). Кнопка 2

Увидеть все объекты

Дальше рис 13-3  Если на сцене вы потерялись, то нажав на эту кнопку все ваши объекты размещаются в вашем одном видовом окне так, что вы их все видите.

Центрирование относительно выделенного объекта (Z)

Выберете объект и нажмете Zoom extends. Кнопка 4 либо Alt+Ctrl+Z. Чтобы это сработало во всех видовых окнах одновременно, то нужна следующая кнопка Zoom extends All – или клавиша Z (одна из популярных клавиш).

Увеличение необходимого фрагмента

Zoom region. Кнопка 5

Перемещение нас в плоскости экрана

Pen View (ладошка). Кнопка 6. Либо, что конечно удобнее – нажать и удерживая  колесико перемещать мышь. Если же еще нажать Alt и колесо мышки то сцену можно будет вращать.

Передвижение по сцене

Walk Through (значок следы) – «пройти насквозь». (Пробел фиксирует горизонт) – передвижение по сцене в окне проекции Perspective или Camera с помощью клавиш курсора или указателя мышки, как в играх от первого лица (клавиши W,A,S,D) Скорость движения с помощью клавиши Q (ускорение),  Z (замедление) или клавиш [ (короче шаг), ] (шире шаг). E и C – соответственно вверх и вниз. Shift + пробел – установка уровня камеры.

Вращение вокруг объектов (Alt и колесо мышки)

Orbit Selected. Кнопка 7. Лучше Alt и колесо мышки. Если выбрать какой то объект то вращение будет именно вокруг него.

Максимизация активного видового окна

Maximize viewport toggle. Кнопка 8. Проще конечно комбинация клавиш Alt+W

Совет: при разных глюках зумирования/масштабирования – жмем Z

Видовые окна (слева вверху надписи)

Left, top, front, perspective, bottom – Думаю перевод не нужен, хотя ладно (вид слева, сверху, спереди, перспектива, снизу).

Переключения – в видовом окне жмем либо L— left, T-top, F-front, P-perspective.

Типы отображения поверхностей (F3)

В самых правых скобках написано.

Wireframe – видим только жесткие ребра

Smooth + Highlights – сглаживание поверхностей + блики

F3 – переключение между этими режимами.

Wireframe + Smooth  + Highlights + Edges faces – включается F4

Активным видовое окно переключается правой кнопкой мышки (чтобы не сбрасывать выделение с объекта)

Создание 3хмерных примитивов

Параметрический тип объекта – можно менять параметры.

Редактируемый – имеем доступ к подобъектным уровням, параметров уже нет.

Создавать лучше либо в окне перспективы, либо на виде сверху (чтобы было выровнено относительно осей).

Как только создали объект, сразу переходим на вкладку Modify и уже там настраиваем объекты.

У объекта есть кол-во сегментов (увидеть можно нажав F4), чем больше полигонов (больше плотность) тем плавнее модель, но и тем сцена весит больше. Нужно смотреть на модель и решать самим, в каком случае нужно большое кол-во полигонов и в каком случае они вообще не нужны.

Убрать сетку – G (greed), иногда она мешает в окне перспективы.

Уроки 3ds Max | Компьютерная графика. За кулисами CG. 3D моделирование

В результате этого урока у вас должны получиться процедурные (т.е. созданные без использования текстур) трещины, как на заглавной картинке (она кликабельная).

Я использовал 3ds Max 2016 Ext.1 + SP1 и V-Ray 3.20.03.

Поскольку это процедурные трещины, то они совсем не зависят от UV-координат, а значит их можно добавлять на 3D объект, который не имеет нормальной UV развёртки.

Но есть и обратная сторона медали — такие трещины зависят от размеров объекта. Поэтому, чтобы у вас получились в точности такие трещины как у меня, вы должны использовать те же самые системные единицы, что и у меня, а также создать сферы такого же радиуса.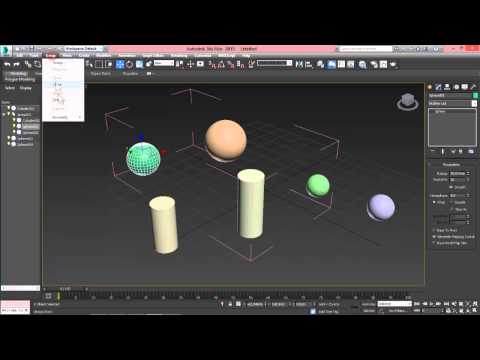

Читать далее »

Впечатлённый рекламным видео под VR от ILM для фильма Warcraft (который вышел в июне 2016)..:

..я решил попробовать сделать подобное. Вот что у меня получилось (озвучка понятно откуда 😉 , а сюжет не критикуйте — его нет 🙂 ).

Чтобы понять в чём вообще суть фишки, то это видео нужно смотреть на новеньком устройстве под iOS или Android с помощью приложения YouTube (если такового девайса нету, то тогда смотрите в Firefox или Chrome на PC).

Процедура такова: вы стоите с телефоном в руках и смотрите это видео, вращаясь вокруг собственной оси (наклоняясь или поднимая телефон/планшет к потолку):

Ниже я расскажу, как я это сделал.

Читать далее »

Я нашел в сети отличный урок по созданию реалистичных микроцарапин с помощью Vray (и 3ds Max). И решил выложить перевод.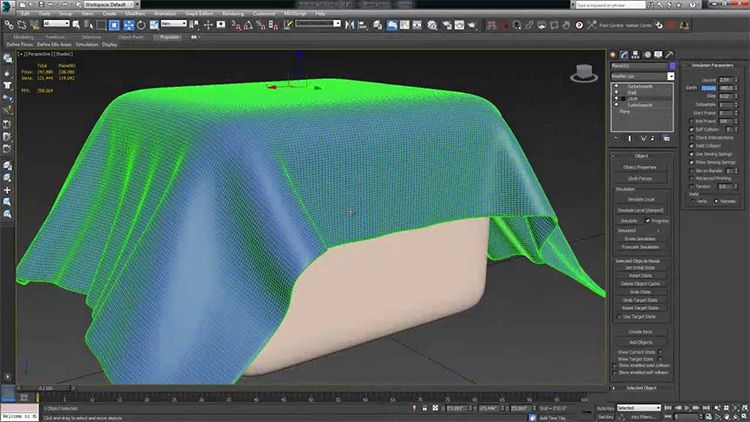 Я исправил некоторые неправильные места в оригинальной статье, а также дополнил.

Принципы создания такого шейдера универсальны, а значит вы сможете их применить не только в V-Ray + 3d Max, но и в любом другом 3D-пакете (Maya, Houdini…)

Радиальная “паутинка” вокруг блика на отражении вызвана микроцарапинами, отражающими свет под разными углами. Мы довольно часто видим этот эффект на потертых, поцарапанных, изношенных поверхностях.

Довольно долго я пытался добиться этого эффекта в VRay, но… безуспешно.

Я поискал решения на форумах, а также поэкспериментировал и думаю, что нашел метод, который дает хорошие результаты. Естественно — сделал урок 🙂

Читать далее »

Метод симуляции, который я опишу ниже, годится для любых длинных 3D волос в 3ds Max, сделанных любым способом.

Сначала смотрите, что у меня получилось (ролик я рендерил VRay’кой в Максе на вот этом компе, на каждый фрейм (1280×720) уходило от 9 до 26 минут в зависимости от количества волос в кадре):

Теперь коротко о том, как я это сделал, а дальше я по каждому пункту пройдусь более подробно.

Читать далее »

Стр. 1 из 7 1 2 3 … 6 7 Старые

Исчисление III — поверхностные интегралы

Показать мобильное уведомление Показать все примечания Скрыть все примечания

Мобильное уведомление

Похоже, вы находитесь на устройстве с «узкой» шириной экрана ( т.е. вы, вероятно, на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.

Раздел 17.3: Поверхностные интегралы

Теперь пришло время подумать об интегрировании функций по некоторой поверхности \(S\) в трехмерном пространстве. Давайте начнем с наброска поверхности \(S\), так как обозначения могут немного запутаться, когда мы в них попадем. Вот набросок некоторой поверхности \(S\).

Область \(S\) будет лежать выше (в данном случае) некоторой области \(D\), лежащей в плоскости \(xy\). Здесь мы использовали прямоугольник, но это, конечно, не обязательно. Заметим также, что мы могли бы так же легко посмотреть на поверхность \(S\), которая находилась перед некоторой областью \(D\) в плоскости \(yz\) или плоскости \(xz\). Не зацикливайтесь на \(xy\)-плоскости настолько, чтобы вы не могли решать задачи с областями в двух других плоскостях.

Теперь то, как мы оцениваем поверхностный интеграл, будет зависеть от того, как нам дана поверхность. По сути, здесь есть два отдельных метода, хотя, как мы увидим, на самом деле они одинаковы. 92} + 1} \,dA}}\]

Здесь нужно быть осторожным, так как оба они выглядят как стандартные двойные интегралы. Фактически интеграл справа является стандартным двойным интегралом. Однако интеграл слева является поверхностным интегралом. Отличить их друг от друга можно, посмотрев на дифференциалы. Поверхностный интеграл будет иметь \(dS\), а стандартный двойной интеграл будет иметь \(dA\).

Чтобы вычислить поверхностный интеграл, мы заменим уравнение поверхности на \(z\) в подынтегральном выражении, а затем добавим часто запутанный квадратный корень. После этого интеграл становится стандартным двойным интегралом, и к этому моменту мы уже должны иметь дело с этим.

Также обратите внимание, что существуют аналогичные формулы для поверхностей, заданных \(y = g\left( {x,z} \right)\) (с \(D\) в \(xz\)-плоскости) и \(x = g\left( {y,z} \right)\) (с \(D\) в \(yz\)-плоскости). Мы увидим одну из этих формул в примерах, а другую предоставим вам для записи.

Второй метод оценки поверхностного интеграла для тех поверхностей, которые заданы параметризацией,

\[\vec r\left( {u,v} \right) = x\left( {u,v} \right)\vec i + y\left( {u,v} \right)\vec j + z \left( {u,v} \right)\vec k\]

В этих случаях поверхностный интеграл равен

\[\iint\limits_{S}{{f\left( {x,y,z} \right)\,dS}} = \iint\limits_{D}{{f\left( {\vec r\left ( {u,v} \right)} \right)\left\| {{{\vec r}_u} \times {{\vec r}_v}} \right\|\,dA}}\]

где \(D\) диапазон параметров, очерчивающих поверхность \(S\).

Прежде чем приступить к работе с некоторыми примерами, заметим, что, поскольку мы можем параметризовать поверхность, заданную \(z = g\left( {x,y} \right)\), как

92} + 1} \]

для таких поверхностей. Возможно, вы захотите проверить это на практике вычисления этих перекрестных произведений.

Давайте рассмотрим несколько примеров.

Пример 1. Вычислите \( \displaystyle \iint\limits_{S}{{6xy\,dS}}\), где \(S\) — часть плоскости \(x + y + z = 1\), которая лежит в октант 1 ^-й и находится перед плоскостью \(yz\).

Показать решение

Итак, поскольку мы ищем часть плоскости, лежащую перед плоскостью \(yz\), нам потребуется записать уравнение поверхности в виде \(x = g\left( {y,z} \справа)\). Это достаточно легко сделать.

\[х = 1 — у — г\]

Далее нам нужно определить, что такое \(D\).

Вот эскиз поверхности \(S\).

Вот набросок региона \(D\).

Обратите внимание, что оси обозначены иначе, чем мы привыкли видеть на эскизе \(D\). Это должно было сохранить соответствие эскиза эскизу поверхности. Мы пришли к уравнению гипотенузы, приравняв \(x\) к нулю в уравнении плоскости и найдя \(z\). Вот диапазоны для \(y\) и \(z\).

\[0 \le y \le 1\hspace{0.25in}0 \le z \le 1 — y\]

Теперь, поскольку поверхность не имеет формы \(z = g\left( {x,y} \right)\), мы не можем использовать приведенную выше формулу. Однако, как отмечалось выше, мы можем изменить эту формулу, чтобы получить ту, которая будет работать для нас. Вот он,

\[\iint\limits_{S}{{f\left( {x,y,z} \right)\,dS}} = \iint\limits_{D}{{f\left( {g\left( { y, z} \right), y, z} \ right) \ sqrt {1 + {{\ left ( {\ frac {{\ partial g}} {{\ partial y}}} \ right)} ^ 2} + {{\left( {\frac{{\partial g}}{{\partial z}}} \right)}^2}} \,dA}}\] 91 = \ frac {{\ sqrt 3}} {4} \ end {align *} \]

Пример 2. Вычислите \( \displaystyle \iint\limits_{S}{{z\,dS}}\), где \(S\) — верхняя половина сферы радиуса 2.

Показать решение

Мы дали параметризацию сферы в предыдущем разделе. Вот параметризация для этой сферы.

\ [\ vec r \ left ( {\ theta , \ varphi } \ right) = 2 \ sin \ varphi \ cos \ theta \, \ vec i + 2 \ sin \ varphi \ sin \ theta \, \ vec j + 2 \cos\varphi\,\veck\]

Поскольку мы работаем над верхней половиной сферы, вот ограничения на параметры.

\[0 \le \theta \le 2\pi \hspace{0.5in}0 \le \varphi \le \frac{\pi} {2}\]

Далее нам нужно определить \({\vec r_\theta} \times {\vec r_\varphi}\). Вот два отдельных вектора.

\[\ begin{align*}{{\vec r}_\theta}\left({\theta,\varphi}\right) & = — 2\sin \varphi\sin\theta\,\vec i + 2 \sin \varphi\cos\theta\,\vec j\\{{\vec r}_\varphi}\left({\theta,\varphi}\right) & = 2\cos\varphi\cos\theta\ ,\vec i + 2\cos \varphi \sin \theta \,\vec j — 2\sin \varphi \,\vec k\end{align*}\] 92}\varphi } \\ & = 4\влево| {\ sin \ varphi } \ right | \\ & = 4 \ sin \ varphi \ end {align *} \]

Мы можем отбросить столбцы абсолютного значения в синусе, потому что синус положительный в диапазоне \(\varphi \), с которым мы работаем. Тогда поверхностный интеграл равен

. \[\iint\limits_{S}{{z\,dS}} = \iint\limits_{D}{{2\cos \varphi \left( {4\sin \varphi } \right)\,dA}} \]

Не забывайте, что нам нужно подставить \(x\), \(y\) и/или \(z\) и в них, хотя в этом случае нам нужно было просто подставить \(z \). Вот оценка для двойного интеграла. 92} = 3\), лежащий между \(z = 0\) и \(z = 6\).

Показать решение

В предыдущем разделе мы настроили цилиндр. Вот параметризация этого цилиндра.

\[\vec r\left( {z,\theta} \right) = \sqrt 3 \cos \theta \,\vec i + \sqrt 3 \sin \theta \,\vec j + z\,\vec k \]

Диапазоны параметров,

\[0 \le z \le 6\hspace{0.25in}0 \le \theta \le 2\pi \]

Теперь нам нужно \({\vec r_z} \times {\vec r_\theta }\). Вот два вектора.

\[\begin{align*}{{\vec r}_z}\left( {z,\theta} \right) & = \,\vec k\\ {{\vec r}_\theta}\left( {z,\theta} \right) & = — \sqrt 3 \sin \theta \,\vec i + \sqrt 3 \cos \theta \,\vec j\end{align*}\]

Вот перекрестное произведение.

\[\begin{align*}{{\vec r}_z} \times {{\vec r}_\theta} & = \left| {\ begin {массив} {* {20} {c}} {\ vec i} & {\ vec j} & {\ vec k} \\ 0 & 0 & 1 \\ { — \ sqrt 3 \ sin \ theta} & {\ sqrt 3 \cos \theta }&0\end{массив}} \right|\\ & = — \sqrt 3 \cos \theta \,\vec i — \sqrt 3 \sin \theta \,\vec j\end{ выровнять*}\] 92} \le 3\) в плоскости \(xy\) и вершиной которого является плоскость \(z = 4 — y\).

Показать решение

Здесь много информации, которую нам нужно отслеживать. Во-первых, мы используем практически ту же поверхность (однако подынтегральная функция другая), что и в предыдущем примере. Однако, в отличие от предыдущего примера, на этот раз мы размещаем на поверхности верх и низ. Начнем с эскиза поверхности.

Здесь нужно быть осторожным. В этом наброске есть нечто большее, чем сама фактическая поверхность. Пусть \({S_1}\) будет частью цилиндра, идущей от \(xy\)-плоскости к плоскости. Другими словами, верхняя часть цилиндра будет находиться под углом. Назовем часть плоскости, лежащую внутри ( т.е. крышка на цилиндр) \({S_2}\). Наконец, дно цилиндра (здесь не показано) представляет собой диск радиуса \(\sqrt 3\) в плоскости \(xy\) и обозначается \({S_3}\).

Чтобы выполнить этот интеграл, нам нужно отметить, что, как и в случае стандартного двойного интеграла, если поверхность разбита на части, мы также можем разделить поверхностный интеграл. Итак, для нашего примера у нас будет

. \[\iint\limits_{S}{{y + z\,dS}} = \iint\limits_{{{S_1}}}{{y + z\,dS}} + \iint\limits_{{{S_2 }}}{{y + z\,dS}} + \iint\limits_{{{S_3}}}{{y + z\,dS}}\]

Здесь нам нужно провести три интеграла. Тем не менее, мы сделали большую часть работы для первого в предыдущем примере, так что давайте начнем с него.

\({S_1}\) : Цилиндр

Параметризация цилиндра и \(\left\| {{{\vec r}_z} \times {{\vec r}_\theta }} \право\|\) есть,

\[\vec r\left( {z,\theta} \right) = \sqrt 3 \cos \theta \,\vec i + \sqrt 3 \sin \theta \,\vec j + z\,\vec k \hspace{0,5 дюйма}\влево\| {{{\vec r}_z} \times {{\vec r}_\theta}} \right\| = \ кв. 3 \]

Отличие этой задачи от предыдущей в ограничениях на параметры. Вот они.

\[\begin{array}{c}0 \le \theta \le 2\pi \\ 0 \le z \le 4 — y = 4 — \sqrt 3 \sin \theta \end{array}\]

Верхним пределом для \(z\) является плоскость, поэтому мы можем просто подключить ее. Однако, поскольку мы находимся на цилиндре, мы знаем, что такое \(y\) из параметризации, поэтому нам также понадобится чтобы подключить это. 9{2\pi }\\ & = \frac{{29\sqrt 3 \,\pi }}{2}\end{align*}\]

\({S_2}\) : Плоскость на вершине цилиндра

В этом случае нам не нужно выполнять какую-либо параметризацию, поскольку она настроена на использование формулы, которую мы дали в начале этого раздела. . Помните, что плоскость задается \(z = 4 — y\). Также обратите внимание, что для этой поверхности \(D\) — это диск радиуса \(\sqrt 3 \) с центром в начале координат.

Вот интеграл для плоскости. 92} + 1} \,dA}}\\ & = \sqrt 2 \iint\limits_{D}{{4\,dA}}\end{align*}\]

Не забывайте, что нам нужно подключиться к \(z\)! Теперь в этот момент мы можем действовать одним из двух способов. Либо мы можем перейти к интегралу, либо мы можем вспомнить, что \(\iint\limits_{D}{{dA}}\) есть не что иное, как площадь \(D\), и мы знаем, что \(D\) круг радиуса \(\sqrt 3 \) и поэтому нет смысла делать интеграл.

Вот оставшаяся часть работы по этой задаче. 92}} \right)\\ & = 12\sqrt 2 \,\pi \end{align*}\]

\({S_3}\) : Дно цилиндра

Опять же, это настроено на использование исходной формулы, которую мы дали в этом разделе, как только мы понимаем, что уравнение для дна задается \(g\ left( {x,y} \right) = 0\) и \(D\) — это диск радиуса \(\sqrt 3 \) с центром в начале координат. {2\pi}\\ & = 0\end{align*}\]

Теперь мы можем получить значение интеграла, которое нам нужно.

\[\begin{align*}\iint\limits_{S}{{y + z\,dS}} & = \iint\limits_{{{S_1}}}{{y + z\,dS}} + \ iint\limits_{{{S_2}}}{{y + z\,dS}} + \iint\limits_{{{S_3}}}{{y + z\,dS}}\\ & = \frac{{ 29\sqrt 3 \,\pi }}{2} + 12\sqrt 2 \,\pi + 0\\ & = \frac{\pi }{2}\left( {29\sqrt 3 + 24\sqrt 2 } \right)\end{align*}\]

Модификация | Горизонт Вики | Фэндом

в: Страницы для обновления, Предметы, Геймплей

Посмотреть источник

«Мне так многому нужно научиться, а времени меньше, чем я надеялся.» В этой статье или разделе не отражены изменения, внесенные новыми выпусками серии. Вы можете помочь, обновив содержимое.

Модификации

• Общий
• Редкий
• Очень редкий

• Нулевой рассвет

Использование

Улучшение оружия и экипировки

Источник(и)

Все машины

Сундуки с сокровищами

Стоимость

Нельзя купить

Стоимость продажи

10222 20 (редкий)
50 (очень редкий)

Модификации — это предметы в наборе Horizon Zero Dawn , которые можно добавить к снаряжению Элой для повышения характеристик и способностей. Катушки — это модификации, применяемые к оружию, а переплетения — к снаряжению.

Сначала их можно использовать после завершения основного квеста «Уроки дикой природы», за исключением Катушки урона от копья, добавленной The Frozen Wilds , которая сначала требует выполнения побочного квеста A Secret Shared. Их можно получить из сундуков с сокровищами и мародерских машин.

Модификации бывают трех типов: Обычные, Редкие и Очень редкие, в зависимости от степени редкости. Некоторые модификации могут повышать сразу несколько характеристик.

Содержимое

• 1 Катушки
• 2 переплетения
• 3 уникальные модификации
  • 3.1 Катушки уникального оружия
  • 3.2 Уникальное переплетение одежды
• 4 Каталожные номера

Катушки

Катушки — это модификации, которые можно добавлять к оружию для увеличения наносимого урона или характеристик обработки.

• Порча Катушка (Элементаль)
• Огонь Катушка (Элементаль)
• Заморозка Катушка (Элементаль)
• Шок Катушка (Элементаль)
• Повреждение Катушка
• Разрыв Катушка
• Транспортировка Катушка
• Копье Урон Катушка

В базовой игре минимальное значение модификации для всех катушек оружия составляет 6%, а максимальное значение варьируется в зависимости от эффекта и его «ранга» в моде:

• Стихийный урон бонусов имеет максимальное значение 50%, если это первичный эффект, и максимальное значение 17%, если это третичный эффект. Элементальный урон бонусов не могут быть переброшены как вторичный эффект.
Бонусы
• Damage и Tear имеют максимальное значение 50%, когда это основной эффект, и максимальное значение 25%, когда это вторичный эффект. Эти бонусы не могут быть выброшены как третичный эффект.
• Бонус обработки имеет максимальное значение 67%, если это основной эффект (=Handling Coil), или максимальное значение 33%, если это вторичный эффект. Его нельзя перевернуть как третичный эффект.
Катушка урона копьем
• всегда дает один бонусный эффект урона с максимальным значением 30%.

Важные примечания:

1. Дополнительным эффектом может быть только Урон , Слеза или Обработка бонусов
2. Третичный эффект может быть только Элементальный урон бонус.
3. Катушка не может иметь два бонуса с одинаковыми эффектами

Катушки оружия можно использовать только для увеличения существующих способностей оружия, но не для добавления новых. Например, огненные змеевики нельзя добавить к остроконечному луку, потому что он не может нанести огненного урона. Если катушка обеспечивает более одного преимущества, основной эффект будет определять, к какому оружию ее можно применить. Это означает, что катушки с несколькими эффектами иногда могут быть добавлены к оружию, которое не получит вторичных и/или третичных преимуществ.

Оружие	Совместимые модификации
Охотничий лук	Повреждение, Разрыв, Огонь, Обращение
Снайперский лук	Повреждение, разрыв, обращение
Боевой лук	Заморозка, Шок, Порча, Обращение
Трипкастер	Урон, Огонь, Шок, Обращение
Канатная машина	Повреждение, разрыв, обращение
Строп	Огонь, Заморозка, Шок, Повреждение, Обращение
Взрывной ремень	Повреждение, обращение
Раттлер	Повреждение, Разрыв, Замораживание, Шок, Обращение
Буревестник	Удар, обращение
Ледяной рельс	Повреждение, Заморозка, Обращение
Кузнечное пламя	Повреждения, Огонь, Обращение

Плетение

Плетение — это модификация, которую можно добавить к экипировке, чтобы повысить устойчивость к различным типам урона или повысить характеристики скрытности.

• Сопротивление Порче Плетение (Элементаль)
• Сопротивление Урону от огня Плетение (Элементаль)
• Сопротивление Урон от замораживания Плетение (Элементаль)
• Сопротивление Урону от электричества Плетение (Элементаль)
• Сопротивление Урон в ближнем бою Плетение (физический)
• Сопротивление Дальнему урону Плетение (Физическое)
• Скрытность Плетение

В базовой игре минимальное значение модификации для всех переплетений экипировки составляет 6%, а максимальное значение варьируется в зависимости от эффекта переплетения и его «ранга» в моде:

• Сопротивление стихиям переплетения имеют максимальное значение 33%, когда это основной эффект, максимальное значение 17%, когда это вторичный эффект, и максимальное значение 12%, когда это третичный эффект.
• Дальний бой и Сопротивление ближнему бою (физическому) переплетения имеют максимальное значение 20%, когда это основной эффект, максимальное значение 10%, когда это вторичный эффект, и максимальное значение 7%, когда это третичный эффект. эффект.
• Скрытность переплетения имеет максимальное значение 15%, когда это основной эффект, максимальное значение 7%, когда это вторичный эффект, и максимальное значение 5%, когда это третичный эффект.

Важные примечания:

1. Вторичный эффект может быть либо типом эффекта, противоположным основному бонусу ( Стихийный <> Физический ), либо быть невидимым бонусом
2. Третичный эффект всегда соответствует основному типу эффекта или является скрытым бонусом .
3. Переплетение не может иметь два бонуса с одинаковыми эффектами

В отличие от оружейных катушек, переплетения снаряжения могут добавлять к снаряжению новые способности и не связаны уже обеспеченной защитой. Например, несмотря на то, что экипировка Nora Protector не дает Сопротивление огню , чтобы добавить эту способность, можно применить плетение Сопротивление Огненному урону .

Уникальные модификации

The Frozen Wilds DLC добавляет в игру одиннадцать уникальных модификаций, которые можно найти в определенных местах. После получения их можно выбросить, разобрать с помощью жука, но нельзя продать.

Каждый из них считается ⁸ ⁄ ₁₁ % (≈0,73%) Frozen Wilds завершение игры.

Катушки уникального оружия

Значок	Имя	Эффекты	Местоположение	Оптимальное оружие
	Оружейная катушка барабанщика	+51% Заморозка +35% Шок +35% Порча	На самом дне Greycatch после слива всей воды	Боевой лук
	Оружейная катушка Hidebound	+51% к урону +35% к шоку +35% к заморозке	Награда за доставку фигурки животного 3 в Эндзюк	Раттлер
	Окрашенная катушка для оружия	+51% Шок +35% Огонь +47% Управляемость	Награда за доставку оксидных пигментов Секули	Трипкастер Вторичный*: строп
	Безупречная катушка для оружия	+51% Урон +35% Разрыв +47% Управляемость	Награда за выполнение задания Out of the Forge	Снайперский лук Вторичный*: Охотничий лук, гремучник
	Катушка непроверенного оружия	+51% Урон +35% Слеза +35% Огонь	Награда за выполнение побочного квеста Трое охотников	Охотничий лук
	Оружейная катушка ветерана	+51% огонь +35% шок +35% заморозка	Награда за получение всего золота на охотничьих угодьях Snowchants	Строп

*: Дополнительное оружие использует все атрибуты мода, но в самом моде отсутствует хотя бы один из элементарных типов оружия. В окрашенной оружейной катушке отсутствует замораживание для пращи, в то время как в нетронутой оружейной катушке отсутствуют удары и замораживание для гремучего, а также огонь для охотничьего лука.

Плетение уникальной одежды

Значок	Имя	Эффекты	Местоположение
	Ткань теплоотвода	+34% к сопротивлению огню +20% к сопротивлению дальним атакам	Примерно на полпути к противопожарному комплексу — в большой комнате, где Аратак и Орея предлагают альтернативные маршруты, это переплетение находится на «маршруте Аратака», с остатками предыдущей экспедиции.
	Ткань для утепленной одежды	+25% к сопротивлению шоку +25% к сопротивлению замораживанию +25% к сопротивлению огню	В ящике с припасами рядом с диспетчерской вышкой на крайнем северо-востоке Зареза. [1]
	Усиленное переплетение экипировки	+20% к сопротивлению дальним атакам +34% к сопротивлению замораживанию	Примерно на полпути через систему пещер вдоль Пути Шамана.
	Ткань для костюма выжившего	+34% к сопротивлению замораживанию +20% к сопротивлению атакам ближнего боя	Награда за получение золота в испытании Икри
	Плетение одежды воина	+20% к сопротивлению атакам ближнего боя +34% к сопротивлению огню	В ящике с припасами в рыбацком лагере Банук к юго-западу от Глубокого Дина.

Ссылки

1. ↑ Из-за ошибки он может появиться только во время выполнения задания Frozen Wilds , The Claws Beneath.

Контент сообщества доступен по лицензии CC-BY-SA, если не указано иное.