Запись чисел в двоичной системе счисления
Пройти занятие
1
Заставка Конспект
2
Правила игры «Расселение зверей» Видео
3
Правила игры «Расселение зверей» Конспект
4
Пример рассления 5 мышей Конспект
5
Игра «Расселение зверей» Задание
6
Запись чисел в двоичной системе Видео
7
Запись числа 5 в двоичной системе Конспект
8
Запись числа 4 в двоичной системе Конспект
9
Игра «Расселение зверей» Задание
10
«Закон сохранения мышей» Видео
11
«Закон сохранения мышей» Конспект
12
Улучшение алгоритма расселения Видео
13
Улучшение алгоритма расселения Конспект
14
Игра «Расселение зверей» Задание
Материалы для скачивания
dwnld_solid0. 51 МБ
51 МБ
Конспект для скачивания
Выпуск этого урока поддержали:
НОУ ИНТУИТ | Лекция | Двоичные числа и двоичная арифметика
Аннотация: Рассматривается двоичная система счисления как частный случай позиционной системы и основные правила двоичной арифметики.
Ключевые слова: вес, целое число, запись, аналогия, выражение, логический, основание, связь, восьмеричная система счисления, обратный код, дополнительный код, прямой, система счисления, сложение, вычитание
Принцип представления чисел в позиционных системах счисления
Позиционной называется система счисления, в которой вес разряда числа определяется его позицией в записи числа [1].
Вспомним нашу привычную десятичную систему счисления, в которой мы с детства производим все расчеты. Уже в начальной школе мы привыкли к терминам «единицы», «десятки», «сотни», «тысячи», «десятые», «сотые», «тысячные» и не задумываемся над тем, что они означают вес разряда, выраженный в виде числа, равного , где — целое число. Например, число 125, 46 можно представить в виде суммы:
Уже в начальной школе мы привыкли к терминам «единицы», «десятки», «сотни», «тысячи», «десятые», «сотые», «тысячные» и не задумываемся над тем, что они означают вес разряда, выраженный в виде числа, равного , где — целое число. Например, число 125, 46 можно представить в виде суммы:
сотни десятки единицы десятые доли сотые доли
Аналогично любое число в десятичной системе счисления можно представить в виде подобной суммы:
| ( 11.1) |
где — количество знаков в целой части числа, — количество знаков в дробной части числа, — вес -го разряда, — весовой коэффициент для -го разряда числа. Количество возможных вариантов значения коэффициента в десятичной системе счисления равно , поскольку для записи чисел в ней используются десять знаков — арабские цифры «0», «1», «2», «3», «4», «5», «6», «7», «8» и «9». Число является основанием системы счисления. Исторически сложилось, что десятичная система получила наибольшее распространение, хотя по этому принципу можно сделать аналогичную запись в любой другой системе счисления c любым другим основанием. В табл. 11.1 прослежива
ется аналогия между позиционными системами счисления.
Количество возможных вариантов значения коэффициента в десятичной системе счисления равно , поскольку для записи чисел в ней используются десять знаков — арабские цифры «0», «1», «2», «3», «4», «5», «6», «7», «8» и «9». Число является основанием системы счисления. Исторически сложилось, что десятичная система получила наибольшее распространение, хотя по этому принципу можно сделать аналогичную запись в любой другой системе счисления c любым другим основанием. В табл. 11.1 прослежива
ется аналогия между позиционными системами счисления.
Основание системы счисления — это число, равное количеству знаков, которые используются в этой системе для записи чисел.
Для числа в системе счисления с основанием выражение (11.1) преобразуется к виду:
(
11. 2) 2) |
| Название системы счисления | Основание системы счисления | Знаки, использующиеся для записи чисел |
|---|---|---|
| Двоичная | 2 | 0, 1 |
| Троичная | 3 | 0, 1, 2 |
| Четверичная | 4 | 0, 1, 2, 3 |
| … | … | |
| Восьмеричная | 8 | 0, 1, 2, 3, 4, 5, 6, 7 |
| … | … | … |
| Десятичная | 10 | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 |
| … | … | … |
| Шестнадцатеричная | 16 | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F |
| … | … | … |
intuit.ru/2010/edi»>С началом развития цифровой вычислительной техники большой интерес стала вызывать двоичная система, поскольку вычислительная машина любого поколения и любой степени сложности — это совокупность логических схем. Работа элементов этих схем основана на ключевом режиме работы транзистора, в котором он может быть только в двух состояниях, принимаемых за логический 0 и логическую 1.
Запись двоичного числа, как будет показано ниже, как правило, довольно длинна и громоздка, поэтому для более короткой записи двоичных чисел применяются восьмеричные и шестнадцатеричные числа. Выбор именно этих систем обусловлен тем, что их основания равны целой степени числа 2. Основание восьмеричной системы , а основание шеснадцатиричной системы — это . Для записи шестнадцатеричных чисел арабских цифр не хватает, поэтому используются первые шесть заглавных букв латинского алфавита.
Итак, далее мы подробно рассмотрим именно эти позиционные системы — двоичную, восьмеричную, шестнадцатеричную и их связь с привычной нам десятичной системой счисления.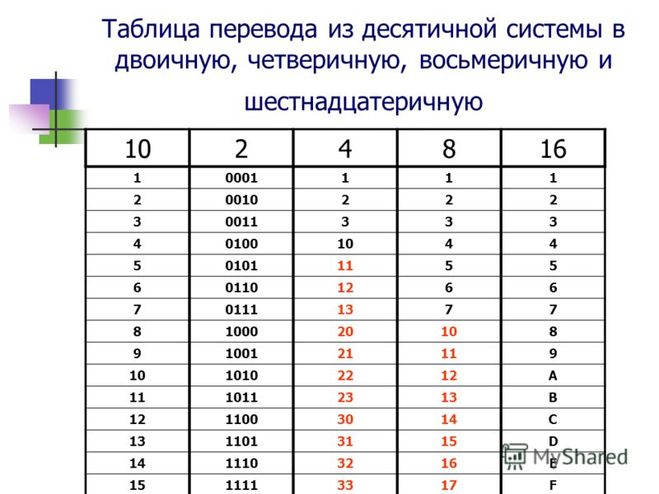
Приведем примеры записи чисел в указанных системах и найдем их десятичные эквиваленты по формуле (11.2).
Для двоичного числа:
Здесь и далее будем придерживаться следующего правила: числа в двоичной, восьмеричной и шестнадцатеричной системах записываются с указанием основания, десятичные — без этой записи.
Для восьмеричного числа:
Для шестнадцатеричного числа:
Округление относится к дробной части числа, целая часть переводится точно. Особенностью перевода из шестнадцатеричного кода в десятичный код является то, что в качестве коэффициента используется десятичный эквивалент шестнадцатеричного знака в соответствии с таблицей 11.2. Для нашего примера вместо знака » » в расчетную формулу (11.2) подставляется десятичное число .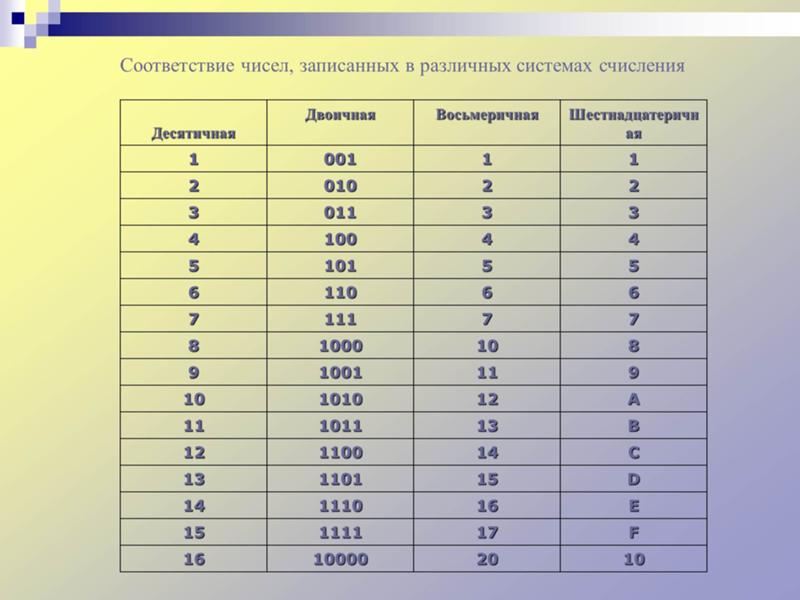
Из рассмотренных примеров видно, что общая формула (11.2) может использоваться для перевода числа из системы счисления с любым основанием в десятичную.
Перевод чисел из одной системы счисления в другую
Перевод из десятичной системы в любую другую. Перевод целых чисел
Целое десятичное число нужно поделить на основание новой системы счисления. Остаток от этого деления является самым младшим разрядом в новой записи числа. Результат деления вновь делится на основание. Остаток от этого деления будет следующим разрядом в новой записи числа, результат деления вновь делится на основание и т.д. до тех пор, пока в результате деления получится число, меньшее по величине, чем основание новой системы. Остаток этого последнего деления будет предпоследним разрядом в новой записи числа, а результат этого последнего деления — самым старшим разрядом в новой записи числа.
intuit.ru/2010/edi»>Проверка перевода осуществляется по формуле (11.2), так, как это показано ниже на примерах.
Пример. Перевести десятичное число 125 в двоичную, восьмеричную и шестнадцатеричную системы счисления. Проверить результаты по формуле (П11.2).
| a) | б) | в) |
Проверка:
- в двоичном коде: ;
- в восьмеричном коде ;
- в шестнадцатеричном коде — .
В рассмотренном примере при переводе вместо коэффициента используется его десятичный эквивалент в соответствии с таблицей 11. 2.
2.
Перевод из двоичной системы в шестнадцатеричную (восьмеричную)
Как уже было сказано выше, шестнадцатеричный и восьмеричный коды используются для более компактной и удобной записи двоичных чисел. Так, программирование в машинных кодах осуществляется в большинстве случаев в шестнадцатеричном коде. Правила перевода для шестнадцатеричной и восьмеричной системы структурно одинаковы, отличия для восьмеричной системы отображаются в скобках.
Двоичная запись числа делится на группы по четыре ( три ) двоичных знака влево и вправо от запятой, отделяющей целые и дробные части Неполные крайние группы (если они есть) дополняются нулями до четырех ( трех ) знаков. Каждая группа заменяется одним шестнадцатеричным ( восьмеричным ) знаком в соответствии с кодом группы (табл. 11.2).
| Двоичная группа | Шестнадцатеричный знак | Десятичный эквивалент | Двоичная группа | Восьмеричный знак |
|---|---|---|---|---|
| 0000 | 0 | 0 | 000 | 0 |
| 0001 | 1 | 1 | 001 | 1 |
| 0010 | 2 | 2 | 010 | 2 |
| 0011 | 3 | 3 | 011 | 3 |
| 0100 | 4 | 4 | 100 | 4 |
| 0101 | 5 | 5 | 101 | 5 |
| 0110 | 6 | 6 | 110 | 6 |
| 0111 | 7 | 7 | 111 | 7 |
| 1000 | 8 | 8 | ||
| 1001 | 9 | 9 | ||
| 1010 | A | 10 | ||
| 1011 | B | 11 | ||
| 1100 | C | 12 | ||
| 1101 | D | 13 | ||
| 1110 | E | 14 | ||
| 1111 | F | 15 |
intuit.ru/2010/edi»>Примеры:
- перевод в шестнадцатеричную систему:
- перевод в восьмеричную систему:
Перевод из шестнадцатеричной (восьмеричной) системы в двоичную
Обычно программы в машинных кодах записаны в шестнадцатеричной системе счисления, реже — в восьмеричной. При необходимости отдельные числа такой программы записываются в двоичном коде, например, при рассмотрении форматов регистров, кодов операции команд и т.п. В этом случае нужен обратный перевод из шестнадцатеричной (восьмеричной) системы счисления в двоичную по следующему правилу.
Каждая цифра (без всяких сокращений!) шестнадцатеричного ( восьмеричного ) числа заменяется одной двоичной группой из четырех ( трех ) двоичных знаков (табл. 11.2).
Примеры:
- intuit.ru/2010/edi»>для шестнадцатеричного числа: ;
- для восьмеричного числа: .
Как показано в примерах, крайние нули слева и справа при желании можно не писать, но такое сокращение делается уже после перевода в двоичную систему.
двоичных цифр
| Двоичная цифра может быть только 0 или 1 |
Двоичный номерДвоичное число состоит из двоичных цифр. |
В компьютерном мире « b inary dig it » часто сокращается до слова « бит «
Более одной цифры
Итак, есть только два способа получить двоичную цифру ( «0» и «1» или » Выкл » и «Вкл» ) .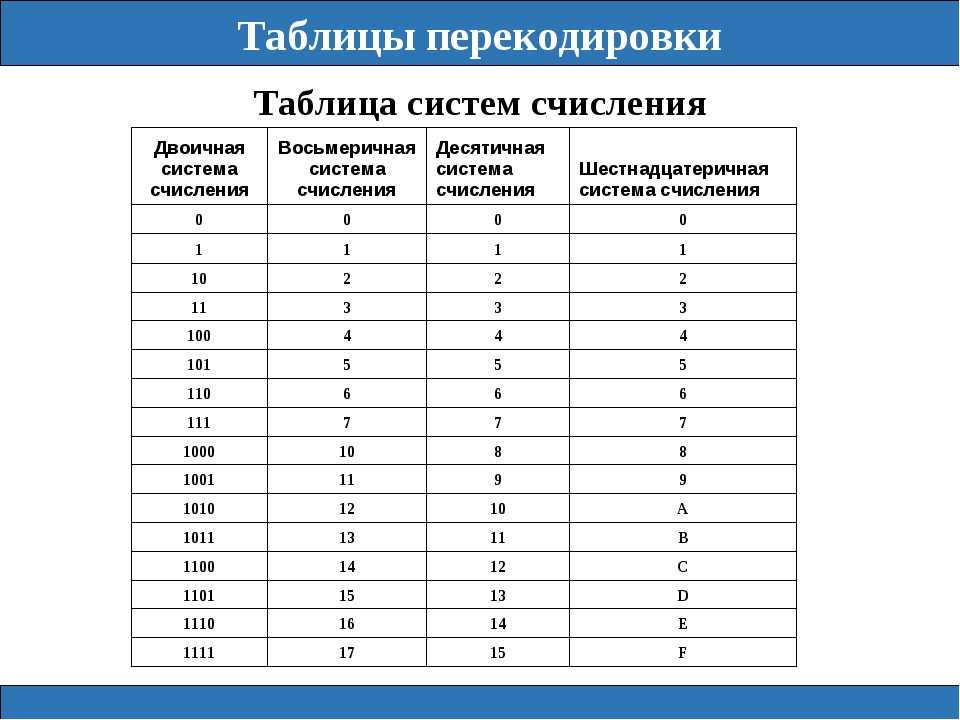 .. но как насчет 2 или больше двоичных цифр?
.. но как насчет 2 или больше двоичных цифр?
Запишем их все, начиная с 1 цифры, а сами можете проверить с помощью переключателей:
| 2 способа получить одну цифру… | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| … 4 способа получить две цифры … |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
. .. 8 способов получить три цифры … .. 8 способов получить три цифры … |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
.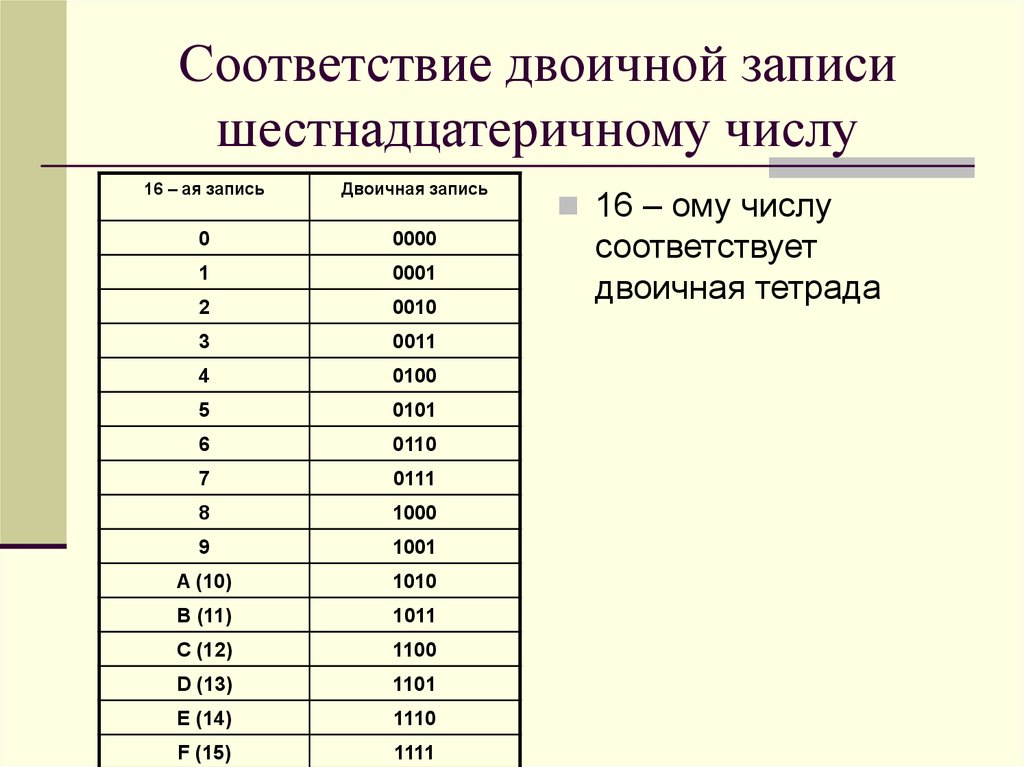 .. и 16 способов получить четыре цифры. .. и 16 способов получить четыре цифры. |
|
Вот этот последний список сбоку:
| 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
И (без ведущих нулей) у нас есть первые 16 двоичных чисел:
| Двоичный: | 0 | 1 | 10 | 11 | 100 | 101 | 110 | 111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Десятичный: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
Это полезно! Чтобы запомнить последовательность двоичных чисел, просто подумайте:
.
- «0» и «1» {0,1}
- , затем снова повторите «0» и «1», но с «1» впереди: {0,1,10,11}
- , затем повторите те с «1» впереди: {0,1,10,11,100,101,110,111}
- и так далее!
На каждом этапе мы повторяем все, что у нас есть до сих пор, но с 1 впереди.
Теперь узнайте, как использовать Binary, чтобы считать на пальцах больше 1000:
Активность: Бинарные пальцы
| Также поиграйте с разными барабанами. |
Двоичные цифры… Они удваиваются!
Также обратите внимание, что каждый раз, когда мы добавляем еще одну двоичную цифру, мы удваиваем возможных значений.
Почему двойной ? Потому что мы берем все предыдущие возможные значения и сопоставляем их с «0» и «1», как указано выше.
- Таким образом, всего одна двоичная цифра имеет 2 возможных значения (0 и 1)
- Две двоичные цифры имеют 4 возможных значения (0, 1, 10, 11)
- Три имеют 8 возможных значений
- Четыре имеют 16 возможных значений
- Пять имеют 32 возможных значения
- Шесть имеют 64 возможных значения
- и т.
 д.
д.
Используя показатели степени, это можно представить как:
| Число цифр | Формула | Настройки |
|---|---|---|
| 1 | 2 1 | 2 |
| 2 | 2 2 | 4 |
| 3 | 2 3 | 8 |
| 4 | 2 4 | 16 |
| 5 | 2 5 | 32 |
| 6 | 2 6 | 64 |
| и т.д… | и т.д. .. | и т. д… д… |
Пример: когда у нас есть 50 двоичных цифр (или 50 вещей, каждая из которых может иметь только две позиции), сколько существует различных способов?
Ответ: 2 50 = 2 × 2 × 2 × 2 × 2 … (пятьдесят из них)
= 1 125 899 906 842 624
Итак, двоичное число из 50 цифр может иметь 1 125 899 906 842 624 различных значения.
Или, другими словами, он может показать число до 1 125 899 906 842 623 (примечание: это на единицу меньше, чем общее количество значений, потому что одно из значений равно 0).
Пример: начните месяц с 1 доллара и удваивайте его каждый день, через 30 дней у вас будет
миллиардер ! 2 30 = 2 × 2 × 2 × 2 … (тридцать из них)
= 1 073 741 824
Шахматная доска
Существует старая индийская легенда о короле, которого пригласил на партию в шахматы приехавший мудрец.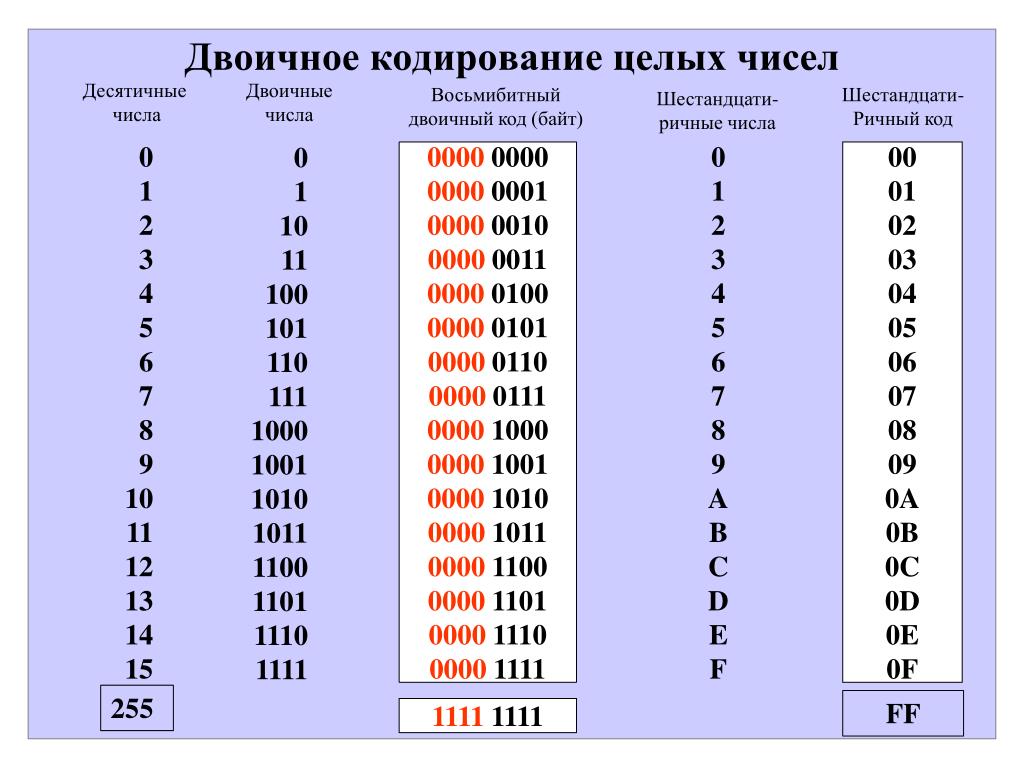 Король спросил: «Какой приз, если вы выиграете?».
Король спросил: «Какой приз, если вы выиграете?».
Мудрец сказал, что ему просто нужно несколько зернышек риса: одно на первой клетке, 2 на второй, 4 на третьей и так далее, удваивая на каждой клетке. Король был удивлен этой скромной просьбой.
Что ж, Мудрец победил, так сколько зернышек риса он должен получить?
На первом квадрате: 1 зерно, на втором квадрате: 2 зерна (всего 3) и так далее:
| Квадрат | Зерновые | Всего |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 2 | 3 |
| 3 | 4 | 7 |
| 4 | 8 | 15 |
| | | |
| 10 | 512 | 1 027 |
| | | |
| 20 | 524 288 | 1 048 575 |
| | | |
| 30 | 53 6870 912 | 1 073 741 823 |
| | | |
| 64 | ??? | ??? |
К 30-му квадрату видно, что риса уже много! Миллиард зерен риса — это около 25 тонн (1000 зерен — это около 25 г… Я немного взвесил!)
Обратите внимание, что Итого любого квадрата на 1 меньше, чем Зерна на следующей клетке (Пример: в клетке 3 всего 7, а в клетке 4 8 зерен). Таким образом, сумма всех квадратов представляет собой формулу: 2 n −1 , где n — номер квадрата. Например, для квадрата 3 сумма равна 2 3 −1 = 8 − 1 = 7
Таким образом, сумма всех квадратов представляет собой формулу: 2 n −1 , где n — номер квадрата. Например, для квадрата 3 сумма равна 2 3 −1 = 8 − 1 = 7
Итак, чтобы заполнить все 64 клетки шахматной доски, потребуется:
2 64 −1 = 18 446 744 073 709 551 615 зерен (460 миллиардов тонн риса),
во много раз больше риса, чем во всем королевстве.
Итак, сила бинарного удвоения не может быть легкомысленной (460 миллиардов тонн — это не свет!)
Зерна риса на каждом квадрате с экспоненциальным представлением
Значения округлены, поэтому
53 6870 912 отображается как 5×10 8
, что означает 5, за которой следуют 8 нулей
(Кстати, в легенде Мудрец оказывается Господь Кришна и говорит королю, что он не обязан платить долг сразу, но может платить ему со временем, просто подавайте рис паломникам каждый день, пока долг не будет погашен. )
)
Шестнадцатеричный
Наконец, давайте рассмотрим особые отношения между двоичным и шестнадцатеричным числами.
Существует 16 шестнадцатеричных цифр, и мы уже знаем, что 4 двоичных цифры имеют 16 возможных значений. Ну, именно так они относятся друг к другу:
| Двоичный: | 0 | 1 | 10 | 11 | 100 | 101 | 110 | 111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Шестнадцатеричный: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | А | Б | С | Д | Е | Ф |
Таким образом, когда люди используют компьютеры (которые предпочитают двоичные числа), гораздо проще использовать одну шестнадцатеричную цифру, а не 4 двоичные цифры.
Например, двоичное число «100110110100» равно «9B4» в шестнадцатеричном формате. Я знаю, что я предпочел бы написать!
бинарных пальцев!
Бинарные пальцы!Показать рекламу
Скрыть рекламу
О рекламе
Забудьте о счете до 10 на пальцах… вы можете считать до 1000, если хотите!
Правая рука
Правой рукой вы можете сосчитать до 31:
Нет пальцев вверху 0
Большой палец 1
Указательный палец 2
2 и 1
= 3
Средний палец 4
Добавьте свой большой палец
на 5
4 и
2 делает 6
4 и 2 и 1
получается 7
Безымянный палец 8
.
|
На самом деле вы считаете в двоичном формате:
| Номер | Сделано | |||||
| 1 | 1 | до | ||||
| 2 | 2 | до | ||||
| 3 | 2+1 | до | до | |||
| 4 | 4 | до | ||||
| 5 | 4+1 | до | до | |||
| 6 | 4+2 | до | до | |||
| 7 | 4+2+1 | до | до | до | ||
| 8 | 8 | до | ||||
| 9 | 8+1 | до | до | |||
| 10 | 8+2 | до | до | |||
| 11 | 8+2+1 | до | до | до | ||
| 12 | 8+4 | до | до | |||
| 13 | 8+4+1 | до | до | до | ||
| 14 | 8+4+2 | до | до | до | ||
| 15 | 8+4+2+1 | до | до | до | до | |
| 16 | 16 | до | ||||
| 17 | 16+1 | до | до | |||
и т.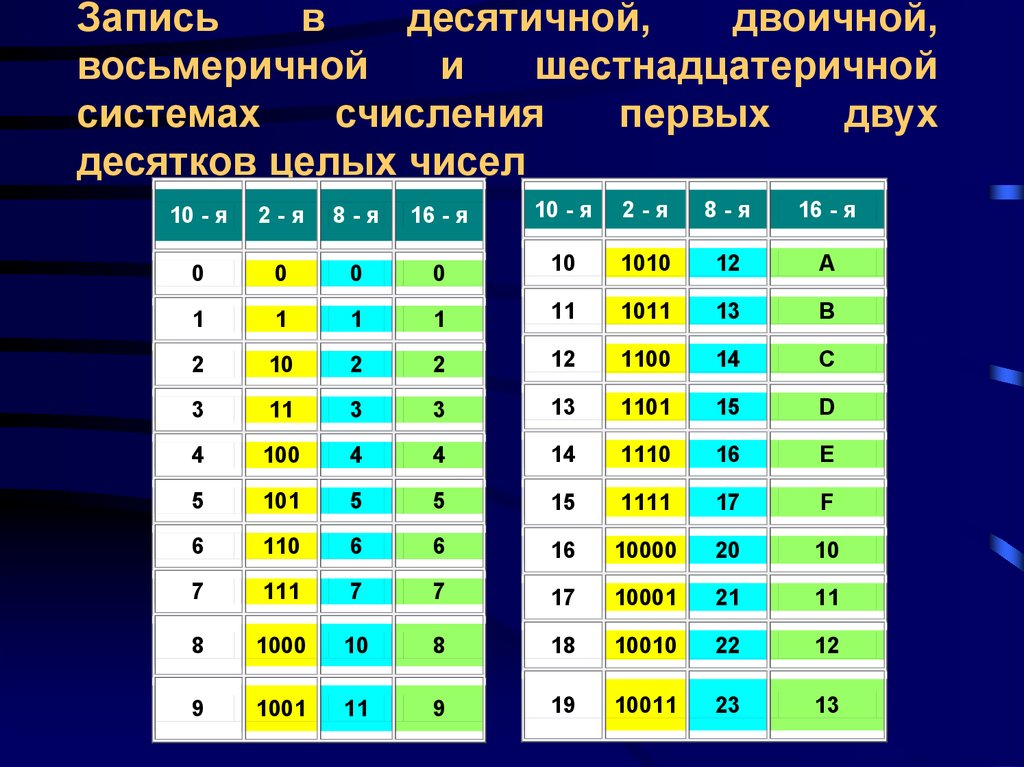 д…. д…. | ||||||
Вот еще несколько примеров:
| 16+8+2 делает 26 |
| 16+8+4+2 делает 30 |
Почему?
Чтобы вы могли считать до большего числа, когда у вас нет карандаша или бумаги.
Вы также можете «запоминать» числа, держа пальцы в правильном положении.
Или вы можете показать кому-то секретный номер, используя только свою руку (или руки, см. далее).
Ваша очередь
Потренируйтесь считать на пальцах от 0 до 31, как описано выше.
Делайте это много раз, пока не станет легко.
Когда у тебя получается хорошо, покажи друзьям!
Левая рука
Хотите большие числа? Ваша левая рука может помочь:
Теперь мы можем использовать все 10 пальцев, чтобы составить такие числа:
| 32+2 делает 34 |
| 32+16+8+4 делает 60 |
| 512+256+32+2+1 делает 803 |
И, наконец, что происходит, когда все пальцы подняты?
| 512+256+128+64+32+16+8+4+2+1 составляет 1 023 |
Итак, теперь вы можете считать до 1000, используя всего 10 пальцев.
 2.
Соответствие двоичных групп, шестнадцатеричных и восьмеричных знаков
2.
Соответствие двоичных групп, шестнадцатеричных и восьмеричных знаков .. и продолжайте узор:
.. и продолжайте узор: