Задачи позиционные – Позиционные задачи.

Позиционные задачи.

Все задачи начертательной геометрии делятся на два больших класса: позиционные и метрические.

Позиционные – это задачи на определение занимаемого положения геометрической фигуры. Они бывают двух типов: задачи на инцидентность (принадлежность) и задачи на пересечение.

Рассмотрим решение одной из важнейших задач на пересечение прямой линии и плоскости, которая называется первая основная позиционная задача.

1. Первая основная позиционная задача.

Содержание: построить на комплексном чертеже точку пересечения прямой l с плоскостью, заданной ΔАВС и определить видимость прямой относительно плоскости АВС на плоскостях П₁ и П₂ (рис. 57).

Рис. 57

Алгоритм графического решения задачи состоит из следующих элементарных операций:

1. Через данную прямую провести вспомогательную плоскость, в большинстве случаев проецирующую. Проведем в данном случае фронтально-проецирующую плоскость Σ, тогда Σ₂ = l₂.

2. Построить линию пересечения MN данной плоскости АВС и вспомогательной Σ. Прямая MN определяется точками М и N пересечения сторон АС и СВ треугольника АВС с проецирующей плоскостью Σ. (). По линиям связи находим горизонтальные проекции М₁ и N₁ точек на А₁С₁ и В₁С₁. Соединив точка М₁

   и N₁ прямой, получим горизонтальную проекцию линии пересечения.

3. Определить точку К пересечения прямой l с линией МN (К₁ = l₁ М₁N₁; К₂ = М₂N₂ К₁К₂).

4. Определить видимость. Определение видимости проводится методом конкурирующих точек.

Возьмем две точки 1 и 2, лежащие на одной горизонтально-проецирующей прямой (рис. 58). Горизонтальные проекции 1 и 2 этих точек совпадают.

Рис. 58 Рис. 59

Так как высота точки 1 больше, чем высота точки 2, т.е. , то точка1₁

на горизонтальной проекции будет видимая, а точка 2₁ – невидимая. Берем ее в скобки. Точка 1 в пространстве лежит ближе к наблюдателю. Аналогично, возьмем две точки 3 и 4, лежащие на одной фронтально-проецирующей прямой (рис. 59). Фронтальные проекции 3₂ и 4₂ этих точек совпадают. Определим, какая из них видимая. Так как глубина точки 4 больше, чем глубина точки 3, т.е. , то фронтальная проекция4₂ точки 4 видимая. Точка 4 в пространстве лежит ближе к наблюдателю. Фронтальную проекцию 3₂ точки 3 берем в скобки. Такое определение видимости называется методом конкурирующих точек, так как точки, лежащие на одной проецирующей прямой, называются конкурирующими.

2. Пересечение двух плоскостей.

Задача. Построить линию пересечения треугольников АВС и DEK на комплексном чертеже. Определить видимость (рис. 60).

Рис. 60

Для того, чтобы построить прямую пересечения двух плоскостей, достаточно построить две общие точки этих плоскостей. В качестве этих точек можно взять точки пересечения двух каких-либо сторон одного треугольника с плоскостью другого или точки пересечения одной стороны одного треугольника с плоскостью другого и одной стороны второго с плоскостью первого.

Таким образом, построение сводится к двукратному решению первой основной позиционной задачи.

Видимость сторон треугольника определяется способом конкурирующих точек.

Однако линию пересечения двух плоскостей можно найти, применяя при решении вспомогательные секущие плоскости (часто горизонтальные или фронтальные плоскости уровня (рис. 61)).

Рис. 61

Плоскость Γ (Γ₂) пересекает заданные плоскости по прямым линиям – горизонталям 12 и 34, которые пересекаются в точке К. Вторая секущая плоскость Δ (Δ₂) пересекает заданные плоскости также по горизонталям, а они, в свою очередь, пересекаются в точке М. Прямая g (g₁, g₂), проходящая через точки К и М, является искомой линией пересечения заданных плоскостей.

studfiles.net

Основные Позиционные Задачи

70

Задача 69. Определить: перпендикулярны плоскости или нет

(рис.91).

Рис.91

СВЕДЕНИЯ ИЗ ТЕОРИИ

Позиционные задачи

В начертательной геометрии задачи на определение взаимного положения заданных оригиналов носят название позиционных (ПЗ).

Во всех позиционных задачах вопрос может быть сформулирован следующим образом: «Определить взаимное положение оригиналов».

Позиционные задачи, в которых участвуют точки, прямые и плоскости называют основными позиционными задачами.

На первом этапе решения задачи необходимо провести полный анализ исходных данных и выразить результаты анализа в символическом

71

виде, т.е. необходимо определить, какие оригиналы участвуют в задаче и какое положение они занимают относительно плоскостей проекций.

Позиционные задачи можно разделять на типы в зависимости от положения заданных оригиналов относительно плоскостей проекций.

ПЗ I типа — оба оригинала занимают проецирующее положение. Например, в задаче, чертёж к которой представлен на рис.92, участвуют горизонтально-проецирующая прямая s и фронтально-проецирующая плоскость .

Рис.92

В этом случае можно сразу ответить на вопрос задачи о взаимном положении оригиналов – есть пересечение или нет; определить, какая фигура получится при пересечении и найти проекции этой фигуры на чертеже (рис.93).

Рис.93.

72

ПЗ II типа — один из оригиналов занимает проецирующее положение. На рис.94 своим горизонтальным следом ( 1) задана горизонтальнопроецирующая плоскость . Плоскость , определителем которой является треугольник АВС, занимает общее положение относительно плоскостей проекций.

Рис.94

В ПЗ II типа также можно ответить на вопрос задачи и найти на чертеже одну из проекций фигуры, получающейся в результате пересечения оригиналов. Вторую проекцию этой фигуры требуется построить (рис.95).

Рис.95

studfiles.net

Глава 10. Позиционные задачи на различные виды отношений между

прямыми и плоскостями и их графические решения

——-

Глава 10. ПОЗИЦИОННЫЕ ЗАДАЧИ

НА РАЗЛИЧНЫЕ ВИДЫ ОТНОШЕНИЙ

МЕЖДУ ПРЯМЫМИ И ПЛОСКОСТЯМИ

И ИХ ГРАФИЧЕСКИЕ РЕШЕНИЯ

10.1. Понятие о позиционных задачах

Определение 10.1. Позиционными называются задачи на определение вида взаимного расположения в прост-ранстве двух геометрических объек-тов по их двухкартинному комплекс-ному чертежу или наоборот, на по-строение обратимого изображения таких двух объектов, взаимное распо-ложение которых в пространстве на-перед задано.

В данном случае под геометричес-кими объектами понимаются прямые линии и плоскости, а под «видом их вза-имного расположения» имеется ввиду то позиционное отношение или связь (принадлежность, пересечение, пер-пендикулярность и параллельность) ме-жду ними, которые конкретизируют их взаимную позицию в пространстве.

Из определения позиционных задач видно, что они делятся на прямые и обратные.

Решение прямых задач даёт ин-формацию о расположении объектов в пространстве и по отношению друг к другу, а решение обратных задач, – информацию о структуре обратимых изображений объектов, взаимное рас-положение которых в пространстве за-дано по условию.

Вполне очевидно, что оба вида за-дач решаются в картинном простран-стве, т.е., в режиме графического моде-лирования тех конкретных ситуаций, ко-торые определяются геометрическими условиями их взаимного расположения в эвклидовом пространстве. Поэтому, как и прежде, графическому модели-рованию ситуации конкретной задачи будет предшествовать её геометричес-кое, т.е., мысленное моделирование.

При этом следует помнить, что в пространстве объекты взаимно распо-лагаются так или иначе, подчиняясь конкретным условиям такого располо-жения, а на комплексном чертеже ин-формация о соблюдении этих условий

кодируется соответствующими графи-

ческими признаками как основой изо-бразительных свойств ортогональных проекций конкретных изображённых объектов.

Два геометрических объекта, рас-полагаясь в пространстве так или ина-че, образуют двухэлементную геоме-трическую систему.

У с л о в и я п р я м ы х з а д а ч:

Задача №1. Определить вид вза-имного расположения двух плоскос-тей в пространстве по их двухкар-тинному комплексному чертежу.

Задача №2. Определить вид вза-имного расположения прямой линии и плоскости по их двухкартинному ком-плексному чертежу.

У с л о в и я о б р а т н ы х з а д а ч:

Задача №3. Построить двухкар-тинный комплексный чертёж точки и прямой, принадлежащих заданной пло-скости.

Задача №4. Построить двухкар-тинный комплексный чертёж прямой линии, пересекающей плоскость в за-данной точке.

Задача №5. Построить двухкар-тинный комплексный чертёж прямой, параллельной заданной плоскости.

Задача №6. Построить двухкар-тинный комплексный чертёж прямой, перпендикулярной к заданной плоскос-ти.

Задача №7.(взаимная задаче №6). Построить двухкартинный комплекс-ный чертёж плоскости, перпендику-лярной к заданной прямой.

Задача №8. Построить двухкар-тинный комплексный чертёж двух взаимно-перпендикулярных прямых

общего положения.

Задача №9. Построить двухкар-тинный комплексный чертёж двух плоскостей, пересекающихся по за-данной прямой.

Задача№10. Построить двухкар-тинный комплексный чертёж двух взаимно-параллельных плоскостей.

Задача №11. Построить двухкар-тинный комплексный чертёж двух вза-имно-перпендикулярных плоскостей.

Вполне логично начинать рассмотре-

ние технологии графичного решения

позиционных задач вообще с решения

Рис. 10.1. Графические модели точки А, принадлежащей плоскости 

перечисленных обратных задач на на-перед заданное взаимное расположе-ние двух объектов в пространстве, так как следует ожидать, что на характере их решения будут сказываться особен-ности положения этих объектов по от—ношению к плоскостям проекций.

В связи с этим будет произведен системный анализ возможных положе-ний прямых и плоскостей в пространст-ве с обработкой его количественных и качественных результатов, на основе которой определятся условия и идеи решения двух прямых позиционных за-дач.

studfiles.net

Решение главных позиционных задач.

3 Случая. 3 алгоритма.

Способ решения главных позиционных задач, или алгоритм решения, зависит от расположения пересекающихся геометрических фигур относительно плоскостей проекций.

Здесь имеет место З случая:

1. обе пересекающиеся фигуры занимают проецирующее положение. Задачи решаются по первому алгоритму.

2. одна из пересекающихся фигур — проецирующая, другая – непроецирующая. Задачи решаются по второму алгоритму.

3. обе пересекающиеся фигуры — непроецирующие. Задачи решаются по третьему алгоритму.

Здесь уместно вспомнить, какие фигуры могут занимать проецирующее положение. Таковыми являются: прямая, плоскость, а из всех известных нам поверхностей проецирующее положение могут занимать только призматическая поверхность (частный случай — призма) и цилиндрическая поверхность (частный случай — прямой круговой цилиндр). На рис. 3-6 показаны примеры горизонтально проецирующих фигур. Напомним, что главными проекциями у них являются: у прямой а— точкаа₁, у плоскости— прямая₁, у призмы— треугольник₁

Рис. 3-6

( а в общем случае — или ломаная линия, или любой многоугольник), у цилиндра Г— окружностьГ₁(в общем случае — замкнутая или разомкнутая кривая). Напомним также, чтоглавные проекциипроецирующих фигур обладают «собирательными» свойствами (рис. 3-6).

1 Алгоритм

Решение задач в случае, когда обе пересекающиеся фигуры занимают проецирующее положение.

Решение рассмотрим на конкретном примере.

Задача: Найти проекции точки пересечения горизонтально-проецирующей плоскости(m || n) с фронтально-проецирующей прямой а (рис. 3-7).

Рис. 3-7

Алгоритм: Так как в пересечении участвует прямая линия (а), то это —первая главная позиционная задача. Обе пересекающиеся фигуры — проецирующие относительно разных плоскостей проекций. Решение начинаем с фронтальной проекции.

1. Точка К является общим элементом плоскостии прямойа, следовательно,К и Ка. Но, еслиКа, тоК₂а₂, а, посколькуа₂— это точка (главная проекция, обладающая собирательными свойствами), тоК₂=а₂.

2. Находим горизонтальную проекцию точки К. Так как плоскостьнаП₁проецируется в прямую линию₁, тоК₁, как общий элементиа, будет располагаться на пересечении₁иа₁.

Выполним краткую алгоритмическую запись вышеизложенного:

(m || n)  а = К; 1 ГПЗ, 1 алгоритм.

1. К  а, а  П₂  К₂ = а₂.

2. К  а, К  ,   П₁  К₁ = ₁  а₁.

Таким образом, решение 1 ГПЗ по первому алгоритму заключается в следующем:

Проекции общего элемента на чертеже уже присутствуют. Они совпадают с главными проекциями проецирующих фигур. Решение сводится к их нахождению и обозначению.

Вторую главную позиционную задачурешим в соответствии с рассмотренным алгоритмом.

Задача: найти проекции линии пересечения горизонтально проецирующего цилиндраФс фронтально проецирующей призмойГ(рис. 3-8).

Рис. 3-8

Алгоритм: Пересекаются две поверхности, это —2 ГПЗ. Вначале анализируем,чтодолжно получиться в результате пересечения. Так как характер пересечения — вмятие, то общим элементом должна быть одна пространственная линия —m.

Обе фигуры проецирующие относительно разных плоскостей проекций. Следовательно, согласно 1 алгоритму, проекции общего элемента должны совпадать с главными проекциями поверхностей. На фронтальной проекции m₂должна совпадать сГ₂. Однако, из чертежа (рис. 3-8) видно, что часть главной проекции призмыГ₂выходит за пределы цилиндра, а это означает, что совпадение проекции линии пересеченияm₂ с главной проекцией призмыГ₂только частичное. Следовательно, нужно найти границы общей части.

На рис. 3-9 линия m₂, совпадающая сГ₂в пределах цилиндра, выделена красным цветом – это фронтальная проекция линии пересечения поверхностей.

Аналогичные рассуждения проведём для нахождения горизонтальной проекции линии пересечения m₁. Она совпадает с главной проекцией цилиндраФ₁в пределах призмы.

Рис. 3-9

Алгоритмическая запись будет выглядеть следующим образом:

Ф  Г = m; 2 ГПЗ, 1 алгоритм.

1. m  Г, Г  П₂  m₂ = Г₂

2. m  ,   П₁  m₁ = ₁

Проанализируем, из чего состоит линия пересечения m. Как мы уже предполагали, это пространственная линия. Она состоит из двух плоских кривыхаиb(рис. 3-10, 3-11), получающихся от пересечения цилиндра двумя гранями призмы, которые на рис. 3-11 обозначены плоскостямии.

Плоскость (₂)— это горизонтальная плоскость уровня. Она параллельна окружности основания цилиндра, поэтому она пересечёт цилиндрФтоже по окружности. Тогда линияаесть дуга окружности, которая спроецируется наП₂в виде прямой (а₂), а наП₁— в натуральную величину, т.е. в виде дуги окружности (а₁).

Рис. 3-10

Плоскость (₂)— фронтально проецирующая и пересечёт цилиндрФпо эллипсу. Тогда линияbесть дуга эллипса, которая спроецируется наП₂в виде прямой (b₂), а наП₁— в виде дуги окружности (b₁).

Таким образом, линия пересечения двух заданных поверхностей есть пространственная линия, состоящая из двух плоских кривых — дуги окружности и дуги эллипса.

Рис. 3-11

Скорректируем алгоритм решения позиционных задач в 1 случае:

Проекции общего элемента на чертеже уже есть. Они совпадают с главными проекциями проецирующих фигур. Если совпадение только частичное, то находят границы общей части. Решение сводится к их нахождению и обозначению.

2 алгоритм.

Решение задач в случае, когда одна из пересекающихся фигур проецирующая, вторая — непроецирующая.

Решение 1 ГПЗ снова рассмотрим на конкретном примере.

Задача: Найти проекции точки пересечения плоскости общего положения(m  n)с фронтально проецирующей прямойа(рис. 3-12).

Рис. 3-12

Графическое условие этой задачи подобно условию 1 ГПЗ, показанному на рис. 3-7. Такая же фронтально проецирующая прямая апересекается с плоскостью(m  n). Только, в данной задаче плоскость — общего положения.

Алгоритм: Решение начинаем, как и в первом случае, с фронтальной проекции. Точно так же, фронтальная проекция точки пересеченияК₂совпадёт с фронтальной проекцией прямойа₂, так кака₂— точка (рис. 3-13).

Рис. 3-13

Горизонтальную проекцию точки пересечения К₁найти так однозначно, как в первом случае, уже невозможно. Поэтому будем находить её по признаку принадлежности плоскости. Точка принадлежит плоскости, если она принадлежит прямой, лежащей в этой плоскости. Возьмём в плоскостилюбую прямую, проходящую через точкуК₂, например,1₂2₂, найдём её горизонтальную проекцию1₁2₁(1m, 2n) и на этой прямой будет располагаться точкаК₁.

Следующим этапом необходимо определить видимость прямой а на горизонтальной проекции. Для этого воспользуемся методом конкурирующих точек(рис. 3-14).

Рис. 3-14

Так как плоскость имеет с прямойатолько одну общую точкуК, то прямыеmиа— скрещивающиеся, а точки3и4на них – горизонтально конкурирующие. Пусть точка3принадлежит прямойm(то есть плоскости), точка4принадлежит прямойа. Находим фронтальные проекции точек. Из чертежа рис. 3-14 видно, что точкаЗ₂расположена выше, чем точка4₂. Следовательно, на данном участке, начиная от точки пересеченияК₁, до прямойm₁прямаяа₁не видна.

Выполним краткую алгоритмическую запись решения:

(m  n)  a = K; 1 ГПЗ, 2 алгоритм

1. К  a , а  П₂  К₂ =а₂.

2. К₁  , К 12, 12    К₁ = а₁  1₁2₁.

Рассмотрим ещё одну задачу: Пересекаются прямая общего положения ас поверхностью горизонтально проецирующего цилиндраГ(рис. 3-15). Найти проекции точек пересечения.

Рис. 3-15

Решение:1 ГПЗ , 2 алг. Горизонтальная проекция цилиндра — окружностьГ₁, следовательно, в результате пересечения получаются 2 точкиМ иN, горизонтальные проекции которыхМ₁иN₁располагаются на пересеченииГ₁иа₁(рис. 3-16).

Рис. 3-16

Фронтальные проекции точек пересечения М₂иN₂находим по принадлежности прямойас использованием линии связи. Видимость наП₂определяем по цилиндру: точкаN₁расположенапередплоскостью фронтального меридианаФ, иN₂— видимая;М₁расположеназаплоскостью фронтального меридианаФ, иМ₂— невидимая. Часть прямойа между точкамиМиNнаходится внутри цилиндра, следовательно, наП₂участок прямой между точкамиМ₂иN₂невидимый. Участок прямой между точкойМ₂и очерковой образующей цилиндраl₂также невидим, так как находитсязаплоскостью фронтального меридиана. Алгоритмическая запись решения:

Г  а = М, N, 1 ГПЗ, 2 алгоритм.

1. М, N  Г, Г  П₁  M₁, N₁ = Г₁  а₁.

2. М, N  a  M₂ ,N₂  a₂.

Вывод: Решение задач по 2 алгоритму сводится к следующему:

1. Выделяют из двух заданных фигур проецирующую и отмечают её главную проекцию .

2. Ставят обозначение той проекции искомого общего элемента, которая совпадает с главной проекцией проецирующей фигуры. Если совпадение только частичное, то находят границы общей части.

3. Вторую проекцию общего элемента находят по условию его принадлежности непроецирующей фигуре.

4. Определяют видимость проекций общих элементов и пересекающихся фигур.

studfiles.net

ЛЕКЦИЯ 5 Позиционные задачи Позиционными задачами называют

ЛЕКЦИЯ 5 Позиционные задачи

Позиционными задачами называют такие, в которых определяется взаимное расположение геометрических фигур в пространстве Существует три типа позиционных задач: 1. Взаимный порядок геометрических фигур. 2. Взаимная принадлежность геометрических фигур. 3. Взаимное пересечение геометрических фигур.

Взаимное пересечение геометрических фигур Две геометрические фигуры, пересекаясь, дают общий элемент: • Прямая с прямой — точку (а b К). • Прямая с плоскостью — точку (а К). • Прямая с поверхностью — одну или несколько точек (а К, М. . . ). • Плоскость с плоскостью — прямую линию ( Г а). • Плоскость с поверхностью — плоскую кривую или плоскую ломаную ( m). • Поверхность с поверхностью — пространственную кривую или несколько пространственных кривых, которые, в свою очередь, могут состоять из плоских кривых или плоских ломаных ( m).

Из всего многообразия этих задач выделяются две общие задачи, которые называют главными позиционными задачами: • Первая главная позиционная задача (1 ГПЗ) — пересечение линии с поверхностью. • Вторая главная позиционная задача (2 ГПЗ) — взаимное пересечение двух поверхностей.

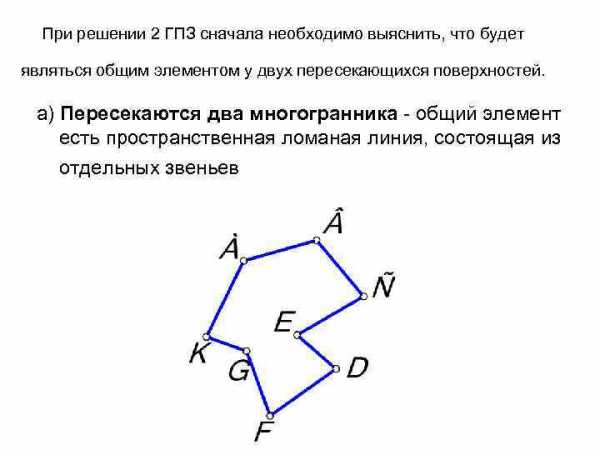При решении 2 ГПЗ сначала необходимо выяснить, что будет являться общим элементом у двух пересекающихся поверхностей. а) Пересекаются два многогранника — общий элемент есть пространственная ломаная линия, состоящая из отдельных звеньев

б) Пересекаются многогранник с кривой поверхностью (например, тор с пирамидой). Общий элемент пространственная кривая линия, состоящая из отдельных звеньев. в) Пересекаются две кривые поверхности (например, сфера с конусом). Общий элемент — пространственная кривая линия.

Далее необходимо определить количество общих элементов пересекающихся поверхностей. Определяется оно в зависимости от характера пересечения поверхностей.

Характер пересечения поверхностей

Такой характер пересечения, когда одна из поверхностей насквозь пронзает другую, называется чистое проницание. В этом случае линий пересечения две (на рис. это m и n).

Когда очерки поверхностей касаются в одной точке, является частным случаем проницания. Линий пересечения две (m и n), но с одной общей точкой (А).

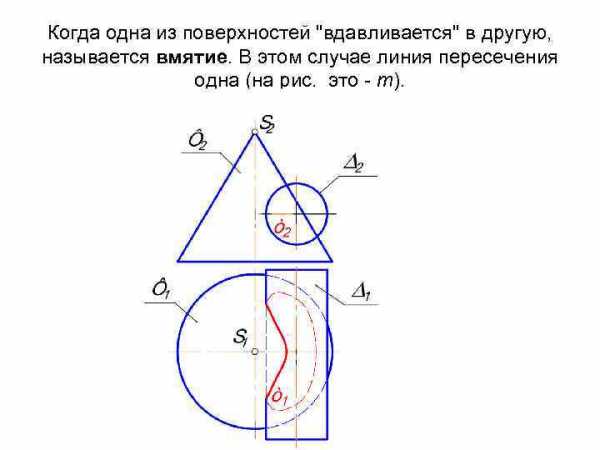Когда одна из поверхностей «вдавливается» в другую, называется вмятие. В этом случае линия пересечения одна (на рис. это — m).

Решение главных позиционных задач. 3 случая. 3 алгоритма. Здесь имеет место З случая: • обе пересекающиеся фигуры занимают проецирующее положение. Задачи решаются по первому алгоритму. • одна из пересекающихся фигур проецирующая, другая – непроецирующая. Задачи решаются по второму алгоритму. • обе пересекающиеся фигуры непроецирующие. Задачи решаются по третьему алгоритму.

Фигуры могут занимать проецирующее положение. Таковыми являются: прямая, плоскость, а из всех известных нам поверхностей проецирующее положение могут занимать только призматическая поверхность (частный случай — призма) и цилиндрическая поверхность (частный случай — прямой круговой цилиндр).

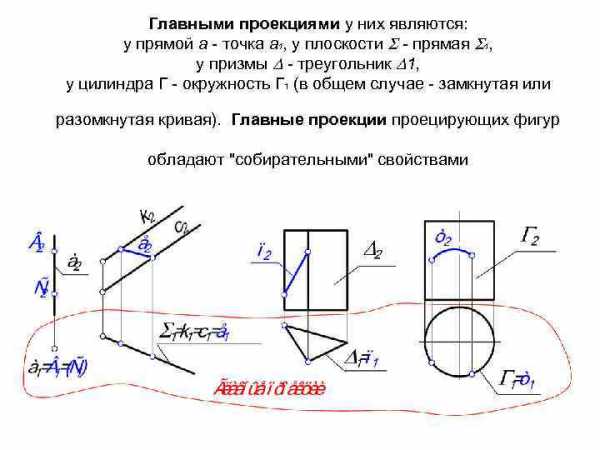Главными проекциями у них являются: у прямой а — точка а 1, у плоскости — прямая 1, у призмы — треугольник 1, у цилиндра Г — окружность Г 1 (в общем случае — замкнутая или разомкнутая кривая). Главные проекции проецирующих фигур обладают «собирательными» свойствами

Решение задач в случае, когда обе пересекающиеся фигуры занимают проецирующее положение. 1 алгоритм Задача : Найти проекции точки пересечения горизонтальнопроецирующей плоскости (m || n) с фронтально-проецирующей прямой а.

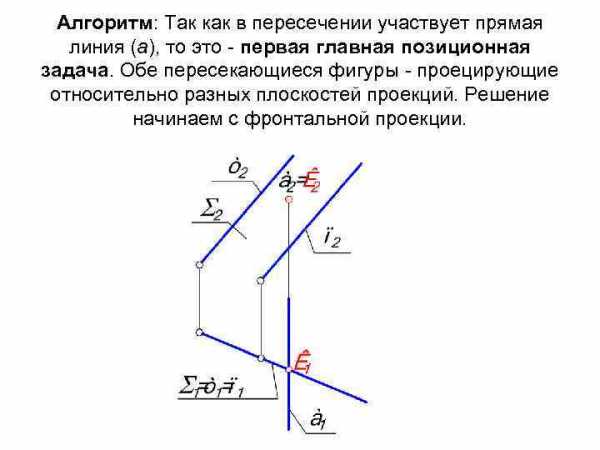Алгоритм: Так как в пересечении участвует прямая линия (а), то это — первая главная позиционная задача. Обе пересекающиеся фигуры — проецирующие относительно разных плоскостей проекций. Решение начинаем с фронтальной проекции.

Выполним краткую алгоритмическую запись вышеизложенного: (m || n) а = К; 1 ГПЗ, 1 алгоритм. 1. К а, а П 2 К 2 = а 2. 2. К а, К , П 1 К 1 = 1 а 1.

Таким образом, решение 1 ГПЗ по первому алгоритму заключается в следующем: Проекции общего элемента на чертеже уже присутствуют. Они совпадают с главными проекциями проецирующих фигур. Решение сводится к их нахождению и обозначению.

Вторую главную позиционную задачу решим в соответствии с рассмотренным алгоритмом. Задача: найти проекции линии пересечения горизонтально проецирующего цилиндра Ф с фронтально проецирующей призмой Г

Алгоритм: Пересекаются две поверхности, это — 2 ГПЗ. Вначале анализируем, что должно получиться в результате пересечения. Так как характер пересечения — вмятие, то общим элементом должна быть одна пространственная линия — m.

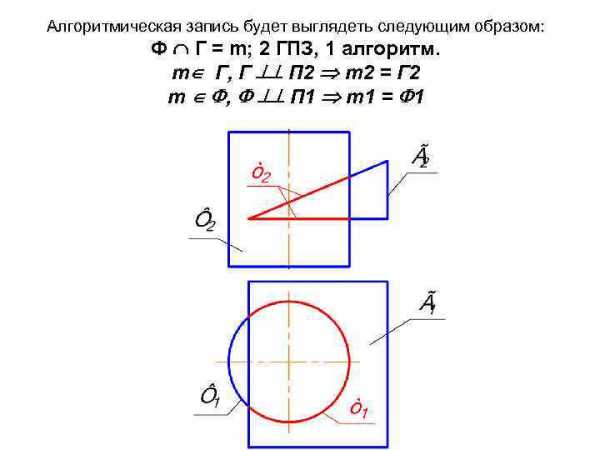Алгоритмическая запись будет выглядеть следующим образом: Ф Г = m; 2 ГПЗ, 1 алгоритм. m Г, Г П 2 m 2 = Г 2 m , П 1 m 1 = 1

Проанализируем, из чего состоит линия пересечения m. Как мы уже предполагали, это пространственная линия. Она состоит из двух плоских кривых а и b, получающихся от пересечения цилиндра двумя гранями призмы, которые на рис. обозначены плоскостями и .

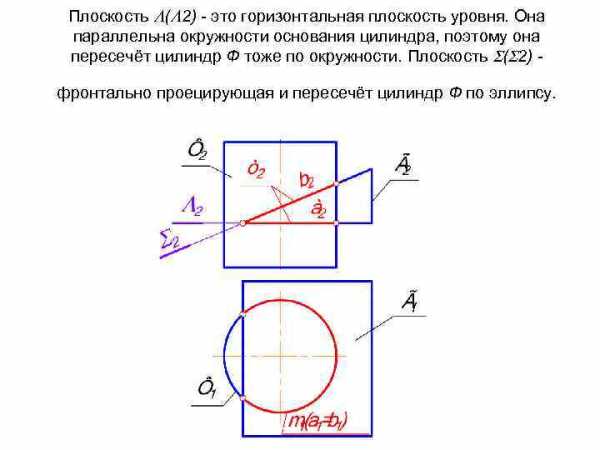Плоскость ( 2) — это горизонтальная плоскость уровня. Она параллельна окружности основания цилиндра, поэтому она пересечёт цилиндр Ф тоже по окружности. Плоскость ( 2) фронтально проецирующая и пересечёт цилиндр Ф по эллипсу.

• Проекции общего элемента на чертеже уже есть. Они совпадают с главными проекциями проецирующих фигур. Если совпадение только частичное, то находят границы общей части. Решение сводится к их нахождению и обозначению.

Решение задач в случае, когда одна из пересекающихся фигур проецирующая, вторая непроецирующая. 2 алгоритм

Задача: Найти проекции точки пересечения плоскости общего положения (m n) с фронтально проецирующей прямой а.

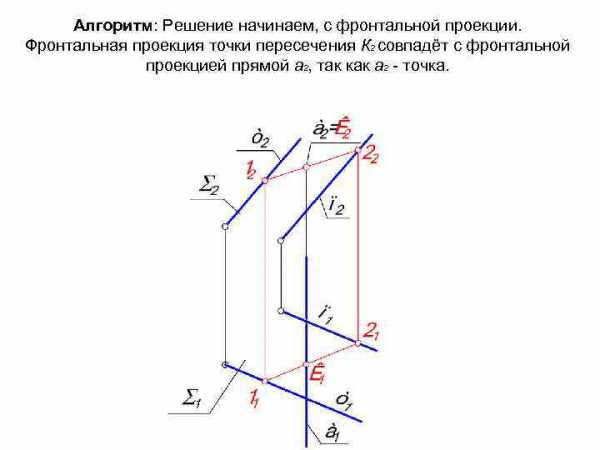Алгоритм: Решение начинаем, с фронтальной проекции. Фронтальная проекция точки пересечения К 2 совпадёт с фронтальной проекцией прямой а 2, так как а 2 — точка.

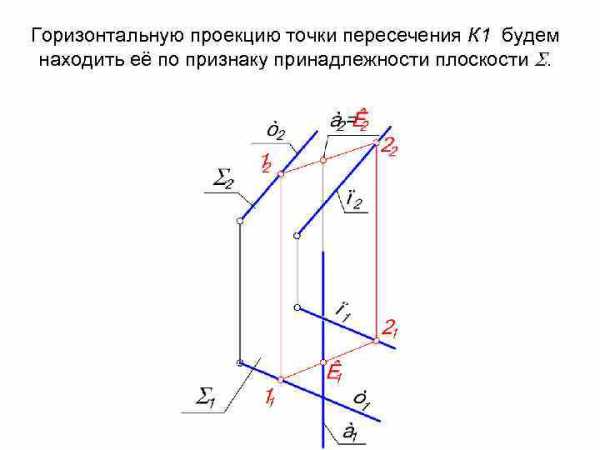Горизонтальную проекцию точки пересечения К 1 будем находить её по признаку принадлежности плоскости .

Следующим этапом необходимо определить видимость прямой а на горизонтальной проекции. Для этого воспользуемся методом конкурирующих точек.

Выполним краткую алгоритмическую запись решения: (m n) a = K; 1 ГПЗ, 2 алгоритм 1. К a , а П 2 К 2 =а 2. 2. К 1 , К 12, 12 К 1 = а 1121. 1

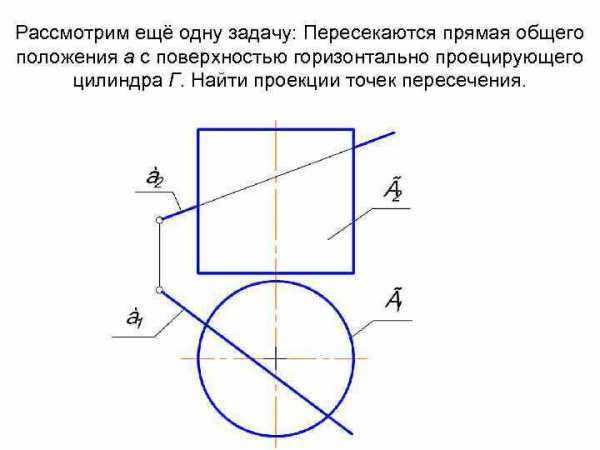Рассмотрим ещё одну задачу: Пересекаются прямая общего положения а с поверхностью горизонтально проецирующего цилиндра Г. Найти проекции точек пересечения.

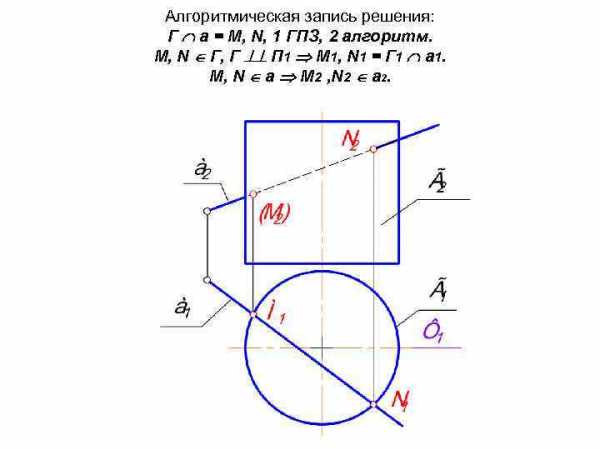Алгоритмическая запись решения: Г а = М, N, 1 ГПЗ, 2 алгоритм. М, N Г, Г П 1 M 1, N 1 = Г 1 а 1. М, N a M 2 , N 2 a 2.

Решение задач по 2 алгоритму сводится к следующему: • • Выделяют из двух заданных фигур проецирующую и отмечают её главную проекцию. Ставят обозначение той проекции искомого общего элемента, которая совпадает с главной проекцией проецирующей фигуры. Если совпадение только частичное, то находят границы общей части. Вторую проекцию общего элемента находят по условию его принадлежности непроецирующей фигуре. Определяют видимость проекций общих элементов и пересекающихся фигур.

Решение 2 ГПЗ по 2 алгоритму рассмотрим на примере конических сечений. При пересечении конуса различными плоскостями можно получить прямые линии, кривые второго порядка и, как вырожденный случай, точку.

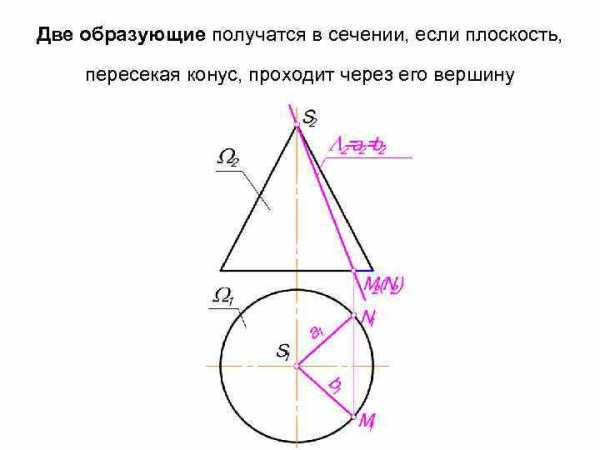Две образующие получатся в сечении, если плоскость, пересекая конус, проходит через его вершину

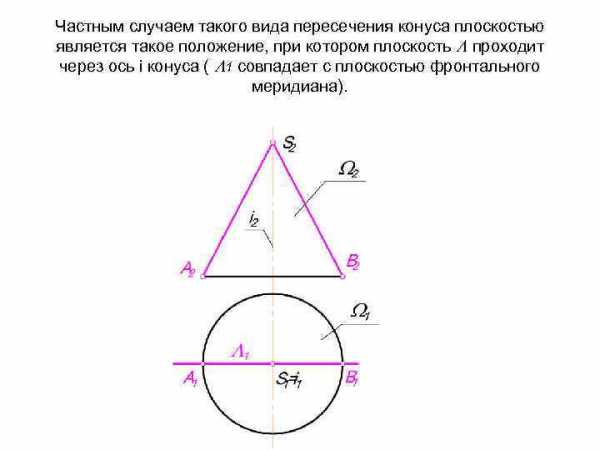Частным случаем такого вида пересечения конуса плоскостью является такое положение, при котором плоскость проходит через ось i конуса ( 1 совпадает с плоскостью фронтального меридиана).

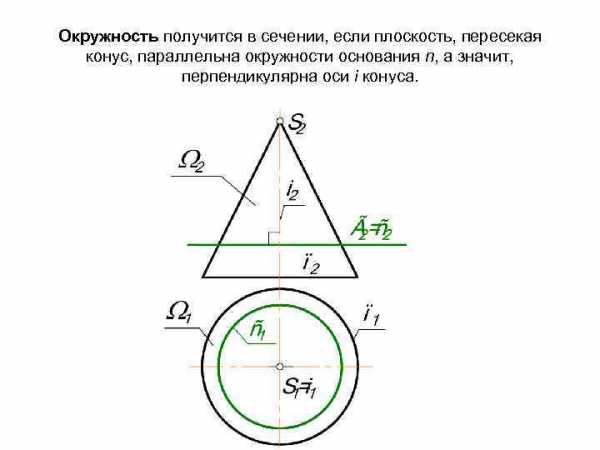Окружность получится в сечении, если плоскость, пересекая конус, параллельна окружности основания n, а значит, перпендикулярна оси i конуса.

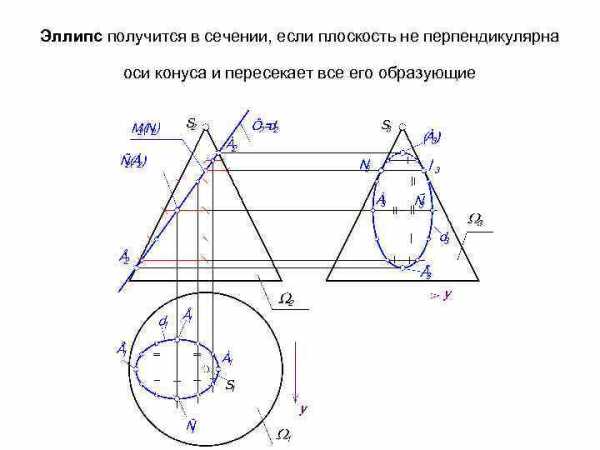Эллипс получится в сечении, если плоскость не перпендикулярна оси конуса и пересекает все его образующие

Парабола получится в сечении, если плоскость, пересекая конус, проходит параллельно только одной его образующей

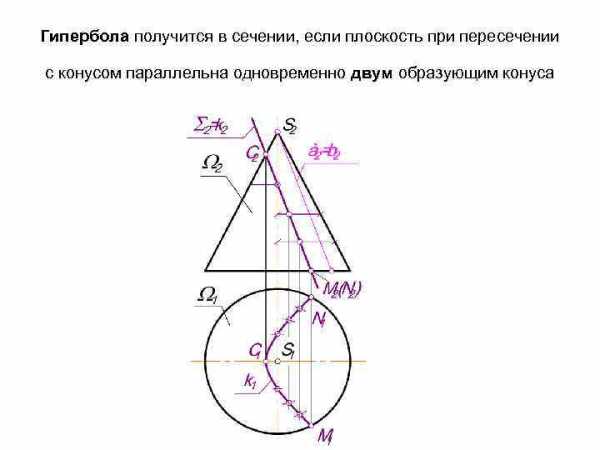Гипербола получится в сечении, если плоскость при пересечении с конусом параллельна одновременно двум образующим конуса

Рассмотрим ещё одну задачу на пересечение поверхностей, из которых одна проецирующая, вторая — непроецирующая. Задача: Построить линию пересечения сферы и горизонтально проецирующей призмы Г

Алгоритм: 2 ГПЗ, 2 алг. 1. Вначале определяем, что должно получиться в результате пересечения. Характер пересечения частный случай вмятия, с одной общей точкой. Призма — трёхгранная, значит можно рассматривать пересечение сферы тремя отдельными плоскостями: , и . Следовательно, линией пересечения является пространственная линия, состоящая из трёх плоских кривых второго порядка: двух дуг эллипсов ( = a, = b) и одной дуги окружности ( = с). 2. Поскольку поверхность призмы – горизонтально проецирующая, то горизонтальная линия пересечения совпадает с Г 1. 3. Фронтальную проекцию линии пересечения сферы с любой из плоскостей, например, Ф, строим по принадлежности сфере. a а 2 2.

Построения начинаем с характерных точек: 1, 2, 3, 4, 5, 6, 7. Промежуточные точки, находим по принадлежности параллелям сферы. Определяем видимости.

Построения начинаем с характерных точек: 1, 2, 3, 4, 5, 6, 7. Промежуточные точки, находим по принадлежности параллелям сферы. Определяем видимости.

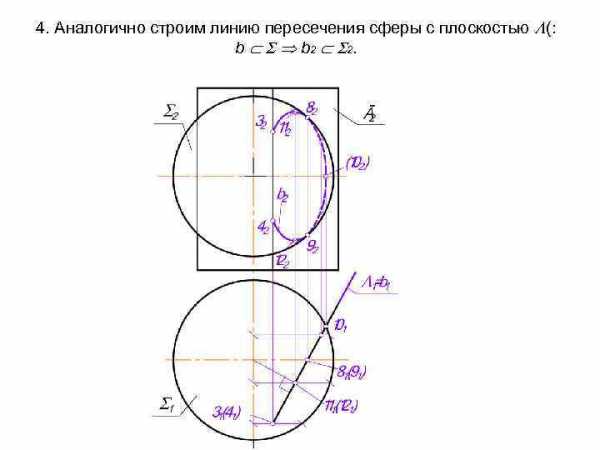4. Аналогично строим линию пересечения сферы с плоскостью (: b b 2 2.

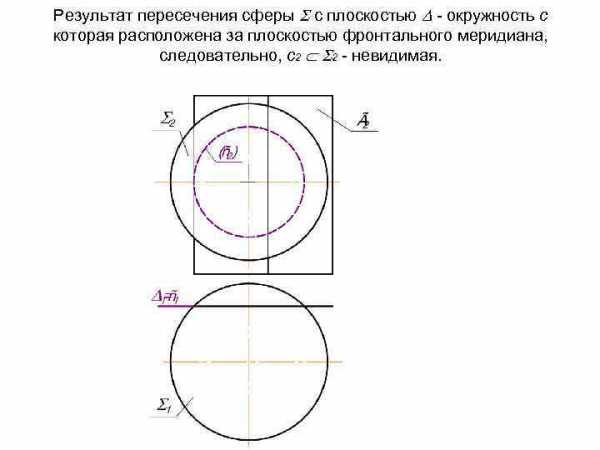Результат пересечения сферы с плоскостью — окружность с которая расположена за плоскостью фронтального меридиана, следовательно, с2 2 — невидимая.

Общий результат решения задачи с учётом видимости поверхностей:

Алгоритм: Г = а, b, с. Г П 1. 2 ГПЗ, 2 алгоритм. 1. Г П 1 а 1, b 1, с1 = Г 1. 2. а 2, b 2, с2 .

Решение задач в случае, когда обе пересекающиеся фигуры непроецирующие. 3 алгоритм

В данном случае задача усложняется тем, что на чертеже нет главной проекции ни у одной из пересекающихся фигур. Поэтому для решения таких задач специально вводят вспомогательную секущую поверхностьпосредник, которая пересекает обе фигуры, выявляя общие точки. Эта поверхность-посредник может быть проецирующей, и тогда решение задачи можно свести ко 2 алгоритму, или непроецирующей (например, сфера посредник). Решение первой и второй ГПЗ рассмотрим отдельно.

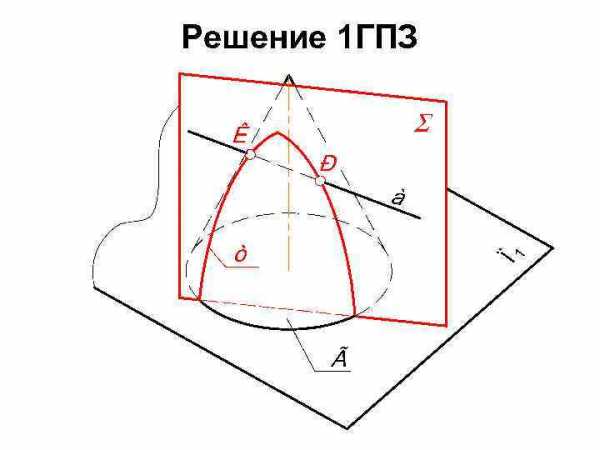Решение 1 ГПЗ

Задача: Найти точку пересечения плоскости Г(АВС) с прямой а. Определить видимость прямой

1 Алгоритм: Возьмём плоскость-посредник так, чтобы она включала в себя прямую а и была бы проецирующей, например, относительно П 1. Тогда 1 совпадёт с а 1

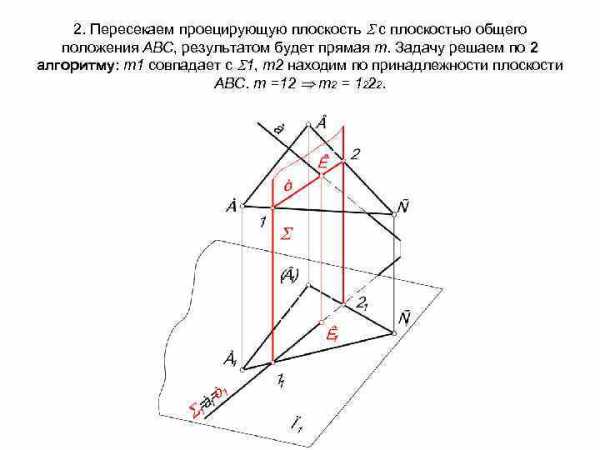2. Пересекаем проецирующую плоскость с плоскостью общего положения АВС, результатом будет прямая m. Задачу решаем по 2 алгоритму: m 1 совпадает с 1, m 2 находим по принадлежности плоскости АВС. m =12 m 2 = 1222.

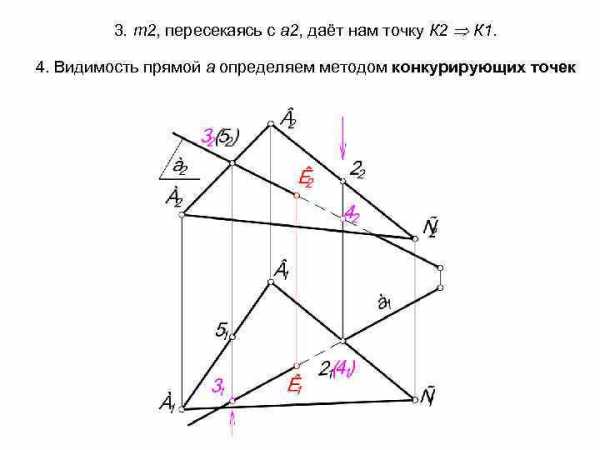3. m 2, пересекаясь с а 2, даёт нам точку К 2 К 1. 4. Видимость прямой а определяем методом конкурирующих точек

Выполним краткую алгоритмическую запись решения задачи: Г(АВС) а = К. 1 ГПЗ, 3 алгоритм. 1. — плоскость-посредник, 2. а, П 1 1= а 1; 2. Г = m. 2 ГПЗ, 2 алгоритм. П 1 m 1 = 1; m 2 Г m 2 а 2 = К 2 К 1.

Такой алгоритм решения приемлем для нахождения точек пересечения любой поверхности с прямой линией. Разница заключается в форме линии m, которая является результатом пересечения плоскостипосредника с заданной поверхностью и зависит от вида поверхности. В рассмотренном примере m — это прямая линия. Если вместо плоскости Г(АВС) возьмём, например, сферу, то линия m будет являться окружностью, которая может проецироваться на какую-либо плоскость проекций в виде эллипса, если с прямой пересекается многогранник, то m — это плоский многоугольник и т. д.

Задача: Найти точки пересечения пирамиды Г(SABC) с прямой а. Определить видимость прямой.

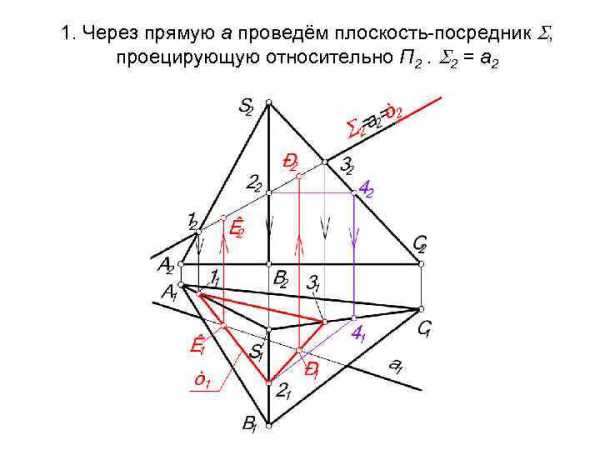1. Через прямую а проведём плоскость-посредник , проецирующую относительно П 2. 2 = а 2

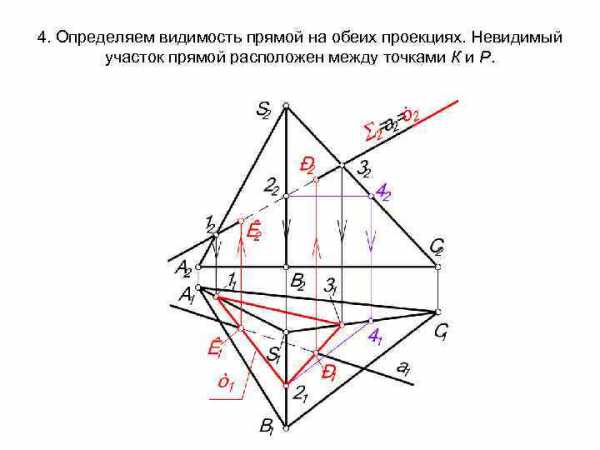4. Определяем видимость прямой на обеих проекциях. Невидимый участок прямой расположен между точками К и Р.

Алгоритм решения: Г(SABC) a = K , P. 1 ГПЗ, 3 алгоритм. 1. — плоскость-посредник, а, П 2 2 = a 2 2. Г = m(123). 2 ГПЗ, 2 алг. П 2 m 2(12, 22, 32) = 2; m 1(11, 21, 31) Г 3. m 1(11, 21, 31) а 1 = К 1, Р 1 К 2, Р 2.

Решение 2 ГПЗ (в случае пересечения непроецирующих фигур) Рассмотрим алгоритм решения на пространственной модели

Алгоритм решения 1. Ф = m; 2 ГПЗ, 3 алгоритм. 2. Отмечаем очевидные точки пересечения — М и Р. 3. Вводим плоскость-посредник (как правило проецирующую. ) 4. Ф = а; = b; 5. а b = K. 6. Для построения линии m нужно найти такое количество точек, которое определяет данную линию. Для этого вводим несколько плоскостейпосредников. 7. Определяем видимость линии пересечения m и поверхностей.

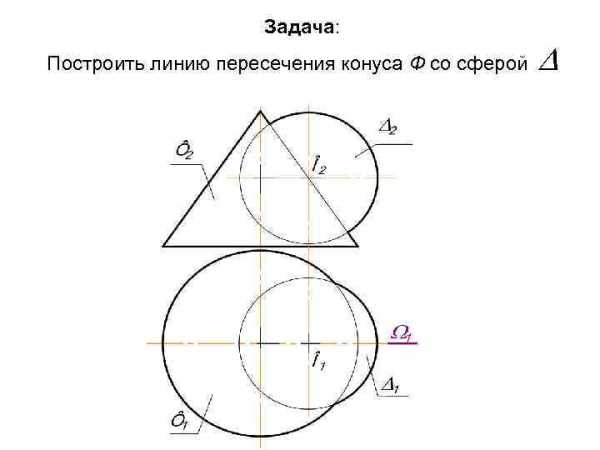Задача: Построить линию пересечения конуса Ф со сферой

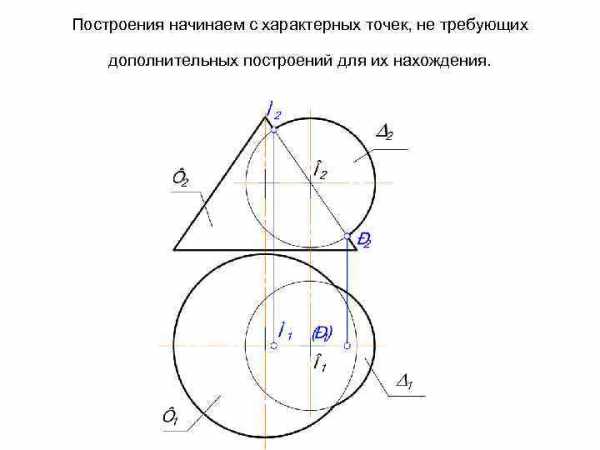Построения начинаем с характерных точек, не требующих дополнительных построений для их нахождения.

3. Все остальные точки находим одинаково: задаём плоскость-посредник .

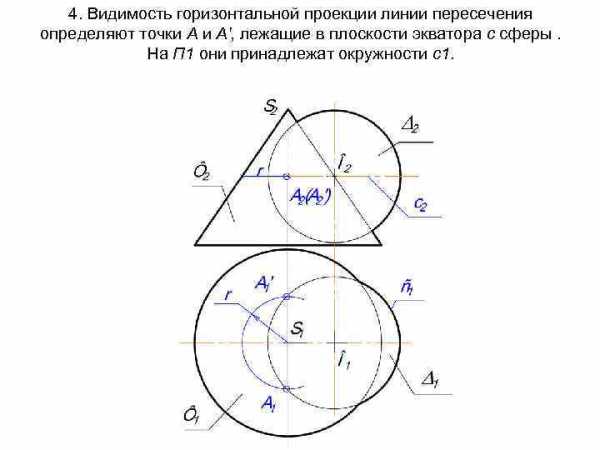4. Видимость горизонтальной проекции линии пересечения определяют точки А и А’, лежащие в плоскости экватора с сферы. На П 1 они принадлежат окружности с1.

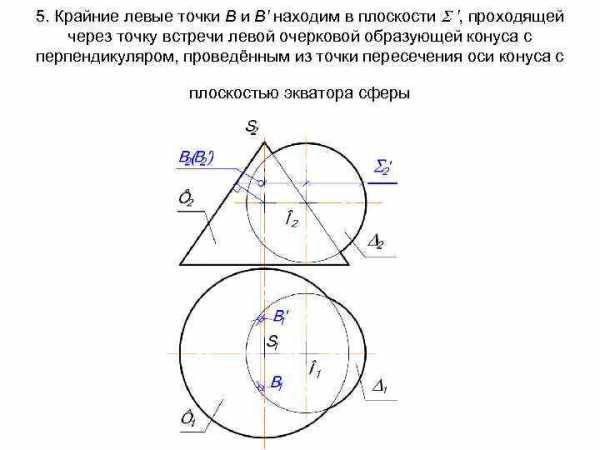5. Крайние левые точки В и В’ находим в плоскости ‘, проходящей через точку встречи левой очерковой образующей конуса с перпендикуляром, проведённым из точки пересечения оси конуса с плоскостью экватора сферы

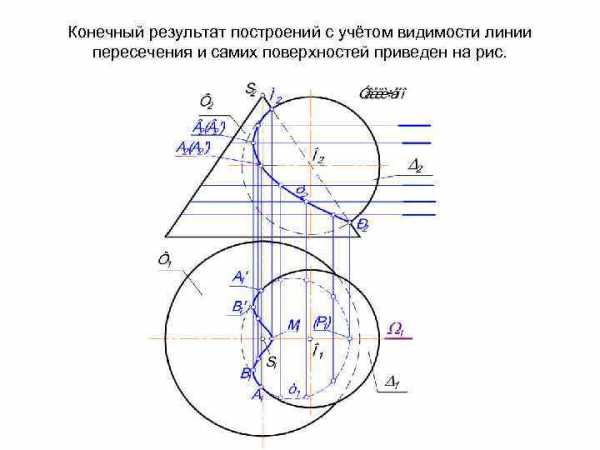Конечный результат построений с учётом видимости линии пересечения и самих поверхностей приведен на рис.

Алгоритмическая запись решения: Ф = m. 2 ГПЗ, 3 алгоритм. 1. Точки М и Р М 2; Р 2 М 1; Р 1. 2. — плоскость-посредник; П 1, 3. Ф = а а 1; = b b 1; b 1 a 1 = K 1; K 1′ K 2; K 2′. 4. Аналогично строим остальные точки: m 1 m 2. 5. Видимость m относительно П 1: точки А, А’ с.

Частные случаи пересечения поверхностей вращения второго порядка Пересечение соосных поверхностей вращения

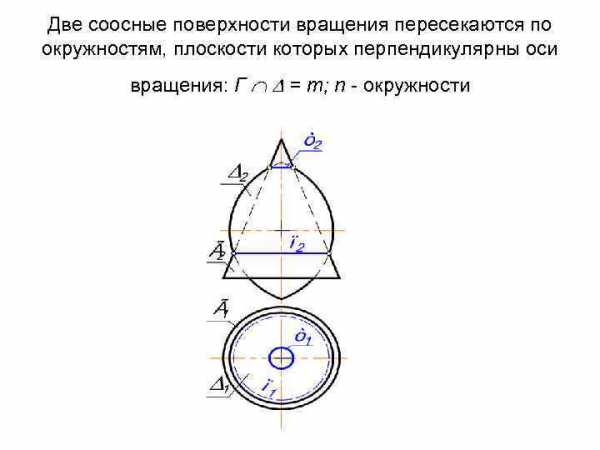Две соосные поверхности вращения пересекаются по окружностям, плоскости которых перпендикулярны оси вращения: Г = m; n — окружности

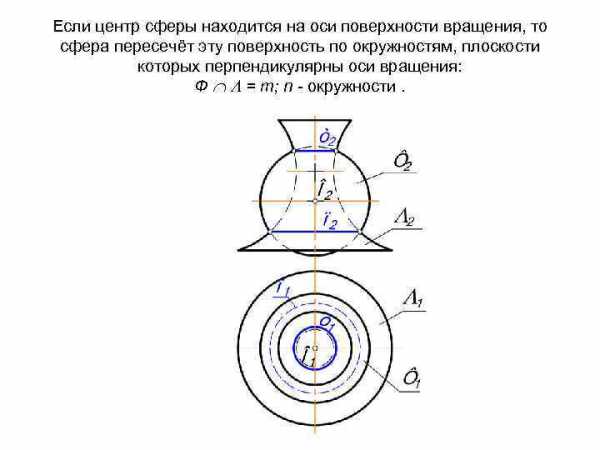Если центр сферы находится на оси поверхности вращения, то сфера пересечёт эту поверхность по окружностям, плоскости которых перпендикулярны оси вращения: Ф = m; n — окружности.

Теорема Монжа • Если две поверхности вращения второго порядка описаны около третьей поверхности вращения второго порядка, или вписаны в неё, то линия их пересечения распадается на две плоские кривые второго порядка. Причём, плоскости кривых проходят через прямую, соединяющую точки двойного соприкосновения.

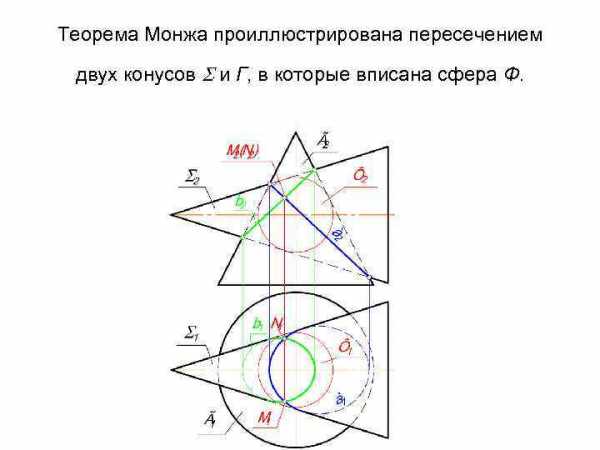Теорема Монжа проиллюстрирована пересечением двух конусов и Г, в которые вписана сфера Ф.

present5.com

23.Позиционные задачи. Две главные позиционные задачи.

1ГПЗ- задача на построение точек пересечения линий и поверхностей.

2ГПЗ- задача на построение линий пересечения поверхностей.

Решение обеих ГПЗ зависит от расположения ГО ( линий поверхности)

Относительно ПП.

Различают 3 случая:

— оба ГО проецирующие

Решать ничего не надо, проекции искомых геометрических элементов известны, их необходимо выделить и обозначить.

— один ГО проецирующий, второй общего положения.

В этом случае одна проекция искомого геометрического элемента известна, она принадлежит основной проекции проецирующего ГО. Вторую проекцию необходимо строить из условия принадлежности не проецирующего ГО.

— оба ГО общего положения

Алгоритм решения:

а)заключить прямую в проецирующую плоскость

б) построить линию пересечения это плоскости заданной (2ГПЗ2)

в) определить точки пересечения заданной прямой с построенной линией пересечения

г) определить видимость заданной прямой относительно заданной плоскости

24. Алгоритм решения главных позиционных задач, если пересекающиеся го занимают проецирущее положение.

1ГПЗ-1 и 2ГПЗ-1 решают по алгоритму: обе проекции точки пересечения (1ГПЗ) или линии пересечения (2ГПЗ) непосредственно заданы на чертеже; они принадлежат основным проекциям пересекающихся ГО ; решение задачи сводится к простановке соответствующих обозначений.

25. Алгоритм решения главных позиционных задач, если один из пересекающихся ГО занимает проецирующее положение.

Согласно алгоритму решения ГПЗ для 2-го случая известной яв-ся только одна проекция точки или линии пересечения, принадлежащая основной проекции проецирующего ГО , а вторая проекция точки или линии пересечения ищется из условия принадлежности их непроецирующему ГО.

26. Алгоритм решения 1-ой главной позиционной задачи, если пересекающиеся ГО не являются проецирующими.

а) заключить прямую в проецирующую плоскость

б) Построить линию пересечения заданной поверхности с этой плоскостью (2ГПЗ2)

в) определить точки пересечения заданной прямой с этой линией пересечения.

г) определить видимость прямой относительно заданной поверхности.

д)оформить чертеж.

27. Алгоритм решения задачи на пересечение прямой и плоскости общего положения.

1.Заключить прямую в проекционную плоскость.

2.Построить линию пресечения заданной поверхности с этой плоскостью.

3.Построить точки пересечения заданной прямой с построенной линией пересечения.

4.Определить видимость прямой относительно поверхности

5.оформить.

28. Алгоритм решения 2-ой главной позиционной задачи, если пересекающиеся ГО не являются проецирующими.

а) определить, какие поверхности заданы.

б) Определить, какая их поверхностей проецирующая, найти ее основную проекцию.

в) выделить и обозначить проекцию линии пересечения, принадлежащую основной прекции проецирующей поверхности.

г) Построить произвольно точку для второй проекции из условия ее принадлежности не проецирующей поверхности.

д) определить характерные точки (точки экстремальные- самая верхняя, нижняя, правая, левая…) (как ведет себя кривая пересечения) построить их.

е) построить необходимое количество точек по своему усмотрению.

ж) соединить построенные точки, обозначить проекцию линии пересечения.

з) Определить видимость линии пересечения и контуров пересекающих поверхностей.

и) оформить чертеж.

studfiles.net

Позиционные задачи

Графические работы, пронумерованная числами первой сотни (с 161 по 199), и графические работы, пронумерованная числами второй сотни (с 261 по 299), содержат по три задачи. Решение этих задач должно быть выполнено непосредственно на листах, содержащих условия задач (см. файл ЗАДАНИЕ). При этом условия задач должны быть формата А4. Обязательным требованием к копиям является максимально точное повторение графических условий оригинала. Все построения выполняются простым карандашом и сохраняются. Ответ задачи выделяется цветным карандашом. На каждом из листов в правом нижнем углу указывается фамилия студента и группа, в которой он числится.

Предоставляемые студентами работы не требуют текстовых пояснений. Однако для более глубокого понимания решений в приводимых примерах графические построения сопровождаются развернутыми пояснениями.

Примеры решения задач

Пример 1 (рис. 1.1).

Задача 1. Построить проекции линии пересечения двух плоскостей, заданных треугольниками АВС и DEF, соблюдая условия видимости.

Анализируя графические условия задачи, можно видеть, что и горизонтальная abc, и фронтальная a’b’c’ проекции треугольника АВС представляют треугольники. Следовательно, плоскость АВС – плоскость общего положения. Горизонтальная проекция треугольника DEF – треугольник def , но фронтальная проекция треугольника DEF – отрезок d’f’. Последнее обстоятельство позволяет придти к заключению: плоскость DEF перпендикулярна к фронтальной плоскости проекции (фронтально-проецирующая плоскость).

Рис. 1.1

Прямая, по которой пересекаются заданные плоскости, принадлежит обеим плоскостям, в частности, и плоскости DEF. Поэтому фронтальная проекция искомой прямой должна совпадать с фронтальной проекцией d’f’, в которую проецируется все множество точек плоскости DEF. Отсюда следует, что фронтальной проекцией линии пересечения мы уже располагаем, и остается достроить лишь ее горизонтальную проекцию.

Проекцию можно достроить по точкам М и N пересечения сторон треугольника АВС с плоскостью DEF: фронтальные проекции m’ и n’ очевидны, а горизонтальные проекции m и n располагаются на соответствующих проекциях сторон треугольника АВС.

Определение видимости значительно упрощается наличием фронтально-проецирующей плоскости. На фронтальной проекции треугольник АВС виден весь, за исключением линии пересечения. На горизонтальной проекции видна та часть треугольника АВС (треугольник АМN), которая выше плоскости DEF.

Задача 2. Построить проекции прямой, проходящей через точку С и пересекающей прямую АВ и ось проекций ОХ.

Ось проекции ОХ перпендикулярна к профильной плоскости проекций. После построения профильных проекций прямой АВ и точки С можно утверждать, что любая прямая, проходящая через точку С и пересекающая ось ОХ, должна иметь профильную проекцию, проходящую через точки c” и О. Такая прямая пересекает ось ОХ в некоторой точкеD, имеющей профильную проекцию d”. Если эта прямая пересекает прямую АВ, то точка e” – профильная проекция точки Е пересечения прямой АВ и прямой CD. Определив фронтальную e’ и горизонтальную e проекции, располагающиеся на соответствующих проекциях прямой АВ, получаем возможность построить недостающие проекции прямойED. Контролем точности графических построений может служить совпадение горизонтальной d и фронтальнойd проекций точкиD.

Задача 3. Построить проекции треугольника АВС, если сторона ВС лежит на прямой MN, параллельной плоскости Н, а сторона АС параллельна плоскости V. Основание D высоты AD делит сторону ВС в отношении BD : DC = 1 : 2.

Поскольку прямая MN параллельна горизонтальной плоскости проекций, то, в соответствии с теоремой о частном случае проецирования прямого угла, прямой угол на плоскость Н проецируется без искажения. Следовательно, перпендикуляр, опущенный из точки А на прямую MN , будет иметь горизонтальную проекцию ad mn, где d – горизонтальная проекция точки D, в которой перпендикуляр AD пересекает прямую MN.

Поскольку сторона АС параллельна плоскости V, то горизонтальная проекция стороны должна быть направлена параллельно оси ОХ, а в безосном чертеже – перпендикулярно к линии связи. Пересечение проведенной прямой с прямой MN позволяет найти точку С (проекции с и с’ ) — вторую вершину треугольника.

В соответствии с условием задачи, расстояние от точки D до вершины В вдвое меньше расстояния от точки D до точки С. Поэтому отрезок CD следует разделить пополам, и одну из его частей отложить на прямой MN. Если в пространстве точка делит отрезок в некотором отношении, то проекции точки делят проекции отрезка в том же отношении. Следовательно, для осуществления намеченных действий можно воспользоваться одной из проекций. На чертеже отрезок cd поделен пополам, найдена его середина 1 и отрезок 1d отложен на прямой mn, что позволило определить горизонтальную b, а затем и фронтальную b’ проекции вершины В. Конечно, для подобных построений можно было бы воспользоваться фронтальной проекцией, но это потребовало дополнительно построить фронтальную d’ проекцию точки D.

Пример 2 (рис. 1.2).

Задача 1. Достроить горизонтальную проекцию плоского четырехугольника ABCD.

Рис. 1.2

Построение недостающей проекции точки В следует основывать на признаке принадлежности точки плоскости: точка принадлежит плоскости, если она лежит на прямой, принадлежащей плоскости. Поэтому через точку В мысленно следует провести прямую, принадлежащую плоскости четырехугольника, построить проекции этой прямой и найти недостающую проекцию точки.

Для осуществления намеченного плана можно воспользоваться многими прямыми, проходящим через точку В, однако наиболее удобным представляется использование диагонали BD. Фронтальная проекция b’d’ очевидна, а для построения горизонтальной проекции следует вначале выяснить направление последней. Учитывая, что задан плоский четырехугольник, можно провести проекции диагонали АС. Диагонали четырехугольника пересекаются, точки 1’ и 1 соответственно фронтальная и горизонтальная проекции точки пересечения. Проведя прямую че-рез точки d и 1, выясним направление горизонтальной проекции диагонали, на которой располагается горизонтальная проекция b точки В. Остается завершить построение горизонтальной проекции четырехугольника.

Примечание. Если считать фронтальные проекции a’b’ и c’d’ сторон АВ и CD параллельными между собой, то, учитывая, что это – стороны плоского четырехугольника, занимающие общее положение относительно плоскостей проекций, следует заключить, что стороны АВ и CD параллельны в пространстве. Такие прямые должны иметь параллельные между собой горизонтальные проекции. Проведя из точки a прямую, параллельную cd, и определив точку b можно соединить ее с точкой с, завершив решение задачи.

Задача 2. Построить проекции прямой, проходящей через точку С и параллельную отрезку АВ.

Если прямые в пространстве параллельны, то параллельны их одноименные проекции. Однако судить по чертежу о взаимном положении прямых, занимающих частное положение относительно плоскостей проекций, можно только в том случае, если имеется проекция прямых на ту плоскость, которой прямые параллельны.

Прямая АВ – профильная прямая, поэтому для решения задачи необходимо располагать профильными проекциями прямой и точки С. Построив с помощью постоянной линии чертежа проекции a”b” и c”, следует через точку c” провести прямую, параллельную a”b”. Зафиксировав профильную проекцию d”, произвольно выбранной точки D, и учитывая, что [ab]  [cd], а [a’b’]  [c’d’] следует закончить построения.

Задача 3. Построить проекции равнобедренной трапеции ABCD, основание AD которой равно 40 мм, а основание ВС равно 80 мм и расположено на прямой MN, параллельной плоскости Н.

Рассмотрим вначале решение задачи при планометрическом задании условий (см. чертеж в правом верхнем углу). Если прямая MN и точка А располагаются в плоскости чертежа, то из точки А следует провести луч, параллельный прямой MN, и отложить на нем 40 мм. Конец этого отрезка – точка D. От оснований Е и F перпендикуляров, опущенных из точек А и D на прямую MN, следует отложить отрезки ВЕ и СF, равные 20 мм. Получим равнобедренную трапецию АВСD с основаниями АD = 40 мм и ВС = 80 мм.

Переходя к решению задачи на чертеже, отражающем пространственную ситуацию, следует учесть, что план решения, рассмотренный выше, не может измениться, но реализация этого плана должна учитывать закономерности проецирования отрезков прямых и углов между прямыми. Поскольку параллельные прямые изображаются параллельными одноименными проекциями, то из точек a и a’ можно провести лучи, параллельные соответственно (mn) и (m’n’). Прямая MN параллельна горизонтальной плоскости проекций, поэтому отрезки этой прямой, а также прямых ей параллельных, проецируются на плоскость Н без искажения. На луче из точки a следует отложить отрезок, равный 40 мм, конец которого даст проекцию d. В проекционной связи на луче из a’ находим проекцию d’.

Поскольку (MN) Н, то, по теореме о частном случае проецирования прямого угла, прямые углы в основании перпендикуляров, проведенных к этой прямой из точек А иD, должны на горизонтальную плоскость проекций проецироваться без искажения. Поэтому из точек a и d проводим перпендикуляры к (mn). От точек e и f откладываем отрезки be и cf, равные 20 мм. По горизонтальным проекциям b и c достраиваем проекции b’ и c’. Проведя проекции прямых АВ и СD, завершаем решение задачи.

studfiles.net