Возведение унимодулярной матрицы в степень. : Высшая алгебра
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Не ищите на этом форуме халяву, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения и указать конкретные затруднения.
Обязательно просмотрите тему Правила данного раздела, иначе Ваша тема может быть удалена или перемещена в Карантин, а Вы так и не узнаете, почему.
| |||
24/04/08 |
| ||
| |||
| Парджеттер |
| |||
07/10/07 |
| |||
| ||||
| bot |
| |||
21/12/05 |
| |||
| ||||
| Парджеттер |
| |||
07/10/07 |
| |||
| ||||
| Профессор Снэйп |
| |||
18/12/07 |
| |||
| ||||
| ||||
13/12/05 |
| |||
| ||||
| Парджеттер |
| |||
07/10/07 |
| |||
| ||||
| BapuK |
| ||
06/03/09 |
| ||
| |||
| Padawan |
| |||
13/12/05 |
| |||
| ||||
| ewert |
| |||
11/05/08 |
| |||
| ||||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 10 ] |
Модераторы: Модераторы Математики, Супермодераторы
Сообщество Экспонента
- Публикация
- 15.
 09.2022
09.2022
Системы управления, Другое
Видел видос на канале экспоненты по созданию топливной системы. Вопрос заключается в наличии более полного описания готового примера или соответсвующее документации. Я новичок в симулинке и ещё многого не знаю. Адекватных и раскрытых пособий по созданию гидрав…
Моделирование гидравлических систем в simulink
- Публикация
- 10.09.2022
Системы управления, Электропривод и силовая электроника, Другое
Планирую написать книгу про модельно-ориентированное программирование с автоматическим генерированием кода применительно к разработке разнообразных микропроцессорных систем управления электроприводов. В этой книге в научно-практическо-методической форме я план…
Планирую написать книгу про модельно-ориентированное программирование с автоматическим генерированием кода применительно к разработке разнообразных микропроцессорных систем управления электроприводов.
- Публикация
- 24.08.2022
Цифровая обработка сигналов, Системы связи, Математика и статистика
&…
Здесь собрана литература по комбинированным методам множественного доступа, в которых используется разделение пользователей в нескольких ресурсных пространствах.
- вопрос
- 23.08.2022
Математика и статистика, Радиолокация, Цифровая обработка сигналов
Есть записанный сигнал с датчика (синус с шумом). Как определить соотношение сигнал/шум?
Есть записанный сигнал с датчика (синус с шумом). Как определить соотношение сигнал/шум?
4 Ответа
- ЦОС
- цифровая обработка сигналов
23.08.2022
- Публикация
- 23.08.2022
Цифровая обработка сигналов, Системы связи, Математика и статистика
&. ..
..
Здесь соборана литература по методам множественного доступа с поляризационным разделением и разделением по орбитальном угловому моменту.
- Публикация
- 16.08.2022
Цифровая обработка сигналов, Системы связи, Математика и статистика
Здесь собрана литература по методам множественного доступа с пространственным разделением.
- вопрос
- 22.07.2022
Изображения и видео, Цифровая обработка сигналов, Математика и статистика, Биология, Встраиваемые системы, Глубокое и машинное обучение(ИИ), Автоматизация испытаний, ПЛИС и СнК, Системы управления, Другое
Здравствуйте. Мне нужно обработать большое количество файлов с похожими названиями, каждый блок файлов относится к отдельному объекту, например: file_1_1.txt file_1_2.txt file_1_3.txt file_1_4.txt fil…
Здравствуйте. Мне нужно обработать большое количество файлов с похожими названиями, каждый блок файлов относится к отдельному объекту, например:
file_1_1.txt
file_1_2.txt
file_1_3.txt
file_1_4.txt
fil…
Мне нужно обработать большое количество файлов с похожими названиями, каждый блок файлов относится к отдельному объекту, например:
file_1_1.txt
file_1_2.txt
file_1_3.txt
file_1_4.txt
fil…
2 Ответа
- чтение
22.07.2022
- вопрос
- 17.07.2022
Математика и статистика, Цифровая обработка сигналов
Уважаемые коллеги, добрый вечер! В общем, возникла проблема следующего характера. Имеется сигнал, достаточно большой объем точек, длительность порядка 35-40 секунд. Он представлят собой последовательн…
Уважаемые коллеги, добрый вечер! В общем, возникла проблема следующего характера. Имеется сигнал, достаточно большой объем точек, длительность порядка 35-40 секунд. Он представлят собой последовательн…
- MATLAB
- Signal Processing
17.07.2022
- вопрос
- 15.07.2022
Системы связи, Цифровая обработка сигналов
Здравствуйте! Сделала в симулинке модель сигнала с модуляцией QPSK. На входе сигнала подала последоватльномть с Генератора Бернули бинарного. Sample time: 1/8000. ПРи выводе сигнала на анализатор спек…
На входе сигнала подала последоватльномть с Генератора Бернули бинарного. Sample time: 1/8000. ПРи выводе сигнала на анализатор спек…
Здравствуйте! Сделала в симулинке модель сигнала с модуляцией QPSK. На входе сигнала подала последоватльномть с Генератора Бернули бинарного. Sample time: 1/8000. ПРи выводе сигнала на анализатор спек…
- сигнал
- модуляция
- qpsk
- скорость бита
- битрейт
- символьная скорость
- скорость передачи информации
- цифровая манипуляция
15.07.2022
- Публикация
- 13.07.2022
Цифровая обработка сигналов, Системы связи, Математика и статистика
&…
Здесь собрана литература по методам множественного доступа с кодовым разделением
Результаты поиска
Нет результатов поиска, попробуйте задать другие параметры.
Используем быстрое возведение матриц в степень для написания очень быстрого интерпретатора простого языка программирования / Хабр
Недавно на хабре появилась неплохая статья про вычисление N-ного числа фибоначи за O(log N) арифметических операций. Разумный вопрос, всплывший в комментариях, был: «зачем это может пригодиться на практике». Само по себе вычисление N-ого числа фибоначи может и не очень интересно, однако подход с матрицами, использованный в статье, на практике может применяться для гораздо более широкого круга задач.
В ходе этой статьи мы разберем как написать интерпретатор, который может выполнять простые операции (присвоение, сложение, вычитание и урезанное умножение) над ограниченным количеством переменных с вложенными циклами с произвольным количеством итераций за доли секунды (конечно, если промежуточные значения при вычислениях будут оставаться в разумных пределах). Например, вот такой код, поданный на вход интерпретатору:
loop 1000000000
loop 1000000000
loop 1000000000
a += 1
b += a
end
end
end
end
Незамедлительно выведет a = 1000000000000000000000000000, b = 500000000000000000000000000500000000000000000000000000, несмотря на то, что если бы программа выполнялась наивно, интерпретатору необходимо было бы выполнить октиллион операций.
Я полагаю, что у читателя есть представление о том, что такое матрица, и что такое произведение матриц. В рамках этой статьи мы будем использовать исключетельно квадратные матрицы и полагаться на очень важное свойство умножения квадратных матриц — ассоциативность.
Для простоты ограничим наш интерпретатор четырьмя переменными — A, B, C и D. Для представления состояния интерпретатора в заданный момент будем использовать вектор размера пять, первые четыре элемента которого будут содержать значения четырех переменных соответственно, а последний будет на протяжении всей работы интерпретатора равен единице.
(A, B, C, D, 1)
В начале работы интерпретатора будем полагать значения всех переменных равными нулю.
(0, 0, 0, 0, 1)
Допустим, что первая операция в коде программы содержит строку
A += 5
Эффект этой команды заключается в том, что значение переменной A увеличится на пять, в то время как значения остальных трех переменных не изменятся. Это можно претставить в виде следующей матрицы:
Это можно претставить в виде следующей матрицы:
1 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 1 0 5 0 0 0 1
Если посмотреть на нее, можно заметить, что она почти идентична единичной матрице (которая, как известно, при умножении любого вектора на нее не меняет его значения), за исключением последнего элемента в первом столбце, который равен пяти. Если вспомнить, как происходит умножение вектора на матрицу, можно понять, что значения всех элементов, кроме первого, не изменятся, в то время как значение первого элемента станет равно
v[0] * 1 + v[4] * 5
Так как v[0] содержит текущее значение в переменной A, а v[4] всегда равен единице, то
v[0] * 1 + v[4] * 5 = A + 5
Если вектор текущего состояния умножить на эту матрицу, полученный вектор будет соответствовать состоянию, в котором A на пять больше, что и требовалось.
Если матрицу поменять немного, убрав единицу в первом элементе первой строки:
0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 1 0 5 0 0 0 1
Как и прежде, значения всех элементов кроме первого не изменятся, в то время как первый элемент станет равным v[4] * 5, или просто пяти. Умножение вектора текущего состояния на такую матрицу эквивалентно выполнению команды
Умножение вектора текущего состояния на такую матрицу эквивалентно выполнению команды
A = 5
Посмотрим на такую матрицу:
1 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 1 0 1 0 0 0 0 0 1
Единственное отличие ее от единичной матрицы — это второй элемент в четвертой строке, который равен единице. Очевидно, что умножение вектора текущего состояния на эту матрицу не изменит значения в первом и последних трех элементах, в то время как значение второго элемента изменится на
v[1] * 1 + v[3] * 1
Так как v[1] содержит текущее значение переменной B, а v[3] содержит текущее значение переменной D, то умножение вектора состояния на такую матрицу эквивалентно выполнению команды B += D
Аналогично рассуждая можно понять, что умножение вектора состояния на следующую матрицу эквивалентно выполнению команды C *= 7
1 0 0 0 0 0 1 0 0 0 0 0 7 0 0 0 0 0 1 0 0 0 0 0 1
Перейдем к комбинированию команд. Пусть вектор v задает текущее состояние, матрица Ma соответствует команде A += 5, а матрица Mm соответствует команде A *= 7. 3
3
Мы вычисляем матрицу, соответствующую телу цикла, только один раз, после чего возводим ее в степень.
Рассмотренных примеров достаточно, чтобы начать работать над интерпретатором простого языка, поддерживающего присваивание, сложение, вычитание, умножение (только на константу) и циклы. Для этого мы научимся представлять любую такую программу в виде матрицы размера N+1 на N+1, где N — это количество переменных, которыми программа оперирует, после чего будем просто умножать вектор с начальным состоянием на эту матрицу.
Правила представления программы в виде матрицы очень просты:
1. Каждая отдельная команда представляется в виде матрицы, отличающейся от единичной одним элементом (или двумя для операции присваивания). Примеры таких матриц рассмотрены выше в этой статье.
2. Несколько подряд идущих команд представляются в виде матрицы, равной произведению матричного представления каждой отдельной команды.
3. Цикл представляется в виде матрицы, представляющей тело цикла, возведенной в степень количества итераций цикла.
Если у нас есть функция identity, возвращающая единичную матрицу:
def identity():
return [[1 if i == j else 0 for j in range(REGS + 1)] for i in range(REGS + 1)]То фукнция, строящая матрицу для команды r1 += r2 (где r1 и r2 — переменные) может выглядеть так:
def addreg(r1, r2):
ret = identity()
ret[r2][r1] = 1
return retА для команды r += val (r — переменная, val — константа) вот так:
def addval(r, val):
ret = identity()
ret[REGS][r] = val
return retФункции для построения матриц других команд выглядят похоже — получается единичная матрица, в которой заменяется один элемент.
Интерпретатор без циклов теперь пишется очень просто — пусть матрица mat соответствует уже прочитанному коду. В начале она равна единичной матрице, потому что пустая программа не меняет состояния. Затем мы считываем команды по одной, разбиваем их на три элемента (левый операнд, оператор, правый операнд), и в зависимости от оператора домножаем матрицу, соответствующую всей программе, на матрицу, соответствующую текущей команде:
def doit():
mat = identity()
while True:
line = sys. stdin.readline().lower()
tokens = line.split()
if tokens[0] == 'loop':
# тут будет код для циклов
elif tokens[0] == 'end':
return mat
else:
r1 = reg_names.index(tokens[0])
try:
r2 = reg_names.index(tokens[2])
except:
r2 = -1
if tokens[1] == '+=':
if r2 == -1: cur = addval(r1, long(tokens[2]))
else: cur = addreg(r1, r2)
elif tokens[1] == '-=':
....
mat = matmul(mat, cur)
stdin.readline().lower()
tokens = line.split()
if tokens[0] == 'loop':
# тут будет код для циклов
elif tokens[0] == 'end':
return mat
else:
r1 = reg_names.index(tokens[0])
try:
r2 = reg_names.index(tokens[2])
except:
r2 = -1
if tokens[1] == '+=':
if r2 == -1: cur = addval(r1, long(tokens[2]))
else: cur = addreg(r1, r2)
elif tokens[1] == '-=':
....
mat = matmul(mat, cur)Осталось дело за малым — добавить поддержку циклов. Цикл возводит матрицу тела цикла в степень количества итераций цикла. Возведение в степень, как известно, требует только O(log N) операций, где N — это степень, в которую матрица возводится. Алгоритм возведения в степень очень прост:
1. Если степень равна нулю, вернуть единичную матрицу.
2. Если степень четная, пусть 2N, то можно рекурсивно вычислить M^N, а затем вернуть квадрат получившейся матрицы. 2N, и вернуть полученную матрицу, умноженную на M.
2N, и вернуть полученную матрицу, умноженную на M.
Так как каждые две итерации степень сокращается в двое, сложность такого алгоритма логарифмическая.
def matpow(m, p):
if p == 0: return identity()
elif p % 2 == 0:
tmp = matpow(m, p / 2)
return matmul(tmp, tmp)
else: return matmul(m, matpow(m, p - 1))В интерпретаторе теперь осталось добавить одну строку:
...
if tokens[0] == 'loop':
cur = matpow(doit(), long(tokens[1]))
...И интерпретатор готов.
Пример интерпретатора доступен на гитхабе. Весь код занимает меньше 100 строк.
Для теста скорости можно вернуться к уже упомянутым числам фибоначи. Например, такой код:
A = 1 B = 1 loop 100 C = A C += B A = B B = C end end
Вычислит 101-ое и 102-ое числа фибоначи:
A = 573147844013817084101, B = 927372692193078999176
Замена 100 на 1000000 вычислит миллион первое и миллион второе числа за четыре секунды. Выполнение такой программы в лоб заняло бы гораздо больше, потому что программе приходится оперировать многотысячезначными числами. Если написать код, которому не приходится оперировать большими числами, например код для вычисления суммы арифметической прогрессии, приведенный в начале статьи, то количество итераций может уходить за рамки разумного, но код будет выполняться за доли секунды
Выполнение такой программы в лоб заняло бы гораздо больше, потому что программе приходится оперировать многотысячезначными числами. Если написать код, которому не приходится оперировать большими числами, например код для вычисления суммы арифметической прогрессии, приведенный в начале статьи, то количество итераций может уходить за рамки разумного, но код будет выполняться за доли секунды
loop 1000000000000000000000000000000000000000000000
loop 1000000000000000000000000000000000000000000000
loop 1000000000000000000000000000000000000000000000
a += 1
b += a
end
end
end
endНа практике этот подход может применяться, например, в оптимизирующих компиляторах, которые могут таким образом сворачивать циклы с большим количеством итераций, оперирующие на небольшом количестве переменных.
| A -1 = |
|
Другой алгоритм нахождения обратной матрицы
Приведем другую схему нахождения обратной матрицы.
- Находим определитель данной квадратной матрицы A .
- Находим алгебраические дополнения ко всем элементам матрицы A .
- Записываем алгебраические дополнения элементов строк в столбцы (транспонирование).
- Делим каждый элемент полученной матрицы на определитель матрицы A .
 T+7E$.
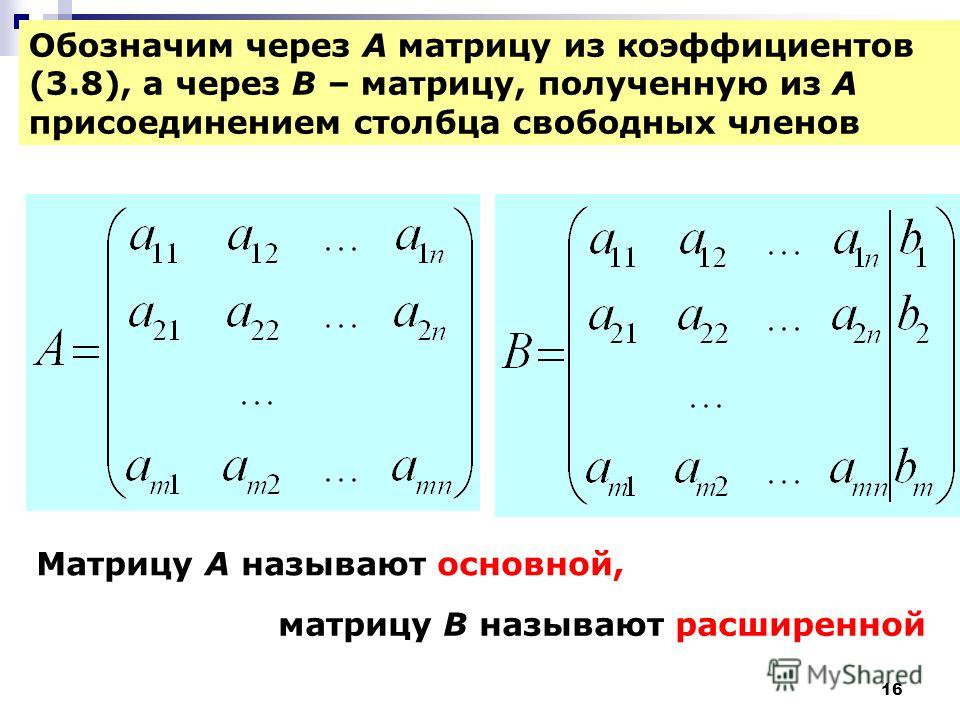
T+7E$.Вычисление матрицы $D$ начнем с нахождения результата произведения $AB$. Матрицы $A$ и $B$ можно перемножать, так как количество столбцов матрицы $A$ равно количеству строк матрицы $B$. Обозначим $F=AB$. При этом матрица $F$ будет иметь три столбца и три строки, т.е. будет квадратной (если этот вывод кажется неочевидным, посмотрите описание умножения матриц в первой части этой темы). Найдем матрицу $F$, вычислив все её элементы:
$$ F=A\cdot B=\left(\begin{array} {cccc} 1 & 0 & -1 & 2 \\ 3 & -2 & 5 & 0 \\ -1 & 4 & -3 & 6 \end{array} \right)\cdot \left(\begin{array} {ccc} -9 & 1 & 0 \\ 2 & -1 & 4 \\ 0 & -2 & 3 \\ 1 & 5 & 0 \end{array} \right)\\ \begin{aligned} & f_{11}=1\cdot (-9)+0\cdot 2+(-1)\cdot 0+2\cdot 1=-7; \\ & f_{12}=1\cdot 1+0\cdot (-1)+(-1)\cdot (-2)+2\cdot 5=13; \\ & f_{13}=1\cdot 0+0\cdot 4+(-1)\cdot 3+2\cdot 0=-3;\\ \\ & f_{21}=3\cdot (-9)+(-2)\cdot 2+5\cdot 0+0\cdot 1=-31;\\ & f_{22}=3\cdot 1+(-2)\cdot (-1)+5\cdot (-2)+0\cdot 5=-5;\\ & f_{23}=3\cdot 0+(-2)\cdot 4+5\cdot 3+0\cdot 0=7;\\ \\ & f_{31}=-1\cdot (-9)+4\cdot 2+(-3)\cdot 0+6\cdot 1=23; \\ & f_{32}=-1\cdot 1+4\cdot (-1)+(-3)\cdot (-2)+6\cdot 5=31;\\ & f_{33}=-1\cdot 0+4\cdot 4+(-3)\cdot 3+6\cdot 0=7.
 T+7E=2\cdot \left(\begin{array} {ccc}
-7 & 13 & -3 \\
-31 & -5 & 7 \\
23 & 31 & 7
\end{array} \right)-3\cdot \left(\begin{array} {ccc}
-5 & 10 & 3 \\
-20 & 12 & -15 \\
13 & 9 & 8
\end{array} \right)+7\cdot \left(\begin{array} {ccc}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array} \right)
$$
T+7E=2\cdot \left(\begin{array} {ccc}
-7 & 13 & -3 \\
-31 & -5 & 7 \\
23 & 31 & 7
\end{array} \right)-3\cdot \left(\begin{array} {ccc}
-5 & 10 & 3 \\
-20 & 12 & -15 \\
13 & 9 & 8
\end{array} \right)+7\cdot \left(\begin{array} {ccc}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array} \right)
$$Умножим матрицы в правой части равенства на соответствующие числа (т.е. на 2, 3 и 7):
$$ 2\cdot \left(\begin{array} {ccc} -7 & 13 & -3 \\ -31 & -5 & 7 \\ 23 & 31 & 7 \end{array} \right)-3\cdot \left(\begin{array} {ccc} -5 & 10 & 3 \\ -20 & 12 & -15 \\ 13 & 9 & 8 \end{array} \right)+7\cdot \left(\begin{array} {ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right)=\\= \left(\begin{array} {ccc} -14 & 26 & -6 \\ -62 & -10 & 14 \\ 46 & 62 & 14 \end{array} \right)-\left(\begin{array} {ccc} -15 & 13 & 9 \\ -60 & 36 & -45 \\ 39 & 27 & 24 \end{array} \right)+\left(\begin{array} {ccc} 7 & 0 & 0 \\ 0 & 7 & 0 \\ 0 & 0 & 7 \end{array} \right) $$
Выполним последние действия: вычитание и сложение:
$$ \left(\begin{array} {ccc} -14 & 26 & -6 \\ -62 & -10 & 14 \\ 46 & 62 & 14 \end{array} \right)-\left(\begin{array} {ccc} -15 & 30 & 9 \\ -60 & 36 & -45 \\ 39 & 27 & 24 \end{array} \right)+\left(\begin{array} {ccc} 7 & 0 & 0 \\ 0 & 7 & 0 \\ 0 & 0 & 7 \end{array} \right)=\\ =\left(\begin{array} {ccc} -14-(-15)+7 & 26-30+0 & -6-9+0 \\ -62-(-60)+0 & -10-36+7 & 14-(-45)+0 \\ 46-39+0 & 62-27+0 & 14-24+7 \end{array} \right)= \left(\begin{array} {ccc} 8 & -4 & -15 \\ -2 & -39 & 59 \\ 7 & 35 & -3 \end{array} \right).
 2+3A-9E=2A\cdot A+3A-9E=2 \left(\begin{array} {cc} -3 & 1 \\ 5 & 0 \end{array} \right)\cdot \left(\begin{array} {cc} -3 & 1 \\ 5 & 0 \end{array} \right)+3 \left(\begin{array} {cc} -3 & 1 \\ 5 & 0 \end{array} \right)-9\left(\begin{array} {cc} 1 & 0 \\ 0 & 1 \end{array} \right)=\\
=2 \left(\begin{array} {cc} (-3)\cdot(-3)+1\cdot 5 & (-3)\cdot 1+1\cdot 0 \\ 5\cdot(-3)+0\cdot 5 & 5\cdot 1+0\cdot 0 \end{array} \right)+3 \left(\begin{array} {cc} -3 & 1 \\ 5 & 0 \end{array} \right)-9\left(\begin{array} {cc} 1 & 0 \\ 0 & 1 \end{array} \right)=\\
=2 \left(\begin{array} {cc} 14 & -3 \\ -15 & 5 \end{array} \right)+3 \left(\begin{array} {cc} -3 & 1 \\ 5 & 0 \end{array} \right)-9\left(\begin{array} {cc} 1 & 0 \\ 0 & 1 \end{array} \right)
=\left(\begin{array} {cc} 28 & -6 \\ -30 & 10 \end{array} \right)+\left(\begin{array} {cc} -9 & 3 \\ 15 & 0 \end{array} \right)-\left(\begin{array} {cc} 9 & 0 \\ 0 & 9 \end{array} \right)=\left(\begin{array} {cc} 10 & -3 \\ -15 & 1 \end{array} \right).
2+3A-9E=2A\cdot A+3A-9E=2 \left(\begin{array} {cc} -3 & 1 \\ 5 & 0 \end{array} \right)\cdot \left(\begin{array} {cc} -3 & 1 \\ 5 & 0 \end{array} \right)+3 \left(\begin{array} {cc} -3 & 1 \\ 5 & 0 \end{array} \right)-9\left(\begin{array} {cc} 1 & 0 \\ 0 & 1 \end{array} \right)=\\
=2 \left(\begin{array} {cc} (-3)\cdot(-3)+1\cdot 5 & (-3)\cdot 1+1\cdot 0 \\ 5\cdot(-3)+0\cdot 5 & 5\cdot 1+0\cdot 0 \end{array} \right)+3 \left(\begin{array} {cc} -3 & 1 \\ 5 & 0 \end{array} \right)-9\left(\begin{array} {cc} 1 & 0 \\ 0 & 1 \end{array} \right)=\\
=2 \left(\begin{array} {cc} 14 & -3 \\ -15 & 5 \end{array} \right)+3 \left(\begin{array} {cc} -3 & 1 \\ 5 & 0 \end{array} \right)-9\left(\begin{array} {cc} 1 & 0 \\ 0 & 1 \end{array} \right)
=\left(\begin{array} {cc} 28 & -6 \\ -30 & 10 \end{array} \right)+\left(\begin{array} {cc} -9 & 3 \\ 15 & 0 \end{array} \right)-\left(\begin{array} {cc} 9 & 0 \\ 0 & 9 \end{array} \right)=\left(\begin{array} {cc} 10 & -3 \\ -15 & 1 \end{array} \right). $$
$$Ответ : $f(A)=\left(\begin{array} {cc} 10 & -3 \\ -15 & 1 \end{array} \right)$.
| A -1 = |
|
Другой алгоритм нахождения обратной матрицы
Приведем другую схему нахождения обратной матрицы.
- Находим определитель данной квадратной матрицы A .
- Находим алгебраические дополнения ко всем элементам матрицы A .
- Записываем алгебраические дополнения элементов строк в столбцы (транспонирование).
- Делим каждый элемент полученной матрицы на определитель матрицы A .
Как видим, операция транспонирования может применяться как в начале, над исходной матрицей, так и в конце, над полученными алгебраическими дополнениями.
Особый случай : Обратной, по отношению к единичной матрице E , является единичная матрица E .
Произведение двух матриц: формула, решения, свойства
- Произведение матриц: определение, формула, способ нахождения
- Примеры нахождения произведения матриц различной размерности
- Возведение матрицы в степень
- Свойства произведения матриц
- Калькулятор произведения матриц онлайн
Будут и задачи для самостоятельного решения, к которым можно
посмотреть ответы.
Определение. Произведением двух матриц А и В называется матрица С, элемент которой, находящийся на пересечении i-й строки и j-го столбца, равен сумме произведений элементов i-й строки матрицы А на соответствующие (по порядку) элементы j-го столбца матрицы В.
Из этого определения следует формула элемента матрицы C:
Произведение матрицы А на матрицу В обозначается АВ.
Пример 1. Найти произведение двух матриц А и B, если
,
.
Решение. Удобно нахождение произведения двух матриц А и В записывать так, как на рис.2:
На схеме серые стрелки показывают, элементы какой строки матрицы А на элементы
какого столбца матрицы В нужно перемножить для получения элементов матрицы С , а линиями цвета
элемента матрицы C соединены соответствующие элементы матриц A и B, произведения
которых складываются для получения элемента матрицы C.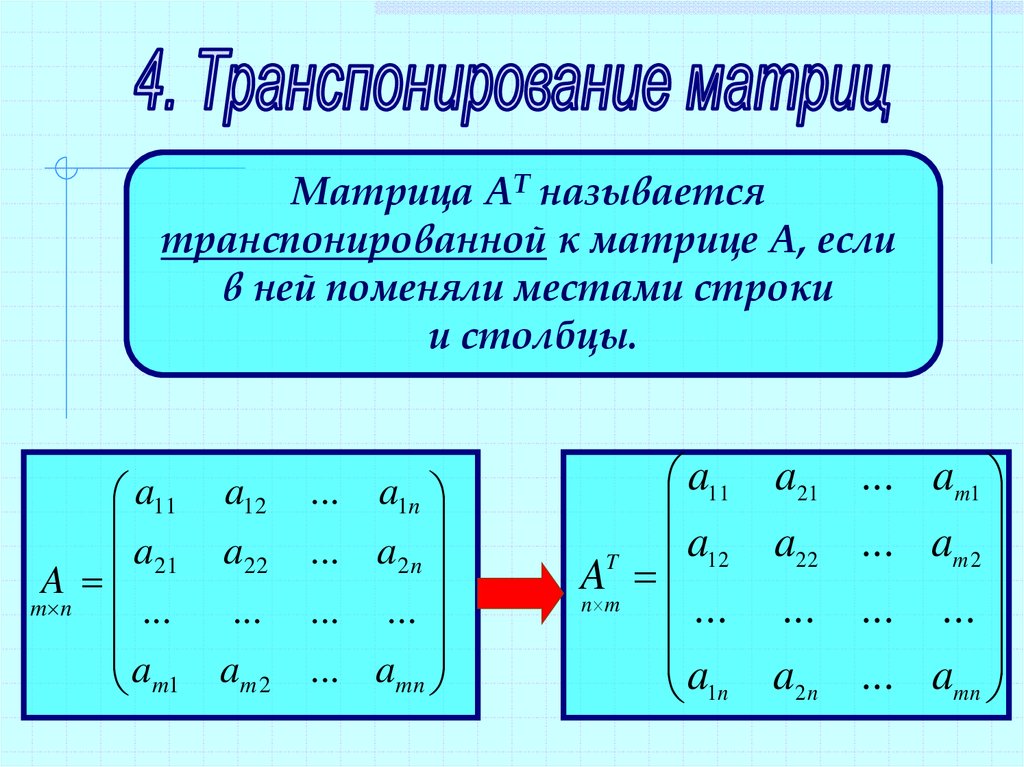
В результате получаем элементы произведения матриц:
Теперь у нас есть всё, чтобы записать произведение двух матриц:
.
Проверить решение этой и других подобных задач можно на калькуляторе произведения матриц онлайн.
Произведение двух матриц АВ имеет смысл только в том случае, когда число столбцов матрицы А совпадает с числом строк матрицы В .
Эту важную особенность будет легче запомнить, если почаще пользоваться следующими памятками:
Имеет место ещё одна важная особенность произведения матриц относительно числа строк и столбцов:
В произведении матриц АВ число строк равно числу строк матрицы А , а число столбцов равно числу столбцов матрицы В .
Пример 2. Найти число строк и столбцов матрицы C, которая является произведением двух матриц A и B следующих размерностей:
а) 2 Х 10 и 10 Х 5;
б) 10 Х 2 и 2 Х 5;
в) 4 Х 4 и 4 Х 10.
Решение:
а) 2 Х 5;
б) 10 Х 5;
в) 4 Х 10.
Пример 3. Найти произведение матриц A и B, если:
.
Решение. Число строк в матрице A — 2, число столбцов в матрице B — 2. Следовательно, размерность матрицы C = AB — 2 X 2.
Вычисляем элементы матрицы C = AB.
Найденное произведение матриц: .
Пример 4. Найти произведение матриц и .
Правильное решение и ответ.
Проверить решение этой и других подобных задач можно на калькуляторе произведения матриц онлайн.
Нет времени вникать в решение? Можно заказать работу!
К началу страницы
Пройти тест по теме Матрицы
Пример 5. Найти произведение матриц A и B, если:
.
Решение. Число строк в матрице A — 2, число столбцов в матрице B — 1. Следовательно, размерность матрицы C = AB — 2 X 1.
Вычисляем элементы матрицы C = AB.
Произведение матриц запишется в виде матрицы-столбца: .
Проверить решение этой и других подобных задач можно на калькуляторе произведения матриц онлайн.
Пример 6. Найти произведение матриц A и B, если:
.
Решение.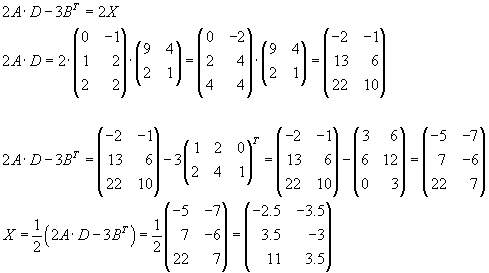 Число строк в матрице A — 3, число столбцов в матрице B — 3.
Следовательно, размерность матрицы C = AB — 3 X 3.
Число строк в матрице A — 3, число столбцов в матрице B — 3.
Следовательно, размерность матрицы C = AB — 3 X 3.
Вычисляем элементы матрицы C = AB.
Найденное произведение матриц: .
Проверить решение этой и других подобных задач можно на калькуляторе произведения матриц онлайн.
Пример 7. Найти произведение матриц A и B, если:
.
Решение. Число строк в матрице A — 1, число столбцов в матрице B — 1. Следовательно, размерность матрицы C = AB — 1 X 1.
Вычисляем элемент матрицы C = AB.
Произведение матриц является матрицей из одного элемента: .
Проверить решение этой и других подобных задач можно на калькуляторе произведения
матриц онлайн.
Программная реализация произведения двух матриц на С++ разобрана в соответствующей статье в блоке «Компьютеры и программирование».
Возведение матрицы в степень определяется как умножение матрицы на ту же самую матрицу. Так как произведение матриц существует только тогда, когда число столбцов первой матрицы совпадает с числом строк второй матрицы, то возводить в степень можно только квадратные матрицы. n-ая степень матрицы путём умножения матрицы на саму себя n раз:
Пример 8. Дана матрица . Найти A² и A³.
Решение:
Найти произведение матриц самостоятельно, а затем посмотреть решение
Пример 9. Дана матрица
Найти произведение данной матрицы и транспонированной матрицы ,
произведение транспонированной матрицы и
данной матрицы.
Правильное решение и ответ.
Свойство 1. Произведение любой матрицы А на единичную матрицу Е соответствующего порядка как справа, так и слева, совпадает с матрицей А , т.е. АЕ = ЕА = А .
Иными словами, роль единичной матрицы при умножении матриц такая же, как и единицы при умножении чисел.
Пример 10. Убедиться в справедливости свойства 1, найдя произведения матрицы
на единичную матрицу справа и слева.
Решение. Так как матрица А содержит три столбца, то требуется найти произведение АЕ , где
—
единичная матрица третьего порядка. Найдём элементы произведения С = АЕ :
Получается, что АЕ = А .
Теперь найдём произведение ЕА , где Е – единичная матрица второго порядка, так как матрица А содержит две строки. Найдём элементы произведения С = ЕА :
Доказано: ЕА = А .
Проверить решение этой и других подобных задач можно на калькуляторе произведения матриц онлайн.
Свойство 2. Произведение матрицы А на нуль-матрицу является нуль-матрицей. Это свойство очевидно, так как все элементы нуль-матрицы равны нулю.
Свойство 3. Произведение матриц некоммутативно:
.
Для этого достаточно показать, что равенство АВ = ВА не выполняется для каких-либо двух матриц.
Пример 11. Найти произведения матриц АВ и ВА, если
,
,
и убедиться в том, что эти произведения не равны друг другу:
.
Решение. Находим:
И действительно, найденные произведения не равны:
.
Проверить решение этой и других подобных задач можно на калькуляторе произведения матриц онлайн.
Свойство 4. Произведение матриц ассоциативно: (АВ)С = А(ВС) .
Свойство 5. Для произведения матриц выполняется дистрибутивный закон: (А + В) С = АС + ВС , С (А + В) = СА + СВ .
Свойство 6. Определитель произведения двух квадратных матриц равен произведению их определителей: если С = АВ , то
.
| Назад | Листать | Вперёд>>> |
Нет времени вникать в решение? Можно заказать работу!
К началу страницы
Пройти тест по теме Матрицы
Поделиться с друзьями
Начало темы «Матрицы»
Понятие матрицы
Продолжение темы «Матрицы»
Обратная матрица
Умножение матрицы на число
Сложение матриц
Найти ранг матрицы: способы и примеры
Решение матричных уравнений
Другие темы линейной алгебры
Определители
Системы линейных уравнений
N)Поиск инструмента
Найдите инструмент в dCode по ключевым словам:Просмотрите полный список инструментов dCode
Matrix Power
Инструмент для вычисления экспоненциальной матрицы в алгебре. Мощность матрицы заключается в возведении матрицы в степень (умножении на себя).
Мощность матрицы заключается в возведении матрицы в степень (умножении на себя).
Результаты
Matrix Power — dCode
Метки: Matrix
Поделиться
dCode и многое другое
dCode бесплатен, а его инструменты являются ценным помощником в играх, математике, геокэшинге, головоломках и задачах для решения любых задач. день! 92 = \begin{bmatrix} 1 и 2 \\ 3 и 4 \end{bmatrix} \times \begin{bmatrix} 1 и 2 \\ 3 и 4 \end{bmatrix} = \begin{bmatrix} 7 и 10 \ \ 15 & 22 \end{bmatrix} $$
Размер полученной матрицы идентичен исходной матрице M; т.е. $m$ строк и $m$ столбцов.
Вычисление степени матрицы работает только для квадратных матриц (2×2, 3×3, 4×4, 5×5 и т. д. из-за ограничений с умножением»> матричных произведений) и используется для некоторых матриц, таких как стохастические матрицы. 9к $.
Исходный код
dCode сохраняет право собственности на исходный код Matrix Power. За исключением явной лицензии с открытым исходным кодом (указано Creative Commons/бесплатно), алгоритма «Matrix Power», апплета или фрагмента (конвертер, решатель, шифрование/дешифрование, кодирование/декодирование, шифрование/дешифрование, транслятор) или «Matrix Power» функции (вычисление, преобразование, решение, расшифровка/шифрование, расшифровка/шифрование, декодирование/кодирование, перевод), написанные на любом информационном языке (Python, Java, PHP, C#, Javascript, Matlab и т. д.) и загрузка всех данных, скрипт, или доступ к API для «Matrix Power» не является общедоступным, то же самое для автономного использования на ПК, мобильных устройствах, планшетах, iPhone или в приложениях для Android!
д.) и загрузка всех данных, скрипт, или доступ к API для «Matrix Power» не является общедоступным, то же самое для автономного использования на ПК, мобильных устройствах, планшетах, iPhone или в приложениях для Android!
Напоминание: dCode можно использовать бесплатно.
Cite dCode
Копирование и вставка страницы «Matrix Power» или любых ее результатов разрешено, если вы цитируете dCode!
Ссылка на источник (библиография):
Matrix Power на dCode.fr [онлайн-сайт], получено 18 сентября 2022 г., https://www.dcode.fr/matrix-power
Сводка
- Сила матрицы
- Что такое сила матрицы? (Определение)
- Как рассчитать мощность матрицы n?
- Зачем диагонализовать матрицу перед вычислением ее мощности?
- Как вычислить отрицательную степень матрицы?
- Как вычислить корень матрицы?
- Как вычислить нецелую степень матрицы?
Similar pages
- Matrix Product
- Matrix Calculator
- Eigenvectors of a Matrix
- Vector Norm
- Complex Conjugate Matrix
- Inverse of a Matrix
- Transpose of a Matrix
- DCODE’S TOOLS LIST
Support
- Paypal
- Patreon
- More
Forum/Help
Keywords
power,exponent,square,matrix
Links
▲
матриц — Как вычислить квадратную матрицу в степени n?
спросил
Изменено 1 месяц назад 9n$ используя обычный матричный экспоненциальный трюк, чтобы сделать это быстро?
Редактировать 1 Также есть еще одно свойство матрицы A, заключающееся в том, что ее диагонали всегда состоят из 0 и других элементов либо из 0, либо из 1. n$ на $P(x)$, характеристический многочлен, чтобы получить остаток $R(x)$, степень которого меньше $ к$. 9n = P(A)Q(A)+R(A) = R(A)$, где R(A) легко найти.
n$ на $P(x)$, характеристический многочлен, чтобы получить остаток $R(x)$, степень которого меньше $ к$. 9n = P(A)Q(A)+R(A) = R(A)$, где R(A) легко найти.
Например, если $n=100$ и $k=3$, то $R(x)$ — полином второй степени.
$\endgroup$
1
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя адрес электронной почты и пароль
Опубликовать как гость
Электронная почта
Обязательно, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Объяснение урока: Сила матрицы
В этом объяснении мы узнаем, как использовать умножение матриц для определить квадрат и куб квадратной матрицы.
Существует множество матричных операций, очень похожих на известные операции из обычной алгебры, такие как сложение, вычитание и масштабирование. Кроме того, хотя умножение матриц принципиально более сложный, чем его обычный аналог, он все же в некоторой степени отражает некоторые алгебраические свойства оригинала.
Одна операция, которая занимает центральное место как в традиционной алгебре, так и в алгебре с использованием
матрицы — это возведение в степень, которое обычно называют взятием степень числа или матрицы. В
обычная алгебра, можно взять почти любое число 𝑥
и возводим в степень 𝑦, что дает 𝑥. За исключением возведения нуля в отрицательную степень, это не имеет значения.
является ли 𝑥 или 𝑦 нулем, отличным от нуля, целым числом,
нецелое, рациональное, иррациональное или сложное, так как вывод всегда может быть
вычислено. То же самое неверно при работе с матрицами, где матрица
𝐴 не всегда можно возводить в степень. Для того, чтобы лучше всего обрисовать
эти потенциальные осложнения, давайте сначала определим простейшую форму
возведение матрицы в степень: возведение матрицы в квадрат.
То же самое неверно при работе с матрицами, где матрица
𝐴 не всегда можно возводить в степень. Для того, чтобы лучше всего обрисовать
эти потенциальные осложнения, давайте сначала определим простейшую форму
возведение матрицы в степень: возведение матрицы в квадрат.
Определение: Квадрат матрицы
Если 𝐴 — квадратная матрица, 𝐴 определяется как 𝐴=𝐴×𝐴.
Другими словами, точно так же, как для возведения чисел в степень (т. е. 𝑎=𝑎×𝑎), квадрат получается умножением Матрица сама по себе.
Как можно заметить, основное требование для возведения матрицы в степень:
определено, что 𝐴 должен быть квадратным. Это потому, что на двоих
общие матрицы 𝐴 и 𝐵, матрица
умножение 𝐴𝐵 корректно определено только при одинаковом количестве столбцов
в 𝐴, так как в 𝐵 есть строки. Если
𝐴 имеет порядок 𝑚×𝑛 и
𝐵 имеет порядок 𝑛×𝑝, то
𝐴𝐵 корректно определен и имеет порядок 𝑚×𝑛. Если бы мы только рассмотрели матрицу 𝐴 и попытались завершить
умножение матриц 𝐴=𝐴×𝐴, то мы были бы
пытаясь умножить матрицу порядка 𝑚×𝑛 на
другая матрица порядка 𝑚×𝑛. Это может быть только хорошо
определяется, если 𝑚=𝑛, а это означает, что 𝐴 должно быть
матрица порядка 𝑛×𝑛 (другими словами, квадратная).
поэтому порядок 𝐴 идентичен исходной матрице
𝐴.
Это может быть только хорошо
определяется, если 𝑚=𝑛, а это означает, что 𝐴 должно быть
матрица порядка 𝑛×𝑛 (другими словами, квадратная).
поэтому порядок 𝐴 идентичен исходной матрице
𝐴.
Существуют и другие ограничения на взятие степеней матриц, которые не существуют для действительных чисел. Например, в отличие от обычных чисел, у нас нет способ определения того, что такое 𝐴, и отрицательная сила матрицу вычислить намного сложнее. Кроме того, обычные законы возведение в степень не обязательно распространяется на матрицы так же, как они делают это для чисел, которые мы рассмотрим позже в этом объяснении.
А пока давайте продемонстрируем, как возведение матрицы в квадрат работает на простом, нетривиальном кейс. Определим матрицу 𝐴=1−325.
Чтобы вычислить матрицу 𝐴, мы умножаем матрицу 𝐴 само собой. Другими словами, мы имеем 𝐴=𝐴×𝐴=1−3251−325.
Как и ожидалось, это умножение корректно определено, так как у нас есть
Матрица 2×2, умноженная на матрицу 2×2
матрица. Теперь осталось завершить умножение матриц, что мы и можем сделать
для каждой записи (𝑖,𝑗) путем умножения элементов
в строке 𝑖 левой матрицы элементами столбца
𝑗 правой матрицы и суммируя их. Мы демонстрируем это
процесс ниже:
Теперь осталось завершить умножение матриц, что мы и можем сделать
для каждой записи (𝑖,𝑗) путем умножения элементов
в строке 𝑖 левой матрицы элементами столбца
𝑗 правой матрицы и суммируя их. Мы демонстрируем это
процесс ниже:
Теперь, когда все записи вычислены, мы можем написать, что 𝐴=−5−181219.
Теперь рассмотрим пример, в котором мы можем применить этот метод возведения в квадрат Матрица для решения проблемы.
Пример 1. Нахождение квадрата матрицы
Для 𝐴=4−54−5, напишите 𝐴 как кратное 𝐴.
Ответ
Перед попыткой записать 𝐴 как кратное 𝐴, нам нужно вычислить саму 𝐴. Заполнение необходимой матрицы умножение дает 𝐴=𝐴×𝐴=4−54−54−54−5=−45−45.
Выходная матрица 𝐴 совпадает с исходной матрицей
𝐴, за исключением того, что каждая запись была умножена на -1. Мы
следовательно, найдите, что 𝐴 может быть записано в терминах самого себя с помощью
выражение 𝐴=−𝐴.
Увидев простой пример взятия степени матрицы, отметим, что мы часто приходится иметь дело с выражениями, которые потенциально включают несколько матрицы, а также другие матричные операции. К счастью, у нас не должно быть проблемы, связанные с такими вопросами, пока мы применяем те же принципы мы только что узнали.
Пример 2. Вычисление матричных выражений с участием степеней
Рассмотрим матрицы 𝑋=−3−35−6,𝑌=136−6. Что такое 𝑋−𝑌?
Ответ
Мы должны начать с вычисления как 𝑋, так и 𝑌 обычным способом. Мы вычисляем, что 136−6=19−15−3054.
Теперь, когда у нас есть и 𝑋, и 𝑌, просто вычислить это 𝑋−𝑌=−627−4521−19−15−3054=−2542−15−33.
Вероятно, неудивительно, что мы можем легко взять, например, третью мощность матрицы, используя наше понимание того, как мы находим вторую степень матрицы, как мы это сделали выше.
Давайте посмотрим, как работает третья степень матрицы. По определению,
третья степень квадратной матрицы 𝐴 определяется выражением
𝐴=𝐴×𝐴×𝐴.
По определению,
третья степень квадратной матрицы 𝐴 определяется выражением
𝐴=𝐴×𝐴×𝐴.
Обратите внимание, что, используя ассоциативное свойство матричного умножения, наряду с определение 𝐴, мы можем написать правую часть это как 𝐴×𝐴×𝐴=(𝐴×𝐴)×𝐴=𝐴×𝐴.
В качестве альтернативы, мы можем использовать ассоциативность двух последних терминов, чтобы записать это как 𝐴×𝐴×𝐴=𝐴×(𝐴×𝐴)=𝐴×𝐴.
Итак, мы показали, что 𝐴=𝐴𝐴=𝐴𝐴. В других словами, как только мы вычислили 𝐴, мы можем найти 𝐴 путем умножения 𝐴 справа (или слева) от 𝐴.
Увидев, как работает возведение в степень для возведения в квадрат и куба, мы можем себе представить мы можем применить те же принципы к любой степени 𝐴. С Следуя определению, это возможно.
Определение: мощность матрицы
Если 𝐴 — квадратная матрица, а 𝑘 — натуральное число, 𝑘-я степень 𝐴 дана по 𝐴=𝐴×𝐴×⋯×𝐴, где имеется 𝑘 копий матрицы 𝐴.
В дополнение к этому определению отметим, что, используя ту же логику, что и выше,
можно вычислить 𝐴 (для любого положительного целого числа 𝑘)
сначала вычислив 𝐴 и умножив на дополнительный 𝐴
справа или слева. Так, например, 𝐴=𝐴×𝐴=𝐴×𝐴,
и так далее.
Так, например, 𝐴=𝐴×𝐴=𝐴×𝐴,
и так далее.
Теперь рассмотрим пример, в котором нам нужно вычислить третью степень числа матрица.
Пример 3: вычисление высших степеней матриц
Учитывая матрицу 𝐴=40−37, вычислить 𝐴−3𝐴.
Ответ
Мы должны начать с вычисления 𝐴, а затем использовать этот результат для рассчитать 𝐴. Мы находим, что 𝐴=40−37,𝐴=160−3349, что означает, что мы можем вычислить 𝐴 как умножение матриц между 𝐴 и 𝐴: 𝐴=𝐴×𝐴=40−37160−3349=640−279343.
Теперь у нас есть все необходимое для вычисления искомого выражения: 𝐴−3𝐴=640−279343−3160−3349=640−279343−480−99147=160−180196.
До сих пор мы видели только расчеты с участием
матрицы 2 × 2, но расширение до более высоких порядков
квадратные матрицы очень естественны. Давайте теперь посмотрим на пример того, как мы могли бы найти
мощность матрицы 3×3.
Пример 4. Возведение в квадрат матрицы 3 × 3
Рассмотрим 𝐴=112101210.
Найти 𝐴.
Ответ
Матрица 𝐴 имеет порядок 3×3, значит, 𝐴 также будет иметь этот заказ. Таким образом, мы ожидаем найти матрицу вида где элементы * должны быть вычислены. Мы заполним матрицу умножение полностью, полностью иллюстрируя каждый шаг.
Сначала вычисляем запись в первой строке и первом столбце самой правой матрицы: 112101210112101210=6∗∗∗∗∗∗∗∗.
Расчет 1×1+1×1+2×2=6. Теперь вычисляем запись в первая строка и второй столбец самой правой матрицы: 112101210112101210=63∗∗∗∗∗∗∗.
Расчет 1×1+1×0+2×1=3. Далее мы сосредоточимся на записи в первая строка и третий столбец самой правой матрицы: 112101210112101210=633∗∗∗∗∗∗.
Расчет
1×2+1×1+2×0=3. Теперь переходим ко второму ряду
самая правая матрица, сбрасываемая в первый столбец:
112101210112101210=6333∗∗∗∗∗.
Расчет 1×1+0×1+1×2=3. Затем мы берем запись во втором строка и второй столбец: 112101210112101210=63332∗∗∗∗,
Расчет 1×1+0×0+1×1=2. Последняя запись во второй строке затем вычислено: 112101210112101210=633322∗∗∗.
Расчет 1×2+0×1+1×0=2. Запись в третьем ряду и первом столбец вычисляется: 112101210112101210=6333223∗∗.
Расчет 2×1+1×1+0×2=3. Тогда предпоследняя запись завершенный: 112101210112101210=63332232∗.
Расчет 2×1+1×0+0×1=2. Затем обрабатывается окончательная запись: 112101210112101210=633322325.
Расчет 2×2+1×1+0×0=5. Теперь, когда все записи самого правого матрица найдена, ответ можно записать в виде 𝐴=633322325.
Учитывая, что получение степени матрицы включает повторяющуюся матрицу
умножение, мы могли бы разумно ожидать, что алгебраические правила матрицы
умножение в некоторой степени повлияло бы на правила возведения матрицы в степень
Аналогичным образом. Несмотря на то, что это до некоторой степени очевидно, опасно
обращаться к правилам обычной алгебры при ответе на вопросы, связанные с
матрицы в предположении, что они сохранятся. В следующих
Например, мы будем рассматривать каждое утверждение отдельно и представим
соответствующие свойства матричного умножения в тандеме, объясняющие, почему
данные утверждения выполняются или не выполняются в результате.
Несмотря на то, что это до некоторой степени очевидно, опасно
обращаться к правилам обычной алгебры при ответе на вопросы, связанные с
матрицы в предположении, что они сохранятся. В следующих
Например, мы будем рассматривать каждое утверждение отдельно и представим
соответствующие свойства матричного умножения в тандеме, объясняющие, почему
данные утверждения выполняются или не выполняются в результате.
Пример 5: Проверка свойств степеней матриц
Какое из следующих утверждений верно для всех 𝑛×𝑛 матрицы 𝐴 и 𝐵?
- 𝐴𝐵 = 𝐴 (𝐴𝐵) 𝐵
- (𝐴 — 𝐵) = 𝐴 — 2𝐴𝐵+𝐵
- (𝐴𝐵) = 𝐴𝐵
- (𝐴+𝐵) = 𝐴+2𝐴𝐵+ 𝐵
- (𝐴+𝐵)(𝐴−𝐵)=𝐴−𝐵
Ответ
- Умножение матриц ассоциативно, т. е.
𝐴(𝐵𝐶)=(𝐴𝐵)𝐶. Мы могли бы продолжить эту роль, чтобы получить результаты
например (𝐴𝐵)(𝐶𝐷)=𝐴(𝐵𝐶)𝐷=𝐴𝐵𝐶𝐷 и так далее. В данном
уравнения, левая часть равна 𝐴𝐵, что по определению
можно записать как 𝐴𝐵=𝐴𝐴𝐵𝐵.
 Учитывая ассоциативность
свойство матричного умножения, мы можем написать, что 𝐴𝐵=𝐴(𝐴𝐵)𝐵 и, следовательно, подтвердить, что данное утверждение верно.
Учитывая ассоциативность
свойство матричного умножения, мы можем написать, что 𝐴𝐵=𝐴(𝐴𝐵)𝐵 и, следовательно, подтвердить, что данное утверждение верно. - Обычная алгебра коммутативна относительно умножения. Для двух действительных чисел 𝑎 и 𝑏, это означает, что 𝑎𝑏=𝑏𝑎. Этот результат позволяет нам принять такое выражение, как (𝑎−𝑏)=𝑎−𝑎𝑏−𝑏𝑎+𝑏 и использовать коммутативное свойство собрать два средних члена правой части: (𝑎−𝑏)=𝑎−2𝑎𝑏+𝑏. Однако, умножение матриц, как правило, не является коммутативным, а это означает, что 𝐴𝐵≠𝐵𝐴, за исключением особых обстоятельств (таких как диагональные матрицы или одновременно диагональные матрицы). Следовательно, расширение (𝐴−𝐵)=𝐴−𝐴𝐵−𝐵𝐴+𝐵 не может упростить в предположении, что 𝐴𝐵=𝐵𝐴. Следовательно, данный утверждение ложно.
- Чтобы завершить умножение матриц (𝐴𝐵), мы можем начать с
запись (𝐴𝐵)=(𝐴𝐵)(𝐴𝐵)=𝐴(𝐵𝐴)𝐵, где мы использовали свойство ассоциативности для организации
окончательное выражение.
 Поскольку умножение матриц не является коммутативным, член в квадратных скобках
(𝐵𝐴) нельзя переставить как (𝐴𝐵), что означает
что мы не можем переписать окончательное выражение как 𝐴𝐴𝐵𝐵, что было бы
допустили упрощение 𝐴𝐵. Учитывая, что это не
случае утверждение ложно.
Поскольку умножение матриц не является коммутативным, член в квадратных скобках
(𝐵𝐴) нельзя переставить как (𝐴𝐵), что означает
что мы не можем переписать окончательное выражение как 𝐴𝐴𝐵𝐵, что было бы
допустили упрощение 𝐴𝐵. Учитывая, что это не
случае утверждение ложно. - У нас есть, что (𝐴+𝐵)=𝐴+𝐴𝐵+𝐵𝐴+𝐵. Поскольку в общем случае 𝐴𝐵≠𝐵𝐴, мы не можем получить упрощение, указанное в вопросе.
- Начнем с завершения расширения (𝐴+𝐵)(𝐴−𝐵)=𝐴+𝐵𝐴−𝐴𝐵−𝐵. Мы знаем, что, вообще говоря, 𝐵𝐴≠𝐴𝐵, а это значит, что мы не можем записать правую часть в виде 𝐴−𝐵 и, следовательно, утверждение в вопросе неверно.
Следовательно, правильный ответ — вариант А.
Несмотря на то, что некоторые общепринятые правила алгебры не выполняются для
матриц, все еще существуют некоторые правила, определяющие степени матриц, которые
мы можем положиться. В частности, законы показателей степени для чисел могут быть
распространяется на матрицы следующим образом.
Свойство: сложение и умножение степеней матрицы
Если 𝐴 — квадратная матрица и 𝑟 и 𝑠 — целые положительные числа, то 𝐴𝐴=𝐴,(𝐴)=𝐴.
В последнем примере мы рассмотрим возведение матрицы в гораздо большую степень и посмотрите, как вышеупомянутые свойства могут быть использованы в сочетании с идентификацией образец того, как матрица ведет себя при возведении в степень.
Пример 6. Нахождение степени матрицы высшего порядка путем исследования шаблона его Полномочий
Заполните пропуск: Если 𝐴=403−4, тогда 𝐴=.
Ответить
Как 𝐴=𝐴×𝐴×⋯×𝐴 (пятьдесят раз), очевидно, нам следует избегать попыток вычислить его напрямую. Вместо этого давайте исследуем эффект от того, что 𝐴 имеет малые степени 𝐴 и см. можем ли мы определить закономерность.
Если мы умножим 𝐴 само на себя, другими словами, если мы найдем
𝐴=𝐴×𝐴, имеем
𝐴=403−4403−4=4004.
Отметим, что, поскольку это диагональная матрица, она может быть полезной для матрица, в которой будет находиться. Продолжая далее, если мы вычислим 𝐴=𝐴×𝐴, имеем 𝐴=4004403−4=404⋅3−4.
Интересно, матрица уже не диагональная. Чтобы продолжить расследование узор, посчитаем 𝐴=𝐴×𝐴. Это 𝐴=404⋅3−4403−4=4004.
В этот момент можно распознать закономерность. Для четных сил 𝐴 мы предполагаем, что матрица является диагональной и ненулевые записи равны 4, где 𝑛 — мощность матрицы. Для нечетных степеней это не так, так как в левом нижнем углу и в правом нижнем углу есть ненулевой элемент запись становится отрицательной. Однако, поскольку нам нужно найти только 𝐴 где 50 — четная степень, нам нужно только рассмотреть первый случай.
Теперь покажем, как можно найти 𝐴, используя четное число.
мощность матрицы, 𝐴. Напомним, что
𝐴=4004.
Напомним, что
𝐴=4004.
Заметим, что скаляр 4 можно вынести за пределы матрицы, переписав его в виде: 𝐴=41001.
Это единичная матрица 2×2 𝐼 раз постоянная. Теперь мы знаем, что единичная матрица имеет имущество 𝐼𝑋=𝑋𝐼=𝑋, где 𝑋 — любая матрица 2 × 2. В частности, если 𝑋=𝐼, имеем 𝐼=𝐼×𝐼=𝐼.
Мы можем распространить это на любую степень 𝐼, то есть 𝐼=𝐼.
Мы можем использовать это свойство для вычисления 𝐴. Давайте также вспомнить свойство (𝐴)=𝐴, что позволяет нам переписать 𝐴 следующим образом: 𝐴=𝐴.
Поскольку мы имеем 𝐴=4𝐼, это означает
Так как 4=2 4=2=2.
Есть много связанных тем, которые подкрепляют обоснованность изучения возведения матриц в степень. При работе с квадратной матрицей ясно, что многократное умножение такой матрицы само по себе приведет к
обычно приводят к результатам, которые последовательно сложнее вычислить, учитывая большие числа
участие, как мы видели в нескольких из приведенных выше примеров. Поэтому выгодно иметь возможность
максимально уменьшить сложность этих вычислений. При определенных
обстоятельств можно диагонализовать матрицу, что значительно уменьшает
сложность вычисления его целых степеней.
Поэтому выгодно иметь возможность
максимально уменьшить сложность этих вычислений. При определенных
обстоятельств можно диагонализовать матрицу, что значительно уменьшает
сложность вычисления его целых степеней.
Давайте закончим рассмотрением основных вещей, которые мы узнали в этом объяснитель.
Ключевые моменты
- Для квадратной матрицы 𝐴 и положительного целого числа 𝑘 мы определяем мощность матрицы повторяющейся матрицей умножение; Например, 𝐴=𝐴×𝐴×⋯×𝐴, где есть 𝑘 копий матрицы 𝐴 с правой стороны.
- Важно признать, что сила матрицы только хорошо определяется, если матрица является квадратной матрицей. Кроме того, если 𝐴 имеет порядок 𝑛×𝑛, то это будет случай для 𝐴, 𝐴 и так далее.
- Матрица высших степеней может быть рассчитана относительно меньшие степени матрицы. Другими словами, 𝐴=𝐴×𝐴, 𝐴=𝐴×𝐴, и так далее.
- Если 𝐴 — квадратная матрица и 𝑟
и 𝑠 — целые положительные числа, то
𝐴𝐴=𝐴,(𝐴)=𝐴.

Как рассчитать мощность (и n-ю степень) матрицы
В этом посте мы объясним, как рассчитать мощность матрицы. Здесь вы найдете примеры и упражнения, решенные шаг за шагом по степеням матрицы, которые помогут вам понять ее в совершенстве. Вы также узнаете, что такое n-я степень матрицы и как ее найти.
Содержание
Как найти степень матрицы?
Чтобы найти степень матрицы, умножьте матрицу на саму себя столько раз, сколько указывает показатель степени.
Следовательно, чтобы вычислить степень матрицы, вы должны сначала знать, как перемножать матрицы. В противном случае вы не сможете вычислить мощность матрицы. Тогда, прежде чем читать дальше, мы рекомендуем вам сначала увидеть алгоритм умножения матриц.
Пример мощности матрицы
Пусть A — квадратная матрица 2×2, 4-я степень матрицы A вычисляется следующим образом:
Существует важное свойство мощности матрицы, которое вы должны знать: вы можете вычислить мощность матрицы только тогда, когда она квадратная матрица.
Мощность матрицы также можно вычислить с использованием собственных значений, то есть путем диагонализации матрицы. Однако вы должны знать, как выполнить диагонализацию матрицы. По этой ссылке вы узнаете, как провести диагонализацию матрицы, а также как вычислить мощность матрицы путем диагонализации.
Что такое энная степень матрицы?
n-я степень матрицы — это выражение, которое позволяет нам легко вычислить любую степень матрицы.
Много раз степени матриц следуют шаблону. Следовательно, если мы найдем последовательность, которой следуют степени матрицы, мы сможем вычислить любую степень без необходимости выполнять все умножения.
Это означает, что мы можем найти формулу , которая дает нам n-ю степень матрицы , не вычисляя все степени.
Формулу некоторых степеней матрицы можно найти следующим образом:
- Четность показателя степени . Может случиться так, что четные степени — это одно, а нечетные — другое.

- Изменение знаков. Например, может быть так, что элементы четных степеней положительны, а элементы нечетных степеней отрицательны, или наоборот.
- Повторение: независимо от того, повторяется ли одна и та же матрица через определенное количество степеней или нет.
- Существует математическая связь между показателем степени и элементами матрицы.
Пример n-й степени матрицы
- Пусть A следующая матрица порядка 2, найдите A n и A 100 :
3 90 Сначала вычислим несколько степеней матрицы A, чтобы попытаться угадать закономерность, по которой следуют степени. Итак, вычисляем пять первых степеней матрицы:
При расчете до А 5 , мы видим, что степени матрицы A следуют закономерности: с каждым увеличением мощности результат умножается на 2. Следовательно, все элементы матриц являются степенями двойки:
Таким образом, по индукции мы можем вывести, что формула для n-й степени матрицы A выглядит следующим образом:
И по этой формуле мы можем вычислить матрицу A, возведенную в 100:
Практическая степень матрицы
Задача 1
Дана следующая матрица размера 2×2:
Возведите матрицу в четвертую степень.
См. решение
Чтобы вычислить степень матрицы, мы должны умножить матрицу одну на одну. Поэтому сначала вычисляем квадрат матрицы A:
Теперь вычисляем куб матрицы A:
И окончательно определяем A 4 :
2 0
0 Задача матрица порядка 2:
Вычислить:
См. решение
A 35 — это слишком большая степень, чтобы ее можно было вычислить вручную, поэтому степени матрицы должны подчиняться закономерности. Итак, мы собираемся вычислить до A 5 , чтобы попытаться вычислить последовательность:
Теперь мы можем видеть закономерность, по которой следуют степени: при каждой степени все числа остаются одинаковыми. , за исключением элемента во втором столбце второй строки, который умножается на 3. Следовательно, все числа всегда остаются одинаковыми, а последний элемент равен степени 3:
Таким образом, формула для n-й степени матрицы A:
2 Формула.
 Мы можем рассчитать 35 :
Мы можем рассчитать 35 :Задача 3
Учитывая следующую матрицу размеров 3 × 3:
. Рассчитайте:
С Проектирование
.0003 A 100 — сила слишком велика, чтобы ее можно было вычислить вручную, а это значит, что силы должны следовать шаблону. Итак, мы собираемся вычислить до A 5 , чтобы попытаться вычислить последовательность: . одна единица в числителе:
Таким образом, формула, определяющая n-ю степень матрицы A:
, и из этой формулы мы можем найти 100 :
Задача 4
Учитывая следующую матрицу размера 2 × 2:
Найти:
.
A 201 — слишком большая степень, чтобы ее можно было вычислить вручную, поэтому степени матрицы должны следовать шаблону. В этом случае мы должны вычислить до A 8 , чтобы узнать их последовательность:
В этом случае мы должны вычислить до A 8 , чтобы узнать их последовательность:
С помощью этих вычислений мы видим, что каждые 4 степени мы получаем единичную матрицу. То есть степени A 4 , A 8 , A 12 , A 16 , … приведут к единичной матрице. Итак, чтобы вычислить A 201 , мы должны разложить 201 на кратные 4:
Таким образом, A 201 будет в 50 раз больше A 4 и один раз A 1 :
Поскольку мы знаем, что A 4 является единичной матрицей:
Кроме того, единичная матрица, возведенная в произвольное число, дает единичную матрицу. Итак:
И, наконец, любая матрица, умноженная на единичную матрицу, дает одну и ту же матрицу. Таким образом:
Итак, A 201 равно A:
Задача 5
Дана следующая квадратная матрица порядка 3:
Вычислить:
См. решение
решение
Очевидно, A 62 слишком большой расчет, чтобы его можно было делать вручную, поэтому мощности матрицы должны следовать шаблону. В этом случае мы должны вычислить до A 6 , чтобы узнать последовательность, которой они следуют:
С этими вычислениями мы можем видеть, что каждые 3 степени мы получаем единичную матрицу . Другими словами, степени A 3 , A 6 , A 9 , A 12 , … приводят к единичной матрице. Таким образом, чтобы вычислить A 62 , мы должны разложить 62 на кратные 3:
Таким образом, A 62 равно 20, умноженному на A 3 , и один раз A 2 :
9000 мы знаем, что A 3 3 — единичная матрица:Кроме того, единичная матрица, возведенная в произвольное число, дает единичную матрицу. Итак:
Наконец, любая матрица, умноженная на единичную матрицу, дает одну и ту же матрицу. Итак:
Итак:
Таким образом, A 62 будет равно A 2 :
сообщить об этом объявлении
Экспонента матрицы
Экспонента матрицыРешение уравнения экспоненциального роста
Естественно спросить, можете ли вы решить постоянный коэффициент линейная система
Аналогичным образом.
Если решение системы должно иметь тот же вид, что и рост решение уравнения должно выглядеть так
Первое, что мне нужно сделать, это разобраться в матричной экспоненте .
Ряд Тейлора для
Он сходится абсолютно для всех z.
Это матрица с вещественными элементами, определите
Степени имеют смысл, так как A — квадратная матрица. Это можно показать, что этот ряд сходится для всех t и всех матрица А.
Дифференцируя ряд почленно,
Это показывает, что решает дифференциальное уравнение
. Вектор начального состояния
дает частное решение
Вектор начального состояния
дает частное решение
Это работает, потому что (по установка в степенном ряду).
Другое известное свойство обычных экспонент справедливо для матричная экспоненциальная: если A и B коммутируют (то есть ), то
Вы можете доказать это, умножив степенной ряд для экспоненты слева. (только с .)
Пример. Вычислить, если
Вычислите последовательные степени A:
Следовательно,
Вы можете вычислить экспоненту произвольной диагональной матрицы в так же:
Пример. Вычислить, если
Вычислите последовательные степени A:
Следовательно,
Вот откуда взялось последнее равенство:
Пример. Вычислить, если
Если вы вычисляете степени A, как в последних двух примерах, не существует
очевидный узор. Поэтому будет сложно вычислить
экспоненциально с помощью степенного ряда.
Поэтому будет сложно вычислить
экспоненциально с помощью степенного ряда.
Вместо этого настройте систему, матрица коэффициентов которой равна A:
Решение
Далее заметим, что если B — матрица,
В частности, это справедливо для . В настоящее время
удовлетворяет ли решение, но
Установите, чтобы получить первый столбец:
Следовательно, , . Так
Установите, чтобы получить второй столбец:
Следовательно, , . Следовательно,
Следовательно,
Я нашел, но мне нужно было решить систему дифференциальные уравнения, чтобы сделать это.
В некоторых случаях можно использовать линейную алгебру для вычисления
экспонента матрицы. Матрица A является диагонализируемой , если она имеет n независимых
собственные векторы. (Это верно, например, если A имеет n различных
собственные значения.)
(Это верно, например, если A имеет n различных
собственные значения.)
Предположим, что A диагонализируется с независимыми собственными векторами и соответствующими собственными значениями. Пусть S — матрица, столбцы являются собственными векторами:
затем
Как я заметил выше,
С другой стороны, поскольку ,
Следовательно,
Я могу использовать этот подход для вычислений в случае, если A диагонализируемо.
Пример. Вычислить, если
Собственные значения , . Так как имеются два различных собственных значения и A — матрица, A диагонализируема. соответствующие собственные векторы и . Таким образом,
Следовательно,
Пример. Вычислить, если
Собственные значения равны и (двойные). Соответствующие собственные векторы для и и для . Поскольку у меня есть 3 независимых собственных вектора, матрица
является диагонализируемым.
Поскольку у меня есть 3 независимых собственных вектора, матрица
является диагонализируемым.
У меня есть
Отсюда следует, что
Вот быстрая проверка вычисления: если вы установите в правой части, вы получите
Это проверяет, так как .
Обратите внимание, что эта проверка не является надежной — только потому, что вы получаете I настройка не означает, что ваш ответ правильный. Однако, если вы не понимаете I, ваш ответ, безусловно, неверен!
Как вычислить, является ли A не диагонализируемым?
Я опишу итеративный алгоритм вычислений, который требует только знания собственных значений А. Существуют различные алгоритмы вычисления матричной экспоненты; этот, принадлежащий Уильямсону [1], кажется мне проще всего для ручного расчета.
(Обратите внимание, что нахождение собственных значений матрицы, вообще говоря,
сложная проблема: с ней придется иметь дело любому методу поиска. )
)
Пусть А — матрица. Пусть будет список собственные значения, причем несколько собственных значений повторяются в соответствии с их множественность.
Позволять
затем
Чтобы доказать это, я покажу, что выражение справа удовлетворяет дифференциальное уравнение . К Для этого мне понадобятся два факта о характеристическом многочлене .
1. .
2. ( Теорема Кэли-Гамильтона ).
Заметим, что если — характеристический полином, затем, используя первый факт и определение B,
По теореме Кэли-Гамильтона
Я буду использовать этот факт в доказательстве ниже.
Пример. Я проиллюстрирую Кейли-Гамильтона теорема с матрицей
Характеристический полином равен . Теорема Кэли-Гамильтона утверждает, что если вы подключите A к , вы получите нулевую матрицу.
Первый,
Следовательно,
Доказательство алгоритма. Во-первых,
Во-первых,
Напомним, что Основная теорема исчисления говорит, что
Применяя это и Правило продукта, я могу дифференцировать, чтобы получить
Следовательно,
Расширьте термины, используя
Делая эту замену и увеличивая сумму, я получил
(Результат (*), доказанный выше, был использован в предпоследнем равенство.) Комбинируя приведенные выше результаты, я показал, что
Это показывает, что удовлетворяет .
Используя разложение степенного ряда, у меня есть . Так
(Помните, что умножение матриц вообще не является коммутативным!) Отсюда следует, что матрица является постоянной.
Установлен . Поскольку , следует, что . Кроме того, . Следовательно, и, следовательно, .
Пример. Используйте экспоненциальную матрицу для решения
Характеристический полином равен . Вы можете
проверить, что существует только один независимый собственный вектор, поэтому я не могу
решить систему путем диагонализации. я мог бы использовать обобщенные собственные векторы для решения системы, но я буду использовать
экспоненциальная матрица для иллюстрации алгоритма.
Вы можете
проверить, что существует только один независимый собственный вектор, поэтому я не могу
решить систему путем диагонализации. я мог бы использовать обобщенные собственные векторы для решения системы, но я буду использовать
экспоненциальная матрица для иллюстрации алгоритма.
Сначала перечислите собственные значения: . Поскольку это двойной корень, он указан дважды.
Сначала я вычислю:
Вот:
Следовательно,
В качестве проверки обратите внимание, что настройка производит личность.)
Решение заданной задачи с начальным значением есть
Вы можете получить общее решение, заменив на .
Пример. Найти, если
Собственные значения, очевидно, (двойные) и .
Сначала я вычислю ‘s. у меня есть, и
Далее я вычислю ‘s. , а также
Следовательно,
Пример. Используйте экспоненциальную матрицу для решения
Используйте экспоненциальную матрицу для решения
Этот пример продемонстрирует, как работает алгоритм для сложных собственных значений.
Характеристический полином равен . Собственные значения равны. я перечислит их как .
Сначала я вычислю ‘s. , а также
Далее я вычислю ‘s. , а также
Следовательно,
я хочу действительное решение , поэтому я буду использовать формулу Де Муавра для упрощать:
Подключив их к приведенному выше выражению, я получил
Обратите внимание, что все i выпали! Это отражает очевидное тот факт, что экспонента действительной матрицы должна быть действительной матрицей.
Наконец, общее решение исходной системы имеет вид
Пример. Я сравню экспоненциальную матрицу и методы решения собственных векторов путем решения следующей системы оба способа:
Характеристический полином равен . Собственные значения равны.
Собственные значения равны.
Рассмотреть возможность :
Поскольку это матрица собственных векторов, она должна быть сингулярной, и, следовательно, ряды должны быть кратными. Так что игнорируйте вторую строку. Я хочу вектор такое что . Чтобы получить такой вектор, поменяйте местами и -1 и инвертируйте один из них: , . Таким образом, является собственным вектором.
Соответствующее решение
Возьмем действительную и мнимую части:
Решение
Теперь я решу уравнение, используя экспоненту. Собственные значения находятся . Вычислите ‘s. , а также
(Здесь и далее я немного лукавлю в сравнении, не показывая всю алгебру, связанную с упрощением. Тебе следует используйте формулу Де Муавра, чтобы исключить сложные экспоненты.)
Затем вычислите ‘s. , а также
Следовательно,
Решение
Принимая во внимание некоторую алгебру, которую я не показал для матрицы
экспоненциальный, я думаю, что подход с собственным вектором проще.
Пример. Решить систему
Для сравнения, сначала я сделаю это, используя обобщенный собственный вектор метод, а затем с помощью матричной экспоненты.
Характеристический полином равен . Собственное значение (двойное).
Игнорируйте первую строку и разделите вторую строку на 2, получив вектор . Я хочу такой. Обмен 1 и -2 и отрицание -2: я получаю. Это собственный вектор для .
Поскольку у меня есть только один собственный вектор, мне нужен обобщенный собственный вектор. Это означает, что мне нужно такое, что
Уменьшить ряд:
Это означает, что . Настройка урожайности. Обобщенный собственный вектор .
Решение
Далее я решу систему, используя экспоненциальную матрицу. собственные значения . Сначала я вычислю ‘s. , а также
Затем вычислите ‘s. , а также
Следовательно,
Решение
В этом случае нахождение решения с использованием матричной экспоненты может
быть немного проще.
[1] Ричард Уильямсон, Введение в дифференциал уравнения . Энглвуд Клиффс, Нью-Джерси: Прентис-Холл, 1986.
Отправить комментарии об этой странице по адресу: Брюс.Икенага@millersville.edu.
Домашняя страница Брюса Икенаги
Copyright 2012 Брюс Икенага
Microsoft Excel — поднять матрицу до мощности без VBA
спросил
Изменено 6 лет, 6 месяцев назад
Просмотрено 6к раз
Мне нужно возвести матрицу в большую степень (скажем, 200), и я не могу использовать VBA, потому что он предназначен для конечного пользователя, чьи ИТ-отделы не позволяют запускать макросы.
Кроме того, поскольку мощность велика, будет недостаточно написать очень большую формулу, например:
=ММНОЖ(m,ММНОЖ(m,ММНОЖ(m..... )))
Где m — диапазон моей матрицы.
Есть ли способ сделать это, не прибегая к VBA?
Я осмотрелся, и пока кажется, что нет.
- microsoft-excel
- worksheet-function
Вы можете сделать это с итеративным вычислением
- поставить галочку: файл — опции — формулы — «включить итерационные вычисления» (от версии Excel 2007)
- установите значение «максимальное число итераций» на достаточно большое число (это максимальная мощность, которую вы можете поднять матрицу)
- Формула во вспомогательной ячейке:
=ЕСЛИ(ЧИСЛО(G2),ЕСЛИ(G2=E2,ТЕКСТ(G2,"0"),G2+1),ЕСЛИ(ЗНАЧЕНИЕ(G2)=E2,G2,1)) - Формула в матрице результатов:
=ЕСЛИ(ЧИСЛО(G2),ЕСЛИ(G2=1,A2:C4,МУМНОЖ(A2:C4,h3:J4)),h3:J4)
(это формула массива , нужно закончить с помощью CTRL+SHIFT+ENTER)
Примечания
- Формула пересчитывается ТОЛЬКО ЕСЛИ ВЫ ИЗМЕНИТЕ МОЩНОСТЬ , она не будет пересчитана ни после изменения только входной матрицы, ни при пересчете всех формул (можно сделать, но требуется более сложная формула и больше вспомогательных ячеек , дайте мне знать, если вы заинтересованы в этом).

- Также, после ввода обеих формул, выходная матрица будет показывать только 0 значений, для ее расчета нужно изменить мощность, от этого лист будет «инициализирован», работать будет без проблем Проверка ошибки
- еще не реализована в формуле:
- если мощность > максимальное количество итераций, то формула будет выполняться только количество итераций, установленное
- аналогично, для нецелых или отрицательных чисел формула не останавливается, а работает до максимального количества итераций
- после того, как достигнуто максимальное количество итераций, формула «переполнится», считает вперед, не начиная с 0, чтобы исправить это, установите мощность, которая будет достигнута в следующем цикле итерации (например, если помощник = 500, максимальное количество итераций = 100, затем установите 500 < мощность < 600, чтобы формула правильно остановилась на этом, и она будет работать правильно для следующей настройки мощности).
- Большинство проблем, описанных выше, при необходимости можно исправить в формуле.

 04.2009, 08:32
04.2009, 08:32  04.2009, 09:03
04.2009, 09:03 
 Математики обычно тоже не в курсе. Поэтому эта информация может быть полезна.
Математики обычно тоже не в курсе. Поэтому эта информация может быть полезна. Так что теперь тему можно каталогизировать.
Так что теперь тему можно каталогизировать. Хоть возведение в степень, хоть синус-косинус-лонарифм, хоть что ещё…
Хоть возведение в степень, хоть синус-косинус-лонарифм, хоть что ещё…
 Хоть возведение в степень, хоть синус-косинус-лонарифм, хоть что ещё…
Хоть возведение в степень, хоть синус-косинус-лонарифм, хоть что ещё… Хоть возведение в степень, хоть синус-косинус-лонарифм, хоть что ещё…
Хоть возведение в степень, хоть синус-косинус-лонарифм, хоть что ещё… Поэтому естественно в качестве значения функции при принять значение , где — такой многочлен, что разность делится на характеристический многочлен матрицы. В качестве можно взят интерполяционный многочлен Лагранжа, если корни хар. многочлена простые. Если же корни кратные, то надо еще потребовать, чтобы на корнях совпадали еще и значения производных и до порядка кратности корня. Это называется интерполяционный многочлен Лагранжа-Сильвестра.
Поэтому естественно в качестве значения функции при принять значение , где — такой многочлен, что разность делится на характеристический многочлен матрицы. В качестве можно взят интерполяционный многочлен Лагранжа, если корни хар. многочлена простые. Если же корни кратные, то надо еще потребовать, чтобы на корнях совпадали еще и значения производных и до порядка кратности корня. Это называется интерполяционный многочлен Лагранжа-Сильвестра.
 Нет просто точки опоры. Нет никакого универсального критерия того, что разумно считать функцией от матрицы.
Нет просто точки опоры. Нет никакого универсального критерия того, что разумно считать функцией от матрицы.



 В образце решения вычисления проведены двумя способами, проанализируйте, какой путь выгоднее и короче.
В образце решения вычисления проведены двумя способами, проанализируйте, какой путь выгоднее и короче.
 Из практического опыта могу сказать, что иногда попадаются примеры на возведение в 4-ю степень, а вот уже пятой степени что-то не припомню. Но на всякий случай приведу оптимальный алгоритм:
Из практического опыта могу сказать, что иногда попадаются примеры на возведение в 4-ю степень, а вот уже пятой степени что-то не припомню. Но на всякий случай приведу оптимальный алгоритм: Плюс некоторые специфические матричные операции, такие, как транспонирование и нахождение обратной матрицы.
Плюс некоторые специфические матричные операции, такие, как транспонирование и нахождение обратной матрицы.
 Это поможет лучше закрепить материал, полученный в теории. Увидев перед собой детальный алгоритм расчётов, вы лучше поймёте все его тонкости и впоследствии сможете не допускать ошибок в ручном вычислении. Кроме того, никогда не будет лишним перепроверить свои расчёты, и это тоже лучше всего осуществлять здесь.
Это поможет лучше закрепить материал, полученный в теории. Увидев перед собой детальный алгоритм расчётов, вы лучше поймёте все его тонкости и впоследствии сможете не допускать ошибок в ручном вычислении. Кроме того, никогда не будет лишним перепроверить свои расчёты, и это тоже лучше всего осуществлять здесь.




 Если матричное умножение осуществимо, то в итоге тоже получится матрица. М-да, хорошо мой преподаватель по алгебре не видит, как я объясняю замкнутость алгебраической структуры относительно её элементов =)
Если матричное умножение осуществимо, то в итоге тоже получится матрица. М-да, хорошо мой преподаватель по алгебре не видит, как я объясняю замкнутость алгебраической структуры относительно её элементов =) В рассматриваемом задании часто возникает иллюзия, что речь идёт о каких-то перестановках матриц. Их здесь нет. Снова напоминаю, что в общем случае ПЕРЕСТАВЛЯТЬ МАТРИЦЫ НЕЛЬЗЯ . Так, во втором пункте на втором шаге выполняем умножение , но ни в коем случае не . С обычными числами такой бы номер прошёл, а с матрицами – нет.
В рассматриваемом задании часто возникает иллюзия, что речь идёт о каких-то перестановках матриц. Их здесь нет. Снова напоминаю, что в общем случае ПЕРЕСТАВЛЯТЬ МАТРИЦЫ НЕЛЬЗЯ . Так, во втором пункте на втором шаге выполняем умножение , но ни в коем случае не . С обычными числами такой бы номер прошёл, а с матрицами – нет. Чтобы возвести квадратную матрицу в куб, нужно вычислить произведение:
Чтобы возвести квадратную матрицу в куб, нужно вычислить произведение:
 При расчётах справедлив знакомый алгебраический приоритет: сначала учитываются скобки , затем выполняется возведение в степень / извлечение корней , потом умножение / деление и в последнюю очередь – сложение /вычитание .
При расчётах справедлив знакомый алгебраический приоритет: сначала учитываются скобки , затем выполняется возведение в степень / извлечение корней , потом умножение / деление и в последнюю очередь – сложение /вычитание .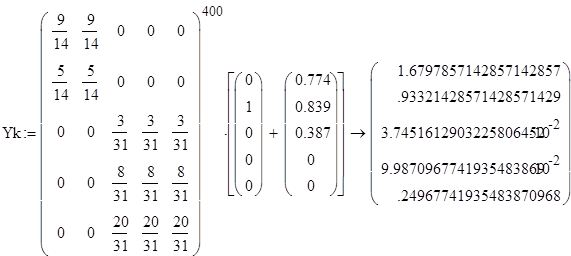 Скобки, как и в числовых выражениях, меняют порядок действий: – тут сначала выполняется умножение , потом полученная матрица транспонируется и умножается на 2.
Скобки, как и в числовых выражениях, меняют порядок действий: – тут сначала выполняется умножение , потом полученная матрица транспонируется и умножается на 2.
 Вот и все. Теперь изучите синтаксис разметки MathML, LaTeX и ASCIIMathML, и вы готовы вставлять математические формулы на веб-страницы своего сайта.
Вот и все. Теперь изучите синтаксис разметки MathML, LaTeX и ASCIIMathML, и вы готовы вставлять математические формулы на веб-страницы своего сайта. T+7E$.
T+7E$. T+7E=2\cdot \left(\begin{array} {ccc}
-7 & 13 & -3 \\
-31 & -5 & 7 \\
23 & 31 & 7
\end{array} \right)-3\cdot \left(\begin{array} {ccc}
-5 & 10 & 3 \\
-20 & 12 & -15 \\
13 & 9 & 8
\end{array} \right)+7\cdot \left(\begin{array} {ccc}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array} \right)
$$
T+7E=2\cdot \left(\begin{array} {ccc}
-7 & 13 & -3 \\
-31 & -5 & 7 \\
23 & 31 & 7
\end{array} \right)-3\cdot \left(\begin{array} {ccc}
-5 & 10 & 3 \\
-20 & 12 & -15 \\
13 & 9 & 8
\end{array} \right)+7\cdot \left(\begin{array} {ccc}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array} \right)
$$ 2+3A-9E=2A\cdot A+3A-9E=2 \left(\begin{array} {cc} -3 & 1 \\ 5 & 0 \end{array} \right)\cdot \left(\begin{array} {cc} -3 & 1 \\ 5 & 0 \end{array} \right)+3 \left(\begin{array} {cc} -3 & 1 \\ 5 & 0 \end{array} \right)-9\left(\begin{array} {cc} 1 & 0 \\ 0 & 1 \end{array} \right)=\\
=2 \left(\begin{array} {cc} (-3)\cdot(-3)+1\cdot 5 & (-3)\cdot 1+1\cdot 0 \\ 5\cdot(-3)+0\cdot 5 & 5\cdot 1+0\cdot 0 \end{array} \right)+3 \left(\begin{array} {cc} -3 & 1 \\ 5 & 0 \end{array} \right)-9\left(\begin{array} {cc} 1 & 0 \\ 0 & 1 \end{array} \right)=\\
=2 \left(\begin{array} {cc} 14 & -3 \\ -15 & 5 \end{array} \right)+3 \left(\begin{array} {cc} -3 & 1 \\ 5 & 0 \end{array} \right)-9\left(\begin{array} {cc} 1 & 0 \\ 0 & 1 \end{array} \right)
=\left(\begin{array} {cc} 28 & -6 \\ -30 & 10 \end{array} \right)+\left(\begin{array} {cc} -9 & 3 \\ 15 & 0 \end{array} \right)-\left(\begin{array} {cc} 9 & 0 \\ 0 & 9 \end{array} \right)=\left(\begin{array} {cc} 10 & -3 \\ -15 & 1 \end{array} \right).
2+3A-9E=2A\cdot A+3A-9E=2 \left(\begin{array} {cc} -3 & 1 \\ 5 & 0 \end{array} \right)\cdot \left(\begin{array} {cc} -3 & 1 \\ 5 & 0 \end{array} \right)+3 \left(\begin{array} {cc} -3 & 1 \\ 5 & 0 \end{array} \right)-9\left(\begin{array} {cc} 1 & 0 \\ 0 & 1 \end{array} \right)=\\
=2 \left(\begin{array} {cc} (-3)\cdot(-3)+1\cdot 5 & (-3)\cdot 1+1\cdot 0 \\ 5\cdot(-3)+0\cdot 5 & 5\cdot 1+0\cdot 0 \end{array} \right)+3 \left(\begin{array} {cc} -3 & 1 \\ 5 & 0 \end{array} \right)-9\left(\begin{array} {cc} 1 & 0 \\ 0 & 1 \end{array} \right)=\\
=2 \left(\begin{array} {cc} 14 & -3 \\ -15 & 5 \end{array} \right)+3 \left(\begin{array} {cc} -3 & 1 \\ 5 & 0 \end{array} \right)-9\left(\begin{array} {cc} 1 & 0 \\ 0 & 1 \end{array} \right)
=\left(\begin{array} {cc} 28 & -6 \\ -30 & 10 \end{array} \right)+\left(\begin{array} {cc} -9 & 3 \\ 15 & 0 \end{array} \right)-\left(\begin{array} {cc} 9 & 0 \\ 0 & 9 \end{array} \right)=\left(\begin{array} {cc} 10 & -3 \\ -15 & 1 \end{array} \right). $$
$$ Первым делом укажите размер матрицы, нажав на иконки «+» или «-» слева от неё. Затем в поле матрицы введите числа. Также нужно указать степень, в которую возводится матрица. А далее вам остаётся лишь кликнуть на кнопку: «Вычислить» в нижней части поля. Полученный результат будет достоверным и точным, если вы внимательно и правильно ввели все значения. Вместе с ним вам будет предоставлена детальная расшифровка решения.
Первым делом укажите размер матрицы, нажав на иконки «+» или «-» слева от неё. Затем в поле матрицы введите числа. Также нужно указать степень, в которую возводится матрица. А далее вам остаётся лишь кликнуть на кнопку: «Вычислить» в нижней части поля. Полученный результат будет достоверным и точным, если вы внимательно и правильно ввели все значения. Вместе с ним вам будет предоставлена детальная расшифровка решения. см. пример оформления .
см. пример оформления . Если он не равен нулю, продолжаем решение, иначе — обратной матрицы не существует.
Если он не равен нулю, продолжаем решение, иначе — обратной матрицы не существует.