Восьмеричная система счисления
Содержание:
Что такое восьмеричная система счисления
Как перевести целое десятичное число в восьмеричную систему счисления
Как перевести десятичную дробь в восьмеричную систему счисления
Как перевести число из восьмеричной системы счисления в десятичную
Как перевести дробное восьмеричное число в десятичное
Таблица значений десятичных чисел от 0 до 100 в восьмеричной системе счисления
Восьмеричная система счисления, является позиционной системой счисления, то есть имеется зависимость от позиции цифры в записи числа. Для записи числа в восьмеричной системе счисления используется восемь цифр 0, 1, 2, 3, 4, 5, 6 и 7. Для определения в какой системе счисления записано число, внизу, справа от числа ставят цифру, которая называется основанием системы счисления. Например, 72318 или 45568
Если вам необходимо перевести число любой системы счисления в другую систему счисления, воспользуйтесь
калькулятором систем счисления с подробным решением онлайн.
Как перевести целое десятичное число в восьмеричную систему счисления
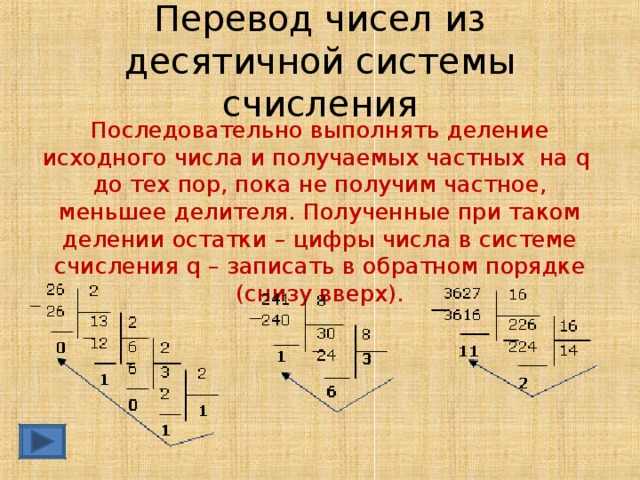
Для того, чтобы перевести целое десятичное число в восьмеричную систему счисления нужно десятичное число делить на 8 до тех пор, пока неполное частное не будет равно нулю. В результате будет получено число из остатков деления записанное справа налево.
Например, переведем число 36910 в восьмеричную систему счисления:
369 : 8 = 46 остаток: 1
46 : 8 = 5 остаток: 6
5 : 8 = 0 остаток: 5
36910 = 5618
Как перевести десятичную дробь в восьмеричную систему счисления
Для того чтобы перевести десятичную дробь в восьмеричную систему счисления необходимо сначала перевести целую часть десятичной дроби в восьмеричную систему счисления,
а затем дробную часть, последовательно умножать на 8, до тех пор, пока в дробной части произведения не получиться ноль (результатом произведения будет целое число)
или не будет достигнуто необходимое количество знаков после запятой.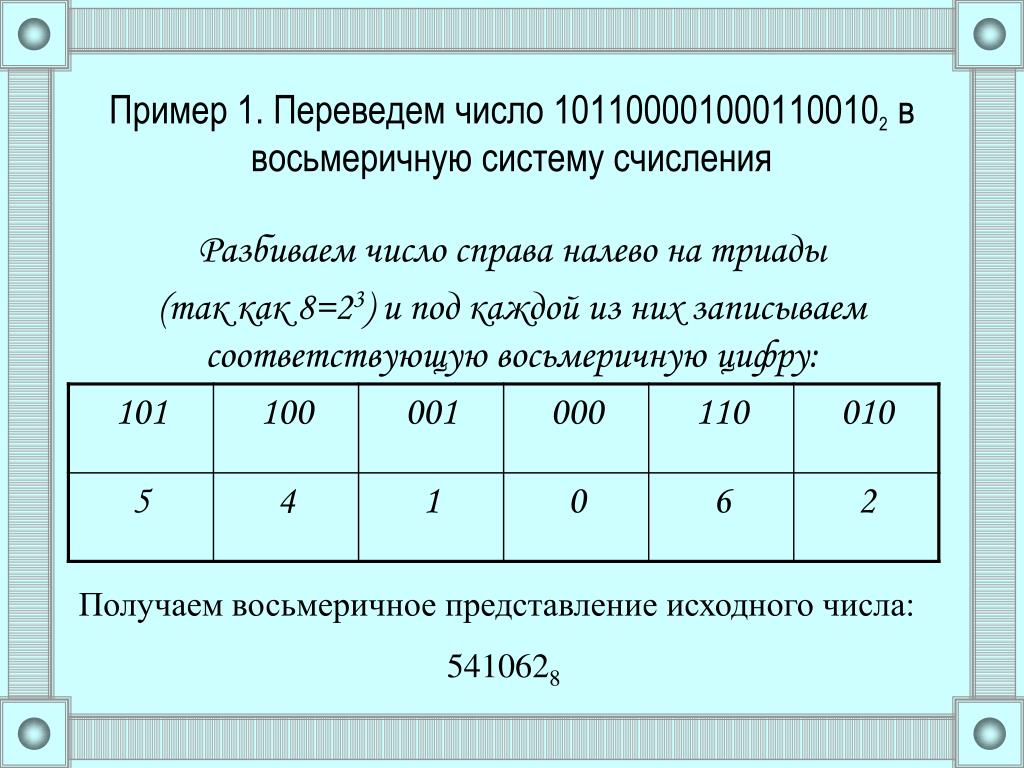
Например, переведем десятичное число 0.210 в восьмеричную систему счисления:
Переведем целую часть
010 = 08
Переведем дробную часть
0.2 · 8 = 1.6
0.6 · 8 = 4.8
0.8 · 8 = 6.4
0.4 · 8 = 3.2
0.2 · 8 = 1.6
0.6 · 8 = 4.8
0.8 · 8 = 6.4
0.4 · 8 = 3.2
0.2 · 8 = 1.6
0.210 = 0.14631463148
Восьмеричные дроби, как и десятичные могут быть как конечными, так и бесконечными. Не всегда конечная десятичная дробь может быть представлена конечной восьмеричной.
В данном примере получается бесконечная периодическая восьмеричная дробь, поэтому умножение на 8 можно производить бесконечное число раз и все равно дробная часть частного не будет равна нулю. В данном случае десятичная дробь 0.2 не может быть точно представлена в восьмеричной системе счисления.
К примеру, дробь 1.510 может быть представлена в восьмеричной системе счисления в виде конечной 2.510 = 1.48.
В данном случае десятичная дробь 0.2 не может быть точно представлена в восьмеричной системе счисления.
К примеру, дробь 1.510 может быть представлена в восьмеричной системе счисления в виде конечной 2.510 = 1.48.
Как перевести число из восьмеричной системы счисления в десятичную
Для того, чтобы перевести число из восьмеричной системы счисления в десятичную систему счисления, необходимо записать позиции каждой цифры в числе с права на лево начиная с нуля. Каждая позиция цифры будет степенью числа 8, так как система счисления 8-ичная. Необходимо последовательно умножить каждое число на 8 в степени соответствующей позиции числа и затем сложить с последующим произведением следующего числа в степени соответствующей его позиции.
Например, переведем число 753108 в десятичную систему счисления:
| Позиция в числе | 4 | 3 | 2 | 1 | 0 |
| Число | 7 | 5 | 3 | 1 | 0 |
753108 = 7 ⋅ 84 + 5 ⋅ 83 + 3 ⋅ 82 + 1 ⋅ 81 + 0 ⋅ 80 = 3143210
Как перевести дробное восьмеричное число в десятичное
Для того, чтобы перевести дробное восьмеричное число в десятичное, необходимо записать дробное восьмеричное число, убрав точку и затем сверху расставить индексы.
Например, переведем дробное восьмеричное число 12.368 в десятичное:
| Позиция в числе | 1 | 0 | -1 | -2 |
| Число | 1 | 2 | 3 | 6 |
12.368 = 1 ⋅ 81 + 2 ⋅ 80 + 3 ⋅ 8-1 + 6 ⋅ 8-2 = 10.4687510
Таблица значений десятичных чисел от 0 до 100 в восьмеричной системе счисления
| Значение числа в десятичной системе счисления | Значение числа в восьмеричной системе счисления |
| 010 | 08 |
| 110 | 18 |
| 210 | 28 |
| 310 | 38 |
| 410 | 48 |
| 510 | 58 |
| 610 | |
| 710 | 78 |
| 810 | 108 |
| 910 | 118 |
| 1010 | 128 |
| 1110 | 138 |
| 1210 | 148 |
| 1310 | 158 |
| 1410 | 168 |
| 1510 | 178 |
| 1610 | 208 |
| 1710 | 218 |
| 1810 | 228 |
| 1910 | 238 |
| 2010 | 248 |
| 2110 | 258 |
| 268 | |
| 2310 | 278 |
| 2410 | 308 |
| 2510 | 318 |
| 2610 | 328 |
| 2710 | 338 |
| 2810 | 348 |
| 2910 | 358 |
| 3010 | 368 |
| 3110 | 378 |
| 3210 | 408 |
| 3310 | 418 |
| 3410 | 428 |
| 3510 | 438 |
| 3610 | 448 |
| 3710 | 458 |
| 468 | |
| 3910 | 478 |
| 4010 | 508 |
| 4110 | 518 |
| 4210 | 528 |
| 4310 | 538 |
| 4410 | 548 |
| 4510 | 558 |
| 4610 | 568 |
| 4710 | 578 |
| 4810 | 608 |
| 4910 | 618 |
| 5010 | 628 |
| Значение числа в десятичной системе счисления | Значение числа в восьмеричной системе счисления |
| 5110 | 638 |
| 5210 | 648 |
| 5310 | 658 |
| 5410 | 668 |
| 5510 | 678 |
| 5610 | 708 |
| 5710 | 718 |
| 5810 | 728 |
| 5910 | 738 |
| 6010 | 748 |
| 6110 | 758 |
| 6210 | 768 |
| 6310 | 778 |
| 6410 | 1008 |
| 6510 | 1018 |
| 6610 | 1028 |
| 6710 | 1038 |
| 6810 | 1048 |
| 6910 | 1058 |
| 7010 | 1068 |
| 7110 | 1078 |
| 7210 | 1108 |
| 7310 | 1118 |
| 7410 | 1128 |
| 7510 | 1138 |
| 7610 | 1148 |
| 7710 | 1158 |
| 7810 | 1168 |
| 7910 | 1178 |
| 8010 | 1208 |
| 8110 | 1218 |
| 8210 | 1228 |
| 8310 | 1238 |
| 8410 | 1248 |
| 8510 | 1258 |
| 8610 | 1268 |
| 8710 | 1278 |
| 8810 | 1308 |
| 8910 | 1318 |
| 9010 | 1328 |
| 9110 | 1338 |
| 9210 | 1348 |
| 9310 | 1358 |
| 9410 | 1368 |
| 9510 | 1378 |
| 9610 | 1408 |
| 9710 | 1418 |
| 9810 | 1428 |
| 9910 | 1438 |
| 10010 | 1448 |
Преобразование чисел в различные системы счисления
Система чисел является систематическим способом представления чисел символьными символами и использует базовое значение для удобной группировки чисел в сжатой форме. Самая распространенная система числов — десятичная, которая имеет базовое значение 10, и набор символов 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9. Однако существуют и другие числовые системы, которые могут быть более эффективными для определенной цели. Например, так как на компьютерах используется логическое значение для вычислений и операций, для выполнения вычислений и операций используется двоичная числовая система, которая имеет базовое значение 2.
Самая распространенная система числов — десятичная, которая имеет базовое значение 10, и набор символов 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9. Однако существуют и другие числовые системы, которые могут быть более эффективными для определенной цели. Например, так как на компьютерах используется логическое значение для вычислений и операций, для выполнения вычислений и операций используется двоичная числовая система, которая имеет базовое значение 2.
Microsoft Office Excel есть несколько функций, которые можно использовать для преобразования чисел в числовые системы и из них:
|
Система номеров |
Базовое значение |
Набор символьных знаков |
|
Двоичный |
2 |
0,1 |
|
Восьмеричном |
8 |
0, 1, 2, 3, 4, 5, 6, 7 |
|
Действительное. |
10 |
0, 1, 2, 3, 4, 5, 6, 7, 8 и 9 |
|
Шестнадцатеричный |
16 |
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F |
Для этого используйте функцию ДВ.В.Е.
|
Для этого используйте функцию ДВ.В.EX.
|
|
Для этого используйте функцию ДВ.В.ВЕХ.
|
|
Для этого используйте функцию DEC2BIN.
|
Для этого используйте функцию DEC2HEX.
|
Для этого используйте функцию DEC2OCT.
|
Для этого используйте функцию HEX2BIN.
|
|
Для этого используйте функцию HEX2DEC.
|
|
Для этого используйте функцию HEX2OCT.
|
|
Для этого используйте функцию ВОСЬМ.В.ДВ.
|
Для этого используйте функцию ВОСЬМ.В.Е.
|
Для этого используйте функцию ВОСЬМ.В.EX.
|
Восьмеричный калькулятор онлайн
Если вам необходимо произвести математические операции в восьмеричной системе счисления воспользуйтесь нашим восьмеричным онлайн калькулятором:
+−×÷ANDORXOR =
Просто введите восьмеричные числа, выберите операцию и получите результат.
Калькулятор может производить следующие действия:
- сложение +
- вычитание −
- умножение ×
- деление ÷
- логическое И (AND)
- логическое ИЛИ (OR)
- исключающее ИЛИ (XOR)
Сложение в восьмеричной системе счисления
Сложение двух восьмеричных чисел производится столбиком, как и в десятичной системе, но по следующим правилам:
| + | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 10 |
| 2 | 2 | 3 | 4 | 5 | 6 | 7 | 10 | 11 |
| 3 | 3 | 4 | 5 | 6 | 7 | 10 | 11 | 12 |
| 4 | 4 | 5 | 6 | 7 | 10 | 11 | 12 | 13 |
| 5 | 5 | 6 | 7 | 10 | 11 | 12 | 13 | 14 |
| 6 | 6 | 7 | 10 | 11 | 12 | 13 | 14 | 15 |
| 7 | 7 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
Пример
Для примера сложим 777 и 15:
| + | 7 | 7 | 7 | ||
| 1 | 5 | ||||
| 1 | 0 | 1 | 4 | ||
7778 + 158 = 10148
(51110 + 1310 = 52410)
Вычитание в восьмеричной системе счисления
Вычитание восьмеричных чисел производится столбиком. Правила вычитания обратны правилам сложения (см. таблицу выше).
Правила вычитания обратны правилам сложения (см. таблицу выше).
Пример
Для примера вычтем из числа 1014 число 777:
| – | 1 | 0 | 1 | 4 | |
| 7 | 7 | 7 | |||
| 1 | 5 | ||||
10148 − 7778 = 158
(52410 − 51110 = 1310)
Умножение чисел в восьмеричной системе счисления
Умножение восьмеричных чисел производится в столбик по следующим правилам:
| × | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2 | 0 | 2 | 4 | 6 | 10 | 12 | 14 | 16 |
| 3 | 0 | 3 | 6 | 11 | 14 | 17 | 22 | 25 |
| 4 | 0 | 4 | 10 | 14 | 20 | 24 | 30 | 34 |
| 5 | 0 | 5 | 12 | 17 | 24 | 31 | 36 | 43 |
| 6 | 0 | 6 | 14 | 22 | 30 | 36 | 44 | 52 |
| 7 | 0 | 7 | 16 | 25 | 34 | 43 | 52 | 61 |
Пример
Для примера перемножим числа 777 и 15:
| × | 7 | 7 | 7 | ||
| 1 | 5 | ||||
| + | 4 | 7 | 7 | 3 | |
| 7 | 7 | 7 | |||
| 1 | 4 | 7 | 6 | 3 | |
7778 × 158 = 147638
(51110 × 1310 = 664310)
Деление чисел в восьмеричной системе счисления
Деление восьмеричных чисел выполняется по тому же принципу, что и деление десятичных, например:
Пример
Для примера разделим число 720 на 4:
7208 ÷ 48 = 1648
(46410 ÷ 410 = 11610)
См.
 также
такжеВосьмеричный
| шестнадцатеричный | декабрь | окт | 3 | 2 | 1 | 0 | шаг |
|---|---|---|---|---|---|---|---|
| 0шестнадцатеричный | 00декабрь | 00окт | 0 | 0 | 0 | 0 | грамм0 |
| 1шестнадцатеричный | 01декабрь | 01окт | 0 | 0 | 0 | 1 | час1 |
| 2шестнадцатеричный | 02декабрь | 02окт | 0 | 0 | 1 | 0 | j3 |
| 3шестнадцатеричный | 03декабрь | 03окт | 0 | 0 | 1 | 1 | я2 |
| 4шестнадцатеричный | 04декабрь | 04окт | 0 | 1 | 0 | 0 | п7 |
| 5шестнадцатеричный | 05декабрь | 05окт | 0 | 1 | 0 | 1 | м6 |
| 6шестнадцатеричный | 06декабрь | 06окт | 0 | 1 | 1 | 0 | k4 |
| 7шестнадцатеричный | 07декабрь | 07окт | 0 | 1 | 1 | 1 | л5 |
| 8шестнадцатеричный | 08декабрь | 10окт | 1 | 0 | 0 | 0 | vF |
| 9шестнадцатеричный | 09декабрь | 11окт | 1 | 0 | 0 | 1 | тыE |
| Ашестнадцатеричный | 10декабрь | 12окт | 1 | 0 | 1 | 0 | sC |
| Bшестнадцатеричный | 11декабрь | 13окт | 1 | 0 | 1 | 1 | тD |
| Cшестнадцатеричный | 12декабрь | 14окт | 1 | 1 | 0 | 0 | о8 |
| Dшестнадцатеричный | 13декабрь | 15окт | 1 | 1 | 0 | 1 | п9 |
| Eшестнадцатеричный | 14декабрь | 16окт | 1 | 1 | 1 | 0 | рB |
| Fшестнадцатеричный | 15декабрь | 17окт | 1 | 1 | 1 | 1 | qА |
В восьмеричный система счисления, или же окт для краткости, это основание -8 система счисления и использует цифры От 0 до 7. {0}}
{0}}
Выполнив приведенное выше вычисление в знакомой десятичной системе, мы поймем, почему 112 в восьмеричной системе счисления равно 64 + 8 + 2 = 74 в десятичной системе счисления.
| × | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 10 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 10 |
| 2 | 2 | 4 | 6 | 10 | 12 | 14 | 16 | 20 |
| 3 | 3 | 6 | 11 | 14 | 17 | 22 | 25 | 30 |
| 4 | 4 | 10 | 14 | 20 | 24 | 30 | 34 | 40 |
| 5 | 5 | 12 | 17 | 24 | 31 | 36 | 43 | 50 |
| 6 | 6 | 14 | 22 | 30 | 36 | 44 | 52 | 60 |
| 7 | 7 | 16 | 25 | 34 | 43 | 52 | 61 | 70 |
| 10 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 100 |
Содержание
- 1 использование
- 1.
 1 Коренными американцами
1 Коренными американцами - 1.2 Европейцами
- 1.3 В компьютерах
- 1.4 В авиации
- 1.
- 2 Преобразование между базами
- 2.1 Преобразование десятичного числа в восьмеричное
- 2.1.1 Метод последовательного евклидова деления на 8
- 2.1.2 Метод последовательного умножения на 8
- 2.1.3 Метод последовательного дублирования
- 2.2 Восьмеричное преобразование в десятичное
- 2.2.1 Метод последовательного дублирования
- 2.3 Восьмеричное преобразование в двоичное
- 2.4 Двоичное преобразование в восьмеричное
- 2.5 Восьмеричное преобразование в шестнадцатеричное
- 2.6 Преобразование шестнадцатеричного числа в восьмеричное
- 2.1 Преобразование десятичного числа в восьмеричное
- 3 Действительные числа
- 3.1 Фракции
- 3.2 Иррациональные числа
- 4 Смотрите также
- 5 Рекомендации
- 6 внешняя ссылка
использование
Коренными американцами
В Язык юки в Калифорния и Памейские языки[1] в Мексика имеют восьмеричную систему, потому что говорящие считают, используя промежутки между пальцами, а не сами пальцы. [2]
[2]
Европейцами
- Было высказано предположение, что реконструированный Протоиндоевропейский Слово «девять» может быть связано со словом ПИРОГ, означающим «новый». Основываясь на этом, некоторые предполагают, что протоиндоевропейцы использовали восьмеричную систему счисления, хотя свидетельств, подтверждающих это, мало.[3]
- В 1668 г. Джон Уилкинс в Эссе о реальном персонаже и философский язык предложено использовать основание 8 вместо 10, «потому что способ Дихотомии или Двучастия является наиболее естественным и легким видом деления, это Число способно на это вплоть до Объединения».[4]
- В 1716 г. король Карл XII Швеции спросил Эмануэль Сведенборг разработать систему счисления, основанную на 64 вместо 10. Сведенборг, однако, утверждал, что для людей с меньшим интеллектом, чем король, такая большая база была бы слишком трудной, и вместо этого предложил 8 в качестве базы. В 1718 году Сведенборг написал (но не опубликовал) рукопись: «En ny rekenkonst som om vexlas wid Thalet 8 i stelle then wanliga wid Thalet 10» («Новая арифметика (или искусство счета), которая меняется на цифру 8 вместо обычный у № 10 «).
 Числа 1-7 там обозначаются согласными l, s, n, m, t, f, u (v), а ноль — гласной o. Таким образом, 8 = «lo», 16 = «so», 24 = «no», 64 = «loo», 512 = «looo» и т. Д. Числа с последовательными согласными произносятся с гласными звуками между ними в соответствии со специальным правилом.[5]
Числа 1-7 там обозначаются согласными l, s, n, m, t, f, u (v), а ноль — гласной o. Таким образом, 8 = «lo», 16 = «so», 24 = «no», 64 = «loo», 512 = «looo» и т. Д. Числа с последовательными согласными произносятся с гласными звуками между ними в соответствии со специальным правилом.[5] - Пишет под псевдонимом «Hirossa Ap-Iccim» в Журнал Джентльмена, (Лондон) июль 1745 г., Хью Джонс предложил восьмеричную систему для британских монет, мер и весов. «Поскольку разум и удобство указывают нам на единый стандарт для всех количеств, который я назову Грузинский стандарт; и это только для деления каждого целого числа в каждом разновидность на восемь равных частей и каждую часть снова на 8 реальных или мнимых частиц, насколько это необходимо. Для всех наций универсально десятки (первоначально обусловлено количеством цифр на обеих руках), но 8 — гораздо более полное и простое число; так как он делится на половины, четверти и половинки четвертей (или единиц) без дроби, из которых подразделение десять неспособен .
 .. «В более позднем трактате о Вычисление октавы (1753) Джонс заключил: «Арифметика Октавы кажется наиболее подходящим для Природы вещей, и поэтому может быть названа естественной арифметикой в противоположность тому, что используется сейчас десятилетиями; которую можно назвать искусственной арифметикой ».[6]
.. «В более позднем трактате о Вычисление октавы (1753) Джонс заключил: «Арифметика Октавы кажется наиболее подходящим для Природы вещей, и поэтому может быть названа естественной арифметикой в противоположность тому, что используется сейчас десятилетиями; которую можно назвать искусственной арифметикой ».[6] - В 1801 г. Джеймс Андерсон критиковал французов за основание метрическая система по десятичной арифметике. Он предложил базу 8, для которой он ввел термин восьмеричный. Его работа была задумана как развлекательная математика, но он предложил чисто восьмеричную систему мер и весов и заметил, что существующая система Английские единицы в значительной степени уже была восьмеричной системой.[7]
- В середине 19 века Альфред Б. Тейлор пришел к выводу, что «наша восьмеричная система счисления с основанием 8, таким образом, вне всякого сравнения»лучший из возможных«для арифметической системы». Предложение включало графическое обозначение цифр и новые названия чисел, предполагая, что мы должны считать «ООН, ду, то, fo, па, se, ки, не-ти, унты-ун, Unty-du«и так далее, с последовательными именами, кратными восьми»не-ти, долг, thety, фоты, пати, Sety, Кити и под.
 «Так, например, число 65 (101 в восьмеричной системе) будет произноситься в восьмеричной системе счисления как под ООН.[8][9] Тейлор также переиздал некоторые из работ Сведенборга по восьмеричной системе в качестве приложения к цитированным выше публикациям.
«Так, например, число 65 (101 в восьмеричной системе) будет произноситься в восьмеричной системе счисления как под ООН.[8][9] Тейлор также переиздал некоторые из работ Сведенборга по восьмеричной системе в качестве приложения к цитированным выше публикациям.
В компьютерах
Octal стал широко использоваться в вычислениях, когда такие системы, как UNIVAC 1050, PDP-8, ICL 1900 и Мэйнфреймы IBM нанятый 6-битный, 12 бит, 24 бит или же 36-битный слова. Восьмеричный был идеальным сокращением двоичного кода для этих машин, потому что размер их слова делится на три (каждая восьмеричная цифра представляет три двоичных цифры). Таким образом, две, четыре, восемь или двенадцать цифр могут кратко отображать весь машинное слово. Это также сокращает расходы, позволяя Nixie трубы, семисегментные дисплеи, и калькуляторы для использования на операторских консолях, где двоичные дисплеи были слишком сложными для использования, десятичные дисплеи требовали сложного оборудования для преобразования радиусов и шестнадцатеричный дисплеи, необходимые для отображения большего количества цифр.
Однако все современные вычислительные платформы используют 16-, 32- или 64-битные слова, далее делится на восьмибитные байты. В таких системах потребуется три восьмеричных цифры на байт, причем наиболее значимая восьмеричная цифра представляет две двоичные цифры (плюс один бит следующего значимого байта, если таковой имеется). Восьмеричное представление 16-битного слова требует 6 цифр, но наиболее значимая восьмеричная цифра представляет (довольно неэлегантно) только один бит (0 или 1). Это представление не дает возможности легко прочитать самый значимый байт, потому что он размазан по четырем восьмеричным цифрам. Поэтому сегодня в языках программирования чаще используется шестнадцатеричный код, поскольку две шестнадцатеричные цифры точно определяют один байт. На некоторых платформах с размером слова степень двойки все еще есть подслова инструкций, которые легче понять, если они отображаются в восьмеричном формате; это включает PDP-11 и Семейство Motorola 68000. Современные повсеместные архитектура x86 также принадлежит к этой категории, но восьмеричное число редко используется на этой платформе, хотя некоторые свойства двоичного кодирования кодов операций становятся более очевидными при отображении в восьмеричном формате, например байт ModRM, который разделен на поля по 2, 3 и 3 бита, поэтому восьмеричные числа могут быть полезны при описании этих кодировок.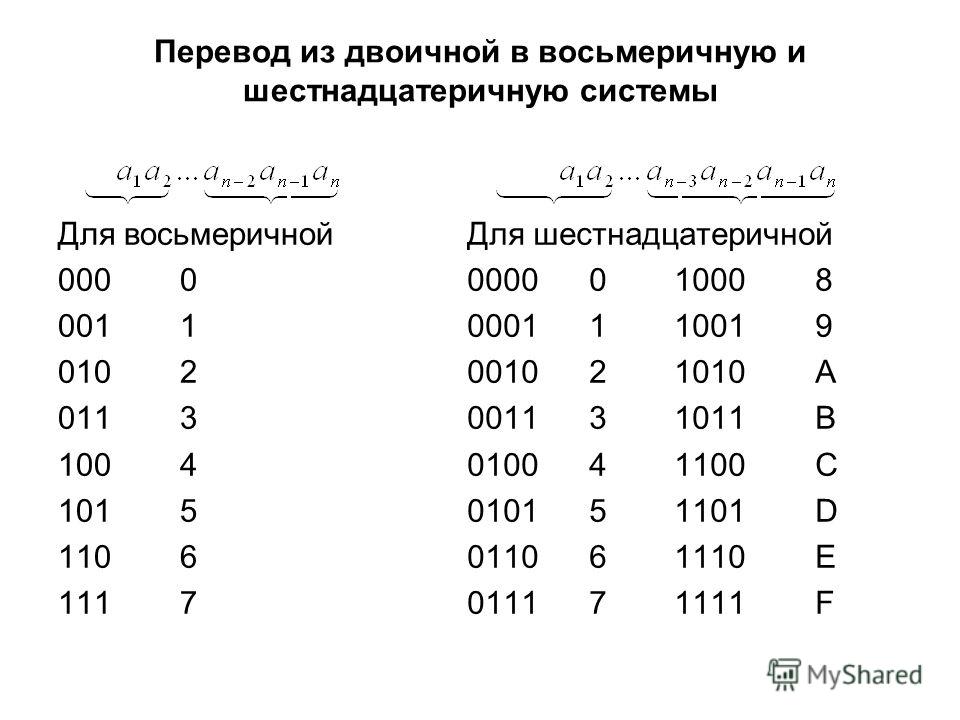 До появления монтажники некоторые программисты вручную кодировали бы программы в восьмеричном формате; например, Дик Уиппл и Джон Арнольд написали Tiny BASIC Extended непосредственно в машинном коде с использованием восьмеричного числа.[10]
До появления монтажники некоторые программисты вручную кодировали бы программы в восьмеричном формате; например, Дик Уиппл и Джон Арнольд написали Tiny BASIC Extended непосредственно в машинном коде с использованием восьмеричного числа.[10]
Восьмеричное число иногда используется в вычислениях вместо шестнадцатеричного, возможно, наиболее часто в наше время в сочетании с права доступа к файлам под Unix системы (см. chmod ). Его преимущество состоит в том, что не требуются какие-либо дополнительные символы в виде цифр (шестнадцатеричная система имеет основание 16 и, следовательно, требует шести дополнительных символов помимо 0–9). Он также используется для цифровых дисплеев.
В языках программирования восьмеричное литералы обычно отождествляются с множеством префиксы, включая цифру 0, письма о или же q, комбинация цифр и букв 0o, или символ &[11] или же $. В Конвенция Motorola, восьмеричные числа имеют префикс @, тогда как малый (или большой[12]) письмо о[12] или же q[12] добавляется как постфикс после Соглашение Intel. [13][14] В Параллельная DOS, Многопользовательская DOS и РЕАЛЬНЫЙ / 32 а также в DOS Plus и DR-DOS разные переменные среды подобно $ CLS, $ ON, $ OFF, $ HEADER или же $ FOOTER поддержать nn запись восьмеричных чисел,[15][16][17] и DR-DOS ОТЛАЖИВАТЬ использует для префикса восьмеричных чисел.
[13][14] В Параллельная DOS, Многопользовательская DOS и РЕАЛЬНЫЙ / 32 а также в DOS Plus и DR-DOS разные переменные среды подобно $ CLS, $ ON, $ OFF, $ HEADER или же $ FOOTER поддержать nn запись восьмеричных чисел,[15][16][17] и DR-DOS ОТЛАЖИВАТЬ использует для префикса восьмеричных чисел.
Например, литерал 73 (основание 8) может быть представлен как 073, o73, q73, 0o73, 73, @73, &73, $73 или же 73o на разных языках.
Новые языки отказались от префикса 0, поскольку десятичные числа часто представляются с ведущими нулями. Префикс q был введен, чтобы избежать префикса о ошибочно принимается за ноль, а префикс 0o был введен, чтобы не начинать числовой литерал с буквенного символа (например, о или же q), так как это может привести к путанице литерала с именем переменной. Префикс 0o также следует модели, заданной префиксом 0x используется для шестнадцатеричных литералов в Язык C; это поддерживается Haskell,[18]OCaml,[19]Python начиная с версии 3. 0,[20]Раку,[21]Рубин,[22]Tcl начиная с версии 9,[23] и он предназначен для поддержки ECMAScript 6[24] (приставка 0 первоначально обозначал базу 8 в JavaScript но мог вызвать путаницу,[25] поэтому он не одобрялся в ECMAScript 3 и был исключен из ECMAScript 5.[26]).
0,[20]Раку,[21]Рубин,[22]Tcl начиная с версии 9,[23] и он предназначен для поддержки ECMAScript 6[24] (приставка 0 первоначально обозначал базу 8 в JavaScript но мог вызвать путаницу,[25] поэтому он не одобрялся в ECMAScript 3 и был исключен из ECMAScript 5.[26]).
Восьмеричные числа, которые используются в некоторых языках программирования (C, Perl, PostScript …) Для текстовых / графических представлений байтовых строк, когда некоторые байтовые значения (не представленные на кодовой странице, неграфические, имеющие особое значение в текущем контексте или иным образом нежелательные) должны быть сбежал в качестве nn. Восьмеричное представление может быть особенно удобно с байтами, отличными от ASCII. UTF-8, который кодирует группы из 6 бит, и где любой начальный байт имеет восьмеричное значение 3nn и любой байт продолжения имеет восьмеричное значение 2nn.
Octal также использовался для плавающая точка в Ферранти Атлас (1962), Берроуз B5500 (1964), Берроуз B5700 (1971), Берроуз B6700 (1971) и Берроуз B7700 (1972) компьютеры.
В авиации
Транспондеры в самолете передать код, выражаемое четырехзначным числом при запросе наземным радаром. Этот код используется для различения разных самолетов на экране радара.
Преобразование между базами
Преобразование десятичного числа в восьмеричное
Метод последовательного евклидова деления на 8
Чтобы преобразовать целые десятичные числа в восьмеричные, разделять исходное число на максимально возможную степень 8 и разделить остатки на последовательно меньшие степени 8, пока степень не станет 1. Восьмеричное представление формируется частными, записанными в порядке, сгенерированном алгоритмом. Например, для преобразования 12510 в восьмеричный:
- 125 = 82 × 1 + 61
- 61 = 81 × 7 + 5
- 5 = 80 × 5 + 0
Следовательно, 12510 = 1758.
Другой пример:
- 900 = 83 × 1 + 388
- 388 = 82 × 6 + 4
- 4 = 81 × 0 + 4
- 4 = 80 × 4 + 0
Следовательно, 90010 = 16048.
Метод последовательного умножения на 8
Чтобы преобразовать десятичную дробь в восьмеричную, умножьте ее на 8; целая часть результата — это первая цифра восьмеричной дроби. Повторите процесс с дробной частью результата, пока она не станет нулевой или находится в пределах допустимых ошибок.
Пример: преобразовать 0,1640625 в восьмеричное:
- 0.1640625 × 8 = 1.3125 = 1 + 0.3125
- 0.3125 × 8 = 2.5 = 2 + 0.5
- 0.5 × 8 = 4.0 = 4 + 0
Следовательно, 0,164062510 = 0.1248.
Эти два метода можно комбинировать для обработки десятичных чисел как с целой, так и с дробной частью, используя первый для целой части, а второй — для дробной части.
Метод последовательного дублирования
Чтобы преобразовать целые десятичные числа в восьмеричные, поставьте перед числом «0». Выполните следующие шаги, пока цифры остаются в правой части системы счисления: Удвойте значение слева от системы счисления, используя восьмеричный rules, переместите точку счисления на одну цифру вправо, а затем поместите удвоенное значение под текущим значением, чтобы точки счисления выровнялись. {i} ight)}
{i} ight)}
В этой формуле ая — это преобразовываемая отдельная восьмеричная цифра, где я — позиция цифры (считая от 0 для самой правой цифры).
Пример: преобразовать 7648 в десятичный:
- 7648 = 7 × 82 + 6 × 81 + 4 × 80 = 448 + 48 + 4 = 50010
Для двузначных восьмеричных чисел этот метод сводится к умножению первой цифры на 8 и добавлению второй цифры, чтобы получить результат.
Пример: 658 = 6 × 8 + 5 = 5310
Метод последовательного дублирования
Чтобы преобразовать восьмеричные числа в десятичные, поставьте перед числом «0». Выполните следующие шаги, пока цифры остаются с правой стороны системы счисления: Удвойте значение слева от системы счисления, используя десятичный rules, переместите точку счисления на одну цифру вправо, а затем поместите удвоенное значение под текущим значением, чтобы точки счисления выровнялись. Вычесть десятичный эти цифры слева от системы счисления и просто опустите эти цифры вправо без изменений.
Вычесть десятичный эти цифры слева от системы счисления и просто опустите эти цифры вправо без изменений.
Пример:
0,1 1 4 6 6 восьмеричное значение -0 ----------- 1,1 4 6 6 - 2 ---------- 9,4 6 6 - 1 8 -------- - 7 6,6 6 - 1 5 2 ---------- 6 1 4,6 - 1 2 2 8 ---------- 4 9 1 8. десятичное значение
Восьмеричное преобразование в двоичное
Чтобы преобразовать восьмеричное число в двоичное, замените каждую восьмеричную цифру ее двоичным представлением.
Пример: преобразовать 518 в двоичный:
- 58 = 1012
- 18 = 0012
Следовательно, 518 = 101 0012.
Двоичное преобразование в восьмеричное
Это процесс, обратный предыдущему алгоритму. Двоичные цифры сгруппированы по тройкам, начиная с младшего разряда и переходя влево и вправо. Добавьте начальные нули (или конечные нули справа от десятичной точки), чтобы заполнить последнюю группу из трех, если необходимо. Затем замените каждое трио эквивалентной восьмеричной цифрой.
Затем замените каждое трио эквивалентной восьмеричной цифрой.
Например, преобразуйте двоичное число 1010111100 в восьмеричное:
001 010 111 100 1 2 7 4
Следовательно, 10101111002 = 12748.
Преобразование двоичного числа 11100.01001 в восьмеричное:
011 100 . 010 010 3 4 . 2 2
Следовательно, 11100.010012 = 34.228.
Восьмеричное преобразование в шестнадцатеричное
Преобразование выполняется в два этапа с использованием двоичного кода в качестве промежуточной базы. Восьмеричное число преобразуется в двоичное, а затем двоичное в шестнадцатеричное, цифры группируются по четыре, каждая из которых соответствует шестнадцатеричной цифре.
Например, преобразовать восьмеричное число 1057 в шестнадцатеричное:
- В бинарный:
1 0 5 7 001 000 101 111
- затем в шестнадцатеричный:
0010 0010 1111 2 2 F
Следовательно, 10578 = 22F16.
Преобразование шестнадцатеричного числа в восьмеричное
Преобразование шестнадцатеричного числа в восьмеричное происходит путем преобразования сначала шестнадцатеричных цифр в 4-битные двоичные значения, а затем перегруппировки двоичных битов в 3-разрядные восьмеричные цифры.
Например, чтобы конвертировать 3FA516:
- В бинарный:
3 F А 5 0011 1111 1010 0101
- затем в восьмеричное:
0 011 111 110 100 101 0 3 7 6 4 5
Следовательно, 3FA516 = 376458.
Действительные числа
Фракции
Из-за того, что множители только два, многие восьмеричные дроби имеют повторяющиеся цифры, хотя они, как правило, довольно просты:
| Основание десятичной дроби Основные факторы базы: 2, 5 Простые множители на единицу ниже основания: 3 Основные множители единицы над базой: 11 Другие основные факторы: 7 13 17 19 23 29 31 | Восьмеричное основание Основные факторы базы: 2 Простые множители на единицу ниже основания: 7 Основные множители единицы над базой: 3 Другие основные факторы: 5 13 15 21 23 27 35 37 | ||||
| Дробная часть | главные факторы знаменателя | Позиционное представительство | Позиционное представительство | главные факторы знаменателя | Дробная часть |
| 1/2 | 2 | 0. 5 5 | 0.4 | 2 | 1/2 |
| 1/3 | 3 | 0.3333… = 0.3 | 0.2525… = 0.25 | 3 | 1/3 |
| 1/4 | 2 | 0.25 | 0.2 | 2 | 1/4 |
| 1/5 | 5 | 0.2 | 0.1463 | 5 | 1/5 |
| 1/6 | 2, 3 | 0.16 | 0.125 | 2, 3 | 1/6 |
| 1/7 | 7 | 0.142857 | 0. 1 1 | 7 | 1/7 |
| 1/8 | 2 | 0.125 | 0.1 | 2 | 1/10 |
| 1/9 | 3 | 0.1 | 0.07 | 3 | 1/11 |
| 1/10 | 2, 5 | 0.1 | 0.06314 | 2, 5 | 1/12 |
| 1/11 | 11 | 0.09 | 0.0564272135 | 13 | 1/13 |
| 1/12 | 2, 3 | 0.083 | 0. 052 052 | 2, 3 | 1/14 |
| 1/13 | 13 | 0.076923 | 0.0473 | 15 | 1/15 |
| 1/14 | 2, 7 | 0.0714285 | 0.04 | 2, 7 | 1/16 |
| 1/15 | 3, 5 | 0.06 | 0.0421 | 3, 5 | 1/17 |
| 1/16 | 2 | 0.0625 | 0.04 | 2 | 1/20 |
| 1/17 | 17 | 0. 0588235294117647 0588235294117647 | 0.03607417 | 21 | 1/21 |
| 1/18 | 2, 3 | 0.05 | 0.034 | 2, 3 | 1/22 |
| 1/19 | 19 | 0.052631578947368421 | 0.032745 | 23 | 1/23 |
| 1/20 | 2, 5 | 0.05 | 0.03146 | 2, 5 | 1/24 |
| 1/21 | 3, 7 | 0.047619 | 0.03 | 3, 7 | 1/25 |
| 1/22 | 2, 11 | 0. 045 045 | 0.02721350564 | 2, 13 | 1/26 |
| 1/23 | 23 | 0.0434782608695652173913 | 0.02620544131 | 27 | 1/27 |
| 1/24 | 2, 3 | 0.0416 | 0.025 | 2, 3 | 1/30 |
| 1/25 | 5 | 0.04 | 0.02436560507534121727 | 5 | 1/31 |
| 1/26 | 2, 13 | 0.0384615 | 0.02354 | 2, 15 | 1/32 |
| 1/27 | 3 | 0.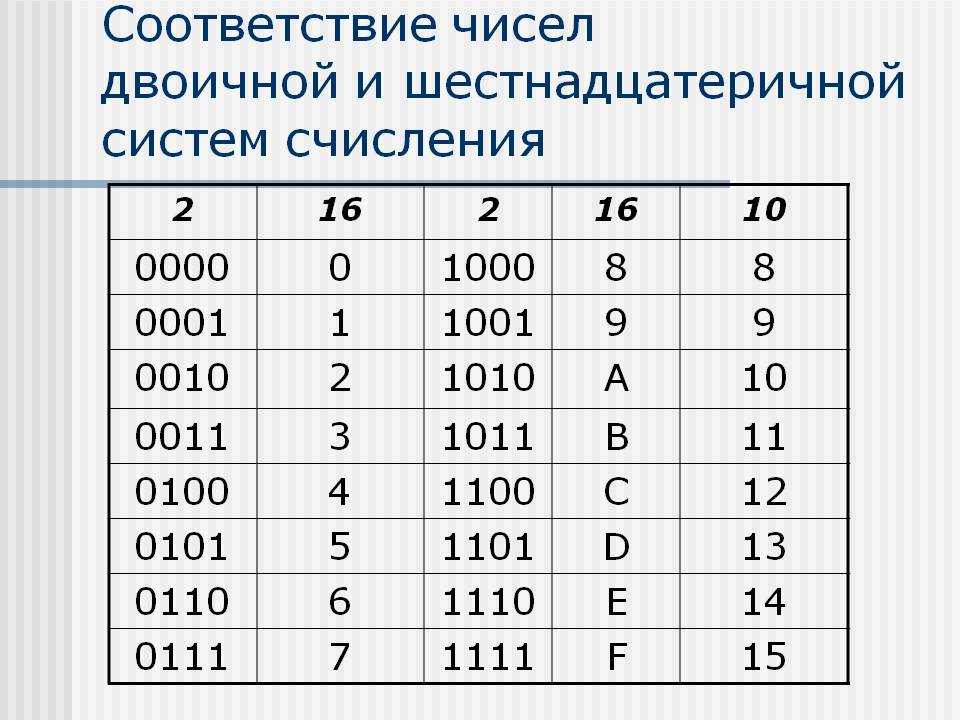 037 037 | 0.022755 | 3 | 1/33 |
| 1/28 | 2, 7 | 0.03571428 | 0.02 | 2, 7 | 1/34 |
| 1/29 | 29 | 0.0344827586206896551724137931 | 0.0215173454106475626043236713 | 35 | 1/35 |
| 1/30 | 2, 3, 5 | 0.03 | 0.02104 | 2, 3, 5 | 1/36 |
| 1/31 | 31 | 0.032258064516129 | 0.02041 | 37 | 1/37 |
| 1/32 | 2 | 0. 03125 03125 | 0.02 | 2 | 1/40 |
Иррациональные числа
В таблице ниже даны расширения некоторых распространенных иррациональные числа в десятичной и восьмеричной системе.
| Число | Позиционное представительство | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Десятичный | Восьмеричный | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| √2 (длина диагональ единицы квадрат ) | 1.414213562373095048… | 1.3240 4746 3177 1674… | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| √3 (длина диагонали агрегата куб ) | 1.732050807568877293… | 1.5666 3656 4130 2312… | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| √5 (длина диагональ 1 × 2 прямоугольник ) | 2.236067977499789696… | 2.1706 7363 3457 7224… | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| φ (фи, Золотое сечение = (1+√5)/2) | 1.618033988749894848… | 1.4743 3571 5627 7512… | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| π (пи, отношение длина окружности к диаметр круга) | 3.141592653589793238462643 383279502884197169399375105. 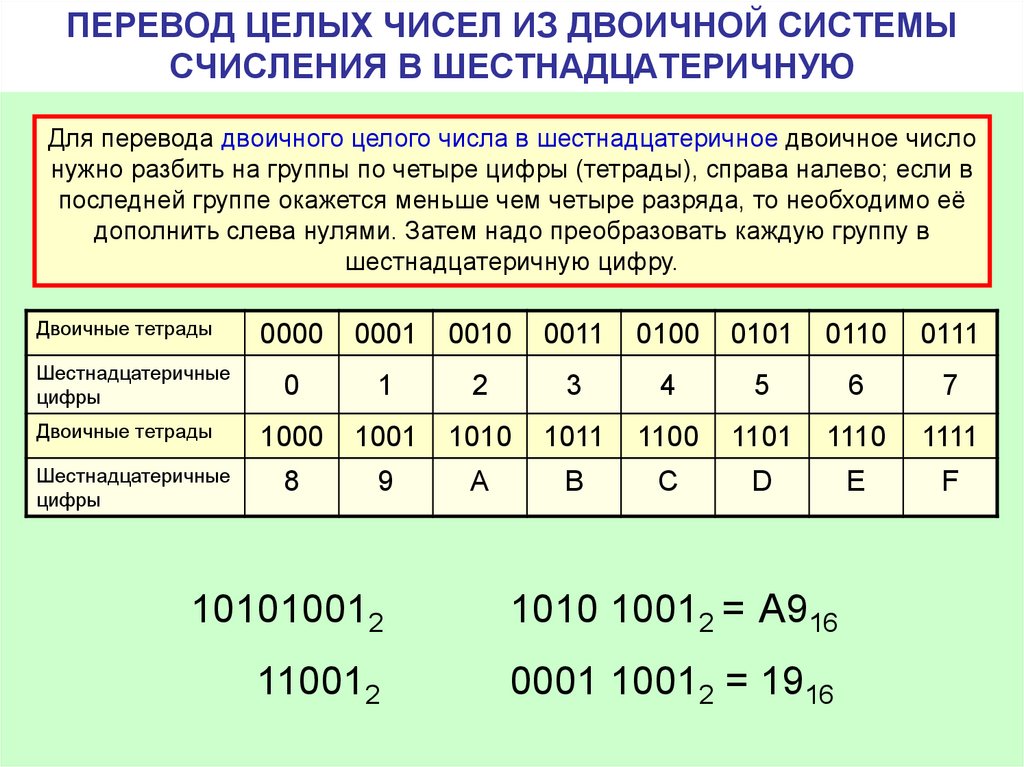 «parseInt ()», Сеть разработчиков Mozilla (MDN), «parseInt ()», Сеть разработчиков Mozilla (MDN), Если входная строка начинается с «0» (ноль), предполагается, что основание системы счисления равно 8 (восьмеричное) или 10 (десятичное). Выбор системы счисления зависит от реализации. ECMAScript 5 поясняет, что следует использовать 10 (десятичное), но пока не все браузеры поддерживают это. внешняя ссылка
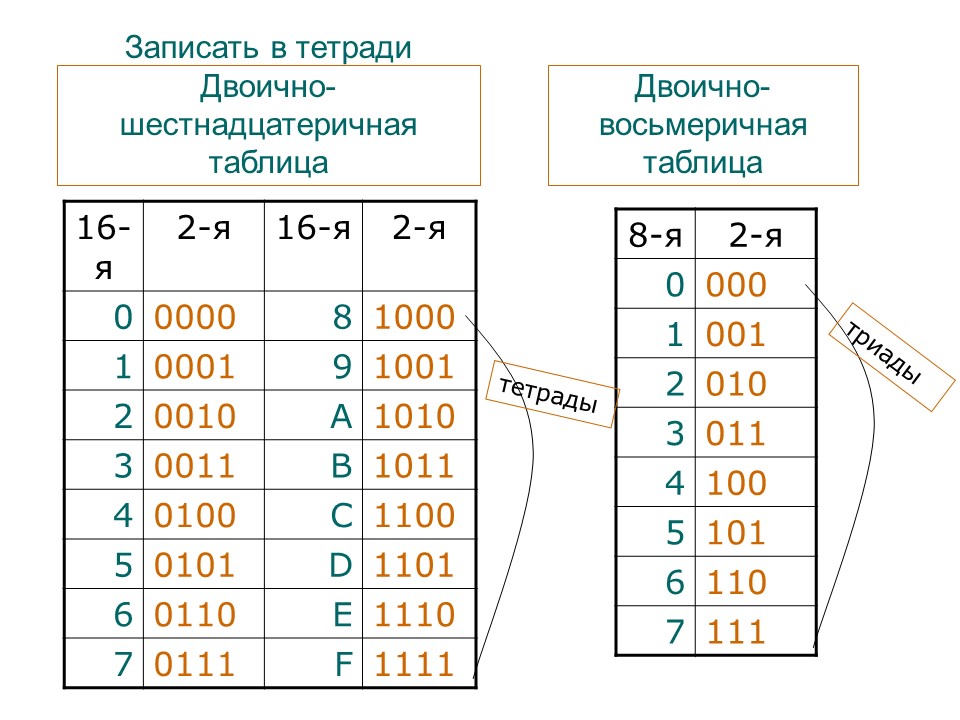
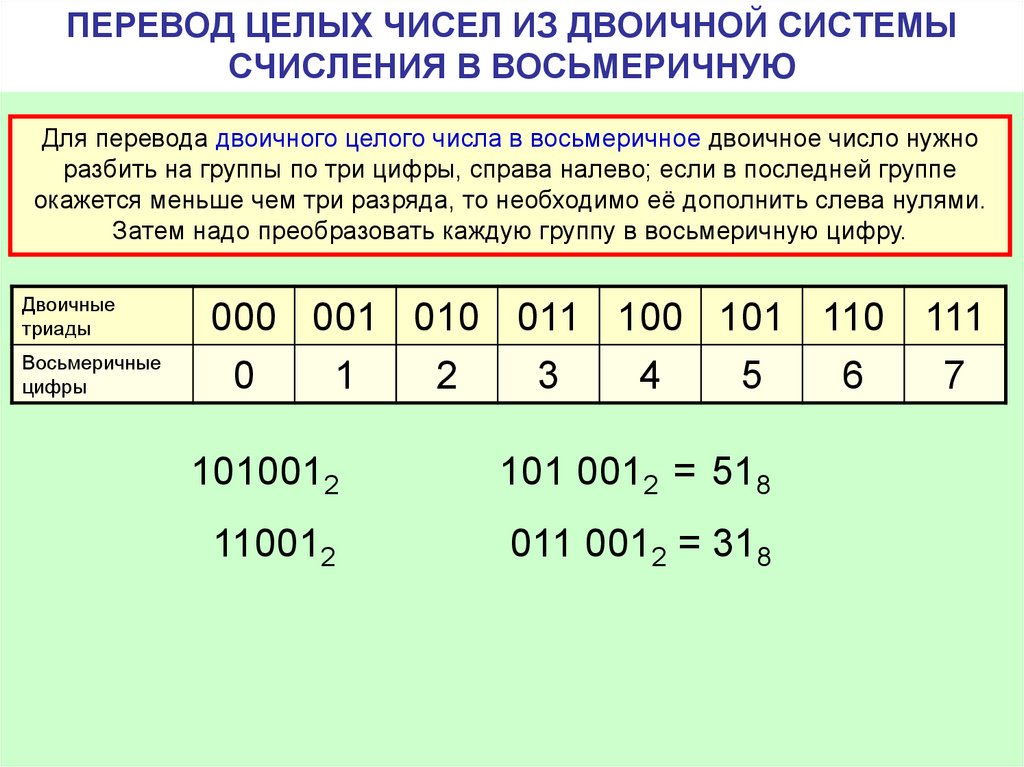
Как перевести число из двоичной системы в восьмеричную и шестнадцатеричную
Перевод чисел из двоичной системы счисления в восьмеричную, шестнадцатеричную или четвертичную и наоборот часто требуется для решения задач по теме Системы счисления. Таблица перевода чисел
Как перевести число из двоичной системы счисленияЧтобы перевести число из двоичной системы счисления в четвертичную, восьмеричную или шестнадцатеричную систему, нужно воспользоваться алгоритмом перевода:
Как перевести число в двоичную систему счисленияЧтобы перевести число из четвертичной, восьмеричной или шестнадцатеричной системы счисления в двоичную, нужно воспользоваться алгоритмом перевода:
Онлайн калькулятор перевода чисел из одной системы счисления в любую другуюВходные данные Введите число:
 Чтобы произвести расчеты, необходимо разрешить элементы ActiveX! Основы Расчёт Справочник Информатика Программирование 66567 Пример 1 Расчёт • Справочник • Информатика • Программирование Перевести число 1111001102 из двоичной системы в четвертичную. Разбиваем число на группы по 2 цифры справа налево и заменяем каждую группу на аналог в четвертичной системе счисления из таблицы: 1111001102 = 01 11 10 01 10 = 132124 Уровень10 класс ПредметИнформатика СложностьПростая Пример 2 Расчёт • Справочник • Информатика • Программирование Перевести число 1111001102 из двоичной системы в восьмеричную. Разбиваем число на группы по 3 цифры справа налево и заменяем каждую группу на аналог в восьмеричной системе счисления из таблицы: 1111001102 = 111 100 110 = 7468 Уровень10 класс ПредметИнформатика СложностьПростая Пример 3 Расчёт • Справочник • Информатика • Программирование Перевести число 1111001102 из двоичной системы в шестнадцатеричную. Разбиваем число на группы по 4 цифры справа налево и заменяем каждую группу на аналог в шестнадцатеричной системе счисления из таблицы: 1111001102 = 0001 1110 0110 = 1E616 Уровень10 класс ПредметИнформатика СложностьПростая Пример 4 Расчёт • Справочник • Информатика • Программирование Перевести число 1203234 из четвертичной системы в двоичную. Выполняем замену каждой цифры на группу из 2 цифр в двоичной системе счисления: 1203234 = 01 10 00 11 10 11 = 110001110112 Уровень10 класс ПредметИнформатика СложностьПростая Пример 5 Расчёт • Справочник • Информатика • Программирование Перевести число 264750308 из восьмеричной системы в двоичную. Выполняем замену каждой цифры на группу из 3 цифр в двоичной системе счисления: 264750308 = 010 110 100 111 101 000 011 000 = 101101001111010000110002 Уровень10 класс ПредметИнформатика СложностьПростая Пример 6 Расчёт • Справочник • Информатика • Программирование Перевести число 2AC0F7416 из шестнадцатеричной системы в двоичную. Выполняем замену каждой цифры на группу из 4 цифр в двоичной системе счисления: 2AC0F7416 = 0010 1010 1100 0000 1111 0111 0100 = 101010110000001111011101002 Уровень10 класс ПредметИнформатика СложностьПростая Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!
простая методика перевода и примеры конвертации чиселМатематика 12.11.21 14 мин. Перевод чисел на язык, который понятен любой электронно-вычислительной машине, осуществляется по определенному алгоритму в некоторое представление. Наиболее востребованными являются двоичная, шестнадцатеричная, а также восьмеричная системы счисления. Однако перед переходом к практике специалисты рекомендуют рассмотреть теорию конвертации первой и последней формы информации (2 и 8).
Перевод чисел на язык, который понятен любой электронно-вычислительной машине, осуществляется по определенному алгоритму в некоторое представление. Общие сведенияДля работы с системами счисления (СС) необходимо разобрать их классификацию, а также базовые определения представления числовой информации. В математике существуют 2 понятия: цифра и число. Первое — базовая единица или символ, при комбинации которого можно записать любое значение. Цифры бывают только двух типов: римскими и арабскими. Однако наибольшее применение получили последние, поскольку используются при выполнении расчетов, записи результатов и т. д. Римские применяются в основном для обозначения величин, на которые требуется обратить внимание. Однако они непрактичны, поскольку не все знают их расшифровку. Кроме того, римские величины невозможно представить в экспоненциальной и степенной форме. Число — количественная характеристика, показывающая фактическое наличие или отсутствие какого-либо предмета, процесса или явления. Каждая величина состоит из разрядной сетки, т. е. единиц, десятков, сотен и т. д. При выполнении различных алгебраических операций важно следить за соответствием разрядов одного значения другому. Например, нельзя складывать сотни и единицы, т. к. это приведет к ошибочным вычислениям. Классификация числовых представленийНекоторые пользователи-практики могут считать, что нет смысла рассматривать классификацию систем исчисления, но это не так. Новички, начинающие знакомство с представлением числовой информации, должны понимать, что порядок (расположение) разрядов в двоичной и восьмеричной имеет значение. Всего бывает 2 вида СС, к которым относятся позиционные и непозиционные. Первые зависят от расположения математических символов, которые их составляют. Непозиционная — СС, в которой расположение знаков не влияет на результат. Для примера можно вспомнить известный фильм «Робинзон Крузо», где главный герой вел счет дней, прожитых на необитаемом острове, при помощи обыкновенных «палочек», которые рисовал на стене. После этого он подсчитывал их общее количество. Следует отметить, что их расположение не влияло на результат. Другим примером непозиционной СС является обучение детей в начальных классах устному счету. Для этой цели применяются палочки, на которых ребенок выполняет операции сложения, вычитания, умножения и даже деления.
Двоичный кодДля работы с двоичным кодом необходимо обратить на его основание. Оно равно 2, поскольку в двоичной системе счисления применяется только два значения 0 и 1. Это позволяет довольно просто реализовать любые алгоритмы на различных устройствах, используемых в вычислительной технике. В первых моделях ЭВМ использовались катушки индуктивности, информация в которых кодировалась наличием (1) или отсутствием (0) электромагнитного поля. Затем человек изобрел конденсатор, что улучшило характеристики компьютерной системы. Последние находились в специальных больших комнатах. Размеры ЭВМ постепенно уменьшались с изобретением новых элементов. Сначала это были транзисторы, а затем интегральные микросхемы. Все компоненты электронно-вычислительной машины или персонального компьютера (ПК) состоят из базовых радиокомпонентов — транзисторов. Последние наносятся методом напыления, а затем «упаковываются» в корпус. В результате получается интегральная микросхема. Кодирование осуществляется при помощи состояний элементов — открытый и закрытый полупроводниковые переходы.
Деление в столбикНаиболее распространенный и простой способ перевода в двоичный код значения из десятичной системы счисления — деление в столбик.
Реализацию алгоритма конвертации необходимо разобрать на практическом примере. Например, требуется перевести 123 в двоичную форму. Для этого необходимо следовать определенной методике:
Для выполнения обратной операции следует воспользоваться степенным представлением числа, которое начинается справа налево. Если указана единица, то 2 в заданной степени есть. В противном случае — указывается ноль. Реализация методики выглядит следующим образом: 2^0+2^1+0^2+2^3+2^4+2^6=123{10}.
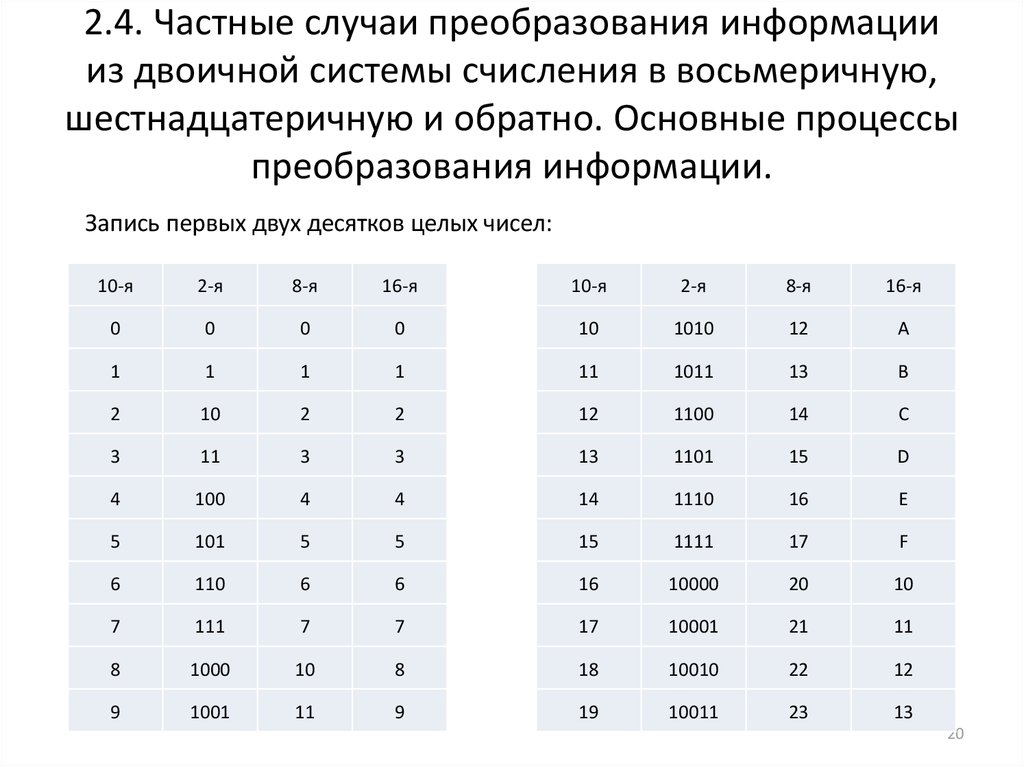
Восьмеричная формаВ отличие от шестнадцатеричной формы представления чисел восьмеричная не содержит букв из английского алфавита. В ее основании присутствует 8. Форма получила широкое применение в кодировании текстовой информации. Кодируются и таблицы в восьмеричную систему счисления, различные цветовые оттенки и прочие данные, обладающие небольшими размерами. Для преобразования из десятичной нужно перевести величину в двоичный код. Далее следовать по такому алгоритму:
Для реализации методики нужно рассмотреть пример конвертации 123. Решение задачи имеет такой вид:
Операция конвертации выполняется аналогично, но в обратном порядке. Например, необходимо преобразовать 173{8}—>{10}. Решение имеет следующий вид:
Специалисты в области информационных технологий рекомендуют проверять все решение на веб-сервисах или калькуляторах, работающих с двоичным, восьмеричным и шестнадцатеричным кодами. Их еще называют инженерными. Программы является компонентом всех операционных систем (Linux, Windows и MacOS). При необходимости в интернете можно найти и более удобные версии программного обеспечения для работы с машинными кодами. Таким образом, восьмеричную СС применяют для кодирования небольших массивов информации. Для конвертации необходимо выполнить промежуточную операцию преобразования десятичной в двоичную форму, а затем разложить последнюю на триады. Конвертер из десятичного числа в восьмеричноеКонвертер десятичного числа в восьмеричноеГлавная›Преобразование›Преобразование чисел›Десятичное число в восьмеричное От BinaryDecimalOctalHexadecimalText Кому BinaryDecimalOctalHexadecimalText Введите десятичное число Восьмеричное число Шестнадцатеричный номер Шаги вычисления десятичного числа в восьмеричное Разделите на 8, чтобы получить цифры из остатков:
Преобразователь восьмеричного числа в десятичное ► Как преобразовать десятичное число в восьмеричноеШаги преобразования:
Пример #1Преобразование 7562 10 в восьмеричное:
SO 7562 10 = 16612 8 Пример № 2Преобразование 35631 10 в октябрь:
So 35631 10 = 105457 8 Таблица преобразования десятичной системы в восьмеричную
См. также также
Напишите как улучшить эту страницуПРЕОБРАЗОВАНИЕ ЧИСЕЛ
RAPID TABLES
Восьмеричная система счисленияСхема Введение В предыдущем разделе мы уже узнали о десятичной, двоичной и шестнадцатеричной системах счисления. [адсенс1] Вернуться к началу Восьмеричная система счисленияВ шестнадцатеричной системе счисления мы представляем двоичные цифры как набор из 4 цифр (2 4 = 16), в восьмеричной системе счисления мы представляем двоичные числа как набор из 3 цифр (2 3 = 8). В восьмеричной системе счисления используется 8 цифр от 0 до 7. Это 0, 1, 2, 3, 4, 5, 6 и 7. Таким образом, каждая цифра восьмеричного числа образована от 0 до 7 цифр в них. Эта система счисления имеет основание 8 в их представлении. Пример: (501) 8 , (480) 8 Вес значения цифры будет увеличиваться с увеличением степени 8. Это показано ниже. Давайте рассмотрим пример, чтобы понять представление восьмеричного числа в виде набора из 3 цифр. Таким образом, число 100011010 представляется в восьмеричном виде как (432) 8 . Наверх [adsense2] Преобразование восьмеричных чиселВосьмеричные числа можно преобразовать в двоичную и десятичную системы счисления, а также в шестнадцатеричные числа. Некоторые из них описаны ниже. Преобразование двоичных чисел в восьмеричныеЧтобы преобразовать двоичное число в восьмеричное, сначала мы должны разделить двоичную строку на набор из 3 двоичных чисел в каждом. Запись соответствующего числа в каждый набор даст восьмеричное число двоичного числа. Пример 1: преобразовать 110111100010 в восьмеричное число. Разделение двоичного числа на набор из 3 цифр 110 111 100 010 6 7 4 2 (110111100010) 2 равен (6742) 8 . Преобразование от Octal Numbers до BINAL Преобразование восьмеричных чисел в двоичные представляет собой процесс, обратный двоичному преобразованию в восьмеричное. EX 1:Преобразование (43628) 8 в двоичный Написание эквивалентного двоичного числа на каждую цифру 4 3 6 2 8 100 011 110 010 SO (43628) 8 . равно (100011110010100) 2 Преобразование десятичных чисел в восьмеричныеДесятичное число можно преобразовать в восьмеричное путем многократного деления на 8. Напоминание на каждом этапе будет давать требуемое восьмеричное число. См. приведенный ниже пример. Пример 1:Преобразовать (159) 10 в восьмеричное число. 159/8 ————-> Коэффициент 19 Напоминание 7——LSB 19/8 ————-> Коэффициент 2 Напоминание 3 2/8 ————-> Коэффициент 0 Напоминание 2—— MSB So (159) 10 = (237)8 Пример 2: Преобразование (80) 10 в восьмеричное число. 80/8 ————-> Частное 9 Напоминание 8—–LSB 9/8 ————-> Частное 1 Напоминание 1 1/8 ————-> Частное 0 Напоминание 1——MSB Итак, (80) 10 = (118) 8 Преобразование восьмеричных чисел в десятичные может быть2 9004 преобразуются в десятичные числа путем умножения каждой цифры на значение ее позиции. Это означает, что каждая цифра умножается на степень 8 с ее позицией.Рассмотрим пример Пример 1:преобразовать (51) 8 в десятичное число Вес позиции 8 1 8 0 Значение положения 8 1 Октальное число 5 1 Эквивалентное десятичное число = 5 x 81 + 1 x 80 = 40 + 1 = 41 (51) 8 = 41 (51) 8 = 41 (51) 8 = 41 (41) 10 Аналогичным образом можно преобразовать восьмеричное число в любую другую систему счисления. В приведенной ниже таблице показаны эквивалентные значения для других систем счисления. Вернуться к началу Представление восьмеричного числаВосьмеричные числа представлены с основанием 8, потому что они используют только 8 цифр, как объяснялось выше. Вес каждого бита в восьмеричном числе показан ниже. Восьмеричные числа представляются аналогично другим системам счисления. Двадцать, это значит {(2×8) + (0×8)} и так далее.
Наверх РезюмеМы представим 3 двоичных разряда в эквиваленте 1 восьмеричного разряда, как показано выше. Точно так же самое старшее двузначное восьмеричное число (77 8 ) может представлять 63 двоичных разряда. Точно так же самое высокое трехзначное восьмеричное число (777 8 ) может представлять 511 двоичных цифр. Наибольшее трехзначное восьмеричное число (7777 8 ) может представлять 4095 двоичных цифр.
Вернуться к началу Восьмеричные числа и пальцыВикискладЕсли бы у нас, как у героев мультфильмов, было по четыре пальца на каждой руке, это могло бы оказать удивительное влияние на то, как мы смотрим на мир. Наша система счисления представляет собой десятичную систему или систему счисления с основанием десять, что означает, что она состоит из десятичных степеней. Числа меньше десяти представлены одной из десяти цифр, числа от десяти до сотни (что равно 10 × 10) состоят из двух цифр, числа от сотни до тысячи (опять же, 10 × 10 × 10) состоят из трех цифр и скоро. Большинство систем счисления по всему миру используют десятичную систему счисления, происхождение этой системы, вероятно, основано на ручном счете: у большинства людей десять пальцев, поэтому у нас десять цифр. Жизнь в мире восьми пальцевПомимо количества пальцев, принадлежащих среднему человеку, в десяти нет ничего особенного. Мы можем взять за основу любое целое число, большее единицы, и получить совершенно хорошую систему счисления. Предположим, мы живем в мире, в котором люди эволюционировали так, что на каждой руке у них обычно четыре пальца вместо пяти. Весьма вероятно, что мы приняли бы восьмеричную систему, или систему с основанием восемь, используя степени восьми вместо степеней десяти. В восьмеричной системе у нас есть восемь цифр — 0, 1, 2, 3, 4, 5, 6 и 7 — и теперь разряды основаны на степенях восьмерки. Восьмеричное число 10 представляет число 8 в десятичном виде. Восьмеричное число 100 представляет 8 × 8, или 64. 1000 – это 8 × 8 × 8, или 512. Один доллар по основанию десять будет конвертирован в 1,44 доллара по основанию восемь и 0,84 доллара по основанию двенадцати. И наоборот, то, что мы назвали бы долларом в нашем мире с восемью пальцами — 1 доллар счисления с основанием восемь, — в нашем мире с основанием 10 будет равно всего 0,64 доллара. Средняя годовая заработная плата в США в 2013 году составляла 35 080 долларов. Если бы у нас было восемь пальцев, это было бы записано как 104 480 долларов. В настоящее время население Земли составляет около 7,2 миллиарда человек. В мире с основанием 8 это будет записано примерно как 66 000 000 000 или 66 «миллиардов», то есть 66, умноженное на восемь, возведенное в девятую степень, точно так же, как миллиард в нашей системе — это десять, возведенное в девятую степень. Год 2014 в нашем мире изменяется на 3736 по основанию 8, так как эквивалент века имеет 64 года, а эквивалент тысячелетия всего 512. Год основания 3000 произошел в нашем десятилетии основания 1536, а восьмеричный следующее тысячелетие мира в 4000 году наступит в нашем 2048 году. Индекс Доу-Джонса 17 000 не является особеннымИспользование восьмеричного числа также изменило бы наши измерения различных вех, поскольку большие круглые числа с основанием восемь сильно отличаются от наших больших круглых чисел. Например, на данный момент индекс DJIA колеблется в паре сотен пунктов от отметки 17 000, впервые за все время, а S&P 500 недалеко от отметки 2 000. Однако в восьмеричном мире трейдеры праздновали бы поздний рождественский подарок, когда восьмеричный DJIA впервые закрылся на отметке 40 000 на следующий день после Рождества 2013 года. Восьмеричное число 40 000 соответствует десятичному числу 16 384, а Индекс DJIA закрылся на отметке 16479.0,88 26 декабря. Население Нью-Йорка, согласно переписи 2010 года, составляло 8 175 133 человека. В мире с основанием восемь мы запишем это как 37 137 035. Город достиг бы большого восьмеричного рубежа в 30 000 000 человек (6 291 456 в десятичном выражении) где-то в конце 1920-х годов: согласно переписи 1930 года, в городе проживало (в десятичном выражении) 6 930 446 человек. В 2010 году население четырех крупнейших городов США — Нью-Йорк, Лос-Анджелес, Чикаго и Хьюстон — превышало большой восьмеричный порог в 10 000 000 человек, или 2,09 человека.7152 в десятичной системе. Деревянная модель Сайлон выглядывает из окна квартиры своего создателя, украинца Дмитрия Баландина, в Запорожье 6 августа 2013 года. REUTERS/Глеб Гаранич У компьютеров нет 10 пальцев Хотя предполагать, как будут выглядеть большие числа в мире, где у нас было бы по четыре пальца на каждой руке, немного глупо, альтернативные системы счисления, в том числе восьмеричная, на самом деле очень важны. Компьютеры построены на основе двоичного кода или основания 2. Это означает, что информация, считываемая или обрабатываемая компьютерами, состоит из длинных цепочек нулей и единиц. Иногда специалистам по информатике и инженерам необходимо анализировать машинный код на этом очень низком уровне, но люди практически не в состоянии разобраться в этих гигантских кучах нулей и единиц. Двоичная природа компьютеров приводит к тому, что с ними связаны на первый взгляд странные числа. Процессоры и операционные системы бывают 32-битными или 64-битными, поскольку они являются степенью двойки: 32 — это 2 5 , или пять двоек, умноженных вместе, а 64 — это 2 6 . Флэш-накопители имеют размер 256 мегабайт или 512 мегабайт, потому что они также являются степенью двойки: 256 — это 2 8 , а 512 — это 2 9 . Поскольку людям трудно читать двоичный код напрямую, специалисты по информатике и инженеры часто смотрят на необработанный компьютерный код, представленный в восьмеричном формате с основанием восемь или в его родственном шестнадцатеричном коде с основанием шестнадцатеричный. Любая группа из трех двоичных цифр или битов соответствует восьмеричной цифре. Двоичное число 010 преобразуется в 2, а 110 — в 6. Точно так же любая группа из четырех битов преобразуется в шестнадцатеричное число: 0011 становится 3, а 1010 становится 10, что обычно представляется в шестнадцатеричном виде как заглавная буква А. Итак , длинная нечитаемая двоичная строка, например 1101 0010 0101 1001, может быть преобразована в более легко читаемую, если вы знаете свои компьютерные коды, шестнадцатеричную цепочку D 2 5 9. c — Литералы восьмеричного числа: Когда? Почему? Всегда?Я никогда не использовал восьмеричные числа в своем коде и не сталкивался ни с одним кодом, который их использовал (несмотря на шестнадцатеричный код и битовую перестановку). Я начал программировать на C/C++ примерно в 1994 году, так что, может быть, я слишком молод для этого? Использует ли старый код восьмеричное число? C включает поддержку для них, добавляя 0 перед кодом, но где код, который использует эти числовые литералы с основанием 8?
6 Недавно мне пришлось написать код сетевого протокола, который обращается к 3-битным полям. Просто для эффекта, не могли бы вы сказать мне, что это за 3-битные поля? 0x492492 С другой стороны, этот же номер в восьмеричной системе: 022222222 Теперь, наконец, в двоичном формате (в группах по 3): 010 010 010 010 010 010 010 010 4 Единственное место, где я сталкиваюсь с восьмеричными литералами в эти дни, это когда я имею дело с битами прав доступа к файлам в Linux, которые обычно представлены в виде 3 восьмеричных цифр, где каждая цифра представляет права доступа для владельца файла, группы и других пользователей соответственно. напр. 0755 (также просто 755 для большинства инструментов командной строки) означает, что владелец файла имеет полные права (чтение, запись, выполнение), а группа и другие пользователи имеют только права на чтение и выполнение. Представление этих битов в восьмеричном формате упрощает определение установленных разрешений. 1 Из Википедии
-Адам
Готов поспорить. Согласно стандарту числовые литералы, начинающиеся с нуля, являются восьмеричными. Это включает в себя, тривиально, 6 Коммерческая авиация использует восьмеричные «метки» (в основном идентификаторы типов сообщений) в почтенном Arinc 429.стандарт автобуса. Так что возможность указывать значения меток в восьмеричном формате при написании кода для приложений авионики — это хорошо… Я также видел восьмеричное использование в транспондерах самолетов. Код транспондера режима 3а представляет собой 12-битное число, которое каждый воспринимает как 4 восьмеричных числа. В Википедии есть немного больше информации. Я знаю, что обычно это не связано с компьютерами, но FAA тоже использует компьютеры :). 1 Полезно для Я связался с Octal через PDP-11, а так, видимо, язык Си 🙂 1 До сих пор существует множество старых систем управления технологическими процессами (Honeywell h5400, h55000 и т. д.) конца 60-х и 70-х годов, которые приспособлены для использования 24-битных слов с восьмеричной адресацией. Подумайте, например, когда в Соединенных Штатах были построены последние атомные электростанции. Замена этих промышленных систем — довольно серьезное мероприятие, поэтому вам может посчастливиться встретить одну из них в дикой природе до того, как они вымрут, и с благоговением взирать на их великолепные настраиваемые форматы с плавающей запятой! 1 файлы tar хранят информацию в виде строки восьмеричного целого числа 2 Нет никаких земных причин изменять стандарт, восходящий к зарождению языка и существующий в бесчисленном количестве программ. То есть я часто использую восьмеричное представление. Теперь, если вы действительно хотите согнуть свою шахту, взгляните на формат слова для PDP-10… Любой, кто учился программировать на PDP-8, имеет теплое сердце к восьмеричным числам. Размер слова составлял 12 бит, разделенных на 4 группы по 3 бита в каждой, поэтому -1 равнялось 7777 восьмеричным числам. Эта схема была увековечена в PDP-11, который имел 16-битные слова, но по-прежнему использовал восьмеричное представление для различных вещей, отсюда и схема разрешений файлов *NIX, которая существует и по сей день. Octal был и был наиболее полезен с первым доступным оборудованием дисплея (7-сегментные дисплеи). Эти оригинальные дисплеи не имели декодеров, доступных позже. Таким образом, выходы цифрового регистра были сгруппированы, чтобы соответствовать доступному дисплею, который мог отображать только восемь (8) символов: 0,1,2 3,4,5,6,7 . Также первые ЭЛТ-дисплеи были дисплеями с растровой разверткой, а простейшие знако-символические генераторы были эквивалентны 7-сегментным дисплеям. Мотивирующим драйвером, как всегда, был самый дешевый дисплей. 1 Преобразование чисел в различные системы счисленияСистема счисления представляет собой систематический способ представления чисел с помощью символьных символов и использует базовое значение для удобной группировки чисел в компактной форме. Наиболее распространенной системой счисления является десятичная, имеющая базовое значение 10 и набор символов 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9. Однако существуют и другие системы счисления. , и их можно более эффективно использовать для определенной цели. Например, поскольку компьютеры используют логическую логику для выполнения вычислений и операций, они используют двоичную систему счисления, базовое значение которой равно 2. Microsoft Office Excel имеет несколько функций, которые можно использовать для преобразования чисел в следующие системы счисления и обратно:
Для выполнения этой задачи используйте функцию BIN2DEC.
Для выполнения этой задачи используйте функцию BIN2HEX.
Для выполнения этой задачи используйте функцию BIN2OCT.
Для выполнения этой задачи используйте функцию DEC2BIN.
Для выполнения этой задачи используйте функцию DEC2HEX.
Для выполнения этой задачи используйте функцию DEC2OCT.
Для выполнения этой задачи используйте функцию HEX2BIN.
Для выполнения этой задачи используйте функцию HEX2DEC.
Для выполнения этой задачи используйте функцию HEX2OCT.
Для выполнения этой задачи используйте функцию OCT2BIN.
Для выполнения этой задачи используйте функцию OCT2DEC.
Для выполнения этой задачи используйте функцию OCT2HEX.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 В.ДЕС(1100100)
В.ДЕС(1100100) В.ШЕСТН(11111011; 4)
В.ШЕСТН(11111011; 4) В.ВОСЬМ(1001; 3)
В.ВОСЬМ(1001; 3) В.ДВ(9;4)
В.ДВ(9;4)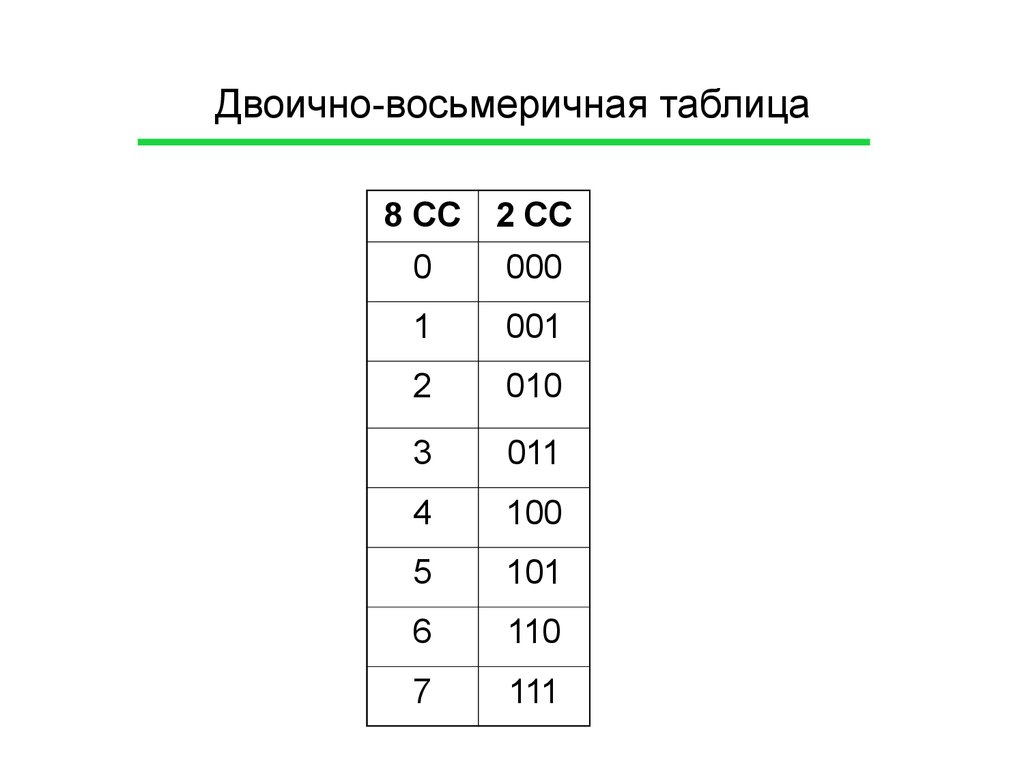 В.ШЕСТН(100;4)
В.ШЕСТН(100;4) В.ВОСЬМ(58;3)
В.ВОСЬМ(58;3)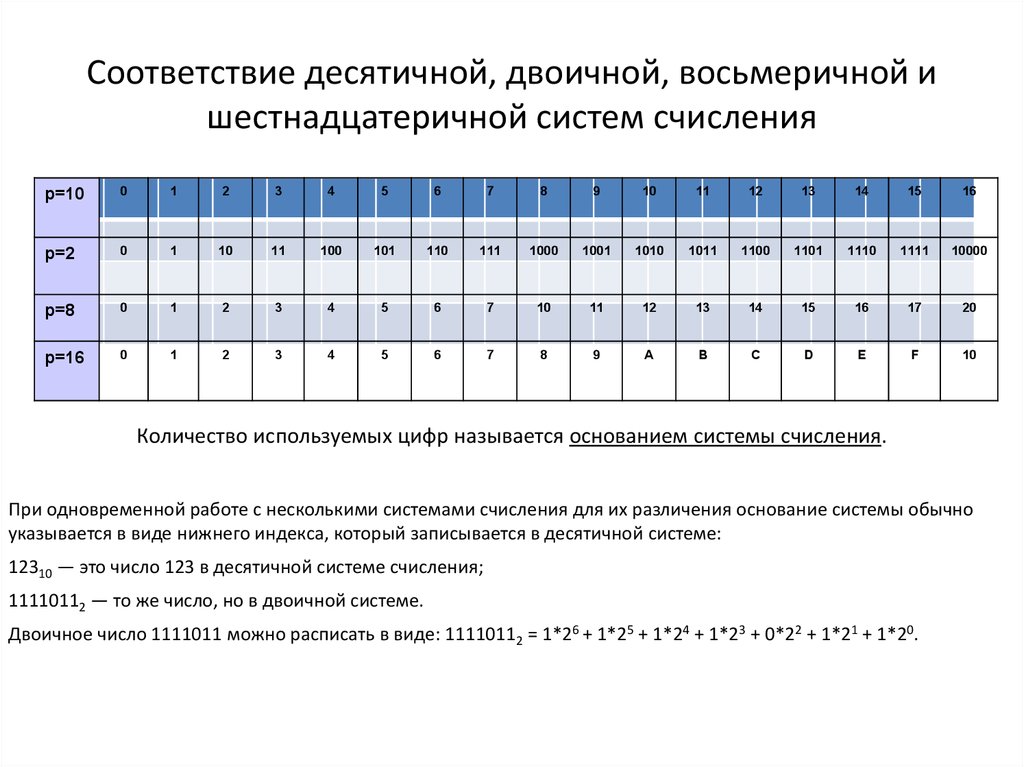 В.ДВ(«F»; 8)
В.ДВ(«F»; 8) В.ДЕС(«A5»)
В.ДЕС(«A5») В.ВОСЬМ(«F»; 3)
В.ВОСЬМ(«F»; 3) В.ДВ(3; 3)
В.ДВ(3; 3) В.ДЕС(54)
В.ДЕС(54) В.ШЕСТН(100; 4)
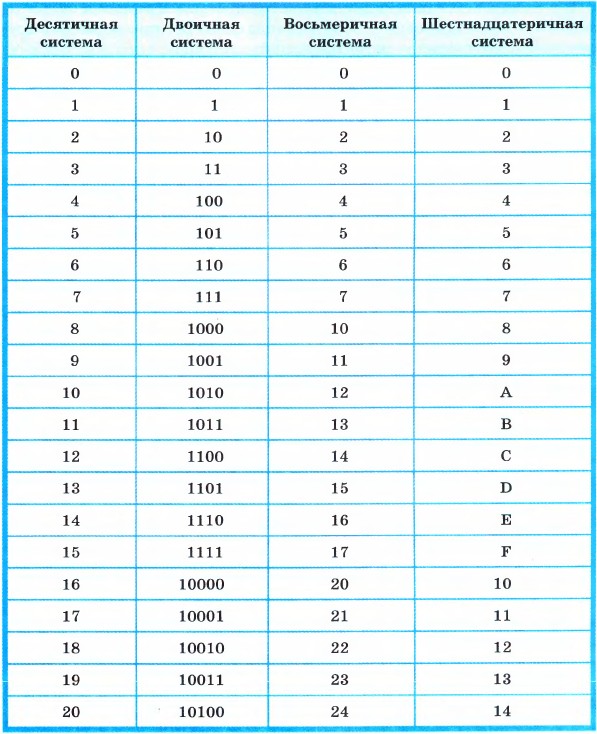
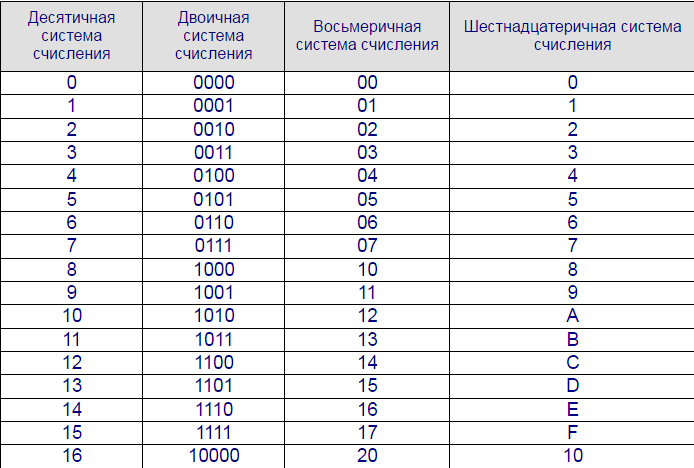
В.ШЕСТН(100; 4)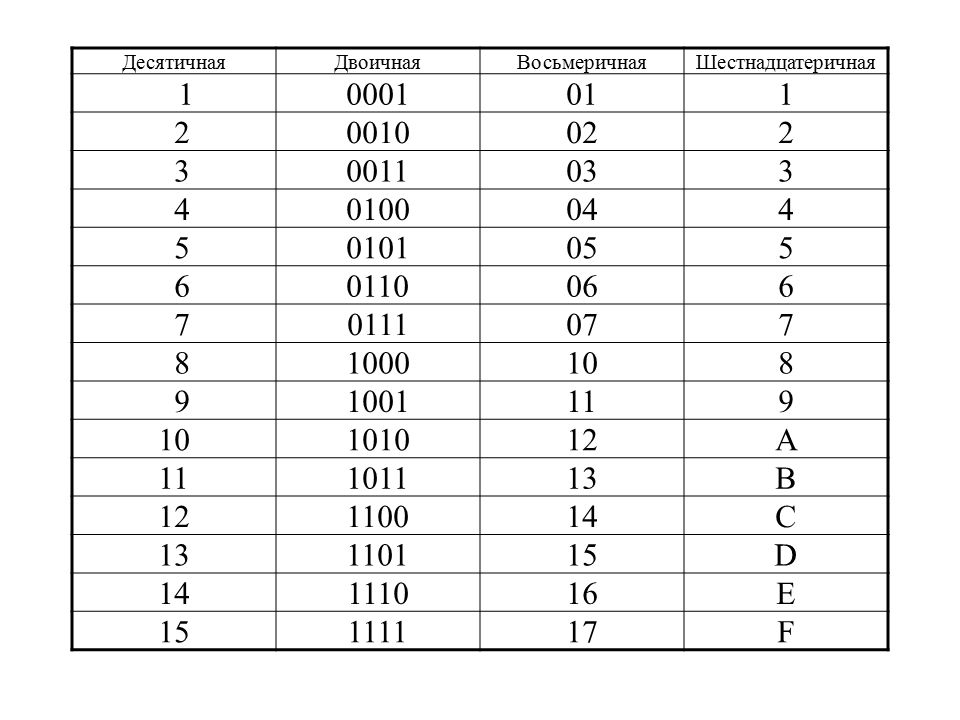 Чтобы перевести число из одной системы в другую, нужно использовать таблицу перевода чисел.
Чтобы перевести число из одной системы в другую, нужно использовать таблицу перевода чисел. Если слева не будет хватать цифр для полной группы, нужно дописать необходимое количество незначащих нулей.
Если слева не будет хватать цифр для полной группы, нужно дописать необходимое количество незначащих нулей.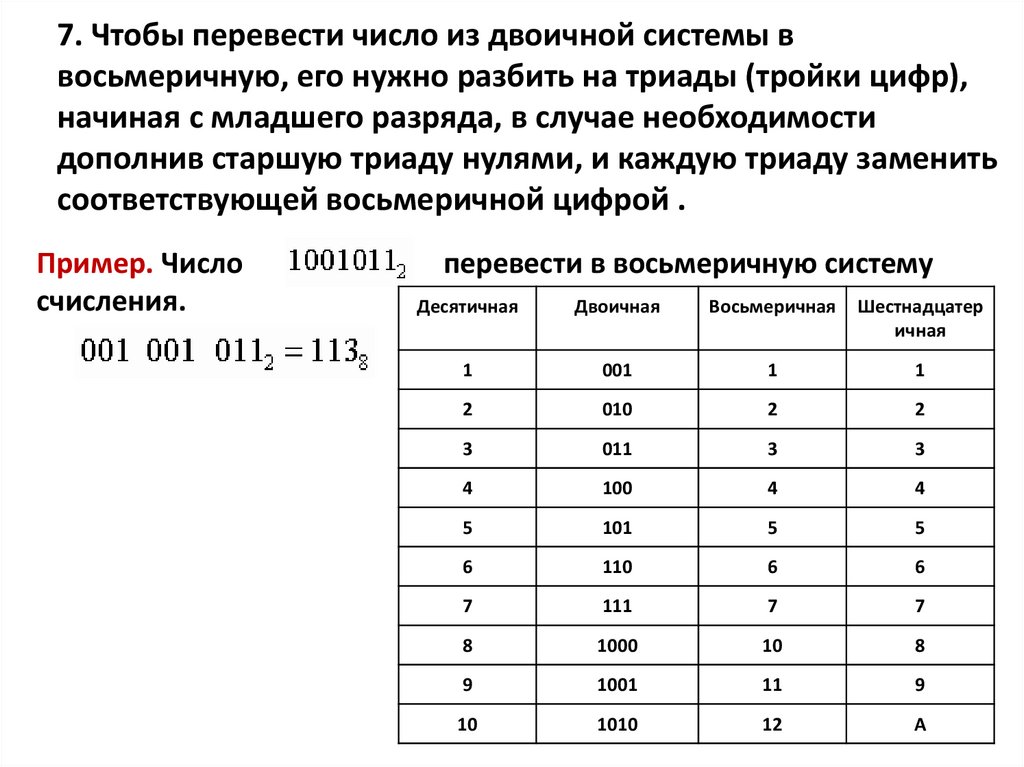


 Чему равен 1 баррель в литрах?
Чему равен 1 баррель в литрах? Наиболее востребованными являются двоичная, шестнадцатеричная, а также восьмеричная системы счисления. Однако перед переходом к практике специалисты рекомендуют рассмотреть теорию конвертации первой и последней формы информации (2 и 8).
Наиболее востребованными являются двоичная, шестнадцатеричная, а также восьмеричная системы счисления. Однако перед переходом к практике специалисты рекомендуют рассмотреть теорию конвертации первой и последней формы информации (2 и 8). Например, микропроцессор состоит из 32 миллиардов транзисторов. В примере числом или значением является 32 млрд.
Например, микропроцессор состоит из 32 миллиардов транзисторов. В примере числом или значением является 32 млрд. Это утверждение довольно просто доказать. Достаточно взять двузначное число (23), а затем образовать из него второе посредством перестановки десятков и единиц, т. е. 32. После этого произвести обычную математическую операцию их разности: 32-23=9. Из расчетов видно, что 2 значения отличаются между собой. Следовательно, расположение цифр имеет значение для позиционной формы представления информации.
Это утверждение довольно просто доказать. Достаточно взять двузначное число (23), а затем образовать из него второе посредством перестановки десятков и единиц, т. е. 32. После этого произвести обычную математическую операцию их разности: 32-23=9. Из расчетов видно, что 2 значения отличаются между собой. Следовательно, расположение цифр имеет значение для позиционной формы представления информации.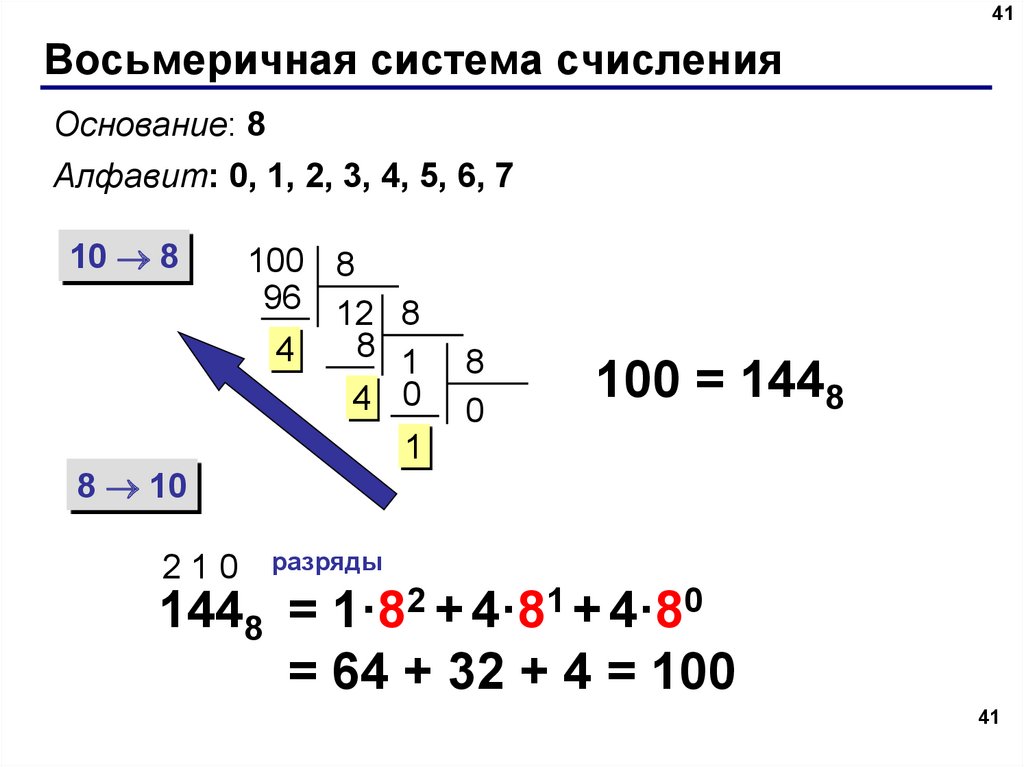 Следует отметить, что у этой формы представления есть недостатки, которые мешают ей вытеснить позиционную. К ним относятся следующие:
Следует отметить, что у этой формы представления есть недостатки, которые мешают ей вытеснить позиционную. К ним относятся следующие:
 Последний имеет такой вид:
Последний имеет такой вид: 1=2.
1=2. Когда не хватает количества разрядов, нужно пополнить его нулями.
Когда не хватает количества разрядов, нужно пополнить его нулями.
 Эта система счисления очень похожа на шестнадцатеричную систему счисления. Мы знаем, что десятичная система основана на 10, так как в ней используются цифры от 0 до 9., основанием двоичной системы является 2, поскольку в ней используются цифры 0 и 1, а в шестнадцатеричной системе счисления используется основание 16, поэтому в этой системе счисления используется 16 цифр, т. е. от 0 до 15. Точно так же «восьмеричная система счисления» использует только 8 чисел для представления чисел, поэтому он имеет название «восьмеричное». (0-7).
Эта система счисления очень похожа на шестнадцатеричную систему счисления. Мы знаем, что десятичная система основана на 10, так как в ней используются цифры от 0 до 9., основанием двоичной системы является 2, поскольку в ней используются цифры 0 и 1, а в шестнадцатеричной системе счисления используется основание 16, поэтому в этой системе счисления используется 16 цифр, т. е. от 0 до 15. Точно так же «восьмеричная система счисления» использует только 8 чисел для представления чисел, поэтому он имеет название «восьмеричное». (0-7). Основное преимущество восьмеричной системы счисления по сравнению с другими системами счисления заключается в том, что при работе с компьютерами проще записать число в восьмеричной форме, чем в двоичной. Особенно, когда мы работаем с большой строкой двоичных чисел, предлагается сгруппировать их как набор из трех цифр, поэтому вероятность возникновения ошибки меньше. Другим преимуществом восьмеричной системы счисления является то, что преобразование восьмеричной системы счисления в двоичную и двоичную в восьмеричную систему счисления очень просто по сравнению с другими преобразованиями.
Основное преимущество восьмеричной системы счисления по сравнению с другими системами счисления заключается в том, что при работе с компьютерами проще записать число в восьмеричной форме, чем в двоичной. Особенно, когда мы работаем с большой строкой двоичных чисел, предлагается сгруппировать их как набор из трех цифр, поэтому вероятность возникновения ошибки меньше. Другим преимуществом восьмеричной системы счисления является то, что преобразование восьмеричной системы счисления в двоичную и двоичную в восьмеричную систему счисления очень просто по сравнению с другими преобразованиями.
 То есть каждая цифра восьмеричного числа должна быть записана в двоичной форме, и объединение всех двоичных цифр приведет к нашему требуемому двоичному числу.
То есть каждая цифра восьмеричного числа должна быть записана в двоичной форме, и объединение всех двоичных цифр приведет к нашему требуемому двоичному числу.

 (0, 1, 2, 3, 4, 5, 6 и 7)
(0, 1, 2, 3, 4, 5, 6 и 7)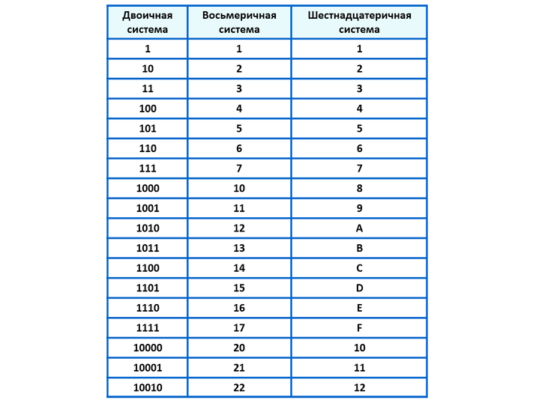




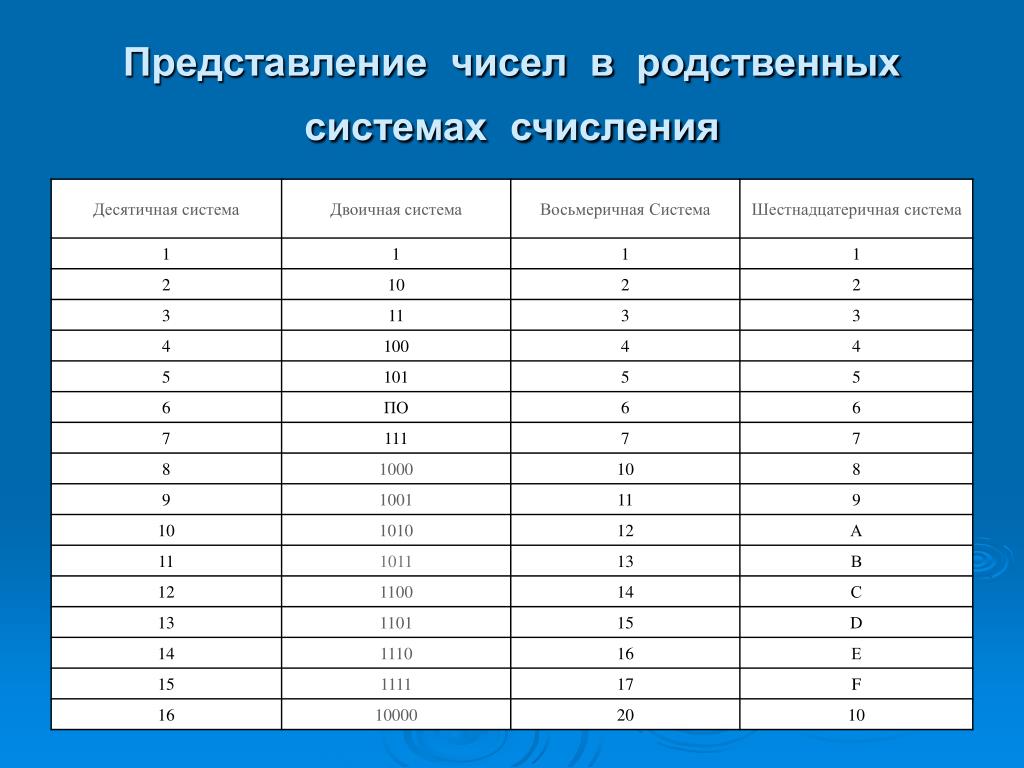 Поскольку восемь и шестнадцать являются степенями двойки (8 = 2 × 2 × 2 и 16 = 2 × 2 × 2 × 2), блоки двоичного кода легко переводятся в эти основания.
Поскольку восемь и шестнадцать являются степенями двойки (8 = 2 × 2 × 2 и 16 = 2 × 2 × 2 × 2), блоки двоичного кода легко переводятся в эти основания. Octal пригодится, когда вы хотите отладить это.
Octal пригодится, когда вы хотите отладить это.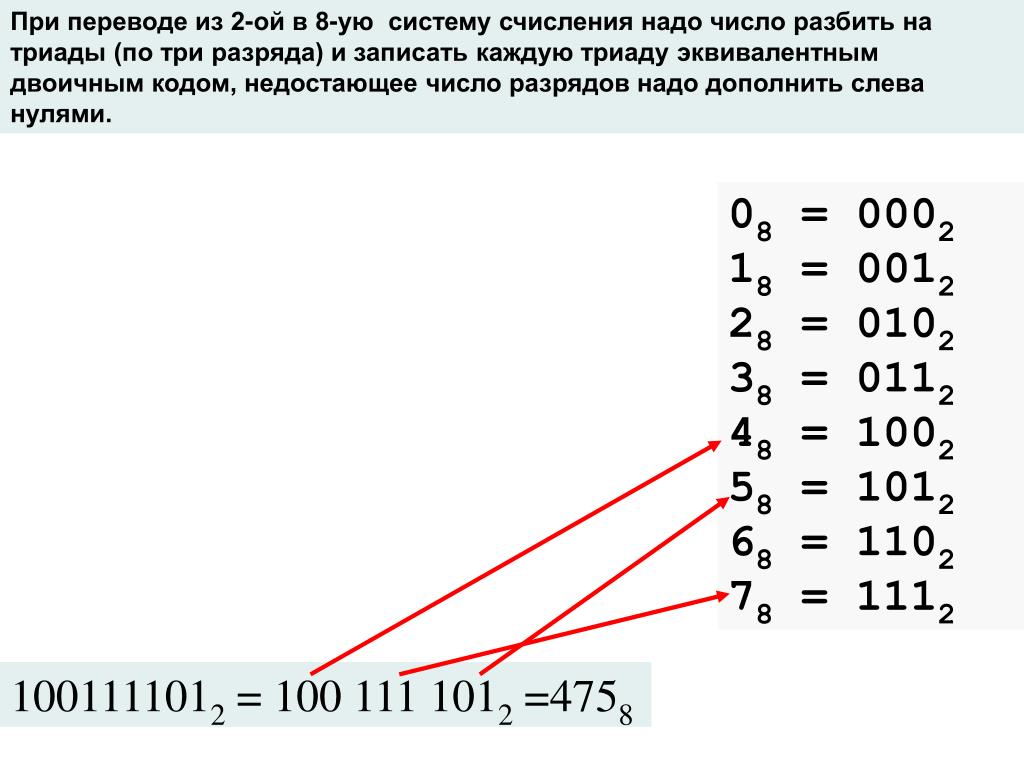 С первого взгляда можно сказать, что означает 0755, но не 493 или 0x1ed.
С первого взгляда можно сказать, что означает 0755, но не 493 или 0x1ed. В таких системах три восьмеричных
потребуются цифры с
старшая восьмеричная цифра
неэлегантно изображая только два
двоичные цифры (а в ряду
одна и та же восьмеричная цифра будет представлять один
двоичная цифра из следующего байта).
Следовательно, шестнадцатеричный код чаще
используемые сегодня в языках программирования,
поскольку шестнадцатеричная цифра охватывает четыре
двоичные числа и все современные вычисления
платформы имеют машинные слова, которые
без остатка делится на четыре. Немного
платформы со степенью двойки
размер все еще имеет подслова инструкции
которые легче понять, если
отображается в восьмеричном формате; это включает
ПДП-11. Современный вездесущий x86
архитектура относится к этой категории
тоже, но восьмеричный почти никогда
используется на этой платформе.
В таких системах три восьмеричных
потребуются цифры с
старшая восьмеричная цифра
неэлегантно изображая только два
двоичные цифры (а в ряду
одна и та же восьмеричная цифра будет представлять один
двоичная цифра из следующего байта).
Следовательно, шестнадцатеричный код чаще
используемые сегодня в языках программирования,
поскольку шестнадцатеричная цифра охватывает четыре
двоичные числа и все современные вычисления
платформы имеют машинные слова, которые
без остатка делится на четыре. Немного
платформы со степенью двойки
размер все еще имеет подслова инструкции
которые легче понять, если
отображается в восьмеричном формате; это включает
ПДП-11. Современный вездесущий x86
архитектура относится к этой категории
тоже, но восьмеричный почти никогда
используется на этой платформе.

 C равен 003…
C равен 003…

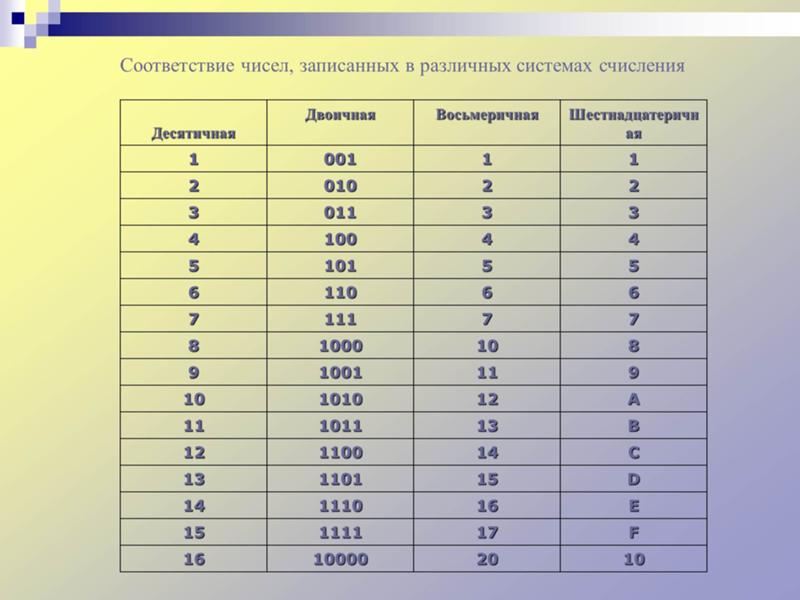
 2ШЕСТ.(11111011, 4)
2ШЕСТ.(11111011, 4)





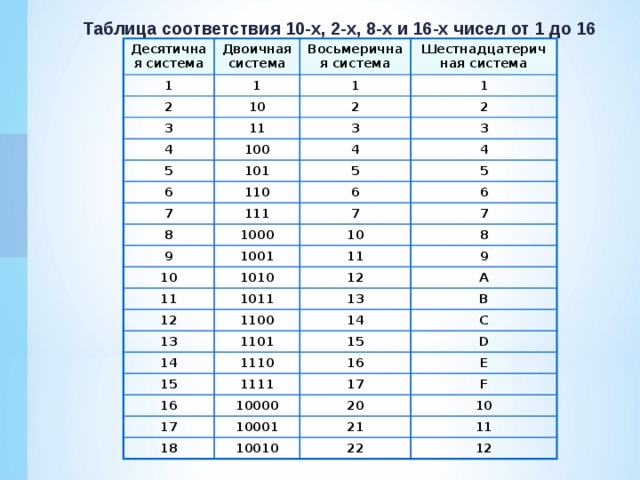 Из-за
связи с двоичной системой, это полезно при программировании некоторых типов
компьютеры.
Из-за
связи с двоичной системой, это полезно при программировании некоторых типов
компьютеры.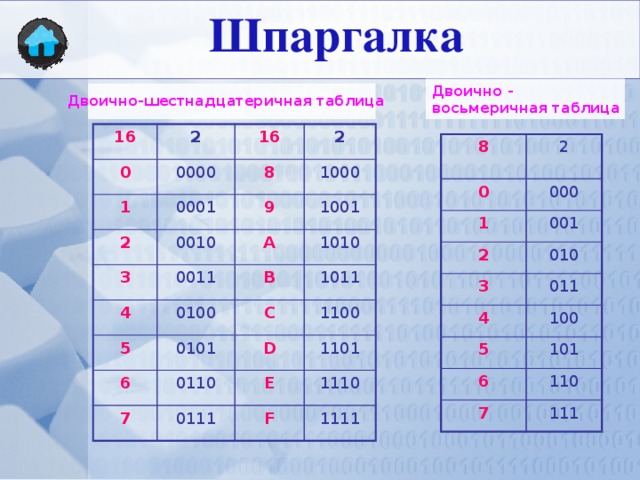 В восьмеричной системе используется восемь символов — от 0 до 7. Основание, или основание,
указывается индексом 8.
В восьмеричной системе используется восемь символов — от 0 до 7. Основание, или основание,
указывается индексом 8. Самая дальняя цифра слева от
точка счисления — это MSD, а самая дальняя справа от точки счисления — это LSD.
Самая дальняя цифра слева от
точка счисления — это MSD, а самая дальняя справа от точки счисления — это LSD.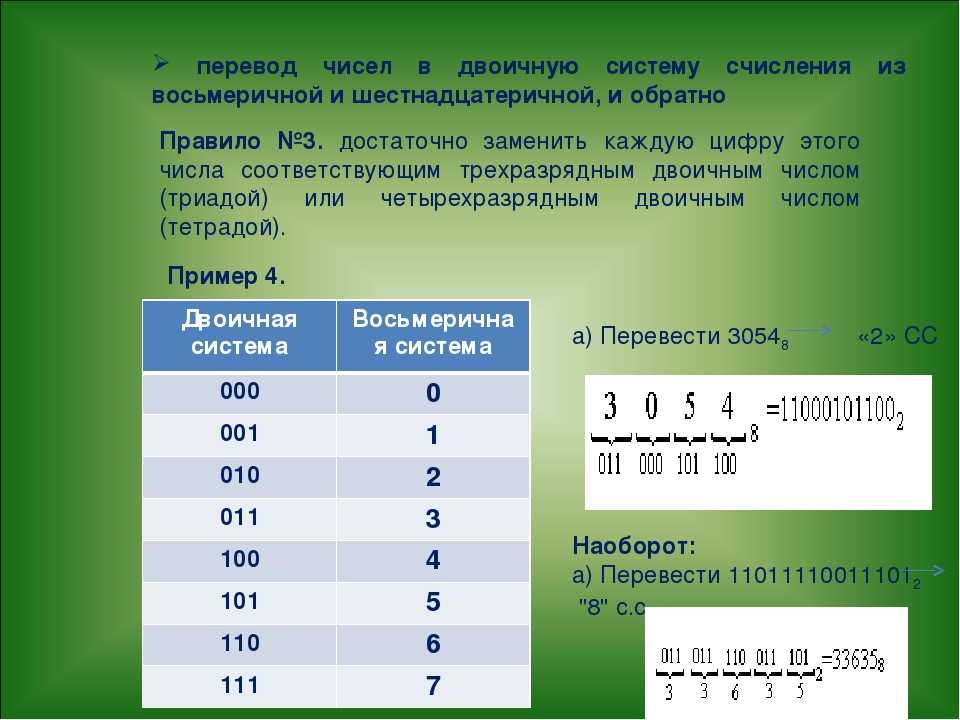 — Восьмеричная таблица сложения
— Восьмеричная таблица сложения