Восьмеричная система счисления
Содержание:Что такое восьмеричная система счисления
Как перевести целое десятичное число в восьмеричную систему счисления
Как перевести десятичную дробь в восьмеричную систему счисления
Как перевести число из восьмеричной системы счисления в десятичную
Как перевести дробное восьмеричное число в десятичное
Таблица значений десятичных чисел от 0 до 100 в восьмеричной системе счисления
Что такое восьмеричная система счисления
Восьмеричная система счисления, является позиционной системой счисления, то есть имеется зависимость от позиции цифры в записи числа. Для записи числа в восьмеричной системе счисления используется восемь цифр 0, 1, 2, 3, 4, 5, 6 и 7. Для определения в какой системе счисления записано число, внизу, справа от числа ставят цифру, которая называется основанием системы счисления. Например, 72318 или 45568Если вам необходимо перевести число любой системы счисления в другую систему счисления, воспользуйтесь
калькулятором систем счисления с подробным решением онлайн.
Как перевести целое десятичное число в восьмеричную систему счисления
Для того, чтобы перевести целое десятичное число в восьмеричную систему счисления нужно десятичное число делить на 8 до тех пор, пока неполное частное не будет равно нулю. В результате будет получено число из остатков деления записанное справа налево.Например, переведем число 36910 в восьмеричную систему счисления:
369 : 8 = 46 остаток: 1
46 : 8 = 5 остаток: 6
5 : 8 = 0 остаток: 5
36910 = 5618
Как перевести десятичную дробь в восьмеричную систему счисления
Для того чтобы перевести десятичную дробь в восьмеричную систему счисления необходимо сначала перевести целую часть десятичной дроби в восьмеричную систему счисления, а затем дробную часть, последовательно умножать на 8, до тех пор, пока в дробной части произведения не получиться ноль (результатом произведения будет целое число) или не будет достигнуто необходимое количество знаков после запятой. Если в результате умножения целая часть не равна нулю, тогда необходимо заменить значение целой части на ноль.
В результате будет получено число из целых частей произведений, записанное слева направо.
Если в результате умножения целая часть не равна нулю, тогда необходимо заменить значение целой части на ноль.
В результате будет получено число из целых частей произведений, записанное слева направо.Например, переведем десятичное число 0.210 в восьмеричную систему счисления:
Переведем целую часть
010 = 08
Переведем дробную часть
0.2 · 8 = 1.6
0.6 · 8 = 4.8
0.8 · 8 = 6.4
0.4 · 8 = 3.2
0.2 · 8 = 1.6
0.6 · 8 = 4.8
0.8 · 8 = 6.4
0.4 · 8 = 3.2
0.2 · 8 = 1.6
0.6 · 8 = 4.8
Восьмеричные дроби, как и десятичные могут быть как конечными, так и бесконечными. Не всегда конечная десятичная дробь может быть представлена конечной восьмеричной.
В данном примере получается бесконечная периодическая восьмеричная дробь, поэтому умножение на 8 можно производить бесконечное число раз и все равно дробная часть частного не будет равна нулю. В данном случае десятичная дробь 0.2 не может быть точно представлена в восьмеричной системе счисления.
К примеру, дробь 1.510 может быть представлена в восьмеричной системе счисления в виде конечной 2.510 = 1.48.
В данном случае десятичная дробь 0.2 не может быть точно представлена в восьмеричной системе счисления.
К примеру, дробь 1.510 может быть представлена в восьмеричной системе счисления в виде конечной 2.510 = 1.48.
Как перевести число из восьмеричной системы счисления в десятичную
Для того, чтобы перевести число из восьмеричной системы счисления в десятичную систему счисления, необходимо записать позиции каждой цифры в числе с права на лево начиная с нуля. Каждая позиция цифры будет степенью числа 8, так как система счисления 8-ичная. Необходимо последовательно умножить каждое число на 8 в степени соответствующей позиции числа и затем сложить с последующим произведением следующего числа в степени соответствующей его позиции. Например, переведем число 753108 в десятичную систему счисления:| Позиция в числе | 4 | 3 | 2 | 1 | 0 |
| Число | 7 | 5 | 3 | 1 | 0 |
753108 = 7 ⋅ 84 + 5 ⋅ 83 + 3 ⋅ 82 + 1 ⋅ 81 + 0 ⋅ 80 = 3143210
Как перевести дробное восьмеричное число в десятичное
Для того, чтобы перевести дробное восьмеричное число в десятичное, необходимо записать дробное восьмеричное число, убрав точку и затем сверху расставить индексы. Индексы в дробной части числа начинаются от -1 и продолжаются на уменьшение вправо, индексы в целой части начинаются с 0 и ставятся с права на лево по возрастанию.
Каждая позиция цифры (индекс) будет степенью числа 8, так как система счисления 8-ичная. Необходимо последовательно умножить каждое число на
8 в степени соответствующей позиции числа и затем сложить с последующим произведением следующего числа в степени соответствующей его позиции.
Индексы в дробной части числа начинаются от -1 и продолжаются на уменьшение вправо, индексы в целой части начинаются с 0 и ставятся с права на лево по возрастанию.
Каждая позиция цифры (индекс) будет степенью числа 8, так как система счисления 8-ичная. Необходимо последовательно умножить каждое число на
8 в степени соответствующей позиции числа и затем сложить с последующим произведением следующего числа в степени соответствующей его позиции.| Позиция в числе | 1 | 0 | -1 | -2 |
| Число | 1 | 2 | 3 | 6 |
12.368 = 1 ⋅ 81 + 2 ⋅ 80 + 3 ⋅ 8-1 + 6 ⋅ 8-2 = 10.4687510
Таблица значений десятичных чисел от 0 до 100 в восьмеричной системе счисления
| Значение числа в десятичной системе счисления | Значение числа в восьмеричной системе счисления |
| 010 | 08 |
| 110 | 18 |
| 210 | 28 |
| 310 | 38 |
| 410 | 48 |
| 510 | 58 |
| 610 | 68 |
| 7 | 78 |
| 810 | 108 |
| 910 | 118 |
| 1010 | 128 |
| 1110 | 138 |
| 1210 | 148 |
| 1310 | 158 |
| 1410 | 168 |
| 1510 | 178 |
| 1610 | 208 |
| 1710 | 218 |
| 1810 | 228 |
| 1910 | 238 |
| 2010 | 248 |
| 2110 | 258 |
| 2210 | 268 |
| 278 | |
| 2410 | 308 |
| 2510 | 318 |
| 2610 | 328 |
| 2710 | 338 |
| 2810 | 348 |
| 2910 | 358 |
| 3010 | 368 |
| 3110 | 378 |
| 3210 | 408 |
| 3310 | 418 |
| 3410 | 428 |
| 3510 | 438 |
| 3610 | 448 |
| 3710 | 458 |
| 3810 | 468 |
| 3910 | 478 |
| 4010 | 508 |
| 4110 | 518 |
| 4210 | 528 |
| 4310 | 538 |
| 4410 | 548 |
| 4510 | 558 |
| 4610 | 568 |
| 4710 | 578 |
| 4810 | 608 |
| 4910 | 618 |
| 5010 | 628 |
| Значение числа в десятичной системе счисления | Значение числа в восьмеричной системе счисления |
| 5110 | 638 |
| 5210 | 648 |
| 5310 | 658 |
| 5410 | 668 |
| 5510 | 678 |
| 5610 | 708 |
| 5710 | 718 |
| 5810 | 728 |
| 5910 | 738 |
| 6010 | 748 |
| 6110 | 758 |
| 6210 | 768 |
| 6310 | 778 |
| 6410 | 1008 |
| 6510 | 1018 |
| 6610 | 1028 |
| 6710 | 1038 |
| 6810 | 1048 |
| 6910 | 1058 |
| 7010 | 1068 |
| 7110 | 1078 |
| 7210 | 1108 |
| 7310 | 1118 |
| 7410 | 1128 |
| 7510 | 1138 |
| 7610 | 1148 |
| 7710 | 1158 |
| 7810 | 1168 |
| 7910 | 1178 |
| 8010 | 1208 |
| 8110 | 1218 |
| 8210 | 1228 |
| 8310 | 1238 |
| 8410 | 1248 |
| 8510 | 1258 |
| 8610 | 1268 |
| 8710 | 1278 |
| 8810 | 1308 |
| 8910 | 1318 |
| 9010 | 1328 |
| 9110 | 1338 |
| 9210 | 1348 |
| 9310 | 1358 |
| 9410 | 1368 |
| 9510 | 1378 |
| 9610 | 1408 |
| 9710 | 1418 |
| 9810 | 1428 |
| 9910 | 1438 |
| 10010 | 1448 |
Восьмеричная система счисления — правила и примеры решений
Общие сведения
Во время изобретения персонального компьютера (ПК) или ЭВМ использовался определенный язык представления данных, который существенно отличался от десятичной системы счисления. Последняя используется человеком при ведении расчетов и является самой удобной.
Последняя используется человеком при ведении расчетов и является самой удобной.
Кодирование данных в современных ЭВМ осуществляется за счет элементов (транзисторов) в интегральных микросхемах. За основу взят полупроводниковый переход, который может быть закрытым или открытым. Следует отметить, что режим «насыщения», присущий радиодетали, не используется. Если он открыт, то в триггер (память) записывается единица, а в противном случае — нуль. В результате этого кодирование осуществляется в двоичном коде (0 или 1), основанием которого является цифра «2».
Для кодирования больших массивов информации использовать двоичную систему счисления не всегда удобно, поскольку количество транзисторов может быть огромным, а устройство будет значительно греться. Чтобы этого избежать, была придумана восьмеричная система счисления.
Для выполнения операции конвертации десятичной системы исчисления в восьмеричный код необходимы некоторые базовые знания. К ним относятся:
- Отличительная особенность числа от цифры.

- Виды систем представления информации.
- Понятие о двоичном коде.
- Алгоритм или методика перевода в восьмеричную систему представления.
- Примеры решения задач.
Специалисты в области информационных технологий рекомендуют разбирать базовые понятия в последовательности, состоящей из пяти шагов.
Число и цифра
При расчетах и выражении количественных характеристик процесса или явления применяются определенные математические символы — числа. Они состоят из разрядной сетки. Каждый ее элемент — цифра, которая принимает значения, в зависимости от выбранной системы счисления (СС). Например, для десятичной используется диапазон от 0 до 9, а девятеричная состоит из интервала с минимальной величиной, равной 0, а максимальной — 8.
Цифра — математический знак, используемый для построения более сложных конструкций. Например, с его помощью можно записать значения различных типов (четырехзначные, пятизначные). Любое число состоит из разрядной сетки, элементами которой и являются математические символы.
Любое число состоит из разрядной сетки, элементами которой и являются математические символы.
При выполнении различных математических операций нужно следить за одинаковыми разрядами. Например, недопустимо складывать сотни и тысячи, поскольку это действие приведет к ошибочным вычислениям. Далее следует разобрать системы представления информации и их примеры.
Виды числовых представлений
Для правильного перевода чисел из одной СС в другую необходимо разобрать классификацию форм представления информации. Они бывают двух типов, в зависимости от расположения цифр:
- Зависимые (позиционные).
- Независимые (непозиционные).
В первом случае значение числа зависит от расположения или комбинации цифр. Этот факт очень просто доказывается на примере обычной десятичной формы представления величины. Например, 25 и 52 — два разных значения. Если бы расположение разрядов не учитывалось, при разности этих двух величин получился нуль. Позиционными СС являются двоичный, восьмеричный и шестнадцатеричный коды. В них также есть разрядная сетка.
Позиционными СС являются двоичный, восьмеричный и шестнадцатеричный коды. В них также есть разрядная сетка.
Независимыми от расположения разрядов называются непозиционные СС. Примером одной из них является унарная форма записи числа. Суть ее заключается в эквивалентности символа какому-либо значению. Например, на предприятиях применяются обыкновенные «крестики» для подсчета количества рабочих дней сотрудников. Каждый символ эквивалентен единице.
На уроках математики в начальных классах также применяется инструмент — счетные палочки. Последние помогают ученикам развивать навык устного счета и являются компонентами непозиционной СС. С их помощью возможно выполнять операции суммы, разности, а также произведения и деления.
Следует отметить, что не во всех случаях один символ может соответствовать единице. Это могут быть десятки, сотни и даже тысячи. Для расчетов при помощи непозиционной СС можно придумать собственные обозначения, как это сделано в римских цифрах. Однако при этом существуют определенные недостатки:
Однако при этом существуют определенные недостатки:
- Сложность работы с большими числами.
- Затрудненный перевод в десятичную и обратно.
- Невозможно работать с дробными величинами (сложение, вычитание, умножение и деление).
- Операции возведения в степень и изъятия корня невозможны.
Достоинством считается сокращение времени записи величины, которая постоянно изменяется. Например, при подсчете количества выходов персонала достаточно поставить крестик или палочку, и это делается без исправлений. В случае с десятичной СС исправлений избежать невозможно.
Чтобы выполнить перевод в восьмеричную систему счисления, необходимо ознакомиться с методикой конвертации десятичной формы в двоичное кодовое представление.
Двоичная кодировка
Для преобразования десятичной величины в двоичную IT-специалистами были разработаны специальные правила или алгоритмы. К ним относятся столбик и степень. Каждому начинающему IT-специалисту необходимо выбрать оптимальную методику преобразования одной формы числа в другую. Каждый из способов удобен в конкретной ситуации. Можно также применять сразу 2 — один для решения, а другой — для проверки результата. Необходимо разобрать каждую методику подробно с практической реализацией алгоритма.
Каждому начинающему IT-специалисту необходимо выбрать оптимальную методику преобразования одной формы числа в другую. Каждый из способов удобен в конкретной ситуации. Можно также применять сразу 2 — один для решения, а другой — для проверки результата. Необходимо разобрать каждую методику подробно с практической реализацией алгоритма.
Метод «столбик»
Первый способ получил широкое применение, поскольку для его выполнения требуется минимум знаний в математической сфере. Он имеет следующий вид:
- Анализ числа на четность и нечетность.
- Запись нуля в первом случае и единицы — во втором.
- Выделение результата (снизу вверх).
Реализация алгоритма проверяется на практическом примере. Для этого требуется решить задачу конвертации числа из десятичной СС в другую, перевод 167{10} в {2}. Решение имеет следующий вид:
- 167/2 ->1.
- 83/2 ->1.
- 41/2 ->1.
- 20/2 ->0.
 0].
0]. - Если сложить все коэффициенты, получится значение, которое равно 167.
- 167{10}.
Переводить системы счисления в другие формы представления возможно при помощи различных онлайн-сервисов. Для этого требуется указать исходную форму числа, а затем конечную. Однако действия рекомендуется совершать только для проверки результата решения задачи.
Способ степени
Для конвертации в двоичный код также применяется метод степени. Суть его заключается в представлении числа в виде отдельных элементов с основанием «2» и некоторым показателем. Алгоритм в этом случае выглядит таким образом:
- Найти наибольшую степень, записав в высший разряд «1».
- Отнять от искомого числа величину, полученную на первом шаге.
- Повторить действия первого и второго пунктов.
Как и во всех остальных случаях, рекомендуется разобрать алгоритм на практическом примере. Решение задачи для числа «167» имеет такой вид:
- Максимальная степень: 2^7<167<2^8 -> 2^7=128 (1).
 0=1 ->1.
0=1 ->1. - Результат: 10100111.
Однако операция преобразования является вспомогательной. Она применяется для дальнейшей конвертации в восьмеричную СС.
Восьмеричная система
Восьмеричная форма представления чисел состоит из основания-восьмерки и триады. Совокупность последних образуют любые значения. Для кодирования информации в этом случае применяется меньше регистров памяти. Этого нельзя сказать о двоичном коде.
Для восьмеричного представления применяются цифры от 0 до 7 (всего 8). Многие новички часто путают ее с шестнадцатеричной СС, в которой содержатся символы латинского алфавита. При выполнении операций конвертации специалисты рекомендуют ознакомиться со списком (таблицей) восьмеричной системы:
- 0 -> 000.
- 1 -> 001.
- 2 -> 010.
- 3 -> 011.
- 4 -> 100.
- 5 -> 101.
- 6 -> 110.

- 7 -> 111.
Он поможет перевести любое числовое сообщение. Для удобства IT-специалисты рекомендуют составить презентацию или записать на лист плотной бумаги перекодировку списка. Заучивать коды нет необходимости, поскольку достаточно решать примеры (информация отложится в памяти). Алгоритм кодирования очень прост:
- Написать величину в десятичной форме.
- Перевести ее в двоичный код одним из методов.
- Разделить двоичную форму на триады (сгруппировать по 3 элемента, начиная справа). Если разрядов не хватает, нужно дописать нули слева (это не влияет на значение).
- Декодировать каждую группу, воспользовавшись списком.
- Записать окончательный результат, указав, что величина записана в восьмеричной форме.
После ознакомления с методикой преобразования нужно проверить ее реализацию на примере. Требуется выяснить, значение 167 {10}. Это делается довольно просто:
- 167{10}.

- Из вышеописанных примеров: 1111011{2}.
- {001}{111}{011}.
- {1}{7}{3}
- 173{8}.
Обратное декодирование выполняется по такой методике:
- Записывается форма: 173{8}.
- Разделяется на группы: {1}{7}{3}.
- Декодируется каждый компонент: {001}{111}{011}.
- Окончательный результат без учета группировочных символов и лишних разрядов: 1111011{2}.
- Переводится в десятичную СС: 167{10}.
На начальных этапах обучения рекомендуется четко следовать по пунктам методики. Однако через некоторое время последние можно опускать.
Таким образом, восьмеричная система применяется для кодирования больших массивов информации, при котором может быть задействовано минимальное количество регистров запоминающего устройства персонального компьютера.
Восьмеричная и шестнадцатеричная системы счисления
Содержание урока
§12. Восьмеричная система счисления
§13. Шестнадцатеричная система счисления
Шестнадцатеричная система счисления
Шестнадцатеричная система счисления
Алгоритм перевода шестнадцатеричного числа в двоичную систему счисления
Алгоритм перевода двоичного числа в шестнадцатеричную систему счисления
Вопросы и задания
Задачи
§13. Шестнадцатеричная система счисления
Шестнадцатеричная система счисления
Шестнадцатеричная система счисления (позиционная система с основанием 16) широко используется для записи адресов и содержимого ячеек памяти компьютера. Её алфавит содержит 16 цифр, вместе с 10 арабскими цифрами (0..9) используются первые буквы латинского алфавита:
А = 10, В = 11, C = 12, D = 13, Е = 14, F = 15.
Таким образом, старшая цифра в шестнадцатеричной системе — F.
Для перевода чисел из десятичной системы в шестнадцатеричную используют алгоритм деления на 16 и взятия остатков. Важно не забыть, что все остатки, большие 9, нужно заменить на буквы:
Важно не забыть, что все остатки, большие 9, нужно заменить на буквы:
Для обратного перехода значение каждой цифры умножают на 16 в степени, равной её разряду, и полученные значения складывают:
Можно также использовать схему Горнера:
1ВС16 = (1 • 16 + 11) • 16 + 12 = 27 • 16 + 12 = 444.
Основания двоичной и шестнадцатеричной систем связаны соотношением 24 = 16, поэтому можно переводить числа из шестнадцатеричной системы в двоичную напрямую. Алгоритмы перевода чисел из шестнадцатеричной системы в двоичную и обратно полностью аналогичны соответствующим алгоритмам для восьмеричной системы. Каждая шестнадцатеричная цифра представляется в виде тетрады (группы из четырёх двоичных цифр) (табл. 2.6).
Следующая страница Алгоритм перевода шестнадцатеричного числа в двоичную систему счисления
Cкачать материалы урока
Восьмеричная система счисления — Википедия. Что такое Восьмеричная система счисления
Что такое Восьмеричная система счисления
| Системы счисления в культуре | |
|---|---|
| Индо-арабская | |
| Арабская Тамильская Бирманская | Кхмерская Лаосская Монгольская Тайская |
| Восточноазиатские | |
| Китайская Японская Сучжоу Корейская | Вьетнамская Счётные палочки |
| Алфавитные | |
| Абджадия Армянская Ариабхата Кириллическая Греческая | Грузинская Эфиопская Еврейская Акшара-санкхья |
| Другие | |
| Вавилонская Египетская Этрусская Римская Дунайская | Аттическая Кипу Майяская Эгейская Символы КППУ |
| Позиционные | |
| 2, 3, 4, 5, 6, 8, 10, 12, 16, 20, 60 | |
| Нега-позиционная | |
| Симметричная | |
| Смешанные системы | |
| Фибоначчиева | |
| Непозиционные | |
| Единичная (унарная) | |
Восьмери́чная систе́ма счисле́ния — позиционная целочисленная система счисления с основанием 8.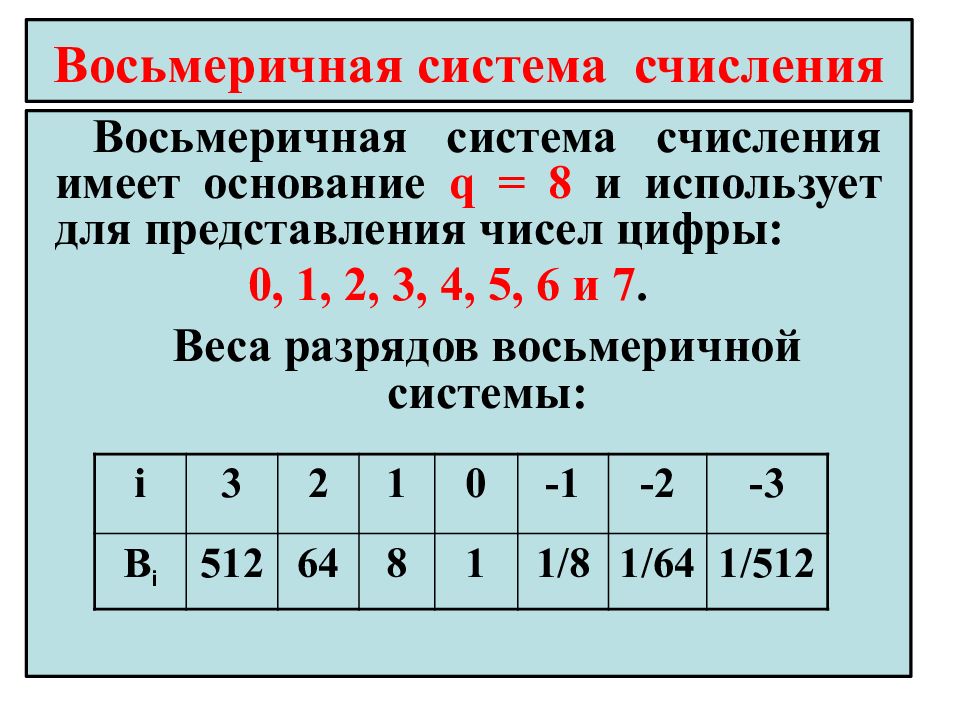 Для представления чисел в ней используются цифры от 0 до 7.
Для представления чисел в ней используются цифры от 0 до 7.
Восьмеричная система чаще всего используется в областях, связанных с цифровыми устройствами. Характеризуется лёгким переводом восьмеричных чисел в двоичные и обратно, путём замены восьмеричных чисел на триплеты двоичных. Широко использовалась в программировании и компьютерной документации, однако позднее была почти полностью вытеснена шестнадцатеричной.
Восьмеричная система применяется при выставлении прав доступа к файлам и прав исполнения для участников в Linux-системах[1][2].
Таблица перевода восьмеричных чисел в двоичные
08 = 0002 18 = 0012 28 = 0102 38 = 0112 48 = 1002 58 = 1012 68 = 1102 78 = 1112
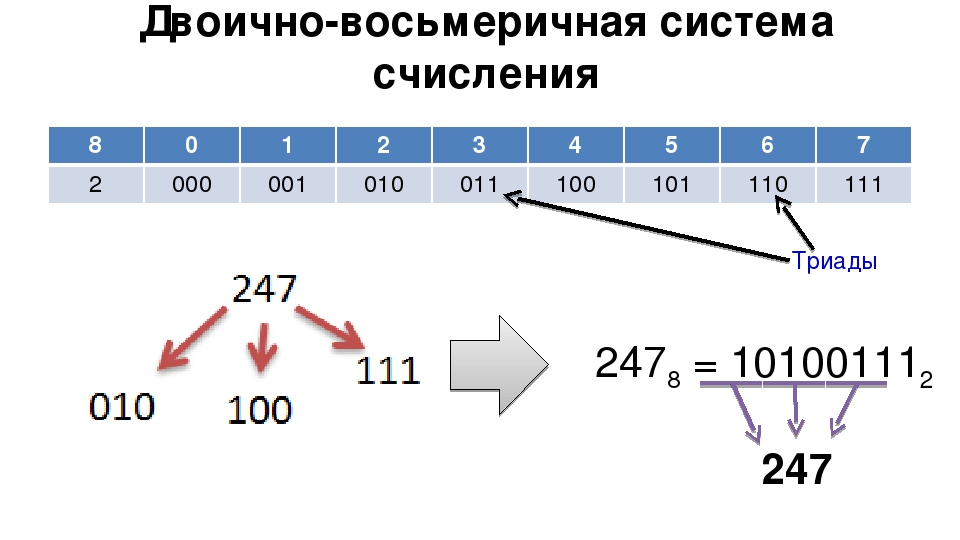
Для перевода восьмеричного числа в двоичное необходимо заменить каждую цифру восьмеричного числа на триплет двоичных цифр. Например:
25418 = [ 28 | 58 | 48 | 18 ] = [ 0102 | 1012 | 1002 | 0012 ] = 0101011000012.
Например:
25418 = [ 28 | 58 | 48 | 18 ] = [ 0102 | 1012 | 1002 | 0012 ] = 0101011000012.
Использование в естественных языках
Языки юки[3] и паме[4] используют восьмеричную систему счисления.
В языках программирования
Ряд языков программирования, в частности, Си/С++, Ada, Perl, Java и Python (до 3.0), имеют специальный синтаксис для записи восьмеричных констант с применением ведущего нуля, например, 0644 представляет собой запись литеральной константы со десятичным значением 42010.
По статистике, применение восьмеричных констант в программах на языке Си чрезвычайно низко (около 0,1 % от всех литеральных констант, без учета константы «0», технически также восьмеричной). Определенную популярность такие константы сохраняют в случае описания прав на файлы в Unix/POSIX стиле (0666, 0750), и при отдельных случаях работы с битовыми масками, когда программисту проще представлять битовое представление восьмеричных чисел, а не шестнадцатиричных или, тем более, десятичных[5].
Подобные правила указания системы счисления могут быть неочевидны для программистов и приводят к ошибкам. В некоторых языках существуют рекомендации не использовать такую запись[6], в других языках такая записи восьмеричных констант запрещена (например, в Python с версии 3 используется префикс 0o[7][8]) или не используется (например Rust и D[9]).
Источники
Ссылки
Урок 1: Системы счисления — 100urokov.ru
План урока:
Системы счисления – виды, особенности
Непозиционные системы счисления, их особенности
Основные позиционные системы счисления, правила перевода
Шестандцатеричная система счисления
Арифметические операции в двоичной системе
Сравнение систем
Таблицы истинности
Развиваясь, древний человек стал испытывать потребность в способах выражения количества. Подсчет убитых животных, количество врагов или соседей – причин становилось все больше. Сначала люди использовали только понятия «один», «много». После стали использовать понятие «пара», чтобы обозначить два предмета, это намного облегчило жизнь.
Сначала люди использовали только понятия «один», «много». После стали использовать понятие «пара», чтобы обозначить два предмета, это намного облегчило жизнь.
Постепенно перешли к использованию подручных средств – пальцев на руках и ногах, зарубок на коре дерева, кости животного или узелков на канате. Именно такие примитивные «счетные машины» позволили через тысячи лет узнать, что предки умели не просто считать, но даже умудрялись фиксировать результаты подсчета.
Кроме зарубок и узелков появилась потребность в символах, выражающих большее количество чего-либо, чем «один». Тогда были придуманы первые знаки для выражения больших значений. Так, египтяне, использовали знаки для цифр 1, 5, 10. Число 324 в их системе выглядело так:
А описание чисел при помощи специальных знаков и является системой счисления.
Системы счисления – виды, особенности
Система счисления (СС) – способ выражения чисел при помощи специальных правил и знаков, которые называются цифрами.
Источник
Все существующие системы делят на 2 группы:
- Позиционные системы счисления – такие, в которых, в зависимости от положения, цифры будет иметь разное значение. К этой группе относится арабская СС, в которой на первом месте справа цифра будет обозначать единицы, на втором – десятки, на третьем – сотни и так далее.
Чтобы выразить число 475, достаточно по порядку написать 3 символа, 475, выражая 5 единиц, 7 десятков и 4 сотни.
К этой группе также относятся СС с различными основаниями (2,8,16).
- Непозиционные СС – имеет значение именно знак, а не его положение. Единицы, десятки, сотни обозначаются определенными символами. Яркий представитель этой группы – римская СС.
Еще одна особенность – чтобы выразить число и не использовать сотни символов, применяется прибавление и вычитание. Написать 475 римскими знаками можно так CCCCXXXXXXXIIIII, но это нерационально. Если отнимать или прибавлять цифры, получится меньшее количество символов – CDLXXV. Цифра слева означает, что ее нужно отнять от большего числа, а справа – прибавить.
Если отнимать или прибавлять цифры, получится меньшее количество символов – CDLXXV. Цифра слева означает, что ее нужно отнять от большего числа, а справа – прибавить.
12 – XII
8 – VIII или IIX
Правильным считается тот вариант, при котором получается меньше символов.
Интересно. Первой позиционной СС была вавилонская и была она шестнадцатиричная! А в 19 веке использовали двенадцатеричную СС.
Алфавит СС – знаки, которые используются для обозначения цифр.
Основание – количество знаков, которыми кодируются числа. Еще оно показывает отличие между цифрами на разных позициях. Основание – целое число, начиная с 2.
Важно. Если в тексте идет речь о различных системах, то чтобы уточнить, какая используется основа, ставится подстрочный знак: 12548, 011001112. Примеры? Если же обозначения нет, по умолчанию это десятичная (12549).
Разряд – положение, позиция обозначения цифры в числе. Пример?
Пример?
Источник
Непозиционные СС, их особенности
Первоначально древние люди ставили отметки (черточки-зарубки, точки), чтобы обозначить количество того или иного предмета. Отклики этого подхода все еще встречаются (полоски у военных, счетные палочки).
Источник
Постепенно от единиц они переходили к группам предметов по 3, 5, 10 единиц. Постепенно такие группы стали обозначаться определенными символами, что позволило сократить размер записи.
Источник
Римская СС
В ней определенным цифрам отвечают латинские буквы. Их сумма и будет числом.
Источник
Основные рекомендации при пользовании римскими цифрами:
- Символы следует писать по убыванию слева направо.
- Нежелательно записывать подряд более 3 одинаковых знаков.
- Положение цифры обозначает, какой ее вклад – отрицательный, если она стоит слева от большего числа, положительный – справа.
Таблица римских цифр Источник
Недостаток этой СС в том, что для больших чисел недоступны операции сложения или другие, ещё она сложная и громоздкая. Зато римские цифры отлично вписались там, где нужна нумерация и эстетика: циферблаты, номера глав, списки, серии документов.
Зато римские цифры отлично вписались там, где нужна нумерация и эстетика: циферблаты, номера глав, списки, серии документов.
Основные позиционные СС, правила перевода
Двоичная система счисления
Систему, на которой основывается работа компьютеров, придумал гениальный немецкий ученый Г.В. Лейбниц (еще до 19 века!). Он придумал и описал СС, в которой все вычисления проводятся при помощи двух простейших символов – 0 и 1.
Компьютер, как механическое устройство, получает команды в виде двоичной кодировки. Он не в силах понять сложные задания, человеческую речь, музыку или тысячи оттенков, а переводя/кодируя всю необходимую информацию при помощи 0 и 1 (сеть, отсутствие сети), можно передать ему любые команды или информацию. Естественно, такие задания выглядят как огромные массивы двух знаков.
Источник
Алгоритм перевода чисел из десятичной в двоичную систему:
- Деление на основу СС до тех пор, пока не останется в остатке значение меньше значения основы.
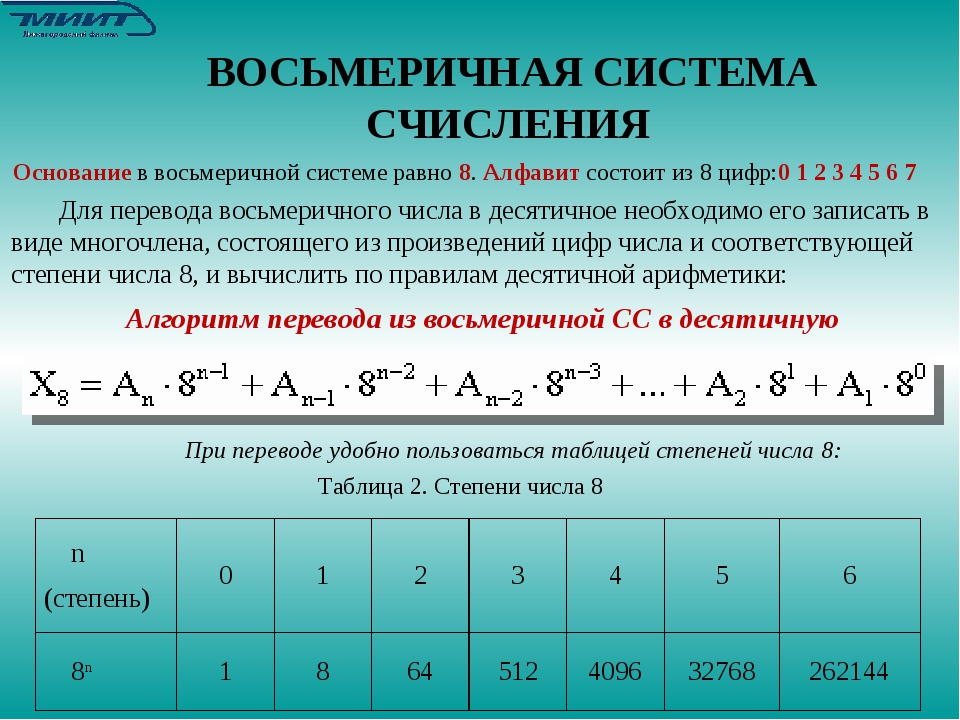
- Записать остатки, от последнего к первому.
- Первый ноль можно не писать.
0111 0100 11002
Этот порядок действия позволят переводить в любую позиционную СС. В данном случае, основа – 2, остаток < или равен =.
Источник
Обратный алгоритм перевода из двоичной в десятичную систему счисления:
Записать число развернуто, то есть, сколько сотен, десятков и единиц в нем, но учитывая основу – 2
Объяснение. Развернутая форма записи 579: 5*102+7*101+9*100 = 57910.
Источник
Обычно мы пользуемся свернутой формой записи чисел, то есть без разбивки на разряды и умножения на основу.
- Умножить и суммировать полученные значения.
А чтобы было легче, пользуются готовой таблицей степеней 2.
Альтернативный способ преобразования для гуманитариев
Для начала нужно написать степени двойки, начиная с самой большой:
Далее нужно отнимать от числа максимальную степень двойки и напротив нее ставить 1, если есть в исходном варианте или 0, если его нет.
Перевод числа 579
Обратно еще проще. Подсчитать количество знаков – это будет степень 2 в степени -1. И так далее. А проще при помощи той же таблицы:
Если же оно на 1 больше, то число будет начинаться и заканчиваться на 1, а внутри – сплошные 0.
Восьмеричная СС
Основой такой системы является 8, а числа восьмеричной системы 0-7. Данная система счисления является позиционной и целочисленной. Применяется в сферах, связанных с цифровыми технологиями, особенно в Linux-программном обеспечении (права доступа, исполнения).
Источник
Пример: Перевести 5798 из десятичной в восьмеричную систему счисления:
Обратный перевод из восьмеричной СС в десятичную:
11038 = 1∙83+1∙82+0∙81+3∙80 = 512+64+0+3 = 57910
Таблица степеней
Альтернативный вариант таблицы степеней
Шестнадцатеричная СС
Это целочисленная система с основанием 16 (символы шестнадцатеричной системы счисления 0-9 и буквы A – F). Используется в реализации компьютерного программирования и документации на низком уровне, так как 8-битный байт, для записи которого удобно использовать 2 цифры из шестнадцатеричной системы.
Используется в реализации компьютерного программирования и документации на низком уровне, так как 8-битный байт, для записи которого удобно использовать 2 цифры из шестнадцатеричной системы.
Стандарт Юникод использует 4 и более символов 16-ой СС.
Ист
Урок 4. Восьмеричная и шестнадцатеричные системы счисления. Компьютерные системы счисления
Урок 4. Восьмеричная и шестнадцатеричные системы счисления. Компьютерные системы счисления
Восьмеричная система счисления
Восьмеричной системой счисления называется позиционная система счисления с основанием 8. Для записи чисел в восьмеричной системе счисления используются цифры: 0, 1, 2, 3, 4, 5, 6, 7.
На основании формулы (1) для целого восьмеричного числа можно записать:
Например: 10638 = 1 • 83 + 0 • 82 + 6 • 81 + 3 • 80 = 56310.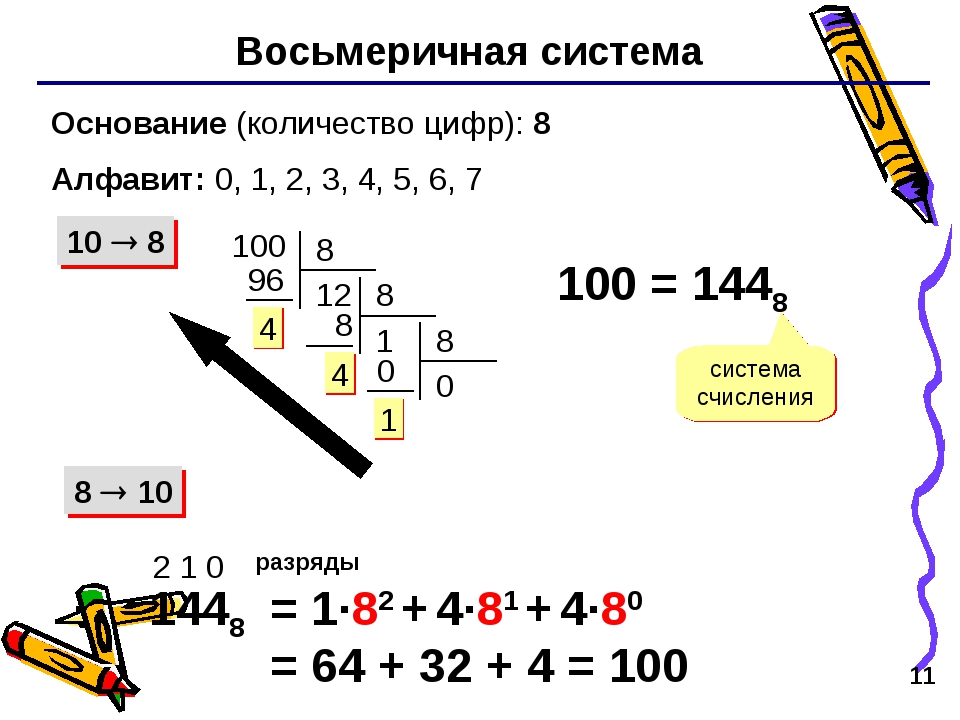
Таким образом, для перевода целого восьмеричного числа в десятичную систему счисления следует перейти к его развёрнутой записи и вычислить значение получившегося выражения.
Для перевода целого десятичного числа в восьмеричную систему счисления следует последовательно выполнять деление данного числа и получаемых целых частных на 8 до тех пор, пока не получим частное, равное нулю. Исходное число в новой системе счисления составляется последовательной записью полученных остатков, начиная с последнего.
Пример 6. Переведём десятичное число 103 в восьмеричную систему счисления.
10310 = 1478
Шестнадцатеричная система счисления
Основание: q = 16.
Алфавит: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, В, С, D, Е, F.
Здесь только десять цифр из шестнадцати имеют общепринятое обозначение 0,…, 9. Для записи цифр с десятичными количественными эквивалентами 10, 11, 12, 13, 14, 15 обычно используются первые пять букв латинского алфавита.
Таким образом, запись 3AF16 означает:
Пример 7. Переведём десятичное число 154 в шестнадцатеричную систему счисления.
15410 = 9А16
Презентация «Системы счисления»
Презентация «Системы счисления» (Open Document Format)
Ссылки на ресурсы ЕК ЦОР
Федеральный центр информационных образовательных ресурсов:
Sistema octal — Wikipedia, la enciclopedia libre
El sistema de numeración posicional cuya base es 8, se llama octal y utiliza los dígitos indio arábigos: 0,1,2,3,4,5,6,7.
En informática a veces se utiliza la numeración octal en vez de la hexadecimal. Tiene la ventaja de que no Requiere utilizar otros símbolos Diferentes de los dígitos. Sin embargo, para trabajar con bytes oConnectos de ellos, asumiendo que un byte es una palabra de 8 битов, suele ser más cómodo el sistema hexadecimal, por cuanto todo byte así Definido es completetamente, представленные шестнадцатеричные данные. {i}}
{i}}
Como el sistema de numeración octal usa la notación posicional entonces para el número 3452,32 tenemos que: 2 * 8 0 + 5 * 8 1 + 4 * 8 2 + 3 * 8 3 + 3 * 8 -1 + 2 * 8 -2 = 2 + 40 + 4 * 64 + 3 * 512 + 3 * 0,125 + 2 * 0,015625 = 2 + 40 + 256 + 1536 + 0,375 + 0,03125 = 1834 + 0,40625d
Entonces, 3452,32q = 1834,40625d; mejor aún: 3452,32 (8) .
El sub índice «q» indica número octal, se usa la letra q para evitar confusión entre la letra ‘o’ y el número 0. En informática, a veces se utiliza la numeración octal en vez de la hexadecimal. Tiene la ventaja de que no Requiere utilizar otros símbolos Diferentes de los dígitos. Es posible que la numeración octal se usara en el pasado en lugar de la decimal, por ejemplo, para contar los espacios interdigitales o los dedos unique de los pulgares.
Es utilizado como una forma abreviada de submitar números binarios que emplean caracteres de seis bit. Cada tres bits (medio carácter) es convertido en un único dígito octal (del griego oktō ‘ocho’).
Cada tres bits (medio carácter) es convertido en un único dígito octal (del griego oktō ‘ocho’).
La numeración octal es tan buena como la binaria y la hexadecimal para operar con fracciones, puesto que el único factor primo para sus базис es 2. Todas las fracciones que tengan un denominador unique de una Potencia de 2 tenden un desarrollo octal periódico.
| Fracción | восьмеричное | Результат в восьмеричном формате |
|---|---|---|
| 1/2 | 1/2 | 0,4 |
| 1/3 | 1/3 | 0,25252525 периодико |
| 1/4 | 1/4 | 0,2 |
| 1/5 | 1/5 | 0,14631463 периодико |
| 1/6 | 1/6 | 0,125252525 периодико |
| 1/7 | 1/7 | 0,111111 периодико |
| 1/8 | 1/10 | 0,1 |
| 1/9 | 1/11 | 0,07070707 периодико |
| 1/10 | 1/12 | 0,063146314 периодико |
Métodos de converión [editar]
Decimal [editar]
Para poder convertir un número en base decimal и base octal se div dicho número entre 8, dejando el остаток y dividiendo el cociente sucesivamente entre 8 hasta obtener cociente 0, luego los de las divations leídos en orden обратное указание на индексы en или обратного индексов.
Ejemplo:
Восьмеричное десятичное число 730
730 ÷ 8 = 91,25
91 = cociente
8 х 91 = 728
730–728 = 2
2 = остаток
91 ÷ 8 = 11.375
11 = cociente
8 х 11 = 88
91-88 = 3
3 = остаток
11 ÷ 8 = 1
1 = cociente
8 х 1 = 8
11-8 = 3
3 = остаток
1 ÷ 8 = 0
0 = cociente
8 х 0 = 0
1 — 0 = 1
1 = остаток
восьмеричное десятичное число 730 = 1332
Восьмеричное десятичное число 179
179 ÷ 8 = 22
22 = cociente
8 х 22 = 176
179–176 = 3
3 = остаток
22 ÷ 8 = 2
2 = cociente
8×2 = 16
22–16 = 6
6 = остаток
2 ÷ 8 = 0
0 = cociente
8×0 = 0
2-0 = 2
2 = остаток
Восьмеричное десятичное число 179 = 263
Бинарио [редактор]
Para pasar de binario a octal, solo hay que agrupar de 3 en 3 los dígitos binarios, así, el número binario 1001010 (74 en decimal), lo agruparíamos como 1/001/010. como al primer dígito le hacen falta dos números para que se cumpla la regla de 3 en 3 le agregamos 2 ceros, de modo que quedaría
como al primer dígito le hacen falta dos números para que se cumpla la regla de 3 en 3 le agregamos 2 ceros, de modo que quedaría
( 00 1) (001) (010)
después obtenemos el número en decimal de cada uno de los paréntesis de los números en binario con la siguiente fórmula:
из derecha a izquierda visualiza un número del 0 al 2 en la parte superior del número binario, para indicar la posición del binario en el paréntesis:
210 <<<
1.(001) posición 0 para el binario 1, posición 1 para el binario 0, posición 2 para el binario 0
210 <<<
2. (001) posición 0 para el binario 1, posición 1 para el binario 0, posición 2 para el binario 0
210 <<<
3. (010) posición 0 para el binario 0, posición 1 para el binario 1, posición 2 para el binario 0
Después se multiplica cada número binario por 2 elevado a la posición del número binario y cada resultado se suma:
- (001) знак равно (0 x 2exp2 {\ displaystyle \ exp 2}) + (0 x 2exp1 {\ displaystyle \ exp 1}) + (1 x 2exp0 {\ displaystyle \ exp 0}) = 0 + 0 + 1 = 1
- (001) знак равно (0 x 2exp2 {\ displaystyle \ exp 2}) + (0 x 2exp1 {\ displaystyle \ exp 1}) + (1 x 2exp0 {\ displaystyle \ exp 0}) = 0 + 0 + 1 = 1
- (010) знак равно (0 x 2exp2 {\ displaystyle \ exp 2}) + (1 x 2exp1 {\ displaystyle \ exp 1}) + (0 x 2exp0 {\ displaystyle \ exp 0}) = 0 + 2 + 0 = 2
001 = 1
001 = 1
010 = 2
De modo que el número binario 1001010 en octal es 112.
Табла преобразования десятичных, двоичных, шестнадцатеричных и восьмеричных [редактор]
| Десятичный | Binario | Шестнадцатеричный | восьмеричный |
|---|---|---|---|
| 0 | 00000 | 0 | 0 |
| 1 | 00001 | 1 | 1 |
| 2 | 00010 | 2 | 2 |
| 3 | 00011 | 3 | 3 |
| 4 | 00100 | 4 | 4 |
| 5 | 00101 | 5 | 5 |
| 6 | 00110 | 6 | 6 |
| 7 | 00111 | 7 | 7 |
| 8 | 01000 | 8 | 10 |
| 9 | 01001 | 9 | 11 |
| 10 | 01010 | А | 12 |
| 11 | 01011 | B | 13 |
| 12 | 01100 | С | 14 |
| 13 | 01101 | D | 15 |
| 14 | 01110 | E | 16 |
| 15 | 01111 | F | 17 |
| 16 | 10000 | 10 | 20 |
| 17 | 10001 | 11 | 21 |
| 18 | 10010 | 12 | 22 |
| 19 | 10011 | 13 | 23 |
| 20 | 10100 | 14 | 24 |
| 21 | 10101 | 15 | 25 |
| 22 | 10110 | 16 | 26 |
| 23 | 10111 | 17 | 27 |
| 24 | 11000 | 18 | 30 |
| 25 | 11001 | 19 | 31 |
| 26 | 11010 | 1A | 32 |
| 27 | 11011 | 1Б | 33 |
| 28 | 11100 | 1С | 34 |
| 29 | 11101 | 1D | 35 |
| 30 | 11110 | 1E | 36 |
| 31 | 11111 | 1 этаж | 37 |
| 32 | 100000 | 20 | 40 |
| 33 | 100001 | 21 | 41 |
Véase también [редактор]
Enlaces externos [редактор]
Восьмеричная система счисления
СИСТЕМА Восьмеричных чисел
Восьмеричная система счисления, или система счисления с основанием 8, широко используется в компьютерах. Потому что
его связь с двоичной системой, это полезно при программировании некоторых типов
компьютеры.
Потому что
его связь с двоичной системой, это полезно при программировании некоторых типов
компьютеры.
Посмотрите внимательно на сравнение двоичной и восьмеричной систем счисления в таблице 1-3. Вы можете видите, что одна восьмеричная цифра эквивалентна трем двоичным цифрам. Следующее примеры преобразования восьмеричного числа 225 8 в двоичное и обратно далее проиллюстрируйте это сравнение:
Таблица 1-3.- Двоичное и восьмеричное сравнение
Блок и номер
Термины, которые вы выучили в десятичной и двоичной части, также используются с восьмеричная система.
Единица остается единым объектом, а число остается символом, используемым для обозначения один или несколько единиц.
Основание (основание)
Как и в других системах, основание — это количество символов, используемых в
система. В восьмеричной системе используются восемь символов — от 0 до 7. Основание или основание системы счисления — это
обозначается нижним индексом 8.
В восьмеричной системе используются восемь символов — от 0 до 7. Основание или основание системы счисления — это
обозначается нижним индексом 8.
Позиционное обозначение
Восьмеричная система счисления — это система счисления с позиционным обозначением. Как десятичный система использует степень 10, а двоичная система использует степень 2, восьмеричная система использует степень 8 для определения значения позиции числа. Следующая гистограмма показывает позиции и мощность базы:
Помните, что степень или экспонента указывает, сколько раз основание умножается на себя.Значение этого умножения выражается в базе 10, как показано ниже:
Все числа слева от точки счисления являются целыми числами, а числа справа дробные числа.
MSD и LSD
При определении старших и младших цифр восьмеричного числа используйте те же
правила, которые вы использовали с другими системами счисления. Крайняя слева цифра от
Точка счисления — это MSD, а крайняя правая точка от точки счисления — LSD.
Крайняя слева цифра от
Точка счисления — это MSD, а крайняя правая точка от точки счисления — LSD.
Пример:
Если число представляет собой целое число, MSD — это ненулевая цифра, крайняя слева от точка счисления, а LSD — цифра слева от точки счисления. И наоборот, если число является только дробью, ненулевая цифра, ближайшая к точке счисления — это MSD, а LSD — это ненулевая цифра, крайняя справа от точки счисления.
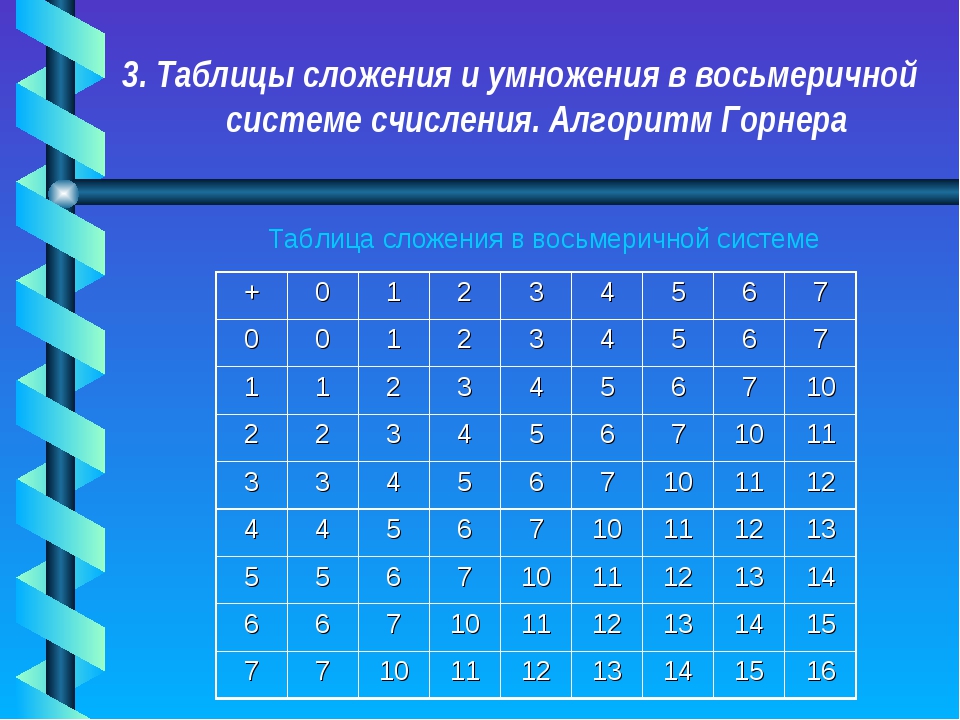
Сложение восьмеричных чисел
Сложить восьмеричные числа несложно, если вы помните, что в любое время сумма двух цифр превышает 7, производится перенос. Сравните два примера, показанных ниже:
Таблица восьмеричного сложения в таблице 1-4 будет полезна вам, пока вы привык складывать восьмеричные числа. Чтобы использовать таблицу, просто следуйте указаниям, приведенным в этот пример:
Добавить: 6 8 и 5 8
Таблица 1-4. — Таблица восьмеричного сложения
— Таблица восьмеричного сложения
Найдите цифру 6 в столбце X на рисунке. Затем найдите 5 в Y столбец. Точка в области Z , где эти два столбца пересекаются, является суммой. Следовательно,
Если вы используете концепции сложения, которые вы уже изучили, вы готовы добавить восьмеричные числа.
Проработайте решения следующих проблем:
Как упоминалось ранее в этом разделе, каждый раз сумма столбца чисел превышает 7, производится перенос.Может быть произведено более одного переноски, если их три или необходимо добавить дополнительные числа, как в этом примере:
Сумма аугенда и первого слагаемого составляет 6 8 с переносом. Сумма 6 8 а второе слагаемое — 5 8 с переносом. Вы должны записать 5 8 и сложите два переноса и уменьшите их до суммы, как показано ниже:
Теперь попробуем несколько практических задач:
Q. 24 Добавить:
24 Добавить:
Q.25 Добавить:
Q.26 Добавить:
Q.27 Добавить:
Q.28 Добавить:
Q.29 Добавить:
Шестнадцатеричная и восьмеричная системы счисления
Системы восьмеричных и шестнадцатеричных чисел на самом деле довольно просты, и я объясню, почему мы на самом деле используем их для программирования.
Теперь давайте посмотрим на нашу собственную систему счисления, у нас есть цифры от 0 до 9.
Если мы посмотрим на число
9
, что переводится в скважину 9.
86
это переводится в 8 * 10 + 6 * 1.
Тогда
475
4 * 100 + 7 * 10 + 5 * 1
здесь вы увидите узор,
примечание ‘^’ — это ‘сила’
9 = 9 * 10 ^ 0
86 = 8 * 10 ^ 1 + 6 * 10 ^ 0
475 = 4 * 10 ^ 2 + 7 * 10 ^ 1 + 5 * 10 ^ 0
Итак, слева направо, используя основание (10), мощность увеличивается на 1, а вы умножаете это на цифру. 0
0
Теперь почему мы используем эти системы счисления? Что ж, они легко переводятся в двоичную форму, поскольку они кратны 2.
В восьмеричном формате каждая цифра преобразуется в 3 двоичных числа.
0–000 90 800 1 — 001 90 800 2–010 90 800 3–011 90 800 4–100 90 800 5–101 90 800 6–110 90 800 7–111
Очень просто,
463–100 110 011
и вместе
142–001100010
и шестнадцатеричный одинаковый, принимаем, что каждая цифра представляет 4 двоичных цифры
0–0000
1–0001
90 800 2 — 00 10
90 800 3–00 11
90 800 4–01 00
5–0101
90 800 6–01 10
90 800 7–0111
90 800 8–1000
90 800 9–100 1
А — 1010
Б — 1011
С — 1100
Д — 1101
E — 1110
F — 1111
473 — 0100 0111 0011
6FA — 0110 1111 1010
Итак, вы понимаете, почему в программировании очень хорошо использовать шестнадцатеричный и восьмеричный числа, иногда нас не беспокоит значение десятичного числа, используя побитовые операции, нас интересует только расположение единиц и нулей в двоичное число
И последнее, чтобы использовать восьмеричные и шестнадцатеричные числа в C
Восьмеричный, у нас просто 0 перед числом
0345 — восьмеричное число 345
0153 — восьмеричное число 153
И в Hex ставим 0x перед числом
0x3F7 — шестнадцатеричное число 3F7
0x2H7 — шестнадцатеричное число 2H7
Чтобы распечатать printf в шестнадцатиричном и окт.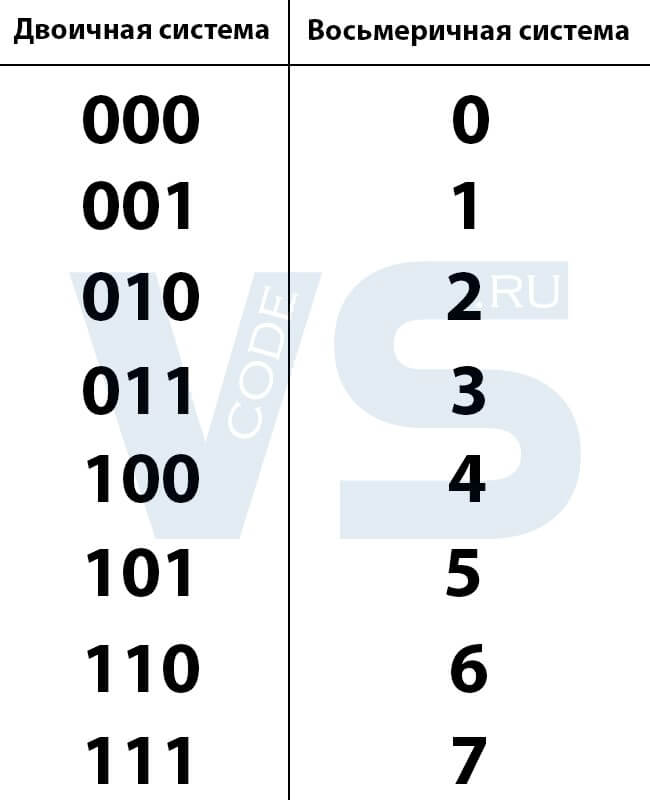
у вас есть операторы для этого
% 0x — шестнадцатеричный
% о — окт.
простой 🙂
3 способа преобразования десятичного числа в восьмеричное в программировании на языке C
Программа на языке C для преобразования десятичного числа в восьмеричное
Узнайте, как преобразовать десятичное число в восьмеричное на языке программирования C.Этот код C для преобразования десятичного числа в восьмеричное использует функцию pow () , цикл While, и цикл For .
Десятичное число
Десятичное число имеет основание 10 и включает следующие цифры: 0 1 2 3 4 5 6 7 8 9
Восьмеричное число
Восьмеричное число имеет основание 8 и включает следующие цифры : 0 1 2 3 4 5 6 7
Примечание: Эта программа на языке C для преобразования десятичных чисел в восьмеричные скомпилирована с помощью компилятора GNU GCC и написана в редакторе gEdit в операционной системе Linux Ubuntu.
Метод 1: C-программа для преобразования десятичного числа в восьмеричное с использованием цикла while
1 2 3 4 5 6 7 8 9 1112 13 14 15 16 17 18 19 | #include #include { int десятичное_число, остаток, восьмеричное_число = 0; int count = 0; printf («Введите десятичное число: \ t»); scanf («% d», & десятичное_число); , а (десятичное_число! = 0) { остаток = десятичное_число% 8; восьмеричное_число = восьмеричное_число + остаток * pow (10, count); десятичное_число = десятичное_число / 8; счет ++; } printf («\ nВосьмеричный эквивалент: \ t% d \ n», восьмеричное_число); возврат 0; } |
Метод 2: Программа C для преобразования десятичного числа в восьмеричное с использованием цикла For
1 2 3 4 5 6 7 7 7 9 10 11 12 13 14 15 16 17 18 | #include #include int main () { int decimal_number, остаток, octal_number = 0; int count; printf («Введите десятичное число: \ t»); scanf («% d», & десятичное_число); для (count = 0; decimal_number> 0; count ++) { остаток = decimal_number% 8; восьмеричное_число = восьмеричное_число + остаток * pow (10, count); десятичное_число = десятичное_число / 8; } printf («\ nВосьмеричный эквивалент: \ t% d \ n», восьмеричное_число); возврат 0; } |
Метод 3: Программа на C для преобразования десятичного числа в восьмеричное с использованием функций
1 2 3 4 5 6 7 7 7 7 9 10 11 12 13 14 15 16 17 18 19 20 21 22 22 | #include #include int decimal_to_octal (int x) { int octal_number, остаток, count = 0; , а (x! = 0) { остаток = x% 8; восьмеричное_число = восьмеричное_число + остаток * pow (10, count); х = х / 8; счет ++; } вернуть восьмеричное_число; } int main () { int decimal_number, результат; printf («Введите десятичное число: \ t»); scanf («% d», & десятичное_число); результат = десятичное_до_октальное (десятичное_число); printf («\ nОктальный эквивалент десятичного числа: \ t% d \ n», результат); возврат 0; } |
Выходные данные
Если у вас есть какие-либо ошибки компиляции или сомнения в этой программе C для преобразования десятичного значения в восьмеричное число, сообщите нам об этом в разделе комментариев ниже.
Связанные
Категория: Программирование на C Теги: Системы счисленияПонимание восьмеричной системы счисления — Видеоурок по Windows Server
Обзор Стенограммы Файлы упражнений Просмотр в автономном режиме
Детали курса
Понимание основ построения сетей имеет первостепенное значение для любого ИТ-профессионала. Когда вы поймете основы, следующим шагом станет IP-адресация. В этом курсе Тимоти Пинтелло рассматривает основные концепции, включая общие системы нумерации, а также логическую и физическую IP-адресацию. Он также обсуждает схемы адресации IPv4 и IPv6 и различные методы разрешения IP-адресации (такие как DHCP и DNS).
Когда вы поймете основы, следующим шагом станет IP-адресация. В этом курсе Тимоти Пинтелло рассматривает основные концепции, включая общие системы нумерации, а также логическую и физическую IP-адресацию. Он также обсуждает схемы адресации IPv4 и IPv6 и различные методы разрешения IP-адресации (такие как DHCP и DNS).
Инструктор
Тимоти Пинтелло
Профессор колледжа Дейтона государственного колледжа
Тимоти Пинтелло — профессор информатики в Государственном колледже Дейтоны и бывший системный администратор.Тимоти — адъюнкт-профессор и ассистент кафедры сетевых технологий в Школе компьютерных наук Государственного колледжа Дейтоны.
Узнать больше Видеть меньше Он также является автором сетевого учебника Introduction to Networking with Network + . До того как стать профессором колледжа, он работал в телекоммуникационной отрасли сначала специалистом по поддержке сети, затем ИТ-аналитиком и, наконец, системным администратором. В свободное время увлекается подводным плаванием с аквалангом и подводной фотографией.
Он также является автором сетевого учебника Introduction to Networking with Network + . До того как стать профессором колледжа, он работал в телекоммуникационной отрасли сначала специалистом по поддержке сети, затем ИТ-аналитиком и, наконец, системным администратором. В свободное время увлекается подводным плаванием с аквалангом и подводной фотографией.
Навыки, описанные в этом курсе
Зрители этого курса
37 479 человек смотрели этот курс
Связанные курсы
Добро пожаловать
« — Последняя система нумерации, на которую я хочу обратить внимание, — это восьмеричная система счисления. Восьмеричная система счисления — это система счисления по основанию 8. Это означает, что у нас есть восемь цифр вместо 10, двух или 16, как в предыдущих системах счисления, о которых мы говорили. Восьмеричная система счисления была разработана по тем же причинам, что и шестнадцатеричная система счисления. Разница в том, что восьмеричное использует только три двоичных разряда, тогда как шестнадцатеричное использует четыре двоичных разряда. Вы можете использовать таблицу, которую мы показали вам в шестнадцатеричной главе, если вы возьмете первый столбец и удалите нули, расположенные слева от чисел в двоичном столбце.Это даст вам трехзначные двоичные значения, а также восьмеричные значения, которые соответствуют этим трехбитным двоичным значениям. Кроме того, восьмеричная система счисления будет использовать только значения от нуля до семи для обозначения двоичных значений, потому что для отображения восьмеричного числа требуется только восемь цифр. О восьмеричной системе счисления следует помнить, что она .
Восьмеричная система счисления — это система счисления по основанию 8. Это означает, что у нас есть восемь цифр вместо 10, двух или 16, как в предыдущих системах счисления, о которых мы говорили. Восьмеричная система счисления была разработана по тем же причинам, что и шестнадцатеричная система счисления. Разница в том, что восьмеричное использует только три двоичных разряда, тогда как шестнадцатеричное использует четыре двоичных разряда. Вы можете использовать таблицу, которую мы показали вам в шестнадцатеричной главе, если вы возьмете первый столбец и удалите нули, расположенные слева от чисел в двоичном столбце.Это даст вам трехзначные двоичные значения, а также восьмеричные значения, которые соответствуют этим трехбитным двоичным значениям. Кроме того, восьмеричная система счисления будет использовать только значения от нуля до семи для обозначения двоичных значений, потому что для отображения восьмеричного числа требуется только восемь цифр. О восьмеричной системе счисления следует помнить, что она .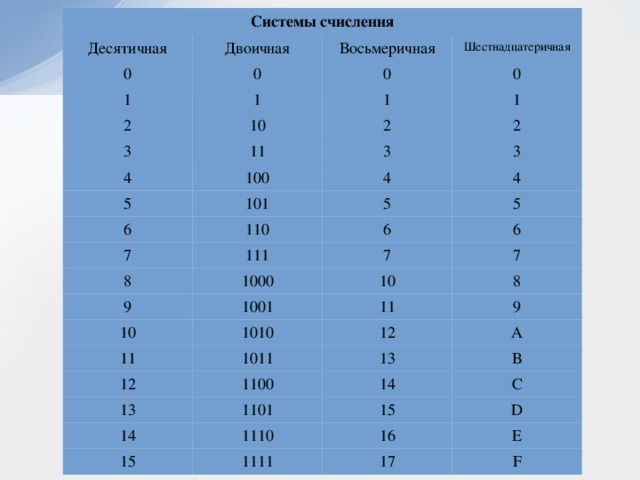 ..
..
Практикуйтесь во время обучения с файлами упражнений
Загрузите файлы, которые инструктор использует для проведения курса.Следуйте и учитесь, наблюдая, слушая и практикуя.
Скачивайте курсы и учитесь на ходу
Смотрите курсы на мобильном устройстве без подключения к Интернету. Загрузите курсы с помощью приложения LinkedIn Learning для iOS или Android.
Неделя 5: ПРЕДСТАВЛЕНИЕ ДАННЫХВ главе 4 вы узнаете, как преобразовывать между десятичным, двоичным и десятичным числами. восьмеричная и шестнадцатеричная системы счисления. Десятичная система счисления:
система нумерации, которую мы используем в повседневной жизни. Двоичная система счисления
это метод, используемый для представления данных в компьютерной системе. Двоичный
Система нумерации состоит из последовательных единиц и нулей. Десятичная система счисления:
система нумерации, которую мы используем в повседневной жизни. Двоичная система счисления
это метод, используемый для представления данных в компьютерной системе. Двоичный
Система нумерации состоит из последовательных единиц и нулей.Так как серию двоичных чисел трудно прочитать, содержимое ячейки памяти или реестра, две сокращенные версии двоичные системы счисления были разработаны для просмотра двоичных чисел Полегче. Для этого были разработаны шестнадцатеричная и восьмеричная системы счисления. цель. Сначала рассмотрим характеристики всех систем счисления. а затем вы узнаете, как переходить из одной системы счисления в другую. Тем:Список характеристики систем нумерацииСписок характеристики каждой системы нумерации: десятичный Система нумерации — База 10 двоичный Система нумерации — База 2 шестнадцатеричный Система нумерации — База 16 восьмеричный
Система нумерации — База 8 десятичный в двоичный двоичный в десятичную систему двоичный до восьмеричного числа восьмеричный в двоичный двоичный в шестнадцатеричный шестнадцатеричный в двоичный Неделя 5 Руководство по курсу | ДомХарактеристики Системы нумерации
ХАРАКТЕРИСТИКИ СИСТЕМА ДЕСЯТИЧНОЙ НУМЕРАЦИИ BASE 10
ХАРАКТЕРИСТИКИ OF БИНАРНАЯ СИСТЕМА НУМЕРАЦИИ BASE 2
ХАРАКТЕРИСТИКИ СИСТЕМА ШЕСТИГРАННОЙ НУМЕРАЦИИ BASE 16
А = 10 В = 11 С = 12 D = 13 E = 14 F = 15 ХАРАКТЕРИСТИКИ Восьмеричная система нумерации BASE 8
Преобразование из десятичной дроби в двоичную систему счисления:Вы будете преобразовывать числа в 8-битные двоичные числа.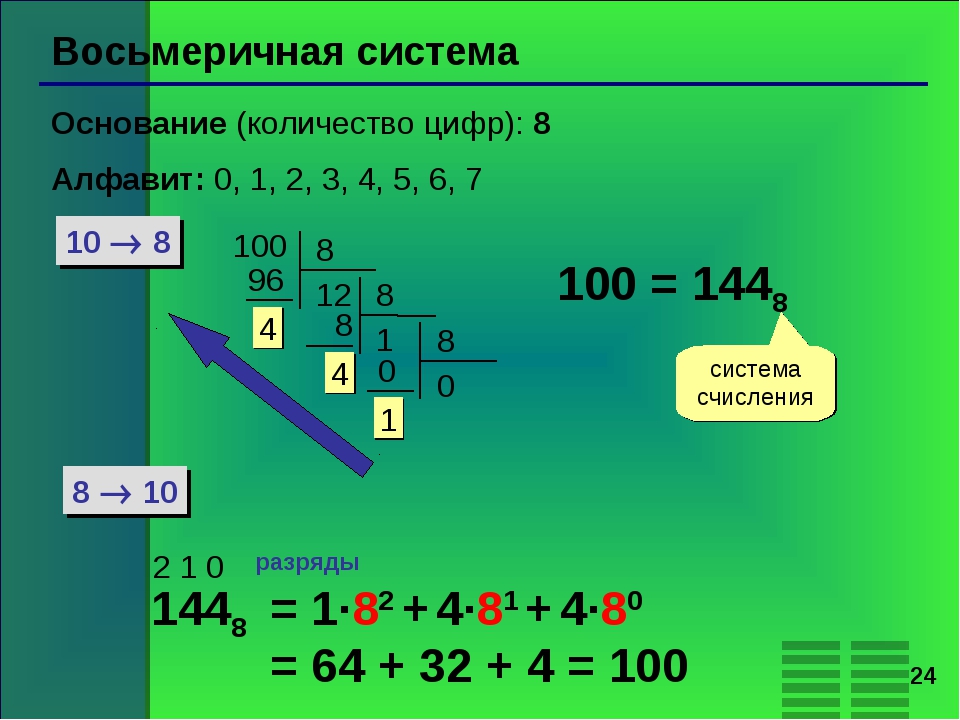 Процесс
преобразовать большие числа точно так же. Процесс
преобразовать большие числа точно так же.
Нам известно число 892 10 (нижний индекс 10 указывает число — десятичное число) имеет значение восемьсот девяносто два, потому что позиции каждой цифры в номере.Крайняя правая позиция — позиция 1, следующая позиция — позиция 10, а крайняя левая позиция — позиция 100 сек. Позиция 1 на самом деле 10 0 все, что в степени 0, всегда равно 1. Позиция 10 на самом деле равна 10 1 — что равно 10. Позиция 100 на самом деле равна 10 2 . Если бы был число перед 8, это будет в позиции 1000 или 10 3 . Те же принципы справедливы и для других систем нумерации.Если
вы смотрите на двоичное число 101 2 (нижний индекс 2 указывает
число — двоичное число). Приступим к конвертации: 2 7 2 6 2 5 2 4 2 3 2 2 2 1 2 0 что на самом деле 128 64 32 16 8 4 2 1 (вы должны увидеть, что шаблон начинается с
1 и удвойте числа для 8 позиций.) номеров (128, 64, 32, 16, 8, 4, 2, 1)
Давайте посмотрим на пример:
Преобразование двоичной в десятичную нумерацию Система:Чтобы преобразовать в десятичное число:
Преобразуйте это число 10101011 2 в десятичное число.
Преобразование двоичной в восьмеричную нумерацию Система:Восьмеричная система счисления разбивает двоичное число на группы.
01010100 знак равно Группа 1 = 100 Группа 2 = 010 Группа 3 = 01 (вы
может добавить дополнительный 0 в крайнюю левую часть, это не изменит значение
номер.
4 2 1 Группа 2 = 0 1 0 = 2 4 2 1 Группа 3 = 0 1 = 1 4 2 1 Преобразование восьмеричной в двоичную нумерацию Система:Чтобы преобразовать двоичное число в восьмеричное, необходимо для перечисления трехзначного двоичного эквивалента каждого восьмеричного числа.
1 1 0Например: 5 — это 4 + 1.Вам нужно поставить 1 в позиции 4 и 1 и 0 в позиции 2. 1 0 1
452 8 4 = 1 0 0 5 = 1 0 1 2 = 0 1 0 Преобразование двоичной в шестнадцатеричную нумерацию Система:Шестнадцатеричная система счисления разбивает двоичное число на группы из четырех и представляет каждую группу из четырех двоичных чисел с одним шестнадцатеричное число.Причина разбиения двоичного числа на группы из четырех потому, что наибольшее шестнадцатеричное число, которое может быть представлено равно 15 (основание 16 минус 1).Давайте посмотрим на пример: 01010100 2 Преобразование из шестнадцатеричной системы в двоичную систему счисления: Чтобы преобразовать шестнадцатеричное число в двоичное, вы необходимо указать четырехзначный двоичный эквивалент для каждого шестнадцатеричного числа.
2 3 2 2 2 1 2 0 или 8 4 2 1 1 0 1 0 8 4 2 1 Например: 9 — это 8 + 1.Вам нужно поставить 1 в позиции 8 и 1 и 0 в позициях 2 и 4. 1 0 0 1 8 4 2 1
8 4 2 1 8 4 2 1 неделя 5 Руководство по курсу | Дом |


 Крайняя правая позиция — позиция 1s,
следующая позиция — это позиция 2s, а крайняя левая позиция — это
4-е место. Позиция 1 на самом деле 2 0 степень 0 всегда равна 1. Позиция 2 на самом деле равна 2 1 — что
равно 2. Позиция 4 на самом деле 2 2 . Если есть
было числом перед крайним левым 1, оно будет в позиции 8 или
2 3 .
Крайняя правая позиция — позиция 1s,
следующая позиция — это позиция 2s, а крайняя левая позиция — это
4-е место. Позиция 1 на самом деле 2 0 степень 0 всегда равна 1. Позиция 2 на самом деле равна 2 1 — что
равно 2. Позиция 4 на самом деле 2 2 . Если есть
было числом перед крайним левым 1, оно будет в позиции 8 или
2 3 .
 (59 32 = 27)
(59 32 = 27) (11 8 = 3)
(11 8 = 3)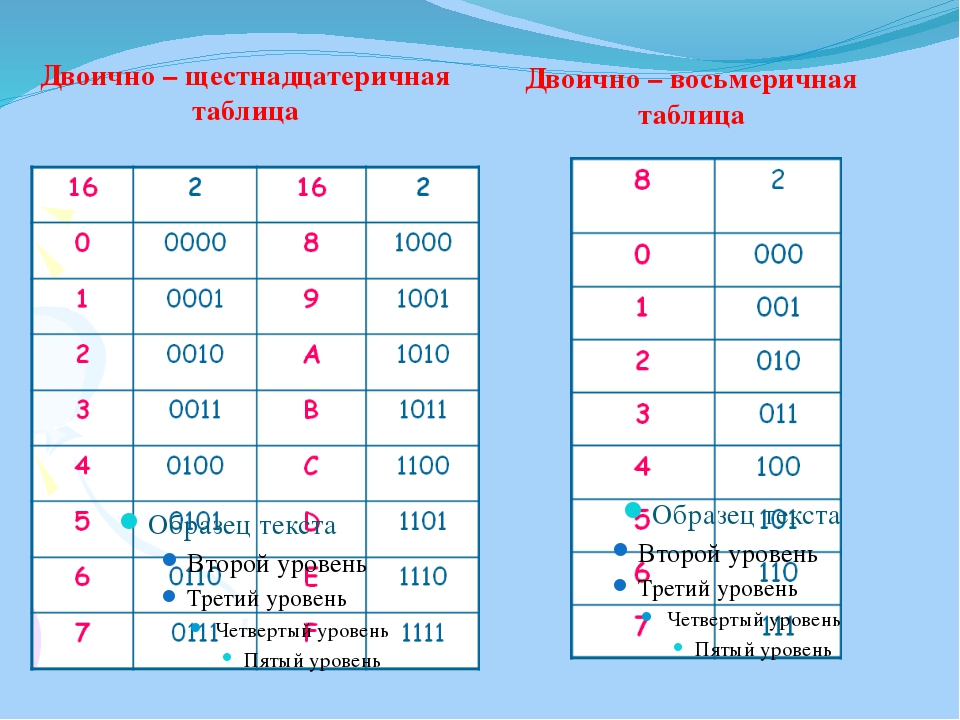
 из трех и представляет каждую группу из трех двоичных чисел с одним восьмеричным
количество. Причина, по которой двоичное число разбито на группы по три
потому что самое большое восьмеричное число, которое может быть представлено, это 7 (основание
8 минус 1).Для представления наибольшего восьмеричного числа требуется всего 3 двоичных цифры.
номер 7.
из трех и представляет каждую группу из трех двоичных чисел с одним восьмеричным
количество. Причина, по которой двоичное число разбито на группы по три
потому что самое большое восьмеричное число, которое может быть представлено, это 7 (основание
8 минус 1).Для представления наибольшего восьмеричного числа требуется всего 3 двоичных цифры.
номер 7. )
) Вам нужно поставить 1 в позиции 4 и 2.
и 0 в позиции 1.
Вам нужно поставить 1 в позиции 4 и 2.
и 0 в позиции 1. 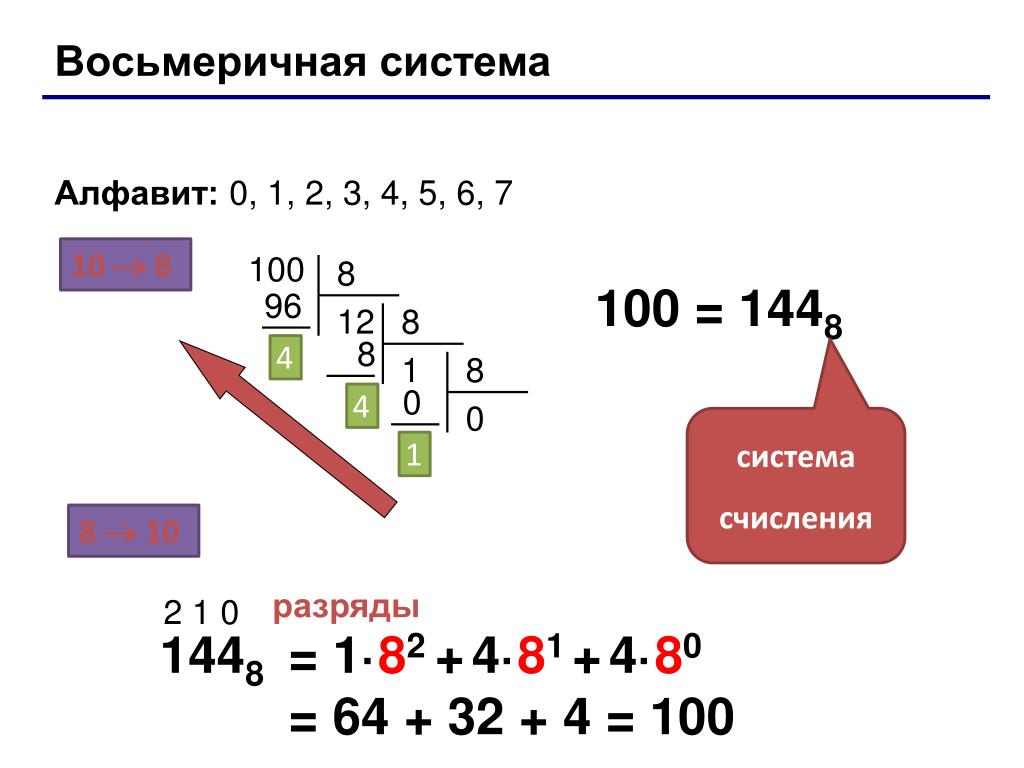 Для представления требуется всего 4 двоичных цифры
наибольшее шестнадцатеричное число 15.
Для представления требуется всего 4 двоичных цифры
наибольшее шестнадцатеричное число 15.