Системы счисления (Теория)
Сегодня разберём теоретический аспект работы с различными системами счисления. Основными системами счисления являются: двоичная, восьмеричная, десятичная (наша родная) и шестнадцатиричная.
Перевод чисел из двоичной системы в шестнадцатиричную систему счисления.
Для начала нужно написать себе в черновик следующую таблицу:
Давайте рассмотрим данную таблицу. В первом столбце идут числа от 0 до 15 в нашей родной десятичной системе счисления. Во втором столбце идут числа так же от 0 до 15, но уже в двоичной системе, а в третьем тоже от 0 до 15 в шестнадцатиричной системе счисления.
Написать числа от 0 до 15 в нашей родной десятичной системе не у кого затруднений не вызовет.
Числа в двоичной же системе лучше всего написать по следующему правилу: в младшем разряде чередуем ноль и единицу, в следующем разряде чередование нулей и единиц происходит в два раза медленнее (два нуля, две единицы, два нуля и т.
д.), в следующем разряде ещё в два раза медленнее чередование (4 нуля, 4 единицы и т.д.) и наконец 8 нулей и 8 единиц — в самом старшем разряде.
В шестнадцатиричной системе счисления помимо наших привычных символов от 0 до 9 придуманы символы A, B, С, D, E, F, и из этих 16 символов (от 0 до 15) составляется любое число, так же как в нашей системе составляется любое число из десяти цифр (от 0 до 9).Соответственно, чтобы посчитать от 0 до 15 — нужно перебрать все символы, которые имеются в шестнадцатиричной системе (от 0 до F).
Теперь рассмотрим, как с помощью данной таблицы переводить из двоичной системы в шестнадцатиричную. Переведём число 100101000 из двоичной системы в шестнадцатиричную.
Чтобы выполнить данную задачу, необходимо разбить наше двоичное число по 4 цифры начиная с правого края, и каждую 4-ку цифр нужно найти в нашей таблице: 1000 — это будет 8, 0010 — 2, 0001 -это 1. В старшем разряде у нас осталась одна единица, мы её дополнили 3-мя нулями.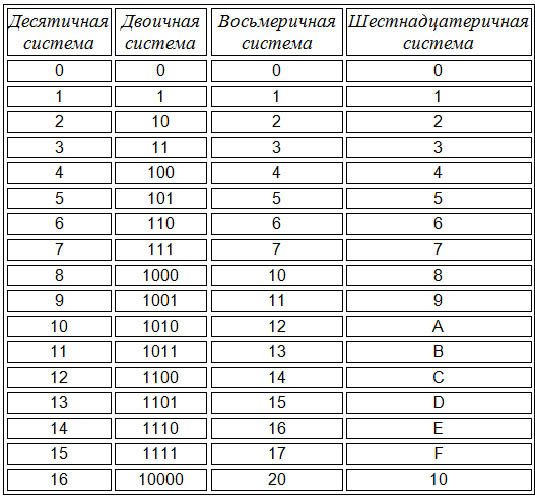
Значит число 1001010002 в двоичной системе счисления будет 12816 в шестнадцатиричной.
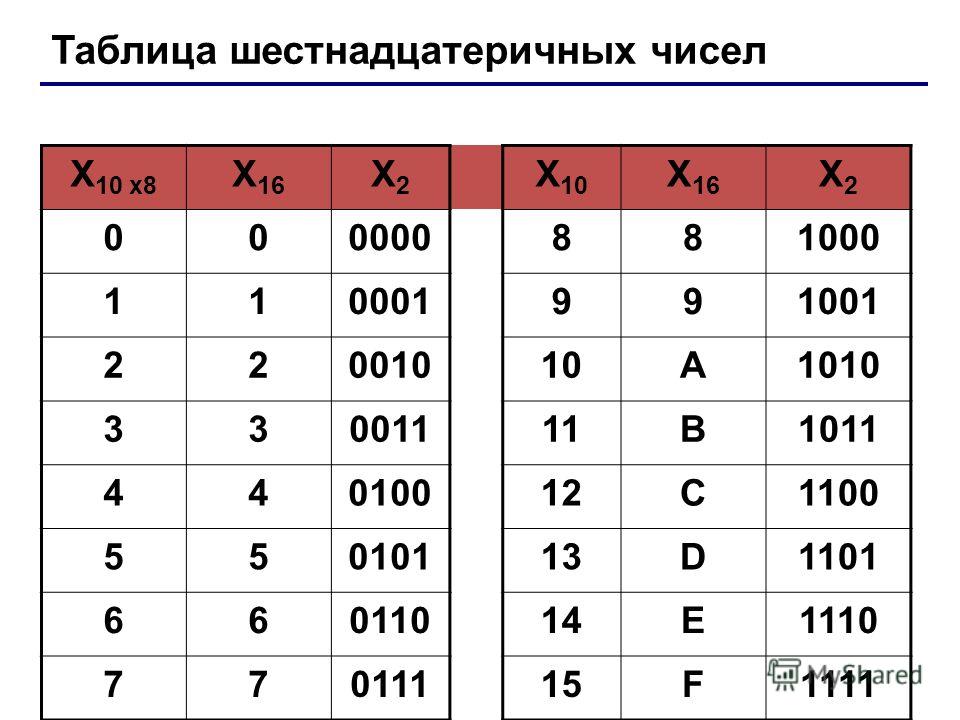
Перевод чисел из двоичной системы в восьмеричную
систему счисления.
Из двоичной системы в восьмеричную систему X2 -> X8 переводим точно так же, только теперь из таблицы берём не по четыре цифры, а по три цифры.
Таким образом, число 10011110012 в двоичной системе будет равно 11718 в восьмеричной системе.
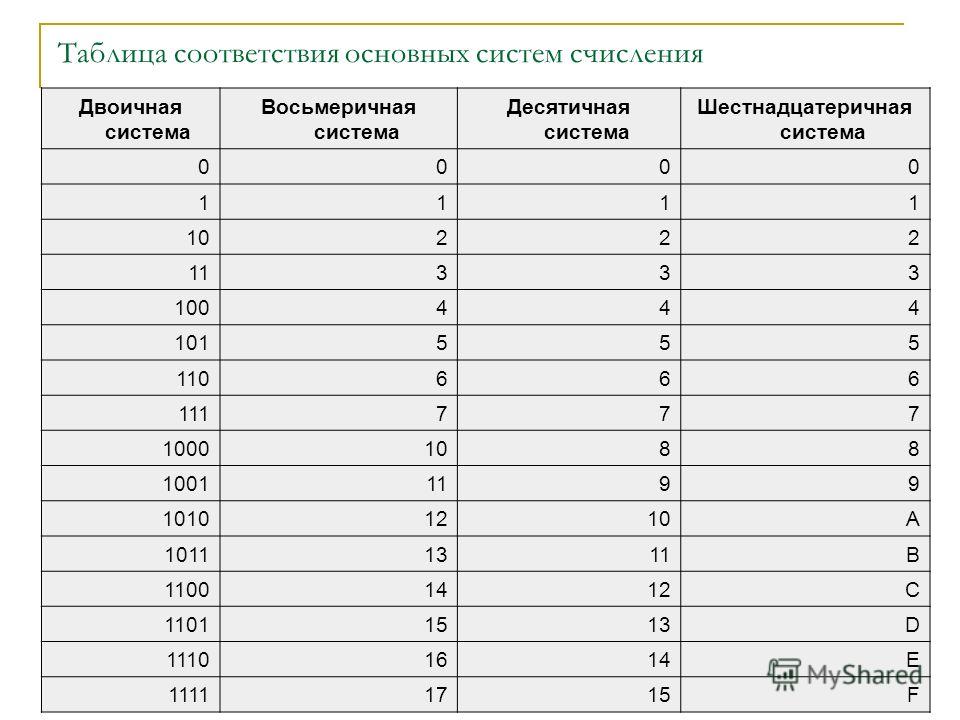
Перевод чисел из шестнадцатиричной системы в двоичную
систему счисления.
Делаем точно так же, как и при переводе чисел из двоичной в шестнадцатиричную, но в обратном порядке. По таблице смотрим: D — 1101, F — 1111, 4 — 0100. Получается число 010011111101. Слева нули мы отбрасываем 10011111101.
4FD16 -> 100111111012.
Перевод чисел из восьмеричной системы в двоичную
систему счисления.
Поступаем, как мы поступали ранее. Разбиваем каждую цифру восьмеричной системы по 3 цифры двоичной системы, используя таблицу, которая приведена в начале статьи. Нули слева откидываем.
3478 -> 111001112.
Перевод чисел из двоичной системы в десятичную
систему счисления.
Переведём число:
Берём цифры двоичного числа, начиная с младшего разряда (т.е. справа), и начинаем умножать на двойку в соответствующей степени. Степень начинается с нуля и с каждым разом увеличивается на 1. Все эти произведения суммируем.
После вычисления получаем число в десятичной системе:
Результат 110100112 -> 21110
Перевод чисел из десятичной системы в двоичную
систему счисления.
Рассмотрим, как перевести из десятичной системы в двоичную. Возьмём число 213.
Перевод чисел из шестнадцатиричной системы в восьмеричную систему
счисления и обратно.
Переведём число A10 из шестнадцатиричной системы в восьмеричную A1016 -> X8.
Разбиваем каждую цифру шестнадцатиричного кода по 4-ри цифры двоичного кода из таблицы в начале статьи (Т.е. переводим число в двоичную систему). Полученное число разбиваем по три цифры — и собираем число уже в восьмеричной системе — как показано на рисунке. Обратно переводим аналогично, только в обратном порядке.
Перевод чисел из шестнадцатиричной системы в десятичную
систему счисления.
Переведём число 5B3 из шестнадцатиричной системы в десятичную систему счисления
Действуем точно также, как при переводе из двоичной системы в десятичную, только умножаем цифры на 16 в соответствующей степени.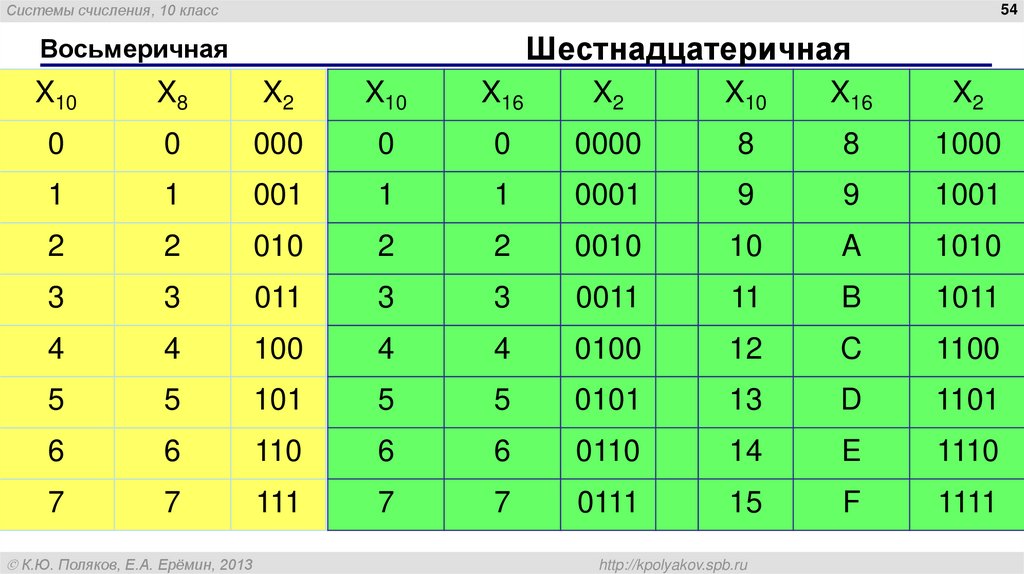
Буквы превращаем в десятичные числа из таблицы. Начинаем, как всегда, справа, т.е. с младшего разряда.
Перевод чисел из десятичной системы в шестнадцатиричную
систему счисления.
Переведём число 203 из десятичной системы в шестнадцатиричную систему счисления 20310 -> X16
Делим число на 16 до тех пор пока не получится число от 1 до 15. Записываем остатки в обратном порядке. Числа от 10 до 15 превращаем в буквы.
Перевод чисел из восьмеричной системы в десятичную
систему счисления.
Переведём число 347 из восьмеричной системы в десятичную систему счисления 3478 -> X10
Делаем аналогично предыдущим примерам, только теперь умножаем на 8 в соответствующей степени.
Перевод чисел из десятичной системы в восьмиричную
систему счисления.
Делаем аналогично предыдущим примерам.
Восьмеричная и шестнацатиричная системы счисления
Двоичная система, в которой работает ЭВМ, не удобна для восприятия человеком. Большое количество разрядов двоичного числа по сравнению с соответствующим десятичным, однообразное чередование единиц и нулей является источником ошибок и затрудняет чтение двоичного числа. Поэтому для удобства записи двоичных чисел необходима такая система счисления, которая, с одной стороны, сохраняла бы свойства двоичной, а с другой — в написании была бы близка к десятичной. Такими свойствами обладают системы счисления с основанием 2
Эти системы удобны тем, что в них обеспечивается чрезвычайно легкий (в уме) перевод из двоичной системы и в тоже время сохраняется привычный для человека вид числа.
Запишем числа в восьмеричной и шестнадцатиричной системах счисления и их представление в двоичной системе.
Таблица 1
Восьмеричный Шестнадцатиричный Двоичное
символ символ представление
0 0 0
1 1 1
2 2 10
3 3 11
4 4 100
5 5 101
6 6 110
7 7 111
————- ———-
8 1000
9 1001
A 1010
B 1011
C 1100
D 1101
E 1110
F 1111
Как видим для представления в двоичной системе счисления любого символа восьмеричной системы достаточно трех (триады) двоичных символов. шестнадцатиричного — четырех (тетрады) двоичных символов. Поэтому процедура перевода состоит в следующем:
1) Разбить исходное двоичное число на группы, состоящие из трех двоичных символов (триады) при переводе в восьмеричную систему, и на группы из четырех двоичных символов (тетрады) при переводе в шестнадцатиричную систему, осуществляя разбивку вправо и влево от запятой. Если крайние левые или правые триады (тетрады) окажутся неполными, то они дописываются справа и слева фиктивными нулями.
2) Каждой триаде (тетраде) ставятся в соответствие восьмеричный (шестнадцатиричный) символ.
Пример 1. Записать в восьмеричной системе двоичное число: 1101011,001110112
Разбиваем число на триады, начиная от запятой. Далее пользуясь таблицей получаем.
Ответ: 1101011,001110112 = 153,1668
Пример 2. Записать в двоичной системе восьмеричное число: 135, 278
Каждую цифру числа представляем в виде двоичной триады в соответствии с таблицей получаем.
Ответ: 135, 278 = 1011101,0101112
Пример 3. Записать в шеснадцатиричной системе двоичное число: 1101011,001110112
Разбиваем число на тетрады от запятой влево и вправо. Затем пользуясь таблицей, записываем каждую тетраду числом в шестнадцатиричной системе.
Ответ: 1101011,001110112 = 6B,3B 16
Пример 4. Записать в двоичной системе шеснадцатиричное число: 1A,CC16
Пользуясь таблицей запишем каждый шестнацатиричный символ тетрадой двоичных.
Ответ: 1A,CC16 = 11010, 1100112
Представление данных в ЭВМ.При вводе информации в ЭВМ каждый символ (буквы, символы, цифры, знаки пунктуации и т.п.) кодируются определенной последовательностью двоичных цифр в соответствии с существующими таблицами кодировки: ДКОИ, КОИ-8, ASCII.
Таблица разбита на 16 строк и 16 столбцов, имеющих двоичные номера от 0000 до 1111 или шестнадцатиричные от 0 до F. на пересечении столбцов и строк записаны символы. Код символа составляется из номера столбца, к которому приписывается номер строки.
Таблица 2
Таблица двоичного кода обработки информации (ASCII)
первая шестнадцатиричная цифра кода
0 1 2 3 4 5 6 7 8 9 A B C D E F
| P | |||||||||||||||
| A | Q | ||||||||||||||
| B | R | ||||||||||||||
| C | S | ||||||||||||||
| D | T | ||||||||||||||
| E | U | ||||||||||||||
| F | V | ||||||||||||||
| G | W | ||||||||||||||
| ( | H | X | |||||||||||||
| ) | I | Y | |||||||||||||
| * | : | J | Z | ||||||||||||
| + | ; | K | [ | ||||||||||||
| L | \ | ||||||||||||||
| M | ] | ||||||||||||||
| N | |||||||||||||||
| O |
Например, буква F, находящаяся в таблице ASCII в столбьце 01002 (416 ) на строке 01102 (616 ), в машине представляется кодом 0100 01102, включающим восемь двоичных разрядов или бит.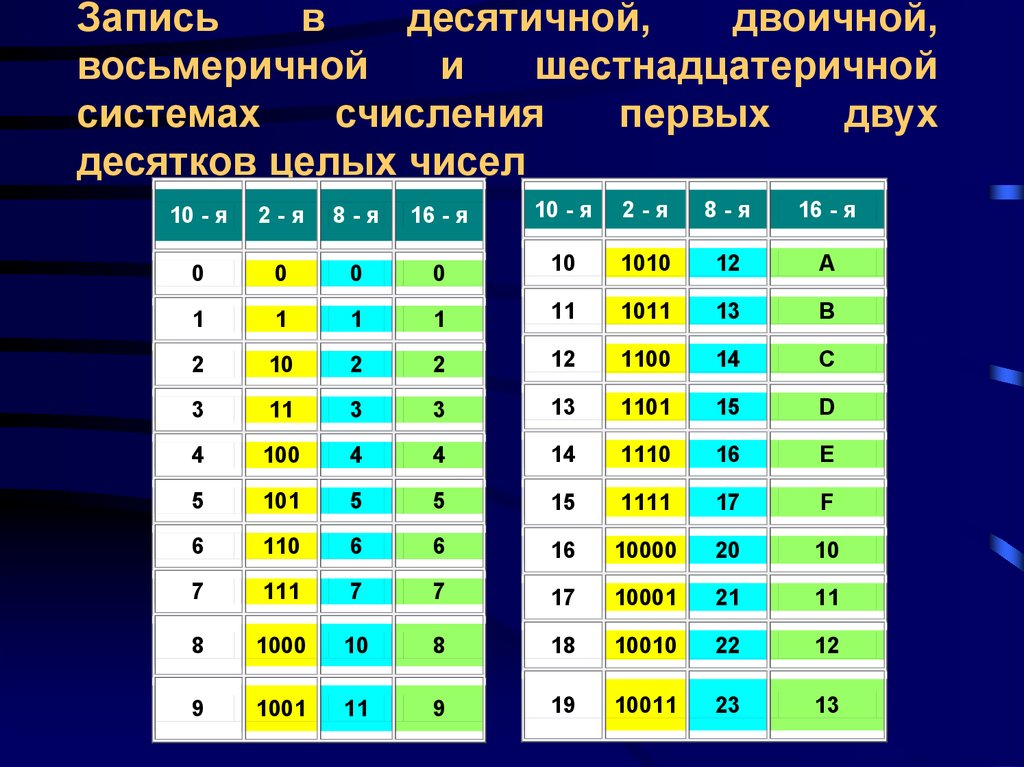
Бит — это количество информации, которое можно записать в одном двоичном разряде. Двоичный разряд может принимать значение либо 1, либо 0. Комбинация из 8 бит называется байтом. Таким образом, в ЭВМ каждый символ входной информации представляется одним байтом.
Объем памяти обычно выражается в килобайтах. 1 Килобайт = 1024 байтам и обозначается буквой К. Например, компьютер с объемом памяти в 64К может хранить 64*1024=65536 символов.
Поскольку объем памяти ПК постоянно возрастает, была введена еще одна единица измерения памяти “мегабайт”, которая означает миллион байт. Например, в 10 мегабайтах может храниться приблизительно 10 млн. символов.
Формы представления числовой информации в ЭВМ.Различают две основные формы представления чисел: с фиксированной и плавающей точкой. Запись числа в форме с фиксированной точкой характеризуется тем, что число представляется как упорядоченная последовательность коэффициентов формулы (1). Каждому коэффициенту ставится в соответствие один разряд, а точка может фиксироваться между какими-то определенными разрядами, причем для точки никакого разряда не требуется.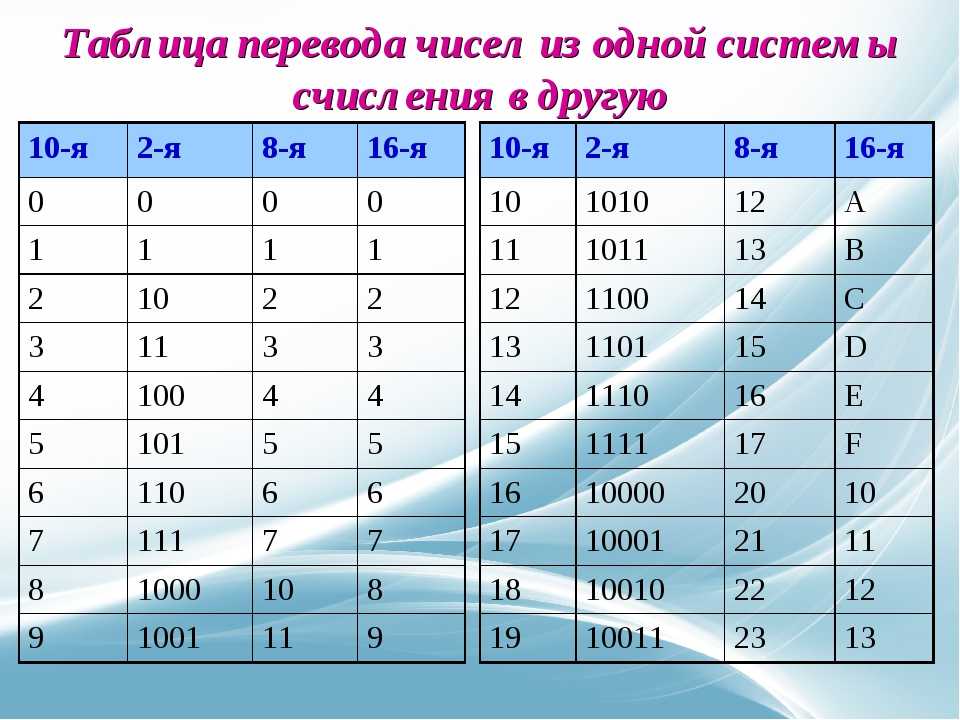
qnqn-1 q1 q0
0 1 … n-1 n
Если точка фиксируется непосредственно правее младшего разряда, то в такой разрядной сетке могут быть представлены только целые числа.
Если точка фиксируется непосредственно левее старшего разряда, то в данной разрядной сетке могут быть представлены только правильные дроби.
В памяти ЭВМ число с фиксированной точкой представляет собой целое число со знаком, у которого условная точка согласно принятому соглашению находится справа от самой младшей цифры числа.
Нулевой разряд отводится под знак числа (0 — положительное, 1 — отрицательное).
знак целая часть числа
0 1 15/31/63
Число в форме с плавающей точкой имеет вид:
A = m q
где m — мантисса числа; q — основание системы счисления; p — порядок числа в системе с основанием q.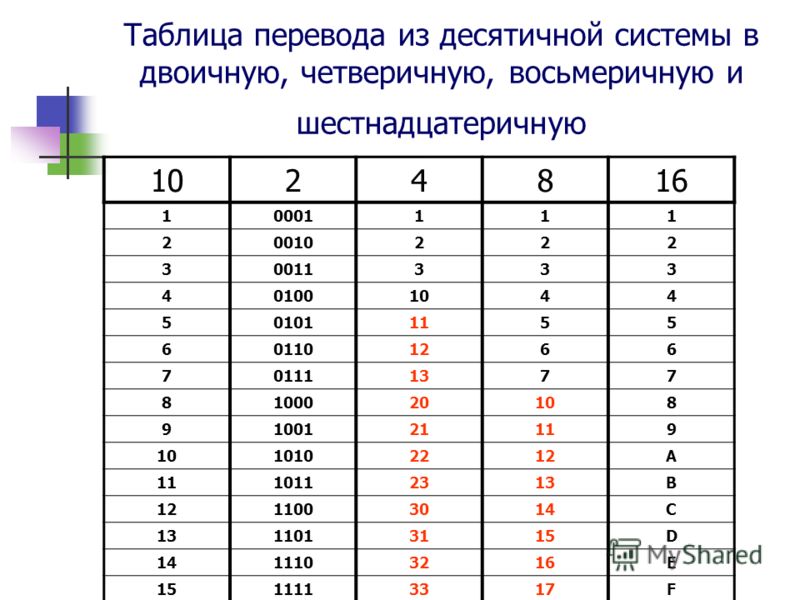
С технической точки зрения более удобно иметь в ЭВМ не порядок, а характеристику числа P*, значение которой связано с порядком числа соотношением, P* = 64 + P. В результате порядок чисел с плавающей точкой в ЭВМ оказывается представленным с избытком 64.
знак характеристика(P*) мантисса(m)
0/1 7 8 31/63
Восьмеричная система счисления в двоичную — преобразование, таблица, примеры
В математике существуют различные системы счисления для записи чисел, например, двоичная система счисления (по основанию 2), восьмеричная система счисления (по основанию 8), десятичная (по основанию 10) и шестнадцатеричная система счисления система (база 16). Восьмеричное преобразование в двоичное определяется как преобразование числа из числа с основанием 8 в основание 2. Это можно сделать двумя способами, о которых вы узнаете в этой статье. Давайте двигаться вперед и изучить преобразование восьмеричной в двоичной.
1. | Что такое восьмеричное преобразование в двоичное? |
| 2. | Восьмеричная таблица в двоичную таблицу |
| 3. | Как преобразовать восьмеричное в двоичное? |
| 4. | Часто задаваемые вопросы о преобразовании восьмеричных чисел в двоичные |
Что такое восьмеричное преобразование в двоичное?
Прежде чем изучать восьмеричное преобразование в двоичное, давайте быстро пройдемся по значениям восьмеричной и двоичной систем счисления. Двоичная система счисления использует только две цифры 0 и 1 для представления чисел. Она также известна как система с основанием 2. Он используется с компьютерной системой, в которой цифры 0 и 1 используются для написания различных сценариев. Каждая цифра, то есть 0 или 1, называется битом в двоичной системе. Например, (01101) 2 , (01000010) 2 , (11000101) 2 — несколько двоичных чисел.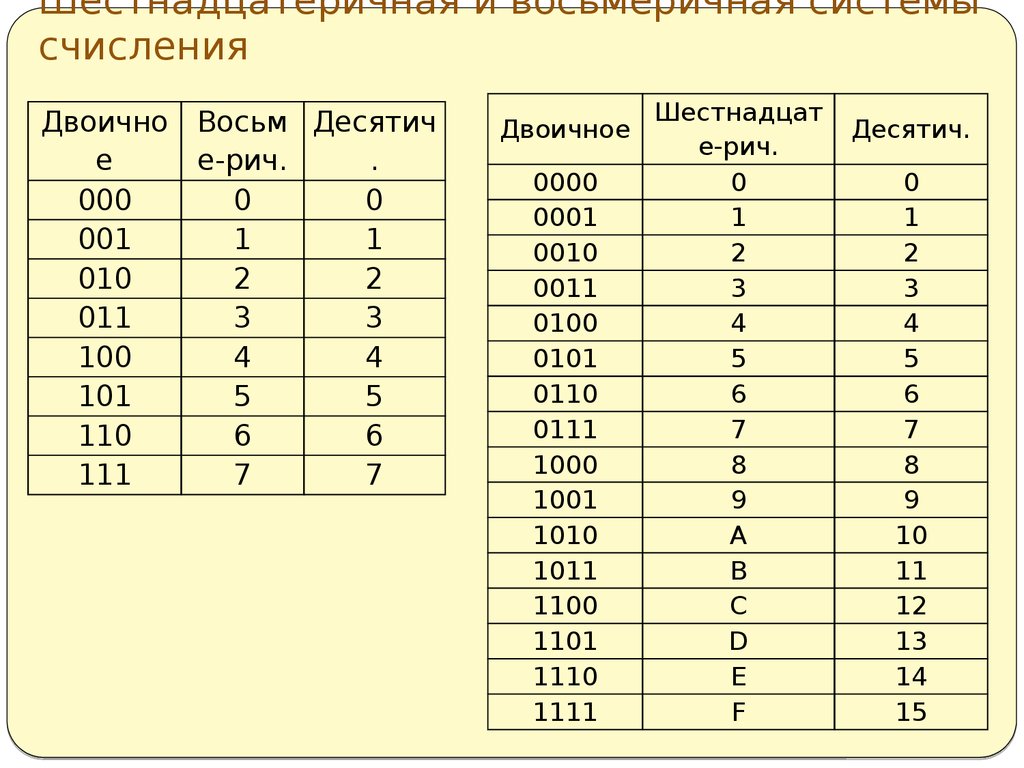
С другой стороны, восьмеричная система счисления включает цифры от 0 до 7. Другие цифры, такие как 8 и 9, не включены в эту систему. Она также известна как система с основанием 8. Как и двоичная, в миникомпьютерах используется восьмеричная система счисления. Например, (73) 8 , (151) 8 , (35) 8 — это несколько восьмеричных чисел.
Преобразование восьмеричного числа в двоичное определяется как преобразование числа с основанием 8 в основание 2 с использованием прямого или косвенного метода. Все цифры в восьмеричном числе находятся в диапазоне от 0 до 7, в то время как все цифры в двоичном числе включают только 0 и 1. Давайте посмотрим на таблицу восьмеричных и двоичных чисел, приведенную в следующем разделе.
Восьмеричная таблица в двоичную таблицу
Обратите внимание на приведенную ниже таблицу восьмеричных и двоичных чисел, которая поможет вам преобразовать восьмеричные числа в двоичные числа. Восьмерично-двоичная таблица показывает число, эквивалентное каждой восьмеричной цифре в двоичной системе, например, 0 в восьмеричной системе эквивалентен 000 в двоичной системе, 1 в восьмеричной системе эквивалентен 001 в двоичной системе, 2 8 соответствует 010 2.
и так далее.
Как преобразовать восьмеричное число в двоичное?
Существует два способа преобразования восьмеричной системы в двоичную, которые объясняются ниже:
- Преобразование восьмеричной системы в десятичную, а затем десятичной в двоичную
- Прямой метод восьмеричного преобразования в двоичный
Давайте подробно разберем каждый метод один за другим.
Метод 1: восьмеричное число в десятичное, а затем десятичное в двоичное
В этом методе мы сначала преобразуем восьмеричное число в десятичное (с основанием 10), а затем преобразуем это десятичное число в двоичное. Чтобы преобразовать число из восьмеричного в десятичное, мы умножаем его цифры, начиная справа, на 8, возведенные в степень, начиная с 0, а затем складываем значения. Итак, первая цифра справа будет умножена на 8 0 , что равно 1, вторая цифра будет умножаться на 8 1 = 8 и так далее.
Возьмем в качестве примера число 56 8 .
Число 8, написанное как основание, означает, что это число с основанием 8. 56 8 можно преобразовать в основание 10 AS,
56 8 = 6 × 8 0 + 5 × 8 1
56 8 = 6 × 1 + 5 × 8
= 6637. + 40
= 46
Следовательно, 56 8 = 46 10 . Теперь мы преобразуем 46, которое является числом с основанием 10, в его двоичный эквивалент. Чтобы преобразовать десятичное число в двоичное, разделите данное число на 2 и запишите частное и напоминание. Снова разделите полученное частное на 2 и запишите остаток. Повторяйте этот процесс, пока не получите 0 в качестве частного. Запишите остатки по порядку справа налево. Преобразуем 46 10 в двоичный формат.
46 разделить на 2 ⇒ 46 ÷ 2 = частное — 23, остаток — 0
23 ÷ 2 = частное — 11, остаток — 1
11 ÷ 2 = Частное — 5, остаток — 1
5 ÷ 2 = Q — 2, R — 1
2 ÷ 2 = Q — 1, R — 0
1 ÷ 2 = Q — 0, R — 1
Расположите все остатки справа налево.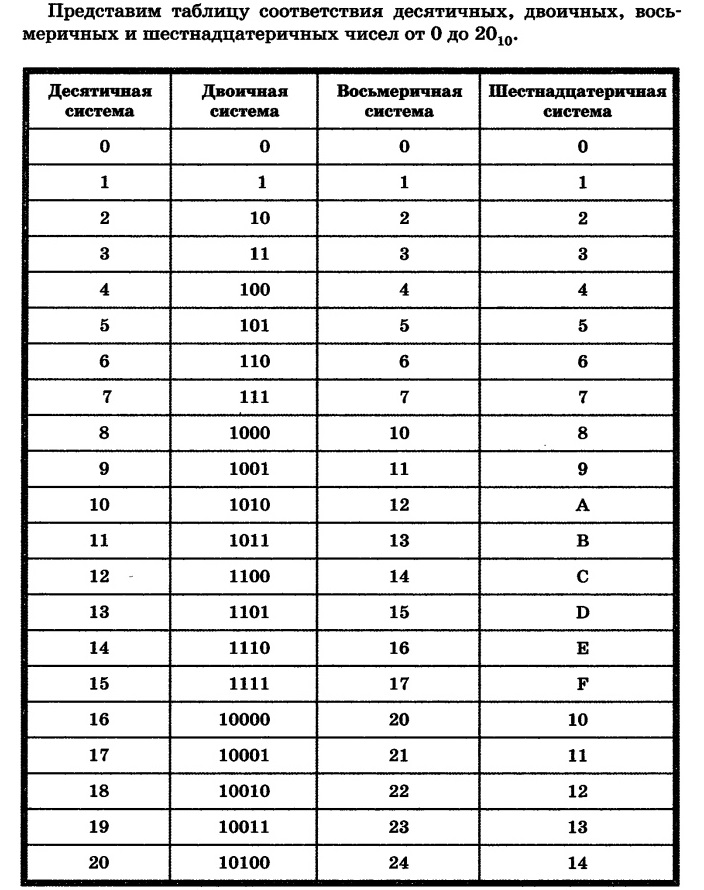
Мы получим
46 10 = 101110 2
Таким образом, мы преобразовали восьмеричное число 56 8 в его двоичный эквивалент 101110 2 .
Метод 2: Прямой метод преобразования восьмеричного числа в двоичное
Другой метод, безусловно, более простой и менее сложный, заключается в прямом преобразовании числа из восьмеричного в двоичное с помощью приведенной выше таблицы восьмеричного числа в двоичное. В этом методе мы преобразуем каждую цифру данного восьмеричного числа в его двоичный эквивалент, обращаясь к приведенной выше таблице. Например, используя этот метод, мы можем напрямую написать 3 8 как 011 2 , 5 8 как 101 2 и т. д.
Преобразуем то же число 56 8 из восьмеричной формы в двоичную прямым методом. В этом числе две цифры, 5 и 6. Ссылаясь на вышеприведенную восьмерично-двоичную таблицу:
5 8 → 101 2
6 8 → 110 2
мы получим, 56 8 = 101110 2 .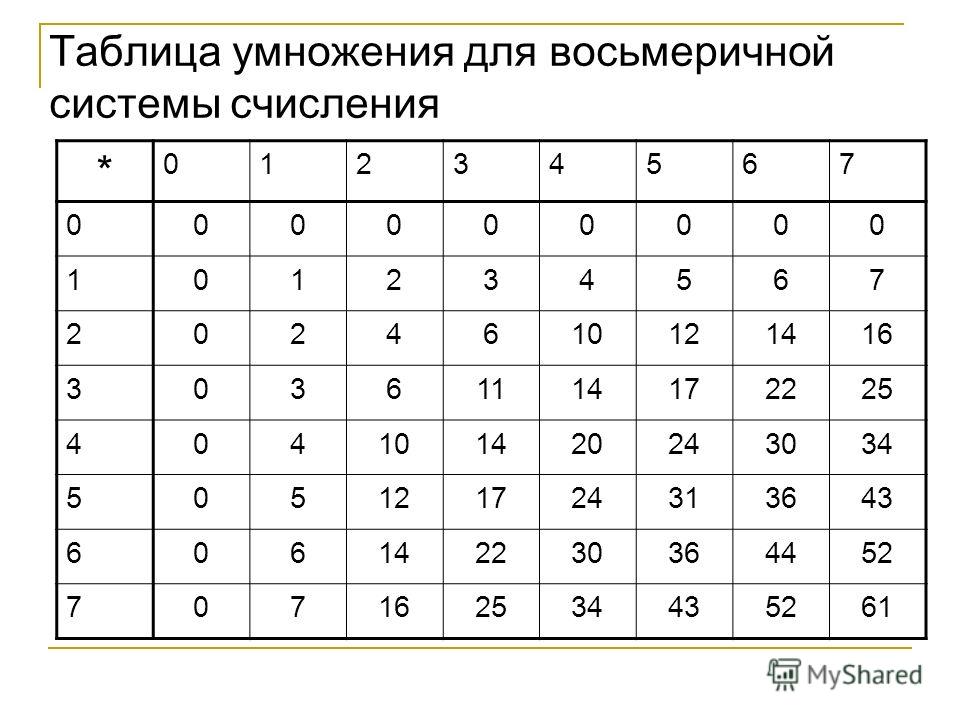
Обратите внимание на изображение, приведенное ниже для справки.► Похожие темы:
Ознакомьтесь с интересными статьями, посвященными преобразованию восьмеричного числа в двоичное в математике.
- Шестнадцатеричный в десятичный
- Десятичный в восьмеричный
- Преобразование двоичного кода в восьмеричный
Часто задаваемые вопросы о преобразовании восьмеричных чисел в двоичные
Что такое восьмеричное преобразование в двоичное?
В математике числа могут быть записаны с использованием различных систем счисления, таких как десятичная, шестнадцатеричная, двоичная и восьмеричная системы счисления. Мы можем преобразовать число из одной системы в другую, следуя определенным правилам и процедурам. Восьмеричное в двоичное — одно из таких преобразований в математике. Чтобы преобразовать число из восьмеричной системы в двоичную, мы можем использовать восьмеричную диаграмму в двоичную или мы можем использовать десятичный метод, сначала преобразовав данное восьмеричное число в десятичное число, а затем преобразовав его в двоичное число.
Как преобразовать восьмеричное число в двоичное?
Чтобы преобразовать восьмеричное число в двоичное, мы можем использовать любой из следующих двух методов:
- Десятичный метод преобразования
- Прямое преобразование
Для конвертации можно использовать любой из вышеперечисленных методов. В первом мы преобразуем заданное восьмеричное число в десятичное, взяв сумму произведений каждой цифры в степени 8, начиная с правой стороны. А затем преобразуйте десятичное число в двоичное, разделив его на 2, а затем разделив последующие частные на 2 на каждом шаге и записав остатки. Расположите остатки в обратном порядке, чтобы получить двоичный эквивалент числа. В то время как в методе прямого преобразования мы обращаемся к восьмеричной диаграмме в двоичную и напрямую записываем двоичные биты каждой из цифр в данном восьмеричном числе.
Как преобразовать восьмеричное число 145 в двоичное?
145 8 эквивалентен 01100101 2 .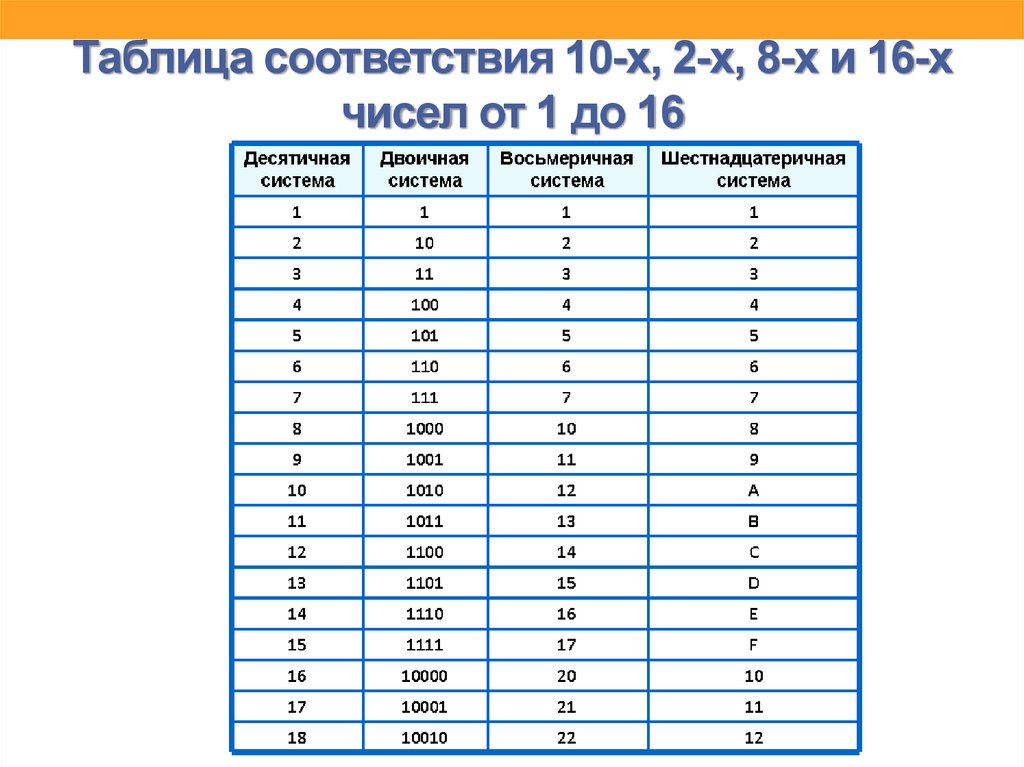
Чтобы преобразовать 145 8 в двоичное число, мы запишем двоичные разряды каждой из его цифр.
1 = 001 2
4 = 100 2
5 = 101 2
Следовательно, 145 8 = 001100101 2 или 011001011 2 .
Как шаг за шагом преобразовать восьмеричную в двоичную?
Пошаговое преобразование восьмеричного числа в двоичное приведено ниже:
- Шаг 1: Преобразование данного восьмеричного числа в его десятичный эквивалент.
- Шаг 2: Преобразуйте полученное десятичное число в двоичное.
Используя эти два шага, мы можем преобразовать любое восьмеричное число в его двоичный эквивалент.
Преобразователь двоичных, десятичных, шестнадцатеричных и восьмеричных чисел с пошаговым решением
Воспользуйтесь нашим калькулятором числовых оснований и изучите преобразование между основаниями с подробным пошаговым решением.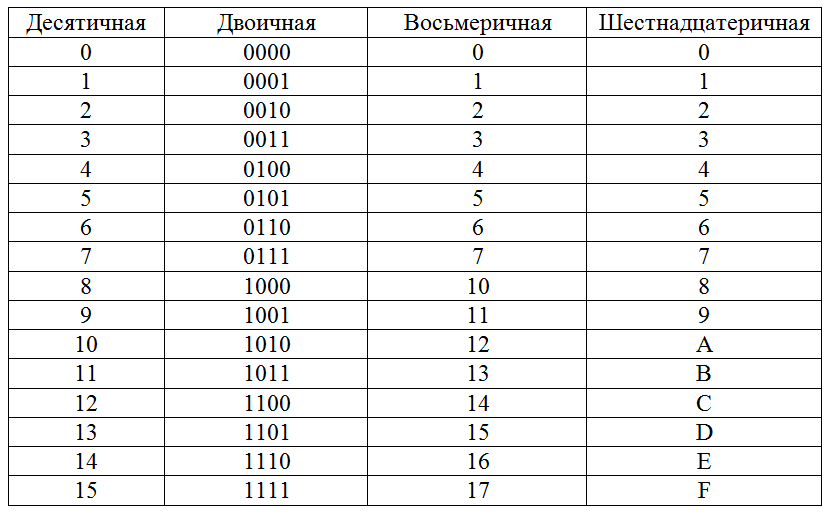
| ||||||||||||||||
Преобразование из/в десятичные, шестнадцатеричные, восьмеричные и двоичные числа. Калькулятор преобразования двоичной базы. Здесь вы можете найти ответы на такие вопросы, как: Преобразование двоичного 0 в десятичное или Преобразование двоичного в десятичное число.
| Dec | Hex | Oct | Bin | |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | |
| 1 | 1 | 1 | 1 | |
| 2 | 2 | 2 | 10 | |
| 3 | 3 | 3 | 11 | |
| 4 | 4 | 4 | 100 | |
| 5 | 5 | 5 | 101 | |
| 6 | 6 | 6 | 110 | |
| 7 | 7 | 7 | 111 | |
| 8 | 8 | 10 | 1000 | |
| 9 | 9 | 11 | 1001 | |
| 10 | A | 12 | 1010 | |
| 11 | B | 13 | 1011 | |
| 12 | C | 14 | 1100 | |
| 13 | D | 15 | 1101 | |
| 14 | E | 16 | 1110 | |
| 15 | 0008 | F | 17 | 1111 |
| Dec | Hex | Oct | Bin |
|---|---|---|---|
| 16 | 10 | 20 | 10000 |
| 17 | 11 | 21 | 10001 |
| 18 | 12 | 22 | 10010 |
| 19 | 13 | 23 | 10011 |
| 0007 20 | 14 | 24 | 10100 |
| 21 | 15 | 25 | 10101 |
| 22 | 16 | 26 | 10110 |
| 23 | 17 | 27 | 10111 |
| 24 | 18 | 30 | 11000 |
| 25 | 19 | 31 | 11001 |
| 26 | 11001 | ||
| 26 | 0007 1A32 | 11010 | |
| 27 | 1B | 33 | 11011 |
| 28 | 1C | 34 | 11100 |
| 29 | 1D | 35 | 11101 |
| 30 | 1E | 36 | 11110 |
| 31 | 1F | 37 | 11111 |
| 8 |
|---|
| 8 |
|---|
| 8 |
|---|
Dec| DEC | HEX | OCT | BIN | 48 48 989 989 98999 | 489 989 989 98999 | 489 9899 989 98999 | 489 989 9899 9899 | ||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
. 0008 | 30 | 60 | 110000 | ||||||||||||||||||||||||||||
| 49 | 31 | 61 | 110001 | ||||||||||||||||||||||||||||
| 50 | 32 | 62 | 110010 | ||||||||||||||||||||||||||||
| 51 | 33 | 63 | 110011 | ||||||||||||||||||||||||||||
| 52 | 34 | 64 | 110100 | ||||||||||||||||||||||||||||
| 53 | 35 | 65 | 110101 | ||||||||||||||||||||||||||||
| 54 | 3667 | ||||||||||||||||||||||||||||||
| 54 | 36 369 9000 | ||||||||||||||||||||||||||||||
| 54 | 36 369 9000 9000 | ||||||||||||||||||||||||||||||
| 54 | 36 369 9000 9000 | ||||||||||||||||||||||||||||||
| 54 | 36 369 | ||||||||||||||||||||||||||||||
| 54 | 369 | 0008 | 66 | 110110 | |||||||||||||||||||||||||||
| 55 | 37 | 67 | 110111 | ||||||||||||||||||||||||||||
| 56 | 38 | 70 | 111000 | ||||||||||||||||||||||||||||
| 57 | 39 | 71 | 111001 | ||||||||||||||||||||||||||||
| 58 | 3A | 72 | 111010 | ||||||||||||||||||||||||||||
| 59 | 3B | 73 | 111011 | ||||||||||||||||||||||||||||
| 60 | 3C | 74 | |||||||||||||||||||||||||||||
| 600008 | 3C | 74 | |||||||||||||||||||||||||||||
| 600008 | 3C | 74 | |||||||||||||||||||||||||||||
| 600008 | 3C | 74 | 111100 | ||||||||||||||||||||||||||||
| 61 | 3D | 75 | 111101 | ||||||||||||||||||||||||||||
| 62 | 3E | 76 | 111110 | ||||||||||||||||||||||||||||
| 63 | 3F | 77 | 111111 |
| Dec | Hex | Oct | Bin |
|---|---|---|---|
| 64 | 40 | 100 | 1000000 |
| 65 | 41 | 101 | 1000001 |
| 66 | 42 | 102 | 1000010 |
| 67 | 43 | 103 | 1000011 |
| 68 | 44 | 104 | 1000100 |
| 69 | 45 | 105 | 1000101 |
| 70 | 46 | 106 | 1000110 |
| 71 | 4710 | ||
| 71 | 47 | 107 | 1000111 |
| 72 | 48 | 110 | 1001000 |
| 73 | 49 | 111 | 1001001 |
| 74 | 4A | 112 | 1001010 |
| 75 | 4B | 113 | 1001011 |
| 76 | 4C | 114 | 1001100 |
| 77 | 4D 9000 | ||
| 4D 9D | 115 | 1001101 | |
| 78 | 4E | 116 | 1001110 |
| 79 | 4F | 117 | 1001111 |
| Dec | Hex | Oct | Bin |
|---|---|---|---|
| 80 | 50 | 120 | 1010000 |
| 51 | 121 | 1010001 | |
| 1010001 | |||
| 52 | 122 | 1010010 | |
| 83 | 53 | 123 | 1010011 |
| 84 | 54 | 124 | 1010100 |
| 85 | 55 | 125 | 1010101 |
| 86 | 56 | 126 | 1010110 |
| 57 | 127 | 101011 | |
| 0007 88 | 58 | 130 | 1011000 |
| 89 | 59 | 131 | 1011001 |
| 90 | 5A | 132 | 1011010 |
| 91 | 5B | 133 | 1011011 |
| 92 | 5C | 134 | 1011100 |
| 93 | 5d | 135 | 1011101 | 0007 94 | 5E | 136 | 1011110 |
| 95 | 5F | 137 | 1011111 |
| Dec | Hex | Oct | Bin | |
|---|---|---|---|---|
| 96 | 60 | 140 | 1100000 | |
| 97 | 61 | 141 | 1100001 | |
| 98 | 62 | 142 | 1100010 98 | 0008 |
| 99 | 63 | 143 | 1100011 | |
| 100 | 64 | 144 | 1100100 | |
| 101 | 65 | 145 | 1100101 | |
| 102 | 66 | 146 | 1100110 | |
| 103 | . 0008 | |||
| 105 | 69 | 151 | 1101001 | |
| 106 | 6A | 152 | 1101010 | |
| 107 | 6B | 153 | 1101011 | |
| 108 | 6C | 154 | 1101100 | |
| 109 | 6d | 155 | 1101101 | |
| 11098 | 6E | 156 | 1101110 | 0008 |
| 111 | 6F | 157 | 1101111 |
| Dec | Hex | Oct | Bin |
|---|---|---|---|
| 112 | 70 | 160 | 1110000 |
| 113 | 71 | 161 | 1110001 |
| 114 | 72 | 162 | 1110010 |
| 115 | 73 | ||
| 0007 163 | 1110011 | ||
| 116 | 74 | 164 | 1110100 |
| 117 | 75 | 165 | 1110101 |
| 118 | 76 | 166 | 1110110 |
| 119 | 77 | 167 | 1110111 |
| 120 | 78 | 170 | 1111000 |
| 121 | 79. | 171 | 1111001 |
| 122 | 7A | 172 | 1111010 |
| 123 | 7B | 173 | 1111011 |
| 124 | 7C | 174 | 1111100 |
| 125 | 7d | 175 | 1111101 |
| 126 | 7E | 176 | 111110 |
| 127 | 0007 7F177 | 1111111 |
| Dec | Hex | Oct | Bin | |||||
|---|---|---|---|---|---|---|---|---|
| 128 | 80 | 200 | 10000000 | |||||
| 129 | 81 | 201 | 10000001 | |||||
| 130 | 82 | 202 | 10000010 | |||||
| 131 | 83 | 203 | 10000011 | 203 | 10011 | 203 | 111 | |
| 132 | 84 | 204 | 10000100 | |||||
| 133 | 85 | 205 | 10000101 | |||||
| 134 | 86 | 206 | 10000110 | |||||
| 135 | 87 | 207 | 1000000111 | |||||
| 136 | 88 | 210 | 10001000 | |||||
| 137 | 89 | 211 | 0007 10001001 | |||||
| 138 | 8A | 212 | 10001010 | |||||
| 139 | 8B | 213 | 10001011 | |||||
| 140 | 8C | 214 | 10001100 | |||||
| 141 | 8d | 215 | 10001101 | |||||
| 142 | 8e | 216 | 10001110 | |||||
| 143 | 8F | 217 | 00810001111 |
| Dec | Hex | Oct | Bin | ||||
|---|---|---|---|---|---|---|---|
| 144 | 90 | 220 | 10010000 | ||||
| 145 | 91 | 221 | 10010001 | ||||
| 146 | 92 | 222 | 10010010 | ||||
| 147 | 93 | 223 | 10010011 | ||||
| 148 | 10010011 | ||||||
| 148 9830008 | 94 | 224 | 10010100 | ||||
| 149 | 95 | 225 | 10010101 | ||||
| 150 | 96 | 226 | 10010110 | ||||
| 151 | 97 | 227 | 10010111 | ||||
| 152 | 98 | 230 | 10011000 | ||||
| 153 | 99 | 231 | 10011001 | ||||
| 9A | 232 | 10011010 | |||||
| 155 | 9B | 233 | 10011011 | ||||
| 156 | 9C | 234 | 10011100 | ||||
| 157 | 9D | 235 | 10011101 | ||||
| 158 | 9E | 236 | 10011110 | ||||
| 159 | 237 | 1001119 | 237 | 10011111 | 0011 |
| Dec | Hex | Oct | Bin | |
|---|---|---|---|---|
| 160 | A0 | 240 | 10100000 | |
| 161 | A1 | 241 | 10100001 | |
| 162 | A2 | 242 | 10100010 | |
| 163 | A3 | 243 | 10100011 | |
| 164 | A4 | |||
| 164 | A4 | 0007 24410100100 | ||
| 165 | A5 | 245 | 10100101 | |
| 166 | A6 | 246 | 10100110 | |
| 167 | A7 | 247 | 10100111 | |
| 168 | A8 | 250 | 10101000 | |
| 169 | A9 | 251 | 10101001 | |
| 170 | AA | |||
| 170 | AA | 252 | 10101010 | |
| 171 | AB | 253 | 10101011 | |
| 172 | AC | 254 | 10101100 | |
| 173 | AD | 255 | 10101101 | |
| 174 | AE | 256 | 10101110 | |
| 175 | AF | 257 | 101011 |
0266
| Dec | Hex | Oct | Bin | |||
|---|---|---|---|---|---|---|
| 192 | C0 | 300 | 11000000 | |||
| 193 | C1 | 301 | 11000001 | |||
| 194 | C2 | 302 | 11000010 | |||
| 195 | C3 | 303 | 11000011 | |||
| 196 | C4 | 304 | 11000100 | |||
| 0007 197 | C5 | 305 | 11000101 | |||
| 198 | C6 | 306 | 11000110 | |||
| 199 | C7 | 307 | 11000111 | |||
| 200 | C8 | 310 | 11001000 | |||
| 201 | C9 | 311 | 11001001 | |||
| 202 | CA | 312 | 110010 | 312 | 11001010 | CA | 3120011
| 203 | CB | 313 | 11001011 | |||
| 204 | CC | 314 | 11001100 | |||
| 205 | CD | 315 | 11001101 | |||
| 206 | CE | 316 | 11001110 | |||
| 207 | CF | 317 | 110011119 |
| Dec | HEX | Dec | HEX | Dec | Dec | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Dec |
Преобразователь базы чисел Пожалуйста, дайте ссылку на эту страницу! Просто щелкните правой кнопкой мыши на изображении выше, затем выберите «Скопировать адрес ссылки», а затем вставьте его в HTML-код. |
0329 Oct