Восьмеричная система счисления — Программирование на C, C# и Java
Оглавление:
Перевод из десятичной системы счисления в восьмеричную
Перевод из восьмеричной системы счисления в десятичную
Перевод из двоичной системы счисления в восьмеричную
Перевод из восьмеричной системы счисления в двоичную
Перевод из восьмеричной системы счисления в шестнадцатеричную и из шестнадцатеричной системы в восьмеричную
Применение восьмеричной системы счисления
Восьмеричная система – одна из основных систем счислений наряду с двоичной, десятичной и шестнадцатеричной, применяемая в информационных технологиях.
Как мы знаем, компьютеры «воспринимают» лишь двоичную систему счисления, состоящую только из нулей и единиц. Однако человеку довольно непривычно и неудобно работать с такими числами. Например, привычное нам десятичное число 2 143 в двоичной системе будет выглядеть как 100001011111. Переводить числа из двоичной системы в десятеричную также не очень удобно и бывает довольно муторно.
В итоге было решено использовать альтернативные и более простые системы счисления: восьмеричную и шестнадцатеричную. Числа 8 и 16 являются степенями двойки (2 в третьей и 2 в четвёртой степени соответственно), поэтому выполнять преобразования из двоичной системы и наоборот гораздо легче, чем при десятичной системе счисления, которая не может похвастаться своей причастностью к степеням числа 2.
Кроме того, числа в восьмеричной системе как минимум более приятны глазу и гораздо короче, чем их аналоги в двоичной системе. Так, например, в восьмеричной системе то же число 2 143 будет записываться как 4137.
В восьмеричной системе счисления, как уже можно было догадаться, основанием является цифра 8 и, соответственно, она вмещает в себя только восемь цифр: от 0 до 7. Поэтому числа в восьмеричной системе счисления очень похожи на десятичные, в отличие от шестнадцатеричных, где присутствуют буквы латинского алфавита или двоичных, состоящих только из двух цифр. Отличают эти две системы тем, что в восьмеричной отсутствуют цифры 8 и 9, а также, очевидно, нижними индексами: у числа в десятичной системе прибавляют нижний индекс с цифрой 10, а к числам в восьмеричной системе приписывают цифру 8, например:
Теперь давайте научимся переводу чисел в восьмеричную систему счисления и наоборот.
Перевод из десятичной системы счисления в восьмеричную
Давайте попробуем изучить перевод десятичного числа в восьмеричное на примере. После этого примера вы без проблем сможете переводить любые числа в эту систему.
Возьмём десятичное число 15 450 и попробуем перевести его в восьмеричную систему счисления.
Для начала нам необходимо разделить исходное число на основание системы, в которую мы хотим это число перевести. Для восьмеричной системы это число 8. То есть мы делим 15 450 на 8.
Происходит деление в столбик, но, в отличие от стандартного деления, мы не находим неполные частные, а делим сразу всё делимое на 8. Наибольшим числом, при котором 15 450 делится без остатка на 8 будет число 1 931. 1931 * 8 = 15 448. Теперь мы вычитаем из 15 450 полученное число 15 448, у нас получился остаток 2. Выделяем эту двойку, так как это уже кусочек нашего числа в восьмеричной системе.
Продолжаем: теперь делим полученное на предыдущем шаге частное на 8:
Всё точно так же: наибольшим числом, при котором 1 931 делится без остатка на 8 будет число 241.
Получается число 30, умножив его на 8, получаем 240. Вычитаем из 241 это число, получается 1. Выделяем единицу.
Продолжаем деление до тех пор, пока частное не станет меньше 8!
Итак, делим 30 на 8, получается 3,75, отбрасываем дробную часть, получается 3. Умножаем 3 на 8, получается 24. 30 — 24 = 6. Выделяем шестёрку. Мы закончили деление так как 3 меньше 8. Обязательно выделяем последнее частное тоже (у нас это цифра 3).
Выделенные красным цифры – это и есть наше число в восьмеричной системе, НО они написаны наоборот. То есть, чтобы правильно прочитать число в восьмеричной системе, необходимо сделать это справа налево.
Таким образом, десятичное число 15 450 10 в восьмеричной системе будет выглядеть как 36 1328.
Итого, алгоритм перевода чисел из десятичной системы в восьмеричную следующий:
- Разделить исходное число на 8.
 Найти максимальное частное и убрать дробную часть от него. Например, исходное число 20 : 8 = 2,5. Значит в частное мы записываем число 2.
Найти максимальное частное и убрать дробную часть от него. Например, исходное число 20 : 8 = 2,5. Значит в частное мы записываем число 2. - Умножить полученное частное на 8. Записать его под исходным числом.
- Найти остаток между этими числами и выделить его — это кусочек переведённого в восьмеричную систему числа.
- Затем разделить в столбик полученное частное на 8, записать ответ и проделать шаги 2 и 3.
- Производить деление до тех пор, пока делимое не станет меньше 8. Выделить это делимое тоже.
- Выписать все выделенные числа справа налево (т.е. последнее делимое будет на первом месте, затем идёт остаток, найденный на последнем шаге, затем остаток, найденный на предпоследнем шаге и т.д.). Полученное при такой записи число и будет нашим искомым восьмеричным.
Теперь перейдём к переводу восьмеричного числа в десятичную систему счисления.
Перевод из восьмеричной системы счисления в десятичную
Перевести восьмеричное число в десятичное даже проще, чем наоборот. Давайте рассмотрим пример: переведём восьмеричное число 36078 в десятичное.
Давайте рассмотрим пример: переведём восьмеричное число 36078 в десятичное.
Для начала мы делаем такую запись: с конца берём каждую цифру нашего исходного числа, каждое из них умножаем на 8, и все в целом складываем. Должно получиться примерно так:
Однако, это ещё не всё! После того, как мы сделали подобную запись, ко всем числам 8, на которые умножаются цифры исходного числа, необходимо добавить степени в порядке возрастания: 0, 1, 2 и т.д. Обязательно необходимо начинать с нулевой степени!
Всё, что остаётся после этого – просто посчитать. В итоге у нас получилось число 1927 в десятичной системе.
Перевод из двоичной системы счисления в восьмеричную
Перевод чисел из двоичной системы счисления в восьмеричную – довольно необычное дело для тех, кто никогда с этим не сталкивался. Однако на деле всё не так пугающе, как может показаться с первого раза.
Давайте попробуем. Допустим, у нас есть двоичное число 1010010001011101100.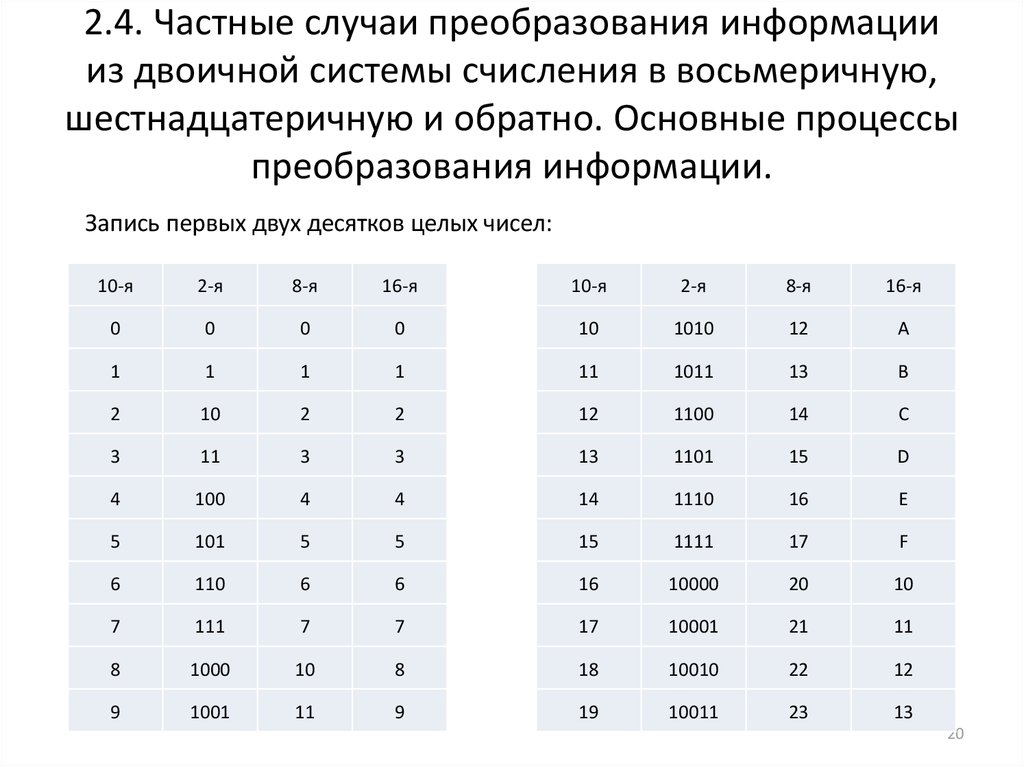
Для начала нам необходимо разбить это число на триады – группы из трёх цифр. Почему именно три цифры? Как мы знаем, у систем счислений имеются основания. И у двоичной системы основание – 2. Нам необходимо перевести двоичное число в восьмеричную систему с основанием 8. Математически это можно записать так:
Найти i, пожалуй, не составит труда: i = 3, то есть, для записи одного восьмеричного числа в двоичной системе необходимо 3 бита или, говоря иначе — 3 двоичные цифры. Поэтому мы и будем разбивать двоичное число на триады. Однако надо запомнить, что делать это надо с младшего бита. Бит – это одна цифра в двоичном числе. Чем дальше бит от начала числа, тем он младше. Самый младший бит – это последняя цифра двоичного числа. Иными словами, мы разбиваем число на триады, начиная с конца.
Внимание: если старшая триада не заполнена, до конца, перед ней необходимо дописать столько нулей, чтобы получилась полноценная триада.
Теперь всё, что нам остаётся – это перевести каждую из этих триад из двоичной системы счисления в восьмеричную. Это можно сделать самостоятельно:
Это можно сделать самостоятельно:
Для этого в каждой отдельной триаде (начиная с первой) нужно каждую цифру (начиная с последней) умножить на 2, возведённую в степени от 0 до 2, и сложить полученные три числа.
Затем, полученные результаты по каждой отдельной триаде надо выписать, начиная с самой первой. Записанное число и будет нашим конечным результатом в восьмеричной системой счисления.
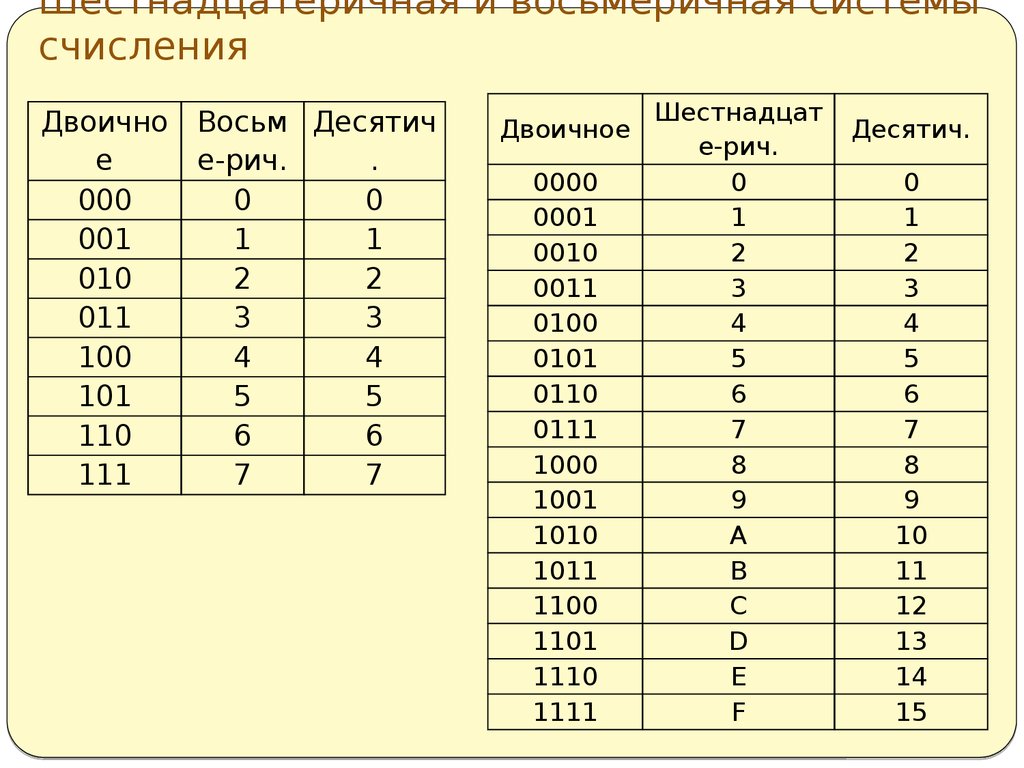
Однако можно сильно облегчить себе задачу, не высчитывая все триады числа, а просто сверяя каждую из них по таблице соответствия двоичных чисел восьмеричным, например, по такой:
Теперь можно просто смотреть на триаду, сверять её с таблицей и записывать число, соответствующее ей в восьмеричной системе.
Перевод из восьмеричной системы счисления в двоичную
Самым удобным способом перевода из восьмеричной системы счисления в двоичную является использование таблицы соответствий. Итак, допустим, мы хотим перевести восьмеричное число 36702 в двоичную систему. Что же нам делать? Мы берём первую цифру нашего исходного числа – 3. Ищем её по таблице соответствия – в двоичной системе это 011. Берём следующую цифру – 6 и ищем её в таблице, находим 110, и так далее. Продолжаем, пока не переведём все восьмеричные цифры в триады. В итоге у нас получится необходимое двоичное число.
Что же нам делать? Мы берём первую цифру нашего исходного числа – 3. Ищем её по таблице соответствия – в двоичной системе это 011. Берём следующую цифру – 6 и ищем её в таблице, находим 110, и так далее. Продолжаем, пока не переведём все восьмеричные цифры в триады. В итоге у нас получится необходимое двоичное число.
Внимание: Если в старших битах (то есть в самом начале двоичного числа) имеются нули, необходимо убрать их до первой единицы. Например, как на изображении ниже. В старшем бите у нас получился ноль при переводе восьмеричной тройки, и мы убрали его. Это делается для удобства, потому что зачем хранить и писать незначащие цифры.
Перевод из восьмеричной системы счисления в шестнадцатеричную и из шестнадцатеричной системы в восьмеричную
К сожалению, несмотря на то, что эти системы счисления близки друг к другу, напрямую перевести друг в друга нельзя. Легче всего при переводе этих двух систем друг в друга воспользоваться посредничеством двоичной системы. То есть, перевести восьмеричную систему счисления в двоичную, разделив число на триады и воспользовавшись таблицей соответствий, а затем перевести это число из двоичной системы в шестнадцатеричную с помощью тетрад. И наоборот: перевести число из шестнадцатеричной системы в двоичную, а затем уже из двоичной системы в восьмеричную описанными выше способами.
То есть, перевести восьмеричную систему счисления в двоичную, разделив число на триады и воспользовавшись таблицей соответствий, а затем перевести это число из двоичной системы в шестнадцатеричную с помощью тетрад. И наоборот: перевести число из шестнадцатеричной системы в двоичную, а затем уже из двоичной системы в восьмеричную описанными выше способами.
Применение восьмеричной системы счисления
В прошлом веке выпускались компьютеры, в которых использовались 12-ти, 24-х и 36-битные слова. Это, например, модель ICT 1900 (1964 год), а также PDP-8, выпущенная в 1965 году — это коммерчески довольно успешная модель миникомпьютера в своё время. Кроме того, некоторые мейнфреймы от компании IBM использовали восьмеричную систему. В компьютерах, размер машинного которых кратен тройке, очень удобно использовать систему с основанием восемь, поскольку всегда все биты из слова можно представить в виде целого количества цифр в восьмеричной системе. Например, слово из 24-х бит, можно записать в виде 8-ми восьмеричных чисел.
Если говорить про использование восьмеричной системы в жизни людей, то известно, что в индейских языках Юки (Калифорния) и Паме (Мексика) использовалась данная система. Индейцы считали предметы не по количеству пальцев на руках, а по количеству промежутков между ними.
Алгоритм, Для начинающих, математические операции, системы счисления, Статья
Поделиться в соц. сетях:
Восьмеричная система счисления — правила и примеры решений » Kupuk.net
Для обеспечения интерфейса «пользователь-компьютер» необходимо переводить числа из одной формы представления в другую. В этом случае может быть полезна восьмеричная система счисления, позволяющая представлять любую информацию в некотором машинном коде. Последний быстро обрабатывается и позволяет расширить объемы декодируемых данных. Однако для этого следует знать определенную методику и немного предыстории развития вычислительной техники.
Общие сведения
Во время изобретения персонального компьютера (ПК) или ЭВМ использовался определенный язык представления данных, который существенно отличался от десятичной системы счисления. Последняя используется человеком при ведении расчетов и является самой удобной.
Последняя используется человеком при ведении расчетов и является самой удобной.
Кодирование данных в современных ЭВМ осуществляется за счет элементов (транзисторов) в интегральных микросхемах. За основу взят полупроводниковый переход, который может быть закрытым или открытым. Следует отметить, что режим «насыщения», присущий радиодетали, не используется. Если он открыт, то в триггер (память) записывается единица, а в противном случае — нуль. В результате этого кодирование осуществляется в двоичном коде (0 или 1), основанием которого является цифра «2».
Для кодирования больших массивов информации использовать двоичную систему счисления не всегда удобно, поскольку количество транзисторов может быть огромным, а устройство будет значительно греться. Чтобы этого избежать, была придумана восьмеричная система счисления.
Для выполнения операции конвертации десятичной системы исчисления в восьмеричный код необходимы некоторые базовые знания. К ним относятся:

Специалисты в области информационных технологий рекомендуют разбирать базовые понятия в последовательности, состоящей из пяти шагов.
Число и цифра
При расчетах и выражении количественных характеристик процесса или явления применяются определенные математические символы — числа. Они состоят из разрядной сетки. Каждый ее элемент — цифра, которая принимает значения, в зависимости от выбранной системы счисления (СС). Например, для десятичной используется диапазон от 0 до 9, а девятеричная состоит из интервала с минимальной величиной, равной 0, а максимальной — 8.
Цифра — математический знак, используемый для построения более сложных конструкций. Например, с его помощью можно записать значения различных типов (четырехзначные, пятизначные). Любое число состоит из разрядной сетки, элементами которой и являются математические символы.
Например, с его помощью можно записать значения различных типов (четырехзначные, пятизначные). Любое число состоит из разрядной сетки, элементами которой и являются математические символы.
При выполнении различных математических операций нужно следить за одинаковыми разрядами. Например, недопустимо складывать сотни и тысячи, поскольку это действие приведет к ошибочным вычислениям. Далее следует разобрать системы представления информации и их примеры.
Виды числовых представлений
Для правильного перевода чисел из одной СС в другую необходимо разобрать классификацию форм представления информации. Они бывают двух типов, в зависимости от расположения цифр:
В первом случае значение числа зависит от расположения или комбинации цифр. Этот факт очень просто доказывается на примере обычной десятичной формы представления величины. Например, 25 и 52 — два разных значения. Если бы расположение разрядов не учитывалось, при разности этих двух величин получился нуль. Позиционными СС являются двоичный, восьмеричный и шестнадцатеричный коды. В них также есть разрядная сетка.
Если бы расположение разрядов не учитывалось, при разности этих двух величин получился нуль. Позиционными СС являются двоичный, восьмеричный и шестнадцатеричный коды. В них также есть разрядная сетка.
Независимыми от расположения разрядов называются непозиционные СС. Примером одной из них является унарная форма записи числа. Суть ее заключается в эквивалентности символа какому-либо значению. Например, на предприятиях применяются обыкновенные «крестики» для подсчета количества рабочих дней сотрудников. Каждый символ эквивалентен единице.
На уроках математики в начальных классах также применяется инструмент — счетные палочки. Последние помогают ученикам развивать навык устного счета и являются компонентами непозиционной СС. С их помощью возможно выполнять операции суммы, разности, а также произведения и деления.
Следует отметить, что не во всех случаях один символ может соответствовать единице. Это могут быть десятки, сотни и даже тысячи. Для расчетов при помощи непозиционной СС можно придумать собственные обозначения, как это сделано в римских цифрах. Однако при этом существуют определенные недостатки:
Для расчетов при помощи непозиционной СС можно придумать собственные обозначения, как это сделано в римских цифрах. Однако при этом существуют определенные недостатки:
Достоинством считается сокращение времени записи величины, которая постоянно изменяется. Например, при подсчете количества выходов персонала достаточно поставить крестик или палочку, и это делается без исправлений. В случае с десятичной СС исправлений избежать невозможно.
Чтобы выполнить перевод в восьмеричную систему счисления, необходимо ознакомиться с методикой конвертации десятичной формы в двоичное кодовое представление.
Двоичная кодировка
Для преобразования десятичной величины в двоичную IT-специалистами были разработаны специальные правила или алгоритмы. К ним относятся столбик и степень. Каждому начинающему IT-специалисту необходимо выбрать оптимальную методику преобразования одной формы числа в другую. Каждый из способов удобен в конкретной ситуации. Можно также применять сразу 2 — один для решения, а другой — для проверки результата. Необходимо разобрать каждую методику подробно с практической реализацией алгоритма.
К ним относятся столбик и степень. Каждому начинающему IT-специалисту необходимо выбрать оптимальную методику преобразования одной формы числа в другую. Каждый из способов удобен в конкретной ситуации. Можно также применять сразу 2 — один для решения, а другой — для проверки результата. Необходимо разобрать каждую методику подробно с практической реализацией алгоритма.
Метод «столбик»
Первый способ получил широкое применение, поскольку для его выполнения требуется минимум знаний в математической сфере. Он имеет следующий вид:
Реализация алгоритма проверяется на практическом примере. Для этого требуется решить задачу конвертации числа из десятичной СС в другую, перевод 167{10} в {2}. Решение имеет следующий вид:
 0].
0].Переводить системы счисления в другие формы представления возможно при помощи различных онлайн-сервисов. Для этого требуется указать исходную форму числа, а затем конечную. Однако действия рекомендуется совершать только для проверки результата решения задачи.
Способ степени
Для конвертации в двоичный код также применяется метод степени. Суть его заключается в представлении числа в виде отдельных элементов с основанием «2» и некоторым показателем. Алгоритм в этом случае выглядит таким образом:
Как и во всех остальных случаях, рекомендуется разобрать алгоритм на практическом примере. 0=1 ->1.
0=1 ->1.
Однако операция преобразования является вспомогательной. Она применяется для дальнейшей конвертации в восьмеричную СС.
Восьмеричная система
Восьмеричная форма представления чисел состоит из основания-восьмерки и триады. Совокупность последних образуют любые значения. Для кодирования информации в этом случае применяется меньше регистров памяти. Этого нельзя сказать о двоичном коде.
Для восьмеричного представления применяются цифры от 0 до 7 (всего 8). Многие новички часто путают ее с шестнадцатеричной СС, в которой содержатся символы латинского алфавита. При выполнении операций конвертации специалисты рекомендуют ознакомиться со списком (таблицей) восьмеричной системы:

Он поможет перевести любое числовое сообщение. Для удобства IT-специалисты рекомендуют составить презентацию или записать на лист плотной бумаги перекодировку списка. Заучивать коды нет необходимости, поскольку достаточно решать примеры (информация отложится в памяти). Алгоритм кодирования очень прост:
После ознакомления с методикой преобразования нужно проверить ее реализацию на примере. Требуется выяснить, значение 167 {10}. Это делается довольно просто:

Обратное декодирование выполняется по такой методике:
На начальных этапах обучения рекомендуется четко следовать по пунктам методики. Однако через некоторое время последние можно опускать.
Таким образом, восьмеричная система применяется для кодирования больших массивов информации, при котором может быть задействовано минимальное количество регистров запоминающего устройства персонального компьютера.
Восьмеричная система счисления — правила и примеры решений
Для обеспечения интерфейса «пользователь-компьютер» необходимо переводить числа из одной формы представления в другую. В этом случае может быть полезна восьмеричная система счисления, позволяющая представлять любую информацию в некотором машинном коде. Последний быстро обрабатывается и позволяет расширить объемы декодируемых данных. Однако для этого следует знать определенную методику и немного предыстории развития вычислительной техники.
В этом случае может быть полезна восьмеричная система счисления, позволяющая представлять любую информацию в некотором машинном коде. Последний быстро обрабатывается и позволяет расширить объемы декодируемых данных. Однако для этого следует знать определенную методику и немного предыстории развития вычислительной техники.
Содержание
- Общие сведения
- Число и цифра
- Виды числовых представлений
- Двоичная кодировка
- Метод «столбик»
- Способ степени
- Восьмеричная система
Общие сведения
Во время изобретения персонального компьютера (ПК) или ЭВМ использовался определенный язык представления данных, который существенно отличался от десятичной системы счисления. Последняя используется человеком при ведении расчетов и является самой удобной.
Кодирование данных в современных ЭВМ осуществляется за счет элементов (транзисторов) в интегральных микросхемах. За основу взят полупроводниковый переход, который может быть закрытым или открытым.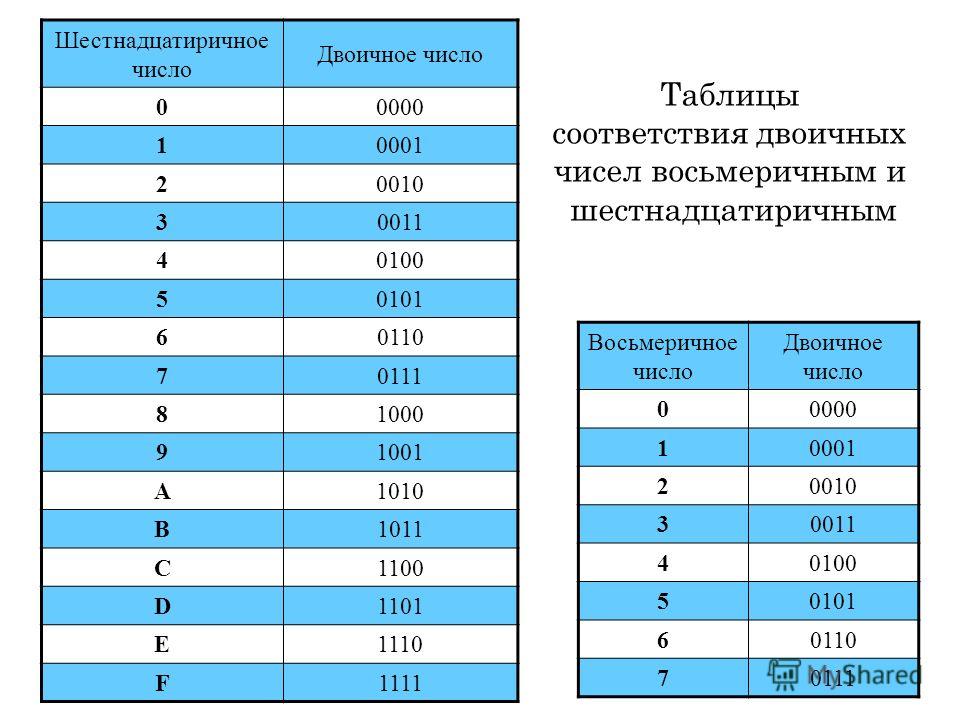 Следует отметить, что режим «насыщения», присущий радиодетали, не используется. Если он открыт, то в триггер (память) записывается единица, а в противном случае — нуль. В результате этого кодирование осуществляется в двоичном коде (0 или 1), основанием которого является цифра «2».
Следует отметить, что режим «насыщения», присущий радиодетали, не используется. Если он открыт, то в триггер (память) записывается единица, а в противном случае — нуль. В результате этого кодирование осуществляется в двоичном коде (0 или 1), основанием которого является цифра «2».
Для кодирования больших массивов информации использовать двоичную систему счисления не всегда удобно, поскольку количество транзисторов может быть огромным, а устройство будет значительно греться. Чтобы этого избежать, была придумана восьмеричная система счисления.
Для выполнения операции конвертации десятичной системы исчисления в восьмеричный код необходимы некоторые базовые знания. К ним относятся:
Специалисты в области информационных технологий рекомендуют разбирать базовые понятия в последовательности, состоящей из пяти шагов.
Число и цифра
При расчетах и выражении количественных характеристик процесса или явления применяются определенные математические символы — числа. Они состоят из разрядной сетки. Каждый ее элемент — цифра, которая принимает значения, в зависимости от выбранной системы счисления (СС). Например, для десятичной используется диапазон от 0 до 9, а девятеричная состоит из интервала с минимальной величиной, равной 0, а максимальной — 8.
Цифра — математический знак, используемый для построения более сложных конструкций. Например, с его помощью можно записать значения различных типов (четырехзначные, пятизначные). Любое число состоит из разрядной сетки, элементами которой и являются математические символы.
При выполнении различных математических операций нужно следить за одинаковыми разрядами. Например, недопустимо складывать сотни и тысячи, поскольку это действие приведет к ошибочным вычислениям.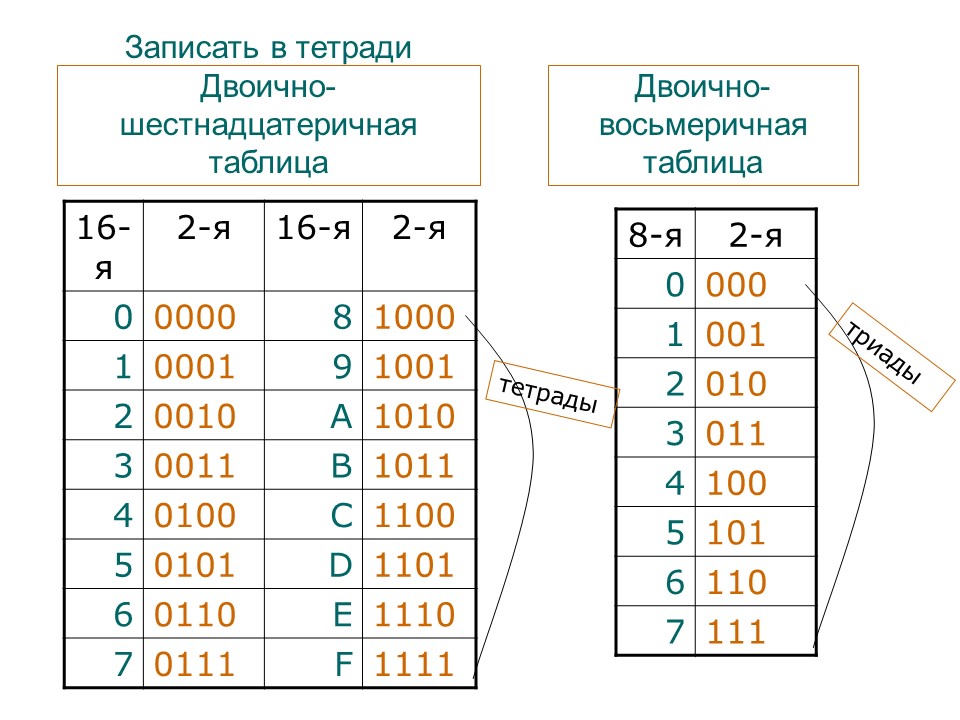 Далее следует разобрать системы представления информации и их примеры.
Далее следует разобрать системы представления информации и их примеры.
Виды числовых представлений
Для правильного перевода чисел из одной СС в другую необходимо разобрать классификацию форм представления информации. Они бывают двух типов, в зависимости от расположения цифр:
В первом случае значение числа зависит от расположения или комбинации цифр. Этот факт очень просто доказывается на примере обычной десятичной формы представления величины. Например, 25 и 52 — два разных значения. Если бы расположение разрядов не учитывалось, при разности этих двух величин получился нуль. Позиционными СС являются двоичный, восьмеричный и шестнадцатеричный коды. В них также есть разрядная сетка.
Независимыми от расположения разрядов называются непозиционные СС. Примером одной из них является унарная форма записи числа. Суть ее заключается в эквивалентности символа какому-либо значению. Например, на предприятиях применяются обыкновенные «крестики» для подсчета количества рабочих дней сотрудников. Каждый символ эквивалентен единице.
Например, на предприятиях применяются обыкновенные «крестики» для подсчета количества рабочих дней сотрудников. Каждый символ эквивалентен единице.
На уроках математики в начальных классах также применяется инструмент — счетные палочки. Последние помогают ученикам развивать навык устного счета и являются компонентами непозиционной СС. С их помощью возможно выполнять операции суммы, разности, а также произведения и деления.
Следует отметить, что не во всех случаях один символ может соответствовать единице. Это могут быть десятки, сотни и даже тысячи. Для расчетов при помощи непозиционной СС можно придумать собственные обозначения, как это сделано в римских цифрах. Однако при этом существуют определенные недостатки:

Достоинством считается сокращение времени записи величины, которая постоянно изменяется. Например, при подсчете количества выходов персонала достаточно поставить крестик или палочку, и это делается без исправлений. В случае с десятичной СС исправлений избежать невозможно.
Чтобы выполнить перевод в восьмеричную систему счисления, необходимо ознакомиться с методикой конвертации десятичной формы в двоичное кодовое представление.
Двоичная кодировка
Для преобразования десятичной величины в двоичную IT-специалистами были разработаны специальные правила или алгоритмы. К ним относятся столбик и степень. Каждому начинающему IT-специалисту необходимо выбрать оптимальную методику преобразования одной формы числа в другую. Каждый из способов удобен в конкретной ситуации. Можно также применять сразу 2 — один для решения, а другой — для проверки результата. Необходимо разобрать каждую методику подробно с практической реализацией алгоритма.
Метод «столбик»
Первый способ получил широкое применение, поскольку для его выполнения требуется минимум знаний в математической сфере. Он имеет следующий вид:
Реализация алгоритма проверяется на практическом примере. Для этого требуется решить задачу конвертации числа из десятичной СС в другую, перевод 167{10} в {2}. Решение имеет следующий вид:
Обратный алгоритм конвертации из двоичной в десятичную форму представления величины основан на соответствии значений степенным показателям двойки. Разбиение на разрядную сетку осуществляется справа налево. Методика имеет такой вид:
 0].
0].Переводить системы счисления в другие формы представления возможно при помощи различных онлайн-сервисов. Для этого требуется указать исходную форму числа, а затем конечную. Однако действия рекомендуется совершать только для проверки результата решения задачи.
Способ степени
Для конвертации в двоичный код также применяется метод степени. Суть его заключается в представлении числа в виде отдельных элементов с основанием «2» и некоторым показателем. Алгоритм в этом случае выглядит таким образом:
Как и во всех остальных случаях, рекомендуется разобрать алгоритм на практическом примере.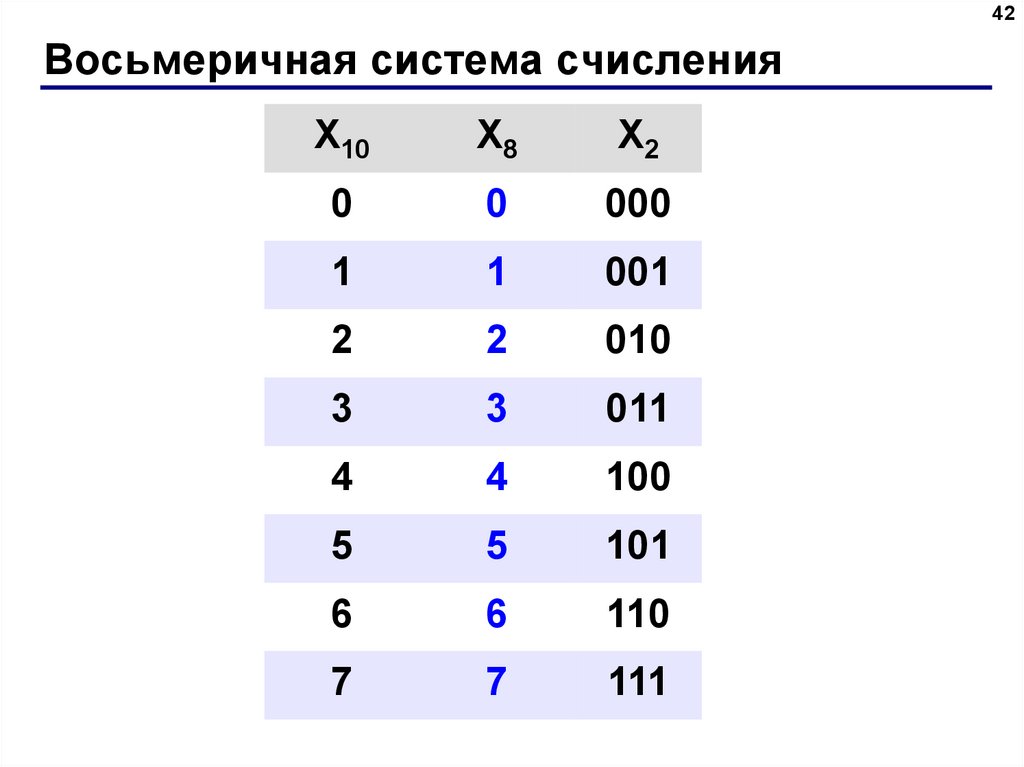 0=1 ->1.
0=1 ->1.
Однако операция преобразования является вспомогательной. Она применяется для дальнейшей конвертации в восьмеричную СС.
Восьмеричная система
Восьмеричная форма представления чисел состоит из основания-восьмерки и триады. Совокупность последних образуют любые значения. Для кодирования информации в этом случае применяется меньше регистров памяти. Этого нельзя сказать о двоичном коде.
Для восьмеричного представления применяются цифры от 0 до 7 (всего 8). Многие новички часто путают ее с шестнадцатеричной СС, в которой содержатся символы латинского алфавита. При выполнении операций конвертации специалисты рекомендуют ознакомиться со списком (таблицей) восьмеричной системы:
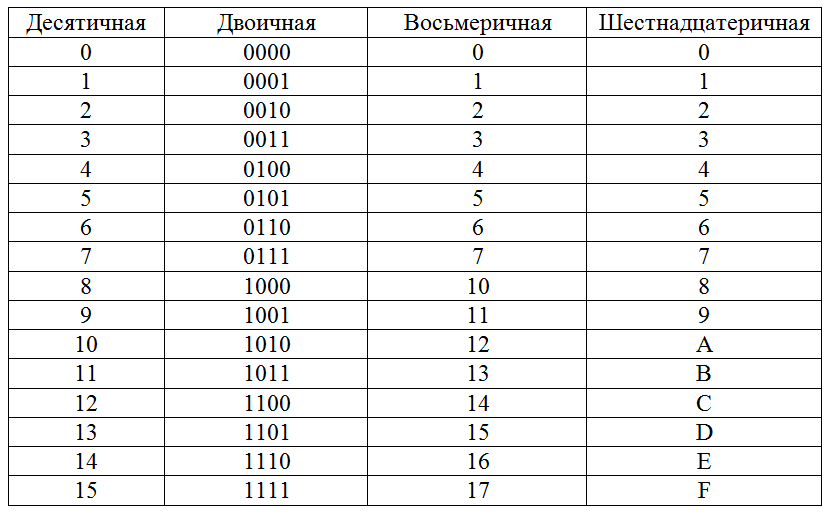
Он поможет перевести любое числовое сообщение. Для удобства IT-специалисты рекомендуют составить презентацию или записать на лист плотной бумаги перекодировку списка. Заучивать коды нет необходимости, поскольку достаточно решать примеры (информация отложится в памяти). Алгоритм кодирования очень прост:
После ознакомления с методикой преобразования нужно проверить ее реализацию на примере. Требуется выяснить, значение 167 {10}. Это делается довольно просто:

Обратное декодирование выполняется по такой методике:
На начальных этапах обучения рекомендуется четко следовать по пунктам методики. Однако через некоторое время последние можно опускать.
Таким образом, восьмеричная система применяется для кодирования больших массивов информации, при котором может быть задействовано минимальное количество регистров запоминающего устройства персонального компьютера.
Предыдущая
ИнформатикаПодходы измерения информации — фоомула, принципы и примеры
Следующая
ИнформатикаОсновные позиции пальцев на клавиатуре при обучении слепой печати
8 Восьмеричная система счисления.
 Запись чисел в восьмеричной системе счисления. Привести примеры.
Запись чисел в восьмеричной системе счисления. Привести примеры.В восьмеричной системе счисления основание равно 8, для записи чисел используются цифры от 0 до 7
A8 A2 |
0 000 |
1 001 |
2 010 |
3 011 |
4 100 |
5 101 |
6 110 |
7 111 |
Для записи каждой цифры восьмеричной с.с. требуется максимум 3 разряда.
Алгоритм перевода из 2-ой в 8-ую систему счисления
При
переводе из 2-ой в 8-ую систему счисления
надо число разбить на триады (по три
разряда) и записать каждую триаду
эквивалентным двоичным кодом, недостающее
число разрядов надо дополнить слева
нулями.
Примеры:
1001111012= 100 111 1012=4758
11000102= 001 100 0102=1428
Алгоритм перевода из 8-ой в 2-ую
Для перевода из 8-ой в 2-ую используется обратное правило.
Каждую цифру 8-ого числа надо записать тремя разрядами соответствующего ей двоичного кода
Примеры:
Перевод из 8-ой в 2-ую | 5638 = 1011100112 |
Перевод из 8-ой в 10-ую | 563 |
9 Шестнадцатеричная система счисления. Запись чисел в шестнадцатеричной системе счисления. Привести примеры.
В шестнадцатеричной системе счисления основание системы равно 16, т.е. для записи чисел используется 16 символов: цифры от 0 до 9 и далее буквы латинского алфавита от AдоF
Ниже
представлена таблица соответствия
кодов чисел четырех систем счисления.
10-ая | 8-ая | 2-ая | 16-ая |
0 | 0 | 00000000 | 0 |
1 | 1 | 00000001 | 1 |
2 | 2 | 00000010 | 2 |
3 | 3 | 00000011 | 3 |
4 | 4 | 00000100 | 4 |
5 | 5 | 00000101 | 5 |
6 | 6 | 00000110 | 6 |
7 | 7 | 00000111 | 7 |
8 | 10 | 00001000 | 8 |
9 | 11 | 00001001 | 9 |
10 | 12 | 00001010 | A |
11 | 13 | 00001011 | B |
12 | 14 | 00001100 | C |
13 | 15 | 00001101 | D |
14 | 16 | 00001110 | E |
15 | 17 | 00001111 | F |
Для
записи 1 цифры шестнадцатеричного числа
в двоичной системе счисления требуется
4 разряда.
Алгоритм перевода чисел из 2-ой в 16-ую систему счисления
При переводе чисел из 2-ой в 16-ую систему счисления надо число разбить на тетрады (по четыре разряда) и записать каждую тетраду эквивалентным двоичным кодом, недостающее число разрядов надо дополнить слева нулями.
Примеры:
1001 11102 = 9E16
0010 00102
= 2216Алгоритм перевода чисел из 16-ой в 2-ую
Для перевода из 16-ой в 2-ую используется обратное правило.
Каждую цифру шестнадцатеричного числа надо записать четырьмя разрядами соответствующего ей двоичного кода
Перевод из 16-ой в 2-ую | 17316 = 1011100112 |
Перевод из 16-ой в 10-ую | 17316 = 1*162 + 7*161 + 3*160 = 256 + 112 + 3 = 37110 |
10 Перевод чисел из десятичной системы счисления в любую другую позиционную систему счисления.
 Привести примеры.
Привести примеры.Для перевода целого десятичного числа N в систему счисления с основанием q необходимо N разделить с остатком («нацело») на q , записанное в той же десятичной системе. Затем неполное частное, полученное от такого деления, нужно снова разделить с остатком на q , и т.д., пока последнее полученное неполное частное не станет равным нулю. Представлением числа N в новой системе счисления будет последовательность остатков деления, изображенных одной q-ичной цифрой и записанных в порядке, обратном порядку их получения.
Пример: Переведем число 75 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:
В двоичную В восьмеричную В шестнадцатеричную
: 7510 = 1 001 0112 = 1138 = 4B16.
Системы счисления
Основные понятия систем счисления
Система счисления — это совокупность правил и приемов записи чисел с помощью набора цифровых знаков. Количество цифр, необходимых для записи числа в системе, называют основанием системы счисления. Основание системы записывается в справа числа в нижнем индексе: ; ; и т. д.
Основание системы записывается в справа числа в нижнем индексе: ; ; и т. д.
Различают два типа систем счисления:
позиционные, когда значение каждой цифры числа определяется ее позицией в записи числа;
непозиционные, когда значение цифры в числе не зависит от ее места в записи числа.
Примером непозиционной системы счисления является римская: числа IX, IV, XV и т.д. Примером позиционной системы счисления является десятичная система, используемая повседневно.
Любое целое число в позиционной системе можно записать в форме многочлена:
где S — основание системы счисления;
— цифры числа, записанного в данной системе счисления;
n — количество разрядов числа.
Пример. Число запишется в форме многочлена следующим образом:
Виды систем счисления
Римская система счисления является непозиционной системой. В ней для записи чисел используются буквы латинского алфавита. При этом буква I всегда означает единицу, буква — V пять, X — десять, L — пятьдесят, C — сто, D — пятьсот, M — тысячу и т. д. Например, число 264 записывается в виде CCLXIV. При записи чисел в римской системе счисления значением числа является алгебраическая сумма цифр, в него входящих. При этом цифры в записи числа следуют, как правило, в порядке убывания их значений, и не разрешается записывать рядом более трех одинаковых цифр. В том случае, когда за цифрой с большим значением следует цифра с меньшим, ее вклад в значение числа в целом является отрицательным. Типичные примеры, иллюстрирующие общие правила записи чисел в римской система счисления, приведены в таблице.
д. Например, число 264 записывается в виде CCLXIV. При записи чисел в римской системе счисления значением числа является алгебраическая сумма цифр, в него входящих. При этом цифры в записи числа следуют, как правило, в порядке убывания их значений, и не разрешается записывать рядом более трех одинаковых цифр. В том случае, когда за цифрой с большим значением следует цифра с меньшим, ее вклад в значение числа в целом является отрицательным. Типичные примеры, иллюстрирующие общие правила записи чисел в римской система счисления, приведены в таблице.
Таблица 2. Запись чисел в римской системе счисления
|
1 |
2 |
3 |
4 |
5 |
|
I |
II |
III |
IV |
V |
|
6 |
7 |
8 |
9 |
10 |
|
VI |
VII |
VIII |
IX |
X |
|
11 |
13 |
18 |
19 |
22 |
|
XI |
XIII |
XVIII |
XIX |
XXII |
|
34 |
39 |
40 |
60 |
99 |
|
XXXIV |
XXXIX |
XL |
LX |
XCIX |
|
200 |
438 |
649 |
999 |
1207 |
|
CC |
CDXXXVIII |
DCXLIX |
CMXCIX |
MCCVII |
|
2045 |
3555 |
3678 |
3900 |
3999 |
|
MMXLV |
MMMDLV |
MMMDCLXXVIII |
MMMCM |
MMMCMXCIX |
Недостатком римской системы является отсутствие формальных правил записи чисел и, соответственно, арифметических действий с многозначными числами. По причине неудобства и большой сложности в настоящее время римская система счисления используется там, где это действительно удобно: в литературе (нумерация глав), в оформлении документов (серия паспорта, ценных бумаг и др.), в декоративных целях на циферблате часов и в ряде других случаев.
По причине неудобства и большой сложности в настоящее время римская система счисления используется там, где это действительно удобно: в литературе (нумерация глав), в оформлении документов (серия паспорта, ценных бумаг и др.), в декоративных целях на циферблате часов и в ряде других случаев.
Десятичня система счисления – в настоящее время наиболее известная и используемая. Изобретение десятичной системы счисления относится к главным достижениям человеческой мысли. Без нее вряд ли могла существовать, а тем более возникнуть современная техника. Причина, по которой десятичная система счисления стала общепринятой, вовсе не математическая. Люди привыкли считать в десятичной системе счисления, потому что у них по 10 пальцев на руках.
Древнее изображение десятичных цифр (рис. 1) не случайно: каждая цифра обозначает число по количеству углов в ней. Например, 0 — углов нет, 1 — один угол, 2 — два угла и т.д. Написание десятичных цифр претерпело существенные изменения. Форма, которой мы пользуемся, установилась в XVI веке.
Десятичная система впервые появилась в Индии примерно в VI веке новой эры. Индийская нумерация использовала девять числовых символов и нуль для обозначения пустой позиции. В ранних индийских рукописях, дошедших до нас, числа записывались в обратном порядке — наиболее значимая цифра ставилась справа. Но вскоре стало правилом располагать такую цифру с левой стороны. Особое значение придавалось нулевому символу, который вводился для позиционной системы обозначений. Индийская нумерация, включая нуль, дошла и до нашего времени. В Европе индусские приёмы десятичной арифметики получили распространение в начале ХIII в. благодаря работам итальянского математика Леонардо Пизанского (Фибоначчи). Европейцы заимствовали индийскую систему счисления у арабов, назвав ее арабской. Это исторически неправильное название удерживается и поныне.
Десятичная система использует десять цифр – 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9, а также символы “+” и “–” для обозначения знака числа и запятую или точку для разделения целой и дробной частей числа.
В вычислительных машинах используется двоичная система счисления, её основание — число 2. Для записи чисел в этой системе используют только две цифры — 0 и 1. Вопреки распространенному заблуждению, двоичная система счисления была придумана не инженерами-конструкторами ЭВМ, а математиками и философами задолго до появления компьютеров, еще в ХVII — ХIХ веках. Первое опубликованное обсуждение двоичной системы счисления принадлежит испанскому священнику Хуану Карамюэлю Лобковицу (1670 г.). Всеобщее внимание к этой системе привлекла статья немецкого математика Готфрида Вильгельма Лейбница, опубликованная в 1703 г. В ней пояснялись двоичные операции сложения, вычитания, умножения и деления. Лейбниц не рекомендовал использовать эту систему для практических вычислений, но подчёркивал её важность для теоретических исследований. Со временем двоичная система счисления становится хорошо известной и получает развитие.
Выбор двоичной системы для применения в вычислительной технике объясняется тем, что электронные элементы — триггеры, из которых состоят микросхемы ЭВМ, могут находиться только в двух рабочих состояниях.
С помощью двоичной системы кодирования можно зафиксировать любые данные и знания. Это легко понять, если вспомнить принцип кодирования и передачи информации с помощью азбуки Морзе. Телеграфист, используя только два символа этой азбуки — точки и тире, может передать практически любой текст.
Двоичная система удобна для компьютера, но неудобна для человека: числа получаются длинными и их трудно записывать и запоминать. Конечно, можно перевести число в десятичную систему и записывать в таком виде, а потом, когда понадобится перевести обратно, но все эти переводы трудоёмки. Поэтому применяются системы счисления, родственные двоичной — восьмеричная и шестнадцатеричная. Для записи чисел в этих системах требуется соответственно 8 и 16 цифр. В 16-теричной первые 10 цифр общие, а дальше используют заглавные латинские буквы. Шестнадцатеричная цифра A соответствует десятеричному числу 10, шестнадцатеричная B – десятичному числу 11 и т. д. Использование этих систем объясняется тем, что переход к записи числа в любой из этих систем от его двоичной записи очень прост. Ниже приведена таблица соответствия чисел, записанных в разных системах.
Ниже приведена таблица соответствия чисел, записанных в разных системах.
Таблица 3. Соответствие чисел, записанных в различных системах счисления
|
Десятичная |
Двоичная |
Восьмеричная |
Шестнадцатеричная |
|
1 |
001 |
1 |
1 |
|
2 |
010 |
2 |
2 |
|
3 |
011 |
3 |
3 |
|
4 |
100 |
4 |
4 |
|
5 |
101 |
5 |
5 |
|
6 |
110 |
6 |
6 |
|
7 |
111 |
7 |
7 |
|
8 |
1000 |
10 |
8 |
|
9 |
1001 |
11 |
9 |
|
10 |
1010 |
12 |
A |
|
11 |
1011 |
13 |
B |
|
12 |
1100 |
14 |
C |
|
13 |
1101 |
15 |
D |
|
14 |
1110 |
16 |
E |
|
15 |
1111 |
17 |
F |
|
16 |
10000 |
20 |
10 |
Правила перевода чисел из одной системы счисления в другую
Перевод чисел из одной системы счисления в другую составляет важную часть машинной арифметики. Рассмотрим основные правила перевода.
Рассмотрим основные правила перевода.
1. Для перевода двоичного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 2, и вычислить по правилам десятичной арифметики:
При переводе удобно пользоваться таблицей степеней двойки:
Таблица 4. Степени числа 2
|
n (степень) |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
1 |
2 |
4 |
8 |
16 |
32 |
64 |
128 |
256 |
512 |
1024 |
Пример . Число перевести в десятичную систему счисления.
Число перевести в десятичную систему счисления.
2. Для перевода восьмеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 8, и вычислить по правилам десятичной арифметики:
При переводе удобно пользоваться таблицей степеней восьмерки:
Таблица 5. Степени числа 8
|
n (степень) |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
8 |
64 |
512 |
4096 |
32768 |
262144 |
Пример . Число перевести в десятичную систему счисления.
Число перевести в десятичную систему счисления.
3. Для перевода шестнадцатеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 16, и вычислить по правилам десятичной арифметики:
При переводе удобно пользоваться таблицей степеней числа 16:
Таблица 6. Степени числа 16
|
n (степень) |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
16 |
256 |
4096 |
65536 |
1048576 |
16777216 |
Пример . Число перевести в десятичную систему счисления.
Число перевести в десятичную систему счисления.
4. Для перевода десятичного числа в двоичную систему его необходимо последовательно делить на 2 до тех пор, пока не останется остаток, меньший или равный 1. Число в двоичной системе записывается как последовательность последнего результата деления и остатков от деления в обратном порядке.
Пример. Число перевести в двоичную систему счисления.
5. Для перевода десятичного числа в восьмеричную систему его необходимо последовательно делить на 8 до тех пор, пока не останется остаток, меньший или равный 7. Число в восьмеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.
Пример. Число перевести в восьмеричную систему счисления.
6. Для перевода десятичного числа в шестнадцатеричную систему его необходимо последовательно делить на 16 до тех пор, пока не останется остаток, меньший или равный 15. Число в шестнадцатеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.
Пример. Число перевести в шестнадцатеричную систему счисления.
7. Чтобы перевести число из двоичной системы в восьмеричную, его нужно разбить на триады (тройки цифр), начиная с младшего разряда, в случае необходимости дополнив старшую триаду нулями, и каждую триаду заменить соответствующей восьмеричной цифрой (табл. 3).
Пример. Число перевести в восьмеричную систему счисления.
8. Чтобы перевести число из двоичной системы в шестнадцатеричную, его нужно разбить на тетрады (четверки цифр), начиная с младшего разряда, в случае необходимости дополнив старшую тетраду нулями, и каждую тетраду заменить соответствующей восьмеричной цифрой (табл. 3).
Пример. Число перевести в шестнадцатеричную систему счисления.
9. Для перевода восьмеричного числа в двоичное необходимо каждую цифру заменить эквивалентной ей двоичной триадой.
Пример. Число перевести в двоичную систему счисления.
10. Для перевода шестнадцатеричного числа в двоичное необходимо каждую цифру заменить эквивалентной ей двоичной тетрадой.
Пример. Число перевести в двоичную систему счисления.
11. При переходе из восьмеричной системы счисления в шестнадцатеричную и обратно, необходим промежуточный перевод чисел в двоичную систему.
Пример 1. Число перевести в восьмеричную систему счисления.
Пример 2. Число перевести в шестнадцатеричную систему счисления.
- Вперёд >
|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. |
⇐ ПредыдущаяСтр 11 из 37Следующая ⇒ Показал полезность применения двоичной системы немецкий математик Г. Лейбниц в 1703 г. Однако лишь благодаря работам Дж. Фон Неймана, опубликованным в 1940-х гг., двоичная система получила практическое использование при создании компьютерных средств. Применение двоичной системы в вычислительной технике было обусловлено такими обстоятельствами, как двухпозиционный характер работы электронных элементов, высокая экономичность двоичной системы счисления и простота выполнения операций с двоичными числами. Как отмечалось в отчете Дж. Фон Неймана (1946 г.): «основное же преимущество двоичной системы по сравнению с десятичной состоит в том, что основная часть машины по своему характеру является не арифметической, а логической. Новая логика, будучи системой типа «да — нет», в основном двоична. Поэтому двоичное построение арифметических устройств существенно содействует построению более однородной машины, которая может быть лучше скомпонована и более эффективна». В современной вычислительной технике, в устройствах автоматики и связи используется в основном двоичная система счисления, что обусловлено рядом преимуществ перед другими системами. Так, для ее реализации нужны технические устройства лишь с двумя устойчивыми состояниями, например материал намагничен или размагничен. Это обеспечивает более надежное и помехоустойчивое представление информации, дает возможность применения аппарата булевой алгебры для выполнения логических преобразований информации. Кроме того, арифметические операции в двоичной системе счисления выполняются наиболее просто. Недостаток двоичной системы – быстрый рост числа разрядов, необходимых для записи больших чисел. Этот недостаток имеет существенное значение. Если возникает необходимость кодировать информацию “вручную”, например при составлении программы на машинном языке, используют восьмеричную или шестнадцатеричную системы счисления. Примеры изображения чисел в данных системах счисления представлены в таблице 4. Таблица 4.2. Представление чисел в двоичной, восьмеричной и Шестнадцатеричной системах счисления
Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему счисления осуществляется путем замены каждой цифры эквивалентной ей двоичной триадой (тройкой цифр) или тетрадой (четверкой цифр). Пример 4 . Переведем число 537,18 в двоичную систему счисления. 537,18 = 101 011 111, 0012 5 3 7 1 Пример 5 . Переведем число 1A3,F16 в двоичную систему счисления. 1A3,F16 = 1 1010 0011, 11112 1 A 3 F Чтобы перевести число из двоичной системы счисления в восьмеричную или шестнадцатеричную, его нужно разбить влево или вправо от запятой на триады ( для восьмеричной) или тетрады (для шестнадцатеричной) и каждую такую группу заменить соответствующей восьмеричной или шестнадцатеричной цифрой. Пример 6 . Переведем число 10101001,101112 в восьмеричную систему счисления. 10101001,101112 = 10 101 001,101 1102 = 251,568 2 5 1 5 6 Пример 7. Переведем число 10101001,101112 в шестнадцатеричную систему счисления. 10101001,101112 = 1010 1001,1011 10002 = A9,В816 A 9 В 8
Выполнение арифметических операций в двоичной, восьмеричной и шестнадцатеричной системах счисления Правила выполнения арифметических операций сложения, вычитания, умножения и деления в 2-, 8- и 16-ичной системах счисления будут такими же, как и в десятичной системе, только надо пользоваться особыми для каждой системы таблицами сложения и умножения. Таблицы сложения для 2-ичной, 8-ичной и 16-ичной систем счисления представлены в таблицах 4.3-4.5. При сложении цифры суммируются по разрядам, и если при этом возникает избыток, то он переносится влево. Таблица 4.3. Сложение в двоичной системе Таблица 4.4. Сложение в восьмеричной системе
Таблица 4.5. ⇐ Предыдущая6789101112131415Следующая ⇒ Читайте также: Как правильно слушать собеседника Типичные ошибки при выполнении бросков в баскетболе Принятие христианства на Руси и его значение Средства массовой информации США |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 2853; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. |
Восьмеричная система счисления — значение, преобразование, решенные примеры, практические вопросы или выражая числа в различных типах форм. Основные способы представления чисел выполняются четырьмя способами: восьмеричной системой счисления, двоичной системой счисления, десятичной системой счисления и шестнадцатеричной системой счисления.
| 1. | Определение восьмеричной системы счисления |
| 2. | Преобразование восьмеричных чисел в двоичные |
| 3. | Преобразование восьмеричного числа в десятичное |
| 4. | Преобразование десятичного числа в восьмеричное |
| 5. | Преобразование восьмеричных чисел в шестнадцатеричные |
6. | Решенные примеры |
| 7. | Практические вопросы |
| 8. | Часто задаваемые вопросы по восьмеричной системе счисления |
Определение восьмеричной системы счисления
Система счисления, основанная на восьми и использующая цифры от 0 до 7, называется восьмеричной системой счисления. Слово восьмеричное используется для обозначения чисел, в основе которых восемь. Восьмеричные числа имеют много применений и важности, например, они используются в компьютерах и цифровых системах счисления. В системе счисления восьмеричные числа можно преобразовать в двоичные числа, а двоичные числа в восьмеричные числа, сначала преобразовав двоичное число в десятичное число, а затем десятичное число в восьмеричное число.
Подобно восьмеричной системе счисления, двоичная система счисления представлена основанием 2, десятичная система счисления представлена основанием 10, а шестнадцатеричная система счисления представлена основанием 16. Несколько примеров этих чисел системы:
Несколько примеров этих чисел системы:
- \((10)_{2}\) — двоичное число
- \((119)_{10}\) — десятичное число
- \((51)_{6}\) — шестнадцатеричное число .
При решении восьмеричного числа каждый разряд равен степени числа восемь. Например: \((347)_{8}\) = 3 x 8 2 + 4 х 8 1 + 7 х 8 0
Преобразование восьмеричных чисел в двоичные
Для процесса преобразования нам нужно преобразовать каждое число из восьмеричного числа в двоичное число. Каждую цифру необходимо преобразовать в 3-битное двоичное число и, следовательно, получить двоичный эквивалент восьмеричного числа. Ниже приведена таблица преобразования двоичных чисел в восьмеричные и наоборот.
Пример 1 — Преобразовать \((14)_{8}\) в двоичное число
Решение — Дано \((14)_{8}\) — восьмеричное число с помощью приведенного выше таблице мы можем написать \((14)_{8}\) = \((001 100)_{2}\). Нули слева не имеют никакого значения. Следовательно, \((14)_{8}\) = \((001 100)_{2}\).
Нули слева не имеют никакого значения. Следовательно, \((14)_{8}\) = \((001 100)_{2}\).
Пример 2 — Преобразование \((11100101)_{2}\) в восьмеричное число.
Решение . Учитывая, что \((11100101)_{2}\) является двоичным числом, с помощью приведенной выше таблицы мы сначала записываем число в его 3-битное двоичное число, так как перед ним необходимо добавить ноль. цифры для формирования 3-битного двоичного числа. Таким образом, число может быть записано как \((011100101)_{2}\). Следовательно, 3-битное двоичное число — это 011, 100, 101. Глядя на ту же таблицу выше, мы можем преобразовать эти двоичные числа в их восьмеричные числа, чтобы получить окончательное число. Следовательно, числа 3, 4, 5
Следовательно, \((11100101)_{2}\) = \((345)_{8}\)
Преобразование восьмеричного числа в десятичное
Преобразование восьмеричных чисел в десятичные осуществляется простым способом. Число расширяется по основанию восемь, где каждое число умножается на уменьшающую степень 8. Десятичная система счисления имеет основание 10 после преобразования.
Десятичная система счисления имеет основание 10 после преобразования.
Например, — преобразовать восьмеричное число \((121)_{8}\) в его десятичную форму.
Решение — \((121)_{8}\) = 1 x 8 2 + 2 x 8 1 + 1 x 8 0
= 1 x 64 + 2 x 8 + 1 х 1
= 64 + 16 + 1
Следовательно, \((121)_{8}\) = \((81)_{10}\)
Преобразование десятичного числа в восьмеричное
Для преобразования десятичного числа в восьмеричное используется другой метод. В этом методе десятичное число делится на 8 каждый раз, когда из предыдущей цифры получается напоминание. Первый полученный остаток представляет собой наименьшую значащую цифру (LSD), а последний остаток — старшую значащую цифру (MSD). Давайте разберемся с конверсией на примере.
Например, — преобразовать десятичное число 321 в восьмеричное.
Решение — Нам нужно начать делить число 321 на 8
321/8 дает частное 40 и остаток 1
40/8 дает частное 5 и остаток 0 а остаток равен 0. Восьмеричное число начинается от MSD до LSD, т. е. 501
Восьмеричное число начинается от MSD до LSD, т. е. 501
Следовательно, \((321)_{10}\) = \((501)_{8}\)
Преобразование восьмеричных чисел в шестнадцатеричные
Шестнадцатеричный код представлен с основанием 16 и состоит как из цифр, так и из букв. Числа от 0 до 9 представляются в обычном виде, а от 10 до 15 обозначаются как A, B, C, D, E, F. Преобразование восьмеричного в шестнадцатеричное выполняется в два шага, т.е. сначала преобразуется восьмеричное число в десятичное число, а затем преобразовать его в шестнадцатеричное число. Давайте рассмотрим пример, чтобы лучше понять этот метод.
Например, — \((121)_{8}\) = \((81)_{10}\)
Решение . У нас уже есть десятичное число 81 10 , поэтому нам нужно только преобразовать его в шестнадцатеричное число. Чтобы определить шестнадцатеричное число, нам нужно разделить число 81 на 16, пока остаток не станет меньше 16. Оно полностью делится с ответом 5 и остатком 1.
Следовательно, \((121)_{8} \) = \((51)_{16}\)
Восьмеричная система счисления Связанные темы
Ознакомьтесь с этими интересными статьями, чтобы узнать больше о восьмеричной системе счисления и связанных с ней темах.
- Система счисления
- База
- 22 в двоичном формате
- Десятичные числа
Важные моменты
- Преобразование восьмеричных чисел в двоичные числа и наоборот очень просто.
- Для преобразования восьмеричных чисел в шестнадцатеричные числа восьмеричное число необходимо преобразовать в десятичное, а затем в шестнадцатеричное.
- Основание каждой из четырех систем счисления очень важно.
Часто задаваемые вопросы по восьмеричной системе счисления
Что такое восьмеричная система счисления?
Система счисления, основанная на восьми и использующая цифры от 0 до 7, называется восьмеричной системой счисления. Слово восьмеричное используется для обозначения чисел, в основе которых восемь. Восьмеричные числа имеют много применений и важности, например, они используются в компьютерах и цифровых системах счисления. Слово Octal — это краткая форма латинского слова Octal, что означает короткий.
Для чего используются восьмеричные числа?
Восьмеричная система счисления широко используется в компьютерных приложениях и цифровых системах счисления. Вычислительные системы используют 16-битное, 32-битное или 64-битное слово, которое далее делится на 8-битные слова. Восьмеричное число также используется в авиационном секторе в виде кода.
Какое значение имеет восьмеричная система счисления?
Восьмеричная система счисления использует цифры от 0 до 7, которые могут быть получены из двоичных чисел путем группировки двоичных цифр в их 3-битном представлении. Восьмеричные числа используют меньшее количество цифр по сравнению с десятичными и шестнадцатеричными, что упрощает вычисление за меньшее количество шагов.
Какие существуют четыре типа системы счисления?
Четыре основных типа системы счисления:
- Двоичная система счисления
- Восьмеричная система счисления
- Десятичная система счисления
- Шестнадцатеричная система счисления
Какие символы используются в восьмеричной системе счисления?
Восьмеричная система счисления — это система счисления с основанием 8, что означает, что для представления любого числа в восьмеричной системе требуется 8 различных символов. Используются символы 0, 1, 2, 3, 4, 5, 6 и 7. Наименьшим двузначным числом в этой системе является \((10)_{8}\), что эквивалентно десятичному числу 8.
Используются символы 0, 1, 2, 3, 4, 5, 6 и 7. Наименьшим двузначным числом в этой системе является \((10)_{8}\), что эквивалентно десятичному числу 8.
Каковы преимущества и недостатки восьмеричной системы счисления?
Преимущества восьмеричной системы счисления в том, что она составляет одну треть от двоичной системы счисления, процесс преобразования восьмеричной системы счисления в двоичную и наоборот очень прост, а в восьмеричной форме просто обрабатывать ввод и вывод . Недостатки восьмеричной системы счисления заключаются в том, что существует дополнительное требование к системе внутри компьютера, которая обеспечивает более простое преобразование восьмеричных чисел в двоичные числа до того, как она будет фактически применена к цифровой платформе.
Как преобразовать восьмеричное число в десятичное?
Чтобы преобразовать восьмеричное число в десятичное, нам нужно расширить число по основанию 8, где каждое число умножается на уменьшающую степень 8. Получив произведение, мы складываем числа, чтобы получить десятичное число. Десятичная система счисления имеет основание 10 после преобразования.
Десятичная система счисления имеет основание 10 после преобразования.
Как преобразовать десятичную систему в восьмеричную?
Чтобы преобразовать десятичное число в восьмеричное, десятичное число делится на 8 каждый раз, когда из предыдущей цифры получается напоминание. Первый полученный остаток представляет собой наименьшую значащую цифру (LSD), а последний остаток — старшую значащую цифру (MSD).
Как преобразовать восьмеричное число в шестнадцатеричное?
Шестнадцатеричный код представлен с основанием 16 и состоит как из цифр, так и из букв. Числа от 0 до 9 представляются в обычном виде, а от 10 до 15 обозначаются как A, B, C, D, E, F. Преобразование восьмеричного в шестнадцатеричное выполняется в два шага, т.е. сначала преобразуется восьмеричное число в десятичное число, а затем преобразовать его в шестнадцатеричное число.
Восьмеричная система счисления — Electronics-Lab.com
Восьмеричная система счисления
Восьмеричная система нумерации — это еще одна цифровая система нумерации, в которой используется система Base-8 , аналогичная обсуждавшейся ранее шестнадцатеричной системе нумерации Base-16 . Oct- — это комбинированная форма, используемая в качестве префикса, означающего «восемь», и поэтому система с основанием 8 (восемь) называется восьмеричной системой счисления. Подобно шестнадцатеричному числу, восьмеричная система счисления уменьшает размер эквивалентного большого двоичного числа и упрощает чтение и запись исходного большого двоичного числа.
Oct- — это комбинированная форма, используемая в качестве префикса, означающего «восемь», и поэтому система с основанием 8 (восемь) называется восьмеричной системой счисления. Подобно шестнадцатеричному числу, восьмеричная система счисления уменьшает размер эквивалентного большого двоичного числа и упрощает чтение и запись исходного большого двоичного числа.
Цифра системы счисления имеет диапазон чисел, которые она может использовать для выражения своего значения. Этот диапазон зависит от базового значения системы счисления, т.е. Системы с основанием 16 имеют диапазоны чисел «10» и «16» соответственно. Точно так же система счисления с основанием 8 (восьмеричная) имеет диапазон только «8» чисел от «0» до «7», то есть 0, 1, 2, 3, 4, 5, 6 и 7. Восьмеричные числа имеют только восемь (8) различных значений для каждой цифры, и каждая цифра имеет вес восемь (8), начиная с младшей значащей цифры (LSD). Для размещения и представления числа «8» в двоичном формате требуется всего три (3) бита. После этого восьмеричные значения (0, 1, 2, 3, 4, 5, 6 и 7) соответствуют двоичным эквивалентным значениям (000, 001, 010, 011, 100, 101, 110 и 111) соответственно.
После этого восьмеричные значения (0, 1, 2, 3, 4, 5, 6 и 7) соответствуют двоичным эквивалентным значениям (000, 001, 010, 011, 100, 101, 110 и 111) соответственно.
Восьмеричное число формируется путем группировки двоичных чисел в наборы по 3 бита. Это следует той же процедуре, которая использовалась ранее в шестнадцатеричном артикле. Однако в шестнадцатеричных числах двоичное число было разделено на группы по 4 бита (поскольку Base-16 использует диапазон от 0 до 15 и требует 4 бита). Восьмеричная система счисления проста по сравнению с шестнадцатеричной системой счисления, поскольку в ней используются только числа по сравнению с шестнадцатеричной системой, использующей числа и алфавиты. Более того, он имеет только восемь различных значений «8» по сравнению с шестнадцатью различными значениями «16» шестнадцатеричной системы счисления. В раннюю эру цифровых вычислений восьмеричная система счисления была очень известна, поскольку цифровые входы (от D0 до D7) и выходы (от Q0 до Q7) исчислялись восемью (8). Однако с увеличением количества цифровых входов и выходов, архитектуры системы и объема памяти и т. д. шестнадцатеричная система счисления стала более удобной для представления больших двоичных значений.
Однако с увеличением количества цифровых входов и выходов, архитектуры системы и объема памяти и т. д. шестнадцатеричная система счисления стала более удобной для представления больших двоичных значений.
Представление восьмеричного числа
Восьмеричная система счисления использует систему с основанием 8, поэтому восьмеричное число представляется нижним индексом «8». Например, (142 8 ) идентифицируется как восьмеричное число, поскольку оно имеет нижний индекс «8». Кроме того, заметно, что каждая цифра восьмеричного числа имеет значение от 0 до 7. Например, восьмеричное число (128 8 ) неверно, поскольку его младшая значащая цифра (LSD) имеет значение «8». Который не относится к восьмеричному диапазону счисления, а относится к десятичной или шестнадцатеричной системе счисления. Таким образом, правильность числа можно определить, проверив его базовое значение и попадание числа каждой цифры в его базовый диапазон.
Восьмеричные числа
В следующей таблице перечислены десятичные числа от 0 до 7 и их эквиваленты в двоичных и восьмеричных числах.
Восьмеричный счет
Каждая цифра восьмеричного числа имеет вес восемь (8) , начиная с младшей значащей цифры. Вес каждой цифры увеличивается в степени восемь при переходе от младшей значащей цифры к старшей значащей цифре. Эквивалентный десятичный вес каждой восьмеричной цифры до 7 й цифра , дана.
Восьмеричная цифра имеет числовой диапазон от «0» до «7» , и для счета сверх этого диапазона слева добавляется еще одна восьмеричная цифра. Добавление второй цифры приводит к счету до (77 8 ) , что в десятичном виде эквивалентно ( 63 10 ). Таким образом, две восьмеричные цифры могут считать до 63. Точно так же трехзначное восьмеричное число может считать до (777 8 ) , который дает диапазон счета до (511 10 ) в десятичной системе.
Добавление нулей к двоичному числу
Поскольку двоичное число разбивается на 3-битные группы для определения эквивалентного ему восьмеричного числа. Для этого требуется двоичное число, состоящее из битов, кратных трем (3), например. 3, 6, 9, 12 и 15 и т. д. Однако это может быть не так, когда речь идет о двоичных числах, а двоичные числа могут различаться по длине в битах. Решение состоит в том, чтобы начать разбивать двоичные числа на группы по 3 бита, начиная с младшего значащего бита (LSB). В случае, если биты двоичного числа не разделены поровну между 3-битными группами, у нас останется менее 3-бит в конце. Ведущие нули добавляются к оставшимся битам, чтобы увеличить их длину до 3 бит. Эта последняя группа из 3 битов составляет старшую значащую цифру (MSD) восьмеричного числа. В следующей таблице нестандартное 13-битное двоичное число (1 0101 1101 101010) преобразуется в 15-битное (делится на 3) двоичное число путем добавления начальных нулей, а затем определяется его эквивалентное восьмеричное число.
Для этого требуется двоичное число, состоящее из битов, кратных трем (3), например. 3, 6, 9, 12 и 15 и т. д. Однако это может быть не так, когда речь идет о двоичных числах, а двоичные числа могут различаться по длине в битах. Решение состоит в том, чтобы начать разбивать двоичные числа на группы по 3 бита, начиная с младшего значащего бита (LSB). В случае, если биты двоичного числа не разделены поровну между 3-битными группами, у нас останется менее 3-бит в конце. Ведущие нули добавляются к оставшимся битам, чтобы увеличить их длину до 3 бит. Эта последняя группа из 3 битов составляет старшую значащую цифру (MSD) восьмеричного числа. В следующей таблице нестандартное 13-битное двоичное число (1 0101 1101 101010) преобразуется в 15-битное (делится на 3) двоичное число путем добавления начальных нулей, а затем определяется его эквивалентное восьмеричное число.
В приведенном выше примере к 13-битному числу необходимо добавить 2 бита с нулевыми значениями в крайнюю левую сторону, чтобы получить 15-битное двоичное число . Точно так же для 11-битного двоичного числа потребуется добавить один (1) нулевой бит. Использование восьмеричных чисел сокращает длину двоичных чисел в три (3) раза.
Точно так же для 11-битного двоичного числа потребуется добавить один (1) нулевой бит. Использование восьмеричных чисел сокращает длину двоичных чисел в три (3) раза.
Преобразование восьмеричного числа в десятичное
Преобразование восьмеричного значения в десятичное достигается с помощью метода взвешенной суммы цифр, описанного в предыдущих статьях. В следующем примере восьмеричное число (4262 8 ) преобразуется в десятичное число.
Преобразование десятичного числа в восьмеричное
Преобразование десятичного числа в восьмеричное требует применения метода повторного деления на 8. Тот же метод использовался для преобразования десятичного числа в его эквивалентные двоичные и шестнадцатеричные значения в предыдущих статьях. Десятичное число (238 10 ) снова используется для получения эквивалентного восьмеричного числа в следующем примере.
Пример преобразования двоичного числа в восьмеричное
Преобразование 8-битного двоичного числа (11011001 2 ) в восьмеричное число показано ниже.
Пример преобразования восьмеричного числа в двоичное и десятичное
Преобразование ( 6271 8 ) в эквивалентное ему двоичное и десятичное число показано ниже в качестве примера.
Заключение
- Восьмеричное число использует систему с основанием 8, и значение каждой цифры находится в диапазоне от 0 до 7, т. е. восемь (8) чисел.
- В восьмеричном числе каждая цифра представляет собой группу или набор из 3 битов. Эквивалент восьмеричного двоичного числа получается путем разбиения двоичного числа на 3-битные группы, и каждой группе присваивается эквивалентное восьмеричное значение от «0» до «7».
- Двоичные числа могут потребовать добавления начальных нулей в крайнюю левую (наиболее значащую) сторону для формирования 3-битных групп.
- Восьмеричное число представляется с помощью «8» в качестве нижнего индекса, например. 735 8 .
- Восьмеричное число можно преобразовать в десятичное число с помощью метода взвешенной суммы цифр.

- Преобразование десятичного числа в восьмеричное требует применения метода повторного деления на 8.
- Восьмеричное число уменьшает длину эквивалентного ему двоичного числа в три (3) раза. Однако сейчас восьмеричные числа используются редко, и, как обсуждалось ранее, их место заняла шестнадцатеричная система счисления.
Восьмеричная система счисления – определение и преобразование
По названию «Восьмеричная система счисления» можно понять, что это разновидность системы счисления. Итак, прежде чем знакомиться с восьмеричной системой счисления, давайте сначала узнаем, что такое система счисления? Система счисления, также известная как система счисления, представляет собой систему наименования, представления или выражения чисел. В математике мы можем называть или представлять числа в различных формах.
Четыре основных способа представления чисел — это двоичная система счисления, десятичная система счисления, шестнадцатеричная система счисления и восьмеричная система счисления. Теперь дайте нам знать все концепции системы счисления вместе с их типами, преобразованиями и примерами.
Теперь дайте нам знать все концепции системы счисления вместе с их типами, преобразованиями и примерами.
Что такое система счисления?
Система счисления — это способ или система записи, которую мы используем для выражения чисел. Это математическая нотация, используемая для представления чисел данного набора с использованием цифр или других символов логическим образом. Система счисления позволяет нам представлять каждое число уникальным образом. Он представляет собой арифметическую и алгебраическую структуру фигур. Не только это, но и позволяет нам выполнять арифметические операции, такие как сложение, вычитание и деление.
Значение цифры в числе обычно определяется:
Типами системы счисления
В математике мы можем представлять числа в различных типах, но четыре основные системы счисления:
Десятичная система счисления ( Основание-10)
Двоичная система счисления (Основание-2)
Восьмеричная система счисления (Основание-8)
Шестнадцатеричная система счисления (Основание-16)
94036 Это система с основанием восемь и использует числа от 0 до 7.
 Это одна из классификаций систем счисления помимо двоичных, десятичных и шестнадцатеричных чисел. Восьмеричный символ используется для представления чисел с основанием 8. Существуют различные приложения и важность восьмеричных чисел. Одно из наиболее распространенных применений — основы работы с компьютером.
Это одна из классификаций систем счисления помимо двоичных, десятичных и шестнадцатеричных чисел. Восьмеричный символ используется для представления чисел с основанием 8. Существуют различные приложения и важность восьмеричных чисел. Одно из наиболее распространенных применений — основы работы с компьютером.Мы можем преобразовать восьмеричные числа в десятичные числа, двоичные числа в восьмеричные числа, где мы сначала должны преобразовать двоичное число в десятичное число и десятичное число в восьмеричное число. Итак, давайте сначала обсудим восьмеричное число с его определением, таблицей, примером и применением.
Что такое восьмеричная система счисления?
Система счисления с основанием «восемь» известна как восьмеричная система счисления и использует числа от 0 до 7, т. е. 0, 1, 2, 3, 4, 5, 6 и 7. Возьмем пример. , чтобы лучше понять концепцию. Как мы уже знаем, любое число с основанием 8 называется восьмеричным числом, например 248, 1098, 558 и т.
 д. с основанием 2, десятичное число с основанием 10 и шестнадцатеричное число представлено с основанием 16. Вот несколько примеров для этих систем счисления:
д. с основанием 2, десятичное число с основанием 10 и шестнадцатеричное число представлено с основанием 16. Вот несколько примеров для этих систем счисления:Двоичное число = 101012
А десятичное число = 12010
Гексадецимное число = 4016
. Мы можем конвертировать, чтобы быть декаменным.
1248 = 1 × 82 + 2 × 81 + 4 × 80
в целом, 83 82 81 80. 8–1 8–2 8–3 … и т. Д.
↑
Октальная точка
, чтобы преобразовать числа из восьмеричной в двоичную, преобразование должно быть выполнено путем преобразования каждого числа из восьмеричной цифры в двоичную цифру. Каждая цифра должна быть преобразована в 3-битное двоичное число, и в результате получится двоичный эквивалент восьмеричного числа.

Преобразование восьмеричного числа в двоичное
Для представления восьмеричного числа используются только 3 бита. Каждая группа будет иметь различное значение от 000 до 111. В таблице ниже представлены восьмеричные значения и эквивалентные двоичные значения.
Octal Symbol
Двоинк.0003
1
001
2
010
3
011
4
100
5
101
.
 Восьмеричная система счисления поддерживает только цифры от 0 до 7. После 7, например 8 и 9не являются восьмеричными цифрами. Например, 29 — не восьмеричное число, а 10 — восьмеричное число.
Восьмеричная система счисления поддерживает только цифры от 0 до 7. После 7, например 8 и 9не являются восьмеричными цифрами. Например, 29 — не восьмеричное число, а 10 — восьмеричное число.Пример 1) Преобразование (145,56)8 в двоичный формат.
Решение: Чтобы преобразовать восьмеричное число в двоичное и наоборот, нам понадобится эта таблица преобразования. Согласно таблице, восьмеричное значение (145,56)8
можно преобразовать в двоичное как (001100101.101110)2
Преобразование из двоичного в восьмеричное
Эту же таблицу можно использовать для преобразования двоичного числа в восьмеричное. А для этого нам сначала нужно сгруппировать двоичное число в группу из трех битов и записать его восьмеричный эквивалент.
Пример 2) Преобразование двоичного числа (11001111)2 в восьмеричное.
Решение. Трехбитную группу двоичных чисел можно записать как 011 001 111, потому что нам нужно добавить ноль перед каждым числом, чтобы завершить группировку в виде трех двоичных цифр.
 Следовательно, восьмеричные числа будут 3, 1, 7, т. е. (317)8
Следовательно, восьмеричные числа будут 3, 1, 7, т. е. (317)8Преобразование восьмеричного числа в десятичное
Метод, который мы используем для преобразования восьмеричного числа в его десятичный эквивалент, чрезвычайно прост. Нам просто нужно расширить число в основании восьми с его позиционным весом и готово! Результирующее значение будет десятичным числом.
Пример 3) Преобразование (317)8 в десятичное число.
Решение. Преобразование восьмеричного числа в десятичное можно выполнить следующим образом: (317)8 = 3 × 82+ 1 × 81 + 7 × 80 = 207
Преобразование десятичного числа в восьмеричное
Мы можем преобразовать число из десятичного числа в восьмеричное путем деления числа на 8 с использованием метода повторного деления, который обычно известен как метод двойного мазка. Делаем повторное деление и находим остаток. Вот пример.
В этом методе десятичное число делится на 8 каждый раз, когда получается остаток.
 Первое напоминание находится в младшей значащей цифре (LSD), а последний остаток называется старшей значащей цифрой (MSD).
Первое напоминание находится в младшей значащей цифре (LSD), а последний остаток называется старшей значащей цифрой (MSD).Пример 4) Преобразование десятичного числа 158 в восьмеричное.
Решение. Нам нужно разделить число 158 на 8 следующим образом:
(Изображение будет загружено в ближайшее время)
Следовательно, в восьмеричном формате значение будет 2368
Преобразование восьмеричного числа в шестнадцатеричное число
xШестнадцатеричные числа состоят из цифр и букв. Эти числа представлены числом 16 в основании. Числа от 0 до 9 представляются в обычном виде, а числа от 10 до 15 обозначаются как A, B, C, D, E, F. Преобразование восьмеричного числа в шестнадцатеричное состоит из двух шагов.
На первом этапе нам нужно преобразовать восьмеричные числа в десятичные.
На втором этапе преобразуйте десятичные числа в шестнадцатеричные числа.

Octal Multiplication Table
Following is the octal multiplication table:
*
0
1
2
3
4
5
6
7
0
0
0
0
0
0
0
0
0
1
0 1
1
1
9 1
1
0 1
1
1
.
 0003
00031
2
3
4
5
6
7
2
0
2
4
6
10
12
14
16
16
16
3
0
3
6
11
14
17
22
25
4
0
4
10
14
20
24
406 30 34
5
0
5
12
17
24
31
36
43
6
0
6
14
22
99 22
0406 30 36
44
52
7
0
7
16
25
34
43
52
61
Применение Octal Number System
Система Octal широко используется в World Applications и также в авиационном штуке.
 в виде кода.
в виде кода.На основе приложений восьмеричной системы счисления было разработано несколько вычислительных систем. Все вычислительные системы современного поколения используют 16-битные, 32-битные или 64-битные слова, которые далее делятся на 8-битные слова. Точно так же для различных языков программирования восьмеричные числа используются для целей кодирования или для хранения данных на зашифрованном языке, который может быть понят только вычислительной машиной.
Также в авиационной промышленности транспондеры, используемые в самолетах, передают код, который выражается в виде четырех восьмеричного числа. Затем эти коды анализируются и запрашиваются наземным радаром.
Важность восьмеричной системы счисления
Восьмеричная система счисления использует меньше цифр (3 бита) по сравнению с шестнадцатеричной системой счисления (4 бита), что является одним из ее основных преимуществ. Это также приводит к меньшему количеству вычислений и меньшей вероятности возникновения ошибки.

Из-за меньшего количества цифр также легко преобразовать восьмеричные числа в любую другую систему счисления и наоборот.
Одним из ограничений восьмеричной системы счисления является то, что компьютеры не воспринимают восьмеричные числа напрямую, и поэтому их необходимо сначала преобразовать в двоичные числа.
Это все о восьмеричной системе счисления и ее преобразованиях в различные другие системы счисления. Сосредоточьтесь на решенных примерах, чтобы понять, как выполняются преобразования. Изучите его применение в современном мире.
Двоичная система счисления, Десятичная система счисления, Восьмеричная система счисления, Шестнадцатеричная система счисления: Pharmaguideline
В двоичной системе число определяется с помощью двоичной системы счисления. Двоичная система использует только две цифры, 0 и 1, для представления числа.
Двоичная система счисления
В двоичной системе число определяется с использованием двоичной системы счисления.
 Двоичная система использует только две цифры, 0 и 1, для представления числа. Многие компьютерные языки используют двоичные системы счисления, включая Java и C++. Компьютер может понимать только двоичный язык (0 или 1), то есть 0 и 1, поэтому все входные данные перед дальнейшей обработкой преобразуются в последовательность 0 и 1. Чтобы понять смысл информации в этом уроке, я преобразовал десятичное число в двоичное число, а затем вернул двоичное число в десятичное число.
Двоичная система использует только две цифры, 0 и 1, для представления числа. Многие компьютерные языки используют двоичные системы счисления, включая Java и C++. Компьютер может понимать только двоичный язык (0 или 1), то есть 0 и 1, поэтому все входные данные перед дальнейшей обработкой преобразуются в последовательность 0 и 1. Чтобы понять смысл информации в этом уроке, я преобразовал десятичное число в двоичное число, а затем вернул двоичное число в десятичное число.Двоичный символ «Би» означает «два». Таким образом, линия возвращается к 0 и 1 как к единственным способам представления числа. Двоичные числа могут быть легко выражены в виде десятичных чисел. Различия между двоичной и десятичной системами счисления. Двоичные числа представлены по основанию двойки, а десятичные числа представлены по основанию 10.
Ниже показано, как числа от 1 до 10 выражаются в двоичной системе счисления:
Десятичная система счисления
Числа представлены своими основаниями в системе счисления.
 Существует четыре основы для чисел: двоичная, восьмеричная, десятичная и шестнадцатеричная. Если основание равно 2, оно двоичное, если 8 — восьмеричное, если 10 — десятичное, а если 16 — шестнадцатеричное. Взять десятичные числа и преобразовать их в другую систему счисления несложно. Однако преобразование десятичных чисел из других систем счисления требует практики.
Существует четыре основы для чисел: двоичная, восьмеричная, десятичная и шестнадцатеричная. Если основание равно 2, оно двоичное, если 8 — восьмеричное, если 10 — десятичное, а если 16 — шестнадцатеричное. Взять десятичные числа и преобразовать их в другую систему счисления несложно. Однако преобразование десятичных чисел из других систем счисления требует практики.В этой статье мы более подробно рассмотрим десятичные числа и то, как их можно преобразовать в другие системы. Основа 10 представляет десятичные числа в десятичной системе счисления. Также известная как десятичная запись, это способ представления десятичных чисел с основанием 10. Многие компьютерные программы используют этот числовой формат. База-10 — это система счисления, состоящая из 10 цифр, например, 0,1,2,3,4,5,6,7,8,9. Десятичные числа имеют четкую позицию для каждой цифры, и каждая цифра в 10 раз значительнее, чем любая предыдущая цифра. Два в десять раз больше, чем пять, если 25 — десятичное число. Число в десятичной системе представляет собой число от 0 до 9 с использованием цифр от 0 до 9.

В системе счисления с основанием 10 число записывается с нулем или первыми девятью положительными целыми числами, представляющими каждое значение. В конце каждого значения ставится степень 10. Десятикратный размер цифры в разряде десятков означает, что он в десять раз больше десятого в разряде единиц. Подсчет в порядке убывания мощности каждой цифры, которая следует за десятичным нулем (.) в десятичном числе.
Восьмеричная система счисления
В восьмеричной системе счисления цифры от 0 до 7 представляют собой восьмизначные числа. Всякий раз, когда восьмеричные числа сгруппированы по три, в качестве представления используются двоичные числа. Системы счисления с основанием «восемь» называются восьмеричными числами. Эта система работает с числами от нуля до семи. По основанию 2 двоичное число является десятичным, по основанию 10 и по основанию 16 — шестнадцатеричным числом. Основание 2 такое же, как основание 8, когда дело доходит до описания восьмеричного числа.

Группируя последовательные двоичные числа в группы по три (для целых чисел, начиная справа), восьмеричные числа легко преобразуются из двоичных представлений (аналогично четверичным числам). Двоичное представление десятичного числа 74, например, 1001010. Добавляя два нуля слева: (00)1 001 010, что соответствует восьмеричным числам 1 1 2, можно получить восьмеричное число 112.
Число с основанием 8, такое как 248, 1098 или 558, является восьмеричным. количество. В восьмеричной системе счисления используются только семь цифр. Больше 7, например 8 или 9, восьмеричные цифры не используются. Единица, деленная на 10, называется восьмеричным числом. Число 19 не представляет собой восьмеричное число.
Шестнадцатеричная система счисления
В шестнадцатеричной системе счисления существует значение основания 16 для метода представления чисел. Единственными возможными значениями являются 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.
 Например, A представляет собой однобитовое представление десятичных значений 10. , 11, 12, 13, 14 и 15, тогда как B представляет собой двухбитное представление десятичных значений 14 и 15. Значение любой цифры может быть представлено только 4 битами. Префиксы 0x и суффиксы h используются в качестве шестнадцатеричной записи. Вес каждой цифры в степени 16,
Например, A представляет собой однобитовое представление десятичных значений 10. , 11, 12, 13, 14 и 15, тогда как B представляет собой двухбитное представление десятичных значений 14 и 15. Значение любой цифры может быть представлено только 4 битами. Префиксы 0x и суффиксы h используются в качестве шестнадцатеричной записи. Вес каждой цифры в степени 16,Шестнадцатеричные числа имеют в 16 раз большее значение, чем предшествующие позиции, поэтому для вычисления значения шестнадцатеричного числа умножьте каждую цифру на значение позиции, в которой она стоит, а затем сложите произведения. Помимо взвешенной системы счисления, у нас также есть позиционная система счисления. Для шестнадцатеричных чисел используется только четыре бита, причем каждая группа битов имеет разные значения от 0000 (для 0) до 1111 (для F = 15 = 8+4+2+1). Ниже приведена таблица в двоичной форме эквивалентов шестнадцатеричных чисел.
Как и восьмеричные числа, шестнадцатеричные числа также являются системой чисел. Используя шестнадцатеричные числа, можно преобразовать большие двоичные числа в более мелкие и компактные группы.
Используя шестнадцатеричные числа, можно преобразовать большие двоичные числа в более мелкие и компактные группы.Получить тематические печатные документы в формате pdfПросмотреть здесь
Системы счисления (двоичная, восьмеричная, десятичная, шестнадцатеричная)
Прежде чем мы сможем объяснить некоторые конкретные системы счисления, нам нужно знать, что такое система счисления. Проще говоря, система счисления — это способ представления чисел.
Мы можем классифицировать системы счисления по типу записи в зависимости от того, используют ли они позиционную запись (также известную как запись разрядного значения), а также проводить дальнейшую категоризацию по системе счисления или основанию.
1. Непозиционная система счисления
Чтобы объяснить непозиционную систему счисления, в качестве примера возьмем римские цифры. В таблице ниже вы можете найти десятичные значения основных символов в римской системе счисления.
Вы можете спросить, есть ли какой-то шаблон для формирования всех остальных символов? Ответ положительный.

- Когда символ с меньшим значением помещается после символа, имеющего равное или большее значение, значения складываются. Примеры приведены в таблице ниже.
- Когда символ с меньшим значением помещается перед символом с большим значением, меньшее значение вычитается из большего. Примеры приведены в таблице ниже.
2. Позиционная система счисления
Позиционная система счисления позволяет расширить исходный набор символов, чтобы их можно было использовать для представления любого произвольно большого (или малого) значения. Число может быть представлено по-разному в разных системах.
Например, два числа $(2A)_{16}$ и $(52)_{8}$ относятся к одному и тому же количеству, $(42)_{10}$.Система счисления, которую мы используем каждый день, называется десятичной системой счисления или системой счисления с основанием десять. Как видно из названия системы счисления, основание определяет всю систему.

Десятичная система счисления имеет основание 10, потому что мы работаем с 10 цифрами (0, 1, 2, 3, 4, 5, 6, 7, 8, 9), и любое другое большее число может быть составлено из этих 10 цифр. Другими словами, мы используем тот же набор символов, но присваиваем символу другое значение в зависимости от его положения в числе.
Положение символа по отношению к другим символам в номере позволяет отдельному символу представлять большее (или меньшее) значение. Это также означает, что каждая цифра умножается на соответствующую степень числа 10 в зависимости от ее положения в числе. 9{0} $
$= 3 \cdot 100+4 \cdot 10+2 \cdot 1$
$=300 + 40 + 2$
В этом уроке мы не будем подробно объяснять десятичную систему, так как она много уроков на странице, посвященной этому.
Помимо десятичной системы счисления существует множество других систем счисления. Мы упомянем только три из них, поскольку они являются наиболее часто используемыми системами счисления после десятичной.
 Это: двоичная система счисления, восьмеричная система счисления и шестнадцатеричная система счисления. Мы дадим краткое объяснение каждому из них и научимся преобразовывать числа из одной системы в другую.
Это: двоичная система счисления, восьмеричная система счисления и шестнадцатеричная система счисления. Мы дадим краткое объяснение каждому из них и научимся преобразовывать числа из одной системы в другую.2.1. Двоичная система счисления
Двоичная система счисления содержит две уникальные цифры (0 и 1). Таким образом, эта система является системой счисления с основанием 2. Относительные величины символов равны 0 < 1. Символы в этой системе часто называют двоичными цифрами или просто битами. Двоичная система счисления является позиционной системой счисления. Позже мы увидим, что, например, $1010_{2}\neq 1100_{2}$.
2.2. Восьмеричная система счисления
Восьмеричная система счисления содержит 8 уникальных цифр (0, 1, 2, 3, 4, 5, 6, 7). Таким образом, эта система является системой счисления с основанием 8. Относительные величины символов равны 0 < 1 < 2 < 3 < 4 < 5 < 6 < 7. Восьмеричная система счисления — еще один пример позиционной системы счисления.

2.3. Шестнадцатеричная система счисления
Шестнадцатеричная система счисления содержит 16 уникальных цифр. Поскольку в десятичной системе всего 10 арабских цифр, нам нужно использовать другие символы для представления оставшихся 6 цифр. Мы используем алфавитные
символов от A до F, чтобы расширить систему до 16 цифр. 16 цифр в шестнадцатеричной системе: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E и F. Относительные величины символов равны
0 < 1 < 2 < 3 < 4 < 5 < 6 < 7 < 8 < 9< A < B < C < D < E < F.
Шестнадцатеричная система счисления также является позиционной системой счисления.3. Преобразование основания
Каждая позиция цифры в числе с основанием b представляет собой степень $b$. Таким образом, когда мы записываем число с основанием b, каждая цифра с основанием b умножается на соответствующую степень $b$ в зависимости от позиции в числе.
3.1. Преобразование в десятичное число
Преобразование числа из любой системы счисления в десятичное число довольно просто.
 Мы знаем, что значение каждой цифры в числе основано на значении отдельной цифры и позиции цифры. Мы узнали это, изучая десятичные числа. Используя это правило, мы можем преобразовать число из любой системы счисления в десятичное число. 9{-2}=3\cdot 8+4\cdot 1+1\cdot \displaystyle{\frac{1}{8}}+5\cdot \displaystyle{\frac{1}{64}}=28,203125$
Мы знаем, что значение каждой цифры в числе основано на значении отдельной цифры и позиции цифры. Мы узнали это, изучая десятичные числа. Используя это правило, мы можем преобразовать число из любой системы счисления в десятичное число. 9{-2}=3\cdot 8+4\cdot 1+1\cdot \displaystyle{\frac{1}{8}}+5\cdot \displaystyle{\frac{1}{64}}=28,203125$3.2. Преобразование десятичного числа в любое другое основание
Мы можем преобразовать десятичное число в любое другое основание, выполнив всего несколько простых шагов:
- Разделите десятичное число, которое необходимо преобразовать, на значение нового основания.
- Запишите остаток в сторону
- Разделите частное от предыдущего деления на новое основание.
- Записать остаток в сторону
- Повторяйте шаги 3 и 4, пока частное не станет равным нулю на шаге 3.
Требуемое число состоит из остатков, записанных снизу вверх и слева направо.
Пример 2. Преобразование 25 в двоичное число.

Следуя правилу преобразования десятичных чисел в любую другую систему счисления, необходимое число равно $11001_{2}$.
Пример 3. Преобразование 2489 в шестнадцатеричное число.
Помните, что эквивалентом числа 11 в шестнадцатеричной системе счисления является буква B.
Следуя правилу преобразования десятичных чисел в любую другую систему счисления, требуемое число равно $9B9_{16}$.
3.3. Эквивалентность между различными системами счисления
4. Сочетания клавиш для переключения между основанием 2 и основанием 8 и между основанием 2 и основанием 16
Мы узнали, что можем преобразовать число из любого основания в число с любым основанием с помощью сначала преобразовать его в десятичное. Например, если мы хотим преобразовать число с основанием 3 в число с основанием 7, первым шагом будет преобразование числа с основанием 3 в десятичное, а затем преобразование этого десятичного числа в число с основанием 7.

Мы можем использовать ту же процедуру для преобразования двоичного числа в восьмеричное или шестнадцатеричное число, но есть несколько полезных сокращений, которые упростят этот процесс. Давайте рассмотрим следующий пример:
Пример 4. Преобразование $100100010101111_{2}$ в шестнадцатеричное число.
Чтобы преобразовать двоичное число в шестнадцатеричное, мы могли бы просто разбить двоичное число на группы из 4 цифр (начиная справа и добавив начальные нули, если цифры заканчиваются), а затем интерпретировать эти группы из 4 цифр как шестнадцатеричные значения. перечислены в таблице выше. При этом имеем:
$ 10010001010111111111111111111111111111 гг. к этому, чтобы преобразовать двоичное число в восьмеричное число, мы могли бы просто разбить двоичное число на группы из 3 цифр, а остальная часть процедуры такая же, как преобразование двоичного числа в шестнадцатеричное число. Преобразуем то же двоичное число в восьмеричное:
$100100010101111_{2}=100 100 010 101 111$
$100=4$
$010=2$
$101=5$
$111=7$
$100100010101111_{2}=44257_{8}$
Обратный процесс еще проще.
 Предположим, мы хотим преобразовать $FC7_{16}$ в двоичную форму. Из таблицы мы можем прочитать двоичные значения для каждой цифры шестнадцатеричного числа:
Предположим, мы хотим преобразовать $FC7_{16}$ в двоичную форму. Из таблицы мы можем прочитать двоичные значения для каждой цифры шестнадцатеричного числа:$F_{16} = 1111_{2}$ $C_{16} = 1100_{2}$ $7_{16} = 0111_{2} $
$FC7_{16}=111111000111_{2}$
Процесс преобразования восьмеричного числа в двоичную форму точно такой же.
Знать шаги преобразования с примерами решения
Восьмеричная система счисления — это один из типов методов представления чисел, в котором их основание равно 8. Восьмеричные числа обозначаются добавлением либо префикса 0, либо суффикса 8. Каждое место в восьмеричной системе в 8 раз значительнее предыдущего, поэтому числовое значение восьмеричного числа вычисляется путем умножения каждой цифры на значение позиции, в которой стоит цифра, с последующим сложением произведений. В результате это также взвешенная (или позиционная) система счисления.
В этой статье мы изучим определение восьмеричной системы счисления, как определить восьмеричную систему счисления, сколько цифр в ней используется, таблицу преобразования, восьмеричное в двоичное, шестнадцатеричное и десятичное преобразование, решенные примеры, использование в линейной алгебре.
 , исчисление, общая математика, физика и т. д., а также преимущества восьмеричной системы счисления и часто задаваемые вопросы.
, исчисление, общая математика, физика и т. д., а также преимущества восьмеричной системы счисления и часто задаваемые вопросы.Восьмеричная система счисления
Восьмеричная система счисления представлена с основанием 8, то есть использует цифры от 0 до 7, т.е. 0, 1, 2, 3, 4, 5, 6 и 7 для представления чисел. Термин восьмеричный используется для описания чисел с восьмизначным основанием. Восьмеричные числа имеют широкий спектр применения и значения, включая использование в компьютерах и цифровых системах счисления. Группируя двоичные цифры в тройки, он часто используется в вычислительных контекстах как более короткое представление двоичных чисел.
Узнайте здесь о различных концепциях биномиальной теоремы.
Восьмеричная система счисления Таблица
Восьмеричные числа представляются с использованием только трех битов. Each group will be assigned a unique number between 000 and 111.
Octal Digital Value Binary Equivalent 0 000 1 001 2 010 3 011 4 100 5 101 6 110 7 111 Base of Octal Number System
Восьмеричная система счисления, или, сокращенно, восьмеричная, использует цифры от 0 до 7, то есть \(10_{восьмеричное}\) представляет восемь, а \(100_{восьмеричное}\) представляет шестьдесят четыре.
 Следовательно, основание восьмеричной системы счисления равно 8. Восьмеричная система счисления — это система счисления с основанием 8, где диапазон чисел составляет 0,1,2,3,4,5,6,7.
Следовательно, основание восьмеричной системы счисления равно 8. Восьмеричная система счисления — это система счисления с основанием 8, где диапазон чисел составляет 0,1,2,3,4,5,6,7.Цифры, используемые в восьмеричной системе счисления
В результате восьмеричные числа состоят только из «8» цифр (0, 1, 2, 3, 4, 5, 6, 7) и, таким образом, представляют собой систему счисления с основанием 8, с q равно «8».
Основные характеристики восьмеричной системы счисления состоят в том, что существует только восемь уникальных счетных цифр от 0 до 7, каждая из которых имеет вес или значение только восемь, начиная с наименее важного бита (LSB). Поскольку он работал в счете до восьми, входы и выходы производились в счете до восьми, побайтно, восьмеричные числа и восьмеричная система счисления были особенно популярны на заре компьютеров для подсчета входов и выходов.
Восьмеричная таблица умножения
Простое правило для умножения двух цифр в любой системе счисления в восьмеричных числах состоит в том, чтобы умножить их в десятичной системе счисления.
 Считаем результат, если произведение меньше основания. Если произведение превышает основание, мы делим его на основание и используем оставшуюся часть для определения младшей значащей цифры. В следующей значащей цифре передается частное. Описанное в таблице правило используется для умножения двух восьмеричных чисел.
Считаем результат, если произведение меньше основания. Если произведение превышает основание, мы делим его на основание и используем оставшуюся часть для определения младшей значащей цифры. В следующей значащей цифре передается частное. Описанное в таблице правило используется для умножения двух восьмеричных чисел.X 0 1 2 3 4 5 6 7 0 0 0 0 0 0 0 0 0 1 0 1 9 20 1 2 3 4 5 6 7 2 0 2 4 6 10 12 14 16 3 0 3 6 11 14 17 22 25 4 0 4 10 14 20 24 30 34 5 0 5 12 17 24 31 36 43 6 0 6 14 22 30 36 44 52 7 0 7 16 25 34 43 52 61 Преобразование восьмеричной системы счисления
На экзаменах часто требуется преобразовать одну форму системы счисления в другую форму.
 Давайте посмотрим, как мы можем преобразовать восьмеричную систему счисления в двоичную, шестнадцатеричную и десятичную.
Давайте посмотрим, как мы можем преобразовать восьмеричную систему счисления в двоичную, шестнадцатеричную и десятичную.Преобразование восьмеричного числа в шестнадцатеричное
При преобразовании восьмеричного числа в шестнадцатеричное обычно выполняется преобразование восьмеричного числа в шестнадцатеричное путем преобразования восьмеричного целого числа в двоичное число, а затем из двоичного в шестнадцатеричное.
Также прочтите эту статью о наборах после прочтения этой статьи.
Преобразование восьмеричного числа в десятичное
Чтобы преобразовать число из восьмеричного в десятичное, выполните следующие действия:
Сначала расположим восьмеричное число со степенью 8, поскольку восьмеричное число может состоять только из цифр от 0 до 7. Мы записываем значение каждого восьмеричного числа после оценки всех степеней 8 значений, например, 80 равно 1, 81 равно 8 и т. д. Мы умножаем каждое число, когда получаем значение. Десятичное число получается сложением произведения всех чисел.

Преобразование восьмеричного числа в двоичное
Для преобразования восьмеричного числа в двоичное требуется два шага. Мы должны сначала преобразовать заданное восьмеричное число в его десятичный аналог, а затем преобразовать десятичное число в двоичное. Мы уже научились переводить восьмеричное число в десятичное. Давайте посмотрим, как преобразовать десятичное число в двоичное.
Остатки следует читать снизу вверх, чтобы получить двоичный эквивалент.
\(43_{8} = 100011_{2}\)
Использование восьмеричной системы счисления
В компьютерных приложениях и цифровых системах счисления обычно используется восьмеричная система счисления. Восьмеричная система счисления в компьютере использует 16-битные, 32-битные или 64-битные слова, каждое из которых разделено на восемь битов. В авиационной промышленности восьмеричное число также используется в качестве кода. Поскольку каждая шестнадцатеричная цифра представляет 4 двоичных цифры (16 = 24), а каждая восьмеричная цифра представляет 3 (8 = 23), восьмеричная и шестнадцатеричная цифры используют преимущество человека, заключающееся в возможности работать с большим количеством символов, при этом легко конвертируясь.
 к бинарному.
к бинарному.Решенные примеры восьмеричной системы счисления
Давайте посмотрим на некоторые примеры восьмеричной системы счисления, которые используются на экзаменах.
Решающий пример : 777) 8 x 33) 8
Решение:
777) 8 x 33) 8
2 2 ← Перенос
7 7 70003
x 3 3
1 10003
7 7 70003
x 3 3
1 10003 ← перенос
2 7 7 5
2 7 7 5 X
3 2 7 4 5
— Десятичный0194 Octal equivalent Sum/remainder Carry/quotient 7×3 21 21÷8=25 5 2 7× 3 21+2 23 ÷ 8 = 27 7 2 7 × 3 21+2 23 ÷ 8 = 27 7 2 759 2 71110 5 12 12÷8=14 4 1 7+7+1 15 15 ÷ 8 = 17 7 1 2+7+1 10 10 ÷ 12 .
2 1 Ответ: 32745) 8
Решенный пример : Добавьте два восьмирождения: 23) 8 + 7651) 8
Раствор:
23) 8 +) 7651)8
1 2 3
+ 7 6 5 1
7 7 7 4 90\)
= 128 + 56 + 3
= 18710
Пример Преобразование 536 из восьмеричного в шестнадцатеричный.
Когда мы преобразуем 536 (восьмеричное) в двоичное, мы получаем (536)8 = (101) (011) (110) = (101011110)
Чтобы получить его шестнадцатеричный эквивалент, создайте группу из четырех двоичных битов (101011110) = (0001) (0101) (1110) = (0001) (0101) (1110) = (0001) (0101) (1110) (15E)
В результате шестнадцатеричное значение 536 равно 15E.
Надеюсь, эта статья о восьмеричной системе счисления была информативной. Попрактикуйтесь в том же в нашем бесплатном приложении Testbook. Скачать сейчас!
Часто задаваемые вопросы о восьмеричной системе счисления
В.
 1 Сколько цифр используется в восьмеричной системе счисления?
1 Сколько цифр используется в восьмеричной системе счисления? Ответ 1 В результате восьмеричные числа состоят только из «8» цифр (0, 1, 2, 3, 4, 5, 6, 7) и, таким образом, представляют собой систему счисления с основанием 8, с q равно «8».
Q.2 Как вы кратко объясните восьмеричную систему счисления?
Ответ 2 Восьмеричная система счисления представлена с основанием 8, то есть использует цифры от 0 до 7, т.е. 0, 1, 2, 3, 4, 5, 6 и 7 до представлять числа. Термин восьмеричный используется для описания чисел с восьмизначным основанием.
Q.3 Какие существуют 4 типа систем счисления?
Ответ 3 Четыре распространенных типа систем счисления:
Десятичная система счисления: имеет основание 10.
Двоичная система счисления: имеет основание 2. Система счисления: имеет основание 16.Q.4 Что такое двоичные числа?
Ответ 4 Двоичная система счисления или система с основанием 2 состоит только из двух цифр 0 и 1.