Восьмеричная система счисления это: Восьмеричная система счисления | это… Что такое Восьмеричная система счисления?

Военно-техническая подготовка

4.1. Системы счисления

Система счисления (СС) — это система записи чисел с помощью определенного набора цифр.

4.1.1. Двоичная система счисления

Двоичная система счисления — это система, в которой для записи чисел используются две цифры: 0 и 1. Основанием двоичной системы счисления является число 2.

Двоичный код числа — запись этого числа в двоичной системе счисления. Пример:

• 0=0;
• 1=1;
• 2=10;
• 3=11;
• 7=111;
• 120=1111000;.

4.

1.2. Восьмеричная система счисления

Восьмеричная система счисления — это система, в которой для записи чисел используются цифры от 0 до 7.

4.1.3. Десятичная система счисления

Десятичная система счисления — это система, в которой для записи чисел используются цифры от 0 до 9. Это привычная нам система счисления, используемая для записи чисел в повседневной жизни.

4.1.4. Шестнадцатеричная система счисления

Шестнадцатеричная система счисления — это система, в которой для записи чисел используются цифры от 0 до 9 и латинские буквы A, B, C, D, E, F.

Двоичные числа	Восьмеричные числа	Десятичные числа	Шестнадцатеричные числа
0	0	0	0
1	1	1	1
10	2	2	2
11	3	3	3
100	4	4	4
101	5	5	5
110	6	6	6
111	7	7	7
1000	10	8	8
1001	11	9	9
1010	12	10	A
1011	13	11	B
1100	14	12	C
1101	15	13	D
1110	16	14	E
1111	17	15	F

Таблица представления чисел от 0 до 15 в различных системах счисления.

4.1.5. Элементы булевой алгебры

Булева алгебра — раздел математики, изучающий логические выражения и операции. Логические выражения представляют собой высказывания — некоторые утверждения, которым всегда можно сопоставить одно из двух логических значений:

ложь или истина (их можно обозначать как 0 и 1 , false и true).
Основными логическими операциями являются операции отрицания , логического И (конъюнкция) и логического ИЛИ (конъюнкция) . Именно с помощью них наиболее удобно оперировать с логическими выражениями. Производные логические операции могут быть выражены через них.
Отрицание — операция, применяемая к одному операнду, т.е. унарная операция. Выражение не A записывается как ­­­­­­­­­­­­­ ¬­A , A ̅ или ! A . Операции отрицания задается следующей таблицей истинности:

A	¬ A
0	1
1	0

Логическое И (конъюнкция) — операция, применяемая к двум операндам, т. е. бинарная операция. Выражение A и B записывается как A˄B , A ⋅ B или A&&B . Конъюнкция задается следующей таблицей истинности:

A	B	A ˄B
0	0	0
0	1	0
1	0	0
1	1	1

Логическое ИЛИ (дизъюнкция) — еще одна бинарная операция.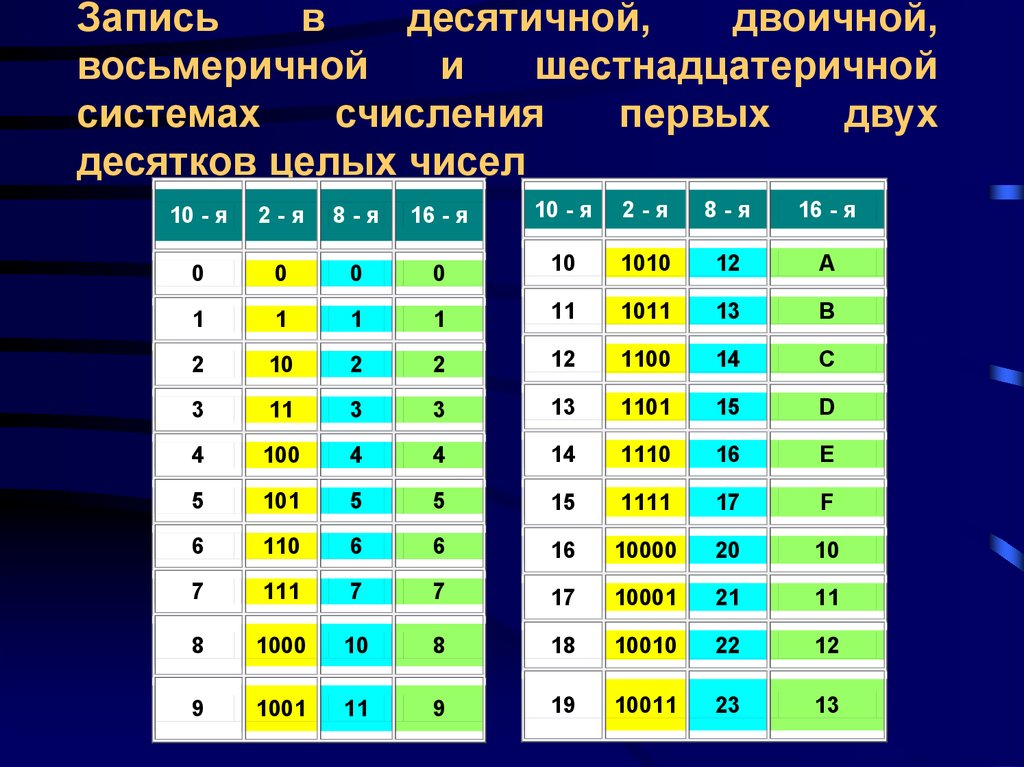 Выражение A или B записывается как A˅B , A+B или A||B . Дизъюнкция задается следующей таблицей истинности:

A	B	A˅B
0	0	0
0	1	1
1	0	1
1	1	1

Остальные операции булевой алгебры могут быть записаны с использованием лишь этих трех операций. Приоритеты основных логических операций соответствуют приоритетам аналогичных операций в элементарной алгебре.

1. Отрицание.
2. Конъюнкция.
3. Дизъюнкция.

Восьмеричная система счисления. Шестнадцатеричная система счисления. Правило перевода целых десятичных чисел в систему счисления с основанием

Для начала вспомним, что такое позиционная система счисления.

Позиционная система счисления – это система счисления, в которой количественный эквивалент цифры зависит от её положения (позиции) в записи числа.

На этом уроке мы с вами познакомимся с восьмеричной и шестнадцатеричной системами счисления, узнаем правила перевода из восьмеричной и шестнадцатеричной систем счисления в десятичную и наоборот. Также изучим правило перевода целых десятичных чисел в систему счисления с основание q.

Начнём с восьмеричной системы счисления.

Восьмеричная система счисления – это позиционная система счисления с основанием 8. В алфавит восьмеричной системы счисления входят цифры от 0 до 7 включительно.

Мы с вами уже узнали, как записывается развёрнутая форма записи числа. Она выглядит следующим образом:

Из этой формулы можно вывести развёрнутую форму записи целого восьмеричного числа:

Посмотрим, как это выглядит на примере. Нам дано следующее число: 4153₈. Давайте распишем его по формуле. Ставим равно. Для начала проставим над цифрами степени для восьмёрки справа налево, начиная с нуля.

После равно пишем первую цифру 4 и умножаем её на 8³. Ставим плюс. Далее запишем вторую цифру 1, умноженную на 8². Снова ставим плюс. Записываем цифру 5 и умножаем её на 8¹. И плюс последняя цифра 3, умноженная на 8⁰.

Мы с вами расписали исходное число в развёрнутой форме целого восьмеричного числа.

Правило для перевода из восьмеричной системы счисления в десятичную очень простое. Достаточно расписать число в развёрнутой форме записи, а затем вычислить значение получившегося выражения.

Давайте переведём наше число из восьмеричной системы счисления в десятичную. Оно уже у нас расписано в развёрнутой записи. Нам осталось сосчитать. Обратимся к математике и распишем степени числа восемь.

Теперь осталось всё посчитать. Ставим равно.

Мы получили число 2 155. Это число представлено в десятичной системе счисления.

А теперь давайте переведём число 125 из десятичной системы счисления в восьмеричную.

Это правило похоже на перевод из десятичной в двоичную систему счисления, но в данном случае мы будем делить на число 8.

Само правило звучит следующим образом: для перевода целого десятичного числа в восьмеричную систему счисления следует последовательно выполнять деление данного числа и получаемых целых частных на 8 до тех пор, пока не получим частное, равное 0.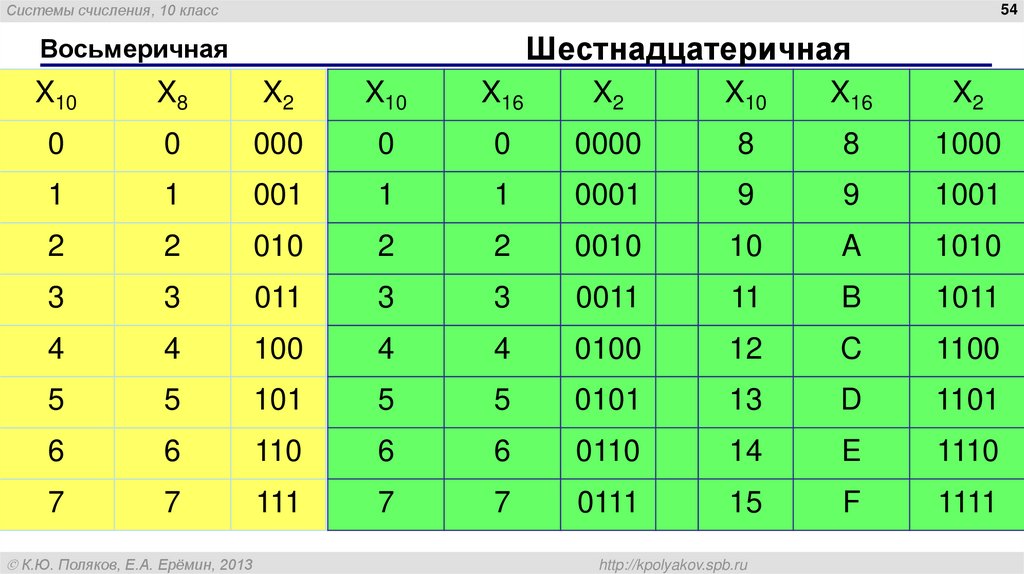 В результате нужно записать в одну строку, справа налево все остатки, начиная с последнего.

Переведём наше число. Делим его на 8. Получим 15, а в остатке 5. Обведём остаток в кружок.

Теперь число 15 делим на 8. Получим 1. В остатке 7. Снова обведём это число.

1 больше 0. Значит делим число 1 на 8. Получим 0. А в остатке 1. Обводим наш остаток.

Теперь осталось после равно записать все остатки справа налево.

125₁₀ = 175₈

Мы перевели число 125 в восьмеричную систему счисления.

А теперь давайте узнаем, что такое шестнадцатеричная система счисления.

Шестнадцатеричная система счисления – это позиционная система счисления с основанием 16. В алфавит этой системы входят цифры от 0 до 9 и буквы А, B, C, D, Е, F. Эти буквы обозначают в десятичной системе числа от 10 до 15 соответственно.

Для представление целого шестнадцатеричного числа в развёрнутой форме записи нужно использовать следующую формулу:

Распишем предоставленное шестнадцатеричное число A6E в развёрнутой форме.

Ставим знак равно. Снова проставим степени для шестнадцати над цифрами нашего числа справа налево.

Пишем букву А и умножаем её на 16². Ставим плюс. Пишем цифру 6, умноженную на 16¹ и прибавляем букву Е, умноженную на 16⁰.

Для перевода целого шестнадцатеричного числа в десятичную систему счисления нужно перейти к его развёрнутой записи, заменить буквы на соответствующие им цифры в десятичной системе счисления и вычислить значение получившегося выражения.

Наше число уже записано в развёрнутой форме. Нам осталось заменить буквы на соответствующие им десятичной системе числа и сосчитать. Ставим равно. Буква А соответствует числу 10 в десятичной системе счисления. Запишем число 10 и умножаем его на 16².

Ставим плюс и перепишем число 6, умноженное на 16¹.

Снова ставим плюс. Букве Е соответствует число 14 в десятичной системе счисления.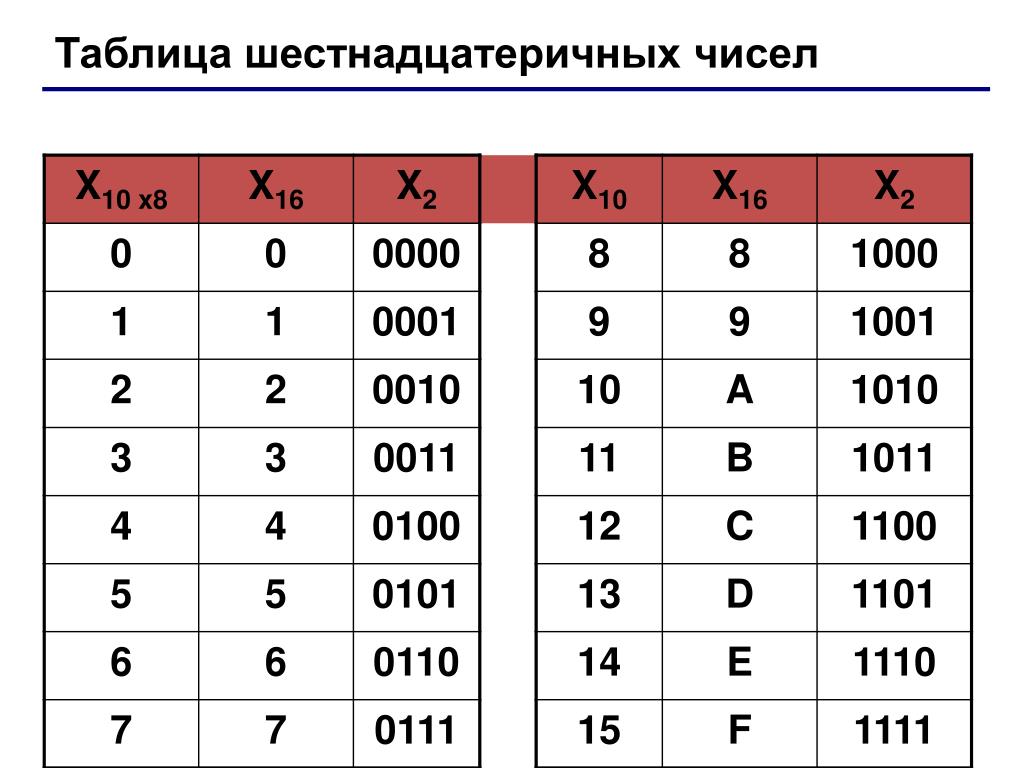 Пишем число 14, умноженное на 16⁰. Ставим равно.

Прежде, чем всё это сосчитать снова обратимся к математике и распишем степени числа шестнадцать.

16² = 256.

16² ·10 = 2 560

Ставим плюс.

16¹ = 16.

16¹ · 6 = 96.

Снова ставим плюс.

16⁰ = 1.

16⁰ · 14 = 14.

Ставим равно.

Мы получили 2 670 в десятичной системе счисления.

Для перевода целого десятичного числа в шестнадцатеричную систему счисления следует последовательно выполнять деление данного числа и получаемых целых частных на 16 до тех пор, пока не получим частное, равное 0. В результате нужно записать в одну строку, справа налево все остатки, начиная с последнего, при необходимости, заменяя цифры на соответствующие им буквы в шестнадцатеричной системе счисления.

Переведём число 350 в шестнадцатеричную систему счисления.

Делим наше число на 16, получим 21, остаток 14. Выделим его.

Делим 21 на 16. Получим 1 и 5 в остатке. Обводим наш остаток.

1 больше 0. Делим 1 на 16, получим 0 и 1 в остатке. И снова выделяем остаток 1.

Теперь запишем все числа справа налево. Записываем следующие цифры: 1, 5.

350₁₀ = 15.

Так как в шестнадцатеричной системе счисления числу 14 соответствует буква Е, то пишем её после 5.

350₁₀ = 15E₁₆.

Мы с вами перевели число 350 в шестнадцатеричную систему счисления.

Вы, наверное, заметили, что все правила перевода целого десятичного числа в любую систему счислению с другим основанием похожи.

Давайте изучим общее правило перевода целых десятичных чисел в любую систему счисления с основание q.

Для того, чтобы перевести целое десятичное число в систему счисления с основанием q нужно:

1. Последовательно выполнять деление данного числа и получаемых целых частных на основание новой системы счисления до тех пор, пока не получим частное, равное нулю.

2. Полученные остатки, которые являются цифрами числа в новой системе счисления, привести в соответствии с алфавитом новой системы счисления.

3. Составить число в новой системе счисления, записывая его, начиная с последнего полученного остатка.

Вам предоставлена таблица соответствия десятичных, двоичных, восьмеричных и шестнадцатеричных чисел от 0 до 20. Числа от 0 до 20 подразумевают собой десятичную систему счисления.

А теперь давайте выполним задание.

Переведём одно и то же число 247 в двоичную, восьмеричную и шестнадцатеричную системы счисления и сравним получившиеся числа.

Для начала переведём из десятичной в двоичную систему счисления. Для этого будем использовать таблицу, так как число большое. В ней будет две строки. В первую строку первого столбца запишем наше число.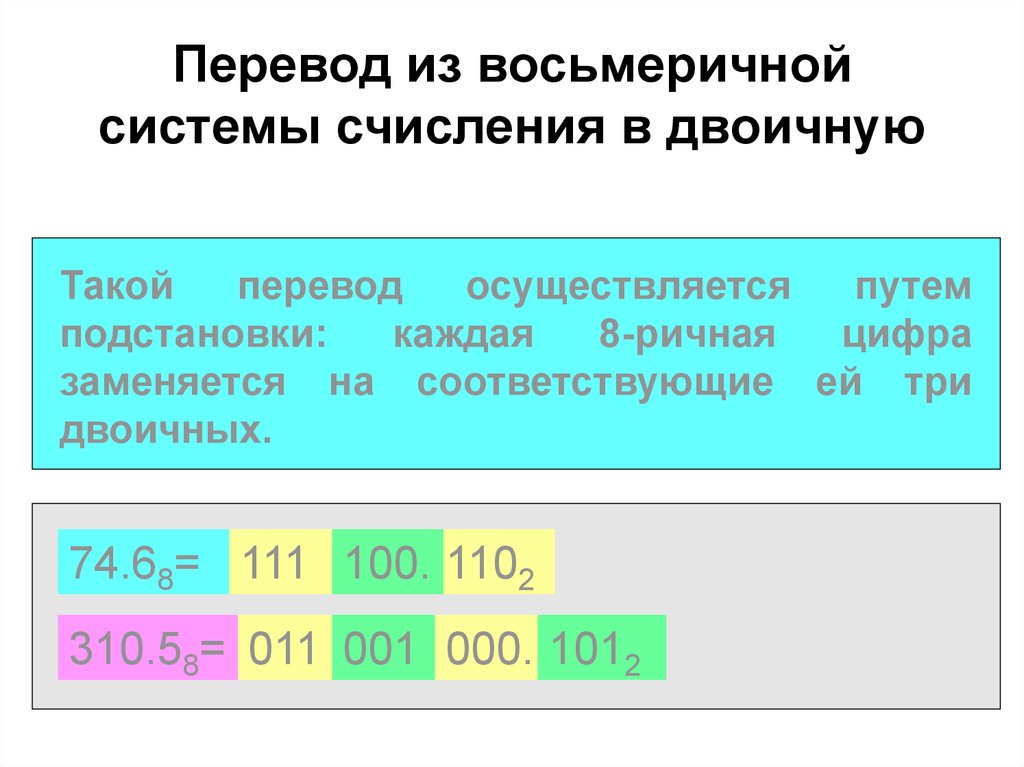

Делим его на 2. Получим 123 и 1 в остатке. 123 запишем во вторую ячейку первой строки, а 1 – в первую ячейку второй строки.

Далее 123 разделить на 2 и получим 61 и 1 в остатке. 61 запишем после числа 123, а остаток один под число 123.

Далее 61 : 2 = 30 и остаток – 1. Запишем их в таблицу.

30 : 2 = 15, а остаток равен 0. Снова запишем их в таблицу в соответствующие ячейки.

При делении 15 на 2 получим 7 и 1 в остатке. Снова заполняем таблицу.

Далее 7 : 2 = 3 и 1 в остатке. Запишем в соответствующие ячейки наши числа.

3 :2 = 1 и 1 в остатке. Занесём данные в таблицу.

И делим 1 на 2, получим 0 и 1 в остатке. 0 писать не будет. Занесём только наш остаток в ячейку.

А теперь соберём все наши цифры в число в двоичной системе. Записываем их поочерёдно справа налево.

247₁₀ = 11110111₂.

А сейчас переходим к переводу в восьмеричную систему счисления числа 247.

Делим 247 на 8. Получим 30 и 7 в остатке. Обведём остаток от деления.

Далее 30 делим на 8, получим 3 и 6 в остатке. Выделяем остаток.

3 делим на 8, получаем 0 и 3 в остатке. Обводим остаток.

Теперь запишем все остатки справа налево и получим число в восьмеричной системе счисления.

247₁₀ = 367₈.

Нам осталось перевести наше число в шестнадцатеричную систему счисления. Делим 247 на 16. Получим 15 и 7 в остатке. Обведём остаток.

Теперь делим 15 на 16, получим 0. А остаток от деления равен 15. Выделим его.

А сейчас запишем наши цифры справа налево в соответствии с алфавитом шестнадцатеричной системы счисления. Число 15 — это буква F в этой системе счисления. Ставим её на первое место. А затем пишем число 7.

247₁₀ = F7₁₆

Задание выполнено. Давайте сравним все наши получившиеся числа.

Как можем видеть – все они одинаковые, но записаны разными цифрами, потому что они представлены в различных системах счисления.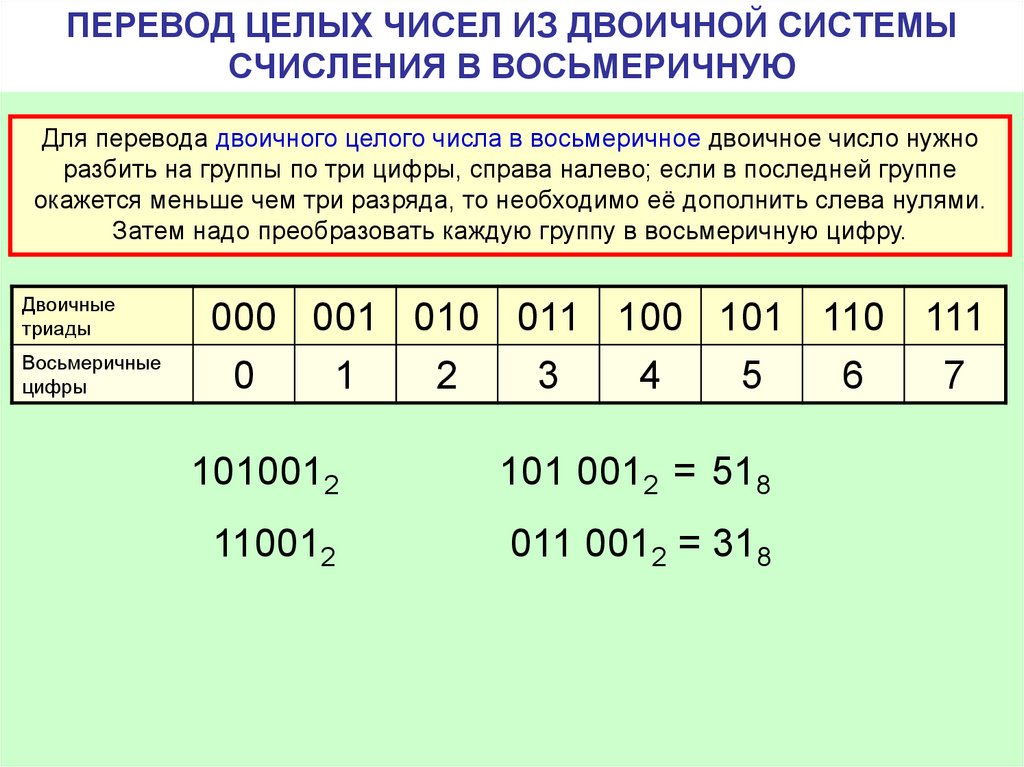 Это можно увидеть, если обратить внимание на основания чисел.

А теперь пришла пора довести итоги урока. Сегодня мы узнали, что такое восьмеричная и шестнадцатеричная системы счисления, какие действия нужно выполнить для перевода целого десятичного числа в систему счисления с основанием q.

Также мы сегодня научились переводить числа из восьмеричной и шестнадцатеричной систем счисления в десятичную и наоборот.

Восьмеричная система счисления

Восьмеричная система счисления — это система счисления с основанием 8. В ней используются цифры от 0 до 7. Эта система похожа на двоичную (основание 2) и шестнадцатеричную (основание 16). Восьмеричные числа записываются с использованием буквы o перед цифрой, например, o04 или o1242. Восьмеричные числа также иногда записываются с маленькой буквой 8 в правом нижнем углу, как, например, 1242₈.

В свое время восьмеричная система использовалась в основном для работы с компьютерами. Она обеспечивала более простой способ работы с двоичными числами. Когда компьютеры перешли от использования 24-битных систем к 32- и 64-битным, шестнадцатеричная система заменила восьмеричную в большинстве случаев. Некоторые группы, например, коренные американцы, использующие язык юки в Калифорнии и языки памеан в Мексике, также используют восьмеричную систему счисления. Они делают это потому, что при счете они используют промежутки между пальцами, а не считают сами пальцы.

Восьмеричные и шестнадцатеричные

Восьмеричная система схожа с шестнадцатеричной, поскольку обе они легко преобразуются в двоичную. Если восьмеричное число равно трехзначному двоичному, то шестнадцатеричное равно четырехзначному двоичному. Если восьмеричные цифры начинаются с буквы «о», то шестнадцатеричные цифры заканчиваются буквой «h». Самый простой способ перевода из одной системы в другую — перевести в двоичную, а затем в другую.

Octal	Бинарные									Шестнадцатеричная
	трёхзначный					четырёхзначное число
o4					100				0100	04h
o15				001	101				1101	0Dh
o306			011	000	110			1100	0110	C6h
o54253	101	100	010	101	011	0101	1000	1010	1011	58ABh

Похожие страницы

• Двоичная система счисления
• Шестнадцатеричная система счисления
• Десятичная система счисления

Восьмеричные и десятичные

В десятичной системе (основание 10) каждая цифра в восьмеричной системе равна этой цифре, умноженной на экспоненту 8, которая равна ее расположению минус единица.

	Местонахождение
	6	5	4	3	2	1
Значение	32768 (85)	4096 (84)	512 (83)	64 (82)	8(81)	1 (80)

Пример: o3425 в десятичную систему

Octal Десятичный o3425 = ( 5 × 1 ) + ( 2 × 8) + ( 4 × 64 ) + ( 3 × 512) = 5 + 16 + 256 + 1536 o3425 = 1813

Восьмеричные и двоичные

В восьмеричной системе счисления используется «трехразрядное» двоичное кодирование. Каждая цифра в восьмеричной системе счисления равна трем цифрам в двоичной системе счисления. Группировка двоичных цифр осуществляется справа налево. Первые три двоичные цифры справа группируются в последнюю часть восьмеричного числа, затем следующие три цифры образуют предпоследнюю часть числа.

Octal Бинарные 1 001 2 010 3 011 4 100 5 101 6 110 7 111 10 001 000

Octal Бинарные 11 001 001 12 001 010 36 011 110 45 100 101 53 101 011 64 110 100 100 001 000 000 357 011 101 111

Бинарные Группировки Octal 11 011 3 010111 010 111 27 101000110 101 000 110 506 01011010101 001 011 010 101 1325

Автор

Alegsaonline. com — Восьмеричная система счисления — Leandro Alegsa — 18/01/2022 — url: https://ru.alegsaonline.com/art/71885

Библиографические ссылки

— linguistics.berkeley.edu — «The typology of Pame number systems and the limits of Mesoamerica as a linguistic area»

Что такое восьмеричная система счисления? Определение, примеры преобразования, преимущества и недостатки восьмеричной системы счисления

Определение : Восьмеричная система счисления представляет собой цифровую систему счисления с основанием 8. Эта система счисления имеет 8 чисел, начиная с 0 до 7 в своем диапазоне. Числа 0, 1, 2, 3, 4, 5, 6, 7 имеют то же значение, что и в случае десятичной системы счисления.

Октябрь означает 8, и это система счисления с основанием или основанием 8. Отсюда она так и называется.

Положение цифр в восьмеричной системе счисления задается как:

Теперь нам приходит в голову вопрос, что цифровые схемы понимают только двоичные значения. Тогда

зачем нужно восьмеричное представление?

Ответ на этот вопрос заключается в том, что иногда становится трудно управлять длинными строками двоичных данных или результатов. Это приводит к ошибочным результатам.

Поэтому иногда двоичные данные представляются в восьмеричном формате, чтобы избежать громоздкости информации.

Однако здесь следует отметить, что цифровые схемы обрабатывают только двоичные данные, т. е. в форме 0 и 1. Таким образом, при использовании требуемой информации в цифровых системах необходимо восьмеричное преобразование в двоичное.

Длина восьмеричной системы счисления составляет в основном одну треть длины двоичной системы счисления.

Рассмотрим пример восьмеричного представления числа

(745) ₈ 

Здесь основание 8 ясно показывает, что это восьмеричное представление. Всегда необходимо представлять определенное число с его определенной основой. В случае, если в восьмеричном представлении основание 8 не указано, то по умолчанию число считается системой десятичным.

Поэтому всегда важно представлять число в любой системе счисления с желаемой основой.

Подсчет восьмеричного числа

В предыдущей статье о двоичной системе счисления мы обсудили основную концепцию системы счисления. И мы знаем, что восьмеричная система счисления состоит из 8 цифр, от 0 до 7.

В приведенной ниже таблице представлены восьмеричные числа. Наряду с этим двоичное представление каждого восьмеричного числа также представлено ниже:

Теперь давайте рассмотрим несколько примеров и разберемся с преобразованием чисел.

Преобразование восьмеричного числа в двоичную форму

При преобразовании восьмеричного числа в двоичное каждый восьмеричный бит преобразуется в эквивалентную ему двоичную форму. В качестве основания восьмеричного числа, то есть 8, является результатом 2, возведенного в степень 3. Мы уже обсуждали двоичный эквивалент восьмеричных цифр от 0 до 7.

Давайте рассмотрим пример, чтобы лучше понять восьмеричное преобразование в десятичное.

(427) ₈

Предположим, это восьмеричное число, которое нужно преобразовать в двоичный эквивалент.

Рассмотрев приведенную выше таблицу, мы можем преобразовать каждый восьмеричный бит в эквивалентный ему двоичный формат.

Возьмем другой пример восьмеричного числа в дробной форме:

(541,63) ₈

Рассмотрим приведенное выше восьмеричное число, которое нужно преобразовать в его эквивалентное дробное двоичное значение.

Преобразование двоичного числа в восьмеричную форму

При выполнении преобразования из двоичного в восьмеричное выполняется процесс, обратный описанному выше.

Всякий раз, когда задано двоичное число, и мы должны выполнить его восьмеричное преобразование, общее количество битов двоичного эквивалента делится на группу из 3, начиная с младшего бита до старшего бита.

Как мы уже упоминали, восьмеричная система счисления есть не что иное, как третья степень двоичной системы счисления. Поэтому делится на группы по 3.

Итак, когда группы разделены, каждому двоичному значению группы присваивается восьмеричное эквивалентное значение.

Иногда, чтобы получить полную группу из 3 битов, при необходимости к двоичным значениям добавляются нули.

Давайте рассмотрим пример, чтобы понять преобразование двоичного значения в восьмеричное значение.

Предположим, что двоичное значение, которое должно быть преобразовано в восьмеричное эквивалентное, равно

(11010110) ₂

Затем, начиная с LSB, биты должны быть сгруппированы по 3 бита каждый

11 010 110

Как мы видим, третья группа в двоичном значении неполная, из-за отсутствия третьего бита. Таким образом, в данном случае мы ставим дополнительный ноль, чтобы завершить третью группу.

Рассмотрим пример дробного двоичного значения, которое необходимо преобразовать в восьмеричный эквивалент.

(100111001.101010) ₂

Итак, снова выполняется группировка битов

Преобразование восьмеричного числа в десятичное

Во время преобразования восьмеричного числа в десятичный эквивалент каждая цифра восьмеричного числа умножается на его позиционное значение. Мы уже видели диаграмму позиционной стоимости во введении.

Итак, теперь давайте возьмем пример для преобразования восьмеричного числа в десятичный эквивалент.

(541.21) ₈

Преобразование десятичного числа в восьмеричное

Всякий раз, когда требуется преобразовать десятичное число в эквивалентное ему двоичное значение, выполняется повторное деление этого числа для получения желаемого восьмеричного эквивалента. Но в отличие от двоичного, здесь деление выполняется на 8, несмотря на использование 2.

Метод также известен как метод двойного мазка.

Давайте возьмем пример и поймем, как достигается преобразование десятичного числа в восьмеричное.

(478) ₁₀

Во время записи эквивалентного восьмеричного термина мы записываем полученные биты переноса в восходящем направлении.

Иногда встречаются дробные десятичные значения. Итак, возникает вопрос, как мы можем преобразовать дробные десятичные значения в дробные восьмеричные значения.

Рассмотрим пример, приведенный ниже

(0,54) ₁₀

При записи дробно-восьмеричного эквивалента результат должен быть записан в нисходящем направлении. Здесь мы выполнили умножение до 8 цифр. Следовательно, мы получаем приблизительное значение, а не точное значение.

Преимущества

• Небольшой размер строки в восьмеричном представлении.
• Из-за малой длины строки вероятность ошибки в результате меньше.
• Биты можно легко преобразовать в соответствии с необходимостью.

Недостатки

Каждый раз требуется дополнительный блок преобразования, так как цифровые схемы работают только с двоичными значениями. Таким образом, данные в восьмеричной форме должны быть преобразованы в двоичный формат.

Восьмеричные факты для детей

Детская энциклопедия Факты

Восьмеричная система счисления — это система счисления с основанием 8. В нем используются цифры от 0 до 7. Система аналогична двоичной (основание 2) и шестнадцатеричной (основание 16). Восьмеричные числительные записываются с использованием буквы или перед числительным, например, о04 или о1242. Восьмеричные числа также иногда пишутся с маленькой восьмеркой справа внизу, например, 1242 ₈ .

В свое время восьмеричная система использовалась в основном для работы с компьютерами. Это обеспечило более простой способ работы с двоичными числами. Поскольку компьютеры перешли от использования 24-битных систем к 32- и 64-битным системам, шестнадцатеричная система заменила восьмеричную для большинства применений. Некоторые группы, например, коренные американцы, использующие язык юки в Калифорнии и памейские языки в Мексике, также используют восьмеричную систему счисления. Они делают это потому, что при счете используют промежутки между пальцами, а не сами пальцы.

Содержание

• Восьмеричный и двоичный код
• Восьмеричный и десятичный
• Восьмеричный и шестнадцатеричный
• Связанные страницы

Восьмеричная и двоичная

Восьмеричная система счисления использует «трехбитное» двоичное кодирование. Каждая цифра восьмеричного числа соответствует трем цифрам двоичного числа. Группировка двоичных цифр выполняется справа налево. Первые три двоичных разряда справа группируются в последнюю часть восьмеричного числительного, затем следующие три разряда образуют предпоследнюю часть числительного.

Восьмеричный Двоичный 1 001 2 010 3 011 4 100 5 101 6 110 7 111 10 001 000

Восьмеричный Двоичный 11 001 001 12 001 010 36 011 110 45 100 101 53 101 011 64 110 100 100 001 000 000 357 011 101 111

Двоичный Группировки Восьмеричный 11 011 3 010111 010 111 27 101000110 101 000 110 506 01011010101 001 011 010 101 1325

Восьмеричная и десятичная

В десятичной системе (с основанием 10) каждая восьмеричная цифра равна той цифре, умноженной на показатель степени 8, который равен ее положению минус один.

	Местоположение
	6	5	4	3	2	1
Значение	32768 (8 5 )	4096 (8 4 )	512 (8 3 )	64 (8 2 )	8(8 1 )	1 (8 0 )

Пример: o3425 до десятичного числа

Восьмеричный Десятичный о3425 = ( 5 × 1 ) + (2 × 8) + ( 4 × 64 ) + (3 × 512) = 5 + 16 + 256 + 1536 о3425 = 1813

Восьмеричный и шестнадцатеричный

Восьмеричный похож на шестнадцатеричный, поскольку оба они легко преобразуются в двоичные.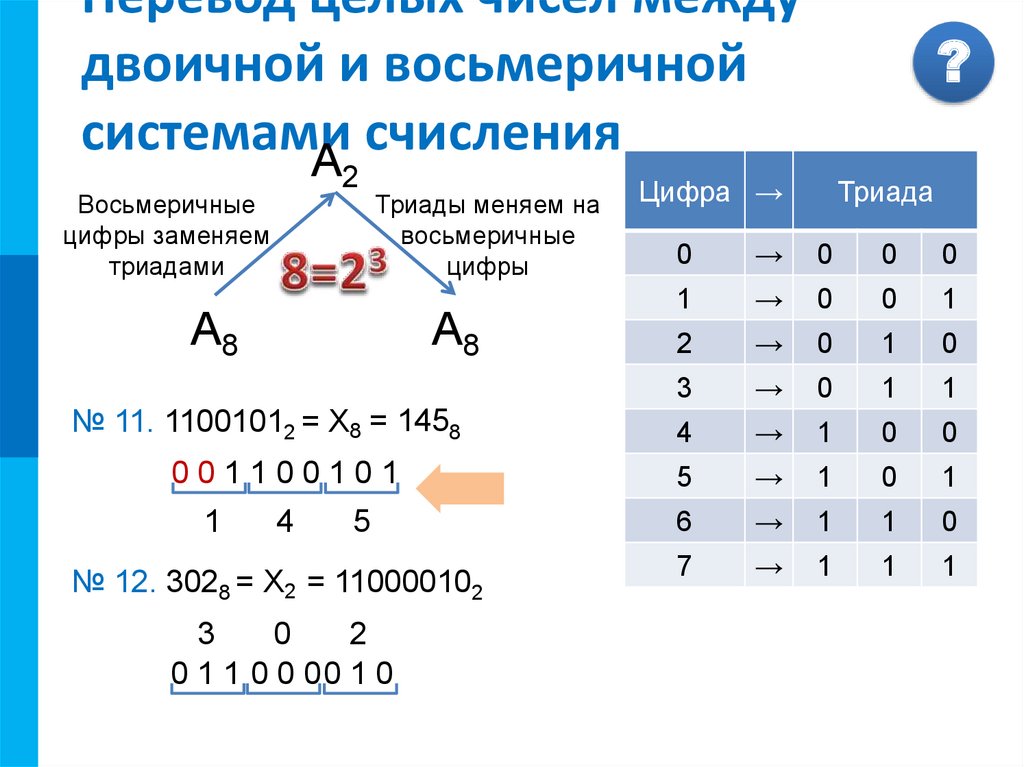 Где восьмеричное равно трехзначному двоичному, шестнадцатеричное равно четырехзначному двоичному. Если восьмеричные числа начинаются с буквы «о», шестнадцатеричные числа заканчиваются буквой «h». Самый простой способ преобразовать одну систему в другую — преобразовать ее в двоичную, а затем в другую систему.

Восьмеричный	Двоичный									Шестнадцатеричный
	трехзначный					четыре цифры
о4					100				0100	04ч
о15				001	101				1101	0Дх
о306			011	000	110			1100	0110	C6h
о54253	101	100	010	101	011	0101	1000	1010	1011	58ABh

Связанные страницы

• Двоичная система счисления
• Шестнадцатеричная система счисления
• Десятичная система счисления

Все содержимое статей энциклопедии Kiddle (включая изображения статей и факты) можно свободно использовать по лицензии Attribution-ShareAlike, если не указано иное. Процитируйте эту статью:

Восьмеричные факты для детей. Энциклопедия Киддла.

Восьмеричная система счисления и ее преобразование в двоичную систему счисления

Система счисления, состоящая из «8» цифр, может быть известна как восьмеричная система счисления. Эта система почти такая же, как и шестнадцатеричная система. При этом каждое число кодируется тремя сгруппированными битами. В аналогичной другой системе кодирование основано на позициях. Распределение позиций начинается с LSB. Вес каждой позиции равен степени числа 8. В этой системе присутствуют числа 0, 1, 2, 3, 4, 5, 6, 7.

На ранних стадиях вычислений на «мини-компьютерах» предпочтительнее использовать эту систему нумерации. Преимущество этой системы в том, что из этого формата число можно легко преобразовать в двоичное.

Восьмеричная система счисления Использование Как правило, компьютер или процессор в нем работает с двоичными значениями.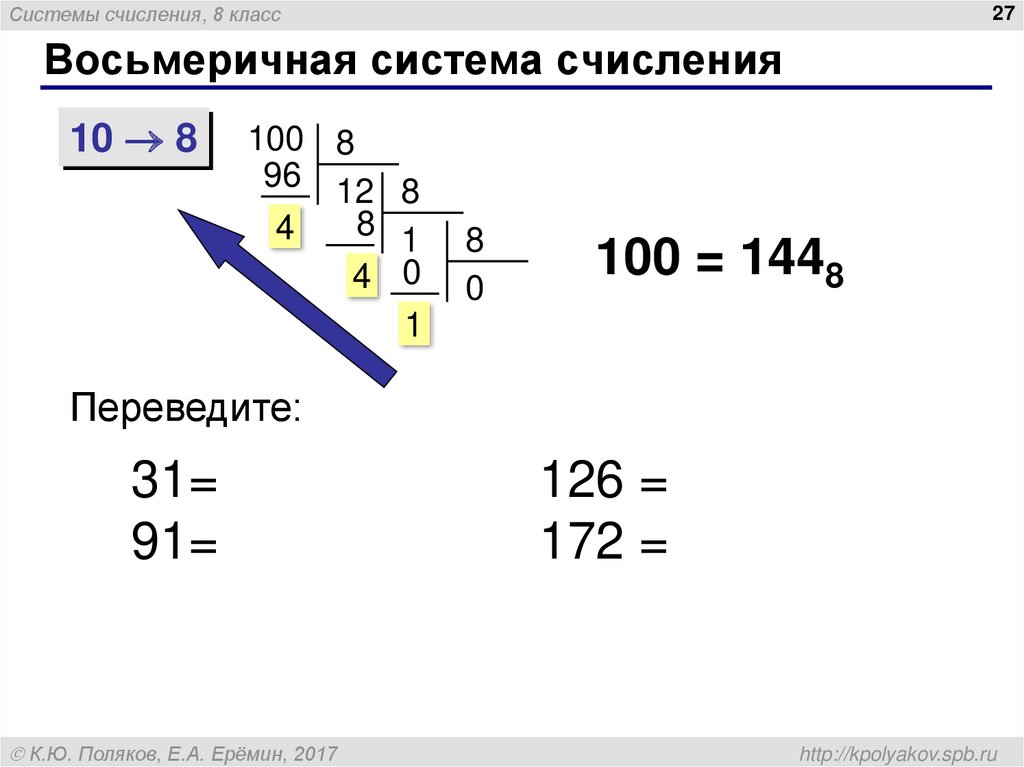 Тем не менее, для удобства использования такое кодирование предпочтительнее. Длина кодирования этой системы составляет одну треть двоичной системы.

Используя двоичные цифры, мы можем показать зашифрованные данные. Но, безусловно, чтобы оператор понял, необходимо некоторое кодирование и декодирование. Для таких целей могут быть написаны программы на определенных языках для преобразования одного формата нумерации в другой.

В таких секторах, как авиация и вычислительная техника, предпочтение отдается этим системам кодирования. Модернизированные системы используют «16-битные, 32-битные, 64-битные слова», которые далее подразделяются на 8-битные. В методах шифрования предпочтение отдается восьмеричному кодированию. Этот тип шифрования возможен с помощью определенных устройств, называемых кодировщиками.

На практике транспондеры, используемые в самолетах, используют формат восьмеричной нумерации для передачи кода. Далее эти коды опрашиваются с радара, находящегося в земле.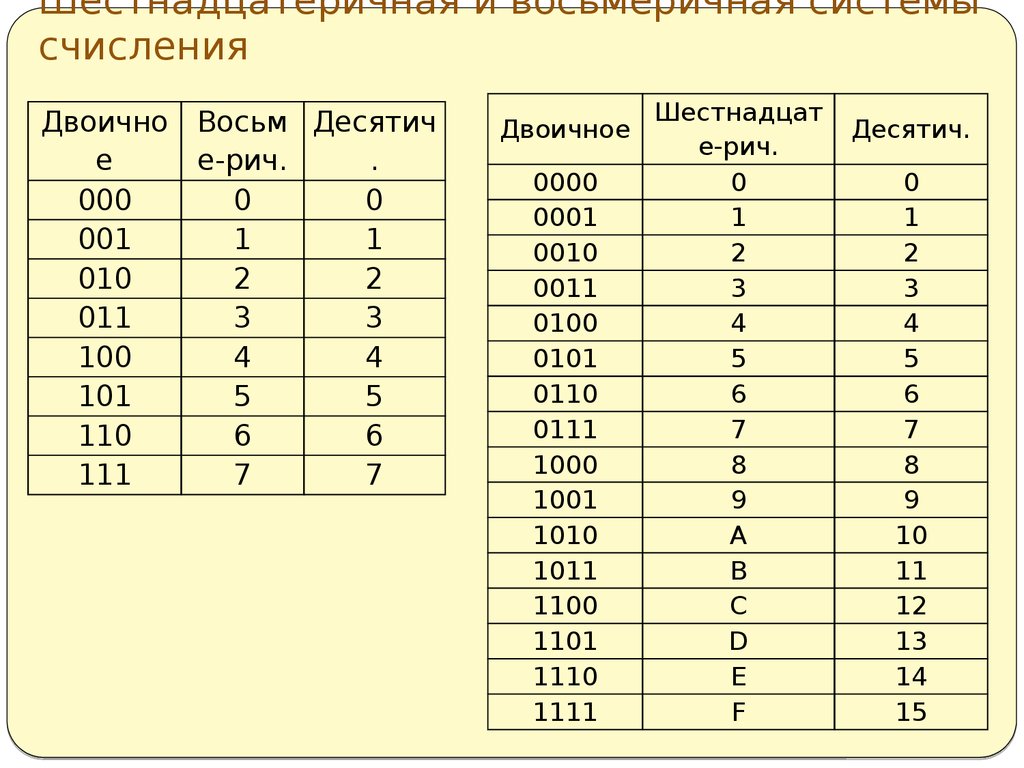 3=8.

Шаги, связанные с преобразованием двоичного числа в восьмеричное, следующие:

1. Наиболее важным шагом является определение формата данного числа. Представление двоичного числа можно понять по его индексу 2.
2. Другой шаг включает в себя группировку этих двоичных цифр с правой стороны.
3. В случае, если при группировке какая-либо группа не заполняется тремя цифрами. Затем к этой группе добавляются 0 бит.
4. Наконец, полученное число представляется нижним индексом восьмеричной системы, то есть «8».

 

Примеры

Давайте подробно обсудим приведенные выше преобразования, а затем приведем примеры.

1. Преобразовать данный код, который находится в двоичном формате 010011, в восьмеричный. Преобразование начинается с группировки цифр по три. Это

010            011

2. После завершения группировки. Проверьте, присутствуют ли три цифры в группе или нет. Если этот шаг подтвержден, начинается преобразование.
3. Так как он основан на позициях, каждая группа преобразуется путем сложения двоичных кодированных чисел. Это 421 для каждой группы.

010      011

421      421

4. Двоичное число, в котором присутствует 0. Окончательное число после полученной перекодировки будет равно нулю. Если число равно 1 после преобразования, это будет тот же закодированный номер.
5. Для 010 полученное число равно 020, а для 011 полученное число равно 021.
6. После того, как закодированные числа получены, их необходимо добавить в соответствующие группы. То есть для 010 это 0+2+0=2. Для 011 это 0+2+1=3.
7. Таким образом, окончательное полученное число равно 23 в восьмеричном формате.

Далее, если число имеет какие-либо десятичные значения. Тогда лучше отдать предпочтение значениям таблицы преобразования. Следовательно, с помощью описанного выше метода одна форма двоичных значений может быть преобразована в восьмеричную.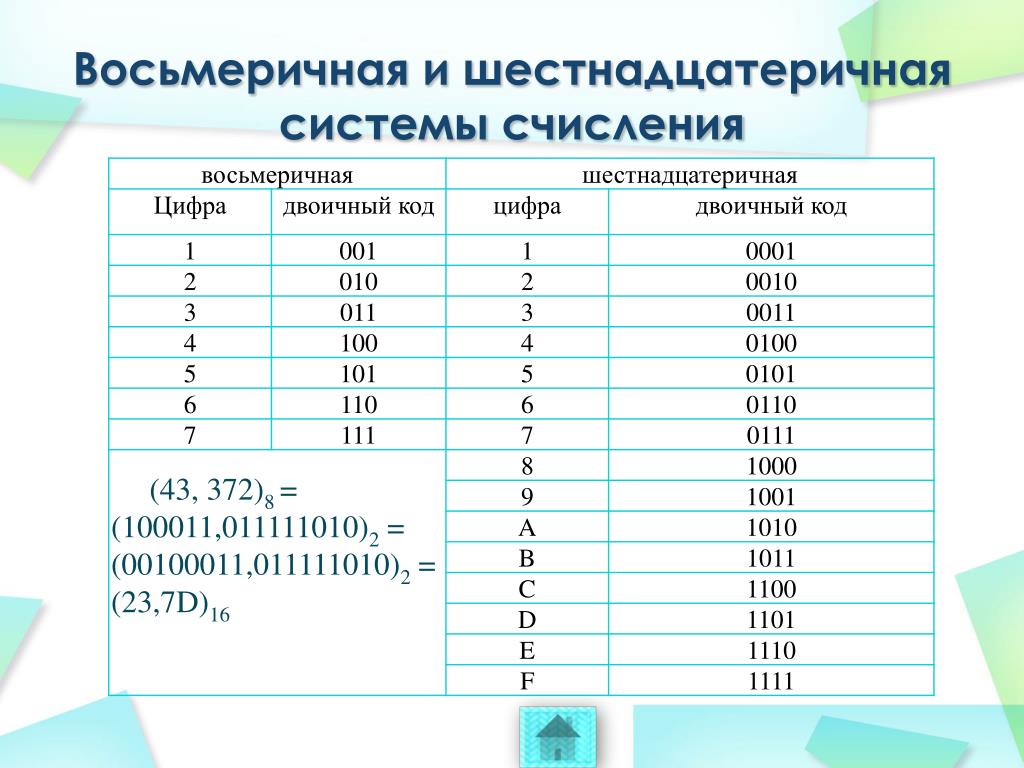 Иногда в вычислительных системах предпочтение отдается восьмеричному языку.

Восьмерично-двоичная таблица

Целью этой таблицы является узнать, для каких значений двоичного формата назначаются значения восьмеричного формата. Это делает преобразование простым. Как уже обсуждалось в отношении преобразования десятичных цифр, можно предпочесть это.

Восьмеричная система счисления Таблица преобразования

Преобразование восьмеричной системы счисления в двоичную

Числа можно преобразовать из двоичной в восьмеричную, даже двоичные значения можно преобразовать в восьмеричную. Это абсолютно обратимый процесс. Важным моментом, который следует учитывать при преобразовании, является то, что каждое восьмеричное число должно содержать три цифры двоичного числа. На основе чисел, приведенных в восьмеричной форме, записываются в степени 8. В зависимости от их положения они преобразуются в двоичные числа. Это становится очень просто с помощью таблицы преобразования, как обсуждалось выше.

Другой альтернативный алгоритм заключается в преобразовании данного восьмеричного числа в десятичный формат. Затем эти десятичные числа можно преобразовать в двоичные.

Примеры

Преобразование можно подробно понять с помощью этого примера.

Преобразовать восьмеричное число 150 в двоичное.

Глядя на таблицу преобразования восьмеричного числа в двоичное, 150 можно преобразовать как

1          5          0

001      101      000

Следовательно, 150 в восьмеричном представлении может быть представлено как 01010.0005

Преобразование восьмеричного числа 270,54 в двоичное.

На основе представления цифр в таблице преобразования его можно преобразовать как

2 7 0. 5 4

010 111 000 101 100

Следовательно, восьмиугольное значение 270,54 может быть преобразовано как 010111000.101100 в бинар.

Существуют различные форматы нумерации, каждый из которых имеет определенный образец представления и применения в различных секторах.